Flavor-changing top quark rare decays in the Bestest Little Higgs Model

Abstract

This paper investigates rare flavor-changing decays of the top quark in the Bestest Little Higgs Model (BLHM). As a result, flavor-changing phenomena are introduced in the BLHM for the first time. In this study, we incorporate new flavor mixing terms between the light quarks of the Standard Model (SM) and the fermions and bosons of the BLHM. We compute the one-loop contributions from the heavy quark (B) and the heavy bosons $(W^{\prime \pm }, \phi ^{\pm }, \eta ^{\pm },H^{\pm })$. Our findings demonstrate that the branching ratios of decays $t\rightarrow qV$ and $t\rightarrow qh^0$, where $q=u,c$ and $V=Z, \gamma , g$, can reach larger branching ratios compared to their counterparts in the SM, except for the gluon case. Moreover, we observe that the processes with the highest sensitivity are $Br(t\rightarrow cZ)\sim 10^{-5}$, $Br(t\rightarrow c\gamma )\sim 10^{-6}$ and $Br(t \rightarrow ch^0) \sim 10^{-8}$ within the appropriate parameter space.

1 Introduction

As the heaviest elementary particle in nature, the top quark provides the best opportunity to discover evidence of new physics Beyond the Standard Model (BSM). On the other hand, Electroweak Symmetry Breaking (EWSB) is a mechanism adaptable to various extensions of the SM that yields fields whose properties characterize the physics of these models. These components represent the primary theoretical foundations in different SM extensions for proposing new physics [1,2,3,4,5,6,7,8]. The BLHM [9, 10] is a type I Two Higgs Doublets Model (2HDM) that offers an exciting solution to the hierarchy problem without fine-tuning and is formulated to solve some issues present in the great majority of Little Higgs models, such as the problem of dangerous singlets in the scalar sector, a pathology where collective symmetry breaking does not suppress quadratically divergent corrections to the Higgs mass; and strong constraints from electroweak precision data. Instead, the BLHM generates a successful quartic Higgs coupling where the real singlet field $\sigma$ is no longer a dangerous singlet, meaning that it no longer develops a divergent tadpole from radiative corrections [9, 11]. On the other hand, it avoids the tight constraints from precision measurements through the implementation of a custodial SU(2) symmetry [12] that protects the model from developing large deviations to electroweak precision measurements and dissociates the masses of the new quarks and heavy gauge bosons. The latter is achieved by incorporating two separate symmetry-breaking scales, f and F with $F>f$. This leads to top quark partners with masses proportional only to the f scale, while the new heavy gauge bosons develop large masses proportional to the combination of f and F, which reduces their contribution to the precision electroweak observables. Some of the early Little Higgs type models that precede the BLHM are the Littlest Higgs Model [1], the Little Higgs Model [13], the Simplest Little Higgs Model [14], and the Littlest Higgs Model with T-parity [15]. These models were proposed between 2002 and 2005, while the BLHM [9, 10] was introduced by Schmaltz in 2010. The recent creation of the BLHM makes it an underexplored and under-recognized model. Additionally, not all Feynman rules for the interaction vertices in the BLHM, which are an essential element to study any process in particle physics, are provided in the literature [16,17,18,19]. These particularities of the BLHM and its quite promising features mentioned above motivate our research in such a scenario. On the other hand, it is worth mentioning that in the experimental aspect, it is more difficult to produce the heavy particles predicted in the BLHM than the light particles of the Simplest Little Higgs Model or Littlest Higgs Model with T-parity. At colliders, the probability of generating heavier particles is tiny because few collisions are sufficiently energetic to produce new heavy particles. This is another reason the BLHM is less frequently considered than other more popular Little Higgs models. Currently, research on the BLHM has been intensified by calculating its effects on some observables. The reported results have yielded promising predictions, challenging experimental data in the chromomagnetic dipole moment of the top quark (${\hat{\mu }}_t \sim -10^{-4}$) [16], the sensitivity of the weak dipole moments of the top quark ($a^W_t \sim 10^{-4}$) [17], the electromagnetic and weak dipole moments of the $\tau$ lepton ($a_{\tau } \sim 10^{-10}$, $a^W_{\tau } \sim 10^{-9}$) [18], and the electromagnetic and weak dipole moments of the top quark ($a_{t} \sim 10^{-4}$, $a^W_{t} \sim 10^{-5}$) [19].

Regarding Flavor Changing Neutral Currents (FCNC), there have been studies primarily in the Little Higgs Model with T-parity (LHT). In Ref. [20], they calculate some observables involving particle-antiparticle mixing in the LHT for the first time. In [21], the first study on rare decays of the top quark is presented, yielding significant results such as $Br(t\rightarrow cg)\sim 10^{-2}$, $Br(t\rightarrow cZ)\sim 10^{-5}$, and $Br(t\rightarrow c\gamma )\sim 10^{-7}$. Thorough examinations of the decays of K, B, and D mesons are conducted in [22,23,24], utilizing various parametrizations of the Cabibbo–Kobayashi–Maskawa (CKM) [25] extended matrices within the LHT.

In the article [26], rare decays of the Higgs boson and the Z boson are investigated, yielding interesting results such as $Br(Z\rightarrow b{\bar{s}})\sim 10^{-7}$. In Ref. [27], the authors calculate the branching ratios of the decays $t\rightarrow cX$ and $t\rightarrow cXX$, where $(X=Z,\gamma , g, h)$, with results of $Br(t\rightarrow cX)\sim 10^{-2}-10^{-5}$ and $Br(t\rightarrow cXX)\sim 10^{-3}-10^{-8}$. These results represent significant improvements over their counterparts in the SM, often by several orders of magnitude.

Our research focuses on the rare decays $t\rightarrow qV$ and $t\rightarrow qh^0$, where $q=u,c$ and $V=g, \gamma , Z$, within the theoretical framework of BLHM. We calculate their respective branching ratios to quantify the contributions of heavy quarks and heavy bosons in flavor-violating processes within a model that represents an improvement over the previous LHM. Additionally, our study allows us to constrain new parameters in BLHM, such as angles and phases of proposed CKM-like matrices, and explore their potential applications in other flavor and CP-violation studies.

The article is structured as follows: Sect. 2 introduces the BLHM, covering both the gauge boson and fermionic sectors. Section 3 considers the flavor mixing in the BLHM. Section 4 is dedicated to constructing the parameter space utilized in our study. Moving on to Sect. 5, we delve into the phenomenology of flavor-changing rare decays of the top quark within the BLHM framework, employing various extended CKM matrices. Lastly, we present our conclusions in Sect. 6. Appendix 1 contains the graphs of the individual contributions of each field $(W^{\prime \pm },\phi ^{\pm },\eta ^{\pm }, H^{\pm })$ to the total branching ratio and Appendix 1 includes the Feynman rules for flavor mixing in the BLHM.

2 Brief review of the BLHM

The BLHM [9] originates from a symmetry group $SO(6)_A\times SO(6)_B$, which breaks at the scale f towards $SO(6)_V$ when the non-linear sigma field $\Sigma$ acquires a vacuum expectation value (VEV), denoted as $\langle \Sigma \rangle =1$. This leads to the emergence of 15 pseudo-Nambu Goldstone bosons, parameterized by the electroweak triplet $\phi ^a$ with zero hypercharges $(a=1,2,3)$ and the triplet $\eta ^a$, where $(\eta _1,\eta _2)$ form a complex singlet with hypercharge, and $\eta _3$ is a real singlet,

$$\begin{aligned}{} & {} \Sigma =e^{i\Pi /f}e^{2i\Pi _h/f}e^{i\Pi /f}, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \Pi =\begin{pmatrix} \phi _a T^a_L+\eta _aT^a_R &{} 0 &{} 0\\ 0 &{} 0 &{} i\sigma /\sqrt{2}\\ 0 &{} -i\sigma /\sqrt{2} &{} 0 \end{pmatrix}, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \Pi _h=\begin{pmatrix} 0_{4\times 4} &{} h_1 &{} h_2\\ -h^T_1 &{} 0 &{} 0\\ -h^T_2 &{} 0 &{} 0 \end{pmatrix}, \end{aligned}$$

(3)

where $h_i^T=(h_{i1},h_{i2},h_{i3},h_{i4})$, $(i=1,2)$, represent Higgs quadruplets of SO(4). The scalar field $\sigma$¹ is required to generate a collective quartic coupling [9]. $T_{L,R}^a$ denote the generators of $SU(2)_L$ and $SU(2)_R$.

2.1 Scalar sector

In the BLHM, two operators are required to generate the quartic coupling of the Higgs through collective symmetry breaking; none of these operators alone allows the Higgs to acquire a potential:

$$\begin{aligned} P_5=diag(0,0,0,0,1,0),\nonumber \\ P_6=diag(0,0,0,0,0,1). \end{aligned}$$

(4)

In this way, we can write the quartic potential as [9]

$$\begin{aligned} V_q= & {} \frac{1}{4}\lambda _{65}f^4Tr(P_6\Sigma P_5\Sigma ^T)+\frac{1}{4}\lambda _{56}f^4Tr(P_5\Sigma P_6 \Sigma ^T)\nonumber \\= & {} \frac{1}{4}\lambda _{65}f^4(\Sigma _{65})^2+\frac{1}{4}\lambda _{56}f^4(\Sigma _{56})^2, \end{aligned}$$

(5)

where $\lambda _{56}$ and $\lambda _{65}$ are coefficients that must be nonzero to achieve collective symmetry breaking and generate a Higgs quartic coupling. The first part of Eq. (5) breaks $SO(6)_A\times SO(6)_B\rightarrow SO(5)_{A5}\times SO(5)_{B6}$, with $SO(5)_{A5}$ preventing $h_1$ from acquiring a potential and $SO(5)_{B6}$ doing the same for $h_2$. The second part of Eq. (5) breaks $SO(6)_A\times SO(6)_B\rightarrow SO(5)_{A6}\times SO(5)_{B5}$. If we expand Eq. (1) in powers of 1/f and substitute it into Eq. (5), we obtain

$$\begin{aligned} V_q= & {} \frac{\lambda _{65}}{2}\left( f\sigma -\frac{1}{\sqrt{2}}h_1^Th_2+\cdots \right) ^2\nonumber \\{} & {} +\frac{\lambda _{56}}{2}\left( f\sigma +\frac{1}{\sqrt{2}}h_1^Th_2+\cdots \right) ^2. \end{aligned}$$

(6)

From Eq. (6), each term alone seems to generate a quartic coupling for the Higgses, this can be eliminated by a redefinition of the field $\sigma \rightarrow \pm \frac{h^{T}_1 h_2}{\sqrt{2} f}$, where the upper and lower signs of this transformation correspond to the first and second operators in Eq. (6), respectively. Collectively, though, the two terms in Eq. (6) produce a tree-level quartic Higgs; this occurs after integrating out $\sigma$ [9, 11, 28]:

$$\begin{aligned} V_q=\frac{\lambda _{56} \lambda _{65}}{\lambda _{56}+ \lambda _{65}} \left( h_1^Th_2 \right) ^2= \frac{1}{2}\lambda _{0}\left( h_1^Th_2 \right) ^2. \end{aligned}$$

(7)

The expression obtained has the desired form of a collective quartic potential [9, 11].

In this way, we obtain the form of a quartic collective potential proportional to two different couplings [9]. We can observe that $\lambda _0$ will be zero if $\lambda _{56}$, $\lambda _{65}$, or both are zero. This illustrates the principle of collective symmetry breaking.

If we exclude gauge interactions, not all scalars gain mass, and therefore, we need to introduce the potential,

$$\begin{aligned} V_s= & {} -\frac{f^2}{4}m_4^2Tr\left( \Delta ^{\dagger }M_{26}\Sigma M^{\dagger }_{26}+\Delta M_{26}\Sigma ^{\dagger }M^{\dagger }_{26}\right) \nonumber \\{} & {} -\frac{f^2}{4}\left( m_5^2\Sigma _{55}+m_6^2\Sigma _{66}\right) , \end{aligned}$$

(8)

where $m_4$, $m_5$, and $m_6$ are mass parameters, and $(\Sigma _{55},\Sigma _{66})$ are matrix elements of Eq. (1). Here, $M_{26}$ is a matrix that contracts the SU(2) indices of $\Delta$ with the SO(6) indices of $\Sigma$,

$$\begin{aligned} M_{26}=\frac{1}{\sqrt{2}} \begin{pmatrix} 0 &{} 0 &{} 1 &{} i &{} 0 &{} 0\\ 1 &{} -i &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}. \end{aligned}$$

(9)

The $\Delta$ operator arises from a global symmetry $SU(2)_C\times SU(2)_D$ that is broken to a diagonal SU(2) at the scale $F>f$ when it develops a VEV, $\langle \Delta \rangle =1$. We can parameterize it in the form

$$\begin{aligned} \Delta =e^{2i\Pi _d/F},\hspace{0.3cm}\Pi _d=\chi _a\frac{\tau _a}{2}\hspace{0.3cm}(a=1,2,3), \end{aligned}$$

(10)

where the matrix $\Pi _d$ contains the scalars of the triplet $\chi _a$ that mix with the triplet $\phi _a$, and $\tau _a$ represents the Pauli matrices. $\Delta$ is connected to $\Sigma$ in such a way that the diagonal subgroup of $SU(2)_A\times SU(2)_B\subset SO(6)_A\times SO(6)_B$ is identified as the SM $SU(2)_L$ group. If we expand the operator $\Delta$ in powers of 1/F and substitute it into Eq. (8), we obtain

$$\begin{aligned} V_s=\frac{1}{2}\left( m^2_{\phi }\phi ^2_a+m^2_{\eta }\eta ^2_a+m^2_1h^T_1h_1+m^2_2h^T_2h_2\right) , \end{aligned}$$

(11)

where

$$\begin{aligned} m^2_{\phi }= & {} m^2_{\eta }=m^2_4,\nonumber \\ m^2_1= & {} \frac{1}{2}(m^2_4+m^2_5),\nonumber \\ m^2_2= & {} \frac{1}{2}(m^2_4+m^2_6). \end{aligned}$$

(12)

To trigger EWSB, the next potential term is introduced [9]:

$$\begin{aligned} V_{B_{\mu }}=m_{56}^2f^2\Sigma _{56}+m_{65}^2f^2\Sigma _{65}, \end{aligned}$$

(13)

where the mass terms $m_{56}$ and $m_{65}$ correspond to the matrix elements $\Sigma _{56}$ and $\Sigma _{65}$, respectively. Finally, we have the complete scalar potential,

$$\begin{aligned} V=V_q+V_s+V_{B_{\mu }}. \end{aligned}$$

(14)

We need a potential for the Higgs doublets; therefore, we minimize Eq. (14) concerning $\sigma$ and substitute the result back into Eq. (14), obtaining the expression:

$$\begin{aligned} V_H=\frac{1}{2}\left[ m_1^2h_1^Th_1+m_2^2h_2^Th_2 -2B_{\mu }h_1^Th_2+\lambda _0(h_1^Th_2)^2\right] , \end{aligned}$$

(15)

where

$$\begin{aligned} B_{\mu }=2\frac{\lambda _{56}m_{65}^2+\lambda _{65}m_{56}^2}{\lambda _{56}+\lambda _{65}}. \end{aligned}$$

(16)

The potential (15) has a minimum when $m_1m_2 > 0$, and EWSB requires that $B_{\mu } > m_1m_2$. Here, we can observe that the term $B_{\mu }$ disappears if $\lambda _{56}=0$ or $\lambda _{65}=0$ or both are zero in Eq. (16). After EWSB, Higgs doublets acquire VEVs given by

$$\begin{aligned} \langle h_1\rangle =v_1,\hspace{0.3cm}\langle h_2\rangle =v_2. \end{aligned}$$

(17)

The two terms in (17) must minimize Eq. (15), resulting in the following relationships

$$\begin{aligned} v_1^2=\frac{1}{\lambda _0}\frac{m_2}{m_1}(B_{\mu }-m_1m_2),\end{aligned}$$

(18)

$$\begin{aligned} v_2^2=\frac{1}{\lambda _0}\frac{m_1}{m_2}(B_{\mu }-m_1m_2), \end{aligned}$$

(19)

and it is defined the $\beta$ angle between $v_1$ and $v_2$ [9], such that,

$$\begin{aligned} \tan \beta =\frac{\langle h_{11}\rangle }{\langle h_{21}\rangle }=\frac{v_1}{v_2}=\frac{m_2}{m_1}, \end{aligned}$$

(20)

in this way, we have

$$\begin{aligned} v^2= & {} v_1^2+v_2^2\nonumber \\= & {} \frac{1}{\lambda _0}\left( \frac{m_1^2+m_2^2}{m_1m_2}\right) (B_{\mu }-m_1m_2)\nonumber \\\simeq & {} (246\;GeV)^2. \end{aligned}$$

(21)

After the EWSB, the scalar sector [9, 28] produces massive states of $h^0$ (SM Higgs), $A^0$, $H^{\pm }$ and $H^0$ with masses

$$\begin{aligned}{} & {} m^2_{G^0}=m^2_{G^{\pm }}=0, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} m^2_{A^0}=m^2_{H^{\pm }}=m^2_1+m^2_2, \end{aligned}$$

(23)

$$\begin{aligned}{} & {} m^2_{H^0}=\frac{B_{\mu }}{\sin 2\beta }\nonumber \\{} & {} +\sqrt{\frac{B^2_{\mu }}{\sin ^22\beta }-2\lambda _0\beta _{\mu } v^2\sin 2\beta +\lambda _0^2v^4\sin ^22\beta }, \end{aligned}$$

(24)

where $G^0$ and $G^{\pm }$ are Goldstone bosons that are eaten to give masses to the $W^{\pm }, Z$ bosons of the SM.

2.2 Gauge boson sector

The gauge kinetic terms are given by the Lagrangian [9, 28]

$$\begin{aligned} {\mathcal {L}}=\frac{f^2}{8}Tr\left( D_{\mu }\Sigma ^{\dag }D^{\mu }\Sigma \right) +\frac{F^2}{4}Tr\left( D_{\mu }\Delta ^{\dag }D^{\mu }\Delta \right) , \end{aligned}$$

(25)

where $D_{\mu }\Sigma$ and $D_{\mu }\Delta$ are covariant derivatives,

$$\begin{aligned} D_{\mu }\Sigma= & {} i\sum _a\left( g_AA_{1\mu }^aT_L^a\Sigma -g_BA_{2\mu }^a\Sigma T^a_L\right) \nonumber \\{} & {} +ig'B_3\left( T^3_R\Sigma -\Sigma T^3_R\right) ,\end{aligned}$$

(26)

$$\begin{aligned} D_{\mu }\Delta= & {} \frac{i}{2}\sum _a\left( g_AA^a_{1\mu }\tau _a\Delta -g_BA^a_{2\mu }\Delta \tau _a\right) , \end{aligned}$$

(27)

while $(A^a_{1\mu },A^a_{2\mu })$ are gauge boson eigenstates, $g'$ is the coupling of $U(1)_Y$, and g is the coupling of the $SU(2)_L$. They are related to $SU(2)_A\times SU(2)_B$ couplings $g_A$ and $g_B$ in the following way

$$\begin{aligned} g=\frac{g_Ag_B}{\sqrt{g_A^2+g_B^2}},\end{aligned}$$

(28)

$$\begin{aligned} s_g=\sin \theta _g=\frac{g_A}{\sqrt{g_A^2+g_B^2}},\end{aligned}$$

(29)

$$\begin{aligned} c_g=\cos \theta _g=\frac{g_B}{\sqrt{g_A^2+g_B^2}}, \end{aligned}$$

(30)

here, $\theta _g$ is the mixing angle, and if $g_A = g_B$, then $\tan \theta _g = 1$.

In the BLHM, both the masses of the heavy gauge bosons $W^{\prime \pm }$, $Z'$ and those of the SM bosons are also generated [9, 28].

2.3 Fermion sector

The fermion sector of the BLHM is governed by the Lagrangian [9]

$$\begin{aligned} {\mathcal {L}}_t= & {} y_1fQ^TS\,\Sigma \, SU^c+y_2fQ_a^{\prime T}\Sigma \,U^c\nonumber \\{} & {} +y_3fQ^T\Sigma \, U_5^{\prime c}+y_bfq_3^T(-2iT_ R^3\Sigma )U_b^c+\text {h.c.}, \end{aligned}$$

(31)

where $(Q,Q')$ and $(U,U')$ are multiplets of $SO(6)_A$ and $SO(6)_B$, respectively, given by:

$$\begin{aligned} Q^T= & {} \frac{1}{\sqrt{2}}\Big [-(Q_{a1}+Q_{b2}),i(Q_{a1}-Q_{b2}),\nonumber \\{} & {} (Q_{a2}-Q_{b1}),i(Q_{a2}+Q_{b1}),Q_{5},Q_6\Big ], \end{aligned}$$

(32)

where $(Q_{a1},Q_{a2})$ and $(Q_{b1},Q_{b2})$ are $SU(2)_L$ doublets. $(Q_5,Q_6)$ are singlets under $SU(2)_L\times SU(2)_R=SO(4)$. While

$$\begin{aligned} (U^c)^T= & {} \frac{1}{\sqrt{2}}\Big [-(U^c_{b1}+U^c_{a2}),i(U^c_{b1}-U^c_{a2}),\nonumber \\{} & {} (U^c_{b2}-U^c_{a1}),i(U^c_{b2}+U^c_{a1}),U^c_5,U^c_6\Big ], \end{aligned}$$

(33)

where $(U^c_{a2},-U^c_{a1})$ and $(-U^c_{b2},U^c_{b1})$ are doublets of $SU(2)_L$ along with the singlets $(U_5,U_6)$. And

$$\begin{aligned} Q^{\prime T}_{a}= & {} \frac{1}{\sqrt{2}}\left( -Q'_{a1},iQ'_{a1},Q'_{a2},iQ'_{a2},0,0\right) \end{aligned}$$

(34)

$$\begin{aligned} U^{\prime c T}_5= & {} (0,0,0,0,U^{\prime c}_5,0), \end{aligned}$$

(35)

are a doublet of $SU(2)_A$ and a singlet of $SU(2)_{A,B}$, respectively. $S=diag(1,1,1,1,-1,-1)$ is a symmetry operator, $(y_1,y_2,y_3)$ represent Yukawa couplings, and the term $(q_3,U_b^c)$ in Eq. (31) contains information about the bottom quark. The BLHM implements new physics in the gauge, fermion, and Higgs sectors, which implies the existence of partner particles for most SM particles. Since top quark loops provide the most significant divergent quantum corrections to the Higgs mass in the SM, the new heavy quarks, in the BLHM scenario, will be crucial for solving the hierarchy problem. Those heavy quarks are: T, $T^5$, $T^6$, $T^{2/3}$, $T^{5/3}$, and B, all of which have associated masses [9]:

$$\begin{aligned} m_{T}^2= & {} (y_1^2+y_2^2)f^2+\frac{9v_1^2y_1^2y_2^2y_3^2}{(y_1^2+y_2^2)(y_2^2-y_3^2)}, \end{aligned}$$

(36)

$$\begin{aligned} m_{T^{5}}^2= & {} (y_1^2+y_3^2)f^2 -\frac{9v_1^2y_1^2y_2^2y_3^2}{(y_1^2+y_3^2)(y_2^2-y_3^2)}, \end{aligned}$$

(37)

$$\begin{aligned} m_{T^{6}}^2= & {} m_{T^{2/3}}^2=m_{T^{5/3}}^2=y_1^2f^2, \end{aligned}$$

(38)

$$\begin{aligned} m_{B}^2= & {} y_B^2f^2=(y_1^2+y_2^2)f^2. \end{aligned}$$

(39)

In the quark sector Lagrangian [9], the Yukawa couplings must satisfy $0<y_ {i}<1$. The masses of t and b are also generated by the Yukawa couplings $y_t$ and $y_b$ [28].

$$\begin{aligned} m^2_t= & {} y_t^2v_1^2, \end{aligned}$$

(40)

$$\begin{aligned} m^2_b= & {} y_b^2v_1^2-\frac{2y^2_b}{3\sin ^2\beta }\frac{v^4_1}{f^2}. \end{aligned}$$

(41)

The coupling $y_t$,

$$\begin{aligned} y_t^2=\frac{9y_1^2y_2^2y_3^2}{(y_1^2+y_2^2)(y_1^2+y_3^2)}, \end{aligned}$$

(42)

is part of the measure of fine-tuning in the BLHM, $\Psi$, defined by [28]

$$\begin{aligned} \Psi =\frac{27f^2}{8\pi ^2v^2\lambda _0\cos ^2\beta }\frac{|y_1|^2|y_2|^2|y_3|^2}{|y_2|^2-|y_3|^2} \log \frac{|y_1|^2+|y_2|^2}{|y_1|^2+|y_3|^2}. \end{aligned}$$

(43)

Table 1 A measure of the fine-tuning in the BLHM for different values of the f scale

According to the numerical values listed in Table 1, we find that the size of the fine-tuning when the energy scale $f=1.5$ TeV is $\Psi \simeq 1.2$ indicates that there is no fine-tuning in the BLHM. The absence of the fine-tuning prevails up to $\Psi \simeq 2.2$ [9], i.e., for values of the scale f close to 2 TeV. Even though fine-tuning starts to become significant above $f=2$ TeV, our best results for the branching ratios are found within $1\le f\le 2$ TeV, giving enough margin for the possible detection of the rare decays of the top quark. On the other hand, if the new particles surpass the $f=2$ TeV limit, this would only affect the exotic quark sector but not the scalar bosons or the gauge bosons that can be adjusted with the second scale F.

3 Flavor mixing in the BLHM

In the SM, FCNCs are highly suppressed due to the GIM mechanism, leading to rare decays. In the original development of the BLHM, the authors [9] avoided introducing interactions between the heavy quarks and the two lighter generations of SM quarks. This omission prevents the construction of extended CKM matrices and the calculation of rare decays.

Our goal is to maintain the intrinsic properties of the BLHM. To achieve this, we will detail a specific procedure. We restrict our focus to interactions involving the light quarks of the SM with both vector and scalar-charged gauge bosons, as well as the heavy $B$ quark. In the BLHM, the couplings $q_dW'^{\pm }q_u$ and $q_dS^{\pm }q_u$ do not exist, where $q_d=(d,s,b)$, $q_u=(u,c)$, and $S^{\pm }=(H^{\pm },\phi ^{\pm },\eta ^{\pm })$. This limitation holds even with the extension proposed in this work. As a result, there is no avenue to introduce additional Feynman diagrams.

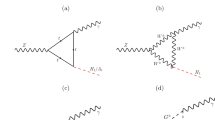
If we were to introduce couplings between the heavy partners of the top quark and the light SM quarks, it would necessitate modifications to the fundamental multiplets of $SO(6)_{A, B}$. This could drastically change the current couplings due to new contributions that emerge from combinations of the SM and BLHM fields. However, with the $B$ quark, this issue is circumvented since its original multiplet is straightforward and provides the required interactions for the Feynman diagrams shown in Figs. 1 and 2.

Fig. 1

Feynman diagrams for the flavor-changing top quark rare decays in the BLHM considered in this paper: $t\rightarrow qV$ and $t \rightarrow qh^o$ vertices, with $V= Z,\gamma , g$, and $q= u, c$

Fig. 2

Feynman diagrams for the flavor-changing top quark rare decays in the BLHM considered in this paper: $t\rightarrow qV$ and $t \rightarrow qh^o$ vertices, with $V= Z,\gamma , g$, and $q= u, c$

Within the BLHM framework for $(Z,Z')$, there are no couplings like $QZq$ or $QZ'q$, where $Q = (T,T^5,T^6,T^{2/3},T^{5/3})$ and $q = (u,c)$. Such couplings are vital for the decays $t \rightarrow qZ$. Altering the multiplets associated with the heavy partners of the top quark would lead to implications similar to the rationale we provided for our exclusive focus on the $B$ quark.

Therefore, we introduce the necessary terms to these interactions by adding the following terms to the Lagrangian (31)

$$\begin{aligned} y_Bfq_1(-2iT_R^2\Sigma )d_B^c,\hspace{0.2cm}y_Bfq_2(-2iT_R^2\Sigma )d_B^c, \end{aligned}$$

(44)

where $y_B^2=y_1^2+y_2^2$ is the Yukawa coupling of heavy B quark, $q_1$ and $q_2$ are multiplets of light SM quarks

$$\begin{aligned} q_1^T= & {} \frac{1}{\sqrt{2}}(-u,iu,d,id,0,0),\nonumber \\ q_2^T= & {} \frac{1}{\sqrt{2}}(-c,ic,s,is,0,0), \end{aligned}$$

(45)

and $d_B^c$ is the new multiplet that we have introduced

$$\begin{aligned} d_B^{c T}=(0,0,0,0,B,0). \end{aligned}$$

(46)

This inclusion facilitates the mixing between scalar fields $(H^{\pm },\phi ^{\pm },\eta ^{\pm })$ and the $B$ quark with the $(u,c,d,s)$ quarks, which significantly enriches the phenomenology associated with the BLHM. The Lagrangian (31) retains its gauge invariance, ensuring that the new terms do not intermingle with the heavy partners of the top quark. To delineate the interactions of the quarks $(u, c, d, s)$ with the $(W^{\pm }, W^{\prime \pm })$ bosons and the $B$ quark, we introduce the following terms:

$$\begin{aligned} Q_3^T=\frac{1}{\sqrt{2}}(0,0,B,iB,0,0), \end{aligned}$$

(47)

and

$$\begin{aligned} q_i^{\prime T}=(0,0,0,0,q_i^c,0), \end{aligned}$$

(48)

where $q_i^c$ represents the quarks (u, c, d, s), in the part of the Lagrangian for gauge–fermion interactions that involve the fields $W^{\pm }$ and $W^{\prime \pm }$ [28]

$$\begin{aligned} {\mathcal {L}}= & {} \sum _{i=1}^2 i{\bar{\sigma }}_{\mu }q^{\dag }_iD^{\mu }q_i+i{\bar{\sigma }}_{\mu }Q^{\dag }D^{\mu }Q\nonumber \\{} & {} + i{\bar{\sigma }}_{\mu }Q^{\prime \dag }D^{\mu }Q^{\prime }+i{\bar{\sigma }}_{\mu }U^{c\dag }D^{\mu }U^c, \end{aligned}$$

(49)

such that we have the extended Lagrangian

$$\begin{aligned} {\mathcal {L}}= & {} \sum _{i=1}^2 i{\bar{\sigma }}_{\mu }q^{\dag }_iD^{\mu }q_i+i{\bar{\sigma }}_{\mu }Q^{\dag }D^{\mu }Q\nonumber \\{} & {} + i{\bar{\sigma }}_{\mu }Q^{\prime \dag }D^{\mu }Q^{\prime }+i{\bar{\sigma }}_{\mu }U^{c\dag }D^{\mu }U^c\nonumber \\{} & {} +\sum _{i=1}^2 i{\bar{\sigma }}_{\mu }Q_3^{\dag }D^{\mu }q_i+\sum _{i=1}^4 i{\bar{\sigma }}_{\mu }q^{\prime \dag }_{i}D^{\mu }U^c, \end{aligned}$$

(50)

where $(q_1, q_2)$ are defined as in Eq. (45). The ${\bar{\sigma }}^{\mu }$ is given by $-\sigma ^{\mu }$, representing the Pauli matrices, and $D_{\mu }$ encapsulates information regarding $(W^{\pm }, W^{\prime \pm })$. The extended Lagrangian (50) maintains gauge invariance and avoids mixing with the top quark’s heavy partners. Expressing the Lagrangian (50) in Dirac notation, we have:

$$\begin{aligned} {\mathcal {L}}= & {} i\sum _{i=1}^2{\bar{\Psi }}_{qi}\gamma _{\mu }P_LD^ {\mu }\Psi _{qi}+i{\bar{\Psi }}_{Q}\gamma _{\mu }P_LD^{\mu }\Psi _{Q}\nonumber \\{} & {} +i{\bar{\Psi }}_{Q'}\gamma _{\mu }P_LD^{\mu }\Psi _{Q'} +i{\bar{\Psi }}_{U^c}\gamma _{\mu }P_R\Psi _{U^c}\nonumber \\{} & {} +i\sum _{i=1}^2{\bar{\Psi }}_{Q_3}\gamma _{\mu }P_LD^ {\mu }\Psi _{qi}+i\sum _{i=1}^4{\bar{\Psi }}_{q'i}\gamma _{\mu }P_RD^{\mu }\Psi _{U^c}.\nonumber \\ \end{aligned}$$

(51)

From Lagrangian (51), any of its covariant derivatives in the mass eigenstate basis takes the form [28]:

$$\begin{aligned} D^{\mu }= & {} \partial ^{\mu }+i\sum _{a=1}^2g_AA^{a\mu }_1T^a_L\nonumber \\= & {} \partial ^{\mu }\nonumber \\{} & {} +\frac{ig_A}{\sqrt{2}}\left[ \rho _{11}(W^{+\mu }+W^{-\mu })+\delta _{11}(W^{\prime +\mu }+W^{\prime -\mu })\right] \nonumber \\{} & {} +\frac{ig_A}{\sqrt{2}}\left[ \rho _{12}(W^{+\mu }-W^{-\mu })+\delta _{12}(W^{\prime +\mu }-W^{\prime -\mu })\right] ,\nonumber \\ \end{aligned}$$

(52)

where $(\rho _{11},\rho _{12})$ and $( \delta _{11},\delta _{12} )$ encompass model constants and a dependency on ${\mathcal {O}}(v^2/(f^2+F^2))$. To elucidate the generation of the elements of the extended CKM matrix $V_{Hu}$ within the charged currents of the BLHM, we focus on the fifth term of the Lagrangian (51) and examine the $W^{\prime -}{\bar{B}}q_i$ interaction:

$$\begin{aligned} \frac{ig_A}{\sqrt{2}}{\bar{\Psi }}_BV_{Bu}\gamma _{\mu }P_LW^{\prime -}\Psi _{qi}, \end{aligned}$$

(53)

where

$$\begin{aligned} V_{Bu}=\delta _{11}-\delta _{12}\approx k\left( \frac{v^2}{f^2+F^2}\right) , \end{aligned}$$

(54)

where k depends on the model constants in such a way that it can be constrained by the values of the extended CKM matrix.

4 Parameter space of the BLHM

The initial parameter spaces for the BLHM were constructed based on the decays of heavy quarks into final states within the SM, adopting an intertwined parametrization of the Yukawa couplings $(y_1, y_2, y_3)$ [28, 29]. The same parameter space is employed in the work of [30], but constraints are solely applied to the heavy quarks following experimental limits. The study in [10] suggests a comparable parameter space for the BLHM, imposing the constraint $m_{h^0} = 125.25$ GeV and permitting both $A^0$ and $H^0$ to span across all the production modes and decay channels examined by ATLAS and CMS at that juncture. This eliminates potential degeneracy between these fields.

In subsequent studies [16,17,18,19], a parameter space devoid of degeneracy is articulated for the neutral Higgs states. The Yukawa couplings remain unchanged, yet the model constants retain their values as in preceding works. This compliance aligns with the prevailing experimental constraints on heavy quarks and bosons.

Notably, the BLHM posits five heavy partners for the top quark and merely one for the bottom quark. Empirical research has ruled out masses for these entities below the thresholds outlined in Table 2.

Table 2 ATLAS experiment searches set 95% C.L. upper exclusion limits for heavy quark searches [31]

In this study, we manipulate the angle corresponding to the ratio of the VEVs of the two Higgs doublets, $\tan \beta$, to dictate all non-fixed parameters while satisfying the experimental bounds.

We initiate by confining the Yukawa couplings within the domain $0< y_i < 1$ [9]. This ensures conformity with both Eq. (40) and Eq. (42), such that $m_t = 172.13$ GeV [32]. Concurrently, we resolve Eqs. (23) and (24), ensuring that the parameters $\lambda _0$, $m_{H^0}$, $m_{A^0}$, and $\beta$ uphold $m_{h^0} = 125.25$ GeV [33], alongside the conditions $\lambda _0 < 4\pi$, $\tan \beta \gtrsim 1$, as informed by the findings in [10].

$$\begin{aligned} \left( \tan \beta \right) ^2< & {} -1+\dfrac{2+2\left( 1-\dfrac{m_{h^0}^2}{m_{A^0}^2}\right) ^{\frac{1}{2}}\left( 1-\dfrac{m_{h^0}^2}{4\pi v^2}\right) ^{\frac{1}{2}}}{\dfrac{m_{h^0}^2}{m_{A^0}^2}\left( 1+\dfrac{m_{A^0}^2-m_{h^0}^2}{4\pi v^2}\right) }. \end{aligned}$$

(55)

The BLHM designates the parameter $m_4$ as a free variable, ensuring that both $m_{\phi ^0}$ and $m_{\eta ^0}$ remain unconstrained, especially given that their one-loop corrections are insignificant [9]. Accordingly, we delineate the range $30< m_4 < 800$ GeV, leading to the masses tabulated in Table 2. Furthermore, the BLHM incorporates the mixing angle $\alpha$ between $h^0$ and $H^0$.

$$\begin{aligned} \tan \alpha= & {} \frac{1}{B_{\mu }-\lambda _0 v^2\sin 2\beta }\left( B_{\mu }\cot 2\beta \right. \nonumber \\{} & {} \left. +\sqrt{\frac{B_{\mu }^2}{\sin ^22\beta }-2\lambda _0 B_{\mu }v^2\sin 2\beta +\lambda _0^2 v^4\sin ^22\beta }\ \right) ,\nonumber \\ \end{aligned}$$

(56)

in a manner such that the condition $\sin (\beta -\alpha ) \approx 1$ is met. In Table 3, we showcase the initial parameters with $y_1 = 0.7$ and $y_2 = 0.9$ kept constant.

Table 3 BLHM parameters

With the calculated Yukawa couplings and satisfying all the conditions that led us to the results in Table 3, we present the masses of the heavy quarks in Table 4 according to Eqs. (36)–(39).

Table 4 Masses of the heavy quarks in the BLHM

The most recent reports [34] with the same dataset from the period 2015–2018 from the ATLAS detector for the $T\rightarrow Ht$ and $T\rightarrow Zt$ processes exclude masses below 1.6 and 2.3 TeV at $95\%$ C.L., respectively, for the production of the singlet T, according to the chosen parameters, and 1.7 and 1 TeV for the production of the doublet T under the same considerations. In [35], masses of the B quark below 1.33 TeV at $95\%$ C.L. are excluded according to the $B\rightarrow Wt$ process. In both cases, the masses of the top and bottom quark partners in the BLHM are within the limits.

There have been recent and compelling experimental results and simulations regarding the neutral bosons $H^0$ and $A^0$. In the study conducted by ATLAS [36], the process $A^0\rightarrow Zh^0$ is analyzed, ruling out the mass of $A^0$ below $1$ TeV at $95\%$ C.L. for all types of 2HDM. The CMS study [37] also excludes the boson’s mass $A^0$ below 1 TeV.

In [38], type I 2HDMs are studied by simulating the process $e^{-}e^{+}\rightarrow A^0\,H^0\rightarrow ZH^0\,H^0\rightarrow jjb{\bar{b}}b{\bar{b}}$ for the SiD detector at the ILC with an integrated luminosity of $500$ fb$^{-1}$. This gives ranges of $200< m_{A^0} < 250$ GeV and $150< m_{H^0} < 250$ GeV. The experimental evidence and simulations in the realm of neutral scalar bosons support our usage of the discovered ranges for the masses of $A^0$ and $H^0$. The neutral scalar bosons $\phi ^0$ and $\eta ^0$ in the BLHM were introduced with anticipated masses below $100$ GeV [9]. However, even though these types of light scalar mediators are more prevalent in dark matter models [39], we have also opted to use the range $30< m_4 < 800$ GeV and specifically $m_4=500$ GeV [17], which has minimal influence on the masses $m_{\phi ^\pm }$ and $m_{\eta ^\pm }$ [10].

We have adopted values for $f$ in the range [1, 3] TeV and set $F = 5$ TeV. These choices align with the current experimental constraints, as illustrated in Tables 3 and 4. However, it is worth noting that adjusting these values to accommodate future experimental results would be feasible, ensuring the model’s requisite condition $f < F$ is maintained. Both $F$ and $f$ have a pronounced impact on the masses of the vector bosons $W^{\prime \pm }$ and $Z^{\prime }$, as well as on the masses of the scalar bosons $(\phi ^{\pm },\eta ^{\pm })$. Using the parameters we derived, the masses of these vector and scalar bosons are enumerated in Table 5.

Table 5 Masses of the heavy bosons in the BLHM

Where the mass of the bosons $\phi ^{\pm }$ and $\eta ^{\pm }$ are dominated by one-loop corrections [10].

In the $e\nu$ channel, both the ATLAS and CMS collaborations have constrained the mass of $m_{W'}$ to be below the 7 TeV at $95\%$ C.L., based on data collected at $\sqrt{s}= 13$ TeV with an integrated luminosity of $139 \text { fb}^{-1}$ [40, 41]. These experimental constraints on the $W^{\prime \pm }$ boson mass maintain the BLHM in a favorable position, as the mass of $W^{\prime \pm }$ has the potential to increase with $F$.

Searches by ATLAS and CMS collaborations for $Z'$ decays into $e^+e^-$ and $\mu ^+\mu ^-$ have set a lower bound of 4.9 TeV on the $Z'$ mass [42, 43]. On a different note, the $Z'\rightarrow \tau ^+\tau ^-$ decay process sets a constraint where $m_{Z'}>2.4$ TeV [44] at $95\%$ C.L. In the decay channel $Z'\rightarrow b{\bar{b}}$, CMS has analyzed a mass value of $1.8<m_{Z'}<8$ TeV [45], while ATLAS has covered values between $1.3<m_{Z'}<5$ TeV [46]. Across all the mentioned channels, our calculated results for the $Z'$ mass are consistent and fit comfortably within these bounds.

The mass of the charged scalar boson $H^{\pm }$ also emerges naturally through the variation of the $\beta$ angle. The range we obtained encompasses experimental studies, particularly in processes like $H^{\pm }\rightarrow h^0W^{\pm }$. The outcomes from these studies fall within the values $0.3 \, \text {TeV} \le m_{H^{\pm }} \le 0.7 \, \text {TeV}$ [47].

5 Phenomenology of flavor-changing top quark rare decays

The permissible Feynman diagrams for the decays $t\rightarrow qV$ and $t\rightarrow qh^0$, where $q=(u,c)$ and $V=(Z,\gamma ,g)$, are illustrated in Figs. 1 and 2. For both Case II and Case III, we computed fifty-two amplitudes utilizing the Mathematica packages FeynCalc [48] and Package X [49].

Each amplitude for the decay $t\rightarrow qV$ adopts the following structure:

$$\begin{aligned} {\mathcal {M}}^{\mu } = {\bar{u}}(p_j)\left( F_1p_i^\mu {\textbf{1}}+F_2p_i^\mu \gamma ^5+F_3\gamma ^\mu +F_4\gamma ^\mu \gamma ^5 \right) u(p_i). \end{aligned}$$

(57)

The form factors $F_1, F_2, F_3,$ and $F_4$ encapsulate the masses and momenta of the external and internal quarks and gauge bosons in both the BLHM and the SM. These are incorporated within the Passarino–Veltman scalar functions. For the decay $t\rightarrow qh^0$, each amplitude displays a unique structure

$$\begin{aligned} {\mathcal {M}}^{\mu } = {\bar{u}}(p_j)\left( f_1+f_2\gamma ^5\right) u(p_i), \end{aligned}$$

(58)

$f_{1,2}$ contains terms from the BLHM and SM with Passarino–Veltman scalar functions.

5.1 Cases for the CKM matrix in the BLHM

In various BSM theories, the mass eigenstates do not necessarily align with those of the SM. This misalignment introduces new contributions from both vector and scalar fields to processes involving FCNCs. A salient advantage of these models is that they circumvent suppression via the GIM mechanism [50]. Within the BLHM framework, one must consider radiative corrections to capture the essence of flavor violation, as the model inherently lacks it at the tree level. Our analysis uses the methodology delineated in [20, 22, 23] to craft the extended CKM matrices.

We need two CKM-like unitary matrices

$$\begin{aligned} V_{Hu},\;V_{Hd} \end{aligned}$$

(59)

such that

$$\begin{aligned} V_{CKM}=V_{Hu}^{\dagger }V_{Hd}. \end{aligned}$$

(60)

Actually, we are familiar with $V_{CKM}$; hence, the relation $V_{Hd} = V_{Hu}V_{CKM}$ holds true. The matrices presented in Eq. (59) characterize flavor-violating interactions between SM fermions (u, c) and bosons $(Z,\gamma ,g,h^0)$. In the context of this paper, the interactions also involve the BLHM fermion B mediated by bosons $(W^{\prime \pm },\phi ^{\pm }, H^{\pm })$. We can generalize the CKM extended matrix as the product of three rotation matrices, as documented in [22, 51].

$$\begin{aligned} V_{Hd}= & {} \begin{pmatrix} 1&{}0&{}0\\ 0&{}c_{23}^d&{}s_{23}e^{-i\delta _{23}^d}\\ 0&{}-s_{23}^de^{i\delta _{23}^d} &{}c_{23}^d \end{pmatrix}\nonumber \\{} & {} \times \begin{pmatrix} c_{13}^d&{}0&{}s_{13}^de^{-i\delta _{13}^d}\\ 0&{}1&{}0\\ -s_{13}e^{i\delta _{13}^d}&{}0&{}c_{13}^d \end{pmatrix}\nonumber \\{} & {} \times \begin{pmatrix} c_{12}^d&{}s_{12}^de^{-i\delta _{12}^d}&{}0\\ -s_{12}^de^{i\delta _{12}^d}&{}c_{12}^d&{}0\\ 0&{}0&{}1 \end{pmatrix}. \end{aligned}$$

(61)

where the $c^d_{ij}$ and $s^d_{ij}$ are in terms of the angles $(\theta _{12},\theta _{23},\theta _{13})$ and the phases $(\delta _{12},\delta _{23},\delta _{13})$. We choose the following cases:

Case I. $V_{Hu}={\textbf{1}}$, this implies $V_{Hd}=V_{CKM}$.

In this case, the condition $V_{Hu}={\textbf{1}}$ does not allow for the contribution of the extended matrix or the CKM matrix since there are no quarks or bosons from the SM within the calculated loops. Only the model constants and the masses of the charged scalar bosons will be present.

Case II. $V_{Hd}={\textbf{1}}$, this implies $V_{Hu}=V_{CKM}^{\dagger }$.

In this case, the contribution comes from the CKM matrix, in which we will have suppression due to more minor terms such as $V_{ub}$ and $V_{cb}$.

Case III. $s_{23}^d=1/\sqrt{2}$, $s_{12}^d=s_{13}^d=0$, $\delta _{12}^d=\delta _{23}^d=\delta _{13}^d=0$.

Substituting the values of case III into the matrix $V_{Hd}$ in Eq. (61), we obtain the matrix:

$$\begin{aligned} V_{Hd}= \begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 1/\sqrt{2}\\ 0 &{} -1/\sqrt{2} &{} 1 \end{pmatrix}, \end{aligned}$$

(62)

and through the product $V_{Hd}V_{CKM}^{\dagger }$, we obtain the matrix:

$$\begin{aligned} V_{Hu}= \begin{pmatrix} 1.08 &{} -0.25 &{} 0.00\\ -0.25 &{} 1.05 &{} 0.66\\ 0.17 &{} -0.81 &{} 1.03 \end{pmatrix}. \end{aligned}$$

(63)

In case III, we follow the parametrization made in [20, 22]. Of all the matrix elements, the only one suppressed is $|V_{Bu}|=0.006$; however, the branching ratios of the decays turned out to be much larger than their counterparts in the SM. We have not considered other scenarios for the extended CKM matrix because one of the objectives of this study was to broaden the flavor structure in the BLHM. Future studies on CP violation will consider other cases.

5.2 Branching ratios for the reactions $t \rightarrow qV$ and $t \rightarrow qh^0$ in the BLHM

Using the parameter space detailed in Sect. 5 and the matrix $V_{Hu}$ from the second and third cases in Sect. 5.1, we have calculated the branching ratios of the processes $t\rightarrow qV$ and $t\rightarrow qh^0$, where $q=u,c$ and $V=Z,\gamma , g$. Our results are shown in Tables 6 and 7.

5.2.1 Case II

In this section, we present the branching ratios calculated using the extended matrix $V_{Hu}=V_{CKM}^{\dag }$. The numerical results for the top quark decay branching ratios are listed in Table 6, where we observe that the smallest ratios involve the up quark. The decays involving the charm quark are also small compared to those obtained through the matrix of Case III. Thus, it is evident that the contribution of the extended matrix and the model itself increase the branchings.

Table 6 Case II. The branching ratios for the top-quark decay via flavor-changing neutral current couplings at the BLHM

In Fig. 3, we plot $B(t\rightarrow cV,ch^0)$ against the breaking scale f, with lower intensities compared to the equivalent branchings in Fig. 5. In Fig. 4, we observe a different situation as the $B(t\rightarrow uV,uh^0)$ have similar magnitudes to their counterparts in Fig. 6, indicating that the form of the extended matrix for Case III practically did not increase the sensitivity in the up quark branching ratios.

Table 7 Case III. The branching ratios for the top-quark decay via flavor-changing neutral current couplings at the BLHM

Fig. 3

Case II. Total contributions to $Br(t\rightarrow cZ, c\gamma , cg, ch^0)$ as a function of the scale of energy f, with $m_B=(1.14)f$ and $F=5$ TeV

This difference in contributions from the extended matrices will allow us to study more cases where obtaining larger magnitudes in these same decays relative to experimental limits is possible.

Fig. 4

Case II. Total contributions to $Br(t\rightarrow uZ, u\gamma , ug, uh^0)$ as a function of the scale of energy f, with $m_B=(1.14)f$ and $F=5$ TeV

5.2.2 Case III

In this section, we present the branching ratios for the extended matrix of Case III, along with the corresponding graphs. We consider it necessary to showcase the individual contributions of the fields $(W^{\prime \pm },\phi ^{\pm },\eta ^{\pm }, H^{\pm })$ in the BLHM to the branching of each field $(Z,\gamma ,g,h^{0})$ and the quarks u, c, B in Appendix 1. We can observe that the scalar field $\phi ^{\pm }$ was the most significant contribution to the branching ratios for both decay processes $t\rightarrow cV$ and $t\rightarrow ch^0$. This highlights the significance of the scalar field contributions in the BLHM in conjunction with the extended CKM matrix.

The best sensitivity on the branching ratios might reach up to the order of magnitude of ${\mathcal {O}}(10^{-8}-10^{-5})$. As can be seen from Table 7, the decay channels $t \rightarrow cZ$, $t \rightarrow c\gamma$, and $t \rightarrow ch^0$ exhibit good sensitivities compared to the branching ratios reported in the literature [21, 27]. Experimentally, the data provided by ATLAS and CMS place the latest searches for $t\rightarrow qZ$ with a limit of $10^{-4}$ [52]. In [53], for the decay of the top quark to a photon accompanied by a charm quark or an up quark, they report $Br(t\rightarrow q\gamma )\sim 10^{-5}$. For the process $t\rightarrow qg$, the branching ratio is around $10^{-4}$ [54]. In [55], the estimation $Br(t\rightarrow qh^0)\sim 10^{-3}$ is published.

Fig. 5

Case III. Total contributions to $Br(t\rightarrow cZ, c\gamma , cg, ch^0)$ as a function of the scale of energy f, with $m_B=(1.14)f$ and $F=5$ TeV

Figure 5 shows the branching ratio of the decays $t\rightarrow cV$ and $t\rightarrow ch^0$, where $V=(Z,\gamma ,g)$, as a function of the breaking scale energy f in the range [1, 3] TeV. Since the masses of the bosons $(W^{\prime \pm },\phi ^{\pm },\eta ^{\pm }, H^{\pm })$ and the quark B depend on the scale f, they also vary their contribution for each point of the branching ratio in the plot of Fig. 5. It is important to emphasize that for the parameters $(\beta ,\alpha ,\lambda _0,y_3)$, their lower limits given in Table 3 were used. In general, we could calculate the branchings for any value of $\beta$ within the range [1.35, 149], but even though the masses of $A^0$ and $H^0$ would be more significant, this would not significantly alter the scenario in the plot of Fig. 5 since the masses of $W^{\prime \pm }$ and $Z'$ reach much higher values as a function of f and F.

Fig. 6

Case III. Total contributions to $Br(t\rightarrow uZ, u\gamma , ug, uh^0)$ as a function of the scale of energy f, with $m_B=(1.14)f$ and $F=5$ TeV

In the case of the decays $t\rightarrow uV$ and $t\rightarrow uh^0$, under the same parameters, the branching ratios were found to be more suppressed, as shown in Fig. 6. Given the records mentioned in the literature, it was expected that the BLHM would produce similar ranges for these decays. On the other hand, we can compare our results with those calculated in the SM, Table 8. We also summarize the current experimental limits for the investigated branching ratios in Table 9.

Table 8 SM Branching ratios for $t \rightarrow qV$ and $t \rightarrow qh^0$ where $q = (u, c)$ and $V = (Z, \gamma , g)$ [56]

Table 9 Experimental upper limits on the $Br(t\rightarrow qV)$ and $Br(t\rightarrow qh^0)$ [54, 57]

6 Conclusions

In this paper, we investigate the impact of one-loop contributions from heavy gauge bosons $W^{\prime \pm }$, the heavy quark B, and the new scalars $(\phi ^{\pm },\eta ^{\pm }, H^{\pm })$ predicted by the BLHM on the top quark rare decay processes $t\rightarrow qV$ and $t\rightarrow qh^0$. We summarize our results for $Br(t \rightarrow qV)$ and $Br(t \rightarrow qh^0)$ in Tables 6 and 7 and illustrate them in Figs. 3, 4, 5, 6, 7, 8, 9 and 10. Our analysis reveals that the dominant contributions to the branching ratios are observed in the channels $Br(t\rightarrow cZ)=3.7\times 10^{-5}$, $Br(t\rightarrow c\gamma )=2.6\times 10^{-6}$, and $Br(t\rightarrow ch^0)=8.5\times 10^{-8}$, assuming symmetry-breaking scales $f=[1,3]$ TeV and $F=5$ TeV within the BLHM.

We establish a relationship between the scale f and fine-tuning, as shown in Table 3, which guides our choice of the f range. However, the scale F is only required to satisfy the condition $F>f$ to adhere to the model’s properties. It can also be adjusted to match experimental requirements for the masses of heavy gauge bosons. The rare decay modes $t \rightarrow cZ$ and $t\rightarrow c\gamma$ studied in this article could be probed with high sensitivity in the High Luminosity (HL) and High Energy (HE) phases at the LHC [58]. These processes may also be accessible in the Future Circular Hadron-Hadron Collider (FCC-hh). Lepton colliders such as the Compact Linear Collider (CLIC) [59, 60] and the muon Collider with HL and HE [61] have also included top quark physics in their research agendas.

In summary, this study explores the potential to constrain the branching ratios $Br(t \rightarrow uZ, u\gamma , ug, uh^0)$ and $Br(t \rightarrow cZ, c\gamma , cg, ch^0)$ within the BLHM framework. Furthermore, we provide the first estimates for constraining these couplings. Considering the solid theoretical basis and convincing phenomenological characteristics that the model presents, it is desirable that the BLHM could be a good motivation for possible future experimental initiatives. In addition, our results complement other studies on the flavor-changing top quark rare decays in the context of the LHMs and other extensions on the SM.

Appendices

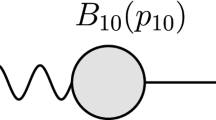
Appendix A: Individual contributions from $W^{\prime \pm },\phi ^{\pm },\eta ^{\pm },H^{\pm }$

In this appendix, we present the graphs corresponding to the individual contributions of the fields $(W^{\prime \pm },\phi ^{\pm },\eta ^{\pm }, H^{\pm })$ in the BLHM to each field $(Z,\gamma ,g,h^0)$ in the SM, where the quarks (u, c) and B are also involved.

Fig. 7

Individual contributions from $W^{\prime \pm },\phi ^{\pm },\eta ^{\pm },H^{\pm }$ to $t\rightarrow qZ$

Fig. 8

Individual contributions from $W^{\prime \pm },\phi ^{\pm },\eta ^{\pm },H^{\pm }$ to $t\rightarrow q\gamma$

Fig. 9

Individual contributions from $W^{\prime \pm },\phi ^{\pm },\eta ^{\pm },H^{\pm }$ to $t\rightarrow qg$

Fig. 10

Individual contributions from $W^{\prime \pm },\phi ^{\pm },\eta ^{\pm },H^{\pm }$ to $t\rightarrow qh^0$

In Fig. 7, the contributions of $\phi ^{\pm }_c$ dominate. In Fig. 8, $H_c^{\pm }$ and $\phi _c^{\pm }$ are the largest contributors. In Fig. 9, $\phi _c^{\pm }$ is the dominant contributor. Finally, in Fig. 10, $\phi _c^{\pm }$ has the highest contribution to the branching ratio.

Appendix B: Feynman rules in the BLHM

In this appendix, we derive and present the Feynman rules for the BLHM necessary to calculate the flavor-changing top quark rare decays.

Tables 10, 11 and 12 summarize the Feynman rules for the 3-point interactions: fermion-fermion-scalar (FFS), fermion-fermion-gauge (FFV), gauge-gauge-gauge (VVV), and scalar-gauge-gauge (SVV) interactions.

Table 10 Essential Feynman rules in the BLHM for studying the flavor-changing top quark rare decays are the 3-point interactions fermion-fermion-scalar (FFS), fermion-fermion-gauge (FFV), gauge-gauge-gauge (VVV), and scalar-gauge-gauge (SVV) interactions

Table 11 Factors from Table 10

Table 12 Factors from Table 11