Study on the possible molecular states composed of $\Lambda _c{\bar{D}}^*$, $\Sigma _c{\bar{D}}^*$, $\Xi _c{\bar{D}}^*$ and $\Xi _c'{\bar{D}}^*$ in the Bethe–Salpeter frame based on the pentaquark states $P_c(4440)$, $P_c(4457)$ and $P_{cs}(4459)$

Abstract

The measurements on a few pentaquarks states $P_c(4440)$, $P_c(4457)$ and $P_{cs}(4459)$ excite our new interests about their structures. Since the masses of $P_c(4440)$ and $P_c(4457)$ are close to the threshold of $\Sigma _c{\bar{D}}^*$, in the earlier works, they were regarded as molecular states of $\Sigma _c{\bar{D}}^*$ with quantum numbers $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$ and $\frac{1}{2}(\frac{3}{2}^-)$, respectively. In a similar way $P_{cs}(4459)$ is naturally considered as a $\Xi _c{\bar{D}}^*$ bound state with $I=0$. Within the Bethe-Salpeter (B-S) framework we systematically study the possible bound states of $\Lambda _c\bar{D}^*$, $\Sigma _c{\bar{D}}^*$, $\Xi _c{\bar{D}}^*$ and $\Xi _c'{\bar{D}}^*$. Our results indicate that $\Sigma _c{\bar{D}}^*$ can form a bound state with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$, which corresponds to $P_c(4440)$. However for the $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$ system the attraction between $\Sigma _c$ and ${\bar{D}}^*$ is too weak to constitute a molecule, so $P_{c}(4457)$ may not be a bound state of $\Sigma _c{\bar{D}}^*$ with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$. As $\Xi _c{\bar{D}}^*$ and $\Xi _c'{\bar{D}}^*$ systems we take into account of the mixing between $\Xi _c$ and $\Xi '_c$ and the eigenstets should include two normal bound states $\Xi _c{\bar{D}}^*$ and $\Xi _c'{\bar{D}}^*$ with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$ and a loosely bound state $\Xi _c{\bar{D}}^*$ with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$. The conclusion that two $\Xi _c{\bar{D}}^*$ bound states exist, supports the suggestion that the observed peak of $P_{cs}(4459)$ may hide two states $P_{cs}(4455)$ and $P_{cs}(4468)$. Based on the computations we predict a bound state $\Xi _c'{\bar{D}}^*$ with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$ but not that with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$. Further more accurate experiments will test our approach and results.

1 Introduction

In recent years several pentaquark states have been successively measured in experiment, which broaden our scope of view on hadron physics. In 2019 the LHCb collaboration [1] observed a pentaquark state $P_c(4312)$ in $J/\psi p$ invariant mass spectrum and found two narrow overlapping peaks $P_c(4440)$ and $P_c(4457)$ which hid in the structure of the former observed $P_c(4450)$ [2]. In 2021 two similar states $P_{cs}(4338)$ [3] and $P_{cs}(4459)$ [4] were announced in the $J/\psi \Lambda$ channel by the LHCb collaboration and their masses and widthes are collected in Table 1. According to their masses and the channels where they were found, they are regarded as pentaquark states rather than conventional excited baryonic states. In fact in 2003 a baryon was measured at LEPS [5] which was conjectured as a pentaquark state, however later the allegation was negated by further more accurate experiments. On the theoretical aspect Gell-Mann clearly indicated possible existence of pentaquark in his first paper on the quark model [6]. Later some theoretical works have been addressed to this topic [7,8,9,10,11,12,13,14]. For these new states people have all reasons to doubt about their inner structure because more constituents involved would bring up more possible combinations, unlike the simplest $q{\bar{q}}$ and qqq for meson and baryon, respectively. In fact until now most researchers do not agree with each other on the inner structures of those exotic states recently found in experiments [15,16,17,18,19]. Those discoveries on pentaquarks have stimulated vigorous discussions on their properties [20]. Indeed the theoretical exploration is crucial for getting a better understanding on their structures in the quark model and obtaining valuable information about non-perturbative physics. Definitely, more accurate data achieved from experiments would help theorists to make progress on the route.

Table 1 $P_c$ and $P_{cs}$ states observed by LHCb

Now let us turn to some concrete subjects where charm physics is referred because relatively larger database is collected nowadays. There have been many papers which address to these hidden charm pentaquark states [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. For $P_c(4318)$ most authors suggest that it is a $\Sigma _c$ and ${\bar{D}}$ bound state. As for $P_c(4440)$ and $P_c(4457)$ they were regarded as the $\Sigma _c-{\bar{D}}^*$ molecular states with $J=\frac{1}{2}$ and $J=\frac{3}{2}$, respectively in the concerned papers [33,34,35,36,37,38,39]. Certainly about $P_c(4457)$ there are still some different opinions about its inner structure [32, 41]. The authors [30, 39] think $P_{cs}(4338)$ to be a $\Xi _c{\bar{D}}$ bound state, while they suggest that the observed $P_{cs}(4459)$ should correspond to two states $P_{cs}(4455)$ and $P_{cs}(4468)$ as $\Xi _c{\bar{D}}^*$ bound state with $I(J)=0(\frac{1}{2})$ and $0(\frac{3}{2})$, respectively. In that situation it requires further theoretical studies on the structures of $P_c(4440)$, $P_c(4457)$ and $P_{cs}(4459)$.

In Ref. [42] we studied two possible molecular states $\Lambda _c{\bar{D}}$ and $\Sigma _c{\bar{D}}$ within the Bethe-Salpeter (B-S) framework. Our results indicate that the $\Sigma _c{\bar{D}}$ molecular state with $I=0$ can exist which corresponds to the pentaquark state $P_c(4318)$. In this paper we still employ the same framework (B-S equation) to study the possible bound state of a charmed baryon ($\Lambda _c,\,\Sigma _c,\,\Xi _c$ or $\Xi '_c$) and ${\bar{D}}^*$. The B-S equation is a relativistic equation and established on the basis of quantum field theory thus is adapted to deal with the bound states [43]. Some authors have employed the B-S equation to study the bound state of two fermions [44, 45], the system of one-fermion-one-boson [46,47,48,49] and two bosons [50,51,52,53]. In Ref. [33] the authors studied possible bound states of $\Sigma _c$ and ${\bar{D}}^*$ within their B-S framework. In this work we follow the approach adopted in [42] to study the possible bound states of $\Sigma _c{\bar{D}}^*$, $\Lambda _c{\bar{D}}^*$, $\Xi _c {\bar{D}}^*$ and $\Xi _c {\bar{D}}^*$. Though our approach is a little similar to that in [33] there is an evident difference between them: we deduce the B-S equation and the corresponding kernel from the Feynman diagrams directly with the effective interactions; instead, in [33] the authors directly wrote down the potentials for exchanging different particles and then insert the kernel into these B-S equations.

The pentaquark states $P_c(4440)$ and $P_c(4457)$ have been measured in the invariant mass spectrum of $J/\psi p$ so their isospins are confirmed as $\frac{1}{2}$ because of isospin conservation. As for $P_{cs}(4459)$ the isospin is 0 since it is observed in $J/\psi \Lambda$ production. Thus we conjecture that the two hadron constituents reside in an isospin eigenstate. For the $\Lambda _c{\bar{D}}^*$ system its isospin must be $\frac{1}{2}$ but the $\Sigma _c{\bar{D}}^*$ system may reside in either isospin $\frac{1}{2}$ or $\frac{3}{2}$. As for $\Xi _c{\bar{D}}^*$ and $\Xi '_c{\bar{D}}^*$ systems, the total isospin is 0 or 1. Certainly, for a bound system composed of a spin-parity $\frac{1}{2}^+$ baryon and $1^-$ meson the total spin-parity is $\frac{1}{2}^-$ or $\frac{3}{2}^-$ if the two constituents are in the $S-$wave.

If two particles can mutually bind the interactions between them needs to be sufficiently strong. According to the quantum field theory two particles interact via exchanging certain mediate particles. Since in our study two constituents are color-singlet hadrons the exchanged particles are some light hadrons such as $\pi$, $\eta$, $\sigma$, $\rho$ or (and) $\omega$ etc.. The effective interactions for the concerned heavy hadrons are deduced in Refs. [54,55,56,57] and some of them we use are collected in the appendix A. Using the effective interactions we obtain the corresponding B-S equation by the Feynman diagrams.

Inputting the corresponding parameters, one can solve the B-S equation numerically. For a spin-isospin eigenstate, if the equation possesses a solution with these reasonable parameters, then we would conclude that the corresponding bound state could exist in the nature, by contraries, no solution of the B-S equation implies the supposed bound state cannot form.

This paper is organized as follows: after this introduction we will derive the B-S equations related to possible bound states composed of a charmed baryon and ${\bar{D}}^*$. Then in Sect. 3 we will solve the B-S equation numerically and present our results by figures and tables. Section 4 is devoted to a brief summary.

2 The bound states of $\Lambda _c{\bar{D}}^*$, $\Sigma _c{\bar{D}}^*$, $\Xi _c{\bar{D}}^*$ and $\Xi '_c{\bar{D}}^*$

Fig. 1

The bound states of $\mathcal {B} {\bar{D}}^*$ formed by exchanging light pseudoscalar meson (a) or vector meson (b)

Since the pentaquark states $P_c(4440)$, $P_c(4457)$ and $P_{cs}(4459)$ contain hidden charms and their masses are close respectively to the sums of the masses of single charmed baryons $\Lambda _c$, $\Sigma _c$, $\Xi _c$ or $\Xi '_c$ and a charmed meson ${\bar{D}}^*$, it is obviously tempted to attribute those pentaquark states to molecules of a charmed baryon and a charmed meson. Below we will focus on the molecular structures composed of a single charmed baryon and ${\bar{D}}^*$. Concretely, in this paper we study $\Lambda _c{\bar{D}}^*$. $\Sigma _c{\bar{D}}^*$, $\Xi _c{\bar{D}}^*$ and $\Xi '_c{\bar{D}}^*$ systems where the spatial wave function between two constituents is in $S-$wave i.e. its spin-parity ($J^P$) is $\frac{1}{2}^-$ or $\frac{3}{2}^-$.

2.1 The isospin states of $\Lambda _c{\bar{D}}^*$ and $\Sigma _c{\bar{D}}^*$

Since the isospins of $\Lambda _c$ and ${\bar{D}}^*$ are 0 and $\frac{1}{2}$, the isospin structure of the possible bound state $\Lambda _c{\bar{D}}^{*}$ is

$$\begin{aligned} \left| \frac{1}{2},\frac{1}{2}\right\rangle =|\Lambda _c{\bar{D}}^{*0}\rangle . \end{aligned}$$

(1)

There also exists another state $|\frac{1}{2},-\frac{1}{2}\rangle =|\Lambda _c D^{*-}\rangle$ belonging to the doublet of $I=\frac{1}{2}$.

However the isospins of $\Sigma _c$ is 1, so the possible bound states of $\Sigma _c{\bar{D}}^*$ could be in one of three isospin assignments i.e. $|I,I_3\rangle$ are $|\frac{1}{2},\frac{1}{2}\rangle$ $|\frac{3}{2},\frac{1}{2}\rangle$ and $|\frac{3}{2},\frac{3}{2}\rangle$. The explicit isospin states are

$$\begin{aligned} \left| \frac{1}{2},\frac{1}{2}\right\rangle= & {} \sqrt{\frac{2}{3}}|\Sigma _c^{++} D^{*-}\rangle -\sqrt{\frac{1}{3}}|\Sigma _c^+{\bar{D}}^{*0}\rangle , \end{aligned}$$

(2)

$$\begin{aligned} \left| \frac{3}{2},\frac{1}{2}\right\rangle= & {} \sqrt{\frac{1}{3}}|\Sigma _c^{++} D^{*-}\rangle +\sqrt{\frac{2}{3}}|\Sigma _c^+{\bar{D}}^{*0}\rangle , \end{aligned}$$

(3)

and

$$\begin{aligned} \left| \frac{3}{2},\frac{3}{2}\right\rangle =|\Sigma _c^{++}{\bar{D}}^{*0}\rangle . \end{aligned}$$

(4)

Similarly there are also three isospin adjoint states $|\frac{1}{2},-\frac{1}{2}\rangle$, $|\frac{3}{2},-\frac{1}{2}\rangle$ and $|\frac{3}{2},-\frac{3}{2}\rangle$.

2.2 The isospin states of $\Xi _c{\bar{D}}^*$ and $\Xi '_c{\bar{D}}^*$

Since the isospins of $\Xi _c$ ($\Xi '_c$) and ${\bar{D}}^*$ are both 1/2, the total isospin of the possible bound state of $\Xi _c{\bar{D}}^{*}$ ($\Xi '_c{\bar{D}}^{*}$) is 0 or 1. For the $\Xi _c{\bar{D}}^{*}$ system the explicit isospin states are

$$\begin{aligned} |0,0\rangle= & {} \frac{1}{\sqrt{2}}|\Xi ^+_c D^{*-}\rangle -\frac{1}{\sqrt{2}}|\Xi ^0_c D^{*0}\rangle \,, \end{aligned}$$

(5)

$$\begin{aligned} |1,0\rangle= & {} \frac{1}{\sqrt{2}}|\Xi ^+_c D^{*-}\rangle +\frac{1}{\sqrt{2}}|\Xi ^0_c D^{*0}\rangle , \end{aligned}$$

(6)

$$\begin{aligned} |1,1\rangle= & {} |\Xi ^+_c D^{*0}\rangle \rangle , \end{aligned}$$

(7)

and

$$\begin{aligned} |1,-1\rangle =|\Xi ^0_c D^{*-}\rangle . \end{aligned}$$

(8)

For the $\Xi '_c{\bar{D}}^{*}$ system one can replace $\Xi _c$ by $\Xi '_c$ to obtain the isospin states.

2.3 The Bethe–Salpeter (B-S) equation for $J^P=\frac{1}{2}^-$ and $\frac{3}{2}^-$ molecular states

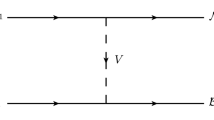
In the effective theory two hadrons interact via exchanging light hadrons. For our concerned structures the Feynman diagrams at the leading order are depicted in Fig. 1 where $\mathcal {B}$, $\mathcal {P}$ and $\mathcal {V}$ denote the charmed baryon, light pseudoscalar and vector mesons, respectively. For exchanging a light scalar meson (such as $\sigma$) the Feynman diagram is the same as Fig. 1a, so we omit it. The total and relative momenta of the bound state are read as

$$\begin{aligned}{} & {} P = p_1 + p_2 =q_1 + q_2, \,\quad p = \eta _2p_1 - \eta _1p_2,\nonumber \\{} & {} q = \eta _2q_1 - \eta _1q_2, \end{aligned}$$

(9)

where P is the total momentum of the bound state, $q_1$ ($q_2$) and $p_1$ ($p_2$) are those momenta of the constituents, q and p are the relative momenta at the two sides of the effective vertex, k is the momentum of the exchanged meson, $\eta _i = m_i/(m_1+m_2)$ and $m_i\, (i=1,2)$ is the mass of the i-th constituent meson.

The bound state composed of a baryon and a vector meson is written as

$$\begin{aligned} \chi ^\mu _P(x_1,x_2) =\langle 0|T\mathcal {B}(x_1)\mathcal {M}^\mu (x_2)|P\rangle . \end{aligned}$$

(10)

The B-S wave function is a Fourier transformation of that into the momentum space

$$\begin{aligned} \chi ^\mu _P(x_1,x_2) =e^{-iPX}\int \frac{d^4p}{(2\pi )^4}\chi ^\mu _P(p)e^{-ipx}. \end{aligned}$$

(11)

By the so-called ladder approximation the corresponding B-S equation is deduced as

$$\begin{aligned} \chi ^\mu _{{P}}({ p}) =S_B(p_1)\int {d^4{q}\over (2\pi )^4}\,K_{\tau \nu }(P,p,q)\chi ^\nu _{_{P}}(q)S^{\mu \tau }_M(p_2),\nonumber \\ \end{aligned}$$

(12)

where $S_B(p_1)$ is the propagator of the baryon ($\Lambda _c$, $\Sigma _c$, $\Xi _c$ or $\Xi '_c$), $S^{\nu \tau }_M(p_2)$ is that of the meson (${\bar{D}}^*$) and $K_{\tau \mu }(P,p,q)$ is the kernel which is obtained by calculating the Feynman diagram in Fig. 1. For the later convenience the relative momentum p is decomposed into the longitudinal $p_l$ ($\equiv p\cdot v$) and transverse projection $p^\mu _t$ ($\equiv p^\mu -p_lv^\mu$)=(0, $\textbf{p}_T$) according to the momentum of the bound state P ($v=\frac{P}{M}$). The two propagators are

$$\begin{aligned} S_B(\eta _1 P+p)= & {} \frac{i[(\eta _1M+p_l)v\!\!\!/+p_t\!\!\!/+m_1]}{[(\eta _1M+p_l)^2-\omega ^2_1+i\epsilon ]}, \end{aligned}$$

(13)

$$\begin{aligned} S^{\mu \tau }_M(\eta _2 P-p)= & {} \frac{i(-g^{\tau \mu }+p_2^\tau p_2^\mu /m_2^2)}{[(\eta _2M-p_l)^2-\omega ^2_2+i\epsilon )]}, \end{aligned}$$

(14)

where M is the total energy of the bound state, $\omega _i = \sqrt{ m_i^2-{ p_t}^2 }$ and $m_1$ ($m_2$) are the energy and the mass of the baryon (meson). Apparently the contribution of the tensor term in $S^{\nu \tau }_M$ is much smaller than that of the first term for heavy meson, thus it can be ignored in numerical computations.

By the Feynman diagram the kernel $K_{\tau \nu }(P,p,q)$ is written as

$$\begin{aligned} K_{\tau \nu }(P,p,q)= & {} \sum _\mathcal {P} K^{\mathcal {P}}_{\tau \nu }(P,p,q)+\sum _\mathcal {S} K^{\mathcal {S}}_{\tau \nu }(P,p,q)\nonumber \\{} & {} +\sum _\mathcal {V} K^{\mathcal {V}}_{\tau \nu }(P,p,q), \end{aligned}$$

(15)

with

$$\begin{aligned} K^{\mathcal {P}}_{\tau \nu }(P,p,q)= & {} C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}} \varepsilon _{\alpha \beta \mu \lambda }\gamma ^\alpha \gamma ^\beta k^\mu (p_1+q_2)^\lambda \varepsilon _{\theta \tau \nu \kappa }\\{} & {} \times (p_2+q_2)^\theta k^\kappa \Delta (k,m_\mathcal {P})F^2(k,m_{\mathcal { P}}),\\ K^{\mathcal {S}}_{\tau \nu }(P,p,q)= & {} C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}} g_{_{2\mathcal {S}}}g_{\tau \nu }\Delta (k,m_\mathcal {S})F^2(k,m_{\mathcal { S}}),\\ K^{\mathcal {V}}_{\tau \nu }(P,p,q)= & {} C_{{I\mathcal {V}}}[g_{_{1\mathcal {V}}}(p_1+q_1)^\alpha \\{} & {} -g'_{_{1\mathcal {V}}} \gamma _\mu \gamma _\nu (k^\mu g^{\nu \alpha }-k^\nu g^{\mu \alpha })]\\{} & {} \times [-g_{_{2\mathcal {V}}}g_{\tau \nu }(p_2+q_2)^\beta \\{} & {} +g'_{_{2\mathcal {V}}}g_{\tau \theta }g_{\nu \delta }(k^{\theta }g^{\delta \beta } -k^{\delta }g^{\theta \beta })]\\{} & {} \times \Delta _{\alpha \beta }(k,m_\mathcal {V})F^2(k,m_{\mathcal {V}}), \end{aligned}$$

Table 2 The isospin factors for $\Sigma _c{\bar{D}}^*$ systems

Table 3 The isospin factors for $\Xi '_c{\bar{D}}^*$ and (or) $\Xi _c{\bar{D}}^*$ systems

where $m_\mathcal {P}$ or $m_\mathcal {V}$ is the mass of the exchanged meson, $g_{_{1\mathcal {P}}}$, $g_{_{2\mathcal {P}}}$, $g_{_{1\mathcal {S}}}$, $g_{_{2\mathcal {S}}}$, $g_{_{1\mathcal {V}}}$, $g'_{_{1\mathcal {V}}}$, $g_{_{2\mathcal {V}}}$ and $g'_{_{2\mathcal {V}}}$ are the concerned coupling constants, $C_{I\mathcal {M}}$ ($\mathcal {M}$ represent $\mathcal {P}$ where $\mathcal {S}$ or $\mathcal {V}$) are the isospin coefficients. We collect the isospin coefficients in Tables 2 and 3 and one can refer to the appendix B of our early paper [42] about how to obtain the isospin coefficients. The propagator of the exchanging mesnons are $\Delta (k,m_\mathcal {M})=i/(k^2-m_\mathcal {M}^2)$ and $\Delta _{\alpha \beta }(k,m_\mathcal {M})=i(-g_{\alpha \beta } +k_{\alpha }k_{\beta }/m_\mathcal {M}^2)/(k^2-m_\mathcal {M}^2)$. In our study the exchanging particles are limited to only a few light mesons. Of course, exchanging two light mesons between two hadrons may also induce a correction to the potential, but it undergoes a loop suppression, therefore, we do not consider that contribution. It is noted for $\Lambda _c {\bar{D}}^*$ system only $\omega$ and $\sigma$ can be exchanged, however for $\Sigma _c {\bar{D}}^*$ system $\eta$, $\pi$, $\sigma$, $\rho$ and $\omega$ can be mediators. Simiary for $\Xi _c {\bar{D}}^*$ system only $\rho$, $\omega$ and $\sigma$ can be exchanged, but for $\Xi '_c {\bar{D}}^*$ system $\eta$, $\pi$, $\sigma$, $\rho$ and $\omega$ can be mediators. When we write down the B-S equation (similar for the transition matrix element) in terms of the Feynman diagrams we need to pay attention to the direction of the fermion line flow, following the Feynman rules we put the B-S wave function of the final state in the left side of the equation and the BS wave function of the initial state at the right side of the equation. The treatment is contrary to the common convention adopted for B-S equation.

Since the constituents of the molecule (meson and baryon) are not point particles, a form factor at each effective vertex should be introduced. The form factor is suggested by many researchers as in the form:

$$\begin{aligned} F({k},m_{\mathcal { M}}) = {\Lambda ^2 - m_{ \mathcal {M}}^2 \over \Lambda ^2 - { k}^2},\quad { k} = { q}-{p} , \end{aligned}$$

(16)

where $\Lambda$ is a cutoff parameter which usually is taken as about 1 GeV.

The three-dimension B-S wave function is obtained after integrating over $p_l$

$$\begin{aligned} \chi ^\mu _{{P}}({ p_t}) =\int \frac{dp_l}{2\pi }\chi ^\mu _{{P}}({ p}). \end{aligned}$$

(17)

For the S-wave system, the completely spatial wave function can be found in Refs. [47,48,49]. However for the heavy hadrons case a simple version can be used

$$\begin{aligned} \chi ^\mu _{{P}}({ p_t}) =[f_1(|\textbf{p}_T|)+f_2(|\textbf{p}_T|)p_t\!\!\!/]u^\mu (v,s), \end{aligned}$$

(18)

where $f_1(|\textbf{p}_T|)$ and $f_2(|\textbf{p}_T|)$ are the radial wave functions, $u^\mu (v,s)$, v and s are the spinors, velocity and total spin of the bound state respectively. $u^\mu (v,s)=\frac{1}{\sqrt{2}}(\gamma ^\mu +v^\mu )\gamma _5u(v,s)$ when the spin of the state is $\frac{1}{2}$ and $u^\mu (v,s)$ is Rarita-Schwinger vector spinor for a $J=\frac{3}{2}$ state.

In the following, let us substitute Eq. (15) into Eq. (12) and employ the so-called covariant instantaneous approximation where $q_l=p_l$ i.e. $p_l$ takes the place of $q_l$ in the kernel K(P, p, q), and then K(P, p, q) no longer depends on $q_l$. Then we are performing a series of manipulations: integrate over $q_l$ on the right side of Eq. (12); multiply $\int \frac{dp_l}{(2\pi )}$ on the both sides of Eq. (12), and integrate over $p_l$ on the left side in the Eq. (12). Finally, substituting Eq. (18) we obtain

$$\begin{aligned}{} & {} [f_1(|\textbf{p}_T|)+f_2(|\textbf{p}_T|)p_t\!\!\!/]u^\mu (v,s)\nonumber \\{} & {} \quad =\int \frac{dp_l}{(2\pi )}\int \frac{d^3\textbf{q}_T}{(2\pi )^3}\frac{ [(\eta _1M+p_l)v\!\!\!/+p_t\!\!\!/+m_1](g^{\mu \tau })}{P_\mathcal{B}\mathcal{M}}\nonumber \\{} & {} \qquad \times \left\{ \sum _\mathcal {P} K^{\mathcal {P}}_{\tau \nu }(P,p,q_t)+\sum _\mathcal {S} K^{\mathcal {S}}_{\tau \nu }(P,p,q_t)\right. \nonumber \\ {}{} & {} \left. \qquad +\sum _\mathcal {V} K^{\mathcal {V}}_{\tau \nu }(P,p,q_t)\right\} \nonumber \\{} & {} \qquad \times {[}f_1(|\textbf{q}_T|)+f_2(|\textbf{q}_T|)q_t\!\!\!/]u^\nu (v,s), \end{aligned}$$

(19)

with

$$\begin{aligned} P_{\mathcal{B}\mathcal{M}}= & {} [(\eta _1M+p_l)^2-\omega ^2_l+i\epsilon ][(\eta _2M-p_l)^2\\ {}{} & {} -\omega ^2_2+i\epsilon )],\\ K^{\mathcal {S}}_{\tau \nu }(P,p,q_t)= & {} C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}} \frac{ig_{\tau \nu }F^2(k)}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {S}^2},\\ K^{\mathcal {P}}_{\tau \nu }(P,p,q_t)= & {} C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}} \varepsilon _{\delta \theta \phi \omega }\gamma ^\delta \gamma ^\phi (p_{t}^\theta -q_{t}^\theta )\\{} & {} \times [(2\eta _1P+2p_l)v^\omega +p^\omega _t+q^\omega _t]\\ {}{} & {} \times [(2\eta _2P-2p_l)v^\beta -p^\beta _t-q^\beta _t]\\{} & {} \times \frac{(p_t^\alpha -q_t^\alpha )\varepsilon _{\alpha \tau \nu \beta }iF^2(k)}{-(\textbf{p}_T -\textbf{q}_T)^2-m_\mathcal {P}^2},\\ K^{\mathcal {V}}_{\tau \nu }(P,p,q_t)= & {} C_{{I\mathcal {V}}}\{[g_{{1\mathcal {V}}}(2\eta _1P+2p_l)v^\alpha +p^\alpha _t+q^\alpha _t]\\{} & {} +g'_{_{1\mathcal {V}}}\gamma _\omega \gamma _\phi [(p_{t}^\omega -q_{t}^\omega )g^{\phi \alpha }-(p_{t}^\phi -q_{t}^\phi )g^{\omega \alpha }]\}\\{} & {} \times \{-g_{_{2\mathcal {V}}}g_{\tau \nu }[(2\eta _2P-2p_l)v^\beta -p^\beta _t-q^\beta _t]\\{} & {} -g'_{_{2\mathcal {V}}}(g_{\tau \theta }g_{\nu \delta })[(p_{t}^{\theta }-q_{t}^{\theta })g^{\delta \beta } -(p_{t}^{\delta }-q_{t}^{\delta })g^{\theta \beta }] \}\\{} & {} \times F^2(k)\frac{i[-g_{\alpha \beta }+(p_{t\alpha }-q_{t\alpha })(p_{t\beta }-q_{t\beta })/m_\mathcal {V}^2]}{{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {V}^2}}. \end{aligned}$$

Now let us finally extract the expressions of $f_1(|\textbf{p}_T|)$ and $f_2(|\textbf{p}_T|)$. Multiplying ${\bar{u}}^\mu (v,s)$ on both sides of Eq.(19), then by taking a trace, we get an expression which only contains $f_1$ on the left side whereas multiplying ${\bar{u}}^\mu (v,s)p_t\!\!\!/$ to the expression, $f_2$ is obtained on the left side, the resultant formulaes are

$$\begin{aligned} f_1(|\textbf{p}_T|)= & {} \int \frac{dp_l}{(2\pi )}\int \frac{d^3\textbf{q}_T}{(2\pi )^3}\frac{i}{P_{\mathcal{B}\mathcal{M}}}\left[ \sum _\mathcal {P}\frac{C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}} F^2(k,m_\mathcal {P})K^\mathcal {P}_{1}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {P}^2}+ \frac{C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}F^2(k,m_\mathcal {S})K^\mathcal {S}_{1}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {S}^2}\right. \nonumber \\{} & {} \left. +\sum _\mathcal {V}C_{{I\mathcal {V}}} \frac{F^2(k,m_\mathcal {V})(-g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},a}_{1} -g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},b}_{1}-g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}} K^{\mathcal {V},c}_{1}-g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},d}_{1})}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {V}^2}\right] , \end{aligned}$$

(20)

$$\begin{aligned} f_2(|\textbf{p}_T|)= & {} \int \frac{dp_l}{(2\pi )}\int \frac{d\textbf{q}_T}{(2\pi )^3}\frac{i}{P_{\mathcal{B}\mathcal{M}}}\left[ \sum _\mathcal {P}\frac{C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}} F^2(k,m_\mathcal {P})K^\mathcal {P}_{2}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {P}^2} +\frac{C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}F^2(k,m_\mathcal {S})K^\mathcal {S}_{2}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {S}^2}\right. \nonumber \\{} & {} \left. +\sum _\mathcal {V}C_{{I\mathcal {V}}}\frac{F^2(k,m_\mathcal {V})(-g_{_{1\mathcal {V}}} g_{_{2\mathcal {V}}}K^{\mathcal {V},a}_{2}-g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},b}_{2} -g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},c}_{2}-g'_{_{1\mathcal {V}}} g'_{_{2\mathcal {V}}}K^{\mathcal {V},d}_{2})}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {V}^2}\right] , \end{aligned}$$

(21)

Table 4 The factors $C_{J\mathcal {M}}$ where $\mathcal {M}$ represents $\mathcal {P}$, $\mathcal {S}$, a, b, c and d

Table 5 The coupling constants of $\mathcal{B}\mathcal{B}M$

with

$$\begin{aligned} K^\mathcal {S}_{1}= & {} C_{J\mathcal {S}}[ {f_1} ({\eta _1} M+p_l+m_1)-f_2{\textbf{p}_T\cdot \textbf{q}_T}],\\ K^\mathcal {S}_{2}= & {} C_{J\mathcal {S}}[{f_1} +f_2({\eta _1} M+p_l-m_1){\textbf{p}_T\cdot \textbf{q}_T}/\textbf{p}_T^2],\\ K^\mathcal {P}_{1}= & {} \frac{16C_{J\mathcal {P}}}{3} {f_1} ({p_l}-{\eta _2} M)\\{} & {} \times [({\eta _1} M+p_l)({\eta _1} M+p_l+m_1){(\textbf{p}_T-\textbf{q}_T)^2}\\{} & {} +{\textbf{p}_T \cdot \textbf{q}_T}^2-{\textbf{p}_T^2} {\textbf{q}_T^2}]\\{} & {} +\frac{16C_{J\mathcal {P}}}{3} {f_2}({p_l}-{\eta _2} M) [({\textbf{p}_T \cdot \textbf{q}_T}-{\textbf{p}_T^2}) \\{} & {} \times ({\textbf{p}_T\cdot \textbf{q}_T}-{\textbf{q}_T^2}) ({\eta _1} M+{p_l})+{m_1}\\{} & {} \times ({\textbf{p}_T\cdot \textbf{q}_T}^2-{\textbf{p}_T^2} {\textbf{q}_T^2})],\\ K^\mathcal {P}_{2}= & {} \frac{16C_{J\mathcal {P}}}{3 {\textbf{p}_T^2}} {f_1} ({p_l}-{\eta _2} M) \\{} & {} \times [({\textbf{p}_T\cdot \textbf{q}_T} -{\textbf{p}_T^2})^2 ({\eta _1} M+{p_l})\\{} & {} +{m_1} ({\textbf{p}_T^2} {\textbf{q}_T^2} -{\textbf{p}_T\cdot \textbf{q}_T}^2)]\\{} & {} -\frac{16C_{J\mathcal {P}}}{3 {\textbf{p}_T^2}} {f_2} ({p_l}-{\eta _2} M)\{({\eta _1} M+p_l)\\ {}{} & {} \times ({\eta _1} M+p_l-m_1)\\{} & {} \times [{\textbf{p}_T\cdot \textbf{q}_T} ({\textbf{p}_T^2}+{\textbf{q}_T^2})-2 {\textbf{p}_T^2} {\textbf{q}_T^2}]\\{} & {} +{\textbf{p}_T^2}[{\textbf{p}_T^2} {\textbf{q}_T^2}-{\textbf{p}_T\cdot \textbf{q}_T}^2]\},\\ K^{\mathcal {V},a}_{1}= & {} \frac{{f_1C_{Ja}}}{{m_\mathcal {V}}^2}({\eta _1} M+{m_1}+{p_l}) \{{m_\mathcal {V}}^2 \\{} & {} \times [-4 {\eta _1} {\eta _2} M^2+4 M {p_l} ({\eta _1}-{\eta _2})+4 {p_l}^2-({\textbf{p}_T}\\{} & {} +{\textbf{q}_T)^2}]-({\textbf{p}_T^2}-{\textbf{q}_T^2})^2\}\\{} & {} + {f_2C_{Ja}}{\textbf{p}_T \cdot \textbf{q}_T} [4 {\eta _1} {\eta _2} M^2+4 M {p_l} ({\eta _2}-{\eta _1})\\{} & {} +\frac{({\textbf{p}_T^2} -{\textbf{q}_T^2})^2}{{m_\mathcal {V}}^2}-4 {p_l}^2+({\textbf{p}_T}+{\textbf{q}_T)^2}],\\ K^{\mathcal {V},b}_{1}= & {} -\frac{4C_{Jb}}{3}{f_2} \left( {\textbf{p}_T\cdot \textbf{q}_T}^2-{\textbf{p}_T^2} {\textbf{q}_T^2}\right) ,\\ K^{\mathcal {V},c}_{1}= & {} 4{f_1C_{Jc}} ({\textbf{p}_T\cdot \textbf{q}_T}-{\textbf{p}_T^2}) ({p_l}-{\eta _2} M)\\{} & {} +4{f_2C_J} \{[-{\eta _2} M ({\eta _1} M+{m_1}+{p_l})\\ {}{} & {} \times +{\eta _1} M {p_l} +{m_1} {p_l}+{p_l}^2]\\{} & {} \times ({\textbf{p}_T\cdot \textbf{q}_T}- {\textbf{q}_T^2})-{\textbf{p}_T \cdot \textbf{q}_T}^2+{\textbf{p}_T^2} {\textbf{q}_T^2}\},\\ K^{\mathcal {V},d}_{1}= & {} -\frac{8C_{Jd}}{3}{f_1} ({\textbf{p}_T}-{\textbf{q}_T)^2} ({\eta _1} M+{m_1}+{p_l})\\{} & {} +\frac{8C_J}{3} {f_2} ({\textbf{p}_T\cdot \textbf{q}_T} -{\textbf{p}_T^2}) ({\textbf{p}_T\cdot \textbf{q}_T}-{\textbf{q}_T^2}),\\ K^{\mathcal {V},a}_{2}= & {} -\frac{f_1C_{Ja}}{{m_\mathcal {V}}^2}\{{m_\mathcal {V}}^2 [4 {\eta _1} {\eta _2} M^2+4 M {p_l} ({\eta _2}-{\eta _1})\\{} & {} -4 {p_l}^2+({\textbf{p}_T} +{\textbf{q}_T)^2}]+({\textbf{p}_T^2}-{\textbf{q}_T^2})^2\}\\{} & {} -\frac{f_2C_{Ja}}{{m_\mathcal {V}}^2 {\textbf{p}_T^2}}{\textbf{p}_T\cdot \textbf{q}_T} (-{\eta _1} M+{m_1}-{p_l}) \\{} & {} \times \{{m_\mathcal {V}}^2 [4 {\eta _1} {\eta _2} M^2+4 M {p_l} ({\eta _2}-{{\eta _1}})-4 {p_l}^2\\{} & {} +({\textbf{p}_T}+{\textbf{q}_T)^2}]+({\textbf{p}_T^2}-{\textbf{q}_T^2})^2\},\\ K^{\mathcal {V},b}_{2}= & {} \frac{f_2C_{Jb}}{3 {\textbf{p}_T^2}}4 \left( {\textbf{p}_T \cdot \textbf{q}_T}^2-{\textbf{p}_T^2} {\textbf{q}_T^2}\right) (-{\eta _1} M+{m_1}-{p_l}),\\ K^{\mathcal {V},c}_{2}= & {} -\frac{4f_1C_{Jc}}{{\textbf{p}_T^2}} ({\textbf{p}_T \cdot \textbf{q}_T}-{\textbf{p}_T^2})\\ {}{} & {} \times ({p_l}-{\eta _2} M) (-{\eta _1} M+{m_1}-{p_l})\\{} & {} -\frac{4 f_2C_{Jc}}{{\textbf{p}_T^2}}\{M [{\eta _1} {\textbf{p}_T\cdot \textbf{q}_T}^2 +{\eta _2} \\{} & {} \times {\textbf{p}_T\cdot \textbf{q}_T} {\textbf{p}_T^2}-{\textbf{p}_T^2} {\textbf{q}_T^2} ({\eta _1}+{\eta _2})]\\ {}{} & {} +{m_1} \left( {\textbf{p}_T^2} {\textbf{q}_T^2}-{\textbf{p}_T\cdot \textbf{q}_T}^2\right) \\{} & {} +{p_l} {\textbf{p}_T\cdot \textbf{q}_T} ({\textbf{p}_T\cdot \textbf{q}_T}-{\textbf{p}_T^2})\},\\ K^{\mathcal {V},d}_{2}= & {} -\frac{8f_1C_{Jd}}{3} ({\textbf{p}_T}-{\textbf{q}_T)^2}\\{} & {} -\frac{8f_2 C_{Jd}}{3 {\textbf{p}_T^2}}({\textbf{p}_T\cdot \textbf{q}_T}-{\textbf{p}_T^2}) ({\textbf{p}_T\cdot \textbf{q}_T}\\{} & {} -{\textbf{q}_T^2}) (-{\eta _1} M+{m_1}-{p_l}) \end{aligned}$$

where the factors $C_{J\mathcal {P}}$, $C_{J\mathcal {S}}$, $C_{Ja}$, $C_{Jb}$, $C_{Jc}$ and $C_{Jd}$ are introduced to include the two cases of total spin: $J=$1/2 or 3/2, and their values are presented in Table 4.

Now we integrate over $p_l$ on the right side of Eqs. (20) and (21) where four poles exist at $-\eta _1M-\omega _1+i\epsilon$, $-\eta _1M+\omega _1-i\epsilon$, $\eta _2M+\omega _2-i\epsilon$ and $\eta _2M-\omega _2+i\epsilon$. By choosing an appropriate contours we calculate the residuals at $p_l=-\eta _1M-\omega _1+i\epsilon$ and $p_l=\eta _2M-\omega _2+i\epsilon$. The coupled equations after performing contour integrations are obtained and collected in appendix (Eqs. (B1) and (B2)). One can carry out the azimuthal integration and reduce Eqs. (B1) and (B2) to two one-dimensional integral equations

$$\begin{aligned}{} & {} f_1(|\textbf{p}_T|)=\int {d|\textbf{q}_T|}[A_{11}(|\textbf{q}_T|,|\textbf{p}_T|) f_1(|\textbf{q}_T|)\nonumber \\{} & {} \quad +A_{12}(|\textbf{q}_T|,|\textbf{p}_T|)f_2(|\textbf{q}_T|)], \end{aligned}$$

(22)

$$\begin{aligned}{} & {} f_2(|\textbf{p}_T|)=\int {d|\textbf{q}_T|}[A_{21}(|\textbf{q}_T|,|\textbf{p}_T|) f_1(|\textbf{q}_T|)\nonumber \\{} & {} \quad +A_{22}(|\textbf{q}_T|,|\textbf{p}_T|)f_2(|\textbf{q}_T|)], \end{aligned}$$

(23)

where $A_{11}$, $A_{12}$, $A_{21}$ and $A_{22}$ are presented in Appendix (see Eqs. (B6), (B7), (B8) and (B9)).

3 Numerical results

In order to solve the B-S equation numerically some parameters are needed to be pre-set. The mass $m_{\Lambda _c}$, $m_{\Sigma _c}$, $m_{\Xi _c}$, $m_{\Xi '_c}$, $m_{D^*}$, $m_{\pi }$, $m_\sigma$,$m_\omega$, $m_\rho$ are taken from the particle databook [58]. We follow Ref. [54] to determine the parameters for the coupling constants of baryon-meson-baryon which are presented in Tables 5 and 6. The coupling constants among mesons are collected in Table 7 and Appendix A.

Table 6 Some parameter in coupling constants

Table 7 The coupling constants of ${\bar{D}}^* {\bar{D}}^*M$

With these parameters, including the corresponding spin factors and the isospin factors, the coupled equations for the B-S wavefunction (Eqs. (22) and (23)) are established. Since the coupled equations are complicated integral equations, we shall solve them numerically. The standard way is to discretize them, thus one is able to convert them into algebraic equations. Concretely, within a reasonable finite range (we set it from 0 to 2 GeV), we let $\mathbf |p_T|$ and $\mathbf |q_T|$ take n discrete values $Q_1$, $Q_2$,...$Q_n$ which distribute with equal gap from $Q_1$=0.001 GeV to $Q_n$=2 GeV. The gap between two adjacent values is $\Delta Q=1.999/(n-1)$ GeV (we set n=129 in our calculation). At this time the integral can be turned into summing the right sides of Eqs. (24) and (25),

$$\begin{aligned}{} & {} f_1(Q_i)=\sum _{j=1}^n \Delta Q [A_{11}(Q_j,Q_i) f_1(Q_j)\nonumber \\{} & {} \quad +A_{12}(Q_j,Q_i)f_2(Q_j)], \end{aligned}$$

(24)

$$\begin{aligned}{} & {} f_2(Q_i)=\sum _{j=1}^n \Delta Q [A_{21}(Q_j,Q_i) f_1(Q_j)\nonumber \\{} & {} \quad +A_{22}(Q_j,Q_i)f_2(Q_j)]. \end{aligned}$$

(25)

Since $Q_i$ can take the sequential values $Q_1$, $Q_2$,...$Q_n$, the total number of the algebraic equations from Eqs. (24) and (25) is 2n and they can be written as a matrix equation

$$\begin{aligned} \left( \begin{array}{c} f_1(Q_1) \\ ... \\ f_1(Q_{n})\\ f_2(Q_1)\\ ... \\ f_2(Q_{n}) \end{array}\right) =A(\Delta E,\Lambda )\left( \begin{array}{c} f_1(Q_1) \\ ... \\ f_1(Q_{n})\\ f_2(Q_1)\\ ... \\ f_2(Q_{n}) \end{array}\right) , \end{aligned}$$

where $A(\Delta E,\Lambda )$ is a $2n\times 2n$ matrix whose elements are the coefficients of $f_1(Q_{j})$ and $f_2(Q_{j})$ given in Eqs. (24) and (25).

As a matter of fact, it is a homogeneous linear equation group. As long as there exist non-trivial solutions, the necessary and sufficient condition is that the coefficient determinant should be zero. In our case, it is $|A(\Delta E,\Lambda )-I|=0$ where I is the unit matrix and $\Delta E=m_1+m_2-M$ is the binding energy. $\Delta E$ and $\Lambda$ are two variables in the determinant. When we set the value of $\Delta E$, by requiring $|A(\Delta E,\Lambda )-I|=0$, we obtain a corresponding $\Lambda$ if the equation group possesses solution. Generally $\Lambda$ should be close to 1 GeV. If the obtained $\Lambda$ is much beyond the value or does not exist, we would conclude that the resonance cannot exist. With this strategy, we investigate the molecular structure of $\Lambda _c$ and ${\bar{D}}^*$, $\Sigma _c$ and ${\bar{D}}^*$, $\Xi _c$ and ${\bar{D}}^*$ as well as that of $\Xi '_c$ and ${\bar{D}}^*$.

3.1 The numerical results on $\Lambda _c{\bar{D}}^*$ and $\Sigma _c{\bar{D}}^*$

Now we begin discussng the phenomenological consequences of the theoretical results. For $\Lambda _c$ and ${\bar{D}}^*$ system, the isospin of $\Lambda _c$ is 0 and it belongs to baryon anti-triplet of flavor ($\mathcal {B}_{{\bar{3}}}$), so only $\omega$ and $\sigma$ can be exchanged between $\Lambda _c$ and ${\bar{D}}^*$. We cannot find a solution for the B-S equation within a large range of $\Lambda$ when we set some different binding energies $\Delta E$, therefore we would conjecture that the total interaction is repulsive between $\Lambda _c$ and ${\bar{D}}^*$.

With the same procedure, we study a molecule composed of $\Sigma _c$ and ${\bar{D}}^*$. Since the isospin could be either $\frac{1}{2}$ or $\frac{3}{2}$ and the total spin could be either $\frac{1}{2}$ or $\frac{3}{2}$, there are four possible states whose $I(J^P)$ are $\frac{1}{2}(\frac{1}{2}^-)$, $\frac{1}{2}(\frac{3}{2}^-)$, $\frac{3}{2}(\frac{1}{2}^-)$ and $\frac{3}{2}(\frac{3}{2}^-)$. In this case $\pi$, $\eta$, $\sigma$, $\omega$ and $\rho$ exchanges between the two ingredients are allowed. For different binding energies the values of $\Lambda$ are presented in Table 8 where the symbol “–” means the value is larger than that for small $\Delta E$. We find for $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$ state when the binding energy is below 30 MeV the value of $\Lambda$ is close to 1, so a $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$ state should exist. The wavefunction for different binding energy are plotted in Fig. 2. However for $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$ state even the binding energy is 1 MeV, the value of $\Lambda$ is much larger than 1, the fact means the abstractive interaction between $\Sigma _c$ and ${\bar{D}}^*$ with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$ is too weak to form a bound state. For $I(J^P)=\frac{3}{2}(\frac{1}{2}^-)$ and $\frac{3}{2}(\frac{3}{2}^-)$ systems the B-S equations have no solution.

Table 8 The cutoff parameter $\Lambda$ and the corresponding binding energy $\Delta E$ for the bound state $\Sigma _c {\bar{D}}^*$ with $I=\frac{1}{2}$

We study the interactions coming from different meson exchange $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$ for $\Sigma _c{\bar{D}}^*$ state. When we ignore the interaction from $\pi$ in our calculation the value of $\Lambda$ will increase to about 1.339 GeV with $\Delta E=1$ MeV. That means the interaction from $\pi$ exchange is attractive in this case. There is the same situation for $\rho$ exchange, i.e. the interaction from $\rho$ exchange also is attractive. Since the isospin factor is opposite between $\rho$ exchange and $\omega$ exchange, but the interaction forms are same, the $\omega$ exchange contributes a repulsive interaction. For $\Sigma _c {\bar{D}}^*$ molecule with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$, the total interaction can be attractive due to a larger contribution from the $\rho$ and $\pi$ exchange.

Fig. 2

The unnormalized wave function $f_1(|\textbf{p}_T|)$ and $f_2(|\textbf{p}_T|)$ for $\Sigma _c{\bar{D}}^*$ system with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$

Apparently when $\Delta E$ is very small the obtained $\Lambda$ is close to 1, so $\Sigma _c$ and ${\bar{D}}^*$ should form a bound state with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$. At present the pentaquark $P_c(4440)$ has been experimentally observed in $\Lambda _b\rightarrow J/\psi pK$ channel, which peaks at the invariant mass spectrum of $J/\psi p$ and has the invariant mass of about 4440.3 MeV. Apparently its isospin is $\frac{1}{2}$, and the majority of authors [33,34,35,36,37,38,39] regarded this pentaquark as a bound state of $\Sigma _c$ and $\bar{D}^*$. We agree with it. In experiment there is another state $P_c(4457)$ in company with $P_c(4440)$. Some authors suggest that $P_c(4457)$ should be a bound state $\Sigma _c$ and $\bar{D}^*$ with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$. Our calculation indicates even for $\Delta E=1$ the value of $\Lambda$ is 1.927 GeV which deviates 1 GeV too much. The value of $\Lambda$ means the attractive interaction is very weak between two constituents so the system of $\Sigma _c\bar{D}^*$ with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$ should not a resonance unless there is a special mechanism to enhance the attractive interaction.

By our observation given above, for the state with $I=\frac{3}{2}$ the isospin factor is 1 for exchanging either $\omega$ or $\rho$, therefore the total interaction is repulsive, it means that $\Sigma _c$ and ${\bar{D}}^*$ cannot form a bound state with $I=\frac{3}{2}$.

3.2 The numerical results on $\Xi _c{\bar{D}}^*$ and $\Xi '_c{\bar{D}}^*$

For the $\Xi _c {\bar{D}}^*$ system, if the other effects are not included the corresponding $\Lambda$-values are presented in Table 9. One can find that even for a small binding energy the value of $\Lambda$ is a bit too large. It seems $\Xi _c$ and ${\bar{D}}^*$ only may form two very loose bound states. In our calculation the two states $I(J^P)=0(\frac{1}{2}^-)$ and $0(\frac{3}{2}^-)$ are also degenerated which is consistent with those in Ref. [30]. Since only $\sigma$, $\rho$ and $\omega$ can be exchanged, the interactions are different only from the tensor item in the $\mathcal {L}_{{\bar{\mathcal {D}}^*\bar{\mathcal {D}}^*\mathcal {V}}}$ (see the values of $C_{\frac{1}{2}b}$ and $C_{\frac{3}{2}b}$ in Table 4), which indicates that the tensor coupling has little contribution to the interaction between $\Xi _c$ and ${\bar{D}}^*$.

For the $\Xi '_c {\bar{D}}^*$ system in terms of the original value of $\Lambda$ in Table 10 one can find that the $I(J^P)=0(\frac{1}{2}^-)$ system can be a bound state but $I(J^P)=0(\frac{3}{2}^-)$ system is not.

In Ref. [30] with the coupled channel effect being taken into account for their initial results, the values of $\Lambda$ apparently changed and the degeneration between the two states $I(J^P)=0(\frac{1}{2}^-)$ and $0(\frac{3}{2}^-)$ disappeared. In this article we employ another mechanism to achieve the same effect. We consider the effect of the mixing between $\Xi _c$ and $\Xi '_c$ which has been discussed in some recent papers [59,60,61,62]. Since the flavor symmetry of SU(3) is broken the physical states $\Xi _c$ and $\Xi '_c$ should be the mixing of $\Xi _c^{{\bar{3}}}$ and $\Xi _c^{6}$ where the superscripts ${\bar{3}}$ and 6 correspond to $SU(3)_F$ anti-triple and sextet. Under the picture of mixing $\Xi _c^{{\bar{3}}}$ and $\Xi _c^{6}$ should replace the $\Xi _c$ and $\Xi '_c$ in the representations $\mathcal {B}_{{\bar{3}}}$ and $\mathcal {B}_6$ in Appendix A. By introducing a mixing angle $\theta$ the physical states $\Xi _c$ and $\Xi '_c$ can be expressed by $\Xi _c^{{\bar{3}}}$ and $\Xi _c^{6}$ i.e. $\Xi _c=\textrm{cos}\theta \,\Xi _c^{{\bar{3}}}+\textrm{sin}\theta \,\Xi _c^{6}$ and $\Xi '_c=-\textrm{sin}\theta \,\Xi _c^{{\bar{3}}}+\textrm{cos}\theta \,\Xi _c^{6}$. In Ref. [59] we fix the value of $\theta$ to be $16.27^\circ$ using the data of $\Gamma (\Xi _{cc}\rightarrow \Xi _c)/\Gamma (\Xi _{cc}\rightarrow \Xi '_c)$. The results including the mixing effect are presented in Tables 11 and 12. One can find

1. for the $\Xi _c{\bar{D}}^*$ system the values of $\Lambda$ drop but those for $\Xi '_c{\bar{D}}^*$ system raise;

2. for the $\Xi _c{\bar{D}}^*$ system the degeneration of the two states $I(J^P)=0(\frac{1}{2}^-)$ and $0(\frac{3}{2}^-)$ disappear;

3. $\Xi _c{\bar{D}}^*$ should be form two states $I(J^P)=0(\frac{1}{2}^-)$ and $0(\frac{3}{2}^-)$ but $\Xi '_c{\bar{D}}^*$ only can form a $I(J^P)=0(\frac{1}{2}^-)$ bound state.

Table 9 The cutoff parameter $\Lambda$ and the corresponding binding energy $\Delta E$ for the bound state $\Xi _c {\bar{D}}^*$ with $I=0$

Table 10 The cutoff parameter $\Lambda$ and the corresponding binding energy $\Delta E$ for the bound state $\Xi '_c {\bar{D}}^*$ with $I=0$

Table 11 The cutoff parameter $\Lambda$ and the corresponding binding energy $\Delta E$ for the bound state $\Xi _c {\bar{D}}^*$ with $I=0$ when the effect of the mixing between $\Xi _c$ and $\Xi '_c$ is included

Table 12 The cutoff parameter $\Lambda$ and the corresponding binding energy $\Delta E$ for the bound state $\Xi '_c {\bar{D}}^*$ with $I=0$ when the effect of the mixing between $\Xi _c$ and $\Xi '_c$ is included

At present $P_{cs}(4459)$ was measured in experiment which is close to the threshold of $\Xi _c{\bar{D}}^*$, so it seems $P_{cs}(4459)$ is one bound state of $\Xi _c{\bar{D}}^*$ with $I=0$. If the structure includes two states: $P_{cs}(4455)$ and $P_{cs}(4468)$ they are just corresponding to two states of $\Xi _c{\bar{D}}^*$ with $I(J^P)=0(\frac{1}{2}^-)$ and $0(\frac{3}{2}^-)$, it seems the suggestion in Refs. [30, 39] is reasonable. For $I=1$ systems there are no solutions can be obtained, so these states cannot exist.

4 Conclusion and discussion

With more and more exotic states (tetraquarks and pentaquarks) being experimentally discovered, the new hadron “zoo” gradually emerges, do we face the same situation Gell-Mann did half century ago? Even though the whole picture is still vague, the shape might be encouraging that the time of establishing a unique theory on the exotic states which would be an extension of the Gell-Manns SU(2) quark model, is coming. Nowadays, the task of high energy physicists is to carefully study every newly discovered exotic state, namely find out its inner structure and production/decay characteristics. The procedure will definitely enrich our understanding. Our present work is just along the route forward.

Within the B-S framework we explore the possible bound states which are composed of a baryon ($\Lambda _c$, $\Sigma _c$, $\Xi _c$ or $\Xi '_c$) and ${\bar{D}}^*$. In our work the orbital angular momentum between two constituents is 0 (S-wave) so the total spin and parity is $\frac{1}{2}^-$ or $\frac{3}{2}^-$. By solving the corresponding B-S equations of $\Lambda _c {\bar{D}}^*$, $\Sigma _c {\bar{D}}^*$, $\Xi _c {\bar{D}}^*$ and $\Xi '_c {\bar{D}}^*$ we get possible information of bound states. If the B-S equation for a supposed molecular structure has a solution and the parameters are reasonable, we would conclude that the concerned pentaquark could exist in the nature, oppositely, no-solution or the unreasonable parameter(s) means the supposed pentaquark cannot appear as a resonance or the molecular state is not an appropriate postulate. The solution can apply as a criterion for the structures of the pentaquark states which have already been or will be experimentally measured. In this work, the two constituents interact by exchanging some light mesons. For the $\Lambda _c{\bar{D}}^*$ system only $\omega$ and $\sigma$ are the exchanged mediate mesons, while for the $\Sigma _c{\bar{D}}^*$ system $\pi$, $\eta$ $\sigma$, $\rho$ and $\omega$ contribute. Similarly, for $\Xi _c {\bar{D}}^*$ system only $\rho$, $\omega$ and $\sigma$ can be exchanged, however for $\Xi '_c {\bar{D}}^*$ system $\pi$, $\eta$, $\sigma$, $\rho$ and $\omega$ can be mediators. The chiral interaction determines if those molecular states can be formed.

The key strategy we adopt in this work is that since two constituents are heavy hadrons, the B-S wave function contains two scalar functions $f_1(|\mathbf {p_T}|)$ and $f_2(|\mathbf {p_T}|)$ which should be solved numerically. After some manipulations the B-S equation turn into two coupled integral equations. Discretizing the two coupled integral equations, we simplify them into two algebraic equations about $f_1(Q_i)$ and $f_2(Q_i)$ $(i=1,2,...,n)$. As $|\mathbf {p_T}|$ can take n discrete values the two coupled equations are converted into 2n algebraic equations which constitute a homogeneous linear equation group and can be easily solved numerically in terms of available softwares. When all known parameters are input there still is one undetermined parameter $\Lambda$. Our strategy is inputting binding energies within a range and then fixing $\Lambda$ by solving the matrix equation. If $\Lambda$ is located in a reasonable range one can expect the bound state to exist. We find the B-S equation of the state $\Lambda _c {\bar{D}}^*$ system has no solution for $\Lambda$ when the binding energy takes experimentally allowed values. For the $\Sigma _c {\bar{D}}^*$ system there are four states with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$, $\frac{1}{2}(\frac{3}{2}^-)$, $\frac{3}{2}(\frac{1}{2}^-)$ and $\frac{3}{2}(\frac{3}{2}^-)$. We find the equation for $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$ has a solution for $\Lambda$ falling into the reasonable range. The result supports that $P_c(4440)$ maybe is a molecular state of $\Sigma _c {\bar{D}}^*$ with $I(J^P)=\frac{1}{2}(\frac{1}{2}^-)$. Some authors suggest that $P_c(4457)$ should be a bound state $\Sigma _c$ and $\bar{D}^*$ with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$. Our calculation indicates even for $\Delta E=1$ the value of $\Lambda$ is 1.927 GeV which deviates 1 GeV too much so the systme of $\Sigma _c\bar{D}^*$ with $I(J^P)=\frac{1}{2}(\frac{3}{2}^-)$ should not a resonant.

We also study the possible $\Xi _c\bar{D}^*$ and $\Xi '_c\bar{D}^*$ bound states. When no other effect is included the system $\Xi '_c\bar{D}^*$ with $I(J^P)=0(\frac{1}{2}^-)$ can be a typical bound state, $\Xi _c\bar{D}^*$ with $I(J^P)=0(\frac{1}{2}^-)$ and $0(\frac{3}{2}^-)$ may be two very weak bound states at most but $\Xi '_c\bar{D}^*$ with $I(J^P)=0(\frac{3}{2}^-)$ shouldn’t exist. However after the effect of the mixing of $\Xi _c$ and $\Xi '_c$ is included the situation changed apparently. $\Xi _c\bar{D}^*$ with $I(J^P)=0(\frac{1}{2}^-)$ and $\Xi '_c\bar{D}^*$ with $I(J^P)=0(\frac{1}{2}^-)$ may be two typical bound states but $\Xi _c\bar{D}^*$ with $I(J^P)=0(\frac{3}{2}^-)$ may be a weak bound state.

It is noted, we ignore the coupled channel effects in the Bethe–Salpeter. If the coupled channel interaction is taken into account, just as the authors of Refs. [30, 63] did, the value of $\Lambda$ may change a little bit.

Within the B-S framework, we investigate the bound state of a charmed baryon and ${\bar{D}}^*$. We pay a special attention to the systems $\Lambda _c {\bar{D}}^*$, $\Sigma _c {\bar{D}}^*$, $\Xi _c {\bar{D}}^*$ and $\Xi '_c {\bar{D}}^*$ because experimentally well measured $P_c(4440)$, $P_c(4457)$ and $P_{cs}(4459)$ may be related to them. From that study, we have accumulated valuable knowledge on probable molecular structure of pentaquarks which can be applied to the future research. Definitely, the discovery of pentaquarks opens a window for understanding the quark model established by Gell-Mann and several other predecessors. Deeper study on their structures and concerned effective interaction which binds the ingredients to form a molecule would greatly enrich our theoretical aspect.

Appendices

Appendix A: The effective interactions

The effective interactions $\mathcal {BBM}$ can be found in [64,65,66]

$$\begin{aligned} \mathcal {L}_{\mathcal {B}_{{\bar{3}}}\mathcal {B}_{{\bar{3}}}\sigma }= & {} l_\mathcal {B}\langle \bar{\mathcal {B}}_{{\bar{3}}}\sigma \mathcal {B}_{{\bar{3}}}\rangle \end{aligned}$$

(A1)

$$\begin{aligned} \mathcal {L}_{\mathcal {B}_{{\bar{3}}}\mathcal {B}_{{\bar{3}}}\mathcal {V}}= & {} \frac{\beta _{\mathcal {B}}g_{\mathcal {V}}}{\sqrt{2}}\langle \bar{\mathcal {B}}_{{\bar{3}}}v \cdot \mathcal {V}\mathcal {B}_{{\bar{3}}}\rangle ,\end{aligned}$$

(A2)

$$\begin{aligned} \mathcal {L}_{\mathcal {B}_6\mathcal {B}_6\sigma }= & {} -l_\mathcal {S}\langle \bar{\mathcal {B}}_6\sigma \mathcal {B}_6\rangle ,\end{aligned}$$

(A3)

$$\begin{aligned} \mathcal {L}_{\mathcal {B}_6\mathcal {B}_6\mathcal {P}}= & {} i\frac{g_1}{2f_\pi }\varepsilon ^{\mu \nu \alpha \beta }v_\beta l_\mathcal {S} \langle \bar{\mathcal {B}}_6\gamma _\mu \gamma _\alpha \partial _\nu \mathcal {P}\mathcal {B}_6\rangle ,\end{aligned}$$

(A4)

$$\begin{aligned} \mathcal {L}_{\mathcal {B}_6\mathcal {B}_6\mathcal {V}}= & {} -\frac{\beta _{\mathcal {S}}g_{\mathcal {V}}}{\sqrt{2}}\langle \bar{\mathcal {B}}_6v \cdot \mathcal {V}\mathcal {B}_6\rangle -i\frac{\lambda _{\mathcal {S}}g_{\mathcal {V}}}{3\sqrt{2}}\nonumber \\{} & {} \quad \times \langle \bar{\mathcal {B}}_6\gamma _\mu \gamma _\nu (\partial ^\mu \mathcal {V}^\nu -\partial ^\nu \mathcal {V}^\mu )\mathcal {B}_6\rangle \end{aligned}$$

(A5)

where $\mathcal {B}_{\bar{{\bar{3}}}}=\left( \begin{array}{ccc} 0&{}\Lambda _c^+ &{}\Xi _c^+ \\ -\Lambda _c^+ &{} 0&{}\Xi _c^0\\ - \Xi _c^+ &{} \Xi _c^0 &{}0 \end{array}\right)$, $\mathcal {B}_6=\left( \begin{array}{ccc} \Sigma _{c}^{+}&{} \frac{\Sigma _{c}^{+}}{\sqrt{2}}&{}\frac{\Xi _c^{'+}}{\sqrt{2}} \\ \frac{\Sigma _{c}^{+}}{\sqrt{2}}&{} \Sigma _{c}^{0}&{}\frac{\Xi _c^{'0}}{\sqrt{2}} \\ \frac{\Xi _c^{'+}}{\sqrt{2}} &{} \frac{\Xi _c^{'0}}{\sqrt{2}} &{}\Omega _c^0 \end{array}\right)$, $\mathcal {P}=\left( \begin{array}{ccc} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{}\pi ^+ &{}K^+ \\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}&{}K^0\\ K^-&{} \bar{K^0} &{} -\sqrt{\frac{2}{3}}\eta \end{array}\right)$ and $\mathcal {V}=\left( \begin{array}{ccc} \frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}} &{}\rho ^+ &{}K^{*+} \\ \rho ^- &{} -\frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}}&{}K^{*0}\\ K^{*-}&{} \bar{K^{*0}} &{} \phi \end{array}\right)$, respectively.

The effective interactions ${\bar{D}}{\bar{D}} \mathcal {M}$ can be found in [55,56,57]

$$\begin{aligned} \mathcal {L}_{_{{\bar{D}}^*{\bar{D}}^*\sigma }}{} & {} =g_{_{{\bar{D}}^*{\bar{D}}^*\sigma }}({\bar{D}}^{*\mu }_{b} {\bar{D}}^{*\dag }_{a\mu }\sigma ),\end{aligned}$$

(A6)

$$\begin{aligned} \mathcal {L}_{_{{\bar{D}}^*{\bar{D}}^*\mathcal {P}}}{} & {} =g_{_{{\bar{D}}^*{\bar{D}}^*\mathcal {P}}}({\bar{D}}^{*\mu }_{b}{\mathop {\partial }\limits ^{\leftrightarrow }}^{\beta } {\bar{D}}^{*\alpha \dag }_{a})(\partial ^\nu \mathcal {P})_{ab}\varepsilon _{\nu \mu \alpha \beta },\end{aligned}$$

(A7)

$$\begin{aligned} \mathcal {L}_{_{{\bar{D}}^*{\bar{D}}^*\mathcal {V}}}{} & {} =ig_{_{{\bar{D}}^*{\bar{D}}^*\mathcal {V}}}({\bar{D}}^{*\nu }_{b}{\mathop {\partial }\limits ^{\leftrightarrow }}_{\mu } {\bar{D}}^{*\dag }_{a\nu })( \mathcal {V})_{ab}^\mu \nonumber \\{} & {} \quad +ig'_{_{{\bar{D}}^*{\bar{D}}^*\mathcal {V}}}{\bar{D}}^{*\mu }_{b} {\bar{D}}^{*\nu \dag }_{a}(\partial _\mu \mathcal {V}_\nu -\partial _\nu \mathcal {V}_\mu )_{ab} \end{aligned}$$

(A8)

where a and b represent index of SU(3) flavor group for three light quarks. In the flavor SU(3) symmetry and heavy quark limit, the above coupling constants are given by$g_{_{D^*D^*\sigma }}=2g_\sigma M_{D^*},$ $g_{_{D^*D^*P}}=\frac{2g}{f_\pi },$ $g_{_{{\bar{D}}^*{\bar{D}}^*V}}=\beta g_V/\sqrt{2},\,\, g'_{_{{\bar{D}}^*{\bar{D}}^*V}}=2\sqrt{2}\lambda g_V M_{D^*}$ with $g_\sigma =-0.76$ [67], $f_\pi =132$ MeV [56], $\beta =0.9$, $g_V=5.9$ [68] and $\lambda =0.56$ GeV$^{-1}$ [37].

Appendix B: The coupled equation of $f_1(|\textbf{p}_T|)$ and $f_2(|\textbf{p}_T|)$ after integrating over $p_l$ and some formulas for azimuthal integration

The coupled equation of $f_1(|\textbf{p}_T|)$ and $f_2(|\textbf{p}_T|)$ after integrating over $p_l$ are

$$\begin{aligned} f_1(|\textbf{p}_T|)= & {} \int \frac{d^3\textbf{q}_T}{(2\pi )^3}\frac{1}{P_{\mathcal {R}1}}\Bigg \{\Bigg [\sum _\mathcal {P}\frac{C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}F^2(k,m_\mathcal {P})K^\mathcal {P}_{1}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {P}^2} +\frac{C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}F^2(k,m_\mathcal {S})K^\mathcal {S}_{1}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {S}^2}\nonumber \\{} & {} +\sum _\mathcal {V} \frac{-C_{{I\mathcal {V}}}F^2(k,m_\mathcal {V})(g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},a}_{1}+g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},b}_{1} +g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},c}_{1}+g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},d}_{1})}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {V}^2} \Bigg ]_{p_l=-\eta _1M-\omega _1}\Bigg \}\nonumber \\{} & {} +\int \frac{d^3\textbf{q}_T}{(2\pi )^3}\frac{1}{P_{\mathcal {R}2}}\Bigg \{\Bigg [\sum _\mathcal {P}\frac{C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}F^2(k,m_\mathcal {P})K^\mathcal {P}_{1}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {P}^2}+\frac{C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}F^2(k,m_\mathcal {S})K^\mathcal {S}_{1}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {S}^2}\nonumber \\{} & {} -\sum _\mathcal {V}\frac{C_{{I\mathcal {V}}}F^2(k,m_\mathcal {V})(g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},a}_{1}+g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},b}_{1} +g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},c}_{1}+g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},d}_{1})}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {V}^2}\Bigg ]_{p_l=\eta _2M-\omega _2}\Bigg \}. \end{aligned}$$

(B1)

$$\begin{aligned} f_2(|\textbf{p}_T|)= & {} \int \frac{d^3\textbf{q}_T}{(2\pi )^3}\frac{1}{P_{\mathcal {R}1}}\Bigg \{ \Bigg [\sum _\mathcal {P}\frac{C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}F^2(k,m_\mathcal {P})K^\mathcal {P}_{2}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {P}^2}+\frac{C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}F^2(k,m_\mathcal {S})K^\mathcal {S}_{2}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {S}^2}\nonumber \\{} & {} +\sum _\mathcal {V} \frac{-C_{{I\mathcal {V}}}F^2(k,m_\mathcal {V})(g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},a}_{2}+g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},b}_{2} +g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},c}_{2}+g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},d}_{2})}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {V}^2} \Bigg ]_{p_l=-\eta _1M-\omega _1}\Bigg \}\nonumber \\{} & {} +\int \frac{d^3\textbf{q}_T}{(2\pi )^3}\frac{1}{P_{\mathcal {R}2}}\Bigg \{\Bigg [\sum _\mathcal {P}\frac{C_{{I\mathcal {P}}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}F^2(k,m_\mathcal {P})K^\mathcal {P}_{2}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {P}^2}+\frac{C_{{I\mathcal {S}}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}F^2(k,m_\mathcal {S})K^\mathcal {S}_{2}}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {S}^2}\nonumber \\{} & {} -\sum _\mathcal {V} \frac{C_{{I\mathcal {V}}}F^2(k,m_\mathcal {V})(g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},a}_{2}+g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},b}_{2} +g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}K^{\mathcal {V},c}_{2}+g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}K^{\mathcal {V},d}_{2})}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {V}^2}\Bigg ]_{p_l=\eta _2M-\omega _2}\Bigg \}, \end{aligned}$$

(B2)

with $P_{\mathcal {R}1}=2\omega _1(M+\omega _1+\omega _2)(M+\omega _1-\omega _2)$ and $P_{\mathcal {R}2}=2\omega _2(M+\omega _1-\omega _2)(M-\omega _1-\omega _2)$.

Since $d^3\textbf{q}_T=\textbf{q}_T^2\textrm{sin}(\theta )d|\textbf{q}_T|d\theta d\phi$ and $\textbf{p}_T\cdot \textbf{q}_T=|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )$ one can carry out the azimuthal integration for Eqs. (B1) and (B2) analytically. Some useful integrations are defined as follow

$$\begin{aligned} J_0{} & {} \equiv \int _0^\pi \textrm{sin}(\theta )d\theta \frac{1}{-(\textbf{p}_T-\textbf{q}_T)^2 -m_\mathcal {M}^2}\left[ \frac{\Lambda ^2-m^2_\mathcal {M}}{\Lambda ^2-{(\textbf{p}_T-\textbf{q}_T)^2}}\right] ^2\nonumber \\{} & {} =\int _0^\pi \frac{\textrm{sin}(\theta )d\theta }{-[\textbf{p}_T^2+\textbf{q}_T^2-2|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )]-m_\mathcal {M}^2}\nonumber \\{} & {} \quad \times \left\{ \frac{\Lambda ^2-m^2_\mathcal {M}}{\Lambda ^2-{[\textbf{p}_T^2+\textbf{q}_T^2-2|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )]}}\right\} ^2\nonumber \\{} & {} =-\frac{2(m_\mathcal {M}^2-\Lambda ^2)}{[(|\textbf{p}_T|-|\textbf{q}_T|)^2+\Lambda ^2][(|\textbf{p}_T| +|\textbf{q}_T|)^2 +\Lambda ^2]}\nonumber \\{} & {} \quad +\frac{1}{2|\textbf{p}_T||\textbf{q}_T|}\left\{ \textrm{Ln}\left[ \frac{(|\textbf{p}_T|+|\textbf{q}_T|)^2 +\Lambda ^2}{(|\textbf{p}_T|-|\textbf{q}_T|)^2+\Lambda ^2}\right] \right. \nonumber \\{} & {} \quad \left. -\textrm{Ln}\left[ \frac{(|\textbf{p}_T|+ |\textbf{q}_T|)^2+m_\mathcal {M}^2}{(|\textbf{p}_T|-|\textbf{q}_T|)^2+m_\mathcal {M}^2}\right] \right\} , \end{aligned}$$

(B3)

$$\begin{aligned} J_1{} & {} \equiv \int _0^\pi \textrm{sin}(\theta )d\theta \frac{\textbf{p}_T\cdot \textbf{q}_T}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {M}^2} \left[ \frac{\Lambda ^2-m^2_\mathcal {M}}{\Lambda ^2-{(\textbf{p}_T-\textbf{q}_T)^2}}\right] ^2\nonumber \\{} & {} =\int _0^\pi \frac{|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )\textrm{sin}(\theta )d\theta }{-[\textbf{p}_T^2+\textbf{q}_T^2-2|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )]-m_\mathcal {M}^2}\nonumber \\{} & {} \quad \times \left\{ \frac{\Lambda ^2-m^2_\mathcal {M}}{\Lambda ^2-{[\textbf{p}_T^2 +\textbf{q}_T^2-2|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )]}}\right\} ^2\nonumber \\{} & {} =-\frac{(m_\mathcal {M}^2-\Lambda ^2)(|\textbf{p}_T|^2+|\textbf{q}_T|^2 +\Lambda ^2)}{[(|\textbf{p}_T|-|\textbf{q}_T|)^2+\Lambda ^2][(|\textbf{p}_T|+|\textbf{q}_T|)^2 +\Lambda ^2]}\nonumber \\{} & {} \quad +\frac{(|\textbf{p}_T|^2+|\textbf{q}_T|^2 +m_\mathcal {M}^2)}{4|\textbf{p}_T||\textbf{q}_T|}\left\{ Ln\left[ \frac{(|\textbf{p}_T|+|\textbf{q}_T|)^2 +\Lambda ^2}{(|\textbf{p}_T|-|\textbf{q}_T|)^2+\Lambda ^2}\right] \right. \nonumber \\{} & {} \quad \left. -Ln\left[ \frac{(|\textbf{p}_T|+ |\textbf{q}_T|)^2+m_\mathcal {M}^2}{(|\textbf{p}_T|-|\textbf{q}_T|)^2+m_\mathcal {M}^2}\right] \right\} , \end{aligned}$$

(B4)

$$\begin{aligned} J_2{} & {} \equiv \int _0^\pi \textrm{sin}(\theta )d\theta \frac{(\textbf{p}_T\cdot \textbf{q}_T)^2}{-(\textbf{p}_T-\textbf{q}_T)^2-m_\mathcal {M}^2}\left[ \frac{\Lambda ^2-m^2_\mathcal {M}}{\Lambda ^2-{(\textbf{p}_T-\textbf{q}_T)^2}}\right] ^2\nonumber \\{} & {} =\int _0^\pi \frac{|\textbf{p}_T|^2|\textbf{q}_T|^2\textrm{cos}^2(\theta )\textrm{sin}(\theta )d\theta }{-[\textbf{p}_T^2+\textbf{q}_T^2-2|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )]-m_\mathcal {M}^2}\nonumber \\{} & {} \quad \times \left\{ \frac{\Lambda ^2-m^2_\mathcal {M}}{\Lambda ^2-{[\textbf{p}_T^2 +\textbf{q}_T^2-2|\textbf{p}_T||\textbf{q}_T|\textrm{cos}(\theta )]}}\right\} ^2\nonumber \\{} & {} =-\frac{(m_\mathcal {M}^2-\Lambda ^2)(|\textbf{p}_T|^2+|\textbf{q}_T|^2 +\Lambda ^2)^2}{2[(|\textbf{p}_T|-|\textbf{q}_T|)^2+\Lambda ^2][(|\textbf{p}_T|+|\textbf{q}_T|)^2 +\Lambda ^2]}\nonumber \\{} & {} \quad +\frac{1}{8|\textbf{p}_T||\textbf{q}_T|}\Bigg \{(|\textbf{p}_T|^2+|\textbf{q}_T|^2 +2m_\mathcal {M}^2-\Lambda ^2)\nonumber \\{} & {} \quad \times (|\textbf{p}_T|^2+|\textbf{q}_T|^2 +\Lambda ^2)\textrm{Ln}\Bigg [\frac{(|\textbf{p}_T|+|\textbf{q}_T|)^2+\Lambda ^2}{(|\textbf{p}_T|-|\textbf{q}_T|)^2+\Lambda ^2}\Bigg ]\nonumber \\{} & {} \quad -(|\textbf{p}_T|^2+|\textbf{q}_T|^2 +m_\mathcal {M}^2)^2\textrm{Ln}\Bigg [\frac{(|\textbf{p}_T|+ |\textbf{q}_T|)^2+m_\mathcal {M}^2}{(|\textbf{p}_T|-|\textbf{q}_T|)^2+m_\mathcal {M}^2}\Bigg ]\Bigg \}.\nonumber \\ \end{aligned}$$

(B5)

The detail expressions of $A_{11}(\mathbf {p_T},\mathbf {q_T})$, $A_{12}(\mathbf {p_T},\mathbf {q_T})$, $A_{21}(\mathbf {p_T},$$\mathbf {q_T})$ and $A_{22}(\mathbf {p_T},\mathbf {q_T})$ are

$$\begin{aligned}{} & {} A_{11}(\mathbf {p_T},\mathbf {q_T})=\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}1}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}A_{11}^{\mathcal {P}}\nonumber \\{} & {} \quad +C_{{I\mathcal {S}}}C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{11}^{\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{11}^{\mathcal {V},a}+C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{11}^{\mathcal {V},b}\nonumber \\{} & {} \quad +C_{Jc}g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{11}^{\mathcal {V},c}+C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{11}^{\mathcal {V},d})\Bigg ]\nonumber \\{} & {} \quad +\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}2}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}A_{11}^{'\mathcal {P}} \nonumber \\{} & {} \quad + C_{{I\mathcal {S}}}C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{11}^{'\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{11}^{'\mathcal {V},a}\nonumber \\{} & {} \quad +C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{11}^{'\mathcal {V},b}+C_{Jc}g'_{_{1\mathcal {V}}} g_{_{2\mathcal {V}}}A_{11}^{'\mathcal {V},c}\nonumber \\{} & {} \quad +C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{11}^{'\mathcal {V},d})\Bigg ], \end{aligned}$$

(B6)

$$\begin{aligned}{} & {} A_{12}(\mathbf {p_T},\mathbf {q_T})=\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}1}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}A_{12}^{\mathcal {P}}\nonumber \\{} & {} \quad +C_{{I\mathcal {S}}}C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{12}^{\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{12}^{\mathcal {V},a}+C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{12}^{\mathcal {V},b}\nonumber \\{} & {} \quad +C_{Jc}g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{12}^{\mathcal {V},c}+C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{12}^{\mathcal {V},d})\Bigg ]\nonumber \\{} & {} \quad +\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}2}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}A_{12}^{'\mathcal {P}} \nonumber \\{} & {} \quad +C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{12}^{'\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{12}^{'\mathcal {V},a}+C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{12}^{'\mathcal {V},b}\nonumber \\{} & {} \quad +C_{Jc}g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{12}^{'\mathcal {V},c}+C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{12}^{'\mathcal {V},d})\Bigg ], \end{aligned}$$

(B7)

$$\begin{aligned}{} & {} A_{21}(\mathbf {p_T},\mathbf {q_T})=\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}1}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}}A_{21}^{\mathcal {P}}\nonumber \\{} & {} \quad +C_{{I\mathcal {S}}}C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{21}^{\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{21}^{\mathcal {V},a} +C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{21}^{\mathcal {V},b}\nonumber \\{} & {} \quad +C_{Jc}g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{21}^{\mathcal {V},c} +C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{21}^{\mathcal {V},d})\Bigg ]\nonumber \\{} & {} \quad +\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}2}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}} g_{_{2\mathcal {P}}}A_{21}^{'\mathcal {P}} \nonumber \\{} & {} \quad +C_{{I\mathcal {S}}}C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{21}^{'\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{21}^{'\mathcal {V},a} +C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{21}^{'\mathcal {V},b}\nonumber \\{} & {} \quad +C_{Jc}g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{21}^{'\mathcal {V},c} +C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{21}^{'\mathcal {V},d})\Bigg ], \end{aligned}$$

(B8)

$$\begin{aligned}{} & {} A_{22}(\mathbf {p_T},\mathbf {q_T})=\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}1}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}} A_{22}^{\mathcal {P}}\nonumber \\{} & {} \quad +C_{{I\mathcal {S}}}C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{22}^{\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{22}^{\mathcal {V},a} +C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{22}^{\mathcal {V},b}\nonumber \\{} & {} \quad +C_{Jc}g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{22}^{\mathcal {V},c} +C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{22}^{\mathcal {V},d})\Bigg ]\nonumber \\{} & {} \quad +\frac{\textbf{q}_T^2}{(2\pi )^2}\frac{1}{P_{\mathcal {R}2}}\Bigg [\sum _\mathcal {P} C_{{I\mathcal {P}}}C_{J\mathcal {P}}g_{_{1\mathcal {P}}}g_{_{2\mathcal {P}}} A_{22}^{'\mathcal {P}} \nonumber \\{} & {} \quad +C_{{I\mathcal {S}}}C_{J\mathcal {S}}g_{_{1\mathcal {S}}}g_{_{2\mathcal {S}}}A_{22}^{'\mathcal {S}}\nonumber \\{} & {} \quad -\sum _\mathcal {V} C_{{I\mathcal {V}}}(C_{Ja}g_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{22}^{'\mathcal {V},a} +C_{Jb}g_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{22}^{'\mathcal {V},b}\nonumber \\{} & {} \quad +C_{Jc}g'_{_{1\mathcal {V}}}g_{_{2\mathcal {V}}}A_{22}^{'\mathcal {V},c} +C_{Jd}g'_{_{1\mathcal {V}}}g'_{_{2\mathcal {V}}}A_{22}^{'\mathcal {V},d})\Bigg ]. \end{aligned}$$

(B9)

with

$$\begin{aligned} A_{11}^{\mathcal {S}}= & {} (m_1-\omega _1)J_0,\nonumber \\ A_{11}^{'\mathcal {S}}= & {} (M+m_1-\omega _2)J_0,\nonumber \\ A_{11}^{\mathcal {P}}= & {} \frac{16}{3}J_0 (M+{\omega _1}) \nonumber \\{} & {} \times \left\{ {\textbf{p}_T}^2[{\omega _1} (m_1-{\omega _1}) +{\textbf{q}_T}^2]+{\textbf{q}_T}^2\omega _1 (m_1-{\omega _1})\right\} \nonumber \\{} & {} +\frac{32}{3}J_1\omega _1 (M+{\omega _1}) ({\omega _1}-m_1)-\frac{16}{3}J_2 (M+{\omega _1}), \nonumber \\ A_{11}^{'\mathcal {P}}= & {} \frac{16}{3}J_0\omega _2 \left\{ -[(M-\omega _2)^2+(M-\omega _2) m_1] ({\textbf{p}_T}^2+ {\textbf{q}_T}^2)\right. \nonumber \\{} & {} \left. +{\textbf{p}_T}^2 {\textbf{q}_T}^2\right\} \nonumber \\{} & {} +\frac{32}{3}J_1\omega _2 [ M^2+ M (m_1-\omega _2)+2\omega _2 ({\omega _2}-m_1)]\nonumber \\{} & {} -\frac{16}{3}J_2\omega _2,\nonumber \\ A_{11}^{\mathcal {V},a}= & {} -J_0 (m_1-{\omega _1}) [-4 {m_\mathcal {V}}^2\omega _1 (M+{\omega _1}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2{\textbf{q}_T}^2+({\textbf{p}_T}^2-{\textbf{q}_T}^2)^2]/{{m_\mathcal {V}}^2}\nonumber \\{} & {} -2J_1 (m_1-{\omega _1}),\nonumber \\ A_{11}^{'\mathcal {V},a}= & {} -J_0 (M+m_1-{\omega _2}) [4 {m_\mathcal {V}}^2\omega _2 (M-{\omega _2}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2 {\textbf{q}_T}^2+({\textbf{p}_T}^2-{\textbf{q}_T}^2)^2]/{{m_\mathcal {V}}^2}\nonumber \\{} & {} -2J_1 (M+m_1-{\omega _2}), \nonumber \\ A_{11}^{\mathcal {V},b}= & {} A_{11}^{'\mathcal {V},b}=0,\nonumber \\ A_{11}^{\mathcal {V},c}= & {} 4J_0 {\textbf{p}_T}^2 (M+{\omega _1})-4J_1 (M+{\omega _1}),\nonumber \\ A_{11}^{'\mathcal {V},c}= & {} 4J_0 {\textbf{p}_T}^2\omega _2-4J_1\omega _2,\nonumber \\ A_{11}^{\mathcal {V},d}= & {} \frac{8}{3}J_0 (m_1-{\omega _1}) (-{\textbf{p}_T}^2 -{\textbf{q}_T}^2)\nonumber \\{} & {} +\frac{16}{3}J_1 (m_1-{\omega _1}), \nonumber \\ A_{11}^{'\mathcal {V},d}= & {} \frac{8}{3}J_0 (-{\textbf{p}_T}^2-{\textbf{q}_T}^2) (M+m_1-{\omega _2})\nonumber \\{} & {} +\frac{16}{3}J_1 (M+m_1-{\omega _2}), \end{aligned}$$

(B10)

$$\begin{aligned} A_{12}^{\mathcal {S}}= & {} -J_1,\nonumber \\ A_{12}^{'\mathcal {S}}= & {} -J_1,\nonumber \\ A_{12}^{\mathcal {P}}= & {} \frac{16}{3}[J_0 (M+{\omega _1}) (m_1 +\omega _1){\textbf{p}_T}^2 {\textbf{q}_T}^2\nonumber \\{} & {} -J_1(M+{\omega _1}) ({\textbf{p}_T}^2 +{\textbf{q}_T}^2)\omega _1+J_2 (M+{\omega _1}) ({\omega _1}-m_1)],\nonumber \\ A_{12}^{'\mathcal {P}}= & {} -\frac{16}{3}[J_0\omega _2 ( M-{\omega _2}-m_1){\textbf{p}_T}^2 {\textbf{q}_T}^2\nonumber \\{} & {} -J_1\omega _2 ({\textbf{p}_T}^2 +{\textbf{q}_T}^2 )(M-{\omega _2})+J_2\omega _2 (M+m_1-{\omega _2})],\nonumber \\ A_{12}^{\mathcal {V},a}= & {} J_1 [-4 {m_\mathcal {V}}^2\omega _1 (M+{\omega _1}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2 {\textbf{q}_T}^2 +({\textbf{p}_T}^2-{\textbf{q}_T}^2)^2]/{m_\mathcal {V}}^2+2 J_2,\nonumber \\ A_{12}^{'\mathcal {V},a}= & {} J_1 [4 {m_\mathcal {V}}^2\omega _2 (M-{\omega _2}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2 {\textbf{q}_T}^2 +({\textbf{p}_T}^2-{\textbf{q}_T}^2)^2]/{{m_\mathcal {V}}^2}+2 J_2,\nonumber \\ A_{12}^{\mathcal {V},b}= & {} A_{12}^{'\mathcal {V},b}=\frac{4}{3}[J_0 {\textbf{p}_T}^2 {\textbf{q}_T}^2-J_2], \nonumber \\ A_{12}^{\mathcal {V},c}= & {} 4[J_0{\textbf{q}_T}^2 [(M+{\omega _1}) (m_1-{\omega _1})+ {\textbf{p}_T}^2]\nonumber \\{} & {} -J_1 (M +{\omega _1}) (m_1-{\omega _1})-J_2], \nonumber \\ A_{12}^{'\mathcal {V},c}= & {} 4[J_0 {\textbf{q}_T}^2 [{\omega _2} (M+m_1-{\omega _2}) +{\textbf{p}_T}^2]\nonumber \\{} & {} -J_1\omega _2 (M+m_1-{\omega _2})-J_2],\nonumber \\ A_{12}^{\mathcal {V},d}= & {} A_{12}^{'\mathcal {V},d}=\frac{8}{3}[J_0 {\textbf{p}_T}^2 {\textbf{q}_T}^2\nonumber \\{} & {} +J_1 -({\textbf{p}_T}^2+{\textbf{q}_T}^2)+J_2], \end{aligned}$$

(B11)

$$\begin{aligned} A_{21}^{\mathcal {S}}= & {} J_0,\nonumber \\ A_{21}^{\mathcal {S}}= & {} J_0,\nonumber \\ A_{21}^{\mathcal {P}}= & {} \frac{16}{3}J_0 (M+{\omega _1}) [{\textbf{p}_T}^2\omega _1 -m_1 {\textbf{q}_T}^2]\nonumber \\{} & {} -\frac{32}{3}J_1 \omega _1 (M+{\omega _1})+\frac{16}{3{\textbf{p}_T}^2}J_2 (M+{\omega _1}) (m_1+{\omega _1}),\nonumber \\ A_{21}^{'\mathcal {P}}= & {} \frac{16}{3}J_0\omega _2[{\textbf{p}_T}^2 ({\omega _2}-M) -m_1 {\textbf{q}_T}^2]\nonumber \\{} & {} -\frac{32}{3}J_1 {\omega _2 ({\omega _2}-M)+\frac{16}{3\textbf{p}_T}^2}J_2 \omega _2 (-M+m_1+{\omega _2}), \nonumber \\ A_{21}^{\mathcal {V},a}= & {} -J_0 [-4 {m_\mathcal {V}}^2\omega _1 (M+{\omega _1}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2 {\textbf{q}_T}^2+({\textbf{p}_T}^2-{\textbf{q}_T}^2)^2]/{{m_\mathcal {V}}^2}-2J_1, \nonumber \\ A_{21}^{'\mathcal {V},a}= & {} -J_0 [4 {m_\mathcal {V}}^2\omega _2 (M-{\omega _2}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2 {\textbf{q}_T}^2+({\textbf{p}_T}^2-{\textbf{q}_T}^2)^2]/{{m_\mathcal {V}}^2}-2J_1, \nonumber \\ A_{21}^{\mathcal {V},b}= & {} A_{21}^{'\mathcal {V},b}=0,\nonumber \\ A_{21}^{\mathcal {V},c}= & {} -4J_0 (M+{\omega _1}) (m_1+{\omega _1})\nonumber \\{} & {} +\frac{4}{{\textbf{p}_T}^2}J_1 (M+{\omega _1}) (m_1+{\omega _1}),\nonumber \\ A_{21}^{'\mathcal {V},c}= & {} -4J_0 \omega _2 (-M+m_1+{\omega _2})\nonumber \\{} & {} +\frac{4}{{\textbf{p}_T}^2}J_1\omega _2 (-M+m_1+{\omega _2}),\nonumber \\ A_{21}^{\mathcal {V},d}= & {} A_{21}^{'\mathcal {V},d}=\frac{-8}{3}J_0 \left( {\textbf{p}_T}^2+{\textbf{q}_T}^2\right) +\frac{16}{3}J_1, \end{aligned}$$

(B12)

$$\begin{aligned} A_{22}^{\mathcal {S}}= & {} (m_1+\omega _1)J_1/\textbf{p}_T^2,\nonumber \\ A_{22}^{\mathcal {'S}}= & {} (m_1+\omega _2-M)J_1/\textbf{p}_T^2,\nonumber \\ A_{22}^{\mathcal {P}}= & {} \frac{16}{3}\{J_0 {\textbf{q}_T}^2 (M+{\omega _1}) [{\textbf{p}_T}^2 -2\omega _1 (m_1+{\omega _1})]\nonumber \\{} & {} \times J_1\omega _1 (M+{\omega _1}) (m_1+{\omega _1})(1+{\textbf{q}_T}^2/{\textbf{p}_T}^2)\nonumber \\ \nonumber \\{} & {} -J_2 (M+{\omega _1})\},\nonumber \\ A_{22}^{'\mathcal {P}}= & {} \frac{16}{3}\{J_0\omega _2 {\textbf{q}_T}^2[-2 M^2+2 M (m_1+2\omega _2)\nonumber \\{} & {} + {\textbf{p}_T}^2-2\omega _2 (m_1+{\omega _2})]\nonumber \\{} & {} +J_1\omega _2 (1+{\textbf{q}_T}^2/{\textbf{p}_T}^2)\nonumber \\{} & {} [M^2 -M (m_1+2\omega _2) +{\omega _2} (m_1+{\omega _2})]-J_2 \omega _2\},\nonumber \\ A_{22}^{\mathcal {V},a}= & {} -J_1 (m_1+{\omega _1})[-4 {m_\mathcal {V}}^2\omega _1 (M+{\omega _1}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2 {\textbf{q}_T}^2+\left( {\textbf{p}_T}^2-{\textbf{q}_T}^2\right) ^2]/({{m_\mathcal {V}}^2}{\textbf{p}_T}^2)\nonumber \\{} & {} -\frac{2}{{\textbf{p}_T}^2}J_2 (m_1+{\omega _1}),\nonumber \\ A_{22}^{'\mathcal {V},a}= & {} J_1 (M-m_1-{\omega _2}) [4 {m_\mathcal {V}}^2\omega _2 (M-{\omega _2}) +{m_\mathcal {V}}^2 {\textbf{p}_T}^2\nonumber \\{} & {} +{m_\mathcal {V}}^2 {\textbf{q}_T}^2+\left( {\textbf{p}_T}^2-{\textbf{q}_T}^2\right) ^2]/({{m_\mathcal {V}}^2} {\textbf{p}_T}^2)\nonumber \\{} & {} +\frac{2}{{\textbf{p}_T}^2}J_2 (M-m_1-{\omega _2}),\nonumber \\ A_{22}^{\mathcal {V},b}= & {} \frac{-4}{3}[J_0 {\textbf{q}_T}^2 (m_1+{\omega _1})-J_2 (m_1+{\omega _1})/{\textbf{p}_T}^2], \nonumber \\ A_{22}^{'\mathcal {V},b}= & {} \frac{-4}{3}[J_0 {\textbf{q}_T}^2 (-M+m_1+{\omega _2})\nonumber \\{} & {} -J_2 (-M+m_1+{\omega _2})/{\textbf{p}_T}^2 ], \nonumber \\ A_{22}^{\mathcal {V},c}= & {} -4[J_0 {\textbf{q}_T}^2 (m_1 -M )+J_1 (M +\omega _1)\nonumber \\{} & {} +J_2(-m_1-{\omega _1})/{\textbf{p}_T}^2], \nonumber \\ A_{22}^{'\mathcal {V},c}= & {} 4[J_0 {\textbf{q}_T}^2 (M-m_1)-J_1 \omega _2\nonumber \\{} & {} -J_2 (M-m_1-{\omega _2})/{\textbf{p}_T}^2], \nonumber \\ A_{22}^{\mathcal {V},d}= & {} \frac{-8}{3}[J_0 {\textbf{q}_T}^2 (m_1+{\omega _1})\nonumber \\{} & {} -J_1 (m_1+{\omega _1}) (1+{\textbf{q}_T}^2/{\textbf{p}_T}^2)+J_2 (m_1+{\omega _1})/{\textbf{p}_T}^2],\nonumber \\{} & {} A_{22}^{'\mathcal {V},d}=\frac{-8}{3}[J_0 {\textbf{q}_T}^2 (-M+m_1+{\omega _2})\nonumber \\{} & {} -J_1 (1+{\textbf{q}_T}^2/{\textbf{p}_T}^2) (-M+m_1+{\omega _2})\nonumber \\{} & {} +J_2(-M+m_1+{\omega _2})/{\textbf{p}_T}^2]. \end{aligned}$$

(B13)