On some new black hole, wormhole and naked singularity solutions in the free Dirac–Born–Infeld theory

Abstract

In this paper, we present some new static and spherically symmetric solutions of the Einstein equation in which the matter sector is accounted for by a free Dirac–Born–Infeld field. Our novel spacetimes can describe either a black hole, a wormhole, or a naked singularity depending on certain boundary conditions. By tracking the dynamical gravitational collapse, we enlighten the importance of the isotropy of the pressure for having an horizon as a result, as required by the Cosmic Censorship Conjecture. Our new spacetime solutions, the amount of exotic matter, its “complexity”, and the equation of state along the tangential direction are analytical and written in closed forms. We identify a taming of the breaking of the null energy condition, customary for wormhole spacetimes in General Relativity, along both the radial and tangential direction. We assess the astrophysical applicability and perform a comparative analysis between our solutions and other literature ones, by identifying an ISO-like density profile of the matter field, which provides a flattening of the rotation curves, by discussing the motion of test particles, and the shadow properties. In our model, those effects are interpreted as a manifestation of a topological defect, and since they can observationally mimic the signatures of other spacetimes, a study of the perturbations is performed within the quasi-normal modes formalism. Having identified the Reissner–Nordström-like quasi-resonance, our paper is intended also to provide some insights on which combinations of background and perturbation properties should be observed, for claiming the nature of astrophysical compact objects.

1 Introduction

A phantom fluid, whose energy density $\rho$ and pressure p are such that $\rho +p<0$, may tame some cosmological observational tensions without the need of modifying gravity beyond General Relativity [1, 2]. The null energy condition might be broken as well in the early universe, during the so-called inflationary epoch. It is therefore important to investigate the possible occurrence of a local collapse in some space region of such phantom material by clarifying whether a configuration of gravitational equilibrium can be established. Compact objects like wormholes and naked singularities, whose main characteristic is to be without an event horizon, can be supported by this type of equilibrium condition, and their existence has not yet been conclusively ruled out by astrophysical observations. In fact, they can mimic some observational signatures usually attributed to black hole spacetimes; indeed, the Event Horizon Telescope Collaboration has devoted attention to the testing of the Janis–Newman–Winicour [3] and of the Joshi–Malafarina–Narayan naked singularities [4], among other spacetimes [5], without ruling them out. On the other hand, the features of the shadow, as size and shape, of some wormholes have been thus far studied theoretically, which results are expected to be astrophysically testable by more precise future datasets [6]. As explained in [7, Footnote.9], the shadow phenomenon, which occurs at length scales of some kiloparsecs, constitutes an excellent arena for testing the previously mentioned cosmological degrees of freedom because that is the length scale at which screening mechanisms, required for preserving the validity of local physics laws, are expected to be triggered. Thus, the mathematical search (and their testing) of new wormhole and naked singularity solutions supported by some matter fields with a well-posed cosmological applicability is in order.

Degeneracy at the background level between physically different spacetime metrics can be broken by looking at the evolution of their perturbations. For example, the propagation of gravitational waves generated by scalar and electromagnetic perturbations has been studied in [8] by identifying the specific imprints on the echoes spectra generated by the equation of state of the exotic material in the surroundings. Specifically, an anomalous decay of the perturbations distinguishes the Bronnikov-Ellis and Morris-Thorne wormholes [9]. Furthermore, a mathematical algorithm for reconstructing the shape function of a wormhole in proximity of its throat by knowing the frequency of its quasi-normal modes of oscillation has been presented in [10], and a relationship between the frequency of the quasi-normal modes and the size of the shadow has been discovered in [11]. The influence of the symmetries of the spacetime on the frequencies of the quasi-normal modes has been investigated in [12] with an application to the stability properties of those objects.

In this paper, we will exhibit some novel wormhole and naked singularity solutions supported by the free Dirac–Born–Infeld field, and also propose a re-interpretation of the Schwarzschild-(anti) de Sitter black hole within this model. Therefore, we will assume a field theory whose potential is vanishing, but based on a scalar field with a non-canonical kinetic term, as formulated in [13], via a certain fluid correspondence that we will outline in Sect. 2. In fact, the Dirac–Born–Infeld scalar field has been invoked both as the mechanism responsible for the inflationary dynamics [14], and as providing the phantom energy in the late universe [15]. The Dirac–Born–Infeld theory can be regarded also as a non-linear theory of electromagnetism, for which black hole solutions are allowed [16], and on which matter accretion phenomena have been investigated as well [17]. Some wormhole solutions (e.g. spacetime admitting a “throat”) have already been discovered in the Dirac–Born–Infeld theory [18, 19], but they have been claimed to be unstable [20]. The specific matter content we will assume to support the spacetime will be effectively treated as obeying to the equation of state of a generalized polytrope with an infinite adiabatic index, and therefore our analysis complements that of [21] in which new wormhole solutions supported by a polytropic fluid have been discovered. More specifically, our new solution will allow us to interpret one of the parameter entering the supporting equation of state as a generator of a topological defect, while we will show that the second parameter actually tames the breaking of the null energy condition both in the radial and tangential directions, with an equation of state provided in a closed form for the tangential pressure. The effects of the free equation of state parameters on the frequencies of the quasi-normal modes of oscillation in the eikonal limit are also analyzed for establishing the stability properties of our configuration. We will as well elucidate the role of the isotropy of the pressure in generating a black hole or a naked singularity as the result of a gravitational collapse. Moreover, we will show that our new solution can pass some relevant astrophysical tests concerning the flattening of rotation curves for the newtonian rotation velocity or the size of the shadow depending on whether we decide to match it with a vacuum Schwarzschild spacetime in its exterior. We deliver analytical results both for the amount of exotic matter supporting our spacetime and find a relationship between the Christodoulou-Rovelli volume and the “complexity” of our spacetime, also by showing an astrophysically relevance of the latter, at least as far as our model is concerned, in reconstructing the size of the throat. Finally, we show that our solution is characterized by an ISO-like (but for phantom energy) density profile.

Our paper is organized as follow: in Sect. 2 we will outline our assumptions on the geometry of the spacetime and on its matter content and write down the relevant field equations, whose novel solutions are then presented in Sect. 3. In this latter section, we will analyze the properties of our solutions at the background level by proposing some new interpretations of the free parameters entering the equation of state accounting for the matter content, by discussing the shadow properties, the density profile, and the motion of test particles. We will also assess the possibilities of having black holes vs. naked singularities supported by the (Modified) Berthelot fluid depending on the isotropy of the pressure, which is an important aspect in reference to the Cosmic Censorship Conjecture. Analytical results are presented for the amount of exotic matter supporting our novel spacetimes, and the null energy condition is inspected. Since some properties at the background level of our solutions are shared by other literature configurations, we break this degeneracy in Sect. 4 by computing the quasi-normal modes of oscillation in the eikonal limit. Finally, we conclude in Sect. 5 by summarizing our results with a discussion about the specific roles of each of our assumption, and by further commenting on the relevance of our new results with respect to recent literature.

2 Modeling a static and spherically symmetric spacetime

To describe a static and spherically symmetric spacetime, we start from the metric ansatz

$$\begin{aligned} \textrm{d}{s}^2 = -e^{2 \Phi (r)} \textrm{d}{t}^2 + \frac{\textrm{d}{r}^2}{1-\frac{b(r)}{r}} + r^2 (\textrm{d}{\theta }^2 + \sin ^2 \theta \textrm{d}{\phi }^2 ) \,, \end{aligned}$$

(1)

where $\Phi (r)$ and b(r) are the redshift and shape functions, respectively. Depending on appropriate boundary conditions, this class of geometries can describe black holes (if an horizon exists), wormholes (if a throat exists), naked singularities (if at least one curvature invariant diverges in some spatial point and there are no horizons), stars (if there are no curvature singularities, no horizons, but a spatial surface in which the pressure of the supporting matter content vanishes) or a gas cloud (like a star, but the energy density vanishes as well on the spatial boundary on which the pressure vanishes). Furthermore, we consider the spacetime to be supported by an anisotropic fluid accounted for by the stress-energy tensor $T^{\mu }{}_{\nu }=\textrm{diag}[-\rho (r),\, p_r(r), \, p_t(r), \, p_t(r)]$ in which $\rho (r)$ is the energy density, $p_r(r)$ is the radial pressure and $p_t(r)$ is the tangential pressure. Therefore, the solutions we will construct in this paper describe “transparent” wormhole/black hole because $T^0_r=0$ and there is no matter either falling into nor being emitted by the central configuration [22,23,24,25].

Then, the Einstein equation

$$\begin{aligned} R_{\mu \nu } - \frac{1}{2} g_{\mu \nu } R = 8 \pi T_{\mu \nu } \end{aligned}$$

(2)

provides the field equations

$$\begin{aligned} \Phi '&= \frac{8\pi p_r r^3+b}{2 r(r-b)} \,, \end{aligned}$$

(3)

$$\begin{aligned} b'&= 8 \pi r^2 \rho \,, \end{aligned}$$

(4)

where a prime denotes a derivative with respect to the radial coordinate r. The conservation of the stress-energy tensor $\nabla ^\mu T_{\mu \nu }=0$ yields the following equation governing the radial evolution of the pressure:

$$\begin{aligned} p'_r = - \left( \rho + p_r \right) \Phi ' + \frac{2 \left( p_t -p_r \right) }{r}\,. \end{aligned}$$

(5)

Finally, we assume the radial pressure to depend functionally on the energy density as

$$\begin{aligned} p_r = \frac{\beta \rho }{1+ \alpha \rho } \,, \end{aligned}$$

(6)

where $\alpha$ and $\beta$ are constants. This equation of state is known as the (Modified) Berthelot model [26], and following previous literature we will restrict our next considerations to the range $\alpha \ge 0$ because this parameter is related to the temperature at which a thermodynamic phase transition occurs [27]; thus, being the denominator always larger than 1, this equation of state may be useful in taming some of the causality and stability issues troubling dark/phantom energy models. In fact, this equation of state with $\beta <0$ has already been adopted in cosmological contexts as a form of time-evolving dark energy [27,28,29,30,31], and at the background level it constitutes the hydrodynamical realization of the free (e.g. with vanishing potential) Dirac–Born–Infeld theory [32]. Actually, recent studies according to which dark matter may exhibit some non-negligible pressure effects at galactic scales [33] allow us to consider astrophysically relevant also the regime in which $\beta >0$. Equation of state (6) is a particular subcase of the generalized polytropic model

$$\begin{aligned} p_r = \frac{\beta \rho ^{1+1/n}}{ 1+\alpha \rho ^{1+1/n}} \,, \end{aligned}$$

(7)

in which the adiabatic index $n=\infty$.

3 Some new black hole, naked singularity and wormhole solutions, and their background characterization

It is straightforward to check that the spacetime

$$\begin{aligned}&\textrm{d}{s}^2 =-f(r) \textrm{d}{t}^2 + \frac{\textrm{d}{r}^2}{f(r)} + r^2 (\textrm{d}{\theta }^2 + \sin ^2 \theta \textrm{d}{\phi }^2)\,,\nonumber \\&f(r) = 1-\frac{2M}{r} + \frac{\Lambda _{\textrm{eff}}}{3}r^2\,, \end{aligned}$$

(8)

is a solution for our model. Here M is an arbitrary constant of integration that we can interpret as the black hole mass parameter, and the “effective” cosmological constant reads as $\Lambda _{\textrm{eff}}=\frac{8 \pi (\beta +1)}{\alpha }$. Thus, we can reproduce both the Schwarzschild-(anti) de Sitter and the Schwarzschild-de Sitter spacetimes should it be $\beta >-1$ or $\beta <-1$, respectively. Interestingly, the Schwarzschild solution can be obtained either for $\beta =-1$ or in the limit $\alpha \rightarrow \infty$. Black hole geometries shaped by an “effective” cosmological constant, combination of some “microscopic” model parameters, have been discovered also when the supporting fluid is given by the Anton–Schmidt model [34]. Solution (8) constitutes a limiting case of our model in which pressure and energy density are constant, and the former is isotropic: $p_r=p_t=-\rho =\frac{1+\beta }{\alpha }$.

We will now assume

$$\begin{aligned} \Phi (r) = \frac{1}{2} \ln \left( \frac{r_1}{r} \right) \,, \end{aligned}$$

(9)

where $r_1$ is a renormalization constant for the time t, for the redshift function in (1). This specific decay of the redshift functional has been chosen as well in the modeling of wormholes supported by an ideal (e.g. with pressure and energy density linearly proportional to each other) phantom fluid [35], the Chaplygin gas [36], and the Shan–Chen fluid [37]. By computing the Newman–Penrose curvature scalars¹ [38] we obtain $4 \Phi _{11} - \Phi _{22}=\frac{1}{r^2}$, which shows that this spacetime metric comes with a curvature singularity located in $r=0$. For the Newman–Penrose spin coefficients accounting for the focussing properties of a bundle of light rays we obtain

$$\begin{aligned} \mu _{\textrm{NP}} = \rho _{\textrm{NP}} = \sqrt{\frac{r-b(r)}{2 r^3}}\,, \end{aligned}$$

(11)

and thus our class of spacetimes are horizonless because there are no sign changes in these quantities (e.g. there is no transition from a diverging to a converging behavior). On the other hand, there might exist a suitable surface located at $r_0$ such that $b(r_0)=r_0$, and correspondingly $\mu _{\textrm{NP}}(r_0)=\rho _{\textrm{NP}}(r_0)=0$: we will show in what follow that $r_0$ is actually the throat of a wormhole. To summarize, once the condition (9) is assumed, we can obtain either (and only) a naked singularity or a wormhole solution depending on how we fix the previously mentioned boundary condition.

The curvature and physical properties we have identified in the previous paragraph follow from purely geometrical considerations, and therefore will keep holding also in modified gravity paradigms. Likewise, also the geodesic motion of test particles is sensitive only to the spacetime curvature and not to the specific physical interpretation of the solution (as long as couplings are neglected). For example, the radius of the photon sphere can be computed once the redshift function is known and astrophysical measurements in this regard do not allow to fully reconstruct the specific spacetime metric [7]. A similar reasoning applies also to the inner stable circular orbit (ISCO). For completeness we mention that their locations can be estimated from the effective potential [39, 40]

$$\begin{aligned} V_{\text {eff}} = e^{2 \Phi } \left( \frac{L^2}{r^2} - \kappa \right) \,, \end{aligned}$$

(12)

where L is the (conserved) angular momentum of the test particle and $\kappa =0,-1$ for massless and massive particles, respectively. The locations of the photon sphere and ISCO are found by solving $V_{\text {eff}}'= V_{\text {eff}}''=0$, which explicitly provide

$$\begin{aligned} \frac{3L^2 -\kappa r^2}{r^4}=0 \,, \qquad \frac{2(6L^2 -\kappa r^2)}{r^5} =0 \,, \end{aligned}$$

(13)

once (9) is implemented, which can be satisfied only at spatial infinity. We remark that this result will apply both to the naked singularity and wormhole interpretation of our new solutions, and for this reason we will investigate the quasi-normal modes of oscillations in Sect. 4 for obtaining a sharper physical characterization of our spacetimes.

For an other than (9) redshift function, we could obtain the black hole solution (8); thus, the same symmetries (1) and the same matter content (6) are consistent with both naked singularity and black hole spacetimes. Whether the fluid collapse leads to one or the other of these configurations is an intriguing question in light of the Cosmic Censorship Conjecture [41]. We can model the fluid collapse by adopting the metric

$$\begin{aligned} \textrm{d}{s}^2{ =} {-}e^{2\nu (t,r)} \textrm{d}{t}^2 {+}e^{2 \psi (t,r)} \textrm{d}{r}^2 {+}R^2(t,r) (\textrm{d}{\theta }^2 {+} \sin ^2 \theta \textrm{d}{\phi }^2) \,, \end{aligned}$$

(14)

whose corresponding field equations are [42]:

$$\begin{aligned} \rho (t,r)= & {} \frac{2 M_{\textrm{MS}}'(t,r)}{R^2(t,r) R'(t,r)}, \end{aligned}$$

(15)

$$\begin{aligned} p(t,r)= & {} - \frac{2 \dot{M}_{\textrm{MS}}(t,r)}{R^2(t,r) \dot{R}(t,r)}, \end{aligned}$$

(16)

where an overdot denotes a derivative with respect to the time, $M_{\textrm{MS}}$ is the Misner–Sharp mass [43], and where we have considered the pressure to be isotropic. Next, by implementing the equation of state (6) we obtain:

$$\begin{aligned} - \frac{\dot{M}_{\textrm{MS}}(t,r)}{\dot{R}(t,r)} =\frac{\beta M_{\textrm{MS}}'(t,r) R^2(t,r) }{R^2(t,r) R'(t,r) +2\alpha M'(t,r)} \,. \end{aligned}$$

(17)

Assuming now $M_{\textrm{MS}}=M_{\textrm{MS}}(R(t,r))$ provides:

$$\begin{aligned} \frac{\textrm{d}{M}_{\textrm{MS}}}{\textrm{d}{R}} =-\frac{\beta + 1}{2\alpha }R^2\,, \end{aligned}$$

(18)

and then $M_{\textrm{MS}}=-\frac{\beta + 1}{6\alpha }R^3$, which is well-defined for $\beta \le -1$ only. The apparent horizon would be located at $R(t,r)=2M_{\textrm{MS}}(t,r)$ (see [42] and references [11,12,23,24] therein), e.g. at $R=\sqrt{-3\alpha /(1+\beta )}$ which exists as long as the Misner-Sharp mass is well-defined. Thus, the isotropy of the pressure in the collapse of the (Modified) Berthelot fluid leads to the formation of a black hole, consistently with the characterization of our solution (8). The naked singularity solution we will present below will be indeed supported by an anisotropic pressure.

Under the assumption (9), the field equations (3), (4), together with (6), reduce to:

$$\begin{aligned} b' = -\frac{8 \pi r^2}{8 \pi \beta r^2 + \alpha }\,, \end{aligned}$$

(19)

which can be integrated into

$$\begin{aligned} b(r) = \frac{r}{ \beta } \left( \frac{\arctan ( C_1 r )}{C_1 r} -1 \right) - C_2 \end{aligned}$$

(20)

for the shape function, where we have defined $C_1:=2 \sqrt{ 2 \pi \beta /\alpha }$ and $C_2:= {\tilde{C} }/(4 \beta \sqrt{\pi \alpha \beta })$, $\tilde{C}$ being the arbitrary constant arising from the integration. Recalling that $\alpha$ is non-negative, we understand that this solution is meaningful for positive $\beta$ only. However, just assuming (1) and (9) we can compute $G^{r }{ }_{r }=-\frac{1}{r^2}$, and therefore from the Einstein equations with (6) we conclude that a consistent solution (with a positive energy density $\rho$) actually requires a negative $\beta$. Therefore, we apply the “trick” $\arctan (i x)=i\, \text {arctanh}(x)$, where i is the imaginary unit, and write

$$\begin{aligned} b(r) = \frac{r}{ \beta } \left( \frac{\text {arctanh} (C_1 r )}{C_1 r} -1 \right) - C_2 \end{aligned}$$

(21)

with $C_1:=2 \sqrt{ - 2 \pi \beta /\alpha }$ and $C_2:= {\tilde{C} }/(4 \beta \sqrt{-\pi \alpha \beta })$. A direct computation of the components of the Einstein equation can now be made for confirming the correctness of the solution. The astrophysical regimes in which our solutions can be applied should be understood by their position inside the Baker–Psaltis–Skordis curvature vs. potential diagram [44], which position in our case would be along a straight line going through the origin. In fact, the square root of the Kretschmann scalar (10) asymptotically goes as $\sim 1/r^3$ (like for the Schwarzschild black hole), while the gravitational potential (12) falls as $\sim 1/r^3$ (and so faster than the Newtonian and Schwarzschild potentials $\sim 1/r$). Our new mathematical solutions are therefore important because a remarkable progress has been achieved by the Event Horizon Telescope which has opened new windows of possibilities of testing solutions in the O(1) range of the latter quantity. We also need to recall that a naked singularity solution of the Einstein equation was discovered by Tolman [45], the so-called Tolman VI (see also [46, 47]), which is supported by a photon gas obeying to the equation of state $p=\frac{\rho }{3}$: while this equation of state is contained as a particular subcase of our (6), our choice of the redshift (9) has made our new solution to belong to a completely different family being supported by a negative pressure. In the asymptotic far-field region $r \rightarrow \infty$ we obtain $g_{rr} \sim \frac{\beta }{1+\beta }$, whose Lorentzian signature is correct for $\beta <-1$ further restricting the range of this parameter. Asymptotic spatial flatness can be achieved only in the limiting case $\beta \rightarrow -\infty$ or by matching with an exterior spatially flat spacetime. We note that the gravitational field in this regime if fully accounted for by the parameter $\beta$, with $\alpha$, ${\tilde{C}}$, and $r_1$ playing no roles. While for the latter quantity this result is not a surprise, as it can be re-absorbed into an appropriate re-definition of the time, deviations from an ideal fluid behavior $p \propto \rho$ and the physical interpretation of the solution (21) (that we will assess below depending on the choice of the integration constant $\tilde{C}$) do not influence the asymptotic properties of the spacetime. We can also note that

$$\begin{aligned} 1-\frac{b(r)}{r} \approx 1+\frac{1}{\beta } -\frac{2 {\mathcal {M}}}{r} + \frac{{\mathcal {Q}}^2}{r^2} \qquad \textrm{for} \,\, r \rightarrow \infty \,, \end{aligned}$$

(22)

where we have introduced an “effective” mass parameter ${{\mathcal {M}}}=\frac{\pi -2C_1 C_2 \beta }{4\beta C_1}$ and an “effective” electric charge-like parameter ${{\mathcal {Q}}}^2=-\frac{1}{\beta C_1^2}$, where as usual the arbitrary integration constant $\tilde{C}$ is related to the former only. The latter term arises as well in some black hole solutions of the Quartic Horndeski theory [48] and of Modified Gravity MOG [49]: our solution has nevertheless a different redshift function, whose role in distinguishing it by studying the quasi-normal modes will be presented in Sect. 4. More interestingly, we can enlighten the role of the equation of state parameter $-1/\beta$ which behaves in the same way of a topological defect arising from the breaking of a global O(3) symmetry [50].

By enforcing the Einstein equations we can compute the energy density, radial and tangential pressure obtaining

$$\begin{aligned}&\rho = - \frac{1}{8 \pi \beta r^2 + \alpha }\,, \qquad p_r=-\frac{1}{8 \pi r^2}\,, \nonumber \\&p_t =\frac{8 \pi (\beta +1) r^2 +\alpha }{32 \pi r^2 (8\pi \beta r^2 +\alpha )}\,, \end{aligned}$$

(23)

respectively, all of which vanish asymptotically for $r \rightarrow \infty$, while only the radial pressure diverges in correspondence of the singularity $r=0$. The radial pressure being negative signifies that the spacetime is supported by an exotic type of matter. The requirement of a positive energy density restricts the applicability of our solutions to the region $r> \sqrt{-\alpha /(8\pi \beta )}$: the parameter $\alpha$, which quantifies the deviation from an ideal fluid $p \propto \rho$, tames the singularity in the energy density (nevertheless the solutions can be adopted in a spherical crown only, possibly matched in their interior with some other regular metric for removing the region with negative energy density²). We should recall that also by studying the collapse of the (Modified) Berthelot fluid we had obtained that a naked singularity cannot occur for $\beta <-1$ if the pressure is isotropic. We can also note that the radial profile of the energy density is formally the same as in the ISO model of galactic dark matter $\rho (r) =\frac{\tilde{\rho }}{1 + \left( \frac{r}{\tilde{r}}\right) ^2}$ [51] with the free parameters³$\tilde{\rho }=-1/\alpha$ and $\tilde{r}^2=\alpha /(8\pi \beta )$. The Newtonian velocity of a massive astrophysical object in rotational motion within this gravitational field at a distance r from the center of the configuration is [33, Eq.(10)]

$$\begin{aligned} v_{\textrm{N}}(r)&= \sqrt{\frac{4 \pi \int r^2 \rho (r) dr}{r}} = \sqrt{\frac{b(r)}{2r}} \nonumber \\&\rightarrow \quad \sqrt{-\frac{1}{2\beta }} + o(\sqrt{r}) \,\,\, \textrm{for} \,\,\, r \rightarrow \infty \,. \end{aligned}$$

(24)

Thus, should we allow for the distribution of the matter content to extend up to spatial infinity without performing any spacetime matching, the rotation velocity approaches a constant value asymptotically. It should be remarked that this value is well defined (e.g. $v<1$) because $\beta <-1$, and recalling (22) the flatness of the galactic rotation curves is now interpreted as a manifestation of a topological defect; we also note that consistently $p_r,\,p_t\, \rightarrow 0$, behaving as pressureless fluid in the far field regime.

Moreover, we can compute the decay of the gravitational potential V(r) generated by our solution by applying the continuity and Euler equations describing the fluid flow [55]:

$$\begin{aligned} (\rho A \tilde{v})'=0\,, \qquad \rho \tilde{v} {\tilde{v}}' =- p_r' -\rho V'\,, \end{aligned}$$

(25)

where $\tilde{v}$ is the speed of the fluid molecules, and $A=4\pi r^2$ the area of the cross section available for the flow, and where we have assumed a spherically symmetric configuration. By writing $p_r'=\frac{\textrm{d}{p}_r}{\textrm{d}{\rho }} \cdot \rho '$, and by using the energy density profile (23), we arrive at:

$$\begin{aligned} \tilde{v}' = - \frac{2\alpha \tilde{v}}{r(8\pi \beta r^2+\alpha )} \end{aligned}$$

(26)

for the former, which can be integrated into

$$\begin{aligned} \tilde{v}(r)= C_3 \left( 8\pi \beta + \frac{\alpha }{r^2}\right) \,, \end{aligned}$$

(27)

with $C_3$ a constant of integration. The Euler equation now becomes

$$\begin{aligned} V' = \frac{(8 \pi \beta r^2 +\alpha ) (8\pi \alpha C_3^2 +r^2)}{4 \pi r^5}\,, \end{aligned}$$

(28)

which can be integrated into

$$\begin{aligned} V(r)= -\frac{\alpha [1+ (8\pi C_3 )^2\beta ] }{8 \pi r^2} -\frac{1}{2}\left( \frac{\alpha C_3}{r^2} \right) ^2 + 2 \beta \ln (r) +C_4\,, \end{aligned}$$

(29)

where $C_4$ is another constant of integration. Finally, in a configuration of equilibrium we need to set $C_3=0$, and we can consistently identify an attractive potential $V(r)<0$.

Furthermore, the tangential pressure switches its sign from negative to positive at $r_t=\sqrt{-\alpha /[8 \pi (\beta +1)]}$. We can provide an analytical expression in closed form for the supporting equation of state in the tangential direction as

$$\begin{aligned} p_t = - \frac{(1+\beta +\alpha \rho ) \rho }{4(1+ \alpha \rho )} =-\frac{\rho }{4}-\frac{\beta \rho }{4(1 + \alpha \rho )} \,, \end{aligned}$$

(30)

which interestingly is given by a re-scaled (Modified) Berthelot fluid (6) plus an ideal fluid contribution, the latter constituting the anisotropic stress. The coefficient of pressure anisotropy is consequently obtained as

$$\begin{aligned} \Delta := p_r - p_t = - \frac{8\pi (5\beta +1)r^2 +5\alpha }{32 \pi r^2 (8\pi \beta r^2 +\alpha )}\,, \end{aligned}$$

(31)

which vanishes not only asymptotically but also on the surface

$$\begin{aligned} r_*=\sqrt{-\frac{5\alpha }{8 \pi (5\beta +1)}}\,. \end{aligned}$$

(32)

Hence, a surface in which radial and tangential pressure are equal to each other can exist if $\beta <-1/5$, which condition is guaranteed by the previously identified range $\beta <-1$. Furthermore, the complexity factor, which quantifies the deviations of the geometry from homogeneity and isotropy, is given by [56]

$$\begin{aligned} y_{tf}&:= \Delta - \frac{1}{2 r^3} \int ^r_{r_0} s^3 \rho '(s) ds\nonumber \\&= \frac{1}{16 \pi \beta r^2} \left[ 2 + \frac{\alpha }{8 \pi \beta r^2 + \alpha } + \frac{3 \textrm{arctanh}(C_1 r)}{C_1 r} \right] _r^{r_0}\nonumber \\&\quad - \frac{8\pi (5\beta +1)r^2+5\alpha }{32 \pi r^2 (8\pi \beta r^2 +\alpha )}\,, \end{aligned}$$

(33)

where $r_0$ is the lower bound of the radial coordinate.

The null energy condition along the radial and tangential direction read as

$$\begin{aligned}&\rho +p_r = - \frac{8 \pi (\beta +1) r^2 + \alpha }{8\pi r^2 (8 \pi \beta r^2 + \alpha )} \,,\nonumber \\&\rho + p_t = \frac{8 \pi (\beta -3)r^2 + \alpha }{32 \pi r^2 (8\pi \beta r^2 +\alpha )}\,, \end{aligned}$$

(34)

respectively. The former holds in the region⁴$r_*< r <\sqrt{-\alpha /[8 \pi (\beta +1)]}$, while the latter for $r > \sqrt{-\alpha /[8 \pi (\beta -3)]}$, e.g. for $r>r_*$. Recalling that $\beta <-1$, this analysis confirms quantitatively that the (positive) parameter $\alpha$ tames some of the well known issues troubling phantom fluids. For our spacetime, the Visser-Kar-Dadhich integral quantifier [61]

$$\begin{aligned} I_V&= \int _{r_0}^{+\infty } |\rho + p_r| dV\nonumber \\&= \left| \frac{(\beta +1)r}{2} -\frac{1}{2 \beta C_1} \textrm{arctanh} (C_1 r) \right| \Big |_{r_0}^{+\infty } \,, \end{aligned}$$

(35)

where the areal volume element $dV=4\pi r^2 dr$ has been used, diverges linearly at infinity. This result suggests that an infinite amount of exotic matter would be required to support the spacetime; however this divergence can be cured by an appropriate matching with a suitable exterior spacetime. Traversable and stable wormhole spacetimes whose existence does not require any amount of exotic matter at all have been discovered by relaxing the assumption of General Relativity as the relevant gravitational framework. Indeed some extensions of Einstein gravity might be needed also for curing its shortcomings at IR and UV energy scales. For example, allowing contributions to the spacetime curvature from geometric entities beyond the Ricci curvature, as in the metric-affine approach in which the torsion and non-metricity fields are considered, empty-space wormhole solutions could be found because the stress-energy tensor entering the field equations enjoys also an effective contribution stemming from those geometrical fields [62]. Another possibility investigated in [63] builds upon the Non-local Integral Kernel Theories of Gravity in which case a suitable function of the d’Alembertian (e.g. of the derivatives) of the Ricci scalar enters the Action of the theory; in this latter scenario, it has been checked that both the energy conditions and the hydrodynamical stability, e.g. a well-defined value of the speed of sound within the fluid, hold by looking at the average (between the tangential and radial contributions) pressure. Confirmation of the stability of such configurations has been of crucial importance for guaranteeing the throat to exist for a long enough period of time making the wormhole to be actually traversable.

Should we impose

$$\begin{aligned} \tilde{C}= 4 \sqrt{-\pi \alpha \beta } r_0 \left( \frac{ \mathrm{arctanh (C_1 r_0)} }{C_1 r_0} -1 -\beta \right) \end{aligned}$$

(36)

for the arbitrary constant stemming from the integration of the Einstein equation (21), we would obtain $b(r_0)=r_0$. Thus, we can provide a physical interpretation to our solution as a wormhole with a throat in $r_0$. We can now compute

$$\begin{aligned} b'(r_0) = \frac{ (C_1 r_0)^2}{ [1-(C_1 r_0)^2] \beta } \end{aligned}$$

(37)

obtaining that the flare-out condition $b'(r_0)<1$ is fulfilled if the location of the throat is such that $r_0<1/C_1$ or $r_0>1/(\sqrt{-(1+\beta )} C_1)$, where in the latter case the region with a negative energy density is automatically removed for $\beta \in (-1,-2]$. We also recall that the singularity in $r=0$ does not belong to the wormhole spacetime since the coordinate system is $r\in [r_0, \infty )$. Geometrically, we can note that the surface (32) on which the pressure is isotropic would be located outside the throat provided that $r_*>r_0$, e.g. if the location of the throat is such that $r_0<\sqrt{-5\alpha /8/\pi (5\beta +1)}$; moreover, the complexity factor (33), where now we interpret $r_0$ to be the throat location, is generally nonzero, consistently with the claim that wormhole solutions with zero complexity factor cannot exist [64]. Nevertheless, if we search for a specific surface $\tilde{r}_*$ on which the complexity factor is zero, in the approximation of small $\alpha \approx 0$, e.g. close to an ideal fluid behavior $p \approx \beta \rho$ for the matter field, such surface would be located at $40\beta (\beta +1)\pi r_0 \tilde{r}_*^2+8(4\pi \beta r_0^2+\alpha ) \tilde{r}_*-7\alpha r_0=0$, e.g. at

$$\begin{aligned}&\tilde{r}_* {\approx } \nonumber \\&\quad {\approx } ~\frac{2(4 \pi \beta r_0^2 {+}\alpha ) {+}\sqrt{(8 \pi \beta r_0^2)^2{-}2(35 \beta {+}19) \pi \alpha \beta r_0^2{+}4 \alpha ^2}}{20 \beta (\beta +1)\pi r_0}\nonumber \\&\quad \approx ~\frac{4 r_0}{5(1+\beta )} - \frac{(3 + 35 \beta ) \alpha }{160 \beta (1+\beta ) \pi r_0}\,. \end{aligned}$$

(38)

Thus, this surface would carry an astrophysical relevance if $r_0 <\sqrt{-\frac{(3+35\beta )\alpha }{32\pi \beta (1+5\beta )}}$ (e.g. if it is located outside the throat): this enlightens an astrophysical interpretation of the complexity factor as a quantity from which it is possible to reconstruct information on the size of the throat, should we observationally detect a point at which it vanishes.

Should we assume the wormhole to have finite size, e.g. its supporting material to fill only the region of space between the throat up to a certain border located at $R_b$, we would be required to match our solution to an exterior spacetime, the exterior Schwarzschild being one possibility. This matching is specifically needed for having an isotropic (in the far limit) and asymptotically flat wormhole solution [65]. A smooth radial evolution of the gravitational field at this border requires continuity of the metric coefficients, and thus we need to impose (see for example [37, Eqs. (21)–(22)]):

$$\begin{aligned}{} & {} (g_{tt})_{\textrm{int}}(R_b)=(g_{tt})_{\textrm{ext}}(R_b) \,, \nonumber \\{} & {} (g_{rr})_{\textrm{int}}(R_b)=(g_{rr})_{\textrm{ext}}(R_b)\,, \end{aligned}$$

(39)

the latter in particular providing

$$\begin{aligned} 1- \frac{b(R_b)}{R_b} = 1- \frac{2M}{R_b}\,. \end{aligned}$$

(40)

This condition allows us to obtain the wormhole mass as a function of the fluid parameters $\alpha$ and $\beta$, of the throat size $r_0$ and of boundary $R_b$ of the matter distribution as:

$$\begin{aligned} M= & {} \frac{b(R_b)}{2} = \frac{1}{2} \left[ \frac{R_b}{ \beta } \left( \frac{\text {arctanh} ( C_1 R_b )}{C_1 R_b} -1 \right) - C_2 \right] \end{aligned}$$

(41)

$$\begin{aligned}= & {} \frac{1}{2 } \left[ \frac{R_b}{ \beta } \left( \frac{\text {arctanh} ( 2 \sqrt{ - 2 \pi \beta /\alpha } R_b )}{2 \sqrt{ - 2 \pi \beta /\alpha } R_b}-1\right) \right. \nonumber \\{} & {} \left. - r_0 \left( \frac{ \textrm{arctanh} (2 \sqrt{ - 2 \pi \beta /\alpha } \textrm{r}_0)}{2\sqrt{ - 2 \pi \beta /\alpha } r_0} -1 -\beta \right) \right] , \end{aligned}$$

(42)

where we have used Eqs. (21) and (36). For having a positive mass, the shape function should be positive at the boundary; this can be interpreted as a (implicit) condition setting the size of the boundary. At lowest order in $\alpha \approx 0$, the positivity of the mass requires $8 \beta \pi R_b^2 r_0-8 \pi \beta (\beta +1) r_0^2 R_b + \alpha (r_0 -R_b) <0$, which then delivers the constraint

$$\begin{aligned} R_b > \frac{8\pi \beta (\beta +1) r_0+ \alpha -\sqrt{[8 \pi \beta (\beta +1) r_0^2 ]^2+ \beta \alpha \pi (\beta -1) (4 r_0)^2+ \alpha ^2}}{16 \pi \beta r_0} \,, \end{aligned}$$

(43)

where the well-posedeness of the square root is guaranteed if $r_0< \sqrt{\frac{(\beta -1 -2\sqrt{-\beta }) \alpha }{8\pi \beta (1+\beta )^2}}$. Furthermore, we remark that our wormhole is now supported by a finite amount of matter because the upper endpoint in the integral (35) should now actually be $R_b$. Then, the amount of “complexity” contained in our wormhole solution can be computed via the Christodoulou–Rovelli volume⁵ [66, Eq.(27)]:

$$\begin{aligned} V_{\textrm{CR}}=3\sqrt{3} \pi M^2 v. \end{aligned}$$

(44)

Considering the location of the boundary $R_b$ as the upper endpoint in the integration for the complexity factor (35), we can recast

$$\begin{aligned} V_{\textrm{CR}} = 3 \sqrt{3} \pi \left[ 2I_V -R_b +\left( \frac{1}{\beta } -\beta \right) (R_b-r_0)\right] ^2 v,\nonumber \\ \end{aligned}$$

(45)

providing a quadratic dependence between complexity factor and Christodoulou–Rovelli volume. It is also interesting to compare the behaviors of these two quantities for thinner and thinner matter shells supporting the wormhole, e.g. for $R_b - r_0 \approx 0$,:

$$\begin{aligned}&I_V \approx \frac{\beta (\beta + 1) + \alpha \rho _0}{2 \beta } (r_0 - R_b) \,, \nonumber \\&V_{\textrm{CR}} \approx 3 \sqrt{3} \pi r_0^2 v + 48 \sqrt{3} \pi ^2 \rho _0 r_0^3 (R_b -r_0)\,, \end{aligned}$$

(46)

where $\rho _0$ is the energy density (23) evaluated on the throat $r_0$. While the complexity factor vanishes in this regime, consistently with the lack of any matter field within the spacetime, the Christodoulou-Rovelli volume does not (as indeed it is non-zero even for vacuum spacetimes as Schwarzschild).

A shadow of size $r_{\textrm{sh}}=3\sqrt{3}M$ is cast by our wormhole spacetime if the light rays generating the photon sphere actually travel inside the exterior Schwarzschild region⁶ [7], which condition can be realized if the shadow is located outside the boundary of the black hole. This condition can be translated into a relationship between the border and the throat as $R_b < r_{\textrm{sh}}= 3\sqrt{3} M=\frac{3\sqrt{3} b(R_b)}{2}$, which at the lowest order in $\alpha$ becomes

$$\begin{aligned}{} & {} 8 \beta \pi (3\sqrt{3}+2\beta ) r_0 R_b^2- [24 \pi \beta (\beta +1) r_0^2 + 3\alpha ] R_b\nonumber \\{} & {} \quad +3 \sqrt{3}\alpha r_0 <0 \,. \end{aligned}$$

(47)

This sets the upper constraint on the boundary location⁷

$$\begin{aligned} R_b < \frac{3 [8 \pi \beta (\beta +1) r_0^2+\alpha ] \sqrt{3} -\sqrt{1728[\pi \beta (\beta +1)r_0^2]^2 +48 \pi \alpha \beta [9(\beta -1)-4 \sqrt{3}\beta ] r_0^2 +27\alpha ^2}}{16 \pi \beta r_0 (3 \sqrt{3}+2 \beta )} \,. \end{aligned}$$

(48)

Likewise, we can claim that our wormhole solution bends the light rays by an angle $\hat{\alpha } \approx 4M/ {{\mathcal {B}}}$ where ${{\mathcal {B}}}$ is the impact parameter, and that the perihelion of the orbits of massive particles advances by $\Delta \phi = 6\pi M/r$ from one closed orbit to the next. Once again, we have used that light rays are traveling in the exterior Schwarzschild region [67, Sect.6.3], but invoking our wormhole mass (41). Thus, for an observer located in the exterior region, our wormhole solution is fully characterized by only one meaningful astrophysical parameter, its mass M, in terms of which the phenomena of shadow and light bending are accounted for, and not two ($\alpha$ and $\beta$ from the equation of state of the matter field supporting the wormhole): this is consistent with the no-hair theorem for solutions of the Einstein field equations [68, p.876]. However, the physical mechanism behind those very same astrophysical phenomena is completely different in the two scenarios (wormhole vs. Schwarzschild black hole), calling for a study of the perturbations of our wormhole solution in Sect. 4: this will help us to identify specific astrophysical signatures of our solution.

The study of the motion of test particles in our wormhole solution should be further complemented by investigating whether a massive body starting its motion inside the fluid distribution can escape to the exterior region. For answering to this question, we will consider a radial motion, for which:

$$\begin{aligned} \frac{\textrm{d}{t}}{\textrm{d}{\tau }}~{=}~\gamma \,, \qquad \frac{\textrm{d}{r}}{\textrm{d}{\tau }}\equiv \frac{\textrm{d}{r}}{\textrm{d}{t}} \cdot \frac{\textrm{d}{t}}{\textrm{d}{\tau }}~{=}~ \gamma v \,, \qquad \frac{\textrm{d}{\theta }}{\textrm{d}{\tau }}{=}0\,, \qquad \frac{\textrm{d}{\phi }}{\textrm{d}{\tau }}~{=}~0\,, \end{aligned}$$

(49)

where $\tau$ is the proper time, and $\gamma = 1/\sqrt{1-v^2}$ the Lorentz factor. Applying a timelike normalization $\textrm{d}{s}^2=-1$ to (1) with (9), we can find the radial dependence of the particle spatial velocity:

$$\begin{aligned} v^2 = \frac{(b(r)-r)(r-r_1)}{b(r) r} \,. \end{aligned}$$

(50)

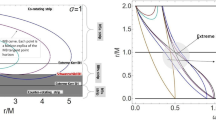
First of all, we note that on the throat the velocity vanishes, while $\frac{\textrm{d}{v}}{\textrm{d}{r}} \Big |_{r_0} \rightarrow \infty$, and that massive particles can be accelerated to ultrarelativistic speed by the wormhole geometry⁸. We depict in Fig. 1, the radial evolution of the velocity (50) with the shape function (21), and setting $r_1=10.0$, $r_0=2.0$, and $\alpha =0.5$. We can identify a maximum in the profile of the velocity, but most importantly the massive body is allowed to reach only a certain maximum distance from the throat due to the latter requirement of the physical constraint $0 \le v^2 \le 1$; thus massive objects can escape into the vacuum exterior region only if the size $R_b$ of the wormhole is small enough (by changing $\alpha$ the main characteristics of the plot remain almost unaffected, while decreasing the value of $r_0$ makes the physically allowed region larger). Specifically, the more phantom the fluid (6) is, e.g. the more negative $\beta$, the smaller the wormhole should be for allowing the test particle to cross the border to an exterior region.

Fig. 1

In this figure, we depict the radial profile of the square of the spatial velocity $v^2$ of a massive test particle traveling inside the region of our wormhole spacetime filled by the matter field, as given by (50) with (21), and setting $r_1=10.0$, $r_0=2.0$, and $\alpha =0.5$. We identify a maximum, and the possibility of the particle to reach an exterior region only for certain sizes of the wormhole due to the physical requirement $v^2>0$. Specifically, larger values of $|\beta |$ would require a smaller wormhole for allowing an escape of the massive body

We will now deepen our discussion about the properties of the boundary $R_b$. The Darmois-Israel surface stresses [69,70,71,72,73] (see also [37, Eqs. (30)–(31)] for their computations in the scenario of a wormhole supported by a Shan–Chen phantom fluid) can be obtained via the Lanczos equations:

$$\begin{aligned} \sigma= & {} -\frac{1}{4\pi R_b} \left( \sqrt{1-\frac{2M}{R_b}} - \sqrt{1-\frac{b(R_b)}{R_b}} \right) \end{aligned}$$

(51)

$$\begin{aligned} {{\mathcal {P}}}= & {} \frac{1}{8\pi R_b} \left( \frac{1-\frac{M}{R_b}}{\sqrt{1-\frac{2M}{R_b}}} -[1+R_b \Phi '(R_b)] \sqrt{1-\frac{b(R_b)}{R_b}}\right) ,\nonumber \\ \end{aligned}$$

(52)

where the former vanishes, as in the mentioned Shan–Chen scenario, because of the matching condition (40). For the latter we obtain:

$$\begin{aligned} {{\mathcal {P}}} = \frac{1}{16 \pi R_b} \cdot \frac{1-\frac{b(R_b)}{2 R_b}}{\sqrt{1-\frac{b(R_b)}{R_b}}} = \frac{1}{16 \pi R_b} \cdot \frac{1-\frac{M}{ R_b}}{\sqrt{1-\frac{ 2M}{R_b}}} \,, \end{aligned}$$

(53)

in which we have used (9), (41), and where (21) is understood; thus, the surface tangential pressure is positive, due to the Lorentzian signature of the metric, as for the Shan–Chen wormhole [37].

The radial and azimuthal epicyclic frequencies are related to the radial and azimuthal epicyclic angular velocities via $\nu _r =\Omega _r/(2\pi )$ and $\nu _\phi =\Omega _\phi /(2\pi )$, respectively. Epicyclic frequencies correspond to the particle oscillation frequencies, should the particle be moving along a closed orbit disturbed by some small perturbations [74]. The radial and azimuthal epicyclic angular velocities for our wormhole solution can be computed by applying [75, 76, 77, Eqs.(22)-(23)]:

$$\begin{aligned} \Omega _r^2= & {} e^{2\Phi (r_0)}\frac{b(r_0) -r_0}{r_0} \left[ 2\Phi '^2(r_0) - \frac{3 \Phi '(r_0)}{r_0} -\Phi ''(r_0)\right] , \nonumber \\ \end{aligned}$$

(54)

$$\begin{aligned} \Omega _\phi= & {} e^{\Phi (r_0)}\sqrt{\frac{\Phi '(r_0)}{r_0}}. \end{aligned}$$

(55)

These results hold for static and spherically symmetric wormholes, and therefore can be applied to our new solution. The former vanishes due to the requirement $b(r_0)=r_0$ on the wormhole throat (the quantity within square brackets is regular for our choice $\Phi (r)=\frac{1}{2}\ln \frac{r_1}{r}$). For the latter we obtain $\Omega _\phi = \frac{i}{\sqrt{2}r_0}$ where i denotes the imaginary unit. It is now worthwhile to recall that for a Kerr black hole [74, Eq.(10.51)]

$$\begin{aligned} \Omega _\phi =\frac{M^{1/2}}{r^{3/2} \pm a M^{1/2}} \end{aligned}$$

(56)

is a real quantity for every possible value of angular momentum a and mass M. Thus, the astrophysical measurement of the azimuthal epicyclic frequency allows to discriminate between our wormhole solution and a Kerr black hole. However, this would not necessarily be the case for the radial epicyclic frequency. For a Kerr black hole it reads as [74, Eq.(10.52)]

$$\begin{aligned} \Omega _r = \frac{M^{1/2}}{r^{3/2} \pm a M^{1/2}} \sqrt{1-\frac{6M}{r} \pm \frac{8 a M^{1/2}}{r^{3/2}} -\frac{3 a^2}{r^2}} \,, \end{aligned}$$

(57)

where the positive/negative sign applies to co/counter rotating orbits, respectively. The radial epicyclic angular velocity for a Kerr black hole vanishes not only for an observer located at spatial infinity, but also for an observer located at $r_*$ such that:

$$\begin{aligned} x^4 -6M x^2 \pm 8 a M^{1/2} x -3a^2=0\,, \qquad x=r_*^{1/2}\,. \end{aligned}$$

(58)

The existence of real roots should be checked by studying the sign of the discriminant, which however is not necessary for this equation. In fact, two (distinct) real solutions are guaranteed if $\Delta <0$; in our case real roots (specifically four and distinct or two and double) are guaranteed also if $\Delta >0$ or if $\Delta =0$ because⁹$P:=8AC=-48M<0$ [78]. While their mathematical form might be not so friendly, the astrophysical consideration behind this analysis should be clear: measuring only the radial epicyclic frequency is, for some observers, not conclusive for discriminating between our wormhole solution and a Kerr black hole. On the other hand, unlike the previously identified degeneracies, we can rule out the occurrence of the 3:2 resonance of the quasi-periodic oscillations in our model [79].

4 Perturbations, and quasi-normal modes of oscillation

In this section, we will search for specific signatures of our novel spacetimes by investigating the time evolution of the quasi-normal modes of oscillation due to scalar and electromagnetic perturbations. This requires us to compute the eigenvalues $\omega$ of the Schrödinger-like equation [10]

$$\begin{aligned} \left( \frac{d ^2}{d r^2_*} +\omega ^2 -V(r_*) \right) \Psi (r_*)=0\,, \end{aligned}$$

(59)

where

$$\begin{aligned} r_*(r) := \int \frac{\textrm{d}{r}'}{e^{\Phi (r')} \sqrt{1-b(r')/r'}} \end{aligned}$$

(60)

is the tortoise coordinate, and the potentials for electromagnetic and massless scalar field perturbations read as [80]

$$\begin{aligned} V_{\textrm{ele}}(r)= & {} e^{2 \Phi (r)}\frac{l(l+1)}{r^2} , \end{aligned}$$

(61)

$$\begin{aligned} V_{\textrm{ms}}(r)= & {} V_{\textrm{ele}}(r) + \frac{1}{2r}\frac{d}{dr} \left[ e^{2 \Phi (r)} \left( 1-\frac{b(r)}{r}\right) \right] , \end{aligned}$$

(62)

respectively. We can note that these potentials depend on the metric coefficients of our solution, but not on the physical interpretation we choose to give to the supporting matter content of our spacetime, e.g. a (Modified) Berthelot fluid or a free Dirac–Born–Infeld scalar field [32]. Keeping in mind the mitigating role that the parameter $\alpha$ has on the null energy condition (34), we consider appropriate to tackle the computation of the frequencies of the quasi-normal modes in the WKB approximation as formulated in [81, 82]:

$$\begin{aligned} i \frac{\omega ^2 -V_0}{\sqrt{-2V''_0}}-\sum _{j=2}^k \Lambda _j = k+\frac{1}{2}\,, \end{aligned}$$

(63)

where $V_0$ and $V_0''$ denote the maxima of the potential and of its second derivative (with respect to the tortoise radial coordinate), k is the order of perturbation, and $\Lambda _j$ are the higher-order corrections. For example, this method has been applied to the previously mentioned Casimir wormholes in [83] and to the reconstruction problem for the wormhole geometry from information about the quasi-normal modes in [10]. At second order the frequency of oscillation is [84]:

$$\begin{aligned} \omega ^2= V_0 - i \left( n +\frac{1}{2}\right) \sqrt{-2V_0''}\,. \end{aligned}$$

(64)

For finding the maxima with respect to the tortoise radial coordinate we use the chain rule for derivatives and notice that $\frac{\textrm{d}{r}}{\textrm{d}{r}_*} = \frac{\sqrt{r_1(r-b(r))}}{r}>0$. The potential governing the electromagnetic perturbations (61) is fully determined by the redshift function, and by using (9), it specifies as

$$\begin{aligned} V_{\textrm{ele}}(r)= \frac{l(l+1)r_1}{r^3}\,. \end{aligned}$$

(65)

Thus $V_{\textrm{ele 0}}=\frac{l(l+1)r_1}{r_0^3}$ since the maximum is achieved on the throat (the potential is monotonically decreasing with respect to the radial coordinate r, which itself is monotonically increasing with respect to the tortoise coordinate $r_*$). Next, we can compute

$$\begin{aligned} \frac{\textrm{d}{V}_{\textrm{ele}}}{\textrm{d}{r}_*} = - \frac{3 r_1^{3/2}l(l+1) \sqrt{r - b(r)}}{r^5}\,, \end{aligned}$$

(66)

and then

$$\begin{aligned} \frac{{d} ^2 V_{\textrm{ele}}}{d r_*^2}= & {} \frac{3l(l+1) r_1^2 }{r^6} \left[ \frac{9}{2}-\frac{5 b(r)}{r} + \frac{\textrm{d}{b}(r)}{2\textrm{d}{r}} \right] \nonumber \\= & {} \frac{ 3l(l+1)r_1^2 }{r^6} \left[ \frac{9}{2} -\frac{5b(r)}{r} + 4 \pi r^2 \rho (r) \right] \end{aligned}$$

(67)

$$\begin{aligned}= & {} \frac{3 l(l+1) r_1^2 }{r^6} \left[ \frac{9}{2} -\frac{5 b(r)}{r} -\frac{4 \pi r^2}{8 \pi \beta r^2 + \alpha }\right] , \end{aligned}$$

(68)

where (4) and (19) have been used, and (21) (or (23)) is understood. The second derivative of the elctromagnetic potential achieves its maximum on the throat as well.¹⁰ Therefore, we obtain the frequency of the quasi-normal modes of oscillation for electromagnetic perturbations at the second order of approximation to be:

$$\begin{aligned} \omega _{\textrm{ele}}^2&= \left[ l(l+1) - i \left( n +\frac{1}{2}\right) r_1 \right. \nonumber \\&\quad \times \left. \sqrt{3 l(l+1)\left( 1+\frac{8\pi r_0^2}{8 \pi \beta r_0^2 +\alpha } \right) }\right] \frac{r_1}{r_0^3}. \end{aligned}$$

(69)

The following properties are worthy commenting: (i) the frequency is purely real and inversely proportional to the size of the throat, and so the wormhole is stable, if $r_0 \le \sqrt{-\frac{\alpha }{8 \pi (1+\beta )}}$ showing that large values of (negative) $\beta$, e.g. strong breaking of the null energy condition, play a stabilizing role; (ii) thus, due to the vanishing of the imaginary part, the quasi-resonance characterizing massive scalar fields in the Reissner–Nordström black hole background [80] can be mimicked, which is a property shared with Casimir wormholes [83] (this might be due to the common feature of the maxima of the potential and its second derivative occurring all on the throat); (iii) in the case of a complex frequency, both the real and imaginary parts are still inversely proportional to the size of the throat; (iv) nothing can be claimed about the size $R_b$ of the wormhole; (v) the frequency of the quasi-normal modes of oscillations under electromagnetic perturbations are complex both in the limit of negligible (recalling that $\beta <-1$) and strong deviation from an ideal fluid equation of state supporting our wormhole solution:

$$\begin{aligned} \lim _{\alpha \rightarrow 0} \omega _{\textrm{ele}}^2&{=}\left[ l(l+1) {-} i \left( n {+}\frac{1}{2}\right) r_1 \sqrt{\frac{3 l(l{+}1) (\beta {+} 1)}{\beta } }\right] \frac{r_1}{r_0^3}\,,\nonumber \\&\quad \times \lim _{\alpha \rightarrow \infty } \omega _{\textrm{ele}}^2 =\left[ l(l+1) - i \left( n +\frac{1}{2}\right) \right. \nonumber \\&\quad \left. \times r_1 \sqrt{3 l(l+1) }\right] \frac{r_1}{r_0^3}\,. \end{aligned}$$

(70)

By using Eqs. (4), (9), (21), after some algebraic manipulations, we can recast the potential for massless scalar field perturbations (62) for our specific wormhole solution into the following form:

$$\begin{aligned}&V_{\textrm{ms}}(r)= \frac{r_1}{r} \left[ \frac{\ell }{2 r^2} + \frac{b(r) }{r^3} - 4 \pi \rho (r) \right] \nonumber \\&= \frac{r_1}{r} \left[ \frac{\ell }{2 r^2} + \frac{b(r) }{r^3} + \frac{4 \pi }{ 8 \pi \beta r^2 + \alpha }\right] \,,\nonumber \\ \ell&=2 l(l+1) - 1\,. \end{aligned}$$

(71)

By using again the chain rule for computing the derivative with respect to the tortoise coordinate, and (19) for expressing the derivative of b(r), we obtain:

$$\begin{aligned}{} & {} \frac{\textrm{d}{V}_{\textrm{ms}}}{ \textrm{d}{r}_*} =\nonumber \\{} & {} {=} {-} \frac{ r_1^{3/2} \sqrt{r{-}b(r)}[128\pi ^2\beta r^5 \rho ^2{-}24\pi r^3 \rho {+}3\ell r{+}8b(r)]}{2 r^6}\nonumber \\ \end{aligned}$$

(72)

$$\begin{aligned}= & {} -\frac{96 r_1^{3/2}\sqrt{r-b(r)}}{r^6 (8\pi \beta r^2 +\alpha )}\nonumber \\{} & {} \times \left[ \frac{(8\pi \beta r^2 +\alpha )^2 b(r)}{24}\right. \nonumber \\{} & {} \left. +\left( \frac{\pi ^2\beta (3\ell \beta +5)r^4}{3} +\frac{\pi \alpha (2\ell \beta +1)r^2}{8} +\frac{\ell \alpha ^2}{64}\right) r\right] ,\nonumber \\ \end{aligned}$$

(73)

and

$$\begin{aligned} \frac{d^2 V_{\textrm{ms}}}{ d r_*^2}&= \frac{6 r_1^2}{r^8} \Bigg [ -4b^2(r)+\frac{5rb(r)}{4}\times \left( \frac{4096 \pi ^3 \beta ^2 r^6 \rho ^3 -512\pi ^2\beta r^4 \rho ^2 +44}{15}+\frac{56\pi r^2 \rho }{5}-\ell \right) \nonumber \\&\quad + r^2 \left( \frac{128 \pi ^3 \beta \rho ^3 r^6(8\beta -1) +8 \pi ^2\rho ^2 r^4(14 \beta -3) +\pi \rho r^2 (3\ell -31)}{3}+\frac{9 \ell }{8}\right) \Bigg ] \end{aligned}$$

(74)

$$\begin{aligned}&= \frac{3456 r_1^2}{r^8 (8\pi \beta r^2 +\alpha )^3} \sum _{k=0}^{2} A_k(r) r^{2-k} b^k(r)\,, \end{aligned}$$

(75)

$$\begin{aligned} A_0(r)&:= \beta \pi ^3 r^6 \left( \ell \beta ^2 + \frac{(61-3 \ell )\beta -5}{27} \right) +\frac{3 \pi ^2 \alpha r^4}{8}\left( \ell \beta ^2 +\frac{(38 -3 \ell )\beta -3}{81} \right) +\frac{3\pi \alpha ^2 r^2}{64} \left( \ell \beta +\frac{31 -3\ell }{81} \right) +\frac{\ell \alpha ^3}{512} \,, \end{aligned}$$

(76)

$$\begin{aligned} A_1(r)&:= \frac{2\beta ^2 \pi ^3 r^6(44\beta -15\ell \beta -37)}{27}+ \frac{\beta \pi ^2 \alpha r^4 (132 \beta -45\ell \beta -50)}{108}+ \frac{\pi \alpha ^2 r^2 (44 \beta -15\ell \beta -7)}{288} +\frac{\alpha ^3 (15\ell -44)}{6912}\,, \end{aligned}$$

(77)

$$\begin{aligned} A_2(r)&:= -\frac{32}{9} \left( \pi \beta r^2 +\frac{\alpha }{8} \right) ^3. \end{aligned}$$

(78)

At this stage it becomes necessary to devise some numerical technique for computing the maxima of the potential (71) and of its second derivative (74) for specific couples of values of ($\alpha$, $\beta$). We think that it might be more insightful to provide some closed form results, albeit approximated, rather than numerical. We will consider $\alpha \approx 0$ and obtain:

$$\begin{aligned}{} & {} V_{\textrm{ms}}(r)=\nonumber \\{} & {} =\frac{r_1 [16 \pi \beta (\beta +1)r r_0^2 \!+\!(8\pi \beta (\ell \beta \!-\!1)r^2\!-\!3\alpha )r_0\!+\!2\alpha r]}{16 \pi \beta ^2 r_0 r^5} \nonumber \\{} & {} + O(\alpha ^2), \end{aligned}$$

(79)

whose maximum is located at the throat.¹¹ Next, we compute

$$\begin{aligned}{} & {} \frac{d^2 V_{\textrm{ms}}}{ d r_*^2} = \sum _{i=6}^9 \frac{A_i}{r^i} + O(\alpha ^2), \end{aligned}$$

(80)

$$\begin{aligned}{} & {} A_6 = \frac{27 [\ell \beta -1 ](1+\beta )}{4 \beta ^2} , \end{aligned}$$

(81)

$$\begin{aligned}{} & {} A_7 = \frac{[8 \pi \beta (1+\beta ) r_0^2 +\alpha ] [59+(44-15\ell )\beta ]}{16 \pi \beta ^3 r_0} , \end{aligned}$$

(82)

$$\begin{aligned}{} & {} A_8 \nonumber \\{} & {} {=} {-}\frac{768\pi r_0^2 \beta ^3{+}1536\pi r_0^2\beta ^2 {+}[768 \pi r_0^2{+}(387{-}33\ell )\alpha ]\beta {+}420 \alpha }{32 \pi \beta ^3} , \nonumber \\ \end{aligned}$$

(83)

$$\begin{aligned}{} & {} A_9 =\frac{157 \alpha (1+\beta ) r_0}{16 \pi \beta ^3}. \end{aligned}$$

(84)

By noticing that $A_6>0$ and that the numerators are given by some constants independent of r, for maximizing the function we minimize the denominator and obtain once again¹²$r=r_0$. Therefore, for the frequency of the quasi-normal modes of oscillation for massless perturbations, we obtain:

$$\begin{aligned}&\omega ^2_{\textrm{ms}}= \frac{r_1}{r_0^4} \left[ \frac{ 8 \pi r_0^2 \beta [(\ell +2) \beta + 1] -\alpha }{\pi \beta ^2 }- \frac{i}{4} \left( n +\frac{1}{2}\right) \right. \nonumber \\&\quad \left. {\times } \sqrt{\frac{8\pi r_0^2 \beta [3 \ell \beta (1+\beta ){+} (8\beta +13)\beta +5] {-}3[(\ell +5)\beta +4]\alpha }{ \pi \beta ^3}}\right] \nonumber \\&\quad +O(\alpha ^2)\,, \end{aligned}$$

(85)

where we can note that the argument of the square root is positive for large $\ell$. This result provides a consistency check with the previously identified lack of circular orbits for massless particles when we inspected Eq. (13). In fact, the Lyapunov exponent $\gamma$ which governs the stability of the orbit as $\delta r_n =e^{\gamma n}\delta r_{\textrm{in}}$, where $\delta r_{\textrm{in}}$ and $\delta r_n$ are the initial perturbation and the perturbation after n turns to the radius of such orbit, is $\gamma \sim \sqrt{-2 V''_{\textrm{ms0}}}>0$ indicating that these orbits are quickly destroyed [85, 86].

5 Conclusion

Wormhole geometries have been studied recently both from the purely theoretical and the astrophysical perspectives. In the former context, an invariant procedure for locating the throat via appropriate curvature scalars has been proposed in [87], while a mechanism for realizing multithroat spacetimes has been discovered in [88]. On the other hand, the possibility of distinguishing astrophysically a wormhole from other compact objects by tracking the motion of nearby stars has been put forward in [89]: this procedure relies on the lack of energy conservation on one side of the throat, should matter falls into it and end up on the other-side connected universe. Thus, the finding of new wormhole geometries is in order because it can help in advancing the understanding of such compact objects.

In this paper, we have presented new solutions of the Einstein equation for a transparent static spherically symmetric spacetime supported by a (Modified) Berthelot fluid. They are constituted by Eq. (1) with (9) and (21). We have specifically explained that the former two equations, which can be assumed independently on considerations about the specific matter content of the spacetime, already allow to identify some properties of the novel solutions as the possible existence of a singularity and the lack of a photon sphere. We have also clarified that the existence of an horizon hiding the singularity depends, for our fluid modeling, on having a gravitational collapse governed by an isotropic pressure, while we can have a wormhole throat for a suitable choice of the integration constant. We could provide analytical results for the amount of “complexity” of the spacetime and relate it to the Christodoulou-Rovelli volume. We also proposed an interpretation of the former, as far as our model in concerned, as a quantity setting the size of the throat of the wormhole. We have proposed as well some possible astrophysical applications of our solutions depending on whether we choose to match them with an exterior spacetime (analyzing the shadow) or not (by identifying the asymptotically flatness of rotation curves). The taming of the breaking of the null energy condition has been pointed out, and an equation of state for the tangential pressure could be found in a closed form. We emphasize that we have not “cooked up” a new equation of state for the radial pressure, but we have actually adopted the (Modified) Berthelot model (6) because it has already received attention in the cosmological literature [27,28,29,30,31], also being shown to correspond to the hydrodynamical realization of the free Dirac–Born–Infeld model [32]. We have analyzed the stability of our wormhole solution by computing analytically the frequency of the quasi-normal modes of oscillation in the eikonal limit, which have revealed that actually their analysis alone might be inconclusive for identifying the nature of an astrophysical compact object due to the identification, for some sets of the free parameters, of a quasi-resonance which is typical also of the Reissner–Nordström black hole.

In this paper, we have investigated the features of our novel wormhole solution from the astrophysical perspective only, without relying on field-theoretic considerations. For example, nothing has been claimed about the entropy, temperature and possible evaporation of our wormhole. We should nevertheless mention Hod’s conjecture according to which the temperature T might be essentially given by the real part of the frequency of the quasi-normal modes [90]: by applying it to our Eq. (85), we would obtain that a wormhole with a throat size such that $r_0 \sim \sqrt{\alpha /(8\pi \ell \beta ^2)}$ would exist at $T=0$. Furthermore, having in hand an manageable exact solution constituted by our Eqs. (1), (9), (21) can allow for an inspection of the ER=EPR correspondence conjecture [91]. All these topics are left for future investigations.