1 Introduction

Expansion and density fluctuation among galaxies characterize the vast structure of the universe. In our galaxy, there exist billions of white dwarfs, a few hundred million neutron star clusters, and millions of black holes. Only a tiny percentage of these white dwarfs, neutron stars, and black holes have been observationally detected by astronomers. It is observed by scientists that every center of a galaxy has super-massive black holes [2]. The main ingredients of galaxies are stars, gas, dust, dark matter, and dark energy that are held together by gravity. Ordinary matter is made up of protons, neutrons, and electrons. Everything, we can see or detect with telescopes is normal matter. Approximately 95 percent of the total matter content is attributed to dark matter, making it the dominant force in the mass budget. Galaxies come in an abundance of patterns and sizes, and they can be generally described into three main categories based on their shape: elliptical galaxies, spiral galaxies, and irregular galaxies [3].

Albert Einstein introduced general relativity (GR) as the geometric theory of gravitation [4]. There are three fundamental postulates that constitute a framework for Einstein’s theory that are the principle of general covariance, the relativity principle, and the equivalence principle. The theory of GR is most effective in explaining weak gravitational fields, but it lacks a comprehensive detail of strong field regimes [5]. The set of Einstein field equations (FEs) is a direct consequence of GR. The gravitational interaction between compact objects is described by these FEs which helps us to explain the light propagation and motion of particles.

General relativistic FEs are significant in the description of the dynamics of the universe. Although GR gives accurate results for small distances, it has some limitations when it comes to to explain the behavior of the universe at later times [6]. The constituents of the universe, dark matter and dark energy have been extensively combined through modified gravity theories. There are many theories related to modified gravity have been presented and some of these are f(G), f(T), f(R), f(G, T), f(R, T) gravity, etc. f(R) gravity is the extension of GR in which R be the Ricci scalar and it is introduced by the Sotiriou and Faraoni [7,8,9,10,11,12].

By extending the concept of f(R), Harko [13] introduced f(R, T) gravity. In f(R, T) gravity, the action covers a function that is arbitrary with respect to the Ricci scalar R and the trace of the energy–momentum tensor T, allowing for the formation of exotic matter. This theory explains that matter and geometry both have equally proportioned in celestial objects. After its introduction a lot of work have been done by authors who explain various properties including energy conditions, dynamical implication, galaxy clustering, and weak lensing. The f(R, T) theory has been suggested as another description for the identified quick extension of the universe, which is described by the presence of dark energy [14,15,16,17].

There exist a extensive works in literature in the field of cosmology regarding the applications of f(R, T) gravity. Jamil et al. [18] have developed some cosmological frameworks in f(R, T) gravity by using f(R, T)=\(R^2+f(T)\). Shabani and Farhoudi [19] explained the results of f(R, T) gravity models by using the Hubble parameter, weight function and equation of state (EoS) parameters. The authors in [20, 21] discussed the evolution of axially symmetric anisotropic sources and shear-free condition and dynamical instability in f(R, T) gravity. Zubair et al. [22] also discussed the stability of cylindrically symmetric object with anisotropic fluid in f(R, T) gravity.

The stability analysis of stellar models holds significant importance in gravitational theories. If the opposing forces of inward and outward attraction are balanced, a compact object reaches a stable condition. Neutron stars, white dwarfs, stellar mass, and super-massive black holes can be formed through the gravitational collapse of compact objects [23]. No developed model can be employed to describe stars unless stability is thoroughly discussed. The astronomical bodies remain stable if they show resistance against fluctuations. The first step towards establishing the stability of gravitating compact objects through the criteria of the adiabatic index was presented by Bondi [24]. Chandrasekhar [25] conducted preliminary investigations on the dynamical stability of spherical bodies at a primary level. He points out that the condition of instability of compact object having radius r and mass M by a component gamma \(\Gamma \) consideration to the inequality \(\Gamma \ge \frac{4}{3}+n\frac{M}{r}\).

The stability of the gravitating system can be well explained by some suitable perturbation approach. In stability analysis of mathematical models of stars, perturbation plays a critical role [26]. It estimates the complete structure of the phases of stars that explain the stability and instability range of compact objects. Regge and Wheeler [27] stated a metric perturbation approach using the stability criteria for the relativistic objects. Local density perturbation (LDP) is also used to investigate the stability of compact objects in which all parameters are examined to be density dependent. Noureen et al. [28] introduced f(R) model of dynamical instability that demonstrates a greater chance for correcting higher-order curvatures.

Herrera and his coworker [29, 30] introduced the cracking technique as an alternate method to analyze the instabilities that occurs in compact objects. Whenever there is a change in the sign of perturbations within radial forces, cracking takes place in gravitating compact objects due to the evolution of these forces. When the equilibrium condition of compact objects is disturbed, the inner fluid distribution of compact objects shows cracking. It contributes significantly to the improvement of the stability regions of the compact star model.

Gonzalez et al. [31] studied the physical characteristics that depend on density and included local density LDP to both isotropic and anisotropic matter distributions. By adding changes to the physical parameters, Azam and Mardan [32, 33] observed cracking in charged spherical polytropes. Sharif and Sadiq [34] explored how density fluctuations affect both isotropic and anisotropic matter configurations using a barotropic equation of state within the framework of general relativity. Malik et al. [35] explain the cracking techniques by using local density perturbation in the framework of f(R, T) gravity.

The authors in [36,37,38,39] explained the structure of stellar models of compact objects in the modified gravities. The internal structure such as mass–radius relationship of neutron stars and other structural properties in f(R) gravity are studied in [40, 41]. The rotation of neutron stars in the modified gravities such as \(f(R), R, R^2\) -gravity and also scalar tensor theories gives the description of compact objects in [42,43,44,45,46,47]. The structure of compact objects such as neutron star, white dwarf in the framework of modified gravity theories is discussed in [48,49,50].

This work is devoted to study the levels of stability/instability in compact objects via cracking technique in modified f(R, T) theory of gravity. The arrangement of manuscript is as follows: modified FEs and generalized TOV equation are constructed in Sect. 2. Section 3 covers assumption of density dependent perturbations of physical parameters and their application to generalized TOV equation that leads to mathematical expression for distribution of forces. Analysis of stability regions is presented with the help of graphical representation of forces for five different realistic stars in Sect. 4. The findings of research conducted are summarized in Sect. 5. The bibliography is given at the end of last section.

2 Modified field equations

In this article, we deal with f(R, T) gravity model to workout instability problem for anisotropic physically viable model. Harko et al. [13] describes the modified action for f(R, T) gravity as follows:

$$\begin{aligned}{} & {} S=\int \Big [\frac{1}{16\pi }f(R,T)+\pounds _m\Big ]\sqrt{-g}d^4 x. \end{aligned}$$
(1)

Here energy momentum tensor is denoted by \(T_{\mu \upsilon }\), \(\pounds _m\) represents the Lagrangian density and \(g_{\mu \upsilon }\) represents the determinant of the metric g. The following spherically symmetric line element explains the geometry in curvature coordinates \((t,r,\theta ,\phi )\).

$$\begin{aligned} ds^2=e^\upsilon dt^2-e^\xi dr^2-r^2 d\theta ^2-r^2 \sin ^2\theta d\varphi ^2. \end{aligned}$$
(2)

Here \(\upsilon (r)\) and \(\xi (r)\) be the metric potentials. To represent the energy–momentum tensor \(T_{\mu \upsilon }\), we use the anisotropic fluid form with four velocity \(u_\mu =(e^{\frac{\upsilon }{2}},0,0,0)\). Assuming the anisotropic nature of the matter, we can express the corresponding energy–momentum tensor as follows,

$$\begin{aligned} T_{\mu \upsilon }=(P_t+\rho )u_\mu u_\upsilon +(P_r-P_t)\upsilon _\mu \upsilon _\upsilon +P_t g_{\mu \upsilon }, \end{aligned}$$
(3)

where \(u^\mu \nabla _\upsilon u_\mu =0\) and \(u^\mu u_\upsilon =1\). Here \(\upsilon _\mu \), \(P_t(r)\), \(P_r(r)\) and \(\rho (r)\) be the radial four-vector, tangential pressure, radial pressure and energy density respectively. The equation below represents the field equations of f(R, T) gravity, which correspond to action (1).

$$\begin{aligned}{} & {} \frac{\partial f(R,T)}{\partial R} R_{\mu \upsilon }-\frac{1}{2}g_{\mu \upsilon } f(R,T)\nonumber \\{} & {} \qquad +(g_{\mu \upsilon }\Box -\nabla _\mu \nabla _\upsilon )\frac{\partial f(R,T)}{\partial R}\nonumber \\{} & {} \quad =8\pi T_{\mu \upsilon }-\frac{\partial f(R,T)}{\partial T}( T_{\mu \upsilon }+ \Theta _{\mu \upsilon }). \end{aligned}$$
(4)

Here \(\nabla _\upsilon \) shows the covariant derivative linked with the Levi-Civita connection of \(g_{\mu \upsilon }\), \(\Box =\frac{1}{\sqrt{-g}}\partial _\mu (\sqrt{-g}g^{\mu \upsilon }\partial _v)\) shows the D’ Alembertian operator, \(R_{\mu \upsilon }\) represent the Ricci tensor, \(\Theta =\frac{g^{\alpha \beta }\delta T_{\alpha \beta }}{\delta g^{\mu \upsilon }}\) and \(T_{\mu \upsilon }=g_{\mu \upsilon \pounds _m}-2\frac{\partial \pounds _m}{\partial g^{\mu \upsilon }}\).

\(T=g^{\mu \upsilon }T_{\mu \upsilon }\) provides the value of the trace of the energy momentum tensor. By applying the covariant divergence to Eq. (4), we can derive the divergence of the energy momentum tensor \(T_{\mu \upsilon }\) as follows:

$$\begin{aligned} \nabla ^\mu T_{\mu \upsilon }= & {} \frac{f_T(R,T)}{8\pi -f_T(R,T)}[( T_{\mu \upsilon }+ \Theta _{\mu \upsilon }) \nabla ^\mu \ln f_T(R,T)\nonumber \\{} & {} -\frac{1}{2}g_{\mu \upsilon } \nabla ^\mu T+\nabla ^\mu \Theta _{\mu \upsilon }]. \end{aligned}$$
(5)

It is clear from Eq. (5), \(\nabla ^\mu T_{\mu \upsilon }\ne 0\) and \(f_T(R,T)\ne 0\). We have another condition \(\Theta =-2T_{\mu \upsilon }-\rho g_{\mu \upsilon }\). By following Harko et al. [13], the selected f(R, T) model has form,

$$\begin{aligned} f(R,T)=R+2\gamma T. \end{aligned}$$
(6)

The coupling constant \(\gamma \) represents the interaction strength between matter and geometry. For the line element Eq. (2), we can derive the modified FEs as,

$$\begin{aligned}{} & {} 8\pi \rho ^{eff}=\frac{\xi ^{\prime }}{r} e^{-\xi }+\frac{1}{r^2} (1-e^{-\xi }), \end{aligned}$$
(7)
$$\begin{aligned}{} & {} 8\pi P_r^{eff}=\frac{1}{r^2} (e^{-\xi }-1)+\frac{\upsilon ^{\prime }}{r} e^{-\xi }, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} 8\pi P_t^{eff}=\frac{1}{4} e^{-\xi }(2\upsilon ^{\prime \prime }+{\upsilon ^{\prime }}^2-\xi ^{\prime }+\frac{2}{r}(\upsilon ^{\prime }-\xi ^{\prime })), \end{aligned}$$
(9)

where, \(P_r^{eff}\), \(P_t^{eff}\) and \(\rho ^{eff}\) are respectively the effective pressures and energy density, given by

$$\begin{aligned}{} & {} \rho ^{eff}=\rho +\frac{\gamma }{8\pi }(\rho -P_r-2P_t), \end{aligned}$$
(10)
$$\begin{aligned}{} & {} P_t^{eff}=P_r+\frac{\gamma }{8\pi }(\rho +3P_r+2P_t), \end{aligned}$$
(11)
$$\begin{aligned}{} & {} P_r^{eff}=P_t+\frac{\gamma }{8\pi }(\rho +P_r+4P_t). \end{aligned}$$
(12)

Here, (\({\prime }=\frac{\partial }{\partial r}\)). The FEs provide information on the curvature of space-time in the presence of matter and energy, allowing us to understand gravitational interaction within compact objects. We assume that the density and radial pressure have a linear relationship to determine the field equations in modified gravity.

$$\begin{aligned} P_r(r)=\frac{1}{3}[\rho (r)-4B_g], \end{aligned}$$
(13)

where,

$$\begin{aligned} B_g=\frac{12(a-B)\pi -5B+a}{64\pi ^2+64\pi +12}. \end{aligned}$$
(14)

By putting \(\upsilon (r)=Br^2+\ln C\) and \(\xi (r)=\ln (1+ar^2+br^4)\), which are Tolman–Kuchowicz metric potentials [51] in Eqs. (7)–(9)

$$\begin{aligned} 8\pi \rho ^{eff}= & {} \frac{2a+4br^2}{(1+ar^2+br^4)^2}+\frac{a+br^2}{(1+ar^2+br^4)}, \end{aligned}$$
(15)
$$\begin{aligned} 8\pi P_r^{eff}= & {} \frac{2B}{(1+ar^2+br^4)}-\frac{a+br^2}{(1+ar^2+br^4)}, \end{aligned}$$
(16)
$$\begin{aligned} 8\pi P_t^{eff}= & {} \frac{1}{(1+ar^2+br^4)}\nonumber \\{} & {} \times \left[ B(2+Br^2)-\frac{(a+2br^2)(1+Br^2)}{(1+ar^2+br^4)}\right] . \end{aligned}$$
(17)

Solving Eqs. (10)–(12), the final expression for matter density, radial pressure and tangential pressure in modified gravities as,

$$\begin{aligned} \rho= & {} \frac{3}{4(\gamma +4\pi )(1+ar^2+br^4)}\nonumber \\{} & {} \times \Big [\frac{a+2br^2}{1+ar^2+br^4}+B\Big ]+B_g, \end{aligned}$$
(18)
$$\begin{aligned} P_r= & {} \frac{1}{4(\gamma +4\pi )(1+ar^2+br^4)}\nonumber \\{} & {} \times \Big [\frac{a+2br^2}{1+ar^2+br^4}+B\Big ]-4B_g, \end{aligned}$$
(19)
$$\begin{aligned} P_t= & {} \frac{1}{(6\gamma +8\pi )}\Bigg [(24\pi -2\gamma )\nonumber \\{} & {} \times \Bigg \{\frac{1}{4(\gamma +4\pi )(1+ar^2+br^4)}\Bigg (\frac{a+2br^2}{1+ar^2+br^4}\nonumber \\{} & {} +B\Bigg )\Bigg \}+(8\pi +2\gamma )B_g-\frac{1}{(1+ar^2+br^4)} \nonumber \\{} & {} \times \Big [\frac{(a+2br^2)(3+Br^2)}{1+ar^2+br^4}\!+\!a\!+\!br^2-B(2\!+\!Br^2)\Big ]\Bigg ].\nonumber \\ \end{aligned}$$
(20)

We derive hydrostatic equilibrium equation by anisotropic fluid distribution as follows:

$$\begin{aligned} \Omega= & {} P_r^{\prime }\Big [1+\frac{(64\pi -6\gamma )\gamma }{8\pi (8\pi -2\gamma )}\Big ]\nonumber \\{} & {} +\rho ^{\prime }\Bigg [\frac{64\pi -6\gamma }{8\pi (8\pi -2\gamma )}\Bigg ] +P_t^{\prime }\Bigg [\frac{64\pi -6\gamma }{8\pi (8\pi -2\gamma )}\Bigg ] \nonumber \\{} & {} +\frac{2\gamma \rho }{8\pi -2\gamma }\Bigg (\frac{r^3\{\rho (8\pi +\gamma )-\gamma P_r-2\gamma P_t\}-2M}{r^2-2Mr}\Bigg )\nonumber \\{} & {} +\frac{4(16\pi ^2+8\gamma \pi -\gamma ^2)}{8\pi (8\pi -2\gamma )} \nonumber \\{} & {} \times \Bigg [\Bigg (\frac{r^3\{P_r(8\pi +3\gamma )+\gamma P_r+2\gamma P_t\}+2M}{r^2-2Mr}\Bigg )\nonumber \\{} & {} \times (\rho +P_r)-\frac{2}{r}(P_t-P_r)\Bigg ]. \end{aligned}$$
(21)

3 Local density perturbation scheme (LDP)

LDP scheme refers to a small fluctuation in the density of a physical system over a small spatial region. It can be caused by various factors such as the presence of a nearby object or a change in the temperature or pressure of the system. In Eq. (21), we incorporated the LDP into all relevant physical quantities, including mass, radial pressure, tangential pressure, and their derivatives respectively.

$$\begin{aligned}{} & {} P_t(\rho +\delta \rho )=P_t(\rho )+\frac{d P_t}{d\rho }\delta \rho , \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \frac{d P_t}{dr}(\rho +\delta \rho )\!=\!\frac{d P_t}{dr}(\rho )\!+\!\Big [\frac{d}{dr}\Big (\frac{d P_t}{d\rho }\Big ) \!+\!\frac{d P_t}{d\rho }\frac{d^2\rho }{dr^2}\frac{dr}{d\rho }\Big ]\delta \rho ,\nonumber \\ \end{aligned}$$
(23)
$$\begin{aligned}{} & {} P_r(\rho +\delta \rho )=P_r(\rho )+\frac{d P_r}{d\rho }\delta \rho , \end{aligned}$$
(24)
$$\begin{aligned}{} & {} \frac{d P_r}{dr}(\rho +\delta \rho )\!=\!\frac{d P_r}{dr}(\rho )\!+\!\Big [\frac{d}{dr}\Big (\frac{d P_r}{d\rho }\Big ) +\frac{d P_r}{d\rho }\frac{d^2\rho }{dr^2}\frac{dr}{d\rho }\Big ]\delta \rho ,\nonumber \\ \end{aligned}$$
(25)
$$\begin{aligned}{} & {} M(\rho +\delta \rho )=M(\rho )+\frac{d M}{d\rho }\delta \rho . \end{aligned}$$
(26)

The tangential and radial sound speed are defined as

$$\begin{aligned} V_t^2=\frac{d P_t}{d\rho }, \quad V_r^2=\frac{d P_r}{d\rho }. \end{aligned}$$
(27)

The Eq. (21) in its perturbed form is given by

Table 1 Determination of model parameters \(a,b,B,B_g\), radius R (km), mass M \((M_{q})\) for stars under consideration
Full size table
Fig. 1
figure 1

A graphical illustration of \(\frac{\delta \Omega ^{}}{\delta \rho }\) for PSR J1614-2230 \(a=0.00459\) (km)\(^{-2}\), \(b=0.000018\) (km)\(^{-2}\), \(B=0.00292\) (km)\(^{-2}\), \(R=10.3\) km

Full size image
$$\begin{aligned} \Omega =\Omega _\circ (M,\rho ,P_t,P_r,\rho ^{\prime },P_t^{\prime },P_r^{\prime })+\delta \Omega , \end{aligned}$$
(28)

where,

$$\begin{aligned} \delta \Omega= & {} \frac{\partial \Omega }{\partial M}\delta M+\frac{\partial \Omega }{\partial \rho }\delta \rho + \frac{\partial \Omega }{\partial P_r}\delta P_r+\frac{\partial \Omega }{\partial P_r^{\prime }}\delta P_r^{\prime } \nonumber \\{} & {} +\frac{\partial \Omega }{\partial P_t}\delta P_t +\frac{\partial \Omega }{\partial P_t^{\prime }}\delta P_t^{\prime }, \end{aligned}$$
(29)

which can also be written as

$$\begin{aligned} \frac{\delta \Omega }{\delta \rho }= & {} \frac{\partial \Omega }{\partial \rho } +\frac{\partial \Omega }{\partial \rho ^{\prime }}\Big (\frac{\rho ^{\prime \prime }}{\rho ^{\prime }}\Big )\nonumber \\{} & {} + \frac{\partial \Omega }{\partial P_r}(V_r)^2+\frac{\partial \Omega }{\partial P_r^{\prime }}\Big ((V_r^2)^{\prime }+(V_r)^2\Big (\frac{\rho ^{\prime \prime }}{\rho ^{\prime }}\Big )\Big )\nonumber \\{} & {} + \frac{\partial \Omega }{\partial P_t}(V_t)^2+\frac{\partial \Omega }{\partial P_t^{\prime }}\Big ((V_t^2)^{\prime } +(V_t)^2\Big (\frac{\rho ^{\prime \prime }}{\rho ^{\prime }}\Big )\Big )\nonumber \\{} & {} +4\pi r^2\frac{\partial \Omega }{\partial M}\Big (\frac{\rho }{\rho ^{\prime }}\Big ). \end{aligned}$$
(30)

This equation is utilized to find out the impact of LDP on the cracking of an anisotropic fluid. For various parameter values in the model, we shall show graphical representation of \(\frac{\delta \Omega }{\delta \rho }\) as a function of the radius ‘r’ for different stars. Making use of using Eq. (21), we found the derivatives involved in above Eq. (30) is given by

$$\begin{aligned} \frac{\partial \Omega }{\partial \rho }= & {} \frac{1}{(8\pi -2\gamma )(r^2-2Mr)}\nonumber \\{} & {} \times \Bigg [2\gamma [r^3\{\rho (8\pi +\gamma )-\gamma P_r-2\gamma P_t\}-2M] \nonumber \\{} & {} +2\gamma \rho r^3(8\pi +\gamma )\nonumber \\{} & {} +\frac{4(16\pi ^2+8\gamma \pi -\gamma ^2)}{2(8\pi )}\times \bigg [r^3\bigg \{(\rho +P_r)\gamma \nonumber \\{} & {} +P_r(8\pi +3\gamma )+\gamma \rho +2\gamma P_t\bigg \}+2M\bigg ]\Bigg ], \end{aligned}$$
(31)
$$\begin{aligned} \frac{\partial \Omega }{\partial P_r}= & {} \frac{1}{(8\pi -2\gamma )(r^2-2Mr)}\nonumber \\{} & {} \times \Bigg [-2\gamma ^2r^3\rho +\frac{4(16\pi ^2+8\gamma \pi -\gamma ^2)}{2(8\pi )}\nonumber \\{} & {} \times \bigg [r^3\{(8\pi +3\gamma )P_r+\gamma \rho +2\gamma P_t\}+2M\nonumber \\{} & {} + r^3(\rho +P_r)(8\pi +3\gamma )+4(r-2Mr)\bigg ]\Bigg ], \end{aligned}$$
(32)
$$\begin{aligned} \frac{\partial \Omega }{\partial P_t}= & {} \frac{1}{(8\pi -2\gamma )(r^2-2Mr)}\nonumber \\{} & {} \times \Bigg [-4\gamma ^2r^3\rho +\frac{4(16\pi ^2+8\gamma \pi -\gamma ^2)}{2(8\pi )} \nonumber \\{} & {} \times \{(\rho +P_r)\gamma r^3-2(r-2M)\}\Bigg ], \end{aligned}$$
(33)
$$\begin{aligned} \frac{\partial \Omega }{\partial \rho ^{\prime }}= & {} 1+\frac{(64\pi -6\gamma )\gamma }{8\pi (8\pi -2\gamma )}, \end{aligned}$$
(34)
$$\begin{aligned} \frac{\partial \Omega }{\partial P_r^{\prime }}= & {} \frac{(16\pi -2\gamma )\gamma }{8\pi (8\pi -2\gamma )}, \end{aligned}$$
(35)
$$\begin{aligned} \frac{\partial \Omega }{\partial P_t^{\prime }}= & {} \frac{(16\pi -2\gamma )2\gamma }{8\pi (8\pi -2\gamma )}, \end{aligned}$$
(36)
$$\begin{aligned} \frac{\partial \Omega }{\partial M}= & {} \frac{1}{(8\pi -2\gamma )(r^2-2Mr)}\nonumber \\{} & {} \times \Bigg [2\gamma \rho \Bigg (-2(r^2-2Mr)+2r\bigg [r^3\bigg \{\rho (8\pi +\gamma ) \nonumber \\{} & {} -\gamma P_r-2\gamma P_t\bigg \}-2M\bigg ]\Bigg )\nonumber \\{} & {} + \frac{4(16\pi ^2+8\gamma \pi -\gamma ^2)}{16\pi }(\rho +P_r) \nonumber \\{} & {} \Bigg (2(r^2-2Mr)+2r\bigg [r^3\bigg \{(8\pi +3\gamma )P_r\nonumber \\{} & {} +\gamma P_r+2\gamma P_t\bigg \}+2M\bigg ]\Bigg )\Bigg ]. \end{aligned}$$
(37)

Above derivatives shall be used in Eq. (30) to plot graph of forces distribution for considered realistic stars.

Table 2 Analysis of cracking/overturning points and singularities for \(\gamma \) in PSR J1614-2230
Full size table
Fig. 2
figure 2

A graphical illustration of \(\frac{\delta \Omega ^{}}{\delta \rho }\) for Vela X-1 \(a=0.0044\) (km)\(^{-2}\), \(b=0.000011\) (km)\(^{-2}\), \(B=0.00275\) (km)\(^{-2}\), \(R=9.99\) km

Full size image

4 Physical analysis

Here, we have considered an already developed logical MIT bag model [51] to identify refinements in stability criterion. For this purpose variation in force distribution defined mathematically as \(\frac{\delta \Omega }{\delta \rho }\) has been plotted with variation in ‘r’. Five strange stars have been studied in this regard namely Star 1: PSRJ1614-2230, Star 2: Vela X-1, Star 3: PSRJ1903+327, Star 4: Cen X-3 and Star 5: SMC X-1. Values for various physical parameters are list in the Table 1 given below.

4.1 Star 1: PSRJ1614-2230

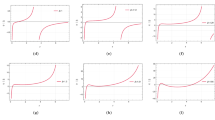
The Parkes Radio Telescope detected PSRJ1614-2230 during a radio survey aimed at identifying unknown EGRET gamma-ray sources. Later on, X-ray emission from Newton XMM and gamma rays emission from Fermi Gamma Ray Large Area Space Telescope was observed. The PSRJ1614-2230, a millisecond pulsar with a mass \(1.97 M{\bigodot }\) and 95-day orbital period in binary star systems. It is an important compact object for studying the behavior of matter under high pressure and the emission of radiation from highly magnetized objects [52]. For this star, we have plotted \(\frac{\delta \Omega }{\delta \rho }\) from Eq. (30) by taking different value of \(\gamma \) given in Fig. 1. The Fig. 1a describes certain disruptions in the form of cracking and singularities for \(\gamma \in [0,12.9]\). The Fig. 1b shows stability for \(\gamma \in (12.9,30.2]\). After that the overturning occurs when we increase value of \(\gamma \), we can see that in Fig. 1c. Regions pertaining cracking are summarized in Table 2.

Table 3 Analysis of cracking/overturning points and singularities for \(\gamma \) in Vela X-1
Full size table
Fig. 3
figure 3

A graphical illustration of \(\frac{\delta \Omega ^{}}{\delta \rho }\) for PSR J 1903+327 \(a=0.0043\) (km)\(^{-2}\), \(b=0.000016\) (km)\(^{-2}\), \(B=0.00267\) (km)\(^{-2}\), \(R=9.82\) km

Full size image

4.2 Star 2: Vela X-1

Sako et al. [53] presented the initial design for the Vela X-1’s global X-ray emission line spectrum. Vela X-1 is the high mass X-ray binary (HMXB), consisting of a massive companion star and neutron star. Since its discovery, it gained a lot of attention among the compact objects in this field of study. The massive companion star in Vela X-1 is a blue supergiant, which has a mass of approximately \(30M_{\bigodot }\) and a radius of about \(16M_{\bigodot }\). The companion star is so massive that it loses material through its outer layers, which is then captured by the neutron star [54]. We have plotted \(\frac{\delta \Omega }{\delta \rho }\) through Eq. (30) for different value of \(\gamma \) which is illustrated in Fig. 2. We have seen that the instabilities in the form of singularities and cracking for the values of \(\gamma \in [0,13]\) in Fig. 2a. Plot of \(\frac{\delta \Omega }{\delta \rho }\) and ‘r’ for \(\gamma \in (13,30.2]\) shows stable behavior as shown in Fig. 2b. The above values of \(\gamma \) shows unstable behavior due to overturning also summarized in Table 3.

Fig. 4
figure 4

A graphical illustration of \(\frac{\delta \Omega ^{}}{\delta \rho }\) for star 4 (Cen X-3), \(a=0.0042\) (km)\(^{-2}\), \(b=0.0000099\) (km)\(^{-2}\), \(B=0.002523\) (km)\(^{-2}\), \(R=9.51\) km

Full size image
Fig. 5
figure 5

A graphical illustration of \(\frac{\delta \Omega ^{}}{\delta \rho }\) for SMC X-1 \(a=0.00397\) (km)\(^{-2}\), \(b=0.0000091\) (km)\(^{-2}\), \(B=0.002363\) (km)\(^{-2}\), \(R=9.13\) km

Full size image

4.3 Star 3: PSR J 1903+327

In (2006), a Millisecond pulsar PSR J1903+0327 was discovered in the ongoing Arecibo L-band Feed Array (ALFA) pulsar survey. The pulsar has a mass of approximately \(1.67 M_{\bigodot }\), but its diameter is only about 20 kms, making it incredibly dense. It rotates at a very high speed, completing a full rotation in just 2.15 ms, or over 460 times per second. It has 95 days orbital motion for the binary companion pulsar [55].

Plot of \(\frac{\delta \Omega }{\delta \rho }\) through Eq. (30) for the different value of \(\gamma \) as shown in Fig. 3. The graph shows the cracking points and singularities around the center for \(\gamma \in [0,13.2]\) in Fig. 3a. The graph shows stable behavior for \(\gamma \in (13.2,30.2]\) in Fig. 3b. The above value of \(\gamma \) shows again unstable behavior and overturning occurs as shown in Fig. 3c.

4.4 Star 4: Cen X-3

The Cen X-3 was detected by JEM-X only in 4 SCWs (Science Windows) and by ISGRI in 11 SCWs. It was observed by integral a few times during the GPS. Its pulsation period is 4.8 s and orbital period is 2.1 days. The companion star of Cen X-3 is a supergiant (V779) of radius 12 \(R_{\bigodot }\) and mass 17-19 \(M_{\bigodot }\). It shows spin-up and a secular decay of the orbital period [56].

The graphical explanation of \(\frac{\delta \Omega }{\delta \rho }\) through Eq. (30) for the different value of \(\gamma \) as shown in Fig. 4. There are so many cracking points and also singularity for \(\gamma \in [0,13.1]\) in Fig. 4a shows unstable behavior. The value of \(\gamma \in (13.1,30.3]\) force stability of 4th star as shown in Fig. 4b and by increasing the value of \(\gamma \) overturning occurs.

4.5 Star 5: SMC X-1

An X-ray binary star system called SMC X-1, often referred to as Small Magellanic Cloud X-1, is located within the Small Magellanic Cloud (SMC), which is a satellite galaxy of the Milky Way. The neutron star in SMC X-1 is a highly magnetized, rapidly spinning pulsar. It emits regular pulses of electromagnetic radiation as it rotates. It has mass \(M=1.29M_{\bigodot }\) and its radius \(R=9.13\) km [57].

We have set the graph of \(\frac{\delta \Omega }{\delta \rho }\) through Eq. (30) for the different value of \(\gamma \) as shown in Fig. 5. there are many cracking points and also singularity for \(\gamma \in [0,13.3]\) that shows instability in Fig. 5a. The graph shows stable behavior of 5th star for \(\gamma \in (13.3,30.2]\) as shown in Fig. 5b. When we increase the value of \(\gamma \) then overturning occurs shows in Fig. 5c.

5 Conclusion

In order to understand the phenomenon of cosmic acceleration, it is essential to consider the significant contributions of dark matter and dark energy, which plays a significant role for a large fraction of the universe. Understanding cosmic variation in terms of higher-order curvature is best accomplished with modified gravity theories. In this article, we have considered a non-minimal connection of matter and geometry in f(R, T) gravity. It is beneficial to consider f(R, T) for the dynamical analysis, which includes the trace of the energy–momentum tensor and higher order curvature [22].

Herein, we intend to generalize the concept of cracking in considered modified theory of gravity, the mathematical foundation to arrive at cracking criterion has been developed for modified FEs. The LDP are taken into account for the development of expression for forces distribution among the compact source. The graphical representation of forces distribution with variation in radial coordinate defines cracking or overturning in the compact source, it appears whenever forces change their sign from negative to positive or vice versa.

The limitations of the f(R, T) form arise with non-linear components of the trace in the analytical formulation of FEs. This work uses cracking techniques to test the instabilities of compact astronomical objects in the context of the modified theory of f(R, T) gravity. Cracking shows how fluid distribution works when the equilibrium condition is disturbed by a change in the direction of the radial forces. Using the LDP on the hydrostatic equilibrium equation, we have developed mathematical distribution force models for this purpose.

Table 4 Analysis of cracking/overturning points and singularities for \(\gamma \) in PSR J 1903+327
Full size table
Table 5 Analysis of cracking/overturning points and singularities for \(\gamma \) in Cen X-3
Full size table
Table 6 Analysis of cracking/overturning points and singularities for \(\gamma \) in SMC X-1
Full size table

We have chosen f(R, T) model of Tolman–Kuchowicz metric that covers the expression of curvature invariant i.e., \(f(R,T)=R+2\gamma T\), In which \(\gamma \) has a positive value. Its occurs due to coupling between matter and geometry in modified gravity. The modified FEs are constructed in the form of Eqs. (7)–(9) for a spherically symmetric matter configuration. We have constructed hydrostatic TOV generalized equation Eq. (21) for different compact objects by applying MIT Bag model on modified FEs.

The cracking points or intervals are identified with the LDP scheme by perturbing the parameters involved in the generalized TOV equation Eq. (21). The results of LDP in the support of GR is beneficial for anisotropic matter distribution to point out the cracking and overturning in the system. The stability analysis for a developed model with LDP tends to be more appropriate for compact objects. For the f(R, T) gravity model, we have developed a density-dependent perturbation that is described in Eqs. (22)–(26). We use the LDP scheme to analyze the distribution of forces that operate on a gravitational system given by Eq. (30) and apply it to the hydrostatic equilibrium equation that distinguishes minimal fluctuations in the system.

To analyze the cracking of various compact objects, we generate a plot of force distribution \(\frac{\delta \Omega }{\delta \rho }\) against radius ‘r’ by taking different values of the \(\gamma \) for the compact objects in the following order: PSR J1614-2230, Vela X-1, PSR J1903+327, SMC X-1 and Cen X-3. Tables 2, 3, 4 and 5 shows the behavior of all stars by using local density perturbation scheme to identify the instability region. If we increased the value of involved parameter \(\gamma \) then all compact objects have cracking points and singularities that identify the instabilities. By further increasing the value of parameter \(\gamma \) in a specific interval there are no cracking points and singularity that shows stability of these compact objects. After that again by increasing the value of \(\gamma \), overturning occurs that shows instability. So, we conclude that the stability of compact objects in a specific interval that are also shown in Figs. 1, 2, 3, 4 and 5 and Tables 2, 3, 4, 5 and 6.

Extension of present work to charged compact sources is an interesting and important problem.