1 Introduction

One of the famous approach is to study the cosmological evolution from small scale to large scale in modern physics based on general relativity (GR) and quantum field theory [1]. Many cosmic phenomena were studied on the basis of GR like bending of light, gravitational waves, mercury orbit precession, gravitational lensing etc [2, 3]. Despite all these achievements, the GR has faced limitations to explain the latest cosmic observations like two dark phenomena of the modern cosmology i.e dark matter (DM) [4] and dark energy (DE) [5], and black hole singularities. This is the reason of motivation for physicists to propose the modified or alternative gravity theories or introduce new components of energy/matter to explain the recent observational scenarios of cosmology.

Serious attentions have been taken for the development of modified theories of gravity to explain the unsolved problems of GR [6,7,8,9,10] and [17]. One of the approach to modify GR that goes outside the limitations of Remannian geometry is to introduce the torsional spacetime and form new geometrical degrees of fredom based on an asymmetric affine connection. Therefore, in new formulation it consists of metric in addition to the independent geometric torsion field [11]. As regard the experimentation point of view, no evidence against or in favor the presence of torsion. Technically the main difficulty in detecting torsion is due to the reason that at high energy densities significant evidences of torsion appear. These high energy densities possible in neutron starts, black holes, interior highly compact objects or in the early stage of the Universe’s expansion [11]. Some authors have presented suggestions to test experimentally gravitational theories with non-zero torsion [12,13,14,15]. Tsamparlis was the first who derived the equations with torsion for the FRW Universe [16]. Using the assumption that torsion is considered as a scalar function of time allows us to build the torsional analogues with the Friedmann Universe [11]. Nojiri et al. [17] discussed the evolution of the Universe from early phase to late time and analyzed it by introducing torsion scalar in the gravitational action. In [18], the expansion of the Universe was analyzed and observed that \(\Lambda \)CDM model mimicked with the torsion effects in a homogenous and isotropic framework.

For a torsion dependent model, the restriction on the parameters with CMB, BAO, Hubble and type Ia Supernova was discussed in [19, 20], this study reveals that this kind of model is valid to describe all epochs i.e radiation, matter dominant era and accelerated phase of the Universe. In [21, 22] the behavior of neutrinos are discussed under torsional effects. In [23], it was studied that torsion could be camouflaged as DM. In the early stage of the Universe torsion could be associated with matter–antimatter [24]. Different cosmological issues under the Einstein–Cartan framework for torsional spacetime and the Friedmann cosmology respectively were analyzed [25, 26]. Different DE models were analyzed under the framework of different modified gravity theories [27,28,29,30,31,32,33,34,35]. In [36], the authors investigated the thermodynamics outcomes with torsion, they considered two choices for torsional term and found that model shows phantom or quintessence regime behavior. Furthermore they found the cosmic expansion is not adiabatic. Jawad et al. [37] discussed that stability of different DE models with the non-zero torsion using dynamical system approach. They found that the cosmic solutions indicate different evolution phases of the Universe, mathematically these models are stable and their phase plots show the attractor behavior.

There is ample indication that the Universe is composed of DM and DE [38,39,40]. DE has an anti-gravity aspect and negative pressure, due to these facts, DE is responsible to push the Universe for acceleration. Hence, DE is the source for recent cosmic accelerated expansion of the Universe. Two important aspects depend on DM in the evolution of the Universe. These aspects are, DM is responsible to produce appropriate gravity that rotate the galaxies cluster and DM has an important part in matter growth perturbations which is the source for structure formation in the early phase of the Universe. One of the primary difficulties in modern cosmology has been comprehending the origin and physical mechanism driving the perturbation’s growth in galaxies and galaxy clusters. It is widely accepted that large scale structures like galaxies and galaxy clusters that we observe, emerge from gravitational instability, which amplifies minute density irregularities during the evolution of the Universe. These irregularities gradually expand with time until they attain sufficient strength to disassociate from the overall expansion. Subsequently, they undergo gravitational collapse and form bounded systems like galaxies and galaxy clusters. In essence, these initial cosmic seeds originating from ancient collapsed regions serve as the foundation for the development of the Universe’s large scale structures [41, 42].

Spherical Collapse (SC) model is a suitable approach for investigating the growth of perturbations and the development of structures. According to observational data [43] it is evident that the majority of structures originate from nonlinear evolution of perturbations during dark age phase (\(10<z<100\)) [44]. The dark age phase refers to time frame spanning from the emission of CMB to the point when Universe’s evolution caused the gravitational collapse of objects ultimately leading to the formation of the first galaxies. The symmetrical nature of the SC model allows us to analyze the spherical perturbation within the context of FRW Universe. In simple words, we can discuss the growth of perturbations within a spherical region with the utilization of same Friedmann equations of underlying gravitational theory for the model [45]. The specific mechanism of collapse caused by gravitational instability is highly influenced by the dynamics of the background Hubble flow [46]. The detailed discussion has been conducted to explore the impact of DE on the formation of structures in different scenarios [47]. In [48], they used SC formalism and analyzed the matter perturbations with the impact of DE. The matter growth perturbations are discussed with entropies in the early phase of the Universe [49]. Under the framework of Chern-Simons gravity study of cosmic analysis and matter growth index was analyzed [50]. In [51], they analyzed the matter perturbation using SC model approach in context of generalized Rastall framework. Papagiannopoulos et al. discussed the dynamical analysis as well as the growth of matter perturbation in the context of Finsler-Randers cosmology [52]. In [53] they discussed the linear growth index behavior in perturbations and dynamical analysis with the Rastall framework. Cosmological perturbations were discussed under the framework of mimetic gravity [54, 55]. In [54], Newton gauge formalism used while in [55] SC formalism applied. In [56], the authors analyzed the matter growth perturbation in the context of f(T) gravity. Motivated by the above works on matter growth perturbation with the SC model approach, we are analyzing the matter growth perturbation using SC model formalism and cosmographic analysis in the context of the non-zero torsion cosmology.

The outline of this article is as follows. In Sect. 2, we discuss the Friedmann equations for non-zero torsion cosmology. Section 3 relates to the formulation of model-1 whereas in Sect. 3.1, we analyze the density contrast and growth function for the matter growth perturbation of first model. Sect. 3.2 is concerned with the study of cosmic evolution based on cosmographic parameters for model-1. Formulation for the second model is discussed in Sect. 4. Section 4.1 relates the matter growth perturbation analysis of model-2, while cosmographic analysis for model-2 is discussed in Sect. 4.2. Section 5 interprets the conclusion in which we present our results and some comparison with other works.

2 Structure formation in non-zero torsion cosmology

The Einstein–Cartan field equations with non-zero torsion are

$$\begin{aligned} R_{ji}-\frac{g_{ji}R}{2}=\kappa T_{ji}, \end{aligned}$$
(1)

where matter and curvature are interlinked with each other. However, in the presence of torsion, the Ricci tensor \(R_{ji}\) and matter tensor \(T_{ji}\) are asymmetric, i.e., \(R_{[ji]}\ne 0\) and \(T_{[ji]}\ne 0\). The time-like 4-velocity field \(u_k\) is such that \(u^ku_k=-1\) which further implies the metric tensor decomposition as \(g_{ji}=h_{ji}-u_ju_i\) and \(\kappa =8\pi G=1\) is considered here. The projection tensor \(h_{ji}\) is orthogonal to 4-velocity vector field and symmetric as \(h_{ji}=h_{(ji)},~h_{ji}u^i=0,~h^{~j}_j=3\). For this time-like 4-velocity vector field along with non-zero torsion cosmology and FRW Universe model, the torsion tensor is taken as [11, 36, 37]

$$\begin{aligned} S_{ijk}=2\phi h_{_i[_j} u_{{k}]}, \end{aligned}$$
(2)

which holds the homogeneity and isotropy of the rest-space of observers living along the time-like congruence tangent to \(u_k\). The antisymmetric torsion tensor \(S^j_{~ik}\) holds only one non-trivial contraction as \(S_j=S^j_{~ij}=-S^j_{~ji}\). Also, the scalar function \(\phi \) is the function of time only i.e \(\phi =\phi (t)\) which fulfills the homogeneity property. In order to address isotropy of the system, the torsion vector associated with torsion tensor becomes \(S_j=-3\phi u_j\) which further divided into two parts based on sign of \(\phi \). That is, for \(\phi <0\), it gives \(S_j\uparrow \uparrow u_j\) (\(S_j\) is future directed) while \(\phi >0\) shows \(S_j\downarrow \uparrow u_j\) (\(S_j\) is past directed).

The line element for flat FLRW spacetime is given by

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(dr^{2}+r^{2}d\theta ^{2}+r^{2}\sin ^{2}\theta d\vartheta ^{2}). \end{aligned}$$

Using the above metric with metricity condition (\(\nabla _{k}g_{ji}=0\)) along with Eq. (2), we first calculate \(\Gamma ^{j}_{(ik)}\) and then evaluate \(\Gamma ^{j}_{ik}=\Gamma ^{j}_{(ik)}+S^{j}_{ik}\) [11]. The Ricci tensor and scalar are calculated by the following relations \(R_{ji}=-\partial _{i}\Gamma ^{k}_{jk}+\partial _{k}\Gamma ^{k}_{ji}-\Gamma ^{m}_{jk}\Gamma ^{k}_{mi}+\Gamma ^{m}_{ji}\Gamma ^{k}_{mk}\) and \(R=g^{ji}R_{ji}\). The energy momentum tensor relates to matter is \(T_{ji}={diag }[-\rho ,P,P,P]\). Finally substitute the obtained values of \(R_{ji},~R\) and \(T_{ji}\) in Eq. (1). Thus in the underlying setup, the Friedmann equations for flat FLRW spacetime and perfect fluid matter distribution are given by [11, 36, 37]

$$\begin{aligned}{} & {} 3H^{2}=(\rho _{_m} +\rho _{_D})-12\phi (\phi +H), \end{aligned}$$
(3)
$$\begin{aligned}{} & {} {\dot{H}}+H^{2}=-\frac{1}{6}\{\rho _{_m}+\rho _{_D}+3(P_{_m}+P_{_D})\}-2({\dot{\phi }}+\phi H), \nonumber \\ \end{aligned}$$
(4)

where \( \rho _{_m}\) and \(\rho _{_D}\) are density of matter and dark energy (DE) respectively while \(P_{_m}\) and \(P_{_D}\) denote the pressure of matter and DE respectively. Also, \(H=\frac{{\dot{a}}}{a}\) is Hubble parameter where a denotes the scale factor. We consider the expression of \(\phi \)

$$\begin{aligned} \phi =\lambda H, \end{aligned}$$
(5)

where \(\lambda \) is restricted as \(\lambda \in [-0.005813,0.019370]\) consistent with the data of Big Bang Nucleosynthesis (BBN) [36]. The dimensionless ratio \(\frac{\phi }{H}\) describes the strength of torsional effects.

3 Model-1 formulation

For Model-1, we consider the pressureless matter also known as cold DM (CDM) (i.e \(P_{_m}=0\)) and the vacuum DE for which Eqs. (3) and (4) become

$$\begin{aligned} 3H^{2}= & {} \rho _{_m} +\rho _{_D}-12\phi (\phi +H), \end{aligned}$$
(6)
$$\begin{aligned} {\dot{H}}+H^{2}= & {} -\frac{1}{6}(\rho _{_m}+\rho _{_D}+3P_{_D})-2({\dot{\phi }}+\phi H), \end{aligned}$$
(7)

where \( \rho _{_m}\) and \(\rho _{_D}\) are densities of pressureless matter and the vacuum DE while \(P_{_D}\) denotes pressure of vacuum DE (for which \(\omega _{D}=-1\)). Therefore the conservation equations under these assumptions and by using Eq. (5) are

$$\begin{aligned} {\dot{\rho }}_{_m}+(3+2\lambda )H\rho _{_m}=0, \end{aligned}$$
(8)
$$\begin{aligned} {\dot{\rho }}_{_D}-4\lambda H\rho _{_D}=0, \end{aligned}$$
(9)

which yield the solutions as

$$\begin{aligned} \rho _{_m}= & {} \rho _{_{m,0}}a^{-(3+2\lambda )}, \end{aligned}$$
(10)
$$\begin{aligned} \rho _{_D}= & {} \rho _{_{D,0}}a^{4\lambda }, \end{aligned}$$
(11)

where subscripts m, 0 and D, 0 indicate the present-day values of densities. For the underlying scenario, Eqs. (5) and (6) take the following form

$$\begin{aligned} 3H^{2}=\frac{\rho _{_m}+\rho _{_D}}{(2\lambda +1)^{2}}. \end{aligned}$$
(12)

The above equation in terms of fractional energy densities becomes

$$\begin{aligned} 1=\Omega _{_m}+\Omega _{_D}, \end{aligned}$$
(13)

where

$$\begin{aligned} \Omega _{_m}=\frac{\rho _{_m}}{(2\lambda +1)^{2}3H^{2}}, \quad \Omega _{_D}=\frac{\rho _{_D}}{(2\lambda +1)^{2}3H^{2}}. \end{aligned}$$
(14)

Using Eqs. (10)–(12) and by considering the relation between scale factor and redshift \(({1+z}=a^{-1})\), we obtain the Hubble parameter as

$$\begin{aligned} H^{2}(z)=\frac{\rho _{_m,_0}~(1+z)^{3+2\lambda }+\rho _{_D,_0}~(1+z)^{-4\lambda }}{3(2\lambda +1)^{2}}. \end{aligned}$$
(15)

In the following we will discuss the density contrast parameter, growth function w.r.t redshift and cosmographic parameters for model-1.

3.1 Growth of perturbation analysis

Using Eqs. (5) and (7), assumptions of model-1 and \(\frac{\ddot{a}}{a}={\dot{H}}+H^{2}\), we obtain

$$\begin{aligned} \frac{\ddot{a}}{a}=-\frac{\rho _{_m}}{6(1+2\lambda )}+\frac{2\rho _{_D}}{6(1+2\lambda )}. \end{aligned}$$
(16)

For the analysis of the growth of perturbation, we use SC approach by considering a spherically symmetric perturbed region with radius \(a_{p}\) and homogenous density \(\rho _{_m}^{c}(t)\) for which \(\rho _{_m}^{c}(t)-\rho _{_m}(t)=\delta \rho _{_m}\) [51]. For matter dominant era of the Universe, the region which is denser expanded slowly as compared to whole Universe. The conservation equation in the case of spherically perturbed region, similar to Eq. (8) is given by

$$\begin{aligned} {\dot{\rho }}_{m}^{c}+(3+2\lambda )h\rho _{_m}^{c}=0, \end{aligned}$$
(17)

where \(h=\frac{{\dot{a}}_p}{{a}_p}\) = local rate of expansion of perturbed spherical region of radius \(a_{p}\). For the analysis of the evolution of perturbations, density contrast \(\delta _{m}\) is a useful and dimensionless quantity which is defined as [51]

$$\begin{aligned} \delta _{m}=\frac{\rho _{_m}^{c}}{\rho _{_m}}-1=\frac{\delta \rho _{_m}}{\rho _{_m}}. \end{aligned}$$
(18)

Here \(\rho _{_m}^{c}\) is the energy density of spherically perturbed cloud and \(\rho _{_m}\) represents the background density. In SC model, a spherical region under consideration will finally collapse under own gravitational pull or will expand faster than Hubble average rate implying a void depending on \(\delta \rho _{_m}\) greater or less than zero respectively [55]. Differentiating Eq. (18) along with Eqs. (8) and (17), we get

$$\begin{aligned} {\dot{\delta }}_{m}=-\frac{(3+2\lambda )h\rho _{_m}^{c}}{\rho _{_m}}+\frac{\rho _{_m}^{c}}{\rho _{_m}}(3+2\lambda )H. \end{aligned}$$
(19)

Using Eqs. (18) and (19), finally we obtain

$$\begin{aligned} {\dot{\delta }}_{m}=(3+2\lambda )(1+\delta _{m})(H-h). \end{aligned}$$
(20)

Differentiating Eq. (20), it yields

$$\begin{aligned} \ddot{\delta }_{m}=(3+2\lambda )(1+\delta _{m})({\dot{H}}-{\dot{h}})+\frac{{{\dot{\delta }}_{m}}^{^{^2}}}{(1+\delta _{m})}. \end{aligned}$$
(21)

For SC model, a homogenous sphere with uniform density of radius \(a_{p}\) can be modeled by using same evolution as Eq. (16), we get

$$\begin{aligned} \frac{\ddot{a}_p}{{a}_p}=-\frac{\rho _{_m}^{c}}{6(1+2\lambda )}+\frac{2\rho _{_D}}{6(1+2\lambda )}, \end{aligned}$$
(22)

where \(\frac{\ddot{a}_p}{{a}_p}={\dot{h}}+h^{2}\). Subtracting Eq. (22) from (16) and by using Eq. (18), we obtain

$$\begin{aligned} {\dot{H}}-{\dot{h}}=\frac{\rho _{_m}\delta _{m}}{6(1+2\lambda )}-H^{2}+h^{2}. \end{aligned}$$
(23)

Using Eqs. (20), (21) and (23) (also considering linear regime), it yields

$$\begin{aligned} \ddot{\delta }_{m}+2H{\dot{\delta }}_{m}-\frac{(3+2\lambda )}{6(1+2\lambda )}\rho _{_m}\delta _{m}=0. \end{aligned}$$
(24)

Now changing the variable, we get

$$\begin{aligned} {\dot{\delta }}_{m}= & {} aH\delta _{m}', \end{aligned}$$
(25)
$$\begin{aligned} \ddot{\delta }_{m}= & {} a^{2}H^{2}\delta _{m}''+a\bigg (\frac{-\rho _{_m}}{6(1+2\lambda )} +\frac{2\rho _{_D}}{6(1+2\lambda )}\bigg ), \end{aligned}$$
(26)

where \(\delta _{m}'=\frac{d\delta _{m}}{da}\). Using Eqs. (25) and (26), Eq. (24) gives

$$\begin{aligned} \delta _{m}''+\Bigg [\frac{2\rho _{_D}-\rho _{_m}}{6(1+2\lambda )a H^{2}}+\frac{2}{a}\Bigg ]\delta _{m}'-\Bigg (\frac{(3+2\lambda )\rho _{_m}}{6(1+2\lambda )a^{2}H^{2}}\Bigg )\delta _{m}=0.\nonumber \\ \end{aligned}$$
(27)

Considering Eq. (12), linear regime for \(\delta _{m}\), early phase of Universe in which \(\frac{\rho _{_D}}{\rho _{_m}}<1\) and after some simplifications, above equation converts to

$$\begin{aligned}{} & {} \delta _{m}''+\bigg (\frac{3-2\lambda }{2a}+\frac{3(1+2\lambda )}{2a}\frac{\rho _{_D}}{\rho _{_m}}\bigg )\delta _{m}' \nonumber \\{} & {} \quad +\frac{(3+2\lambda )(1+2\lambda )}{2a^{2}}\bigg (\frac{\rho _{_D}}{\rho _{_m}}-1\bigg )\delta _{m}=0. \end{aligned}$$
(28)

To obtain the standard cosmology result, we take \(\lambda =0\) and in the absence of \(\rho _{_D}=\Lambda =0\) in the early Universe, Eq. (28) yields the following equation that matches with the standard cosmology equation as discussed in [48]. It is \(\delta _{m}''+\frac{3}{2a}\delta _{m}'-\frac{3}{2 a^{2}}\delta _{m}=0\).

In terms of redshift function and by applying chain rule, we obtain

$$\begin{aligned} \delta _{m}'= & {} -(1+z)^{2}\frac{d\delta _{m}}{dz}, \end{aligned}$$
(29)
$$\begin{aligned} \delta _{m}''= & {} (1+z)^{4}\frac{d^{2}\delta _{m}}{dz^{2}}+2(1+z)^{3}\frac{d\delta _{m}}{dz}. \end{aligned}$$
(30)

Taking into account the equations and Eq. (28), we obtain the following initial value problem

$$\begin{aligned}{} & {} \frac{d^{2}\delta _{m}}{dz^{2}}+\frac{1+2\lambda }{2(1+z)}\bigg (1-3\frac{\Omega _{D,0}}{\Omega _{m,0}} (1+z)^{-3(1+2\lambda )}\bigg )\frac{d\delta _{m}}{dz} \nonumber \\{} & {} \quad +\frac{(3+2\lambda )(1+2\lambda )}{2(1+z)^{2}}\bigg (\frac{\Omega _{D,0}}{\Omega _{m,0}} (1+z)^{-3(1+2\lambda )}-1\bigg )\delta _{m}=0,\nonumber \\ \end{aligned}$$
(31)

with initial conditions [55]

$$\begin{aligned} \delta _{m}|_{(z=z_{i})}=0.0001, \quad {and }\quad \frac{d\delta _{m}}{dz}\bigg |_{(z=z_{i})}=-\frac{\delta _{m}|_{(z=z_{i})}}{1+z_{i}},\nonumber \\ \end{aligned}$$
(32)

here \(\delta _{m}(z_{i})\) is the initial value of density contrast. Solving this problem numerically, here we assume \(\Omega _{m,0}=0.3~and~\Omega _{D,0}=1-\Omega _{m,0}=0.7\), the density contrast with respect to redshift parameter is shown in Fig. 1. The fig reveals that, with different values of non-zero torsion field parameter \(\lambda \), density contrast increases from high to low redshifts. It implies from Fig. 1 that the plot of density contrast with different values of \(\lambda \) grows from its initial value with the Universe’s expansion. At low redshifts, the difference between the plots is more visible, for positive choice of non-zero torsion field parameter (\(\lambda \)) the growth of density contrast is greater and for the negative choice of \(\lambda \), the growth of density contrast is lower than the standard \(\Lambda \)CDM model (\(\lambda =0\)). Our observations are, with the increase of parameter \(\lambda \) the matter growth perturbation increases that physically implies the effect of non-zero torsion field on matter growth perturbation and here the density contrast is positive and \(\delta _{m}<1\). Therefore, it yields that region under consideration for matter growth perturbation will expand with the expansion of Universe in lieu of gravitational collapse.

Fig. 1
figure 1

Plot between density contrast and redshift parameter (z) for model-1 with three different choices of \(\lambda \)

Full size image

To further discuss the growth of matter perturbations, we evaluate the growth function which is defined as [50, 55]

$$\begin{aligned} f(a)=\frac{d\ln \delta _{m}}{dx}, \end{aligned}$$
(33)

where \(x=\ln a\). As \(\delta _{m}'=\frac{d\delta _{m}}{da}\), applying chain rules and some simplifications, we get

$$\begin{aligned} \delta _{m}'= & {} \frac{\delta _{m}f}{a}, \end{aligned}$$
(34)
$$\begin{aligned} \delta _{m}''= & {} \frac{\delta _{m}}{a^{2}}\frac{df}{dx}+\frac{f^{2}\delta _{m}}{a^{2}}-\frac{\delta _{m}f}{a^{2}}. \end{aligned}$$
(35)

Using Eqs. (28), (34), (35), (\(\delta _{m}\ne 0\)) finally we get

$$\begin{aligned}{} & {} f^{2}-(1+z)\frac{df}{dz}\nonumber \\{} & {} \quad {+}\bigg (-1{+}\frac{3-2\lambda }{2}{+}\frac{3(1{+}2\lambda )}{2}\frac{\Omega _{D,0}}{\Omega _{m,0}}(1+z)^{-3(1+2\lambda )}\bigg )f \nonumber \\{} & {} \quad {=} \frac{(3+2\lambda )(1+2\lambda )}{2}\bigg (1-\frac{\Omega _{D,0}}{\Omega _{m,0}}(1+z)^{-3(1+2\lambda )}\bigg ). \end{aligned}$$
(36)
Fig. 2
figure 2

Plot between growth function and redshift parameter (z) for model-1 with three different choices of \(\lambda \)

Full size image

We solve the above equation numerically for growth function for three different values of \(\lambda \).Plot between the growth function and redshift parameter is shown in Fig. 2 by using three different values of parameter \(\lambda \). Figure 2 indicates that at high redshits, the matter growth function approaches unity and at low redshift, all trajectories start from smaller values. The trajectory for \(\lambda =0.019\) approaches unity with high growth perturbations compare to \(\lambda =0.0\) (\(\Lambda \)CDM for GR). Similarly, the matter growth perturbations for \(\lambda =0.0\) is little higher than \(\lambda =-0.005\). Hence, the role of non-zero torsion field affects the growth function in matter growth perturbations.

3.2 Cosmographic analysis

In this section, we analyze the behavior of different cosmographic parameters for non-zero torsion cosmology. Using Eqs. (14) and (15), the normalized Hubble parameter is given by

$$\begin{aligned} E(z)=\frac{H}{H_{0}}=\sqrt{\Omega _{m}~(1+z)^{3+2\lambda }+\Omega _{D}~(1+z)^{-4\lambda }}. \end{aligned}$$
(37)

The plot between E w.r.t z for three different choices of parameter \(\lambda \) is shown in Fig. 3. The normalized Hubble parameter increases with the increase of non-zero torsion field parameter \(\lambda \) at high redshifts, as it is evident from Fig. 3 for \(\lambda =0.019\), normalized Hubble parameter is greater than \(\lambda =0\) and \(\lambda =-0.005\).

Fig. 3
figure 3

Plot between normalized Hubble parameter (E) and redshift (z) for model-1 with three different choices of \(\lambda \)

Full size image

Using Eqs. (14), (15) and (37), we obtain a relation for matter density \(\Omega _{m}(z)\) as below

$$\begin{aligned} \Omega _{m}(z)=\frac{\Omega _{m,0}}{E^{2}(z)}(1+z)^{3+2\lambda }. \end{aligned}$$
(38)
Fig. 4
figure 4

Plot between matter density (\(\Omega _{m}(z)\)) and redshift (z) for model-1 with three different choices of \(\lambda \)

Full size image

Figure 4 represents the matter density abundance for different values of \(\lambda \) w.r.t redshift. It is revealed from Fig. 4 with the increase of parameter \(\lambda \) the density abundance of matter increases. All three trajectories of \(\Omega _{m}(z)\) at present \(z=0\) show same behavior. The relation for DE density is obtained by using Eqs. (14), (15) and (37) as

$$\begin{aligned} \Omega _{D}(z)=\frac{\Omega _{D,0}}{E^{2}(z)}(1+z)^{-4\lambda }. \end{aligned}$$
(39)
Fig. 5
figure 5

Plot between DE density (\(\Omega _{D}(z)\)) and redshift (z) for model-1 with three different choices of \(\lambda \)

Full size image

The evolution of DE density w.r.t redshift z is shown in Fig. 5, we observe that with smaller values of parameter \(\lambda \), the plot of density abundance of DE reaches faster than the higher choice of \(\lambda \) to present-day value of \(\Omega _{D,0}\) from high redshift.

An important parameter in cosmographic analysis is deceleration parameter (q) that determines the acceleration or deceleration rates of the Universe. The relation between deceleration parameter and parameter of redshift is given by

$$\begin{aligned} q=-1-\frac{{\dot{H}}}{H^{2}}=-1+\frac{(1+z)}{H(z)}\frac{dH}{dz}. \end{aligned}$$
(40)

Using Eqs. (15) and (40), we obtain the required relation of deceleration parameter in non-zero torsion field cosmology as

$$\begin{aligned} q{=}{-}1{+}\frac{(3+2\lambda )(1+z)^{3+2\lambda }\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0}}{2(\Omega _{m,0} (1+z)^{3+2\lambda }+\Omega _{D,0}(1+z)^{-4\lambda })}.\nonumber \\ \end{aligned}$$
(41)
Fig. 6
figure 6

Plot between parameters deceleration (q) and redshift (z) for model-1 with three different choices of \(\lambda \)

Full size image

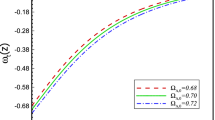
Plot of deceleration parameter q w.r.t z is given in Fig. 6 for three different choices of \(\lambda \). We observe that the Universe faces a transition from deceleration phase \((q>0)\) for \(z>z_{t}\) to acceleration phase (\(q<0\)) for \(z<z_{t}\), here \(z_{t}\) is the transition point on the redshift Fig. 6 shows that with different values of \(\lambda \), the transition from decelerating phase to accelerating phase appears at low redshift signifies around \(z=z_{t}\approx 0.6\). At the present stage, the deceleration parameter approaches to \(q\approx -0.6\). This behavior is compatible with the recent observational data [57]. A dimensionless quantity known as jerk parameter (j) is supportive to understand the different phases of the Universe’s expansion and it also helpful for the comparison of various models of DE with \(\Lambda \)CDM model for which \(j=1\). Jerk parameter is defined [55] as

$$\begin{aligned} j=\frac{1}{a H^{3}}\frac{d^{3}a}{dt^{3}}=q(2q+1)+(1+z)\frac{dq}{dz}. \end{aligned}$$
(42)

Using Eqs. (41) and (42), we obtain the required expression of jerk parameter for model-1 as follows

$$\begin{aligned} j= & {} \Bigg (-1+\frac{((3+2\lambda )(1+z)^{3+2\lambda }\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0})}{2(\Omega _{m,0} (1+z)^{3+2\lambda }+\Omega _{D,0}(1+z)^{-4\lambda })}\Bigg )\nonumber \\{} & {} \times \Bigg (-1+\frac{((3+2\lambda )(1+z)^{3+2\lambda }\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0})}{(\Omega _{m,0}(1+z)^{3+2\lambda }+\Omega _{D,0}(1+z)^{-4\lambda })}\Bigg ) \nonumber \\{} & {} +\frac{1}{2N^{2}}\Bigg (((3+2\lambda )^{2}(1+z)^{3+2\lambda }\Omega _{m,0}+16\lambda ^{2}(1+z)^{-4\lambda }\Omega _{D,0})\nonumber \\{} & {} \times N-M(((3+2\lambda )(1+z)^{3+2\lambda }\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0}))\Bigg ),\nonumber \\ \end{aligned}$$
(43)

where \(M=(3+2\lambda )(1+z)^{3+2\lambda }\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0}\) and \(N=(1+z)^{3+2\lambda }\Omega _{m,0}+(1+z)^{-4\lambda }\Omega _{D,0}\).

Fig. 7
figure 7

Plot between parameters jerk (j) and redshift (z) for model-1 with three different choices of \(\lambda \)

Full size image

Figure 7 indicates that the deviation of the behavior of jerk parameter for \(\lambda =-0.005\) and \(\lambda =0.019\) from \(\Lambda \)CDM \((j=1)\) is due to presence of non-zero torsion. We see that with the increase of non-zero torsion parameter \(\lambda \), the jerk parameter also increases.

4 Model-2 formulation

In model-2, we assume non-zero pressure of matter i.e \(p_{m}=\alpha \rho _{_m}\) and by using \(\phi =\lambda H,~{\dot{H}}+H^{2}=\frac{\ddot{a}}{a}\), we get Friedmann equations (6) and (7) as

$$\begin{aligned}{} & {} 3H^{2} = \frac{\rho _{_m}+\rho _{_D}}{(1+2\lambda )^{2}}, \end{aligned}$$
(44)
$$\begin{aligned}{} & {} \frac{\ddot{a}}{a} = -\frac{(1+3\alpha )\rho _{_m}}{6(1+2\lambda )}+\frac{2\rho _{_D}}{6(1+2\lambda )}. \end{aligned}$$
(45)

The conservation equations for model-2 take the following form

$$\begin{aligned} {\dot{\rho }}_{_m}+(3+2\lambda )H\rho _{_m}+3\alpha H(1+2\lambda )\rho _{_m}= & {} 0, \end{aligned}$$
(46)
$$\begin{aligned} {\dot{\rho }}_{_D}-4\lambda H\rho _{_D}= & {} 0, \end{aligned}$$
(47)

which yield the solutions

$$\begin{aligned} \rho _{_m}= & {} \rho _{_{m,0}}(1+z)^{((3+2\lambda )+3\alpha (1+2\lambda ))}, \end{aligned}$$
(48)
$$\begin{aligned} \rho _{_D}= & {} \rho _{_{D,0}}(1+z)^{-4\lambda }. \end{aligned}$$
(49)

Taking Eqs. (44), (48) and (49) in terms of redshift function, we get

$$\begin{aligned}{} & {} H^{2}(z)=\nonumber \\{} & {} \frac{\rho _{_m,_0}~(1+z)^{((3+2\lambda )+3\alpha (1+2\lambda ))}+\rho _{_D,_0}~(1+z)^{-4\lambda }}{3(2\lambda +1)^{2}}.\nonumber \\ \end{aligned}$$
(50)

Using Eqs. (14) and (50), it yields

$$\begin{aligned} H(z){} & {} =H_{0}(z)((\Omega _{m,0}(1+z)^{((3+2\lambda )+3\alpha (1+2\lambda ))}\nonumber \\{} & {} \quad +\Omega _{D,0}(1+z)^{-4\lambda })^{\frac{1}{2}}. \end{aligned}$$
(51)

In similar way to model-1, here we discuss growth of matter perturbation and cosmographic analysis for model-2 in the following.

4.1 Growth of perturbations analysis

Conservation equation in this case similar to Eq. (46) is

$$\begin{aligned} {\dot{\rho }}_{m}^{c}+\{(3+2\lambda )+3\alpha (1+2\lambda )\}h\rho _{_m}^{c}=0. \end{aligned}$$
(52)

Now using Eq. (52) and repeating procedure parallel (from Eq. (19) to (27) and considering linear regime for \(\delta _{m}\), we obtain

$$\begin{aligned}{} & {} \delta _{m}''+\Bigg (\Bigg (-\frac{(1+3\alpha )(1+2\lambda )}{2a}\Bigg )\nonumber \\{} & {} \quad +\Bigg (\frac{(1+3\alpha )(1+2\lambda )}{2a}\Bigg ) \Bigg (\frac{\rho _{_D}}{\rho _{_m}}\Bigg )+\frac{(1+2\lambda )}{a}\Bigg (\frac{\rho _{_D}}{\rho _{_m}}\Bigg ) +\frac{2}{a}\Bigg )\delta _{m}'\nonumber \\{} & {} \quad -\left( \frac{((3+2\lambda )+3\alpha (1+2\lambda ))\Bigg )(1+3\alpha )(1+2\lambda )}{2a^{2}}\right) \nonumber \\{} & {} \quad \Bigg (1-\frac{\rho _{_D}}{\rho _{_m}}\Bigg )\delta _{m}=0. \end{aligned}$$
(53)

To obtain the standard cosmology result by considering \(\alpha =0,~\lambda =0,~\rho _{_D}=\Lambda =0\), above equation yields the same standard equation. Using Eqs. (29), (30), (48), (49) and (53), we get

$$\begin{aligned}{} & {} \frac{d^{2}\delta _{m}}{dz^{2}}+\frac{1}{(1+z)}\bigg [\frac{(1+3\alpha )(1+2\lambda )}{2}\nonumber \\{} & {} \quad -\frac{3(1+2\lambda )(1+\alpha )}{2} \frac{\Omega _{D,0}}{\Omega _{m,0}}P\bigg ]\frac{d\delta _{m}}{dz}\nonumber \\{} & {} \quad -\frac{((3+2\lambda )+3\alpha (1+2\lambda ))(1+3\alpha )(1+2\lambda )}{2(1+z)^{2}} \bigg [1-\frac{\Omega _{D,0}}{\Omega _{m,0}}P\bigg ]\delta _{m}\nonumber \\{} & {} =0. \end{aligned}$$
(54)

where \(P=(1+z)^{-3(1+2\lambda )(1+\alpha )}\). We solve this equation for \(\delta _{m}(z)\) numerically with same initial conditions given in Eq. (32). Figure 8 indicates the density contrast \(\delta _{m}\) w.r.t z, here we consider \(\alpha =1,~\Omega _{m,0}=0.3,~\Omega _{D,0}=1-\Omega _{m,0}\).

Fig. 8
figure 8

Plot between density contrast and redshift parameter (z) for model-2 with three different choices of \(\lambda \)

Full size image

Plot of density contrast (i.e Fig. 8) shows that density contrast grows from higher redshift to low redshift, particularly in the range \(5<z<8\) density contrast grows very fast for non-zero pressure and non-zero torsion (i.e \(\lambda =0.015\) \(\lambda =0.01\) and \(\lambda =0.005\)) as compare to zero torsion (i.e \(\lambda =0.00\)) with pressureless matter. Physically, it implies that matter growth of perturbations are very high due to non-zero pressure of DM as well as non-zero torsion, as a result of it the perturbed region under consideration is going to expand more faster than the overall Universe’s expansion force, eventually this region will collapse under its own gravitational force and form new large scale matter or galaxy.

Since \(\delta _{m}\ne 0\), using Eqs. (34), (35), (54) and \(a=\frac{1}{1+z}\), we finally obtain

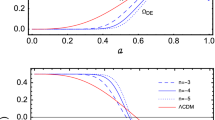
$$\begin{aligned}&f^{2}-(1+z)\frac{df}{dz}+\bigg (-1-\frac{(4-(1+3\alpha )(1+2\lambda ))}{2}\nonumber \\&\quad +\frac{(3+3\alpha ) (1+2\lambda )}{2}\frac{\Omega _{D,0}}{\Omega _{m,0}}A\bigg )\nonumber \\&\quad f= \bigg (\frac{((3+2\lambda )+3\alpha (1+2\lambda ))(1+3\alpha ) (1+2\lambda )}{2}\bigg )\bigg (1-\frac{\Omega _{D,0}}{\Omega _{m,0}}A\bigg ),\nonumber \\ \end{aligned}$$
(55)

where \(A=(1+z)^{(-4\lambda -((3+2\lambda )+3\alpha (1+2\lambda )))}\). Plot of growth function f(z) w.r.t redshift parameter z is shown in Fig. 9.

Fig. 9
figure 9

Plot between growth function and redshift parameter (z) for model-2 with three different choices of \(\lambda \) and \(\lambda =0\)

Full size image

It is clear from Fig. 9 that the behavior of the growth function for three different non-zero choices of \(\lambda \) with DM having non-zero pressure deviates from \(\lambda =0\) with pressureless matter. The deviation in the profiles of the growth function is due to matter growth perturbations.

The formation of cosmic structures is studied under the framework of the SC model. When the density contrast is positive and greater than 1, the gravitational forces within the perturbed region are stronger than the overall expansion of the Universe that tends to pull matter apart and lead to the formation of structures such as new large scale matter or galaxy or supercluster [51]. The Universe undergoes multiple phase transitions, cosmic reionization represents one phase in the cosmic evolution, where ultraviolet and X-ray radiation emanated from the initial generations of galaxies [58]. This took place approximately 150 million to one billion years following the Big Bang, in terms of redshift this range is \( 6<z<20\) [58]. These findings indicate that the Universe was nearing the conclusion of the reionization epoch at \(z\approx 6\). Specifically for model-2, it is clear from Fig. 8 that the density contrast for non-zero pressure and torsion grows faster than the standard \(\Lambda \)CDM (zero torsion and pressureless DM) from high to low redshifts. Figure 9 reflects that the trajectories of the growth function for non-zero pressure and torsion have large values as compare to zero torsion and pressureless DM in low redshifts. The most important outcome of our model-2 (DM with non-zero pressure i.e \(\alpha =1\) and non-zero torsion) is, the density contrast grows smoothly with the expansion of the Universe between \(8<z<30\) but in the range \(5<z<8\) due to non-zero pressure and torsion the matter growth perturbation increases rapidly. This implies expeditious growth in density contrast (Fig. 8) that indicates the formation of new large scale matter or galaxy. In future prospect for this model, if we increase the value of the parameter \(\alpha \) for non-zero pressure, we can obtain new large scale matter formation or galaxy at high redshift \(z=10\) or greater.

In our model-2, we consider DM with non-zero pressure which suggests the collisional nature of matter. In [59, 60], the authors studied the models of collisional nature for matter under the context of f(R) gravity. In the article [59], the differential equation related to matter growth function contains a term \(\frac{G_{eff}(a(z),k)}{G}\), where k is comoving wavenumber and they considered the subhorizon approximation \((\frac{k^{2}}{a^{2}}>>H^{2})\). Similar work in the context f(R) has been studied for matter growth function in which \(\frac{G_{eff}(a(z),k)}{G}\approx 1\) for different choices of comoving number k and \(z\ge 4\) [61]. The article [62] suggests that in the context of subhorizon scale, we may ignore dependence on k and observation limit of \(\frac{G_{eff}(a(z),k)}{G}\approx 1\) for high redshifts. The role of the subhorizon approximation is less important when perturbations are considered on very large scales, such as the behavior of the Universe as a whole. The SC formalism is designed to study matter growth perturbations and formation of new large scale structures on subhorizon scale (smaller scale than the Hubble horizon), therefore the subhorizon approximation is not necessary when analyzing the matter growth perturbations within the framework of the SC formalism for large scale structure formation. In model-2, we analyze the matter growth perturbation with the SC formalism for large scale matter formation under the framework of non-zero torsion cosmology. We solve the related differential equation of the matter growth function by considering the same initial condition used in [59]. The trajectories of the growth function for nonzero torsion with DM of nonzero pressure show the deviation from pressureless DM (CDM) with zero torsion (Fig. 9), this behavior signifies the difference in collisional and noncollisional nature of matter with torsion.

4.2 Cosmographic analysis

In this section, we analyze the effects of non-zero torsion and non-zero pressure on the the different cosmographic parameters. Considering Eq. (40), derivative of Eq. (51) and after some simplification, we obtain the required expression for deceleration parameter as

$$\begin{aligned} q{=}{-}1{+}\frac{((3+2\lambda )+3\alpha (1+2\lambda ))B\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0}}{2(\Omega _{m,0}B+\Omega _{D,0}(1+z)^{-4\lambda })}.\nonumber \\ \end{aligned}$$
(56)

where \(B=(1+z)^{((3+2\lambda )+3\alpha (1+2\lambda ))}\). The plot between q and z for model-2 is shown in Fig. 10.

Fig. 10
figure 10

Plot between deceleration parameter (q) and redshift parameter (z) for model-2 with four different choices of \(\lambda \)

Full size image

In Fig. 10, we observe the behavior of deceleration parameter for different choices of \(\lambda \) as \(\lambda =0.015,~\lambda =0.001~\lambda =0.005\) with \(\alpha =1\) that physically indicates the effects of non-zero pressure and torsion on deceleration parameter. This reveals that due to non-zero pressure and non-zero torsion, the matter dominance is more significant and at present \(z=0\), the acceleration phase of the Universe is just started as \(q<0\) indicates power-law expansion rate of accelerating Universe. This plot also signifies the difference in the trajectories behavior of q for non-zero pressure and torsion with \(\Lambda \)CDM model \((\lambda =0,~ \alpha =0)\).

The expression for jerk parameter of model-2 is obtained by using Eq. (42) and derivative of Eq. (56) as

$$\begin{aligned} j&=\Bigg (-1+\frac{(((3+2\lambda )+3\alpha (1+2\lambda ))B\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0})}{2(\Omega _{m,0}B+ \Omega _{D,0}(1+z)^{-4\lambda })}\Bigg )\nonumber \\&\quad \times \Bigg (\!{-}1{+} \frac{(((3+2\lambda )+3\alpha (1+2\lambda ))B\Omega _{m,0}-4\lambda (1+z)^{-4\lambda }\Omega _{D,0})}{(\Omega _{m,0}B+\Omega _{D,0}(1+z)^{-4\lambda })}\!\Bigg )\nonumber \\&\quad +\frac{1}{2D^{2}}\Bigg ((B \times ((3+2\lambda )+3\alpha (1+2\lambda ))^{2}\Omega _{m,0}\nonumber \\&\quad -16\lambda ^{2} (1+z)^{-4\lambda \Omega _{D,0}})D-C(\Omega _{m,0}B\nonumber \\&\quad \times ((3+2\lambda )+3\alpha (1+2\lambda ))-4\lambda (1+z)^{-4\lambda }\Omega _{D,0})\Bigg ), \end{aligned}$$
(57)

where \(B=(1+z)^{((3+2\lambda )+3\alpha (1+2\lambda ))},~C=((3+2\lambda )+3\alpha (1+2\lambda ))\Omega _{m,0}B-4\lambda \Omega _{D,0} (1+z)^{-4\lambda }\) and \(D=\Omega _{m,0}B+\Omega _{D,0}(1+z)^{-4\lambda }\). Plot between jerk parameter j and redshift z is shown in Fig. 11.

Fig. 11
figure 11

Plot between (j) and redshift parameter (z) for model-2 with four different choices of \(\lambda \)

Full size image

It is clear from Fig. 11 that the behavior of jerk parameter for non-zero pressure and torsion (i.e \(\alpha =1\) and \(\lambda =0.005,~\lambda =0.01~\lambda =0.015\)) is different from \(\Lambda \)CDM in past (\(z>0\)) and present times (\(z=0\)) but in future (\(z<0\)), the behavior of jerk parameter for both cases coincides.

5 Conclusions

The latest research on cosmology deals with the accelerated expansion of the Universe. Another open area is to investigate the gravitational collapse for the formulation of galaxies, clusters due to perturbations growth in early and past era of the Universe. The dark sector (DM and DE) affects the cosmic evolution of the Universe. In the present article, we have explored the cosmic evolution of matter growth perturbations under the framework of non-zero torsion cosmology. To investigate the matter growth perturbations, we have formulated two models with two choices of DM (pressureless and non-zero pressure) and DE (vacuum) and applied the SC formalism, considering the linear regime for density contrast. In literature, mainly matter growth perturbations are discussed only for pressureless matter. Additionally, we have analyzed some cosmic parameters for these models.

Following are the outcomes of this research work:

  • In model-1, the pressureless matter is considered as DM to observe the density contrast. Density contrast with three different choices of torsion parameter (\(\lambda \)) increases from high to low redshift, it remains positive and less than 1. Physically this observation implies that matter growth perturbation are within the control limits for the region under consideration and it will expand with the Universe’s overall expansion instead of collapse. The growth function for model-1 increases from low to high redshift with three different values of \(\lambda \). Different cosmographic parameters of model-1 i.e normalized Hubble parameter, DM and DE density abundance behavior for different choices of \(\lambda \) is similar. The declaration parameter q shows transformation of declaration to acceleration phase of the Universe and at present \(z=0\), \(q\approx -0.6\), therefore value of q compilable with the observed schemes BAO+ Masers + TDSL + Pantheon and BAO + Masers + TDSL + Pantheon +\(H_{0}\) [57] for model-1. The jerk parameter for model-1 shows its deviation from \(\Lambda \)CDM due to non-zero torsion \(\lambda \).

  • In model-2, matter with non-zero pressure is taken as DM for which we have observed that the density contrast grows from high to low redshift and this growth is very fast in the past era (\(5<z<8\)) as compare to pressureless DM with zero torsion. Physically this signifies that due to non-zero pressure and non-zero torsion density contrast growth is enormous as compare to Universe’s overall expansion force, finally perturbed region collapse and form new super cluster or galaxy. The trajectories of matter growth function for non-zero pressure and torsion deviate from torsion free and pressureless DM (\(\Lambda \)CDM) due to matter growth perturbations. In model-2, the behavior of deceleration q and jerk j parameters deviate from standard \(\Lambda \)CDM due to non-zero torsion and pressure as shown in Figs. 10 and 11 respectively. For non-zero pressure \(\alpha =1\) and three different values of \(\lambda \), the parameter q shows acceleration phase of the Universe just begin at present (\(z=0\)) as compare to \(\Lambda \)CDM for which the acceleration phase of the Universe begins at \(z=0.6\) that physically indicate the matter dominance. Similarly non-zero pressure and non-zero torsion \(\lambda \) effects jerk parameter parameter, Fig. 11 indicate its deviation from \(\Lambda \)CDM (j=1) in the present, past era but it is compatible for future era of the Universe.

In the present work under the framework of non-zero torsion cosmology, the behavior of both parameters related to matter growth perturbations i.e., density contrast \(\delta _{m}\) and growth function f(z) with the restriction of pressureless DM (model-1) are similar and more closer to \(\Lambda \)CDM as compared to some other related works under the framework of Tasllis and Barrow cosmology [49] and mimetic gravity framework [55]. The matter growth perturbation and cosmographic analysis with DM of non-zero pressure (model-2) with torsion are discussed in the present article which provides us the possible identification of large scale matter formation or galaxy or supercluster.