1 Introduction

One of the main challenges in modern cosmology is understanding the origin and physics of the growth of perturbations in the early stages of the universe. Indeed, these perturbations eventually lead to large-scale structures such as galaxies and clusters of galaxies. It is a general belief that the large-scale structures of the universe originate from gravitational instability that amplifies very small initial density fluctuations during the evolution of the universe. Such fluctuations then grow slowly over time until they are robust enough to be detached from the background expansion. Finally, they collapse into gravitationally bound systems such as galaxies and clusters of galaxies. In fact, the collapsed primordial regions serve as the initial cosmic seeds from which the large-scale structures are developed [1, 2]. This provides sufficient motivation to study the perturbations of matter and dark energy (DE) at the early stages of the universe in the linear and nonlinear regimes. It was argued that the perturbations of DE may form halo structures which can influence the dark matter (DM) collapsed region nonlinearly [3]. Studies of the mutual interactions between dark sectors of the universe at the perturbation level can aid in understanding the nature of both dark components of the universe. The influence of the DE on structure formation at both the background level (no fluctuations) and the perturbed level has been widely explored in the literature [4,5,6,7,8]. An appropriate approach for investigating the growth of perturbations and structure formation is the so-called top-hat spherical collapse (SC) model [3]. In this approach, one considers a uniform and spherically symmetric perturbation in an expanding background and describes the growth of perturbations in a spherical region using the same Friedmann equations for the underlying theory of gravity [9,10,11,12].

According to thermodynamics–gravity conjecture [13,14,15,16,17,18,19,20,21], one can write the Friedmann equations in any gravity theory in the form of the first law of thermodynamics, \(\textrm{d}E = T_{\textrm{h}}\textrm{d}S_{\textrm{h}} +W \textrm{d}V\), on the apparent horizon and vice versa [22,23,24,25,26,27,28,29,30,31,32,33]. For this purpose, one should pick up the entropy expression of the black hole in each gravity theory and replace the black hole horizon radius \(r{+}\) with the apparent horizon radius \({\tilde{r}}_{\textrm{A}}\). While it is more convenient to apply the Bekenstein–Hawking area law relation defined as \(S_{\textrm{h}}=A/(4G)\) for the black hole entropy (with the black hole horizon area \(A=4 \pi r_{+}^{2}\)), it should be noted that there are several types of corrections to the area law of entropy. Two possible corrections that occur from the inclusion of quantum effects are known as logarithmic and power-law corrections. Logarithmic correction arises from the loop quantum gravity due to thermal equilibrium fluctuations and quantum fluctuations [34,35,36,37,38], and the power-law corrections appear in dealing with the entanglement of quantum fields inside and outside the horizon [39,40,41].

Another type of correction to the area law of entropy comes from the fact that, in divergent partition function systems such as gravitational systems, Boltzmann–Gibbs additive entropy should be generalized to non-additive entropy [42,43,44,45]. Based on this, and using the statistical arguments, Tsallis and Cirto [46] argued that the microscopic mathematical expression of the thermodynamic entropy of a black hole does not obey the area law and is modified as \(S_{\textrm{h}} \sim A^{\beta }\), where \(\beta \) is a non-extensive parameter which quantifies the degree of non-extensivity of the system [46]. Tsallis’s definition of entropy plays a crucial role in studying gravitational and cosmological systems in the framework of generalized statistical mechanics [47,48,49]. Some phenomenological aspects as well as observational constraints on the modified Friedmann equations based on Tsallis entropy were explored in [50]. It was argued that this model is compatible with observations [50]. Modified cosmology through Tsallis holographic DE (THDE) has also been explored [51,52,53,54,55]. It was shown that, depending on the value of the \(\beta \) parameter, the THDE model can explain the current accelerated cosmic expansion and alleviate the age problem [54].

Recently, Barrow suggested a fractal structure for the black hole horizon and argued that the area of the horizon may increase due to quantum gravitational deformation [56]. As a result, the area law of entropy is modified as \(S_{\textrm{h}} \sim A^{ 1+\Delta /2}\), where \(\Delta \) quantifies the quantum gravitational deformation. The modified cosmological field equations based on Barrow entropy were explored in [28, 57]. More recently, new developments have appeared in the literature aiming to test the performance of the Barrow entropy in the cosmological framework [58]. The validity and the constraints imposed by the generalized second law of thermodynamics, including the matter–energy content and the horizon entropy, were investigated in [58]. Additionally, the Barrow holographic DE (BHDE) model was proposed in [59,60,61,62] and was tested against the latest cosmological data in [63, 64]. It was found that BHDE very efficiently describes the late accelerated expansion of the universe, having additionally the correct asymptotic behavior [65]. It is worth noting that although the Barrow entropy resembles the Tsallis entropy, their physical motivation and origin are completely different. Indeed, Tsallis non-additive entropy correction is motivated by generalizing standard thermodynamics to a non-extensive one, while the Barrow correction to entropy originates from intricate, fractal structure on the horizon induced by quantum gravitational effects.

Our aim in this paper is to determine the influence of the Tsallis and Barrow entropy corrections on the growth of perturbations in the early stage of the universe. For this purpose, using thermodynamics–gravity conjecture, we extract the modified Friedmann equations based on Tsallis/Barrow entropy [27, 28]. We then employ the SC approach, and investigate the evolution of DM and DE perturbations in the framework of Tsallis and Barrow cosmology.

The paper is structured as follows. In Sect. 2, we provide a review on the modified Friedmann equations in Tsallis and Barrow cosmology. In Sect. 3, we examine the growth of matter perturbations in Tsallis cosmology using the SC approach. In Sect. 4, we explore the growth of perturbations against the background of Barrow cosmology. We finish our paper with concluding remarks in Sect. 5.

2 Modified Friedmann equations in Tsallis and Barrow cosmology

We start with a spatially homogeneous and isotropic spacetime with line elements

$$\begin{aligned} \textrm{d}s^2={h}_{\mu \nu }\textrm{d}x^{\mu } \textrm{d}x^{\nu }+{\tilde{r}}^2(\textrm{d}\theta ^2+\sin ^2\theta \textrm{d}\phi ^2), \end{aligned}$$
(1)

where \({\tilde{r}}=a(t)r\), \(x^0=t, x^1=r\), and \(h_{\mu \nu }\) = diag \((-1, a^2/(1-kr^2))\) represents the two-dimensional metric. The open, flat, and closed universe corresponds to \(k = -1,0, 1\), respectively. We assume that our universe is bounded by an apparent horizon with a radius of [29]

$$\begin{aligned} {\tilde{r}}_{\textrm{A}}=\frac{1}{\sqrt{H^2+k/a^2}}. \end{aligned}$$
(2)

The apparent horizon is a suitable boundary foe which the first and second law of thermodynamics hold. The temperature associated with the apparent horizon has the form [23, 29]

$$\begin{aligned} T_{\textrm{h}}=-\frac{1}{2 \pi {\tilde{r}}_\textrm{A}}\left( 1-\frac{\dot{\tilde{r}}_\textrm{A}}{2H{\tilde{r}}_\textrm{A}}\right) . \end{aligned}$$
(3)

We further assume that the energy content of the universe is in the form of perfect fluid,

$$\begin{aligned} T_{\mu \nu }=(\rho +p)u_{\mu }u_{\nu }+pg_{\mu \nu }, \end{aligned}$$
(4)

where \(\rho \) and p are the energy density and pressure of the matter inside the universe, respectively. The total energy content of the universe satisfies the conservation equation, \(\nabla _{\mu }T^{\mu \nu }=0\), which yields the continuity equation,

$$\begin{aligned} {\dot{\rho }}+3H(\rho +p)=0. \end{aligned}$$
(5)

In the above relation, \(H=\dot{a}/a\) stands for the Hubble parameter which measures the rate of the universe expansion. In an expanding universe, as a thermodynamic system, we must define a work term in the first law of thermodynamics. The work density for an expanding universe may be obtained as [66]

$$\begin{aligned} W=-\frac{1}{2} T^{\mu \nu }h_{\mu \nu },\ \ \Rightarrow \ \ W=\frac{1}{2}(\rho -p). \end{aligned}$$
(6)

We further assume that the first law of thermodynamics on the apparent horizon is satisfied and has the form

$$\begin{aligned} \textrm{d}E = T_\textrm{h} \textrm{d}S_\textrm{h} + W\textrm{d}V, \end{aligned}$$
(7)

where \(V=\frac{4\pi }{3}{\tilde{r}}_{\textrm{A}}^{3}\) is the volume enveloped by a three-dimensional sphere, and \(T_{\textrm{h}}\) and W are given by (3) and (6). In the above expression, \(S_{\textrm{h}}\) stands for the entropy associated with the apparent horizon. The total energy of the universe is \(E=\rho V\), which after taking the differential and using the continuity equation (5), leads to

$$\begin{aligned} \textrm{d}E=4\pi {\tilde{r}}_{\textrm{A}}^{2}\rho \textrm{d}{\tilde{r}}_{\textrm{A}}-4\pi H {\tilde{r}}_{\textrm{A}}^{3}(\rho +p) \textrm{d}t. \end{aligned}$$
(8)

In order to derive the Friedmann equations from the first law of thermodynamics (7), we need to define the entropy expression associated with the boundary of the universe. In this paper, we consider two modification for the area law, known as Tsallis and Barrow entropy.

2.1 Modified Friedmann equations through Tsallis entropy

The Tsallis entropy associated with the boundary of the universe is given by [46]

$$\begin{aligned} S_{\textrm{h}}= \gamma A^{\beta }, \end{aligned}$$
(9)

where A is the apparent horizon area, \(\gamma \) is an unknown constant, and \(\beta \) is known as the Tsallis parameter or non-extensive parameter, which is a real parameter that quantifies the degree of non-extensivity [46]. When \(\beta =1\) and \(\gamma =1/(4L_p^2)\), the well-known area law of entropy is recovered. Using Tsallis entropy in the first law of thermodynamics on the apparent horizon, we derive the differential form of the modified Friedmann equation [27]

$$\begin{aligned} -\frac{2}{{\tilde{r}}_{\textrm{A}}^3} \left( 4\pi \tilde{r}_{\textrm{A}}^2\right) ^{\beta -1} \textrm{d}{\tilde{r}}_{\textrm{A}} = \frac{2\pi }{3\gamma \beta }\textrm{d}\rho . \end{aligned}$$
(10)

Integrating, we arrive at the modified Friedmann equation based on Tsallis entropy [27]

$$\begin{aligned} \left( H^2+\frac{k}{a^2}\right) ^{2-\beta } = \frac{8\pi L_p^2}{3} \rho +\frac{\Lambda }{3}, \end{aligned}$$
(11)

where \(\Lambda \) is the integration constant which can be interpreted as the cosmological constant, and we have defined

$$\begin{aligned} \gamma \equiv \frac{2-\beta }{4\beta L_p^2 } \left( 4\pi \right) ^{1-\beta }. \end{aligned}$$
(12)

The above Friedmann equation can be rewritten as

$$\begin{aligned} \left( H^2+\frac{k}{a^2}\right) ^{2-\beta } = \frac{8\pi L_p^2}{3} (\rho +\rho _{\Lambda }), \end{aligned}$$
(13)

where \(\rho _{\Lambda }=\Lambda /(8\pi L_p^2)\) is the energy density of the cosmological constant. Since \(\gamma >0\), from Eq. (12) we have \(\beta <2\). The second modified Friedmann equation can be easily derived by combining the continuity equation (5) with the first Friedmann equation (13). We find [27]

$$\begin{aligned}{} & {} (4-2\beta ) \frac{\ddot{a}}{a}\left( H^2+\frac{k}{a^2}\right) ^{1-\beta }+(2\beta -1) \left( H^2+\frac{k}{a^2}\right) ^{2-\beta }\nonumber \\{} & {} \quad =-8\pi L_{p}^{2} (p+p_{\Lambda }). \end{aligned}$$
(14)

where \(p_{\Lambda }=-\Lambda /(8\pi L_p^2)\) is the vacuum (cosmological constant) pressure. As usual, we define the density parameters as

$$\begin{aligned} \Omega _m=\frac{\rho _m}{\rho _{c}}, \ \ \ \Omega _{\Lambda }=\frac{\rho _{\Lambda }}{\rho _{c}}, \ \ \ \rho _{c}=\frac{3H^{4-2\beta }}{8\pi L_{p}^{2}}. \ \ \end{aligned}$$
(15)

Therefore, in terms of the density parameters, the first Friedmann equation (13) can be written as

$$\begin{aligned} \Omega _m+ \Omega _{\Lambda }=(1+\Omega _k)^{2-\beta }, \end{aligned}$$
(16)

where the curvature density parameter is defined as usual, \(\Omega _k=k/(a^2H^2)\), and we have assumed \(\rho =\rho _m\) by neglecting the radiation.

2.2 Modified Friedmann equations through Barrow entropy

The Barrow entropy associated with the apparent horizon is given by [56]

$$\begin{aligned} S_{\textrm{h}}= \left( \frac{A}{A_{0}}\right) ^{1+\Delta /2}, \end{aligned}$$
(17)

where A is the apparent horizon area and \(A_0\) is the Planck area. The exponent \(\Delta \) ranges as \(0\le \Delta \le 1\) and stands for the amount of the quantum gravitational deformation effects [56]. When \(\Delta =0\), the area law is restored and \(A_{0}\rightarrow 4G\), while \(\Delta =1\) represents the most intricate and fractal structure of the horizon. Using the thermodynamics–gravity conjecture, the differential form of the Friedmann equation derived from the first law of thermodynamics, based on Barrow entropy, is given by [28]

$$\begin{aligned} -\frac{2+\Delta }{2\pi A_0 }\left( \frac{4\pi }{A_0}\right) ^{\Delta /2} \frac{\textrm{d}\tilde{r}_{\textrm{A}}}{{\tilde{r}}_{\textrm{A}}^{3-\Delta }}= \frac{\textrm{d}\rho }{3}. \end{aligned}$$
(18)

After integration, we find the first modified Friedmann equation in Barrow cosmology,

$$\begin{aligned} \left( H^2+\frac{k}{a^2}\right) ^{1-\Delta /2} = \frac{8\pi G_{\textrm{eff}}}{3} \rho +\frac{\Lambda }{3}, \end{aligned}$$
(19)

where \(\Lambda \) is a constant of integration which can be interpreted as the cosmological constant, and \(G_{\textrm{eff}}\) stands for the effective Newtonian gravitational constant,

$$\begin{aligned} G_{\textrm{eff}}\equiv \frac{A_0}{4} \left( \frac{2-\Delta }{2+\Delta }\right) \left( \frac{A_0}{4\pi }\right) ^{\Delta /2}. \end{aligned}$$
(20)

If we define \(\rho _{\Lambda }={\Lambda }/(8\pi G_{\textrm{eff}})\), Eq. (19) can be rewritten as

$$\begin{aligned} \left( H^2+\frac{k}{a^2}\right) ^{1-\Delta /2} = \frac{8\pi G_{\textrm{eff}}}{3}(\rho +\rho _{\Lambda }). \end{aligned}$$
(21)

Combining the modified Friedmann equation (21) with the continuity equation (5), we arrive at

$$\begin{aligned}{} & {} (2-\Delta )\frac{\ddot{a}}{a} \left( H^2+\frac{k}{a^2}\right) ^{-\Delta /2}+(1+\Delta )\left( H^2+\frac{k}{a^2}\right) ^{1-\Delta /2} \nonumber \\{} & {} \quad =-8\pi G_{\textrm{eff}}(p+p_{\Lambda }), \end{aligned}$$
(22)

where \(p_{\Lambda }=-{\Lambda }/(8\pi G_{\textrm{eff}})\). This is the second modified Friedmann equation governing the evolution of the universe based on Barrow entropy. In the limiting case where \(\Delta =0\) (\(G_{\textrm{eff}}\rightarrow G\)), Eqs. (21) and (22) reduce to the Friedmann equation in standard cosmology.

In this case, we define the critical density parameter as \(\rho _{\textrm{c}}=3H^{2-\Delta }/(8\pi G_{\textrm{eff}})\), and thus the first Friedmann equation (21) can be rewritten as

$$\begin{aligned} \Omega _m+ \Omega _{\Lambda }=(1+\Omega _k)^{1-\Delta /2}. \end{aligned}$$
(23)

Now we are going to show that the modified Friedmann equations based on Tsallis/Barrow entropy derived in Eqs. (13) and (21) can describe the late-time accelerated expansion. For a flat universe filled with pressureless matter (\(p=p_m=0\)) and cosmological constant, we have \(\Omega _m+ \Omega _{\Lambda }=1.\) The total equation of state parameter can be written

$$\begin{aligned}{} & {} \omega _{\textrm{t}}=\frac{p_{\Lambda }}{\rho _m+\rho _{\Lambda }}=-\frac{1}{\rho _m/\rho _{\Lambda }+1}, \nonumber \\{} & {} \quad \Rightarrow \omega _{\textrm{t}} (z)=-\frac{\Omega _{\Lambda ,0}}{(1-\Omega _{\Lambda ,0}) (1+z)^3+\Omega _{\Lambda ,0}}, \end{aligned}$$
(24)

where \(\rho _{\Lambda }=\rho _{\Lambda ,0}\), and \(\rho _m=\rho _{m,0} (1+z)^{3}\). If we take \(\Omega _{\Lambda ,0} \simeq 0.7 \) and \(\Omega _{m,0} \simeq 0.3\), we have

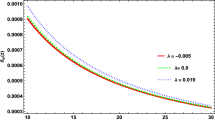
$$\begin{aligned}{} & {} \omega _{\textrm{t}} (z)=-\frac{0.7}{0.7+0.3 (1+z)^3}. \end{aligned}$$
(25)

At the present time, where \(z\rightarrow 0\), we have \(\omega _{\textrm{t}}=-0.7\), while at the early universe where \(z\rightarrow \infty \), we obtain \(\omega _{\textrm{t}}=0\). This implies that at the early stages, the universe undergoes a decelerated phase while at the late time it experiences an accelerated phase. In Fig. 1 we have plotted the \(\omega _{\textrm{t}}\) versus z for different values of \(\Omega _{\Lambda ,0}\). This figure confirms an accelerated universe at the late time.

Fig. 1
figure 1

The behavior of \(\omega _{\textrm{t}}\) in terms of redshift z for different values of \(\Omega _{\Lambda ,0}\)

Full size image

3 Growth of perturbation in Tsallis cosmology

In a spatially flat universe, the modified Friedmann equation (13) can be written as

$$\begin{aligned}{} & {} H^{4-2\beta }=\dfrac{1}{3}\left( \rho _{m}+\Lambda \right) , \end{aligned}$$
(26)

where we have taken \(8 \pi L_p^2 =1\) and hence \(\rho _{\Lambda }=\Lambda \). The second Friedmann equation (14) based on Tsallis entropy is given by

$$\begin{aligned}{} & {} (4-2\beta )\dfrac{\ddot{a}}{a}H^{2-2\beta }+(2\beta -1)H^{4-2\beta }=\Lambda , \end{aligned}$$
(27)

where \(p_{m}=0\) and \(p_{\Lambda }=-\Lambda \). The Hubble expansion rate can be obtained as

$$\begin{aligned} H^{2}=\left( \dfrac{\rho _{m}+\Lambda }{3}\right) ^{1/(2-\beta )}. \end{aligned}$$
(28)

We can also define the normalized Hubble parameter as

$$\begin{aligned} E(z)=\frac{H(z)}{H_{0}}=\left[ (1-\Omega _{\Lambda ,0})(1+z)^{3}+\Omega _{\Lambda ,0}\right] ^{1/(4-2\beta )}. \end{aligned}$$
(29)

The evolution of the normalized Hubble parameter versus z for different values of \(\beta \) is plotted in Fig. 2. As we can see, in Tsallis cosmology the Hubble parameter is smaller than in the \(\Lambda \)CDM model, implying that in this model our universe expands more slowly. Also, the Hubble parameter decreases with the decrease in the non-extensive parameter \(\beta \). The deceleration parameter in terms of the redshift can be written as

$$\begin{aligned}{} & {} q=-1-\dfrac{\dot{H}}{H^2}=-1+\dfrac{(1+z)}{H(z)}\dfrac{dH(z)}{dz} \nonumber \\{} & {} \quad =-1+\dfrac{3}{2}\dfrac{(1+z)^{3}(1-\Omega _{\Lambda ,0})}{(2-\beta )[(1-\Omega _{\Lambda ,0})(1+z)^{3}+\Omega _{\Lambda ,0}]}. \end{aligned}$$
(30)
Fig. 2
figure 2

The behavior of the normalized Hubble rate E(z) for different values of \(\beta \) in Tsallis cosmology, where we have taken \(\Omega _{\Lambda ,0}=0.70\)

Full size image

We have plotted the behavior of the deceleration parameter q(z) for different \(\beta \) parameters in Fig. 3. We observe that the universe experiences a transition from a decelerating phase (\(q>0\)) to an accelerating phase (\(q<0\)) at a redshift around \(z_{\textrm{tr}}\approx 0.6\), compatible with observations. It is seen that \(z_{\textrm{tr}}\) depends on the non-extensive parameter \(\beta \) and decreases with increasing \(\beta \).

Fig. 3
figure 3

The behavior of the deceleration parameter q(z) as a function of redshift for different \(\beta \) (\(\beta =1\) corresponds to \(\Lambda \)CDM model). Here we have taken \(\Omega _{\Lambda ,0}=0.70\)

Full size image

Another quantity which is helpful in understanding the phase transitions of the universe is called the jerk parameter. This is a dimensionless quantity obtained by taking the third derivative of the scale factor with respect to the cosmic time, and provides a comparison between different DE models and the \(\Lambda \)CDM \((j=1)\) model. The jerk parameter is defined as

$$\begin{aligned} j=\dfrac{1}{aH^{3}}\dfrac{\textrm{d}^{3}a}{\textrm{d}t^{3}}=q(2q+1)+(1+z)\dfrac{\textrm{d}q}{\textrm{d}z}. \end{aligned}$$
(31)

For the \(\Lambda \)CDM model, the value of j is always unity. A non-\(\Lambda \)CDM model occurs if there is any deviation from the value of \(j=1\). From Fig. 4 we observe that the jerk parameter is smaller (larger) than \(\Lambda \)CDM for \(\beta <1\) (\(\beta >1\)).

Fig. 4
figure 4

Evolution of the jerk parameter with respect to redshift for different values of \(\beta \) parameter

Full size image

Combining Eqs. (26) and (27), we arrive at

$$\begin{aligned} \dfrac{\ddot{a}}{a}= & {} \dfrac{1}{4-2\beta }\Bigg \{(1-2\beta )\left( \dfrac{\rho _{m}+\Lambda }{3}\right) ^{1/(2-\beta )} \nonumber \\{} & {} +\Lambda \left( \dfrac{\rho _{m}+\Lambda }{3}\right) ^{(\beta -1)/(2-\beta )}\Bigg \} . \end{aligned}$$
(32)

The conservation equations take the form

$$\begin{aligned} {\dot{\rho }}_{m}+3H\rho _{m}=0. \end{aligned}$$
(33)

This equation describes the density evolution of pressureless matter labeled by m with background density \(\rho _{m}\). The SC model describes a spherical region with uniform density so that at time t, \(\rho _{m}^{c}=\rho _{m} (t)+\delta \rho _{m}\). We can write the conservation equation for the spherical perturbed region of radius \(a_p\) as

$$\begin{aligned} {\dot{\rho }}_{m}^{c}+3h\rho _{m}^{c}=0, \end{aligned}$$
(34)

where \(h=\dot{a_{p}}/a_{p}\) is the local expansion rate of the spherical perturbed region of radius \(a_{p}\). Since Eq. (32) is valid for the entire spacetime region, we further assume that it holds for the spherical perturbed region with radius \(a_{p}\), namely,

$$\begin{aligned} \dfrac{\ddot{a}_{p}}{a_{p}}= & {} \dfrac{1}{4-2\beta }\Bigg \{ (1-2\beta )\left( \dfrac{\rho _{m}^{c}+\Lambda }{3}\right) ^{{1}/(2-\beta )} \nonumber \\{} & {} +\Lambda \left( \dfrac{\rho _{m}^{c}+\Lambda }{3}\right) ^{(\beta -1)/(2-\beta )}\Bigg \} , \end{aligned}$$
(35)

where for simplicity we assume that \(\beta ^{c}=\beta \). The density contrast of a single fluid labeled by \(\delta _m\) is defined as [10]

$$\begin{aligned} \delta _{m}=\dfrac{\rho _{m}^{c}}{\rho _{m}}-1=\dfrac{\delta \rho _{m}}{\rho _{m}}. \end{aligned}$$
(36)

Taking the time derivative of Eq. (36) and using Eqs. (33) and (34) yields

$$\begin{aligned} \dot{\delta _{m}}=3(1+\delta _{m})(H-h). \end{aligned}$$
(37)

If we take the second derivative with respect to time, we find

$$\begin{aligned} \ddot{\delta }_{m}-\dfrac{{\dot{\delta }}_{m}^{2}}{1+\delta _{m}}=3(\dot{H}-\dot{h})(1+\delta _{m}), \end{aligned}$$
(38)

where we have used Eq. (37). Combining Eqs. (32), (35) and (36), we can find the following equation

$$\begin{aligned} \dot{H}-\dot{h}= & {} -H^{2}+h^{2}+\dfrac{2\beta -1}{2(2-\beta )^{2}} \left( \dfrac{\rho _{m}}{3}\right) ^{1/(2-\beta )}\delta _{m} \nonumber \\{} & {} +\dfrac{\Lambda (1-\beta )}{2(2-\beta )^{2}} \left( \dfrac{\rho _{m}}{3}\right) ^{(\beta -1)/(2-\beta )}\delta _{m}, \end{aligned}$$
(39)

where we have expanded the first and second terms in the matter-dominated era and in the linear term of \(\delta _{m}\). This is because we work in the early universe where \(\rho _{\Lambda }/\rho _{m}<1\) and in the linear regime where \(\delta _{m} <1\). Therefore, Eq. (38) using Eqs. (37) and (39) in the linear regime can be rewritten as

$$\begin{aligned}{} & {} \ddot{\delta }_{m}+2H{\dot{\delta }}_{m}-\dfrac{3}{2}\dfrac{2\beta -1}{(2-\beta )^{2}}\left( \dfrac{\rho _{m}}{3}\right) ^{1/(2-\beta )}\delta _{m}\nonumber \\{} & {} \quad -\dfrac{3}{2}\dfrac{(1-\beta )\Lambda }{(2-\beta )^{2}}\left( \dfrac{\rho _{m}}{3}\right) ^{(\beta -1)/(2-\beta )}\delta _{m} =0, \end{aligned}$$
(40)

where the matter energy density is given by \(\rho _{m} =\rho _{m,0}a^{3}\). In order to study the evolution of the density contrast \(\delta _{m}\) in terms of the redshift parameter, \(1 + z = a^{-1}\), we first replace the time derivatives with the derivatives with respect to the scale factor a. It is a matter of calculations to show that

$$\begin{aligned}{} & {} {\dot{\delta }}_{m}=aH\delta ^{\prime }_{m}, \nonumber \\{} & {} \ddot{\delta }_{m}=aH^{2}\left( \dfrac{1-2\beta +\Lambda H^{2\beta -4}}{4-2\beta } \right) \delta ^{\prime }_{m} +a^{2}H^{2}\delta ^{\prime \prime } _{m} \end{aligned}$$
(41)

where the prime stands for the derivative with respect to the scale factor a. Combining Eqs. (40) and (41), we arrive at

$$\begin{aligned}{} & {} \delta ^{\prime \prime }_{m}+\dfrac{1}{a(4-2\beta )}\left[ (9-6\beta )+\Lambda H^{2\beta -4}\right] \delta ^{\prime }_{m}\nonumber \\{} & {} \quad +\Bigg \{(1-2\beta )\rho ^{{1}/(2-\beta )}_{m}-3(1-\beta )\Lambda \rho ^{(\beta -1)/(2-\beta )}_{m}\Bigg \}\nonumber \\{} & {} \quad \times \dfrac{3^{(1-\beta )/(2-\beta )}}{a^2H^2}\dfrac{\delta _{m}}{2(2-\beta )^{2}}=0. \end{aligned}$$
(42)

It should be noted that in standard cosmology (\(\beta =1\)), and in the absence of the cosmological constant (\(\Lambda =0\)), Eq. (42) reduces to

$$\begin{aligned} \delta ^{\prime \prime }_{m}+\dfrac{3}{2a}\delta ^{\prime }_{m}-\dfrac{3}{2a^{2}}\delta _{m}=0, \end{aligned}$$
(43)

which is the result obtained in standard cosmology [3]. In Fig. 5, we plot the matter density contrast \(\delta _m\) as a function of redshift for different values of \(\beta \) parameter and for redshifts \(10<z<100\). We can see that non-extensive parameter \(\beta \) affects the growth of matter perturbations, in particular in the lower redshifts. Indeed, the growth of perturbations increases with the increase in the non-extensive Tsallis parameter \(\beta \). Further, we find that in lower redshifts, the matter perturbations for \(\beta <1\) grow more slowly than in standard cosmology (\(\beta =1\)), while for \(\beta >1\) they grow more rapidly.

Fig. 5
figure 5

Growth of matter perturbations (density contrast \(\delta _m\)) for different values of \(\beta \) in Tsallis cosmology, where the dashed line for \(\beta =1.06\), the solid line for \(\Lambda \)CDM (\(\beta =1\)), and the dash-dotted line for \(\beta =0.94\). Here we take \(\delta _{m}(z_{i})=0.0001\)

Full size image

4 Growth of perturbation in Barrow cosmology

In a flat Friedmann–Robertson–Walker (FRW) universe, the modified Friedmann equations, based on Barrow entropy, can be rewritten as

$$\begin{aligned}{} & {} H^{2-\Delta }=\Gamma (\rho _{m}+\rho _{\Lambda }), \end{aligned}$$
(44)
$$\begin{aligned}{} & {} \left( 2-\Delta \right) \dfrac{\ddot{a}}{a}H^{-\Delta }+\left( 1+\Delta \right) H^{2-\Delta }\nonumber \\{} & {} \quad =-3\Gamma (p_{m}+p_{\Lambda }), \end{aligned}$$
(45)

where

$$\begin{aligned} \Gamma \equiv \dfrac{1}{3}\left( \dfrac{2-\Delta }{2+\Delta } \right) \left( \dfrac{1}{8\pi ^2}\right) ^{{\Delta }/{2}}. \end{aligned}$$
(46)

Note that here we work in the unit where \(k_{B}=c=\hslash =1\), and thus \(A_{0}=4G\). We also assume, for simplicity, that \(8\pi G=1\). In terms of the density parameters, the first Friedmann equation (44) can be written as \(\Omega _{m}+\Omega _{de}=1\), where the dimensionless density parameters are now defined as

$$\begin{aligned} \Omega _{m}\equiv \dfrac{\Gamma \rho _{m}}{H^{2-\Delta }}, \ \ \ \ \ \Omega _{de}\equiv \dfrac{\Gamma \rho _{de}}{H^{2-\Delta }}. \end{aligned}$$
(47)

We can write the normalized Hubble parameter as

$$\begin{aligned} E(z)=\dfrac{H(z)}{H_{0}}=\left[ (1-\Omega _{\Lambda ,0})(1+z)^{3}+\Omega _{\Lambda ,0}\right] ^{1/(2-\Delta )}. \end{aligned}$$
(48)

The evolution of the normalized Hubble parameter versus z for different values of \(\Delta \) is plotted in Fig. 6. It is seen that the Hubble parameter is larger than the \(\Lambda \)CDM \((\Delta =0)\) model, indicating that in Barrow cosmology the universe expands more rapidly. Also, the Hubble parameter decreases with the decrease in the Barrow parameter \(\Delta \).

Fig. 6
figure 6

The behavior of the normalized Hubble rate for different values of \(\Delta \), where we have taken \(\Omega _{\Lambda ,0}=0.7\)

Full size image

The deceleration parameter in terms of the redshift can be written as

$$\begin{aligned}{} & {} q=-1-\dfrac{\dot{H}}{H^2}=-1+\dfrac{(1+z)}{H(z)}\dfrac{dH(z)}{dz} \nonumber \\{} & {} \quad =-1+\dfrac{3(1+z)^{3}(1-\Omega _{\Lambda ,0})}{(2-\Delta )\left( (1-\Omega _{\Lambda ,0})(1+z)^{3}+\Omega _{\Lambda ,0} \right) }. \end{aligned}$$
(49)

We have plotted the behavior of the deceleration parameter q(z) for different \(\Delta \) parameter in Fig. 7. We observe that the universe experiences a transition from decelerating phase (\(z>z_{\textrm{tr}}\)) to accelerating phase (\(z<z_{\textrm{tr}}\)). Also, we can see that with the increase in \(\Delta \), the phase transition between deceleration and acceleration takes place at lower redshifts.

Fig. 7
figure 7

The behavior of the deceleration parameter as a function of redshift for different \(\Delta \). Here we take \(\Omega _{\Lambda ,0}=0.7\)

Full size image

Similar to the previous section, we can find the jerk parameter in this model. From Fig. 8 we observe that the jerk parameter for all values of the \(\Delta \) parameter is greater than in the \(\Lambda \)CDM model.

Fig. 8
figure 8

The evolution of jerk parameter with respect to redshift for different values of the \(\Delta \) parameter

Full size image

Combining Eqs. (44) and (45), we find

$$\begin{aligned} \dfrac{\ddot{a}}{a}= & {} \frac{\Gamma ^{2/(2-\Delta )}}{\Delta -2}\Bigg \{ (1+\Delta )\left( \rho _{m}+\Lambda \right) ^{2/(2-\Delta )} \nonumber \\{} & {} -3\Lambda \left( \rho _{m}+\Lambda \right) ^{\Delta /(2-\Delta )}\Bigg \}. \end{aligned}$$
(50)

In order to study the growth of perturbations in Barrow cosmology, following the approach of the previous section, we employ the SC method. For the spherical perturbed region of radius \(a_p\), we can write

$$\begin{aligned} \frac{\ddot{a}_{p}}{a_{p}}= & {} \frac{\Gamma ^{2/(2-\Delta )}}{\Delta -2}\Bigg \{ (1+\Delta )\left( \rho _{m}^{c}+\Lambda \right) ^{2/(2-\Delta )} \nonumber \\{} & {} -3\Lambda \left( \rho _{m}^{c}+\Lambda \right) ^{\Delta /(2-\Delta )}\Bigg \} , \end{aligned}$$
(51)

Combining Eqs. (36), (50), and (51), we arrive at

$$\begin{aligned}{} & {} \dot{H}-\dot{h}+H^{2}-h^{2}=\Bigg \{\dfrac{2(1+\Delta )}{(2-\Delta )^{2}}(\Gamma \rho _{m})^{2/(2-\Delta )}\nonumber \\{} & {} \quad -\dfrac{3\Delta }{(2-\Delta )^{2}}\Lambda (\Gamma \rho _{m})^{\Delta /(2-\Delta )}\Bigg \}\delta _{m}. \end{aligned}$$
(52)

Using Eqs. (37), (38) and (52), after a simple calculation, we find

$$\begin{aligned}{} & {} \ddot{\delta }_{m}+2H{\dot{\delta }}_{m}-\Bigg \{\dfrac{6(1+\Delta )}{(2-\Delta )^{2}}(\Gamma \rho _{m})^{2/(2-\Delta )}\nonumber \\{} & {} \quad -\dfrac{9\Delta }{(2-\Delta )^{2}}\Lambda (\Gamma \rho _{m})^{\Delta /(2-\Delta )}\Bigg \}\delta _{m}=0. \end{aligned}$$
(53)

Changing our variable from time to the scale factor, we can rewrite the above equations as

$$\begin{aligned}{} & {} \delta ^{\prime \prime }_{m}+\dfrac{3}{a(2-\Delta )}\left[ (1-\Delta )+\Gamma \Lambda H^{\Delta -2}\right] \delta ^{\prime }_{m}\nonumber \\{} & {} \quad -\Bigg \{2(1+\Delta )(\Gamma \rho _{m})^{2/(2-\Delta )}-3\Delta \Lambda (\Gamma \rho _{m})^{\Delta /(2-\Delta )}\Bigg \}\nonumber \\{} & {} \quad \times \dfrac{3}{a^2H^2}\dfrac{\delta _{m}}{(2-\Delta )^{2}}=0. \end{aligned}$$
(54)

It should be noted that in standard cosmology (\(\Delta =0\)), and with the absence of the cosmological constant (\(\Lambda = 0\)), this equation reduces to Eq. (43). In Fig. 9, we have plotted the matter density contrast as a function of redshift for different values of the \(\Delta \) parameter and for redshifts \(10< z < 100\). We can see that the Barrow exponent \(\Delta \) affects the growth of total perturbations, in particular in the lower redshifts. Indeed, in low redshifts, the total density contrast increases with increasing \(\Delta \) parameter. This implies that in Barrow cosmology, the perturbations grow more rapidly than in standard cosmology. This is because, in Barrow cosmology, the spacetime has quantum gravitational deformation and intricate fractal structure, which can support the growth of perturbations in energy density.

Fig. 9
figure 9

Growth of matter perturbations (density contrast \(\delta _m\)) for different values of \(\Delta \), where the dashed line for \(\Delta =0.1\), the dash-dotted line for \(\Delta =0.05\) and the solid line for \(\Lambda CDM\). Here we take \(\delta _{m}(z_{i})=0.0001\)

Full size image

5 Concluding remarks

In this paper, we have investigated the modified cosmological field equations of a flat FRW universe when the entropy associated with the apparent horizon is in the form of Tsallis/Barrow entropy. We have explored the growth of perturbations in the context of Tsallis/Barrow cosmology. We have considered the energy/matter content of the universe in the form of matter (baryonic matter and DM) and cosmological constant. Employing the SC approach for the growth of perturbations, we extracted the differential equation for the evolution of the matter perturbations. Further, for the matter density contrast, we observed that the profile of the growth of perturbations differs from standard cosmology. Indeed, in Tsallis cosmology and in lower redshifts, the perturbations grow more slowly for \(\beta <1\) than in standard cosmology (\(\beta =1\)), while they grow more rapidly for \(\beta >1\). In Barrow cosmology, however, the growth rate of the total perturbations was always faster than in standard cosmology.

Also, we find that both Tsallis and Barrow cosmology can explain the phase transition from a decelerating to an accelerating universe. In contrast to Tsallis cosmology, we observed that Barrow cosmology predicts that the universe expands at a greater rate than in the \(\Lambda \)CDM model.

It is important to note that although the modified Friedmann equations based on Tsallis and Barrow entropy are similar to each other, the growth of perturbation differs in some cases in these models. This is because the non-extensive Tsallis parameter \(\beta \) takes a different value from the Barrow exponent \(\Delta \). Indeed, the non-extensive Tsallis parameter has an upper bound, \(\beta <2\), while the Barrow exponent ranges as \(0\le \Delta \le 1\). In addition, the origins of these two corrections to the entropy are completely different.

Finally, it is worth mentioning that Barrow entropy correction to the area law is just a first approximation on the subject of quantum gravitational implications of the black hole horizons. In reality, the underlying spacetime foam deformation will be complex, wild and dynamic. Therefore, one could think of an exponent \(\Delta \) that depends on time and scale, as has already been done with the Tsallis entropy exponent [67]. In order to constrain the Barrow exponent \(\Delta \) and Tsallis non-extensive parameter \(\beta \), one may perform a full observational confrontation using data from supernovae type Ia data (SNIa), cosmic microwave background (CMB) shift parameters, baryonic acoustic oscillations (BAO), growth rate and Hubble data observations. These issues are beyond the scope of the present work, and we leave them for future investigations.