1 Introduction

Quark transverse-momentum dependent distribution functions (TMDs for short) are the basic ingredients for parametrizing the hadronic quark-quark correlator (see the seminal Ref. [1] and for the complete parametrization Ref. [2], while Refs. [3, 4] for correlators involving gluons), and represent direct generalization of the parton distribution functions (PDFs), so that both longitudinal and transverse degrees of freedom (dof) can be addressed (see, e.g., Refs. [5, 6] for an extensive introduction to the transverse dof and related distribution functions). Clearly, with respect to the PDF, the access to the 3D imaging of hadrons allows us to achieve a deeper and deeper understanding of the non-perturbative regime of QCD, also exploiting the non-trivial coupling to the spin dof (see, e.g., Refs. [7, 8] and references therein). Hence, by means of TMDs, one can gather unique information on QCD at work in hard semi-inclusive reactions (both unpolarized and polarized) at low transverse-momentum, like low-\(q_\perp \) Drell–Yan (DY) processes, vector/scalar boson productions or semi-inclusive deep inelastic scattering (SIDIS) (see, e.g., Refs. [8,9,10,11] for a status-report on the experimental measurements).

Indeed, the extraction of TMDs from the experimental cross-section is a highly challenging task, as shown by the intense theoretical work on the factorization of the cross sections into transverse-momentum dependent matrix elements (see, e.g., Refs. [12,13,14,15,16]) and the TMDs evolution that becomes a two-scale problem, since the rapidity \(\zeta \) comes into play in addition to the renormalization scale \(\mu \) (see, e.g., Refs. [12, 17,18,19] and Ref. [20] for a recent review that covers also the factorization). Noteworthy, one has to mention the efforts for obtaining reliable global fits (see, e.g., Refs. [21,22,23,24] and also Ref. [8] for a general discussion), early-stage lattice-QCD (LQCD) calculations (see, e.g., Refs. [25,26,27,28,29] and also Refs. [8, 30,31,32]) and, finally, the broad set of phenomenological models, that we can only partially list: the bag model (see, e.g., Ref. [33] and references therein), covariant model (see, e.g., Ref. [34] and references therein), light-front (LF) constituent quark models (see, e.g., Refs. [35, 36]) and the basis LF quantization framework [37], the approaches based on the Nambu–Jona-Lasinio interaction (see, e.g., Refs. [38, 39]), the holographic models (see,e.g., Refs. [40, 41]), etc. In view of our study, one has to separately mention the approaches developed within the so-called continuum-QCD, that are based on solutions (actually in Euclidean space) of dynamical equations like the 4D homogeneous Bethe–Salpeter equation (BSE) [42, 43] in combination or not with the quark gap-equation (see, e.g. Refs. [44,45,46,47]).

It should be recalled that the proton is the elective target of much experimental (see, e.g., Refs. [9,10,11]) and theoretical research (see, e.g., Refs. [48,49,50] and references therein). While the pion, given the experimental challenges its study poses, has surely attracted less efforts in spite of its intriguing double-nature, being both a Goldstone boson (and hence fundamental for investigating the dynamical chiral-symmetry breaking) and a quark–antiquark bound system (i.e. the simplest bound system in QCD). In particular, a first extraction of the pion unpolarized leading-twist TMD from Drell–Yan data can be found in Ref. [51], where the results of the E615 Collaboration [52] has been used, and in Ref. [53], where both the previous data and the E537 Collaboration cross-sections [54] have been included. As to the phenomenological calculations, a broad overview, embracing different approaches, can be gained from Refs. [35, 38, 40, 41, 44,45,46,47, 55,56,57,58,59] (see also Ref. [60] for the generalized TMDs in a spin-0 hadron).

As a conclusion to the above schematic introduction, it has to be emphasized that the vast amount of nowadays theoretical studies on TMDs finds its strong motivation in the very accurate measurements that will come from forthcoming electron-ion colliders, that promise to achieve greatly expected milestones in the experimental investigation of non-perturbative QCD, given the planned high energy and luminosity [61, 62].

Our aim is to obtain, for the first time, T-even leading- and subleading-twist unpolarized TMDs (uTMDs) of the pion, by solving a dynamical equation directly in Minkowski space, namely relying on a genuinely relativistic quantum field theory framework based on the 4D homogeneous BSE [42, 43] (see also the recent Ref. [59] for an approach based on diagonalizing the LF QCD Hamiltonian). The 4D homogeneous BS integral equation is suitable for dealing with the fundamentally non-perturbative nature of bound states. One should not get confused by the use of an interaction kernel expressed in a perturbative series, since an integral equation has a peculiar feature of infinitely many times iterating the boson exchanges contained in each term of the kernel, just what one needs for obtaining a pole in the relevant Green’s function. In our approach (see Ref. [63] for details and references therein), based on the 4D homogeneous BSE in Minkowski space and the Nakanishi integral representation (NIR) of the BS-amplitude [64, 65], the interaction kernel is given by the exchange of a massive vector boson in the Feynman gauge, with three input parameters, inferred from LQCD calculations (see, e.g. Refs. [66,67,68]): (i) the constituent-quark and gluon masses, and (ii) a scale parameter featuring the extended quark-gluon vertex. It should be pointed out that the ladder kernel, i.e. the first term in a perturbative series, can be a reliable approximation to evaluate the pion bound state, as suggested by the suppression of the non-planar contributions for \(N_c=3\) within the BS approach in a scalar QCD model [69], and the presence of massive quarks and gluons, featuring the confinement effects in a relatively large system (\(r_{ch} \sim 0.66\) fm).

There is another important consequence stemming from the use of the BS-amplitude. Although in the definition of the \(q\bar{q}\)-pair BS-amplitude there is a simple dependence upon two interacting fermionic fields, one ends up dealing with an infinite content of Fock states (the use of the Fock space allows one to recover a probabilistic language within the BS framework). In particular, by exploiting the Fock expansion of the pion state, one can establish a formal link between the LF-projected BS-amplitude (see, e.g., Refs. [70,71,72]), and the amplitude of the Fock component of the pion state with the lowest number of constituents. Therefore, in our approach, it is natural to call the LF-projected BS-amplitude: LF valence wave function (LFWF), to be distinguished from the valence wave function, when a SU(3)-flavor language is adopted. In the latter case, the pion is composed by only two fermionic constituents, suitably dressed. One should keep in mind that within our framework, the pion LFWF contributes only with 70% [63] of the normalization, and consequently a significant role of the higher Fock components has to be highlighted, and possibly analyzed in-depth, as illustrated in what follows. Finally, we would emphasize that the first evaluation of the uTMDs strengthens the reliability of our approach and makes sound the ground for the next step, already in progress, i.e. taking into account the self-energy of the quarks (see Refs. [73,74,75,76]).

Indeed, in spirit, our approach is similar to the one developed in Ref. [45] for evaluating the leading-twist uTMD, where it was also taken into account the self-energy of the quark propagator (solving the gap equation) and a confining interaction, but in Euclidean space. In this case, one resorts to a suitable method (based on the moments and a parametrization of the Euclidean BS-amplitude) to get the Minkowski-space distribution function. Differently, in our approach the NIR of the BS-amplitude allows one to successfully deal with the analytic structure of the BS-amplitude itself, obtaining an integral equation formally equivalent to the initial 4D homogeneous BSE in Minkowski space, but more suitable for the numerical treatment. Many and relevant applications of our approach to the pion, such as the electromagnetic form factor [77], the PDF [78] and the 3D imaging [63], have confirmed its reliability and encouraged to broad the scope of our investigation. It should be pointed out that (it will become clear in what follows) the evaluation of quantities that depend not only upon the longitudinal dof but also the transverse ones leads to sharply increase the sensitivity to the dynamical content of a given phenomenological description of the pion, namely to increase its predictive power. Furthermore, the joint use of the Fock expansion, meaningful in the Minkowski space, allows one to resolve the gluonic content of the pion state.

The paper outline is as follows. In Sect. 2, the general formalism and the notations are introduced, highlighting the ingredients of our dynamical approach, namely (i) the Bethe–Salpeter amplitude, solution of the 4D homogeneous Bethe–Salpeter equation in Minkowski space, and (ii) the Nakanishi integral representation of the BS-amplitude. In Sect. 3, the expressions of leading- and subleading-twist uTMDs are given in terms of the Bethe–Salpeter amplitude of the pion. In Sects. 4 and 5, the leading and subleading-twist uTMDs are shown and compared with outcomes from other approaches. Finally, in Sect. 6, the conclusions are drawn, and the perspectives of our approach are presented.

2 Generalities

For a pion with four-momentum \(P\equiv \{P^-,P^+,\textbf{P}_\perp \}\) (where \(P^2=P^+P^--|\textbf{P}_\perp |^2=M^2\) and the LF coordinates are \(a^\pm =a^0\pm a^3\)), and by adopting both i) a frame where \(\textbf{P}_\perp =0\) and ii) the light-cone gauge \(A^+_g = 0\), the quark leading-twist uTMD, \(f^q_1(\gamma , \xi )\), is defined as follows (for a general introduction see, e.g., Refs. [1, 6])

$$\begin{aligned}{} & {} f^q_1(\gamma , \xi ) \nonumber \\{} & {} \quad ={N_c\over 4}\int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \int _{-\infty }^\infty {dy^- d\textbf{y}_\perp \over 2 (2\pi )^3}\nonumber \\{} & {} \qquad \times e^{i [\xi P^+\frac{y^-}{2} - \textbf{k}_\perp \cdot \textbf{y}_\perp ] } \langle P| \bar{\psi }_q (- \tfrac{y}{2}) \gamma ^+ \psi _q(\tfrac{y}{2}) |P \rangle \big |_{ y^+=0}, \end{aligned}$$
(1)

where \(N_c\) is the number of colors,Footnote 1\(\phi _{\hat{\textbf{k}}_\perp }\) is the azimuthal angle in the plane swept by \( \textbf{k}_\perp \), \(\psi _q\) is the fermionic field, and the quark four-momentum is given in terms of LF coordinates by \(p_q\equiv \{p^-_q, \xi P^+,\textbf{k}_\perp +\textbf{P}_\perp /2\} \), with \(\gamma =|\textbf{k}_\perp |^2\). The antiquark uTMD is obtained by using the proper four-momentum \(p_{\bar{q}}\equiv \{p^-_{\bar{q}}, (1-\xi ) P^+,-\textbf{k}_\perp +\textbf{P}_\perp /2\} \), recalling that \(P=p_q+p_{\bar{q}}\) and \(k=(p_q-p_{\bar{q}})/2\).

The normalization of \(f^q_1(\gamma , \xi )\) is given by

$$\begin{aligned}{} & {} \int _{-\infty }^\infty d\xi \int _0^\infty d\gamma ~f^q_1(\gamma , \xi )\nonumber \\{} & {} = {N_c \over 2}\int d {\textbf {p}}_{q_\perp }\int _{-\infty }^\infty {dp^+_q\over P^+}\int _{-\infty }^\infty {dp^-_q\over 2} \nonumber \\{} & {} \qquad \times \int _{-\infty }^\infty {d^4y \over (2\pi )^4}e^{i \, p_q\cdot y } \langle P| \bar{\psi }_q (- \tfrac{y}{2}) \gamma ^+ \psi _q(\tfrac{y}{2}) |P \rangle \nonumber \\{} & {} \quad =N_c~{\langle P| \bar{\psi }_q (0) \gamma ^+ \psi _q(0) |P \rangle \over 2P^+} =F^q_\pi (0)=1, \end{aligned}$$
(2)

where \(F^q_\pi (t)\) is the quark contribution to the electromagnetic (em) form factor of the pion. The latter results to be equal to \(F_\pi (t)=e_q F^q_\pi (t)+e_{\bar{q}}F^{\bar{q}}_\pi (t)\), with \(t=(P'-P)^2\), and is related to the matrix element of the four-current by \(N_c~\langle P| \bar{\psi }_q (0) \gamma ^\mu \psi _q(0) |P \rangle =2P^\mu ~F_\pi (t=0)\). Finally, it should be pointed that inserting a complete basis in Eq. (1) and exploiting the good and bad components of the fermionic field one can easily demonstrate that \(f^q_1(\gamma ,\xi )\ge 0\) (see Ref. [79]).

In order to describe the pion by taking into account at some extent the QCD dynamics in the non-perturbative regime, it is useful to resort to the Mandelstam framework [80], where the interacting quark-pion vertex is expressed in terms of the (reduced) BS-amplitude, i.e. the solution of the 4D homogeneous BSE in Minkowski space, and defined by

$$\begin{aligned} {\varPhi }(k,P)=\int d^4x~e^{i k\cdot x}\, \langle 0|T\bigl \{\psi (\tfrac{x}{2})\,\bar{\psi }(-\tfrac{x}{2}) \bigr \}|P\rangle , \end{aligned}$$
(3)

where the fermionic field fulfills the Poincaré translation \(\psi (x)=e^{i\hat{P}\cdot x} \psi (0) e^{-i\hat{P}\cdot x}\) (recall that only the component \(\hat{P}^-\) is interacting in the LF dynamics, see, e.g., Ref. [81]).

Thus, by using the Feynman-like diagrammatic picture inherent to the Mandelstam framework (see, e.g., Ref. [77] for the application to the em form factor), one can write the following expression for \(f^q_1(\gamma , \xi )\)

$$\begin{aligned}{} & {} f^q_1(\gamma , \xi ) \nonumber \\{} & {} \quad = {N_c \over 4(2\pi )^3} \int _{-\infty }^\infty {dk^+\over 2(2\pi )} \delta \Big (k^+ + \frac{P^+}{2}- \xi P^+\Big )\int _{-\infty }^\infty dk^- \nonumber \\{} & {} \qquad \times \int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \text {Tr}\left[ S^{-1}(-p_{\bar{q}}) {\bar{{\varPhi }}}(k,P)\, \gamma ^+ \,{\varPhi }(k,P) \right] ,\nonumber \\ \end{aligned}$$
(4)

where

$$\begin{aligned} p_{q(\bar{q})}=\pm \, k+\frac{P}{2}. \end{aligned}$$
(5)

For the sake of completeness, let us write the BSE in ladder approximation, i.e. the one we are adopting for the numerical calculations, viz.

$$\begin{aligned} {\varPhi }(k; P)= & {} S\bigl (p_q\bigr ) \int \frac{d^4k'}{(2\pi )^4}S^{\mu \nu }(q){\varGamma }_{\mu }(q) \nonumber \\{} & {} \times ~ {\varPhi }(k';P)\widehat{\varGamma }_{\nu }(q)S\bigl (-p_{\bar{q}}\bigr ), \end{aligned}$$
(6)

where quark and antiquark momenta are off-shell, i.e. \(p^2_{q(\bar{q})}=(\pm k +\tfrac{P}{2})^2\ne m^2\), and \(q = k - k'\) is the gluon four-momentum. In Eq. (6), the fermion propagator, the gluon propagator in the Feynman gauge and the quark-gluon vertex, dressed through a simple form factor, are

$$\begin{aligned}{} & {} S(p) = {i \over /\! \!\! {p} - m + i\epsilon }, \quad S^{\mu \nu }(q) = -i \frac{g^{\mu \nu }}{q^2 - \mu ^2 + i\epsilon }, \nonumber \\{} & {} {\varGamma }^\mu = i g\gamma ^\mu ~ \frac{\mu ^2 - {\varLambda }^2}{q^2 - {\varLambda }^2 + i\epsilon }, \end{aligned}$$
(7)

where g is the coupling constant, \(\mu \) the mass of the exchanged vector-boson and \({\varLambda }\) is a scale parameter, featuring the extension of the color distribution in the interaction vertex of the dressed constituents. Moreover, in Eq. (6), one has \(\widehat{\varGamma }_{\nu }(q)=C~{\varGamma }^T_{\nu }(q) ~C^{-1}\), where \(C=i\gamma ^2\gamma ^0\) is the charge-conjugation operator.

The normalization of the BS-amplitude reads (cf. Refs. [63, 82] for details)

$$\begin{aligned}{} & {} N_c~\text {Tr} \Biggl [ \int {d^4k\over (2\pi )^4}~{\partial \over \partial P^{\prime \mu }}\Biggl \{ S^{-1}\Big (k-\tfrac{P'}{2}\Big )\,{\bar{{\varPhi }}}(k,P) \nonumber \\{} & {} \quad \times \,S^{-1}\Big (k+\tfrac{P'}{2}\Big ) ~{\varPhi }(k,P)\Biggr \}\Biggr ]_{P'=P}=-2iP_\mu . \end{aligned}$$
(8)

The antiquark uTMD is given by

$$\begin{aligned}{} & {} f^{\bar{q}}_1(\gamma , 1-\xi )\nonumber \\{} & {} \quad =-{N_c \over 4(2\pi )^3} \int _{-\infty }^\infty {dk^+\over 2 (2\pi )} \delta (k^+ + \tfrac{P^+}{2}- \xi P^+)\int _{-\infty }^\infty dk^- \nonumber \\{} & {} \qquad \times \int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \text {Tr}\left[ S^{-1}(p_q) {\varPhi }(k,P) \gamma ^+ {\bar{{\varPhi }}}(k,P) \right] , \end{aligned}$$
(9)

where the minus sign results from the property of the normal-ordered em current to be odd under the action of the charge conjugation operator. It is noteworthy that in subsection Appendix C.1, it is proven the identity of the normalization condition, Eq. (8), and the half sum of Eqs. (1) and (9).

Within a SU(3)-flavor symmetry framework, one describes a pion as a bound system of a massive \(q\bar{q}\) pair. This leads to introduce the so-called valence-quark PDF in the pion, that is charge symmetric (once the isospin breaking is disregarded [83]) as well as fulfills the charge conjugation. From those properties one deduces that the SU(3)-valence PDFs in the charged pions must verify: \(u^v_{\pi ^+}(\xi )=d^v_{\pi ^-}(\xi )=\bar{d}^v _{\pi ^+}(\xi )\). In our BS framework, in addition to the fermionic dof (still massive) one introduces also gluonic dof, by adding an explicit dynamical description of the binding. This amounts to the ladder exchange of infinite number of massive gluons. Therefore, at the initial scale, the quark and anti-quark longitudinal-momentum fraction distributions are not expected to be symmetric with respect to \(\xi =1/2\) (as it follows from the charge symmetry), given the gluon-momentum flow in the composite pion (see Sect. 4). The symmetric combination of quark and anti-quark contribution allows one to fulfill the charge symmetry, and hence it is relevant in the comparison with experimental data (see Ref. [78]). In what follows, in addition to the quark distributions, symmetric and anti-symmetric combinations are introduced for all the uTMDs we are going to analyze.

The half sum (difference) of the quark and anti-quark contributions, Eqs. (1) and (9), yields the following charge-symmetric (anti-symmetric) expression for the leading-twist uTMD inside a \(\pi ^+\) meson

$$\begin{aligned}{} & {} f^{S(AS)}_1(\gamma , \xi )\nonumber \\{} & {} \quad ={f^q_1(\gamma , \xi ) \pm f^{\bar{q}}_1(\gamma , 1-\xi ) \over 2} \nonumber \\{} & {} \quad = {N_c \over 8(2\pi )^3} \int _{-\infty }^\infty {dk^+\over 2 (2\pi )} \delta \left( p^+_q- \xi P^+\right) \int _{-\infty }^\infty dk^- \nonumber \\{} & {} \qquad \times \int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \text {Tr}\Big [ S^{-1}(-p_{\bar{q}}) {\bar{{\varPhi }}}(k,P)~ \gamma ^+ ~{\varPhi }(k,P) \nonumber \\{} & {} \qquad \mp \,S^{-1}(p_q) {\varPhi }(k,P)~ \gamma ^+ ~ {\bar{{\varPhi }}}(k,P)\Big ]. \end{aligned}$$
(10)

Analogously to Eq. (1), one can define the T-even subleading quark uTMDs, starting from the decomposition of the pion correlator [6, 84]. To be specific, one has two twist-3 uTMDs (see, e.g., Ref. [35] for the pion case)

$$\begin{aligned}&{M\over P^+ }~e^q(\gamma ,\xi )\nonumber \\&\quad ={N_c\over 4}\int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \int _{-\infty }^\infty {dy^- d\textbf{y}_\perp \over 2 (2\pi )^3}\nonumber \\&\qquad \times e^{i [\xi P^+\frac{y^-}{2} - \textbf{k}_\perp \cdot \textbf{y}_\perp ] } \langle P| \bar{\psi }_q (-\tfrac{y}{2})\,{\mathbbm {1}}\,\psi _q(\tfrac{y}{2}) |P \rangle \big |_{ y^+=0},\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned}&{M\over P^+ }~f^{\perp q}(\gamma ,\xi )\nonumber \\&\quad ={M\over \gamma }~{N_c \over 4}\int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \int _{-\infty }^\infty {dy^- d\textbf{y}_\perp \over 2 (2\pi )^3}\nonumber \\&\qquad \times e^{i [\xi P^+\frac{y^-}{2} - \textbf{k}_\perp \cdot \textbf{y}_\perp ] } \, \langle P| \bar{\psi }_q (-\tfrac{y}{2})\,\textbf{k}_ \perp \!\cdot \!{\varvec{\gamma }}_\perp \, \psi _q(\tfrac{y}{2}) |P \rangle \big |_{ y^+=0}.\nonumber \\ \end{aligned}$$
(12)

In analogy to Eq. (2), one gets for the twist-3 \(e^q(\xi )\) (see Refs. [35, 79, 84] for the pion in phenomenological models)

$$\begin{aligned}{} & {} \int _{-\infty }^\infty d\xi \int _0^\infty d\gamma ~e^q(\gamma , \xi )\nonumber \\{} & {} \quad = {N_c \over 2}\int d{\textbf {p}}_{q_\perp }\int _{-\infty }^\infty {dp^+_q\over P^+} \int _{-\infty }^\infty {dp^-_q\over 2} \nonumber \\{} & {} \qquad \times \int _{-\infty }^\infty {d^4y \over (2\pi )^4}e^{i \, p_q\cdot y } ~ \langle P| \bar{\psi }_q (- \tfrac{y}{2})\, {\mathbbm {1}}\, \psi _q(\tfrac{y}{2}) |P \rangle \nonumber \\{} & {} \quad =N_c~{\langle P| \bar{\psi }_q (0) ~{\mathbbm {1}}~ \psi _q(0) |P \rangle \over 2P^+}, \end{aligned}$$
(13)

where the matrix element \(\langle P| \bar{\psi }_q (0) ~{\mathbbm {1}}~ \psi _q(0) |P \rangle \) has to be proportional to the pion sigma term, once a QCD framework is adopted. As a matter of fact, one gets

$$\begin{aligned} \sum _q\int _0^1 d\xi \int _0^\infty d\gamma ~e^q(\gamma ,\xi )={\sigma _\pi \over m_{cur}} \end{aligned}$$
(14)

where \(m_{cur}\) is the quark current mass and \(\sigma _{\pi }\) is the pion sigma term, that becomes \(\sigma _{\pi }=M/2\), in the leading order of the chiral expansion, i.e. the Gell-Mann–Oakes–Renner relation [85]. It should be pointed that recent LQCD calculations [86] confirm, with high accuracy, the Gell-Mann–Oakes–Renner relation in the range of the explored pion masses. Indeed, the QCD equations of motion gives a decomposition of the subleading collinear PDF \(e(\xi )= \int d\gamma ~e(\gamma ,\xi )\) in three terms. Among them, there is a singular term proportional to the pion sigma term, that reads (see, e.g., Ref. [87])

$$\begin{aligned} e_{sing}(\xi )=\delta (\xi )~{\langle P| \bar{\psi }_q (0) ~{\mathbbm {1}}~ \psi _q(0) |P \rangle / 2P^+}, \end{aligned}$$
(15)

while the other two terms, one is due to \(q\bar{q}\)-gluon correlations and the other is proportional to the quark mass, do not contribute to Eq. (14) (see Ref. [87], where the issue is analyzed, taking the nucleon as actual case). In our phenomenological model the strength is distributed over the whole range of \(\xi \) (as in Ref. [35]), without the singularity at \(\xi =0\), as it will be shown in Sect. 5. Moreover, one has for the first moment [87]

$$\begin{aligned} \int _0^1 d\xi \int _0^\infty d\gamma ~\xi ~e^q(\gamma ,\xi )=N_q~{m_{cur}\over M}, \end{aligned}$$
(16)

where the singular term and the gluonic contribution vanish, and only the term proportional to the quark mass contributes.

As shown in Refs. [35, 88], one deduces the following relations between the above uTMDs

$$\begin{aligned}{} & {} \xi ~e^q_{EoM}(\gamma ,\xi )= \xi ~\tilde{e}^q(\gamma ,\xi )+{m\over M}~f^q_{1;EoM}(\gamma ,\xi ) \nonumber \\{} & {} \xi ~f^{\perp q}_{EoM}(\gamma ,\xi )= \xi ~\tilde{f}^{\perp q}(\gamma ,\xi )+f^q_{1;EoM}(\gamma ,\xi ), \end{aligned}$$
(17)

where the rightmost terms are obtained by applying the equations of motion of a free-quark model and the uTMDs with a tilde are the gluonic contributions. There, the relevant point is the dependence of all the subleading-twist uTMDs from only the leading one, modulo the gluonic terms. For a derivation of the first line of Eq. (17), consistent with QCD, one should apply the formalism presented in Ref. [87], as already pointed above Eq. (15). In our interacting framework, one can anticipate that we get large differences between lhs expressions and the rightmost ones (see Sect. 5), pointing to relevant gluonic effects.

Following Eq. (10), one readily writes down charge-symmetric and the anti-symmetric combinations for the subleading TMDs. One has to take care how the scalar and vector operators behave under the charge conjugation that impose a different combination of signs (cf. below Eq. (9)). Namely, one gets

$$\begin{aligned}{} & {} {M\over P^+ }~e^{S(AS)}(\gamma ,\xi )\nonumber \\{} & {} \quad = {N_c \over 8(2\pi )^3} \int _{-\infty }^\infty {dk^+\over 2 (2\pi )} \delta (p^+_q- \xi P^+)\int _{-\infty }^\infty dk^- \nonumber \\{} & {} \qquad \times \int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \text {Tr}\Big [ S^{-1}(-p_{\bar{q}}) {\bar{{\varPhi }}}(k,P)~ {\mathbbm {1}} ~{\varPhi }(k,P) \nonumber \\{} & {} \qquad \pm \, S^{-1}(p_q) {\varPhi }(k,P)~ {\mathbbm {1}} ~ {\bar{{\varPhi }}}(k,P) \Big ]. \end{aligned}$$
(18)
$$\begin{aligned}{} & {} {M\over P^+ }~f^{S(AS) \perp }(\gamma ,\xi )\nonumber \\{} & {} \quad ={N_c M\over 8(2\pi )^3\gamma } \int _{-\infty }^\infty {dk^+\over 2 (2\pi )} \delta (p^+_q- \xi P^+)\int _{-\infty }^\infty dk^- \nonumber \\{} & {} \qquad \times \int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \text {Tr}\Big [ S^{-1}(-p_{\bar{q}}) {\bar{{\varPhi }}}(k,P)\, {\varvec{\gamma }}_\perp \,{\varPhi }(k,P)\nonumber \\{} & {} \qquad \pm \, S^{-1}(p_q) {\varPhi }(k,P)\, {\varvec{\gamma }}_\perp \, {\bar{{\varPhi }}}(k,P) \Big ]\cdot \textbf{k}_\perp . \end{aligned}$$
(19)

2.1 The BS-amplitude and its Nakanishi integral representation

It is useful to briefly recall some features of our approach for obtaining the actual solution of the ladder BSE given in Eq. (6). The basic ingredient is the NIR of the BS-amplitude (see Ref. [65] for the general introduction, Refs. [63, 78, 89,90,91] for the application to a two-fermion), but let us first introduce the general decomposition of the BS-amplitude, \({\varPhi }(k; P)\), for a \(0^-\) bound state, viz. [89, 92]

$$\begin{aligned}{} & {} {\varPhi }(k;P)\nonumber \\{} & {} \quad = S_1(k;P) \phi _1(k;P)+S_2(k;P) \phi _2(k;P) \nonumber \\{} & {} \qquad +S_3(k;P) \phi _3(k;P)+S_4(k;P) \phi _4(k;P), \end{aligned}$$
(20)

where \(\phi _i\)’s are unknown scalar functions, that depend upon the kinematical scalars at disposal (\(k^2\), \(k\cdot P\) and \(P^2\)), and \(S_i\)’s are suitable Dirac structures, given by

$$\begin{aligned}{} & {} S_1(k;P) = \gamma _5, \,\, S_2(k;P) = \frac{/\! \! \!\! {P}}{M}{\gamma _5},\nonumber \\{} & {} S_3(k;P) = \frac{k\cdot P}{M^3}/\! \! \!\! {P}\gamma _5 -\frac{1}{M}/\! \!\! {k}\gamma _5, \nonumber \\{} & {} S_4(k;P) =\frac{i}{M^2}\sigma ^{\mu \nu }P_\mu k_\nu \gamma _5. \end{aligned}$$
(21)

The functions \(\phi _i\) must be even for \(i=1,2,4\) and odd for \(i=3\), under the change \(k \rightarrow - k\), as dictated by the anti-commutation rules of the fermionic fields and the considered SU(2)-flavor symmetry. They can be written in terms of the NIR as follows

$$\begin{aligned} \phi _i(k; P)= & {} \int _{-1}^1 dz'\int _0^\infty d\gamma ' \nonumber \\{} & {} \times \frac{g_i(\gamma ',z';\kappa ^2)}{[k^2 + z'(P\cdot k) - \gamma ' - \kappa ^2 + i \epsilon ]^3}, \end{aligned}$$
(22)

where \(\kappa ^2 = m^2 -{M^2/4}\). The real functions \(g_i(\gamma ',z';\kappa ^2)\), the unknowns of the problem under scrutiny, are the Nakanishi weight functions (NWFs), and assumed to be unique, following the uniqueness theorem from Ref. [65]. The properties of the scalar functions \(\phi _i\) under the exchange \(k\rightarrow -k\) translate to properties of the NWFs, but under the exchange \(z'\rightarrow -z'\).

Finally, it should be mentioned that NWFs are determined by solving a system of integral equation, so that one is able to non-perturbatively embed dynamical information that characterize the BS interaction kernel. The system of integral equations is formally deduced from the initial BSE, by exploiting the analytic structure of the scalar functions \(\phi _i\), made explicit by means of the NIR. In fact, after inserting Eqs. (20) and (22) in the BSE, Eq. (6), and performing both the Dirac traces and a LF projection, i.e. the integration over the \(k^-=k^0-k^3\) component of the relative momentum, one gets a coupled system of integral equations for the NWFs (see details in Ref. [91]). Once the NWFs are known, the BS-amplitude can be fully reconstructed through an inverse path, i.e. Eqs. (22) and (20) (see, e.g. Ref. [93] for the application of the NIR framework by means of the pion self-energy).

3 The unpolarized TMDs and the pion BS-amplitude

The evaluation of the leading- and subleading-twist uTMDs, given in Eqs. (10), (18) and (19), can be performed by inserting the decomposition of the BS-amplitude in Eq. (20), obtaining

$$\begin{aligned}{} & {} {\mathcal {T}}^{S(AS)}_i(\gamma ,\xi )\nonumber \\{} & {} \quad ={N_c \over 8 (2\pi )^3} \int _{-\infty }^\infty {dk^+\over 2 } \delta (p^+_q- \xi P^+) \int _{-\infty }^\infty {d k^{-}\over 2 \pi }\nonumber \\{} & {} \qquad \times \int _0^{2\pi } d\phi _{\hat{\textbf{k}}_\perp } \Biggl \{\text {Tr} \Big [ S^{-1}(-p_{\bar{q}}) \, {\bar{{\varPhi }}}(k,P)\, {\mathcal {O}}_i \,{\varPhi }(k,P) \Big ] \nonumber \\{} & {} \qquad +\eta ^{S(AS)}_i \, \text {Tr} \Big [S^{-1}(p_q) \,{\varPhi }(k,P)\, {\mathcal {O}}_i \,\bar{\varPhi }(k,P) \Big ]\Biggr \} \nonumber \\{} & {} \quad ={i\,N_c \over 8 (2\pi )^2} \sum _{\ell j} \int _{-1}^1 dz \, \delta ( z - \left( 1- 2\xi \right) ) \, F^i_{\ell j}(\gamma , z;{S(AS)}),\nonumber \\ \end{aligned}$$
(23)

where the new variable z is defined as \(z=-2k^+/P^+\) and the three quantities: (i) the functions \({\mathcal {T}}_i(\gamma ,\xi )\), (ii) the operators \({\mathcal {O}}_i\) and (iii) the phase \(\eta ^{S(AS)}_i\) are given by

$$\begin{aligned}{} & {} {\mathcal {T}}^{S(AS)}_0(\gamma ,\xi )\equiv ~f^{S(AS)}_1(\gamma ,\xi ), {\mathcal {O}}_0=\gamma ^+,\eta ^{S(AS)}_0=\mp 1,\nonumber \\{} & {} {\mathcal {T}}^{S(AS)}_1(\gamma ,\xi )\equiv {M\over P^+}~e^{S(AS)}(\gamma ,\xi ), {\mathcal {O}}_1={\mathbbm {1}} , \eta ^{S(AS)}_1=\pm 1, \nonumber \\{} & {} {\mathcal {T}}^{S(AS)}_2(\gamma ,\xi )\equiv {M\over P^+}~f^{S(AS) \perp }(\gamma ,\xi ), {\mathcal {O}}_2={M\over |\textbf{k}_\perp |^2}~\textbf{k}_\perp \cdot {\varvec{\gamma }}_\perp ,\nonumber \\{} & {} \eta ^{S(AS)}_2=\pm 1. \end{aligned}$$
(24)

Finally, the integrand \(F^i_{\ell j}\) in Eq. (23) reads

$$\begin{aligned}{} & {} F^i_{\ell j}(\gamma , z;{S(AS)})\nonumber \\{} & {} \quad = \int _{-\infty }^\infty {d k^{-}\over 2 \pi } ~a^i_{\ell j}(k^{-},\gamma ,z;{S(AS)}) ~\phi _{\ell }(k,P) \, \phi _j(k,P) \nonumber \\{} & {} \quad =2M\int _{-\infty }^\infty {d k^{-}\over 2 \pi } ~\phi _\ell (k,P) \, \phi _j(k,P) \nonumber \\{} & {} \qquad \times \Biggl [b^i_{0; \ell j}(\gamma ,z;S(AS)) + b^i_{1; \ell j} (\gamma ,z;S(AS)) {k^{-}\over 2M} \nonumber \\{} & {} \qquad + b^i_{2; \ell j}(\gamma ,z;S(AS)) \Biggl ({k^{-}\over 2M}\Biggr )^2\nonumber \\{} & {} \qquad +b^i_{3; \ell j}(\gamma ,z;S(AS)) \Biggl ({k^{-}\over 2M}\Biggr )^3\Biggr ], \end{aligned}$$
(25)

where the expressions of both \(a^i_{\ell j}(k^{-}, \gamma ,;S(AS))\), that are polynomial in \(k^-\) up to the cubic power, and \(b^i_{n; \ell j}(\gamma ,z;S(AS))\) can be found in Appendix A, for each uTMDs we are considering. By exploiting the NIR, Eq. (22), one can perform the integration on \(k^-\). This integration amounts to restrict the LF-time to \(x^+=0\), and it is also known as LF-projection (see, e.g., Refs. [71, 72, 94]). After carrying out the \(k^-\)-integration, the expression of each \({\mathcal {T}}^{S(AS)}_i(\gamma ,\xi )\) can be decomposed as follows (the details of this formal step can be found in Appendix B)

$$\begin{aligned} {\mathcal {T}}^{S(AS)}_i(\gamma ,\xi )= & {} {3N_c \over (2\pi )^2}~\sum _{\ell j}~\Bigl [{\mathcal {F}}^{i}_{0;\ell j}(\gamma ,z;S(AS)) \nonumber \\{} & {} +\,{\mathcal {F}}^{i}_{1;\ell j}(\gamma ,z;S(AS))+{\mathcal {F}}^{i}_{2;\ell j} (\gamma ,z;S(AS))\nonumber \\{} & {} +\,{\mathcal {F}}^{i}_{3;\ell j}(\gamma ,z;S(AS))\Bigr ], \end{aligned}$$
(26)

where \(\xi =(1-z)/2\) and the functions \({\mathcal {F}}^{i}_{n;\ell j} (\gamma , z;S(AS))\) \((n=1,2,3,4)\) are given in Eqs. (B.19), (B.20), (B.21) and (B.22), respectively.

4 The leading-twist \(f_1^{S(AS)}(\gamma ,\xi )\)

The symmetric and anti-symmetric combinations of the T-even leading-twist uTMD, \(f_1^{S(AS)}(\gamma ,\xi )\), allow us to address the evaluation of both quark and anti-quark contributions, \(f_1^{q(\bar{q})}(\gamma ,\xi )\), that in the BS framework plus the Fock expansion of the pion state have interesting features, distinct from the ones of \(f_1^{S(AS)}(\gamma ,\xi )\).

After integrating the leading-twist \(f_1^{q(\bar{q})}(\gamma ,\xi )\) on \(\gamma \), one gets the quark PDF \(u^q(\xi )\), while the symmetric combination provides the charge-symmetric PDF \(u^S(\xi )\), i.e. the one is expected to have relevance at the valence scale (see, e.g., Ref. [83]). Indeed, in the Mandelstam approach the quark and antiquark PDFs do not have in general a symmetry with respect to \(\xi =1/2\), since each receives contributions from states containing an infinite number of gluons, as a consequence of the ladder-interaction kernel. If we restrict to the contribution from the first Fock component in the expansion of the pion state, one gets the LF-valence \(u^{LF}_{val}(\xi )\), that is given by the BS-amplitude projected onto the null plane [81] and is fully compliant with the charge symmetry (see below the discussion on the differences among \(u^q(\xi )\), \(u^S(\xi )\) and \(u^{LF}_{val}(\xi )\)).

To illustrate general features and relations, in this section we give some details, referring to Appendix C for a more complete discussion.

The symmetric and anti-symmetric leading-twist uTMDs, can be decomposed as follow

$$\begin{aligned}{} & {} f^{S(AS)}_1(\gamma ,\xi )\nonumber \\{} & {} \quad ={\mathcal {I}}_N(\gamma ,\xi ;S(AS))+{\mathcal {I}}_d(\gamma ,\xi ;S(AS))\nonumber \\{} & {} \qquad +\,{\mathcal {I}}_{2d}(\gamma ,\xi ;S(AS))+{\mathcal {I}}_{3d}(\gamma ,\xi ;S(AS)), \end{aligned}$$
(27)

where the non-vanishing symmetric contributions are given by Eqs. (C.2), (C.3), (C.4) and \({\mathcal {I}}_{3d}(\gamma ,\xi ;S)=0\), respectively. The anti-symmetric terms are shown in Eqs. (C.5), (C.6), (C.7) and (C.8), respectively.

Two comments are in order. The symmetry properties of the above quantities with respect to the transformation \(z\rightarrow -z\) are demonstrated in Appendix C, and can be translated into the symmetry with respect to \(\xi \rightarrow 1-\xi \) (that implements the charge-symmetry). A relevant feature is given by the presence in the expressions of \({\mathcal {I}}_{d,2d,3d}\) of the partial derivatives \(\partial ^n/\partial z^n\), that should be considered dual of the n-th moment in \(k^-\) of the relevant functions, generated by the formal step of the LF-projection (cf Eq. (25)). This is not a surprise since the variable z is proportional to \(k^+\).

Fig. 1
figure 1

Left panel: The symmetric pion PDF, \(u^S(\xi )\), with its contributions \(u^S_N(\xi )\), \(u^S_d(\xi )\) and \(u^S_{2d}(\xi )\) (cf Eq. (29)). Dash-dotted line: \(u^S(\xi )\). Dashed line: \(u^S_N(\xi )\). Dotted line: \(u^S_d(\xi )\). Dash-double-dotted line: \(u^S_{2d}(\xi )\). Right panel: \(u^q(\xi )\), \(u^S(\xi )\), \(u^{AS}(\xi )\) and the LF-valence PDF of the pion, \(u^{LF}_{val}(\xi )\). Solid line: Quark PDF, Eq. (30). Dashed line: \(u^S(\xi )\). Dotted line: \(u^{AS}(\xi )\). Dash-dotted line: \(u^{LF}_{val}(\xi )\) (see Ref. [78]), with normalization equal to \(P_{val}=0.7\) (see text)

Full size image

A first consistency check of our formalism has been carried out in Appendix C.1, where it is shown that, within the Mandelstam approach, \(f^{S}_1(\gamma ,\xi )\) and in turn \(f^q_1(\gamma ,\xi )\) are normalized to 1, as naturally follows from the canonical BS-amplitude normalization [82, 95], performed according to Eq. (8) (see also Ref. [63]). In particular, the integral on \(\gamma \) and \(\xi \) of \({\mathcal {I}}_N(\gamma ,\xi ;S)\) saturates the normalization, while the other two terms provide vanishing contributions. Hence, one gets

$$\begin{aligned}{} & {} \int _{0}^1 d\xi \int _0^\infty d\gamma ~f^S_1(\gamma ,\xi ) \nonumber \\{} & {} \quad =\int _{0}^1 d\xi \int _0^\infty d\gamma ~{\mathcal {I}}_N(\gamma ,\xi ;S)\nonumber \\{} & {} \quad =\int _{0}^1 d\xi \int _0^\infty d\gamma ~f^q_1(\gamma ,\xi )=1 . \end{aligned}$$
(28)

It should be recalled that all the calculated uTMDs vanish outside the interval \(0\le \xi \le 1\), as dictated by the conservation of the plus components of the four-momenta of both pion and constituents (cf. Eq. (10)). It is understood that the integral of \(f^{AS}_1(\gamma ,\xi )\) is vanishing, given the antisymmetry with respect to \(\xi \rightarrow 1-\xi \).

4.1 Longitudinal degree of freedom

The symmetric and the anti-symmetric PDFs, \( u^{S(AS)}(\xi )\) (for the explicit expressions see Appendix D) are defined by

$$\begin{aligned}{} & {} u^{S(AS)}(\xi )\nonumber \\{} & {} \quad = \int _0^\infty d\gamma ~f^{S(AS)}_1(\gamma ,\xi )\nonumber \\{} & {} \quad =u^{S(AS)}_N(\xi )+u^{S(AS)}_d(\xi )+u^{S(AS)}_{2d}(\xi )+u^{S(AS)}_{3d}(\xi ),\nonumber \\ \end{aligned}$$
(29)

with the normalization that follows from Eq. (28) and the vanishing result of the double integration of \(f^{AS}_1(\gamma ,\xi )\). Finally, the quark and anti-quark PDFs are evaluated through

$$\begin{aligned} u^{q(\bar{q})}(\xi )=u^{S}(\xi )\pm u^{AS}(\xi ), \end{aligned}$$
(30)

with the normalization still given by Eq. (28). Within the SU(3)-flavor symmetry, one has to implement the charge symmetry (see, e.g. Ref. [83]) at the initial scale, and therefore \(u^S(\xi )\) is the PDF to be compared, after the proper evolution, with the experimental data, as it has been shown in Ref. [78].

In the left panel of Fig. 1, \(u^S(\xi )\) and its three contributions (see Eqs. (D.4), (D.5) and (D.6)) are shown. The calculation has been carried out by adopting the BS-amplitude obtained by using the solution of the BSE as described in Ref. [63], using the following values of the three input parameters: \(m= 255\) MeV, \(\mu =637.5\) MeV and \({\varLambda }=306\) MeV, able to reproduce the pion decay constant \(f^{PDG}_\pi = 130.50(1)(3)(13)\) MeV [96] (recall that the pion charge radius results to be \(r_{ch}=0.663\) fm [77], in excellent agreement with \(r^{PDG}_{ch}= 0.659\pm 0.004\) fm [97]). A remarkable cancellation among the contributions takes place, and this represents a common feature for all the integrated quantities generated by the uTMDs we are considering. In the right panel, one can see the comparison between the quark PDF, \(u^{S(AS)}(\xi )\) and the LF-valence PDF, resulting from the one-to-one relation between the LF-projected BS amplitude and the valence amplitude of the Fock expansion of the pion state. In particular, the LF-valence PDF (see Refs. [63, 78]), is given by

$$\begin{aligned} u^{LF}_{val}(\xi )= \int _0^\infty {d\gamma \over (4\pi )^2}~\Bigl [|\psi _{\uparrow \downarrow }(\gamma ,z)|^2+|\psi _{\uparrow \uparrow }(\gamma ,z)|^2\Bigr ], \end{aligned}$$
(31)

where \(\xi =(1-z)/2\), \( \psi _{\uparrow \downarrow }(\gamma ,z)\) is the anti-aligned component of the LF-valence amplitude and \( \psi _{\uparrow \uparrow }(\gamma ,z)\) the aligned one (of purely relativistic nature having an orbital angular momentum equal to 1). These amplitudes are suitable combinations of the LF-projected scalar functions \(\phi _i(k;P)\), Eq. (22). The integral on \(\xi \) of LF-valence PDF gives the probability of the valence state in the Fock expansion and amounts to

$$\begin{aligned} P_{val}=\int _0^1 d\xi ~u^{LF}_{val}(\xi )=0.7 . \end{aligned}$$
(32)

The striking feature shown in the left panel is the shift toward low \(\xi \) of the quark PDF, so that for this quantity the symmetry \(\xi \rightarrow 1-\xi \) is slightly violated.

4.2 Analysing the shift and the gluon content

The PDF calculations based on the BS-amplitude are able to capture an explicit gluonic effect, to be taken distinct from the one responsible for the effective mass of the constituents. In particular, the difference between the two symmetric PDFs, i.e. \(u^S(\xi )\) and \(u^{LF}_{val}(\xi )\) (recall that has \(P_{val}=0.7\)), can be traced back to the non negligible probability of the higher Fock states (HFS), where a \(q\bar{q}\) pair interacts by exchanging any number of gluons. Interestingly, the difference can be effectively described only by a factor, since it turns out that \(u^{LF}_{val}(\xi )/P_{val}\) largely overlaps \(u^S(\xi )\). Finally, also the small, but relevant, shift of the quark PDF with respect to \(u^S(\xi )\) has to be ascribed to the presence of HFS, as discussed in what follows.

To get a qualitative view, we remind that the pion state can be, in principle, decomposed in Fock-components, which are schematically written in ladder approximation as

$$\begin{aligned} |\pi \rangle =|q\bar{q}\rangle + |q\bar{q} g\rangle + |q\bar{q} \, 2g\rangle + \cdots \end{aligned}$$
(33)

Due to the charge symmetry, each Fock-component is invariant by \(q\leftrightarrow \bar{q}\), and hence the valence state \(|q\bar{q}\rangle \) provides a symmetric contribution to \(u^q(\xi )\), identified with \(u_{val}^{LF}(\xi )\). The following terms contain gluons up to infinity. In our model, the gluon has an effective mass about twice the quark mass, so that the HFS cumulative effect results in a small shift of the \(u^q(\xi )\) peak at \(\xi <1/2\), as shown in the right panel of Fig. 1. Actually, a similar effect, related to the increasing mass of the remnant, can be also recognized in the nucleon, where one has a valence parton distribution with a peak around 1/3 due to the presence of the other two constituent quarks. In the case of the pion, the effect is small since the valence component \(|q\bar{q}\rangle \) has 70% of probability (as generated by our dynamical calculation), and hence is largely dominant.

To become more quantitative and illustrate this effect, we schematically write the quark PDF by using the Fock expansion of the pion state, Eq. (33), and inserting LF variables [81], one has

$$\begin{aligned} u^q(\xi )= & {} \sum _{n=2}^\infty \, \Bigg \{ \prod _{i}^n \int \frac{d^2k_{i\perp }}{(2\pi )^2} \int ^1_0 d\xi _i\Bigg \}\, \nonumber \\{} & {} \times \delta \left( \xi -\xi _1\right) \delta \left( 1-\sum _{i=1}^n \xi _i\right) \, \delta \left( \sum _{i=1}^n \textbf{k}_{i\perp }\right) \nonumber \\{} & {} \times \big |{\varPsi }_n(\xi _1, \textbf{k}_{1\perp },\xi _2, \textbf{k}_{2\perp },\ldots )\big |^2, \end{aligned}$$
(34)

where \(\xi _{1(2)}\) is the longitudinal-momentum fraction of the quark (antiquark) in each Fock state, composed by a \(q\bar{q}\) pair and \(n-2\) gluons, generated by the iteration of the one-gluon exchange. Moreover, \({\varPsi }_n(\xi _1,\textbf{k}_{1\perp },\xi _2, \textbf{k}_{2\perp },\ldots )\) is the probability amplitude of the corresponding Fock component and fulfills a normalization condition that follows from the one of the pion state. In the n-th state one has

$$\begin{aligned} \xi _1=1 -\xi _2 -\sum _{g=3}^{n} \xi _{g}. \end{aligned}$$
(35)

Since \(\xi _i > 0\) for massive particles, the average value of \(\xi _1\) starts to decreases while the number of gluons increases, as quantitatively shown in what follows.

Looking at the right panel of Fig. 1, one can realize that while the valence term, with probability \(P_{val}=0.7\), has a peak at \(\xi _1=\xi _2=1/2\), given the symmetry of \(|{\varPsi }_2(\xi _1,\textbf{k}_{1\perp },\xi _2,\textbf{k}_{2\perp })|^2\) all the HFS shift the peak to \(\xi _1<1/2\), and decrease the tail, due to the constraint of the overall normalization. This is reflected in the evaluation of the first moment (recall \(\xi _q\equiv \xi _1\))

$$\begin{aligned} \langle \xi _q\rangle= & {} P_{val}~\langle \xi _q\rangle _{val} + \sum _{n>2} P_n~\langle \xi _q\rangle _n \nonumber \\= & {} P_{val}~\langle \xi _q\rangle _{val} +(1-P_{val})~\langle \xi _q\rangle _{HFS}, \end{aligned}$$
(36)

where \(P_n\) is the probability of the n-th Fock state beyond the valence one. The first term in Eq. (36) is equal to 0.35, since 1/2 is weighted by \(P_{val}\), and the rest is weighted by 0.3. Notice that for each HFS, normalized to 1, one has

$$\begin{aligned} \langle \xi _q\rangle _n= & {} 1- \langle \xi _{\bar{q}}\rangle _n- \sum _{i=3}^{n}\langle \xi _{g_i}\rangle _n \nonumber \\= & {} 1-\langle \xi _{\bar{q}}\rangle _n- (n-2) \langle \xi _g\rangle _n , \end{aligned}$$
(37)

where the gluon bosonic nature leads to the factor \(n-2\).

The actual value of the first moment of \(u^q(\xi )\) is

$$\begin{aligned} \langle \xi _q\rangle =\int _0^1d\xi \int _0^\infty d\gamma ~\xi ~f^q_1(\gamma ,\xi ) =0.471 , \end{aligned}$$
(38)

that amounts to an average of \(\langle \xi _q\rangle _{HFS}\) equal to 0.40.

Fig. 2
figure 2

Left panel: Pion longitudinal distributions, with different scales (see text for details). Dashed line: \(\xi \,u^S(\xi )\), with an assigned initial scale equal to 360 MeV, and first moment equal to 0.5. Solid line: \(\xi \,u^q(\xi )\), with a deduced scale equal to 389 MeV obtained by using a backward evolution of the first moment from \(\langle \xi _q \rangle =0.471\) to \(\langle \xi _q \rangle =0.5\). Dot-dashed line \(\xi ~u^q(\xi )\) backward-evolved from 389 MeV to 360 MeV. Right panel: Comparison with the experimental data at the scale 5.2 GeV. Solid line: Evolved \(u^S(\xi )\) starting from 360 MeV. Dot-dashed line: Evolved \(u^q(\xi )\), starting from 389 MeV. Dashed line: DSE calculation from Fig. 5 of Ref. [98]. Dotted line: basis light-front quantization result at 4.0 GeV [99]. Shaded area: LQCD calculation extracted via Mellin moments from Ref. [100]. Full squares: reanalyzed data by using the ratio between the fit 3 of Ref. [101], evolved to 5.2 GeV, and the experimental data [52], at each data point (see Ref. [78] for details)

Full size image

We can further analyse \(\langle \xi _q\rangle _{HFS}\), aiming at extracting a quantitative estimate of the exchanged-gluon contribution, \(\langle \xi _g\rangle \). From the momentum sum rule Eq. (36), and recalling Eq. (35), we get

$$\begin{aligned} \langle \xi _q\rangle _{HFS}= & {} {1 \over 1-P_{val}}\sum _{n>2} P_n~\langle \xi _q\rangle _n \nonumber \\= & {} 1 -\langle \xi _{\bar{q}}\rangle _{HFS}-\langle \xi _g\rangle , \end{aligned}$$
(39)

where

$$\begin{aligned} \langle \xi _g\rangle ={1 \over 1-P_{val}} \sum _{n\ge 3} P_n (n-2)~\langle \xi _g\rangle _n. \end{aligned}$$
(40)

Moreover, since each Fock component fulfills the charge symmetry, i.e. \(q\leftrightarrow \bar{q}\), the corresponding quark and antiquark momentum densities are equal and hence for the Mellin moments one has \(\langle \xi _q^{k}\rangle _{HFS}=\langle \xi _{\bar{q}}^{k}\rangle _{HFS}\) (this property does not imply the charge symmetry of the total density, given the presence of the gluon contribution, cf. Eq. (36)). From Eq. (39), it follows that the gluon contribution reads

$$\begin{aligned} \langle \xi _g\rangle =1 -2~ \langle \xi _q\rangle _{HFS}. \end{aligned}$$
(41)

Then, in our model one has \(\langle \xi _{g} \rangle =0.2\). We should note that (i) \(\langle \xi _q\rangle >\langle \xi _q\rangle _{HFS}\), as it should be, and (ii) the massive gluons carry 20% of the HFS momentum fraction and contribute to the total longitudinal fraction by 6% (recalling that \(P_{HFS}=0.3\)). This result indicates that the exchanged gluons in the pion are not soft (differently from the ones considered in Ref. [102] where the subtraction of the effect due to soft gluons is advocated for getting a symmetric PDF from the LF projected BS amplitude).

It has to be emphasized that the above analysis, made transparent by the adopted LF variables, is valid in any gauge (both covariant gauges or the light-cone one), and the only difference is the amount of the shift one gets. The possibility to regain the full gauge-invariance by taking into account the additional gluon exchanges that could affect the interaction between the knocked-out quark and the spectator one (see, e.g., the analysis of the gauge-invariance and the hand-bag contribution in Refs. [14, 103]) will be explored elsewhere.

The real test of the longitudinal dof is obviously given by the comparison between the PDF and the experimental E615 data [52]. In particular, we have considered the original data reanalyzed by taking into account logarithmic resummation effects in the hard part of the Drell–Yan cross-section, as performed in Ref. [101], at a new scale of 5.2 GeV as suggested by the studies in Ref. [104]. As it is shown in Ref. [78], our result compares very satisfactorily with the experimental data, after evolving \(u^S(\xi )\) from an assigned initial scale of 360 MeV. This is further illustrated in the right panel of Fig. 2, where the data (squares) has been obtained by rescaling the experimental E615 data [52], at each \(\xi \), by the ratio between (i) the fit 3 in Ref. [101] with resummation effects, evolved to the scale of 5.2 GeV [104] through a leading-order DGLAP plus an effective running charge, as given in Ref. [105],Footnote 2 and (ii) the fit of E615 experimental data, which were assigned a scale of 4.0 GeV [52] (the parameters of the fit correspond to the ones in the first column of Table I of Ref. [104]). Moreover, we have achieved a nice agreement with other dynamical calculations, such as the Dyson–Schwinger result of Ref. [98], the basis light-front quantization calculation of Refs. [109, 110], and also the recent LQCD outcomes of Ref. [100]. In particular, both the overall shape and, importantly, the tail for \(\xi \rightarrow 1\), gives great confidence in our formalism, and encourages the further steps we have undertaken in this work.

Fig. 3
figure 3

Left panel: Normalized pion transverse distribution function, Eq. (42), vs \(\gamma /m^2\). The normalization is given by \(D_\perp (0)=22.945\,{\text {GeV}^{-2}}\). Thick solid line: Full calculation. Dashed line: The same as the full line, but times \((\gamma /m^2)^4\). Dash-dotted line: The same as the full line, but times \((\gamma /m^2)^2\). Dash-double-dotted line: Exponential form \(e^{-\gamma /(m~0.42)^2}\), with the parameter from Table 1 of Ref. [35], corresponding to a Gaussian Ansatz for \(f_1(\gamma ,\xi )\) (see text). Right panel: Pion unpolarized transverse-momentum distribution \(f^S_1(\gamma ,\xi )\), Eq. (10), for \(\xi =0.5\). Solid line: Full calculation as in Fig. 4. Dashed line: LF constituent quark model [35, 56]. Dash-dotted line: LF wave function from DSE calculations [45]. Dash-Double-dotted line: NJL model [38]. The adopted quark mass \(m=255\) MeV

Full size image

In Fig. 2, one can observe a further comparison, involving the product \(\xi \,u(\xi )\), that sheds more light on the link between the shift of the peak and the gluon dynamics taken explicitly into account in the ladder kernel of the BSE. In particular, we get a scale of 389 MeV for \(u^q(\xi )\), the solid line in the left panel of Fig. 1, by backward-evolving its first moment, \(\langle \xi _q\rangle =0.471\) (cf. Eq. (38)), to 0.5, i.e. the first moment of \(u^S(\xi )\), that has an assigned hadronic scale of 360 MeV, as above mentioned and thoroughly discussed in Ref. [78]. In the left panel, the comparison at 360 MeV between \(\xi \,u^S(\xi )\) and the backward-evolved \(\xi \,u^q(\xi )\) shows that the effect of the interaction taken into account in the ladder BSE is reproduced at large extent by applying a leading-order DGLAP evolution with an effective running charge as suggested in Ref. [105] and already applied to our PDF in Ref. [78]. This is not surprising once we remind that the dressing of the quark-gluon vertex, as expressed by the effective charge, is governed by the same interaction kernel present in the BSE (i.e. the \(q\bar{q}\) amputated T-matrix). Notice that the right panel also shows the comparison at 5.2 GeV between the evolved \(u^S(\xi )\), starting from the scale of 360 MeV, and the evolved \(u^q(\xi )\), starting from the scale of 389 MeV. Nicely, the difference is even smaller.

4.3 Transverse degree of freedom

In the left panel of Fig. 3, it is shown the transverse distribution defined by

$$\begin{aligned} {\mathcal {D}}_\perp (\gamma )=\int _0^1 d\xi ~f^{S}_1(\gamma ,\xi )=\int _0^1 d\xi ~f^{q}_1(\gamma ,\xi ). \end{aligned}$$
(42)

It has to be pointed out that the integration on \(\xi \) eliminates the anti-symmetric term \(f^{AS}_1(\gamma ,\xi )\), and therefore one gets the same transverse distribution also by using \(f^{q}_1(\gamma ,\xi )\). In order to emphasize the analysis of the general pattern, we have presented \({\mathcal {D}}_\perp (\gamma )/{\mathcal {D}}_\perp (0)\), so that the widely adopted exponential or power-like fall-off can be readily compared to our result.

In addition, in the left panel of Fig. 3 one can find: (i) an exponential form \({\mathcal {D}}_{\perp }(\gamma )/{\mathcal {D}}_{\perp }(0)= e^{-\gamma /(m\,0.42)^2}\), with the parameter given in Table 1 of Ref. [35], corresponding to the so-called Gaussian Ansatz (recall \(\gamma =|\textbf{k}_\perp |^2\)), amounting to a factorized form for \(f^{S}_1(\gamma ,\xi )\sim u^S(\xi ) e^{-\gamma /(m~0.42)^2}\) very often adopted in phenomenological studies; (ii) our full results multiplied by \((\gamma /m^2)^2\) and (iii) our full results multiplied by \((\gamma /m^2)^4\). This panel contains two relevant comparisons. The first one is between the output of our dynamical calculation (solid line) and the Gaussian Ansatz (dash-double-dotted line). One observes that the behaviour are sharply different even at small and intermediate values of \(\gamma /m^2\). A second comparison, somewhat implicit, is the one between the asymptotic behavior of our dynamical result and a power-like tail, which is accomplished by multiplying our calculation by a suitable power of \(\gamma /m^2\). If the product becomes constant for large values of \(\gamma /m^2\), then one can validate a power-like fall-off of our dynamical calculation. As the dashed line shows, this is exactly what happens. Indeed, the proper power is different from the one expected by the action of only a one-gluon exchange, that should govern the ultraviolet behavior and lead to a \((\gamma /m^2)^2\) (as suggested by a generalized counting rule in Ref. [111]). Indeed, the adopted form-factor featuring the extension of the quark-gluon interaction vertex (cf. Eq. (7)) generates a different power-like fall-off, namely \((\gamma /m^2)^4\), as already pointed out in Refs. [90, 91]. Finally, it is worth noticing that, unlike the PDF, the two terms in \(f^S_1(\gamma ,\xi )\) containing derivatives of the delta-function do not contribute, as it is discussed at the end of Appendix C.1.

Table 1 The average value \(\langle \gamma /m^2\rangle \) (with \(m=0.255\) GeV), \(u^S(\xi =0.5)\) and the pion charge radius are presented for: (i) \(f^S_1(\gamma ,\xi =0.5)\) from the present approach (NIR+BSE); (ii) the outcome from the LF wave function obtained by using DSE calculation [45] (LFDSE); (iii) the LF constituent quark-model of Refs. [35, 56] (LFCQM) and (iv) the NJL with Pauli–Villars regulator [38]. (Recall that the most recent PDG value of the charge radius is \(r^{PDG}_{ch}=0.659\pm 0.004\) fm [97])
Full size table

In the right panel of Fig. 3, it is presented the quantitative comparison between \(f^S_1(\gamma ,\xi )\) at \(\xi =0.5\) and some phenomenological outcomes from (i) the approach based on the LF wave function obtained by using the DSE calculation in Ref. [45]; (ii) the LF constituent quark-model of Refs. [35, 56]; (iii) the NJL model with Pauli–Villars regulator as given in Ref. [38]. For \(\gamma /m^2\rightarrow 0\), there are remarkable differences that, indeed, are present also on the tails. This last feature impacts the value of \(\langle \gamma /m^2\rangle ^\frac{1}{2}\), as shown in Table 1, where, for the sake of completeness, the value of \(u^S(\xi =0.5)\) and the pion charge radius are also presented. As can be expected, the larger the average transverse moment, the smaller the radius of charge. The current model has the smaller \(\langle \gamma /m^2\rangle ^\frac{1}{2}\) (of the order of the infrared scale \({\varLambda }_{QCD}\), effectively incorporated in the QCD-inspired choice of our parameters) which in turn leads to a larger charge radius, in agreement with the experimental value.

Fig. 4
figure 4

Pion unpolarized transverse-momentum distribution \(f^S_1(\gamma ,\xi )\), Eq. (10), at the initial scale. The normalization is \(\int _0^1d\xi \int _0^\infty d\gamma ~f^S_1(\gamma ,\xi )=1\)

Full size image

In Fig. 4, the uTMD \(f^S_1(\gamma ,\xi )\) is shown in full, in order to appreciate the main features, i.e. (i) the peak at \(\xi =0.5\) for running \(\gamma /m^2\), (ii) the vanishing values at the end-points and (iii) the order of magnitude fall-off already for \(\gamma /m^2> 2 \). Comparing to other approaches, one can notice the sharp difference with the results from the LF constituent model in Ref. [56] and the LF holographic framework, like in Refs. [40, 57] where a double-humped structure is found due to the \(\xi \)-dependence in the holographic wave functions. Also the value at \(\xi =0.5\) and small \(\gamma /m^2\) is substantially lower than ours (almost an order of magnitude less). Differently, the shape of our \(f^S_1(\gamma ,\xi )\) is more similar, i.e. without any double-humped structure, to the one obtained in Ref. [45], where the pion LF-wave function is determined from a beyond rainbow-ladder Dyson–Schwinger equations (DSE) in Euclidean space, by exploiting the \(\gamma \)-dependent moments in \(\xi \) and a suitable parametrization of the BS-amplitude.

5 The subleading-twist uTMDs

Fig. 5
figure 5

Left panel: Pion unpolarized collinear PDFs: (i) \(e^q(\xi )\) (solid line), Eq. (45), (ii) \(e^S(\xi )\) (dashed line) and \(e^{AS}(\xi )\) (dotted line), Eqs. (44). It is also shown \(e^q_{EoM}(\xi )\) (dash-dotted line), Eq. (46). Right panel: Quark unpolarized collinear PDFs: \(\xi ~e^q(\xi )\). Solid line: Full calculation as in the left panel. Dashed line: \(m/M~u^q(\xi )\), with \(u^q(\xi )\) shown in the right panel of Fig. 1. Double-dot-dashed line: \(\xi ~e^q_{EoM}(\xi )\), Eq. (46)

Full size image

In this section we present the numerical results for (T-even) uTMDs beyond the leading-twist. The detailed expressions can be found in the Appendix E, but it is useful to recall that the decomposition in symmetric and antisymmetric combinations adopted for \(f_1(\gamma ,\xi )\) remains still valid, as well as the relations with the quark and anti-quark contributions.

As introduction to the outcomes of our dynamical approach, it is worth anticipating that the comparison between full calculations and naive estimates one can infer from Eq. (17) by using a valence approximation of the leading-twist \(f_1(\gamma ,\xi )\), highlights the inspiring statement one can read in Ref. [79]: the higher-twist distributions are naturally related to multiparton distributions. The role of the exchanged gluons becomes definitely clear through a remarkable shift of the peak in all the sub-leading uTMD we have analyzed, as already discussed in the previous section, as well as through the sharp difference with the naive estimates, which exclude the effect of the one-gluon exchange.

5.1 Twist-3 uTMD: \(e(\gamma ,\xi )\)

In the frame where \(\textbf{P}_\perp =0\) and hence \(P^+=M\), by using Eq. (26), (B.19), (B.20), (B.21) and (B.22), with \(i=1\) and the functions \(b^1_{n;\ell j}\) given in Table 7, one gets the twist-3 uTMDs \(e^{S(AS)}(\gamma ,\xi )\), decomposed as follows

$$\begin{aligned}{} & {} e^{S(AS)}(\gamma ,\xi )\nonumber \\{} & {} \quad = {\mathcal {E}}_0(\gamma ,\xi ;S(AS))+{\mathcal {E}}_d(\gamma ,\xi ;S(AS)) \nonumber \\{} & {} \qquad +{\mathcal {E}}_{2d}(\gamma ,\xi ;S(AS))+{\mathcal {E}}_{3d}(\gamma ,\xi ;S(AS)), \end{aligned}$$
(43)

where the functions in the rhs are given in Appendix E.

5.1.1 Longitudinal degree of freedom

In the left panel of Fig. 5, the following collinear PDFs are shown

$$\begin{aligned} e^{(S,AS)}(\xi )=\int _0^\infty d\gamma ~e^{(S,AS)}(\gamma ,\xi ) \end{aligned}$$
(44)

and

$$\begin{aligned} e^q(\xi )=e^{S}(\xi )+e^{AS}(\xi ). \end{aligned}$$
(45)

Moreover, in the spirit of Ref. [35], we also present the subleading collinear PDF, \( e^q_{EoM}(\xi )\), obtained by integrating the first line in Eq. (17), but disregarding the gluon contribution, viz

$$\begin{aligned} e^q_{EoM}(\xi )\sim & {} {m\over M \xi }\int _0^\infty d\gamma ~ f^q_{1;EoM}(\gamma ,\xi ) \nonumber \\\sim & {} {m\over M \xi }~{u^{LF}_{val}(\xi )\over P_{val}}, \end{aligned}$$
(46)

where \(u^{LF}_{val}(\xi )/P_{val}\), normalized to 1 (cf. Eq. (32)), approximates the integral of \(f^q_{1;EoM}(\gamma ,\xi )\). The large difference between our \(e^q(\xi )\) and \((m/M\xi ) u^{LF}_{val}(\xi )/P_{val}\) indicates the sizable role of the gluon contribution from the HFS generated by our dynamical model. In addition, one should point out that the strength of \(e^q(\xi )\) is spread out on the whole range of \(\xi \), and not concentrated at the end-point \(\xi =0\) as QCD investigations indicate. The latter feature leads to the singular contribution given in Eq. (15) (see, e.g., Ref. [87], for a detailed discussion, but notice that the focus is on the nucleon).

In the right panel of Fig. 5, the comparison between \(\xi \,e(\xi )\) and the other two approximations: (i) \((m/M) f^{q}_1(\xi )\) and (ii) \((m/M) u^{LF}_{val}(\xi )\) (cf. Eq. (46)) is carried out. The relevance of such a comparison is given by the possibility of more directly assessing the gluon role, since the factor \(\xi \) eliminates the singular term present in the QCD analysis of \(e(\xi )\), and one remains with the mass contribution \((m/M) f^{q}_1(\xi )\) and the term from the quark–gluon–antiquark correlator.

Still within the QCD framework (see, e.g., Ref. [87]), the moments \(\langle \xi ^n\rangle _{e^q}\), for \(n\le 2\), read as follow

$$\begin{aligned}{} & {} \sum _q\int _{0}^{1} d\xi ~ e^q(\xi ) ={\sigma _\pi \over m_{cur}}\nonumber \\{} & {} \int _{0}^{1} d\xi ~ \xi ~e^q(\xi ) =N_q~{m_{cur}\over M}\nonumber \\{} & {} \int _{0}^{1} d\xi ~ \xi ^2~e^q(\xi ) ={m_{cur}\over M}\int _{0}^{1} d\xi ~ \xi ~f^q_1(\xi ), \end{aligned}$$
(47)

and, for \(n>2\), they receive contributions not only from the \((n-1)\)-th moment of \(f^q_1(\gamma ,\xi )\) , but also from the n-th moment of the twist-3 contribution pertaining to the quark–gluon–antiquark correlator. Given the highly non trivial dynamical content of the \(e^q(\xi )\) moments, it is interesting to show the results obtained with our dynamical model.

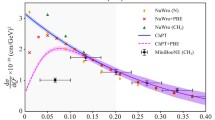
Table 2 The moments \(\langle \xi ^n\rangle _{e^q}\) of the quark twist-3 \(e^q(\gamma ,\xi )\) for \(n<4\), and the ratio \(R(n,e^q,f^q_1)=\langle \xi ^n\rangle _{e^q}/ \langle \xi ^{n-1}\rangle _{f^q_1} \) (it is assumed \(\langle \xi ^{-1}\rangle _{f^q_1}=\langle \xi ^{0}\rangle _{f^q_1}=1\), and the values of \(\langle \xi ^{1}\rangle _{f^q_1}=0.471\) and \(\langle \xi ^{2}\rangle _{f^q_1}=0.266\) have been numerically evaluated)
Full size table

In Table 2, both the moments up to \(n=3\) and the ratio \(R(n,e^q,f^q_1)=\langle \xi ^n\rangle _{e^q}/ \langle \xi ^{n-1}\rangle _{f^q_1}\) are presented. In particular, as to the first two moments, to get rid of the dependence upon \(m_{cur}\) it is helpful to compare the result obtained by multiplying the zero-th and the first moment, (cf. Eq. (47)), with final outcome \(\sigma _\pi /M\). The estimate of \(\sigma _\pi \) at the leading order of the chiral expansion leads to \(\sigma _\pi /M=1/2\), as satisfactorily confirmed by the LQCD calculations in Ref. [86], where \(\sigma ^{lat}_\pi =78.2\pm 4.2\) MeV, for \(M=149.5\pm 1.3\) MeV and \(m_{cur} \sim 4.9\) MeV. Eliminating the current quark mass, that is outside our approach, through the above product, we get \(\sigma _\pi /M=1.78\), instead of \(\sim 0.5\). Such a conspicuous difference is surely influenced by the different distribution of the \(e^q(\xi )\) strength, as already mentioned, and points to a needed enrichment of the gluon dynamics in our approach. However, it is worth mentioning that for a simple non relativistic constituent quark model one has \(\sigma _\pi ^{NR}=2 m\), so that \(\sigma _\pi ^{NR}/M=3.64\) (with \(m=255\) MeV the constituent mass), almost twice the result obtained in the BS framework.

In QCD, the ratios \(R(1,e^q,f^q_1)\) and \(R(2,e^q,f^q_1)\) are equal and amount to \(m_{cur}/M\) (see Eq. (47)), while \(R(3,e^q,f^q_1)=m_{cur}/M+{\varDelta }^3_g\), where \({\varDelta }^3_g\) contains the contribution from the twist-3 gluonic contribution. In our calculation, the ratios for \(n=1,2\) are almost equal, but different from the naive expectation \(m/M=1.82\) with the adopted \(m=255\) MeV. The difference with the third ratio indicates the onset of the contribution from the twist-3 gluonic term.

Fig. 6
figure 6

Left panel: Normalized transverse distribution function \(E_\perp (\gamma )/E_\perp (0)\) (cf. Eq. (48)). Dotted line: full calculation. Solid line: \(D_\perp (\gamma )/D_\perp (0)\) for the sake of comparison. Dash-double-dotted line: The same as in the left panel of Fig. 3. Right panel: Pion unpolarized transverse-momentum distribution \(e^S(\gamma ,\xi )\), Eq. (43), for \(\xi =0.5\). Solid line: Full calculation. Dashed line: LF constituent quark model of Refs. [35, 56], but multiplied by m/(M 0.5) (cf. Eq. (46)). Dash-dotted line: The same as the dashed line but with the LF wave function from DSE calculations [45]. Dash-Double-dotted line: The same as the dashed line but with the NJL model [38]. The adopted quark mass \(m=255\) MeV

Full size image

5.1.2 Transverse degree of freedom

The transverse dof can be analyzed globally by introducing the following transverse distribution function, as already accomplished with the leading-twist uTMD, viz.

$$\begin{aligned} E_\perp (\gamma )=\int _0^1 d\xi ~ e^S(\gamma ,\xi )= \int _0^1 d\xi ~ e^q(\gamma ,\xi ). \end{aligned}$$
(48)

In the left panel of Fig. 6, it is presented our calculation and the ratio \(D_\perp (\gamma )/D_\perp (0)\) to show the similar fall-off, as generated from gluon dynamics and the form-factor featuring the quark-gluon vertex.

A more close view of the decreasing as a function of \(\gamma /m^2\) is provided by the right panel of Fig. 6, where it is shown the comparison between our calculation of \(e(\gamma ,\xi =0.5)\) and the outcomes obtained by using Eq. (46) with ((i) the LF wave function from the constituent quark model of Refs. [35, 56], (ii) the LF wave function from DSE calculations [45] and (iii) the PDF from the NJL model [38]. The differences again point to the role of the interaction in the various approaches, and highlight the relevance of an experimental investigation of the transverse dof.

In Fig. 7, the full dependence of \(e^S(\gamma ,\xi )\) is presented, displaying a double-hump shape that for larger \(\gamma /m^2\) becomes smoother and smoother.

5.2 Twist-3 uTMD: \(f^\perp (\gamma ,\xi )\)

In an analogous way, for \(i=2\) and using Table 8, one gets the twist-3 \(f^{S(AS) \perp }(\gamma ,\xi )\), with the following decomposition

$$\begin{aligned}{} & {} f^{S(AS) \perp }(\gamma ,\xi )\nonumber \\{} & {} \quad ={\mathcal {P}}_0(\gamma ,\xi ;S(AS)) + {\mathcal {P}}_d(\gamma ,\xi ;S(AS)) \nonumber \\{} & {} \qquad +{\mathcal {P}}_{2d}(\gamma ,\xi ;S(AS)) \end{aligned}$$
(49)

where the above functions are given in Appendix E. Notice that in this case \({\mathcal {P}}_{2d}(\gamma ,\xi ;S(AS))=0\).

Fig. 7
figure 7

Pion unpolarized transverse-momentum distribution \(e^S(\gamma ,\xi )\), Eq. (44), at the initial scale

Full size image

5.2.1 Longitudinal degree of freedom

In the left panel of Fig. 8, the following subleading collinear PDFs are shown

$$\begin{aligned} f^{S(AS) \perp }(\xi )=\int _0^\infty d\gamma ~ f^{S(AS) \perp }(\gamma ,\xi ), \end{aligned}$$
(50)

and the corresponding quark combination. As a reference, it is also presented \(f^{\perp q}_{EoM}(\xi )\), obtained from the second line of Eq. (17), without the gluon term, as follows

$$\begin{aligned} f^{\perp q}_{EoM}(\xi ) \sim {1 \over \xi } \int _0^\infty d\gamma f^{\perp q}_{EoM}(\gamma ,\xi ) \sim {u^{LF}_{val}(\xi ) \over \xi }. \end{aligned}$$
(51)

For the sake of completeness, in the right panel of Fig. 8, the product \(\xi \,f^{\perp q}(\xi )\) is compared to \(f^q_1(\xi )\) and \(u^{LF}_{val}(\xi )\) that represents the approximation to \(f^{\perp q}_{EoM}(\xi )\) as given in Eq. (51). Also for \(f^{\perp q}(\xi )\), the full calculation substantially differs from approximated evaluations, prompting further investigation of the gluon contributions.

Fig. 8
figure 8

Left panel: The same as in Fig. 5, but for \(f^{\perp q}(\xi )\), \(f^{S \perp }(\xi )\) and \(f^{AS \perp }(\xi )\), Eq. (50), and \(f^{\perp q}_{EoM}(\xi )\) as given in Eq. (51). Right panel: Quark unpolarized collinear PDFs \(\xi \,f^{\perp q}(\xi )\). Solid line: Full calculation as in left panel. Dashed line: \(\xi \,f^{\perp q}(\xi )\) obtained by using the second line in Eq. (17) and our \(f^q_1(\xi )\). Double-dot-dashed line: The same as the dashed line but using the valence approximation of the PDF, \(u^{LF}_{val}(\xi )\), with norm equal to 1

Full size image
Fig. 9
figure 9

Left panel: Normalized transverse distribution function \(P_\perp (\gamma )/P_\perp (0)\) (cf. Eq. (52)). Dotted line: Full calculation. Solid line: \(D_\perp (\gamma )/D_\perp (0)\) for the sake of comparison. Dash-double-dotted line: The same as in the left panel of Fig. 3. Right panel: Pion unpolarized transverse-momentum distribution \(f^{S\perp }(\gamma ,\xi )\), Eq. (49), for \(\xi =0.5\). Solid line: Full calculation. Dashed line: By using \(f_1(\gamma ,\xi =0.5)\) in Fig. 3 from the LF constituent quark model of Refs. [35, 56] (cf. the second line in Eq. (17), without the gluonic term). Dash-dotted line: The LF wave function from DSE calculations [45]. Dash-Double-dotted line: The NJL model [38]. The adopted quark mass \(m=255\) MeV

Full size image

5.2.2 Transverse degree of freedom

Also for \(f^\perp (\gamma ,\xi )\), we introduce the transverse distribution function, viz.

$$\begin{aligned} P_\perp (\gamma )=\int _0^1 d\xi ~ f^{S\perp }(\gamma ,\xi )= \int _0^1 d\xi ~ f^{\perp q}(\gamma ,\xi ). \end{aligned}$$
(52)

In the left panel of Fig. 9, a comparison, built with the same spirit as in the left panel of Fig. 6, is shown for the ratio \(P_\perp (\gamma )/P_\perp (0)\).

A more detailed view of the fall-off can be gained from the right panel of Fig. 9, where \(f^{S\perp }(\gamma ,\xi =0.5)\) is compared with the results obtained by using (i) the LF constituent quark model of Refs. [35, 56] (cf. the second line in Eq. (17), without the gluonic term). (ii) the LF wave function from DSE calculations [45] and (iii) the NJL model [38].

Fig. 10
figure 10

Pion unpolarized transverse-momentum distribution \(f^{S\perp }(\gamma ,\xi )\), Eq. (49)

Full size image

Finally in Fig. 10, the full dependence of \(f^{S\perp }(\gamma ,\xi )\) is shown. Also in this uTMD, the double-hump shape decreases when \(\gamma /m^2\) increases.

To summarize, a coherent view of the tail in \(\gamma \) is plainly provided by Figs. 3, 6 and 9. Namely, the interaction taken into account in the ladder kernel together with the extended structure of the quark-gluon vertex governs the fall-off of both the leading and subleading-twist uTMDS. Therefore, the quantitative estimates obtained through our dynamical model, in Minkowski space, is shown to be in a favorable position to provide insights into the interplay between transverse dof and the role of gluons.

6 Conclusions

The twist-2 (leading) and twist-3 (subleading) unpolarized (T-even) transverse-momentum dependent parton distribution functions have been calculated for the pion within an approach based on the solution of the Bethe–Salpeter equation in Minkowski space, namely, within a genuinely relativistic quantum field theory framework. We achieved this goal by exploiting the Nakanishi integral representation of the BS-amplitude in order to get actual solution of the 4D homogeneous ladder BSE in Minkowski space through a system of integral equations that determine the Nakanishi weight functions relevant for the problem under scrutiny [63, 90, 91]. After obtaining the pion electromagnetic form factor [77], and the pion PDF [78], we extended the yield of our approach by exploring the dependence of the parton distributions upon the transverse momentum. This additional step has its-own importance in view of the planned experimental efforts to achieve a fully three-dimensional investigation of hadrons (mainly of the nucleon and, more challenging, the pion).

The relevant message one gets from our calculations is given by the essential role of the gluon exchange, that cannot be captured by purely phenomenological model. The joint use of the Fock expansion of the pion state, allows us to shed light on the gluonic content of the quark PDF obtained through the BS amplitude, even determining a quantitative estimate, \(\sim 6\%\) of the average longitudinal momentum fraction \(\langle \xi ^q\rangle \). Moreover, the latter analysis explains also the source of the small, but theoretically relevant, shift between the \(u^q(\xi )\) and the PDF that fulfills the charge symmetry (an issue already investigated within the Dyson–Schwinger approach, e.g., in Ref. [102], where a different interpretation was proposed). As to the transverse degree of freedom, a power-like fall-off of the transverse distributions, obtained by integrating on \(\xi \) the uTMDs, is supported by the one-gluon exchange interaction that governs the ultraviolet region, according to our calculations. This outcome could suggest to reconsider exponential or Gaussian Ansätze for describing the high-momentum content \((\gamma \gg m^2)\) of the uTMDS.

Clearly, the presented first evaluation of the uTMDs has to be considered a reliable starting point for the next step we are elaborating, i.e. the introduction of the quark self-energy in the 4D ladder BSE in Minkowski space (see Refs. [73,74,75,76].

Summarizing, our approach can be placed among those in which the dynamics can be studied in Minkowski space and in some detail. Moreover, the additive construction of the interaction kernel allows one to address step-by-step recognized effects, achieving an implementation of the dynamics in a controlled way.