Effects of exact kinematics and the Sudakov form factor on the dipole amplitude

Abstract

We investigate the effects of exact gluon kinematics on the parameters of the Golec-Biernat–Wüsthoff, and Bartels–Golec-Biernat–Kowalski saturation models. The resulting fits show some differences, particularly, in the normalization of the dipole cross section $\sigma _0$. The refitted models are used for the dijet production process in DIS to describe HERA data and investigate the effects of the Sudakov form factor at the future Electron Ion Collider.

1 Introduction

Factorization of scales plays central role in Quantum Chromodynamics (QCD). In particular, within collinear factorization approach, long-distance effects can be isolated into objects called collinear parton distribution functions (PDFs) [1, 2]. The collinear PDFs are not fully perturbatively calculable but they obey perturbative evolution equations and are process-independent [2]. That is to say that one needs to determine initial condition by fit to data, and the obtained PDFs can be used universally.

One of the main type of processes that is suited particularly well to the studies of proton structure is the deep inelastic scattering (DIS) [1, 2]. The data from HERA has enabled us to answer many questions in that domain and largely improved our picture of interior of a proton. It is therefore very exiting that the next generation of DIS machines, the Election Ion Collider (EIC) [3] is making its way and will soon allow us to uncover more details about hadron structure.

At large center of mass energy and fixed value of the photon virtuality, Q, one probes the region of small Bjorken scaling variable, x. In that region, which is dominated by gluons [1, 2, 16], the approach of High Energy Factorization, also called $k_T$-factorization [4,5,6,7,8,9], has proven to be suited particularly well. In this framework, the interaction of the photon with gluons happens through boson-gluon fusion or quark impact factor, as depicted in Fig. 1. An object, which is central to the description of such process is called the dipole gluon density, ${\mathcal {F}}^{\textrm{dipole}}(x,k_T^2)$, and it is a type of transverse momentum dependent (TMD) [10,11,12,13] PDF. Due to its clear picture, one often uses a position-space counterpart of the gluon density, called dipole cross section. It appears in the $k_T$-factorization formula [5, 11,12,13], which we shall discuss in the next section, and plays a role similar to that of the collinear parton distribution function in the collinear factorization.

Much effort has been made to study this object, notably the work of Balitsky, Fadin, Kuraev and Lipatov (BFKL) [14, 15] has predicted sharp rise of cross sections with 1/x. However, such rise violates unitarity and the Froissart bound [1, 2, 16, 17]. In Ref. [18] it has been recognized that gluon recombination can tame the growth of gluons. The interplay of linear and nonlinear terms leads to a phenomenon called gluon saturation and corresponding evolution equations are known as Balitsky–Kovchegov (BK) [19, 20] equation or JIMWLK [21,22,23,24,25,26] equation.

Despite the success of the aforementioned evolution equations, there exist a number of phenomenological models of the dipole cross section, which are popular due to their simplicity. A notable example is the model proposed by Golec-Biernat and Wüsthoff (GBW) [27] and its extension by Bartels, Golec-Biernat and Kowalski (BGK) [28]. We will use these two specific models in our study. We note, however, that other saturation models have been discussed in the literature [29,30,31,32].

In the present study, we fit the GBW and BGK models to HERA data [33] in the $k_T$-factorization formula for $F_2$, instead of the original dipole factorization [34] formula. As discussed below, this allows us to relatively easy investigate the role of the exact gluon kinematics. Since inclusive observables do not reveal the $k_T$ dependence well, in order to demonstrate the effects of exact kinematics we consider a less inclusive observable which is more sensitive to the $k_T$ dependence of the gluon distribution. The resulting models are used for predictions of dijet production in DIS at Electron Ion Collider (EIC) [35], including effects of the Sudakov form factor, which resums logarithms of the small transverse momentum. This process is known to be sensitive to another type of gluon density, called Weizsäcker–Williams (WW) [11, 12]. For that process, we study, in particular, the angular correlation of jets, and that of the scattered electron and the jets. For other papers addressing dijet production at the EIC we refer the Reader to [36,37,38,39,40].

The paper is organized as follows. In the next section, we present theoretical framework which we use and outline differences between the $k_T$-factorization and the dipole factorization. In Sect. 3, results of the new fits to HERA data in the $k_T$-factorization formula are presented. In Sect. 4, we apply the results from the previous section to compute distributions for dijet production in DIS at the EIC and make comparisons to our earlier study of Ref. [41].

Fig. 1

Kinematic variables of the inclusive DIS

2 The framework

The DIS cross section (structure function) factorises and can be written in a form

$$\begin{aligned} d\sigma = \sum _{a} \phi _{a/h} \otimes H_{\gamma a \rightarrow X} , \end{aligned}$$

(1)

where the hard function, $H_{\gamma a \rightarrow X}$, involving a parton a in the initial state, is calculable perturbatively, and $\phi _{a/h}$ is the parton distribution function of a in a hadron h. The symbol $\otimes$ denotes appropriate convolution. All non-perturbative effects are absorbed in $\phi _{a/h}$, while $H_{\gamma a \rightarrow X}$ can be computed order by order in $\alpha _s$.

We will study factorization in two versions: defined in momentum and position space, respectively. As mentioned earlier, in the fit, we use the GBW and BGK models. The models were originally formulated in the position-space version of the $k_T$-factorization formula. In the GBW model, the dipole cross section has the form [27]

$$\begin{aligned} \sigma _{\textrm{GBW}}(x,r)=\sigma _0\left( 1-e^{-r^2/R^2_0}\right) \quad \text {where}\ R^{-2}_0=\frac{Q_0^{2}}{4}\left( \frac{x_0}{x}\right) ^{\lambda }. \end{aligned}$$

(2)

The dipole cross section is related to the dipole gluon density by the Fourier transform

$$\begin{aligned} \alpha _s{\mathcal {F}}^{\textrm{dipole}}(x,k_T^2)=\frac{N_c}{4\pi }\int \frac{d^2{\textbf{r}}}{(2\pi )^2}e^{i{\textbf{k}}_T\cdot {\textbf{r}} }\nabla _{{\textbf{r}}}^2\sigma _{\textrm{dipole}}(x,r). \end{aligned}$$

(3)

The essence of the GBW model is encoded in the x-dependent saturation scale $Q_s^2(x)=Q^2_0(x_0/x)^{-\lambda }$, which separates the saturation region and the scaling region. An extension of the above model was proposed by Bartels et al. [28] who incorporated the DGLAP evolution in the GBW dipole cross section (2) by modifying the exponent to

$$\begin{aligned} R_0^{-2}=\frac{\pi ^2\alpha (\mu ^2)xg(x,\mu ^2)}{3\sigma _0}, \end{aligned}$$

(4)

where

$$\begin{aligned} \mu ^2=\frac{C}{r^2}+\mu _0^2\quad \text {and}\quad xg(x,Q^2_0)=A_g x^{-\lambda _g}(1-x)^{5.6}, \end{aligned}$$

(5)

thus improving the description of data at higher $Q^2$.

While these models enjoyed much success in the phenomenology of DIS, including the diffractive and photo-production processes [27, 42], it is worth mentioning that they both use certain kinematic approximation which is specific to LO dipole factorization and are not there in the $k_T$-factorization. This was recognized in [43]. In the following, we will investigate effects of these approximations.

Firstly, let us outline the factorization formulas. With $q'\equiv q+x p$, one decomposes k and $\kappa$, defined in Fig. 1, as

$$\begin{aligned} \kappa =\alpha p-\beta q'+\kappa _T\quad \text {and}\quad k=a p- bq'+k_T. \end{aligned}$$

(6)

For the contribution depicted in Fig. 1, the structure function $F_2$ factorizes with a change of variable ${{\varvec{\kappa }}'}_T\equiv {{\varvec{\kappa }}_T}-(1-\beta ){\textbf{k}}_T$, to the form [44, 45]

$$\begin{aligned} F_2(x,Q^2)= & {} \sum _f e_f^2 \frac{Q^2}{2\pi }\int \frac{dk^2_T}{k_T^2}\int ^1_0d\beta \int d{\kappa '}_T\alpha _s(\mu ^2)\nonumber \\{} & {} \times {\mathcal {F}}^{\textrm{dipole}}(x/z,k_T^2)\Theta (1-x/z)\nonumber \\{} & {} \times \left[ \left( \beta ^2+(1-\beta )^2\right) \left( \frac{I_1}{2\pi }-\frac{I_2}{2\pi }\right) \right. \nonumber \\{} & {} \left. +\left( m_f^2+4Q^2\beta ^2(1-\beta )^2\right) \left( \frac{I_3}{2\pi }-\frac{I_4}{2\pi }\right) \right] , \nonumber \\ \end{aligned}$$

(7)

where

$$\begin{aligned} \frac{1}{z}=1+\frac{{\kappa '}^2_T+m_f^2}{\beta (1-\beta )Q^2}+\frac{k^2_T}{Q^2}. \end{aligned}$$

(8)

One should note that the gluons are not probed directly, thus the argument of the gluon density is x/z rather than x. If one, instead, uses $1/z=1+4 m_f^2/Q^2$ and assumes that $\mu$ is independent of $\kappa '$ and $k_T$, the above formula can be written in the impact parameter space [27, 46] (i.e. as a dipole factorization formula)

$$\begin{aligned} F_2\left( x,Q^2\right)= & {} \sum _f e_f^2 \frac{Q^2}{4\pi ^2} \int ^1_0d\beta \int \frac{d^2{\textbf{r}}}{(2\pi )^2}\nonumber \\{} & {} \times \left| \Psi \left( {\tilde{x}},\beta ,Q^2\right) \right| ^2\sigma _{\textrm{dipole}}\left( {\tilde{x}},r\right) , \end{aligned}$$

(9)

where the photon wave function, $\left| \Psi \left( \tilde{x},\beta ,Q^2\right) \right| ^2$, describes splitting of the incoming photon into a $q{\overline{q}}$ pair with light-cone momenta fractions $\beta$ and $1-\beta$ respectively, and the dipole cross section, $\sigma _{\textrm{dipole}}\left( {{\tilde{x}}},r\right)$, describes the interaction of the colour dipole of size r with the proton. In Ref. [27], ${\tilde{x}}=x(1+4m_f/Q^2)$ with nonzero value of $m_f$ was used even for light flavours, which is necessary to partially substitute $k_T$ and ${\kappa '}_T$ in Eq. (8). In the present study, we use Eq. (7) to fit the models, where the gluon density is obtained by evaluating Eq. (3).

Considering the small-r limit of the GBW model

$$\begin{aligned} \left. \sigma _{\textrm{GBW}}\left( x,r\right) \right| _{r\ll Q_s}\approx r^2 Q_s^2/4, \end{aligned}$$

(10)

comparison to

$$\begin{aligned} \left. \sigma _{\textrm{BGK}}\left( x,r\right) \right| _{r\ll Q_s}\approx \frac{r^2 \pi ^2\alpha _s(\mu ^2)xg(x,\mu ^2)}{3}, \end{aligned}$$

(11)

from BGK, suggests that the GBW model is an approximation in which $\alpha _s(\mu ^2)$ and $xg(x,\mu ^2)$ are independent of r [28]. For this reason, in one version of the model discussed below, we shall account for the running coupling in Eq. (7) by assuming that $\alpha _s$ in Eq. (3) is constant for the GBW model, and thus explicitly multiply it by the running coupling

$$\begin{aligned} \alpha _s(\mu ^2){\mathcal {F}}^{\textrm{dipole}}(x,k_T^2)\rightarrow \alpha _s(\mu )\frac{\alpha _s{\mathcal {F}}^{\textrm{dipole}}(x,k_T^2)}{0.2}, \end{aligned}$$

(12)

where

$$\begin{aligned} \alpha _s(\mu ^2)=\frac{1}{\frac{11 C_A-2n_f}{12\pi }\log \left( \frac{\mu ^2}{\Lambda _{\textrm{QCD}}^2 }\right) }, \end{aligned}$$

(13)

and $\Lambda _{\textrm{QCD}}^2=0.09\;\textrm{GeV}^2$.

The factor 0.2 is an arbitrary normalization, whose effect is absorbed by $\sigma _0$, and hence bears no importance. (For a more detailed analysis of the dipole gluon density from the BGK model see Ref. [47]¹) While there is some ambiguity on what the argument of $\alpha _s(\mu ^2)$ should be, we follow Ref. [45] and use

$$\begin{aligned} \mu ^2=k_T^2+{\kappa '}_T^2+m_f^2+\mu ^2_0, \end{aligned}$$

(14)

where we add $\mu ^2_0=4\;\textrm{GeV}^2$ in order to freeze the coupling at low scales.

3 Fits to $F_2$ data

We fitted the GBW and BGK models to the $F_2$ data from HERA [33].² A numerical program was written with help of CERNLIB (DPSIPG) [49], GSL [50], CUBA [51] and ROOT [52] libraries to evaluate $F_2$. The fitting was performed using MnMigrad and MnSimplex of ROOT::Minuit2 [53].

The data were selected to be in the range $0.045\le Q^2\le 650~\text {GeV}^2$, $x<0.01$. As with the previous fit [54], the c and b flavours were taken into account with the mass 1.3 and $4.6~\text {GeV}$, respectively. As discussed earlier, we take the light quarks to be massless.

We studied the following cases

• GBW model with the fixed coupling in $k_T$-factorization ($k_T$-GBW),

• GBW model with the running coupling in $k_T$-factorization (rc-$k_T$-GBW),

• BGK model in $k_T$-factorization ($k_T$-BGK),

and, as a reference, we provide the following results from Ref. [54]

• GBW model with massless light quarks in the dipole factorization (r-GBW),

• GBW model with massive light quarks in the dipole factorization (r-GBW-massive),

• BGK model in the dipole factorization (r-BGK).

Table 1 Fit parameters of respective models. The parameters of the dipole factorization cases are from Ref. [54]

The results of the fits are summarized in Table 1. The fit quality of $k_T$-GBW is almost unchanged w.r.t. r-GBW, while rc-$k_T$-GBW shows remarkable improvement, almost halving the $\chi ^2$ value. This is in line with the observation made in Refs. [55,56,57] that in the BK evolution, the running coupling corrections have considerable effect.

Another notable point is that, except for the normalization $\sigma _0$, the parameters are very similar, particularly those of rc-$k_T$-GBW are almost identical to those of r-GBW. While the GBW model remains almost unaffected, the BGK model seems to show slightly more change. The difference in $\sigma _0$ is similar to that of GBW and other parameters changed moderately.

In Fig. 2, the plots of the dipole cross section, the dipole gluon density and the saturation scale for the GBW and BGK models are shown. The dipole cross section and the gluon density are both normalized by $\sigma _0$ in order to show the effects of other parameters better, and the saturation scale is defined as a ridge of the dipole gluon density in the $(x,k_T^2)$ plane.

In the plots on the left hand side, one can see the effects of changes in the parameters of the GBW model. The difference between the rc-$k_T$-GBW and r-GBW is negligible, while the $k_T$-GBW is slightly shifted, compared to others, by the change in $x_0$.

On th right hand side of Fig. 2, the same plots are shown for the BGK model. Unlike in the GBW case, the connection between the differences shown in the plots and the differences in the parameters is less clear. Nevertheless, the differences are more prominent in the small-x region.

Comparisons of the results with the $F_2$ data are shown in Figs. 3 and 4. In Fig. 3, the differences between r-GBW and $k_T$-GBW are not visible, while rc-$k_T$-GBW shows sizable difference from the others, particularly in the large-$Q^2$ region. Recalling that the parameters of rc-$k_T$-GBW and r-GBW are very similar, the difference in $F_2$ is almost entirely due to the coupling constant. The improvement in the fit quality is depicted as a histogram of the $\chi ^2$-vale per number of points at the bottom of Fig. 3. Here, the improvement in the large-$Q^2$ region is very clear. In Fig. 4, the differences between r-BGK and $k_T$-BGK are hardly visible. In the histogram at the bottom, one can see some differences, but they cancel out mostly, making little improvement overall.

Fig. 2

The dipole cross section, the dipole gluon density at $x=10^{-2},\; 10^{-6}$, and the saturation scale for the GBW (left) and the BGK (right) models. Note that the dipole cross section and the gluon density are normalized with $\sigma _0^{-1}$

Fig. 3

Comparison of $F_2$ from GBW with HERA data. The histogram shows the $\chi ^2$ value per data point in each frame. Improvement by the running coupling (rc-$k_T$) is clearly visible in the high-$Q^2$region, while the new fit ($k_T$) shows only marginal improvement

Fig. 4

Comparison of $F_2$ from BGK with HERA data. The histogram shows the $\chi ^2$ value per data point in each frame. The overall fit quality remain similar but the quality in each frame changes noticeably. In particularly, the $k_T$-formula $(k_T)$ shows better quality at small $Q^2$

Let us now take a closer look at the parameter $\sigma _0$. Recall that the difference between the $k_T$-factorization formula and the dipole factorization formula is in x/z, and this enters in the GBW formalism as ${\tilde{x}}$. It is easy to see that, as x grows, the dipole cross section gets suppressed. (Keeping in mind the suppression by the photon wave function in the large-r region.) Such effect was discussed previously in Ref. [58] in the context of the BK equation. In fact, this suppression is the motivation given in Ref. [27] for such modification of x, so that, in the small-$Q^2$ limit, the total cross section remains finite. Since

$$\begin{aligned} \left( 1+\frac{4 m_f^2}{Q^2}\right) \le \left( 1+\frac{k_T^2}{Q^2}+ \frac{{\kappa '}_T^2+m_f^2}{\beta (1-\beta )Q^2}\right) , \end{aligned}$$

(15)

the $k_T$-factorization case receives more suppression. Consequently, the normalization factor $\sigma _0$ rises to compensate the suppression. Therefore, one can understand the change in $\sigma _0$ as a direct consequence of the key difference between the $k_T$-factorization and the dipole factorization.

4 Dijet production at EIC

The $F_2$ structure function is an inclusive object and it is weakly sensitive to the shape of the gluon density. To probe that shape better, we shall now apply the dipole cross sections obtained in the previous section to the jet correlations at the EIC, following closely the method of Ref. [41].

Fig. 5

Weizsäcker–Williams gluon density at $x=10^{-3}$. Top row: Comparison of the dipole factorization fit and $k_T$-factorization fit results. Bottom row: Comparison of the respective models with and without the Sudakov factor, at $\mu =17,\;67~\text {GeV}$.The green dotted line is the KS gluon [41], and the green dashed line is the rcBK gluon [59]

We consider dijet production in DIS

$$\begin{aligned} e+p\rightarrow e+J_1+J_2+X. \end{aligned}$$

(16)

At the leading order, in the small-x limit, this process is dominated by $q{\overline{q}}$ jets [12]. It is therefore closely related to the dipole picture we discussed earlier. In the Breit frame, where the photon momentum is given by $q=(0,0,0,Q)$, at the leading order, the jets momentum imbalance $p_T\equiv \left| p_{1T}+p_{2T}\right|$ equals the gluon transverse momentum $k_T$, where $p_{1T}$ and $p_{2T}$ are transverse momenta of the jets. This makes dijets an interesting process. For the region where $p_T\ll P_T\sim p_{1T},\,p_{2T}$, one may use power counting to take leading order in $p_T/P_T$, which leads to the transverse-momentum-dependent (TMD) factorization.

In the large-$N_c$ limit of the TMD factorization, there are two types of gluon densities, namely the dipole gluon density and the Weizsäcker–Williams (WW) gluon density [11, 12, 60, 61]. It was shown in Ref. [12], that the dijet process in DIS can directly probe the WW gluon, ${\mathcal {F}}^{\textrm{WW}}(x,k^2)$, where the differential cross section factorizes as

$$\begin{aligned} \frac{d\sigma ^{\gamma ^*p\rightarrow q{\overline{q}}X}}{d \text {P.S.}}={\mathcal {F}}^{\textrm{WW}}(x,k_T^2)H_{\gamma ^*g^*\rightarrow q{\overline{q}}}, \end{aligned}$$

(17)

with the hard function $H_{\gamma ^*g^*\rightarrow q{\overline{q}}}$ describing interactions of an off-shell photon with an off-shell gluon producing a $q{\overline{q}}$ pair. ${\mathcal {F}}^{\textrm{WW}}(x,k^2)$, has an interpretation as a number density of gluons inside a proton, while ${\mathcal {F}}^{\textrm{dipole}}(x,k_T^2)$ does not have such an interpretation [11, 12, 61].

We carry out our study in the framework of the Improved Transverse-Momentum-Dependent (ITMD) factorization [60, 62].³ This is implemented in the program KaTie [63], which we use to compute the cross sections. The ITMD factorization is a generalization of the TMD factorization, where the momentum imbalance in TMD is restricted to be small [60, 62]. That is to say, ITMD resums $(Q_s/k_T)^n$ and $(k_T/P_T)^n$ [60, 62], thus extends the region of applicability up to $k_T\sim P_T$. The difference of Eq. (17) from the regular TMD is that the hard function has an off-shell gluon, $g^*$, thus rendering the $k_T$ dependence in the hard function as well [62].

Under the Gaussian approximation and assuming $\theta$-like profile of the proton, one can write [11, 12, 60, 61]

$$\begin{aligned} {\mathcal {F}}^{\textrm{WW}}(x,k^2)= \frac{C_F}{2\pi ^3\alpha _s}\int ^\infty _0\frac{dr}{r}J_0(r k) \sigma _{\mathrm {dipole\,Adj.}}(x,r), \end{aligned}$$

(18)

with the adjoint dipole cross section

$$\begin{aligned} \sigma _{\mathrm {dipole\,Adj.}}(x,r)=\sigma _0\left( 1-\left( 1-\frac{\sigma _{\textrm{dipole}}(x,r)}{\sigma _0}\right) ^{C_A/C_F}\right) .\nonumber \\ \end{aligned}$$

(19)

For the region where the TMD factorization is applicable, $Q_s\sim k_T\ll P_T\sim Q$, one needs to resum the large Sudakov logarithms $\log (k_T/Q)$, as well as $\log (1/x)$ [12]. It was shown in Refs. [13, 64, 65] that consistent resummation of such logarithms is possible owing to the separation of corresponding regions (see also Ref. [66]). Resummation of the Sudakov logarithms is achieved by the formula

$$\begin{aligned}{} & {} {\mathcal {F}}^{\textrm{WW}}(x,k^2,\mu ^2)\nonumber \\{} & {} \quad =\frac{C_F}{2\pi ^3\alpha _s}\int ^\infty _0\frac{dr}{r}J_0(r k) e^{-S(r,\mu ^2)} \sigma _{\mathrm {dipole\,Adj.}}(x,r), \end{aligned}$$

(20)

where, we use the Sudakov form factor [13, 65],

$$\begin{aligned} S(r,\mu ^2)=\frac{\alpha _s N_c}{4\pi }\ln ^2\left( \frac{\mu ^2r^2}{4e^{-2\gamma _E}}\right) , \end{aligned}$$

(21)

in which $\gamma _E$ is the Euler-Mascheroni constant, and we set $\alpha _s=0.2$. The obtained gluon densities are shown in Fig. 5.

Fig. 6

Comparison of calculation with the GBW and BGK models, fitted in the dipole (r) and $k_T$ factorization formulae to the HERA dijet data [67]

Fig. 7

Effects of Sudakov factor in the BGK model, fitted in the $k_T$ factorization formula to the HERA dijet data [67]. Uncertainty was estimated by varying renormalization scale by multiplying by 0.5 and 2

Fig. 8

Azimuthal correlation of the jets and the scattered electron in the Breit frame. Top: Comparison of dipole factorization fit and $k_T$-factorization fit. Middle and bottom: Effect of the Sudakov form factor. The green dotted line is the KS gluon [41], and the green dashed line is the rcBK gluon [59]

Fig. 9

Azimuthal correlation of the jets and the scattered electron in the lab frame. Top: Comparison of dipole factorization fit and $k_T$-factorization fit. Middle and bottom: Effect of the Sudakov form factor. The green dotted line is the KS gluon [41], and the green dashed line is the rcBK gluon [59]

4.1 Comparison to HERA data

Before discussing dijet production at the EIC, we compare our model with inclusive dijet data from HERA [67]. The kinematical cuts chosen for this study read

$$\begin{aligned}{} & {} E_p=27.6\, \textrm{GeV},\quad E_e=920\, \textrm{GeV},\nonumber \\{} & {} p_{2T}>4\, \textrm{GeV},\quad 5.0<\left<p_T\right>_2<50\, \textrm{GeV},\nonumber \\{} & {} 0.2<y<0.6,\quad -1.0<\eta _{1\text {Lab}}^{\text {jet}},\,\eta _{2\text {Lab}}^{\text {jet}}<2.5,\nonumber \\{} & {} 5.5<Q^2<80\, \textrm{GeV}^2,\nonumber \\{} & {} R=\sqrt{\left( \Delta \eta ^{\text {jet}}_{\text {Lab}}\right) ^2+ \left( \Delta \phi ^{\text {jet}}_{\text {Lab}}\right) ^2}<1, \end{aligned}$$

(22)

where the average transverse momentum of jets in the Breit frame is given by

$$\begin{aligned} \left<p_T\right>_2\equiv \frac{1}{2}\left( p_{1T}+p_{2T}\right) , \end{aligned}$$

(23)

and $\eta$ and $\phi$ denote pseudo-rapidity and azimuthal angle, respectively. The processes under consideration are of the type

$$\begin{aligned} g\rightarrow q{\overline{q}}, \end{aligned}$$

(24)

where we take five massless quark flavours [67].

The renormalization and factorization scales are given by⁴

$$\begin{aligned} \mu =\frac{1}{2}\left( Q+\left<p_T\right>_2 \right) . \end{aligned}$$

(25)

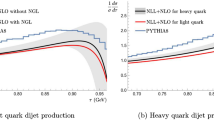
The comparison of the new and the old fits of the GBW and BGK models is shown in Fig. 6, in which we plot differential dijet cross sections in bins of $\left<p_T\right>_2$ and $Q^2$. In both cases of the GBW and BGK models, we observe that in the low- and moderate-$Q^2$ region, the new fits agree better with the data, except for large $\left<p_T\right>_2$. At large $Q^2$ and large jet-transverse momenta, our predictions overshoot the data but this is expected, as this kinematic configurations lay beyond the validity region of the saturation models.

Figure 7 shows the effects of the Sudakov form factor in the case of the BGK model. Here, we plot the BGK model predictions with an uncertainty estimated by varying the renormalization scale by the factors 0.5 and 2. We see that the Sudakov form factor has a sizeable effect by making the $\left<p_T\right>_2$-spectra steeper. This leads to lowering the high-$\left<p_T\right>_2$ region, which improves agreement with the data. Hence, we can conclude that the BGK model with exact kinematics and Sudakov resummation provides a good description of dijet production at HERA energies.

Fig. 10

Azimuthal correlation of the jets in the Breit frame. Top: Comparison of dipole factorization fit and $k_T$-factorization fit. Middle and bottom: Effect of the Sudakov form factor. The green dotted line is the KS gluon [41], and the green dashed line is the rcBK gluon [59]

4.2 Dijet processes at EIC

Following Ref. [41], we study the azimuthal correlations of jets and the final state electron in DIS , where it was argued that this observable is sensitive to the soft emissions and the saturation effects. In this study we focus only on the proton case. The kinematical cuts suggested in Ref. [41] are

$$\begin{aligned}&E_e=15\textrm{GeV},\quad E_p=135\textrm{GeV},\quad Q^2>1\textrm{GeV}^2,\\&0.1<\nu<0.85,\quad \Delta R_{\textrm{Breit}}<1,\quad p^{\textrm{Breit}}_{1,2\,T}>3\textrm{GeV},\\&-4<y_{1,2\,{\textrm{lab}}}<-1. \end{aligned}$$

Grids of the Weizsäcker–Williams gluon density were produced by evaluating Eqs. (18) and (20). The gluon density at $x=10^{-3}$ is plotted in Fig. 5 with the hard-scale-independent Kutak–Sapeta (KS) gluon [41, 68, 69] and the running-coupling BK (rcBK) gluon density [57, 59, 70]. Both of these gluon densities are solutions of evolution equations and treat better perturbative tail at large $k_T$. Furthermore, the KS gluon takes into account resummed corrections of higher orders, i.e. kinematical constraint and nonsingular (at low z) elements of DGLAP splitting functions [45].

Clearly, as shown in Fig. 5, the GBW and BGK models fall much more quickly than the KS and rcBK gluon densities. In general, expected behaviour in the large-$k_T$ region is $\sim k_T^{-2}$ [11, 12], while $\sigma _{\textrm{GBW}}$ behaves like $\sim e^{-k_T^2}$. As in Ref. [41], the Sudakov factor enhances in the small-$k_T$ region and suppresses in the large-$k_T$ region. In other words, it broadens the distribution. In comparison to the result of Ref. [41], the effect of broadening by the Sudakov factor is significantly more pronounced in the case of the GBW and BGK models. The hard-scale-dependent GBW and BGK models, as a consequence, become closer to the KS and rcBK gluons, cf. Fig. 2 of Ref. [41].

Figures 8 and 9 show electron-jets azimuthal correlation in the Breit and in the Lab frame, respectively. In the top row of Fig. 8, we see, for both the GBW and BGK models, better agreements of results with the KS and rcBK for the new $k_T$-factorization fits. However the overall normalization of the gluon density depends on the coupling $\alpha _s$, which we assumed to be 0.2. Nevertheless, it shows clearly the effect of the parameter $\sigma _0$. In the middle and the bottom row, it shows the effects of the Sudakov form factor, which qualitatively agrees with that of Ref. [41], by lowering the cross section.

Figure 9 shows the electron-jets correlation in the Lab frame. Here, the difference between KS and GBW and BGK is more prominent, while rcBK shows similar pattern to the GBW and BGK models and therefore we can attribute the effects to importance of higher order corrections, as are accounted for in KS gluon. The effects of the Sudakov factor are similar to those in Ref. [41] at relatively high $\Delta \phi$, while at smaller $\Delta \phi$, the effect is reversed (i.e. the cross sections were slightly lowered in Ref. [41], while here, they are significantly increased).

Finally, Fig. 10 shows the jet–jet correlations in the Breit frame. Again, the GBW and BGK models exhibit considerable deviation from the KS gluon. The difference from the previous plot is the disagreement of the GBW/BGK models and the rcBK in the small-$\Delta \phi$ region. Similarly to the previous plots, the Sudakov factor affects the models somewhat differently from the KS gluon in Ref. [41]. The effect enhances the cross section considerably in the small-$\Delta \phi$ region, making it closer to KS gluon result.

The results shown in Figs. 9 and 10 are natural, as back-to-back configuration in the respective observable corresponds to the small-$k_T$ region of gluon densities and, as it can be seen clearly in Fig. 5, the GBW and BGK gluons do not fare well in the large-$k_T$ region. That is to say that the enhancement in the small-$\Delta \phi$ region is a direct consequence of the broadening by the Sudakov factor.

5 Summary

We have fitted the GBW and BGK saturation models to HERA data [33] using the $k_T$-factorization for the structure function $F_2$. The main difference between the $k_T$-and the dipole factorizations is an argument of the gluon, x/z, appearing in the former and being replaced by $x\,(1+4m_f^2/Q^2)$ in the latter. In fact, the massive light quarks used in Ref. [27] partially simulate the factor 1/z, and our fit result indicates such effect, as expected.

We found that the dipole factorization can reproduce the result of the $k_T$-factorization formula quite well. The only major difference is in the normalization parameter $\sigma _0$, which increases significantly for the $k_T$-factorization case. We argued that this change is a direct consequences of the kinematic approximation used in the dipole factorization formula. We have also observed that the explicit inclusion of the running coupling in the GBW model has a significant effect on fit quality, particularly in the large-$Q^2$ region, where the GBW model performs poorly.

We have applied the new results from our fits to description of the transverse momentum spectra of the dijet processes in DIS at HERA. The description of the data is fairly good with all used models. However, the best results are obtained within the $k_T$-BGK model with the Sudakov form factor, indicating the relevance of exact kinematics, DGLAP corrections, and resummation.

Furthermore, we provided predictions for dijet production at the EIC. Results of the electron-jets correlation in the Breit frame agrees qualitatively with those of Ref. [41]. Other results, namely the electron-jets in the Lab frame and the jet-jet correlation in the Breit frame, shows considerable effects of the Sudakov form factor, which broadens the gluon density.

Appendix: \(I_i\) in Eq. (7)

The functions $I_1,\, I_2,\, I_3,\, I_4$ used in Eq. (7) are defined as [44]

$$\begin{aligned} \frac{I_1}{2\pi }= & {} \frac{N_1N_2+N_3^2}{\left( N^2_1+2N_1N_2+N_3^2\right) ^{3/2}}, \nonumber \\ \frac{I_2}{2\pi }= & {} \frac{N_3-(1-2\beta )N_1}{(N_1+N_4)\sqrt{ N^2_1+2N_1N_2+N_3^2}},\nonumber \\ \frac{I_3}{2\pi }= & {} \frac{N_1+N_2}{\left( N^2_1+2N_1N_2+N_3^2\right) ^{3/2}},\nonumber \\ \frac{I_4}{2\pi }= & {} \frac{2(1-\beta )}{(N_1+N_4)\sqrt{ N^2_1+2N_1N_2+N_3^2}}, \end{aligned}$$

(26)

for

$$\begin{aligned} N_1\equiv & {} \beta (1-\beta )Q^2+m_f^2,\nonumber \\ N_2\equiv & {} {\kappa '}_T^2+(1-\beta )^2k_T^2,\nonumber \\ N_3\equiv & {} {\kappa '}_T^2-(1-\beta )^2k_T^2, \nonumber \\ N_4\equiv & {} {\kappa '}_T^2+\beta (1-\beta )k_T^2. \end{aligned}$$

(27)