Impact of a newly parametrized deceleration parameter on the accelerating universe and the reconstruction of f(Q) non-metric gravity models

Abstract

This article presents a novel parametrization of the deceleration parameter (DP) to investigate the cosmological scenario. The newly proposed parametric form of the DP is both physically plausible and model-independent. Constrained by a combined dataset of 31 cosmic chronometers (CC) data points, 26 non-correlated baryonic acoustic oscillations (BAO) points, and 1701 Pantheon$+$ data points from supernovae type Ia (SNeIa), we determine the model parameters using a Markov Chain Monte Carlo (MCMC) method. The analysis explores the kinematic behavior of the model, including the transition from deceleration to acceleration. The results indicate that the Universe is currently in an accelerated phase. Furthermore, we apply the obtained parameter values to constrain f(Q) gravity models and compare them with observations. This study provides valuable insights into the accelerating Universe and underscores the importance of employing a model-independent approach in cosmological investigations.

1 Introduction

The $\Lambda$CDM model is a fundamental framework in cosmology, explaining various observations with minimal parameters. However, recent studies [1] expose its limitations, challenging its reliability, including fine-tuning the cosmological constant and tensions between model predictions and observations [2,3,4]. While still important, the model requires refinement to overcome its shortcomings. Recently, studies are exploring alternative frameworks, modifying General Relativity or introducing new fields, to build on $\Lambda$CDM’s success while addressing its limitations.

In light of these considerations, a new approach known as “reconstruction” has emerged as a response, whereby observational data is directly incorporated into the process of constructing cosmological models. This approach holds significant promise in enriching our understanding of the Universe and enhancing the accuracy and efficiency of future cosmological surveys.

The reconstruction approach offers the key advantage of being independent of the specific gravity model underlying cosmological studies. It encompasses two methods: non-parametric reconstruction, which involves deriving models directly from observational data through statistical procedures, and parametric reconstruction, which establishes a kinematic model with free parameters and subsequently constrains these parameters through statistical analysis of observational data. The parametric reconstruction approach has been successfully employed in studying the accelerating Universe through various cosmological entities, including the jerk parameter, the deceleration parameter (DP), and the Hubble parameter, shedding light on the behavior of dark energy. Also, numerous works have focused on parametrizing physical parameters, such as pressure, energy density, and EoS. These parametrizations aid in obtaining precise solutions to the Einstein field equations (see [5,6,7,8,9,10,11,12,13,14]).

Furthermore, the remarkable observations from cosmological surveys, including those by Riess et al. [15] and Perlmutter et al. [16], have confirmed the current acceleration of the Universe’s expansion following a period of deceleration characterized by structure formation. The DP is a vital quantity in explaining this phenomenon, and parametrizing it offers an appropriate approach compared to other kinematic quantities. Several works have proposed parametrizations of the DP [12,13,14, 17, 18] (one can see the references therein). In addition, more prominently, the redshift-based DP is advantageous as it directly relates to the Universe’s expansion rate and facilitates comparisons among different observational datasets.

Additionally, in recent years, significant attention has been given to modified gravity theories such as f(R), f(T), and f(Q) theories. One innovative approach to exploring gravitational interactions is through non-metricity, where both curvature and torsion vanish. This approach is valuable for understanding gravity at a fundamental level, as it treats gravity as a gauge theory without presuming the preeminence of the Equivalence Principle. Investigating f(Q) theories can provide insights into the cosmic acceleration resulting from different geometries compared to Riemannian geometry. The connection between the disformation tensor and the Levi–Civita connection in f(Q) gravity highlights the intricate interplay between non-metricity and the geometry of spacetime. Ongoing research aims to explore the consequences and potential applications of f(Q) gravity in deepening our understanding of the fundamental nature of gravity and its effects on the large-scale structure of the universe. In the literature, one can see several prominent studies on f(Q) gravity [19,20,21,22,23].

In this study, we propose a newly reconstructed form of the deceleration parameter that aligns with both physical considerations and theoretical arguments. This parameterization is independent of the specific gravity model. The free parameters are constrained via statistical analysis of observational data using the Bayesian approach and Markov Chain Monte Carlo (MCMC) analysis. Specifically, we utilize data sets including Cosmic Chronometers, Baryonic Acoustic Oscillations, and the latest $\hbox {Pantheon}^+$ dataset. Based on these constraints, we study the kinematics of the model. More interestingly, with these obtained parameters, we constrain f(Q) gravity models and compare the results with observational data.

Article organization: The basic field equations in f(Q) gravity are discussed in Sect. 2. The newly proposed parameterization and its characteristics are explained in Sect. 3. The detailed statistical analysis of the data sets is given in Sects. 4 and 5. Further, using the results obtained from the statistical method, we interpret the behavior of the Universe for our newly defined DP model in Sect. 6. With the obtained parameter values we constrain f(Q) gravity models in Sect. 7. Finally, we conclude our results in Sect. 8.

2 The basic field equations in gravity

A general affine connection can be written in terms of three components, namely, the Levi–Civita connection, the contorsion tensor, and the disformation tensor. The Levi–Civita connection is a unique connection that is derived from the metric tensor of the space. It has the property that it is torsion-free, which means that the derivative of a vector field along a curve depends only on the endpoints of the curve. The Levi–Civita connection $\Gamma ^\alpha _{\mu \nu }$ of the metric $g_{\mu \nu }$ is defined by

$$\begin{aligned} \Gamma ^\alpha _{\mu \nu }=\frac{1}{2}g^{\alpha \lambda }(g_{\mu \lambda ,\nu }+g_{\lambda \nu ,\mu }-g_{\mu \nu ,\lambda }). \end{aligned}$$

(1)

The contortion tensor $K^\alpha _{\mu \nu }$ is a tensor field that describes the deviation of a given affine connection from the Levi–Civita connection. It is defined as

$$\begin{aligned} K^\alpha _{\;\;\mu \nu }=\frac{1}{2}(T^\alpha _{\;\;\mu \nu } +T_{\mu \;\;\nu }^{\;\;\alpha }-T_{\nu \;\;\mu }^{\;\;\alpha }). \end{aligned}$$

(2)

where $T^\alpha _{\;\;\mu \nu }$ is the torsion tensor given by

$$\begin{aligned} T^\alpha _{\;\;\mu \nu }=Y^\alpha _{\;\;\mu \nu }-Y^\alpha _{\;\;\nu \mu }. \end{aligned}$$

(3)

The disformation tensor $L^\alpha _{\;\;\mu \nu }$ is a tensor field that describes the deviation of the metric tensor from its Euclidean form. It is defined as

$$\begin{aligned} L^\alpha _{\;\;\mu \nu }=\frac{1}{2}(Q^\alpha _{\;\;\mu \nu } +Q_{\mu \;\;\nu }^{\;\;\alpha }-Q_{\nu \;\;\mu }^{\;\;\alpha }), \end{aligned}$$

(4)

where the non-metricity tensor $Q_{\alpha \mu \nu }$ is defined by $Q_{\alpha \mu \nu }=\nabla _\alpha g_{\mu \nu }$.

Putting these components together, the general affine connection $Y^\alpha _{\mu \nu }$ can be written in the form

$$\begin{aligned} Y^\alpha _{\;\;\mu \nu }=\Gamma ^\alpha _{\;\;\mu \nu } +L^\alpha _{\;\;\mu \nu }+K^\alpha _{\;\;\mu \nu }. \end{aligned}$$

(5)

This form of the affine connection allows for a more general description of the geometry of a curved space than the Levi–Civita connection alone, and it is used in modified gravity theories where the deviation from General Relativity is described by the contorsion and disformation tensors.

Recently, a research paper by Jimenez et al. [24] introduced a novel approach to gravity known as f(Q) gravity. This theory is distinctive as it is solely defined by the non-metricity $\nabla _\alpha g_{\mu \nu }\ne 0$ of the spacetime, where both curvature and torsion vanish and $Y^\alpha _{\;\;\mu \nu }=0$. One noteworthy result in f(Q) gravity is the equivalence between the disformation tensor and the Levi–Civita connection, albeit with a sign change:

$$\begin{aligned} L^\alpha _{\;\;\mu \nu }=-\Gamma ^\alpha _{\;\;\mu \nu }. \end{aligned}$$

(6)

This finding implies a direct relationship between the disformation tensor, which characterizes the deviation of the metric tensor from its Euclidean form, and the Levi–Civita connection derived from the metric tensor.

In f(Q) gravity, the gravitational interactions are described by the following action:

$$\begin{aligned} S=\int \left[ -\frac{1}{2}f(Q)+{\mathcal {L}}_m\right] \sqrt{-g}d^4x, \end{aligned}$$

(7)

where g represents the determinant of the metric $g_{\mu \nu }$, $L_m$ denotes the matter Lagrangian, and f(Q) is an arbitrary function of Q. Here, we assume the natural units $k^2=8\pi G=1$. The selection of the non-metricity scalar and the action described above in f(Q) gravity is motivated by the desire to reproduce General Relativity (GR) in a certain limit [24]. Specifically, when the function f is chosen as $f=Q$, the action (7) yields, up to a boundary term, the so-called Symmetric Teleparallel Equivalent of GR (STEGR) which is known to be equivalent to GR in the classical regime, albeit with some differences in the mathematical formalism. This classical correspondence with GR provides a significant motivation for this particular choice. This allows for a seamless transition between the two theories and ensures that f(Q) gravity remains consistent with the well-established framework of GR. The action in Eq. (7) incorporates both the gravitational and matter sectors, where the former is described by the function f(Q) and the latter by the matter Lagrangian $L_m$.

The non-metricity of the spacetime is characterized by two independent traces, given by:

$$\begin{aligned} Q_\alpha =Q_{\alpha \;\;\nu }^{\;\;\nu }\text { and } \tilde{Q}_\alpha =Q^{\nu }_{\;\;\alpha \nu }. \end{aligned}$$

(8)

In accordance with the work by [24], the conjugate of non-metricity is defined as:

$$\begin{aligned} 4P^\alpha _{\;\;\mu \nu }=-Q^\alpha _{\;\;\mu \nu } +2Q^{\;\;\;\alpha }_{(\mu \;\;\nu )}+(Q^\alpha -\tilde{Q}^\alpha )g_{\mu \nu }-\delta ^\alpha _{(\mu }Q_{\nu )}. \nonumber \\ \end{aligned}$$

(9)

Using this definition, the non-metricity scalar is further defined as $Q=-Q_{\alpha \mu \nu } P^{\alpha \mu \nu }$.

The energy–momentum tensor, denoted as ${\mathcal {T}}_{\mu \nu }$, is a fundamental quantity in the study of gravitational interactions. It characterizes the distribution and flow of energy and momentum within a given system. In the context of general relativity and curved spacetime, the energy–momentum tensor is derived from the matter Lagrangian, denoted as ${\mathcal {L}}_m$.

The expression for the energy–momentum tensor is given by:

$$\begin{aligned} {\mathcal {T}}_{\mu \nu }=-\dfrac{2}{\sqrt{-g}} \dfrac{\delta (\sqrt{-g}{\mathcal {L}}_m)}{\delta g^{\mu \nu }}, \end{aligned}$$

(10)

where $\delta (\sqrt{-g}{\mathcal {L}}_m)/\delta g^{\mu \nu }$ represents the functional derivative of the Lagrangian with respect to the metric tensor components $g^{\mu \nu }$. The functional derivative captures how the Lagrangian varies as a result of infinitesimal changes in the metric tensor. The field equation for f(Q) gravity, which describes the gravitational dynamics in this modified theory, can be obtained by varying the action integral (7) with respect to the metric tensor $g_{\mu \nu }$. The resulting equation is given by:

$$\begin{aligned} \begin{aligned}&f_Q(P_{\mu \beta \gamma }Q_{\nu }^{\;\;\beta \gamma } -2Q_{\beta \gamma \mu }P^{\beta \gamma }_{\;\;\;\;\;\nu })+\frac{1}{2}g_{\mu \nu }f\\&\quad +\frac{2}{\sqrt{-g}}\nabla _\alpha (\sqrt{-g}f_Q P^\alpha _{\;\;\mu \nu }) ={\mathcal {T}}_{\mu \nu }, \end{aligned}\nonumber \\ \end{aligned}$$

(11)

where $f_Q$ represents the partial derivative of the function f with respect to Q. These field equations play a fundamental role in f(Q) gravity, governing the behavior of the metric tensor and the connection. They establish the relationship between the non-metricity of spacetime, the matter-energy distribution encoded in the energy–momentum tensor ${\mathcal {T}}_{\mu \nu }$, and the functional form of f(Q). In addition to varying the action with respect to the metric tensor, we can also vary it with respect to the connection. This variation yields the equation:

$$\begin{aligned} \nabla _\mu \nabla _\nu (\sqrt{-g}f_Q P^{\mu \nu }_{\;\;\;\;\;\gamma })=0. \end{aligned}$$

(12)

2.1 The cosmological model

To investigate the evolution of the universe, it is often useful to make the assumption that the background spacetime is isotropic and homogeneous. This assumption allows us to employ the Friedmann–Lemaitre–Robertson–Walker (FLRW) metric, which describes a homogeneous and isotropic universe. In the case of an isotropic and homogeneous universe, we specifically consider the flat FLRW metric, given by:

$$\begin{aligned} ds^2=-dt^2+a^2(t)(dx^2+dy^2+dz^2), \end{aligned}$$

(13)

where a(t) is the scale factor that quantifies the size of the expanding universe and is related to the Hubble parameter as $H=\frac{{\dot{a}}}{a}$. Here, overhead dot indicates derivative with cosmic time t and the same convention is used throughout the article. This framework allows us to study the behavior of cosmological models, analyze the dynamics of matter and energy within the universe, and investigate phenomena such as cosmic expansion, the age of the universe, and the behavior of different components like dark matter and dark energy. In this case, the non-metricity scalar is given by $Q = 6H^2$.

By employing the FLRW metric, the equations governing the dynamics of the universe can be derived. These equations are known as the cosmological equations of motion. In this context, the cosmological equations of motion are given by:

$$\begin{aligned} 6f_{Q} H^2-\frac{1}{2}f= & {} \rho , \end{aligned}$$

(14)

$$\begin{aligned} {\dot{H}}(12 f_{QQ}H^2+f_{Q})= & {} -\frac{1}{2}(\rho + p). \end{aligned}$$

(15)

Here, $f_{Q}$ represents the first derivative of the function f partially with respect to Q, while $f_{QQ}$ denotes the second partial derivative. The variables $\rho$ and p correspond to the energy density and pressure of the matter fluid, respectively. In the absence of any interaction, the conservation equation ${\dot{\rho }}+3H(\rho + p)=0$ holds true, ensuring consistency with the aforementioned cosmological equations. To provide a more familiar form, these cosmological equations can be written in the standard Friedman equations format:

$$\begin{aligned}{} & {} 3H^2=\rho _{eff}, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} 2{\dot{H}}+3H^2=-p_{eff}, \end{aligned}$$

(17)

by defining the effective pressure $p_{eff}$ and effective density $\rho _{eff}$ of the total fluid as

$$\begin{aligned} \rho _{eff}= & {} \frac{1}{2f_Q}\left( \frac{f}{2}+\rho \right) , \end{aligned}$$

(18)

$$\begin{aligned} p_{eff}= & {} \frac{1}{f_Q}\left( p-\frac{f}{2}+3H^2(f_Q+8{\dot{H}} f_{QQ}) \right) . \end{aligned}$$

(19)

An important quantity of interest is the effective equation of state (EoS), denoted as $\omega _{eff}$. It is defined as the ratio of the effective pressure $p_{eff}$ to the effective density $\rho _{eff}$:

$$\begin{aligned} \omega _{eff}=\frac{p_{eff}}{\rho _{eff}}=\frac{4p-2f +12H^2(f_Q+8{\dot{H}}f_{QQ})}{f+2\rho }. \end{aligned}$$

(20)

The value of $\omega _{eff}$ in f(Q) gravity can play a significant role in addressing issues related to dark energy (DE). It allows for the investigation of the nature of DE and its impact on the expansion of the universe. It is worth noting that for an accelerating universe, one requires $\omega _{eff} < -\frac{1}{3}$. These equations provide a comprehensive framework for studying the behavior of the universe within the context of f(Q) gravity. They offer insights into the effective energy density, pressure, and equation of state, which play essential roles in understanding the dynamics and properties of dark energy.

3 New parametrization of deceleration parameter

The deceleration parameter (q) plays a fundamental role in characterizing the evolution of the homogeneous and isotropic cosmos, making it a crucial parameter in cosmology. It is directly associated with the second time derivative of the scale factor in the FLRW metric and can be expressed as:

$$\begin{aligned} q=-\frac{\ddot{a}}{H^2a}=-\left( \frac{{\dot{H}}}{H^2}+1\right) . \end{aligned}$$

(21)

The DP provides insight into the rate at which the Universe’s expansion is accelerating or decelerating. A positive value of q indicates a decelerating expansion, while a negative value signifies an accelerating expansion. The relationship between the Hubble parameter and the DP is given by:

$$\begin{aligned} H(z)=H_0 \exp \left( \int _0^z (q(\xi )+1)d\ln (\xi +1)\right) , \end{aligned}$$

(22)

where $H_0$ denotes the value of the Hubble parameter at $z=0$, and z represents the redshift, which is related to the scale factor a through $z=-1+\frac{1}{a}$.

The choice of a specific parametric form for the DP q(z) allows us to investigate various cosmological models and explore the properties of dark energy and modified gravity theories. The DP plays a crucial role in understanding the dynamics of the Universe, and therefore, several authors have proposed parametrized forms of q(z) based on practical and theoretical considerations, as discussed in the introduction. It is important to note that different parametric forms of q(z) have different ranges of applicability. Some parametrizations work well when the redshift z is much smaller than 1 ($z \ll 1$), while others may not accurately predict the future evolution of the Universe. Ideally, the chosen parametric form should be valid and predictive for all ranges of redshifts, encompassing both the early and late stages of the Universe’s evolution. This ensures that the parametrization captures the full dynamics and behavior of dark energy and provides reliable insights into the expansion history of the Universe.

The parametrization of the DP offers several advantages over other kinematic models, making it a valuable tool for studying the dynamics of the universe. The DP provides a direct physical interpretation, allowing us to understand the formation and evolution of cosmic structures. By choosing a suitable form for q(z), we can capture the behavior of cosmic expansion across different epochs, shedding light on the intricate processes involved in the growth of large-scale structures. Crucially, the DP must approach 1/2 at high redshifts to meet the requirements of cosmic structure formation, ensuring that the universe undergoes the necessary deceleration for structures to develop over cosmic timescales. The adherence of the universe to the second law of thermodynamics is another important aspect that the parametrization of q(z) can address. The second law imposes constraints on the dynamics of the universe, and incorporating thermodynamic considerations into the parametrization allows us to satisfy these constraints. One such constraint is that the Friedmann–Lemaître–Robertson–Walker (FLRW) universe approaches thermodynamic equilibrium in the distant future, ensuring the consistency of the cosmological model. By incorporating these thermodynamic aspects, we can refine the parametrization of q(z) and ensure its adherence to the underlying principles of thermodynamics. Moreover, the parametrization of q(z) offers predictive power, enabling us to accurately describe the past and present cosmic expansion and make reliable predictions about the future evolution of the universe. By carefully selecting an appropriate parametric form, we can extrapolate the behavior of q(z) beyond the range of observed redshifts, providing insights into the long-term fate of the universe. This predictive capability is particularly valuable in understanding whether the cosmic expansion will continue to accelerate, decelerate, or undergo a transition to a different regime in the future.

Considering the factors discussed above, we propose a new parametric expression for the DP q(z) that satisfy several important criteria. Firstly, we ensure that q(z) remains finite for all redshifts within the range $z\in [-1,\infty ]$. This condition guarantees that the parametrized form remains well-defined and applicable across a wide range of cosmic epochs. Additionally, we impose the requirement that $q(z)\ge -1$ for all $z\in [-1,\infty ]$, $q(z)\rightarrow -1$ and $dq/dz>0$ as $z\rightarrow -1$ indicating that the FLRW universe approaches thermodynamic equilibrium in the distant future, as discussed in a previous study by Campo et al. [17] and Capozziello et al. [6]. To ensure an effective and reliable analysis, we focus on just two parameters, motivated by the challenges of higher-dimensional spaces and the potential for degeneracies that hinder parameter determination and increase uncertainties. Exploring high-dimensional spaces becomes computationally demanding and time-consuming, while a smaller parameter space enables more efficient sampling and convergence checks. Taking into account these considerations, we introduce a parametrized model for the DP q(z) as given by the expression:

$$\begin{aligned} q(z)=-1+a\left( \frac{(1+z)^3}{z^3+5z^2+b}\right) , \end{aligned}$$

(23)

where a and b are model parameters. These parameters control the shape and behavior of the DP and allow for customization based on specific cosmological scenarios. By adopting this parametric forms for q(z), we meet the requirements of finiteness, positivity of $q(z)+1$, and convergence of FLRW universe to thermodynamic equilibrium in the distant future. The next step involves comparing these parametric expressions with observational data to determine the best-fit values for the model parameters and assess their agreement with empirical evidence. This analysis will provide insights into the dynamics and future evolution of the Universe within the framework of this parametrized model.

It is important to note that the cubic polynomial $z^3+5z^2+b$ exhibits distinct root characteristics depending on the value of b. When $b>0$, the polynomial will possess one negative root (which is less than -5) and two complex roots. On the other hand, when $b<0$, it can have at most one positive real root. Consequently, when $b>0$, we observe that the equation $z^3+5z^2+b\ne 0$ holds true for any $z\in [-1,\infty )$. In order to ensure the finite nature of the DP across all redshifts, it becomes necessary to impose the condition $b>0$ in the parametric form. By adhering to this condition, we guarantee that the DP remains free from divergences, thereby upholding the validity of the model throughout the entire range of redshifts. This provides a solid foundation for using this parametrized model to analyze and interpret observational data on the expansion history of the Universe.

4 Observational data and methodology

In order to build a cosmological model that accurately describes the behavior of our Universe, it is crucial to rely on robust observational data and employ appropriate methodologies for parameter estimation. In this section, we outline the observational data sets used and the methodology adopted to constrain the model parameters a, b, and $H_0$. The data utilized in this analysis consists of cosmic chronometers (CC), baryonic acoustic oscillations (BAO), and the Pantheon$+$ sample derived from observations of Supernovae type Ia (SNeIa). By leveraging these diverse and complementary data sets, we can effectively constrain the model parameters a and b, enabling a comprehensive analysis of the Universe’s evolution and providing valuable insights into its underlying dynamics and properties.

4.1 Cosmic chronometers (CC)

The CC method plays a crucial role in measuring the Hubble rate by utilizing ancient and slowly evolving galaxies that are separated by a small interval of redshift. This method employs the concept of differential aging, which involves measuring the difference in ages of these galaxies at different redshifts. By utilizing the definition of the Hubble rate within an FLRW metric, given by $H=-\frac{1}{1+z}\frac{dz}{dt}$, the CC method enables the measurement of the Hubble parameter H(z) independently of any specific cosmological assumptions. This attribute makes CC a powerful tool for testing cosmological models, as it provides an independent measurement of the Universe’s expansion rate.

In our study, we have collected a comprehensive set of 31 data points from various sources [25,26,27,28,29,30,31,32] using the cosmic chronometers (CC) method. These data points span a wide range of redshifts, from 0.1 to 2, allowing for a detailed analysis of the expansion history of the Universe. To perform the Markov Chain Monte Carlo (MCMC) analysis, we employ the chi-square function for the cosmic chronometers, given by:

$$\begin{aligned} \chi ^2_{CC}(\Theta )=\sum _{i=1}^{31}\left[ \frac{(H_{th} (z_i,\Theta )-H_{obs}(z_i))^2)}{\sigma _H^2(z_i)}\right] . \end{aligned}$$

(24)

Here, $H_{th}$ represents the theoretical value of the Hubble parameter for a specific model with model parameters $\Theta$, while $H_{obs}$ represents the corresponding observed Hubble parameter. The term $\sigma _H$ represents the error associated with the observed value of H at each redshift $z_i$.

4.2 Baryonic acoustic oscillations (BAO)

Baryonic Acoustic Oscillations (BAO) serve as a significant cosmological probe for studying the large-scale structure of the Universe. These oscillations originate from acoustic waves in the early Universe, which compress baryonic matter and radiation in the photon-baryon fluid. This compression leads to a distinctive peak in the correlation function of galaxies or quasars, providing a standard ruler for measuring cosmic distances. The comoving size of the BAO peak is determined by the sound horizon at the time of recombination, which relies on the baryon density and the temperature of the cosmic microwave background.

At a given redshift z, the position of the BAO peak in the angular direction determines the angular separation $\Delta \theta = r_d/((1+z)D_A(z))$, while in the radial direction, it determines the redshift separation $\Delta z=r_d/D_H(z)$. Here, $D_A$ represents the angular distance, $D_H = c/H$ corresponds to the Hubble distance, and $r_d$ denotes the sound horizon at the drag epoch. By accurately measuring the position of the BAO peak at different redshifts, we can constrain combinations of cosmological parameters that determine $D_H/r_d$ and $D_A/r_d$. By selecting an appropriate value for $r_d$, we can estimate H(z). In this study, we employ a dataset comprising 26 non-correlated data points obtained from line-of-sight BAO measurements [33,34,35,36,37,38,39,40,41,42,43,44].

Similar to the cosmic chronometers (CC) method, the BAO data is incorporated into the analysis through the computation of the chi-square function,

$$\begin{aligned} \chi ^2_{BAO}(\Theta )=\sum _{i=1}^{26}\left[ \frac{(H_{th} (z_i,\Theta )-H_{obs}^{BAO}(z_i))^2)}{\sigma _H^2(z_i)}\right] , \end{aligned}$$

(25)

where $H_{th}$ represents the theoretical values of the Hubble parameter for a specific model with model parameters $\Theta$. On the other hand, $H_{obs}^{BAO}$ corresponds to the observed Hubble parameter obtained from the BAO method, and $\sigma _H$ denotes the error associated with the observed values of $H^{BAO}$.

For the CC and BAO dataset, the total chi-square function, $\chi ^2_T$, is defined as the sum of the individual chi-square functions:

$$\begin{aligned} \chi ^2_T=\chi ^2_{CC}+\chi ^2_{BAO}. \end{aligned}$$

(26)

The combined analysis allows for a more comprehensive constraint on the model parameters a, b, and $H_0$ by incorporating complementary information from both cosmic chronometers and baryonic acoustic oscillations.

4.3 Pantheon$+$ (SNeIa)

The Pantheon$+$ dataset contains distance moduli estimated from 1701 light curves of 1550 SNeIa with a redshift range of $0.001\le z\le 2.2613$, acquired from 18 distinct surveys. Notably, 77 of the 1701 light curves are associated with Cepheid-containing galaxies. Pantheon$+$ has the benefit of being able to constrain $H_0$ in addition to the model parameters. We extremize the $\chi ^2$ function as shown below to fit the parameter of the model from the Pantheon$+$ samples.

$$\begin{aligned} \chi ^2_{SNeIa}= \Delta \mu ^T (C_{stat+sys}^{-1})\Delta \mu , \end{aligned}$$

(27)

where $C_{stat+sys}$ is the covariance matrix of Pantheon$+$ dataset formed by adding the systematic and statistic uncertainties and $\Delta \mu$ is the distance residual given by

$$\begin{aligned} \Delta \mu _i=\mu _i-\mu _{th}(z_i), \end{aligned}$$

(28)

where $\mu _i$ is the distance modulus of the ith SNeIa. Note that $\mu _i=m_{Bi}-M$, where $m_{Bi}$ is the apparent magnitude of ith SNeIa and M is fiducial magnitude of an SNeIa. The theoretical distance modulus $\mu _{th}$ can be calculated from the following expression

$$\begin{aligned} \mu ^{th}(z,\Theta )=5\log _{10}\left( \frac{d_L(z,\Theta )}{1Mpc} \right) +25, \end{aligned}$$

(29)

where $d_L$ is the model-based luminosity distance in Mpc given by

$$\begin{aligned} d_L(z,\Theta )=\frac{c(1+z)}{H_0}\int _0^z \frac{d\xi }{E(\xi )}, \end{aligned}$$

(30)

where c is the speed of light and $E(z)=\frac{H(z)}{H_0}$.

When analyzing SNeIa data alone, there exists a degeneracy between the parameters $H_0$ and M. To address this issue, a modification is made to the SNeIa distance residuals presented in Eq. (27) as shown in previous studies [45, 48]. Specifically, the modified residuals $\Delta \tilde{\mu }$ are defined as:

$$\begin{aligned} \Delta \tilde{\mu }={\left\{ \begin{array}{ll} \mu _i-\mu _i^{Ceph}, &{} \quad \text {if }i\in \text { Cephied hosts}\\ \mu _i-\mu _{th}(z_i), &{} \quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(31)

where $\mu _i^{Ceph}$ indicates Cepheid host of the ith SNeIa which is provided by SH0ES. It is to be noted that $\mu _i-\mu _i^{Ceph}$ is sensitive to the Hubble constant $H_0$ and M. In our analysis, we take $M=-19.253$ which has been determined from SH0ES Cepheid host distances (see [49]).

For a comprehensive analysis incorporating the CC, BAO, and SNeIa datasets, we combine the individual $\chi ^2$ functions to obtain the total $\chi ^2_{\text {tot}}$ function:

$$\begin{aligned} \chi ^2_{\text {tot}}=\chi ^2_{CC}+\chi ^2_{BAO}+\chi ^2_{SNeIa}. \end{aligned}$$

(32)

To determine the best-fit parameters of our cosmological model, we adopt the approach of minimizing the $\chi ^2$ function. It is important to note that minimizing the $\chi ^2$ is equivalent to maximizing the likelihood, which in turn is equivalent to minimizing the negative log-likelihood. In order to obtain numerical constraints on the model parameters, we employ the Markov Chain Monte Carlo (MCMC) sampling method. This approach allows us to explore the parameter space and obtain a statistical distribution of the parameter values that are consistent with the observational constraints. In our analysis, we utilize the widely-used MCMC package called emcee [50], which provides efficient and reliable sampling techniques.

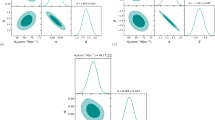
The results of our analysis are presented in the form of contour plots, which illustrate the joint constraints on the model parameters. These contour plots depict regions in the parameter space that are consistent with the observational data at different confidence levels. In particular, we present the contours up to $3\sigma$ ($99.7\%$) confidence level, indicating the regions where the model is in good agreement with the observed data.

5 Observational constraints

The dynamics of the Universe can be better understood with the help of cosmological surveys and observational data. In order to derive physically meaningful parameter space for the free parameters, statistical analysis of the observed datasets is performed in the context of parametric reconstruction. In the previous section, we discussed various observational data sets that were used for the analysis. In this section, we will use these datasets to constrain the model parameters a, b, and $H_0$ for the parametrization of DP presented earlier. Furthermore, we will attempt to reconstruct the DP q by finding the best-fit parameter values. To achieve this, we will use the expression of DP (23) and numerically compute the Hubble parameter using equation (22), where $H_0$ is also a free parameter.

The MCMC method is employed for the analysis, and the results are presented in the form of contour plots in Fig. 1. These contour plots illustrate regions in the parameter space that are consistent with the observational data at various confidence levels. Specifically, we present the contours up to $3\sigma$ ($99.7\%$) confidence level, indicating the regions where the model agrees well with the observed data. Based on our analysis, the mean values of the model parameters a, b, and $H_0$ are determined to be $1.513^{+0.073}_{-0.073}$, $5.04^{+0.44}_{-0.37}$, and $74.43^{+0.18}_{-0.18}$ (with 1$\sigma$ error), respectively. Notably, the obtained value of $a=1.513^{+0.073}_{-0.073}$ leads to an interesting consequence. At high redshifts, the DP approaches nearly 1/2, which is significant for the cosmic structure formation. This finding suggests that the universe undergoes the necessary deceleration required for the development of cosmic structures over vast timescales. The agreement between the obtained value of a and the requirements for cosmic structure formation further strengthens the consistency of our model with observational data.

Fig. 1

2D-contour plot of the model parameters a, b, and $H_0$, indicating the most likely values and confidence regions upto $3\sigma$ obtained from the combined analysis of CC, BAO and SNeIa datasets

In Fig. 3a, we present the observed data on H(z), accompanied by error bars, as well as the best-fit theoretical curves represented by a red line. The shaded regions in blue indicate $1\sigma$, $2\sigma$, and $3\sigma$ error bands of the Hubble function H(z). The agreement between the model predictions and the observed data is evident from the consistency of the error bars with the shaded regions. This visual representation confirms the accuracy of our model in capturing the observed behavior of the Hubble function. Furthermore, in Fig. 3b, we display the error plot of the distance modulus. The observed distance modulus of the 1701 SNeIa dataset is depicted, along with the best-fit theoretical curves of the distance modulus function $\mu (z)$ shown as a red line. The blue shaded regions correspond to the error bands at a confidence level of up to 99.7%. The consistency observed in these plots further strengthens the confidence in the reliability of our results.

Table 1 Results of MCMC for parameters a, b and $H_0$ (km/s/Mpc) with $1\sigma$-$3\sigma$ errors

Fig. 2

A plot illustrating the current values of $H_0$ along with their corresponding error bars obtained from various studies is presented. The orange-red shaded strips represent the $H_0$ value with $1\sigma$, $2\sigma$, and $3\sigma$ errors obtained in this work

Fig. 3

Comparison of the obtained best-fit theoretical curves (red line) of the Hubble function H(z) and distance modulus function $\mu (z)$ with their corresponding $1\sigma$, $2\sigma$, and $3\sigma$ error bands (blue shaded regions) against the $\Lambda$CDM model (orange dotted line) with $\Omega _\Lambda =0.7$, $\Omega _m=0.3$, and $H_0=67.8$ km s$^{-1}$ Mpc$^{-1}$

In addition to analyzing the model parameters, we have successfully constrained the present value of the Hubble parameter $H_0$. Utilizing the combined CC+BAO+SNeIa dataset, we determine the value of $H_0$ to be $74.43^{+0.18}_{-0.18}$ $km\,s^{-1}Mpc^{-1}$, accompanied by a 1-$\sigma$ error. The results of this constrained $H_0$ value are presented in Fig. 2, where we compare our findings with the outcomes of previous studies.

6 Dynamics of the model

The dynamics of a cosmological model provide valuable insights into the behavior and evolution of the Universe. In this section, we explore the dynamics of our model through three key aspects: the transition from a deceleration to an acceleration phase, the analysis of the jerk parameter, and the examination of the Om diagnostics. Each of these subsections sheds light on different aspects of the model’s behavior and helps us better understand the underlying dynamics of the Universe. By studying these aspects, we gain a deeper understanding of the fundamental processes that govern the expansion and evolution of our Universe.

Fig. 4

Deceleration parameters as a function of redshift for proposed parametric model, obtained from the combined CC, BAO, and SNeIa datasets, with shaded zones representing $68\%$, $95\%$, and $99.7\%$ confidence levels

Table 2 Summary of the results for DP, effective EoS, $z_t$, and jerk parameter obtained from constrained values of model parameter with $1\sigma$-$3\sigma$ errors

6.1 Transition from deceleration to acceleration phase

The transition from a deceleration to an acceleration phase holds significant importance in understanding the dynamics of the Universe. Prior to this transition, the Universe was characterized by a decelerating expansion, driven by the gravitational interaction between matter and radiation. However, as the cosmos continued to expand and matter became more dispersed, the gravitational force gradually weakened, leading to a shift in the cosmic dynamics. This transition marks a turning point in the evolution of the Universe, as it entered a phase of cosmic acceleration. The current accelerating action of the Universe can be quantified by estimating negative values of the DP. Exploring this transition is essential for comprehending the underlying mechanisms driving the expansion and evolution of the cosmos. By studying the transition from deceleration to acceleration, we gain valuable insights into the dynamic nature of our Universe.

In Fig. 4, we present the results, showcasing three DP curves accompanied by their corresponding $1\sigma$, $2\sigma$, and $3\sigma$ error bands. The displayed curves clearly depict a transition of the Universe from a decelerating phase to an accelerating phase. Notably, we observe that the occurrence of this phase transition is influenced by the variations in the model parameters a and b. The specific redshift value at which the transition takes place is determined as $z_t = 0.789^{+0.186}_{-0.165}$, based on the constrained parameters derived from the combined CC+BAO+SNeIa dataset, with a $1-\sigma$ error. Remarkably, these values align with those reported by several other researchers in diverse scenarios [17, 18, 51]. Furthermore, the current estimate of the DP is $q_0=-0.7^{+0.045}_{-0.033}$, with a 1-$\sigma$ error. These findings consistently agree with values previously reported in the literature [52, 53]. To facilitate reference, these values are compiled in Table 2. Further, we present the obtained $q_0$ in Fig. 5 and compare them with the results of previous studies.

Fig. 5

A graph displaying the present values of DP, accompanied by their corresponding error bars, as obtained from several studies is presented [8, 13, 17, 18, 54,55,56,57,58]. The blue shaded regions on the graph indicate the $q_0$ value, along with their $1\sigma$, $2\sigma$, and $3\sigma$ errors obtained in this study

6.2 Jerk parameter (j)

The jerk parameter serves as a significant quantity in our understanding of the accelerating Universe. It is defined as the dimensionless third-order derivative of the cosmic scale factor a(t). Furthermore, we can express the jerk parameter as a function of redshift z(t) using the DP q(z), which can be given by the equation:

$$\begin{aligned} j(z)=q(z)(2q(z)+1)+\frac{dq}{dz}(1+z). \end{aligned}$$

(33)

The jerk parameter plays a crucial role in discerning various dark energy models [44], as deviations from the value of $j=1$ would favor non-$\Lambda$CDM models. For our specific model, the expression for the jerk parameter can be derived from the expression for the DP. It takes the form:

$$\begin{aligned} j(z)= \frac{2 a^2 (z+1)^6-a z (3 z+10) (z+1)^4}{\left( b+(z+5) z^2\right) ^2}+1. \end{aligned}$$

(34)

The equation provides insights into the behavior of the jerk parameter within the framework of our model.

Figure 6 presents the evolution of the jerk parameter, j(z), within the $3\sigma$ error regions for the combined CC+BAO+SNeIa dataset. The results depicted in Fig. 6 indicate that our model only exhibits slight deviations from the concordance $\Lambda$CDM model at the present epoch. These deviations, observed in the value of $j_0$, prompt further investigation as the underlying cause of cosmic acceleration remains unknown. Furthermore, our analysis demonstrates that the future behavior of our model is marginally consistent with the $\Lambda$CDM model. The current value of the jerk parameter, along with its corresponding $1\sigma$ error, is estimated as $j_0=1.18^{+0.058}_{-0.038}$, which is consistent with the results obtained in [18, 59]. These findings, presented in Table 2, provide validation for our model and lend support to the notion of an accelerating Universe.

Fig. 6

Jerk parameters as a function of redshift for the proposed model, obtained from the combined CC, BAO, and SNeIa datasets, with shaded zones representing $68\%$, $95\%$, and $99.7\%$ confidence levels

6.3 Om(z) diagnostic

The Om(z) diagnostic is an effective tool in differentiating between different dark energy (DE) or cosmological models from the standard $\Lambda$CDM model. Sahni et al. introduced this diagnostic in 2008 [60], and it has since been studied extensively by numerous researchers. The function Om(z) relates the observed Hubble parameter, which is a measure of the rate of expansion of the Universe, to the density of matter in the Universe. A constant value of Om(z) at any redshift indicates that the DE behaves like a cosmological constant. However, if Om(z) varies with redshift, it suggests that the DE is dynamic and changes its form over time. Furthermore, the slope of Om(z) can distinguish between two distinct types of dynamic DE models: quintessence and phantom. A positive slope in Om(z) implies a phantom phase, while a negative slope implies a quintessence phase. In general, the Om(z) diagnostic is an influential tool for studying various DE and cosmological models and provides important insights into the expansion of the Universe.

In a Universe with flat spatial geometry, the Om(z) diagnostic can be expressed as

$$\begin{aligned} Om(z)=\frac{E^2(z)-1}{(1+z)^3-1}, \end{aligned}$$

(35)

where $E(z)=H(z)/H_0$ and H(z) is obtained numerically using the Eq. (22). By utilizing the mean values of the constrained parameters derived from the combined CC+BAO+SNeIa dataset, we plot the evolution of Om(z) with respect to z in Fig. 7. The resulting graph illustrates that Om(z) exhibits a negative slope for all redshift ranges, indicating a quintessence phase. This suggests that our model displays distinct behavior compared to the standard $\Lambda$CDM model.

Fig. 7

The behavior of the Om(z) diagnostic vs. redshift z

Table 3 Summary of the findings for constraints on f(Q) gravity models

7 Constraints on f(Q) models

The exploration of alternative theories of gravity, such as f(Q) gravity models, provides valuable insights into the fundamental nature of the Universe. In this section, we aim to constrain the parameters of two specific f(Q) gravity models using the observed values of the DP $q_0$ and the Hubble constant $H_0$. The first model we consider is the power-law form of f(Q) gravity and the second model is the logarithmic form of f(Q) gravity. To derive constraints on these models, we utilize the generalized Friedmann equations in the present-day values, taking into account the contribution of pressureless matter while neglecting the influence of radiation. By analyzing the available observational data, we aim to determine the parameter values that best describe the dynamics of the Universe within the framework of f(Q) gravity models. Thus, (14) and (15) take the forms

$$\begin{aligned} 6f_{Q} H_0^2-\frac{1}{2}f_0= & {} \rho _0, \end{aligned}$$

(36)

$$\begin{aligned} (12 f_{QQ_0}H_0^2+f_{Q_0})\dot{H_0}= & {} -\frac{1}{2}\rho _0, \end{aligned}$$

(37)

where a subscript 0 indicates the present-day value of the corresponding parameter. We make use of (36) and (37) to set constraints on the parameter of f(Q) model.

7.1 Power-law form of f(Q) gravity model

In this subsection, we focus on the power-law form of the f(Q) gravity model, given by the equation

$$\begin{aligned} f(Q)=Q+\alpha Q_0\left( \frac{Q}{Q_0}\right) ^\beta , \end{aligned}$$

(38)

where $\alpha$ and $\beta$ are scalars. Though there are models like $f(Q)=Q+\alpha Q^\beta$ in the literature [61, 62], we chose the above specific form because it allows us to express the parameters $\alpha$ and $\beta$ as dimensionless quantities. By substituting the Eq. (38) into the Eqs. (36) and (37), we obtain

$$\begin{aligned}{} & {} \alpha (2 \beta -1)-\Omega _{m_0}+1=0, \end{aligned}$$

(39)

$$\begin{aligned}{} & {} 2 (q_0+1) (\alpha \beta (2 \beta -1)+1)-3 \Omega _{m_0}=0, \end{aligned}$$

(40)

where $\Omega _{m_0}$ is the dimensionless matter density parameter. By substituting the values $q_0=-0.7$, $H_0=74.43$ obtained in this study along with $\Omega _{m_0}=0.315$ [63], into Equations (39) and (40), we find the corresponding parameter values for the power-law f(Q) gravity model as $\alpha =0.255708$ and $\beta =-0.839416$. Alternatively, considering the observational constraints from Planck2018 [63] results, with values $q_0=-0.5275$, $H_0=67.4$, and $\Omega _{m_0}=0.315$, we obtain parameter values of $\alpha = 0.685$ and $\beta =3.09284\times 10^{-16}$. Similarly, by using the observational constraints from the SH0ES team [49] with values $q_0=-0.51$, $H_0=73.3$, and $\Omega _{m_0}=0.326$, we find parameter values of $\alpha =0.678107$ and $\beta =0.00302792$. These parameter values are summarized in Table 3.

Figure 8 displays the reconstructed f(Q) functions for the power-law f(Q) gravity model in comparison to the $\Lambda$CDM model with $\Omega _{m_0}=0.3$ and $H_0=70$. The f(Q) curves corresponding to the parameter sets $\alpha =0.685$, $\beta =3.09284\times 10^{-16}$ and $\alpha =0.678107$, $\beta =0.00302792$ closely align with the $\Lambda$CDM model. These curves exhibit a strong similarity to the standard cosmological scenario. However, the f(Q) curve corresponding to $\alpha =0.255708$ and $\beta =-0.839416$ shows a small deviation from the $\Lambda$CDM model. While still resembling the standard cosmological scenario, this particular parameter set exhibits a slight departure from the expected behavior.

7.2 Logarithmic form of f(Q) gravity model

As our second specific example, we examine the f(Q) gravity model expressed as

$$\begin{aligned} f(Q)=\alpha Q+\beta Q_0\log (Q/Q_0). \end{aligned}$$

(41)

A similar kind of model has also been explored in recent studies, such as the work by [62]. By substituting this model into the Eqs. (36) and (37), we obtain the following

$$\begin{aligned}{} & {} \alpha +2 \beta -\Omega _{m_0}=0, \end{aligned}$$

(42)

$$\begin{aligned}{} & {} 2 (q_0+1) (\alpha -\beta )-3 \Omega _{m_0}=0. \end{aligned}$$

(43)

By employing the values $q_0=-0.7$ and $H_0=74.43$ obtained in this study, along with $\Omega _{m_0}=0.315$, we derive the parameter values for the logarithmic f(Q) gravity model as $\alpha =1.155$ and $\beta =-0.42$. On the other hand, when considering the values $q_0=-0.5275$, $H_0=67.4$, and $\Omega _{m_0}=0.315$ based on the observational constraints from Planck Collaboration [63], the resulting parameter values are $\alpha = 0.771667$ and $\beta =-0.228333$. Additionally, adopting the values $q_0=-0.51$, $H_0=73.3$, and $\Omega _{m_0}=0.326$ following the observational constraints by the SH0ES team [49], yields the parameter values of $\alpha =0.773973$ and $\beta =-0.223986$. These parameter values are summarized in Table 3.

Figure 9 depicts the reconstructed f(Q) function for the logarithmic form of the f(Q) gravity model, compared to the $\Lambda$CDM model with $\Omega _{m_0}=0.3$ and $H_0=70$. The plot showcases the minor deviations of the logarithmic form of the f(Q) model from the standard cosmological scenario. Notably, the f(Q) curve corresponding to $\alpha =1.155$ and $\beta =-0.42$ closely resembles the $\Lambda$CDM model. However, the f(Q) curves associated with the other two parameter sets, $\alpha = 0.771667$, $\beta =-0.228333$, and $\alpha =0.773973$, $\beta =-0.223986$, exhibit increasing deviations from the $\Lambda$CDM model as the redshift increases. These findings underscore the capability of the logarithmic form of the f(Q) gravity model to reproduce the standard cosmological scenario while also manifesting deviations from it within specific parameter regimes.

Fig. 8

Comparison between the reconstructed $f(Q)=Q+\alpha Q_0\left( \frac{Q}{Q_0}\right) ^\beta$ and $\Lambda$CDM model

Fig. 9

Graph of $f(Q)=\alpha Q+\beta Q_0\log (Q/Q_0)$ against $\Lambda$CDM model

Overall, our analysis of both the power-law and logarithmic forms of f(Q) gravity models reveals their ability to reproduce the standard cosmological scenario while also exhibiting departures from it in specific parameter regimes. The derived parameter constraints and the corresponding reconstructed f(Q) functions provide insights into the behavior of these models and their compatibility with observational data. These findings contribute to our understanding of modified gravity theories and their implications for cosmology.

8 Concluding remarks

The investigation of cosmic evolution through reconstruction methods has shed light on the dynamics of the Universe, providing valuable insights into its expansion history and the nature of dark energy and modified gravity. Building upon the advancements in parametric reconstruction and considering the importance of a suitable deceleration parameter model, this study has made significant contributions to our understanding of the cosmological scenario. The choice of a parametric form for q(z) is a critical step in cosmological analysis. It must be done thoughtfully, considering both observational constraints and theoretical considerations, to ensure that the parametrization is valid and predictive across all ranges of redshifts. This ensures robust investigations of the Universe’s dynamics and facilitates the exploration of dark energy and modified gravity theories. In this paper, we introduced a new parametrization for the DP, offering a more flexible and model-independent approach to studying the dynamics of the universe. The proposed DP model in this article is capable of explaining several physical phenomena, such as satisfying the second law of thermodynamics and describing the entropy of the Universe.

In this work, the utilization of observational probes including 31 data sets of Cosmic Chronometers (CC), 26 non-correlated points from Baryon Acoustic Oscillations (BAO), and 1701 newly updated type Ia supernovae data points has enabled the constraint of cosmological parameters and validation of the viability of the proposed model. The Bayesian statistical inference techniques and MCMC methods used to constrain the model parameters have allowed us to accurately analyze the data and derive meaningful conclusions. The best fits (see Table 1) obtained from this procedure are used to analyze the kinematic behavior of the Universe. Our findings demonstrate that the best-fit parameters of our models align well with the observed data. This success in constraining the model’s parameters showcases the importance of utilizing observational data and statistical methods to improve our understanding of the Universe’s behavior.

Table 4 CC data used for analysis

Table 5 BAO data used for analysis

Through the investigation of the proposed model’s dynamics, which includes examining the transition from deceleration to acceleration, analyzing the Jerk Parameter (j), and utilizing the Om(z) diagnostic, we gain a better understanding of the Universe’s behavior and its evolutionary processes. The results of the cosmological quantities for the statistically estimated values of model parameters are in Table 2. The current DP value, upto $3\sigma$ error, is presented and compared with earlier studies in Fig. 5. Moreover, our study effectively constrained both the model parameters and the Hubble constant ($H_0$). Notably, our obtained Hubble constant values align with those derived from other studies that employed reconstruction methods (both parametric and non-parametric) [17, 59, 64,65,66,67] and observational data (including the distance ladder method, TRGB technique, and H0LiCOW) [49, 68,69,70,71,72,73,74,75,76,77,78,79]. We present our findings of the constrained $H_0$ in Fig. 2 and compare them with the results of previous studies.

By employing a careful analysis of the observational constraints, we obtained substantial findings into the behavior of the power-law and logarithmic f(Q) gravity models. We presented the parameter values of f(Q) gravity models for three different sets of observational constraints: one obtained in the present work, one following the Planck2018 observational constraints, and one based on the SH0ES team’s observational constraints. We summarized these parameter values in the Table 3 and demonstrated their impact on the reconstructed f(Q) function. Notably, we found that the power-law f(Q) model closely resembles the $\Lambda$CDM model for certain parameter sets, while others exhibit increasing deviations as redshift increases.

Overall, this paper offers valuable cosmological perspectives utilizing observational data and a novel deceleration parameter, providing meaningful astrophysical insights. These findings will aid in the continued exploration of the nature of dark energy and the future trajectory of the cosmos. In future research, we plan to explore the behavior of the Universe from a different perspective by constructing parametric models for various cosmological models. We also intend to investigate the different modified gravity theories using reconstructed kinematic models. Furthermore, we believe it would be interesting to adopt a non-parametric approach to reconstruct the Universe, which can offer additional insights into the cosmic evolution beyond the limitations of parametric models. Future investigations and observations will further refine and expand our understanding of f(Q) gravity and its implications for the nature of the universe.

Appendix

See Tables 4 and 5.