1 Introduction

It has been shown that a mysterious entity known as dark energy is speeding up the expansion of our universe. As its composition cannot be determined by sight, dark energy might be made of any material. One of the things that might be thought of as a dark-energy model is quintessence. It is represented as a scalar field that controls the fast expansion of the universe and generates negative pressure [1, 3]. Moreover, the scalar field is investigated in several gravity theories on both the local astrophysical manifestations [4,5,6,7] and the cosmic scale [8,9,10,11,12,13,14,15]. It’s interesting to note that Kiselev [16] has investigated the scalar field in a black hole framework using certain arbitrary assumptions. Further research has also been done on a few more widespread scenarios involving black holes under modified gravity [17,18,19,20,21,22,23].

The string theory is one of the theories that aim to combine quantum physics with gravitational theory. It makes the assumption that one-dimensional strings are the essential component of our universe in an effort to explain all the theories. Letelier [24] has attempted to apply the concept of a string to a black hole, the characteristics of which could be affected by the manifestation of the string’s existence. As far as we are aware, revolving black holes fit the observational evidence for their existence rather well [25,26,27,28,29]. There hasn’t been any research, in particular, on the revolving and twisting charged black hole amid a cloud of strings. Whilst some research has been done on a cloud of strings within a black hole system, it will be more quantifiable to take into account the cloud of strings for spinning black holes under Einstein’s gravity. The twisting parameter or the NUT charge should also be taken into account to provide a more comprehensive answer.

The Kerr hypothesis states that the Kerr metric [30] represents the only stationary, vacuum, axisymmetric solution of Einstein’s field equations which is asymptotically flat and devoid of pathologies outside the event horizon [31,32,33]. It may be challenging to rule out other Kerr-like black holes [34] that are acknowledged by modified theories of gravity because direct evidence for the theorem is still uncertain. Moreover, basic problems with general relativity (GR) at sizes similar to the event horizon continue to be unresolved.

Gravitational lensing occurs when an item traveling around a black hole with a certain radius falls into it. Nevertheless, if the traveling object is a photon, it casts a shadow on the plane, which can be seen at infinity and was originally discovered by Bardeen [35]. If the black hole is spherically symmetric, a circular shadow will be created [36, 37], whereas spinning black holes will cast a distorted shadow [38, 39]. Reference [40] first investigated the angular radius of the Schwarzschild black hole, whereas Hioki [41] subsequently presented the two observable parameters. As a result, the analysis of black hole shadows resulted in a wide range of instances [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58].

Data collection from the Milky Way and close-by galaxies of supermassive black holes is being done as part of the Event Horizon Telescope (EHT) project [59]. The picture of M87 was released in 2019 by a team of EHT researchers [60]. Everyone was able to glimpse the black hole’s picture for the first time because of this revelation. One of the first quantitative recommendations for testing the Kerr metric with black hole shadows was made by Johannsen and Psaltis [61]. The event horizon is only accessible for indirect tests using strong-field phenomena [62], such as a black hole shadow [35, 37]. With the publication of the very first horizon-scale image of the black hole M87* by the Event Horizon Telescope (EHT) collaboration in 2019 [60, 63,64,65,66], black holes were made physically tangible, and limits could be set on the size of the compact emission region with angular diameter \(\theta _d = 42\pm 3\) and the central flux depression with a factor of \( > rsim 10\), which is known as the shadow [60, 65].

With regard to stellar dynamical priors on its mass and distance, the EHT collaboration, in turn, revealed the photograph of the black hole Sgr A* in the Milky Way in 2022 [67,68,69,70], displaying an angular shadow of diameter (\(d_{sh} = 48.7\pm 7 \mu a s\)). The two black holes’ recorded pictures, M87* and Sgr A*, are in line with the expected characteristics of a Kerr black hole, according to General Relativity [60, 65, 69]. The relative deviation of quadrupole moments and the existing measurement error of spin or angular momentum do not, however, completely rule out Kerr-like black holes originating under modified gravities [60, 65, 71]. Moreover, Sgr A* shows consistency with GR predictions spanning three orders of magnitude in central mass when compared to the EHT results for M87* [69].

The remaining sections of the paper are organized as follows. In Sect. 2, using a cloud of strings and quintessence, we consider the solution for a charged black hole obtained in Ref. [72] and derived the geodesics equations. The shadow of the rotating and twisting solution is then shown in Sect. 3, along with an examination of the restrictions obtained from EHT Findings on Sgr A* and M87* in Sect. 4. Section 5 discusses the black hole’s energy emission rate. Lastly, in the final part, we provide a summary of our article.

2 Rotating black hole

In Ref. [72], the spinning and twisting solution of a charged spherically symmetric black hole with the existence of a cloud of strings and quintessence was determined using the DJN method. As a result, the universal twisted rotating metric in Boyer-Linquist coordinates read as

$$\begin{aligned} dS^{2}= & {} -\frac{\varDelta }{\rho ^2}\left[ dt-\left( a \sin ^2\theta +2n(1-cos\theta )\right) d\phi \right] ^2 \nonumber \\{} & {} {+}\frac{\rho ^2}{\varDelta }dr^2 {+}\rho ^2 d\theta ^2 {+} \frac{\sin ^2 \theta }{\rho ^2}\left[ adt{-}{r^2 {+} (a{+}n)^2 }d\phi \right] ^2,\nonumber \\ \end{aligned}$$
(1)

with

$$\begin{aligned} \rho ^2= & {} r^2+(n+a\cos \theta )^2, \end{aligned}$$
(2)
$$\begin{aligned} \varDelta= & {} r^2 -2Mr +a^2 +q^2 -n^2 -C r^{(1-3\omega _q)} -br^2. \end{aligned}$$
(3)

The above solution comprises a cloud of strings and quintessence that contributes similarly to the metric when \(\omega _q = -\frac{1}{3}\) for perfect fluid dark matter dominance. This parameter is important in determining perfect-fluid matter dominance in the case of accelerated universe expansion. We can impose \(-1< \omega _q<-1/3\) to establish quintessential dark energy dominance [72]. Yet, because there is no limitation in the black hole solution, \(\omega _q\) can take any value. Here, b and \(\omega _q\) are related to the strength of clouds and the state parameter of quintessence, respectively. Moreover, \(q^2=e^2 + g^2\), where e and g are respectively representing electric and magnetic charge. Finally, M, C, a, and n are denoting the mass, quintessential intensity, spin, and the NUT charge parameters of the black hole.

Fig. 1
figure 1

Radial profiles of \(\varDelta (r)\) with respect to a (upper row) and b (middle row) at \(\omega _{q}=-3/5\) (left) \(\omega _{q}=-1/2\) (middle) and \(\omega _{q}=-2/5\) (right). The lower row is plotted by varying \(\omega _{q}\) (left), n (middle), and q (right)

Full size image

In Fig. 1, we draw the radial profile of \(\varDelta (r)\) for different spacetime parameters. The upper row is plotted by varying the spin parameter for three different cases of \(\omega _q\) (that is, \(\omega _q =-3/5\),\(-1/2\) and \(-2/5\)). Similarly, the middle row is plotted by varying parameter b for three different cases of parameter \(\omega _q\). Finally, the third row shows the behaviour of \(\varDelta (r)\) with respect to parameter \(\omega _q\) (left), n (middle) and q (right). The graphs show that increasing the spin parameters increases \(\varDelta (r)\), whereas increasing the b parameter decreases them (middle row). Furthermore, the parameter \(\omega _q\) and q increases \(\varDelta (r)\) with increasing increment, while the parameter b decreases \(\varDelta (r)\).

Fig. 2
figure 2

Dependence of black hole horizons from the black hole charge for various values of the parameters q, n C and \(\omega _q\) at \(b=0.01\) (left panels) and \(b=0.0\) (right panels)

Full size image

Furthermore, the relationships between the horizon radius and black hole charge for the fixed value of the black hole spin \(a=0.5\) are shown in Fig. 2. The left panel is plotted at \(b=0.01\) while the right panel is plotted at \(b=0\). The graphs are plotted for different cases of parameter a (first row), n (second row), C (third row), and \(\omega _q\) (last row). The result shows that the radius decreases in all cases by increasing the values of the spin parameter. The presence of \(\omega _q\), and C parameters do not change the inner (Cauchy) horizon, while the event horizon decreases when both quintessential parameters C and \(\omega _q\) increase. Whereas, the radius increases by increasing values of parameter n. A slight difference in the range of radii can be observed for \(b=0.01\) and 0.

Geodesic motion around a black hole is the most important factor in projecting the probable shape of a black hole shadow. This section looks at the geodesic equations that surround a revolving charged black hole. The geodesic of a moving particle is often obtained by solving the geodesic equations or using the Hamilton-Jacobi methodology. The particle is described by the Hamilton-Jacobi equation, which can be written as

$$\begin{aligned} \frac{\partial H}{\partial \tau }+\frac{1}{2}g^{\mu \sigma }\frac{\partial H}{\partial x^{\mu }}\frac{\partial H}{\partial x^{\sigma }}=0, \end{aligned}$$
(4)

here \(\tau \) represents an affine parameter. This black hole is linked to two different killing vectors, \(\partial _t\) and \(\partial _\phi \). This gives us the formulas for two constants: particle energy (\(\mathcal {E}\)) and orbital angular momentum (L), as shown below.

$$\begin{aligned} -\mathcal {E}=g_{t\mu } \dot{x}^\mu , \qquad L=g_{\phi \mu } \dot{x}^\mu . \end{aligned}$$
(5)

Therefore, Eq. (4) takes the form [73]

$$\begin{aligned} H=H_{r}(r)-\mathcal {E} t+L\phi +H_{\theta }(\theta )+\frac{1}{2}m_{0}^{2}\tau . \end{aligned}$$
(6)

In Eq. (6), \(H_{r}(r)\) and \(H_{\theta }(\theta )\) denote the function of radial r and angular \(\theta \) coordinates, respectively. \(m_0^2\), on the other hand, denotes the particle’s rest mass. By inserting Eq. (4), into Eq. (6), we get

$$\begin{aligned} H_{r}(r)=\int ^{r}\frac{\sqrt{Z(r)}}{\varDelta (r)}dr,\qquad H_{\theta }(\theta )=\int ^{r}\sqrt{W(\theta })d\theta , \end{aligned}$$
(7)

in which,

$$\begin{aligned} Z(r)= & {} \left( \mathcal {E}(r^{2}+a^2)-a L\right) ^2 \nonumber \\{} & {} -\varDelta \left( \kappa +r^{2}m_{0}^{2}+(L-a\mathcal {E})^{2}\right) , \end{aligned}$$
(8)
$$\begin{aligned} W(\theta )= & {} \kappa -L^{2}\cot ^{2}\theta +a^2 \cos ^2\theta (\mathcal {E}^2 -m_0^2). \end{aligned}$$
(9)

The Carter constant is denoted by \(\kappa \). The aforementioned equations can be used to illustrate the geodesic equations of motion of particles in the backdrop of the rotating black hole.

$$\begin{aligned} \rho ^{2}\frac{dt}{d\tau }= & {} a(L-a\mathcal {E}\sin ^2\theta )+\frac{a^2 +r^2}{\varDelta } \nonumber \\\times & {} \left( \mathcal {E}(a^2 +r^2)-aL\right) , \end{aligned}$$
(10)
$$\begin{aligned} \rho ^{4}\left( \frac{d\theta }{d\tau }\right) ^2= & {} {\kappa -L^{2}\cot ^{2}\theta +a^2 \cos ^2\theta (\mathcal {E}^2 -m_0^2)}, \end{aligned}$$
(11)
$$\begin{aligned} \rho ^{4}\left( \frac{d r}{d\tau }\right) ^2= & {} \left( (a^{2}+r^2)\mathcal {E}-a L\right) ^2 \nonumber \\{} & {} -\varDelta \left( \kappa +r^{2}m_{0}^{2}+(L-a\mathcal {E})^{2}\right) , \end{aligned}$$
(12)
$$\begin{aligned} \rho ^{2}\frac{d \phi }{d\tau }= & {} \frac{a}{\varDelta }\left( (a^2 +r^2)\mathcal {E}-aL\right) -a\mathcal {E}+L\csc ^2\theta .\nonumber \\ \end{aligned}$$
(13)

The aforementioned equations are the required geodesic equations. Furthermore, if \(m_{0}^{2}=0\), the corresponding geodesic equations followed by photons around the black hole may be obtained as [74]

$$\begin{aligned} \rho ^{2}\frac{d\theta }{d\tau }= & {} \sqrt{\kappa +a^2 \cos ^2\theta \mathcal {E}^2-L^{2}\cot ^{2}\theta }, \end{aligned}$$
(14)
$$\begin{aligned} \rho ^{2}\frac{d r}{d\tau }= & {} \sqrt{\left( \mathcal {E}(a^{2}+r^2)-a L\right) ^2 -\varDelta \left( \kappa +(a\mathcal {E}-L)^{2}\right) }.\nonumber \\ \end{aligned}$$
(15)

Equation (15) can be further expressed as

$$\begin{aligned} \rho ^4\left( \frac{d r}{d \tau }\right) ^{2}+V_\textrm{eff}=0. \end{aligned}$$
(16)

In Eq. (16), the effective potential (\(V_\textrm{eff}\)) has the following form.

$$\begin{aligned} \frac{1}{\mathcal {E}^2} V_\textrm{eff}=\varDelta [(\xi -a)^2 +\eta ]-[-a\xi +(a^2 +r^2)]^2. \end{aligned}$$
(17)

Where, \(\eta ={\kappa }/{\mathcal {E}^{2}}\) and \(\xi ={L}/{\mathcal {E}}\) [73]. Then, to discover the unstable circular orbits, we must apply the following constraints

$$\begin{aligned} V_\textrm{eff}(r_{ph})=V_\textrm{eff}^{'}(r_{ph})=0, \end{aligned}$$
(18)

here \(r_{ph}\), to represent the radius of photonsphere. Solving these conditions, we get

$$\begin{aligned} \xi= & {} \frac{\varDelta ^{'}(r^{2}+a^{2})-4r\varDelta }{a\varDelta ^{'}}, \end{aligned}$$
(19)
$$\begin{aligned} \eta= & {} \frac{r^{2}[16\varDelta (a^{2}-\varDelta )-r^{2}\varDelta ^{'^{2}}+8r\varDelta \varDelta ^{'}]}{a^{2}\varDelta ^{'^{2}}}, \end{aligned}$$
(20)

where

$$\begin{aligned} \varDelta '= & {} 2(r-M)-2br-C r^{-3\omega _q} (1-3\omega _q). \end{aligned}$$
Fig. 3
figure 3

The radial profile of black hole’s shadow concerning spin parameter (upper row) and inclination angle (lower row) at \(\omega _{q}=-2/5\) (left) \(\omega _{q}=-1/2\) (middle) and \(\omega _{q}=-2/3\) (right). The middle row is plotted by varying \(\omega _{q}\) (left), n (middle), and b (right) for different values of spacetime parameters

Full size image

3 The shadow of rotating black hole

Fig. 4
figure 4

Dependence of the shadow size \(R_s\) with respect to parameter q at \(a=0.5\) (left panel) and \(a=0.0\) (right panel) for different values of parameter n (1st row) b (2nd row), C (3rd row) and \(\omega _q\) (4th row)

Full size image
Fig. 5
figure 5

Dependence of the shadow size \(\delta _s\) with respect to parameter q at \(a=0.5\) (left panel) and \(a=0.0\) (right panel) for different values of parameter n (1st row) b (2nd row), C (3rd row) and \(\omega _q\) (4th row)

Full size image
Fig. 6
figure 6

Relationships between the spin and charge parameters of rotating charged black holes for different values of the black hole shadow size and distortion parameters at \(\omega _{q} = -2/3\) (left), \(\omega _{q} = -1/2\) (right) for \(b = 0.01\) (upper row) and \(b=0.0\) (lower row) for \(n=0.1\) and \(C=0.1\)

Full size image
Fig. 7
figure 7

Relationship between spin and charge parameter for zero distortion in shadow shape of the charged rotating black hole at \(b=0.01\) (left panel) and \(b=0.0\) (right panel)

Full size image

The spinning black hole’s shadow will be analyzed next. When a photon is guided from infinity toward the black hole, there are two possibilities. In the first case, a photon with a high orbital angular momentum is involved. It will reappear in specific areas and be seen by an observer who is a significant distance away from the black hole. Low orbital angular momentum photons, on the other hand, will fall into the black hole and not reach the observer. During this process, a dark zone in the sky known as the black hole’s shadow is created, with the two conditions defining its boundary. Examining the geodesic of a photon yields the geometry of the shadow. In addition, we will establish the new celestial coordinates (\(\alpha ,\beta \)) to investigate this dark region or black hole shadow, called celestial coordinates described by [75] as

(21)
(22)

In the above equation, the observer’s inclination angle is denoted by \(\theta _{0}\). Furthermore, from the geodesic equations, the above set of equations becomes

$$\begin{aligned} \alpha= & {} -\xi \csc \theta _{0}, \end{aligned}$$
(23)
$$\begin{aligned} \beta ^2= & {} {a^{2}\cos ^{2}\theta _{0}+\eta -\xi ^{2}\cot ^{2}\theta _{0}}. \end{aligned}$$
(24)

For the rotating black hole in the equatorial plane (\(\theta _{0}=\pi /2\)), the equations for celestial coordinates can be expressed in the following form,

$$\begin{aligned} \alpha= & {} \frac{4r\varDelta -\varDelta ^{'}(r^{2}+a^{2})}{a\varDelta ^{'}}, \end{aligned}$$
(25)
$$\begin{aligned} \beta= & {} \pm \sqrt{\frac{r^{2}[(a^{2}-\varDelta )16\varDelta -r^{2}\varDelta ^{'^{2}}+8r\varDelta \varDelta ^{'}]}{a^{2}\varDelta ^{'^{2}}}}, \end{aligned}$$
(26)

Therefore, expression of the shadow radius (\(R_{sh}\)) can be calculated in the following form,

$$\begin{aligned} R^{2}_{sh}=\alpha ^{2}+\beta ^{2}. \end{aligned}$$
(27)

and we have

$$\begin{aligned} R_{sh}^2=a^{2}+\frac{2r}{(\varDelta ')^{2}}\left\{ r\left[ 8\varDelta +(\varDelta ')^{^2}\right] -4\varDelta \varDelta '\right\} . \end{aligned}$$
(28)

The graphical representation of the shadow radius under different spacetime parameters is shown in Fig. 3. The upper and lower row is plotted by varying spin and inclination angle parameter, respectively, at three different values of parameter \(\omega _q\) (\(-2/5\) (left), \(-1/2\) (middle), and \(-2/3\) (right)). The graphs show that the shadow radius decreases by increasing the value of the spin parameter. A similar pattern of shadow radius can be seen in the case of inclination angle. The middle row of Fig. 3 is plotted by the varying parameter \(\omega _q\) (left), parameter n (middle), and parameter b (right). Here we can see that increasing \(\omega _q\) decreases shadow radius, whereas, the shadow radius increases by increasing parameters b and n.

Now we introduce two observable parameters of the black hole shadow, the radius \(R_s\) and the distortion \(\delta _s\) [41]:

$$\begin{aligned} R_s= & {} \frac{(\alpha _t-\alpha _r)^2+\beta _t^2}{2|\alpha _r-\alpha _t|} \end{aligned}$$
(29)
$$\begin{aligned} \delta _s= & {} \frac{|\alpha _l-\alpha '_l|}{R_s} \end{aligned}$$
(30)

where subscripts r,l and t stands for the right, left and top boundaries if the shadow, respectively.

The relationship between the shadow size and the distortion parameter concerning black hole charge is respectively shown in Figs. 4 and 5. The graphs are plotted at \(a=0.5\) (left) and \(a=0\) (right) by varying values of the other spacetime parameters. The result shows that both shadow size and distortion decrease by increasing the value of parameter n for both cases. However, the shadow size and distortion parameter increases along black hole charge concerning parameters n, b, C, and \(\omega _q\). Similarly, the relationship between spin and charge parameters of the black hole at \(b=0.01\) (upper row) and \(b=0\) (lower row) for \(\omega _q = -2/3\) (left) and \(\omega _q =-1/2\) (right) is shown in Fig. 6. Finally, Fig. 7 shows the results for the relationship between the spin and charge parameter of the black hole with zero distortion in shadow shape by varying parameter n (first row), C (second row) and \(\omega _q\) (last row) at \(b=0.01\) (left panel) and \(b=0\) (right panel).

In Fig. 6 we demonstrate contour-plots of shadow radius and distortion parameter in the spin and charge parameters space for different values of b and \(\omega _q\) for fixed values of \(n=0.1\) and \(C=0.1\). It is observed from the figure that there are negative distortion parameters at \(a<0.8M\) when \(\omega _q=-2/3\) in the absence of cloud strings \(b=0\), while it is negative at \(a<0.7\) when \(\omega _q=-1/2\). Moreover, the shadow size enlarges when the black hole rotates fast and be accumulated a bigger charge.

Now, we are interested in which values of spin and charge parameters of the black hole with string clouds and quintessence, the black hole shadow takes a circular shape with zero distortion parameter. It is observed from Fig. 7 that the ratio of the charge and spin parameter increase with quintessence C & \(\omega _q\), and the cloud of strings b.

4 Constraints from EHT observations

Now we can get the constraints from observational data of EHT results. Foremost, we ought to define the observable parameters that can describe the size and shape of the black hole shadow. The shadow of the spherically symmetric black hole will be a perfect circle, but for an axially symmetric black hole, there will be some distortion. Hioki and Maedia first introduced two observables the radius to describe the size of shadow and the deviation parameter to describe distortion [41]. However, there were other approaches, and we can use a simple method of black hole parameter estimation using the shadow observables, shadow area A, and oblateness D which is based on the coordinate independent formalism [78, 79].

One may introduce the area enclosed within the shadow silhouette and the shadow oblateness observable as [79, 80]

$$\begin{aligned} A= & {} 2\int _{r_-}^{r_+} \Big (\beta (r) \frac{d\alpha (r)}{dr}\Big ) dr, \end{aligned}$$
(31)
$$\begin{aligned} D= & {} \frac{\varDelta \alpha }{\varDelta \beta }\, \end{aligned}$$
(32)

where \(r_\pm \) refers to the prograde and retrograde radii of stable circular orbits obtained as the roots of the equation \(\eta _c=0\), outside the event horizon [81].

By using Eqs. (31)–(32) one can find the dependencies of shadow observables from the black hole parameters with the help of numerical calculations. Since there are now two shadow images of supermassive black holes (Sgr A* and M87*), one may estimate the black hole parameters of the different gravity models through these EHT observation results.

Now we can determine the constraints for the charge and spin parameter of the black hole Sgr A* and M87* considering them the twisting charged black hole with the cloud of strings and quintessence using the angular diameter of their shadow image measured by an observer at a distance d from the black hole can be expressed as [82, 83]

$$\begin{aligned} \theta _d =2 \frac{R_a}{d}, \qquad R_a^2 = {\frac{A}{\pi }} \end{aligned}$$
(33)

where \(R_a\) is the areal shadow radius. If we take into account the Eq. (31) the angular diameter of the shadow can depend on the parameters of the black hole and the observation angle. Besides, it implicitly depends on the mass of the black hole.

The angular diameter of the image of the black hole M87* is \(\theta _d = 42\pm 3 \mu \)as [84]. The mass of M87* and the distance from the solar system can be considered as \(M=6.5\times 10^9 M_\odot \) and \(d=16.8\) Mpc, respectively. [65, 85]

Note that for simplicity, in the numerical estimations, we do not consider the possible uncertainties in the mass and distance measurements of the black holes.

Fig. 8
figure 8

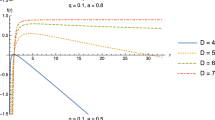
Angular diameter observable \(\theta _d\) for the black hole shadows as a function of parameters a/M and q/M at inclinations \(90^\circ \) (left panels) and \(17^\circ \) (right panels). The black curve corresponds to \(\theta _d = 39\mu \)as within \(1\sigma \) region of the measured angular diameter, \(\theta _d = 42 \pm 3\mu \)as, of the M87* black hole reported by the EHT

Full size image

In Fig. 8, we present the density plots of the spin and charge parameter of the black hole which are fitted with the measured value of the angular diameter of M87*, for the different fixed values of the NUT charge, cloud of strings and quintessence parameters. The inclination angle between the rotation axis and observation direction is chosen as \(90^\circ \) on the left panels, while on the right ones, the angle is \(17^\circ \) and between the two cases there is some difference in terms of distribution, as one can notice from the plots. Black curves correspond to the value of the shadow size \(39\mu \)as which is the lower bound of the angular diameter of the supermassive black hole M87*. It is observed from the figure that there is a quantitative change in the distribution of the angular size of the shadow for the various values of the black hole parameters. In the previous section, we obtained that with the increase of parameters C, \(\omega _q\), the shadow radius of the black hole also increases. Accordingly, the constrained area with M87* enlarges as the black hole parameters change. One can also see from the top panels that the presence of quinte the lower limit for the spin parameter increase from about 0.65 (0.5) to 0.92 (0.75) at the NUT charge parameter \(n=0.1\) and \(\chi =90^\circ \) (\(\chi =17^\circ \)). However, the charge limits also increase in the presence of C and b parameters.

The observational data from the angular diameter of the shadow of the supermassive black hole Sgr A* is \(\theta _d = 48.7\pm 7 \mu \)as [69]. Below, we provide constraints on the spin and charge parameters of the black hole varying the NUT charge, quintessence, and cloud strings parameters.

Fig. 9
figure 9

Angular diameter observable \(\theta _d\) for the black hole shadows as a function of parameters a/M and q/M at inclinations \(90^\circ \) (left panels) and \(50^\circ \) (right panels). The black curve corresponds to \(\theta _d = 41.7\mu \)as within \(1\sigma \) region of the measured angular diameter, \(\theta _d = 48.7 \pm 7\mu \)as, of the Sgr A* black hole reported by the EHT. The blue dashed curve corresponds to \(48.7\mu \)as

Full size image

In Fig. 9, the constraints from Sgr A* are illustrated for the charged black hole that we are studying. Here, the mass of Sgr A* and the distance from Earth be considered as \(M\simeq 4\times 10^6 M_\odot \) and \(d\simeq 8\) kpc, respectively. [69, 70]. In this case, we would like to add the mean value of angular diameter, \(48.7\mu \)as with blue dashed curves to easily describe changes among different plots. Black curves correspond to lower bound of angular diameter of Sgr A*. The inclination angle is \(90^\circ \) and \(50^\circ \) for the left and right panels, respectively. Generally, we tried to take smaller values for the parameters related to quintessence which is more realistic. The plots show that non-zero values of C, \(\omega _q\) parameters cause the rise of the corresponding angular diameter of the BH. We realized that if we take larger numbers for these parameters, the results cannot be constrained with EHT observations any more.

To be concluded, these all constraints can give us information about in which values of the black hole parameters shadow image can be compared with EHT results of M87* and Sgr A* supermassive black holes.

5 The energy emission rate

Fig. 10
figure 10

The graphical representation of energy emission rate with respect to frequency \(\omega \), for different values of the parameter a (upper left) and b (upper right) \(\omega _q\) (lower left) and n (lower right)

Full size image

The rate of energy emission from spinning black holes is a fascinating and complicated phenomenon that results from a number of different causes, such as Hawking radiation and accretion. According to Stephen Hawking’s ground-breaking theory, black holes produce heat radiation because of quantum phenomena close to their event horizons, therefore they are not completely black. Black holes gradually lose mass and energy due to this phenomenon, called Hawking radiation. Smaller spinning black holes generate more radiation and dissipate energy more quickly than bigger ones because the rate of energy emission via Hawking radiation is inversely related to the black hole’s mass. This has important effects on black hole lifetimes and ultimate outcomes.

Observations of black hole shadows can aid in the understanding of physics and its fascinating aspects in astrophysical processes. In reality, for an infinite observer, the shadow’s radius is proportional to the cross-section of electromagnetic wave absorption, and the shadow’s shape is the same as the geometric cross-section of photon absorption in the region of the so-called photon sphere. In addition, the Hawking radiation inside the region near the horizon causes the black hole to evaporate, producing and destroying particles.

We are now looking at the spinning charged black hole’s energy emission rate. The value of the limiting constant for the absorption cross-section is given by,

$$\begin{aligned} \rho _\textrm{lim}=\pi R^{2}_{sh}. \end{aligned}$$
(34)

Since it is generally understood that the black hole shadow is responsible for the huge energy absorption cross-section for the distinct observer. As a result, the conventional form describing the energy emission rate may be expressed as follows [76], with the value of the limiting constant as

$$\begin{aligned} \frac{d^{2}E(\omega )}{d\omega dt}=\frac{2\pi ^{3} R^{2}_{sh}}{e^{\frac{\omega }{T_{h}}}-1}\omega ^{3}. \end{aligned}$$
(35)

In Eq. 35, \(T_{h} (r=r_h)\) represents the Hawking temperature of the black hole, and \(r=r_h\) represents the event horizon’s radius. Furthermore, \(\omega \) and \(E(\omega )\) stands for the black hole’s frequency and energy, respectively. The Hawking temperature is calculated as follows [77]

$$\begin{aligned} 4\pi T_{h}|_{r=r_h}= & {} \frac{2(r-M)-2br-C r^{-3w} (1-3w)}{r^2+(n+a)^2}. \end{aligned}$$
(36)

The radial profile of energy emission rate with respect to frequency \(\omega \) is shown in Fig. 10. The graphs are plotted by varying parameters a (upper left), b (upper right), \(\omega _q\) (lower left), and n (lower right). The result shows that, as we increase the value of spin parameter, the energy emission rate of the black hole decreases. On the other hand, parameter b increases energy emission rate as the parameter b increases. Finally, parameters \(\omega _q\) and n both decrease the rate of energy emission of the rotating black hole.

6 Conclusions

One of the excellent and natural laboratories in the Universe for studying gravitational properties of the spacetime geometry around black holes and testing them in both strong and weak gravitational field regimes is the EHT observations of the shadow of the supermassive black hole such as Sgr A*, located at the heart of the Milky Way and M87* located the nearby galaxy called Meissner 87. In this work, we have studied the shadow cast by the spinning and twisting charged spherically symmetric black hole surrounded by clouds of strings and the quintessential field. First, we have started by considering the rotating black hole solution with electric and NUT charges in the presence of the cloud of strings and quintessence, using DJN algorithm obtained in Ref. [72] and have studied the radial profile of the radial function of the rotating metric under the effect of spacetime parameters. We have provided graphical analyses of the behaviour of \(\varDelta (r)\) by varying the spacetime parameters a, b,n and q for three different cases of \(\omega _q=-2/5,-1/2\) and \(-2/3\). The obtained results have shown that an increase in the rotating parameter of the black hole a, causes increasing in the radial profile of the metric function, whereas the parameter b decreases them upon increment. Moreover, the presence of both parameters q and \(\omega _q\) causes increasing them as well. Additionally, we have also obtained the relationship between the event horizon radius and the black hole charge for the variations of the spin parameter. The two cases of the parameter b have been discussed, and the graphical results are depicted in the plots.

Then, we have derived null-geodesic equations in the spacetime around the rotating black hole with the existence of a cloud of strings and quintessential field. After that, we calculated celestial coordinate equations to study the shadow cast by the aforementioned black hole using the obtained null geodesics. We have provided plots of different cases for the shadow radius to study its behaviour under the influence of spacetime parameters. The acquired graphs have shown that, as we increase the spin value, the shadow shape begins to distort as expected. The inclination angle has also shown a similar effect of increasing the shadow radius upon increment. The parameter \(\omega _q\), on the other hand, causes the decrease in shadow radius, while, the presence of parameters b and n increases them as well. We have also studied the relationship between the black hole spin and charge parameters for different values of black hole shadow size and the distortion parameter. The figures are plotted for both rotating and non-rotating cases. The obtained results on shadow size and distortion parameter demonstrated that raising the value of the NUT parameter n reduces to increase in both the shadow size and distortion parameter.

Furthermore, we have also obtained the constraints on the spin and charge parameters of the black hole for different values of the clouds of string, quintessential field, and the NUT charge parameters using the observational data of EHT outcomes. First and foremost, we have established the observable characteristics that may be used to characterize the shape and size of the black hole shadow. In fact, for a spherically symmetric black hole, the shadow is a complete circle, but for one that is axially symmetric, there are some distortions. For the various fixed values of the other black hole characteristics, we have drawn the density plots of possible values of the black hole’s spin and charge parameters, and solid black lines which are fitted with the observed value of the angular diameter of M87*. The outcome demonstrates that, for different values of the black hole parameters, there is a quantifiable variation in the distribution of angular diameter. As the black hole’s parameters change, the constrained region around M87* also shifts as well in the charge-spin space. Additionally, the supermassive black hole \(Sgr A^* \) constraints depicted by the charged black hole are investigated as well, with similar results graphically presented. The figures demonstrate that non-zero values of the parameters C and q result in an increase in the black hole’s angular diameter. Actually, we realized that the results would no longer be constrained by EHT observations if we used larger values for these parameters.

Finally, we studied the energy emission rate around the rotating black hole with the existence of a cloud of strings and a quintessential field. The radial profile of the energy emission rate versus the frequency of the black hole radiation has also been obtained and depicted graphically. The obtained results have shown that the energy emission rate decreases by increasing the spin parameter, while, the presence of the other parameters b, \(\omega _q\), and n cause decreasing in the energy emission rate value. The EHT Collaboration depicts M87* and says that it supports General Relativity. We anticipate that studies of the black hole shadow in future astronomical observation efforts will provide insights and consequences for the quintessential dark energy model and string theory.