Black holes with cloud of strings and quintessence in Lovelock gravity

Abstract

The Lovelock gravity is a natural extension of the Theory of General Relativity (TGR) to higher dimensions, which presents the criteria of general covariance and whose field equations are of second order. Its action contains higher order curvature terms and is reduced to the Einstein–Hilbert action when we consider a four dimensional spacetime. In this work, we obtain solutions corresponding to static spherically symmetric black holes with a cloud of strings and surrounded by quintessence. The study of the thermodynamical properties of these black holes is performed, with special emphasis on the mass, entropy, Hawking temperature and heat capacity. The graphs corresponding to the mass and the Hawking temperature are shown for different dimensions of spacetime, namely, $D = 4, 5, 6$ and 7. Concerning Hawking radiation, it is shown that the radiation spectrum is related to the change of entropy which codifies the presence of the cloud of strings as well as of the quintessence.

1 Introduction

The Theory of General Relativity (TGR) is indubitable the theory that describes the gravitational phenomena at large distances. On the other limit, namely at short distances, we expect that some corrections should be done in order to describe gravity appropriately. Thus, taking into account that TGR is a low energy effective theory, we can, in principle, extend it in order to describe the regime of high energy. One of those extensions is obtained by introducing high powers of curvature tensors in the standard Einstein–Hilbert action, in such way that we recover this action by taking the dimension of spacetime equal to four. Among this class of extensions for higher dimensional gravity, we can mention Lovelock gravity [1], which can be obtained as the low energy limit of a string theory [2].

The Lovelock gravity is a natural extension of the TGR for $D \ge 5$, in the sense that it contains the most general tensor satisfying properties of the Einstein tensor in high dimensional spacetime [1]. This extension, which represents one of a class of general higher order curvature theories [3], has some desirable characteristics, as for example, it satisfies the general covariance criteria and its fields equations are of second order in the derivatives of the metric. In addition, it is free from ghosts, which means that there is no problem in which concerns unitarity.

Black holes are very important and fascinating structures which appear in any theory of gravity. They can provide some insight with respect to the understanding of aspects concerning an eventual formulation of quantum gravity, as well as some comprehension of their thermodynamical properties. In view of these points and many others, there has been during last years an interest in these structures, specially in the context of higher dimensions. Then, there are good reasons to obtain black hole solutions in different theories of gravity. In special, some exact solutions describing black holes were obtained in the framework of Lovelock gravity [4,5,6,7,8,9], when a cloud of strings is taken into account [10,11,12] as well as when the black holes are surrounded by quintessence [13, 14]. Others studies concerning the scenario with a cloud of strings include the analysis of the thermodynamical properties [15] and the tensor quasinormal modes [16].

The main idea of the string theory is that the building blocks of nature are one-dimensional strings, instead of particles, which are zero-dimensional objects. An extension of this idea is to consider a cloud of strings and study its possible measurable effects on long range gravitational fields of some sources, as for example, black holes. On the other hand, the possible existence of strings in the early universe is in accordance with observations. These two points suggest us that it is necessary and important take these objects into account with the proposal to know all the features of strings in different scenarios, in gravitational and cosmological scales.

The theoretical analysis of these cloud of strings was performed by Letelier [17]. In this context, Letelier [17] obtained a generalization of the Schwarzschild solution corresponding to a black hole surrounded by a spherically symmetric cloud of strings as well as some others interesting results [18, 19]. Thus, assuming that these strings are fundamental objects, it seems natural to consider their extension to gravitational theories that go beyond Einstein’s gravity, since the low energy limit of string theory implies the natural generalization of the TGR to higher dimensions, as for example in Lovelock gravity [1] which we are interested in this paper.

In the last twenty years, high-precision data obtained through the observation have confirmed the possible existence of a kind of cosmic dark energy which is gravitationally repulsive at global scale and for this reason should be the source responsible for the accelerated expansion [20]. This possible candidate for dark energy, which is characterized by a equation of state $p_q = \omega _q \rho _q$, where $p_q$ is the pressure, $\rho _q$ is the energy density and $\omega _q$ is a parameter assuming values in the interval $-1< \omega _q < -1/3$, has nature and origin still unknown. It is called quintessential dark energy or simply quintessence. Its effects has been measured accurately [20]. The quintessence is not the only possible candidate to produce this accelerated expansion. In fact, there are other candidates as the cosmological constant [21, 22], among others.

At astrophysics scales, the presence of quintessence surrounding black holes should produces some additional effects, as for example, the shift of light coming from distant stars [23]. Therefore, in order to understand these effects produced by black holes in any theory of gravity and know the different insights they could provide, it is necessary to consider a scenario in which black hole surrounded by quintessence are considered and, for this source, solve the Einstein equations. The analytical solutions with spherical symmetry were first obtained by Kiselev [24], in which case quintessence surrounds a static black hole. It was also obtained the generalization of the Kiselev solutions [24] by constructing their rotating counterpart [25, 26].

Therefore, taking into account the role played by Lovelock gravity among the class of generalizations of TGR to higher dimensions and the importance of black holes, it seems to be relevant to analyse how higher order curvature corrections changes substantially the gravitational field generated by these objects and, as a consequence, their physical properties.

The study of black hole thermodynamics is a powerful tool to give us some insights about different aspects of the black hole physics, specially, due to the fact that the thermodynamical properties of the black holes are strongly related to statistical mechanics [27,28,29]. In this scenario, we find a result which tells us that black holes emit radiation with a black body spectrum [30]. This radiation is called Hawking radiation.

It is the purpose of this paper to obtain exact solutions corresponding to static spherically symmetric black holes with a cloud of string and surrounded by quintessence in the Lovelock gravity and explicitly show the effect of the cloud of strings as well as of quintessence in this context. Thus, we analyse some aspects of thermodynamics of these black holes through the calculation of entropy, heat capacity and Hawking temperature.

This paper is organized as follows. In Sect. 2, we present a brief review of the Lovelock gravity, cloud of strings and quintessence. In Sect. 3, we obtain the static black hole solutions with a cloud of strings and surrounded by quintessence. Section 4 is devoted to thermodynamics and Sect. 5 to Hawking radiation. Finally, in Sect. 6, we present the concluding remarks. We will adopt units for which $G = c = 1$ and the metric signature $(+,-,-,-)$.

2 Lovelock gravity

Lovelock gravity represents a generalization of TGR to higher dimensions. It was proposed in the early seventies of the last century by Lovelock [1] and corresponds to the most general extension of the TGR to higher dimensions that preserves the order of derivatives in relation to metric, and thus the equation of motion are of second order. It is also connected with string theory [31].

In Lovelock gravity in D-dimensions, the action is given by [13, 32]:

$$\begin{aligned} \mathcal {I} = \mathcal {I}_L+\mathcal {I}_M = \frac{1}{2} \int _{\mathcal {M}} d x^D \sqrt{-g}\mathcal {L}+\mathcal {I}_M \end{aligned}$$

(1)

where $\mathcal {I}_M$ is the action related to the matter fields and

$$\begin{aligned} \mathcal {L} =\sum _{p=0}^{(D-1)/2}\alpha _p \mathcal {L}_p, \end{aligned}$$

(2)

where $\alpha _p$ are coupling constants and

$$\begin{aligned} \mathcal {L}_p = \frac{1}{2^p}\delta ^{\mu _1 \cdots \mu _p \nu _1\cdots \nu _p}_{\alpha _1\cdots \alpha _p \beta _1\cdots \beta _p} R^{\alpha _1 \beta _1}_{\phantom {xxx}\mu _1 \nu _1}\cdots R^{\alpha _p \beta _p}_{\phantom {xxx}\mu _p \nu _p}. \end{aligned}$$

(3)

The generalized Kronecker delta, $\delta ^{\mu _1 \cdots \mu _p \nu _1\cdots \nu _p}_{\alpha _1\cdots \alpha _p \beta _1\cdots \beta _p}$, is totaly antisymmetric by permutation of any index and could be obtained by

$$\begin{aligned} \delta ^{\mu _1 \cdots \mu _p }_{\alpha _1\cdots \alpha _p} = p! \delta ^{\mu _1 \cdots \mu _p}_{[\alpha _1\cdots \alpha _p]}. \end{aligned}$$

(4)

For $\mathcal {L}_1 = R$ and $\alpha _p = 0$, for $p \ne 1$, we reobtain the Einstein–Hilbert action. In the particular case where $\alpha _p = 0$, for $p >3$, we get the Lagrangian of Gauss–Bonnet gravity. The parameter $\alpha _0$ is such that $\alpha _0 = - 2 \varLambda$, where $\varLambda$ is the cosmological constant. Taking the variation of the Lovelock action with respect to the metric, we find the generalized Einstein equation

$$\begin{aligned} G_{\mu \nu } = -\frac{\alpha _0}{2} g_{\mu \nu } + G^E_{\mu \nu } + \mathcal {G}_{\mu \nu } = T_{\mu \nu }, \end{aligned}$$

(5)

where $G_{\mu \nu }^E$ is the Einstein tensor, $T_{\mu \nu }$ is the energy-momentum tensor given by

$$\begin{aligned} T_{\mu \nu } = \frac{2}{\sqrt{-g}}\frac{\delta \mathcal {I}_M}{\delta g^{\mu \nu }}, \end{aligned}$$

(6)

and

$$\begin{aligned} G_{\mu \nu } = \frac{2}{\sqrt{-g}}\frac{\delta \mathcal {I}_L}{\delta g^{\mu \nu }}. \end{aligned}$$

(7)

3 Cloud of strings and quintessence

3.1 Cloud of strings

The first studies concerning a formalism to treat gravity with a cloud of strings as source, in the framework of TGR, was presented by Letelier [17]. By using this formalism, he obtained a generalization of the Schwarzschild solution corresponding to a black hole surrounded by a spherically symmetric cloud of strings, whose energy-momentum tensor is given by

$$\begin{aligned} T^t_{\phantom {t}t}= & {} T^r_{\phantom {r}r} = \rho _c = \frac{a}{r^2} \end{aligned}$$

(8a)

$$\begin{aligned} T^\theta _{\phantom {t}\theta }= & {} T^\phi _{\phantom {t}\phi } = 0, \end{aligned}$$

(8b)

where $\rho _c$ is the energy density of the cloud and a is an integration constant associated with the presence of the string. Solving the Einstein’s equations taking into account the source given by Eq. (8), he found that the space-time metric is given by [17]

$$\begin{aligned} ds^2= & {} \left( 1 -a-\frac{2 M}{r}\right) dt^2 -\left( 1 -a-\frac{2 M}{r} \right) ^{-1}\nonumber \\&dr^2 - r^2 d\varOmega ^2. \end{aligned}$$

(9)

On the other hand, the solution corresponding to a black hole with a cloud of strings, in a D-dimensional spacetime, is given by the general form [11]

$$\begin{aligned} ds^2 = f(r) dt^2 -\frac{1}{f(r)} dr^2 - r^2 d \varOmega _{D-2}^2, \end{aligned}$$

(10)

with the energy–momentum tensor corresponding to a spherically symmetric cloud of strings being given by[11, 12]

$$\begin{aligned} T^\mu _{\phantom {x} \nu } = \frac{a}{r^{D-2}}[1,1,0,\ldots ,0]. \end{aligned}$$

(11)

In this case, we find

$$\begin{aligned} f(r) = 1-\frac{\mu }{r^{D-3}} - \frac{2a}{(D-2)r^{D-4}}, \end{aligned}$$

(12)

where

$$\begin{aligned} \mu = \frac{2M}{(D-2)\varSigma _{D-2}}, \end{aligned}$$

(13)

and

$$\begin{aligned} \varSigma _{D-2} = \frac{2 \pi ^{(D-1)/2}}{\varGamma [(D-1)/2]}. \end{aligned}$$

(14)

is the volume of a $D-2$ dimensional sphere with radius equal to unit. In this work we will consider, for simplicity, $M = 8 \pi M_o$, where $M_o$ is the black hole mass in the Schwarzschild solution.

3.2 Quintessential dark energy

Recently, it was obtained the solution corresponding to a black hole immersed in quintessence, whose line element is given by [24]

$$\begin{aligned} ds^2= & {} \left( 1 -\frac{2 M}{r} - \frac{q}{r^{3\omega _q+1}}\right) dt^2 \nonumber \\&-\left( 1 -\frac{2 M}{r} - \frac{q}{r^{3\omega _q+1}}\right) ^{-1}dr^2 - r^2 d \varOmega ^2 \end{aligned}$$

(15)

where M is the mass of the black hole, $\omega _q$ is the quintessential state parameter and q is the quintessential parameter associated to the density of quintessence defined bellow. The pressure and density of quintessence are related by the equation of state $p_q = \omega _q \rho _q$, with $\rho _q$ given by

$$\begin{aligned} \rho _q = - \frac{q}{2} \frac{3 \omega _q}{r^{3 ( \omega _q +1)}}. \end{aligned}$$

(16)

In order to get the scenario of accelerated expansion, it is necessary to impose that $- 1<\omega < - 1/3$. As to q, it is a positive parameter and note that, when $q = 0$, we recover the Schwarzschild solution.

Following the results given by Kiselev [24], the energy–momentum tensor will be given by

$$\begin{aligned} T^t_{\phantom {t}t}= & {} T^r_{\phantom {r}r} = \rho _q \end{aligned}$$

(17a)

$$\begin{aligned} T^\theta _{\phantom {t}\theta }= & {} T^\phi _{\phantom {t}\phi } = -\frac{1}{2} \rho _q (3 \omega _q+1). \end{aligned}$$

(17b)

Thus, in D-dimensions, the solution corresponding to a black hole surrounded by quintessence is written in the same form of Eq. (9), where [13]

$$\begin{aligned} f(r) = 1 -\frac{\mu }{r^{D-3}} - \frac{q}{r^{(D-1)\omega _q +D-3}}, \end{aligned}$$

(18)

where $\mu$ and q are constants. The energy-momentum tensor is given by

$$\begin{aligned} T^t_{\phantom {t}t}= & {} T^r_{\phantom {r}r} = \rho _q = -\frac{\omega _q q (D-1)(D-2)}{2r^{(D-1)(\omega _q+1)}} \end{aligned}$$

(19a)

$$\begin{aligned} T^{\theta _1}_{\phantom {t}\theta _1}= & {} \cdots = T^{\theta _{D-2}}_{\phantom {t}\theta _{D-2}} = -\frac{1}{D-2} \rho _q [(D-1) \omega _q+1], \end{aligned}$$

(19b)

where $\theta _i (i=1,2,\ldots ,D-2)$ are the $D-2$ variables which describe the space-time section with constant curvature.

4 D-dimensional Lovelock black holes with a cloud of strings and surrounded by quintessence

Let us assume that [6, 9, 13]

$$\begin{aligned} f(r) = \kappa - r^2F(r), \end{aligned}$$

(20)

where F(r) is a solution of the polynomial equation

$$\begin{aligned} P(F)= & {} \sum _{p=0}^m \widetilde{\alpha }_p F^p = \frac{2M}{(D-2)\varSigma _{D-2}r^{D-1}} \nonumber \\&+\frac{q}{r^{(D-1)(\omega _q+1)}}-\frac{2a}{(D-2)r^{D-2}}, \end{aligned}$$

(21)

with

$$\begin{aligned} \widetilde{\alpha }_0= & {} \frac{\alpha _0}{(D-1)(D-2)} \end{aligned}$$

(22a)

$$\begin{aligned} \widetilde{\alpha }_1= & {} 1 \end{aligned}$$

(22b)

$$\begin{aligned} \widetilde{\alpha }_p= & {} \prod ^{2p}_{i=3} (D-i) \alpha _p, \quad p>1. \end{aligned}$$

(22c)

Thus, we get the results for 4-dimensional space-time, in which case f(r) is written as

$$\begin{aligned} f(r) = 1 -a -\frac{2M}{r} -\frac{q}{r^{3 \omega _q+1}}, \end{aligned}$$

(23)

when we take $\kappa = 1$ and $\alpha _p = 0$ for $p \ge 2$. In general, for $D>4$ and $\kappa = 1$, $\alpha _p = 0$, $p \ge 2$, we find

$$\begin{aligned} f(r) = 1 - \frac{\mu }{r^{D-3}} -\frac{q}{r^{(D-1)\omega _q+D-3}}- \frac{2 a}{(D-2)r^{D-4}}. \end{aligned}$$

(24)

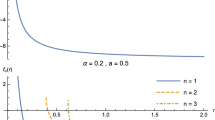
The behaviour of this function, for different values of $\omega _q$ and a, are represented by Figs. 1 and 2 in the case of D-dimensional gravity.

Fig. 1

The function f(r) in D-dimensional gravity for $\omega _q = -2/3$, $q = 0.1$, $M = 1$ and for differents values of a and D

Fig. 2

The function f(r) in D-dimensional gravity for $\omega _q = -2/3$, $a = 0.8$, $M = 1$ and for differents values of q and D

The Gauss–Bonnet solution is obtained when $\alpha _2 \ne 0$ and $\alpha _p = 0$, for $p \ge 3$.

Considering the method above described, we obtain two classes of black holes appropriately described by taking the function $f_+(r)$ or $f_-(r)$, which are given by

$$\begin{aligned}&f_{\pm } = 1+\frac{r^2}{2 \widetilde{\alpha }_2} \nonumber \\&\quad \times \left( 1 \pm \sqrt{1+ \frac{8 \widetilde{\alpha }_2 M}{(D-2)\varSigma _{D-2}r^{D-1}}+\frac{4q \widetilde{\alpha }_2}{r^{(D-1)(\omega _q+1)}}-\frac{8a \widetilde{\alpha }_2}{(D-2)r^{D-2}}} \right) .\nonumber \\ \end{aligned}$$

(25)

where

$$\begin{aligned} \widetilde{\alpha }_2 = (D-3)(D-4) \alpha _2. \end{aligned}$$

(26)

Note that when $r \rightarrow \infty$ and taking $q = 0$, which means that there is no quintessence, we obtain [11]:

$$\begin{aligned} f_+ \rightarrow 1 + \frac{r^2}{\widetilde{\alpha }_2}, \quad f_- \rightarrow 1. \end{aligned}$$

(27)

Thus, we verified that $f_-$ tends to the flat spacetime very far from the black hole. Otherwise, $f_+$, at large distances from the black hole, gives us the anti-de Sitter metric. If we take into account the quintessence ($q \ne 0$), we have the behaviors influenced by this quantity, as explicitly shown in Eq. (25). For different values of $\omega _q$ and a, the function $f_+(r)$ is represented in Figs. 3 and 4 in the case of Gauss–Bonnet gravity.

Fig. 3

The function f(r) in the Gauss–Bonnet gravity for $\omega _q = -2/3$, $M = 1$ and $\alpha _2 = 1$

Fig. 4

The function f(r) in the Gauss–Bonnet gravity for $\omega _q = -2/3$, $M = 1$ and $\alpha _2 = 1$

5 Black hole thermodynamics

In this section, we will analyze the thermodynamics of black holes with a cloud of strings and surrounded by quintessence in the Lovelock gravity in D-dimensions, following straightforwardly the results recently obtained in the literature [6, 9, 13]. From Eq. (20), we find that the coordinates $r_h$ of the event horizon are calculated from

$$\begin{aligned} r^2_h = \frac{\kappa }{F(r_h)}. \end{aligned}$$

(28)

Thus, using Eq. (21), we find that the mass of the black hole is

$$\begin{aligned} M= & {} \frac{(D-2)\varSigma _{D-2}}{2} \left[ \sum ^{m}_{p=0} \frac{\widetilde{\alpha }_p \kappa ^p}{r_h^{-(D-2p-1)}}\right. \nonumber \\&\left. -\frac{q}{r_h^{(D-1)\omega _q}} - \frac{2a r_h}{D-2} \right] . \end{aligned}$$

(29)

The Hawking temperature is calculated from the expression

$$\begin{aligned} T= & {} \frac{f'(r)}{4 \pi } =\frac{1}{4 \pi N(r_h)}\left[ \sum _{p = 0}^{m}\frac{\widetilde{\alpha }_p \kappa ^p(D-2p-1)}{r_h^{2p+2}}\right. \nonumber \\&\left. +\frac{q \omega _q(D-1)}{r_h^{(D-1)\omega _q+D+1}} -\frac{2a}{(D-2)r_h^{D}}\right] , \end{aligned}$$

(30)

where

$$\begin{aligned} N(r_h) = \sum ^{m}_{p = 1} \frac{\widetilde{\alpha }_p p \kappa ^{p-1}}{r_h^{2p+1}}. \end{aligned}$$

(31)

According to the first law of thermodynamics, the entropy is calculated using the following expression

$$\begin{aligned} S = \int \frac{dM}{T} = \int \frac{1}{T} \frac{dM}{dr_h} dr_h, \end{aligned}$$

(32)

and is given explicitly by [13]

$$\begin{aligned} S = 2 \pi (D-2) \varSigma _{D-2} \sum ^m_{p=1} \frac{\widetilde{\alpha }_p \kappa ^{p-1}p}{(D-2)r_h^{-(D-2p)}}. \end{aligned}$$

(33)

From the above result, we conclude that the area law is fulfilled when $\kappa = 0$. In this case, we find

$$\begin{aligned} S = 2 \pi r_{h}^{D-2}\varSigma _{D-2} = 2 \pi A_{D-2} = \frac{A_{D-2}}{4}. \end{aligned}$$

(34)

The heat capacity is given by

$$\begin{aligned} C = \frac{dM}{dT} = \frac{dM}{dr_h}\frac{dr_h}{dT} = 2 \pi (D-2)\varSigma _{D-2}\frac{c_1 c_2^2}{c_3}, \end{aligned}$$

(35)

where

$$\begin{aligned} c_1= & {} \sum _{p=0}^{m} \frac{(D-2p-1)\widetilde{\alpha }_p \kappa ^p}{r_h^{-D+2p+2}} +\frac{(D-1)\omega _q q}{r^{(D-1) \omega _q +1}} -\frac{2a}{D-2} \end{aligned}$$

(36a)

$$\begin{aligned} c_2= & {} \sum _{p=1}^{m} \frac{\widetilde{\alpha }_pp \kappa ^{p-1}}{r_h^{-(D-2p-1)}} \end{aligned}$$

(36b)

$$\begin{aligned} c_3= & {} \sum _{p,s = 0}^{m}(D-2s-1)(2p-2s-1) \frac{\widetilde{\alpha }_p \widetilde{\alpha }_s \kappa ^{p+s-1}s}{r_h^{-2(D-s-p-2)}}\nonumber \\&-\sum _{p=1}^{m} \left[ (D-1) \omega _q +1 + (D-2p-1)\right] \nonumber \\&\times \frac{q \omega _q(D-1)}{r_h^{(D-1)\omega _q+1}} \frac{\widetilde{\alpha }_pp \kappa ^{p-1}}{r_h^{-(D-2p-2)}} \nonumber \\&+ \frac{2a}{D-2}\frac{\widetilde{\alpha }_pp \kappa ^{p-1}}{r_h^{-(D-2p-2)}}. \end{aligned}$$

(36c)

5.1 D-dimensional black hole

In this section, we will use previous results to analyze the thermodynamics of a D-dimensional black hole with a cloud of strings and surrounded by quintessence, by considering $\alpha _p = 0$, $p \ge 2$, and $D>4$. Note that, in this case, the mass of the black hole (Figs. 5, 6) can be written as

$$\begin{aligned} M =\frac{(D-2)\varSigma _{D-2}}{2} \left[ r_h^{(D-3)} -\frac{q}{r_h^{(D-1)\omega _q}} - \frac{2a r_h}{D-2} \right] . \end{aligned}$$

(37)

Fig. 5

Mass of black holes in D-dimensional TGR as a function of $r_h$ for different values of a

Fig. 6

Mass of black holes in D-dimensional TGR as a function of $r_h$ for different values of q

The Hawking temperature (Figs. 7, 8) is given by

$$\begin{aligned} T= \frac{r_h^3}{4 \pi } \left[ \frac{D-3}{r_h^{4}} +\frac{q\omega _q(D-1)}{r_h^{(D-1)\omega _q+D+1}} -\frac{2a}{(D-2)r_h^D} \right] . \end{aligned}$$

(38)

It is worth calling attention to the fact that, in this case, the entropy is proportional to the area of the event horizon, namely,

$$\begin{aligned} S= 2 \pi \varSigma _{D-2}r_h^{D-2}, \end{aligned}$$

(39)

as in the case of TGR in 4-dimensions.

Fig. 7

The Hawking temperature in D-dimensional TGR as function of $r_h$ for different values of a

Fig. 8

The Hawking temperature in D-dimensional TGR as function of $r_h$ for different values of q

For a black hole in D-dimensional spacetime, we can calculate the heat capacity using Eq. (35), with

$$\begin{aligned} c_1= & {} \frac{D-3}{r_h^{-D+4}} +\frac{(D-1)\omega _q q}{r^{(D-1)\omega _q +1}} -\frac{2a}{D-2} \end{aligned}$$

(40a)

$$\begin{aligned} c_2= & {} \frac{1}{r_h^{-D+3}} \end{aligned}$$

(40b)

$$\begin{aligned} c_3= & {} \frac{3-D}{r_h^{-2(D-4)}} -[(D-1)\omega _q+1+(D-3)] \nonumber \\&\times \frac{(D-1)q\omega _q}{r_h^{(D-1)\omega _q+1}} \frac{1}{r_h^{-(D-4)}} \frac{2a}{D-2}\frac{1}{r_h^{-(D-4)}}. \end{aligned}$$

(40c)

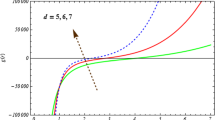
In Figs. 9 and 10, we show the heat capacity of the black hole for different values of the quintessential parameter as well as for the parameter which takes care of the presence of the cloud of strings.

The heat capacity can be used as criterium to study the stability of a thermodynamical system [13, 33]. As an example, we can mention that when the heat capacity is negative, then the system is thermodynamically unstable, as in the case of Schwarzschild black hole. Otherwise, the presence of quintessence can induces the stabilization of a Reissner–Nordstrom black hole [34].

Fig. 9

The heat capacity in D-dimensional TGR as function of $r_h$ for different values of q

Fig. 10

The heat capacity in D-dimensional TGR as function of $r_h$ for different values of q

Analyzing Figs. 9 and 10, we conclude that there are some regions of stability which depends on the values of q, as well as on the dimension of spacetime. It is worth calling attention to the fact that there is a phase transition for a certain value of the coordinate of the horizon, $r_h$. In Fig. 9, it is shown separately the particular case $D=4$, in which is evident the existence of regions in which the black hole is unstable, as well as regions in which it is stable, from the thermodynamical point of view. In the same way, it is shown in Fig. 10 the particular case $D=4$, separately, in order to evidentiate the fact that for the chosen value of q, the black hole is thermodynamically unstable.

5.2 Black hole in Gauss–Bonnet gravity

Now, let us consider the same black holes in the framework of Gauss–Bonnet gravity (Figs. 11, 12). In this case, we impose that $\widetilde{\alpha }_1 =\widetilde{\alpha }_2= 1$ and $\widetilde{\alpha }_p =0$, for $p>2$. The mass parameter will be given by

$$\begin{aligned} M =\frac{(D-2)\varSigma _{D-2}}{2} \left[ r_h^{D-3}+r_h^{D-5} -\frac{q}{r_h^{(D-1)\omega _q}} - \frac{2a r_h}{D-2} \right] , \end{aligned}$$

(41)

whose behavior is given in Fig. 9.

Fig. 11

Mass in Gauss–Bonnet gravity as function of $r_h$, for $a = 0.8$ and $q = 0.1$

Otherwise, the Hawking temperature is given by

$$\begin{aligned} T= & {} \frac{r_h^5}{4 \pi (2+r_h^2)} \left[ \frac{D-3}{r_h^{4}}+\frac{D-5}{r_h^6} \right. \nonumber \\&\left. +\frac{q\omega _q(D-1)}{r_h^{(D-1)\omega _q+D+1}} -\frac{2a}{(D-2)r_h^D} \right] . \end{aligned}$$

(42)

Fig. 12

Hawking temperature in Gauss–Bonnet gravity as function of $r_h$, for $a = 0.8$ and $q = 0.1$

In the case of Gauss–Bonnet gravity, the heat capacity is given by Eq. (35), where the parameters $c_1$, $c_2$ and $c_3$ are

$$\begin{aligned} c_1= & {} \frac{D-3}{r_h^{-D+4}}+ \frac{D-5}{r_h^{-D+6}} +\frac{(D-1)\omega _q q}{r^{(D-1)\omega _q +1}} -\frac{2a}{D-2} \end{aligned}$$

(43a)

$$\begin{aligned} c_2= & {} \frac{1}{r_h^{-D+3}}+\frac{2}{r_h^{-D+5}} \end{aligned}$$

(43b)

$$\begin{aligned} c_3= & {} \frac{3-D}{r_h^{-2(D-4)}}+\frac{-6(D-5)+D-3}{r_h^{-2(D-5)}} +\frac{2(5-D)}{r_h^{-2(D-6)}}\nonumber \\&-[(D-1)\omega _q+1 +(D-3)]\frac{(D-1)q\omega _q}{r_h^{(D-1)\omega _q+1}} \frac{1}{r_h^{-(D-4)}} \nonumber \\&-[(D-1)\omega _q+1 +(D-5)]\frac{(D-1)q\omega _q}{r_h^{(D-1)\omega _q+1}} \frac{1}{r_h^{-(D-6)}} \nonumber \\&+\frac{2a}{D-2}\frac{1}{r_h^{-(D-4)}}+\frac{2a}{D-2} \frac{1}{r_h^{-(D-6)}}. \end{aligned}$$

(43c)

From Fig. 13, we conclude that there are regions which are thermodynamically stables and unstables depending on the dimension of the spacetime.

Fig. 13

Heat capacity in Gauss–Bonnet gravity as function of $r_h$, for $a = 0.8$ and $q = 0.1$

5.3 Black hole in third order Lovelock gravity

In this section, we will analyze the behaviors of the mass parameter and the Hawking temperature in the third order Lovelock gravity, that is for $\widetilde{\alpha }_1 =\widetilde{\alpha }_2=\widetilde{\alpha }_3= 1$ and $\widetilde{\alpha }_p =0$for $p>3$. In this case, the mass parameter is given by Fig. 11.

(44)

whose behavior is represented in Fig. 11.

Fig. 14

Mass in third order Lovelock gravity as function of $r_h$, for $a = 0.8$ and $q = 0.1$

In this case, the Hawking temperature is given by

$$\begin{aligned} T= & {} \frac{r_h^7}{4 \pi (3+2r_h^2+r_h^4)} \left[ \frac{D-3}{r_h^{4}}+\frac{D-5}{r_h^6}+\frac{D-7}{r_h^8} \right. \nonumber \\&\left. +\frac{q\omega _q(D-1)}{r_h^{(D-1)\omega _q+D+1}} -\frac{2a}{(D-2)r_h^D} \right] . \end{aligned}$$

(45)

Fig. 15

Hawking temperature in third order Lovelock gravity as function of $r_h$, for $a = 0.8$ and $q = 0.1$

Finally, the heat capacity in the third order Lovelock gravity, which was obtained using Eq. (35), and coefficients $c_1$, $c_2$ and $c_3$ given by

$$\begin{aligned} c_1= & {} \frac{D-3}{r_h^{-D+4}}+ \frac{D-5}{r_h^{-D+6}}+ \frac{D-7}{r_h^{-D+8}} \nonumber \\&+\frac{(D-1)\omega _q q}{r^{(D-1)\omega _q +1}} -\frac{2a}{D-2} \end{aligned}$$

(46a)

$$\begin{aligned} c_2= & {} \frac{1}{r_h^{-D+3}} +\frac{2}{r_h^{-D+5}}+\frac{3}{r_h^{-D+7}} \end{aligned}$$

(46b)

$$\begin{aligned} c_3= & {} \frac{3-D}{r_h^{-2(D-4)}}+\frac{-6(D-5) +D-3}{r_h^{-2(D-5)}}\nonumber \\&+\frac{-12(D-7)-2(D-5)+3(D-3)}{r_h^{-2(D-6)}} \nonumber \\&+\frac{-9(D-7)+3(D-5)}{r_h^{-2(D-7)}} +\frac{-3(D-7)}{r_h^{-2(D-8)}}\nonumber \\&-[(D-1)\omega _q+1 +(D-3)]\frac{(D-1)q\omega _q}{r_h^{(D-1)\omega _q+1}} \frac{1}{r_h^{-(D-4)}} \nonumber \\&-[(D-1)\omega _q+1 +(D-5)]\frac{(D-1)q\omega _q}{r_h^{(D-1)\omega _q+1}} \frac{1}{r_h^{-(D-6)}} \nonumber \\&-[(D-1)\omega _q+1 +(D-7)]\frac{(D-1)q\omega _q}{r_h^{(D-1)\omega _q+1}} \frac{1}{r_h^{-(D-8)}} \nonumber \\&+\frac{2a}{D-2}\frac{1}{r_h^{-(D-4)}}+\frac{2a}{D-2} \frac{1}{r_h^{-(D-6)}} +\frac{2a}{D-2}\frac{1}{r_h^{-(D-8)}} , \end{aligned}$$

(46c)

which shows us the existence of phase transitions for the different dimensions of spacetime (Figs. 14, 15, 16).

Fig. 16

Heat capacity in third order Lovelock gravity as function of $r_h$, for $a = 0.8$ and $q = 0.1$

6 Hawking radiation

Now, let us consider the phenomenon pointed by Hawking [29] concerning the radiation of particles by a black hole. Taking $r_+$, the coordinate r of the event horizon far away from the black hole,we can write [35]:

$$\begin{aligned} dT = dt + \frac{1}{f(r)}\sqrt{\frac{r_+}{r}}dr. \end{aligned}$$

(47)

Thus, the metric given by Eq. (10) turns into:

$$\begin{aligned} ds^2= & {} -f(r) dT^2 + 2\sqrt{\frac{r_+}{r}}dT dr\nonumber \\&+\frac{r-r_+}{r}\frac{1}{f(r)}dr^2 + r^2 d \varOmega _{D-2}. \end{aligned}$$

(48)

As we can verify, $r=r_+$ is not a singularity of this spacetime [35]. The null radial geodesic is obtained from

$$\begin{aligned} \frac{dr}{dT} = f(r) \left( 1+ \sqrt{\frac{r_+}{r}} \right) ^{-1}. \end{aligned}$$

(49)

Therefore, the imaginary part of the action corresponding to the particle which crosses the horizon is given by:

$$\begin{aligned} Im Z= & {} Im \int ^{T_f}_{T_i} L dT = Im \int ^{r_f}_{r_i} p_r dr \nonumber \\= & {} Im \int ^{r_f}_{r_i} \int ^{p_r}_{0} dp_r dr, \end{aligned}$$

(50)

where $p_r$ is the canonical momentum associated with the coordinate r. Thus, using the relation $\dot{r} = \frac{dH}{dp_r} \big |_r$ and the fact that $(dH_r) = dM$, we find the following result:

$$\begin{aligned} Im Z= & {} Im \int ^{M_f}_{M_i} \int ^{r_f}_{r_i}\frac{dr}{\dot{r}}dM \nonumber \\= & {} Im \int ^{M_f}_{M_i} \int ^{r_f}_{r_i}\frac{1+\sqrt{r_+/r}}{f(r)}drdM, \end{aligned}$$

(51)

where $M_i = M$ is the original mass of the black hole and $M_f = M-\omega$ the mass after the emission of a particle with energy $\omega$. Note that the integrand has a pole at $r=r_+$, and thus we can calculate the contour integral around that pole as

$$\begin{aligned} ImZ= & {} -2 \pi \int ^{M_f}_{M_i} \frac{1}{f'(r_+)}dM \nonumber \\= & {} -2 \pi \int ^{r_{+f}}_{r_{+i}} \frac{1}{f'(r_+)}\frac{dM}{dr_+}dr_+. \end{aligned}$$

(52)

From Eqs. (20) and (29), we find

$$\begin{aligned} ImZ= & {} -\pi (D-2) \varSigma _{D-2} \sum ^m_{p=1} \frac{\widetilde{\alpha }_p \kappa ^{p-1}p}{(D-2)r_+^{-(D-2p)}}\Bigg |_{r_{+i}}^{r_{+f}}\nonumber \\= & {} -\frac{\varDelta S}{2}. \end{aligned}$$

(53)

Using a result from the WKB method, which tell us that the probability that a particle emitted by the black hole experience a tunneling is given by

$$\begin{aligned} \varGamma \sim exp(-2 Im Z), \end{aligned}$$

(54)

we find that

$$\begin{aligned} log \varGamma\sim & {} -\pi (D-2) \varSigma _{D-2} \left[ \sum ^m_{p=1} \frac{\widetilde{\alpha }_p \kappa ^{p-1}p}{(D-2)r_{+f}^{-(D-2p)}}\right. \nonumber \\&\left. - \sum ^m_{p=1} \frac{\widetilde{\alpha }_p \kappa ^{p-1}p}{(D-2)r_{+i}^{-(D-2p)}} \right] \end{aligned}$$

(55)

or

$$\begin{aligned} \varGamma \sim e^{\varDelta S}, \end{aligned}$$

(56)

which means that this probability is related to the change of the entropy of the black hole. Thus it depends on the event horizon which is influenced by the parameters associated with the presence of the cloud of strings as well as of the quintessence.

7 Concluding remarks

Lovelock theory consists in a natural generalization of the Theory of General Relativity to higher dimensions satisfying the criteria of general covariance and containing field equations with derivatives of the metric up to second order. In addition to this mathematical motivation, we can mention one of physical origin related to the fact that string theory, which contains higher order curvature corrections to the Einstein–Hilbert action, reduces to the Theory of General Relativity in the low energy limit.

Thus, we expect to naturally extend the TGR to those with higher powers of curvature in a D-dimensional spacetime, where $D>4$, which can be mapped into the Lovelock gravity.

In this framework, we obtained exact solutions corresponding to a static, spherically symmetric black hole with a cloud of strings and surrounded by quintessence in Lovelock gravity in a D-dimensional spacetime. Those solutions generalizes the ones corresponding to a black hole with a cloud of strings in the sense that quintessence was included and the dimensions of spacetime were enlarged. These solutions have a lot of rich properties and in appropriate limits reduces to black holes in the Theory of General Relativity.

The presence of the string cloud as well as of the quintessence affects the horizon in terms of which all thermodynamical quantities are given. Thus, the quantities are influenced by the presence of the cloud of strings and of the quintessence, for different values of the spacetime dimensions, namely $D=4,5,6$ and 7. Those values of dimensions were chosen in such a way to compare with the case $D=4$, which corresponds to the TGR.

Concerning the stability of the black holes, we obtained the heat capacity in terms of the horizon radius and through different figures we showed when this quantity is negative and when it is positive, that implies that the black holes are thermodynamically instable or stable, emphasizing the role played by the presence of the cloud of strings as well as of the quintessence in relation to the stabilization of the black hole, with special emphasis to the important role played by the dimension of the spacetime under consideration, for a particular set of values.

As to Hawking radiation, we discussed that radiation rate and showed that this quantity depends of the change of entropy which is given in terms of the event horizon which is strongly influenced by the presence of the cloud of strings as well as of the quintessence. Therefore, the Hawking radiation spectrum depends strongly on the presence of the cloud of strings and on the quintessence.