1 Introduction

The accelerated cosmic expansion is a crucial area of interest in cosmology and astrophysics, and various theories have been proposed to explain its current state. This expansion is mainly attributed to the impact of dark energy, which accounts for a significant portion of the universe’s total energy and has significant negative pressure. Despite extensive research, the nature of dark energy remains a significant challenge in cosmology [1,2,3]. Einstein’s theory of relativity has significantly contributed to unveiling the mysteries of the universe and revolutionized our understanding of space, time, and gravity [4]. Despite being a fundamental concept in modern physics, the theory of relativity has limitations in analyzing strong gravitational fields, explaining cosmic acceleration, and accounting for dark matter. To address these limitations, researchers have explored modified theories of gravity, which can provide better explanations than the classical theory in specific scenarios. Hence, it has become evident that the classical theory requires some modifications, to investigate cosmic expansion. Consequently, numerous theories have been put forth by modifying general relativity, including the f(R) [5,6,7,8], f(G) [9, 10], f(R, T) [11,12,13], f(R, G) [14], f(G, T) [15], f(Q) [16], and \(f(R,\phi , X)\) [17,18,19] theories of gravity. By presenting new cosmological perspectives and concepts, these theories not only aim to overcome the shortcomings of classical theory but also offer valuable insights into important issues such as dark energy and cosmic acceleration [20,21,22,23,24]. Bahamonde et al. [25] proposed \(f(R,\phi , X)\) theory of gravity, as an extension of f(R) gravity, which incorporates a scalar field \(\phi \) and a kinetic term X. The \(f(R,\phi , X)\) gravity has been extensively studied in recent years for its potential to explain and accelerate the cosmic expansion while still satisfying the weak energy condition [26,27,28,29].

Compact stars are the subject of extensive research in the field of astrophysics [30,31,32,33,34,35,36,37]. Hewish et al. [38] discovered the first pulsar by detecting a highly magnetized neutron star emitting periodic radio waves, revolutionizing the field of astrophysics. Consequently, this discovery of pulsars led to a paradigm shift in our understanding of regular stars, and prompted researchers to investigate physical processes that resulted in the formation of compact stars like neutron stars, white dwarfs, and black holes. When a star consumes its nuclear fuel, it undergoes stellar demise and forms a compact star, which is characterized by a higher density, a smaller radius, and the inability to resist gravitational collapse [39]. The discovery of anisotropic properties within the compact structures of stars was a significant development in astrophysics, pioneered by Ruderman [40]. In the literature [41], the stellar structures with anisotropic pressure have been investigated by means of the equation of state. While studying compact stars, it is highly appropriate to take into account the anisotropic form of modified gravity. Kalam et al. [42] used the Krori and Barua metrics to address the effects of anisotropic matter on compact objects. Bhar et al. [43] analyzed the possibility of compact stars in higher dimensions by examining the noncommutative anisotropic stars. The nature of compact stars can be further investigated through both general relativity and modified theories of gravity [44,45,46].

The fluid with anisotropic pressure, characterized by unequal principal stresses, has been a fundamental consideration in our study. The importance of anisotropic pressure as a starting point has been discussed, serving as a foundation for further investigation. Recent advancements in our understanding, as highlighted in Reference [47], have presented a new perspective on the justification of anisotropic pressure in fluid configurations. The results presented in [47] demonstrate that, even when the initial configuration is assumed to be isotropic, physical processes fundamental to star evolution will always tend to produce pressure anisotropy, especially in relativistic contexts. This insight reinforces the fact that anisotropic pressure is not only a plausible outcome but an expected feature in fluid systems undergoing dynamic changes.The important point to highlight is that equilibrium states in fluid systems are the outcomes of dynamic stages. Crucially, any anisotropy acquired during these dynamic stages persists, no matter how small, as the system reaches equilibrium. This idea is consistent with the ideas put forth in [47], where stellar evolution-related physical processes result in anisotropic pressure that is fundamental to the equilibrium configuration of the system.

Stability analysis of compact stars is a crucial aspect of modern astrophysics, providing insights into the internal structure, evolution, and dynamics of celestial objects. The stability of a compact star refers to its ability to maintain a balance between inward and outward forces. Fusion processes within compact objects generate energy, creating an outward pressure that counters the inward forces and prevents gravitational collapse. However, once the energy is consumed, the inward forces become dominant, causing the celestial object to collapse and leading to the formation of compact stars. Bondi [48] made a pioneering and significant contribution to investigating the stability of self-gravitating spheres by employing the adiabatic criterion. Chandrasekhar [49] employed the theoretical framework proposed by Bondi and utilized the adiabatic index to investigate the stability of compact objects, inspiring further research into the impact of physical variables on the stability of compact objects. Herrera et al. [50] investigated the effects of dissipation on the dynamical instability of fluid with spherically symmetric in the Newtonian and relativistic limits and concluded that instability is increased by Newtonian correction whereas relativistic correction reduced it. Chan et al. [51] investigated the effects of local anisotropy on the stability of compact objects and concluded that even small anisotropies in the unperturbed fluid can greatly impact system stability in both Newtonian and relativistic limits. The same authors [52] examined the impact of shearing forces and their corresponding viscosity and demonstrated that both factors decrease fluid instability in both the Newtonian and relativistic contexts.

One of the crucial techniques for analyzing stability in literature is perturbation analysis, which involves introducing perturbations to the physical variables of a compact object and analyzing their effects on its stability. The central theme of perturbation analysis is to comprehend the impact of perturbations in physical parameters on the stability of a compact object. This technique provides insights into the underlying physical processes that govern the behavior of self-gravitating compact objects. Regge et al. [53] analyzed the stability of relativistic objects by introducing a metric perturbation within the framework of general relativity and provided insights into the behavior of relativistic objects and their stability under different conditions.

The cracking and overturning approach was developed by Herrera [54], as an alternative approach to analyze the instabilities within the configuration of compact objects. When the equilibrium condition is disturbed, this approach aims to analyze the behavior of the fluid configuration within the object. It explicitly addresses the point of departure from equilibrium, where non-zero radial forces with different signs appear within the system. Cracking occurs when the perturbed radial force is directed inward in the inner part of the configuration and changes sign at a specific point \(\big (\frac{\delta \Omega }{\delta \rho }<0 \rightarrow \frac{\delta \Omega }{\delta \rho } >0\big )\). On the other hand, if the force is directed inward in the inner part and changes sign in the outer part \(\big (\frac{\delta \Omega }{\delta \rho } >0 \rightarrow \frac{\delta \Omega }{\delta \rho }<0\big )\), we refer to it as overturning. The cracking technique was elaborated on by Di Prisco et al. [55], who employed the Raychaudhuri equation to determine the necessary limitations for cracking. Herrera et al. [56] examined the effects of variations in local anisotropy on the cracking of compact objects through a Jeans instability analysis. Herrera and Varela [57] proposed the method to analyze the cracking in non-spherical systems by introducing axisymmetric perturbations in an ideal fluid configuration. Di Prisco et al. [58] examined the occurrence of cracking by employing perturbations in local anisotropy of self-gravitating compact objects. Abreu et al. [59] analyzed the occurrence of cracking by perturbing the density and local anisotropy of compact objects with the local and non-local equation of state. Abreu et al. [60] studied the stability of compact objects by analyzing the occurrence of cracking, utilizing the concept of density fluctuations and sound speeds. Azam et al. [61] investigated the effects of electromagnetic fields on the stability of charged compact objects through the concept of cracking. Azam et al. [62] investigated the cracking of PSR J1614-2230 in quadratic regime in the presence of electromagnetic fields and concluded that star exhibits cracking in the presence of charge. Sharif and Sobia [63] investigated the cracking of charged anisotropic fluid configuration using polytropic equation of state in the presence of electromagnetic field. Gonzalez et al. [64, 65] extended the notion of cracking by assuming density-dependent physical parameters and employing local density perturbations to both anisotropic and isotropic matter distributions. Azam et al. [66] investigated the impacts of density fluctuations on the stability of compact objects using the cracking technique in a linear regime. Azam and Mardan [67] investigated cracking in charged spherical polytropes by perturbing the physical parameters. Azam and Mardan [68] also analyzed the occurrence of cracking for certain values of density and other parameters in two distinct types of charged cylindrical polytropes. Gonzalez et al. [69] investigated the effects of density perturbations on the stability of isotropic and anisotropic matter configuration with barotropic equation of state in general relativity utilizing the concept of cracking. Sharif and Sobia [70] studied the stability of charged cylindrically symmetric compact object with anisotropic matter configuration by utilizing the concept of cracking and demonstrated that the models with a specific form of Chaplygin equation of state exhibits cracking and instability increases with higher charge parameter. Sharif and Sobia [71] investigated the cracking in anisotropic spherically symmetric matter configurations with a polytropic equation of state by employing density perturbations in matter variables. León et al. [72] discussed the occurrence of cracking in polytropic spherical compact objects by analyzing the effects of perturbations in energy density and local anisotropy, with the implication for the various astrophysical scenarios. Azam et al. [73] investigated the stability of anisotropic generalized polytropic models with charge using the concept of cracking and concluded that all the models retains stability when local density perturbation is applied. Noureen et al. [74] proposed a technique to observe cracking points by employing local density perturbation in f(R) gravity and investigated the stability of self-gravitating compact objects.

In this paper, we aim to investigate the stability of compact stars in \(f(R,\phi , X)\) gravity using the cracking technique. To achieve this, we employ local density perturbation in spherically symmetric spacetime with anisotropic matter distribution and examine the configuration for cracking and overturning points. This paper is structured in the following manner: In Sect. 2, we present the field equations of \(f(R,\phi , X)\) theory of gravity and formulate the expression for the hydrostatic equilibrium equation. Within this section, we also employ Krori Barua spacetime coefficients for the hydrostatic equilibrium equation. In Sect. 3, we acquire the expression of the distribution of radial forces to examine cracking within the configuration, by perturbing all physical variables using local density perturbation (LDP). Section 4 presents the matching conditions to acquire constants resulting from the Krori Barua approach. Section 5, presents the physical analysis via graphical illustrations of the distribution of radial forces for all the considered compact stars to validate the effectiveness of our developed technique. In Sect. 6, the fundamental physical motivation that underlies our research is discussed. Section 7, presents our concluding remarks, as well as an appendix and list of references.

2 Development of field equations in \(f({{\mathcal {R}}},\phi ,X)\) gravity

The Einstein Hilbert (EH) action for \(f(R,\phi ,X)\) is presented as [75,76,77],

$$\begin{aligned} S= \int d^4x \sqrt{-g} \bigg [\dfrac{1}{2K^{2}} f(R,\phi ,X)+ L_m\bigg ], \end{aligned}$$
(1)

here, \(L_{m}\) refers to the matter Lagrangian, g is the determinant of \(g_{\xi \eta }\), R represents the Ricci Scalar, \(\phi \) expressed as \(\phi \equiv \phi (r)\) and signifies the scalar field and X refers to the kinetic term expressed as

$$\begin{aligned} X= -\frac{\epsilon }{2}\partial _{\eta }\phi \partial ^{\eta }\phi , \end{aligned}$$
(2)

In this study, we employed the canonical scalar field by assigning a value of 1 to the parameter \(\epsilon \), which is given in Eq. (2) with the conditions that \(\epsilon =1\) signifies the canonical scalar field and \(\epsilon =-1\) corresponds to a non-canonical scalar field. Varying EH in Eq. (1) with respect to \(g_{\xi \eta }\), we obtain a modified set of field equations for the \(f({{\mathcal {R}}},\phi ,X)\) gravity, illustrated as

$$\begin{aligned}{} & {} f_{R}R_{\xi \eta }- \frac{1}{2}f g_{\xi \eta } - \nabla _\xi \nabla _\eta f_{R} + g_{\xi \eta }\nabla ^\alpha \nabla _\alpha f_{R} \nonumber \\{} & {} \quad - \frac{\epsilon }{2}f_{X}(\nabla _{\xi }\phi )(\nabla _{\eta }\phi ) = \kappa ^2 T^m_{\xi \eta }. \end{aligned}$$
(3)

To simplify the notation, we will use \(f\equiv f(R,\phi , X)\), where f is referred to as an analytic function that depends on R, \(\phi \), and X. Additionally, we will use \(f_{R}=\dfrac{\partial f}{ \partial R}\), \(f_{\phi }=\dfrac{\partial f}{ \partial \phi }\), and \(f_{X}=\dfrac{\partial f}{ \partial X}\). In the case of an anisotropic matter distribution, the corresponding energy-momentum tensor is expressed as

$$\begin{aligned} T^{m}_{\xi \eta }=(\rho +p_{t})u_{\xi }u_{\eta }-p_{t}g_{\xi \eta }+(p_{r}-p_{t})\upsilon _{\xi }\upsilon _{\eta }, \end{aligned}$$
(4)

\(T^{m}_{\xi \eta }\) incorporates the density, tangential, and radial pressures signified by \(\rho \), \(p_{t}\), and \(p_{r}\) respectively, and the four-velocity vectors specified as, \(u_{\xi }=e^{a/2}\delta ^{0}_{\xi }\) and \(\upsilon _{\eta }=e^{b/2}\delta ^{1}_{\eta }\). However, for dark matter in \(f(R,\phi , X)\) gravity, the energy-momentum tensor is expressed as.

$$\begin{aligned} T^{D}_{\xi \eta }= & {} \dfrac{1}{f_{R}}\bigg [\dfrac{1}{2}g_{\xi \eta }(f-Rf_{R})+\nabla _{\xi }\nabla _{\eta }f_{R}-g_{\xi \eta }\nabla _{\alpha }\nabla ^{\alpha }\nonumber \\{} & {} +\frac{\epsilon }{2}f_{X}(\nabla _{\xi }\phi )(\nabla _{\eta }\phi )\bigg ]. \end{aligned}$$
(5)

For our present analysis, we will analyze a static spherically symmetric spacetime, characterized by a line element given by:

$$\begin{aligned} d{s}^{2}=e^{a(r)}dt^{2}-e^{b(r)}d{r}^{2}-r^2(d{\theta }^{2}+sin^2{\theta }d{\phi }^{2}), \end{aligned}$$
(6)

here \(e^{a(r)}\) and \(e^{b(r)}\) signifies metric coefficients. An alternative formulation of the modified field equations, which incorporate both dark matter Eq. (5) and ordinary matter Eq. (4) is stated as

$$\begin{aligned} G_{\xi \eta }=R_{\xi \eta }-\dfrac{1}{2}R g_{\xi \eta }=\dfrac{1}{f_{R}}\bigg [T^{m}_{\xi \eta }+T^{D}_{\xi \eta }\bigg ]. \end{aligned}$$
(7)

The line element Eq. (6) and the energy-momentum tensor are used to develop the field equations, expressed as

$$\begin{aligned} G_{00}= & {} \dfrac{e^{a}}{f_{R}}\bigg [\rho +\dfrac{1}{2}f-\dfrac{1}{2}Rf_{R}\nonumber \\{} & {} +e^{-b}f_{R}^{''}+e^{-b}\bigg (\dfrac{b^{'}}{2}+\dfrac{2}{r}\bigg )f_{R}^{'}\bigg ], \end{aligned}$$
(8)
$$\begin{aligned} G_{11}= & {} \dfrac{1}{f_{R}}\bigg [p_{r}-\dfrac{e^{b}}{2}\bigg (f-Rf_{R}\bigg )\nonumber \\{} & {} -\bigg (\dfrac{a^{'}}{2}+b^{'}+\dfrac{2}{r}\bigg )f_{R}^{'}+\dfrac{1}{2}f_{X}\phi ^{'2}\bigg ], \end{aligned}$$
(9)
$$\begin{aligned} G_{22}= & {} \dfrac{r^{2}}{f_{R}}\bigg [p_{t}+\dfrac{1}{2}Rf_{R}-e^{-b}f_{R}^{''}\nonumber \\{} & {} -e^{-b}\bigg (\dfrac{a^{'}}{2}+\dfrac{b^{'}}{2}+\dfrac{1}{r}\bigg )f_{R}^{'}\bigg ], \end{aligned}$$
(10)
$$\begin{aligned} G_{33}= & {} \dfrac{r^{2}sin^{2}\theta }{f_{R}}\bigg [p_{t}+\dfrac{1}{2}Rf_{R}-\dfrac{1}{2}f\nonumber \\{} & {} -e^{-b}f_{R}^{''}-e^{-b}\bigg (\dfrac{a^{'}}{2}+\dfrac{b^{'}}{2}+\dfrac{1}{r}\bigg )f_{R}^{'}\bigg ]. \end{aligned}$$
(11)

Here we considered \(k=1\), \(f_{R}=\dfrac{\partial f}{ \partial R}\), \(f_{\phi }=\dfrac{\partial f}{ \partial \phi }\), and \(f_{X}=\dfrac{\partial f}{ \partial X}\) and used the prime symbol (\(\prime \)) to indicate derivatives with respect to ”r”. After manipulating the field equations Eqs. (7)–(11), we derived the hydrostatic equilibrium equation expressed as,

$$\begin{aligned}{} & {} \dfrac{dp_{r}}{dr}=e^{b}f_{R}\bigg [\dfrac{e^{-2b}}{f_{R}}\bigg (\dfrac{f-Rf_{R}}{2}e^{b}\nonumber \\{} & {} \quad +\bigg (\dfrac{a^{'}}{2}+b^{'}+\dfrac{2}{r}\bigg )f_{R}^{'}-\dfrac{f_{X}\phi ^{'2}}{2}\bigg )\bigg ]_{,1} \nonumber \\{} & {} \quad -\dfrac{\rho a^{'}}{2}-\bigg (\dfrac{a^{'}}{2}+\dfrac{2}{r}-\dfrac{f_{R}^{'}R^{'}}{f_{R}^{2}\rho ^{'}}\bigg )p_{r}\nonumber \\{} & {} \quad +\dfrac{2p_{t}}{r} -e^{-b}\bigg (\dfrac{a^{'}}{2}+\dfrac{2}{r}\bigg )f_{R}^{''}\nonumber \\{} & {} \quad +e^{-b}\bigg (\dfrac{3}{4}a^{'}b^{'}+\dfrac{a^{'2}}{4}+\dfrac{3b^{'}}{r}+\dfrac{2}{r^{2}}+b^{'2}\bigg )f_{R}^{'} \nonumber \\{} & {} \quad -b^{'}\bigg (\dfrac{Rf_{R}-f}{2}\bigg )-e^{-b}\bigg (b^{'}+\dfrac{a^{'}}{2}+\dfrac{2}{r}\bigg )f_{X}\phi ^{'2}, \end{aligned}$$
(12)

which leads to

$$\begin{aligned}{} & {} \Omega =-\dfrac{dp_{r}}{dr}-\dfrac{\rho a^{'}}{2}-\bigg (\dfrac{a^{'}}{2}+\dfrac{2}{r}-\dfrac{f_{R}^{'}R^{'}}{f_{R}^{2}\rho ^{'}}\bigg )p_{r}\nonumber \\{} & {} \quad +\dfrac{2p_{t}}{r}-e^{-b}\bigg (\dfrac{a^{'}}{2}+\dfrac{2}{r}\bigg )f_{R}^{''}\nonumber \\{} & {} \quad +e^{-b}\bigg (\dfrac{3}{4}a^{'}b^{'}+\dfrac{a^{'2}}{4}+\dfrac{3b^{'}}{r}+\dfrac{2}{r^{2}}+b^{'2}\bigg )f_{R}^{'} \nonumber \\{} & {} \quad -b^{'}\bigg (\dfrac{Rf_{R}-f}{2}\bigg )-e^{-b}\bigg (b^{'}+\dfrac{a^{'}}{2}+\dfrac{2}{r}\bigg )f_{X}\phi ^{'2}\nonumber \\{} & {} \quad + \bigg [\dfrac{e^{-2b}}{f_{R}}\bigg (\dfrac{f-Rf_{R}}{2}e^{b}\nonumber \\{} & {} \quad +\bigg (\dfrac{a^{'}}{2}+b^{'}+\dfrac{2}{r}\bigg )f_{R}^{'}-\dfrac{f_{X}\phi ^{'2}}{2}\bigg )\bigg ]_{,1}. \end{aligned}$$
(13)

The equilibrium state of the anisotropic compact star is characterized by equation Eq. (13), which we will employ to discuss cracking and overturning by analyzing its perturbed form. To accomplish this, we will incorporate the Krori Barua spacetime coefficients [78, 79] in Eq. (12) specified as, \(a=Br^2 + C\) and \(b=Ar^2\), where A, B,  and C are constants.

$$\begin{aligned}{} & {} \Omega =-\dfrac{dp_{r}}{dr} -Br\rho -\bigg (Br+\dfrac{2}{r}-\dfrac{f_{R}^{'}R^{'}}{f_{R}^{2}\rho ^{'}}\bigg )p_{r}+\dfrac{2p_{t}}{r}\nonumber \\{} & {} \quad -e^{-Ar^{2}}\bigg (Br+\dfrac{2}{r}\bigg )f_{R}^{''}-e^{-Ar^{2}}\bigg (Br+2Ar+\dfrac{2}{r}\bigg )f_{X}\phi ^{'2} \nonumber \\{} & {} \quad -(2Ar)\bigg (\dfrac{Rf_{R}-f}{2}\bigg )\nonumber \\{} & {} \quad +e^{-Ar^{2}}\bigg (3ABr^{2}+B^{2}r^{2}+6A+4A^{2}r^{2}+\dfrac{2}{r^{2}}\bigg )f_{R}^{'} \nonumber \\{} & {} \quad + \bigg [\dfrac{e^{-2Ar^{2}}}{f_{R}}\bigg (\dfrac{f-Rf_{R}}{2}e^{-Ar^{2}}\nonumber \\{} & {} \quad +\bigg (Br+2Ar+\dfrac{2}{r}\bigg )f_{R}^{'}-\dfrac{f_{X}\phi ^{'2}}{2}\bigg )\bigg ]_{,1}. \end{aligned}$$
(14)

After simplifying Eq. (14), we get

$$\begin{aligned}{} & {} \Omega =-\dfrac{dp_{r}}{dr}-Br\rho -\bigg (Br+\dfrac{2}{r}-\dfrac{f_{R}^{'}R^{'}}{f_{R}^{2}\rho ^{'}}\bigg )p_{r}+\dfrac{2p_{t}}{r}\nonumber \\{} & {} \quad +e^{-Ar^{2}}\bigg (-Br-\dfrac{2}{r}+\dfrac{BrR^{'}}{\rho ^{'}}+\dfrac{2ArR^{'}}{\rho ^{'}}+\dfrac{2R^{'}}{r\rho ^{'}}\bigg )f_{R}^{''}\nonumber \\{} & {} \quad +\bigg (-ABr^{2}e^{-Ar^{2}}+B^{2}r^{2}e^{-Ar^{2}}-4A^{2}r^{2}e^{-Ar^{2}}\nonumber \\{} & {} \quad +Be^{-Ar^{2}}-\dfrac{fR^{'}f_{R}}{2f_{R}\rho ^{'}} \bigg )f_{R}^{'} -e^{-Ar^{2}}\bigg (Br+\dfrac{2}{r}\bigg )f_{X}\phi ^{'2}\nonumber \\{} & {} \quad -\bigg (Br+2Ar+\dfrac{2}{r}\bigg )\dfrac{e^{-Ar^{2}}(f_{R^{'}})^{2}R^{'}}{f_{R}\rho ^{'}}\nonumber \\{} & {} \quad +\dfrac{1}{2}\bigg [f_{\phi }+f_{X}X^{'}-f_{X}^{'}X^{'}e^{-Ar^{2}}-\phi ^{''}f_{X}e^{-Ar^{2}}\bigg ]\phi ^{'}. \end{aligned}$$
(15)

Equation (15) refers to the basic equation that is essential in analyzing both the stability and instability of the system by employing density perturbations.

3 Local density perturbation technique in \(f(R, \phi , X)\)

This section outlines the basic formulation of the LDP technique in the framework of \(f(R, \phi , X)\) theory of gravity to determine the stability of an anisotropic system with barotropic equations of state, i.e., \(p_{r}=p_{r}(\rho )\) and \(p_{t}=p_{t}(\rho )\). LDP is employed in the system to perturb all the physical variables, which are assumed to be density-dependent in this study. Subsequently, the configuration is disturbed from its hydrostatic equilibrium state due to LDP resulting in the occurrence of radial forces \(\delta \Omega \). Our present study focuses on analyzing the change in the signs of radial forces \(\frac{\delta \Omega }{\delta \rho }\), where cracking occurs due to inwardly directed radial forces changing sign from negative to positive \((\frac{\delta \Omega }{\delta \rho }<0 \rightarrow \frac{\delta \Omega }{\delta \rho }>0)\), while outwardly directed forces changing sign from positive to negative \((\frac{\delta \Omega }{\delta \rho } >0 \rightarrow \frac{\delta \Omega }{\delta \rho }<0)\) lead to overturning within the configuration. To perturb all physical variables within the configuration, we apply the LDP \(\rho \rightarrow \rho +\delta \rho \), as follows

$$\begin{aligned} \rho (\rho +\delta \rho )= & {} \rho (\rho )+\delta \rho . \end{aligned}$$
(16)
$$\begin{aligned} \rho '(\rho +\delta \rho )= & {} \rho '(\rho )+\dfrac{\rho ''}{\rho '}\delta \rho . \end{aligned}$$
(17)
$$\begin{aligned} p_{r}(\rho +\delta \rho )= & {} p_{r}(\rho )+\dfrac{ dp_{r}}{d\rho }\delta \rho =p_{r}(\rho )+v_{r}^{2}\delta \rho . \end{aligned}$$
(18)
$$\begin{aligned} \dfrac{d p_{r}}{dr}(\rho +\delta \rho )= & {} \dfrac{d p_{r}}{dr}+\bigg [\dfrac{d}{dr}\bigg ( \dfrac{d p_{r}}{d\rho }\bigg )+\dfrac{d^{2}\rho }{dr^{2}}\bigg ( \dfrac{d p_{r}}{d\rho }\bigg ).\dfrac{d r}{d\rho } \bigg ]\nonumber \\= & {} \dfrac{d p_{r}}{dr}+v_{r}'^{2}+v_{r}^{2}.\rho '' (\rho ')^{-1}. \end{aligned}$$
(19)
$$\begin{aligned} p_{t}(\rho +\delta \rho )= & {} p_{t}(\rho )+\dfrac{ dp_{t}}{d\rho }\delta \rho =p_{t}(\rho )+v_{t}^{2}\delta \rho . \end{aligned}$$
(20)
$$\begin{aligned} f (\rho +\delta \rho )= & {} \bigg [\dfrac{ R'}{\rho '} f_{R}+\dfrac{ \phi '}{\rho '} f_{\phi } \bigg ] \delta \rho . \end{aligned}$$
(21)
$$\begin{aligned} f_{R}(\rho +\delta \rho )= & {} f_{R}(\rho )+\dfrac{ R'}{\rho '} f_{R}'\delta \rho . \end{aligned}$$
(22)
$$\begin{aligned} f_{R}'(\rho +\delta \rho )= & {} f_{R}'(\rho )+\dfrac{ R'}{\rho '} f_{R}''\delta \rho . \end{aligned}$$
(23)
$$\begin{aligned} f_{R}''(\rho +\delta \rho )= & {} f_{R}''(\rho )+\dfrac{ R'}{\rho '} f_{R}'''\delta \rho . \end{aligned}$$
(24)
$$\begin{aligned} f_{\phi }(\rho +\delta \rho )= & {} f_{\phi }(\rho )+\dfrac{ \phi '}{\rho '} f_{\phi }'\delta \rho . \end{aligned}$$
(25)
$$\begin{aligned} f_{X}(\rho +\delta \rho )= & {} f_{X}(\rho )+\dfrac{ f_{X}^{'}{X}^{'}\phi '}{\rho '} \delta \rho . \end{aligned}$$
(26)
$$\begin{aligned} f_{X}^{'}(\rho +\delta \rho )= & {} f_{X}^{'}(\rho )+\dfrac{ f_{X}^{''}{X}^{'}\phi '}{\rho '} \delta \rho . \end{aligned}$$
(27)
$$\begin{aligned} R'(\rho +\delta \rho )= & {} R'(\rho )+\dfrac{ R''}{\rho '} \delta \rho . \end{aligned}$$
(28)
$$\begin{aligned} \phi '(\rho +\delta \rho )= & {} \phi '(\rho )+\dfrac{ \phi ''}{\rho '} \delta \rho . \end{aligned}$$
(29)
$$\begin{aligned} \phi ''(\rho +\delta \rho )= & {} \phi ''(\rho )+\dfrac{ \phi '''}{\rho '} \delta \rho . \end{aligned}$$
(30)
$$\begin{aligned} X^{'}(\rho +\delta \rho )= & {} X'(\rho )+\dfrac{ X'' \phi '}{\rho '} \delta \rho . \end{aligned}$$
(31)

Expanding Eq. (15) for its perturbed form by employing LDP, will enable us to examine the distribution of radial forces that occur due to perturbations in the system.

$$\begin{aligned} \Omega= & {} \,\Omega _{0}\bigg (\rho ,\ \rho ',\ p_{r},\ p_{r}',\ p_{t},\ f,\ f_{R},\ f_{R}',\ f_{R}'',\ f_{\phi },\ f_{X},\nonumber \\{} & {} \, f_{X}',\ X^{'}(\phi ), R^{'},\ \phi ',\ \phi '' \bigg )+\ \delta \Omega . \end{aligned}$$
(32)

where

$$\begin{aligned} \delta \Omega= & {} \dfrac{\partial \Omega }{\partial \rho }\delta \rho \ +\dfrac{\partial \Omega }{\partial \rho '}\delta \rho ' \ + \dfrac{\partial \Omega }{\partial p_{r}}\delta p_{r} \nonumber \\{} & {} \quad +\dfrac{\partial \Omega }{\partial p_{r}'}\delta p_{r}' \ + \dfrac{\partial \Omega }{\partial p_{t}}\delta p_{t} \ +\dfrac{\partial \Omega }{\partial f}\delta f \nonumber \\{} & {} \quad + \dfrac{\partial \Omega }{\partial f_{R}}\delta f_{R} \ + \dfrac{\partial \Omega }{\partial f_{R}'}\delta f_{R}' \ + \dfrac{\partial \Omega }{\partial f_{R}''}\delta f_{R}'' \nonumber \\{} & {} \quad + \dfrac{\partial \Omega }{\partial f_{\phi }}\delta f_{\phi } \ + \dfrac{\partial \Omega }{\partial f_{X}}\delta f_{X} \ +\dfrac{\partial \Omega }{\partial f_{X}'}\delta f_{X}' \ + \dfrac{\partial \Omega }{\partial R'}\delta R' \nonumber \\{} & {} \quad + \dfrac{\partial \Omega }{\partial X'}\delta X' \ +\dfrac{\partial \Omega }{\partial \phi '}\delta \phi ' \ + \dfrac{\partial \Omega }{\partial \phi ''}\delta \phi ''. \end{aligned}$$
(33)

Equation (33) simplifies to

$$\begin{aligned} \dfrac{\delta \Omega }{\delta \rho }= & {} \dfrac{\partial \Omega }{\partial \rho }\ + \dfrac{\partial \Omega }{\partial \rho '} \bigg (\ \rho '' (\rho ')^{-1}\ \bigg ) \ + \dfrac{\partial \Omega }{\partial p_{r}}\ \bigg (\ \dfrac{dp_{r}}{d\rho } \ \bigg ) \nonumber \\{} & {} + \dfrac{\partial \Omega }{\partial p_{r}'} \ \bigg (\ \bigg (\dfrac{dp_{r}}{d\rho }\bigg )^{'} \ +\bigg (\dfrac{dp_{r}}{d\rho }\bigg ) \ \rho '' (\rho ')^{-1}\ \bigg ) \ \nonumber \\{} & {} + \dfrac{\partial \Omega }{\partial p_{t}} \ \bigg (\ \dfrac{dp_{t}}{d\rho }\ \bigg ) + \dfrac{\partial \Omega }{\partial f} \bigg (\ \dfrac{f_{R} R^{'}}{\rho '} + \dfrac{f_{X}X^{'}\phi '}{\rho '} \ + \dfrac{f_{\phi } \phi ^{'}}{\rho '} \bigg ) \nonumber \\{} & {} + \dfrac{\partial \Omega }{\partial f_{R}} \bigg ( \dfrac{f_{R}'R^{'}}{\rho '} \bigg ) + \dfrac{\partial \Omega }{\partial f_{R}'} \bigg (\ \dfrac{f_{R}''R^{'}}{\rho '} \bigg ) \nonumber \\{} & {} + \dfrac{\partial \Omega }{\partial f_{R}''} \bigg ( \dfrac{f_{R}'''R^{'}}{\rho '} \bigg )+\dfrac{\partial \Omega }{\partial f_{\phi }} \bigg ( \ f_{\phi }' \ \dfrac{\phi ^{'}}{\rho '} \bigg ) \nonumber \\{} & {} + \dfrac{\partial \Omega }{\partial f_{X}} \bigg ( \ \dfrac{ f_{X}'X^{'}\phi '}{\rho '} \bigg )+\dfrac{\partial \Omega }{\partial f_{X}'} \bigg ( \ \dfrac{ f_{X}''X^{'}\phi '}{\rho '} \bigg )\nonumber \\{} & {} +\dfrac{\partial \Omega }{\partial X'} \bigg (\ \dfrac{X^{''}\phi ^{'}}{\rho '} \bigg ) +\dfrac{\partial \Omega }{\partial R'} \bigg (\ \dfrac{R^{''}}{\rho '} \bigg ) \nonumber \\{} & {} + \dfrac{\partial \Omega }{\partial \phi '} \bigg ( \ \dfrac{\phi ^{''}}{\rho '} \bigg ) +\dfrac{\partial \Omega }{\partial \phi ''} \bigg ( \ \dfrac{\phi ^{'''}}{\rho '} \bigg ). \end{aligned}$$
(34)

The partial derivatives in Eq. (34) are specified as,

$$\begin{aligned} \dfrac{\partial \Omega }{\partial \rho }= & {} -Br. \end{aligned}$$
(35)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial \rho '}= & {} -\dfrac{f_{R}'R'p_r}{f_{R}^{2}(\rho ')^{2}}-e^{-Ar^{2}}\bigg (\dfrac{-BrR^{'}}{(\rho ')^{2}}\nonumber \\{} & {} +\dfrac{2AR^{'}}{(\rho ')^{2}}+\dfrac{-2R'}{(r\rho ')^{2}}\bigg )f_{R}^{''} +\bigg (\dfrac{f R' f_{R}}{2f_{R}{(\rho ')^{2}}}\bigg ) f_{R}'\nonumber \\{} & {} +\dfrac{e^{-Ar^{2}}f_{R}^{'2}R' }{{ f_{R}(\rho ')^{2}}}\bigg (2Ar+Br+\dfrac{2}{r}\bigg ). \end{aligned}$$
(36)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial p_{r}}= & {} \dfrac{f_{R}'R'}{f_{R}^2\rho '}-\dfrac{2}{r}-Br. \end{aligned}$$
(37)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial p_{r}'}= & {} -1. \end{aligned}$$
(38)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial p_{t}}= & {} \dfrac{2}{r}. \end{aligned}$$
(39)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial f}= & {} -\dfrac{f_{R}'R'}{2f_{R}\rho ^{'}}. \end{aligned}$$
(40)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial f_{R}}= & {} \dfrac{e^{-Ar^{2}} (f_{R}')^{2}R'}{(f_{R})^{2}\rho '}\bigg (2Ar+Br+\dfrac{2}{r}\bigg )\nonumber \\{} & {} +\dfrac{-f_{R}^{'}R'p_{r}}{(f_{R})^2\rho '}+\dfrac{fR'f_{R}'}{2(f_{R})^{2}\rho '}. \end{aligned}$$
(41)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial f_{R}'}= & {} \dfrac{R'p_{r}}{{f_{R}}\rho '}-\dfrac{fR^{'}}{2f_{R}\rho ^{'}}\nonumber \\{} & {} +e^{-Ar^{2}}\bigg (-ABr^{2}+B^{2}r^{2}-4A^{2}r^{2}-B\bigg )\nonumber \\{} & {} +\dfrac{2e^{-Ar^{2}} f_{R}'R'}{f_{R}\rho '}\bigg (-Br-2Ar-\dfrac{2}{r}\bigg ). \end{aligned}$$
(42)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial f_{R}''}= & {} e^{-Ar^{2}}\bigg (\dfrac{BrR^{'}}{\rho ^{'}}+\dfrac{2ArR^{'}}{\rho ^{'}}+\dfrac{2R^{'}}{r\rho ^{'}}-\dfrac{2}{r}-Br\bigg ).\nonumber \\ \end{aligned}$$
(43)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial f(\phi )}= & {} \dfrac{\phi '}{2}. \end{aligned}$$
(44)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial f_{X}}= & {} \dfrac{1}{2}\bigg (X^{'}-\phi ^{''}e^{-Ar^{2}}\bigg )\phi ^{'}-e^{-Ar^{2}}\bigg (Br+\dfrac{2}{r}\bigg )\phi ^{'2}.\nonumber \\ \end{aligned}$$
(45)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial f_{X}^{'}}= & {} -\dfrac{1}{2}\bigg (X^{'}e^{-Ar^{2}}\bigg )\phi ^{'}. \end{aligned}$$
(46)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial X^{'}}= & {} \dfrac{1}{2}\bigg (f_X-f_{X}^{'}e^{-Ar^{2}}\bigg )\phi ^{'}. \end{aligned}$$
(47)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial R'}= & {} \dfrac{p_{r}f_{R}'}{{(f_{R})^2}\rho '}- \dfrac{ff_{R}'}{2f_{R}\rho ^{'}} \nonumber \\{} & {} +e^{-Ar^{2}}\bigg (\dfrac{Br}{\rho ^{'}}+\dfrac{2Ar}{\rho ^{'}}+\dfrac{2}{r\rho ^{'}}\bigg )f_{R}^{''}\nonumber \\{} & {} -\dfrac{e^{-Ar^{2}} ( f_{R}')^{2}}{f_{R}\rho '} \bigg (2Ar+Br+\dfrac{2}{r}\bigg ). \end{aligned}$$
(48)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial \phi '}= & {} 2e^{-Ar^{2}}\bigg (-Br-\dfrac{2}{r}\bigg )\phi '\phi ''f_{X}\nonumber \\{} & {} +\dfrac{1}{2}\bigg (f_{\phi }+f_{X}X'-f_{X}'X'e^{-Ar^{2}}-\phi ''f_{X}e^{-Ar^{2}}\bigg ).\nonumber \\ \end{aligned}$$
(49)
$$\begin{aligned} \dfrac{\partial \Omega }{\partial \phi ''}= & {} -\dfrac{1}{2}f_{X}e^{-Ar^{2}}\phi '. \end{aligned}$$
(50)

Equtions (A1)–(A25) in the Appendix presents the values of the remaining parameters expressed in Eq. (34).

Table 1 Calculated values of A, B, M and R of compact stars
Full size table
Fig. 1
figure 1

Plots of \(\dfrac{\delta \Omega }{\delta \rho }\) for Her X-1: \(A= 0.0069062764281 \,\textrm{km}^{-2}\), \(B=0.0042673646183 \,\textrm{km}^{-2}\), \(V_{0}=-0.5\), \( m=-1\)

Full size image
Fig. 2
figure 2

Plots of \(\dfrac{\delta \Omega }{\delta \rho }\) for SAXJ1808.4-3658: \(A= 0.018 231 569 740\,\textrm{km}^{-2}\), \(B=0.014 880 115 692\,\textrm{km}^{-2}\), \(V_{0}=-0.5\), \(m=-1 \)

Full size image
Fig. 3
figure 3

Plots of \(\dfrac{\delta \Omega }{\delta \rho }\) for 4U 1820-30: \(A= 0.010906441192\,\textrm{km}^{-2}\), \(B=0.009880 9,523,811\,\textrm{km}^{-2}\), \( m=-1\), \(V_{0}=-0.5\)

Full size image
Fig. 4
figure 4

Plots of \(\dfrac{\delta \Omega }{\delta \rho }\) for PSR J 1614-2230: \(A=0.003689961987 \,\textrm{km}^{-2}\), \(B=0.002323332389\,\textrm{km}^{-2}\), \(V_{0}=-0.5\), \(m=-1\)

Full size image
Fig. 5
figure 5

Plots of \(\dfrac{\delta \Omega }{\delta \rho }\) for Vela X-1: \(A=0.003558090580\,\textrm{km}^{-2}\), \(B=0.002191967045\,\textrm{km}^{-2}\), \(V_{0}=-0.5\), \( m=-1\)

Full size image
Fig. 6
figure 6

Plots of \(\dfrac{\delta \Omega }{\delta \rho }\) for Cen X-3: \(A=0.003388625404 \,\textrm{km}^{-2}\), \(B=0.002026668572 \,\textrm{km}^{-2}\), \(V_{0}=-0.5\) and \( m=-1\)

Full size image

4 Matching conditions

In this section, we aim to estimate the numerical values of constants A and B involved in solution set, which have obtained in the previous section. There are many choices for the matching conditions but we consider Schwarzschild exterior solution for the present work [80,81,82]. Therefore, the Schwarzschild metric is presented as

$$\begin{aligned} \begin{aligned} d{s}^{2}=&\, \bigg (1-\dfrac{2M}{r} \bigg )dt^{2}-\dfrac{1}{1-\dfrac{2M}{r}}d{r}^{2}\\&-r^2(d{\theta }^{2}+sin^2{\theta }d{\phi }^{2}). \end{aligned} \end{aligned}$$
(51)

Now for solving the field equations at \(r = R\), the interior metric Eq. (6) requires these matching conditions

$$\begin{aligned} g^-_{tt}=g^+_{tt},~ ~ ~ ~ g^-_{rr}=g^+_{rr}, ~ ~ ~ ~ \dfrac{\partial g^-_{tt}}{\partial r}=\dfrac{\partial g^+_{tt}}{\partial r}. \end{aligned}$$
(52)

where (+) and (-) represent the exterior and interior solutions, respectively. Now by comparing both interior and exterior spacetime metrics, we get the constants A, B and C as

$$\begin{aligned} A= & {} ln\bigg (1-\dfrac{2M}{R} \bigg )^{(-1/R^2)}, \end{aligned}$$
(53)
$$\begin{aligned} B= & {} \dfrac{M}{R^3}-\dfrac{2M^2}{R^4}, \end{aligned}$$
(54)
$$\begin{aligned} C= & {} ln\bigg (1-\dfrac{2M}{R} \bigg )-\bigg (\dfrac{M}{R}-\dfrac{2M^2}{R^2} \bigg ) \end{aligned}$$
(55)

where R is the Schwarzschild radius and M is the Schwarzschild mass. Thus using the above expressions, the numerical values of A and B are given in Table 1 for different compact stars.

5 Discussion

This section discusses the occurrence of cracking and overturning by analyzing the effects of LDP in the framework of \(f({{\mathcal {R}}},\phi , X)\). Equation (34) signifies the perturbed state of the configuration and will be used to examine the effects of LDP. We will investigate cracking and overturning points by observing the change in signs of this perturbed state after employing LDP. To accomplish this, we consider the following already developed physical viable model [83].

$$\begin{aligned} f(R,\phi ,X) = R + \alpha R^2- V(\phi ) + X(\phi ), \end{aligned}$$
(56)

We assume \(V(\phi )=V_{0}\phi ^{m}\) and \(\phi =r^\beta \), where \(\alpha , \beta \) and m are arbitrary constants. We will analyze the cracking and overturning of Her-XI, SAXJ1808.4-3658, 4U 1820-30, PSR J 1614 2230, Vela X-1, and Cen X-3 by plotting the distribution of forces \(\dfrac{\delta \Omega }{\delta \rho }\). The mass, radii, and values of other constants for all stars are listed in Table 1. The graphical analysis of cracking and overturning for each star corresponding to different values of the model parameter \(\beta \) is illustrated by Figs. 1, 2, 3, 4, 5 and 6 in the subsequent subsections. A significant point to mention is that we carried out our current analysis using the software MATHEMATICA.

5.1 Star 1: Her X-1

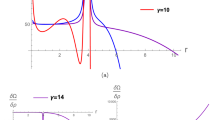
Her XI is a pulsating X-ray source that was initially observed by Tanabaum et al. [84], pulsates every 1.24 s and has an orbital period of 1 day. Deeter et al. [85] analyzed the pulse period of Her XI by examining the observational data of 7 years. To comprehend the neutron star’s development, Taam et al. [86] analyzed the gradual dissipation of magnetic field strength on the surface of a neutron star. Soong et al. [87] investigated the beaming pattern of the Her X-1 by analyzing the radiation emitted by it over a wide range of frequencies. The mass-radius ratio of Her X1 was theoretically calculated by Li et al. [88], who concluded that it matched the observational data of Her X-1. Kuster et al. [89] observed the intensity and distribution of X-ray photons emitted by Her X-1 to investigate its evolution over time. Maurya and collaborators [90] contributed to enhance the understanding by developing an anisotropic theoretical framework and refining the previously known parameters. The distribution of radial forces \(\dfrac{\delta \Omega }{\delta \rho }\) is plotted versus radius for Her X-1 with the parameter \(\beta \) varied and the remaining parameters fixed as shown in Fig. 1. Figure 1a–k demonstrates that star exhibit cracking within the interval \(\beta \in (0, 2.90)\), while Fig. 1b–f, i–k depicts that star experiences overturning within the intervals \(\beta \in (0.59, 1.3)\) and \(\beta \in (1.63, 2.30)\), respectively causing instability in the configuration. Additionally, Fig. 1l illustrates that a star maintains stability for noticeably large values of parameter \(\beta \) starting at \(\beta =2.90\) and continuing upwards. Table 2 presents a concise summary of Fig. 1a–l, highlighting the precise values at which the Her X-1 become unstable.

5.2 Star 2: SAXJ1808.4-3658

SAXJ1808.4-3658 is a low-mass X-ray binary star with an orbital period of 2 h. It was initially observed by Zand et al. [91] who reported it as an X-ray transient. Li et al. [92] analyzed the mass-radius relation of SAXJ1808.4 3658 relative to the mass-radius relation of neutron stars and suggested that it is likely a strange star. Recently, Peter et al. [93] investigated the thermal evolution of SAXJ1808.4-3658 by analyzing data from an X-ray telescope.

The graphical analysis of \(\dfrac{\delta \Omega }{\delta \rho }\) for SAXJ1808.4-3658 with the other parameters of model held constant and parameter \(\beta \) varied, is illustrated in Fig. 2. The graphs of \(\dfrac{\delta \Omega }{\delta \rho }\) for SAXJ1808.43658 demonstrate that cracking appears for \(\beta \in (0, 3.1)\), as seen in Fig. 2a–k. Moreover, Fig. 2b–f, i–k depict that star undergo overturning at \(\beta \in (0.60, 1.25)\) and \(\beta \in (1.6, 2.5)\), leading to instability in the configuration. Figure 2l, further demonstrates that the star retains stability for substantially large values of the parameter \(\beta \), starting at \(\beta =3.1\) and increasing upward. Table 3 summarizes Fig. 2a–l concisely, highlighting the specific values at which the SAXJ1808.4-3658 becomes unstable.

5.3 Star 3: 4U 1820-30

The 4U 1820 30, exhibiting significant luminosity variability and an extremely short orbital period of 685 s, is a unique compact X-ray binary in the globular cluster NGC 6624. Guver et al. [94] estimated the radius and mass of 4U 1820-30 to be \(9.11 \pm 0.40\,\textrm{km}\) and \(1.58 \pm 0.06\) \(M_{\odot }\), respectively by analyzing its spectral data obtained from thermonuclear bursts. Recently, Suvorov et al. [95] observed the thermonuclear bursts of 4U 1820-30 and employed numerical simulations, revealing significant details about the dynamics of a neutron star.

The plots of \(\dfrac{\delta \Omega }{\delta \rho }\) 4U 1820-30 for a range of model parameters are illustrated in Fig. 3. For 4U 1820-30, cracking appears at \(\beta \in (0, 0.285)\), as seen in Fig. 3a–k, whereas overturning appears at \(\beta \in (0.59, 1.5)\) and \(\beta \in (1.7, 2.65)\), illustrated in Fig. 3c–g, i–k, resulting in instability within the configuration. Notably, Fig. 3l illustrates that no cracking or overturning appears at \(\beta =2.85\) suggesting that the star retains stability for relatively large values of \(\beta \). Table 4 presents a concise summary of Fig. 3a–l, highlighting the specific values at which the 4U 1820-30 becomes unstable.

5.4 Star 4: PSR J 1614-2230

PSR J1614-2230 is a highly magnetized dense pulsar with a spin period of 3.15 milliseconds and was initially discovered through Parkes telescope [96]. Demorest et al. [97] investigated the physical properties of PSR J1614-2230 using the Green Bank Telescope and determined its mass to be \(1.97\pm 0.04 M_{\odot }\). Moreover, Takisa et al. [98] investigated its physical properties by developing a model using a quadratic equation of state. The graphs representing \(\dfrac{\delta \Omega }{\delta \rho }\) for PSR J1614-2230 illustrate that the star undergoes cracking and overturning for a specific range of parameter \(\beta \) as shown in Fig. 4. PSR J1614-2230 exhibit cracking at \(\beta \in (0, 3.56)\), as shown in Fig. 4a–l, whereas overturning occurs at \(\beta \in (0.59, 1.6)\) and \(\beta \in (1.65, 2.45)\) as illustrated in Fig. 4b–f, h–k respectively. Additionally, Fig. 4l illustrates that the star retains stability for the relatively large values of parameter \(\beta \), starting at \(\beta =3.56\) and continuing upwards. Table 5 presents a concise summary of Fig. 4a–l, highlighting the precise values at which the PSR J 1614 2230 becomes unstable.

5.5 Star 5: Vela X-1

Vela X-1 is a massive X-ray binary star that constitutes an orbital period of 8.964 days and was initially discovered by Gursky et al. [99] in the Vela constellation. Nagase et al. [100] investigated the physical characteristics of Vela X-1 and determined that it constitutes an elliptical orbit and pulsates every 283.4 s. The mass and radius of Vela X-1 were initially estimated by Quaintrell et al. [101] through Doppler spectroscopy and spectroscopic data of nearby orbiting stars. Later, Kalam et al. [102] used the stiff equation of state and precisely determined the radius of Vela X-1 to be \((9.92-10.31) \,\textrm{km}\). The plots Fig. 5 illustrating perturbed force \(\dfrac{\delta \Omega }{\delta \rho }\) for Vela X-1 demonstrate that cracking and overturning appear for a particular range of parameter \(\beta \), suggesting instability within the configuration. The cracking for Vela X-1 is observed at \(\beta \in (0, 3)\) as illustrated in Fig. 5a–l, whereas overturning is observed at \(\beta \in (0.59, 1.57)\) and \(\beta \in (1.8, 2.5)\) as illustrated in Fig. 5b–g, i, j respectively. However, the star retains stability at a considerably large values of \(\beta \) starting at \(\beta =2.5\). Table 6 presents a concise summary of Fig. 5a–l, illustrating the specific values at which the Vela X-1 becomes unstable.

Table 2 Cracking and overturning points in Her X-1
Full size table
Table 3 Cracking and overturning points in SAXJ1808.4-3658
Full size table
Table 4 Cracking and overturning points in 4U 1820-30
Full size table
Table 5 Cracking and overturning points in PSR J 1614-2230
Full size table
Table 6 Cracking and overturning points in Vela X-1
Full size table

5.6 Star 6: Cen X-3

Cen X-3 is a massive X-ray binary star comprised of an intensely magnetized neutron star with an orbital period of 2.087 days. Cen X-3 was initially observed by Chodil et al. [103], in 1967 during the analysis of the X-ray profile obtained by sound rocket. Giacconi et al. [104] made further observations in this context and discovered that it pulsates every 4.84 s. The plots Fig. 6 demonstrate the behavior of radial forces \(\dfrac{\delta \Omega }{\delta \rho }\) for specific values of model parameters. Figure 6a–k demonstrates that Cen X-3 undergoes cracking at \(\beta \in (0, 2.85)\), whereas overturning is observed at \(\beta \in (0.58, 1.52)\) and \(\beta \in (1.7, 2.5)\) as depicted in Fig. 6b–f, i, j respectively. Notably, no cracking or overturning is observed for relatively large values of parameter starting at \(\beta =2.85\), implying stability within the configuration as shown in Fig. 6l. Table 6 presents a concise summary of Fig. 6a–l, illustrating the specific values at which the configuration becomes unstable.

Table 7 Cracking and overturning points in Cen X-3
Full size table

6 Physical motivation

In this work, we have analyzed the stability of anisotropic compact stars characterized by a barotropic equation of state, by employing the concept of cracking introduced by Herrera [54]. The cracking technique is a quite useful stability analysis technique, as this technique enhances our understanding of the stability properties of compact objects and facilitates to identify cracking and overturning points within the configuration by permitting a more thorough stability analysis of the configuration. It is important to investigate how cracking relates to the perturbation framework and the conditions under which these critical points can change and impact the stability and structure of compact stars.

We analyze the impact of LDP on the stability of compact objects in the framework of \(f(R,\phi , X)\) gravity, by perturbing the Ricci scalar, scalar potential function, kinetic term, and other physical parameters within the configuration. We have considered the changes in curvature, dynamics of the scalar field, and variations in kinetic energy by perturbing the Ricci scalar, scalar potential function, and kinetic term. The distribution of forces within the object is influenced by the perturbations in the Ricci scalar, which presents the changes in spacetime curvature. The perturbations in the scalar potential function demonstrate the changes in the dynamics of the scalar field, ultimately affecting the equilibrium and radial forces. Similarly, the perturbation in the kinetic term accounts for the changes in the kinetic energy of the scalar field and its impact on the total forces. By taking into account these perturbations, together with the perturbation in the physical parameters, and getting equations for the radial forces, we identified the cracking and overturning points by studying changes in the sign of radial forces. The numerical values of cracking and overturning points presented in Tables 2,3, 4, 5, 6 and 7 demonstrate the stable and unstable regions within the configuration of considered compact stars.

The current stability analysis demonstrates the sensitivity of radial forces to local density perturbations that could cause gravitational collapse. In addition, this study offers important insights into how changes in the kinetic term, Ricci scalar, scalar potential function, and other physical parameters might affect the stability of the compact object. This technique enables us to comprehend the effects of the \(f(R,\phi , X)\) theory on the stability characteristics of the compact object more thoroughly. To conclude our study, we would like to speculate on scenarios in which cracking might occur, influencing the evolution of the system. The implosion of a supermassive star might be one of these circumstances. In some situations, the conditions for the expulsion of the outer mantle in a supernova event would probably change as a result of the inner core cracking. In certain cases, this effect will hold true for both the prompt mechanism as mentioned in [105, 106] and the long-term mechanism as mentioned in [107,108,109]. Furthermore, the cracking phenomenon is considered to be a viable explanation for the occurrence of quakes in neutron stars [110,111,112]. In particular, it has been intensively investigated how the cracking of crust in neutron stars on a large scale affects the occurrence of glitches, X-ray bursts, and gamma-ray bursts [113].

However, it is crucial to emphasize that our goal here is not to extensively model any of the above-mentioned scenarios. Instead, we want to emphasize the occurrence of cracking and how it is related to local density perturbations in the framework of \(f(R,\phi , X)\). However, it should be obvious that the existence of these occurrences could significantly impact the evolution of the system. The current study offers valuable insights into how perturbations in the kinetic term, Ricci scalar, scalar potential function, and other physical parameters can affect the stability or instability of the compact object. Using this method, we gain a deeper understanding of the stability of self-gravitating systems in the context of \(f(R,\phi , X)\) gravity and make a significant contribution to a more thorough explanation of the behaviors exhibited by modified theories of gravity.

7 Conclusion

In this manuscript, we analyzed the stability of anisotropic compact stars with a barotropic equation of state in the framework \(f(R,\phi , X)\) gravity, by employing cracking technique introduced by Herrera [54]. For this, we formulated the field equations Eqs. (8)–(11) for anisotropic matter distribution with spherically symmetric spacetime in the framework of the \(f(R,\phi , X)\) theory of gravity. Further, in this context, we developed the hydrostatic equilibrium equation Eq. (13) by employing energy conservation law and subsequently employed Krori and Barua metric potentials [78, 79]. We then perturb the configuration from its hydrostatic equilibrium state by employing LDP on all the physical variables within the configuration, which are assumed to be density-dependent in this study. Subsequently, we analyzed the perturbed state of configuration Eq. (35), to identify cracking or overturning points by investigating the changes in the signs of radial forces at perturbed state. Specifically, we observed the cracking of Her X-1, SAXJ1808.4-3658, 4U 1820-30, PSR J 1614-2230, Vela X-1and Cen X-3. For this, we consider the following model: \(f(R,\phi ,X) = R + R^2 \alpha - V(\phi ) + X(\phi )\). We plotted the distribution of radial forces \(\dfrac{\delta \Omega }{\delta \rho }\) at perturbed state to analyze cracking for each star corresponding to different values of the model parameter illustrated by Figs. 1, 2, 3, 4, 5 and 6 in the preceding section. Tables 2,3, 4, 5, 6 and 7 presents a concise summary of Figs. 1, 2, 3, 4, 5 and 6, highlighting the precise values of the model parameters at which cracking and overturning is observed for each star. In brief, we summarize our analysis as

  • For Her X-I, cracking is observed at \(\beta \in (0, 2.90)\) and overturning at \(\beta \in (0.59, 1.3)\) and \(\beta \in (1.63, 2.30)\), resulting in instability within the configuration. However, stars retain stability at \(\beta =2.90\) as illustrated in Fig. 1.

  • SAXJ1808.4-3658 undergoes cracking at \(\beta \in (0, 3.1)\), while overturning occurs at \(\beta \in (0.60, 1.25)\) and \(\beta \in (1.6, 3.1)\), leading to unstable configuration for certain range of model parameter \(\beta \). Nonetheless, at \(\beta =3.1\) the configuration remains stable as shown in Fig. 2.

  • For 4U 1820-30, cracking occurs at \(\beta \in (0, 2.85)\), although overturning occurs at \(\beta \in (0.59, 1.5)\) and \(\beta \in (1.7, 2.65)\), causing instability within the configuration. Nonetheless, at \(\beta =2.85\) star exhibits stable behavior as illustrated in Fig. 3.

  • PSR J 1614-2230 exhibits cracking at \(\beta \in (0, 3.56)\) and overturning at \(\beta \in (0.59, 1.6)\) and \(\beta \in (1.65, 2.45)\), while retains stability at at \(\beta =3.56\) as shown in Fig. 4.

  • Vela X-1 exhibits cracking at \(\beta \in (0, 3)\) and overturning at \(\beta \in (0.59, 1.57)\) and \(\beta \in (1.8, 2.5)\), however at \(\beta =3\) configuration retains stability as illustrated in Fig. 5.

  • For Cen X-3, the instability is observed within configuration caused by cracking at \(\beta \in (0, 2.85)\), whereas overturning occurs at \(\beta \in (0.58, 1.52)\) and \(\beta \in (1.7, 2.5)\). However, at \(\beta =2.85\) the configuration remains stable as illustrated in Fig. 6.

These results imply that all the considered stars exhibit cracking and overturning for a certain range of model parameters, resulting in instability within the configuration. Notably, the current stability analysis demonstrates the sensitivity of radial forces to local density perturbations that could cause gravitational collapse. In addition, this study offers important insights into how perturbations in the kinetic term, Ricci scalar, scalar potential function, and other physical parameters might affect the stability of the compact object. This technique is therefore quite suitable for refining physically viable compact star models as it effectively identifies the stable and unstable regions within the configuration.