1 Introduction

The application of the canonical quantization of gravity to the cosmological problem in the metric approach [1,2,3,4] has not implied the hoped-for removal of the initial singularity. In fact, the Wheeler–DeWitt equation is associated to quasi-classical states which follow the Einsteinian classical behaviour of the corresponding cosmological solutions [5,6,7,8]. A different situation came out from the cosmological application of Loop Quantum Gravity [4, 9], especially for what concerns the isotropic Universe dynamics [10,11,12,13]. Actually, the quantum dynamics of an isotropic Universe is associated to quasi-classical states which outline a clear bouncing picture, i.e. the symmetrical re-connection of the collapsing and expanding branches of the dynamics in correspondence of a minimum Universe volume. A clear picture for a bouncing cosmology also emerges for more general homogeneous models, as discussed in [14,15,16] (more in general, for bouncing models obtained in modified gravity theories, see for example [17,18,19]). However, this important feature of replacing the initial Big Bang with a primordial Big Bounce is affected by some criticisms [20,21,22] (for a more general critique point of view on the Loop Quantum Gravity approach see [23]). A simpler approach is provided by the implementation of PQM [24] to the Minisuperspace [25]. This formulation is still able to induce a bouncing cosmology, both in a metric and in a connection approach. For a discussion on the emergence of the polymer quantum dynamics from the Loop Quantum Cosmology paradigm see [26]. Also, see [27] and [28,29,30,31,32] for many interesting cosmological scenarios in effective Loop Quantum/Polymer Cosmology respectively.

Here we face a central theme about the real nature of the bouncing isotropic cosmology, namely the question concerning the quantum behaviour of the anisotropic degrees of freedom across the Big Bounce. Actually, the tendency of the Universe anisotropies to highly increase towards the primordial Bounce could affect the robustness of the picture proposed by the Ashtekar School. Some attempts to overcome this problem can be found in [33,34,35] that led to the formulation of the so-called Ekpyrotic Cosmology [36] (see also [37] in which the Big Bounce is treated as a quantum relativistic scattering and no semiclassical approach is used). Our proposal of studying the anisotropies behaviour of a quantum Universe refers to the original Vilenkin idea, presented in [38] (see also [39] for a review on this theme), in which the Minisuperspace is separated into a quasi-classical background and a small quantum subsystem (for a precise derivation about the physical meaning of the word “small” see [40]). The important difference between the present study and previous cosmological implementations of the Vilenkin idea [41,42,43,44] consists of the semiclassical polymer dynamics of the background, which allows the emergence of a bouncing dynamics (pioneering works in the same spirit are [45]). As a first step, we derive the proposed formulation in its general setting with the only assumption of dealing with a Minisuperspace scenario in the polymer formulation. In this respect, we generalize the equations obtained in [38] by addressing the momentum representation, the only viable in the construction of a continuum limit of the theory [24]. This part of the analysis is rather challenging from a mathematical point of view and actually we perform it with the ansatz that all the momentum functions are series expandable. The second part of the paper is dedicated to the implementation of the derived formalism to the Bianchi I and Bianchi IX models, when the anisotropic degrees of freedom are regarded as small variables. Actually, we deal with a semiclassical bouncing isotropic dynamics on which small anisotropies live (freely in the case of the Bianchi I model and subjected to a harmonic potential for the Bianchi IX one). For the Bianchi I model, the Schrödinger equation describing the anisotropic variables dynamics resembles that one of a free two-dimensional particle. However, the bouncing dynamics enters in the definition of the time variable and regularizes the divergences of the anisotropies towards the singularity. Despite this, the anisotropies mean value is not confined and the standard deviation monotonically increases along the dynamics. Analogous results are obtained even when the anisotropies are considered as discrete in the polymer formulation. Therefore, in this picture we can conclude that the anisotropies are not under control during the Universe collapse, i.e. the semiclassical isotropic bouncing cosmology loses its reliability. Furthermore, when the Universe anisotropies increase enough the Vilenkin idea can be no longer applied.

In the second case, when we analyze a Bianchi IX model with small enough anisotropies the Schrödinger equation acquires a harmonic potential term (due to the model spatial curvature). Actually, in the polymer representation we deal with a time-dependent pendulum. In this respect, according to [38, 40] the anisotropic variables phase space is small and so we can approximate the polymer-like kinetic term with the ordinary quadratic one, so that we get a viable time-dependent harmonic oscillator. Then, we construct a complete base of eigenfunctions for the system and we show that in such states (including the low-energy one) the average value of the anisotropies is exactly zero with a standard deviation that oscillates with a constant amplitude. Differently from the previous case, here we see that the anisotropic degrees of freedom remain limited in amplitude during the bouncing dynamics of the background. This analysis shows that the presence of a small spatial curvature in the Bianchi IX model at a quantum level guarantees the physical robustness of a semiclassical isotropic bouncing cosmology. In other words, if we start with a quasi-isotropic Universe in the collapsing branch, then the quantum spatial curvature is able to preserve the smallness of the anisotropies across the Bounce. Since we have demonstrated the validity of this statement in the case of a Bianchi IX Universe (that reduces to a closed Robertson–Walker dynamics in the isotropic limit), this behaviour could concern more general cosmological scenarios in the context of the so-called BKL conjecture [46].

The paper is structured as follows. In Sect. 2 we present PQM and in Sect. 3 we describe our original version of the Vilenkin approach in the polymer formalism. In Sect. 4 we apply the polymer formalism to the Bianchi IX model and we solve the quasi-classical dynamics. Then, in Sects. 5 and 6 we perform the quantum analysis of the Bianchi I and IX models respectively. Finally, in Sect. 7 we report the main results and we present some concluding remarks.

2 The polymer representation of quantum mechanics

PQM is an alternative representation of quantum mechanics introduced by Corichi in [24]. Its formalism is based on the assumption that the configurational variables are discrete. Hence, it results non-equivalent to the Schrödinger representation and its main applications regard the investigation of cut-off physics effects in quantum gravity and primordial cosmology theories.

2.1 Polymer kinematics

PQM can be introduced without making any reference to the standard Schrödinger representation. By considering abstract kets \(|\mu \rangle \) labelled by the real parameter \(\mu \in {\mathbb {R}}\), a generic state in the Hilbert space \({\mathcal {H}}_{poly}\) can be defined through a finite linear combination of them, i.e.

$$\begin{aligned} |\psi \rangle =\sum _{i=1}^Na_i|\mu _i\rangle , \end{aligned}$$
(1)

where \(\mu _i\in {\mathbb {R}},\;i=1,\dots ,N\in {\mathbb {N}}\). The inner product can be chosen as

$$\begin{aligned} \langle \mu |\nu \rangle =\delta _{\mu \nu }, \end{aligned}$$
(2)

in order to guarantee the orthonormality between the basis kets. It can be demonstrated that such a Hilbert space \({\mathcal {H}}_{poly}\) is non-separable.

The two fundamental operators on \({\mathcal {H}}_{poly}\) are the symmetric operator \({\hat{\epsilon }}\) that labels the kets and the unitary operator \({\hat{s}}(\lambda )\) with \(\lambda \in {\mathbb {R}}\) that shifts them. Their action is

$$\begin{aligned} {\hat{\epsilon }}|\mu \rangle :=\mu |\mu \rangle \end{aligned}$$
(3)

and

$$\begin{aligned} {\hat{s}}(\lambda )|\mu \rangle :=|\mu +\lambda \rangle , \end{aligned}$$
(4)

respectively. Since the kets \(|\mu \rangle \) and \(|\mu +\lambda \rangle \) are orthogonal \(\forall \lambda \), the shift operator \({\hat{s}}(\lambda )\) is discontinuous in \(\lambda \) and therefore no Hermitian operator can represent it by exponentiation.

To give an explicit representation of these two main operators, let us consider a one-dimensional system (q, p) in which the configurational coordinate q has a discrete character. It is easy to see that in the p-polarization the shift operator acts as

$$\begin{aligned} {\hat{s}}(\lambda )\cdot \psi _{\mu }(p)= e^{\frac{i\lambda p}{\hslash }}e^{\frac{i\mu p}{\hslash }}=e^{\frac{i(\mu +\lambda ) p}{\hslash }}=\psi _{\mu +\lambda }(p), \end{aligned}$$
(5)

so \({\hat{s}}(\lambda )\) can be identified with the operator \(e^{\frac{i\lambda {\hat{p}}}{\hslash }}\) but \({\hat{p}}\) cannot be defined rigorously. On the other hand, the operator \({\hat{q}}\) acts as a differential operator

$$\begin{aligned} {\hat{q}}\cdot \psi _{\mu }(p)= -i\frac{\partial }{\partial p} \psi _{\mu }(p)= \mu \psi _{\mu }(p) \end{aligned}$$
(6)

and corresponds to the label operator \({\hat{\epsilon }}\). We notice that the eigenvalues of \({\hat{q}}\) can be considered as a discrete set, since they label kets that are orthonormal \(\forall \lambda \).

2.2 Polymer dynamics

Let us consider a one-dimensional system described by the Hamiltonian

$$\begin{aligned} H=\frac{p^2}{2m}+V(q) \end{aligned}$$
(7)

in the p-polarization. In order to deal with a well-defined dynamics, we have to find a proper definition for the physical operators \({\hat{p}}\) and \({\hat{q}}\). The main point of the kinematical analysis performed above is that we have to find an approximate representation for \({\hat{p}}\) when \({\hat{q}}\) has a discrete character. The standard procedure consists in the introduction of a lattice with a constant spacing \(\mu \)

$$\begin{aligned} \gamma _{\mu }=\{q \in {\mathbb {R}} : q=n\mu , \; \forall \; n \in {\mathbb {Z}}\}. \end{aligned}$$
(8)

In order to remain in the lattice, the permitted states \(|\psi \rangle =\sum _{n}b_n|\mu _n\rangle \in {\mathcal {H}}_{\gamma _{\mu }}\) are such that \(\mu _n=n\mu \). The action of the operator \(e^{\frac{i\lambda {\hat{p}}}{\hslash }}\), after been restricted to the lattice, is well-defined and can be used to define an approximate version of \({\hat{p}}\)

$$\begin{aligned} {\hat{p}}_{\mu }|\mu _n\rangle= & {} \frac{\hslash }{2i\mu }[e^{\frac{i\mu {\hat{p}}}{\hslash }}-e^{-\frac{i\mu {\hat{p}}}{\hslash }}]|\mu _n\rangle \nonumber \\= & {} \frac{\hslash }{2i\mu }(|\mu _{n+1}\rangle -|\mu _{n-1}\rangle ). \end{aligned}$$
(9)

Actually, for \(\mu p\ll \hslash \) one gets \(p\backsim \sin (\mu p)/\mu =\hslash (e^{\frac{i\mu p}{\hslash }}-e^{-\frac{i\mu p}{\hslash }})/2i\mu \). Accordingly, for \({\hat{p}}^2\) we obtain

$$\begin{aligned} \nonumber {\hat{p}}^2_{\mu }|\mu _n\rangle{} & {} \equiv {\hat{p}}_{\mu }\cdot {\hat{p}}_{\mu }|\mu _n\rangle \\ \nonumber{} & {} =\frac{\hslash ^2}{4\mu ^2}[-|\mu _{n-2}\rangle +2|\mu _{n}\rangle -|\mu _{n+2}\rangle ]\\{} & {} =\frac{\hslash ^2}{\mu ^2}\sin ^2(\mu p)|\mu _n\rangle . \end{aligned}$$
(10)

We remind that \({\hat{q}}\) is well-defined, so the regularized version of the Hamiltonian is

$$\begin{aligned} {\hat{H}}_{\mu }:=\frac{1}{2m}{\hat{p}}_{\mu }^2+{\hat{V}}(q) \end{aligned}$$
(11)

and represents a symmetric and well-defined operator on \({\mathcal {H}}_{\gamma _{\mu }}\).

3 Vilenkin approach in the polymer formalism

In this section we present the procedure we developed to reproduce the Vilenkin picture in the polymer framework. The original Vilenkin proposal was firstly presented in [38] and is about the probabilistic interpretation of the Universe wave function. In the same spirit, we start by separating the total Hamiltonian of the considered system in its classical and quantum parts

$$\begin{aligned} H=H_0+H_q,H_0=p_ip_jH^{ij}(i\hslash \partial p)+V(i\hslash \partial p). \end{aligned}$$
(12)

The basic idea is that the concept of time, and hence a probabilistic interpretation of the wave function, can be introduced only in a system with small quantum fluctuations. So, the fundamental requirement is dealing with some quasi-classical degrees of freedom and other quantum ones. In (12), \(H_0\) is the quasi-classical part of the total Hamiltonian H and \(H_q\) the quantum one, whereas \(H_{ij}\) is the Supermetric. In the case of one-dimensional systems we get

$$\begin{aligned} H=H_0+H_q,H_0=p^2g(i\hslash \partial p)+V(i\hslash \partial p), \end{aligned}$$
(13)

We note that the use of the momentum representation is required to implement the polymer representation. Moreover, p is multiplicative and the chosen ordering is the normal one. However, \(H_0\) must satisfy some regularity criteria in order the formalism to be developed. In particular, it is required that

$$\begin{aligned} g(i\hslash \partial p)=\sum _{n=0}^{+\infty }a_n(i\hslash )^n(\partial p)^n \end{aligned}$$
(14)

and

$$\begin{aligned} V(i\hslash \partial p)=\sum _{n=0}^{+\infty }b_n(i\hslash )^n(\partial p)^n. \end{aligned}$$
(15)

Actually, every analytic function can be expanded in power series and hence the following procedure will be valid inside the radius of convergence.

By following the Vilenkin approach as in [38], we consider the Universe wave function to be the product of a quantum contribution \(\chi (q,p)\) times a quasi-classical WKB one \(\psi (p)\), i.e.

$$\begin{aligned} \Psi (p,q)=\psi (p)\chi (p,q)=A_k(p)e^{-i/\hslash S_k(p)}\chi (p,q), \end{aligned}$$
(16)

in which we consider p as a quasi-classical variable and q as a quantum one. In order to guarantee that the quantum effects on the quasi-classical system are negligible, we impose

$$\begin{aligned} \frac{\langle H_q\rangle }{\langle H_0\rangle }=o(\hslash ), \end{aligned}$$
(17)

i.e. we consider the case in which \(H_0\) has a larger expectation value (in absolute terms) with respect to \(H_q\). This means that the quantum degrees of freedom constitute a small subsystem compared to the quasi-classical phase space. In addition, we make a Born–Oppenheimer hypothesis by considering the dependence of \(\chi (p,q)\) from p as parametric. Thanks to these hypotheses, we can derive the Vilenkin equations in the momentum space and demonstrate that the quasi-classical dynamics is completely described by a Hamilton-Jacobi together with a continuity equation and that a Schrödinger equation emerges at a quantum level.

We remark that in this scheme the semiclassical polymer substitution \(p\rightarrow \sin {(\mu p)}/\mu \) can be easily implemented since the variable p acts multiplicatively on the left in (12). Hence, the expression of the polymer-modified Hamiltonian becomes

$$\begin{aligned} H^{pol}= & {} H_0^{pol}+H_q,H_0^{pol}=\frac{1}{\mu ^2}\sin ^2(\mu p)g(i\hslash \partial p)\nonumber \\{} & {} +V(i\hslash \partial p). \end{aligned}$$
(18)

The first polymer Vilenkin equation represents the annihilation of the quasi-classical Hamiltonian \(H_0^{pol}\) on the quasi-classical part of the Universe wave function \(\psi \), i.e.

$$\begin{aligned} H_0^{pol}\psi (p)=H_0^{pol}A(p)e^{-i/\hslash S(p)}=0. \end{aligned}$$
(19)

By using (14), at the lowest order in \(\hslash \) we have

$$\begin{aligned}&\frac{\sin ^2(\mu p)}{\mu ^2}\sum _na_n\bigg (\frac{\partial S(p)}{\partial p}\bigg )^nA(p)e^{-i/\hslash S(p)}\nonumber \\&\quad +V(i\hslash \partial p)A(p)e^{-i/\hslash S(p)}=0 \end{aligned}$$
(20)

and after summing the series we get

$$\begin{aligned} H_0^{pol}\bigg (p,\frac{\partial S}{\partial p}\bigg )= \frac{\sin ^2(\mu p)}{\mu ^2}g\bigg (\frac{\partial S}{\partial p}\bigg )+V(i\hslash \partial p)=0, \end{aligned}$$
(21)

i.e. the Hamilton-Jacobi equation. At the next order we obtain

$$\begin{aligned} \frac{\sin ^2(\mu p)}{\mu ^2}\sum _na_ni\hslash \frac{\partial }{\partial p}\bigg [n\,A(p)\bigg (\frac{\partial S(p)}{\partial p}\bigg )^{n-1}\bigg ]e^{-i/\hslash S(p)}=0\nonumber \\ \end{aligned}$$
(22)

and by using (21) we get

$$\begin{aligned} \sum _na_n\frac{\partial }{\partial p}\bigg [n\,A(p)\bigg (\frac{\partial S(p)}{\partial p}\bigg )^{n-1}\bigg ]=0 \end{aligned}$$
(23)

that corresponds to the continuity equation. By solving both (21) and (23) we can derive the quasi-classical action S(p) and the amplitude A(p) and then characterize the quasi-classical contribution to the Universe wave function \(\psi (p)\) in the polymer scheme.

The second polymer Vilenkin equation leads to the emergence of a Schrödinger dynamics at the first order in \(\hslash \) and hence to the definition of a time variable for the system. In particular, it represents the annihilation of the total Hamiltonian \(H^{pol}\) on the Universe wave function \(\Psi (p,q)\), i.e.

$$\begin{aligned}{} & {} H^{pol}\psi (p)\chi (p,q)\nonumber \\{} & {} \quad =(H_0^{pol}+H_q)A(p)e^{-i/\hslash S(p)}\chi (p,q)=0. \end{aligned}$$
(24)

Thanks to the Born–Oppenheimer assumption we neglect the action of \(H_q\) on p, so by using (14) we can write

$$\begin{aligned}&\frac{\sin ^2(\mu p)}{\mu ^2}\sum _na_n(i\hslash )^n(\partial p)^n[A(p)e^{-i/\hslash S(p)}\chi (q,p)]\nonumber \\&\quad =-A(p)e^{-i/\hslash S(p)}H_q\chi (q,p) \end{aligned}$$
(25)

and at the first order in \(\hslash \) we obtain

$$\begin{aligned} \frac{\sin ^2(\mu p)}{\mu ^2}\sum _na_ni\hslash \,n\bigg (\frac{\partial S}{\partial p}\bigg )^{n-1}\frac{\partial \chi }{\partial p}=-H_q\chi (q,p)\,\, \end{aligned}$$
(26)

in which we have used (21) and (23). Now, we can rewrite the l.h.s of (26) as

$$\begin{aligned}&\frac{\sin ^2(\mu p)}{\mu ^2}\sum _na_ni\hslash \,n\frac{\partial \chi }{\partial p}\bigg (\frac{\partial S}{\partial p}\bigg )^{n-1} \nonumber \\&\quad =\frac{\partial }{\frac{\partial S}{\partial p}} \sum _na_ni\hslash \frac{\partial \chi }{\partial p}\bigg (\frac{\partial S}{\partial p}\bigg )^n=i\hslash \frac{\partial \chi }{\partial p}\frac{\partial }{\frac{\partial S}{\partial p}} H_0^{pol}\bigg (\frac{\partial S}{\partial p}\bigg ), \end{aligned}$$
(27)

thus obtaining

$$\begin{aligned} i\hslash \frac{\partial \chi }{\partial p}\frac{\partial }{\frac{\partial S}{\partial p}}H_0^{pol}\bigg (\frac{\partial S}{\partial p}\bigg )=-H_q\chi . \end{aligned}$$
(28)

We also remind that \(q=\partial S/\partial p\), so by definition we have

$$\begin{aligned} \frac{\partial H_0^{pol}}{\frac{\partial S}{\partial p}}=\frac{\partial H_0^{pol}}{\partial q}=-{\dot{p}}/N \end{aligned}$$
(29)

where N is the lapse function, and therefore we can rewrite (26) as

$$\begin{aligned} i\hslash \frac{\partial \chi }{\partial p}\frac{\partial p}{\partial t}=NH_q\chi . \end{aligned}$$
(30)

Hence, we have recovered a Schrödinger equation for the system, i.e.

$$\begin{aligned} i\hslash \frac{\partial \chi }{\partial t}=NH_q\chi . \end{aligned}$$
(31)

It is worth noting that both \(H_0\) and \(H_q\) form the Hamiltonian constraint, i.e. the Wheeler–DeWitt equation for the system. However, according to the original analysis in [38], we imposed the WKB-expanded Wheeler–DeWitt equation for the quasi-classical component separately (for a physical justification see [47]). In practice, the quantum Hamiltonian form a constraint with the \(\hslash \) contribution of the quasi-classical dynamics, thus giving consistency to the hypothesis (17). Then, the only remnant of the background physics entering the quantum constraint is the time derivative: this term comes out from the application of the background Hamiltonian on the product of the two wavefunctions.

4 Formulation for a Bianchi IX model

Our aim is to investigate the quantum behaviour of the anisotropies when PQM is implemented to a quasi-classical cosmological setting and hence a semiclassical Big Bounce emerges. In order to describe the primordial Universe as accurately as possible, let us consider a Bianchi IX model with a free scalar field \(\phi \). In this respect, we consider the regime of small anisotropies far from the Bounce, in order to describe them as the quantum subsystem in the Vilenkin approach.

Let us start with the Bianchi IX Hamiltonian in the semiclassical polymer formulationFootnote 1

$$\begin{aligned} \nonumber H_{IX}^{pol}&=\frac{A^{-3/2}\sqrt{2}}{2}\bigg [-\frac{2}{3\sqrt{2}(4\pi )^2}\frac{A^2\sin ^2(\mu p_A)}{\mu ^2}+p_\phi ^2\\&\quad +p_+^2+p_-^2+A^2(\beta _+^2+\beta _-^2)\bigg ], \end{aligned}$$
(32)

where \(\beta _+,\beta _-\) are the anisotropies and \(A=e^{2\alpha }\) (\(\alpha \) being the isotropic Misner variable) is the degree of freedom related to the Universe area and chosen as discrete in the polymer framework. We remark that in (32) the Bianchi IX potential has been expanded up to the second order in the anisotropies [48] thanks to the Vilenkin hypothesis \(\beta _+,\beta _-\ll 1\). We also note that \(8\pi G=1\) and some irrelevant constants have been taken out by canonically redefining the coordinates.

It is important to stress that a change of configurational variables is a really subtle question in PQM because it is not immediate to generalize the concept of canonical transformations and find a class of equivalence (for a detailed discussion see [29]). Moreover, it is worth stressing that no privileged variables can be assigned in PQM. This problem also concerns the Loop Quantum Cosmology analyses [13] to some extent. In particular, the difficulty of giving a physical ground to the choice of a preferred configurational variable comes from the fact that the Ashtekar–Barbero–Immirzi connection is associated to the non-Abelian SU(2) group in Loop Quantum Gravity [1, 9]. This symmetry cannot be implemented in the Minisuperspace both for diagonal and non-diagonal Bianchi models [21, 22, 49, 50], since in Loop Quantum Cosmology (as well as in PQM) the underlying group of symmetry is an Abelian U(1) one. As a consequence, implementing the original SU(2) connection in the Minisuperspace is a prescription for a privileged representation, but it can not be a physical requirement. In particular, in [29] the relation between the two Loop Quantum Cosmology schemes (the original \(\mu _0\) formulation and the improved \({\bar{\mu }}\) one) is deeply analyzed, mainly focusing on their physical meaning for the isotropic Universe in PQM. Basically, in [29] it is shown that the two schemes mentioned above simply correspond to which configurational variable is polymerized. Therefore, since PQM is isomorphic to Loop Quantum Cosmology (except for the inverse triad effect [51]), the area variable A we consider here can be considered as related to the Ashtekar–Barbero–Immirzi connection and hence our configurational space for the quasi-classical system as a viable choice. Moreover, its capability to describe a bouncing picture (see [32]) is a sufficient property to consider our formulation properly assessed, although not the only possible choice.

A certain degree of ambiguity also concerns the anisotropic variables, but it has a minor physical impact in the present context since \(\beta _{\pm }\) are here not involved in the Bounce picture directly. Their choice is rather natural in a Hamiltonian formulation of the Bianchi models and their identification as the real gravitational degrees of freedom gives them a meaningful nature.

By following the Vilenkin approach of Sect. 3, we consider \(A,\phi \) as the classical degrees of freedom and \(\beta _+,\beta _-\) as the quantum ones. Therefore, the classical evolution will be dictated by

$$\begin{aligned} H_0^{pol}=-\frac{2}{3\sqrt{2}(4\pi )^2}\frac{A^2\sin ^2(\mu p_A)}{\mu ^2}+p_\phi ^2 \end{aligned}$$
(33)

and the quantum evolution by

$$\begin{aligned} H_q^{pol}=p_+^2+p_-^2+A^2(\beta _+^2+\beta _-^2). \end{aligned}$$
(34)

The classical dynamics can be obtained by integrating the Hamilton equations

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle {\dot{A}}=N\frac{\partial {H_0^{pol}}}{\partial p_A}=-\frac{1}{\sqrt{288}\pi ^2}\frac{A^2}{\mu }\sin {(\mu p_A)}\cos {(\mu p_A)}\\ \displaystyle \dot{p_A}=-N\frac{\partial H_0^{pol}}{\partial A}=\frac{1}{\sqrt{288}\pi ^2}\frac{A\sin ^2(\mu p_A)}{\mu ^2} \end{array}\right. }\nonumber \\ \end{aligned}$$
(35)

in which the time gauge has been fixed by choosing \(N=2A^{3/2}/\sqrt{2}\). The analytical solutions for \((A,P_A)\) are

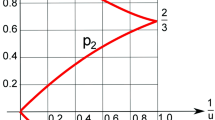
$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle A(\tau )=\cosh {\bigg (\frac{\sin (\frac{3\mu \pi }{2})\tau }{\sqrt{288}\pi ^2\mu }\bigg )}-\cos {\bigg (\frac{3\mu \pi }{2}\bigg )}\sinh \bigg (\frac{\sin (\frac{3\mu \pi }{2})\tau }{\sqrt{288}\pi ^2\mu }\bigg ) \\ \displaystyle p_A(\tau )=\frac{2}{\mu }{{\,\textrm{arccot}\,}}\bigg [\exp {\bigg (-\frac{\sin (\frac{3\mu \pi }{2})\tau }{\sqrt{288}\pi ^2\mu }\bigg )}\cot \bigg (\frac{3\mu \pi }{4}\bigg )\bigg ] \end{array}\right. }\nonumber \\ \end{aligned}$$
(36)

with initial conditions \(A(0)=1,\,p_A(0)=3\pi /2\). As expected, the Universe evolution traces a bouncing one, as shown in Fig. 1. We notice that this result would not have been obtained by simply polymerizing the isotropic Misner variable \(\alpha \) [30, 52]. Moreover, by analyzing the Friedmann equation

$$\begin{aligned}&\bigg (\frac{{\dot{A}}}{2A}\bigg )^2=\frac{\sqrt{2}}{24\pi ^2}A^3\rho _\phi \bigg (1-\frac{\rho _\phi }{A\rho _c}\bigg ), \end{aligned}$$
(37)
$$\begin{aligned}&\rho _\phi =\frac{p_\phi ^2}{2A^3},\quad \rho _c=\frac{1}{3\sqrt{2}(4\pi )^2\mu ^2} \end{aligned}$$
(38)

we can see that the critical point depends only on the variable A and not on the initial conditions on the scalar field. Therefore, the existence of the Bounce is ensured for all the initial configurations that avoid nonphysical cosmological predictions (e.g. too large values of A(0) or \(A(0)=0\)). We remark that the presence of A in (37) does not violate the rescaling symmetry of the line element, since the polymer parameter scales as a length and hence \(A/\mu ^2\) is an invariant (see [29] for a discussion on the meaning of the polymer parameter in relation to the two LQC schemes).

Fig. 1
figure 1

Plot of the bouncing solution \(A(\tau )\) for \(\mu =1/3\)

Full size image

Now, let us derive the Vilenkin equations for the considered model. As discussed in Sect. 3, regarding the first Vilenkin equation (19) at the zero order we recover the Hamilton-Jacobi equation

$$\begin{aligned} -\frac{2}{3\sqrt{2}(4\pi )^2}\frac{\sin ^2(\mu p_A)}{\mu ^2}\bigg (\frac{\partial S}{\partial p_A}\bigg )^2+p_\phi ^2=0, \end{aligned}$$
(39)

whereas at the first order we have

$$\begin{aligned} i\frac{\partial }{\partial p_A}\bigg (A\frac{\partial S}{\partial p_A}\bigg )=0, \end{aligned}$$
(40)

i.e. the continuity equation. Then, by solving (39) and (40) we get the analytical expressions of the action S and the amplitude A, i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle S(p_A,p_\phi )=\pm \ln {(\tan (\mu p_A/2)^{2\pi \mu p_\phi \sqrt{6\sqrt{2}}})}\\ \displaystyle A(p_A,p_\phi )=\frac{\sin (\mu p_A)}{2\pi \mu p_\phi \sqrt{6\sqrt{2}}} \end{array}\right. } \end{aligned}$$
(41)

Hence, for the portion of the phase space in which \(\partial S/\partial p_A>0\) the classical part of the Universe wave function results to be

$$\begin{aligned} \psi (p_A,p_\phi )=\frac{\sin (\mu p_A)e^{-i\ln {(\tan (\frac{\mu p_A}{2})^{2\pi \mu p_\phi \sqrt{6\sqrt{2}}})}}}{2\pi \mu p_\phi \sqrt{6\sqrt{2}}} \end{aligned}$$
(42)

in which it is encoded all the information on the quasi-classical phase space dynamics.

In order to obtain the full description of the Universe, we have to solve the second Vilenkin equation (24). In particular, at the first order it emerges a Schrödinger evolution

$$\begin{aligned}{} & {} \bigg [p_+^2+p_-^2-A^2(\tau )\bigg (\frac{\partial ^2}{\partial p_+^2}+\frac{\partial ^2}{\partial p_-^2}\bigg )\bigg ]\chi (p_\pm ,\tau )\nonumber \\{} & {} \quad =i\frac{\partial \chi (p_\pm ,\tau )}{\partial \tau } \end{aligned}$$
(43)

that resembles a time-dependent quantum harmonic oscillator in which the time parameter is defined through the relation

$$\begin{aligned} \frac{\partial }{\partial \tau }=N\frac{\partial }{\partial t}=\frac{2A^{3/2}}{\sqrt{2}}\frac{\partial }{\partial t}. \end{aligned}$$
(44)

To be accurate, the anisotropies are the real quantum degrees of freedom and therefore should be affected by the polymer modifications. In that case, (43) would be

$$\begin{aligned}&\bigg [\frac{1-\cos {(\mu p_+)}}{\mu _+^2}+\frac{1-\cos {(\mu p_-)}}{\mu _-^2}+ \end{aligned}$$
(45)
$$\begin{aligned}&-A^2(\tau )\bigg (\frac{\partial ^2}{\partial p_+^2}+\frac{\partial ^2}{\partial p_-^2}\bigg )\bigg ]\chi (p_\pm ,\tau )=i\frac{\partial \chi (p_\pm ,\tau )}{\partial \tau }, \end{aligned}$$
(46)

i.e. a time-dependent quantum pendulum. However, the hypothesis \(\beta _+,\beta _-\ll 1\) makes it possible to consider the regime of small oscillations in the pendulum dynamics, i.e. the aforementioned harmonic oscillator. Regarding the sensitive issue of the continuum limit, in [53] it is widely investigated the issue of recovering the Schrödinger quantum picture from the polymer one for the polymer harmonic oscillator, i.e. a quantum pendulum.

Now, we have to shed light on one of the basic assumption in the original formulation [38] and on how it impacts our study. Actually, the separation of the dynamics into a quasi-classical sector and a quantum one strictly relies on the “smallness” of the phase space of the quantum system with respect to that one of the classical component (see the analysis in [40] for a validation of this statement). This assumption is not valid for both a Bianchi I and a Bianchi IX model in general, since the anisotropic degrees of freedom can approach arbitrarily large values near the singularity. However, the situation in which the Universe anisotropic variables are small, i.e. \(|\beta _{\pm }|\ll 1\), and the spatial curvature term can be expanded in Taylor series turns to be appropriate to our study. In fact, we are interested in investigating the behaviour of the anisotropies near the quasi-isotropic configuration of the Universe, in order to verify if such approximation remains valid across the Big Bounce. By other words, we study the emergence of the Universe anisotropies as a natural tendency of the isotropic Universe during the collapse and hence the implementation of the ideas in [38] are well-grounded. We will show that such a scheme is a well-established dynamical picture, under certain conditions, and that the anisotropies do not arbitrarily increase throughout the minimal volume configuration, when a Bianchi IX model is considered by virtue of the presence of a harmonic potential. In the case of a Bianchi I model it is also true that the Universe anisotropies can freely develop and sooner or later the proposed quasi-classical vs quantum decomposition is going to fail.

5 Quantum behaviour of the anisotropies for the Bianchi I model

In this section we first analyze the anisotropies quantum behaviour by neglecting the quadratic potential, i.e. by restricting the cosmology to the simpler Bianchi I model. In this case, the Schrödinger equation in the coordinate representation reduces to

$$\begin{aligned} -\bigg (\frac{\partial ^2}{\partial \beta _+^2}+\frac{\partial ^2}{\partial \beta _-^2}\bigg )\chi (\beta _\pm ,\tau )=i\frac{\partial \chi (\beta _\pm ,\tau )}{\partial \tau } \end{aligned}$$
(47)

whose solution can be written as a linear combination of

$$\begin{aligned} \varphi (\beta _\pm ,\tau )=e^{ik_+\beta _+}e^{ik_-\beta _-}e^{-i(k_+^2+k_-^2)\tau } \end{aligned}$$
(48)

Then, we construct a Gaussian wave packet (\({\mathcal {N}}\) is the normalization constant)

$$\begin{aligned} \chi (\beta _\pm ,\tau )&=\frac{1}{{\mathcal {N}}}\iint _{-\infty }^{+\infty }e^{-\frac{(k_+-{\bar{k}}_+)^2}{2\sigma _+^2}}e^{-\frac{(k_--{\bar{k}}_-)^2}{2\sigma _-^2}}\nonumber \\&\quad \times e^{ik_+\beta _+}e^{ik_-\beta _-}e^{-i(k_+^2+k_-^2)\tau }dk_+\,dk_- \end{aligned}$$
(49)

and we study the evolution of the probability density distribution \(|\chi |^2=\chi (\beta _\pm ,\tau )\chi ^*(\beta _\pm ,\tau )\). Actually, the position of the peak and the width of the probability function give the information about the quantum behaviour of the anisotropies, i.e. their mean values and standard deviation.

We notice that the presence of the Bounce enters in the definition of the time variable, since the relation between the synchronous time t and the time variable \(\tau \) is fixed by the choice of the lapse function \(N=2A^{3/2}/\sqrt{2}\) and hence it depends on how the Universe volume evolves with time. Thus, polymer effects on the anisotropies can appear when returning to the synchronous time picture. In particular, in the bouncing picture we have (see (36))

$$\begin{aligned} V^{pol}(\tau )=A(\tau )^{3/2}, \end{aligned}$$
(50)

whereas in the absence of the semiclassical polymer scenario we get the two singular trajectories (depending on the sign of the initial condition on \(p_A\))

$$\begin{aligned} V^\pm (\tau )=A^{\pm }(\tau )^{3/2}=\big (e^{\pm \frac{|p_A(0)|\tau }{\sqrt{288}\pi ^2}}\big )^{3/2} \end{aligned}$$
(51)

that can be obtained by taking the limit of the polymer solution (50) for \(\mu \rightarrow 0\). Therefore, by using the relation (44) we have

$$\begin{aligned} t=\int \frac{2V^{pol}(\tau )}{\sqrt{2}}\,d\tau \end{aligned}$$
(52)

in the polymer case and

$$\begin{aligned} t=\int \frac{2V^\pm (\tau )}{\sqrt{2}}\,d\tau \end{aligned}$$
(53)

for the two singular branches. Thus, after computing the integrals, the obtained functions can be inverted to find the relation between \(\tau \) and t in the two cases.

Fig. 2
figure 2

Plot of the bouncing trajectory for the Universe volume in function of \(\tau \) (green line), together with the trajectories for the classical limits \(\tau \rightarrow \pm \infty \) (orange and blue lines)

Full size image

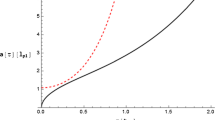
In order to provide a generic bouncing scenario, here the initial conditions are such that the Bounce occurs at \(\phi =1\) (see Fig. 2). Actually, the trajectory for the Universe volume is formally equivalent to the translation of (50) for \(\tau \rightarrow \tau -1\). We note that the exponential behaviour of the classical limit is recovered for large times. Then, by means of numerical and analytical methods respectively we have found the inverse functions \(\tau ^{pol}(t)\) and \(\tau ^\pm (t)\). In particular, from Fig. 3 we point out that the divergence of \(\tau ^\pm (t)\) in correspondence of the singularity \(t=0\) is regularized in the bouncing trajectory \(\tau ^{pol}(t)\). Moreover, \(\tau ^+(t)\) is not simply the reflection of \(\tau ^-(t)\) with respect to the bisector \(\tau =t\) since the Bounce does not occur at \(\phi =0\).

Fig. 3
figure 3

Plot of \(\tau (t)\) for the three relevant cases: \(\tau ^{pol}(t)\) (green line) for the bouncing trajectory, \(\tau ^+(t)\) (orange line) for the expanding branch and \(\tau ^-(t)\) (blue line) for the collapsing one

Full size image

For the sake of completeness, we also report the Universe volume trajectory in the synchronous time obtained by using the numerical solution \(\tau ^{pol}(t)\) (see Fig. 4). We notice that the Bounce occurs for \(t=0\) and that the linear behaviour of the classical solution is recovered for large times.

Fig. 4
figure 4

Plot of the bouncing trajectory for the Universe volume in function of t (green line), together with the trajectories for the classical limits \(t\rightarrow \pm \infty \) (orange and blue lines)

Full size image

Now, by using \(\tau ^{pol}(t)\) and \(\tau ^{\pm }(t)\) in (49) we have studied the two different evolution of the probability density function \(|\chi (\beta _\pm ,t|^2\) in the synchronous time, thus recovering the quantum information on the anisotropies in the bouncing picture and in the singular one respectively. Actually, it is well-known that the Schrödinger solutions are characterized by a spreading behaviour and, restricting to the one-dimensional picture, it can be easily demonstrated that the Gaussian standard deviation grows linearly with time. Since (47) is separable, the total Universe wave function (49) is factorized as \(\chi (\beta _\pm ,t)=\chi ^+(\beta _+,t)\chi ^-(\beta _-,t)\) in which

$$\begin{aligned} \chi ^+(\beta _+,t)=\frac{1}{{\mathcal {N}}_+}\int _{-\infty }^{+\infty }e^{-\frac{(k_+-{\bar{k}}_+)^2}{2\sigma _+^2}}e^{ik_+\beta _+}e^{-ik_+^2t}dk_+ \end{aligned}$$
(54)

and

$$\begin{aligned} \chi ^-(\beta _-,t)=\frac{1}{{\mathcal {N}}_-}\int _{-\infty }^{+\infty }e^{-\frac{(k_--{\bar{k}}_-)^2}{2\sigma _-^2}}e^{ik_-\beta _-}e^{-ik_-^2t}dk_-. \end{aligned}$$
(55)

Hence, we can restrict the analysis to a single anisotropic degree of freedom and same considerations will be valid for the other one. Thus, if we consider the anisotropy \(\beta _+\) we have that the standard deviation of the Universe wave function \(\chi ^+(\beta _+,t)\) goes linearly with \(\tau (t)\) and therefore in the singular picture it diverges towards the singularity \(t\rightarrow 0\) (that corresponds to the initial Big Bang in the singular expanding branch and to the future Big Crunch in the singular collapsing one). On the other hand, in the bouncing picture the divergence is regularized at the Bounce \(t=0\) in which the two branches are symmetrically reconnected. However, the Universe wave packet is still affected by the spreading behaviour and the anisotropic standard deviation is not confined but it grows along the dynamics, even if the Universe initial state is sufficiently localized before the bouncing point.

Fig. 5
figure 5

Left side: Evolution of \(|\chi ^+(\beta _+,\tau ^+(t))|^2\) in function of the anisotropy \(\beta _+\) from the initial singularity for \(t=10^{-180},10^{-120},10^{-60}\) (blue, orange and green lines respectively). Right side: Evolution of \(|\chi ^+(\beta _+,\tau ^-(t))|^2\) in function of the anisotropy \(\beta _+\) towards the future singularity for the corresponding symmetric values of time (yellow, light-blue and red lines respectively). The purple graph corresponds to \(|\chi ^+(\beta _+,0)|^2\) and is in common to the expanding and collapsing branches

Full size image
Fig. 6
figure 6

Evolution of \(|\chi ^+(\beta _+,\tau ^{pol}(t))|^2\) in function of the anisotropy \(\beta _+\) in the bouncing scenario for \(t=-10^5,0,10^{15},10^{60},10^{90}\) (left-to-right)

Full size image

In Fig. 5 we can see the behaviour of the Universe wave packet along the expanding branch (left side) and collapsing one (right side) that shows the spreading behaviour towards the singularities. From the position of the peak we can infer that the more the wave packet spreads the higher the anisotropy mean value is (in absolute value). Even if the quantum behaviour is regularized at the Bounce, the anisotropic standard deviation grows indefinitely for \(t\rightarrow +\infty \) (see Fig. 6). In particular, states with higher anisotropic standard deviation are associated to higher (absolute) mean values for the anisotropy. The only difference is that the Universe wave packet spreads slowly when considering the bouncing evolution for the semiclassical sector (see Fig. 7) and therefore the anisotropic standard deviation can remain confined for a finite time interval if the initial Universe wave packet is sufficiently localized. However, even if the quantum behaviour is regularized at the Bounce the anisotropic standard deviation grows indefinitely for \(t\rightarrow +\infty \) (see Fig. 6). In particular, states with higher anisotropic standard deviation are associated to higher (absolute) mean values for the anisotropy. Finally, we repeat the analysis above considering the anisotropies as discrete. Accordingly, the Schödinger equation in the semiclassical polymer framework writes as

$$\begin{aligned}{} & {} \bigg [\frac{\sin ^2({\mu _+p_+})}{\mu _+^2}+\frac{\sin ^2({\mu _-p_-})}{\mu _-^2}\bigg ]\chi _{pol}(p_\pm ,\tau )\nonumber \\{} & {} \quad =i\frac{\partial \chi _{pol}(p_\pm ,\tau )}{\partial \tau }, \end{aligned}$$
(56)

in which we have recovered the momentum representation. Thus, after a Fourier transformation the solution can be written as a factorized Gaussian superposition of plane waves

$$\begin{aligned} \chi _{pol}(\beta _\pm ,\tau )&=\chi _{pol}^+(\beta _+,t)\chi _{pol}^-(\beta _-,t)\nonumber \\&=\frac{1}{{\mathcal {N}}}\iint _{-\infty }^{+\infty }e^{-\frac{(k_+-{\bar{k}}_+)^2}{2\sigma _+^2}}e^{-\frac{(k_--{\bar{k}}_-)^2}{2\sigma _-^2}}\nonumber \\&\quad \times e^{ik_+\beta _+}e^{ik_-\beta _-}e^{-i\left[ (k_+^\mu )^2+(k_-^\mu )^2\right] \tau }dk_+\,dk_- \end{aligned}$$
(57)

in which \({\mathcal {N}}\) sets the norm and \(k^\mu _\pm =\sin (\mu _\pm k_\pm )/\mu _\pm \) (Fig. 7).

Now we can study the evolution of the probability density \(|\chi _{pol}^+(\beta _+,t)|^2\) as before, and analyze the different behaviour in the singular or bouncing background picture by respectively considering \(\tau ^\pm (t)\) or \(\tau ^{pol}(t)\). In particular, in Fig. 8 we can see the behaviour of the Universe wave packet along the expanding branch (left side) and the bouncing one (red lines), whose evolution in the latter case is not appreciable at these time scales. More specifically, in Fig. 9 it is highlighted the slower, but still present, spreading behaviour of the bouncing case too. Thus, the unlimited growth of the anisotropies standard deviation is not prevented even when they are represented in the polymer formalism.

Fig. 7
figure 7

Evolution of \(|\chi ^+(\beta _+,\tau ^+(t))|^2\) in function of the anisotropy \(\beta _+\) along the expanding branch for \(t=10^{-180},10^{-120},10^{-60}\) (blue, orange and green lines respectively) compared with that of \(|\chi ^+(\beta _+,\tau ^{pol}(t))|^2\) in function of the anisotropy \(\beta _+\) along the bouncing trajectory for \(t=10^{-180},10^{-120},10^{-60}\) (red lines). The evolution of the Universe wave packet in the bouncing scenario is not appreciable at these time scales. For the Gaussian coefficients we have set \(\sigma _+=1/\sqrt{2}\), \({\bar{k}}_+=+5\) in the left figure and \({\bar{k}}_+=-5\) in the right figure

Full size image

6 Quantum behaviour of the anisotropies for the Bianchi IX model

In this section we analyze the anisotropies quantum behaviour in the full model, i.e. by including the harmonic potential \(A^2(\tau )(\beta _+^2+\beta _-^2)\). The analytical method to solve the time-dependent quantum oscillator (see (43)) is widely described in [54]. In particular, by means of the exact invariant method it can be demonstrated that the normalized eigenfunctions of the Hamiltonian can be written as

$$\begin{aligned} \chi _n(\beta _+,\beta _-,\tau )=\chi _n^+(\beta _+,\tau )\chi _n^-(\beta _-,\tau ) \end{aligned}$$
(58)

with

$$\begin{aligned} \chi _n^\pm (\beta _\pm ,\tau )=\frac{e^{i\gamma _n(\tau )}}{\sqrt{\sqrt{\pi }n!2^n\rho }}{\mathcal {H}}\bigg (\frac{\beta _\pm }{\rho }\bigg )e^{\frac{i}{4}(\frac{{\dot{\rho }}}{\rho }+\frac{2i}{\rho ^2})\beta _\pm ^2} \end{aligned}$$
(59)

in which \({\mathcal {H}}\) are the usual Hermite polynomials, the \(\gamma \) function is defined as

$$\begin{aligned} \gamma _n(\tau )=-\bigg (n+\frac{1}{2}\bigg )\int _0^\tau \frac{2}{\rho ^2}d\tau ' \end{aligned}$$
(60)

and \(\rho \) solves the differential equation

$$\begin{aligned} \ddot{\rho }+4A(\tau )^2\rho =0. \end{aligned}$$
(61)

Actually, in our model the role of the time-dependent frequency is played by the solution for the Universe area \(A(\tau )\). Thus, the semiclassical behaviour of the model directly enters in the quantum dynamics thanks to the presence of the Bianchi IX potential.

Fig. 8
figure 8

Evolution of \(|\chi _{pol}^+(\beta _+,\tau ^+(t))|^2\) in function of the anisotropy \(\beta _+\) along the expanding branch for \(t=10^{-180},10^{-120},10^{-60}\) (blue, orange and green lines respectively) compared with that of \(|\chi _{pol}^+(\beta _+,\tau ^{pol}(t))|^2\) in function of the anisotropy \(\beta _+\) along the bouncing trajectory (red lines) for \(t=10^{-180},10^{-120},10^{-60}\) (we set \(\sigma _+=1/\sqrt{2}\), \({\bar{k}}_+=-5\))

Full size image
Fig. 9
figure 9

Evolution of \(|\chi _{pol}^+(\beta _+,\tau ^{pol}(t))|^2\) in function of the anisotropy \(\beta _+\) in the bouncing scenario for \(t=-10^5,0,10^{15},10^{60},10^{90}\) (left-to-right)

Full size image

By solving (61) (in which for \(A(\tau )\) we have used the expression in (36) with \(\mu =1/3\)) we get

$$\begin{aligned} \rho (\tau )= & {} c_1{\mathcal {M}}_C\bigg (-\frac{1}{288},\frac{1}{576},24i\tau \bigg )\nonumber \\{} & {} -c_2{\mathcal {M}}_S\bigg (-\frac{1}{288},\frac{1}{576},24i\tau \bigg ), \end{aligned}$$
(62)

where \(c_1,c_2\) are constants and \({\mathcal {M}}_C\) and \({\mathcal {M}}_S\) are the Mathieu functions, i.e. elliptic cosine and the elliptic sine respectively. Then, we have constructed a basis of real solutions and performed an expansion of the elliptic functions up to the first order, i.e.

$$\begin{aligned}&{\mathcal {M}}_C\bigg (-\frac{1}{288},\frac{1}{576},24i\tau \bigg )\sim \cos \bigg (\sqrt{-\frac{1}{288}}24i\tau \bigg ), \end{aligned}$$
(63)
$$\begin{aligned}&{\mathcal {M}}_S\bigg (-\frac{1}{288},\frac{1}{576},24i\tau \bigg )\sim \sin \bigg (\sqrt{-\frac{1}{288}}24i\tau \bigg ). \end{aligned}$$
(64)

This approximation is justified since the second argument of \({\mathcal {M}}_{C,S}\) tends to zero in the continuum limit, i.e. for \(\mu \ll 1\). We remark that it also remains valid arbitrarily close to the Bounce, since a bouncing dynamics emerges for any positive value of the polymer parameter, however small. Moreover, this case is very different from that one in which the singular solution for the Universe area is considered in (61), as we will see below.

Fig. 10
figure 10

Plot of \(\epsilon _{1,2}\) in function of t for two different initial conditions (the continuous lines are referred to (63) and (64)). The relative error goes to zero as \(\lambda _2\rightarrow 0\)

Full size image

In particular, in Fig. 10 it can be noticed that the relative errors

$$\begin{aligned}&\epsilon _1=\left| \frac{{\mathcal {M}}_{C}(\lambda _1,\lambda _2,x)-\cos (\sqrt{\lambda _2}x)}{\cos (\sqrt{\lambda _2}x)}\right| , \end{aligned}$$
(65)
$$\begin{aligned}&\epsilon _2=\left| \frac{{\mathcal {M}}_{S}(\lambda _1,\lambda _2,x)-\sin (\sqrt{\lambda _2}x)}{\sin (\sqrt{\lambda _2}x)}\right| \end{aligned}$$
(66)

decrease towards the Bounce and can be made smaller than one for a time interval depending on the initial conditions.

Thanks to the expansions (63) and (64) we are able to analytically compute the integral in (60). Thus, we have an explicit expression for the eigenstates \(\chi _n(\beta _+,\beta _-,\tau )\) through which computing the mean value and the standard deviation of the anisotropies \(\beta _\pm \).

Fig. 11
figure 11

Plot of \(|\chi (\beta _+,0)|^2\) for \(n=0\) (blue line), \(n=1\) (orange line) and \(n=2\) (green line)

Full size image

In Fig. 11 we show the probability density distribution \(|\chi _n^+(\beta _+,0)|^2\) for the obtained eigenfunctions in the anisotropy \(\beta _+\) with \(n=0,1,2\). In order to compute the expectation value of the anisotropies and their standard deviation, we write \({\hat{\beta }}_\pm \) by means of the creation and annihilation operators \({\hat{a}}_\pm ^+\) and \({\hat{a}}_\pm \) for the time-dependent harmonic oscillator (see [55]), i.e.

$$\begin{aligned}&{\hat{\beta }}_\pm =\frac{\rho }{\sqrt{2}}({\hat{a}}_\pm +{\hat{a}}_\pm ^+), \end{aligned}$$
(67)
$$\begin{aligned}&{\hat{p}}_\pm =-\frac{i}{\sqrt{2}}\bigg [\bigg (\frac{1}{\rho }+i{\dot{\rho }}\bigg ){\hat{a}}_\pm -\bigg (\frac{1}{\rho }-i{\dot{\rho }}\bigg ){\hat{a}}_\pm ^+\bigg ], \end{aligned}$$
(68)

in which \(\rho \) is the solution of (61). Now we are able to easily write the action of the operators \({\hat{\beta }}_\pm \) on the eigenstates \(|n \rangle \). In particular, the anisotropies expectation value is equal to zero since

$$\begin{aligned} {\hat{\beta }}_\pm |n \rangle =\frac{\rho }{\sqrt{2}}(\sqrt{n}|n-1\rangle +\sqrt{n}|n+1\rangle ), \end{aligned}$$
(69)

while their standard deviation results to be

$$\begin{aligned} \varDelta \beta _\pm =\sqrt{\langle \hat{\beta ^2_\pm }\rangle -\langle {\hat{\beta }}_\pm \rangle ^2}=\bigg (n+\frac{1}{2}\bigg )\rho ^2. \end{aligned}$$
(70)
Fig. 12
figure 12

Left figure: Behaviour of \(\varDelta \beta _+\) in function of \(\tau \) for \(n=0,1,2,3,4,5\) (bottom-up) in the semiclassical bouncing picture. Right figure: Behaviour of \(\varDelta \beta _+\) in function of \(\tau \) for \(n=0\) in the bouncing picture

Full size image
Fig. 13
figure 13

Left figure: Behaviour of \(\langle {\hat{Q}}\rangle \) in function of \(\tau \) for \(n=0,1,2,3,4,5\) (bottom-up) in the semiclassical bouncing picture. Right figure: Behaviour of \(\varDelta {\hat{Q}}\) in function of \(\tau \) for \(n=0,1,2,3,4,5\) (bottom-up) in the semiclassical bouncing picture

Full size image

In Fig. 12 it is highlighted the confined character of \(\varDelta \beta _+\) in function of the time variable \(\tau \). In particular, \(\varDelta \beta _+\) oscillates around a constant values that grows with n (together with the amplitude) but remains one order of magnitude smaller than \(\sigma _+\) in the case of the two-dimensional free particle, i.e. Bianchi I (see Fig. 7 in which both the singular and the bouncing pictures are reported). Thus, the presence of the harmonic potential maintains the anisotropies small, differently from the previous case (see Sect. 5). Obviously, all the analysis is analogous if performed for \(\beta _-\).

In order to strengthen this result, we also compute both the expectation value and the standard deviation of the shear, i.e. the geometrical quantity

$$\begin{aligned} Q=(H_1-H_2)^2+(H_2-H_3)^2+(H_3-H_1)^2 \end{aligned}$$
(71)

representing the anisotropic term in the Bianchi I Friedmann equation (here \(H_i\) is the Hubble parameter along the i-direction). It can be demonstrated that in the Misner variables the shear writes as [8, 48]

$$\begin{aligned} Q=18(\dot{\beta _+}^2+\dot{\beta _-}^2)=72(p_+^2+p_-^2), \end{aligned}$$
(72)

in which we have used the Hamilton equations \({\dot{\beta }}_\pm =2p_\pm \). Hence, by using (68) we can compute the shear expectation value

$$\begin{aligned} \langle {\hat{Q}}\rangle =144\bigg (\frac{1}{\rho ^2}+{\dot{\rho }}^2\bigg ) \end{aligned}$$
(73)

and its standard deviation

$$\begin{aligned} \varDelta {\hat{Q}}=\sqrt{\langle \hat{Q^2}\rangle -\langle {\hat{Q}}\rangle ^2}=144\sqrt{\frac{n^2+n+1}{2}}\bigg (\frac{1}{\rho ^2}+{\dot{\rho }}^2\bigg )\nonumber \\ \end{aligned}$$
(74)

on the eigenstates \(|n\rangle \). In Fig. 13 it is evident that they both oscillate around a constant value that grows with n (together with the amplitude), as it happens for the anisotropies standard deviation (see Fig. 12). Thus, we can conclude that the oscillatory and confined character of the anisotropies is a robust result of the present analysis.

We finally notice that, differently from the case of the Bianchi I model, here it is not necessary to construct a wave packet in order to demonstrate that the anisotropic degrees of freedom (as well as the shear) remain small in their mean value with a correspondingly small standard deviation. In fact, since the fundamental states we construct for the time-dependent harmonic oscillator have these both features, the superposition principle (that stems from the linear nature of the time-dependent Schrödinger equation) ensures that any generic state for the anisotropies has a localized and oscillatory structure.

Fig. 14
figure 14

Behaviour of \(\varDelta \beta _+\) in function of \(\tau \) for \(n=0\) along the collapsing (singular) branch

Full size image

The corresponding behaviour of \(\varDelta \beta _+\) in the absence of the regularized semiclassical bouncing evolution is represented in Fig. 14. In this case, we have considered \(A^-(\tau )\) (see (51)) as the time-dependent frequency of the harmonic oscillator in (43), i.e. the collapsing singular solution obtained from the considered bouncing solution \(A(\tau )\) in the limit \(\mu \rightarrow 0\). Then, by following the same procedure explained above we have found the complete set of eigenstates of the corresponding Hamiltonian. In particular, (61) turn to be a Bessel-type one and therefore we can write

$$\begin{aligned} \rho (\tau )=c_1{\mathcal {B}}_J(0,A^-(\tau )/6\pi )+c_22{\mathcal {B}}_Y(0,A^-(\tau )/6\pi ), \end{aligned}$$
(75)

in which \({\mathcal {B}}_J\) and \({\mathcal {B}}_Y\) are the Bessel functions of the first and second kind respectively. Therefore, \(\varDelta \beta _+\) loses its oscillatory and confined character and grows monotonically towards the singularity (see Fig. 14). As a consequence, because of the divergence of \(\varDelta \beta _+\) the quantum behaviour of the shear (72) is not crucial here. Thus, we can conclude that the only presence of the harmonic potential is not sufficient to confine the trajectory of the anisotropies but it is necessary to introduce the regularizing polymer effects and remove the divergences in the semiclassical background.

To summarize, here the general formulation of the idea proposed in [38] has been implemented to a Minisuperspace regulated by PQM on a very general ground. In fact, we considered as “polymerized” both the quasi-classical and the quantum generalized coordinates. In this respect, it is worth noting that the major impact of a polymer approach is clearly on the quasi-classical setting, since a Bounce can emerge and replace the cosmological singularity. This feature affects the dynamics of the quantum variables on a basic level, with respect to the modifications introduced by polymerizing their own Hilbert space that mainly concern the nature of the obtained spectrum (see [24, 53]). More specifically, we analyzed the Bianchi I model coherently with the general prescriptions, i.e. both the surface-like variable and the small anisotropies are treated via a polymer approach. When studying the Bianchi IX model we polymerize the background setting only, while the quantum dynamics of the anisotropies is treated via standard quantum mechanics. In practice, this corresponds to approximate the quantum equation of a pendulum with the corresponding one of a harmonic oscillator, in order to provide an explicit (and otherwise prevented) analytical solution. This kind of harmonic reduction is well-known also in fundamental classical physics and it is commonly justified via the so-called “regime of small oscillations” in the pendulum dynamics. When transferred to our polymer model, this typical assumption is well-grounded, since the idea in [38] is applicable only when the phase-space of the quantum system is “small”. Actually, when the range of the momentum variables is intrinsically restricted the sine function is well-approximated by its argument and the harmonic oscillator becomes a reliable a good approximation. The possibility of passing from the eigenfunctions of the polymer (time-independent) harmonic oscillator (the facto a quantum pendulum) to a standard theory, in the limit discussed above, is satisfactory described in [53]. Furthermore, we stress that if our approximation fails, it also breaks down the idea itself of the present study and of the analysis in [40]. Such an eventuality could concern the Bianchi I dynamics only. In fact, in our model the Bianchi IX quantum dynamics is assumed to be close to that of an isotropic Universe and the anisotropies growth is somehow “frozen” thanks to the presence of a potential.

7 Concluding remarks

In this work we consider a new theoretical paradigm to investigate the decoupling of a quantum gravity system into a quasi-classical background and a small quantum subsystem. In particular, we generalize the original idea in [38] in the case of a polymer quantum formulation of the Minisuperspace [24, 25]. The main goal of the present analysis is the quantum characterization of the Universe anisotropic degrees of freedom across a Big Bounce configuration [13, 32].

The first part of the manuscript is dedicated to the challenging question of reformulating the Vilenkin idea in the momentum representation, i.e. the only viable to semiclassically implement the polymer formulation. In fact, the Hamiltonian kinetic term is always quadratic in the momenta and hence in the standard Vilenkin approach it transforms into a second derivative in the coordinate representation. On the other hand, the potential term has a generic form and so in the momentum representation we have to deal with non-local differential operators. Nonetheless, we manage this difficulty by requiring that all the functions of the momenta be series expandable.

In the second part of this study we apply the derived theoretical paradigm to the description of the quantum behaviour of small Universe anisotropies during a semiclassical bouncing picture. In particular, we first consider a Bianchi I model (to be thought as the limit of any Bianchi Universe when the spatial curvature is neglected [56, 57]), whose background corresponds to a flat isotropic Universe. Then, we consider the evolution of a Bianchi IX model in the limit of small anisotropies, whose quantum potential contains the positive spatial curvature contribution.

In the first case, we see that thanks to the presence of the Bounce the anisotropies quantum standard deviation grows slowly without diverging at \(t=0\) (differently from what happens along the singular trajectories) but it still monotonically increases. So, the concept of a quasi-isotropic Universe (as well as the Vilenkin approximation scheme) is essentially lost since the anisotropies are not under control, even when represented on the polymer lattice.

In the second case, the resulting Schrödinger equation for the anisotropic variables in the polymer formalism would correspond to a time-dependent quantum pendulum, reduced to a simpler and treatable time-dependent harmonic oscillator by virtue of the fundamental assumption of the present Vilenkin analysis, i.e. the smallness of the anisotropic phase space. The important result is that the anisotropies standard deviation of the Hamiltonian eigenstates is no longer monotonically increasing across the Bounce, but it oscillates with a constant amplitude. The main difference between the two cases is that the polymer bouncing effect alone is not able to maintain the smallness of the anisotropies (both of their mean value and standard deviation), whereas the quantum emergence of a small positive curvature confines the anisotropies standard deviation if the quasi-classical background is regularized at the singularity.

Thus, by limiting the anisotropies to a small quantum effect we have demonstrated that the bouncing evolution preserves the quasi-isotropic nature of the classical background, thanks to the presence of a spatial curvature term that induces a localizing potential. We remark that the anisotropic mean values on the Hamiltonian eigenstates is zero, hence our analysis is consistent with the quasi-isotropic ansatz. By concluding, since the Bianchi IX model is the prototype for constructing the dynamics of a generic inhomogeneous cosmological model [46, 58,59,60] we can infer the general validity of the present analysis.