Investigating $R_D$ and $R_{D^*}$ anomalies in a left–right model with an inverse seesaw

Abstract

We investigate $R_D$ and $R_{D^*}$ anomalies in a low scale left–right symmetric model based on $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$ with a simplified Higgs sector consisting of only one bidoublet and one $SU(2)_R$ doublet. The Wilson coefficients relevant to the transition $b\rightarrow c\tau \nu$ are derived by integrating out the charged Higgs $H^\pm$ boson, which gives the dominant contributions. We emphasize that the charged Higgs effects, with the complex right-handed quark mixing matrix, can account for both $R_D$ and $R_{D^*}$ anomalies simultaneously, while adhering to a set of significant constraints including, for instance, $\textrm{BR}(B^-_c \rightarrow \tau ^- \bar{\nu }_\tau )$ and $B_{s(d)}-\bar{B}_{s(d)}$ mixing. In relation to this, we show that the predicted values of the $D^*$, $\tau$ longitudinal polarizations and $P_\tau (D)$ can be affected for the set of the parameters of the model resolving the $R_{D,D^*}$ anomalies.

1 Introduction

In flavor physics, the two ratios $R_D$ and $R_{D^*}$ are among several long-term tensions between the Standard Model (SM) and the related experimental measurements. These ratios are defined by

$$\begin{aligned} R_{D^*,D} \equiv \frac{\mathcal {B}(B_q\rightarrow \{D^*,D\} \tau \nu )}{\mathcal {B}(B_q\rightarrow \{D^*,D\} l\nu )}, \end{aligned}$$

(1)

where $l=e,\mu$. The processes $B_q\rightarrow \{D^*,D\} \ell \nu$ with $\ell =l,\tau$ arise at tree-level from the four fermion transition $b\rightarrow c\tau \nu$. Upon combining different experimental data by BaBar Collaboration [1, 2], Belle Collaboration [3,4,5,6] and LHCb Collaboration [7,8,9], the Heavy Flavor Averaging Group (HFLAV) obtained the average of $R_D$ and $R_{D^*}$ for 2021 as [10],

$$\begin{aligned} R_D&= 0.339 \pm 0.026 \pm 0.014, \end{aligned}$$

(2)

$$\begin{aligned} R_{D^*}&= 0.295 \pm 0.010 \pm 0.010. \end{aligned}$$

(3)

Recently, with the announcement of the LHCb collaboration new results of $R_D$ and $R_{D^*}$ in autumn 2022 using the Run 1 data sample of a luminosity of $2 fb^{-1}$, the HFLAV obtained a new averages of $R_D$ and $R_{D^*}$ for 2023 as [11],

$$\begin{aligned} R_D&= 0.356 \pm 0.029, \end{aligned}$$

(4)

$$\begin{aligned} R_{D^*}&= 0.284 \pm 0.013 . \end{aligned}$$

(5)

The corresponding averages of SM predictions as reported by HFLAV [10] based on the predictions obtained in Refs.  [12,13,14] are given by

$$\begin{aligned} R_D^{\textrm{SM}}&= 0.298 \pm 0.003, \end{aligned}$$

(6)

$$\begin{aligned} R_{D^*}^{\textrm{SM}}&= 0.254 \pm 0.005. \end{aligned}$$

(7)

Clearly, the listed results of $R_D$ and $R_{D^*}$ in Eqs. (2, 3) exceed the SM predictions given above, by $1.4\sigma$ and $2.9\sigma$ respectively. Moreover, as reported by HFLAV [10], the difference with the SM predictions reported above, corresponds to about $3.4\sigma [R_D-R_{D^*}]$ combination. In Ref. [15], the authors used all the available experimental data and took the higher derivative QCDSR constraints on HQET parameters into account to fit $B_q\rightarrow \{D^*,D\}$ form factors, and gave the accurate SM prediction of $R_{D^*}$ and $R_D$. The result of their investigation indicated a $4\sigma$ discrepancy in $R_{D^*}$ and $R_D$. All this may serve as a hint for a violation of lepton-flavor universality.

In the literature, many theoretical models have been investigated aiming to explain the $R_D$ and $R_{D^*}$ anomalies. Based on the remark that the measured ratio $R_{D^*}$ is higher than its value in the SM, attempts in many models have focused on enhancing the rate of $b\rightarrow c\tau \nu$ transition through extra contributions arising from the new particles mediating the transition. This turns to be much easier than reducing the rate of $b\rightarrow c (e,\mu ) \nu$ transitions, given the much more severe restraints on the couplings of new physics to muons and electrons [16].

The new particles mediating the $b\rightarrow c\tau \nu$ can be spin-0 or spin-1. In addition, they can either carry baryon and lepton number (leptoquarks) or be B/L neutral (charged Higgs and $W'$). As reported in Ref. [16], the existing models can be classified into three main categories:

• Models with charged Higgs [17,18,19,20,21,22]. In these class of models, integrating out the charged Higgs, that mediates $b\rightarrow c\tau \nu$ transition at tree-level results in scalar–scalar operators contributing to decay rates. The contributions of these additional operators can be constrained using the measured $B_c$ lifetime. This leads to the upper limits $\textrm{BR}(B_c^{-} \rightarrow \tau ^{-} \bar{\nu }_\tau ) \le 40\%$ [23], $\textrm{BR}(B_c^{-} \rightarrow \tau ^{-} \bar{\nu }_\tau ) \le 30\%$ [24] and a much stronger bound $\textrm{BR}(B_c^{-} \rightarrow \tau ^{-} \bar{\nu }_\tau ) \le 10 \%$ was obtained from the LEP data taken at the Z peak [25]. Later on, the bounds using the measured $B_c$ lifetime had been critically investigated and relaxed upper limit of $\le 39 \%$ [26] and $\le 60 \%$ [27, 28] were obtained. An analysis of the LHC sensitivity of the charged Higgs that can explain $R_D$ and $R_{D^*}$ anomalies showed that the bound $400\, \textrm{GeV} < m_{H^\pm }$ is more stringent than $B_c$ lifetime bound [29]. Based on the finding of Ref. [29] and other investigations carried out later in Refs. [30, 31], the available charged Higgs mass range for the explanation of the $R_D$ and $R_{D^*}$ anomalies within 1 $\sigma$ range is bounded from the above as $m_{H^\pm } \le 400$ GeV. It should be remarked that $m_{H^\pm } > 400$ GeV is ruled out by the $\tau \nu$ resonance search at the LHC [29, 32], the low-mass bottom flavored di-jet search [33, 34] and a conventional search for tau sleptons [35] set constraint on the available parameter region. Recently, the analysis has been extended to cover the mass range $180\, \textrm{GeV}< m_{H^\pm } < 400 \, \textrm{GeV}$ [30, 36]. Experimentally, searches for charged Higgs bosons at high-energy colliders such as the Large Hadron Collider (LHC) have set model-dependent limits on their masses. ATLAS and CMS collaborators have searched for charged Higgs bosons that have large couplings only to the third generation, looking for multijet events with one lepton and at least 2 b-jets. They have carried out dedicated searches only for charged Higgses that dominantly couple to tb quarks. In addition, there is no dedicated searches looking for a charged Higgs with sizable couplings to both q b and t b quarks [37]. The production of charged Higgs bosons is influenced by the particle’s mass and its couplings to other particles, which are determined by the specific beyond the Standard Model (BSM) scenario being considered. When the charged Higgs boson is heavier than the top quark, the experimental constraints on its mass become weaker. Certain regions of the charged Higgs boson mass parameter space have been excluded by experimental searches, even for masses higher than the top quark mass. However, these constraints depend on the couplings to other particles, particularly top and bottom quarks. We have ensured that our coupling parameter, $g_{H^- t \bar{b}}$, is below the limits obtained from previous model-independent analyses in Ref. [37]. Therefore, the mass of the charged Higgs boson can fall within the range of 200 GeV to 1 TeV.

• Models with heavy charged vector bosons [38, 39]. In such class of models, integrating out $W'$’s yields new contributions to the vector-vector operators. Simultaneous explanation of both $R_D$ and $R_{D^{*}}$ with left-handed neutrinos requires non zero values for the associated new contributions. It should be noted that, these class of models are subjected to constraints originating from the presence of an accompanying $Z'$ mediator. Thus, the vertex $Z'b_Ls_L$ can be inferred from the $W'b_Lc_L$ vertex through the SU(2) invariance. The $Z'b_Ls_L$ term in the Lagrangian can lead to tree-level flavor-changing neutral currents (FCNCs) and hence there is a need to some mechanism to subdue the contributions of this term. One way to do that is to assume minimal flavor violation (MFV) as considered in Refs. [40, 41]. However, adopting this choice in general can not suppress $Z'bb$ and $Z'\tau \tau$ vertices. Consequently, LHC direct searches for $Z'\rightarrow \tau \tau$ resonances can result in stringent restraints on the related parameters of the models. However, as shown in Refs. [41, 42], selecting unnaturally high $Z'$ widths helps to avoid these severe constraints.

• Models with leptoquarks [18, 43]. Either scalar and vector leptoquarks can be potentially favored as an explanations for the $R_{D^{(*)}}$ anomaly [42, 44]. These models are subjected also to many important constraints including those from $b\rightarrow s \nu \nu$ restraints [42], searches at the LHC for $\tau \tau$ resonances [41, 42], and the measured $B_c$ life-time [24, 25]. However, these constraints turn to be weaker compared to the corresponding ones imposed on the alternative models described above [16].

In this study, we aim to derive the effective Hamiltonian resulting from the four fermion transition $b\rightarrow c\tau \nu$ in the minimal left–right model with an inverse-seesaw (LRIS). At tree-level, the transition is mediated by the exchanging of the charged Higgs boson in the model. The large neutrino Yukawa, which measures the strength of the charged Higgs–lepton interaction, and the charged Higgs–quark interaction, which is proportional to right-handed mixing matrix $V^{CKM}_{R}$, are notable features of this class of left–right model with an inverse seesaw mechanism that motivate it to solve $R_D$ and $R_{D^*}$.

Having the effective Hamiltonian, we will proceed to show the dominant Wilson coefficients contributing to the ratios $R_D$ and $R_{D^*}$. Consequently, we will display the dependency of the ratios on the parameters of the model to determine the most relevant ones. Moreover, we reexamine the relation between the observable $R_{D^*}$ and $\textrm{BR}(B_c \rightarrow \tau \bar{\nu }_\tau )$, reported in Refs. [24, 25], in light of Belle combination [6] and LHCb [8] experimental results, and the projection at Belle II experiment with an integrated luminosity of 50 $\mathrm ab^{-1}$ [45]. This turns to be very important because the constraint on $\textrm{BR}(B_c \rightarrow \tau \bar{\nu }_\tau )$ affects substantially the contributions from scalar operators [26,27,28]. The $B_{s(d)}-\bar{B}_{s(d)}$ mixing can lead to possible constraints on the parameter space related to the the ratios $R_D$ and $R_{D^*}$. These constraints will be investigated in this study also. Finally, we will also investigate the possibility of resolving the anomalies after including the new contributions to the Wilson coefficients of the total effective Hamiltonian in the presence of the LRIS model and give predictions of the $D^*$ and $\tau$ longitudinal polarizations.

This paper is organized as follows. In Sect. 2, we give a brief review of the left–right model with inverse seesaw. In the review, we discuss the gauge structure and the particle content of the model. We also discuss the fermion interactions with charged Higgs and with the charged $W,W'$ gauge bosons. These interactions are required to derive the effective Hamiltonian governs the processes contributing to $R_D$ and $R_{D^*}$. Then, in Sect. 3, we present the effective Hamiltonian describing $b\rightarrow c\tau \nu$ transition in the presence of a general New Physics (NP) beyond the SM. Particularly, we derive the analytic expressions of the Wilson coefficients up to one loop level originating from the charged Higgs mediation in LRIS model under study in this paper. Based on the Hamiltonian, we show the total expressions of $R_D$ and $R_{D^*}$. In Sect. 4, we give our estimation of $R_D$, $R_{D^*}$, the $D^*$ and $\tau$ longitudinal polarizations and their dependency on the parameter space. Finally, in Sect. 5, we give our conclusion.

2 Left–right model with inverse seesaw (LRIS)

The gauge sector of the minimal left–right model with an inverse-seesaw (LRIS) is based on the symmetry $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$. The particle content of the model includes the usual particles in the SM in addition to extra fermions, scalars and gauge bosons. Regarding the fermion content of the model, it is the same as its counterpart in the conventional left–right models [46,47,48,49,50,51,52,53]. The scalar sector consists of only one Bidoublet $\phi$ and one doublet $\chi _R$, which is more minimal and able to circumvent the stringent FCNC constraints placed on the conventional left–right model. Additionally, we abandon using the left-handed doublet in order to prevent the severe fine tuning in the VEV of the neutral component of the left-handed doublet scalar, $v_L$, caused by light neutrino masses. As a result, our model is $SU(2)_L \times SU(2)_R$ gauge invariant but not symmetric in left–right parity.

The implementation of the IS mechanism for neutrino masses can be carried out via introducing three SM singlet fermions $S_1$ with $B-L$ charge $=-2$ and three singlet fermions $S_2$ with $B-L$ charge $=+2$. It should be remarked that, this particular choice of the $B-L$ charges of the pair $S_{1,2}$ assures that the $U(1)_{B-L}$ anomaly is free.

The scalar sector of the LRIS model contains $SU(2)_R$ scalar doublet $\chi _R$ with $B-L$ charge equals -1, and a scalar bidoublet $\phi$ with zero $B-L$ charge. The extra doublet and bidoublet are essential for breaking the symmetries of the model upon having nonvanishing VEVs. We define $\langle \chi _R\rangle =v_R/\sqrt{2}$ and assume that $v_R$ of an order TeV to break the right-handed electroweak sector together with $B-L$. Regarding the VEV of the scalar bidoublet $\phi$, we use the parametrization $\langle \phi \rangle =\text {diag}(k_1/\sqrt{2},k_2/\sqrt{2})$ where $k_1=v s_{\beta },~k_2=v c_{\beta }$ and hence $v^2 =k_1^2 + k_2^2$ with v of an order $\mathcal {O}(100)~\text {GeV}$ to break the electroweak symmetry of the SM. Here and after we use the definitions $s_x=\sin x,~c_x=\cos x$, $t_x=\tan x$ and $ct_x=\cot x$.

The scalar–fermion interactions in the LRIS model can be inferred from the left–right symmetric Yukawa Lagrangian which can be generally expressed as

$$\begin{aligned} \mathcal {L}_{\text {Y}}= & {} \sum _{i,j=1}^3 y_{ij}^L \bar{L}_{Li}\phi L_{Rj} +\tilde{y}_{ij}^L \bar{L}_{Li} \tilde{\phi } L_{Rj} + y_{ij}^Q \bar{Q}_{Li}\phi Q_{Rj} \nonumber \\{} & {} +\tilde{y}_{ij}^Q \bar{Q}_{Li} \tilde{\phi } Q_{Rj} +y^s_{ij} \bar{L}_{Ri} \tilde{\chi }_R S^c_{2j}+H.c., \end{aligned}$$

(8)

here i and j are family indices that run from $1\ldots 3$, $y^Q$ and $\tilde{y}^Q$ represent the quark Yukawa couplings while $y^L$ and $\tilde{y}^L$ stand for the lepton Yukawa couplings. It should be noted that a $Z_4$ discrete symmetry is implemented in order to forbid a mixing mass term $M \bar{S^c_1} S_{2}$ and thus preserving the IS mechanism in a way similar to imposing $Z_2$ symmetry discussed in [54]. Under this discrete $Z_2$ symmetry, $S_1$ has a charge $-1$ and all other fields have a charge $+1$. The fields in Eq. (8) are defined as

$$\begin{aligned} \chi _R= & {} \begin{pmatrix} \chi _R^+\\ \chi _R^0 \\ \end{pmatrix},\,\,\,\, \phi = \begin{pmatrix} \phi _1^0 &{}\phi _1^+\\ \phi _2^-&{}\phi _2^0\\ \end{pmatrix},\,\,\,\,\nonumber \\ Q_{A}= & {} \begin{pmatrix}u_{A} \\ d_{A} \\ \end{pmatrix},\,\,\, L_{A}=\begin{pmatrix}\nu _{A} \\ e_{A}\\ \end{pmatrix},\,\,\,\, for\,\,\, A=L,R. \end{aligned}$$

(9)

The dual bidoublet $\widetilde{\phi }$ and doublet $\widetilde{\chi }_{R}$ are defined as $\widetilde{\phi }=\tau _2\phi ^*\tau _2$ and $\widetilde{\chi }_{R}=i\tau _2\chi ^*_{R}$ respectively. Clearly, from the scalar sector of the model and before symmetry breaking, there are 12 scalar degrees of freedom: 4 of $\chi _R$ and 8 of $\phi$. After symmetry breaking, six scalars out of these 12 degrees of freedom remain as physical Higgs bosons while the other degrees of freedom are eaten by the neutral gauge bosons: $Z_\mu$ and $Z'_\mu$ and the charged gauge bosons: $W^\pm _\mu$ and $W'^\pm _\mu$ to acquire their masses. The physical Higgs bosons are two charged Higgs bosons, one pseudoscalar Higgs boson, and the remaining three are CP-even neutral Higgs bosons. For a detailed discussion about the Higgs sector of the LRIS model we refer to Ref. [55].

We turn now to the neutrino sector of LRIS model. After breaking the $B-L$ symmetry, one finds that the neutrino Yukawa interaction terms lead to the following mass terms[54]:

$$\begin{aligned} \mathcal{L}_m^{\nu } = m_D \bar{\nu }_L \nu _R + M_R \bar{\nu }^c_R S_2 + h.c., \end{aligned}$$

(10)

where $M_{R}$ and $M_D$ are $3\times 3$ matrices related to $v_R$ and Dirac neutrino masses respectively via $M_{R}=y^s v_R/\sqrt{2}$ and $M_D=v(y^L s_{\beta }+\tilde{y}^L c_{\beta })/\sqrt{2}$. In addition one may generate very small Majorana masses for $S_{1,2}$ fermion through possible non-renormalizable terms. This tiny mass is required in the standard inverse seesaw mechanism for generating light neutrino masses  [56,57,58,59]. Thus, the Lagrangian of neutrino masses can be expressed as

$$\begin{aligned} \mathcal{L}_m^\nu = M_D \bar{\nu }_L \nu _R + M_R \bar{\nu }^c_R S_2 + \frac{1}{2}\mu _{s_2} \bar{S^c_2} S_2+H.c., \end{aligned}$$

(11)

where $\mu _s \lesssim 10^{-6}$ GeV, as it is suppressed by high non-renormalizable scale. The inverse seesaw mechanism actually depends on small mass scale $\mu _2$, which violates the residual Lepton number symmetry after breaking the LR symmetry. The light neutrino masses vanish identically in the limit of $\mu _2 \rightarrow 0$, and the lepton number is restored. According to ’t Hooft criteria, such a small scale is natural. We demonstrated that this mass parameter can be generated using a non-renormalizable dimension 7 operator [54], and despite its small size, it plays an important role in generating very small neutrino masses in this mechanism. In this context, the neutrino mass matrix can be written as $\mathcal{M}_{\nu } \bar{\psi }^c \psi$ with $\psi =(\nu _L^c,\nu _R, S_2)$ and $\mathcal{M}_{\nu }$ is given by

$$\begin{aligned} {\mathcal {M}}_\nu = \begin{pmatrix} 0 &{} M_D &{} 0 \\ M_D^T &{} 0 &{} M_{R}\\ 0 &{} M_{R}^T &{} \mu _{s_2} \end{pmatrix}. \end{aligned}$$

(12)

Note that in order to avoid a possible large mass term $m S_1 S_2$ in the Lagrangian (8), that would spoil the above inverse seesaw structure, one assumes that $L_R$, $\chi _R$, and $S_2$ are even under a $Z_2$-symmetry, while $S_1$ is an odd particle. Furthermore, similar to $S_2$, the fermion $S_1$ can acquire a mass via another renormalizable term. As discussed in Ref. [60], $S_1$ can be a natural candidate for warm dark matter. It is a kind of sterile neutrino that has no mixing with active neutrinos and hence can only interact with $Z'$ gauge boson. As a consequence, $S_1$ is not subjected to all constraints imposed on sterile neutrinos due to their mixing with the active neutrinos. On the the hand, the mass of $S_1$ has to be of order $O(10 \, \textrm{keV})$ to satisfy the combined constraints from Lyman-$\alpha$ forest data [61] and phase space arguments for fermionic dark matter [62]. This can be accommodated by choosing $\mu _{s_1}=O(10 \, \textrm{keV})$ without any conflict with the mass parameter $\mu _{s_2}$ contributing to the neutrino mass matrix given below which is required in our analysis. Moreover, for $S_1$ being hot dark matter, any related expected constraints will be set on its mass $\mu _{s_1}$ and its couplings to the $Z'$ gauge boson which have no effects on the tau couplings to neutrinos or neutrino masses or neutrino mixings needed in this study.

Following the standard procedure, the diagonalization of $\mathcal {M}_\nu$ results in the light and heavy neutrino mass eigen states $\nu _{\ell _i},\nu _{h_j}$ with the mass eigenvalues given by:

$$\begin{aligned} m_{\nu _{\ell _i}}&=M_D M_{R}^{-1} \mu _{s_2} (M_{R}^T)^{-1} M_D^T,\quad i=1\ldots 3, \end{aligned}$$

(13)

$$\begin{aligned} m_{\nu _{h_j}}^2&=M_{R}^2+M_D^2,\quad j=1\ldots 6. \end{aligned}$$

(14)

The light neutrino mass matrix in Eq. (13) must be diagonalized by the physical neutrino mixing matrix $U_{\!M\!N\!S}$ [63], i.e.,

$$\begin{aligned} U_{\!M\!N\!S}^T m_{\nu _{\ell _i}} U_{\!M\!N\!S} = m_{\nu _{\ell _i}}^\textrm{d} \equiv \textrm{diag}\{m_{\nu _e}, m_{\nu _\mu }, m_{\nu _\tau }\}. \end{aligned}$$

(15)

Thus, one can easily show that the Dirac neutrino mass matrix can be defined as:

$$\begin{aligned} M_D=U_{\!M\!N\!S}\, \sqrt{m_{\nu _{\ell _i}}^\textrm{d}}\, R\, \sqrt{\mu ^{-1}_{s_2}}\, M_R, \end{aligned}$$

(16)

where R is an arbitrary orthogonal matrix. Clearly, for $M_R$ at TeV scale and $\mu _{s_2} \ll M_R$ the light neutrino masses can be of order eV. The $9\times 9$ neutrino mass matrix $\mathcal{M}_\nu$, can be diagonalized with the help of the matrix V satisfying $V^T \mathcal{M}_\nu V = \mathcal{M}_\nu ^\textrm{diag}$. The matrix can be expressed as [64]

$$\begin{aligned} V= \left( \begin{array}{cc} V_{3\times 3} &{} V_{3\times 6}\\ V_{6\times 3} &{} V_{6\times 6} \\ \end{array} \right) . \end{aligned}$$

(17)

As a good approximation, the matrix $V_{3\times 3}$ can be given a

$$\begin{aligned} V_{3\times 3} \simeq \left( 1-\frac{1}{2} F F^T \right) U_{\!M\!N\!S} \, . \end{aligned}$$

(18)

where $F = M_D M^{-1}_R$. Generally F, as one can see from the expression of $V_{3\times 3}$, is not unitary matrix. This unitarity violation, i.e., the deviation from the standard $U_{\!M\!N\!S}$ matrix, depends on the size of $\frac{1}{2} F F^T$ [65]. The matrix $V_{3\times 6}$ is given by

$$\begin{aligned} V_{3\times 6}=\left( \textbf{0}_{3\times 3},F \right) V_{6\times 6}. \end{aligned}$$

(19)

In addition, $V_{6\times 3}= (V_{3\times 6})^\dagger$. Finally, the matrix $V_{6\times 6}$ is the one that diagonalize the $\{\nu _R, S_2\}$ mass matrix.

The neutral scalar fields and their masses can be obtained if one expands the neutral components of the bidoublet $\phi$ and the doublet $\chi _{R}$ around their vacua as follows

$$\begin{aligned} \phi _i^0 = \frac{1}{\sqrt{2}} ( v_i +\phi _i^{0R} +i \phi _i^{0I}), \end{aligned}$$

(20)

where $\phi _i=\phi _{1,2},\chi _{R}$ and $v_i=k_{1,2},v_{R}$. In this case, the symmetric mass matrix of the CP-odd Higgs bosons in the basis $(\phi _1^{0I}, \phi _2^{0I}, \chi _R^{0I})$ is given as

$$\begin{aligned} M_{A}^2=\frac{1}{2}\left( \frac{v_R^2 \alpha _{32}}{c_{2\beta }}-4v^2(2\lambda _2-\lambda _3)\right) \begin{pmatrix} c_{\beta }^2 &{} s_\beta c_\beta &{} 0 \\ . &{} s_{\beta }^2 &{} 0 \\ . &{} . &{} 0 \end{pmatrix}, \end{aligned}$$

(21)

which can be diagonlized by a unitary matrix in the form

$$\begin{aligned} Z^A=\begin{pmatrix} 0 &{} 0 &{} 1 \\ -s_{\beta } &{} c_{\beta } &{} 0 \\ c_{\beta } &{} s_{\beta } &{} 0 \end{pmatrix}, \end{aligned}$$

(22)

leading to $Z^A M_A^2 Z^{AT}=\text {diag}(0,0,m_A^2)$ with the physical mass of the pseudoscalar boson A, $m_{A}^2$, given by

$$\begin{aligned} m_{A}^2 =\frac{1}{2}\left( \frac{v_R^2}{c_{2\beta }}\alpha _{32}-4v^2(2\lambda _2-\lambda _3)\right) . \end{aligned}$$

(23)

Similar to the CP-odd Higgs bosons, the elements of the $(3\times 3)$ symmetric mass matrix of the CP-even Higgs bosons are given by

$$\begin{aligned} m_{11}&= 2v^2 (\lambda _{1}s_\beta ^2+\lambda _{23}c_\beta ^2+\lambda _{4} s_{2\beta })+\frac{1}{4}\left( \frac{1}{c_{2\beta }}+1\right) \alpha _{32} v_R^2, \end{aligned}$$

(24)

$$\begin{aligned} m_{12}&=m_{21}= v^2 ((\lambda _{1}+\lambda _{23})s_{2\beta }+2\lambda _{4})-\frac{1}{4} \alpha _{32} v_R^2 t_{2\beta }, \end{aligned}$$

(25)

$$\begin{aligned} m_{13}&=m_{31}= v v_R (\alpha _{13} s_{\beta }+\alpha _4 c_{\beta }), \end{aligned}$$

(26)

$$\begin{aligned} m_{22}&= 2v^2 (\lambda _{1}c_\beta ^2+\lambda _{23}s_\beta ^2+\lambda _{4} s_{2\beta })+\frac{1}{4}\left( \frac{1}{c_{2\beta }}-1\right) \alpha _{32} v_R^2, \end{aligned}$$

(27)

$$\begin{aligned} m_{23}&=m_{32}= v v_R (\alpha _{12} c_{\beta }+\alpha _4 s_{\beta }), \end{aligned}$$

(28)

$$\begin{aligned} m_{33}&= 2 \rho _1 v_R^2, \end{aligned}$$

(29)

where the potential parameter $\alpha _{1i}=\alpha _1+\alpha _i,~i=2,3$ and $\lambda _{23}=2\lambda _2+\lambda _3$. This matrix can be diagonalized by a unitary transformation matrix $Z^{H}$ such that $Z^H M_H^2 Z^{HT}=\text {diag}(m_{H_1}^2,m_{H_2}^2,m_{H_3}^2)$. For more details, we refer to Ref. [55].

The process under study can receive dominant contributions from the charged Higgs mediation at tree level as we will show in the following. Thus, below, we list the relevant charged Higgs couplings related to our study following Ref. [55]. In the flavor basis $(\phi _1^{\pm },\phi _2^{\pm },\chi _R^{\pm })$, the charged Higgs bosons symmetric mass matrix takes the form

$$\begin{aligned} M_{H^\pm }^2=\frac{\alpha _{32}}{2}\begin{pmatrix} \frac{v_R^2 s_{\beta }^2}{c_{2\beta }} &{} \frac{v_R^2 s_{2\beta }}{2c_{2\beta }} &{} -v v_R s_{\beta } \\ . &{} \frac{v_R^2 c_{\beta }^2}{c_{2\beta }} &{} -v v_R c_{\beta } \\ . &{} . &{} v^2 c_{2\beta } \end{pmatrix}. \end{aligned}$$

(30)

The above matrix can be diagonalized by the unitary matrix,

$$\begin{aligned} Z^{H^\pm }=\begin{pmatrix} \frac{v c_{2\beta }}{\sqrt{v^2c_{2\beta }^2+v_R^2s_{\beta }^2}} &{} 0 &{} \frac{v_R s_{\beta }}{\sqrt{v^2c_{2\beta }^2+v_R^2s_{\beta }^2}} \\ -\frac{\frac{1}{2}v_R^2 s_{2\beta }}{\sqrt{(v^2c_{2\beta }^2+v_R^2s_{\beta }^2)(v^2c_{2\beta }^2+v_R^2)}} &{} \sqrt{\frac{v^2c_{2\beta }^2+v_R^2s_{\beta }^2}{v^2c_{2\beta }^2+v_R^2}} &{} \frac{v v_R c_{\beta }c_{2\beta }}{\sqrt{(v^2c_{2\beta }^2+v_R^2s_{\beta }^2)(v^2c_{2\beta }^2+v_R^2)}} \\ -\frac{v_R s_{\beta }}{\sqrt{v^2c_{2\beta }^2+v_R^2}} &{} -\frac{v_R c_{\beta }}{\sqrt{v^2c_{2\beta }^2+v_R^2}} &{} \frac{v c_{2\beta }}{\sqrt{v^2c_{2\beta }^2+v_R^2}} \end{pmatrix}. \end{aligned}$$

(31)

The mass eigenstates basis can be obtained using the rotation $(\phi _1^{\pm },\phi _2^{\pm },\chi _R^{\pm })^T=Z^{H^\pm T}(G_1^{\pm },G_2^{\pm },H^{\pm })^T$ such that $Z^{H^\pm }M_{H^\pm }^2Z^{H^\pm T}=\text {diag}(0,0,m_{H^\pm }^2)$. Here $G_1^{\pm }$ and $G_2^{\pm }$ represent the massless charged Goldstone bosons and $H^{\pm }$ is a massive physical charged Higgs boson. The massless Goldstone bosons are eaten by the charged gauge bosons $W_\mu$ and $W'_\mu$ to acquire their masses via the familiar Higgs mechanism. On the other hand, the mass of the charged Higgs boson $H^{\pm }$ is given by:

$$\begin{aligned} m_{H^{\pm }}^2 = \frac{\alpha _{32}}{2}\left( \frac{ v_R^2}{c_{2\beta }}+v^2c_{2\beta }\right) , \end{aligned}$$

(32)

where $\alpha _{32}=\alpha _3-\alpha _2$ is a potential parameter Ref. [55]. Clearly, the charged Higgs boson mass can be of the order of hundreds GeV if we pick out the values $v_R\sim \mathcal {O}(\text {TeV})$ and $\alpha _{32}\sim \mathcal {O}(10^{-2})$. It is clear to see that, the physical charged Higgs boson is a linear combination of the flavor basis fields $\phi _1^{\pm },\phi _2^{\pm },\chi _R^{\pm }$, namely given as

$$\begin{aligned} H^\pm =Z^{H^\pm }_{13}\phi _1^\pm +Z^{H^\pm }_{23}\phi _2^\pm +Z^{H^\pm }_{33}\chi _R^\pm . \end{aligned}$$

(33)

The effective Lagrangian, in the LRIS model, describing the charged Higgs and the charged gauge bosons W and $W'$ couplings to quarks and leptons can be expressed as

$$\begin{aligned} \mathcal {L}_{eff}= \mathcal {L}^{\bar{q} q' H^\pm }_{eff}+\mathcal {L}^{\bar{\nu }\ell H^\pm }_{eff}+\mathcal {L}^{ W,W'}_{eff} \end{aligned}$$

(34)

The Lagrangians $\mathcal {L}^{\bar{q} q' H^\pm }_{eff}$ and $\mathcal {L}^{\bar{\nu }\ell H^\pm }_{eff}$ can be obtained from expanding $\mathcal {L}_{\text {Y}}$, given in Eq. (8), and rotating the fields to their corresponding ones in the mass eigenstates basis. It is direct to obtain

$$\begin{aligned} \mathcal {L}^{\bar{q} q' H^\pm }_{eff}= & {} \bar{u}_i {\Gamma _{u_i d_j }^{H^\pm \,LR\,{\textrm{eff}} } }P_R d_j H^\pm \,\nonumber \\ {}{} & {} + \bar{u}_i {\Gamma _{u_i d_j }^{H^\pm \,RL\,{\textrm{eff}} } }P_L d_j H^\pm + h.c., \end{aligned}$$

(35)

where

$$\begin{aligned} {\Gamma _{u_i d_j }^{H^\pm \,LR\,{\textrm{eff}} } }= & {} \sum _{a=1}^3 (V^R_{CKM})^*_{j a} y^Q_{i a} Z_{{3 2}}^{H^{\pm }} \nonumber \\{} & {} + \sum _{a=1}^3 (V^R_{CKM})^*_{j a} \tilde{y}^Q_{i a} Z_{{3 1}}^{H^{\pm }} \nonumber \\ {\Gamma _{u_i d_j }^{H^ \pm \,RL\,{\textrm{eff}} } }= & {} \sum _{a=1}^{3}(V^L_{CKM})^*_{j a} y^{Q^*}_{a i} Z_{{3 1}}^{H^{\pm }}\nonumber \\{} & {} + \sum _{a=1}^{3}(V^L_{CKM})^*_{j a} \tilde{y}^{Q^*}_{a i} Z_{{3 2}}^{H^{\pm }}. \end{aligned}$$

(36)

In the LRIS model and after electroweak symmetry breaking, quarks and charged leptons acquire their masses via Higgs mechanism. Consequently, we can express the quark Yukawa couplings in terms of the quark masses and CKM matrices in the left and right sectors as

$$\begin{aligned} y^Q= & {} \frac{1}{(t_\beta -ct_\beta )}\bigg (\frac{M^{diag}_u V_{\text {CKM}}^{R \dag }}{v_d} -\frac{V^L_{\text {CKM}} M^{diag}_d}{v_u} \bigg )\nonumber \\ \tilde{y}^Q= & {} \frac{1}{(ct_\beta -t_\beta )}\bigg (\frac{M^{diag}_u V_{\text {CKM}}^{R \dag }}{v_u} - \frac{V^L_{\text {CKM}} M^{diag}_d }{v_d} \bigg ), \end{aligned}$$

(37)

with $v=246$ GeV, $v_u= \frac{v s_{\beta }}{\sqrt{2}}$, $v_d= \frac{v c_{\beta }}{\sqrt{2}}$. In the above equation, $M^{diag}_{u} (M^{diag}_{d})$ is the diagonal up (down) quark mass matrix, $V^L_{\text {CKM}}$ and $V^R_{\text {CKM}}$ are the CKM matrices in the left and right sectors respectively. The mixing matrices for left and right quarks result in the CKM matrices in the left and right sectors $V_{\text {CKM}}^{L,R}=V^{u\dag }_{L,R} V^d_{L,R}$. We can choose the bases where $V^u_L=I$ and as a result, in this basis, $V_{\text {CKM}}^L=V^d_L$. Turning now to the right sector, we follow Ref. [66], where the matrix $V^R_{\text {CKM}}$ can be written as a unitary matrix similar to $V^L_{CKM}$, but with new mixing angles $\theta ^R_{ij}$ and a new Dirac phase $\delta ^R$, as follows:

$$\begin{aligned} V^R_{\text {CKM}} = K ~ V^L_{\text {CKM}}\left( \theta ^R_{12}, \theta ^R_{23},\theta ^R_{13}, \delta _R \right) ~ \tilde{K}^+, \end{aligned}$$

(38)

here the diagonal matrices K and $\tilde{K}$ contain five of six non-removable phases in $V^R_{\text {CKM}}$. It was emphasized that CP violation and FCNC in the right-handed sector can be under control if the $V^R_{\text {CKM}}$ is of the form

$$\begin{aligned} V^R_{\text {CKM}}= \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} c_{\theta ^R_{13}} &{} s_{\theta ^R_{13}} e^{i \alpha } \\ 0 &{} s_{\theta ^R_{13}} &{} -c_{\theta ^R_{13}} e^{i\alpha } \end{array} \right) , \end{aligned}$$

(39)

where $c_{\theta ^R_{13}}= \cos (\theta ^R_{13})$ and $s_{\theta ^R_{13}}= \sin (\theta ^R_{13})$ and as we will see that, in the following, the phase $\alpha$ in the third column plays an important role in increasing the values of $R_{D^*}$. It is also possible to have a non-vanishing phase in the second column, which turns out to be irrelevant and has no effect on the $R_D$ or $R_{D^*}$ results. Therefore, we set it to zero. We work in the bases where $V^d_R=I$ and thus $V_{\text {CKM}}^R=V^u_R$, similar to the left-handed quark sector.

We proceed now to the lepton-neutrinio charged Higgs interactions in the model under study. These interactions contribute to the effective Lagrangian $\mathcal {L}^{\bar{\nu }\ell H^\pm }_{eff}$ and generally, can be written as

$$\begin{aligned} \mathcal {L}^{\bar{\nu }\ell H^\pm }_{eff}= & {} \bar{\nu }_i {\Gamma _{\nu _i \ell _j }^{H^\pm \,LR\,{\textrm{eff}} } }P_R \ell _j H^\pm \,\nonumber \\ {}{} & {} + \bar{\nu }_i {\Gamma _{\nu _i \ell _j }^{H^\pm \,RL\,{\textrm{eff}} } }P_L \ell _j H^\pm + h.c., \end{aligned}$$

(40)

with

$$\begin{aligned} {\Gamma _{\nu _i \ell _j }^{H^\pm \,LR\,{\textrm{eff}} } }= & {} \sum _{a=1}^{3} \tilde{y}^L_{a j} V_{{i a}} Z_{{3 1}}^{H^{\pm }} - \sum _{a=1}^{3}y^L_{a j} V_{{i a}} Z_{{3 2}}^{H^{\pm }}\nonumber \\{} & {} -\sum _{a=1}^{3}y^{s *}_{j a} V_{{i 6 + a}} Z_{{3 3}}^{H^{\pm }} \nonumber \\ {\Gamma _{\nu _i \ell _j }^{H^ \pm \,RL\,{\textrm{eff}} } }= & {} - \sum _{a=1}^{3} V^{*}_{{i 3 + a}} y^{L *}_{j a} Z_{{3 1}}^{H^{\pm }} \nonumber \\{} & {} + \sum _{a=1}^{3} V^{*}_{{i 3 + a}} \tilde{y}^{L *}_{j a} Z_{{3 2}}^{H^{\pm }}. \end{aligned}$$

(41)

The lepton Yukawa couplings $y^L$ and $\tilde{y}^L$ can be expressed as

$$\begin{aligned} y^L&=\frac{t_{2\beta }}{\sqrt{2}\,v_u}\bigg (M_\ell -t_\beta M_D \bigg ), \end{aligned}$$

(42)

$$\begin{aligned} \tilde{y}^L&=\frac{t_{2\beta }}{\sqrt{2}\,v_u}\bigg (M_D -t_\beta M_\ell \bigg ), \end{aligned}$$

(43)

where $M_\ell$ is charged lepton diagonal mass matrix. Finally, the leptons and quarks gauge interactions related to our processes at tree-level can be deduced from the effective Lagrangian $\mathcal {L}^{ W,W'}_{eff}$ given by

$$\begin{aligned} \mathcal {L}^{ W,W'}_{eff}= & {} \frac{1}{\sqrt{2}} g_2 \cos \phi _W (V_{\text {CKM}}^L)_{ij} W_\mu \bar{u}_i \gamma _{\mu } P_L d_j\nonumber \\ {}{} & {} - \frac{1}{\sqrt{2}} g_R \sin \phi _W (V_{\text {CKM}}^R)^*_{ji} W_\mu \bar{u}_i \gamma _{\mu } P_R d_j\nonumber \\ {}{} & {} +\frac{1}{\sqrt{2}} g_2 \sin \phi _W (V_{\text {CKM}}^L)_{ij} W'_\mu \bar{u}_i \gamma _{\mu } P_L d_j \nonumber \\ {}{} & {} - \frac{1}{\sqrt{2}} g_R \cos \phi _W (V_{\text {CKM}}^R)^*_{ji} W'_\mu \bar{u}_i \gamma _{\mu } P_R d_j\nonumber \\ {}{} & {} +\frac{1}{\sqrt{2}} g_2 \cos \phi _W V_{{i j}} W_\mu \bar{\nu }_i \gamma _{\mu } P_L e_j \nonumber \\ {}{} & {} - \frac{1}{\sqrt{2}} g_R \sin \phi _W V^{*}_{{i 3 + j}} W_\mu \bar{\nu }_i \gamma _{\mu } P_R e_j \nonumber \\ {}{} & {} +\frac{1}{\sqrt{2}} g_2 \sin \phi _W V_{{i j}} W'_\mu \bar{\nu }_i \gamma _{\mu } P_L e_j \nonumber \\ {}{} & {} - \frac{1}{\sqrt{2}} g_R \cos \phi _W V^{*}_{{i 3 + j}} W'_\mu \bar{\nu }_i \gamma _{\mu } P_R e_j+ h.c., \end{aligned}$$

(44)

where $\phi _W$ is the mixing angle between $W_L$ and $W_R$, which is of order $10^{-3}$. We have now all the ingredient required for deriving the effective Hamiltonian contributing to the transition $b\rightarrow c\tau \nu$. In next section, we derive this Hamiltonian and list the expressions of the Wilson coefficients corresponding to this Hamiltonian.

3 The effective Hamiltonian relevant to the processes in the LRIS

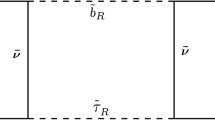
In the presence of NP beyond SM, the effective Hamiltonian governs $\vert \Delta c \vert =1$ B decays transition relevant to our processes up to one-loop level derived from the diagrams in Fig. 1, can be expressed as

$$\begin{aligned} {\mathcal H}_{eff}= & {} -\frac{4 G_F}{\sqrt{2}}V_{cb}\bigg ( (1+g_V^{LL})\,(\bar{c} \gamma _\mu P_L b) (\bar{\ell }_j \gamma ^\mu P_L \nu _i)\nonumber \\{} & {} + g_V^{RR}(\bar{c} \gamma _\mu P_R b) (\bar{\ell }_j \gamma ^\mu P_R \nu _i) \nonumber \\{} & {} + g_V^{LR}(\bar{c} \gamma _\mu P_L b) (\bar{\ell }_j \gamma ^\mu P_R \nu _i)\nonumber \\{} & {} + g_V^{RL} (\bar{c} \gamma _\mu P_R b) (\bar{\ell }_j \gamma ^\mu P_L \nu _i)\nonumber \\{} & {} +g_S^{LL}(\bar{c} P_L b) (\bar{\ell }_j P_L \nu _i)\nonumber \\{} & {} + g_S^{RR}(\bar{c} P_R b) (\bar{\ell }_j P_R \nu _i)+g_S^{LR}(\bar{c} P_L b) (\bar{\ell }_j P_R \nu _i)\nonumber \\{} & {} +g_S^{RL}(\bar{c} P_R b) (\bar{\ell }_j P_L \nu _i)\nonumber \\{} & {} + g_T^{LL}(\bar{c}\sigma _{\mu \nu } P_L b) (\bar{\ell }_j \sigma ^{\mu \nu }P_L{\nu }_i)\nonumber \\{} & {} +g_T^{RR}(\bar{c}\sigma _{\mu \nu } P_R b) (\bar{\ell }_j\sigma ^{\mu \nu } P_R{\nu }_i)\bigg ), \end{aligned}$$

(45)

where $V_{cb}$ is the cb Cabibbo–Kobayashi–Maskawa (CKM) matrix element, $P_{L,R}=\frac{1}{2}(1\mp \gamma _5)$, $\sigma _{\mu \nu }= \frac{i}{2} [\gamma _\mu , \gamma _\nu ]$ and as mentioned in Ref. [43] the tensor operator with chirality $(\bar{c}\sigma _{\mu \nu } P_R b) (\bar{\ell }_j \sigma ^{\mu \nu } P_L{\nu }_i)$ vanishes. In case of $\ell =\tau$ we find that the Wilson coefficients at the high energy scale $\mu = m_{H^\pm }$ can be expressed as

Fig. 1

Diagrams contributing to ${\mathcal H}_{eff}$, in Eq. (45) up to one loop-level due to charged Higgs mediation with V can be Z or $\gamma$ or both of them depending on the fermion lines connecting them. In the figure when A and B represent b and c quarks the other two external lines will represent $\nu _\tau$ and $\tau$. In the case that A and B represent $\nu _\tau$ and $\tau$, the other two external lines should be understood as representing b and c quarks respectively

$$\begin{aligned} g_V^{LL}(\mu )= & {} \frac{m^2_W}{m^2_{W'}} \sin ^2\phi _W Z_{M,{i 3}}^{v},\nonumber \\ g_V^{RR}(\mu )= & {} \frac{1}{V_{cb}} \Bigg (\sin ^2\phi _W + \frac{m^2_W}{m^2_{W'}} \cos ^2\phi _W \Bigg )(V_{\text {CKM}}^R)^*_{32} Z^{v,*}_{M,{i 6}},\nonumber \\ g_V^{LR}(\mu )= & {} - \Bigg (1 + \frac{m^2_W}{m^2_{W'}} \Bigg ) Z^{v,*}_{M,{i 6}}\cos \phi _W \sin \phi _W,\nonumber \\ g_V^{RL}(\mu )= & {} -\frac{1}{V_{cb}} \Bigg (1 + \frac{m^2_W}{m^2_{W'}} \Bigg ) (V_{\text {CKM}}^R)^*_{32} Z_{M,{i3}}^{v}\cos \phi _W \sin \phi _W,\nonumber \\ g_S^{LL} (\mu )= & {} -\frac{\sqrt{2}}{4 G_F V_{cb} m^2_{H^\pm }} {\Gamma _{u_2 d_3 }^{H^\pm \,RL\,{\textrm{eff}} } }{(\Gamma _{\nu _i \ell _3 }^{H^\pm \,LR\,{\textrm{eff}}})^* },\nonumber \\ g_S^{RR} (\mu )= & {} -\frac{\sqrt{2}}{4 G_F V_{cb} m^2_{H^\pm }}{\Gamma _{u_2 d_3 }^{H^\pm \,LR\,{\textrm{eff}} } }{(\Gamma _{\nu _i\ell _3}^{H^\pm \,RL\,{\textrm{eff}} })^* },\nonumber \\ g_S^{LR} (\mu )= & {} -\frac{\sqrt{2}}{4 G_F V_{cb} m^2_{H^\pm }}{\Gamma _{u_2 d_3 }^{H^\pm \,RL\,{\textrm{eff}} } } {(\Gamma _{\nu _i \ell _3}^{H^\pm \,RL\,{\textrm{eff}} })^* },\nonumber \\ g_S^{RL} (\mu )= & {} -\frac{\sqrt{2}}{4 G_F V_{cb} m^2_{H^\pm }} {\Gamma _{u_2 d_3 }^{H^\pm \,LR\,{\textrm{eff}} } } {(\Gamma _{\nu _i \ell _3 }^{H^\pm \,LR\,{\textrm{eff}} })^* },\nonumber \\ g_T^{LL} (\mu )= & {} -\frac{\sqrt{2} \alpha _E}{96\pi G_F V_{cb} m^2_{H^\pm }} {\Gamma _{u_2 d_3 }^{H^\pm \,RL\,{\textrm{eff}} }}{(\Gamma _{\nu _i \ell _3 }^{H^\pm \,LR\,{\textrm{eff}} })^* }\nonumber \\{} & {} \bigg ( f(x_c,x_\tau )+\frac{1}{2} f(x_b,x_\tau )\bigg ) +\Delta g^{LL\,Z,Z'}_{{T}},\nonumber \\ g_T^{RR}(\mu )= & {} -\frac{\sqrt{2} \alpha _E}{96 \pi G_F V_{cb}m^2_{H^\pm }} {\Gamma _{u_2 d_3 }^{H^\pm \,LR\,{\textrm{eff}} } } {(\Gamma _{\nu _i \ell _3 }^{H^\pm \,RL\,{\textrm{eff}} })^* }\nonumber \\{} & {} \bigg ( f(x_c,x_\tau )+\frac{1}{2} f(x_b,x_\tau )\bigg )+\Delta g^{RR\,Z,Z'}_{ T},\, \end{aligned}$$

(46)

where i refers to the neutrino flavor, $x_k =\frac{m_k^2}{m^2_H}$, $f(x_i,x_j)= \frac{1}{(x_i-x_j)}\Big (\frac{x_i}{1-x_i}log x_i-(x_i\leftrightarrow x_j)\Big )$ and we set the energy scale $\mu = 1$ TeV. In our numerical analysis, where all results are evaluated at the bottom scale $m_b = 4.2$ GeV, the evolution down of the Wilson coefficients from the scale $\mu = 1$ TeV to the bottom scale can be inferred from the renormalization group evolution (RGE). It should be noted that in Eq. (46), the tensor contributions to the Wilson coefficients $g_T^{LL}(\mu )$ and $g_T^{RR}(\mu )$ are generated from the one-loop diagrams in the figure. Moreover, in the same equation, we kept only the dominant contributions to the scalar Wilson coefficients $g_S^{AB}$, with A, B run over L, R, which originate from tree-level diagrams in Fig. 1. As we will show below, only these tree-level scalar contributions will have sizable effects on the ratios $R_{D,D^*}$ and other observables under concern in this work.

As can be seen from Eq. (46), the coefficients $g_S^{LL}(\mu )$ and $g_S^{RL}(\mu )$ have the same lepton vertex $(\Gamma _{\nu _i \ell _3 }^{H^\pm \,LR\,{\textrm{eff}}})^*$. Therefore, they are expected to have different values due to receiving different contributions of the quark vertices $\Gamma _{u_i d_j }^{H^ \pm \,RL\,{\textrm{eff}} }$ and $\Gamma _{u_i d_j }^{H^\pm \,LR\,{\textrm{eff}} }$ expressed in Eq. (36) in terms of $y^Q$ and $\tilde{y}^Q$. Furthermore, Eq. (37) shows that the contributions from the terms proportional to $V^L_{CKM}$ to both $y^Q$ and $\tilde{y}^Q$ are suppressed by the small down quark masses appear in the matrix $M^{diag}_d$.

In the processes under consideration, the corresponding Wilson coefficient $g_S^{LL}(\mu )$ ($g_S^{RL}(\mu )$) receives contributions only from the elements in the second column (row) of the matrix $M^{diag}_u V_{\text {CKM}}^{R \dag }$, which are present in both of $y^Q$ and $\tilde{y}^Q$. With the texture of $V_{\text {CKM}}^{R}$ given previously, we find that

$$\begin{aligned} M^{diag}_u V_{\text {CKM}}^{R \dag } = \left( \begin{array}{ccc} m_u &{} 0 &{} 0 \\ 0 &{} m_c\, c_{\theta ^R_{13}} &{} m_c\, s_{\theta ^R_{13}} \\ 0 &{} m_t\,s_{\theta ^R_{13}} e^{-i\alpha } &{} m_t\,c_{\theta ^R_{13}} e^{-i\alpha } \\ \end{array} \right) . \end{aligned}$$

(47)

In this regard, one can show that $R_D$, $R_{D^*}$ and $\textrm{BR}(B^-_c \rightarrow \tau ^- \bar{\nu }_\tau )$ receive contributions from the terms proportional to $m_t\,s_{\theta ^R_{13}} e^{-i\alpha }$ which originate from $g_S^{LL}(\mu )$ only and not from $g_S^{RL}(\mu )$. The other contributions generated from the Wilson coefficient $g_S^{RL}(\mu )$ are proportional to the charm quark mass which is small compared to the top quark mass.

Finally in Eq. (46), the quantities $\Delta g^{LL(RR)\,Z,Z'}_{ T}$ refer to the suppressed contributions, comparing to photon ones, originating from Z and $Z'$ mediating the diagrams. Upon neglecting the small contributions $\Delta g^{LL,RR\,Z,Z'}_{T }$ we find the following relations

$$\begin{aligned} g_T^{LL}(\mu )= & {} - \frac{\alpha _E}{24\pi } \bigg ( f(x_c,x_\tau )+\frac{1}{2} f(x_b,x_\tau )\bigg ) g_S^{LL}(\mu ),\nonumber \\ g_T^{RR}(\mu )= & {} - \frac{\alpha _E}{24\pi } \bigg ( f(x_c,x_\tau )+\frac{1}{2} f(x_b,x_\tau )\bigg ) g_S^{RR}(\mu ). \end{aligned}$$

(48)

For a charged Higgs of a mass 300 GeV we find that $g_T^{LL}(\mu ) \simeq 1.4 \times 10^{-3} g_S^{LL}(\mu )$ and $g_T^{RR} \simeq 1.4 \times 10^{-3} g_S^{RR}(\mu )$. Clearly the tensor contributions to the processes under study can be safely neglected. This is the case also regarding the vector Wilson coefficients $g_V^{AB}(\mu )$, where AB can be any combination of the L and R chiralities, as they are suppressed by either $\frac{m^2_W}{m^2_{W'}}\lesssim 6.4\times 10^{-3}$ for $m_{W'} \simeq \mathcal {O} (1 \, \textrm{TeV})$ or by $\sin \phi _W\simeq \phi _W \simeq \mathcal {O} (10^{-3})$ or both of them. Consequently, we are left only with contributions of the scalar Wilson coefficients.

In the given expressions below, the quantities $g_{S}^{LL}, g_{S}^{RL}, g_{S}^{LR}$ and $g_{S}^{RR}$ refer to the Wilson coefficients at the bottom scale $\mu = m_b$. In terms of these quantities, the ratios $R_M$ ($M=D,D^*)$ are given as  [16, 67, 68]:

$$\begin{aligned} R_D= & {} R_D^{\textrm{SM}} \Big [1+ 1.49 \ \text {Re}(g_{S}^{RL}+ g_{S}^{LL})\nonumber \\{} & {} + 1.02 \big ( |g_{S}^{RL}+ g_{S}^{LL}|^2 + |g_{S}^{LR}+ g_{S}^{RR}|^2 \big )\Big ], \end{aligned}$$

(49)

$$\begin{aligned} R_{D^*}= & {} R_{D^*}^{\textrm{SM}} \Big [1+ 0.11 \ \text {Re}(g_{S}^{RL}- g_{S}^{LL}) \nonumber \\{} & {} + 0.04 \big ( |g_{S}^{RL}- g_{S}^{LL}|^2 + |g_{S}^{LR}- g_{S}^{RR}|^2 \big ) \Big ]. \end{aligned}$$

(50)

It should be noted that in the above expressions of $R_{D,D^*}$ we assumed that NP effects are only present in the third generation of leptons ($\tau , \nu _\tau$). This assumption is motivated by the absence of deviations from the SM for light lepton modes $\ell = e$ or $\mu$.

The $D^*$ and $\tau$ longitudinal polarizations depend on the same Wilson coefficients affecting the $R_{D,D^*}$ ratios. Thus, it is relevant to our investigation to show their predicted values for the set of the parameters of the model resolving the $R_{D,D^*}$ anomalies. The two observables have been measured at Belle experiment. Their expressions can be written as  [16, 67, 68]

$$\begin{aligned} F_L(D^*)= & {} F^{\textrm{SM}}_L(D^*) \ r_{D^*}^{-1} \Big [1+ 0.24 \ \text {Re}(g_{S}^{RL}- g_{S}^{LL}) \nonumber \\{} & {} + 0.08 \big ( |g_{S}^{RL}- g_{S}^{LL}|^2 + |g_{S}^{LR}- g_{S}^{RR}|^2 \big )\Big ], \end{aligned}$$

(51)

$$\begin{aligned} P_\tau (D)= & {} P^{\textrm{SM}}_\tau (D) \ r_{D}^{-1} \Big [1 +4.65 \ \text {Re}(g_{S}^{RL}+ g_{S}^{LL}) \nonumber \\{} & {} +3.18 \big ( |g_{S}^{RL}+ g_{S}^{LL}|^2 + |g_{S}^{LR}+ g_{S}^{RR}|^2\big )\Big ], \end{aligned}$$

(52)

$$\begin{aligned} P_\tau (D^*)= & {} P^{\textrm{SM}}_\tau (D^*) \ r_{D^*}^{-1} \Big [1 - 0.22 \ \text {Re}(g_{S}^{RL}- g_{S}^{LL}) \nonumber \\{} & {} - 0.07 \big ( |g_{S}^{RL}- g_{S}^{LL}|^2 + |g_{S}^{LR}- g_{S}^{RR}|^2\big )\Big ], \end{aligned}$$

(53)

with $r_{D^{(*)}} = R_{D^{(*)}} / R^{\textrm{SM}}_{D^(*)}$. In our analysis we use the measured values of the $D^*$ and $\tau$ longitudinal polarizations reported by Belle collaborations namely, $F^{Expt}_L(D^*) = 0.60 \pm 0.08 \pm 0.035$ [69] and $P^{Expt}_\tau (D^*) = - 0.38 \pm 0.51^{+0.21}_{-0.16}$ [4, 5, 70]. On the other hand their SM predictions are estimated as $F^{\textrm{SM}}_L(D^*)= 0.464 \pm 0.010$, $P^{\textrm{SM}}_\tau (D)=0.321 \pm 0.003$ and $P^{\textrm{SM}}_\tau (D^*)=-0.496 \pm 0.015$ [14]. Although the tau polarization observable $P_\tau (D)$ is known to be a good discriminator of scalar contributions originated in many beyond SM physics, (for instances the leptoquark (LQ) scenarios [71] ) there is no available experimental measurements of this observable so far. However, it is important to show its prediction in the model under study.

The tree-level charged Higgs boson exchange also modifies the branching ratio of the tauonic decay $B_c^- \rightarrow \tau ^- \bar{\nu }_{\tau }$ as follows [16, 67, 68]

$$\begin{aligned}{} & {} {\textrm{BR}}(B_c^- \rightarrow \tau ^- \bar{\nu }_{\tau }) = {\textrm{BR}}(B_c^- \rightarrow \tau ^- \bar{\nu }_{\tau })_{\text {SM}} \nonumber \\ {}{} & {} \quad \times \left[ \bigg | 1 + \frac{m_{B_c}^2}{m_\tau (m_b+m_c)} (g_{S}^{RL}- g_{S}^{LL})\bigg |^2 \nonumber \right. \\ {}{} & {} \quad \left. + \bigg |\frac{m_{B_c}^2}{m_\tau (m_b+m_c)} (g_{S}^{LR}- g_{S}^{RR})\bigg |^2\right] , \end{aligned}$$

(54)

where $m_{B_c}^2/m_\tau (m_b+m_c) = 4.065$ and

$$\begin{aligned}{} & {} {\textrm{BR}}(B^-_c \rightarrow \tau ^- \bar{\nu }_\tau )_{{\textrm{SM}}} \nonumber \\{} & {} \quad =\tau _{B_c} \dfrac{G_F^2}{8\pi } |V_{cb}|^2 f_{B_c}^2 m_{B_c} m_{\tau }^2 \Big (1- \dfrac{m_{\tau }^2}{m_{B_c}^2}\Big )^2, \end{aligned}$$

(55)

where $V_{cb}$ stands for the CKM matrix element, $\tau _{B_c}$ and $f_{B_c}$ denote the $B^-_c$ meson lifetime and decay constant, respectively. The SM prediction of $\textrm{BR}(B^-_c \rightarrow \tau ^- \bar{\nu }_\tau )_{\textrm{SM}} = (2.25 \pm 0.21)\times 10^{-2}$ [72]. Unfortunately, no direct constraints from upper bounds on the leptonic $B_c$ branching ratios are available from the LHC. In view of this, an estimate of a bound on $\textrm{BR}(B^-_c \rightarrow \tau ^- \bar{\nu }_\tau )$ has been derived from LEP data at the Z peak in Ref. [25]. The bound turns to be strong $\textrm{BR}(B_c^{-} \rightarrow \tau ^{-} \bar{\nu }_\tau ) \le 10 \%$. Later on, the bounds using the measured $B_c$ lifetime had been critically investigated and relaxed upper limit of $\le 39 \%$ [26] and $\le 60 \%$ [27, 28] were obtained. Thus we will follow Ref. [72] and take in our analysis the bound: $\textrm{BR}(B^-_c \rightarrow \tau ^- \bar{\nu }_\tau )< 60\%$.

The processes $B_s \rightarrow \ell _{A}^{+} \ell _{A}^{-}$, where $\ell _{A}^{-}$ denotes a charged lepton, can be used to derive constraints on the parameter space on the model under concern in this work as we discuss in the following. These processes are mediated at tree-level by the neutral Higgs ($H_{k}^{0}=H^{0},h^{0},A^{0}$) exchange. Their branching ratios, including tree-level neutral Higgs contributions, can be written as

$$\begin{aligned}{} & {} \mathcal{{B}}\left[ B^0_s \rightarrow \ell _{A}^{+} \ell _{A}^{-} \right] = \dfrac{G_{F}^{4} M_{W}^{4} }{8 \pi ^{5}} \, \sqrt{1-4 x_{i}} \, M_{ B_s} \, f_{ B_s}^{2} \,m^{2}_{l_{A}} \, \tau _{ B_s} \nonumber \\ {}{} & {} \qquad \times \left\{ \left| \dfrac{M_{B_s}^{2} \left( C^{b s}_{P}-C^{' b s}_{P}\right) }{2 m_{l_{A}}\left( m_{s}+m_{b}\right) } -\left( C^{b s}_{A}-C^{' b s}_{A}\right) \right| ^{2} \right. \nonumber \\ {}{} & {} \qquad + \left. \left| \dfrac{M_{ B_s}^{2} \left( C^{ b s }_{S}-C^{' b s}_{S}\right) }{2 m_{l_{A}} (m_{s}+m_{b})} \right| ^{2}\times \left[ 1-4 x^2_{A}\right] \right\} , \end{aligned}$$

(56)

where $x_{i}=\frac{m_{\ell _{i}}}{M_{B_s}}$, $\tau _{B_s}$ and $f_{B_s}$ stand for the $B^-_s$ meson lifetime and decay constant, respectively. In the above equation, the neutral Higgs non-vanishing Wilson coefficients only include $C^{b s}_{P,S}$ $C^{' b s}_{P,S}$. Their expressions are listed in Eq. (69) in Appendix A.1. On the other hand and within SM, up to one loop-level, we have $C^{b s}_{P}=C^{' b s}_{P}=C^{' b s}_{A}=0$ [73] and

$$\begin{aligned} { C^{bs}_{A} = -V^{\star }_{tb}V_{ts} Y\left( \dfrac{ m^{2}_{t}}{ M^{2}_{W}}\right) -V^{\star }_{cb}V_{cs} Y\left( \dfrac{ m^{2}_{c}}{ M^{2}_{W}}\right) , } \end{aligned}$$

(57)

The function $Y =\eta _{Y} Y_{0}$ is defined in a way that the NLO QCD effects are included in $\eta _{Y}=1.0113$ [74].The expression of the one loop Inami-Lim function $Y_{0}$ is given as [75]

$$\begin{aligned} Y_{0}(x)= \dfrac{x}{8} \, \left[ \dfrac{4-x}{1-x}+ \dfrac{3\,x}{(1-x)^{2}}\,{\ln (x)} \right] . \end{aligned}$$

(58)

It should be remarked that, the SM Wilson coefficient $C^{bs}_{A}$ is scale independent as its corresponding effective operator corresponds to conserved vector current with vanishing anomalous dimensions [73].

In our analysis we use the numerical values of the CKM matrix elements reported in Ref. [76]. Moreover, the numerical values of the mass and life time of $B_s$ are taken from Ref. [77] and we take the value $f_{B_s}=0.230$ GeV [78]. Setting the neutral Higgs Wilson coefficients to zero in Eq. (56), we find that $B_{SM}(B^0_s\rightarrow \mu ^{+} \mu ^{-}) = 4.1 \times 10^{-9}$ and $B_{SM}(B^0_s\rightarrow \tau ^{+} \tau ^{-}) = 8.7 \times 10^{-7}$. We note that the SM prediction for the process $B^0_s\rightarrow \mu ^{+} \mu ^{-}$ obtained here is larger than the well known one by Misiak et al. (2013) reading $B_{SM}(B^0_s\rightarrow \mu ^{+} \mu ^{-}) = (3.65 \pm 0.23) \times 10^{-9}$ [79]. This can be attributed to the fact that the authors of Ref. [79] performed extensive study and included $\mathcal{}O(\alpha _{em})$ and $\mathcal{}O(\alpha _s^2)$ corrections to the amplitude of the process. Experimentally, from the non observation of the decay $B^0_s\rightarrow \tau ^{+} \tau ^{-}$, we have the upper limit $B(B^0_s\rightarrow \tau ^{+} \tau ^{-}) < 6.8 \times 10^{-3}$ [77]. This result allows new physics to have large contributions to $B(B^0_s\rightarrow \tau ^{+} \tau ^{-})$ and hence one obtains very loose constraints. This is not the case regarding the process $B^0_s\rightarrow \mu ^{+} \mu ^{-}$ for which the experimental measurements $\mathcal {B} \left( B_s \rightarrow \mu ^+ \mu ^- \right) _{\textrm{LHCb}} = (3.09^{+0.46+0.15}_{-0.43-0.11})\times 10^{-9}$ [80]. We refer to Ref. [10] for the results reported by the CMS, ATLAS and CDF collaborations. Using the $2\sigma$ range of the HFLAV average $\mathcal {B} \left( B_s \rightarrow \mu ^+ \mu ^- \right) _{\textrm{HFLAV}} = (3.45\pm 0.29)\times 10^{-9}$ [11] and with the help of Eq. (56), we can derive the required constraints on our parameter space

In the model under consideration in this work, the $B_{s(d)}-\bar{B}_{s(d)}$ neutral meson mixing receives new contributions from tree-level diagrams mediated by the exchange of neutral Higgs bosons, box diagrams mediated by the charged Higgs only, the $W'$ bosons only, both charged Higgs and $W'$ or $W^\pm$ together and finally both $W'$ and $W^\pm$ together. In Appendix A.1.1, we list the set of the operators contributing to the effective Hamiltonian governing the $B_{s(d)}-\bar{B}_{s(d)}$ mixing and their corresponding Wilson coefficients. Following the analysis in Ref. [81], we can use the reported experimental and SM values of $\Delta M_{B_{s,d}}$ and $\Delta M_{B_{s,d}}^{\textrm{SM}}$ respectively to impose the constraints $0.85<{\Delta M^{SM+H^\pm }_{B_s}}/{\Delta M_{B_s}^{\textrm{SM}}} <1.10$ and $0.81<{\Delta M^{SM+H^\pm }_{B_d}}/{\Delta M_{B_d}^{\textrm{SM}}} <1.03$ up to $2 \sigma$ level.

The $b \rightarrow s \gamma$ can lead to constraints on the parameter space of the model under consideration. In our investigation of these constraints, we work in leading logarithmic (LL) precision. Charged Higgs can mediate a loop diagram similar to the one in the SM but with replacing the charged W bosons with the charged Higgs. On the other hand, the contributions of the neutral Higgs boson to $b \rightarrow s \gamma$ are suppressed and thus can be neglected. This can be explained as the flavor off-diagonal elements in the down sector can be stringently constrained from the tree-level decays. Thus, we are left with the contributions originating from charged Higgs mediating the loop diagram.

Fig. 2

Left (right) $R_{D^*}$ ($R_D$) variation with $g_{S}^{LL}$ where the shaded green regions represent the allowed $2\sigma$ region of their experimental values

In the small $t_\beta$ and $\alpha _{32}$ scheme adopted in this study, we find that the effective couplings $\Gamma _{c b }^{H^\pm \,LR\,{\textrm{eff}} }$ and $\Gamma _{c s }^{H^\pm \,LR\,{\textrm{eff}} }$ appearing in Eq. (36) are so tiny, regardless the values of the parameters $\alpha$ and $\theta _{13}$. This is not the case if one considers $\Gamma _{c s }^{H^\pm \,RL\,{\textrm{eff}} }$ and $\Gamma _{c b }^{H^\pm \,RL\,{\textrm{eff}} }$ which can be of order $\mathcal{}O(10^{-2})$ or larger than that. Consequently, in our analysis, we keep only the dominant contributions to $b \rightarrow s \gamma$ in the following. Upon, neglecting the operators with mass dimension higher than six, one obtains the same effective Hamiltonian as in the case of the SM [82]

$$\begin{aligned} \mathcal{{H}}_{eff}^{b \rightarrow s \gamma }= -\dfrac{4G_F }{\sqrt{2}} V_{tb}V_{ts}^\star \sum _i C_{i} \, O_{i}\, . \end{aligned}$$

(59)

In the approximation we adopted above, charged Higgs, propagating in the loop, contributes only to the Wilson coefficients $C^{H^\pm }_7$ and $C^{H^\pm }_8$ corresponding to the operators

$$\begin{aligned} O_7&= \dfrac{e}{{16\pi ^2 }}m_b \bar{s} \sigma ^{\mu \nu } P_R b F_{\mu \nu } ; \nonumber \\ O_8&= \dfrac{{g_s }}{{16\pi ^2 }}m_b \bar{s}\sigma ^{\mu \nu } T^{a} P_R b G^{a}_{\mu \nu } \end{aligned}$$

(60)

The Wilson coefficients $C^{H^\pm }_7$ and $C^{H^\pm }_8$ are given as

$$\begin{aligned} C_{7}^{H^\pm }\simeq & {} \frac{v^2}{\lambda _t} \sum _{j=1}^{3}~ \Gamma ^{RLH^\pm \star }_{u_j d_2} \, \Gamma ^{RLH^\pm }_{u_j d_3} \frac{C_{7,YY}^{0}(y_{j})}{m_{u_{j}}^{2}} , \\ C_{8}^{H^\pm }\simeq & {} \frac{v^2}{\lambda _t} \sum _{j=1}^{3}~ \Gamma ^{RLH^\pm \star }_{u_j d_2} \, \Gamma ^{RLH^\pm }_{u_j d_3} \frac{C_{8,YY}^{0}(y_{j})}{m_{u_{j}}^{2}} , \end{aligned}$$

where $y_j=m_{u_j}^2/m_{H^+}^2$ and $\lambda _t=V_{tb} \, V_{ts}^\star$. The expressions of $C_{7,YY}^{0}$ and $C_{8,YY}^{0}$ read [82];

$$\begin{aligned}&C_{7,YY}^{0}(y_j) \nonumber \\&= \frac{y_j}{72} \, \left[ \frac{-8y_j^3+3y_j^2+12y_j-7+(18y_j^2-12y_j)\ln y_j}{(y_j-1)^4} \right] \quad , \nonumber \\&C_{8,YY}^{0}(y_j) \nonumber \\&= \frac{y_j}{24} \, \left[ \frac{-y_j^3+6y_j^2-3y_j-2-6y_j \ln y_j}{(y_j-1)^4} \right] \quad . \end{aligned}$$

(61)

From [83,84,85] we have

$$\begin{aligned} \dfrac{{{\mathcal B}^{\textrm{exp}}}(b\rightarrow s\gamma )}{{\mathcal B^{{\textrm{SM}}}}(b\rightarrow s\gamma )}-1= & {} - 2.87\, \left[ C^{H^\pm }_7+0.19\,C^{H^\pm }_8\right] \nonumber \\= & {} (-0.7\pm 8.2)\times 10^{-2}, \end{aligned}$$

(62)

leading to [83]

$$\begin{aligned} |C^{H^\pm }_7+0.19\,C^{H^\pm }_8 | \lesssim 0.06\,\quad (2\,\sigma ). \end{aligned}$$

(63)

Here, we used $C^{H^\pm }_{7,8}$ at a matching scale of 1 TeV as input. Again, these constraints are so stringent that the effect of $C^{H^\pm }_{7,8}$ on the flavour anomalies can be mostly neglected.

Finally, It is worth to recall that, due to the requirement of having light neutrino masses we found that the contributions of the right neutrino sector to the corresponding Wilson coefficients $g_S^{RR}(\mu )$ and $g_S^{LR}(\mu )$ are very small and thus can be safely ignored, leaving us with only $g_S^{LL}(\mu )$ and $g_S^{RL}(\mu )$.

4 Numerical results and analysis

Having discussed all relevant constraints related to the ratios $R_{D,D^*}$, we are ready now to estimate their predictions in the model under concern in this investigation. To proceed, we need first to show, numerically, the RGE running effect of $g^{RL,LL}_S (\mu )$ from $\mu = 1$ TeV to $m_b = 4.2$ GeV scale. According to the estimation carried out in Refs. [86, 87], we have

$$\begin{aligned} \left( \begin{array}{c} g_S^{RL}\\ g_S^{LL} \\ \end{array} \right) =\left( \begin{array}{cc} 1.71 &{} 0 \\ 0 &{} 1.71 \\ \end{array} \right) \left( \begin{array}{c} g_S^{RL} (\mu = 1 \, \textrm{TeV})\\ g_S^{LL} (\mu = 1 \, \textrm{TeV})\\ \end{array} \right) . \end{aligned}$$

(64)

Furthermore, we have checked that $g_S^{RL}$ is about one order of magnitude smaller than $g_S^{LL}$; thus for real $g_S^{LL}$ (i.e., $Re(g_S^{LL}) = g_S^{LL}$), one finds

$$\begin{aligned} R_D\simeq & {} R_D^{{\textrm{SM}}} \Big [1+ 1.49 g_{S}^{LL}+ 1.02 |g_{S}^{LL}|^2 \Big ], \end{aligned}$$

(65)

$$\begin{aligned} R_{D^*}\simeq & {} R_{D^*}^{\textrm{SM}} \Big [1- 0.11 g_{S}^{LL} + 0.04 |g_{S}^{LL}|^2 \Big ]. \end{aligned}$$

(66)

This expression clearly shows that enhancing the values of $R_{D^*}$ to be in the range of the given experimental results, while keeping the limit $-1\lesssim g_S^{LL} \lesssim 1$ in mind is possible for a range of negative values of $g_S^{LL}$ as can be seen from the left plot in Fig. 2. However, as can be remarked from the right plot in Fig. 2, these negative values reduce $R_D$ below their allowed $2\sigma$ region of the experimental results shown by the shaded green region in the plot. Clearly, we deduce that the phase $\alpha$ of the mixing matrix $V^R_{CKM}$ is crucial to solve the concerned anomalies for the processes under consideration.

Fig. 3

$R_D$ and $R_{D^*}$ as function of the charged Higgs mass where the parameters as stated in the text are chosen as follows: $c_{\theta ^R_{13}} \in [-1,1]$, $\alpha \in [0,\pi ]$, $\alpha _{32} \in [0.00166,0.00716]$ and $t_\beta \in [0.15,0.25]$

Fig. 4

$R_D$ and $R_{D^*}$ as function of the sin of mixing angle $\theta ^R_{13}$ left and the phase $\alpha$ of the $V^R_{CKM}$ matrix right and other parameters are fixed as in the previous figure

The attainable values of the Wilson coefficients $g_S^{LL}$ and $g_S^{RL}$ are affected by the charged Higgs mass. As a result, to enhance these coefficients and thus the values of $R_D$ and $R_{D^*}$ while adhering to direct search constraints, the charged Higgs masses should not be too heavy, namely of the order of hundreds GeV. According to Eq. (32), this can be accomplished by considering $v_R\sim \mathcal {O}(\text {TeV})$, $\alpha _{32}\sim \mathcal {O}(10^{-2})$ and $t_\beta$ less than one. Remarkably, from the pre factor $1/(t_\beta -ct_\beta )$ in Eq. (37), it is direct to see that small $t_\beta$ values can enhance also the quark Yukawa couplings and hence together with the angle $\theta ^R_{13}$ and the complex phase $\alpha$ of the right-quark mixing $V^R_{CKM}$, defined in Eq. (39), play crucial roles in increasing the values of $R_D$ and $R_{D^*}$, and allow them to take values that are compatible with the limit of the experiments at the same time. In our scan of the parameter space we take $\alpha _{32} \in [0.007,0.016]$, $t_\beta \in [0.15,0.25]$, $c_{\theta ^R_{13}} \in [-1,1]$, $\alpha \in [0,\pi ]$ and $v_R=6400$ GeV. With this in hand, we show below our results corresponding to the scanned points in the parameter space respecting all the bounds discussed in the previous section. It should be noted that, in these results we only select the points that lead to values of $F_L(D^*)$ and $P_{\tau }(D^*)$ within their $2\sigma$ range of the corresponding experimental results. Moreover, we have checked that, for these parameters in the chosen ranges and values, the contribution of the $g_S^{RL}$ are irrelevant and can be safely neglected. This confirms our previous conclusion that only the Wilson coefficient $g_S^{LL}$ plays the major role through the terms proportional to $m_t\,s_{\theta ^R_{13}} e^{-i\alpha }$. In the following, we present a set of elucidative plots of $R_D$ and $R_{D^*}$ versus some selected relevant parameters of the model. It should be noted that these plots were generated through a random scan and therefore do not reflect any specific correlations with the chosen parameter.

Fig. 5

Allowed region in the $(\theta ^R_{13},\alpha )$ plane by all considered constraints in green color. The red region satisfies the $2\sigma$ experimental results of $R_{D^*}$ and $R_D$ together for $t_\beta \simeq 0.2074$, $\alpha _{32} = 0.00416$ which result in $m_{H^\pm } = 305$ GeV and the other parameters are fixed as before

Table 1 A set of selective benchmarks of the parameters and intended predictions resulting from the scan after taking into account the constraints discussed in the previous section and requirements stated in the beginning of this section

In Fig. 3, we display the variation of $R_D$ and $R_{D^*}$ with the charged Higgs mass. As can be seen from the figure, it is possible to account for the experimental results of $R_D$ and $R_{D^*}$ within $2\sigma$ range, while respecting the the mentioned constraints in the previous section and the $2\sigma$ range of $F_L(D^*)$ and $P_{\tau }(D^*)$ mentioned in the previous section, with charged Higgs masses $m_{H^\pm }$ can be chosen of order 300 GeV. On the other hand, the dependence of $R_D$ and $R_{D^*}$ on the sin of the mixing angle $\theta ^R_{13}$ and the phase $\alpha$ of the $V^R_{CKM}$ matrix is depicted in Fig. 4. It is clear from left plot in the figure that, moderate and large values of $s_{\theta ^R_{13}}$ are preferable to satisfy the experimental results of $R_D$ and $R_{D^*}$ within $2\sigma$ range while respecting the bounds and the requirements considered in the scan. On the other hand, regarding the phase $\alpha$, large phases are favored as can be seen from the right plot in the figure. The explicit dependence of $R_D$ and $R_{D^*}$ on the parameters $\alpha _{23}$, which determines the mass of the charged Higgs $M_{H^\pm }$, $\theta _{13}$, and the phase $\alpha$, can be understood through the following approximate analytical expressions:

$$\begin{aligned} R_D= & {} 0.298+\Gamma _{l,\nu }^{H^\pm } \sin (\theta _{13})\nonumber \\{} & {} \times \left( \frac{8.854\times 10^{-4} \Gamma _{l,\nu }^{H^\pm } \sin (\theta _{13})}{(\alpha _{23})^2}-2.39\right. \nonumber \\{} & {} \times \left. 10^{-2} \Re \left( \frac{e^{-i \alpha }}{\alpha _{23}}\right) \right) \end{aligned}$$

(67)

$$\begin{aligned} R_D^*= & {} 0.254+\Gamma _{l,\nu }^{H^\pm } \sin (\theta _{13})\nonumber \\ {}{} & {} \times \left( \frac{2.936\times 10^{-5} \Gamma _{l,\nu }^{H^\pm } \sin (\theta _{13})}{(\alpha _{23})^2}+1.496\right. \nonumber \\ {}{} & {} \times \left. 10^{-3} \Re \left( \frac{e^{-i \alpha }}{\alpha _{23}}\right) \right) \end{aligned}$$

(68)

We can obtain the regions in the $(\theta ^R_{13},\alpha )$ parameter space in which the anomalies are satisfied through varying $\theta ^R_{13}$ and $\alpha$ while assigning fixed values of the other parameters. As an example, we take the fixed values $t_\beta \simeq 0.2074$ and $\alpha _{32} = 0.00416$ which result in $m_{H^\pm } = 305$ GeV and the other parameters are fixed as before. In Fig. 5, we show the experimentally allowed $2\sigma$ region in the $(\theta ^R_{13},\alpha )$ plane satisfying $R_{D^*}$ and $R_D$ together in red color. In the same plot, the regions in green color are the allowed regions, in the $(\theta ^R_{13},\alpha )$ plane for the set of the input parameters we use, by all constraints discussed above in the previous section. Clearly, the imposed constraints have a sensible effect on the parameter space as large part of this space is excluded by the constraints. Moreover, as shown in the plot, their is a small region in the parameter space which is allowed by all the aforementioned constraints in which $R_{D^*}$ and $R_D$ anomalies are satisfied together. Specifically, this region is the intersection region of the two colored regions in the plot. It should be noted that this conclusion corresponds to our particular example of the input parameters stated above. Taking other values of the input parameters $t_\beta$, $\alpha _{32}$ and $v_R$ may lead to another regions in $(\theta ^R_{13},\alpha )$ plane that respect all constraints and satisfy $R_{D^*}$ and $R_D$ anomalies together. For instances, in Table 1, we list several benchmarks obtained upon variation of $\alpha _{32}$ while keeping other input parameters as before.

In Fig. 6, we present the correlation between $R_D$ and $R_{D^*}$ for the same set of the parameter space considered in the scan over the values and ranges mentioned in the beginning of this section. Only points that satisfy all the bounds discussed in Sect. 3 and the $2\sigma$ range of $F_L(D^*)$ and $P_{\tau }(D^*)$ are included here. It is remarkable from this figure that both $R_D$ and $R_{D^*}$ are satisfied for a lot of points in the parameter space, thanks to the complex mixing of right-handed quarks.

Fig. 6

The correlation between $R_D$ and $R_{D^*}$ for the same set of parameter space considered in Fig. 3. The dashed red line represents the $\Delta \chi ^2 = 1.0$ contour, which is consistent with the 2023 latest results from HFLAV [11]

Table 2 $Re(C^{NP}_{9\mu })/C^{SM}_{9\mu }$ and $Re(C^{NP}_{10\mu })/C^{SM}_{10\mu }$ for the set of benchmark points considered in Table 1

It should be noted that, if the $t b H^+$ Yukawa coupling is non-negligible ($c_{\theta 13}^R$ is non-zero), there will be non-negligible $tt \phi$ couplings thanks to the SU(2) invariance where $\phi$ stands for the neutral extra scalars: H and A. As a consequence, $gg \rightarrow \phi \rightarrow \tau \tau$ would also impose constraints on the parameter space. To consider this possibility, we have analyzed the processes $gg\rightarrow \phi \rightarrow \tau \tau$. We have found that the corresponding cross-sections are less than $10^{-8}$ Pb, indicating that they do not impose any significant constraints on our analysis.

We turn now to the discussion of our predictions of the $D^*$ and $\tau$ longitudinal polarizations and tau polarization observable $P_\tau (D)$. For this purpose we list in Table 1 a selective set of 6 benchmarks representing part of our results. Recall that the corresponding measurements, reported by Belle collaborations, are $F^{Expt}_L(D^*) = 0.60 \pm 0.08 \pm 0.035$ [69] and $P^{Expt}_\tau (D^*) = - 0.38 \pm 0.51^{+0.21}_{-0.16}$ [4, 5, 70]. Clearly, the uncertainty in the measurement of $P^{Expt}_\tau (D^*)$ is so large and thus we only restrict ourselves to $F_L(D^*)$. The SM prediction is estimated to be $F^{\textrm{SM}}_L(D^*)= 0.464 \pm 0.010$ [14]. Clearly from Table 1, the new contributions of the model under concern can increase the central value of the SM by about $11\%$ for the listed set of the benchmarks. We also noted there are points in our scan that imply a larger enhancement which makes our predictions closer to the experimentally measured central value. On the other hand, the enhancement in the tau polarization $P_\tau (D)$ can reach 6 times its SM predicted value as can be noted from the same table. This can serve as test of the model under consideration once this observable is measured.

Searching for new physics via B meson exclusive decays originating at the quark level from the $b\rightarrow s\ell ^{+}\ell ^{-}$ transitions has gained a lot of attention in the last decades. In the framework of the SM, these transitions take place only at loop-level. Consequently, their amplitudes are suppressed, for instances, by factors accounting for the integration over the momenta running in the loop. This in turn leads to deviations of the measured branching ratios of $B\rightarrow K\mu ^{+}\mu ^{-}$, $B\rightarrow K^{*}\mu ^{+}\mu ^{-}$, and $B_{s}\rightarrow \phi \mu ^{+}\mu ^{-}$ decays. from their SM predictions. Also, the angular observable $P_{5}^{\prime }$ in the $B^{0}\rightarrow K^{*0}\mu ^{+}\mu ^{-}$ decay, [88, 89], has shown tension with the SM values. For instance, ATLAS [90], and LHCb [91, 92], measured the value of $P_{5}^{\prime }$ in the kinematical region $4.0<q^{2}<6.0$ $\text {GeV}^{2}$ and found departure from the SM value to be more than $3\sigma$ [93]. Furthermore Belle [94, 95] and CMS [96] measured the value of $P_{5}^{\prime }$ for the same decay mode in $q^{2}$ bin $4.0<q^{2}<8.0$ $\text {GeV}^{2}$ and $6.0<q^{2}<8.68$ $\text {GeV}^{2}$ respectively. Belle measurement shows the deviation of $2.6\sigma$ from the SM prediction and CMS measurement shows a discrimination of $1\sigma$ from the SM value. Their is a possibility that the tensions between the measurements and the SM predictions of all these observables can be relaxed if one considers NP models affecting the $b\rightarrow s\ell ^{+}\ell ^{-}$ transitions. In the literature, various performed model independent global fit analyses [97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114] based on the assumption that NP present only in the muon sector revealed that two simple one-dimensional (1D) NP scenarios (S1) $C_{9\mu }^{\text {NP}}$ or (S2) $C_{9\mu }^{\text {NP}}=-C_{10\mu }^{\text {NP}}$, that give better fit to all the data, with preferences reaching $\approx 5-6\sigma$ compared to the SM [115].

The observable $P '_5$ is sensitive to the real parts of $C_{9\mu }^{\text {NP}}$ and $C_{10\mu }^{\text {NP}}$. On the other hand, the ratios $R_{K^{(*)}}$, defined as $R_{K^{(*)}}=\frac{\mathcal {B}(B\rightarrow K^{(*)}\mu ^{+}\mu ^{-})}{\mathcal {B}(B\rightarrow K^{(*)}e^{+}e^{-})}$, are also sensitive to $C_{9\mu }^{\text {NP}}$ and $C_{10\mu }^{\text {NP}}$. Recently the updated measurements of $R_{K^{(*)}}$, [116, 117] have put stringent constraints on the NP couplings and the NP models. This in turn lead to a strong constraints on the Wilson coefficients $C_{9\mu }^{\text {NP}}$ and $C_{10\mu }^{\text {NP}}$ which affect the aforementioned observables. In the model under concern we found that it is not possible to accommodate $P '_5$ and other observables related to the $b\rightarrow s\ell ^{+}\ell ^{-}$ transitions through $Re(C^{NP}_{9\mu })$ and $Re(C^{NP}_{10\mu })$. To make it more clear, we show in Table 2$Re(C^{NP}_{9\mu })/C^{SM}_{9\mu }$ and $Re(C^{NP}_{10\mu })/C^{SM}_{10\mu }$ for the set of benchmark points in Table 1. As can be seen from the table there is no sizable enhancement due to the new contributions of the model under consideration compared to the corresponding SM Wilson coefficients.

5 Conclusion

In this work we have explored the possibility of resolving the tension between the SM prediction and the experimental results of the $R_D$ and $R_{D^*}$ ratios using a low scale left–right symmetric model based on $SU(3)_C\times SU(2)_L\times SU(2)_R\times U(1)_{B-L}$. The scalar sector of the model contains charged Higgs boson with masses that can be chosen in the order of hundreds GeV without any conflict with direct search constraints. We have shown that integrating out the charged Higgs mediating the tree-level diagrams generates a set of non vanishing scalar Wilson coefficients contributing to the effective Hamiltonian governing the transition $b\rightarrow c\tau \bar{\nu }$ and hence to the ratios $R_{D^*}$ and $R_D$ and the $D^*$ and $\tau$ polarizations.

The dependency of the scalar Wilson coefficients on the matrix elements of the quark mixing angle in the right sector turns to be important. We emphasized that the mixing element $(V^R_{CKM})_{23}$ should be complex in order to satisfy both $R_D$ and $R_{D^*}$. We have also shown the complex phase associated with this mixing element is essential to accommodate the experimental results of the ratios for charged Higgs masses of order 300 GeV while respecting the constraints from $\textrm{BR}(B^-_c \rightarrow \tau ^- \bar{\nu }_\tau )$, $B_{s(d)}-\bar{B}_{s(d)}$ mixing and other relevant constraints discussed above.

Appendix

1.1 A.1 Wilaon coefficients relevant to the process $B_s \rightarrow \ell _{A}^{+} \ell _{A}^{-}$

Following Ref. [73], the neutral Higgs non-vanishing Wilson coefficients can be expressed as

$$\begin{aligned} \begin{array}{l} C_S^{b s}= \dfrac{{ \pi ^{2}}}{2 G_{F}^{2} M_{W}^{2}}\sum \limits _{k = 1}^3 \dfrac{1}{m^{2}_{H_{k}^{0}}}\, \left( \Gamma _{\ell _{A} \ell _{A}}^{LR\, H_{k}^{0}} + \Gamma _{\ell _{A} \ell _{A}}^{RL \, H_{k}^{0}} \right) \, \Gamma _{b s}^{RL\, H_{k}^{0}} \\ C_P^{b s} = \dfrac{{ \pi ^{2}}}{2 G_{F}^{2} M_{W}^{2}}\sum \limits _{k = 1}^3 \dfrac{1}{m^{2}_{H_{k}^{0}}}\, \left( \Gamma _{\ell _{A} \ell _{A}}^{LR\, H_{k}^{0}} - \Gamma _{\ell _{A} \ell _{A}}^{RL \, H_{k}^{0}} \right) \, \Gamma _{b s}^{RL\, H_{k}^{0}} \\ C_S^{' b s}= \dfrac{{ \pi ^{2}}}{2 G_{F}^{2} M_{W}^{2}}\sum \limits _{k = 1}^3 \dfrac{1}{m^{2}_{H_{k}^{0}}}\, \left( \Gamma _{\ell _{A} \ell _{A}}^{LR\, H_{k}^{0}} + \Gamma _{\ell _{A} \ell _{A}}^{RL \, H_{k}^{0}} \right) \, \Gamma _{ b s}^{LR\, H_{k}^{0}} \\ C_P^{' b s} = \dfrac{{ \pi ^{2}}}{2 G_{F}^{2} M_{W}^{2}}\sum \limits _{k = 1}^3 \dfrac{1}{m^{2}_{H_{k}^{0}}}\, \left( \Gamma _{\ell _{A} \ell _{A}}^{LR\, H_{k}^{0}} - \Gamma _{\ell _{A} \ell _{A}}^{RL \, H_{k}^{0}} \right) \, \Gamma _{ b s}^{LR\, H_{k}^{0}} \, . \end{array} \end{aligned}$$

(69)

with vertex

$$\begin{aligned} {\Gamma _{b s}^{RL\, A^0 } }= & {} - \frac{1}{\sqrt{2}} \left( \sum _{b=1}^{3}(V^R_{CKM})^*_{3 b} \sum _{a=1}^{3}(V^L_{CKM})^*_{2 a} y^{Q^*}_{a b} Z_{{3 2}}^{A}\right. \nonumber \\{} & {} + \left. \sum _{b=1}^{3}(V^R_{CKM})^*_{3 b} \sum _{a=1}^{3}(V^L_{CKM})^*_{2 a} \tilde{y}^{Q^*}_{a b} Z_{{3 1}}^{A} \right) \end{aligned}$$

(70)

$$\begin{aligned} {\Gamma _{ b s}^{LR \, A^0 } }= & {} \frac{1}{\sqrt{2}} \left( \sum _{b=1}^{3}\sum _{a=1}^{3}(V^L_{CKM})_{3 a} y^{Q}_{a b} (V^R_{CKM})_{2 b} Z_{{3 2}}^{A}\right. \nonumber \\{} & {} + \left. \sum _{b=1}^{3}\sum _{a=1}^{3}(V^L_{CKM})_{3 a} \tilde{y}^{Q}_{a b} (V^R_{CKM})_{2 b} Z_{{3 1}}^{A} \right) \end{aligned}$$

(71)

$$\begin{aligned} {\Gamma _{b s}^{RL \,h^k} }= & {} i \frac{1}{\sqrt{2}} \left( - \sum _{b=1}^{3}(V^R_{CKM})^*_{3 b} \sum _{a=1}^{3}(V^L_{CKM})^*_{2 a} y^{Q^*}_{a b} Z_{{k 2}}^{H}\right. \nonumber \\{} & {} + \left. \sum _{b=1}^{3}(V^R_{CKM})^*_{3 b} \sum _{a=1}^{3}(V^L_{CKM})^*_{2 a} \tilde{y}^{Q^*}_{a b} Z_{{k 1}}^{H} \right) \end{aligned}$$

(72)

$$\begin{aligned} {\Gamma _{b s}^{LR \,h^k } }= & {} i \frac{1}{\sqrt{2}} \Bigg (- \sum _{b=1}^{3}\sum _{a=1}^{3}(V^L_{CKM})_{3 a} y^{Q}_{a b} (V^R_{CKM})_{2 b} Z_{{k 2}}^{H} \nonumber \\{} & {} + \left. \sum _{b=1}^{3}\sum _{a=1}^{3}(V^L_{CKM})_{3 a} \tilde{y}^{Q}_{a b} (V^R_{CKM})_{2 b} Z_{{k 1}}^{H} \right) \end{aligned}$$

(73)

$$\begin{aligned} {\Gamma _{\ell _A, \ell _A}^{RL\,A^0 } }= & {} \frac{1}{\sqrt{2}} \Bigg (- y^{L^*}_{A A} Z_{{3 2}}^{A} + \tilde{y}^{L^*}_{A A} Z_{{3 1}}^{A} \Bigg ) \end{aligned}$$

(74)

$$\begin{aligned} {\Gamma _{\ell _A \ell _A}^{LR \,A^0 } }= & {} - \frac{1}{\sqrt{2}} \Bigg (- y^{L}_{A A} Z_{{3 2}}^{A} + \tilde{y}^{L}_{A A} Z_{{3 1}}^{A} \Bigg ) \end{aligned}$$

(75)

$$\begin{aligned} {\Gamma _{\ell _A \ell _A}^{RL\,h^k } }= & {} -i \frac{1}{\sqrt{2}} \Bigg ( y^{L^*}_{A A} Z_{{k 2}}^{H} + \tilde{y}^{L^*}_{A A} Z_{{k 1}}^{H} \Bigg ) \end{aligned}$$

(76)

$$\begin{aligned} {\Gamma _{\ell _A \ell _A}^{LR\, h^k } }= & {} -i \frac{1}{\sqrt{2}} \Bigg ( y^{L}_{A A} Z_{{k 2}}^{H} + \tilde{y}^{L}_{A A} Z_{{k 1}}^{H} \Bigg ) \end{aligned}$$

(77)

The expressions of $Z_{{ij}}^{A,H}$ can be found in Ref. [55]. The Wilson coefficients at low energy scale $\mu _{{low}},$ $C_{S,P}^{(\prime )bs}(\mu _{{low}})$, can be obtaining from their corresponding ones listed in Eq. (69) using the relation [73]

$$\begin{aligned} C_{S,P}^{(\prime )bs}(\mu _{{low}})=\frac{m_{q}(\mu _{{low}})}{m_{q}(\mu _{{high}})} \, C_{S,P}^{(\prime )bs}(\mu _{{high}}), \end{aligned}$$

(78)

here $m_q$ represents the running quark mass with the appropriate number of active flavors. Finally, it should be noted that since the Wilson coefficients are given at the matching scale, $m_b$ and $m_t$ must be evaluated at this scale [73].

1.1.1 A.1.1 $B_{q}-\bar{B}_{q}$ mixing

The contributions of the NP to the effective hamiltonian generating $\Delta B=2$ transitions, q = d, s, can be written as

$$\begin{aligned} \mathcal {H}^{\Delta Q=2}_\textrm{eff} = -\frac{4 G_F}{\sqrt{2}} |V_{tb}V_{tq}^*|^2 \left\{ \sum ^5_{i=1} C^{NP}_i Q_i+\sum ^3_{i=1} \tilde{C}^{NP}_i \tilde{Q}_i \right\} . \end{aligned}$$

(79)

The four-quark operators are given as

$$\begin{aligned} Q_1= & {} \left( \bar{q}\gamma ^{\mu } P_L b\right) \left( \bar{q}\gamma _{\mu } P_L b\right) \nonumber \\ Q_2= & {} ({\bar{q}}_{\alpha } P_{L} b_{\alpha })\, ({\bar{q}}_{\beta } P_{L} b_{\beta }) \nonumber \\ Q_3= & {} ({\bar{q}}_{\alpha } P_{L} b_{\beta })\, ({\bar{q}}_{\beta } P_{L} b_{\alpha }) \nonumber \\ Q_4= & {} ({\bar{q}}_{\alpha } P_{L} b_{\alpha })\, ({\bar{q}}_{\beta } P_{R} b_{\beta }) \nonumber \\ Q_5= & {} \left( \bar{q}_{\alpha } P_L b_{\beta }\right) \left( \bar{q}_{\beta } P_R b_{\alpha }\right) \end{aligned}$$

(80)

The operators $\tilde{Q}_{1,2,3}$ can be obtained from the operators $Q_{1,2,3}$ by the replacement $L \leftrightarrow R$. At tree-level, we have contributions to $\mathcal {H}^{\Delta Q=2}_\textrm{eff}$ from only neutral Higgs bosons mediation. Denoting these contributions by $C_i^{H_{k}^{0}}$, we find that their expressions can be written as

$$\begin{aligned} C_2^{H_{k}^{0}}(\mu _{H_{k}^{0}})= & {} \frac{\sqrt{2}}{4 G_F |V_{tb}V_{tq}^*|^2} \sum \limits _{k = 1}^3 \, \dfrac{ 1}{2 m_{H_{k}^{0}}^{2}} \, (\Gamma _{\;b q}^{LR\,H_{k}^{0}\star })^{2}\nonumber \\ C_2^{\prime \,H_{k}^{0}} (\mu _{H_{k}^{0}})= & {} \frac{\sqrt{2}}{4 G_F |V_{tb}V_{tq}^*|^2}\sum \limits _{k = 1}^3 \, \dfrac{ 1}{2 m_{H_{k}^{0}}^{2}} \, (\Gamma _{\;q b}^{LR\,H_{k}^{0}})^{2} \nonumber \\ C_4^{\,H_{k}^{0}} (\mu _{H_{k}^{0}})= & {} \frac{\sqrt{2}}{4 G_F |V_{tb}V_{tq}^*|^2} \sum \limits _{k = 1}^3 \, \dfrac{ 1}{m_{H_{k}^{0}}^{2}} \, \Gamma _{\;q b}^{LR\,H_{k}^{0}} \, \Gamma _{\;b q}^{LR\,H_{k}^{0}\star } \nonumber \\ \end{aligned}$$

(81)

The quantities $\Gamma _{\;q b}^{AB\,H_{k}^{0}}$ are defined as before. We remark from the above expressions that, the neutral Higgs bosons contributes only to the scalar color singlet four-quark operators in Eq. (80). In Ref. [81], it was pointed out that the contributions of the operators that contains scalar and tensor Dirac structures are highly disfavored by the fits to $b \rightarrow s$ data and hence their contributions can be neglected. The charged Higgs contributions to $\mathcal {H}^{\Delta Q=2}_\textrm{eff}$ originate at one loop-level and can be expressed as

$$\begin{aligned} C^{H^\pm }_{1}(\mu _{H^\pm })= & {} -\frac{1}{256\sqrt{2} \pi ^2 G_F m_{H^+}^2 (V_{tb}V_{t q}^*)^2} \nonumber \\ {}{} & {} \quad \times \sum _{k,\ell } \Gamma _{\ell b }^{H^\pm \,RL\,{\textrm{eff}}} \Big (\Gamma _{k q }^{H^\pm \,RL\,{\textrm{eff}}}\Big )^* \nonumber \\{} & {} \times \bigg [ \Gamma _{k b }^{H^\pm \,RL\,{\textrm{eff}}} \Big (\Gamma _{\ell q }^{H^\pm \,RL\,{\textrm{eff}}}\Big )^* G_1(x_k,x_\ell )\nonumber \\ {}{} & {} -\frac{4g^2m_{u_k} m_{u_\ell } }{m_{H^+}^2} V_{k b}V^*_{\ell q}G_2(x_k,x_\ell ,x_W)\nonumber \\{} & {} +\frac{g^2 m_{u_k}m_{u_\ell }}{m_W^2} V_{k b} V^*_{\ell q}G_3(x_k,x_\ell ,x_W) \bigg ], \end{aligned}$$

(82)

where the loop functions $G_i$ for $i=1,2,3$ are given as

$$\begin{aligned}&G_1(x,y) \nonumber \\&=\frac{1}{x-y}\left[ \frac{x^2\log x}{(1-x)^2}+\frac{1}{1-x}- \frac{y^2\log y}{(1-y)^2}-\frac{1}{1-y} \right] , \end{aligned}$$

(83)

$$\begin{aligned}&G_2(x,y,z) \nonumber \\&=-\frac{1}{(x-y)(1-z)} \nonumber \\&\quad \times \left[ \frac{x \log x}{1-x}-\frac{y\log y}{1-y}-\frac{x\log \frac{x}{z}}{z-x} +\frac{y\log \frac{y}{z}}{z-y} \right] , \end{aligned}$$

(84)

$$\begin{aligned}&G_3(x,y,z)\nonumber \\&=-\frac{1}{x-y} \left[ \frac{1}{1-z}\left( \frac{x\log x}{1-x}-\frac{y\log y}{1-y}\right) \right. \nonumber \\&\left. \quad -\frac{z}{1-z}\left( \frac{x\log \frac{x}{z}}{z-x}-\frac{y\log \frac{y}{z}}{z-y}\right) \right] . \end{aligned}$$

(85)

and $x_W=m_W^2/m_{H^+}^2$ and $x_k=m_{u_k}^2/m_{H^+}^2$. The next step is to calculate the matrix elements of the operators $Q_i$ at the scale $\mu =\mu _b$ and to run the Wilson coefficients from the electroweak scale to the scale $\mu =\mu _b$. The contribution to the $B_{q}-\bar{B}_{q}$ mixing amplitudes induced by a given NP scale coefficient $C_i(\mu =\mu _{NP})$, denoted by $\langle B_q | \mathcal {H}^{\Delta B=2}_\textrm{eff} |\bar{B}_q\rangle _i$, as a function of $\alpha _s(\mu _{NP})$ and the scale $\mu =\mu _b$ is given as [118] (see also [119])

$$\begin{aligned}{} & {} \langle B_q | \mathcal {H}^{\Delta B=2}_\textrm{eff} |{\bar{B}}_q\rangle _i\nonumber \\ {}{} & {} \quad = \sum _{j=1}^5 \sum _{r=1}^5\, \left( b_j^{(r,i)}+ \eta \, c_j^{(r,i)}\right) \,\eta ^{a_j}\, \nonumber \\ {}{} & {} \qquad \times C_i(\mu _{NP})\,B_i^{B_q}\, \langle B_s | Q_r | {\bar{B}}_q\rangle , \end{aligned}$$

(86)

where $\eta = \alpha _s(\mu _{NP}))/\alpha _s(m_t)$, $a_j, b_j^{(r,i)}$ and $c_j^{(r,i)}$ are magic numbers given in [118] and $B_{B_s}^i$ are the B parameters that can be found in Table 9 in Ref. [120]. It should be noted that the magic numbers for the evolution of the Wilson coefficients $\tilde{C}_{1-3}$ are the same as the ones for the evolution of $C_{1-3}$ [119]. Moreover, in the basis $\tilde{Q}_{i}$, the $\,B_i^{B_q}$ parameters and the hadronic matrix elements $\langle B_q | \tilde{Q}_r | \bar{B}_q\rangle$ are equal to their corresponding ones in the basis $Q_{i}$ [121]. The matrix elements are given by

$$\begin{aligned} \langle B_q | Q_1 | \bar{B}_q\rangle&=\frac{1}{3}M_{B_q}\, f_{B_q}^2, \nonumber \\ \langle B_q | Q_r | \bar{B}_q\rangle&=N_r\,\left( \frac{M_{B_q}}{m_q+m_b}\right) ^2\, M_{B_q} f_{B_q}^2, \end{aligned}$$

(87)

with $N_r= (-5/24, 1/24, 1/4, 1/12)$ for $r=(2,3,4,5)$. With all this in hand, it is direct to calculate the quantity $\Delta M_{q}$ [122, 123] and thus derive the bounds on the parameter space using the measured value of $\Delta M_{q}$.

The $K-\bar{K}$ mixing can be studied in a similar way used above in the $B_q-\bar{B}_q$ mixing. In fact, it is possible to have a non-vanishing phase in the second column of the $V^R_{\text {CKM}}$ matrix, which turns out to be irrelevant and has no effect on the $R_D$ and $R_D^*$ result. However, this imaginary phase can affect the bound from other flavor observables e.g. $\epsilon _K$. In particular, through the contributions from the neutral Higgs mediating the tree-level diagrams. In order to provide the ingredient required for the estimation of $\epsilon _K$, we define

$$\begin{aligned} C_{\epsilon _K}=\frac{Im \,\langle K^0| \mathcal{H}_\text {full}^{\Delta S=2}| \bar{K}^0 \rangle }{Im \,\langle K^0| \mathcal {H}_\textrm{SM}^{\Delta S=2}| \bar{K}^0 \rangle }, \end{aligned}$$

(88)

where $\mathcal{H}_\text {full}^{\Delta S=2} = \mathcal {H}_\textrm{SM}^{\Delta S=2} +\mathcal{H}_\text {NP}^{\Delta S=2}$. The calculation of $\langle K^0| \mathcal{H}_\text {full}^{\Delta S=2}| \bar{K}^0 \rangle _i$ can be done in a similar manner to $\langle B_q | \mathcal {H}^{\Delta B=2}_\textrm{eff} |\bar{B}_q\rangle _i$ with the replacement of $bs \leftrightarrow s d$ in the Wilson coefficients listed above. The $K-\bar{K}$ mixing can be evaluated using [118]

$$\begin{aligned}{} & {} \langle \bar{K} | \mathcal {H}^{\Delta S=2}_\textrm{eff} | K\rangle _i\nonumber \\ {}{} & {} \quad = \sum _{j=1}^5 \sum _{r=1}^5\, \left( b_j^{(r,i)}+ \eta \, c_j^{(r,i)}\right) \,\eta ^{a_j}\, \nonumber \\ {}{} & {} \qquad \times C_i^{sd}(\mu )\,B_i^K\, \langle \bar{K} | Q_r^{sd} | K\rangle , \end{aligned}$$

(89)

as before $a_i, b_j^{(r,i)}$ and $c_j^{(r,i)}$ are “magic numbers” listed in [124] and $B_K^i$ are the B parameters collected in Table 8. The matrix elements are given by

$$\begin{aligned} \langle \bar{K} | Q_1^{sd} | K\rangle&=\frac{1}{3}M_K\, f_k^2, \nonumber \\ \langle \bar{K} | Q_r^{sd} | K\rangle&=N_r\,\left( \frac{M_K}{m_d+m_s}\right) ^2\, M_K f_k^2, \end{aligned}$$

(90)

with $N_r= (-5/24, 1/24, 1/4, 1/12)$ for $r=(2,3,4,5)$. In the next step, the Wilson coefficients are evolved down from the mass scale of the Higgs scalars to the scale $\mu = 2$ GeV at which the hadronic matrix elements are evaluated using the RG equations in [124]. Doing so, it is quite forward and direct to compute the constraint on the non-vanishing phase in the second column of the $V^R_{\text {CKM}}$ matrix using the bound from $\epsilon _K$.