1 Introduction

Despite the enormous success of Newtonian gravity, it entirely failed in several situations when there were strong gravitational effects, such as when Mercury’s movement was taken into account [1]. In 1915, Einstein discovered the General Theory of Relativity (GR), which enabled the Mercury problem to be resolved [2]. Since then, GR has gained recognition as the fundamental theory of gravitational physics. However, GR contains a variety of shortcomings such as the dark energy issue that demonstrate that it is not a comprehensive theory of gravity [3, 4]. Moreover, GR contradicts current discoveries as well as the strong gravitational field [5,6,7]. Therefore, appropriate modifications to GR are needed. Einstein predicted his formulation of GR on the curvature of spacetime, but there are two more comparable formulations that use torsion and nonmetricity for spacetime. Curvature and torsion disappear in the nonmetricity approach, and only the contribution of nonmetricity is used to convey gravitational information. Jiménez et al. [8] have suggested symmetric teleparallel gravity, namely f(Q) gravity, which is a well-motivated theory of gravity in which the gravitational interaction in spacetime is governed by nonmetricity. Research on f(Q) gravity has been growing continuously since it was first proposed. A convincing set of constraints are imposed on f(Q) gravity by Lazkoz et al. [9], where Lagrange f(Q) is written as a polynomial function of redshift z. The constraints of these models have been effectively determined using observational data such as type Ia supernovae, baryon acoustic oscillation data, quasars, gamma-ray bursts, and cosmic microwave background distance data.

In f(Q) symmetric teleparallel gravity, Errehymy et al. [10] investigated the characteristics of anisotropic, spherically symmetric compact stars, particularly electrically charged strange stars. From the perspective of the Friedmann–Laîmatre–Robertson–Walker (FLRW) evolution history, Gadbail et al. [11] propose a number of fascinating explicit reconstructions for f(Q) gravity. In the context of f(Q) gravity, Maurya et al. [12] have studied the gravitationally decoupled anisotropic solutions for strange stars by combining the Massachusetts Institute of Technology (MIT) bag model equation of state for hadronic matter with the Tolman metric ansatz. Lymperis [13] investigated the cosmic implications in f(Q) gravity, motivated by the interesting characteristics and a recently proposed general form of the function of nonmetricity scalar Q. In f(Q) gravity, Hassan et al. [14] discovered a new class of wormhole solutions. Arora and Sahoo [15] look into the possibility of crossing a phantom dividing line in the extension of symmetric teleparallel gravity or f(Q) gravity, where Q is the nonmetricity. Exponential, logarithmic, and combined f(Q) theories are used to examine the evolution of the effective equation of state parameter for dark energy throughout cosmic evolution. Hu and Katsuragawa [16] showed how to correct the coincident gauge condition and perform a Hamiltonian analysis of f(Q) gravity. They demonstrate that the f(Q) gravity has 8 physical degrees of freedom using the common Dirac–Bergmann algorithm. Capozziello [17] believes that nonmetricity, with vanishing curvature and torsion, controls gravity. In order to describe the consequences of dark energy, the gravitational action is examined, incorporating an arbitrary function of the nonmetric scalar. In the context of f(Q) gravity, Anagnostopoulos et al. [18] proposed a novel model that includes a gravitational modification class that results from the inclusion of nonmetricity. The model has the same number of free parameters as the \(\Lambda \)-cold dark matter (CDM). In another work, in order to extract constraints on various classes of f(Q) models, Anagnostopoulos et al. [19] used the Big Bang Nucleosynthesis (BBN) formalism and observations.

The universe is expanding more rapidly than initially assumed, as indicated by observations made by high-redshift supernova Ia and later verified by cosmic microwave radiation [3, 4]. One possible explanation for the fast expansion of the universe takes into account the existence of dark energy or dark matter [20]. Although a telescope cannot detect dark matter, its gravitational effects on visible matter and gravitational lensing of background radiation provide us evidence of its existence. Dark energy (DE) is characterized by a state parameter \(\omega = p/\rho \). If \(-1< \omega < -1/3 \), then it is referred to as quintessence DE, and if \(\omega <-1\), then it is called phantom DE, producing the Big Rip singularity and violating the null energy condition. There are numerous references that discuss the phantom DE [21,22,23]. \(\omega = -1\) in particular provides the equation of state of “Gravastar.” With the normal matter that surrounds a black hole, Kiselev [24] presents a new static, spherically symmetric exact solution to the Einstein equations. It is possible to obtain exact limits to the known solutions for the electromagnetic static field, which suggests the relativistic relation between energy density and pressure, as well as for the extraordinary case of the cosmological constant, by introducing a condition of additivity and linearity in the energy–momentum tensor. Simeon Hellerman [25] explains the challenges in establishing the set of observable properties that would be required to define string theory in an expanding universe. These properties would be similar to an S-matrix. They demonstrate that the quintessence models with the equations of state \(-1<\omega <-1/3\) contain future horizons and may not be better suited to an S-matrix or S-vector description. Review of the cosmic dynamics of quintessence with a special focus on the development of the dark energy equation of state \(\omega \), Shinji Tsujikawa [26] constrains quintessence models using the observations of supernovae of type Ia, the cosmic microwave background, and baryon acoustic oscillations by using the analytical formulation of \(\omega \). Hussain and Ali [27] investigate the marginally stable circular orbits (MSCOs) of a massive test particle in the spacetime geometry of the Schwarzschild black hole surrounded by quintessence. In order to address this issue, the authors take into account three crucial situations in which the equation of state parameter, \(\omega _q\), has one of the following forms: (i) \(\omega _q=-1\), (ii) \(\omega _q=-2/3\), or (iii) \(\omega _q=-1/3\). The solution for a static, spherically symmetric black hole with a cloud of strings (Letelier spacetime) immersed in a quintessence fluid is found by Costa et al. [28]. The authors describe some of its thermodynamics and complete proceeding studies in the Schwarzschild spacetime with quintessence and a solid deficit angle. The quintessential matter surrounding a black hole has an additional parameter (\(\omega \)) due to the quintessential matter, in addition to the mass (M), which Ghosh [29] discussed in terms of spherically symmetric exact solutions of the Einstein equations. For a statically charged black hole (Reissner-Nordström black hole) surrounded by quintessence and a cloud of strings, Toledo and Bezerra [30] found the solution, investigated its thermodynamics, and determined the quasinormal frequencies for a scalar field in this background spacetime. Anisotropic compact stars have been studied by Das and Debnath [31] within the context of modified Gauss–Bonnet gravity, usually known as the f(G) theory of gravity. The equations characterizing the interior geometry of the compact stellar object, the anisotropic mode of the matter distribution in the presence of the electromagnetic field, and the quintessence field were established. Pradhan [32] considered an anisotropic viscous cosmological model having locally rotationally symmetric (LRS) Bianchi type I spacetime with f(Q) gravity. According to Agostino et al. [33], if the thermodynamics for a generalized scalar (dark) matter field is expressed in terms of a quasi-quintessence representation, the vacuum energy contribution can be removed. For the scalar field dark energy models, Roy et al. [34] suggested a simple generalized parameterization approach of the Hubble parameter. With their method, it is possible to write down relevant cosmological parameters that are independent of the scalar field’s nature while incorporating both the quintessence and phantom scalar fields into a single analytical scheme. In their study, Mandal et al. [35] take into account an anisotropic fluid distribution in a spherically symmetric spacetime. To investigate the solution of compact stars in f(Q) gravity, the quintessence field is used in the energy–momentum tensor, in particular. A quintessence scalar field on the brane was taken into account by Ravanpak [36] as the dark energy component of a normal branch of the Dvali–Gabadadze–Porrati (DGP) cosmological model. They investigate the stability characteristics of the model using the dynamical system technique and discover that \(\lambda \), one of their new dimensionless variables that are specified in terms of the quintessence potential, plays a significant role in the development of the universe. Ndongmo [37] proposed the thermodynamics of a revolving, nonlinear magnetically charged black hole in the quintessence field. Compact stars were proposed to exist in the context of f(T) modified gravity, where T is a scalar torsion, by Saha and Debnath [38]. Within the context of modified f(T) gravity, they obtain the equations of motion using the anisotropic property of the spherically compact star’s electromagnetic field, quintessence field, and modified Chaplygin gas. Examples of two exact solutions are given that can be used to illustrate inflation and a significant decline of the dynamical “cosmological constant,” which is provided by the scalar quintessence proposed by Kiselev [39]. Three exact solutions to the Einstein gravity equation that are minimally connected to a quintessence field are shown by Zhou [40] to possess certain characteristics. Guo [41] uses the third-order Wentzel–Kramers–Brillouin (WKB) approximation approach to evaluate the Schwarzschild black hole’s quasi-normal frequencies in the quintessence background. Bhar [42] developed a new model of an anisotropic superdense star that allows conformal motions in the presence of a quintessence field that is defined by the parameter \(\omega _q\). Inspired by all of this previous work, in this paper we want to propose a new anisotropic compact stellar model in the presence of a quintessence field characterized by \(\omega _q\) in f(Q) gravity.

The structure of this paper is as follows: In Sect. 2, we derive the field equations in the context of quadratic f(Q) gravity with anisotropic matter distribution in the presence of a quintessence field. For solving the field equations, we also took into account the linear equation of state along with the gravitational potentials of Krori and Barua. The matching condition is employed in Sect. 3 to determine the parameter values that are necessary for our construction. We examine the physical study of our developed star model by choosing the compact star SAXJ1808.4-3658, in Sect. 4. A physical analysis is discussed including the mass function, compactness factor, and redshift function. To check the viability of the model, many physical properties like the nature of the metric potential, matter density and pressure components, anisotropy, causality, Herrera’s stability analysis, the behavior of the quintessence field, equation of state parameters, and anisotropy are discussed in details. The mass–radius relationship and variation of mass with the help of contour plots are presented in the next section. Finally, by combining all the findings, we conclude our analysis of the compact star in Sect. 6.

2 Field equations for spherically symmetric objects within f(Q) theory

We consider the action for f(Q) gravity given by [8],

$$\begin{aligned} S=\int \left[ \frac{1}{2}f(Q)+\mathcal {L}_m\right] \sqrt{-g}d^{4}x, \end{aligned}$$
(1)

where f(Q) represents a general function of Q, g is the determinant of the metric \(g_{\mu \nu }\), and \(\mathcal {L}_m\) is the matter Lagrangian density. The nonmetricity tensor can be written as

$$\begin{aligned} Q_{\alpha \mu \nu }=\nabla _{\alpha }g_{\mu \nu }=-L^{\rho }_{\alpha \mu }g_{\rho \nu }-L^{\rho }_{\alpha \nu }g_{\rho \mu }, \end{aligned}$$
(2)

where the two independent traces of the nonmetricity tensor are given by

$$\begin{aligned} Q_{\alpha }=Q^{~\beta }_{\alpha ~\beta },~~ \tilde{Q}_{\alpha }=Q^{\beta }_{~~\alpha \beta }, \end{aligned}$$
(3)

and the deformation term is given by

$$\begin{aligned} L^{\alpha }_{\mu \nu }=\frac{1}{2}Q^{\alpha }_{\mu \nu }-Q^{~~~\alpha }_{(\mu \nu )}. \end{aligned}$$
(4)

The nonmetricity scalar is defined by

$$\begin{aligned} Q=-g^{\mu \nu }\left( L^{\alpha }_{\beta \nu }L^{\beta }_{\mu \alpha }-L^{\beta }_{\alpha \beta }L^{\alpha }_{\mu \nu }\right) =-P^{\alpha \beta \gamma }Q_{\alpha \beta \gamma }, \end{aligned}$$
(5)

where \(P^{\alpha \beta \gamma }\) is the nonmetricity conjugate, and the corresponding tensor is written as

$$\begin{aligned} P^{\alpha }_{~~\mu \nu }= & {} \frac{1}{4}\left[ -Q^{\alpha }_{~~\mu \nu }+2Q^{\alpha }_{(\mu \nu )}-Q^{\alpha }g_{\mu \nu }\right. \nonumber \\{} & {} \left. -\tilde{Q}^{\alpha }g_{\mu \nu }-\delta ^{\alpha }_{(\mu }Q_{\nu })\right] . \end{aligned}$$
(6)

The field equation of f(Q) gravity is obtained by varying (1) with respect to \(g_{\mu \nu }\) as

$$\begin{aligned}{} & {} -\frac{2}{\sqrt{-g}}\nabla _a \left( \sqrt{-g}f_QP_{\mu \nu }^{\alpha }\right) +f_Q\left( P_{\nu }^{\alpha \beta }Q_{\mu \alpha \beta }-2P^{\alpha \beta }_{~~\mu }Q_{\alpha \beta \nu }\right) \nonumber \\{} & {} \quad +\frac{1}{2}g_{\mu \nu }f=\kappa \mathcal {T}_{\mu \nu }, \end{aligned}$$
(7)

where \(\kappa =8\pi \) \(f_Q=\frac{\partial f}{\partial Q}\), and the energy–momentum tensor \(\mathcal {T}_{\mu \nu }\) is given by

$$\begin{aligned} \mathcal {T}_{\mu \nu }= & {} -\frac{2}{\sqrt{-g}}\frac{\delta \sqrt{-g}\mathcal {L}_m}{\delta \sqrt{g_{\mu \nu }}}. \end{aligned}$$
(8)

Then by varying the action with respect to the affine connection, one can obtain the following equation:

$$\begin{aligned} \nabla _{\mu }\nabla _{\nu }\left( \sqrt{-g}f_QP^{\mu \nu }_{~~~\alpha }\right) =0. \end{aligned}$$
(9)

The field equations ensure the conservation of the energy–momentum tensor within the formalism of f(Q) gravity, and for the choice of \(f(Q)=Q\), the Einstein equations are recovered.

Let us now assume that our model includes an anisotropic pressure that represents regular matter and a field that represents the quintessence, and therefore the energy–momentum tensor becomes

$$\begin{aligned} \mathcal {T}_{\mu }^{ \nu }=T_{\mu }^{ \nu }+\tau _{\mu }^{ \nu }, \end{aligned}$$

where \(\tau _{\mu }^{ \nu }\) corresponds to the energy–momentum tensor for the quintessence field, and its expression is given by

$$\begin{aligned} \tau _{r}^{r}= & {} \tau _{t}^{t}=-\rho _q,\\ \tau _{\theta }^{\theta }= & {} \tau _{\phi }^{\phi }=\frac{(3\omega _q+1)\rho _q}{2}, \end{aligned}$$

where \(\rho _q\) represents the energy density for the quintessence field characterized by the parameter \(\omega _q\), with (\(-1<\omega _q <-\frac{1}{3}\)), and \(T_{\mu }^{ \nu }\) represents the energy–momentum tensor of the ordinary matter having the expression

$$\begin{aligned} T_{\nu }^{\mu }=(\rho +p_r)u^{\mu }u_{\nu }-p_t g_{\nu }^{\mu }+(p_r-p_t)\eta ^{\mu }\eta _{\nu }, \end{aligned}$$
(10)

with \(u^{i}u_j =-\eta ^{i}\eta _j= 1\) and \(u^{i}\eta _j= 0\). Here, the vector \(u_i\) is the fluid 4-velocity, and \(\eta ^{i}\) is the space-like vector which is orthogonal to \(u_i\), \(\rho \) is the matter density, \(p_r\) and \(p_t\) are, respectively, the radial and the transversal pressure of the underlying fluid, and \(p_t\) lies in the orthogonal direction to \(p_r\).

In this paper, our goal is to discuss a model that describes an anisotropic matter distribution. The following line element can be used to illustrate static, spherically symmetric spacetime for this purpose:

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(11)

Assuming \(G=c=1\), the field equations in f(Q) gravity are given as follows:

$$\begin{aligned} \kappa \rho ^{\text {Total}}= & {} \frac{e^{-\lambda }}{2r^2}\Big [2rf_{QQ}Q'(e^{\lambda } - 1) + f_Q\Big ((e^{\lambda } - 1)(2 + r\nu ')\nonumber \\{} & {} + (1 + e^{\lambda })r \lambda '\Big ) + f r^2 e^{\lambda }\Big ], \end{aligned}$$
(12)
$$\begin{aligned} \kappa p_r^{\text {Total}}= & {} -\frac{e^{-\lambda }}{2r^2}\Big [2rf_{QQ}Q'(e^{\lambda } - 1)\nonumber \\{} & {} +f_Q\Big ((e^{\lambda } - 1)(2 + r \lambda ' + r\nu ') - 2r\nu '\Big ) + fr^2e^{\lambda }\Big ],\nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned} \kappa p_t^{\text {Total}}= & {} -\frac{e^{-\lambda }}{4r}\Big [-2rf_{QQ}Q'\nu ' + f_Q\Big (2\nu '(e^{\lambda } - 2) \nonumber \\{} & {} - r\nu '^2 + \lambda '(2e^{\lambda } + r\nu ') - 2r\nu ''\Big ) + 2fre^{\lambda }\Big ]., \end{aligned}$$
(14)

where the expressions for \(\rho ^{\text {Total}}\), \(p_r^{\text {Total}}\), and \(p_t^{\text {Total}}\) are given by

$$\begin{aligned} \rho ^{\text {Total}}{=}\rho {+}\rho _q,\,p_r^{\text {Total}}{=}p_r{-}\rho _q,\,p_t^{\text {Total}}{=}p_t{+}\frac{3\omega _q{+}1}{2}\rho _q. \end{aligned}$$

The nonmetricity scalar is given by [43]

$$\begin{aligned} Q=\frac{1}{r}(\nu '+\lambda ')(e^{-\lambda }-1). \end{aligned}$$
(15)

Now we define a quadratic function for f(Q) gravity, which is expressed as

$$\begin{aligned} f(Q)=Q+aQ^2, \end{aligned}$$
(16)

where “a” is a constant. This form of f(Q) was used earlier by Lin and Zhai [43] to model compact stars in f(Q) gravity.

In the field Eqs. (12)–(14), there are six unknowns. For four distinct values of the coupling constant “a,” our goal is to develop an anisotropic uncharged solution and determine its viability. To achieve this, we need to apply some constraints. Hence, under the f(Q) scenario, we use the metric potentials which Krori and Barua [44] proposed. These potentials were originally utilized to analyze charged star formations, and their non-singular character generated considerable interest in astrophysics. The solution has the form

$$\begin{aligned} \lambda = Ar^2,\, \nu = Br^2 + C. \end{aligned}$$
(17)

The ansatz contains three unknown constants, \(A,\, B\), and C, whose values can be determined by boundary conditions. In terms of the Krori–Barua ansatz, the field Eqs. (12)–(14) become

$$\begin{aligned}{} & {} \kappa \left( \rho +\rho _q\right) =\frac{e^{-2 A r^2}}{r^2}\Big [e^{A r^2} ( e^{A r^2}-1 + 2 A r^2) \nonumber \\{} & {} \quad - 2 a (A + B) ( e^{A r^2}-1)\nonumber \\{} & {} \quad \times \Big \{ (7 A - B) r^2-2 +e^{A r^2} \big (2 + (A + B) r^2\big )\Big \}\Big ], \end{aligned}$$
(18)
$$\begin{aligned}{} & {} \kappa \left( p_r-\rho _q\right) =\frac{e^{-2 A r^2}}{r^2}\Big [ e^{A r^2} (1 - e^{A r^2} + 2 B r^2) \nonumber \\{} & {} \quad + 2 a (A + B) ( e^{A r^2}-1)\nonumber \\{} & {} \quad \times \Big \{ (3 A - 5 B) r^2 -2+ e^{A r^2} (2 + (A + B) r^2)\Big \}\Big ], \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \kappa \left( p_t+\frac{3\omega _q+1}{2}\rho _q\right) \nonumber \\{} & {} \quad =e^{-2 A r^2}\Big [-e^{A r^2} \big (A - 2 B + (A - B) B r^2\big ) \nonumber \\{} & {} \qquad + 2 a (A + B) \Big \{-A + 5 B + (A + B) e^{2 A r^2} \nonumber \\{} & {} \qquad - 6 A B r^2 + 2 B^2 r^2- 2 B e^{A r^2} \big (3 + (-A + B) r^2\big )\Big \}\Big ].\nonumber \\ \end{aligned}$$
(20)

To better understand the physical properties of a massive body, it is important to consider a number of constraints, also known as the equation of state (EoS), that serve to link the matter variables of the fluid configuration to the pressure. For our present model, let us assume that the radial pressure \(p_r\) maintains a linear equation of state with the matter density \(\rho \) as

$$\begin{aligned} p_r=\alpha \rho -\beta , \end{aligned}$$
(21)

where \(\alpha \) and \(\beta \) are numeric constants, and their values will be obtained in the coming section. The EoS proposed in (21) is a generalized version of the MIT bag model EoS proposed by De Felice et al. [45]. The physical characteristics of many compact star models have been extensively studied using the EoS (21) in both general relativity (GR) and modified gravity scenarios.

Now the Eqs. (18)–(20) are solved with the help of Eq. (21) to obtain the expression of \(\rho ,\,\rho _q,\,p_r\), and \(p_t\) as follows:

$$\begin{aligned} \rho= & {} \frac{e^{-2 A r^2} \Big \{8 a (A \!+\! B)^2 \!-\! 2 (A \!+\! B) \big (4 a (A \!+\! B)-1\big ) e^{A r^2} \!+\! \beta e^{2 A r^2} \kappa \Big \}}{(1 + \alpha ) \kappa }, \nonumber \\\end{aligned}$$
(22)
$$\begin{aligned} \rho _q= & {} \frac{e^{-2 A r^2}}{(1 + \alpha ) \kappa r^2} \Big [-e^{A r^2} (1 + \alpha - 2 A \alpha r^2 + 2 B r^2) \nonumber \\{} & {} +e^{2 A r^2} (1 + \alpha - \beta \kappa r^2) - 2 a (A + B) ( e^{A r^2}-1)\nonumber \\{} & {} \times \Big \{3 A r^2-2 - 2 \alpha + 7 A \alpha r^2 - 5 B r^2 - \alpha B r^2 + (1 + \alpha ) e^{A r^2} \nonumber \\{} & {} \big (2 + (A + B) r^2\big )\Big \}\Big ],\end{aligned}$$
(23)
$$\begin{aligned} p_r= & {} \frac{e^{-2 A r^2} \Big \{8 a \alpha (A \!+\! B)^2 \!-\! 2 \alpha (A \!+\! B) ( 4 a (A \!+ \!B)-\!1) e^{A r^2}\! -\!\beta e^{2 A r^2} \kappa \Big \}}{(1 + \alpha ) \kappa }, \nonumber \\ \end{aligned}$$
(24)
$$\begin{aligned} p_t= & {} \frac{e^{-2 A r^2}}{2 (1 + \alpha ) \kappa r^2}\bigg [2 a (A + B) \Big [2 + 2 \alpha + 6 \omega _q + 6 \alpha \omega _q\nonumber \\{} & {} - 5 A r^2 -9 A \alpha r^2 + 15 B r^2 + 11 \alpha B r^2 - 9 A \omega _q r^2 - 21 A \alpha \omega _q r^2 \nonumber \\{} & {} + 15 B \omega _q r^2 + 3 \alpha B \omega _q r^2 - 12 A B r^4 - 12 A \alpha B r^4 + 4 B^2 r^4\nonumber \\{} & {} + 4 \alpha B^2 r^4+ (1 + \alpha ) e^{2 A r^2} \big (2 + 6 \omega _q + 3 (A + B) (1 + \omega _q) r^2\big ) \nonumber \\{} & {} +2 e^{A r^2} \Big \{\big (A (1 + 3 \alpha ) (1 + 3 \omega _q) - B (9 + 7 \alpha + 3 (3 + \alpha ) \omega _q)\big ) r^2\nonumber \\{} & {} -2 (1 + \alpha ) (1 + 3 \omega _q) +2 (1 + \alpha ) (A - B) B r^4\Big \}\Big ] \nonumber \\{} & {} +e^{A r^2} \Big \{1 + 3 \omega _q - 2 \big (A - 3 B (1 + \omega _q)\big ) r^2 + 2 B ( B-A) r^4 \nonumber \\{} & {} +e^{A r^2} (1 + 3 \omega _q) ( \beta \kappa r^2-1) - \alpha \Big (-1 + e^{A r^2} (1 + 3 \omega _q) \nonumber \\{} & {} + \omega _q (-3 + 6 A r^2) +2 (A - B) r^2 (2 + B r^2)\Big )\Big \}\bigg ], \end{aligned}$$
(25)

and the anisotropic factor \(\Delta =p_t-p_r\) for our present model is obtained as

$$\begin{aligned} \Delta{} & {} =\frac{e^{-2 A r^2}}{2 (1 + \alpha ) \kappa r^2}\bigg [e^{A r^2} \Big \{1 + 3 \omega _q - 2 (A - 3 B (1 + \omega _q)) r^2\nonumber \\{} & {} \quad + 2 B (-A+ B) r^4 + e^{A r^2} \Big (-1 - 3 \omega _q + 3 \beta \kappa (1 + \omega _q) r^2\Big )\nonumber \\{} & {} \quad - \alpha \Big (-1 - 3 \omega _q + e^{A r^2} (1 + 3 \omega _q) \nonumber \\{} & {} \quad + 2 A (4 + 3 \omega _q) r^2 + 2 (A - B) B r^4\Big )\Big \}\nonumber \\{} & {} \quad + 2 a (A + B) \Big \{2 + 2 \alpha + 6 \omega _q + 6 \alpha \omega _q - 5 A r^2 \nonumber \\{} & {} \quad - 17 A \alpha r^2 + 15 B r^2 + 3 \alpha B r^2 - 9 A \omega _q r^2 - 21 A \alpha \omega _q r^2 \nonumber \\{} & {} \quad + 15 B \omega _q r^2 + 3 \alpha B \omega _q r^2 - 12 A B r^4 - 12 A \alpha B r^4 \nonumber \\{} & {} \quad + 4 B^2 r^4 + 4 \alpha B^2 r^4 + (1 + \alpha ) e^{ 2 A r^2} \Big (2 + 6 \omega _q \nonumber \\{} & {} \quad + 3 (A + B) (1 + \omega _q) r^2\Big ) + 2 e^{A r^2} \bigg (-2 (1 + \alpha ) (1 + 3 \omega _q) \nonumber \\{} & {} \quad + \Big (-3 (3 + \alpha ) B (1 + \omega _q) + A \big \{1 + 3 \omega _q + \alpha (7 + 9 \omega _q)\big \}\Big ) r^2 \nonumber \\{} & {} \quad + 2 (1 + \alpha ) (A - B) B r^4\bigg )\Big \}\bigg ]. \end{aligned}$$
(26)

In the following section, each model parameter that was obtained through this approach will be thoroughly studied.

3 Boundary condition

To preserve the continuity of spacetime, both the interior and exterior of the stellar model are essential. As a result, at the boundary \(r=r_b\), the interior and exterior spacetimes must coincide. As the problem we have been considering is static, non-rotating, and spherically symmetric, one can note that the exterior solution is described by the Schwarzschild vacuum solution provided by the following line element:

$$\begin{aligned} ds_+^{2}= & {} \left( 1-\frac{2\mathfrak {m}}{r}\right) dt^{2}-\left( 1-\frac{2\mathfrak {m}}{r}\right) ^{-1}dr^{2}\nonumber \\{} & {} -r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\right) , \end{aligned}$$
(27)

where “\(\mathfrak {m}\)” denotes the total mass within the boundary of the compact star corresponding to our interior line element

$$\begin{aligned} ds_-^{2}= & {} e^{Br^2+C}dt^{2}-e^{Ar^2}dr^{2}-r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\right) ,\nonumber \\ \end{aligned}$$
(28)

where the (−) and (\(+\)) signs respectively denote the interior and exterior of spacetime.

The continuity of the metric potentials at the boundary surface \(r = r_b\) leads to the following expressions:

$$\begin{aligned} 1-\frac{2\mathfrak {m}}{r_b}= & {} e^{Br_b^{2}+C}, \end{aligned}$$
(29)
$$\begin{aligned} \left( 1-\frac{2\mathfrak {m}}{r_b}\right) ^{-1}= & {} e^{Ar_b^{2}}, \end{aligned}$$
(30)
$$\begin{aligned} \frac{\mathfrak {m}}{r_b^{2}}= & {} Br_be^{Br_b^{2}+C}. \end{aligned}$$
(31)

Equations (29)–(31) are simultaneously solved to determine the Krori–Barua unknowns \(A,\, B,\,\) C as

$$\begin{aligned} A= & {} -\frac{1}{r_b^{2}}\ln \left( 1-\frac{2\mathfrak {m}}{r_b}\right) , \end{aligned}$$
(32)
$$\begin{aligned} B= & {} \frac{\mathfrak {m}}{r_b^{3}}\left( 1-\frac{2\mathfrak {m}}{r_b}\right) ^{-1},\end{aligned}$$
(33)
$$\begin{aligned} C= & {} \ln \left( 1-\frac{2\mathfrak {m}}{r_b}\right) -\frac{\mathfrak {m}}{r_b}\left( 1-\frac{2 \mathfrak {m}}{r_b}\right) ^{-1}. \end{aligned}$$
(34)

Now, at the boundary (r = \(r_b\)), the pressure in the radial direction inside star systems must vanish. On this basis, we arrive at Eq. (35):

$$\begin{aligned} \frac{e^{{-}2 A r_b^2} \Big \{8 a \alpha (A \!{+}\! B)^2 \!{-}\! 2 \alpha (A \!{+}\! B) ( 4 a (A \!{+}\! B)-\!1) e^{A r_b^2} \!{-}\! \beta e^{2 A r_b^2} \kappa \Big \}}{(1 {+} \alpha ) \kappa }{=}0.\nonumber \\ \end{aligned}$$
(35)

Along with this, we impose another condition that the pressure anisotropic factor \(\Delta \) vanishes at the center of the star, which gives

$$\begin{aligned} \Delta |_{r=0}= & {} \frac{3 (A + 3 A \alpha - 2 B - \beta \kappa ) (1 + \omega _q)}{2 (1 + \alpha ) \kappa }=0. \end{aligned}$$
(36)

Now, solving Eqs. (35) and (36) simultaneously, we obtain the expressions for \(\alpha \) and \(\beta \) as follows:

$$\begin{aligned} \alpha= & {} \frac{(A - 2 B) e^{2 A R^2}}{8 a A^2 + 16 a A B + 8 a B^2 +2 A e^{A R^2} - 8 a A^2 e^{A R^2} + 2 B e^{A R^2} - 16 a A B e^{A R^2} - 8 a B^2 e^{A R^2} - 3 A e^{2 A R^2}}, \end{aligned}$$
(37)
$$\begin{aligned} \beta= & {} \frac{A + 3 A \alpha - 2 B}{\kappa }. \end{aligned}$$
(38)

The unknowns A, B, and C have been calculated using experimental data from five different strange stars and are shown in Table  1, and the numerical values of \(\alpha \) and \(\beta \) for different values of the coupling constants are presented in Table 2.

Table 1 The numerical values of \(A,\,B\), and C for some familiar compact objects have been obtained
Full size table
Table 2 The numerical values of central density, surface density, central pressure, \(\alpha \), \(\beta \), u(R), and \(z_s(R)\) for the compact star SAX J1808.4-3658 [46] for different values of “a,” i.e., \(a=0,\,5,\,10\), and 15
Full size table

4 Physical analysis

In this section, we discuss an extensive number of the characteristics of proposed stellar structures related to anisotropic fluid distribution in f(Q) gravity. Using the relevant experimental and calculated data from Tables 1 and 2, the state variables for the compact star SAX J 1808.4-3658 are graphically analyzed in order to verify the physical validity of the proposed solution. For different values of the coupling parameters \(a=0,\,5,\,10\), and 15, we investigate the behavior of metric functions, anisotropic pressure, energy conditions, mass, redshift and compactness, stability, etc.

4.1 Metric potential, density, and pressure

  • Both metric potentials are singularity-free within the star’s boundary as \(e^{\lambda }|_{r=0}=1\) and \(e^{\nu }|_{r=0}=e^C\). The derivative of the metric coefficients results in the expressions \((e^{\lambda })'=2 A e^{A r^2} r\) and \((e^{\nu })'=2 B e^{C + B r^2} r\). At the core of the star, the derivative of the metric potentials is equal to zero. Also, they are consistent and monotonically increasing inside the star. The profiles of the metric coefficients are shown in Fig. 1.

  • The profiles of total density and total pressures are shown in Fig. 2 for different values of “a.” All these physical parameters are singularity-free and well behaved inside the stellar interior.

  • As a function of the radial coordinate r, the profile of physical quantities such as radial pressure \(p_r\), tangential pressure \(p_t\), matter density due to normal matter \(\rho \), and matter density due to quintessence field \(\rho _q\) are shown in Figs. 3 and 4. We can see from these graphs that the three physical variables \(\rho ,\,p_r\), and \(p_t\) are maximum at the origin and monotonically decrease to reach their minimum values at the surface, demonstrating the physical viability of the predicted stellar model. These figures also demonstrate that at the origin, the energy density and the tangential and radial pressures are positive and regular, confirming that our framework is free of mathematical and physical singularities. On the other hand, \(\rho _q\) takes a negative value throughout the interior for different values of “a.” The central density (\(\rho _c\)) and central pressure (\(p_c\)) for our present model are obtained as

    $$\begin{aligned} \rho |_{r=0}=\rho _c= & {} \frac{2 A + 2 B + \beta \kappa }{\kappa (1 + \alpha ) }, \end{aligned}$$
    (39)
    $$\begin{aligned} p_r|_{r=0}=p_t|_{r=0}=p_c= & {} \frac{2 A \alpha + 2 \alpha B - \beta \kappa }{\kappa (1 + \alpha ) }. \end{aligned}$$
    (40)

    For a physically acceptable model, the central pressure and central density should be positive inside the stellar interior.

    Now, \(p_c>0\) implies

    $$\begin{aligned} \frac{2\alpha (A+B)}{\kappa }>\beta . \end{aligned}$$
    (41)

    Moreover, it must be ensured that any physical fluid meets the Zeldovich [48] condition \(p_c/\rho _c < 1\), which gives

    $$\begin{aligned} \frac{2 \alpha (A + B) - \beta \kappa }{2 (A + B) + \beta \kappa }\le 1 ~~\Rightarrow \beta >~\frac{(\alpha -1)(A+B)}{\kappa }. \end{aligned}$$
    (42)

    Combining the two inequalities given in (41) and (42), we get a suitable range of \(\beta \) as

    $$\begin{aligned} \frac{(\alpha -1)(A+B)}{\kappa }<\beta <\frac{2\alpha (A+B)}{\kappa }. \end{aligned}$$
    (43)

  • The so-called equation of state (EoS) parameter is the next physical quantity that will be investigated. For our present model, the anisotropic EoS parameters are defined as

    $$\begin{aligned} \omega _r=\frac{p_r}{\rho },\,\omega _t=\frac{p_t}{\rho }. \end{aligned}$$

    The profiles of both \(\omega _r\) and \(\omega _t\) are shown in Fig. 5. The EoS plays an important role in describing the nature of the underlying fluid. It should lie between 0 and 1, where unitary refers to a Zeldovich stiff fluid and a disappearing EoS refers to dust. From the profiles of \(\omega _r\) and \(\omega _t\), one can note that \(0<\omega _r,\,\omega _t<1\). Thus, both the tangential and radial EoS exhibit properties of a viable cosmic fluid.

Fig. 1
figure 1

Variation of metric potentials \(e^{-\lambda }\) and \(e^{\nu }\) versus radius “r”

Full size image
Fig. 2
figure 2

Variation of \(\rho ^{\text {Total}}\), \(p_r^{\text {Total}}\), and \(p_t^{\text {Total}}\) versus radius “r”

Full size image
Fig. 3
figure 3

Variation of \(\rho \) and \(\rho _q\) versus radius “r”

Full size image
Fig. 4
figure 4

Variation of radial and transverse pressure versus radius “r”

Full size image
Fig. 5
figure 5

Variation of \(\omega _r\) and \(\omega _t\) versus radius “r”

Full size image

4.2 Nature of the anisotropy factor

In Eq.(26), the expression of the anisotropic factor is given, and it is depicted in Fig. 6. The beauty of this quantity is that it indicates whether the anisotropy will be directed inward or outward depending on whether \(\Delta < 0\) or \(p_t < p_r\), and \(\Delta >0\) or equivalently \(p_t> p_r\), respectively. From the graph corresponding to the anisotropy factor versus radial coordinate r, it is simple to see that anisotropy vanishes at the origin when radial pressure and tangential pressure are equal (\(p_t = p_r\)). Also, for \(a=0,\,5\), the anisotropy stress is positive and reaches its highest value at the boundary surface of the stellar structure, which helps in the formation of a more compact and massive stellar object. On the other hand, for \(a=10\) and 15, some parts of \(\Delta \) are negative. So one can conclude that for the present model, for a smaller value of “a,” the star becomes more compact.

4.3 Mass, redshift, and compactness parameters

We are interested in studying the mass function of our model, which is the solution to the following differential equation with the assumption \(m(0)=0\).

$$\begin{aligned} \frac{{\text {d}}m(r)}{{\text {d}}r}= & {} \frac{\kappa }{2}\rho (r)r^2. \end{aligned}$$

We derive the mass function of the model by solving the aforementioned equation with the specified initial condition as

$$\begin{aligned} m(r)= & {} \frac{e^{-2 A r^2}}{12 A^{3/2} (1 + \alpha )}\Big [2 \sqrt{A} r \Big \{-6 a (A + B)^2 + 3 (A + B) \nonumber \\{} & {} \times \big (-1 + 4 a (A + B)\big ) e^{A r^2} + A \beta e^{2 A r^2} \kappa r^2\Big \} \nonumber \\{} & {} -3 (A + B) e^{2 A r^2} \sqrt{\pi } \Big \{\big (-1 + 4 a (A + B)\big ) \nonumber \\{} & {} \times \text {erf}(\sqrt{A} r)- \sqrt{2}a (A + B) \text {erf}(\sqrt{2A} r)\Big \}\Big ]. \end{aligned}$$
(44)

The physical characteristics of astronomical objects can be investigated in order to learn more about their structural makeup. One of these, the compactness factor u(r), describes the relationship between the mass and radius of a compact star. By matching the interior and exterior spacetimes at the hypersurface \(r = r_b\), Buchdahl [49] presented the upper limit of u(r) and came to the conclusion that the system will remain stable as long as its value is less than 4/9. The expression for the compactness factor is obtained as

$$\begin{aligned} u(r)=\frac{m(r)}{r}. \end{aligned}$$
(45)

Buchdahl [49] and Straumann [50] have demonstrated that the gravitational redshift \(z_s\), in the absence of a cosmological constant in stellar structure, is \(z_s<2\). For an anisotropic star structure along a cosmological constant, Bohmer and Harko [51] have shown that the gravitational redshift can have a noticeably greater value \(z_s<5\). Ivanov [52] demonstrated that the most extreme allowed value might be as high as \(z_s = 5.211\) by altering the last restriction. The surface redshift of our present model is calculated as

$$\begin{aligned} z_s=\frac{1-\sqrt{1-2u}}{\sqrt{1-2u}}. \end{aligned}$$
(46)

Figure 7 depicts the graphical behavior of mass, compactness factor, and surface redshift inside the compact star model for different values of “a.” The profiles of \(m(r),\,u(r)\) and \(z_s\) are monotonically increasing functions of “r”; therefore, they attain maximum value at the boundary of the star. We have also obtained the numerical values of u(r) and \(z_s\) at the boundary for different values of “a” and presented them in Table 2.

4.4 Causality criteria and cracking

The initial observer interprets the relativistic concept of causality as demanding that the cause come before its effect. Therefore there is a time-like gap between the cause and its effect. When two occurrences are separated by a period of time, it is possible for a signal to travel between them more slowly than the speed of light. The causality will be broken if the signal travels faster than the speed of light. Hence, special relativity prevents an object from moving faster than the speed of light. The following are the causality criteria for an anisotropic structure:

$$\begin{aligned} 0\le V_r^2=\frac{p_r'}{\rho '}\le 1,\,0\le V_t^2=\frac{p_t'}{\rho '}\le 1, \end{aligned}$$

where \(V_r\) and \(V_t\) respectively denote the radial and transverse speed of sound. For our proposed model,

$$\begin{aligned} V_r^2= & {} \alpha , \end{aligned}$$
(47)
$$\begin{aligned} V_t^2= & {} \frac{1}{\psi _1(r)}\bigg [-4 a (A + B) \Big [1 + 3 \omega _q + e^{2 A r^2} \nonumber \\{} & {} \times (1 + 3 \omega _q)+2 A (1 + 3 \omega _q) r^2 \nonumber \\{} & {} + \Big \{-2 B^2 + 3 A B (7 + 5 \omega _q) - A^2 (5 + 9 \omega _q)\Big \} r^4 \nonumber \\{} & {} + 4 A B (-3 A + B) r^6 +e^{A r^2} \Big \{-2 - 6 \omega _q \nonumber \\{} & {} -2 A (1 + 3\omega _q) r^2 + \Big (A^2 - 11 A B\nonumber \\{} & {} + 2 B^2 + 3 A (A - 3 B) \omega _q\Big ) r^4 \nonumber \\{} & {} + 2 A (A - B) B r^6\Big \} + \alpha \Big \{1 + 3 \omega _q + e^{2 A r^2} (1 + 3 \omega _q) \nonumber \\{} & {} +2 A (1 + 3 \omega _q) r^2 + \Big \{-2 B^2 + A B (17 + 3 \omega _q)\nonumber \\{} & {} - 3 A^2 (3 + 7 \omega _q)\Big \} r^4 + 4 A B (-3 A + B) r^6 \nonumber \\{} & {} +e^{A r^2} \Big (-2 - 6 \omega _q - 2 A (1 + 3 \omega _q) r^2\nonumber \\{} & {} + \big (2 B^2 - 3 A B (3 + \omega _q) +A^2 (3 + 9 \omega _q)\big ) r^4 \nonumber \\{} & {} + 2 A (A - B) B r^6\Big )\Big \}\Big ] \nonumber \\{} & {} + e^{A r^2} \Big \{-1 - 3 \omega _q + e^{A r^2} (1 + 3 \omega _q) \nonumber \\{} & {} -A (1 + 3 \omega _q) r^2 + 2 \Big (A^2 + B^2 - A B (4 + 3 \omega _q)\Big ) r^4 \nonumber \\{} & {} +2 A (A - B) B r^6 +\alpha \Big (-1 + e^{A r^2} (1 + 3 \omega _q) - A r^2 \nonumber \\{} & {} +3 \omega _q (-1 + A r^2) (1 + 2 A r^2) \nonumber \\{} & {} +2 (A - B) r^4 \big (-B + A (2 + B r^2)\big )\Big )\Big \}\bigg ], \end{aligned}$$
(48)

where

$$\begin{aligned} \psi _1(r)= & {} 4 A (A + B)\\{} & {} \times \Big \{-8 a (A + B) + (-1 + 4 a (A + B)) e^{A r^2}\Big \} r^4. \end{aligned}$$
Fig. 6
figure 6

Variation of the anisotropic factor \(\Delta \) versus radius “r”

Full size image
Fig. 7
figure 7

Variation of m(r), u(r), and \(z_s(r)\) versus radius “r”

Full size image

Figure 8 displays the causality condition plots for the present model. It can be shown that the causality criteria have been fulfilled for our model.

Fig. 8
figure 8

Variation of \(V_r^2\) and \(V_t^2\) versus radius “r”

Full size image

Herrera and collaborators [53,54,55] developed the idea of cracking for self-gravitating isotropic and anisotropic matter configurations in a number of works. It was developed to show how fluid distributions behave when they first begin to deviate from equilibrium and total non-vanishing radial forces of various signs begin to appear in the system. According to Herrera and colleagues, cracking occurs when a radial force is directed inward in the inner part of the sphere. When a radial force is directed outward in the inner part of the sphere and changes sign in the outer part, that phenomenon is known as overturning. Abreu [56] asserts that potentially stable configurations should exist if \(\frac{\delta \Delta }{\delta \rho }\le 0\).

Now,

$$\begin{aligned} \frac{\delta \Delta }{\delta \rho }\sim \frac{\delta (p_t-p_r)}{\delta \rho }\sim \frac{\delta p_t}{\delta \rho }-\frac{\delta p_r}{\delta \rho }\sim V_t^2-V_r^2. \end{aligned}$$
(49)

According to causality, \(0\le V_r^2\le 1\) and \(0\le V_t^2\le 1\), which implies that \(|V_t^2-V_r^2|\le 1\).

By using the Abreu criterion, we reach the following conclusion:

$$ \begin{aligned}{} & {} -1\le V_t^2-V_r^2 \le 1\\{} & {} \quad \Rightarrow \Big \{-1\le V_t^2-V_r^2 \le 0~\rightarrow ~\text {potentially stable}\\{} & {} \quad \& ~~ 0 \le V_t^2-V_r^2 \le 1 \rightarrow ~\text {potentially unstable}\Big \}. \end{aligned}$$

As a result, using the variation in sound propagation within the matter configuration, we can now analyze potentially unstable regions inside anisotropic models. Those regions could be unstable if \(V_t^2>V_r^2\). On the other hand, no cracking will happen if \(V_t^2<V_r^2\) are found everywhere in a matter distribution. The profiles of \(V_r^2-V_t^2\) and \(|V_r^2-V_t^2|\) are depicted in Fig. 9 for different values of coupling constant “a.”

Fig. 9
figure 9

Variation of \(V_r^2-V_t^2\) and \(|V_r^2-V_t^2|\) versus radius “r”

Full size image

4.5 Energy condition

There are some specific restrictions, commonly referred to as energy conditions, that must be followed for the mathematical functions of stress-energy tensors to describe physically plausible matter fields. Energy conditions (ECs) are crucial resources for understanding cosmic geodesics. The well-known Raychaudhury equations can be used to establish such conditions. A thorough study of the energy conditions for f(Q) gravity models is provided by Mandal et al. [57]. The null energy condition (NEC), strong energy condition (SEC), dominant energy condition (DEC), and trace energy condition (TEC) are defined for the weak energy condition (WEC) as follows:

$$\begin{aligned}{} & {} \text {NEC}:~\rho \ge 0,\\{} & {} \text {WEC}:~\rho +p_r\ge 0,\,\rho +p_t\ge 0,\, \text {SEC}:~\rho +p_r+2p_t \ge 0,\\{} & {} \text {DEC}:~\rho -p_r\ge 0,\,\rho -p_t\ge 0,\,\text {TEC}:~\rho -p_r-2p_t\ge 0. \end{aligned}$$
Fig. 10
figure 10

Variations of energy conditions versus radius “r”

Full size image

Figure 10 graphically shows that in the context of the f(Q) gravity theory at different chosen values of “a,” the progression of all these energy conditions against the radial coordinate “r” for the compact stellar structure is well satisfied for our system.

4.6 Adiabatic index

Chandrasekhar [58] was the first to evaluate the stable and unstable regions for spherical stars and to investigate the role of the adiabatic index. Chan et al.’s proposal for the adiabatic index for an isotropic fluid sphere was \(\Gamma =\frac{\rho +p}{p}\frac{dp}{d\rho }\) [59]. In the situation of pressure anisotropy, the expression of the adiabatic index changes as

$$\begin{aligned} \Gamma= & {} \frac{\rho +p_r}{p_r}\frac{dp_r}{d\rho }, \end{aligned}$$
(50)
$$\begin{aligned}= & {} \frac{2 (1 + \alpha ) (A + B) \Big (-4 a (A + B) + ( 4 a (A + B)-1) e^{A r^2}\Big )}{-8 a \alpha (A + B)^2 + 2 \alpha (A + B) \Big (-1 + 4 a (A + B)\Big ) e^{A r^2} +\beta e^{2 A r^2} \kappa }\frac{dp_r}{d\rho }. \end{aligned}$$
(51)

According to Bondi [60], stability occurs if the adiabatic index is greater than 4/3. With the use of a graphical representation, we shall examine the condition of the stability. Figure 11 displays the \(\Gamma \) profile for various values of “a.” \(\Gamma \) takes values greater than 4/3 throughout the fluid sphere, as is evident.

Fig. 11
figure 11

Variations of adiabatic index versus radius “r”

Full size image
Fig. 12
figure 12

\(M-R\) relationship for different values of “a”

Full size image

5 Mass–radius relationship and contour plots

Figure 12 shows the total mass M normalized in \(M_{\odot }\), with the radius R for various values of “a.” Figure 12 shows that the maximum mass decreases as the values of “a” increase. The maximum allowable mass and the corresponding radius have been obtained for different values of “a” and are presented in Table 3. From the literature, we have chosen four different compact stars, namely the lighter component of the GW 190814 event with associated mass \(2.50-2.67~M_{\odot }\) [61], PSR J0952-0607 with associated mass \(2.18-2.52~M_{\odot }\) [62], PSR J0740+6620 with associated mass \(2.01-2.15~M_{\odot }\) [63], and PSR J1614-2230 with associated mass \(1.93-2.01~M_{\odot }\) [64], and from our analysis via graphical representation, we have shown that we have predicted the above mass from our present model for different values of the coupling parameter “a” associated with the f(Q) gravity.

As seen in the left panel of Fig. 13, where the equi-mass contour is plotted for the \(a-\alpha \) plane, the mass decreases in both cases: (i) with an increased value of \(\alpha \) when the coupling parameter “a” is fixed and (ii) with an increased value of “a” when \(\alpha \) is fixed. As a result, we can infer that the supermassive solution is preferable at lower values of \(\alpha \) and a smaller coupling constant “a.” The nature of the equi-mass contour for the \(\alpha -\beta \) plane is depicted in the right panel of Fig. 13. This graph demonstrates how the mass grows as \(\beta \) increases when \(\alpha \) is fixed. At the same time, mass simultaneously decreases when \(\alpha \) increases by keeping \(\beta \) fixed. The nature of the equi-mass contour for the \(a-\beta \) plane is depicted in the left panel of Fig. 14. This figure makes it clear that (i) for a fixed value of “a,” mass increases as \(\beta \) grows, and (ii) for a fixed \(\beta \), mass decreases as “a” increases. The nature of the equi-mass contour for the \(r-a\) plane is depicted in the right panel of Fig. 14. From this figure, it is clear that for a fixed value of “a,” the mass grows as “r” increases, and for a fixed value of “r,” the value of mass nearly stays the same as “a” increases.

Table 3 The maximum mass and the corresponding radius of different values of a
Full size table
Fig. 13
figure 13

(Left) contour plot of mass function in the plane and (right) contour plot of mass function in the plane

Full size image
Fig. 14
figure 14

(Left) contour plot of mass function in the plane and (right) contour plot of mass function in the plane

Full size image

6 Discussion

In this manuscript, we studied the compact stellar objects in well-known modified f(Q) gravity with the presence of a quintessence field. We focused on exploring the compact star model SAX J1808.4-3658 corresponding to the exterior Schwarzchild spacetime and anisotropic source of fluid. To do this, we have considered a quadratic form of f(Q) as \(f(Q) = Q +aQ^2\) and formulated the field equations in f(Q) gravity. Furthermore, the matching condition is used at the boundary to find the different values of parameters, and the numerical values are presented in tabular form. Besides this, the coupling parameter “a” plays an important role in our analysis, as the rest of our study depends on it, and we choose four different values of “a,” namely \(a=0,\,5,\,10\), and 15, to proceed our study where \(a=0\) corresponds to Einstein’s general theory of relativity. The main results are summarized here:

  • The metric potential, radial, and transverse pressure all are well behaved inside the boundary of the stellar object. All the properties of those model parameters have been described both analytically and graphically. One can note that the metric potentials do not depend on the coupling constant “a” of f(Q) gravity. The pressure and densities depend on “a” as can be seen from Figs. 3 and 4. From Table 2, we can check that both the central density and surface density take higher values for the lower value of “a.” On the other hand, for a higher value of “a,” central pressure takes a larger value.

  • The total density and total pressures are shown in Fig. 2. All of them depend on “a” and do not suffer from singularities as can be seen from the figure. The matter density related to quintessence field \(\rho _q\) is shown in Fig. 3, and it is negative throughout the stellar interior for all chosen values of “a.” The equation of state parameters lie in the range (\(0,\,1\)), which confirms that the underlying fluid is non-exotic in nature.

  • The anisotropic factor vanishes at the center of the star as can be seen from Fig. 6. \(\Delta >0\) everywhere inside the stellar interior for \(a=0\) and 5 and positiveness of \(\Delta \) throughout the interior helps to construct a more compact object which was studied in [65]. \(\Delta \) does not maintain a positive sign throughout the interior when \(a>5\). So, from our analysis, we can conclude that for \(0\le a\le 5\), the anisotropic factor is positive, and the stellar structure becomes more stable against gravitational collapse. For \(a=10\) and 15, some portions of the curve of anisotropy are negative, and it renders the configuration unstable at the interior points. This implies that the coupling parameter “a” plays an important role in switching the stellar model from being stable to that of an unstable configuration. We observe that \(\Delta \) becomes negative when “a” takes the value greater than 5 and becomes positive as “a” decreases towards zero from \(a=5\). So we can conclude that the configuration becomes more stable for a smaller value of “a.” The anisotropic factor \(\Delta \) shows the same behavior in Refs. [66,67,68].

  • Figure 7 illustrates the evolutionary behavior of the mass function, compactness factor, and surface redshift for different values of “a.” It is clear that the mass function is always finite at the center (i.e., as r \(\rightarrow \) 0 as m(r) \(\rightarrow ~0\)) and increases positively from the center towards the star’s boundary surface. Evidently, both plots of u(r) and \(Z_s(r)\) reveal that nature is regular (finite) at its center and continues to be positive across its full region of the compact sphere. From the figure, it is clear that \(m(R), \,u(R)\) and \(z_s(R)\) decrease with the increasing values of “a.” The numerical values of \(m(R),\,u(R)\) and \(z_s(R)\) are shown in Table 2 for different values of “a.” Our proposed anisotropic star candidate with its corresponding models is in a better configuration and consistent with the analysis of Buchdahl [49], Bohmer and Harko [51], and Ivanov [52]. This is because the values of u(R) and \(z_s(R)\) always remain within the limit.

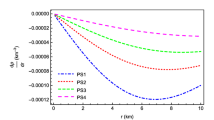
  • The causality condition for our present model is fully met. From Fig. 8, one can check that in the case of radial sound velocity, for a larger value of “a,” \(V_r^2\) takes a lower value; on the other hand, for transverse sound velocity, for a larger value of “a,” \(V_t^2\) takes higher value up to radius 5 km. At approximately \(r=5\), all the profiles of \(V_t^2\) merge, i.e., they take the same value for a while and again spread from that point. One can notice an interesting thing here. From this meeting point when the curves of \(V_t^2\) approach to the boundary again for a larger value of “a,” \(V_t^2\) takes a lower value up to the boundary of the star.

  • Using the cracking concept proposed by Herrera and the causality criterion, the stability analysis has been comprehensively explained. From Fig. 9, it can be noted that the model is potentially stable for \(a=0,\,5\) since for these two values of “a,” \(V_r^2>V_t^2\) everywhere inside the stellar interior. But for \(a=10\) and 15, the inequality \(V_r^2>V_t^2\) does not hold throughout the stellar interior. Inside the stellar model, there is some portion where \(V_r^2<V_t^2\); therefore, the potential stability condition is not satisfied inside the stellar body for \(a=10\) and 15. From this analysis, one can conclude that in f(Q) gravity, for lower values of the coupling parameter “a,” the model is potentially stable, and the instability occurs when \(a>5\). From the graph, it is clear that \(|V_r^2-V_t^2|<1\) holds everywhere inside the boundary. From Fig. 9, it is clear that for \(a=0\), 5, and 10, the profiles of \(V_t^2\) are positive throughout the interior, including at the boundary, and for \(a=15\), the profile of \(V_t^2\) is positive throughout the interior except at the boundary. For \(a=15\), \(V_t^2\) vanishes at \(r=r_b\), \(r_b\) being the stellar boundary. Now if we take \(a>15\), \(V_t^2\) will be negative, which is not physically reasonable. Therefore, for our present model, for SAX J1808.4-3658, the physically viable range for “a” is \(0 \le a \le 15\).

  • All the energy conditions are well satisfied inside the stellar structure and the relativistic adiabatic index \(\Gamma >4/3\) everywhere inside the stellar interior.

From our present analysis, we have discussed all the model parameters for four different values \(a=0,\,5,\,10\), and 15. The values of the free parameters \(A,\, B,\, C,\,\alpha \), and \(\beta \) have been represented in terms of mass, radius, quintessence parameter \(\omega _q\), and coupling constant “a” of f(Q) gravity. As soon as all the plots are drawn for compact star SAX J1808.4-3658 by fixing \(\omega _q=-0.35\), only one free parameter, “a,” is left. The present discussion implies that the potential stability condition is obtained when \(a \in [0,\,5]\). Finally, it is worth mentioning that the model admits and shares all of the crucial physical and mathematical characteristics that are essential to the study of compact stars and which give circumstantial evidence for the evolution of realistic stellar configurations in the high-density regime in the presence of a quintessence field within the framework of f(Q) modified gravity.