Suppression of spin polarization as an indicator of QCD critical point

Abstract

We study the impact of the QCD critical point (CP) on the spin polarization of $\Lambda$-hyperon generated by the thermal vorticity in viscous quark gluon plasma (QGP). The equations of the relativistic causal viscous hydrodynamics have been solved numerically in (3+1) dimensions to evaluate the thermal vorticity. The effects of the CP have been incorporated through the equation of state (EoS) and the scaling behavior of the transport coefficients. We observe a significant suppression of the spin polarization around mid-rapidity region induced by the CP and propose that such changed behaviour of the spin polarization can be used to detect the CP. To the best of our knowledge this is the first study on the effects of critical point on the spin polarization in QCD matter.

1 Introduction

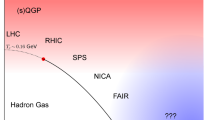
Results from lattice quantum chromodynamics (QCD) and effective field theoretical models at non-zero temperature (T) and baryon chemical potential ($\mu$) reveal a rich and complex phase diagram [1]. While at high T and low $\mu$ $(\rightarrow 0)$ the quark-hadron transition is a crossover, at low T and high $\mu$ the transition is believed to be first order in nature. Therefore, it is expected that between the crossover and the first order transition there exists a point in the $\mu -T$ plane called the Critical End Point or simply the Critical Point (CP) where the first order transition ends and crossover begins [2]. The location of CP is not yet known from first principles [3], however, phenomenological studies indicate its existence [4]. The investigations of the CP and the spin polarization in QCD matter are two frontier areas of research. In the present work we introduce a connection between these two outstanding problems.

At present the general consensus is that the collisions of nuclei at the top Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) energies produce QGP with small $\mu$ and high T which reverts to hadronic phase via a crossover. The ongoing Beam Energy Scan-II program at RHIC and the upcoming Compressed Baryonic Matter experiment at Facility for Anti-proton and Ion Research (FAIR) and Nuclotron based Ion Collider fAcility (NICA) are planned to create system of quarks and gluons with different $\mu$ and T by varying the collision energies to explore the region close to the CP. The non-monotonic variation of the fluctuations in multiplicity with collision energy in the center of mass frame ($\sqrt{s_{NN}}$) [5], the change of sign of the fourth cumulant of order parameter with the variations of rapidity (rapidity scan) [6] and beam energy [7], the appearance of negative sign in the kurtosis of the order parameter fluctuation near the CP [8] are some of the proposed signals of the CP (see [9] for a review and references therein).

Relativistic hydrodynamics has been used to describe the space-time evolution of QGP and explain various experimental data quite successfully. One such crucial observable is the polarization of $\Lambda$-hyperon [10] generated by the thermal vorticity and thermal shear during the hydrodynamic evolution of the QGP. Invigorating theoretical activities have been witnessed (see [11, 12] for review) to understand various aspects of the polarization within the scope of hydrodynamics and transport models after the experimental measurement of the global polarization of the $\Lambda$ hyperon [10].

The magnetization of uncharged objects induced by mechanical rotation, called Barnett effect [13] and its inverse, that is, the rotation generated by varying magnetization, called the Einstein–de Haas effect [14] originate due to the conversion between spin (S) and orbital angular momentum (L) via spin-orbit coupling constrained by the conservation of total angular momentum $\vec {J}\ (=\vec {L}+\vec {S})$. Similar coupling between L and S in QCD matter results in the spin polarization of particles. The initial orbital angular momentum (OAM) imparted by the spectators in non-central heavy ion collisions induce vortical motion locally and this induced vorticity polarize the quarks [15, 16] which gets reflected in the spin polarization of final state hadrons. The coupling of fluid vorticity and quantum mechanical spin has been experimentally demonstrated for the first time in Ref. [17]. The vorticity in the fluid can be generated by other mechanisms (e.g. by the viscous stress as discussed in detail later). Hence, spin polarization of hadrons measured by STAR collaboration [10] has contributions from OAM and from other dynamical effects (e.g. viscosities, etc). The first contribution depends on the details of mechanism of transfer of initial OAM to the fluid and this is sensitive to the initial condition. The second contribution depends on the transport properties of the system and will be sensitive to the EoS. The goal of the present work is to understand the CP induced change in the vorticity and its consequences on the spin polarization of the $\Lambda$ hyperon. In other words if, $\varpi _{\mu \nu }^{\text {CP}}$ ($\varpi _{\mu \nu }$) is the vorticity in the presence (absence) of CP then what is the value of $\Delta \varpi _{\mu \nu }= (\varpi _{\mu \nu }^{\text {CP}}-\varpi _{\mu \nu }$) and the corresponding change on the spin polarization of $\Lambda$-hyperon. We show in this work that as the CP is approached the local vorticity and hence the spin-polarization gets suppressed around the mid rapidity. Relativistic hydrodynamics can be applied to study the problem under consideration by choosing trajectories in the QCD phase diagram which are not too close to the CP but pass through the critical domain.

The presence of CP in the EoS affects the expansion of the system due to suppression of the sound wave and divergence of some of the transport coefficients [18]. This will affect the evolution of local vorticity and hence the $\Lambda$-polarization through vorticity-spin coupling. Apart from polarization, the effect of CP on the separation of baryon and anti-baryon due to chiral vortical effect is another interesting facet [19].

Here we use natural unit $c=\hbar =k_B=1$ where c is the speed of light in vacuum, $h=2\pi \hbar$ is the Planck’s constant and $k_B$ is the Boltzmann’s constant. The signature metric for flat spacetime is taken as $g_{\mu \nu }=\text {diag}(1,-1,-1,-1)$.

The paper is organized as follows. In the next section we describe hydrodynamical model used in this work. In Sect. 3, we discuss the spin-polarization of $\Lambda$-hyperon due to vorticity. Results are presented in Sects. 4 and 5 is devoted to summary and discussions.

2 Relativistic hydrodynamical model

We numerically solve (3+1)-dimensional relativistic viscous causal hydrodynamics using the algorithm detailed in Ref. [20]. The code contains the effect of CP through the EoS and the scaling behavior of the transport coefficients (see [21] for details). The initial condition and the EoS models used here to solve hydrodynamic equations have been extensively tested by reproducing the results available in Refs. [22] and [23] respectively. The CORNELIUS code [24] has been used to find the constant energy-density hyper surface. Our numerical results in the absence of CP have been contrasted with the known analytical results of Ref. [25] and with numerical results from other publicly available codes: AZHYDRO [26], MUSIC [27] and vHLLE [20]. The reliability of our code can be further appreciated by contrasting its output with the transverse momentum and rapidity dependence of various experimental observables, as we show in Sect. 4.

We have solved the following relativistic hydrodynamic equations numerically:

$$\begin{aligned}&\partial _{\mu }T^{\mu \nu }=0, \nonumber \\&\partial _{\mu }N^{\mu }=0, \end{aligned}$$

(1)

where $T^{\mu \nu }$ is the energy-momentum tensor and $N^{\mu }$ is the net-baryon number current. Here we work in the Landau frame of reference where the $T^{\mu \nu }$ and $N^\mu$ are given by

$$\begin{aligned} T^{\mu \nu }&= \varepsilon \,u^\mu \,u^\nu - (p+\Pi )\Delta ^{\mu \nu } +\pi ^{\mu \nu }, \end{aligned}$$

(2)

$$\begin{aligned} N^\mu&= n_B\, u^\mu +V^\mu , \end{aligned}$$

(3)

where $\Pi$ is the bulk pressure, $\pi ^{\mu \nu }$ is the shear-stress tensor which is symmetric, traceless and orthogonal to $u^\mu$, $V^\mu (=0, \text {here})$ is the baryon diffusion 4-current and $\Delta ^{\mu \nu } = g^{\mu \nu }-u^\mu \, u^\nu$. The viscous terms obey the following evolution equations,

$$\begin{aligned} u^{\alpha }\partial _{\alpha }\Pi&=-\frac{\Pi -\Pi _{NS}}{\tau _{\Pi }}-\frac{4}{3}\Pi \partial _{\alpha }u^{\alpha } , \end{aligned}$$

(4)

$$\begin{aligned} \langle u^{\alpha }\partial _{\alpha }\pi ^{\mu \nu }\rangle&=-\frac{\pi ^{\mu \nu }- \pi ^{\mu \nu }_{NS}}{\tau _{\pi }}-\frac{4}{3}\pi ^{\mu \nu }\partial _{\alpha }u^{\alpha }, \end{aligned}$$

(5)

where $\langle \cdot \rangle$ is defined as,

$$\begin{aligned} \langle A^{\mu \nu } \rangle =\left( \frac{1}{2}\Delta ^{\mu }_{\alpha }\Delta ^{\nu }_{\beta }+\frac{1}{2}\Delta ^{\nu }_{\alpha }\Delta ^{\mu }_{\beta }-\frac{1}{3}\Delta ^{\mu \nu }\Delta _{\alpha \beta }\right) A^{\alpha \beta }, \end{aligned}$$

$\Pi _{NS}$ and $\pi _{NS} ^{\mu \nu }$ are the Navier–Stokes limit of $\Pi$ and $\pi ^{\mu \nu }$ respectively, given by

$$\begin{aligned} \Pi _{NS} = -\zeta \theta \quad , \quad \pi _{NS} ^{\mu \nu } = 2\eta \left\langle \partial ^\alpha u^\beta \right\rangle , \end{aligned}$$

(6)

where $\theta =\partial _\mu u^\mu$. The coefficients of shear ($\eta$) and bulk ($\zeta$) viscosities are positive, i.e. $\eta ,\zeta > 0$.

The hydrodynamical equations are solved in $(\tau ,x,y,\eta _s)$ coordinates where, $\tau =\sqrt{t^2-z^2}$ and $\eta _s=\text {tanh}^{-1}(z/t)$. The space-time evolution begins at time $\tau _0$. For lower energies the initial time, $\tau _0$ is taken as the time required by the nuclei to pass through one other, $\sim \frac{2R}{\gamma _zv_z}$ (R is the radius of the colliding nucleus, $\gamma _z=1/\sqrt{1-v_z^2}$ with $v_z$ is the velocity of the nucleus along z direction) and for higher energies ($\sqrt{s_{NN}}\ge 62.4$ GeV), $\tau _0=1$ fm as shown in Table  1. The initial energy density profile at $\tau _0$ is taken as:

$$\begin{aligned} \varepsilon (x,y,\eta _s;\tau _0) = e (x,y) \, f(\eta _s). \end{aligned}$$

(7)

A symmetric rapidity profile, $f(\eta _s)$, with the local energy-momentum conservation puts a constraint on e(x, y) as shown in Ref. [22]. The energy deposited in the transverse plane, e(x, y) depends on the number of wounded nucleons per unit area which has been calculated by using the optical Glauber model for given impact parameter (b) at different $\sqrt{s_{NN}}$. The quantity, e(x, y) is related to the the number of wounded nucleons per unit area in the transverse plane, $n_A(x,y)$ and $n_B(x,y)$ of the colliding nuclei A and B respectively as: $e(x,y)\propto \sqrt{n_A^2+n_B^2+2n_An_B\text {cosh}(2y_\texttt{beam})}$, where $y_\texttt{beam}=\text {cosh}^{-1}(\sqrt{s_{NN}}/2)$. Here we consider Au+Au collisions at $b=5.6$ fm for different $\sqrt{s_{NN}}$ that has been found to correspond to 15–25% centrality [21]. The thickness function of the Au nucleus has been computed by assuming Woods-Saxon profile for nuclear density with nuclear radius, $R=6.37$ fm, and surface thickness, $\delta =0.535$. The p+p inelastic cross-section, $\sigma ^{\texttt {in}}_{NN}(\sqrt{s_{NN}})$, needed for the calculation of the number of wounded nucleons in the Glauber model has been taken from Refs. [28, 29].

The initial velocity profile is taken as:

$$\begin{aligned} u^\mu (x,y,\eta _s; \tau _0)= \left( \cosh (\eta _s),0,0,\sinh (\eta _s)\right) , \end{aligned}$$

(8)

The initial energy density and net baryon number density profiles have been computed with the parameters used in Ref. [22]. The viscous terms have been initialized with their corresponding Navier–Stokes limit.

Table 1 Values of $\tau _0$ used at different colliding energies

The EoS [23] employed here to solve the hydrodynamic equations reproduces the lattice QCD results at zero baryonic chemical potential. The parameters w, $\rho$ and $\alpha _1$ that appear in the linear mapping from Ising model to QCD in Ref. [23] have been fixed as $w=1$, $\rho =2$ and $\alpha _1=3.85^\texttt{o}$. The other parameters are same as that of Ref. [23]. The transport coefficients are expected to diverge near the critical point following a scaling behavior [30]:

$$\begin{aligned} \zeta \sim \xi ^3 \quad , \quad \eta \sim \xi ^{0.05}. \end{aligned}$$

where $\xi (\mu ,T)$ is the equilibrium correlation length, which is obtained through mapping QCD to 3D Ising model in the critical region. In the Ising model, $\xi$ is computed by taking the derivative of equilibrium magnetization, M(r, h), with respect to the magnetic field, h, at fixed $r=(T-T_c)/T_c$ as [30]

$$\begin{aligned} \xi ^2=\frac{1}{H_0}\left( \frac{\partial M}{\partial h}\right) _r, \end{aligned}$$

where $H_0$ is a dimensionful parameter to get the correct dimensions of $\xi$. We shall take $H_0 = 1$ in our calculations and $\left( \frac{\partial M}{\partial h}\right) _r$ is obtained from the EoS model [23] using chain rule of differentiation. The extent of the critical domain in the $\mu -T$ plane is determined by the condition: $\xi (\mu ,T)=\xi _0$, where $\xi _0$ is taken as 1.75 fm. The possibility of divergent behavior is incorporated through the following expressions of the transport coefficients [30]

$$\begin{aligned} \zeta = \zeta _0 \left( \frac{\xi }{\xi _0}\right) ^3 \ , \ \eta = \eta _0 \left( \frac{\xi }{\xi _0}\right) ^{0.05} \end{aligned}$$

(9)

Outside the critical region the values of the shear and bulk viscosities denoted by $\eta _0,\ \zeta _0$ respectively are chosen as [31, 32]:

$$\begin{aligned} \eta _0 (\mu ,T)&= C_\eta \left( \frac{\varepsilon + p}{T}\right) \quad , \quad \zeta _0 (\mu ,T) = 15 \ \eta _0 \left( \frac{1}{3}-c_s^2\right) ^2 \end{aligned}$$

The above parametrization is consistent with the estimates of the temperature-dependent specific shear and bulk viscosity extracted using Bayesian method [33] away from the critical region.

The dependence of the relaxation times appeared in Eqs. (4) and (5) on $\xi$ are parameterized as:

$$\begin{aligned} \tau _\pi = \tau ^0_\pi \left( \frac{\xi }{\xi _0}\right) ^{0.05} \quad ,\quad \tau _\Pi = \tau ^0_\Pi \left( \frac{\xi }{\xi _0}\right) ^3. \end{aligned}$$

(10)

where $\tau ^0_\pi$ and $\tau ^0_\Pi$ are the relaxation times outside the critical region which are given by [31, 32],

$$\begin{aligned} \frac{\tau ^0_\pi }{5} =\tau ^0_\Pi =\frac{C_\eta }{T} \end{aligned}$$

with $C_\eta =0.08$.

3 Thermal vorticity and spin polarization

The thermal vorticity at any space-time point of the fluid is given by [34,35,36]:

$$\begin{aligned} \varpi _{\mu \nu } = \frac{1}{2}\left[ \partial _\nu \beta _\mu - \partial _\mu \beta _\nu \right] \end{aligned}$$

(11)

where $\beta _\mu =u_\mu /T$. The $\Lambda$-polarization is calculated by using the following expression of mean spin vector for a spin-1/2 particle with four-momentum $p_\nu$ [37, 38]:

$$\begin{aligned} S^\mu (x,p) = -\frac{1}{8m}(1-n_F)\epsilon ^{\mu \nu \rho \sigma }p_\nu \varpi _{\rho \sigma } (x) + O (\varpi )^2, \end{aligned}$$

(12)

where m is the mass of the particle, $\epsilon ^{\mu \nu \rho \sigma }$ is the Levi-Civita tensor and $n_F$ is the Fermi-Dirac distribution. As we shall discuss later, the spin polarization is suppressed around mid rapidity in presence of CP. In Ref. [39], it has been shown that the contribution to spin polarization due to thermal shear around mid-rapidity is small. Hence, we have not considered the effect of thermal shear on spin polarization in this work for simplicity. Since the mass of the $\Lambda$ is much larger than the temperature range being considered in this study, we assume that $1-n_F\approx 1$ and $n_F\approx n_B$, where $n_B$ is the Boltzmann distribution. Consequently the expression for the mean spin vector becomes

$$\begin{aligned} S^\mu (x,p) = \frac{1}{8m}\epsilon ^{\mu \nu \rho \sigma }p_\nu \partial _\rho \beta _\sigma . \end{aligned}$$

In the rest frame of the particle, the spin vector is $S^{*\mu } = (0,\mathbf{{S}^*})$, which is obtained by using the Lorentz transformation as:

$$\begin{aligned} \mathbf{{S}^*} =\mathbf{{S}} - \frac{\mathbf{{p}}.\mathbf{{S}}}{E(E+m)}{} \mathbf{{p}} \end{aligned}$$

The mean spin averaged over the hypersurface $\Sigma$ is then given by [34],

$$\begin{aligned} S^\mu (p) = \frac{\int d\Sigma _\lambda p^\lambda \ e^{-\beta (p.u-\mu )} S^\mu (x,p)}{\int d\Sigma _\lambda p^\lambda \ e^{-\beta (p.u-\mu )}} \end{aligned}$$

(13)

The net spin is obtained by integrating over azimuthal angle ($0 \le \phi < 2\pi$), rapidity ($|y| < 1$) and transverse momentum ($0<p_T<3 \text { GeV}$) following the procedure of Ref. [40]. Finally the spin polarization of $\Lambda$ is given by,

$$\begin{aligned} \mathbf{{P}} = 2\mathbf{{S}^*}. \end{aligned}$$

4 Results

In this section, we present results through the following two subsections. First we test results from our newly developed computer code by contrasting with results from other codes available in the literature and experimental data. Then we discuss the effects of CP on spin polarization.

4.1 Testing the computer code

We present below a few test results from our hydrodynamic code. To test the code in (2+1)-dimensions, we compare the energy density obtained from the code with the Gubser’s analytical solution [25] in (2+1) dimension in Fig. 1. We find that the results are in good agreement. There is no analytical result available in (3+1)-dimensions. Therefore, to test the code, we compare our result for the rapidity distribution of positively charged pion with the output from publicly available MUSIC code [41] without the resonance decays in Fig. 2.

Fig. 1

The variation of $\varepsilon$ with x. Results from the present work is compared with Gubser’s analytical results in (2+1) dimension

Fig. 2

The comparison of the rapidity distribution of $\pi ^+$ from our code and the publicly available MUSIC code

Fig. 3

The numerical results for $dN_{\text {ch}}/d\eta$ from our code are compared with experimental data of PHOBOS collaboration in different centralities [42, 43]. Here EoS-CP and noCP denote results with and without the effects of CP respectively (see text)

Using the initial condition model, Eqs. (7) and (8) and EoS mentioned above, we further reproduce the charged particle pseudorapidity distribution for two colliding energies ($\sqrt{s_{NN}}=19.6$ GeV and 62.4 GeV) and different centralities in Fig. 3. To generate the plots of Fig. 3, we use the switching energy density $\varepsilon _{\text {sw}}=0.3$ GeV/fm$^3$. We generate the constant energy density, $\varepsilon _{\text {sw}}$, hypersurface henceforth denoted by $\Sigma _\varepsilon$, using the CORNELIUS code [24] which is then given as input to the UrQMD transport code [44] and generate 1000 events. It should be mentioned here that the width of the experimental distribution is slightly underestimated because we have used a single impact parameter and not an event-by-event simulation that would consist of a mixture of several impact parameters. We next reproduce the PHOBOS data on $p_T$ dependence of elliptic flow in 0–50% centrality of Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV [45] in Fig. 4. The variation of $dN_{\text {ch}}/d\eta$ with pseudorapidity with (EoS-CP) and without (noCP) the critical point in EoS are shown in Fig. 5 for colliding energies 14.5 GeV at impact parameter $b=4$ fm (left), and 19.6 GeV at impact parameter $b=5.6$ fm (right). The effect of the CP is found to be insignificant here.

4.2 Suppression of spin polarization by the CP

In this subsection, we will discuss the suppression of thermal vorticity and consequently of spin-polarization of $\Lambda$-hyperon due to the presence of QCD CP. We will discuss the cases with zero as well as non-zero initial OAM.

We first show the critical region and the trajectories traced by the center of the fireball in the ($\mu -T$) plane at different $\sqrt{s_{NN}}$ in Fig. 6. The black dot inside the critical domain (closed contour) indicates the location of the CP at $(\mu _c,T_c)=(350 \text {MeV},143.2 \text {MeV})$ [23] in this study. The trajectories have been calculated by solving the hydrodynamic equations with (denoted by EoS-CP) and without (denoted by noCP) the effects of CP. The trajectories for $\sqrt{s_{NN}}=$14.5 GeV and 19.6 GeV respectively passes through the critical domain. The trajectories for higher $\sqrt{s_{NN}}$ remain outside the critical domain. We evaluate the thermal vorticity and subsequently the polarization of $\Lambda$ for system evolving along trajectories passing through both inside and outside the critical domain. As the transport code, UrQMD, does not include the spin effects, we stop the hydrodynamic evolution and evaluate the spin polarization on the constant energy density hypersurface $\varepsilon = 0.3$ GeV/fm$^3$. The effect of the CP on the polarization is expected to be larger for $\sqrt{s_{NN}}=14.5$ GeV as the trajectory for this case is closer to the CP compared to other values of $\sqrt{s_{NN}}$ considered here.

Fig. 4

Our numerical result on $p_T$ dependence of elliptic flow, $v_2$, compared to the experimental data from Ref. [45]

Fig. 5

The variation of $dN_{\text {ch}}/d\eta$ is shown as a function of pseudorapidity with (EoS-CP) and without (noCP) the critical point in EoS for colliding energies (left) 14.5 GeV at impact parameter $b=4$ fm, and (right) 19.6 GeV at impact parameter $b=5.6$ fm

Before presenting our results for non-zero initial OAM, some results with zero initial OAM are displayed first. The time evolution of the $x\eta$ component of the thermal vorticity, averaged over the spatial coordinates and weighted by the energy density, with and without the effects of CP are shown in Fig. 7. Initially the system has zero vorticity. The vorticity generated by the viscous effects increase at first to attain some maximum value and then decreases subsequently. The evolution of the vorticity near the CP is affected by several competing factors like enhancement of various transport coefficients, slower expansion, changes in baroclinic torque, vortex stretching etc. Also, absorption of sound wave near the CP affects the expansion directly and the diverging nature of the transport coefficients reduces the vorticity as seen in Fig. 7. The observed suppression of the vorticity due to CP at $\sqrt{s_{NN}}=14.5$ GeV is expected to influence some of the experimental results. As the evolution trajectory for $\sqrt{s_{NN}}=62.4 \text {GeV}$ (and higher energies) remain outside the critical domain the results with and without CP essentially overlap.

The variation of the y-component of the spin-polarization with rapidity (y) has been displayed in Fig. 8. A drastic change is induced by the CP in the rapidity distribution of spin-polarization at $\sqrt{s_{NN}}=14.5$ GeV. At $\sqrt{s_{NN}}=62.4$ GeV, the $P_y$ with and without CP are identical as expected. It is intriguing to note that the CP not only reduces the polarization around mid-rapidity but also introduces strong qualitative changes in the slopes of the curves as shown in Fig. 9.

Fig. 6

Trajectories traced by the center of the fireball i.e. $x=y=\eta _s=0$ in the $\mu -T$ plane for different $\sqrt{s_{NN}}$. The critical point is indicated by solid black dot at $(\mu ,T)=(350,143.2)$ MeV

Fig. 7

Time evolution of the mean of the $x\eta$-component of thermal vorticity for $\sqrt{s_{NN}}=14.5 \text {GeV}$ and $62.4\text {GeV}$ for zero initial OAM

Fig. 8

y-component of $\Lambda$-polarization plotted as a function of momentum rapidity for $\sqrt{s_{NN}}=14.5\,\,\text {GeV}\,\, \text {and}\,\,62.4\text {GeV}$ for the case of zero initial OAM

Fig. 9

Negative slope of the y-component of the polarization of $\Lambda$-hyperon plotted as a function of rapidity for the case of zero initial OAM

Finally, the global polarization is obtained as a function of $\sqrt{s_{NN}}$ upon integration over $p_T$, $\phi$ and y. The suppression of polarization is conspicuous for the trajectories passing through the critical domain at lower $\sqrt{s_{NN}}$ (Fig. 10). The slope of the curve without CP is much steeper than the one with CP at lower $\sqrt{s_{NN}}$. The smaller value of polarization compared to experimental value [10] is because of the zero initial OAM. Inclusion of OAM through the non-zero initial value of the velocity profile [34] will enhance the magnitude of $-P_y$, however, the difference in the rapidity distribution of polarization observed here with and without CP will still persist, as we discuss below.

Fig. 10

Global polarization of $\Lambda$-hyperon plotted as a function of $\sqrt{s_{NN}}$ for the case of zero initial OAM

Now we introduce a non-zero OAM into the system through initial condition. The initial condition model that we use from Ref. [22] has been generalized to include a non-zero OAM in Ref. [46]. This is done by introducing a parameter, f, that takes value in the interval [0,1] and which controls the fraction of longitudinal momentum that can be attributed to the flow velocity. $f=0$ corresponds to the Bjorken flow scenario. The assumption for the initial energy-momentum current in Ref. [46] can be achieved through the following choice of rest frame quantities:

$$\begin{aligned}{} & {} p=\varepsilon \ , \ u^x=u^y=0 \ , \ u^\tau = \cosh \left( \frac{y_L}{2}\right) , \nonumber \\{} & {} u^\eta =\frac{1}{\tau _0}\sinh \left( \frac{y_L}{2}\right) . \end{aligned}$$

(14)

where p, $\varepsilon$, and $u^\mu$, respectively, denote the pressure, energy density, and fluid four flow-velocity. Also, $y_L (=fy_{\text {CM}})$ denotes the local longitudinal rapidity variable and $y_{\text {CM}}$ is the rapidity in local center-of-mass frame.

Fig. 11

The numerical result for y-component of $\Lambda$-polarization as function of pseudorapidity is compared with the experimental data measured by STAR collaboration from Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV in 20–60% centrality [47]. Vertical lines are the statistical uncertainties only

Fig. 12

The numerical result for y-component of $\Lambda$-polarization as function of transverse momentum ($p_T$) is compared with the experimental data by STAR from Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV for 20–60% centrality [47]. Vertical lines are the statistical uncertainties only

The components of the initial energy-momentum tensor then take the following form:

$$\begin{aligned} T^{\tau \tau }&= (\varepsilon +p)(u^\tau )^2 - p = \varepsilon \cosh (y_L),\\ T^{\tau \eta }&= (\varepsilon +p)u^\tau u^\eta = \frac{\varepsilon }{\tau _0} \sinh (y_L),\\ T^{\eta \eta }&= (\varepsilon +p)u^\eta u^\eta = \frac{\varepsilon }{\tau _0^2} \cosh (y_L),\\ \end{aligned}$$

which is consistent with the assumption of Ref. [46]. The trace of the energy-momentum tensor is given by

$$\begin{aligned} T^\mu _\mu = T^{\tau \tau } - \tau ^2T^{\eta \eta } = 0. \end{aligned}$$

Hence, our choice for the rest frame quantities, Eq. (14), does not violate the condition for the trace of the energy-momentum tensor. It was stated in Ref. [46] that the parameter f has negligible effects on most of the global observables such as the pseudorapidity distributions, particle yields, and elliptic flow. We have checked this and conclude the same.

Fig. 13

The left panel shows rapidity dependence of y component of $\Lambda$-hyperon polarization at $\sqrt{s_{NN}}=14.5$ GeV and $b=5.6$ fm with (CP) and without (noCP) critical point EoS, and the right panel shows the derivative as a function of rapidity

By setting the value of $f=0.2$, impact parameter, $b=8.7$ fm, and using the same set of values for other parameters of the IC model for Au+Au collision at $\sqrt{s_{NN}}=200$ GeV, described earlier, we compute the negative y-component of global polarization, $-P_y$, of $\Lambda$-hyperon for 20–60% centrality. We get $-P_y$=0.254% where the corresponding experimental value from STAR is 0.277± 0.040 (stat). By using the updated PDG value of $\alpha _\Lambda$, we get $-P_y=0.243 \pm$ 0.035% (stat) [47]. Having fixed the parameter f with the help of global polarization data, we set out to see if we can reproduce the measurements of local polarization. We show the pseudorapidity and transverse momentum dependence in the 20–60% centrality in Figs. 11 and 12 respectively. It is to be stressed that we have used EoS with CP for the results displayed in Figs. 11 and 12 for $\sqrt{s_{\text {NN}}}=200$ GeV. The change in results for EoS without CP is negligible at such a large energy as expected. Having reproduced the experimental data at $\sqrt{s_{NN}}=200$ GeV further validates our numerical code.

After qualitatively understanding the CP induced effects, we make prediction for the spin polarization as the critical point is approached. For this we choose $\sqrt{s_{NN}}=14.5$ GeV which is close to the CP in our model study. We first tune the parameter f so as to reproduce the STAR measurement of global polarization at this energy [10]. The values of $f=0.45$ with CP and $f=0.53$ without CP corresponds to the same value of $-P_y$=0.92% of $\Lambda$-hyperon for $b=5.6$ which reproduces the experimental value measured by the STAR collaboration for 20–60% centrality. After tuning f we evaluate the rapidity distribution of $P_y$. We plot the rapidity distribution of $-P_y$ in the left panel of Fig. 13 for these values of f. A suppression of about $25\%$ in $-P_y$ is observed at mid-rapidity. The changes in other observables like $p_T$ spectra, elliptic flow, $dN_{\text {ch}}/dy$ is at most 8% on the surface $\Sigma _\varepsilon$ [21]. We also compute the derivative of $P_y$ with respect to rapidity and plot as a function of rapidity in the right panel of Fig. 13. We observe a slight positive slope for $dP_y/dy$ at mid-rapidity opposite to the case when there is no critical point. We cannot confirm the sign of the slope by further approaching the critical point due to the limitations of the EoS model which is valid for $\mu _B < 450$ MeV. The observed suppression of spin polarization at $\sqrt{s_{NN}}= 14.5$ GeV has resulted even though the fireball is 100 MeV away from the critical point along the $\mu _B$ axis. We expect the effect to get enhanced on further approach toward the critical point.

The sensitivity of the spin polarization on the EoS can be understood from the following expression for the spin polarization in the rest frame of $\Lambda$-hyperon at any point on $\Sigma _\varepsilon$ [11]:

$$\begin{aligned} \vec {S}^*(x,p) \propto \frac{\gamma }{T^2}\vec {v}\times \nabla T+\frac{1}{T}\left( \vec {\omega }-(\vec {\omega }\cdot \vec {v})\vec {v}\right) +\frac{1}{T}\gamma \vec {A}\times \vec {v}, \end{aligned}$$

(15)

where $\vec {\omega }$ is the vorticity ($=\nabla \times \vec {v}$), $\gamma$ is the Lorentz factor and A denotes the acceleration of the fluid element. In a nutshell, spin polarization depend on the gradients of temperature and curl of flow-velocity $(=\omega$). These gradients in turn depend on the expansion dynamics of the system and the expansion is strongly influenced by the speed of sound through EoS. Since the sound mode gets suppressed at the critical point, the system undergoes a slow expansion consequently the gradients of temperature and flow-velocity develop slowly. This should then result into a suppression of spin-polarization as confirmed by our simulations.

5 Summary and discussions

The thermal vorticity and consequently the polarization of the $\Lambda$ hyperon for different colliding energies have been estimated and found to be suppressed as the CP is approached. It is well-known that the local vorticity of the fluid couples with the quantum mechanical spin of the particles and polarize them. We have evaluated the spin polarization of $\Lambda$-hyperon with and without the effects of CP and found a strong change in the spin polarization around mid-rapidity as the system approaches the CP. There are various physical processes which collectively contribute to the suppression. Although we have solved the fully relativistic equation to estimate the vorticity, we consider below the evolution equation for vorticity ($\vec {\omega }=\nabla \times \vec {v}$) for a compressible fluid with constant $\zeta$ and $\eta$ in the non-relativistic limit because the contributions from various terms appear more clearly in this limit,

$$\begin{aligned} \frac{\partial \vec {\omega }}{\partial t}&= \left( \vec {\omega }\cdot \vec {\nabla }\right) \vec {v}- \left( \vec {v}\cdot \vec {\nabla }\right) \vec {\omega }-\theta \vec {\omega } +\frac{1}{\rho ^2}\vec {\nabla }\rho \times \vec {\nabla }p\\&\quad - \frac{1}{\rho ^2}\left( \zeta +\frac{1}{3}\eta \right) \vec {\nabla }\rho \times \vec {\nabla }\theta -\frac{\eta }{\rho ^2}\vec {\nabla }\rho \times \nabla ^2 \vec {v}+ \frac{\eta }{\rho } \nabla ^2 \vec {\omega }. \end{aligned}$$

Here $\rho$ denotes the density of fluid and $\theta = \nabla \cdot \vec {v}$. As $\theta$ is a measure of the expansion of the system, a larger expansion results in smaller vorticity as suggested by the negative sign of the term $\theta \vec {\omega }$, the vortex stretching term, $\vec {\omega }\cdot \vec {\nabla }\vec {v}$ enhances it; the baroclinic torque described by $\frac{1}{\rho ^2}\vec {\nabla }\rho \times \vec {\nabla }p$ generates vorticity by creating shear due to different acceleration confronted by the fluid with different densities. The term proportional to $\nabla ^2 \vec {\omega }$ is responsible for spatial diffusion of vorticity, the diffusion coefficient being $\frac{\eta }{\rho }$. The term of particular interest is proportional to $\vec {\nabla }\rho \times \vec {\nabla }\theta$ which suggests that the vorticity dissipates if there is a gradient in expansion rate for fluid cells i.e. the fluid cells having less density and expanding faster will oppose the vorticity of the denser fluid cells expanding slowly. The strength of this effect is proportional to $\left( \zeta +\frac{1}{3}\eta \right)$. It is clear that the suppression of vorticity and hence polarization, is a combined effect of the absorption of sound wave and the enhancement of various transport coefficients in presence of CP. The drastic qualitative and quantitative changes induced by CP in the rapidity distribution of $P_y$ can be used to detect the CP experimentally. It is important to mention at this point that the effects of CP on the $p_T$ spectra of the hadrons and on the $p_T$ and y dependence of directed and elliptic flow are found to be small [21].

Some comments on the application of hydrodynamics near the CP are in order here. Near the CP, the fluctuating modes do not relax faster than the timescale of changes in slow/conserved variables due to which the local thermal equilibrium is not maintained making hydrodynamics inapplicable. The validity of the hydrodynamics can, however, be extended by adding a scalar variable representing the slow non-hydrodynamic modes connected to the relaxation rate of the critical fluctuation (see [48] and [49] for details). It has been explicitly shown that the modes associated with the scalar variable lags behind the hydrodynamic modes resulting in back reactions on the hydrodynamic variables [50]. Further, it has been demonstrated in Ref. [50] that the back reaction has negligible effects on the hydrodynamic variables. In view of this, the results presented in this work will be useful in detecting the CP. The addition of slow non-hydrodynamic modes related to the relaxation of the critical fluctuation will be considered in future studies. Moreover, we may also recall that if a system is not too close to CP then hydrodynamics can still be applied in a domain around the CP [51].