Quasitopological electromagnetism, conformal scalar field and Lovelock black holes

Abstract

In this work, we present the new higher dimensional dyonic black hole solutions of the Lovelock-scalar gravity coupled with quasitopological electromagnetism. First, we concentrate on the dimensionally continued gravity and construct the solution that describes the dyonic black holes with conformal scalar hair in diverse dimensions. We study the physical properties and discuss the effects of the quasitopological electromagnetism and conformal scalar field on the local thermodynamic stability of these dimensionally continued black holes. Next, we derive the solutions that describe the conformal hairy black holes of the Gauss–Bonnet and third order Lovelock gravities in the presence of quasitopological electromagnetism. The basic thermodynamic quantities of these black holes are calculated as well.

1 Background

Einstein’s general relativity (EGR), which describes our Universe at medium and large scales, is the most widely accepted theory of gravity in four dimensions. A century after Einstein’s key predictions, the famous discovery of gravitational waves supports the validity of this theory. However, its modification is still necessary because one does not anticipate EGR to hold up at extremely high energies near the Planck scale. It is known that string theory [1] and brane cosmology [2, 3] offer strong predictions regarding the presence of higher dimensions, hence it sounds beneficial to investigate the gravitational fields in higher dimensions. In this setup, Lovelock theory [4] provides a useful framework for examining gravity. The action of this theory contains higher curvature terms and reduces to Einstein–Hilbert action in four dimensions. It has been established that the field equations, which result from varying the Lovelock action, are of second order in the metric derivatives. This suggests that the quantization of linearized Lovelock gravity is free from ghosts [5]. Lovelock gravity may play a crucial role in a string theory as well because the Gauss–Bonnet term appears in the low energy effective action [5, 6]. The Lovelock action reads

$$\begin{aligned} \mathfrak {I}_g=\int d^dx\sqrt{-g}\sum _{p=0}^{p_{max}}a_p\mathfrak {L}_p, \end{aligned}$$

(1.1)

in which $\mathfrak {L}_p$’s refer to the Euler densities of the 2p-dimensional manifolds such that

$$\begin{aligned} \mathfrak {L}_p=\frac{1}{2^p}\delta ^{\mu _1\nu _1\ldots \mu _{p}\nu _{p}}_{\sigma _1\lambda _1\ldots \sigma _{p}\lambda _{p}}R^{\sigma _1\lambda _1}_{\mu _1\nu _1}\ldots R^{\sigma _p\lambda _p}_{\mu _p\nu _p}. \end{aligned}$$

(1.2)

Note that $p_{max}=[\frac{d-1}{2}]$ in which the brackets are signifying the integer part of $(d-1)/2$, and $a_p$’s are the arbitrary coupling constants. Furthermore, $\delta ^{\alpha _1\beta _1\ldots \alpha _{p}\beta _{p}}_{\kappa _1\rho _1\ldots \kappa _{p}\rho _{p}}$ is the generalized Kronecker delta, $g_{\sigma \beta }$ stands for the metric tensor and $R^{\rho \lambda }_{\sigma \beta }$ denotes the components of the Riemann tensor.

It is strongly believed that Lovelock gravity is a natural extension to EGR, however, this gravity theory may have several problems if the $a_p$’s in the above action (1.1) are selected at random. For example, the dynamical evolution of the fields seems unexpected and the Hamiltonian is also not well-defined [7, 8]. Similarly, the spacetime solutions could describe either a positive energy solution with naked singularity or a negative energy solution having an event horizon [9, 10]. These issues can be tackled by choosing the proper values for $a_p$’s, which require that the spacetime solutions have a distinct AdS vacuum with a fixed cosmological constant $\Lambda$. This presumption results in the development of dimensionally continued gravity (DCG) [11,12,13], a particular version of pure Lovelock gravity. Any model of gravity theory has intriguing and significant structures called black holes. These objects may be able to shed some light on certain features related to the formulation of quantum gravity, and their thermodynamic characteristics as well. In light of these and many other points, different higher dimensional black holes in DCG and their thermodynamic properties were extensively studied [11,12,13,14,15,16,17,18].

As well-known, no-hair theorems deny the formation of asymptotically flat hairy black holes in EGR [19, 20]. Four-dimensional conformal hairy black holes have recently been revealed when $\Lambda =0$, even though the scalar field is observed to be diverging on the event horizon [21]. On the other hand, this sort of gravitating object could not be found in spacetimes with dimensions greater than four [22]. In addition, these objects are discovered in three and four dimensions for $\Lambda \ne 0$ as well [23, 24]. It is remarkable to note that the scalar field is analytic on the event horizon and outside of these objects. However, these black holes have not yet been discovered in higher dimensions when no-go results were portrayed [25]. Recently, a new model for the theory of gravity coupled to the real scalar field was formulated [26, 27]. Defining the participant

$$\begin{aligned} S^{\sigma \tau }_{\rho \kappa }{} & {} =\xi ^2R^{\sigma \tau }_{\rho \kappa }{-}2\delta ^{[\sigma }_{[\rho } \delta ^{\tau ]}_{\kappa ]}\nabla _{\beta }\xi \nabla ^{\beta }\xi {-}4\xi \delta ^{[\sigma }_{[\rho }\nabla _{\kappa ]}\nabla ^{\tau ]}\xi \nonumber \\{} & {} \quad +8\delta ^{[\sigma }_{[\rho }\nabla _{\kappa ]}\xi \nabla ^{\tau ]}\xi ,\nonumber \\ \end{aligned}$$

(1.3)

which transforms homogeneously as $S^{\gamma \alpha }_{\mu \nu }\rightarrow \Omega ^{-4}S^{\gamma \alpha }_{\mu \nu }$ when $g_{\alpha \beta }\rightarrow \Omega ^2g_{\alpha \beta }$ and $\xi \rightarrow \Omega ^{-1}\xi$. Thus, the conformal invariant action can be presented as

$$\begin{aligned} \mathfrak {I}_s\!=\!\int \! d^dx\sqrt{-g}\sum _{p=0}^{p_{max}}\bigg [b_p\xi ^{d-4p}\delta ^{\rho _1\kappa _1\ldots \rho _{p}\kappa _p}_{\sigma _1\tau _1\ldots \sigma _p\tau _p}S^{\sigma _1\tau _1}_{\rho _1\kappa _1}\ldots S^{\sigma _{p}\tau _{p}}_{\rho _{p}\kappa _{p}}\bigg ],\nonumber \\ \end{aligned}$$

(1.4)

where $\xi$ describes the scalar field. It is significant to note that Eqs. (1.1) and (1.4) describe the most comprehensive model for the Lovelock gravity coupled to a conformal scalar field. The field equations for both $g_{\mu \nu }$ and $\xi$ are of order two and hence the resulting theory is free from ghosts. Besides, it recovers the gravity theory with scalar field potential $V(\xi )=\frac{\lambda }{24}\xi ^4$ in four dimensional spacetimes. In this situation the non-minimal coupling term appears as $(-1/12)R\xi ^2$ [27]. Higher dimensional black holes with scalar hair from theory (1.4) have been discovered in Refs. [27,28,29,30,31,32]. The scalar field configurations are also consistent in the exterior or on the horizons of these objects. It is also claimed that the conformal scalar field makes the hairy black holes more thermodynamically stable [28, 29]. Likewise, charged black holes and black holes with quintessence and string-cloud are also studied in Lovelock-scalar gravity [33,34,35,36].

Since Lovelock gravity can be described from the generalization of a 2p-dimensional topological invariants in diverse dimensions, therefore higher curvature terms should be appeared in the Lagrangian (1.2). In the context of Abelian gauge theories, related concepts are also investigated, for example, Liu et al. proposed the model of quasitopological electromagnetism [37]. In this formulation, they modified the classical Maxwellian model by including new terms in the Lagrangian. These additional terms possess a special relationship with the topological invariants and are constructed from the metric tensor and electromagnetic 2 -form $F_{[2]}=dA_{[1]}$. Among them are polynomials like

$$\begin{aligned} V_{[2p]}=F_{[2]}\wedge F_{[2]}\wedge \cdots \wedge F_{[2]}. \end{aligned}$$

(1.5)

The polynomials (1.5) are similar to the Pontryagin densities, and their integrals are entirely topological in even dimensions. Contrarily, for arbitrary dimensions, these 2p-forms can be taken in a fashion that impacts the dynamics of the system. This can be accomplished by taking the squared norm as

$$\begin{aligned} U^{(p)}_{[d]}\sim \left| V_{[2p]}\right| ^2\sim V_{[2p]}\wedge *V_{[2p]}. \end{aligned}$$

(1.6)

The typical kinetic term of the Maxwell’s theory corresponds to the scenario $p=1$ in Eq. (1.6). These invariants typically make non-vanishing contributions to the equations of motion. Because of the two reasons, this theory has been given the label “quasitopological electromagnetism”. First, due to the topological origin of its constituent parts, i.e. the forms $V_{[2p]}$. Secondly, the spectrum of the static solutions with either pure electric or pure magnetic sources agrees with the corresponding spectrum of these solutions in Maxwell’s theory. However, fascinating things appear when dyons are investigated. Recently, the extension of these models has also been explored in a way that the higher-rank $(p-1)$-form field $B_{[p-1]}$ is also taken along with the Abelian gauge field $A_{[1]}$ [38]. The field strength associated with $B_{[p-1]}$ is defined through $H_{[p]}=dB_{[p-1]}$. Depending on the particular circumstances, this new field might have several physical conceptions. For instance, it could mimic the higher-rank fields emerging in string theory, which includes the basic Kalb-Ramond 2-form $B_{[2]}$, the Ramond-Ramond p-forms, or the 3-forms of super-gravity in eleven dimensions. It has also been demonstrated that the coupling of the Maxwell field with the p-forms enables the development of more generic black hole systems than those explored in Ref. [37]. Hence, the purpose of this paper is to derive the dyonic hairy black holes of Lovelock-scalar gravity in the framework of generalized quasitopological electromagnetism.

Our paper is ordered as follows. In Sect. 2, we start with a brief introduction of the generalized quasitopological electromagnetism and Lovelock gravity with a conformally coupled scalar field. Then we investigate the new hairy black holes of DCG sourced by a quasitopological electromagnetic field. We also look into the thermodynamic properties of these hairy black holes. In Sect. 3, we concentrate on the dyonic black holes of the generic Lovelock-scalar gravity. In particular, the hairy black holes and the thermodynamic properties of these systems in the framework of Gauss–Bonnet and third order Lovelock gravities are investigated. Finally, Sect. 4 gives the closing remarks.

2 Dyonic hairy black holes of the dimensionally continued gravity

2.1 Field equations

The action describing the higher curvature gravity with conformal scalar field and matter sources can be written as

$$\begin{aligned} \mathfrak {I}= & {} \int d^dx\sqrt{-g}\left[ \sum _{p=0}^{p_{max}}\frac{1}{2^k}\delta ^{\mu _1\nu _1\cdots \mu _{p}\nu _{p}}_{\sigma _1\lambda _1\cdots \sigma _{p}\lambda _p}\bigg (a_p R^{\sigma _1\lambda _1}_{\mu _1\nu _1}\cdots R^{\sigma _{p}\lambda _{p}}_{\mu _{p}\nu _{p}}\right. \nonumber \\{} & {} \left. + b_p\xi ^{d-4p}S^{\sigma _1\lambda _1}_{\mu _1\nu _1}\cdots S^{\sigma _{p}\lambda _{p}}_{\mu _{p}\nu _{p}}\bigg )+\mathfrak {L}_{qt}\right] , \end{aligned}$$

(2.1)

where $\mathfrak {L}_{qt}$ labels the Lagrangian density of matter, for instance, quasitopological electromagnetism. Moreover, $a_p$’s and $b_p$’s are the arbitrary Lovelock and conformal coupling constants, respectively. One will result in a certain class of the Lovelock gravity, i.e., DCG if one use the assumption [11, 15, 33,34,35]

$$\begin{aligned} a_p=\left( \begin{array}{c} n-1 \\ p \end{array} \right) \frac{(d_1-2p)!}{d_2!l^{-2(p+1-n)}}. \end{aligned}$$

(2.2)

Note that l is related to the cosmological constant through $\Lambda =-\frac{d_1d_2}{2l^2}$, while the positive integer n is associated with the dimensionality parameter d by $d=2n+1$ in odd and by $d=2n+2$ in even dimensions of the spacetime. Note that in Eq. (2.2) and throughout this paper, we have defined $d_j=d-j$ for simplicity. It is significant to note that this theory is equivalent to Born–Infeld gravity for $d=2n+2$ and Chern-Simons gravity for $d=2n+1$ [11,12,13]. The action principle can be employed to derive the gravitational field equations from (2.1) as

$$\begin{aligned} \sum _{p=0}^{p_{max}}\frac{a_p}{2^{p+1}}\delta ^{\alpha \sigma _1\lambda _1\cdots \sigma _p\lambda _{p}}_{\beta \kappa _1\rho _1\cdots \kappa _p\rho _{p}} R^{\kappa _1\rho _1}_{\sigma _1\lambda _1}\cdots R^{\kappa _{p}\rho _{p}}_{\sigma _{p}\lambda _{p}}=-\mathfrak {T}^{(M)\alpha }_{\beta }- \mathfrak {T}^{(S)\alpha }_{\beta }, \nonumber \\ \end{aligned}$$

(2.3)

where the energy–momentum tensor $\mathfrak {T}^{(qt)\alpha }_{\beta }$ corresponding to matter source is defined by

$$\begin{aligned} \mathfrak {T}^{(M)}_{\alpha \beta }=-\frac{2}{\sqrt{-g}}\frac{\delta \mathfrak {I}_{qt}}{\delta g^{\alpha \beta }}. \end{aligned}$$

(2.4)

Note that $\mathfrak {I}_{qt}$ is the action associated with matter. Similarly, the energy–momentum tensor for the conformal scalar field takes the form

$$\begin{aligned} \begin{aligned} \mathfrak {T}^{(S)\alpha }_{\beta }&=\sum _{p=0}^{p_{max}}\frac{b_p}{2^{p+1}}\xi ^{d-4p}\delta ^{\alpha \sigma _1\lambda _1\cdots \sigma _p\lambda _{p}}_{\beta \kappa _1\rho _1\cdots \kappa _p\rho _{p}}S^{\kappa _1\rho _1}_{\sigma _1\lambda _1}\cdots S^{\kappa _p\rho _{p}}_{\sigma _{p}\lambda _{p}}.\end{aligned} \end{aligned}$$

(2.5)

The action principle can be used to construct the following scalar field equation

$$\begin{aligned} \sum _{p=0}^{p_{max}}(d-2p)\frac{b_p}{2^p}\xi ^{d_1-4p}\delta ^{\sigma _1\lambda _1\cdots \sigma _{p}\lambda _p}_{\kappa _1\rho _1\cdots \kappa _{p}\rho _p}S^{\kappa _1\rho _1}_{\sigma _1\lambda _1}\cdots S^{\kappa _{p}\rho _{p}}_{\sigma _{p}\lambda _{p}}=0. \nonumber \\ \end{aligned}$$

(2.6)

By using Eq. (2.6), one may confirm that the energy–momentum tensor (2.5) is trace-free. This demonstrates the conformal invariance of $\xi$.

The notion of quasitopological electromagnetism has been generalized in [38] and analogous structures that resemble (1.6) are designed by utilizing the field strength $H_{[q]}$. To be more specific, one can assume

$$\begin{aligned} \begin{aligned} \digamma _{[2p]}&=F_{[2]}\wedge F_{[2]}\wedge \cdots \wedge F_{[2]}, p\le \lfloor d/2\rfloor ,\\ \mathcal {H}_{[mp]}&=H_{[m]}\wedge H_{[m]}\wedge \cdots \wedge H_{[m]}, p\le \lfloor d/m\rfloor ,\\ \digamma \mathcal {H}_{[2p+ml]}&=\digamma _{[2p]}\wedge \mathcal {H}_{ml}, 2p+ml\le d.\end{aligned} \end{aligned}$$

(2.7)

Taking these as a starting point, one can also present squared norms through the Hodge product; particularly $\left| \digamma _{[2p]}\right| ^2$, $\left| \mathcal { H}_{[mp]}\right| ^2$, and $\left| \digamma \mathcal { H}_{[2p+ml]}\right| ^2$ [38]. Of course, other options besides these squared norms also exist. For instance, one may assume terms like $\digamma _{[2p]}\wedge *\mathcal { H}_{[ml]}$ with $2p=ml$ and $p\le \lfloor d/2\rfloor$, $\digamma _{[2p]}\wedge *\digamma \mathcal { H}_{[2k+ml]}$ with $ml=2(p-k)$ and $p\le \lfloor d/2\rfloor$. Similarly, the invariant $\mathcal {H}_{[mp]}\wedge *\digamma \mathcal { H}_{[2k+ml]}$ with $2k=m(p-l)$ and $p\le \lfloor d/m\rfloor$ could also be used. All of these quantities would typically contribute to the equations of motion, hence they need to be considered in the action.

Nevertheless, we are considering the configurations as

$$\begin{aligned}&F_{\rho \sigma }\sim h'(r)\delta ^{x^0x^1}_{\rho \sigma }, \nonumber \\&H_{\nu _1\nu _2\cdots \nu _m}\sim \delta ^{x^2\cdots x^d}_{\nu _1\nu _2\cdots \nu _m}, \nonumber \\ \end{aligned}$$

(2.8)

with $m=d_2$, in which $F_{\mu \nu }$ and $H_{\nu _1\nu _2\cdots \nu _m}$ are purely electric and purely magnetic, respectively. One may demonstrate that the only nonzero terms for the configuration (2.8) are the kinetic terms $\left| \digamma _{[2]}\right| ^2\sim F_{\mu \nu }F^{\mu \nu }$ and $\left| \mathcal {H}\right| ^2$, and the interacting term $\left| \digamma \mathcal { H}_{[d]}\right| ^2$. This is why we only need to think about the following Lagrangian density for the matter source

$$\begin{aligned} \mathfrak {L}_{qt}=-\frac{1}{4} F_{\rho \sigma }F^{\rho \sigma }-\frac{1}{2m!}H_{\nu _1\nu _2\cdots \nu _m}H^{\nu _1\nu _2\cdots \nu _m}-\eta \mathfrak {L}_{int},\nonumber \\ \end{aligned}$$

(2.9)

in which $\eta$ is the coupling parameter, while $\mathfrak {L}_{int}$ refers to the interaction term defined as

$$\begin{aligned} \mathfrak {L}_{int}=\delta ^{\rho _1\cdots \rho _d}_{\sigma _1\cdots \sigma _d}F_{\rho _1\rho _2}H_{\rho _3\cdots \rho _d}F^{\sigma _1\sigma _2}H^{\sigma _3\cdots \sigma _d}.\nonumber \\ \end{aligned}$$

(2.10)

By substituting Eq. (2.9) in the action (2.1), one can derive the quasitopological electromagnetic field equations from the action principle as

$$\begin{aligned} \nabla _{\gamma }F^{\gamma \rho }-4\eta \delta ^{\rho \gamma \nu _1\cdots \nu _m}_{\sigma _1\sigma _2\cdots \sigma _d}H_{\nu _1\cdots \nu _m}\nabla _{\gamma }\big (F^{\sigma _1\sigma _2}H^{\sigma _3\cdots \sigma _d}\big )=0,\nonumber \\ \end{aligned}$$

(2.11)

and

$$\begin{aligned}{} & {} \nabla _{\rho }H^{\rho \nu _1\cdots \nu _{m-1}}{+}2\eta m!\delta ^{\rho \gamma \beta \nu _1\cdots \nu _{m-1}}_{\sigma _1\cdots \sigma _d}F_{\rho \gamma }\nabla _{\beta }\nonumber \\{} & {} \quad \big (F^{\sigma _1\sigma _2}H^{\sigma _3\cdots \sigma _d}\big ){=}0.\nonumber \\ \end{aligned}$$

(2.12)

Additionally, one may write the energy–momentum tensor corresponding to the Lagrangian density (2.9) in the form

$$\begin{aligned} \mathfrak {T}^{(M)}_{\alpha \beta }= & {} F_{\alpha \rho }F^{\rho }_{\beta }-\frac{1}{4}g_{\alpha \beta }F_{\rho \sigma }F^{\rho \sigma } \nonumber \\{} & {} +\frac{1}{2(m-1)!}H_{\alpha \nu _1\cdots \nu _{m-1}}H^{\nu _1\cdots \nu _{m-1}}_{\beta } \nonumber \\ {}{} & {} -\frac{1}{2(m!)^2}\delta ^{\nu _1\cdots \nu _m\rho }_{\sigma _1\cdots \sigma _m(\alpha }g_{\beta )\rho }H_{\nu _1\cdots \nu _m}H^{\sigma _1\cdots \sigma _m}\nonumber \\{} & {} +\eta g_{\alpha \beta }\mathfrak {L}_{int}. \end{aligned}$$

(2.13)

2.2 Dyonic hairy black hole solution in DCG

Here, we construct the hairy dyonic black hole solutions of the Eqs. (2.3), (2.6), (2.11), and (2.12). To do this, we are employing the condition (2.2) and the following static and spherically symmetric line element

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2d\Upsilon ^{2}_{d_2}. \end{aligned}$$

(2.14)

Note that $d\Upsilon ^{2}_{d_2}$ denotes the metric of the $d_2$-dimensional hyper-surface of curvature $d_2d_3\gamma$, which may be defined as

$$\begin{aligned} \begin{aligned} d\Upsilon ^2_{d_2}{=}\left\{ \begin{array}{lll} d\theta _1^2+\sum _{j=2}^{d-2}\prod _{l=1}^{j-1}\sin ^2\theta _l d\theta _j^2, &{} &{} \gamma =1, \\ d\theta _1^2+\sinh ^2\theta _1d\theta _2^2\\ +\sinh ^2\theta _1\sum _{j=3}^{d-2}\prod _{l=2}^{j-1}\sin ^2\theta _ld\theta ^2_j, &{} &{} \gamma =-1,\\ \sum _{j=1}^{d-2}d\phi _j^2, &{} &{} \gamma =0, \end{array}\right. \end{aligned}\nonumber \\ \end{aligned}$$

(2.15)

This $d_2$-dimensional hyper-surface is garbed with a magnetic field proportional to its intrinsic volume form, i.e.,

$$\begin{aligned} H_{\nu _1\nu _2\cdots \nu _m}=q\sqrt{\Sigma }\delta ^{x^1\cdots x^m}_{\nu _1\cdots \nu _m}. \end{aligned}$$

(2.16)

Similarly, for the purely electric case, we have the following form for the Maxwell tensor

$$\begin{aligned} F_{\alpha \beta }=h'(r)\delta ^{tr}_{\alpha \beta }, \end{aligned}$$

(2.17)

in which prime denotes differentiation with respect to r. Hence, by using Eqs. (2.16) and (2.17) one can get

$$\begin{aligned}{} & {} r^{2d_2}\big (d_2h'(r)+rh''(r)\big )-8\eta (d_2!)^2q^2\nonumber \\{} & {} \quad \times \big (d_2h'(r)-rh''(r)\big )=0. \end{aligned}$$

(2.18)

This equation can be integrated to give

$$\begin{aligned} h'(r)=\frac{Q r^{d_2}}{r^{2d_2}+8\eta (d_2!)^2q^2}. \end{aligned}$$

(2.19)

It is worth noting that the integration constants q and Q are associated with magnetic and electric charges, respectively. Additionally, the screening of the electric field caused by the interaction with the magnetic component is also specified by Eq. (2.19).

Let’s define the configuration of a scalar field as

$$\begin{aligned} \xi (r)=\frac{\mathcal {X}}{r}. \end{aligned}$$

(2.20)

One can confirm that $\xi (r)$ is the solution of Eq. (2.6) if the conditions

$$\begin{aligned} \sum _{p=1}^{p_{max}}pb_p\frac{d_1!}{(d_1-2p)!}\gamma ^{p-1}\mathcal {X}^{2-2p}=0, \end{aligned}$$

(2.21)

and

$$\begin{aligned} \sum _{p=0}^{p_{max}}b_p\frac{d_1!(dd_1+4p^2)}{(d_1-2p)!}\gamma ^p\mathcal {X}^{-2p}=0, \end{aligned}$$

(2.22)

hold. One may examine that there exists one unknown $\mathcal {X}$ in Eqs. (2.21) and (2.22), therefore one of the two equations must constitute a constraint on the constants $b_p$’s. Therefore, it remains to find the solution of the gravitational field equations: for the case of DCG, if we use Eq. (2.2) for $a_p$’s, energy–momentum tensor (2.13) along with (2.19), metric (2.14) and the scalar field (2.20) in the field equations (2.3) then the following first order independent differential equation is obtained

$$\begin{aligned}{} & {} \frac{1}{r^{d_2}}\bigg [r^{d_1}\bigg (\frac{\gamma -f(r)}{r^2}+\frac{1}{l^2}\bigg )^{n-1}\bigg ]'=-\frac{2H}{d_1r^d} \nonumber \\{} & {} \quad +\frac{1}{2d_1d_2}\bigg [\frac{Q^2}{\big (8\eta q^2(\Gamma (d_1))^2+r^{2d_2}\big )}+\frac{q^2}{r^{2d_2}}\bigg ], \end{aligned}$$

(2.23)

with

$$\begin{aligned} H=\sum _{p=0}^{n-1}b_p\frac{d_2!\gamma ^p\mathcal {X}^{d-2p}}{(d_2-2p)!}. \end{aligned}$$

(2.24)

It is easy to see that the value $\gamma =0$ corresponds to $H=0$. Hence, the planer solutions with scalar hair do not exist. By solving the above Eq. (2.23) for f(r) we obtain

$$\begin{aligned}{} & {} f(r)=\gamma +\frac{r^2}{l^2}-r^2\left[ \frac{\mu }{r^{d_1}}-\frac{Q^2}{2d_1d_2r^{2d_2}} F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ], \right. \nonumber \\{} & {} \quad \left. \bigg [\frac{3d_2-1}{2d_2}\bigg ],\frac{-8\eta q^2(\Gamma (d_1))^2}{r^{2d_2}}\bigg ) \right. \nonumber \\{} & {} \quad \left. -\frac{q^2}{2d_1d_2d_3r^{2d_2}}+\frac{2H}{d_1r^d}+\frac{\Delta _d}{r^{d_1}}\right] ^{\frac{1}{n-1}}, \end{aligned}$$

(2.25)

in which the constant $\mu$ is associated with the black hole’s mass M through the relation

$$\begin{aligned} M=\frac{(d-2)\mu \Sigma }{2}, \end{aligned}$$

(2.26)

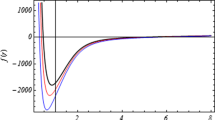
where $\Sigma$ refers to the volume of the $d_2$-dimensional hyper-surface, while $F_1$ denotes the Gaussian hypergeometric function. Furthermore, the constant $\Delta _{d}$ is selected so that the event horizon shrinks to a point when $M\rightarrow 0$ [12, 15, 34,35,36]. Figure 1 exhibits how our solution (2.25) behaves in different dimensions. The intersections of the metric function f(r) and the horizontal axis illustrate the horizon’s locations. For particular values of the parameters l, M, $\delta _{d}$, $\eta$, q, Q, and H, it is revealed that the black hole may have one or more horizons. As a result, the solution (2.25) can be thought of as the dyonic black hole solution of DCG coupled to a conformal scalar field. Similar plots of the solution for various values of the charges Q and q are displayed in Figs. 2 and 3. The quasitopological electromagnetic field has a considerable impact on where the inner horizon $r_-$ is located, while the outer horizon radius $r_+$ is unaffected. For instance, the inner horizon’s radius rises along with the magnitude of q or Q until it meets the outer event horizon. The conformal scalar field, however, affects both of them Fig. 4. It is possible to observe that as the parameter H grows, $r_-$ drops and $r_+$ increases. It should be highlighted that one will encounter the new family of dyonic black holes with no scalar hair when H disappears. Similar to this, if the parameters q, Q, and H disappear the generalized Schwarzschild-type solution of DCG can be restored. Furthermore, the aforementioned family of hairy black holes (2.25) only emerges for $d>4$ since the equations leading to a well-defined scalar field, i.e., (2.21), (2.22) are not relevant in four dimensions. This characteristic of our resulting black hole (2.25) also arises in the hairy black holes that were discovered in the backdrops of electromagnetic fields, quintessential energy, and string-clouds [33,34,35].

Fig. 1

The behaviour of f(r) (Eq. (2.25)) in different dimensions. The fixed values of the parameters are considered as $l=2$, $q=0.5$, $\eta =10^{-1}$, $\Delta _{d}=0.3$, $Q=1$, $\mu =10$, $H=1$, and $d=7$ (solid line), $d=8$ (dotted line), and $d=9$ (dashed line)

Fig. 2

Effect of electric charge Q on the solution (Eq. (2.25)). The parameters are considered as $l=2$, $q=0.05$, $\Delta _{d}=0.3$, $n=2$, $d=5$, $\eta =10^{-2}$, $\mu =10$, $H=1$, and $Q=10^4$ (solid line), $Q=10^5$ (dotted line), and $Q=10^6$ (dashed line)

Fig. 3

Effect of magnetic charge q on the solution (Eq. (2.25)). The parameters are considered as $l=2$, $Q=1$, $\Delta _{d}=0.3$, $n=3$, $d=8$, $\eta =10^{-1}$, $\mu =10$, $H=1$, and $q=0.5$ (solid line), $q=1.5$ (dotted line), and $q=2.5$ (dashed line)

Fig. 4

Effect of conformal scalar field on the solution (Eq. (2.25)). The parameters are considered as $l=2$, $Q=1.5$, $\Delta _{d}=0.3$, $n=3$, $d=7$, $\eta =10^{-1}$, $\mu =10$, $q=1$, and $H=1$ (solid line), $H=2$ (dotted line), and $H=3$ (dashed line)

In accordance to the metric (2.14), the Ricci and Kretschman scalars are expressed, respectively, as

$$\begin{aligned} \begin{aligned} R(r){=}\bigg [d_2d_3\bigg (\frac{\kappa {-}f(r)}{r^2}\bigg ){-}f''(r)-\frac{2d_2}{r}f'(r)\bigg ],\end{aligned} \end{aligned}$$

(2.27)

and

$$\begin{aligned} \begin{aligned} K(r){=}\bigg [2d_2d_3\bigg (\frac{\kappa -f(r)}{r^2}\bigg )^2{-}\big (f''(r)\big )^2{+}\frac{2d_2}{r^2}\big (f'(r)\big )^2\bigg ].\end{aligned}\nonumber \\ \end{aligned}$$

(2.28)

The solution (2.25) and its derivatives can be used to demonstrate that neither of the foregoing curvature invariants converges towards $r=0$. As a result, our solution (2.25) illustrates the occurrence of essential singularity at $r=0$.

2.3 Thermodynamics of the dyonic hairy black holes

Here, we aim to determine the fundamental thermodynamic quantities of the hairy dyonic black hole systems in DCG. Given the condition $f(r_+)=0$, it is simple to depict the mass (2.26) as

$$\begin{aligned} M= & {} \frac{d_2\Sigma r^{d_1}_+}{2}\bigg [\bigg (\frac{\gamma }{r_+^2}+\frac{1}{l^2}\bigg )^{n-1}-\frac{\Delta _{d}}{r_+^{d_1}}-\frac{2H}{d_1r_+^d}\nonumber \\ {}{} & {} +\frac{q^2}{2d_1d_2d_3r_+^{2d_2}} +\frac{Q^2}{2(d^2-3d+2)r_+^{2d_2}}\nonumber \\{} & {} \times F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\bigg [\frac{3d_2-1}{2d_2}\bigg ],\frac{-8\eta q^2(\Gamma (d_1))^2}{r_+^{2d_2}}\bigg )\bigg ]. \nonumber \\ \end{aligned}$$

(2.29)

One might express the Hawking temperature [39] from the notion of surface gravity as

$$\begin{aligned} T_H=\frac{1}{2\pi }\bigg (-\frac{1}{2}(\nabla _{\rho }Y_{\sigma })(\nabla ^{\sigma }Y^{\rho })\bigg )^{\frac{1}{2}}, \end{aligned}$$

(2.30)

with $Y_{\sigma }$ is representing the temporal Killing vector field. Therefore, one could determine $T_H$ as

$$\begin{aligned} T_{H}= & {} \frac{1}{4\pi }\bigg [\frac{\gamma d_{2n-1}}{n_1r_+}+\frac{d_1r_+}{n_1l^2}-\frac{r_+^{2n-3}l^{2n_2}}{n_1(\gamma l^2+r_+^2)^{n-2}}\bigg (\frac{2H}{r_+^d}\nonumber \\{} & {} +\frac{q^2}{r_+^{2d_2}} +\frac{d_3(d^2-3d+2)^{-1}Q^2}{2\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )}\bigg )\bigg ]. \end{aligned}$$

(2.31)

Fig. 5

The Hawking temperature $T_H$ (Eq. (2.31)) is plotted in various dimensions. The parameters have the following values: $l=2$, $\gamma =1$, $q=1$, $Q=1.5$, $\eta =10^{-1}$, $H=1$, and $d=5$ (solid line), $d=7$ (dotted line), and $d=8$ (dashed line)

Fig. 6

Behaviour of the temperature $T_H$ (Eq. (2.31)) for several values of q. The specific values of the parameters are utilized as $l=2$, $H=1$, $\gamma =1$, $n=2$, $d=5$, $Q=1.5$, $\eta =10^{-1}$, and $q=0.5$ (solid line), $q=1$ (dotted line), and $q=1.5$ (dashed line)

Fig. 7

Dependence of the electric charge on the behaviour of $T_H$ (Eq. (2.31)). The parameters have the following values: $\gamma =1$, $l=2$, $n=2$, $d=5$, $q=0.5$, $\eta =10^{-1}$, $H=1$, and $Q=10^3$ (solid line), $Q=10^5$ (dotted line), and $Q=10^7$ (dashed line)

Fig. 8

Impact of the conformal scalar field on the behaviour of the temperature $T_H$ (Eq. (2.31)). The specific values i.e. $\gamma =1$, $l=2$, $n=2$, $q=1$, $d=5$, $Q=1.5$, $\eta =10^{-1}$, and $H=1$ (solid line), $H=2$ (dotted line), and $H=3$ (dashed line) are considered for the parameters

Figure 5 illustrates that the horizon radius of the extreme black hole reduces when the dimensionality parameter d rises. It should be noticed that at the extreme horizon radius $r_{ext}$, the temperature $T_H$ vanishes. Besides, the horizon radii of the physical black holes are those points on which this quantity is non-negative. Similarly, Figs. 6 and 7 illustrate the impacts of the magnetic and electric charges on $T_H$ when the value of d is kept fixed. It is clear that the charges q and Q have a significant effect on the physicality of the smaller black holes, and that when the magnitude of these charges increase, the extreme horizon radius $r_{ext}$ increases as well. On the other hand, the temperature of the greater objects remains unaffected by these parameters. Additionally, Fig. 8 shows how the scalar field alters the temperature (2.31). One can examine that the horizon radius of the extreme black hole grows when the parameter H rises. Since the solution (2.25) defines the hairy black hole in higher curvature gravity, the area law cannot be generally applicable [40, 41]. Therefore, Hamiltonian formalism may be quite effective for the computation of this quantity [42,43,44]. This formalism has also been utilized in the context of higher curvature theories and the entropy is determined through Wald’s methodology [45, 46]. As a result, the entropy can be found as

$$\begin{aligned} S= & {} \frac{\Sigma _{d_2}}{4}\sum _{p=1}^{n-1}\frac{pb_pd_2!\mathcal {X}^{d-2p}}{(d_{2p})!}+\frac{n_1\Sigma r_+^{d}}{4d_{2n-2}\gamma }\bigg [\frac{\gamma }{r_+^2} \nonumber \\{} & {} +\frac{1}{l^2}\bigg ]^{n_1} F_1\bigg (\bigg [1,\frac{d}{2}\bigg ],\bigg [\frac{d_{2n-4}}{2}\bigg ],\frac{-r_+^2}{l^2}\bigg ). \end{aligned}$$

(2.32)

It needs to be remembered that the impact of the matter source in the aforementioned expression comes from the outer horizon radius $r_+$ through the value of M (i.e. Eq. (2.29)). This behaviour, yet again, is similar to that of the higher curvature black holes examined in Refs. [47,48,49,50,51,52].

The fluxes of the $F_{[2]}$ and $H_{[d_2]}$ at infinity, respectively, can be used to compute the electric and magnetic charges. Indeed, they are expressed as

$$\begin{aligned}&Q\sim \int *F_{[2]} ,\nonumber \\ {}&q\sim \int H_{[d_2]}, \end{aligned}$$

(2.33)

with appropriate proportionality constants. By assuming these charges and the conformal constants as extensive thermodynamic variables, one can establish the first law as

$$\begin{aligned} dM=T_HdS+\mathcal {A}dQ+\mathcal {U}dq+\sum _{j=0}^{n-1}\Xi ^{(p)}db_p. \end{aligned}$$

(2.34)

The conjugate quantities associated with the above extensive variables are computed as

$$\begin{aligned} \mathcal {A}= & {} \frac{Q\Sigma }{2d_1r_+^{d_3}}F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\nonumber \\{} & {} \quad \times \bigg [\frac{3d_2-1}{2d_2}\bigg ],\frac{-8\eta q^2(\Gamma (d_1))^2}{r_+^{2d_2}}\bigg ), \end{aligned}$$

(2.35)

$$\begin{aligned} \mathcal {U}= & {} \frac{d_2\Sigma r_+^{d_1}}{2}\left[ \frac{q r_+^{-2d_2}}{d_1(d^2-5d+6)}\right. \nonumber \\{} & {} \left. +\frac{d_3 Q^2\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )^{-1}}{2d_1d_2^2q} -\frac{d_3 Q^2}{2d_1d_2^2qr_+^{2d_2}}\right. \nonumber \\{} & {} \left. F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\bigg [\frac{3d_2-1}{2d_2}\bigg ],\frac{-8\eta q^2(\Gamma (d_1))^2}{r_+^{2d_2}}\bigg )\right] ,\nonumber \\ \end{aligned}$$

(2.36)

and

$$\begin{aligned} \begin{aligned} \Xi ^{(p)}&=-\frac{d_2\Sigma }{r_+}\sum _{p=0}^{n-1}\frac{d_2!\mathcal {X}^{d_{2p}}}{(d_{2}-2p)!}-\frac{\Sigma T_H}{4}\sum _{p=1}^{n-1}\frac{d_2!p\mathcal {X}^{d_{2p}}}{d_{2p}!}.\end{aligned}\nonumber \\ \end{aligned}$$

(2.37)

The specific heat capacity can be expressed as

$$\begin{aligned} C_H=T_{H}\frac{dS}{dT_H}\bigg |_{q,Q}. \end{aligned}$$

(2.38)

Hence, by using Eqs. (2.31) and (2.32) in the above relation of heat capacity we can get

$$\begin{aligned} C_H{} & {} =\frac{\big [(d_{2n}\gamma l^2{+}d_1r_+^2)(\gamma l^2{+}r_+^2)^{n-2}{-}r_+^{2n-2}l^{2n-2}\Upsilon _1(r_+)\big ]}{\big [(d_1(n{-}1)r_+^2{-}nd_{2n}\gamma l^2)(\gamma l^2{+}r_+^2)^{n-1}{-}nl^{2n{-}2}r_+^{2n-2}\Upsilon _3(r_+)\big ]}\nonumber \\{} & {} \quad \times \frac{n\Sigma r_+^{d_{2n-2}}(n-1)(\gamma l^2+r_+^2)^{n-1}\mathcal {S}_1(r_+)}{4d_{2n-2}d_{2n-4}\gamma l^{2n}}, \end{aligned}$$

(2.39)

where

$$\begin{aligned} \Upsilon _1(r_+)= & {} \frac{2H}{r_+^d}+\frac{q^2}{r_+^{2d_2}}+\frac{d_3Q^2}{2d_1d_2\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )}, \nonumber \\ \end{aligned}$$

(2.40)

$$\begin{aligned} \Upsilon _2(r_+)= & {} \frac{2dH}{r_+^d}-\frac{2d_2q^2}{r_+^{2d_2}}+\frac{d_3Q^2r_+^{2d_2}}{d_1\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )^2}, \nonumber \\ \end{aligned}$$

(2.41)

$$\begin{aligned} \Upsilon _3(r_+)= & {} \big ((2n-3)\gamma l^2+(2n-1)r_+^2\big )\Upsilon _1(r_+)\nonumber \\{} & {} -(\gamma l^2+r_+^2)\Upsilon _2(r_+), \end{aligned}$$

(2.42)

and

$$\begin{aligned} \mathcal {S}_1(r_+)= & {} l^2d_{2n-4}\big (d(r_+^2+\gamma l^2)-2\gamma (n-1)l^2\big )F_1\bigg (\bigg [1,\frac{d}{2}\bigg ], \nonumber \\{} & {} \bigg [\frac{d_{2n-4}}{2}\bigg ],\frac{-r_+^2}{\gamma l^2}\bigg ) -2dr_+^2(\gamma l^2+r_+^2)\nonumber \\{} & {} \times F_1\bigg (\bigg [2,\frac{d}{2}+1\bigg ],\bigg [\frac{d_{2n-6}}{2}\bigg ],\frac{-r_+^2}{\gamma l^2}\bigg ). \nonumber \\ \end{aligned}$$

(2.43)

Fig. 9

Dependence of $C_H$ (Eq. (2.39)) on the outer horizon for $\gamma =1$, $q=0.5$, $Q=1.5$, $\Sigma =1$, $H=1$, $\eta =10^{-1}$, and $d=5$ (solid line), $d=6$ (dotted line), and $d=7$ (dashed line)

Fig. 10

Dependence of $C_H$ (Eq. (2.39)) on the outer horizon for $\gamma =1$, $Q=1.5$, $d=5$, $n=2$, $\Sigma =1$, $H=1$, $\eta =10^{-1}$, and $q=0.5$ (solid line), $q=1.5$ (dotted line), and $q=2.5$ (dashed line)

Fig. 11

Impact of the electric charge on the specific heat (Eq. (2.39)) with $\gamma =1$, $q=2.5$, $d=5$, $n=2$, $\Sigma =1$, $H=1$, $\eta =10^{-1}$, and $Q=10^3$ (solid line), $Q=10^4$ (dotted line), and $Q=10^5$ (dashed line)

Fig. 12

Impact of the conformal scalar field on the specific heat $C_H$ (Eq. (2.39)) with $\gamma =1$, $q=0.5$, $d=5$, $n=2$, $\Sigma =1$, $Q=1.5$, $\eta =10^{-1}$, and $H=1$ (solid line), $H=2$ (dotted line), and $H=3$ (dashed line)

Note that the black hole is locally stable if its heat capacity is non-negative. One can observe from Fig. 9 that the black holes given by (2.25) in higher dimensions are more stable than the lower dimensional objects. Correspondingly, the impact of the parameters Q and q on the local stability can be examined in Figs. 10 and 11, respectively. The first order phase transitions correspond to the zeros of $C_H$. It can be concluded from Fig. 10 that the value of $r_+$ corresponding to the first order transition increases when the magnetic charge q increases. Moreover, the second order phase transition occurs when $C_H$ becomes infinite. Hence, Fig. 11 presents that the horizon radius associated with this phase transition of the black hole becomes smaller when the electric charge Q rises. Similarly, Fig. 12 demonstrates how the specific heat (2.39) behaves for various values of parameter H. It is shown that the event horizon of the extremal black hole is getting larger when the magnitude of H grows.

3 Dyonic black holes of the Lovelock-scalar gravity

In this section, we want to investigate the hairy dyonic black holes of the Lovelock gravity coupled to quasitopological electromagnetism. Once more, we consider the gravitational field equations given by (2.3), however, we are choosing the Lovelock parameters $a_p$’s arbitrarily. Thus, by defining the scalar field $\xi (r)$ as (2.20) subject to the Eqs. (2.21) and (2.22) and the energy–momentum tensor (2.13) along with (2.19), we have the following independent equation of motion

$$\begin{aligned}{} & {} \frac{d}{dr}\bigg [\sum _{p=0}^{p_{max}}\alpha _p\bigg (\frac{\gamma -f(r)}{r^2}\bigg )^p\bigg ]+\frac{d_1}{r}\sum _{p=0}^{p_{max}}\alpha _p\bigg (\frac{\gamma -f(r)}{r^2}\bigg )^p \nonumber \\{} & {} \quad =\frac{q^2}{2d_2r^{2d-3}}+\frac{Q^2}{2d_2(r^{2d-3}+8\eta q^2(\Gamma (d_1))^2 r)}-\frac{2H}{r^{d+1}}, \nonumber \\ \end{aligned}$$

(3.1)

where

$$\begin{aligned}&\alpha _0=\frac{a_{0}}{d_1d_2}, \nonumber \\ {}&\alpha _1=1,\nonumber \\ {}&\alpha _p=\prod _{n=3}^{2p}d_na_p. \end{aligned}$$

(3.2)

Note that the above formula of the $\alpha _p$’s in Eq. (3.2) is valid only for $p\ge 2$. By solving Eq. (3.1) one may obtain

$$\begin{aligned} \sum _{p=0}^{p_{max}}\alpha _p\bigg (\frac{\gamma -f(r)}{r^2}\bigg )^p= & {} \frac{\mu }{r_{d_1}}+\frac{2H}{r^d}-\frac{q^2}{2d_2d_3r^{2d_2}}\nonumber \\{} & {} -\frac{Q^2}{2d_2r^{2d_2}}F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\nonumber \\{} & {} \times \bigg [\frac{3d_2-1}{2d_2}\bigg ],\frac{-8\eta q^2(\Gamma (d_1))^2}{r^{2d_2}}\bigg ), \nonumber \\ \end{aligned}$$

(3.3)

with

$$\begin{aligned} H=\sum _{p=0}^{p_{max}}b_p\frac{d_2!\gamma ^p\mathcal {X}^{d-2p}}{(d_2-2p)!}. \end{aligned}$$

(3.4)

The above polynomial (3.3) is very significant because it generates the metric function f(r) that describe hairy black holes in the Lovelock-scalar gravity of arbitrary order.

3.1 Dyonic black holes of the Gauss–Bonnet-scalar gravity

The dyonic solution in this theory can be determined by putting $\alpha _{0,1,2}\ne 0$ and $\alpha _p=0$ for all $p\ge 3$ in Eq. (3.3). Hence, we get

$$\begin{aligned} \begin{aligned} f_{\pm }(r)&=\gamma +\frac{r^2}{2\alpha _2}\bigg [1\pm \sqrt{\mathcal {W}(r)}\bigg ], \end{aligned} \end{aligned}$$

(3.5)

where

$$\begin{aligned} \mathcal {W}(r)= & {} 1-\frac{4\alpha _2}{l^2}+\frac{8\alpha _2M}{\Sigma d_2r^{d_1}}+\frac{8\alpha _2H}{r^d}-\frac{8\alpha _2q^2}{d_2d_3r^{2d_2}} \nonumber \\{} & {} -\frac{2\alpha _2Q^2}{d_2r^{2d_2}}F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\bigg [\frac{3d_2-1}{2d_2}\bigg ],\nonumber \\{} & {} \frac{-8\eta q^2(\Gamma (d_1))^2}{r^{2d_2}}\bigg ). \end{aligned}$$

(3.6)

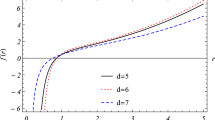
It is important to recall that the parameter l is related to the cosmological constant through $\Lambda =-\frac{d_1d_2}{2l^2}$. When $q=Q=\Lambda =0$ and $M\ne 0$, then the metric which approaches the Schwarzschild metric would be physically realistic. As a result, the solution $f_+(r)$ is not real-valued and physically realistic. To generate real-valued f(r), the function $\mathcal {W}$ must not be negative. Notably, there exist values of the parameters M, $\eta$, Q, q and l for which $\mathcal {W}(r)=0$ has a root say $r=r_b$. This root of $\mathcal {W}$ symbolizes the branch singularity [53, 54] and leads to physically meaningful $f_{-}(r)$ in Eq. (3.5) on the interval $[r_+,\infty )$. Because $\mathcal {W}(r_{\pm })=(1+2\alpha _2/r^2_{\pm })^2$, while $\mathcal {W}(r_b)=0$, the branch singularity $r_b$, outer horizon $r_+$ and inner horizon $r_-$ must satisfy $r_b<r_-<r_+$. The dyonic solution $f_-(r)$ with various values of the parameters d, H, q, and Q is plotted in Figs. 13, 14, 15 and 16. Again, it can be seen that the conformal scalar and quasitopological electromagnetic fields have a substantial impact on the existence of the horizons.

Fig. 13

The behaviour of f(r) (Eq. (3.5)) in different dimensions. The fixed values of the parameters are considered as $l=2$, $q=0.5$, $\eta =10^{-1}$, $\gamma =1$, $Q=1$, $M=10$, $\Sigma =100$, $\alpha _2=3$, $H=1$, and $d=5$ (solid line), $d=6$ (dotted line), and $d=7$ (dashed line)

Fig. 14

Effect of the electric charge Q on the solution (Eq. (3.5)). The fixed values of the parameters are considered as $l=2$, $q=0.5$, $d=5$, $M=10$, $\eta =10^{-2}$, $\Sigma =100$, $\alpha _2=3$, $\gamma =1$, $H=1$, and $Q=0.5$ (solid line), $Q=1.5$ (dotted line), and $Q=2.5$ (dashed line)

Fig. 15

Effect of the magnetic charge q on the solution (Eq. (3.5)). The fixed values of the parameters are considered as $l=2$, $Q=1$, $\Sigma =100$, $d=5$, $M=10$, $\eta =10^{-1}$, $\alpha _2=3$, $\gamma =1$, $H=1$, and $q=1$ (solid line), $q=1.5$ (dotted line), and $q=2$ (dashed line)

Fig. 16

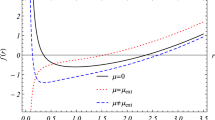
Effect of the conformal scalar field on the solution (Eq. (3.5)). The fixed values of the parameters are considered as $l=2$, $Q=1.0$, $M=10$, $\gamma =1$, $d=5$, $\eta =10^{-1}$, $\Sigma =100$, $\alpha _2=3$, $q=0.5$, and $H=0.5$ (solid line), $H=0.8$ (dotted line), and $H=1$ (dashed line)

The black hole’s mass can be computed from $f_-(r_+)=0$ as

$$\begin{aligned} M= & {} \frac{d_2\Sigma r_+^{d_1}}{8\alpha _2}\bigg [\bigg (1+\frac{2\alpha _2\gamma }{r_+^2}\bigg )^2-1+\frac{4\alpha _2}{l^2}\nonumber \\{} & {} -\frac{8\alpha _2H}{r_+^d}+\frac{2\alpha _2 q^2}{d_2d_3r_+^{2d_2}} +\frac{2\alpha _2Q^2}{d_2r^{2d_2}}\nonumber \\{} & {} F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\bigg [\frac{3d_2{-}1}{2d_2}\bigg ],\frac{{-}8\eta q^2(\Gamma (d_1))^2}{r^{2d_2}}\bigg )\bigg ]. \nonumber \\ \end{aligned}$$

(3.7)

Once more, the Hawking temperature can be calculated from Eq. (2.30) as

$$\begin{aligned} T_H(r_+)= & {} \frac{-\gamma }{2\pi r_+}+\frac{r_+^4}{16\pi \alpha _2(r_+^2+2\gamma \alpha _2)} \nonumber \\{} & {} \times \bigg [\frac{d_1(4\alpha _2-l^2)}{l^2r_+}+\frac{8\alpha _2 H}{r_+^{d+1}} \nonumber \\{} & {} -\frac{2\alpha _2q^2}{d_2r_+^{2d-3}}+\frac{d_1}{r_+}\bigg (1+\frac{2\alpha _2\gamma }{r_+^2}\bigg )^2 \nonumber \\{} & {} -\frac{2\alpha _2d_3Q^2}{d_2r_+\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )}\bigg ]. \end{aligned}$$

(3.8)

Fig. 17

The Hawking temperature $T_H$ (Eq. (3.8)) is plotted in various dimensions. The parameters have the following values: $l=2$, $\gamma =1$, $q=1$, $Q=1.5$, $\eta =10^{-1}$, $\alpha _2=10^{-1}$, $H=3$, and $d=5$ (solid line), $d=6$ (dotted line), and $d=7$ (dashed line)

Fig. 18

Impact of the conformal scalar field on the behaviour of the temperature $T_H$ (Eq. (3.8)) for $\gamma =1$, $l=2$, $q=1$, $d=5$, $Q=1.5$, $\alpha _2=1$, $\eta =10^{-1}$, and $H=0.5$ (solid line), $H=0.6$ (dotted line), and $H=0.7$ (dashed line)

Fig. 19

Impact of the magnetic charge q on the behaviour of the temperature $T_H$ (Eq. (3.8)) for $\gamma =1$, $l=2$, $H=0.7$, $d=5$, $Q=1.5$, $\alpha _2=1$, $\eta =10^{-1}$, and $q=1.3$ (solid line), $q=1.4$ (dotted line), and $q=1.5$ (dashed line)

Fig. 20

Impact of the electric charge Q on the behaviour of the temperature $T_H$ (Eq. (3.8)) for $\gamma =1$, $l=2$, $q=1.3$, $d=5$, $H=0.7$, $\alpha _2=1$, $\eta =10^{-1}$, and $Q=10^3$ (solid line), $Q=10^4$ (dotted line), and $Q=10^5$ (dashed line)

Figures 17, 18, 19 and 20 show the evolution of Hawking temperature (3.8) for distinct values of the parameters d, H, q and Q, respectively. One can see that the extremal black hole is growing in size as spacetime dimension increases. The size of this black hole, however, shrinks as the parameter H rises. The same plots can also be used to investigate how electromagnetic charges q and Q influence the temperature of the extremal and smaller black holes. The conclusion is that the size of the extremal black hole grows as these charges increase. Furthermore, these charges have very little impact on the larger black holes.

In the same way, one can derive the expression for entropy as

$$\begin{aligned} \begin{aligned} S&=\frac{\Sigma r_+^{d_4}}{4}\bigg [r_+^2+\frac{2\gamma \alpha _2d_2}{d_4}\bigg ]+\frac{\Sigma }{4}\sum _{p=0}^{p_{max}}\frac{pb_pd_2!}{d_{2p}!}\gamma ^{p-1}\mathcal {X}^{d_{2k}}.\end{aligned}\nonumber \\ \end{aligned}$$

(3.9)

Finally, by using Eq. (2.38), one can determine the heat capacity as

$$\begin{aligned}{} & {} C_H(r_+)\nonumber \\{} & {} {=}\frac{\Sigma r_{+}^{d_4} (r_{+}^2{+}2\gamma \alpha _2)(d_2r_{+}^2{+}2\gamma \alpha _2d_2)\big (r_{+}^5C_1{-}8\gamma \alpha _2(r_{+}^2{+}2\gamma \alpha _2)\big )}{\big [8\gamma \alpha _2(r_{+}^2{+}2\gamma \alpha _2)^2{+}4\alpha _2(r_{+}^8{+}2\gamma \alpha _2r_{+}^6)C_2{+}2r_{+}^5(r_{+}^2{+}4\gamma \alpha _2)C_1\big ]},\nonumber \\ \end{aligned}$$

(3.10)

with

$$\begin{aligned} C_1= & {} \frac{d_1(4\alpha _2-l^2)}{l^2r_+}+\frac{8\alpha _2 H}{r_+^{d+1}} \nonumber \\{} & {} -\frac{2\alpha _2q^2}{d_2r_+^{2d-3}}-\frac{2\alpha _2d_3Q^2}{d_2r_+\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )}\nonumber \\{} & {} +\frac{d_1}{r_+}\bigg (1+\frac{2\alpha _2\gamma }{r_+^2}\bigg )^2, \end{aligned}$$

(3.11)

and

$$\begin{aligned} C_2= & {} -\frac{d_1(4\alpha _2-l^2)}{l^2r_+^2}-\frac{8\alpha _2 (d+1) H}{r_+^{d+2}}+\frac{2\alpha _2q^2(2d-3)}{d_2r_+^{2d_1}}\nonumber \\{} & {} +\frac{4\alpha _2d_3Q^2r_+^{2d_3}}{\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )^2}\nonumber \\{} & {} +\frac{2\alpha _2d_3Q^2}{d_2r_+^2\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )}-\frac{d_1}{r_+^2}\bigg (1+\frac{2\alpha _2\gamma }{r_+^2}\bigg )^2\nonumber \\{} & {} -\frac{8\alpha _2\gamma d_1}{r_+^6(r_+^2+2\gamma \alpha _2)}. \end{aligned}$$

(3.12)

Fig. 21

Dependence of $C_H$ (Eq. (3.10)) on the outer horizon for various values of d. The values of the parameters are chosen as $\gamma =1$, $q=0.5$, $Q=1.5$, $l=2$, $\Sigma =100$, $H=1$, $\alpha _2=1$, $\eta =10^{-1}$, and $d=5$ (solid line), $d=6$ (dotted line), and $d=7$ (dashed line)

Fig. 22

Dependence of $C_H$ (Eq. (3.10)) on the outer horizon for various values of q. The values of the parameters are chosen as $\gamma =1$, $l=2$, $Q=1.5$, $d=5$, $\Sigma =100$, $H=1$, $\alpha _2=1$, $\eta =10^{-1}$, and $q=0.5$ (solid line), $q=1$ (dotted line), and $q=1.5$ (dashed line)

Fig. 23

Impact of the electric charge on the specific heat (Eq. (3.10)) with $\gamma =1$, $l=2$, $q=1.5$, $d=5$, $\alpha _2=1$, $\Sigma =100$, $H=1$, $\eta =10^{-1}$, and $Q=10^3$ (solid line), $Q=10^4$ (dotted line), and $Q=10^5$ (dashed line)

Fig. 24

Impact of the conformal scalar field on the specific heat $C_H$ (Eq. (3.10)) with $\gamma =1$, $l=2$, $q=0.5$, $d=5$, $Q=1.5$, $\Sigma =100$, $\alpha _2=1$, $\eta =10^{-1}$, $H=1$ (solid line), $H=2$ (dotted line), and $H=3$ (dashed line)

The consequences of the parameters d, q, Q, and H on the local stability of black holes are depicted in Figs. 21, 22, 23 and 24. The local stability of the black hole (3.5) is related to the positive heat capacity, whereas the instability is connected to negative specific heat. The singularities of this quantity refer to the second order phase transition, while the point at which it vanishes corresponds to the first order transition. It is evident that as the dimensionality parameter advances, the outer horizon radius corresponding to the singularity of $C_H$ grows as well. Additionally, it is demonstrated that heat capacity has two types of singularities, termed $r_1$ and $r_2$ such that $r_1<r_2$, for any value of q and Q. As a result, we conclude that the black hole will be stable in $(0, r_1)$, unstable in $(r_1,r_2)$, and stable in $(r_2,\infty )$. It is also evident that when the magnitude of charges q and Q rise, $r_1$ increases and $r_2$ falls. However, as the magnitude of H grows, $r_1$ declines and $r_2$ rises.

3.2 Dyonic black holes in the third order Lovelock-scalar gravity

The solution in this setup can be determined by putting $\alpha _{0,1,2}\ne 0$, $\alpha _3=\alpha _2^2/3$, and $\alpha _p=0$ for all $p\ge 4$ in Eq. (3.3). Hence, we get

$$\begin{aligned} \begin{aligned} f(r)&=\gamma +\frac{r^2}{\alpha _2}\bigg [1- \big (\mathcal {W}_1(r)\big )^{\frac{1}{3}}\bigg ], \end{aligned} \end{aligned}$$

(3.13)

where

$$\begin{aligned} \mathcal {W}_1(r)= & {} 1-\frac{3\alpha _2}{l^2}+\frac{6\alpha _2M}{\Sigma d_2r^{d_1}}+\frac{6\alpha _2H}{r^d}-\frac{3\alpha _2q^2}{2d_2d_3r^{2d_2}} \nonumber \\{} & {} -\frac{3\alpha _2Q^2}{2d_2r^{2d_2}}F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\bigg [\frac{3d_2-1}{2d_2}\bigg ],\nonumber \\{} & {} \frac{-8\eta q^2(\Gamma (d_1))^2}{r^{2d_2}}\bigg ). \end{aligned}$$

(3.14)

The dyonic black hole solution of the third order Lovelock-scalar gravity is plotted in Figs. 25, 26, 27 and 28. When the spacetime dimensions grow, it is visible that the inner and outer horizons are expanding. On the other hand, the size of the black hole and consequently the outer horizon decreases when the charges q and Q grow. We have also observed that the metric function (3.13) can have a single horizon, two horizons, or no horizons for different values of M, q, Q, d, and H. Furthermore, if the parameter H increases the inner horizon radius $r_-$ is falling while the outer horizon radius $r_+$ is growing.

Fig. 25

The behaviour of f(r) (Eq. (3.13)) in different dimensions. The fixed values of the parameters are considered as $l=2$, $q=0.5$, $\eta =10^{-1}$, $\gamma =1$, $Q=1$, $M=10$, $\Sigma =100$, $\alpha _2=3$, $H=1$, and $d=7$ (solid line), $d=8$ (dotted line), and $d=9$ (dashed line)

Fig. 26

Effect of the electric charge Q on the solution (Eq. (3.13)). The parameters are considered as $l=2$, $q=1.5$, $d=7$, $M=10$, $\eta =10^{-1}$, $\Sigma =100$, $\alpha _2=1$, $\gamma =1$, $H=1$, and $Q=10$ (solid line), $Q=20$ (dotted line), and $Q=25$ (dashed line)

Fig. 27

Effect of the magnetic charge q on the solution (Eq. (3.13)). The parameters are considered as $l=2$, $Q=1$, $\Sigma =100$, $d=7$, $M=10$, $\eta =10^{-1}$, $\alpha _2=3$, $\gamma =1$, $H=1$, and $q=0.5$ (solid line), $q=1.0$ (dotted line), and $q=1.5$ (dashed line)

Fig. 28

Effect of the conformal scalar field on the solution (Eq. (3.13)). The parameters are considered as $l=2$, $Q=1.5$, $M=10$, $\gamma =1$, $d=7$, $\eta =10^{-1}$, $\Sigma =100$, $\alpha _2=3$, $q=1.5$, and $H=1$ (solid line), $H=2$ (dotted line), and $H=3$ (dashed line)

Once again, we can derive the expression for the black hole’s mass from $f(r_+)=0$ as

$$\begin{aligned} M= & {} \frac{d_2\Sigma }{2}\bigg [\frac{r_+^{d_1}}{l^2}-\frac{r_+^{d_1}}{3\alpha _2}-\frac{2H}{r_+}+\frac{q^2}{2d_2d_3r_+^{d_3}}+\frac{r_+^{d_1}}{3\alpha _2}\bigg (1+\frac{\alpha _2\gamma }{r_+^2}\bigg )^{\frac{1}{3}} \nonumber \\ {}{} & {} +\frac{Q^2}{2d_2r_+^{d_3}} F_1\bigg (\bigg [1,\frac{d_3}{2d_2}\bigg ],\bigg [\frac{3d_2-1}{2d_2}\bigg ],\nonumber \\ {}{} & {} \frac{-8\eta q^2(\Gamma (d_1))^2}{r_+^{2d_2}}\bigg )\bigg ]. \end{aligned}$$

(3.15)

Correspondingly, the Hawking temperature associated with Eq. (3.13) can be calculated from Eq. (2.30) as

$$\begin{aligned} T_H(r_+)= & {} \frac{-\gamma }{2\pi r_+}+\frac{r_+^6}{4\pi \alpha _2(r_+^2+2\gamma \alpha _2)^2}\bigg [\frac{3\alpha _2d_1}{l^2r_+}-\frac{d_1}{r_+}\nonumber \\{} & {} +\frac{6\alpha _2 H}{r_+^{d+1}} -\frac{3\alpha _2q^2}{2d_2r_+^{2d-3}}+\frac{d_1}{r_+}\bigg (1+\frac{\alpha _2\gamma }{r_+^2}\bigg )^{\frac{1}{3}} \nonumber \\{} & {} -\frac{3\alpha _2d_3Q^2}{2d_2r_+\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )}\bigg ]. \end{aligned}$$

(3.16)

Fig. 29

The Hawking temperature $T_H$ (Eq. (3.16)) is plotted in various dimensions. The parameters have the following values: $l=2$, $\gamma =1$, $q=1$, $Q=1.5$, $\eta =10^{-1}$, $\Sigma =100$, $\alpha _2=1$, $H=3$, and $d=7$ (solid line), $d=9$ (dotted line), and $d=12$ (dashed line)

Fig. 30

Impact of the magnetic charge on the behaviour of the temperature $T_H$ (Eq. (3.16)) for $\gamma =1$, $l=2$, $H=3$, $d=7$, $Q=1.5$, $\Sigma =100$, $\alpha _2=1$, $\eta =10^{-1}$, and $q=1.1$ (solid line), $q=1.3$ (dotted line), and $q=1.5$ (dashed line)

Fig. 31

Impact of the electric charge on the behaviour of the temperature $T_H$ (Eq. (3.16)). The specific values i.e. $\gamma =1$, $l=2$, $\alpha _2=1$, $q=1.5$, $d=7$, $H=3$, $\Sigma =100$, $\eta =10^{-1}$, and $Q=100$ (solid line), $Q=500$ (dotted line), and $Q=800$ (dashed line) are considered for the parameters

Figure 29 expresses that the Hawking temperature (3.16) of the higher dimensional dyonic black holes is greater than their corresponding lower dimensional counterparts. Besides, as the parameter d rises, so does the size of the extremal black hole. Similarly, Figs. 30 and 31 suggest that the charges q and Q are affecting the Hawking temperature of the smaller black holes whereas the temperature of the larger objects is quite unaffected. Additionally, the extremal black hole’s size is increasing with the increase in the magnitude of magnetic charge. On the contrary, when the parameter H is growing, the size of the extremal object shrinks (Fig. 32). The entropy corresponding to the solution (3.13) is obtained as

$$\begin{aligned} S= & {} \frac{\Sigma r_+^{d_6}}{4}\bigg [r_+^4+\frac{2\gamma \alpha _2d_2r_+^2}{d_4}+\frac{\gamma ^2\alpha _2^2}{d_6}\bigg ]\nonumber \\{} & {} +\frac{d_2\Sigma }{4}\sum _{p=0}^{p_{max}}\frac{pb_pd_3!}{d_{2p}!}\gamma ^{p-1}\mathcal {X}^{d_{2k}}. \end{aligned}$$

(3.17)

Similarly, the heat capacity associated with the solution (3.13) can be computed as

$$\begin{aligned}{} & {} \!\!C_H(r_{+})\nonumber \\{} & {} {=}\frac{\Sigma r_{+}^{d_6} (d_2r_{+}^4{+}2\gamma \alpha _2d_2r_{+}^2{+}\gamma ^2\alpha _2^2d_2)\big (r_{+}\mathcal {N}_1{-}2\gamma \alpha _2(r_{+}^2{+}\gamma \alpha _2)\big )}{(r_{+}^2{+}\gamma \alpha _2)^{-1}\big [8\gamma \alpha _2(r_{+}^2{+}\gamma \alpha _2)^3{+}4(r_{+}^4{+}\gamma \alpha _2r_{+}^2)\mathcal {N}_2{-}16r_{+}^3\mathcal {N}_1\big ]},\nonumber \\ \end{aligned}$$

(3.18)

with

$$\begin{aligned} \mathcal {N}_1= & {} \frac{3\alpha _2d_1r_+^5}{l^2}-d_1r_+^5+\frac{6\alpha _2 H}{r_+^{d-5}}+d_1r_+^5\bigg (1+\frac{\gamma \alpha _2}{r_+^2}\bigg )^{\frac{1}{3}} \nonumber \\{} & {} -\frac{3\alpha _2q^2}{2d_2r_+^{2d-9}} \nonumber \\{} & {} -\frac{3\alpha _2d_3Q^2r_+^5}{2d_2r_+\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )}, \end{aligned}$$

(3.19)

and

$$\begin{aligned} \mathcal {N}_2= & {} \frac{5d_1r_+^4}{l^2(3\alpha _2-l^2)^{-1}}+5d_1r_+^4\bigg (1+\frac{\gamma \alpha _2}{r_+^2}\bigg )^{\frac{1}{3}} \nonumber \\{} & {} -\frac{2\alpha _2\gamma d_1r_+^2}{3}\bigg (1+\frac{\gamma \alpha _2}{r_+^2}\bigg )^{\frac{-2}{3}}-\frac{6\alpha _2 d_5 H}{r_+^{d_4}} \nonumber \\{} & {} +\frac{\alpha _2q^2(6d-27)}{2d_2r_+^{2d_4}}-\frac{15\alpha _2d_3Q^2r_+^{4}}{2d_2\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )} \nonumber \\{} & {} +\frac{3\alpha _2Q^2d_3r_+^{2d}}{\big (r_+^{2d_2}+8\eta q^2(\Gamma (d_1))^2\big )^2}. \end{aligned}$$

(3.20)

Fig. 32

Impact of the conformal scalar field on the behaviour of the temperature $T_H$ (Eq. (3.16)). The specific values i.e. $\gamma =1$, $l=2$, $\alpha _2=1$, $q=1.5$, $d=7$, $Q=1$, $\Sigma =100$, $\eta =10^{-1}$, and $H=1.5$ (solid line), $H=2.5$ (dotted line), and $H=3.5$ (dashed line) are considered for the parameters

Fig. 33

Dependence of $C_H$ (Eq. (3.18)) on the outer horizon for various values of d. The values of the parameters are chosen as $\gamma =1$, $l=2$, $q=0.5$, $Q=1.5$, $\Sigma =100$, $\alpha _2=1$, $H=1$, $\eta =10^{-1}$, and $d=7$ (solid line), $d=9$ (dotted line), and $d=10$ (dashed line)

Fig. 34

Dependence of $C_H$ (Eq. (3.18)) on the outer horizon for various values of q. The parameters are chosen as $\gamma =1$, $Q=1.5$, $d=9$, $\alpha _2=1$, $l=2$, $\Sigma =100$, $H=1$, $\eta =10^{-1}$, and $q=1.5$ (solid line), $q=2.5$ (dotted line), and $q=3.5$ (dashed line)

Fig. 35

Impact of the electric charge on the specific heat (Eq. (3.18)) with $\gamma =1$, $q=1.5$, $d=8$, $l=2$, $\Sigma =100$, $\alpha _2=1$, $H=1$, $\eta =10^{-1}$, and $Q=10^2$ (solid line), $Q=10^3$ (dotted line), and $Q=10^5$ (dashed line)

Fig. 36

Impact of the conformal scalar field on the specific heat $C_H$ (Eq. (3.18)) with $\gamma =1$, $q=1.5$, $d=8$, $l=2$, $\Sigma =100$, $Q=1$, $\alpha _2=1$, $\eta =10^{-1}$, and $H=1$ (solid line), $H=2$ (dotted line), and $H=3$ (dashed line)

The dependence of the heat capacity (3.18) of the dyonic black holes in the third order Lovelock-scalar gravity on the parameters d, q, Q, and H is demonstrated in Figs. 33, 34, 35 and 36. Like the dyonic black holes of the Gauss–Bonnet scalar gravity, the heat capacity associated with the black hole solution (3.13) also possesses two singular points, say $r_1$ and $r_2$ with $r_1<r_2$. These singularities are associated with the existence of the second order black hole’s phase transition. It can be examined from Fig. 33 that both the radii $r_1$ and $r_2$ are becoming larger when the parameter d rises. In addition, the higher dimensional black holes of this theory are more stable than their lower dimensional counterparts. Similarly, the slight changes in the strength of q (Fig. 34), and larger variations in the magnitude of Q (35) are also modifying the regions of local stability as well as the positions of the singularities $r_1$ and $r_2$. Additionally, Fig. 36 demonstrates the influence of the conformal scalar field on the local stability of the dyonic black hole. It is determined that the position of $r_1$ is moving to the left while that of $r_2$ is moving to the right when the parameter H is increasing.

4 Closing remarks

Here, we looked into the dyonic black holes of the Lovelock-scalar gravity sourced by quasitopological electromagnetism. In the first part, the novel dyonic hairy black holes of the DCG and their thermodynamic properties are studied. In this setup, we derive the metric function (2.25), which depends on the mass M, electric charge Q, magnetic charge q, and conformal coupling constants $b_p$’s. It is concluded that these parameters are influencing the location and existence of the black holes’ horizons. Additionally, we also calculate the thermodynamic quantities as functions of the outer horizon. It is significant to recognize that these quantities are impacted by the quasitopological and scalar fields. However, the charges q and Q have no direct impact on the entropy of the black hole. In this aspect, quasitopological electromagnetism exhibits behaviour similar to that of the Maxwellian and Born–Infeld electrodynamic theories. Thus, because the horizons depend on the charges q and Q through Eq. (2.29), these charges have an indirect effect on the entropy. To maintain things simpler, we only investigate the local stability of the dyonic black holes with $\gamma =1$. For the analysis of stability, comparable arguments can be made for the cases $\gamma =0,-1$ as well. We plotted the temperature (2.31) and heat capacity (2.39) in diverse dimensions, whereas the particular values for q, Q, l, Q, $\eta$ and H are taken into account. It can be examined from Fig. 5 that the event horizon radius of the extreme black hole decreases when spacetime dimensions increase. The dyonic hairy black hole specified by (2.25) with an outer horizon $r_+$ is shown to be locally stable if the specific heat is non-negative. In contrast, the event horizons of unstable black holes are described by those values that maintain coherence with the negative specific heat. Hence, the higher dimensional black holes of this theory are more stable than the lower dimensional ones, as seen in Fig. 9. Similarly, the effects of the magnetic and electric charges on the black hole’s stability can be seen in Figs. 10 and 11, respectively. Additionally, there are values in the domain of the heat capacity where it can either be zero or infinite. Accordingly, for these objects, both first and second order phase transitions may be occurring. As a result, Fig. 10 showed that the value of $r_+$ linked with the first order phase transition rises as the magnetic charge q increases. Moreover, the second order phase transition takes place when $C_H$ reaches infinity. Consequently, we concluded from Fig. 11 that the horizon radius linked with this phase transition decreases as the electric charge increases. Finally, Fig. 12 demonstrated how the specific heat (2.39) behaved for various values of the parameter H. We noticed that as H grows in magnitude, the extreme black hole’s size increases.

In the second part of the paper, we investigated the hairy black holes of the Lovelock gravity supported by quasitopological electromagnetism. We found the Lovelock polynomial (3.3), which offers the metric functions necessary to describe the new dyonic hairy black holes. We specifically used this polynomial to derive the dyonic hairy black hole solutions of Gauss–Bonnet and third order Lovelock gravities. We also talked about the thermodynamic properties of the black holes in these gravities. Once again, it can be said that the thermodynamic stability of these objects is greatly affected by the scalar hair and quasitopological electromagnetism.

It may be vital to look into how the quasitopological electromagnetism and conformal scalar field affect the critical behaviour and greybody factors of the resultant black holes. Furthermore, the physical characteristics of dyonic black holes in quasitopological gravities may also be very attractive.