1 Introduction

The vertex that describes the interaction of three gluons, known as the “three-gluon vertex”, plays a pivotal role in the dynamics of Yang-Mills theories in general, and of Quantum Chromodynamics (QCD) in particular [1,2,3,4,5]. The last decades have witnessed considerable progress in our understanding of the nonperturbative structure of the three-gluon vertex in the Landau gauge, thanks to the coordinated efforts of lattice simulations [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] and continuous methods, such as Schwinger–Dyson equations (SDEs) [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] and functional renormalization group [38,39,40]. Particularly noteworthy features of this vertex include the suppression of its strength in the low-energy domain [26,27,28,29,30,31,32,33,34, 36,37,38,39,40,41,42,43,44,45], its logarithmic divergence at the origin [27, 33, 34, 36], and the displacement of its Ward identity [37, 46,47,48,49], induced by the action of the Schwinger mechanism [50,51,52,53,54,55,56,57,58,59,60,61].

Recently, a rather striking property of the transversely-projected three-gluon vertex, \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\), denominated planar degeneracy, has received particular attention [20, 37, 49]. This property was first discovered in the SDE analysis of [29], and has been firmly established in a recent lattice simulation that explored a broad array of kinematic configurations [20]. The main observation may be summarized by stating that when \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\) is spanned in a special tensorial basis, the associated form factors depend almost exclusively on a single kinematic variable, \(s^2 = \frac{1}{2}(q^2+r^2+p^2)\), which defines a plane in the coordinate system \((q^2, r^2, p^2)\). Thus, all configurations with a common \(s^2\) are nearly “degenerate”, in the sense that they share, to a high degree of accuracy, the same form factors. In the recent quenched lattice study of [20], the validity of this property was established for the so-called bisectoral kinematics, \(p^2 = r^2 \ne q^2\); its generalization to arbitrary configurations was conjectured on the grounds of an inspection including numerous random configurations. As we will see in detail in what follows, the systematic SDE-based exploration carried out here demonstrates clearly that this special feature persists indeed for general kinematics, i.e., configurations with arbitrary \(q^2\), \(r^2\), and \(p^2\).

The analysis presented in [20] reached an additional important conclusion regarding the relative size of the form factors comprising \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\). Specifically, the form factor associated with the tree-level (“classical”) tensor, \({\overline{\Gamma }}_{0}^{\alpha \mu \nu }(q,r,p)\), dominates numerically over all others. As a result, the particularly compact structure

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p) \approx {\overline{\Gamma }}_{0}^{\alpha \mu \nu }(q,r,p) L_{sg}(s^{2}) , \end{aligned}$$
(1.1)

first used in [30], emerges as an excellent approximation for general kinematics. The function \(L_{sg}(s^{2})\) denotes the form factor associated with the soft-gluon limit of the three-gluon vertex (\(q=0\), \(r=-p)\), and is rather accurately known from various lattice simulations [13,14,15, 18,19,20, 62].

In the present work we employ the SDE that governs the dynamics of the three-gluon vertex, supplemented with inputs from quenched lattice simulations, in order to scrutinize some of the prominent features that arise after these recent developments. The main results of this exploration may be summarized as follows.

(i) A new basis for the expansion of \({\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p)\) is constructed, which, even though it differs only slightly from that of [20], it improves considerably the exactness of the planar degeneracy at the level of the individual form factors. To appreciate this point, note that, in the soft-gluon limit, Eq. (1.1) becomes exact, since only one transverse tensor can be constructed in this configuration. The main advantage of the new basis is that only its classical tensor is nonvanishing in the soft-gluon limit, leading to the equality between the associated form factor and \(L_{sg}(r^2)\). As a consequence, in this new basis the planar degeneracy is more accurately fulfilled for small q, since it is exact, by construction, at \(q = 0\). In contrast, in the basis of [20], \(L_{sg}(r^2)\) emerges as a linear combination of two form factors, both of which deviate markedly from the planar degeneracy at small q.

(ii) One of the prime objectives of our SDE analysis is to establish the extent of validity of Eq. (1.1). To that end, the soft-gluon limit of the SDE is determined, and all fully-dressed vertices appearing in the resulting expressions are replaced by the Ansatz of Eq. (1.1). This procedure provides a dynamical equation for the function \(L_{sg}(r^{2})\), which is solved iteratively, using lattice inputs for most of the remaining ingredients, such as gluon and ghost propagators. The resulting \(L_{sg}(r^{2})\) is in very good agreement with the lattice data of [18, 19, 62]. This fine coincidence indicates that the combined error originating from the truncation of the SDE and potential inaccuracies in the form of Eq. (1.1) is rather negligible.

(iii) The simplifications induced by Eq. (1.1) are exploited at the level of the vertex SDE, in order to determine all the form factors of \({\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p)\) in general kinematics. This is accomplished by simply substituting all three-gluon vertices appearing in the SDE the r.h.s. of Eq. (1.1) and carrying out the corresponding integration (i.e., no iterative procedure is employed). Our results demonstrates that the classical form factor dominates over all others, including the tensor structure not evaluated in the lattice study of [20], for nearly all kinematic regions. The only exception is the soft-gluon limit, where the non-classical form factors grow in magnitude; this is due to a would-be collinear divergence, which, even though tamed by the emergence of a dynamical gluon mass [57, 58, 63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78], leads to a considerable enhancement. Nevertheless, since the tensors associated with these form factors vanish in this limit, Eq. (1.1) is unaffected by this observation. In addition, by charting regions of momenta away from the bisectoral limit, we find that the planar degeneracy persists at a notable degree of accuracy at the level of the classical form factor, but is significantly violated at the level of the remaining three form factors. In particular, in the case of the classical form factor, the largest deviation from the planar degeneracy is \(17.5\%\) at \(q^2 = r^2 = p^2 = 2\) \(\mathrm GeV^2\), rapidly dropping below \(10\%\) away from this point. Finally, we observe that the effect of these deviations is that Eq. (1.1) generally tends to underestimate the true value of the classical form factor.

(iv) An interesting by-product of our analysis is related with the origin of the infrared suppression displayed by the main form factors of the three-gluon vertex, which acquire their tree-level value (unity) at 4.3 GeV (renormalization point), but reduce their size by half at around 1 GeV [13, 15, 27, 31,32,33, 40]. The detailed evaluation of the various diagrams comprising the SDE of the three-gluon vertex, employing Eq. (1.1) as input, leads to a reassessment of the origin of this phenomenon. Specifically, the cause of the suppression has been originally attributed to the infrared divergence of the “unprotected” logarithm stemming from the ghost loop diagram [27, 36]. However, the present analysis reveals that the contribution from the ghost loop becomes discernible only below 0.5 GeV, converting the so-called “swordfish” diagrams (whose logarithms are “protected” by the gluon mass) to the main source of the suppression. Consequently, the true infrared divergence becomes apparent considerably deeper in the infrared than originally thought, in a region of momenta not accessible to current lattice simulations [19, 79, 80].

The article is organized as follows. In Sect. 2 we discuss general features of \({\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p)\), placing special emphasis on the properties of the tensor basis used to decompose the vertex. Then, in Sect. 3 we present the SDE governing the evolution of \({\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p)\), derived from the three-particle irreducible (3PI) three-loop effective action, and discuss its renormalization. In Sect. 4 we solve this SDE in the soft-gluon limit, and compare the result with the \(L_{sg}(r^2)\) obtained from the lattice. Next, in Sect. 5 we discuss the true origin of the infrared suppression of \(L_{sg}(r^2)\), as unraveled through the diagram-by-diagram evaluation of the SDE. In Sect. 6 we carry out the SDE analysis for completely general kinematics. In particular, we determine all form factors of \({\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p)\), analyze in detail their size hierarchy, and the degree of accuracy of the planar degeneracy displayed by the classical form factor. Finally, our conclusions are summarized in Sect. 7, while certain technical details are relegated to an Appendix.

2 Planar degeneracy and form factor hierarchies

The full three-gluon vertex is represented diagrammatically in Fig. 1 and denoted by

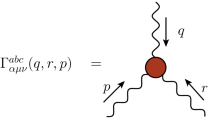
$$\begin{aligned} {\textrm{I}}\!\Gamma ^{abc}_{\alpha \mu \nu }(q,r,p) = g f^{abc} {\textrm{I}}\!\Gamma _{\alpha \mu \nu }(q,r,p), \end{aligned}$$
(2.1)

where g is the gauge coupling, and \(f^{abc}\) are the SU(3) structure constants. The vertex \({\textrm{I}}\!\Gamma ^{abc}_{\alpha \mu \nu }(q,r,p)\) possesses full Bose symmetry, remaining invariant under the exchange of any two sets of indices, e.g., \((a, \alpha , q) \leftrightarrow (c, \nu , p)\). As has been explained in the related literature [2, 20, 29, 33], this particular symmetry imposes numerous constraints on the structure of the form factors comprising this vertex (see, e.g., Eqs. (3.7)–(3.10) in [33]).

Fig. 1
figure 1

Diagrammatic representation of the three-gluon vertex

Full size image

At tree-level, \({\textrm{I}}\!\Gamma ^{\alpha \mu \nu }(q,r,p)\) acquires the standard expression

$$\begin{aligned} \Gamma _{\!0}^{\alpha \mu \nu }(q,r,p)= & {} (q-r)^{\nu }g^{\alpha \mu } + (r-p)^{\alpha }g^{\mu \nu }\nonumber \\ {}{} & {} + (p-q)^{\mu }g^{\alpha \nu }. \end{aligned}$$
(2.2)

The perturbative aspects of \({\textrm{I}}\!\Gamma ^{\alpha \mu \nu }(q,r,p)\) have been explored in various articles, see, e.g., [2,3,4,5, 81,82,83].

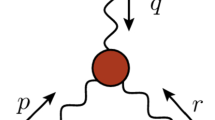
The focal point of the present work is the transversely-projected vertex, \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\), defined as

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p):= & {} P_{\alpha '}^{\alpha }(q) P_{\mu '}^{\mu }(r) P_{\nu '}^{\nu }(p) {\textrm{I}}\!\Gamma ^{\alpha '\!\mu '\!\nu '}(q,r,p),\nonumber \\{} & {} \times P_{\mu \nu }(q):= g^{\mu \nu } - \frac{q^\mu q^\nu }{q^2}. \end{aligned}$$
(2.3)

Evidently, \(f^{abc}\,{\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\) displays also full Bose symmetry, which will play a key role in what follows. Its tree-level value, to be denoted by \({\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p)\), is obtained from Eq. (2.3) through the substitution \({\textrm{I}}\!\Gamma ^{\,\alpha \mu \nu }(q,r,p) \rightarrow \Gamma _{\!0}^{\,\alpha \mu \nu }(q,r,p)\).

In general kinematics, \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\) can be decomposed in terms of four independent tensors, i.e.,

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p) = \sum _{i=1}^4 {G}_i(q^2,r^2,p^2) \, \tau _{i}^{\alpha \mu \nu }(q,r,p), \end{aligned}$$
(2.4)

where the \({G}_i(q^2,r^2,p^2)\) denote scalar form factors, which depend on three Lorentz scalars.

Remarkably, lattice [20, 84, 85] and continuum studies [28, 29, 35] have revealed that with a suitable choice of basis tensors, to be denoted by \(\tau _i^{\alpha \mu \nu }\), the structure of the form factors \(G_i\) is dramatically simplified. Specifically, the basis is required to satisfy the following properties:

(i):

All \(\tau _i^{\alpha \mu \nu }(q,r,p)\) are antisymmetric under the exchange of any pair of external legs of the vertex, e.g.,

$$\begin{aligned}{} & {} \tau _i^{\alpha \mu \nu }(q,r,p) = - \tau _i^{\mu \alpha \nu }(r,q,p) . \end{aligned}$$
(2.5)

Consequently, the Bose symmetry of the vertex manifests itself in a particularly transparent way at the level of the individual form factors. Specifically, all \(G_i(q^2,r^2,p^2)\) are symmetric under the exchange of any pair of momenta.

(ii):

The tensor \(\tau _1^{\alpha \mu \nu }(q,r,p)\) is chosen to be the classical Lorentz structure,

$$\begin{aligned}{} & {} \tau _1^{\alpha \mu \nu }(q,r,p) = {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) ; \end{aligned}$$
(2.6)

thus, at tree-level, the form factors reduce to \({G}_{\!1}^{0}= 1\) and \({G}_{\!j}^{0}=0\), for \(j=2,3,4\).

(iii):

Each tensor \(\tau _i^{\alpha \mu \nu }(q,r,p)\) has mass dimension one, exactly as the vertex itself. Hence, the form factors \(G_i(q^2,r^2,p^2)\) are all dimensionless and can be directly compared to one another.

Given such a basis, it is clear from property (i) above that the form factors \(G_i(q^2,r^2,p^2)\) can only depend on three Bose symmetric combinations of the momenta. Importantly, lattice results [20, 84, 85] have shown that for a large range of kinematic configurations, these form factors can be accurately approximated by functions of a single Bose symmetric variable,

$$\begin{aligned} G_1(q^2,r^2,p^2) \approx G_1(s^2) , \end{aligned}$$
(2.7)

whereFootnote 1

$$\begin{aligned} s^{2}:= \frac{1}{2}(q^2 + r^2 + p^2). \end{aligned}$$
(2.8)

Equation (2.7) defines the property called “planar degeneracy”. Note that in [20] the validity of Eq. (2.8) was proposed also for the remaining form factors, i.e., \(G_{2,3,4}\); however, as we will see in Sect. 6.2, this is a rather poor approximation.

Furthermore, \(G_{2,3,4}\) are found to be subleading compared to \(G_1\), for most kinematic configurations. Evidently, this property holds in perturbation theory, but its validity in the nonperturbative regime is less obvious.

The upshot of the above two observations is that \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\) can be accurately approximated by

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p) \approx G_1(s^2) {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) , \end{aligned}$$
(2.9)

over a wide range of kinematic configurations.

Now, in the soft-gluon limit, \(q \rightarrow 0\), there exists only one transverse tensor structure for the three-gluon vertex [62], namely the tree-level vertex evaluated at \(q \rightarrow 0\),

$$\begin{aligned} \lim _{q\rightarrow 0} {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) = 2 r^{\alpha '}P^{\mu \nu }(r) \lim _{q \rightarrow 0} P^\alpha _{\alpha '}(q) . \end{aligned}$$
(2.10)

Hence, the transverse vertex reduces exactly to

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(0,r,-r) = L_{sg}(r^2) \lim _{q\rightarrow 0} {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p), \end{aligned}$$
(2.11)

where the single form factor \(L_{sg}(r^2)\) can be determined as [13, 15, 19, 62]

(2.12)

At tree-level, \(L_{sg}^{0} = 1\). Note that the limit \(q\rightarrow 0\) of the term \(P^\alpha _{\alpha '}(q)\) in Eq. (2.11) is finite, but path-dependent; nevertheless, as explicitly shown in [47], the path-dependence cancels in the ratio of Eq. (2.12), leading to a well-defined \(L_{sg}(r^2)\).

At this point, if the range of validity of Eq. (2.7) includes the soft-gluon limit, \(q = 0\), then

$$\begin{aligned} G_1(q^2,r^2,p^2) \approx L_{sg}(s^2) . \end{aligned}$$
(2.13)

Under this additional assumption, Eq. (2.9) can be recast in the form given by Eq. (1.1). The advantage of this latter expression is that the soft-gluon form factor, \(L_{sg}(s^2)\), has been extensively studied in large-volume lattice simulations, appropriately refined to eliminate scale-setting and continuum extrapolation artifacts [13,14,15, 18, 19, 62]. Consequently, the shape and size of \(L_{sg}(s^2)\) are currently rather well-known; therefore, Eq. (1.1) serves as a compact and accurate approximation for the general kinematics \({\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p)\).

A tensor basis that satisfies all of the conditions (i)–(iii) above is given by

$$\begin{aligned} \begin{aligned} \tau _1^{\alpha \mu \nu }&= \, {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu },\\ \tau _2^{\alpha \mu \nu }&= \, \frac{3}{2 s^2} \,(q-r)^{\nu '} (r-p)^{\alpha '} (p\\&\quad -q)^{\mu '} P_{\alpha '}^\alpha (q) P_{\mu '}^{\mu }(r) P_{\nu '}^\nu (p),\\ \tau _3^{\alpha \mu \nu }&= - \tau _2^{\alpha \mu \nu }/4 - 3 t_4^{\alpha \mu \nu }/s^2,\\ \tau _4^{\alpha \mu \nu }&=\left( \frac{3}{2 s^2}\right) ^{\!\!2} \left[ t_1^{\alpha \mu \nu } + t_2^{\alpha \mu \nu } + t_3^{\alpha \mu \nu }\right] , \end{aligned} \end{aligned}$$
(2.14)

where we suppress the functional dependence, (q, r, p), of all tensors for compactness, and the \(t_i^{\alpha \mu \nu }\) are given by [33]

$$\begin{aligned} t_1^{\alpha \mu \nu }&= [(q\cdot r)g^{\alpha \mu } - q^{\mu }r^\alpha ][(r\cdot p)q^\nu - (q\cdot p)r^\nu ], \nonumber \\ t_2^{\alpha \mu \nu }&= [(r\cdot p)g^{\mu \nu } - r^{\nu }p^\mu ][(p\cdot q)r^\alpha - (r\cdot q)p^\alpha ], \nonumber \\ t_3^{\alpha \mu \nu }&= [(p\cdot q)g^{\nu \alpha } - p^{\alpha }q^\nu ][(q\cdot r)p^\mu - (p\cdot r)q^\mu ], \nonumber \\ t_4^{\alpha \mu \nu }&= g^{\mu \nu }[ (r\cdot q)p^\alpha - (p\cdot q)r^\alpha ] + g^{\nu \alpha }[ (p\cdot r)q^\mu \nonumber \\&\quad - (q\cdot r)p^\mu ] + g^{\alpha \mu }[ (q\cdot p)r^\nu - (r\cdot p)q^\nu ] \nonumber \\&\quad + r^\alpha p^\mu q^\nu - p^\alpha q^\mu r^\nu . \end{aligned}$$
(2.15)

The basis given in Eq. (2.14) is a minimal modification of the basis employed in [20, 85], where \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\) was decomposed as

(2.16)

the tensors are related to the \(\tau ^{\alpha \mu \nu }_{j}(q,r,p)\) through the simple relations

(2.17)

Hence, the form factors \(G_i(q^2,r^2,p^2)\) and \({\widetilde{\Gamma }}_i(q^2,r^2,p^2)\) of both bases are connected through the transformations

$$\begin{aligned} G_1(q^2,r^2,p^2)&= {\widetilde{\Gamma }}_{1}(q^2,r^2,p^2) + \tfrac{3}{2}{\widetilde{\Gamma }}_{3}(q^2,r^2,p^2), \nonumber \\ G_j(q^2,r^2,p^2)&= {\widetilde{\Gamma }}_{j}(q^2,r^2,p^2), \qquad j=2,3,4. \end{aligned}$$
(2.18)

The motivation for using Eq. (2.14), instead of Eq. (2.17), is that, in the soft-gluon limit, the two tensors survive and become linearly dependent, i.e.,

(2.19)

such that

(2.20)

Hence, in the basis , \(L_{sg}(r^2)\) is not obtained as the limit of \({\widetilde{\Gamma }}_{1}(q^2,r^2,p^2)\) as \(q \rightarrow 0\), but rather as a linear combination of \({\widetilde{\Gamma }}_{1}(0,r^2,r^2)\) and \({\widetilde{\Gamma }}_{3}(0,r^2,r^2)\). However, as we will show in Sect. 6, \(G_3(q^2,r^2,p^2)\), and hence \({\widetilde{\Gamma }}_{3}(q^2,r^2,p^2)\), is sizable at \(q = 0\); such that the equivalent of Eq. (2.13) with \(G_1\) substituted by \({\widetilde{\Gamma }}_{1}\) is a poor approximation in the soft-gluon limit.

In contrast, in the basis of Eq. (2.14), only \(\tau _1^{\alpha \mu \nu }\) is nonvanishing at \(q = 0\), i.e.,

$$\begin{aligned} \tau _1^{\alpha \mu \nu }(0,r,-r)&= 2 r^{\alpha '}P^{\mu \nu }(r) \lim _{q \rightarrow 0} P^\alpha _{\alpha '}(q), \nonumber \\ \tau _j^{\alpha \mu \nu }(0,r,-r)&= 0, \qquad j=2,3,4. \end{aligned}$$
(2.21)

Consequently, comparing Eqs. (2.11) and (2.21), we obtain simply

$$\begin{aligned} G_1(0,r^2,r^2)= L_{sg}(r^2) , \end{aligned}$$
(2.22)

i.e., Eq. (2.13) is promoted to an exact relation in the soft-gluon limit. As a result, we find that the property of the planar degeneracy, as captured by Eq. (2.13), is more accurately realized with the basis of Eq. (2.14) than with that of Eq. (2.16).

Armed with these observations, in the rest of this article we will focus on three key issues, namely the derivation of \(L_{sg}(r^2)\) from the vertex SDE, the dominance of \(G_1(q^2,r^2,p^2)\) over the other three form factors, and the quantification of the planar degeneracy (or the deviations from it) in the case of \(G_1(q^2,r^2,p^2)\), for general kinematics.

3 SDE of the three-gluon vertex

In this section we present the SDE of the three-gluon vertex that we will employ in our analysis, and discuss in detail how its renormalization is implemented.

Fig. 2
figure 2

Diagrammatic representations of: (a) the fully dressed gluon propagator, \(\Delta ^{ab}_{\mu \nu }(q)\); (b) the complete ghost propagator, \(D^{ab}(q)\); (c) the full ghost-gluon vertex, \({\textrm{I}}\!\Gamma ^{abc}_{\mu }(q,r,p)\); (d) the tree-level four-gluon vertex, \(\Gamma _{\!0\,\alpha \beta \mu \nu }^{abcd}\)

Full size image

Throughout this work we adopt the version of the three-gluon SDE obtained within the formalism of the 3PI effective action [86, 87], at the three-loop level [30, 88,89,90,91]; for general reviews on the SDE formalism, see, e.g., [25, 32, 76, 92,93,94].

As has been explained in the related literature, the diagrammatic representations of the SDEs originates from the functional differentiation of this particular action (see Figs. 1-2 of [30]), and involves fully dressed two- and three-point functions (i.e., gluon and ghost propagators, and three-gluon and ghost-gluon vertices). On the other hand, the four-gluon vertex, \({\textrm{I}}\!\Gamma _{\alpha \beta \mu \nu }^{abcd}(q,r,p,t)= -ig^2 {\textrm{I}}\!\Gamma _{\alpha \beta \mu \nu }^{abcd}(q,r,p,t)\), receives no quantum corrections, thus retaining its tree-level (classical) form, given byFootnote 2

$$\begin{aligned} \Gamma ^{abcd}_{\!0\,\alpha \beta \mu \nu }&= f^{adx}f^{cbx}\left( g_{\alpha \mu }g_{\beta \nu }-g_{\alpha \beta }g_{\mu \nu }\right) \nonumber \\&\quad +f^{abx}f^{dcx}\left( g_{\alpha \nu }g_{\beta \mu }-g_{\alpha \mu }g_{\beta \nu }\right) \nonumber \\&\quad +f^{acx}f^{dbx}\left( g_{\alpha \nu }g_{\beta \mu }-g_{\alpha \beta }g_{\mu \nu }\right) . \end{aligned}$$
(3.1)

The diagrammatic representations of all the quantities mentioned above are given in Figs. 1 and 2. In terms of these components, the resulting SDE for the three-gluon vertex acquires the form shown in Fig. 3. Our analysis is restricted to the case of pure Yang-Mills, with no active quark flavours, hence the absence of quark loops in Fig. 3.

Fig. 3
figure 3

Diagrammatic representation of the SDE for the full three-gluon vertex, \({\textrm{I}}\!\Gamma ^{\alpha \mu \nu }\), derived from the 3PI effective action at the three-loop level. Diagrams \(d_3\), \(d_4\), and, \(d_5\) are often referred to as “swordfish diagrams”. The ghost loop with the arrow reversed (equal in contribution to \(d_2\)) is not shown

Full size image

To determine the transversely-projected three-gluon vertex, \({{{\overline{{\textrm{I}}\!\Gamma }}}}^{\alpha \mu \nu }\), defined in Eq. (2.3), the first step is to contract each external leg of the SDE of Fig. 3 with a corresponding transverse projector. Then, since we specialize to the Landau gauge, the gluon propagator \(\Delta ^{ab}_{\mu \nu }(q)=-i\delta ^{ab}\Delta _{\mu \nu }(q)\) assumes the completely transverse form,

$$\begin{aligned} \Delta _{\mu \nu }(q) = \Delta (q^2)P_{\mu \nu }(q). \end{aligned}$$
(3.2)

Therefore, the legs of the three-gluon vertices attached to internal lines are automatically projected transversely as well. Consequently, in the Landau gauge, the SDE of Fig. 3 furnishes a self-consistent equation for \({{{\overline{{\textrm{I}}\!\Gamma }}}}^{\alpha \mu \nu }\), without reference to longitudinal tensor structures [29, 32].

In terms of the diagrams shown in Fig. 3, the transversely-projected three-gluon vertex is given by

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p) = {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) \, + \, \sum _{i=1}^5 {\bar{d}}_i^{\,\alpha \mu \nu }(q,r,p) , \end{aligned}$$
(3.3)

where

$$\begin{aligned} {\bar{d}}_i^{\,\alpha \mu \nu }(q,r,p):= P_{\alpha '}^{\alpha }(q) P_{\mu '}^{\mu }(r) P_{\nu '}^{\nu }(p) \,{d}_i^{\,\alpha '\mu '\nu '} (q,r,p) . \end{aligned}$$
(3.4)

After carrying out the color algebra, the individual contributions of the graphs \({d}_i\) in Minkowski space are given by

$$\begin{aligned}&{\bar{d}}_1^{\,\alpha \mu \nu }(q,r,p)\nonumber \\ {}&\quad = \lambda \!\! \int _k {\overline{{\textrm{I}}\!\Gamma }}^{\alpha \sigma \beta }(q,-k_1, k) {\overline{{\textrm{I}}\!\Gamma }}^{\mu \beta \tau }(r,-k, k_{2}) {\overline{{\textrm{I}}\!\Gamma }}^{\nu \tau \sigma }(p,-k_2,k_1)\nonumber \\ {}&\qquad \times \Delta (k_1^2) \Delta (k^2) \Delta (k_2^2), \nonumber \\&{\bar{d}}_2^{\,\alpha \mu \nu }(q,r,p)\nonumber \\ {}&\quad = - 2\lambda \!\! \int _k {\overline{{\textrm{I}}\!\Gamma }}^{\alpha }(q,-k_1,k){\overline{{\textrm{I}}\!\Gamma }}^{\mu }(r,-k,k_2){\overline{{\textrm{I}}\!\Gamma }}^{\nu }(p,-k_2,k_1)\nonumber \\ {}&\qquad \times D(k_1^2)D(k^2)D(k_2^2), \nonumber \\&{\bar{d}}_3^{\,\alpha \mu \nu }(q,r,p)\nonumber \\ {}&\quad = \frac{3}{2} \lambda [P^{\alpha }_{\sigma }(q)P^{\mu }_{\beta }(r) -P^{\alpha }_{\beta }(q) P^{\mu }_{\sigma }(r)]\!\!\int _k {\overline{{\textrm{I}}\!\Gamma }}^{\nu \sigma \beta }(p,-k_3,k) \nonumber \\ {}&\qquad \times \Delta (k_3^2) \Delta (k^2), \nonumber \\&{\bar{d}}_4^{\,\alpha \mu \nu }(q,r,p) = -\bar{d_3}^{\,\alpha \nu \mu }(q,p,r), \nonumber \\&{\bar{d}}_5^{\,\alpha \mu \nu }(q,r,p) = -\bar{d_3}^{\,\nu \mu \alpha }(p,r,q), \end{aligned}$$
(3.5)

where we define \(k_1=k+q\), \(k_2=k-r\), and \(k_3=k+p\), together with \( \lambda := ig^{2}C_{\textrm{A}}/2\), with \(C_\textrm{A}\) denoting the eigenvalue of the Casimir operator in the adjoint representation [\(C_\textrm{A} = N\) for SU(N)]. In addition, we denote by \(D^{ab}(q)= i\delta ^{ab}D(q^2)\) the ghost propagator, whose dressing function, \(F(q^2)\), is given by

$$\begin{aligned} D(q^2) =\frac{F(q^2)}{q^2}. \end{aligned}$$
(3.6)

Furthermore, \({\textrm{I}}\!\Gamma ^{abc}_\mu (q,r,p) =-g f^{abc} {\textrm{I}}\!\Gamma _\mu (q,r,p)\) stands for the ghost-gluon vertex, whose Lorentz decomposition reads

$$\begin{aligned} {\textrm{I}}\!\Gamma _\mu (q,r,p) = r_\mu B_1(r,p,q) + q_\mu B_2(r,p,q) ; \end{aligned}$$
(3.7)

at tree-level, \(B_1^0 = 1\) and \(B_2^0 = 0\). Note that only \(B_1\) contributes to the transversely-projected form, \({\overline{{\textrm{I}}\!\Gamma }}^{\,\mu }(q,r,p)\), defined as

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\mu }(q,r,p):= & {} P_{\mu '}^{\mu }(q) {\textrm{I}}\!\Gamma ^{\mu '}(q,r,p) \nonumber \\= & {} r^{\mu '}P_{\mu '}^{\mu }(q)B_1(r,p,q) . \end{aligned}$$
(3.8)

Finally, we denote by

$$\begin{aligned} \int _{k}:= \frac{1}{(2\pi )^4} \int \!\!\textrm{d}^4 k \end{aligned}$$
(3.9)

the integration over virtual momenta, where the use of a symmetry-preserving regularization scheme is implicitly assumed.

All quantities appearing in Eq. (3.5) are bare (unrenormalized). The transition to renormalized quantities is implemented by means of the standard relations

$$\begin{aligned} \Delta _{{\scriptscriptstyle R}}(q^2)&= Z^{-1}_{A} \Delta (q^2), \quad {\textrm{I}}\!\Gamma ^{\mu }_{\!\!{\scriptscriptstyle R}}(q,p,r) = Z_1 {\textrm{I}}\!\Gamma ^{\mu }(q,p,r),\nonumber \\ F_{\!{\scriptscriptstyle R}}(q^2)&= Z^{-1}_{c} F(q^2),\quad {\textrm{I}}\!\Gamma ^{\alpha \mu \nu }_{\!\!{\scriptscriptstyle R}}(q,r,p) = Z_3 {\textrm{I}}\!\Gamma ^{\alpha \mu \nu }(q,r,p),\nonumber \\ g_{{\scriptscriptstyle R}}&= Z_g^{-1} g, \quad {\textrm{I}}\!\Gamma ^{abcd}_{\!\!{\scriptscriptstyle R}\,\alpha \beta \mu \nu }(q,r,p,t) = Z_4 {\textrm{I}}\!\Gamma ^{abcd}_{\alpha \beta \mu \nu }(q,r,p,t), \end{aligned}$$
(3.10)

where the subscript “R” denotes renormalized quantities, and \(Z_{A}\), \(Z_{c}\), \(Z_{1}\), \(Z_{3}\), \(Z_{4}\), and \(Z_g\) are the corresponding (cutoff-dependent) renormalization constants. In addition, we employ the exact relations

$$\begin{aligned} Z_g^{-1} = Z_1^{-1} Z_A^{1/2} Z_c\, = Z_3^{-1} Z_A^{3/2} \, = Z_4^{-1/2} Z_A , \end{aligned}$$
(3.11)

which are imposed by the various Slavnov–Taylor identities [95, 96]. Substituting the relations of Eq. (3.10) into Eq. (3.5) and using Eq. (3.11), it is straightforward to derive the renormalized version of Eq. (3.3), given by

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}_{\!\!{\scriptscriptstyle R}}^{\,\alpha \mu \nu }(q,r,p)&= Z_3{\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) \,+ \sum _{i=1}^2 {\bar{d}}^{\,\alpha \mu \nu }_{i,{\scriptscriptstyle R}}(q,r,p) \nonumber \\ {}&\quad + Z_4 \sum _{i=3}^5 {\bar{d}}^{\,\alpha \mu \nu }_{i,{\scriptscriptstyle R}}(q,r,p), \end{aligned}$$
(3.12)

where the subscript “R” in \({\bar{d}}_{i,{\scriptscriptstyle R}}\) denotes that the expressions given in Eq. (3.5) have been substituted by their renormalized counterparts. Of course, when the momentum integration over k is carried out, the \({\bar{d}}_{i,{\scriptscriptstyle R}}\) diverge; their combined divergence will be removed subtractively, by adjusting appropriately the vertex renormalization constant \(Z_3\). Instead, the multiplicative \(Z_4\) will be approximated simply by setting \(Z_4=1\); this is consistent with the fact that, at this level of approximation, the four-gluon vertex receives no quantum corrections.

In order to fix the renormalization constants appearing in Eq. (3.12), we adopt the asymmetric MOM renormalization scheme [19, 97, 98, 98]. This scheme imposes that

$$\begin{aligned} \Delta ^{-1}(\mu ^2) = \mu ^2 , \qquad F(\mu ^2) = 1 , \qquad L_{sg}(\mu ^2) = 1 , \end{aligned}$$
(3.13)

which means that the gluon and ghost propagators assume their tree-level values at the subtraction point \(\mu \), while an analogous condition is imposed on the three-gluon vertex in the soft-gluon limit.

In applying the asymmetric MOM condition at the level of the SDE, we should keep in mind that the transversely-projected vertex becomes ill-defined in the soft-gluon limit. Nevertheless, the form factor \(L_{sg}(r^2)\) is well defined, as mentioned below Eq. (2.12), such that Eq. (3.13) fixes \(Z_3\) uniquely.

To see this, we simply factor out the term \(P^\alpha _{\alpha ^\prime }(q)\) in Eq. (3.12), which becomes ill-defined in the \(q = 0\) limit. Then, Eq. (3.12) becomes (with \(Z_4 = 1\))

$$\begin{aligned}&P_{\mu ^\prime }^\mu (r)P_{\nu ^\prime }^\nu (p){\textrm{I}}\!\Gamma _{\!\!{\scriptscriptstyle R}}^{\,\alpha ^\prime \mu ^\prime \nu ^\prime }(q,r,p) = P_{\mu ^\prime }^\mu (r)P_{\nu ^\prime }^\nu (p)\nonumber \\&\quad \times \left[ Z_3\Gamma _{\!0}^{\,\alpha ^\prime \mu ^\prime \nu ^\prime }(q,r,p) \,+ \sum _{i=1}^5 d^{\,\alpha ^\prime \mu ^\prime \nu ^\prime }_{i,{\scriptscriptstyle R}}(q,r,p) \right] , \end{aligned}$$
(3.14)

which is well-defined as \(q \rightarrow 0\). Moreover, all terms in the above expression have the same tensor structure, of the form \(r^{\alpha ^\prime } P^{\mu \nu }(r)\), which is the only possible Lorentz structure of a generic tensor \(T^{\alpha ^\prime \mu \nu }(0,r,-r)\) that is transverse to \(r^\mu \) and \(r^\nu \). In particular

$$\begin{aligned} \lim _{q\rightarrow 0} P_{\mu ^\prime }^\mu (r)P_{\nu ^\prime }^\nu (p){\textrm{I}}\!\Gamma _{\!\!{\scriptscriptstyle R}}^{\,\alpha ^\prime \mu ^\prime \nu ^\prime }(q,r,p)= & {} 2 r^{\alpha ^\prime } P^{\mu \nu }(r) L_{sg}(r^2) , \nonumber \\ \lim _{q\rightarrow 0} P_{\mu ^\prime }^\mu (r)P_{\nu ^\prime }^\nu (p)\Gamma _{\!0}^{\,\alpha ^\prime \mu ^\prime \nu ^\prime }(q,r,p)= & {} 2 r^{\alpha ^\prime } P^{\mu \nu }(r) , \nonumber \\ \lim _{q\rightarrow 0} P_{\mu ^\prime }^\mu (r)P_{\nu ^\prime }^\nu (p) d^{\,\alpha ^\prime \mu ^\prime \nu ^\prime }_{i,{\scriptscriptstyle R}}(q,r,p)= & {} 2 r^{\alpha ^\prime } P^{\mu \nu }(r) d_{i,{\scriptscriptstyle R}}^{\,\scriptscriptstyle {sg}}(r^2) , \nonumber \\ \end{aligned}$$
(3.15)

where \(d_{i,{\scriptscriptstyle R}}^{\,\scriptscriptstyle {sg}}(r^2)\) denotes the scalar form factors of \(P_{\mu ^\prime }^\mu (r)P_{\nu ^\prime }^\nu (r)d^{\,\alpha ^\prime \mu ^\prime \nu ^\prime }_{i,{\scriptscriptstyle R}}(0,r,-r)\).

Then, the substitution of the above limits into Eq. (3.14) yields

$$\begin{aligned} L_{sg}(r^2)&=Z_{3} + \sum _{i=1}^4 d_{i,{\scriptscriptstyle R}}^{\,\scriptscriptstyle {sg}}(r^2), \end{aligned}$$
(3.16)

where we have used the fact that in the limit \(q\rightarrow 0\), \(d_{5}\) vanishes in its entirety, and, in particular, \(d_{5,{\scriptscriptstyle R}}^{\scriptscriptstyle {sg}}(r^2)=0\). In addition, notice that in this same limit, the diagrams \(d_{3}\) and \(d_{4}\) become equal.

By imposing the renormalization condition of Eq. (3.13), it is straightforward to see that Eq. (3.16) immediately determines that

$$\begin{aligned} Z_{3} = 1-\sum \limits _{i=1}^4 d_{i,{\scriptscriptstyle R}}^{\,\scriptscriptstyle {sg}}(\mu ^2). \end{aligned}$$
(3.17)

Thus, substituting Eq. (3.17) into Eq. (3.12), one obtains the renormalized SDE for \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }\), expressed as

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}_{\!\!{\scriptscriptstyle R}}^{\,\alpha \mu \nu }(q,r,p)&= {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) \left[ 1- \sum _{i=1}^{4} d_{i,{\scriptscriptstyle R}}^{\,\scriptscriptstyle {sg}}(\mu ^2)\right] \nonumber \\&\quad + \sum _{i=1}^{5} {\bar{d}}_{i,{\scriptscriptstyle R}}^{\,\alpha \mu \nu }(q,r,p). \end{aligned}$$
(3.18)

It may seem at this point that the determination of \(Z_3\) through the asymmetric scheme does not completely eliminate the divergences of the SDE, because, while all “swordfish” diagrams diverge in general kinematics, the \(Z_3\) of Eq. (3.17) is independent of \({\bar{d}}_5\). However, a simple one-loop calculation illustrates how Eq. (3.17) cancels correctly all divergences. In particular, using dimensional regularization, with spacetime dimension \(d = 4-2\epsilon \), we find that the divergent parts of \({\bar{d}}_{3,4,5}\) are given by

$$\begin{aligned}{} & {} {\bar{d}}_{3, \mathrm div}^{\,\alpha \mu \nu }(q,r,p)\nonumber \\ {}{} & {} \quad = A\, ( p_{\mu '}g_{\alpha '\nu '} - p_{\alpha '}g_{\mu '\nu '} )P^{\alpha \alpha '}(q)P^{\mu \mu '}(r)P^{\nu \nu '}(p) , \nonumber \\{} & {} {\bar{d}}_{4, \mathrm div}^{\,\alpha \mu \nu }(q,r,p)\nonumber \\ {}{} & {} \quad = A\, ( r_{\alpha '}g_{\mu '\nu '} - r_{\nu '}g_{\alpha '\mu '} )P^{\alpha \alpha '}(q)P^{\mu \mu '}(r)P^{\nu \nu '}(p) , \nonumber \\{} & {} {\bar{d}}_{5, \mathrm div}^{\,\alpha \mu \nu }(q,r,p)\nonumber \\ {}{} & {} \quad = A\, ( q_{\nu '}g_{\alpha '\mu '} - q_{\mu '}g_{\alpha '\nu '} )P^{\alpha \alpha '}(q)P^{\mu \mu '}(r)P^{\nu \nu '}(p) ,\nonumber \\ \end{aligned}$$
(3.19)

where

$$\begin{aligned} A:= - \frac{1}{\epsilon }\left( \frac{15\alpha _s C_{\textrm{A}}}{32\pi } \right) . \end{aligned}$$
(3.20)

Then, we note that the sum of these divergences results in the tree-level tensor structure, for any kinematic configuration, i.e.,

$$\begin{aligned} {\bar{d}}_{3, \mathrm div}^{\,\alpha \mu \nu } + {\bar{d}}_{4, \mathrm div}^{\,\alpha \mu \nu } + {\bar{d}}_{5, \mathrm div}^{\,\alpha \mu \nu } = A\, {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) . \end{aligned}$$
(3.21)

Next, specializing in the soft-gluon limit (\(q=0\), \(p = -r\)), we find

$$\begin{aligned} {\bar{d}}_{3, \mathrm div}^{\alpha \mu \nu }(0,r,-r)&= {\bar{d}}_{4, \mathrm div}^{\,\alpha \mu \nu }(0,r,-r) = A\, r_{\alpha ^\prime }P^{\mu \nu }(r) \lim _{q\rightarrow 0} P^{\alpha \alpha ^\prime }(q), \nonumber \\ {\bar{d}}_{5, \mathrm div}^{\,\alpha \mu \nu }(0,r,-r)&= 0. \end{aligned}$$
(3.22)

Using Eq. (3.15), it follows that the contributions of the \({\bar{d}}_{3,4,5}\) to the form factor \(L_{sg}(r^2)\) are given by

$$\begin{aligned} d_{3, \mathrm div}^{\,\scriptscriptstyle {sg}}= & {} d_{4, \mathrm div}^{\,\scriptscriptstyle {sg}} = \frac{A}{2} , \quad d_{5, \mathrm div}^{\,\scriptscriptstyle {sg}} = 0 , \,\,\Longrightarrow \,\, d_{3,\mathrm div}^{\,\scriptscriptstyle {sg}} + d_{4,\mathrm div}^{\,\scriptscriptstyle {sg}} \nonumber \\{} & {} + d_{5,\mathrm div}^{\,\scriptscriptstyle {sg}} = A. \end{aligned}$$
(3.23)

Finally, using the above expressions in Eq. (3.17), we see that the contribution of \(d_{3, \mathrm div}^{\,\scriptscriptstyle {sg}}\) and \(d_{4, \mathrm div}^{\,\scriptscriptstyle {sg}}\) to the combination \(Z_3{\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p)\) is precisely the negative of \({\bar{d}}_{3, \mathrm div} + {\bar{d}}_{4, \mathrm div} + {\bar{d}}_{5, \mathrm div}\) in general kinematics, given in Eq. (3.21). Hence, the \(Z_3\) defined through the asymmetric MOM scheme captures the correct divergence of all swordfish diagrams, \({\bar{d}}_{3,4,5}(q,r,p)\), despite the vanishing of \({\bar{d}}_5(0,r,-r)\), thus ensuring the finiteness of the renormalized vertex in general kinematics.

In the following sections, we perform different projections of Eq. (3.18) in order to extract different kinematic limits. When no ambiguity can arise we drop the index “R” to avoid notation clutter.

4 Soft-gluon configuration

In this section, we consider the SDE determination of the soft-gluon form factor, \(L_{sg}(r^2)\), from Eqs. (3.16) and (3.17), by explicitly employing the approximation given by Eq. (1.1). Therefore, the level of agreement between the SDE outcome and available lattice data will constitute the first test of the accuracy of Eq. (1.1).

In order to appreciate how the approximation of Eq. (1.1) is used in this context, note that of all vertices \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\) appearing in the SDE of Fig. 3, only one supplies a form factor \(L_{sg}(k^2)\) naturally, i.e., as a result of triggering the first relation of Eq. (3.15): the vertex of diagram \(d_1\) that carries q as its external momentum.Footnote 3 All other three-gluon vertices are evaluated in general kinematics even after setting \(q = 0\), e.g., \((r,-k,k-r)\). Therefore, strictly speaking, the general decomposition of Eq. (2.4) must be employed for all of them, inducing a dependence on all four form-factors \(G_i\left( r^2,k^2,(k-r)^2\right) \). The use of Eq. (1.1) enters at this point, by implementing the substitution

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(r,-k,k-r) \rightarrow {\overline{\Gamma }}_{0}^{\alpha \mu \nu }(r,-k,k-r) L_{sg}(s^{2}) , \end{aligned}$$
(4.1)

with \(s^2 = [r^2+k^2+(k-r)^2]/2 = k^2+r^2 - k\cdot r\), for all these vertices. As a result, the only form factor related to the three-gluon vertex that appears on the r.h.s of the SDE is the \(L_{sg}\). In particular, the SDE reduces to an integral equation for \(L_{sg}\), of the general form

$$\begin{aligned} L_{sg}= 1 + \int _k K_1 + \int _k L_{sg}K_2 + \int _k L_{sg}^3 K_3 , \end{aligned}$$
(4.2)

whose solution provides the momentum evolution of \(L_{sg}(r^2)\).

Specifically, after conversion to Euclidean space and use of hyper-spherical coordinates, and applying standard transformation rules (see, e.g., Eq. (5.1) of [99]), we obtain from Eqs. (3.16) and (3.17)

$$\begin{aligned} L_{sg}(r^2)&= 1 + \sum \limits _{i=1}^4 d_{i,f}^{\,\scriptscriptstyle {sg}}(r^2,\mu ^2), \qquad d_{i,f}^{\,\scriptscriptstyle {sg}}(r^2,\mu ^2):= d_i^{\,\scriptscriptstyle {sg}}(r^2) \nonumber \\&\quad - d_i^{\,\scriptscriptstyle {sg}}(\mu ^2), \end{aligned}$$
(4.3)

with

$$\begin{aligned} d_1^{\,\scriptscriptstyle {sg}}(x)&= \frac{4\lambda '}{3}\!\!\int _{0}^{\infty }\!\!\!\!dy \!\!\int _{0}^{\pi }\!\!\!\!d\phi \, s_{\phi }^4 \,w \left[ xy (c_{\phi }^2+8)\!+\!3(x^2\!+\!y^2)\right. \nonumber \\&\quad \left. -\!6\sqrt{y x}c_{\phi }(x+y)\!\right] \!L_{sg}(y) L_{sg}^2(v)\Delta (u) \Delta ^2(y),\nonumber \\ d_2^{\,\scriptscriptstyle {sg}}(x)&= - \frac{\lambda '}{3}\int _{0}^{\infty }\!\!\!\!dy \int _{0}^{\pi }\!\!\!\!d\phi \, s_\phi ^4(w/y)F^2(y)F(u)B_1^2(u,y,\chi )\nonumber \\&\quad \times B_1(y,y,\pi ),\nonumber \\ d_3^{\,\scriptscriptstyle {sg}}(x)&= d_4^{\,\scriptscriptstyle {sg}}(x) = -\frac{\lambda '}{2}\int _{0}^{\infty }\!\!\!\!dy \!\!\int _{0}^{\pi }\!\!\!\!d\phi \,s_{\phi }^4 \left( {y}/{u}\right) \left[ 3x + 5y \right. \nonumber \\&\quad \left. - 5\sqrt{x y}c_{\phi }\right] L_{sg}(v) \Delta (u) \Delta (y), \end{aligned}$$
(4.4)

where \(\lambda ':= {C_{A}\alpha _s}/{4\pi ^{2}}\) and \(\alpha _s(\mu ^2):=g^2/4\pi \) is the value of the strong charge at the renormalization point \(\mu \). In the above equation, we introduced the auxiliary variables

$$\begin{aligned} x&:= r^2, \qquad y := k^2, \qquad u := (r-k)^2 = x + y - 2\sqrt{xy}c_\phi , \nonumber \\ v&:= x + y - \sqrt{xy}c_\phi , \qquad w:=\left( {y}/{u}\right) \sqrt{{y}/{x}}\,c_{\phi }, \end{aligned}$$
(4.5)

where \(\phi \) denotes the angle between the momenta k and r, while \(s_\phi := \sin \phi \), \(c_\phi := \cos \phi \). Furthermore, we parametrize \(B_1(r,p,q)\), in terms of the squares of their first two arguments and the angle between them. In particular,

$$\begin{aligned}&B_1(k,-k,0) \rightarrow B_1(y,y,\pi ), \nonumber \\&B_1(k-r,-k,r) \rightarrow B_1(u,y,\chi ), \end{aligned}$$
(4.6)

with the angle \(\chi \) defined as \(c_{\chi }:=\left( \sqrt{{x}/{u}}\,c_{\phi } -\sqrt{{y}/{u}}\right) \).

The nonlinear integral equation for \(L_{sg}(r^{2})\) given by Eq. (4.3) is solved by employing the following sequence of steps:

(i):

\(\Delta (r^2)\), \(F(r^2)\), and the ghost-gluon form factor \(B_{1}(r^2, p^2, \theta )\) are treated as external inputs. For \(\Delta (r^2)\) and \(F(r^2)\) we use fits given by Eqs. (C11) and (C6) of [47], respectively, to the lattice results of [62], which have been cured from volume and discretization artifacts [100,101,102,103]. For \(B_{1}(r^2, p^2, \theta )\) we employ the results of [37, 49] (see Figs. 13 and 14 of [37]), which were obtained through the solution of the coupled system of SDEs for the ghost propagator and the ghost-gluon vertex, and reproduce the available lattice data of [104, 105]. All these inputs are renormalized in the asymmetric MOM scheme, defined by Eq. (3.13), at the renormalization point \(\mu =4.3~\text {GeV}\). For this particular \(\mu \) we use \(\alpha _s = 0.27\), as determined by the lattice simulation of [15].

(ii):

To solve Eq. (4.3), we first perform a change of variables

$$\begin{aligned}{} & {} {{\hat{x}}}:= \frac{x - 1}{ x + 1} , \end{aligned}$$
(4.7)

and similarly for all squared momenta appearing in Eq. (4.4), including the integration measure. This procedure transforms the interval \([0,\infty ]\) to the canonical interval \([-1,1]\). Evidently, we can rewrite any function of a squared momentum as a function of its hatted counterpart, e.g., \(L_{sg}(x)\rightarrow L_{sg}({{\hat{x}}})\), and so on.

(iii):

Then we expand \(L_{sg}({{\hat{x}}})\) in terms of the Chebyshev polynomials of the second kind, \(U_i({{\hat{x}}})\), i.e.,

$$\begin{aligned}{} & {} L_{sg}({{\hat{x}}}) = \sum _{i = 0}^{N} c_i U_i({{\hat{x}}}) , \end{aligned}$$
(4.8)

and similarly for \(L_{sg}({{\hat{y}}})\) and \(L_{sg}({{\hat{v}}})\), where we take \(N = 39\). The resulting integrals are evaluated through Gauss–Legendre quadrature at 40 values of squared momenta in the range \([8\times 10^{-4}, 1\times 10^{3}]~\text {GeV}^{2}\).

(iv):

At this point, Eq. (4.3) has been converted to a nonlinear algebraic system for the 40 coefficients \(c_i\), which is solved using a quasi-Newton method. Finally, substituting the solution into Eq. (4.8) and inverting Eq. (4.7) yields \(L_{sg}(x)\).

Fig. 4
figure 4

The soft-gluon form factor \(L_{sg}(r^{2})\) from [19, 79, 80] (lattice data) compared with the SDE result obtained from Eq. (4.3) (blue continuous)

Full size image

The \(L_{sg}(r^2)\) determined through the above procedure is shown in Fig. 4 (blue continuous curve), where it is compared to the lattice data (points) of [19, 79, 80]. The observed agreement is particularly good: the deviation of the SDE solution from the lattice results is below \(5\%\) for most of the momentum range where data exist. The only exception is for \(r\in [0.4,1.2]\) GeV, where the deviation is more pronounced; in particular, at momenta near \(r = 0.6\) GeV the SDE result underestimates the lattice data by \(24\%\) at most.

5 Infrared features revisited

In this section we take advantage of the simplicity offered by Eq. (1.1) and revisit two particular features of \(L_{sg}(r^2)\) in the Landau gauge, namely the infrared suppression of \(L_{sg}(r^2)\) with respect to its tree-level value, and the divergence of this form factor at the origin. Even though both features have been extensively discussed in the recent literature at a qualitative level [13, 15, 18, 19, 27, 36, 37], our results allow for a quantitative analysis of their origin.

To this end, we begin by disentangling the contributions of the individual terms \(d_{i,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\) to the final result for \(L_{sg}(r^2)\). This is achieved by substituting the solution for \(L_{sg}(r^{2})\), shown in Fig. 4, into the expressions for the contributions of each diagram, given in Eqs. (4.3) and (4.4). The outcome of this exercise is presented on the left panel of Fig. 4, where we turn on, one by one, the resulting \(d_{i,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\).

As we can see on the left panel of Fig. 4, diagram \(d_1\) has a positive contribution to \(L_{sg}(r^2)\) in the infrared. On the other hand, both the ghost loops, \(d_2\), and the swordfish diagrams, \(d_3+d_4\), furnish a negative contribution in the infrared, thus suppressing \(L_{sg}(r^2)\). However, it is clear that the bulk of the suppression has its origin in the swordfish terms. In fact, comparing the purple dotted and green dashed curves of Fig. 4, corresponding to \(1 + d_{1,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\) and \(1 + d_{1,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)+ d_{2,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\), respectively, we see that the numerical impact of the ghost loop in \(L_{sg}(r^2)\) is negligible for momenta \(r \gtrapprox 0.3\) GeV. In other words, even if diagram \(d_2\) were to be omitted entirely, the suppression of the vertex in the physically important region of momenta would remain practically unaltered.

Next, we consider the behavior of \(L_{sg}(r^2)\) near the origin. As has been shown in previous studies [27], the nonperturbative masslessness of the ghost makes \(d_{2,f}^{\scriptscriptstyle {sg}}\) diverge at \(r = 0\). While this feature is already visible on the left panel of Fig. 4, it is best appreciated in a logarithmic plot, presented on the right panel of the same figure. In this panel, we see that \(L_{sg}(r^2)\) (blue continuous) displays a behavior consistent with a logarithmic divergence near the origin. To confirm that this divergence originates from \(d_{2,f}^{\scriptscriptstyle {sg}}\), the result of \(L_{sg}(r^2) - d_{2,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\) is plotted in the same panel as a red dot-dashed curve, and clearly saturates to a constant value.

In previous studies [19, 27, 36], the features of infrared suppression and divergence at the origin were thought to be connected: the divergence of \(d_{2,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\) was understood to drive the suppression of \(L_{sg}(r^2)\), since \(d_{2,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\) inevitably acquires values that are negative and large in magnitude for small enough r. Instead, from the results presented in Fig. 4, it is clear that the infrared suppression of \(L_{sg}(r^2)\) is driven by the swordfish diagrams, with the divergence of the ghost loop becoming apparent only at very small momenta.

Fig. 5
figure 5

Left: The sequential inclusion of the diagrammatic contributions \(d_{i,f}^{\scriptscriptstyle {sg}}(r^2,\mu ^2)\) that comprise the soft-gluon form factor \(L_{sg}(r^{2})\). Right: Rate of the logarithmic divergence of \(L_{sg}(r^{2})\) extracted from (i) fitting the lattice data of [19, 79, 80] (yellow dot-dashed curve), and (ii) the SDE calculation leading to Eq. (5.1) (black dotted curve)

Full size image

Given these considerations, it is possible to obtain an exact expression describing the rate of the logarithmic divergence of \(L_{sg}(r^{2})\) in the infrared by studying only the ghost diagram, \(d_2\). This expression is derived in detail in the Appendix A and readsFootnote 4

(5.1)

where \({{\widetilde{Z}}}_1(\mu = 4.3~\text {GeV})=0.933\) is the particular value assumed by the renormalization constant \(Z_1\) of the ghost-gluon vertex in the asymmetric MOM scheme [37, 49]. Lastly, b is a finite constant left unspecified.

On the right panel of Fig. 5, we compare the SDE result for \(L_{sg}(r^2)\) (blue continuous) to the asymptotic behavior given by Eq. (5.1) (black dotted), where we fixed \(b=0.45\) by adjusting it to the full SDE solution. From this comparison, it is clear that the asymptotic behavior is only reached for momenta below 0.3 GeV. For \(r > 0.3\) GeV, the blue continuous and red dot-dashed curves become nearly equal, such that the slope of \(L_{sg}(r^2)\) is clearly contaminated by positive contributions originating from the gluonic diagrams.

The latter observation is relevant for the correct extraction of the asymptotic behavior of \(L_{sg}(r^2)\) from the lattice data. Specifically, in [19], the parameters of Eq. (5.1) were determined by fitting Eq. (5.1) to the lattice data below 0.5 GeV. This procedure yielded the values \(a\rightarrow a^{\prime }=0.117(6)\) and \(b\rightarrow b^{\prime }=0.78(8)\) (yellow dot-dashed line on the right panel of Fig. 5). In particular, \(a^{\prime }\) is 2.25 times larger than the theoretical value found for a in Eq. (5.1).

Now, we note that out of the 52 data points of [19, 79, 80] for \(L_{sg}(r^2)\) with \(r <0.5\) GeV, only 17 (about one-third) lie in the region \(r < 0.3\) GeV, where \(L_{sg}(r^2)\) is well-described by its asymptotic behavior. Moreover, these few points possess larger error bars than the points at higher momenta, thus having smaller weights in the fitting procedure. As such, the value of a obtained through this procedure is polluted by non-asymptotic contributions.

Indeed, if the fitting is repeated using only the 17 data points in the asymptotic region, \(r < 0.3\) GeV, we obtain instead \(a = 0.09(8)\). The latter number is consistent with the theoretical value of Eq. (5.1), albeit with an error that is too large to be conclusive. Evidently, a more reliable comparison between SDE results and lattice would require data points for \(r < 0.3\) GeV, which may be particularly costly.

We conclude this section by emphasizing that the discussed features, and the diagrammatic origin attributed to them, have been explored in the strict confines of the Landau gauge; it would be interesting to explore if any of them persist for different values of the gauge-fixing parameter.

6 General kinematics

In this section we determine from the SDE the structure of the form factors \(G_i(q^2,r^2,p^2)\) for general kinematics. The main goal of this analysis is twofold: first, to establish quantitatively the extent of the dominance of the classical form factor, and second, to determine the accuracy of the planar degeneracy approximation, i.e., of Eq. (2.13).

In general, the four form factors comprise a system of coupled integral equations, since all of the \(G_i(q^2,r^2,p^2)\) contribute to the right-hand side of the SDE of Eq. (3.18). To simplify our analysis, we will instead employ again the approximation given by Eq. (1.1), using for \(L_{sg}(r^2)\) the result of the previous section, shown as a blue continuous line in Fig. 4.

With the above procedure, the task of determining each \(G_i(q^2,r^2,p^2)\) is reduced to the evaluation of a specific static projection of the SDE of Eq. (3.18). Concretely, the form factors can be extracted through

$$\begin{aligned} G_{j}(q^2,r^2,p^2) = {{\mathcal {P}}}_{j}\cdot {\overline{{\textrm{I}}\!\Gamma }}(q,r,p), \qquad {j=1,2,3,4,} \end{aligned}$$
(6.1)

where we have introduced the compact notation \(A\cdot B:= A^{\alpha \mu \nu }B_{\alpha \mu \nu }\). Evidently, the projectors \({{\mathcal {P}}}_{j}^{\alpha \mu \nu }\) can be defined by the requirement

$$\begin{aligned} {{\mathcal {P}}}_{j} \cdot \tau _{i} = \delta _{ij} . \end{aligned}$$
(6.2)

Since the basis elements, \(\tau _i^{\alpha \mu \nu }\), defined in Eq. (2.14), are transversely-projected, the \({{\mathcal {P}}}_{j}^{\alpha \mu \nu }\) are themselves transverse, and may be expanded in the same basis, i.e.,

$$\begin{aligned} {{\mathcal {P}}}_{j}^{\alpha \mu \nu } = \sum _{n}c_{jn} ~\tau _{n}^{\alpha \mu \nu }. \end{aligned}$$
(6.3)

Hence, combining Eqs. (6.2) and (6.3), we obtain

$$\begin{aligned} \sum _{n}c_{jn} ~\tau _{n} \cdot \tau _{i} = \delta _{ij} . \end{aligned}$$
(6.4)

The above expression can be conveniently expressed in matrix form by defining matrices C and T as

$$\begin{aligned}{}[C]_{jn}:= c_{jn} , \qquad [T]_{ni}:= \tau _{n}\cdot \tau _{i} . \end{aligned}$$
(6.5)

Then, Eq. (6.2) is rewritten as

(6.6)

which provides a formal expression for the coefficients \(c_{jn}\). We will not report here the expressions for the individual \(c_{jn}\), since they are rather long.Footnote 5 Following the above steps, these expressions can easily be derived using any conventional program capable of performing Lorentz algebra, such as the Mathematica packages Feyncalc [106] and Package-X [107].

Thus, in order to isolate the contributions of the form factors \(G_{j}(q^2,r^2,p^2)\), defined in Eq. (6.1), we contract Eq. (3.18) with the projectors of Eq. (6.3), which yield (Minkowski space)

$$\begin{aligned} {G}_{1}(q^{2},r^{2},p^{2})&= 1 + \sum _{i=1}^{5} {\mathcal {P}}_1 \cdot \bar{d_i}(q,r,p) - \sum _{i=1}^{4} d_i^{\,\scriptscriptstyle {sg}}(\mu ^2), \nonumber \\ {G}_{j}(q^{2},r^{2},p^{2})&= \sum _{i=1}^{5} {\mathcal {P}}_j\cdot \bar{d_i}(q,r,p), \qquad j=2,3,4, \end{aligned}$$
(6.7)

where we have used the fact that \(\tau _{1}^{\alpha \mu \nu } = {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }\) [see Eq. (2.14)], and have applied the definition of Eq. (6.2) on the first term of Eq. (3.18).

To proceed, we convert the expressions in Eq. (6.7) to Euclidean space and use hyper-spherical coordinates. In doing so, the form factors are re-expressed as functions of \(q^{2}\), \(r^{2}\), and the angle between the four-vectors q and r, \(\theta _{qr}\), i.e., we make the replacement \({G}_{i}(q^{2},r^{2},p^{2})\rightarrow {G}_{i}(q^{2},r^{2},\theta _{qr})\). For the propagators, ghost-gluon vertex, and value of the coupling, we use the results described in item (i) of Sect. 4.

Then, the numerical evaluation of the resulting expressions is performed on a grid of external momenta distributed logarithmically in the interval \(q^2,\,r^2\in [10^{-3}, 10^{3}]\, \text{ GeV}^2\) with 40 points in each dimension, while the angle \(\theta _{qr}\) is uniformly distributed in the interval \([0, \pi ]\) with 20 points. It turns out that in certain kinematic regions, particularly near the soft-gluon limits, the triple integrations require multiple evaluations of the integrand in order to achieve acceptable precision, while, away from the soft-gluon limits, a few evaluations suffice. Thus, to perform the integration efficiently, we employ an adaptive quadrature method, namely the Gauss–Kronrod implementation of [108]. Finally, all the needed interpolations in three variables are performed with B-splines [109].

6.1 Form factor hierarchy

We start our analysis of the general kinematics behavior of the form factors \(G_i(q^2,r^2,\theta _{qr})\) by comparing their general forms and relative sizes.

In Fig. 6 we show the \(G_i(q^2,r^2,\theta _{qr})\) for the specific value of \(\theta _{qr}=0\). For other values of \(\theta _{qr}\), the results are qualitatively similar, with moderate quantitative differences. In the top left panel, we highlight as a blue solid curve the soft-gluon limit (\(q=0\)) of \({G}_{1}(q^{2},r^{2},\theta _{qr})\), for which we recover exactly the \(L_{sg}(r^{2})\) of Fig. 4, in agreement with Eq. (2.22).

Fig. 6
figure 6

The vertex form factors \(G_{i}(q^{2},r^{2},\theta _{qr})\), with \(i= 1,2\) (top row) and \(i=3,4\) (bottom row) plotted as functions of the magnitudes of the momenta q and r, for the specific angle \(\theta _{qr}=0\). In the first panel, we highlight (blue curve) the soft-gluon limit (\(q=0\)), corresponding to the SDE solution for \(L_{sg}(r^{2})\) displayed in Fig. 4

Full size image

From Fig. 6, we make the following observations:

(i):

First, only the classical form factor, \(G_1(q^2,r^2,\theta _{qr})\), displays a divergence at the origin, namely the divergence discussed in Sect. 5 and quantified by Eq. (5.1). The remaining form factors are all found to be finite at the origin.

(ii):

Next, we note that the form factors \(G_{2,3,4}(q^2,r^2,\theta _{qr})\) are subleading in comparison to \(G_1(q^2,r^2,\theta _{qr})\), for most of the kinematic range. In particular, \(G_2(q^2,r^2,\theta _{qr}\)) is found to be the smallest of all, and positive through the entire range, while \(G_3(q^2,r^2,\theta _{qr}\)) and \(G_4(q^2,r^2,\theta _{qr}\)) have comparable magnitudes and opposite signs.

(iii):

In the soft-gluon limit, \(q = 0\) (as well as \(r = 0\) and \(p = 0\), by Bose symmetry), the magnitudes of the form factors \(G_{2,3,4}(0,r^2,\theta _{qr})\) become increasing functions of the remaining momentum, r. Therefore, for sufficiently large r, the \(G_{2,3,4}(0,r^2,\theta _{qr})\) become comparable in magnitude to \(G_{1}(0,r^2,\theta _{qr})\). In particular, at \(r = 5\) GeV the \(G_3\) and \(G_4\) reach values of 0.21 and \(-0.25\), respectively, which correspond to \(20\%\) and \(-25\%\) of the value of \(G_1\) at the same point. For larger r, these proportions increase further, such that \(G_{2,3,4}(0,r^2,\theta _{qr})\) become comparable in magnitude to the classical form factor. As has been discussed in [20] (see Sec. 6 and Fig. 7 therein), the enhancement of the \(G_{2,3,4}(0,r^2,\theta _{qr})\) may be interpreted as a finite remainder of a would-be collinear divergence, averted by the emergence of the nonperturbative gluon mass. Note finally that the above behavior does not invalidate the approximation given by Eq. (1.1), because, as \(q\rightarrow 0\), the associated basis elements \(\tau _{2,3,4}^{\alpha \mu \nu }\) vanish linearly in q.

6.2 Planar degeneracy

We next analyze the accuracy of the planar degeneracy approximation, i.e., Eq. (2.7), and consider whether this property can be generalized to the subleading form factors.

To that end, it is convenient to reparametrize the form factors \(G_i\) in terms of the variable \(s^2\) of Eq. (2.8), rather than the individual momenta q, r and p. This can be achieved by introducing two new angles, \(\alpha \) and \(\beta \), defined byFootnote 6

$$\begin{aligned} \cos \alpha := \frac{\sqrt{3}(r^2 - q^2)}{2 s^2} , \qquad \cos \beta := \frac{q^2 + r^2 - 2 p^2}{2 s^2} . \end{aligned}$$
(6.8)

Note that momentum conservation implies

$$\begin{aligned} \cos ^2\alpha + \cos ^2\beta \le 1 , \end{aligned}$$
(6.9)

i.e., the kinematically allowed range of \(\cos \alpha \) and \(\cos \beta \) is the unit disk, which is represented in gray in each of the panels of Fig. 7.

The form factors can then be expressed as \(G_i(s^2,\alpha ,\beta )\) through the inverse relations

$$\begin{aligned} q^2&= \frac{s^2}{3}(2 + \cos \beta - \sqrt{3}\cos \alpha ), \nonumber \\ r^2&= \frac{s^2}{3}(2 + \cos \beta + \sqrt{3}\cos \alpha ), \nonumber \\ \cos \theta _{qr}&= - \frac{1 + 2 \cos \beta }{\sqrt{(2 + \cos \beta )^2 - 3 \cos ^2\alpha }}. \end{aligned}$$
(6.10)

To facilitate the comparison between the different parametrizations of \(G_i\), we list below how some special kinematic limits are represented in the \((s^2,\alpha ,\beta )\) coordinate system:

(i):

The totally symmetric limit, \(q^2 = r^2 = p^2\), corresponds to the center of the disk, i.e., \(\cos \alpha =\cos \beta = 0\), and is represented by a red dot in each of the panels of Fig. 7.

(ii):

The soft-gluon limit, \(q = 0\), and its Bose symmetric counterparts \(r = 0\) and \(p = 0\) are given by

$$\begin{aligned}&q = 0 \quad \Leftrightarrow&\quad (\cos \alpha , \cos \beta ) = \left( \sqrt{3}/2,-1/2\right) , \nonumber \\&r = 0 \quad \Leftrightarrow&\quad (\cos \alpha , \cos \beta ) = - \left( \sqrt{3}/2,1/2\right) , \nonumber \\&p = 0 \quad \Leftrightarrow&\quad (\cos \alpha , \cos \beta ) = \left( 0,1\right) , \end{aligned}$$
(6.11)

which correspond to the vertices of an equilateral triangle inscribed in the unit circle. These points and the triangle they form are represented by blue dots and black lines, respectively, in each of the panels of Fig. 7.

Fig. 7
figure 7

The form factors \(G_i(s^2,\alpha ,\beta )\), shown as functions of the variables \(s^2\), \(\alpha \) and \(\beta \), defined in Eqs. (2.8) and (6.8)

Full size image

The \(G_i(s^2,\alpha ,\beta )\) are shown in Fig. 7 for general values of \(\alpha \) and \(\beta \) and selected values of s. Specifically, for the case of \(G_1(s^2,\alpha ,\beta )\), we show surfaces corresponding to \(s = 0.5 \) GeV (red), \(s = 1 \) GeV (green), \(s = 2 \) GeV (blue), and \(s = 5\) GeV (yellow). In the case of the subleading form factors, the dense overlap of the resulting surfaces makes their visual distinction difficult; we therefore show only two examples, \(s = 1 \) GeV and \(s = 5\) GeV.

On the top left panel of Fig. 7, we see clearly that for fixed s the classical form factor is rather flat, i.e., nearly independent of \(\alpha \) and \(\beta \). Hence, the approximate planar degeneracy property of Eq. (2.7) is verified at a high level of accuracy.

As for the subleading form factors, \(G_{2,3,4}(s^2,\alpha ,\beta )\), we note that the corresponding surfaces in Fig. 7 are flat for \(s = 1\) GeV, but not so for \(s = 5\) GeV. Instead, in the latter case, the corresponding surfaces increase markedly when one of the momenta vanishes. Evidently, this effect corresponds to the increase in the magnitudes of the \(G_{2,3,4}\) near the soft-gluon limit, already discussed in relation with Fig. 6. From this analysis, we conclude that planar degeneracy would be a poor approximation for the subleading form factors, except at \(s\lessapprox 1\) GeV.

Returning to the classical form factor, it is important to quantify the accuracy of the planar degeneracy approximation. To this end, we define the function

$$\begin{aligned} d(q^2,r^2,\theta _{qr}):= \frac{G_1(q^2,r^2,\theta _{qr}) - L_{sg}(s^2)}{G_1(q^2,r^2,\theta _{qr})}\times 100 \% , \nonumber \\ \end{aligned}$$
(6.12)

which measures in percentages the error made in approximating \(G_1(q^2,r^2,\theta _{qr})\) by \(L_{sg}(s^2)\). Note that, recalling Eq. (2.22), \(d(q^2,r^2,\theta _{qr})\) vanishes whenever one momentum is zero.

Fig. 8
figure 8

Error measure, \(d(q^2,r^2,\theta _{qr})\), defined in Eq. (6.12), for \(\theta _{qr} = 0\) (left), \(\theta _{qr} = 2\pi /3\) (center), and \(\theta _{qr} = \pi \) (right)

Full size image

The maximum error can be found using standard numerical methods and is given by \(d_{{\mathrm{\scriptscriptstyle max}}} = 17.5\%\). This value of error is attained at the symmetric point \(q = r = p = 2.0\) GeV, corresponding to \(\theta _{qr} = 2\pi /3\). For angles away from \(\theta _{qr} = 2\pi /3\), the error diminishes quickly, falling below \(10\%\) for most of the range. This can be seen clearly in Fig. 8, where \(d(q^2,r^2,\theta _{qr})\) is plotted for \(\theta _{qr} = 0\), \(\theta _{qr} = 2\pi /3\) and \(\theta _{qr} = \pi \).

To conclude, we note that the error \(d(q^2,r^2,\theta _{qr})\) in the planar degeneracy approximation is positive, apart from minor fluctuations in the deep infrared, as seen in Fig. 8. Hence, Eq. (2.13) tends to underestimate the value of \(G_1(q^2,r^2,\theta _{qr})\). This is evident on the left panel of Fig. 9, where \(G_1(s^2,\alpha ,\beta )\) is compared to the soft-gluon limit, \(L_{sg}(s^2)\), for 8 randomly chosen values of \(\alpha \) and \(\beta \). Evidently, in all cases, when \(s \gtrapprox 1.4\) GeV, the form factor \(G_1\) exceeds \(L_{sg}(s^2)\). The same behavior can be appreciated more generally on the right panel of Fig. 9, where \(G_1(q^2,r^2,\theta _{qr})\) (yellow) is seen to be above \(L_{sg}(s^2)\) (blue), for the representative angle \(\theta _{qr} = 0\) and values of \(q^2\) and \(r^2\) larger than about 1 GeV.

Fig. 9
figure 9

Left: Comparison of \(G_1(s^2,\alpha ,\beta )\), for 8 randomly chosen values of \(\alpha \) and \(\beta \), to the soft-gluon limit \(L_{sg}(s^2)\). The values of \(\alpha \) and \(\beta \) are given in radians in the legend. Right: Comparison between \(G_1(q^2,r^2,\theta _{qr})\) and \(L_{sg}(s^{2})\), where \(s^{2} = q^{2} + r^{2} + qr\cos \theta _{qr}\), for arbitrary \(q^{2}\) and \(r^{2}\), and the choice of angle \(\theta _{qr} = 0\). Note that in the soft-gluon limit (\(q\rightarrow 0\)) both surfaces become equal; the resulting curve corresponds to \(L_{sg}(r^2)\)

Full size image

6.3 Totally symmetric limit

Our final exercise is to specialize our results to the totally symmetric configuration, defined by the condition \(q^2 = r^2 = p^2:= Q^2\), where \(Q^2\) denotes the single momentum scale available. Note that this condition implies \(q\cdot r = r\cdot p = p\cdot q = - Q^2/2\), and \(\theta _{qr} = \theta _{rp} = \theta _{pq} = 2\pi /3\).

In this limit, the tensors \(\tau _i^{\alpha \mu \nu }(q,r,p)\) of Eq. (2.14) become linearly dependent, such that the tensor decomposition of \({\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)\) collapses to [13, 15, 18, 19]

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p)= & {} {{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2) \lambda _1^{\alpha \mu \nu }(q,r,p) \nonumber \\{} & {} + {{{\overline{\Gamma }}}}_2^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2) \lambda _2^{\alpha \mu \nu }(q,r,p) , \end{aligned}$$
(6.13)

where

$$\begin{aligned} \lambda _1^{\alpha \mu \nu }(q,r,p):= & {} {\overline{\Gamma }}_{\!0}^{\,\alpha \mu \nu }(q,r,p) , \qquad \lambda _2^{\alpha \mu \nu }(q,r,p) \nonumber \\:= & {} \frac{(q-r)^{\nu } (r-p)^{\alpha } (p-q)^{\mu }}{Q^2} . \end{aligned}$$
(6.14)

Then, it is straightforward to show that the form factor \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\), associated with the tree-level tensor structure, can be obtained through the projection [13, 15, 18, 19]

(6.15)

where

$$\begin{aligned} W^{\alpha \mu \nu }(q,r,p):= \lambda _1^{\alpha \mu \nu }(q,r,p) + \frac{1}{2}\lambda _2^{\alpha \mu \nu }(q,r,p) . \end{aligned}$$
(6.16)

The exact correspondence between the form factors \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}\) and \(G_i\) is obtained by using Eq. (6.15) in Eq. (2.4); it reads

$$\begin{aligned} {{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2) = G_1(Q^2) - G_3(Q^2) + G_4(Q^2)/4 , \end{aligned}$$
(6.17)

where we write \(G_i(Q^2,Q^2,Q^2)\rightarrow G_i(Q^2)\) for the symmetric limits of the form factors. Using for the \(G_i\) the results discussed in the previous subsections, we obtain for \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\) the blue continuous line shown on the left panel of Fig. 10.

Then we consider the effect of neglecting the subleading form factors, \(G_3\) and \(G_4\), in Eq. (6.17). In this case, we obtain the approximation

$$\begin{aligned} {{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2) \approx G_1(Q^2) , \end{aligned}$$
(6.18)

which is shown as a purple dotted line on the left panel of Fig. 10.

Lastly, we consider the prediction of the compact expression Eq. (1.1), noting that in the symmetric limit \(s^2\rightarrow 3Q^2/2\). Evidently, in this case

$$\begin{aligned} {{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2) \approx L_{sg}(3Q^2/2) , \end{aligned}$$
(6.19)

which leads to the result displayed as a black dot-dashed line on the left panel of Fig. 10.

Fig. 10
figure 10

Left: SDE result for \({\overline{\Gamma }}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\) obtained from Eq. (6.17) (blue continuous), compared to the two approximations given by Eqs. (6.18) and (6.19) (purple dotted and black dot-dashed, respectively). Right: Lattice data of [19, 79, 80] for \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\), compared to the SDE result combined with Eq. (6.19) (blue continuous line)

Full size image

From the results shown on the left panel of Fig. 10, we see that the approximation in Eq. (6.18) (purple dotted) overestimates the true value of \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\) (blue continuous), given by Eq. (6.17).

Quite remarkably, the approximation given in Eq. (6.19) (black dot-dashed), derived from Eq. (1.1), reproduces the full result to within \(3\%\). The exceptional accuracy of Eq. (6.19) is due the fact that the underestimation of \(G_1(Q^2)\) by \(L_{sg}(3Q^2/2)\), discussed in detail in Sect. 6.2, effectively captures the negative contribution to \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\), furnished by the term \(- G_3(Q^2)+G_4(Q^2)/4\) in Eq. (6.17); recall, from Fig. 6, that \(G_4\) is mostly negative.

This observation suggests that, at least in the symmetric limit, Eq. (1.1) approximates the full \({\overline{{\textrm{I}}\!\Gamma }}^{\alpha \mu \nu }(q,r,p)\) even more accurately than the \(L_{sg}(s^2)\) approximates the \(G_1(q^2,r^2,p^2)\), by effectively capturing part of the contribution of the subleading form factors.

Finally, on the right panel of Fig. 10 we show the lattice result for \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\) from [19, 79, 80] (points). Note that these data are normalized in the so-called “symmetric MOM scheme”, defined by the condition \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(\mu ^2) = 1\), with \(\mu = 4.3\) GeV. Then, on the same panel, we show as a blue continuous line the result of Eq. (6.19) after renormalization in the symmetric scheme.Footnote 7 Clearly, Eq. (6.19) approximates the lattice results quite well, with an error of less than \(10\%\) for most of the range, which increases to \(22\%\) at \(r = 0.6\) GeV. As is evident from the agreement between \({{{\overline{\Gamma }}}}_1^{\,{\mathrm{\scriptscriptstyle sym}}}(Q^2)\) and \(L_{sg}(3Q^2/2)\) on the left panel, the error with respect to the lattice originates from the truncation of the SDE, rather than from the use of the compact approximation given by Eq. (1.1).

7 Conclusions

We have presented an extensive study of the transversely-projected three-gluon vertex by means of the SDE that determines its momentum evolution, making ample use of dynamical ingredients obtained from large-volume lattice simulations. The focal point of this investigation is the notable property of planar degeneracy: after a judicious choice of the tensor basis, the classical form factor of the vertex depends predominantly on a single kinematic variable, which represents a plane in the space spanned by \(q^2\), \(r^2\), and \(p^2\). Our SDE-based approach affords a valuable vantage point on the technical details surrounding this special property, establishing its range of validity and degree of accuracy, for a particularly wide range of kinematic configurations. In fact, our analysis reveals that the planar degeneracy persists to a high degree of accuracy for general kinematics, and in particular for configurations that deviate completely from the bisectoral limit (\(p^2 = r^2\)), considered in [20].

Of central importance in the present study is the simple equation given by Eq. (1.1), which leads to a serious reduction of the technical effort required when dealing with the three-gluon vertex in nonperturbative computations. The relation given in Eq. (1.1) emerges by combining the planar degeneracy with the observation that the classical form factor is considerably larger than all others. The component \(L_{sg}\) appearing in Eq. (1.1) corresponds to the form factor of the soft-gluon limit, a well-known quantity from a variety of lattice studies, and serves as a “benchmark” for the veracity of the SDE results.

The SDE analysis carried out probes the validity of Eq. (1.1), and uses it in order to obtain a plethora of related results, which, in turn, demarcate its applicability. Our findings confirm the previous results found by [29]: the classical form factor clearly dominates over the other three for a wide range of kinematics, with the exception of the region approaching the soft-gluon limit. However, due to the vanishing of the corresponding basis elements in this limit, Eq. (1.1) represents an excellent approximation for all momenta.

One may wonder whether there exists a basis in which the planar degeneracy becomes exact. To be sure, it is always possible to construct such a basis, by absorbing the residual dependence of the \({G}_i(q^2,r^2,p^2)\) on the other two variables into the basis elements themselves, through

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{\,\alpha \mu \nu }(q,r,p) = \sum _{i=1}^4 {{\widetilde{G}}}_i(s^2) \, {{{\widetilde{\tau }}}}_{i}^{\alpha \mu \nu }(q,r,p), \end{aligned}$$
(7.1)

with

$$\begin{aligned} {{{\widetilde{\tau }}}}_{i}^{\alpha \mu \nu }(q,r,p):= {G}_i(q^2,r^2,p^2) \, {{\widetilde{G}}}^{-1}(s^2) \, \tau _1^{\alpha \mu \nu }(q,r,p).\nonumber \\ \end{aligned}$$
(7.2)

Nonetheless, such a basis would be of no practical advantage, since it can only be constructed “a-posteriori”, namely after the form factors have been exactly determined. The truly remarkable observation is that there exists a “simple” basis containing the classical tensor as an element, which exhibits, in a natural way, a rather accurate manifestation of planar degeneracy.

As mentioned in Sect. 3, the SDE for the three-gluon vertex that we use is obtained from the 3PI three-loop effective action. The appropriate variation of this action yields also the SDEs of the gluon and ghost propagator, as well and the SDE of the ghost-gluon vertex. All these equations are dynamically coupled to each other, and, from a strictly SDE-based point of view, they must be solved simultaneously, as a coupled system comprised by numerous integral equations. Instead, in our approach we treat the SDE of the three-gluon vertex in isolation, using lattice ingredients for the gluon and ghost propagators. Evidently, what one is tacitly assuming when adopting this approach is that the lattice results “solve” the corresponding SDEs to a very good approximation; that this is indeed so has been shown in detail in [30], by solving the SDEs and comparing the solutions with the lattice results. We have therefore used the coincidence between 3PI SDEs and lattice, found in [30], as our basic working hypothesis.

Finally, it would be interesting to investigate whether some generalized form of planar degeneracy holds for the transversely-projected four-gluon vertex [110,111,112,113,114,115,116,117,118,119,120], which, just as the three-gluon vertex, is fully Bose-symmetric. Such a study may be particularly timely, given that lattice simulations are commencing to probe the basic structures of this vertex [121].