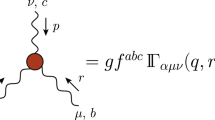Four-gluon vertex in collinear kinematics

Abstract

To date, the four-gluon vertex is the least explored component of the QCD Lagrangian, mainly due to the vast proliferation of Lorentz and color structures required for its description. In this work we present a nonperturbative study of this vertex, based on the one-loop dressed Schwinger–Dyson equation obtained from the 4PI effective action. A vast simplification is brought about by resorting to “collinear” kinematics, where all momenta are parallel to each other, and by appealing to the charge conjugation symmetry in order to eliminate certain color structures. Out of the fifteen form factors that comprise the transversely-projected version of this vertex, two are singled out and studied in detail; the one associated with the classical tensorial structure is moderately suppressed in the infrared regime, while the other diverges logarithmically at the origin. Quite interestingly, both form factors display the property known as “planar degeneracy” at a rather high level of accuracy. With these results we construct an effective charge that quantifies the strength of the four-gluon interaction, and compare it with other vertex-derived charges from the gauge sector of QCD.

1 Introduction

In recent years, our understanding of nonperturbative QCD has advanced considerably thanks to the systematic scrutiny of the fundamental correlation functions (Green’s functions) of the theory. This ongoing exploration proceeds through continuous studies based on functional methods, such as Schwinger–Dyson equations (SDEs) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24] or the function renormalization group [25,26,27,28,29,30,31,32,33,34],¹ and by means of gauge-fixed lattice simulations [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55]. In particular, a great deal of information is available on the two-point sector of QCD (propagators of the gluon, ghost, and quark fields), as well as the three-point sector (ghost-gluon, three-gluon, and quark-gluon vertices); for related reviews see  [1,2,3,4,5,6,7,8,9, 29, 55,56,57,58]. This knowledge, in turn, enables the reliable determination of observables built out of these functions, and allows for the detailed scrutiny of underlying physical mechanisms, associated with the emergence of fundamental mass scales, formation of bound states, and confinement  [5,6,7,8, 30, 59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75].

Instead, the nonperturbative aspects of the four-gluon vertex, to be denoted by ${\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }$, are relatively poorly known [23,24,25, 76,77,78,79,80]; for perturbative studies, see [81,82,83,84,85,86,87,88]. The main reason for this limitation is the large proliferation of Lorentz and color structures, which makes the treatment of this vertex exceedingly cumbersome in the continuum, and overly costly on the lattice. Since this vertex is inextricably connected with all other Green’s functions through the coupled functional equations that govern their evolution, it is certainly desirable to improve our understanding of its dynamics.

Certain new insights gained from recent studies of the three-gluon vertex appear particularly promising for determining the leading nonperturbative features of the four-gluon vertex. In particular, the logistics of the three-gluon vertex are greatly simplified due to the property known as “planar degeneracy”: with an error of less than 10%, the form factor associated with the classical tensor is the same for all momentum configurations lying on a given plane [58, 89,90,91]. Even though the dynamical reason that enforces this feature is not fully understood, its manifestation hinges crucially on the appropriate exploitation of the Bose symmetry of the three-gluon vertex, a symmetry shared also by the four-gluon vertex. It is, therefore, possible that the planar degeneracy may be a property of the four-gluon vertex, leading to a great simplification of practical computations. Parallel to these developments, lattice simulations have been carrying out exploratory studies of the four-gluon vertex in simplified kinematics [92,93,94], and are expected to access a wider array of momentum configurations in the near future.

In the present work we study the quenched four-gluon vertex (no dynamical quarks) in the context of the one-loop SDE derived from the four-particle irreducible (4PI) effective action [95,96,97,98,99] at four loops [100, 101]. Note that, within this formalism, the extremization of the n-loop n-PI effective action with respect to the m-point correlation functions ($m \le n$) generates the corresponding equations of motions (SDEs), which are expressed in terms of $(n-m+1)$-loop diagrams [97, 100, 101]. We emphasize that our analysis does not treat the entire system of coupled SDEs that govern the propagators and vertices entering in the SDE of the four-gluon vertex: instead, we consider the four-gluon SDE in isolation, using lattice results as inputs for all other dynamical components.

The focal point of our attention is the transversely projected four-gluon vertex, $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$, which is precisely the one simulated on the lattice in the Landau gauge [92,93,94], and appears in the majority of physical applications [80, 102, 103]. The analysis is restricted to the case of the “collinear” kinematics, where all vertex momenta are parallel to each other, or, equivalently, proportional to a single momentum p (i.e., $p_i=x_i p$). This kinematic choice, together with the proper exploitation of the charge conjugation symmetry, drastically reduces the tensorial structure of $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$: only 15 elements, $t_{i,\mu \nu \rho \sigma }^{abcd}$, are required for the full description of its Lorentz and color content, with the associated form factors denoted by $G _{i}$ ($i=1,\ldots ,15$). Note that this basis contains as one of its elements the transversely projected classical (tree-level) tensor of the four-gluon vertex; in particular, $t_1 = \overline{\Gamma }_{\!\!0}$.

There is an additional simplification that we will incorporate in our study, prompted by the following two observations. First, the elements $t_1$, $t_2$, and $t_3$ satisfy a special orthogonality condition with respect to the rest of the basis. Second, they depend only on p, being independent of the variables $x_i$. These facts reduce significantly the algebraic complexity of the problem, facilitating the determination of the attendant form factors $G _{1}, G _{2}$, and $G _{3}$; we therefore focus exclusively on this special subset of contributions.

In the 4PI formalism, all propagators and vertices appearing in the one-loop diagrams comprising the SDE that governs the evolution of the $G_i$ are fully dressed, including the four-gluon vertices. This converts the SDE into an integral equation, involving the unknown function $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$ evaluated in different kinematic configurations. The approximation used for dealing with this complication is to assume that the tree-level form factor $G_1$ is dominant, and that it satisfies planar degeneracy, in exact analogy to its three-gluon vertex counterpart.

The results of our study may be summarized as follows:

• (i) Under the approximations mentioned above, the form factor $G _{2}$ vanishes identically.

• (ii) $G _{1}$ and $G _{3}$ are computed for several collinear configurations. We find that $G _{1}$ is suppressed in the infrared with respect to its tree-level value, $G_1^{(0)} =1$, reaching a finite value at the origin, while $G _{3}$ displays a logarithmic divergence in the deep infrared, originating from the ghost loops.

• (iii) For momenta below 1 GeV, our results for $G _{1}$ are compatible with planar degeneracy to within 1.7$\%$. In the case of $G_3$, a similar tendency is observed, albeit with a lesser degree of accuracy.

• (iv) With the help of the $G _{1}$ computed for an extensive set of collinear configurations, we construct a “band” of effective charges, $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(p)$, which may be used to quantify the strength of the four-gluon interaction. The $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(p)$ is then compared with the effective charges $\alpha _{\mathrm{{\scriptscriptstyle 3g}}}(p)$ and $\alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)$, obtained from the soft-gluon limits of the three- and ghost-gluon vertices, respectively. For momenta below 1.5 GeV, we find the clear hierarchy $\alpha _{\mathrm{{\scriptscriptstyle 3g}}}(p)< \alpha _{\mathrm{{\scriptscriptstyle 4g}}}(p) < \alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)$, in agreement with earlier results presented in [8, 25].

The article is organized as follows. In Sect. 2 we summarize the general features of ${\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }$ in collinear configurations. In Sect. 3 we show how the charge conjugation symmetry prohibits the presence of color tensors of the type $f^{abx} d^{cdx}$. In Sect. 4 we define the Lorentz tensor basis for collinear configurations, and determine the projectors that allow us to extract the attendant form factors. In Sect. 5 we present the SDE governing the evolution of ${\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }$, derived from the 4PI effective action at the four-loop level, and its renormalization. In Sect. 6, the SDE is solved for general collinear configurations, and the form factors $G_{1,3}$ are determined and analyzed. In Sect. 7 we compare our results to previous continuum studies, and comment on the impact of the three-gluon vertex in the four-gluon SDE. In Sect. 8 we present an analytic proof of the ultraviolet finiteness of the form factors $G_{1,3}$, which complements our numerical findings. Next, in Sect. 9, we compute the four-gluon effective charge. Finally, our conclusions are discussed in Sect. 10, and certain technical points are summarized in two Appendices.

Fig. 1

Upper panel: Diagrammatic representations of the full four-gluon Green’s function, $\mathcal {G}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4)$, separated into the connected, $\mathcal {\widetilde{C}}^{abcd}_{\mu \nu \rho \sigma }$, and disconnected parts. Lower panel: Schematic decomposition of the amputated four-gluon Green’s function, $\mathcal {C}^{abcd}_{\mu \nu \rho \sigma }$, into the 1PI vertex, $-ig^2{\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4)$, and the 1PR terms of the type ${\textrm{I}}\!\Gamma ^{ade}_{\mu \sigma \lambda } \Delta ^{\lambda \beta } {\textrm{I}}\!\Gamma ^{bce}_{\nu \rho \beta }$ and crossed contributions

2 Four-gluon vertex in collinear kinematics

The starting point is the definition of the four-gluon correlation function as the vacuum expectation value of the time-ordered product of four SU(3) gauge fields, $\widetilde{A}^a_\mu (p)$, in momentum space,

$$\begin{aligned}&\mathcal {G}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4) \nonumber \\&\quad = \langle 0 \vert T [\widetilde{A}^a_\mu (p_1) \widetilde{A}^b_\nu (p_2) \widetilde{A}^c_\rho (p_3)\widetilde{A}^d_\sigma (p_4)] \vert 0\rangle , \end{aligned}$$

(2.1)

with $p_1+p_2+p_3+p_4 = 0$. The diagrammatic representation of $\mathcal {G}^{abcd}_{\mu \nu \rho \sigma }$, shown in the upper panel of Fig. 1, distinguishes between connected and disconnected contributions. The connected Green’s function, denoted by $\mathcal {{\widetilde{C}}}^{abcd}_{\mu \nu \rho \sigma }$, has the general form

$$\begin{aligned}&\mathcal {{\widetilde{C}}}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4)\nonumber \\&\quad = \Delta ^{\mu '}_{\mu }(p_1) \Delta ^{\nu '}_{\nu }(p_2)\Delta ^{\rho '}_{\rho }(p_3)\Delta ^{\sigma '}_{\sigma }(p_4)\nonumber \\&\qquad \times \mathcal {C}^{abcd}_{\mu '\nu '\rho '\sigma '}(p_1,p_2,p_3,p_4), \end{aligned}$$

(2.2)

where $\mathcal {C}^{abcd}_{\mu \nu \rho \sigma }$ is the amputated vertex. $\mathcal {C}^{abcd}_{\mu \nu \rho \sigma }$ may be further separated into one-particle irreducible (1PI) and one-particle reducible (1PR) contributions, namely

$$\begin{aligned} \mathcal {C}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4)&= -ig^2\underbrace{ {\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4)}_{\text {1PI}} \,\nonumber \\&\quad -i \underbrace{{\textrm{I}}\!\Gamma ^{ade}_{\mu \sigma \lambda }\Delta ^{\lambda \beta } {\textrm{I}}\!\Gamma ^{bce}_{\nu \rho \beta } + \textrm{crossed}}_{\text {1PR}}, \end{aligned}$$

(2.3)

where $\Delta _{\mu \nu }^{ab}(q)=-i\delta ^{ab}\Delta _{\mu \nu }(q)$ denotes the gluon propagator, and ${\textrm{I}}\!\Gamma ^{abc}_{\alpha \beta \gamma }(q,r,t)$ the full three-gluon vertex [see lower panel of Fig. 1].

In the Landau gauge that we use from now on and throughout this work, the gluon propagator has the form

$$\begin{aligned} \Delta _{\mu \nu }(q) = \Delta (p^2) P_{\mu \nu }(q), \qquad P_{\mu \nu }(q) = g_{\mu \nu } - q_{\mu } q_{\nu }/q^2, \end{aligned}$$

(2.4)

it is natural to define, at the level of Eq. (2.2),

$$\begin{aligned}&\widetilde{\mathcal {C}}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4) \nonumber \\&\quad =\Delta (p^2_1) \Delta (p^2_2) \Delta (p^2_3)\Delta (p^2_4)\, \overline{\mathcal {C}}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4), \end{aligned}$$

(2.5)

where

$$\begin{aligned}&\overline{\mathcal {C}}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4) \nonumber \\&\quad :=P^{\mu '}_{\mu }(p_1) P^{\nu '}_{\nu }(p_2)P^{\rho '}_{\rho }(p_3)P^{\sigma '}_{\sigma }(p_4)\,\nonumber \\&\qquad \times \mathcal {C}^{abcd}_{\mu '\nu '\rho '\sigma '}(p_1,p_2,p_3,p_4), \end{aligned}$$

(2.6)

is the transversely-projected amputated vertex. Substituting Eq. (2.3) into Eq. (2.6), we obtain (Landau gauge)

$$\begin{aligned} \overline{\mathcal {C}}^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4)&= -ig^2 \overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4) \nonumber \\&\quad -i\left\{ {\overline{{\textrm{I}}\!\Gamma }}^{ade}_{\mu \sigma \lambda } \Delta ^{\lambda \beta } {\overline{{\textrm{I}}\!\Gamma }}^{bce}_{\nu \rho \beta } + \textrm{crossed}\, \right\} , \end{aligned}$$

(2.7)

where

$$\begin{aligned}&\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4) = P^{\mu '}_\mu (p_1)P^{\nu '}_\nu (p_2)P^{\rho '}_\rho (p_3)P^{\sigma '}_\sigma (p_4)\nonumber \\&\quad \times {\textrm{I}}\!\Gamma ^{abcd}_{\mu '\nu '\rho '\sigma '}(p_1,p_2,p_3,p_4), \end{aligned}$$

(2.8)

is the transversely-projected 1PI four-gluon vertex, and

$$\begin{aligned} {\overline{{\textrm{I}}\!\Gamma }}^{abc}_{\alpha \beta \gamma }(q,r,t) = P^{\alpha '}_\alpha (q)P^{\beta '}_\beta (r)P^{\gamma '}_\gamma (t) {\textrm{I}}\!\Gamma ^{abc}_{\alpha '\beta '\gamma '}(q,r,t),\nonumber \\ \end{aligned}$$

(2.9)

is the transversely-projected three-gluon vertex.

In general kinematics, the vertices ${\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }$ and $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$ have a proliferation of tensorial and color structures, which give rise to a large number of form factors. In the present work we restrict ourselves to the nonperturbative study of $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$ in collinear configurations. This type of configurations are defined through a single four-momentum p, and all vertex momenta $p_i$ $(i=1,2,3,4)$ are proportional to it, namely

$$\begin{aligned} p_i = x_i \,p , \end{aligned}$$

(2.10)

where the parameters $x_i$ are real, and satisfy $x_1+x_2+x_3+x_4 =0$ due to four-momentum conservation.

The reason for this particular kinematic choice is twofold. First, the tensorial structure of the four-gluon vertex simplifies enormously, rendering the resulting dynamical equations completely tractable. Second, it allows for the direct comparison with contemporary lattice simulations [92,93,94], where these configurations are employed as benchmarks in the initial stages.

Note, in fact, that, while the SDEs access directly the vertex ${\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }$ or $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$, the lattice computes the full $\mathcal {G}^{abcd}_{\mu \nu \rho \sigma }$. When all momenta are collinear, the disconnected contributions may be eliminated simply by imposing the additional restriction $x_i + x_j\ne 0$, which makes propagator-like transitions impossible, due to the induced momentum non-conservation. Alternatively, appropriate projectors may be chosen [see Sect. 4], which remove the disconnected contributions from the simulation without restricting the values of the $x_i$. As for the 1PI terms, when Eq. (2.10) is fulfilled, all three-gluon vertices in the 1PR diagrams are of the form ${\textrm{I}}\!\Gamma _{\alpha \beta \gamma } (q)= A (q^2)(q_{\alpha }g_{\beta \gamma } + q_{\beta }g_{\alpha \gamma } + q_{\gamma }g_{\alpha \beta }) + B (q^2)q_{\alpha } q_{\beta }q_{\gamma }$, and therefore ${\overline{{\textrm{I}}\!\Gamma }}_{\alpha \beta \gamma } (q) =0$. Thus, the term in the curly bracket of Eq. (2.7) vanishes, and one finally isolates $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$ on the lattice [78].

We end this section by reporting the tree-level expressions of ${\textrm{I}}\!\Gamma ^{abcd}_{\mu \nu \rho \sigma }$ and $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$, namely

$$\begin{aligned} \Gamma ^{abcd}_{\!0\,\mu \nu \rho \sigma }= & {} f^{adx}f^{cbx}\left( g_{\mu \rho }g_{\nu \sigma }-g_{\mu \nu }g_{\rho \sigma }\right) \nonumber \\{} & {} +f^{abx}f^{dcx}\left( g_{\mu \sigma }g_{\nu \rho }-g_{\mu \rho }g_{\nu \sigma }\right) \nonumber \\{} & {} +f^{acx}f^{dbx}\left( g_{\mu \sigma }g_{\nu \rho }-g_{\mu \nu }g_{\rho \sigma }\right) , \end{aligned}$$

(2.11)

where $f^{abc}$ is the totally antisymmetric structure constants of any Lie group, and

$$\begin{aligned}{} & {} \overline{\Gamma }_{\!\!0~\!\!\mu \nu \rho \sigma }^{abcd}(p_{1},p_{2},p_{3},p_{4})\nonumber \\{} & {} \quad =P^{\mu '}_\mu (p_1)P^{\nu '}_\nu (p_2)P^{\rho '}_\rho (p_3)P^{\sigma '}_\sigma (p_4) \Gamma ^{abcd}_{\!0\,\mu '\!\nu '\!\rho '\!\sigma '} . \end{aligned}$$

(2.12)

3 Color structure and charge conjugation symmetry

It is well-known that the color structure of the four-gluon vertex is comprised by the appropriate combinations of three basic elements common to any Lie group, namely $f^{abc}$, the totally symmetric $d^{abc}$, and the identity matrix $\delta ^{ab}$. The 15 combinations built out of these elements, valid for any Lie group, are [78, 81]

$$\begin{aligned} f^{abx}f^{cdx},\qquad d^{abx}d^{cdx}, \qquad f^{abx}d^{cdx} , \qquad \delta ^{ab} \delta ^{cd} . \end{aligned}$$

(3.1)

and their permutations.

We next restrict the discussion to the SU(N) groups. In that case, the number of possible combinations is reduced from 15 to 9, thanks to 6 identities, valid for a general SU(N) group [104], whose derivation we review below.

The generators of the SU(N) group are traceless hermitian matrices, $t^a_r$, where the color index $a = 1, \ldots ,\, \text {dim}(G)$, with $\text {dim}(G)=N^2-1$ the dimension of the group, and r specifies the representation. The $t^a_r$ satisfy the commutation relations

$$\begin{aligned} {[}t^a_r,t^b_r]=if^{abc}t^c_r , \end{aligned}$$

(3.2)

and we define the Dynkin index, $d_r$, by

$$\begin{aligned} \text {Tr}(t^a_r t^b_r ) = d_r \delta ^{ab} . \end{aligned}$$

(3.3)

The symmetric color structures, $d^{abc}$, are defined by

$$\begin{aligned} d^{abc}:= 2 \text {Tr}\left( t^a\left\{ t^b, t^c\right\} \right) , \end{aligned}$$

(3.4)

where $t^a:= t^a_f$ are the SU(N) generators in the fundamental representation. For SU(3), $t^a = \lambda ^a/2$, where $\lambda ^a$ are the Gell–Mann matrices. In this representation, the anticommutator of the generators can be written as²

$$\begin{aligned} \left\{ t^a, t^b\right\} = \frac{2 d_f}{\text {dim}(f)} \delta ^{ab}\mathbb {1}_{\text {dim}(f)} + \frac{1}{2d_f} d^{abc}t^c , \end{aligned}$$

(3.5)

where $\text {dim}(r)$ is the dimension of the representation r, and $\mathbb {1}_{\text {dim}(r)}$ is the $\text {dim}(r)\times \text {dim}(r)$ identity matrix.

Then, we recall the identities

$$\begin{aligned}&\left[ C,\left[ A,B\right] \right] = \left\{ B, \left\{ C, A\right\} \right\} - \left\{ A, \left\{ B, C\right\} \right\} , \nonumber \\&\left[ \left\{ A,B\right\} ,C\right] + \left[ \left\{ B,C\right\} ,A\right] + \left[ \left\{ C,A\right\} ,B\right] = 0, \end{aligned}$$

(3.6)

valid for any three matrices A, B, and C. Next, we take $A = t^a$, $B=t^b$, and $C = t^c$, and substitute Eqs. (3.2) and (3.5) into Eq. (3.6). Multiplying the results by $t^d$, taking the trace, and using Eq. (3.3), yields

$$\begin{aligned}{} & {} f^{abx} f^{cdx} \nonumber \\{} & {} \quad = \frac{4d_f}{\text {dim}(f)}[ \delta ^{ac}\delta ^{bd} - \delta ^{ad}\delta ^{bc}] \nonumber \\{} & {} \qquad + \frac{1}{4 d^2_f}[d^{acx}d^{dbx} - d^{adx} d^{bcx}] , \nonumber \\{} & {} \qquad f^{abx}d^{cdx} + f^{acx}d^{dbx} + f^{adx}d^{bcx} = 0 . \end{aligned}$$

(3.7)

The above result can also be expressed in terms of the Casimir eigenvalue, $C_r$, defined for a general representation by

$$\begin{aligned} t^a_r t^a_r = C_r \mathbb {1}_{\text {dim}(r)} . \end{aligned}$$

(3.8)

To this end, we employ the relation

$$\begin{aligned} C_r = \frac{\text {dim}(G)}{\text {dim}(r)}d_r , \end{aligned}$$

(3.9)

which allows us to recast the first line of Eq. (3.7) as

$$\begin{aligned} f^{abx} f^{cdx}= & {} \frac{4C_f}{\text {dim}(G)}[ \delta ^{ac}\delta ^{bd} - \delta ^{ad}\delta ^{bc}] \nonumber \\{} & {} + \frac{\text {dim}^2(G)}{4 C_f^2 \text {dim}^2(f) }[d^{acx}d^{dbx} - d^{adx} d^{bcx}] .\nonumber \\ \end{aligned}$$

(3.10)

Setting $d_f = 1/2$, $\text {dim}(f) = N$, $\text {dim}(G) = N^2-1$, and $C_f = (N^2-1)/(2N)$, as appropriate for the fundamental representation of SU(N), we obtain

$$\begin{aligned}&f^{abx} f^{cdx} = \frac{2}{N}[ \delta ^{ac}\delta ^{bd} - \delta ^{ad}\delta ^{bc}] + d^{acx}d^{dbx} - d^{adx} d^{bcx} , \nonumber \\&f^{abx}d^{cdx} + f^{acx}d^{dbx} + f^{adx}d^{bcx} = 0 . \end{aligned}$$

(3.11)

Then, from the total (anti-)symmetries of $d^{abc}$ and $f^{abc}$, one obtains two additional linearly independent permutations of each line of Eq. (3.11). Thus, in total Eq. (3.11) yields 6 constraints.³

Moreover, for $N = 3$, the additional identity [104]

$$\begin{aligned}{} & {} \delta ^{ab}\delta ^{cd} + \delta ^{ac}\delta ^{bd} + \delta ^{ad}\delta ^{bc} \nonumber \\{} & {} \quad = 3[d^{abx}d^{cdx} + d^{acx}d^{bdx} + d^{adx}d^{bcx}] , \end{aligned}$$

(3.12)

reduces the number of independent color tensors to 8.

It turns out that the invariance of the theory under charge conjugation prohibits the presence of terms of the type fd, thus eliminating 3 additional color combinations. In earlier works [8, 76, 105], and under special assumptions, such terms have been shown to vanish; however, no exact proof justifying their complete omission has been presented in the literature.

The general implications of charge conjugation symmetry for the Green’s functions of a pure SU(N) theory were worked out in [106]. Specifically, a Green’s function with n color indices, $\Gamma ^{a_1 a_2\ldots a_n}$ (we suppress Lorentz indices and momenta), must satisfy

$$\begin{aligned}&f^{ba_1x}\Gamma ^{x a_2\ldots a_n} + f^{ba_2x}\Gamma ^{a_1 x\ldots a_n} + \cdots + f^{ba_nx}\Gamma ^{a_1 a_2\ldots x} = 0 , \nonumber \\&A^{a_1 b_1} A^{a_2 b_2} \ldots A^{a_n b_n} \Gamma ^{b_1 b_2\ldots b_n}= \Gamma ^{a_1 a_2\ldots a_n} . \end{aligned}$$

(3.13)

In the above equation, $A^{ab}$ is a certain color matrix that conjugates the charges; its concrete form will not be necessary here. It suffices to state the following properties of $A^{ab}$:

• {1} $A^{ab} \not \propto \delta ^{ab}$, i.e., $A^{ab}$ is not proportional to the diagonal matrix.

• {2} A is an orthogonal matrix, i.e., $A^\intercal = A^{-1}$, where $\intercal$ denotes matrix transposition;

• {3} $A^{aa^\prime }A^{bb^\prime }A^{cc^\prime } f^{a^\prime b^\prime c^\prime } = f^{abc}$;

• {4} $A^{aa^\prime }A^{bb^\prime }A^{cc^\prime } d^{a^\prime b^\prime c^\prime } = -d^{abc}$.

To see how Eq. (3.13) can then be used to constrain the color structures of vertex functions, consider first the simpler case of the three-gluon vertex, ${\textrm{I}}\!\Gamma _{\alpha \mu \nu }^{abc}(q,r,t)$. The most general structure possible is given by [81]

$$\begin{aligned} {\textrm{I}}\!\Gamma _{\alpha \mu \nu }^{abc}(q,r,t) = f^{abc} V_{\alpha \mu \nu }(q,r,t) + d^{abc} U_{\alpha \mu \nu }(q,r,t) , \nonumber \\ \end{aligned}$$

(3.14)

where the tensors $V_{\alpha \mu \nu }(q,r,t)$ and $U_{\alpha \mu \nu }(q,r,t)$ may be decomposed in an appropriate basis.

Using the Jacobi identity and the second line of Eq. (3.11), it is easy to verify that the expression in Eq. (3.14) satisfies the first line of Eq. (3.13). Then, substituting Eq. (3.14) into the second line of Eq. (3.13) and using properties {3} and {4}, we obtain

$$\begin{aligned} d^{abc} U_{\alpha \mu \nu }(q,r,t) = 0 \qquad \Longrightarrow \qquad U_{\alpha \mu \nu }(q,r,t) = 0.\nonumber \\ \end{aligned}$$

(3.15)

Hence, charge conjugation symmetry implies that the three-gluon vertex is proportional to $f^{abc}$ only.

Let us now consider the four-gluon vertex. From property {2} follows that

$$\begin{aligned} A^{xa}A^{xb} = A^{ax}A^{bx} = \delta ^{ab} , \end{aligned}$$

(3.16)

and thus

$$\begin{aligned} f^{abx}f^{cdx} = f^{abx}\delta ^{xy}f^{cdy} = f^{abx}(A^{zx}A^{zy})f^{cdy} . \end{aligned}$$

(3.17)

Hence, multiplying by $A^{a a^\prime }A^{b b^\prime }A^{c c^\prime }A^{d d^\prime }$, we find

$$\begin{aligned}{} & {} A^{a a^\prime }A^{b b^\prime }A^{c c^\prime }A^{d d^\prime } f^{abx}f^{cdx} \nonumber \\{} & {} \quad = A^{a a^\prime }A^{b b^\prime }A^{c c^\prime }A^{d d^\prime } f^{abx}(A^{zx}A^{zy})f^{cdy} \nonumber \\{} & {} \quad = (A^{a a^\prime }A^{b b^\prime }A^{zx} f^{a^\prime b^\prime x})( A^{c c^\prime }A^{d d^\prime }A^{zy}f^{c^\prime d^\prime y})\nonumber \\{} & {} \quad =f^{abz}f^{cdz} , \end{aligned}$$

(3.18)

where we used property {3} to obtain the last equality.

Similarly, using property {2}, we get

$$\begin{aligned} A^{a a^\prime }A^{b b^\prime }A^{c c^\prime }A^{d d^\prime } \delta ^{a^\prime b^\prime } \delta ^{c^\prime d^\prime } = \delta ^{ab}\delta ^{cd} . \end{aligned}$$

(3.19)

Finally, using property {4}, it is straightforward to show that

$$\begin{aligned} A^{a a^\prime }A^{b b^\prime }A^{c c^\prime }A^{d d^\prime } d^{a^\prime b^\prime e} d^{c^\prime d^\prime e}= & {} d^{abe} d^{cde} , \nonumber \\ A^{a a^\prime }A^{b b^\prime }A^{c c^\prime }A^{d d^\prime } f^{a^\prime b^\prime e} d^{c^\prime d^\prime e}= & {} - f^{abe} d^{cde} . \end{aligned}$$

(3.20)

Combining the transformation properties given by Eqs. (3.18),(3.19) and (3.20) into the second line of Eq. (3.13), one can easily show that the form factors of the color structures of the form fd must all vanish.

Then, on account of Eq. (3.12), the number of independent color structures in the SU(3) four-gluon vertex is reduced to 5, namely

$$\begin{aligned} f^{abx}f^{cdx}; \quad f^{acx}f^{bdx}; \quad \delta ^{ab} \delta ^{cd} ; \quad \delta ^{ac} \delta ^{bd} ; \quad \delta ^{ad} \delta ^{bc}. \nonumber \\ \end{aligned}$$

(3.21)

For $N>3$, an additional color structure is allowed, which may be chosen to be $f^{adx}f^{bcx}$.

4 Tensor basis and projectors

In this section we discuss the tensorial basis that will be used for describing the four-gluon vertex in collinear configurations, and the projectors that allow us to extract particular form factors.

From this point on, we will employ the short-hand notation

$$\begin{aligned} A(x,p):= A(x_1p,x_2p,x_3p,x_4p) , \end{aligned}$$

(4.1)

to indicate a quantity A (with Lorentz and color indices, as well as scalar form factors) in general collinear kinematics. In the case of a specific configuration, i.e., $(1,1,1,-3)$, we will be reverting to the explicit notation, i.e., $A(p,p,p,-3p)$.

First, notice that in collinear configuration one can form 10 Lorentz tensors with four indices and one independent momentum [25, 85], covering all linearly independent combinations of the forms

$$\begin{aligned}{} & {} g^{\mu \nu }g^{\rho \sigma }\;\text{(3 } \text{ tensors) }; \quad g^{\mu \nu }p^{\rho }p^{\sigma }\;\text{(6 } \text{ tensors) }; \nonumber \\{} & {} p^{\mu }p^{\nu }p^{\rho }p^{\sigma } \;\text{(1 } \text{ tensor) }. \end{aligned}$$

(4.2)

Since $P_{\mu \nu }(x_i p) = P_{\mu \nu }(p)$, for any scalar $x_i$, the Lorentz tensors quadratic and quartic in the momenta [cf. Eq. (4.2)] do not survive the transverse projection (2.8) in the collinear configurations defined in Eq. (2.10). Hence, the Lorentz tensors available to decompose $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(p_1, p_2, p_3, p_4)$ reduce to only 3, namely

$$\begin{aligned} P_{\mu \nu }(p)P_{\rho \sigma }(p) , \quad P_{\mu \rho }(p)P_{\nu \sigma }(p), \quad P_{\mu \sigma }(p)P_{\nu \rho }(p) . \end{aligned}$$

(4.3)

Combining the 5 independent color tensors of Eq. (3.21) with the Lorentz tensors of Eq. (4.3), we see that for collinear configurations $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$ is comprised by 15 color-Lorentz tensors. However, the basis resulting from the tensor product of the building blocks in Eqs. (3.21) and (4.3) is not manifestly Bose symmetric.

To amend this, we use linear combinations of the above elements to construct a basis of 15 new tensors $t_{i,\mu \nu \rho \sigma }^{abcd}$, and associated form factors $G_i$,

$$\begin{aligned} \overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(x,p) = \sum _{i = 1}^{15} G _i (x,p) \, t_{i,\mu \nu \rho \sigma }^{abcd} (x,p). \end{aligned}$$

(4.4)

Notice that in the decomposition given by Eq. (4.4), one has that

• (i) Each $t_i$ is manifestly Bose symmetric. Consequently, the form factors $G _i$ are individually symmetric under the exchange of any two components $x_i$ implicit in x.

• (ii) The $t_i$, and therefore the $G _i$, are all dimensionless. This property prevents the form factors $G _i$ from developing kinematic divergences when one of the momenta vanishes. Moreover, the different form factors can be compared directly.

• (iii) Finally, the tree-level tensor ${{\overline{\Gamma }}}^{0}$ defined in Eq. (2.12) is an element of the basis, namely $t_1 = {{\overline{\Gamma }}}^{0}$.

To construct a basis satisfying the above properties, we employ the $S_4$ permutation group formalism developed in [107]. Specifically, we combine the multiplets of momenta, colors, and Lorentz indices computed there into $S_4$ singlets (invariants). The details are presented in Appendix A, and the expressions for the resulting $t_i$ are given in Eq. (A13).

In order to extract the form factors $G _k$ from the SDE, we construct projectors $\mathcal {P}_k$ that isolate specific elements of the basis. In compact notation, we have

$$\begin{aligned} \mathcal {P}_{k} \odot \overline{{\textrm{I}}\!\Gamma } = G _{k}, ~~~~~k = 1,\ldots , 15, \end{aligned}$$

(4.5)

where the symbol “$\odot$” denotes the full contraction of all tensor and color indices, namely $A \odot B = A^{abcd}_{\mu \nu \rho \sigma } B_{abcd}^{\mu \nu \rho \sigma }$.

To determine the projectors $\mathcal {P}_{k}$, we first contract both sides of Eq. (4.4) with an arbitrary $t_{j}$,

$$\begin{aligned} t_{j}\odot \overline{{\textrm{I}}\!\Gamma }= & {} \sum _{i = 1}^{15} G _i~ (t_{j}\odot t_{i}) \nonumber \\= & {} \sum _{i = 1}^{15} G _i~ [C]_{ji} , ~~~~~j = 1,\ldots , 15 , \end{aligned}$$

(4.6)

where we define the symmetric matrix C with entries $[C]_{ji} = (t_{j}\odot t_{i})$. Next we multiply both sides of Eq. (4.6) by the inverse $[C^{-1}]_{kj}$ thus obtaining

$$\begin{aligned} \sum _{j = 1}^{15}([C^{-1}]_{kj} ~t_{j})\odot \overline{{\textrm{I}}\!\Gamma }= & {} G _{k} \implies \mathcal {P}^{abcd}_{k,\mu \nu \rho \sigma } \nonumber \\:= & {} \sum _{j = 1}^{15}[C^{-1}]_{kj} ~t^{abcd}_{j,\mu \nu \rho \sigma }, \end{aligned}$$

(4.7)

with $k = 1,\ldots , 15$.

The first three tensors, $t_{1,2,3}$, of the basis of Eq. (4.4) form a rather special subset. To begin, they are orthogonal to the remaining tensors, i.e.,

$$\begin{aligned} t_{1}\odot t_{j} = t_{2}\odot t_{j} = t_{3}\odot t_{j} = 0,~~~~~~j=4,\ldots ,15. \end{aligned}$$

(4.8)

In fact, $t_{3}$, is orthogonal to all other $t_{i}$. Furthermore, we find that $t_{1,2,3}$ are the only tensors of the basis that are independent of $x_{i}$.⁴ Indeed, for $t_{1,2,3}$ the expressions in Eq. (A13) reduce to the relatively compact forms

$$\begin{aligned} \begin{aligned} t_{1\,\mu \nu \rho \sigma }^{abcd}&= {{\overline{\Gamma }}}^{0\,abcd}_{\mu \nu \rho \sigma } ,\\ t_{2\,\mu \nu \rho \sigma }^{abcd}&=\delta ^{ad} \delta ^{bc} \left[ 2 P_{\mu \sigma }(p)P_{\nu \rho }(p) -P_{\mu \rho }(p)P_{\nu \sigma }(p)\right. \\&\quad \left. -P_{\mu \nu }(p) P_{\rho \sigma }(p) \right] +\delta ^{ac} \delta ^{bd}\left[ 2 P_{\mu \rho }(p)P_{\nu \sigma }(p)\right. \\&\quad \left. -P_{\mu \sigma }(p)P_{\nu \rho }(p) -P_{\mu \nu }(p) P_{\rho \sigma }(p) \right] \\&\quad +\delta ^{ab}\delta ^{cd} \left[ 2 P_{\mu \nu }(p)P_{\rho \sigma }(p) -P_{\mu \rho }(p)P_{\nu \sigma }(p)\right. \\&\quad \left. -P_{\mu \sigma }(p) P_{\nu \rho }(p) \right] ,\\ t_{3\,\mu \nu \rho \sigma }^{abcd}&= ( \delta ^{ab}\delta ^{cd} + \delta ^{ac}\delta ^{bd} + \delta ^{ad}\delta ^{bc} )\left[ P_{\mu \nu }(p) P_{\rho \sigma }(p) \right. \\&\quad \left. + P_{\mu \rho }(p)P_{\nu \sigma }(p) + P_{\mu \sigma }(p)P_{\nu \rho }(p) \right] . \end{aligned} \end{aligned}$$

(4.9)

These two observations have important consequences for the projectors $\mathcal {P}_{1}, \mathcal {P}_{2}$ and $\mathcal {P}_{3}$ which extract the associated form factors. The orthogonality expressed in Eq. (4.8) gives rise to a significant simplification in the procedure of Eq. (4.7), allowing these projectors to be expressed as linear combinations of only $t_{1,2,3}$; in particular, $\mathcal {P}_{3}$ is simply proportional to $t_{3}$. As a consequence, we find that $\mathcal {P}_{1}, \mathcal {P}_{2}$, and $\mathcal {P}_{3}$, are themselves independent of $x_{1}, x_{2}$ and $x_{3}$; through the procedure outlined, we find that they read

$$\begin{aligned} \mathcal {P}_1 = \displaystyle \frac{ 7 t_1 - 3 t_2}{19440}; \qquad \mathcal {P}_2 = \frac{ 3 t_2 - 2 t_1 }{12960} ; \qquad \mathcal {P}_3 = \frac{ t_3}{10800} . \nonumber \\ \end{aligned}$$

(4.10)

We hasten to emphasize that, since we made explicit use of Eq. (3.12), the above projectors are valid for SU(3), and may not hold for a general SU(N) group.

In what follows we will concentrate on the form factors $G _{1,2,3}(x,p)$, since they do not mix with the remaining form factors in any collinear configuration.

We conclude by pointing out that the projector $\mathcal {P}_1$ completely eliminates disconnected contributions when applied to $\mathcal {G}^{abcd}_{\mu \nu \rho \sigma }$, because its contraction with color structures of the type $\delta ^{ab}\delta ^{cd}$ vanish. Thus, in principle, the tree-level tensor structure can be isolated on the lattice, even for $x_i + x_j = 0$ for all $i \ne j$, by employing $\mathcal {P}_1$. On the other hand, the tensors $t_{2,3}$ mix with disconnected terms in $\mathcal {G}^{abcd}_{\mu \nu \rho \sigma }$, since the projectors $\mathcal {P}_{2,3}$ do not annihilate $\delta ^{ab}\delta ^{cd}$.

5 SDE of the four-gluon vertex

In this section, we set up the SDE that governs the form factors $G _{1,2,3}$ of the four-gluon vertex for an arbitrary collinear configuration, and discuss the renormalization of the resulting equations.

Fig. 2

Diagrammatic representations of: a the fully dressed gluon propagator, $\Delta _{\mu \nu }(q)$; b the complete ghost propagator, $D(q^2)$; c the full three-gluon vertex, ${\textrm{I}}\!\Gamma ^{abc}_{\alpha \mu \nu }(q,r,t) =g f^{abc}{\textrm{I}}\!\Gamma _{\alpha \mu \nu }(q,r,t)$; (d) the full ghost-gluon vertex, ${\textrm{I}}\!\Gamma ^{abc}_\mu (q,r,t) =-g f^{abc} {\textrm{I}}\!\Gamma _\mu (q,r,t)$

We employ the version of the four-gluon SDE derived from the formalism of the 4PI effective action [95,96,97,98,99] at the four-loop level [100, 101]; we remind the reader that, within this formalism, the SDE of a given Green’s function is obtained by extremizing the variation of the effective action with respect to this particular function.

It turns out that the SDE of the four-gluon vertex derived from the 4PI effective action is automatically symmetric with respect to permutations of its external legs, and contains fully dressed propagators and vertices as its ingredients, depicted diagrammatically in Fig. 2. The four-gluon SDE built out of these components is shown in Fig. 3; diagram $(d_1)$ is accompanied by five additional permutations, $(d_2)$ by two, $(d_3)$ by five, and $(d_4)$ by two [78]. In what follows we will denote by

$$\begin{aligned}&\left( {d}_{i}^{s}\right) ^{abcd}_{\mu \nu \rho \sigma }(p_{1},p_{2},p_{3},p_{4})\nonumber \\&\quad =\left( {d}_{i}\right) ^{abcd}_{\mu \nu \rho \sigma }(p_{1},p_{2},p_{3},p_{4}) + \text{ permutations }, \end{aligned}$$

(5.1)

the sum of each representative diagram and its permutations.

Fig. 3

Diagrammatic representation of the SDE for the full four-gluon vertex, ${{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$, derived from the 4PI effective action at the four-loop level. Contributions obtained through the permutations of the external momenta in the various diagrams are omitted

To obtain the SDE of the transversely-projected four-gluon vertex, $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(p_1,p_2,p_3,p_4)$, one simply contracts both sides of the SDE in Fig. 3 by the transverse projectors corresponding to the four external legs; the additional projectors, needed for the internal lines, come automatically from the gluon propagators, which in the Landau gauge, assumes the completely transverse form, $\Delta _{\mu \nu }(q) = \Delta (q^2)P_{\mu \nu }(q)$. Thus, in addition to $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$, the various diagrams depend on the transversely-projected three-gluon and ghost-gluon vertices, $\overline{{\textrm{I}}\!\Gamma }^{\,\alpha \mu \nu }(q,r,t)$ and $\overline{{\textrm{I}}\!\Gamma }^{\,\mu }(q,r,t)$, respectively, defined as

$$\begin{aligned} \overline{{\textrm{I}}\!\Gamma }^{\,\alpha \mu \nu }(q,r,t):= & {} P_{\alpha '}^{\alpha }(q) P_{\mu '}^{\mu }(r) P_{\nu '}^{\nu }(t) {\textrm{I}}\!\Gamma ^{\alpha '\!\mu '\!\nu '}(q,r,t) \nonumber \\ \overline{{\textrm{I}}\!\Gamma }^{\,\mu }(q,r,t):= & {} P_{\mu '}^{\mu }(q) {\textrm{I}}\!\Gamma ^{\mu '}(q,r,t) . \end{aligned}$$

(5.2)

Furthermore, we introduce the ghost propagator, $D^{ab}(q^2)= i\delta ^{ab}D(q^2)$, whose dressing function, $F(q^2)$, is given by $F(q^2) = q^2 D(q^2)$.

Then, the transversely-projected diagrams $(d_i)^{abcd}_{\mu \nu \rho \sigma }$ in Fig. 3, to be denoted by $(\bar{d}_{i})^{abcd}_{\mu \nu \rho \sigma }$, are given by (Minkowski space, omitting a factor $-ig^{2}$)

$$\begin{aligned} \left( \bar{d}_{1}\right) ^{abcd}_{\mu \nu \rho \sigma }&= -2\!\int _k \!\! \overline{{\textrm{I}}\!\Gamma }^{amf}_{\mu }\!(p_{1},k,-k_{1}) \overline{{\textrm{I}}\!\Gamma }^{bnm}_{\nu }\!(p_{2},k_{2},-k)\nonumber \\&\quad \times \overline{{\textrm{I}}\!\Gamma }^{cnt}_{\rho }\!(p_{3},-k_{2},k_{3}) \overline{{\textrm{I}}\!\Gamma }^{dft}_{\sigma }\!(p_{4},k_{1},-k_{3})\nonumber \\&\quad \times f_{D}(k,k_{1},k_{2},k_3), \nonumber \\ \left( \bar{d}_{2}\right) ^{abcd}_{\mu \nu \rho \sigma }&= \int _k \overline{{\textrm{I}}\!\Gamma }_{\mu \alpha \tau }^{amf}(p_{1},k,-k_{1}) \overline{{\textrm{I}}\!\Gamma }_{\nu \beta \alpha }^{bnm}(p_{2},k_{2},-k)\nonumber \\&\quad \times \overline{{\textrm{I}}\!\Gamma }_{\rho \beta \lambda }^{cnt}(p_{3},-k_{2},k_{3}) \overline{{\textrm{I}}\!\Gamma }_{\sigma \tau \lambda }^{dft}(p_{4},k_{1},-k_{3})\nonumber \\&\quad \times f_{\Delta }(k,k_{1},k_{2},k_3), \nonumber \\ \left( \bar{d}_{3}\right) ^{abcd}_{\mu \nu \rho \sigma }&= \int _k \overline{{\textrm{I}}\!\Gamma }_{\nu \tau \alpha }^{btm}(p_{2},k_{2},-k)\overline{{\textrm{I}}\!\Gamma }_{\rho \beta \tau }^{cnt}(p_{3},k_{3},-k_{2})\nonumber \\&\quad \times \overline{{\textrm{I}}\!\Gamma }^{admn}_{\mu \sigma \alpha \beta }(p_{1},p_{4}, k, -k_{3}) \Delta (k^2)\Delta (k_{3}^2)\Delta (k_{2}^2),\nonumber \\ \left( \bar{d}_{4}\right) ^{abcd}_{\mu \nu \rho \sigma }&= \!\! \frac{1}{2}\int _k \overline{{\textrm{I}}\!\Gamma }^{admn}_{\mu \sigma \alpha \beta }(p_{1},p_{4},k,-k_{3})\nonumber \\&\quad \times \overline{{\textrm{I}}\!\Gamma }^{bcmn}_{\nu \rho \alpha \beta }(p_{2},p_{3},-k,k_{3}) \Delta (k^2) \Delta (k_{3}^2), \end{aligned}$$

(5.3)

where we set $k_1:=k+p_{1}$, $k_{2}:=k-p_{2}$, $k_{3}:=k+p_{1}+p_{4}$, and define the products of propagators

$$\begin{aligned} f_{{\Delta }}(k,k_{1},k_{2},k_3):= & {} { \Delta }(k^2){\Delta }(k_{1}^2){\Delta }(k_{2}^2){\Delta }(k_{3}^2) , \nonumber \\ f_{D}(k,k_{1},k_{2},k_3):= & {} { D}(k^2){D}(k_{1}^2){D}(k_{2}^2){D}(k_{3}^2) . \end{aligned}$$

(5.4)

Finally,

$$\begin{aligned} \int _{k}:= \frac{1}{(2\pi )^4} \int \!\!\textrm{d}^4 k , \end{aligned}$$

(5.5)

where the use of a symmetry-preserving regularization scheme is implicitly assumed.

Thus, the SDE for $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }$ may be expressed in the following compact way

$$\begin{aligned} \overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(p_{1},p_{2},p_{3},p_{4})&=\overline{\Gamma }_{\!0\,\mu \nu \rho \sigma }^{abcd}(p_{1},p_{2},p_{3},p_{4})\nonumber \\&\quad + \sum _{i=1}^{4} \left( \bar{d}_{i}^s\right) ^{abcd}_{\mu \nu \rho \sigma }(p_{1},p_{2},p_{3},p_{4}), \end{aligned}$$

(5.6)

where the $(\bar{d}_{i}^s)$ denotes the transversely-projected counterpart of the $(d_i^s)$ defined in Eq. (5.1).

We now turn to the renormalization of the SDE given in Eq. (5.3). All quantities appearing in that equation are bare (unrenormalized); the transition to the renormalized quantities is implemented multiplicatively, by means of the standard relations

$$\begin{aligned}&\Delta _{{\scriptscriptstyle R}}(q^2)= Z^{-1}_{A} \Delta (q^2),\nonumber \\&{\textrm{I}}\!\Gamma ^{\mu }_{\!\!{\scriptscriptstyle R}}(q,r,t) = Z_1 {\textrm{I}}\!\Gamma ^{\mu }(q,r,t),\nonumber \\&F_{\!{\scriptscriptstyle R}}(q^2)= Z^{-1}_{c} F(q^2),\nonumber \\&{\textrm{I}}\!\Gamma ^{\alpha \mu \nu }_{\!\!{\scriptscriptstyle R}}(q,r,t) = Z_3 {\textrm{I}}\!\Gamma ^{\alpha \mu \nu }(q,r,t),\nonumber \\&g_{{\scriptscriptstyle R}} = Z_g^{-1} g, \nonumber \\&{\textrm{I}}\!\Gamma ^{abcd}_{\!\!{\scriptscriptstyle R}\,\alpha \beta \mu \nu }(p_1,p_2,p_3,p_4) = Z_4 {\textrm{I}}\!\Gamma ^{abcd}_{\alpha \beta \mu \nu }(p_1,p_2,p_3,p_4), \end{aligned}$$

(5.7)

where the subscript “R” denotes renormalized quantities, and $Z_{A}$, $Z_{c}$, $Z_{1}$, $Z_{3}$, $Z_{4}$, and $Z_g$ are the corresponding (cutoff-dependent) renormalization constants. In addition, we employ the exact relations

$$\begin{aligned} Z_g^{-1} = Z_1^{-1} Z_A^{1/2} Z_c = Z_3^{-1} Z_A^{3/2} = Z_4^{-1/2} Z_A , \end{aligned}$$

(5.8)

which are imposed by the fundamental Slavnov–Taylor identities (STIs) [108, 109]. Substituting the relations of Eq. (5.7) into Eq. (5.3) and using Eq. (5.8), it is straightforward to derive the renormalized version of Eq. (5.6), given by

$$\begin{aligned} \overline{{\textrm{I}}\!\Gamma }^{abcd}_{{\!\!{\scriptscriptstyle R}}\, \mu \nu \rho \sigma }(p_{1},p_{2},p_{3},p_{4})&= Z_4\overline{\Gamma }_{\!0\,\mu \nu \rho \sigma }^{abcd}(p_{1},p_{2},p_{3},p_{4}) \, \nonumber \\&\quad + \sum _{i=1}^{4} \left( \bar{d}^{s}_{i\,{\scriptscriptstyle R}}\right) ^{abcd}_{\mu \nu \rho \sigma } (p_{1},p_{2},p_{3},p_{4}), \end{aligned}$$

(5.9)

where the subscript “R” in $\left( \bar{d}^{s}_{i\,{\scriptscriptstyle R}}\right) ^{abcd}_{\mu \nu \rho \sigma }$ denotes that the expressions given in Eq. (5.3) have been substituted by their renormalized counterparts. We emphasize that the $Z_4$ multiplied by the tree-level structure is the only renormalization constant to be determined. Note in particular that, because all vertices are fully dressed, none of the renormalization constants appears multiplying any of the contributions $\left( \bar{d}^{s}_{i\,{\scriptscriptstyle R}}\right) ^{abcd}_{\mu \nu \rho \sigma }$; thus, the usual complications associated with multiplicative renormalization are absent [100, 101].

In order to determine $Z_4$ we adopt a variant of the momentum subtraction (MOM) scheme [110, 111]. Within this scheme, the gluon and ghost propagators assume their tree-level values at the subtraction point $\mu$, i.e.,

$$\begin{aligned} \Delta ^{-1}(\mu ^2) = \mu ^2 , \qquad F(\mu ^2) = 1 . \end{aligned}$$

(5.10)

In general studies of vertices, these two conditions are supplemented by an additional one, fixing the value of a form factor (or combination thereof) at some special kinematic configuration [112, 113, 113, 114]. For example, in the recent SDE analysis of [90], the renormalization of the three-gluon vertex was such that the leading form factor would acquire its tree-level value in the soft-gluon configuration [see Eq. (3.13) therein].

For the case of the four-gluon vertex we employ an analogous scheme. In particular, we single out the configuration $(0,p,p,-2p)$, and require that

$$\begin{aligned} G _{1}(0,p,p,-2p)|_{p^{2}=\mu ^{2}} = 1 . \end{aligned}$$

(5.11)

The above kinematic configuration is chosen for numerical simplicity, and is otherwise arbitrary; any other configuration for which $G_1(x,p)$ is infrared finite at the perturbative level would have been equally good. We emphasize that, despite being an exceptional configuration, in the sense that a subset of momenta add to zero [115], $G_1(0,p,p,-2p)$ is infrared finite, thus defining a valid MOM. This was confirmed by the explicit one-loop calculation of Eq. (B10), which contains only the expected ultraviolet divergence.

Note that, when the scheme defined by Eqs. (5.10) and (5.11) is employed, the conditions used for renormalizing the three-gluon and ghost-gluon vertices may not be simultaneously employed, because this would lead to a violation of the relations of Eq. (5.8) imposed by the STIs [116]. The renormalized three-gluon and ghost-gluon vertices used in our calculations as inputs of the four-gluon SDE must undergo finite renormalizations, which will adjust their values such that the relations of Eq. (5.8) are fulfilled. This procedure of finite renormalization is described in detail in Appendix B.

In what follows we will denote the renormalization constants particular to this scheme by a tilde; thus, the set $\{Z_ A, Z_c, Z_1, Z_3, Z_4, Z_g \}$, introduced in Eq. (5.7), is replaced by $\{{{\widetilde{Z}}}_A, {{\widetilde{Z}}}_c, {{\widetilde{Z}}}_1, {{\widetilde{Z}}}_3, {{\widetilde{Z}}}_4, {{\widetilde{Z}}}_g \}$. Note that these constants are restricted by the fundamental relations of Eq. (5.8).

The determination of ${{\widetilde{Z}}}_{4}$ proceeds by first employing the special projection of Eq. (4.10) to define

$$\begin{aligned} {d}^{\,0}_{i}(p^{2}):=\left[ \displaystyle \mathcal {P}_{1} \odot (\bar{d}_{i{\scriptscriptstyle R}}^{s})(x,p) \right] \Big |_{x \rightarrow x_0}; \end{aligned}$$

(5.12)

where $x_0$ denotes the reference configuration $(0,1,1,-2)$ in Eq. (5.11). Then, imposing the condition Eq. (5.11) at the level of Eq. (5.9), we find

$$\begin{aligned} {{\widetilde{Z}}}_{4} = 1 - \sum _{i=2}^{4} {d}^{\,0}_{i}(\mu ^{2}) . \end{aligned}$$

(5.13)

Note that all contributions to ${d}^{\,{0}}_{1}(p^{2})$ originating from the ghost boxes vanish, i.e., $\left[ \displaystyle \mathcal {P}_{1} \odot (\bar{d}_{1{\scriptscriptstyle R}}^{s})(x,p) \right] \Big |_{x \rightarrow x_0} \!\!\!= 0$.

Then, substituting Eq. (5.13) into Eq. (5.9), we obtain the renormalized SDE for $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{{\!\!{\scriptscriptstyle R}}\, \mu \nu \rho \sigma }$ expressed as

$$\begin{aligned} \overline{{\textrm{I}}\!\Gamma }^{abcd}_{{\!\!{\scriptscriptstyle R}}\, \mu \nu \rho \sigma }(x,p)&= \overline{\Gamma }_{\!0\,\mu \nu \rho \sigma }^{abcd}(x,p) \left[ 1 - \sum _{i=2}^{4} {d}^{\,0}_{i}(\mu ^{2}) \right] \, \nonumber \\&\quad + \sum _{i=1}^{4} \left( \bar{d}^{s}_{i\,{\scriptscriptstyle R}}\right) ^{abcd}_{\mu \nu \rho \sigma } (x,p). \end{aligned}$$

(5.14)

When no ambiguity can arise we drop the index “R” to avoid notational clutter.

The final renormalized expressions for both $G _{1,3}(x,p)$ are obtained by acting on Eq. (5.14) with the associated projectors given in Eq. (4.10),

$$\begin{aligned} G _{1}(x,p)= & {} 1 + \sum _{i=2}^{4} \mathcal {P}_{1}\odot \left( \bar{d}_{i}^{s}\right) (x,p)- \sum _{i=2}^{4} {d}^{\,{0}}_{i}(\mu ^{2}),\nonumber \\ G _{j}(x,p)= & {} \sum _{i=1}^{4} \mathcal {P}_{j}\odot \left( \bar{d}_{i}^{s}\right) (x,p), \qquad j=2,3. \end{aligned}$$

(5.15)

The SDEs in Eq. (5.15) will be solved in the next section, under a set of well-founded assumptions, which will be discussed there in detail. It turns out that, under these assumptions, one may demonstrate analytically the ultraviolet finiteness of the resulting $G_i(x,p)$; the detailed proof is presented in Sect. 8.

6 Results: emergence of planar degeneracy

In this section we solve the SDE of the four-gluon vertex under certain simplifying assumptions, and check the extent of validity of the planar degeneracy at the level of the solutions obtained.

6.1 Preliminary considerations

Fig. 4

Upper left: Lattice data of [42, 54] (points) for the gluon propagator, $\Delta (r^2)$, and its fit given by Eq. (C11) of [117] (blue solid lines). Upper right: The lattice ghost dressing function, $F(r^2)$, of [42, 54] (points) together with the fit given by Eq. (C6) of [117] (blue solid lines). Lower left: Lattice data of [114] for $L _{{sg}}(r^{2})$ (points), compared to the fit of Eq. (C12) (black continuous). Lower right: The ghost-gluon form factor, $B_{1}(r^2, q^2, \theta )$, for arbitrary magnitudes of the antighost and gluon momenta, r and q, respectively, and a representative value of $\theta = 2\pi / 3$ for the angle between them

For the SDE treatment, we employ appropriate inputs for the various functions entering in the kernels of Eqs. (6.7) and (6.8). In particular, for the gluon propagator, $\Delta (r^2)$, and the ghost dressing function, $F(r^2)$, we use fits given by Eqs. (C11) and (C6) of [117], respectively, to the lattice results of [42, 54] shown in Fig. 4.

Regarding the three-gluon vertex, we retain only its tree-level tensorial structure, and resort to the planar degeneracy approximation for the associated form factor. Specifically, $\overline{{\textrm{I}}\!\Gamma }^{\,\alpha \mu \nu }(q,r,t)$ can be accurately approximated by the compact form

$$\begin{aligned} \overline{{\textrm{I}}\!\Gamma }^{\,\alpha \mu \nu }(q,r,t)= & {} L _{{sg}}(s^2) \overline{\Gamma }_{\!0}^{\,\alpha \mu \nu }(q,r,t) , \nonumber \\ s^2= & {} \frac{1}{2}(q^2+r^2+t^2), \end{aligned}$$

(6.1)

where $\overline{\Gamma }_{\!0}^{\,\alpha \mu \nu }(q,r,t) = \ P_{\alpha '}^\alpha (q) P_{\mu '}^{\mu }(r) P_{\nu '}^\nu (t) \Gamma _{\!0}^{\,\alpha ' \mu ' \nu '}(q,r,t)$, with $\Gamma _{\!0}$ denoting the three-gluon vertex at tree-level [58, 89,90,91]. The function $L _{{sg}}(s^{2})$ is the form factor associated with the soft-gluon limit of the three-gluon vertex, $(q=0, r =-t)$, and has been accurately determined from various lattice simulations  [49, 50, 54, 89, 114, 118, 119]; its functional form is shown in the lower left panel of Fig. 4. Concretely, we use a fit to the lattice data of [58, 120], which is given by Eq. (C12) of [117], and convert to the renormalization scheme of Eqs. (5.10) and (5.11) using Eq. (B14).

As for the ghost-gluon vertex, its Lorentz decomposition reads

$$\begin{aligned} {\textrm{I}}\!\Gamma _\mu (q,r,t) = r_\mu B_1(q,r,t) + q_\mu B_2(q,r,t) ; \end{aligned}$$

(6.2)

at tree-level, $B_1^0 = 1$ and $B_2^0 = 0$. Only $B_1$ contributes to the transversely-projected form, $\overline{{\textrm{I}}\!\Gamma }^{\,\mu }(q,r,t)$, so we have

$$\begin{aligned} \overline{{\textrm{I}}\!\Gamma }^{\,\mu }(q,r,t)&:= r^{\mu '}P_{\mu '}^{\mu }(q) B_1(q,r,t) . \end{aligned}$$

(6.3)

The form employed for $B_{1}(q,r,t)$ is taken from the SDE results of [58, 120], and has been consistently renormalized using Eq. (B14); it is shown in the lower right panel of Fig. 4.

Finally, for the coupling constant we use the value $\alpha _s(\mu ^2) = g^2/4\pi = 0.23$ [see Eq. (B14)], which corresponds to the renormalization scheme of Eqs. (5.10) and (5.11) and $\mu = 4.3$ GeV.

It is clear that the arguments of the $G_i$ appearing in the integrands of the SDE are comprised by combinations $x_i p$ and the loop momentum k, a fact that complicates the numerical treatment. However, a considerable simplification occurs if (i) the form factor $G_1$ is assumed to be dominant, making negligible all dependence on other form-factors, in particular $G_{2,3}$, and (ii) the $G_1$ is assumed to display “planar degeneracy” at some notable level of accuracy. In such a case, one implements the substitution

$$\begin{aligned}&\overline{{\textrm{I}}\!\Gamma }_{\mu \nu \rho \sigma }^{abcd}(p_1,p_2,p_3,p_4) \nonumber \\&\quad \approx G_1(p_1,p_2,p_3,p_4) \overline{\Gamma }_{\!0~\!\!\mu \nu \rho \sigma }^{abcd}(p_1,p_2,p_3,p_4), \end{aligned}$$

(6.4)

and

$$\begin{aligned} G_1(p_1,p_2,p_3,p_4)\approx G^{*}_1(\bar{s}^{2}) , \end{aligned}$$

(6.5)

where, in general,

$$\begin{aligned} \bar{s}^{2}=\frac{1}{2}(p_{1}^{2}+p_{2}^{2}+p_{3}^{2}+p_{4}^{2}). \end{aligned}$$

(6.6)

The form of $G^{*}_1({\bar{s}}^2)$ will be determined by means of an iterative procedure, outlined in the next subsection. Note that, for a given $G^{*}_1({\bar{s}}^2)$, all four-gluon vertices in the integrands of Eq. (5.15) will be replaced by Eqs. (6.4) and (6.5), and evaluated at the value of ${\bar{s}}^2$ corresponding to each vertex. For example, the ${\bar{s}}^2$ assigned to the vertex $\overline{{\textrm{I}}\!\Gamma }^{admn}_{\mu \sigma \alpha \beta }(p_{1},p_{4},k,-k_{3})$ in the diagram $\left( \bar{d}_{3}\right)$ in Eq. (5.3) is given by $\bar{s}^2= \frac{1}{2}(p_1^2+p_4^2 +k^2 +k_3^2)$, where $k_{3}:=k+p_{1}+p_{4}$.

There are two main consequences stemming from the implementation of these two approximations.

First, the form factor $G _{2}(x,p)$ vanishes identically. Indeed, we find that the diagrams $(\bar{d}_{1,2})$ of Eq. (5.3) cannot generate the particular color combination associated with $G_2$ [cf. Eq. (4.9)], independently of the approximation used for the ghost-gluon and three-gluon vertices. On the other hand, the diagrams $(\bar{d}_{3,4})$ can contribute to $G_2$, but only if non-tree-level tensor structures of the four-gluon vertices therein are dressed. Since a nonzero $G_2$ can only arise from the effect of dressing non-tree level tensor structures, or including higher loop diagrams in the SDE, it is reasonable to expect it to be subleading in comparison to $G_{1,3}$. In particular, it is evident that, perturbatively, $G_2$ can only be nonzero at two loops or higher.

Second, the remaining equations for $G _{1}(x,p)$ and $G _{3}(x,p)$ decouple, assuming the schematic form

$$\begin{aligned} G _{1}(x,p)&= 1 + \left[ \int _{k}\!\! K_{1} + \!\!\int _{k}\!\! G^{*}_1K_{2} + \!\!\int _{k}\!\! G^{*2}_1 K_{3}\right] \nonumber \\&\quad -\left[ \int _k\!\!K_{1} + \!\!\int _k\!\!G^{*}_1K_{2} + \!\!\int _k\!\!G^{*2}_1 K_{3}\right] _{\begin{array}{c} \!\!\!p\rightarrow \mu \\ x\rightarrow x_{0} \end{array}}, \end{aligned}$$

(6.7)

$$\begin{aligned} G _{3}(x,p)&= \left[ \int _{k}\!\! K_{4} + \!\!\int _{k}\!\! G^{*}_1K_{5} + \!\!\int _{k}\!\! G^{*2}_1 K_{6}\right] , \end{aligned}$$

(6.8)

where the $K_i$ are the various kernels defined from the diagrams $\bar{d}_{i}^{s}(x,p)$; all functions other than $G^{*}_1$ have been absorbed into them. The term quadratic in $G^{*}_1({\bar{s}}^2)$ stems from graph ($d_4$); and $x_0$ denotes the configuration $(0,1,1,-2)$ in Eq. (5.11).

In order to proceed with the numerical solution, the Eqs. (6.7) and (6.8) must be passed to Euclidean space, following standard conventions (see, e.g., Eq. (5.1) of [121]). For the numerical treatment, the resulting integrals are expressed in hyper-spherical coordinates.

Fig. 5

Comparison of $G _{1}(x,p)$ expressed as a function of the momentum p (left), and as function of the Bose symmetric variable $\bar{s}$ (right panel), for the four collinear kinematic configurations, defined in (6.9). $G _{1}(x,p)$ was computed employing the approximation $\overline{{\textrm{I}}\!\Gamma } = \overline{\Gamma }_{\!0}$ on the r.h.s. of the Eq. (6.7). The blue curve on the right panel represents $G_1^{\textrm{av}}(\bar{s}^{2})$, the average of these four configurations in terms of $\bar{s}^{2}$, defined in Eq. (6.11)

Numerical integration is performed with the Gauss–Kronrod implementation of [122]. We integrate over a grid of external squared momenta distributed logarithmically over the interval $[10^{-4},10^{4}] ~\text {GeV}^{2}$.

6.2 Planar degeneracy as an infrared feature

The first step in determining $G^{*}_1(\bar{s}^{2})$ is to set $G^{*}_1(\bar{s}^{2}) =1$ everywhere on the r.h.s. of Eq. (6.7). After this substitution, any collinear configurations for $G_1(x,p)$ are obtained from Eq. (6.7) by simply carrying out the corresponding integrations. Thus, we determine numerically $G_1(x,p)$ in four collinear kinematic configurations, whose coordinates $(x_1,x_2,x_3,x_4)$ are given by

$$\begin{aligned} (1,1,1,-3),\quad (0,1,1,-2), \quad (0,1,2,-3),\quad (1,2,3,-6). \end{aligned}$$

(6.9)

This choice is random; there is nothing particular about these four cases. The results are displayed in Fig. 5: on the left panel, where the four configurations are plotted as functions of the momentum p, they lead to clearly distinct curves; however, when plotted in terms of the Bose symmetric variable $\bar{s}$ of Eq. (6.6), they merge into each other in the range $0 \le \bar{s}\lessapprox 1$ GeV, manifesting clearly the onset of the planar degeneracy in this region of momenta. Note that in the case of collinear momenta, Eq. (6.6) reduces to

$$\begin{aligned} \bar{s}^{2}=\frac{1}{2}(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}) \, p^2. \end{aligned}$$

(6.10)

This promising result motivates the iteration of the procedure, in order to obtain the optimal form of $G^{*}_1(\bar{s}^{2})$. In particular, we determine the numerical average, $G_1^{\textrm{av}}(\bar{s}^{2})$, of the four configurations defined in Eq. (6.9), i.e.,

$$\begin{aligned} G_1^{\textrm{av}}(\bar{s}^{2}) = \frac{1}{4} \sum _{j=1}^{4} G _{1}(x_{j},p)\,; \end{aligned}$$

(6.11)

the result of this “averaging” is shown as the blue continuous curve on the right panel of Fig. 5. Then, the second step in the iterative procedure is taken, by setting on the r.h.s. of Eq. (6.7)

$$\begin{aligned} G^{*}_1(\bar{s}^{2}) = G_1^{\textrm{av}}(\bar{s}^{2}) \,; \end{aligned}$$

(6.12)

in this way, the $G_1^{\textrm{av}}(\bar{s}^{2})$ acts now as the new “seed” for obtaining the next generation of results for the same four configurations. These new results will then be averaged and fed back into the r.h.s. of the original set of four equations. This iterative procedure concludes when the relative error between two consecutive averaged solutions is smaller than $0.1\%$; typically, convergence is achieved after about 15 iterations. In Fig. 6, we compare the $G^{*}_1(\bar{s}^{2})$ corresponding to the first (blue dashed curve), and last iterations (red continuous curve). The final result is clearly suppressed with respect to the initial $G^{*}_1(\bar{s}^{2})=1$ (tree-level).

Fig. 6

The first and last iterations of $G^{*}_{1,3}(\bar{s}^{2})$

Note that this particular procedure decouples effectively Eq. (6.7) from Eq. (6.8): the form factor $G _3(x,p)$ may be obtained by means of a single integration, once the final $G^{*}_1(\bar{s}^{2})$ has been computed from Eq. (6.7) and substituted into Eq. (6.8).

However, even though $G_3(x,p)$ is not subject to an iterative procedure, it is advantageous to define a curve $G_3^{*}(\bar{s}^{2})$, which potentially approximates the general collinear $G_3(x,p)$, and allows this form factor to be reconstructed from a single curve (see Fig. 8). Moreover, the curve $G_3^{*}(\bar{s}^{2})$ will serve as a reference for quantifying how well $G_3(x,p)$ satisfies the property of planar degeneracy. Therefore, by analogy with Eqs. (6.11) and (6.12), we set

$$\begin{aligned} G_3^{*}(\bar{s}^{2}) = \frac{1}{4} \sum _{j=1}^{4} G _{3}(x_{j},p), \end{aligned}$$

(6.13)

where the sum is over the same kinematic configurations used to define $G_1^{*}(\bar{s}^2)$, given in Eq. (6.9). The resulting $G_3^{*}(\bar{s}^2)$ is shown on the right panel of Fig. 6 for the case $G^{*}_1(s^2) = 1$ (blue dot-dashed) and for the final $G^{*}_1(s^2)$ (red continuous).

Fig. 7

The form factors $G _{1,3}(x,p)$ for the fourteen random collinear kinematic configurations, defined in Eq. (6.15), plotted as functions of momentum p (left panels) and as functions of the Bose symmetric variable $\bar{s}$ (right panels). The disordered pattern seen on the left panels is to be contrasted with the tight clustering of the curves displayed on the right ones

As is clear from Fig. 6, for $\bar{s}\ge 0.3$ GeV, $G _3^{*}(\bar{s}^2)$ is considerably smaller than $G _1^{*}(\bar{s}^2)$. On the other hand, for $\bar{s}\rightarrow 0$, the form factor $G _3^{*}(\bar{s}^2)$ diverges logarithmically, whereas $G _1^{*}(0)$ is finite. As shown in [78], the divergence of $G _3^{*}(\bar{s}^2)$ results from the massless ghost loop $(d_1)$ of Fig. 3, which contributes to $G _3(x,p)$, but not to $G _1(x,p)$. The rate of divergence can be determined by an asymptotic analysis along the lines of the one performed for the three-gluon vertex in Appendix A of [90]. Specifically, we obtain

$$\begin{aligned} \lim _{p\rightarrow 0} G_{3}(x,p) = -\frac{3\alpha _{s}}{64\pi }F^{4}(0) {{\widetilde{Z}}}_{1}^{4}\ln (p^2/\mu ^2), \end{aligned}$$

(6.14)

where ${{\widetilde{Z}}}_1$ is the renormalization constant of the ghost-gluon vertex. Note that ${{\widetilde{Z}}}_1$ is finite in the Landau gauge [108, 111, 123]; within our renormalization scheme, it turns out to be very close to unity, ${{\widetilde{Z}}}_1 = 1.01$.

In order to test the reliability of the entire procedure, we compute $G_1$ and $G_3$ for fourteen random collinear kinematics, using as input in Eqs. (6.7) and (6.8) the $G^{*}_1(\bar{s}^{2})$ obtained at the end of the iteration procedure (red continuous curve in Fig. 6). Ten of these configurations are obtained by employing a random number generator for the $x_i$, while the last four correspond to those used earlier for the determination of $G^{*}_1(\bar{s}^{2})$; the coordinates $(x_1,x_2,x_3,x_4)$ of all of them are listed below:⁵

$$\begin{aligned}&c_1 =(0.41,5.96,6.77,-13.14)\,; \nonumber \\&c_6=(0.23,3.78,6.17,-10.18)\,; \quad c_{11} =(1,1,1,-3)\,; \nonumber \\&c_2 =(2.26,3.72,6.55,-12.53)\,; \nonumber \\&c_7 =(1.02,3.37,5.10,-9.49)\,; \quad c_{12} =(0,1,1,-2)\,; \nonumber \\&c_3 =(0.71,1.56,2.32,-4.59)\,; \nonumber \\&c_8 =(3.30,4.13,5.53,-12.96)\,; \quad c_{13}=(0,1,2,-3)\,; \nonumber \\&c_4 =(0.74,3.96,4.63,-9.33)\,; \nonumber \\&c_9 =(4.02,4.25,6.09,-14.36)\,; \quad c_{14} =(1,2,3,-6). \nonumber \\&c_5 =(1.42,2.34,6.65,-10.41)\,; \nonumber \\&c_{10} =(2.23,2.55,6.49,-11.27)\,; \end{aligned}$$

(6.15)

In Fig. 7 we plot both form factors $G _{1,3}(x,p)$, for the configurations listed in Eq. (6.15), as functions of the momentum p (left panels) and the Bose symmetric variable $\bar{s}$ (right panels). The remarkable agreement between the fourteen curves when they are plotted as functions of $\bar{s}$ is to be contrasted to the considerable disparity observed when they are plotted as functions of p. Thus, for $\bar{s}< 1$ GeV, the approximation

$$\begin{aligned} G_i(x,p)\approx G^{*}_i(\bar{s}^{2}), \qquad i=1,3, \end{aligned}$$

(6.16)

appears to be particularly robust.

To quantify the level of accuracy of Eq. (6.16) within the range $0<\bar{s}<2$ GeV, we compute the percentage error defined as

$$\begin{aligned} \delta _{i}(\bar{s}_j^2) = \frac{ G _{i}(\bar{s}_j^2)-G^{*}_i(\bar{s}^{2})}{G^{*}_{i}(\bar{s}^2)}\times 100\%, \quad j=1,\ldots ,14, \end{aligned}$$

(6.17)

where $i = 1,\,3$, and $G_{i}(\bar{s}_j^2)$ denotes any one of the fourteen curves shown on the right panels of Fig. 7, while $G^{*}_i(\bar{s}^{2})$ are our reference curves, shown as red continuous lines in Fig. 6.

Starting with the classical form factor, $G _1(x,p)$, we find that for $\bar{s}\le 1$ GeV, the error $\delta _{1}(\bar{s}_j^2)\le 1.7\%$. As can be seen already from Fig. 7, the relative separation between curves of different kinematics grows as $\bar{s}$ increases; consequently, in the range $1\le \bar{s}\le 2$ GeV, $\delta _{1}(\bar{s}_j^2)$ increases, reaching the maximum value of $4.4\%$.

For $G _3(x,p)$, notice that, for all the kinematics shown in Fig. 6, the curves display zero crossings at around $\bar{s}=0.7$ GeV, where the relative error $\delta _3(\bar{s}_j^2)$ becomes ill-defined. Away from the crossing, we find that $\delta _3(\bar{s}_j^2) \le 7.0 \%$ for $\bar{s}\le 0.4$ GeV, whereas for $1\le \bar{s}\le 2$ GeV the $\delta _3(\bar{s}_j^2)$ increases, reaching the value $\delta _3(\bar{s}_j^2) \le 33.7\%$; however, in this latter range of momenta, $G^{*}_{3}(\bar{s}^2)$ is itself rather small.

In addition to the inspection of discrete sets of kinematic configurations, one may visualize the accuracy of the planar degeneracy approximation more generally through 3D plots, where the $x_i$ components vary continuously.

In Fig. 8, we plot $G_{1,3}(x,p)$ (yellow surfaces) as functions of the momenta $x_1p$ and $x_2p$. To make this visualization possible, we reduce the number of independent variables by fixing $p_{3}=(x_1+x_2)p$. In the same figure, we map $G^{*}_{1,3}(\bar{s}^{2})$ into the $(x_1 p$, $x_2p)$ plane, by setting $p_{3}=(x_1+x_2)p$ in Eq. (6.10), such that $\bar{s}^{2} = 3(x_{1}p)^{2} + 3(x_{2}p)^{2} + 5 (x_{1}p)(x_{2}p)$. With this mapping, the curves for $G_i^{*}(\bar{s}^2)$ (red continuous in Fig. 6) become surfaces, shown in blue in Fig. 8. For both form factors, $G_{1,3}(x,p)$, the blue and yellow surfaces show a high degree of overlap in the infrared, in agreement with Eq. (6.16), while differences become visible with increasing momenta.

Fig. 8

Form factors $G _{1,3}(x,p)$ (yellow) compared to the approximation $G^{*}_{1,3}(\bar{s}^{2})$ (blue), mapped into the ($x_1p$, $x_2p$) plane using Eq. (6.10), and setting $x_{3} = x_{1} + x_{2}$. In both cases, the advantage of planar degeneracy becomes evident: entire surfaces are reconstructed, to a great accuracy, from the knowledge of a single curve

Fig. 9

Form factors $G _{1,3}(x,p)$ for $x_1 = 1$, arbitrary $x_2$ and $x_3$, and fixed values of $\bar{s} = 0.5$ GeV (brown), $\bar{s} = 1$ GeV (blue), and $\bar{s} = 2$ GeV (green). For $\bar{s} = 1$ GeV and $\bar{s} = 2$ GeV, both $G _{1,3}(x,p)$ are practically constant, i.e., independent of $x_i$

Let us finally point out that, if planar degeneracy were an exact property of the $G _i(x,p)$, there should be no dependence on x for fixed $\bar{s}$; instead, for an approximate planar degeneracy, the $G _i(x,p)$ should show a mild dependence on x. The residual dependences of the $G _i(x,p)$ on x can be visualized by plotting surfaces corresponding to fixed values of $\bar{s}$; their deviation from the absolute flatness will be then a measure of the exactness of the planar degeneracy.

To this end, first note that for a given vector x, the value of p that gives rise to a given value of $\bar{s}$ can be uniquely determined by inverting Eq. (6.10). Specifically,

$$\begin{aligned} p = \bar{s}\left( x_1^2 + x_2^2 + x_3^2 + x_1 x_2 + x_2 x_3 + x_3 x_1\right) ^{-1/2} , \nonumber \\ \end{aligned}$$

(6.18)

where $x_4$ has been eliminated by using momentum conservation. Hence, we can determine how $G_1(x,p)$ varies as a function of $x_1$, $x_2$ and $x_3$, for fixed $\bar{s}$: from an available array of values for $G_1(x,p)$, we pick the one value that corresponds to the unique p obtained from Eq. (6.18), once an $\bar{s}$ and a set of $(x_1,x_2,x_3)$ have been substituted in it.

In Fig. 9 we first set $x_1=1$, and then plot $G _{1,3}(x,p)$ for fixed values of $\bar{s}$ and general values of $x_2$ and $x_3$. Specifically, we show surfaces corresponding to $\bar{s}= 0.5$ GeV (brown), $\bar{s}= 1$ GeV (blue), and $\bar{s}= 2$ GeV (green). In both panels, it is clear that for $\bar{s} = 0.5$ GeV and $\bar{s} = 1$ GeV, the $G _{1,3}(x,p)$ are almost perfectly constant, i.e., nearly independent of $x_2$ and $x_3$. Hence, we confirm once more the validity of the planar degeneracy property expressed by Eqs. (6.5) and (6.16) in the infrared.

For $\bar{s}= 2$ GeV, the surfaces of $G _{1,3}(x,p)$ in Fig. 9 begin to deviate from perfect flatness, in line with our previous observations that planar degeneracy breaks down with increasing $\bar{s}$. However, even in this case, the surfaces of $G _{1,3}(x,p)$ are rather flat for most values of $x_2$ and $x_3$. The only exceptions occur near the borders of the plot, when at least one of the $x_i$ is small, with particularly stronger dependences on x when both $x_2,\,x_3 \approx 0$.

7 Comparison with previous works: impact of the three-gluon vertex

In this section, we compare our results with previous continuum studies of the four-gluon vertex. We recall that in the present work we employed a 4PI-based truncation of the SDE, given by Fig. 3, where all vertices in the one-loop diagrams appear dressed. On the other hand, in [78] all vertices on the r.h.s. of the SDE are set to tree-level, whereas in [8, 25] one vertex per diagram appears at tree-level. As such, the comparison of these results to ours allows us to assess the effect that the dressing of the vertices, and especially of the three-gluon vertex, has on the four-gluon SDE. Finally, we comment on the recent work of [124], where a single configuration, $(p,p,p,-3p)$, was computed within the Curci–Ferrari model [125], at one-loop.

For this task, we will focus on the configuration $(p,p,p,-3p)$, corresponding to $c_{11}$ of Fig. 7, which has also been studied in [8, 25, 78, 124]; for simplicity, we limit our discussion to the classical form factor $G_1$.

In this kinematic limit, all tensors $t_{i,\mu \nu \rho \sigma }^{abcd} (x,p)$ for $i \ge 4$ vanish.⁶ Then, Eq. (4.4) reduces to

$$\begin{aligned}{} & {} \overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(x,p) = \sum _{i = 1}^{3} G _i (x,p) \, t_{i,\mu \nu \rho \sigma }^{abcd}(x,p) , \nonumber \\{} & {} x = (1,1,1,-3) . \end{aligned}$$

(7.1)

Then, it is straightforward to show that the form factor denoted by $V_{\Gamma ^{(0)}}(p^2)$ in Eq. (4.17) of [78], and shown in Fig. 5 of that reference, corresponds precisely to $G_1(p,p,p,-3p)$.

Similarly, the projection

$$\begin{aligned}{} & {} D^{\mathrm{{\scriptscriptstyle 4g}}}(p_1,p_2,p_3,p_3) \nonumber \\{} & {} \quad := \frac{{{\overline{\Gamma }}}^{0}(p_1,p_2,p_3,p_4)\odot \overline{{\textrm{I}}\!\Gamma }(p_1,p_2,p_3,p_4)}{{{\overline{\Gamma }}}^{0}(p_1,p_2,p_3,p_4)\odot {{\overline{\Gamma }}}^{0}(p_1,p_2,p_3,p_4)}, \end{aligned}$$

(7.2)

computed in [25], reduces to $D^{\mathrm{{\scriptscriptstyle 4g}}}(p,p,p,-3p) = G_1(p,p,p,-3p) + (2/3) G_2(p,p,p,-3p)$. Since under our approximations $G_2 = 0$, we can set $D^{\mathrm{{\scriptscriptstyle 4g}}}(p,p,p,-3p) = G_1(p,p,p,-3p)$, and compare our result to that shown on the upper left panel of Fig. 8 of [25].

Note that [25, 78] employed renormalization schemes different to the one used in the present work, defined by the prescription in Eqs. (5.10) and (5.11). Hence, to perform a meaningful comparison, we rescale all results to be equal to 1 at $\mu = 4.3$ GeV, i.e.,

$$\begin{aligned} G_1(p,p,p,-3p)\rightarrow&\,\, \frac{G_1(p,p,p,-3p)}{G_1(\mu ,\mu ,\mu ,-3\mu )}. \end{aligned}$$

(7.3)

Fig. 10

Comparison of our results (red continuous line) for the configuration $c_{11}$ [Eq. (6.15)] with previous results, obtained in [78] (blue dashed), [25] (green dotted), and [124] (yellow dashed)

In Fig. 10 we show our result for $G_1(p,p,p,-3p)$ as a continuous red curve, the result of [78] is the blue dot-dashed curve, the data of [25] correspond to the green dotted curve, while the result of [124] is given by the yellow dashed curve.

Focusing on the SDE-derived results, let us first point out that they are all qualitatively rather similar; in particular, they reach a finite value at the origin, and remain positive for the entire range of the momentum p. The main reason underlying this qualitative similarity is the gluon propagator, shown in the upper left panel of Fig. 4, which is a common ingredient in all aforementioned SDE computations. Note, in particular, that the infrared finiteness of this propagator, usually associated with the dynamical generation of a gluon mass, has a stabilizing effect on the SDE computations.

The most prominent difference between the SDE results manifests itself for $p<1.5$ GeV. In this region, the results of [25, 78] display a large peak, which is nearly absent in our $G_1(p,p,p,-3p)$. Indeed, in this range of momenta, our result has a local maximum of 0.9 at $p = 0.8$ GeV. In contrast, the result of [78] is strongly enhanced in the infrared, reaching a maximum of 1.5 at 0.4 GeV, while [25] obtains a smaller maximum of 1.1 at 0.6 GeV, and becomes very similar to ours for $p\lessapprox 0.4$ GeV.

To understand the origin of these differences in the infrared behavior, we have computed the individual contributions of each diagram of Fig. 3, and compared to the Fig. 5 of [78] and Fig. 8 of [25]. We find that, in the infrared, the diagrams $(d_2)$ and $(d_3)$ contribute positively to $G_1(p,p,p,-3p)$, in agreement with [25, 78], but vary considerably in size within the different truncations.

Then, we note that both of these diagrams contain three-gluon vertices. As has been firmly established by lattice [43, 49,50,51, 114, 118, 119] and continuum studies [58, 91, 99, 126,127,128], the three-gluon vertex is strongly suppressed in the infrared in comparison to its tree-level value. Hence, in our treatment, the diagrams $(d_2)$ and $(d_3)$ yield minimal contributions, due to the suppressing effect of dressing the three-gluon form factor $L _{{sg}}(s^2)$ [cf. Eq. (6.1)]. Consequently, the shape of our $G_1$ is dominated by the tree-level and the negative $(d_4)$ diagram.

In contrast, in [78], where all vertices on the r.h.s. of the SDE are at tree-level, $(d_2)$ and $(d_3)$ give large contributions, giving rise to the peak seen in Fig. 10. Finally, the truncation of [25] yields a result between ours and that of [78], since there is only one tree-level vertex per diagram.

An additional noteworthy feature is the differences between the values that the various SDE curves reach at the origin, namely $G_1(0,0,0,0)$; evidently, all these values are finite, since no infrared divergences are associated with the computation of the form factor $G_1$. The deviations between the values of $G_1(0,0,0,0)$ in the various SDE approaches may be attributed again to the different approximations employed for the three-gluon vertices entering in the SDE diagrams. In particular, the gluon triangles [($d_3$) in Fig. 3, and permutations] have positive nonzero saturation values (see Fig. 5 of [78] and Fig. 8 of [25] ), which get suppressed when the three-gluon vertices are dressed. This suppression accounts for the fact that the zero-momentum limit found in the present work is smaller than that of [78] and [25].

From these observations we conclude that the approximation employed for the three-gluon vertex has considerable impact on SDE analyses of the four-gluon vertex.

Turning to the result of [124], we notice a clear departure from the general SDE findings, for momenta below 0.5 GeV. In particular, the yellow curve reverses its sign at around 0.3 GeV, and decreases rapidly towards $-1.7$ at $p=0$. The authors of [124] attribute the deviation from the SDE pattern to truncation issues intrinsic to their approach. In that respect, one should note that the Curci–Ferrari model captures some of the basic QCD dynamics by means of introducing a tree-level massive propagator, and subsequently implementing renormalization-group types of resummations. However, the resulting resummations may recover the genuine non-perturbative QCD effects only at higher orders, a fact which may cause discrepancies when specific Green’s functions are considered at a lower level of resummation, as is the case in [124].

Finally, we point out that the four-gluon vertex has also been studied in the context of scaling solutions in [8, 25, 77]. In this case, the classical form factor displays infrared divergences that are absent in our framework.

8 Ultraviolet finiteness of the form factors $G_1$ and $G_3$

Even though the numerical evaluation of the SDEs presented in the previous section gave rise to results that are free of ultraviolet divergences, it would be clearly advantageous to devise an analytic demonstration of this fact. In this section, we show that when the SDE undergoes the renormalization procedure outlined in Sect. 5, and under the assumptions discussed in Sect. 6.1, one obtains ultraviolet finite form factors $G_1$ and $G_3$. In particular, $G_1$ becomes finite after a single subtraction, while $G_3$ turns out to be automatically free of ultraviolet divergences, exactly as expected.

We begin by writing the SDEs in Eq. (5.15) in Euclidean space using hyperspherical coordinates; then, integrating over the angle between k and p, and setting $y:= k^{2}$, we arrive at

$$\begin{aligned} G_i(x,p) = \int _{0}^{\Lambda _{\mathrm{{\scriptscriptstyle UV}}}^2}\!\!\!\!\!\!\! dy \,f_i(y,p^2,x), \qquad i=1,3, \end{aligned}$$

(8.1)

where $\Lambda _{\mathrm{{\scriptscriptstyle UV}}}^2$ is an ultraviolet cutoff, and $f_i(y,p^2,x)$ denotes the sum of the integrands of the projected diagrams. The closed expressions for the $f_i(x,p)$ are rather complicated; however, for the purposes of renormalization, only their behavior for asymptotic y is relevant.

At this point we introduce an arbitrary mass scale M, with $p^2, \mu ^2 \ll M^2$, and split the integrals in Eq. (8.1) into a finite and a potentially divergent part, i.e.,

$$\begin{aligned} \!\!G_{i}(x,p) = \int _{0}^{M^2}\!\!\!\!\!\!\!\! dy \,f_i(y,p^{2},x) \,+\, \underbrace{\int _{M^2}^{\Lambda _{\mathrm{{\scriptscriptstyle UV}}}^2}\!\!\!\!\!\!\! dy \,f_i(y,p^{2},x)}_{\mathrm{potentially \,\, divergent}}. \nonumber \\ \end{aligned}$$

(8.2)

The type of divergence contained in the second integral may be established by performing a Taylor expansion of $f_i(y,p^2,x)$ around $p^2/M^2=0$,

$$\begin{aligned} f_i(y, p^{2}, x)&= f_i(y) + p^{2}\left[ \frac{\partial f_i(y, p^{2}, x)}{\partial p^{2}}\right] _{\!p^2= 0} + \cdots , \end{aligned}$$

(8.3)

where the ellipsis denotes higher derivatives. Note that, upon setting $p^2=0$, all reference to the parameter $x:=(x_1,x_2,x_3,x_4)$ drops out from $f_i(y)$.

Evidently, for the renormalization to go through, the only potential divergence must be isolated in the term $f_i(y)$, whereas the terms with the derivatives must yield finite integrals when substituted into Eq. (8.2).

To check if this indeed so, let us first focus on $f_3(y)$; a detailed calculation reveals that it consists of four contributions, $I_{i}(y)$, one from each diagram $(\bar{d}_{i}^{s})$ $[i=1,2,3,4]$, namely

$$\begin{aligned} f_{3}(y)&= \frac{3\alpha _{s}}{64\pi } \left[ I_{1}(y) -24 \, I_{2}(y) + 40 \, I_{3}(y) -17 \, I_{4}(y) \right] , \end{aligned}$$

(8.4)

where

$$\begin{aligned}&I_1(y) = y^{-1} B_{1}^{4}(y,y,\pi ) F^{4}(y); \quad I_2(y) = y^{3}\Delta ^{4}(y) L _{{sg}}^{4}(y);\nonumber \\&I_3(y) =y^{2}\Delta ^{3}(y) L _{{sg}}^{2}(y) G^{*}_1(y); \quad I_4(y) = y\Delta ^{2}(y) G^{*2}_1(y). \end{aligned}$$

(8.5)

To further evaluate the $I_i(y)$, we assume that, in the limit $y\rightarrow \infty$, the functions comprising them reproduce their one-loop resummed forms [8, 19, 123, 129] i.e.,

$$\begin{aligned}&F(y)\sim L _{\mathrm{{\scriptscriptstyle UV}}}^{-9/44}(y), \quad \Delta (y)\sim y^{-1} L _{\mathrm{{\scriptscriptstyle UV}}}^{-13/22}(y),\nonumber \\&B_{1}(y,y,\pi )\sim 1, \quad L _{{sg}}(y)\sim L _{\mathrm{{\scriptscriptstyle UV}}}^{17/44}(y), \nonumber \\&G^{*}_1(y)\sim L _{\mathrm{{\scriptscriptstyle UV}}}^{2/11}(y), \quad L _{\mathrm{{\scriptscriptstyle UV}}}(y) := c\,\ln (y/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2}), \end{aligned}$$

(8.6)

where $c = 1/\ln (\mu ^2/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2})$, and $\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}$ is the QCD mass-scale in the MOM scheme. Note that this assumption is built into the fits employed for all quantities that serve as inputs for the SDE: indeed, the expressions for F(y), $\Delta (y)$, and $L _{{sg}}(y)$ given respectively in Eqs. (C6), (C11) and (C12) of [117] are designed to capture the correct one-loop resummed anomalous dimension, while the numerical results in Fig. 13 of [58] satisfy $B_1(k,-k,0)\rightarrow 1$ at large k.

The anomalous dimension of $G_1$ can be obtained by standard renormalization group analysis [130] from the one-loop form of the renormalization constant ${{\widetilde{Z}}}_4$, given in Eq. (B9). Specifically, the exponent $d_{\mathrm{{\scriptscriptstyle 4g}}}$ of the logarithm in $G_1$ is given by $d_{\mathrm{{\scriptscriptstyle 4\,g}}} = \gamma _{\mathrm{{\scriptscriptstyle 4\,g}}}^{(0)}/\beta _0$, where $\beta _0 = 11/(4\pi )$ and $\gamma _{\mathrm{{\scriptscriptstyle 4g}}}^{(0)}$ are the lowest order coefficients of the beta function, $\beta (\alpha _s)$, and the four-gluon anomalous dimension, $\gamma _{\mathrm{{\scriptscriptstyle 4g}}}(\alpha _s)$, respectively, i.e.,

$$\begin{aligned} \beta (\alpha )= & {} \frac{\partial \alpha }{\partial \ln \mu ^2} = - \beta _0 \alpha _s + \cdots , \nonumber \\ \gamma _{\mathrm{{\scriptscriptstyle 4g}}}(\alpha _s)= & {} \frac{1}{{{\widetilde{Z}}}_4}\frac{\partial {{\widetilde{Z}}}_4 }{\partial \ln \mu ^2} = - \gamma _{\mathrm{{\scriptscriptstyle 4g}}}^{(0)} \alpha _s + \cdots , \end{aligned}$$

(8.7)

with ellipses denoting higher powers of $\alpha _s$. Then, Eq. (B9) entails $\gamma _{\mathrm{{\scriptscriptstyle 4g}}}^{(0)} = 1/(2\pi )$ and, hence $d_{\mathrm{{\scriptscriptstyle 4g}}} = 2/11$.

Using Eq. (8.6) in Eq. (8.5), we find that all $I_i(y)$ are equal, namely

$$\begin{aligned} I_i(y) = \frac{1}{c^{9/11} y \ln ^{9/11} (y/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2})}:= I(y) , \qquad \forall i . \end{aligned}$$

(8.8)

Note that the individual contributions from each diagram diverge, since the integral

$$\begin{aligned} {{\mathcal {I}}}&:= \int _{\!M^{2}}^{\Lambda _{\mathrm{{\scriptscriptstyle UV}}}^{2}} \!\!dy \,I(y) \nonumber \\&= \frac{11}{2}c^{-9/11}\left[ \ln ^{2/11} (\Lambda _{\mathrm{{\scriptscriptstyle UV}}}^2/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2}) -\ln ^{2/11} (M^2/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2})\right] , \end{aligned}$$

(8.9)

diverges as $\Lambda _{\mathrm{{\scriptscriptstyle UV}}}^2 \rightarrow \infty$. However, the substitution of Eq. (8.8) into Eq. (8.4) reveals that

$$\begin{aligned} f_{3}(y)&= \frac{3\alpha _{s}}{64\pi } \left[ 1-24 + 40 -17 \right] I(y) = 0 , \end{aligned}$$

(8.10)

namely that the full asymptotic integrand $f_3(y)$ vanishes before carrying out any integration.

Turning to the form factor $G_1$, note that only $(\bar{d}_{3}^{s})$ and $(\bar{d}_{4}^{s})$ contribute to it, yielding

$$\begin{aligned} f_{1} (y) = \frac{\alpha _{s}}{2\pi } \left[ I_3(y) - 2 I_4(y)\right] = - \frac{\alpha _{s}}{2\pi } I(y) , \end{aligned}$$

(8.11)

which upon integration yields the divergent contribution of $G_1$, given by the constant

$$\begin{aligned} G_1^{\textrm{div}} = -\frac{\alpha _{s}}{2\pi } \, {{\mathcal {I}}}. \end{aligned}$$

(8.12)

Clearly, the subtraction prescribed by the first relation in Eq. (5.15) will cancel the divergence in Eq. (8.12), giving rise to a finite $G_1$. Specifically, the exact same steps leading from Eqs. (8.1) to (8.12) may be repeated for $f_1(y,\mu ^2, x_0)$, expanding around $\mu ^2/M^2=0$; $x_0$ denotes the reference configuration $(0,1,1,-2)$ in Eq. (5.11).

We end this section by confirming that the higher derivative terms in Eq. (8.3) are ultraviolet finite, and do not interfere with renormalization. In particular, with the aid of Eq. (8.6), we obtain

$$\begin{aligned}&\left[ \frac{\partial f_i(y, p^{2}, x_{i})}{\partial p^{2}}\right] _{\!p^2= 0} \nonumber \\&\quad = \frac{ a_{i} + b_{i}\log (y/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2}) + c_{i}\log ^{2}(y/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2})}{y^2 \log ^{31/11}(y/\Lambda _{\mathrm{{\scriptscriptstyle MOM}}}^{2})} + \cdots , \end{aligned}$$

(8.13)

for constants $a_{i}$, $b_{i}$ and $c_{i}$ that depend in general on x, and the ellipsis denotes terms that are subleading for large y. Integrating the r.h.s. of Eq. (8.13) over y yields a convergent result; keeping higher order derivatives in the expansion of Eq. (8.3) leads to even faster converging integrals.

Fig. 11

Comparison of the nonperturbative solution for $G^{*}_1(y)$ with its one-loop resummed behavior given by Eq. (8.6)

Fig. 12

The lattice data for the gluon dressing function ${{\mathcal {Z}}}(p^2):= p^2\Delta (p^2)$ [42, 54] (points) and the fit given by Eqs. (C11) of [117] (blue solid line) (left panel). The effective charge $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$, defined in Eqs. (9.1) and computed for the fourteen collinear configurations listed in Eq. (6.15) (right panel). In the inset we show a zoom the fourteen $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$ in the deep infrared region

It is important to emphasize that, for asymptotic values of the momentum, our numerical solutions for $G^{*}_1$ are completely compatible with the anomalous dimension of 2/11, quoted in Eq. (8.6); this is shown in Fig. 11.

9 Four-gluon effective charge

Typically, the quantitative description of the strength of a given interaction proceeds through the construction of the corresponding renormalization group invariant (RGI) effective charge [70, 77, 131,132,133,134,135,136,137,138]. In the case of the four-gluon interaction, the appropriate RGI combination is obtained with the aid of the relation $Z_g^{-1} = Z_4^{-1/2} Z_A$ [see Eq. (5.8)]. Specifically, introducing the gluon dressing function ${{\mathcal {Z}}}(p^2):= p^2\Delta (p^2)$ [see left panel of Fig. 12], it is straightforward to establish that the combination

$$\begin{aligned} \alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)= & {} \, \alpha _{s} G _1 (x,p) {{\mathcal {Z}}}^2(p^2) \nonumber \\= & {} \alpha ^{{\scriptscriptstyle R}}_{s}(\mu ^2) G _1^{{\scriptscriptstyle R}} (x,p, \mu ) {{\mathcal {Z}}}^2_{{\scriptscriptstyle R}}(p^2,\mu ^2) , \end{aligned}$$

(9.1)

retains the same form before and after renormalization, and thus, does not depend on the renormalization point $\mu$, even though the individual components are $\mu$-dependent. Then, the quantity $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$ will be constructed using inputs renormalized at a given $\mu$, which we choose $\mu = 4.3$ GeV; evidently, any other choice of $\mu$ would be equally good, since the value of $\alpha ^{{\scriptscriptstyle R}}_{s}(\mu ^2)$ is adjusted to compensate precisely the $\mu$-dependence in the other components.

In order to obtain a concrete realization of a vertex-derived effective charge, one normally specifies a particular kinematic configuration for the vertex form factor entering in it. For instance, in the case of the effective charges $\alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)$ and $\alpha _{\mathrm{{\scriptscriptstyle 3g}}}(p)$, obtained from the ghost-gluon and three-gluon vertices, respectively [70, 77, 132,133,134],

$$\begin{aligned} \alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)= & {} \alpha _s(\mu ^2) B_{sg}^2(p^2)F^2(p^2){{\mathcal {Z}}}(p^2) , \nonumber \\ \alpha _{\mathrm{{\scriptscriptstyle 3g}}}(p)= & {} \alpha _s(\mu ^2) L _{{sg}}^2(p^2){{\mathcal {Z}}}^3(p^2) , \end{aligned}$$

(9.2)

where $B_{sg}(p^2):=B_1(p,-p,0)$ and $L _{{sg}}(p^2)$ are the “soft-gluon” limits of the classical form factors of the ghost-gluon and three-gluon vertices, respectively. Instead, in order to obtain a more representative picture for the strength of the four-gluon interaction, we evaluate $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$ using not one, but all fourteen collinear configurations listed in Eq. (6.15); the results are shown on the right panel of Fig. 12.

We emphasize that the component responsible for the overall shape of all these $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$ is the gluon dressing function, ${{\mathcal {Z}}}(p^2)$, depicted in the left panel of Fig. 12. Note, in particular, that ${{\mathcal {Z}}}(p^2)$ is positive-definite throughout the entire range of space-like momenta considered, except at the origin where it vanishes, due to the fact that $\Delta (0) = \textrm{constant}$ [see upper left panel of Fig. 4]. Then, the minor differences in the various $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$ originate from the multiplication of ${{\mathcal {Z}}}(p^2)$ by the various $G _1 (x,p)$, shown in the upper left panel of Fig. 7. Evidently, given that the $G _1 (x,p)$ are all positive-definite functions in the entire range of the momentum p, the resulting family of $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$ is positive for all p, approaching zero at the origin with rates proportional to $p^2$, but with different proportionality factors, i.e., the $c_{4g}$ in Eq. (9.3).

In Fig. 13 we present a comparison between the family $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$ and the two effective charges $\alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)$ and $\alpha _{\mathrm{{\scriptscriptstyle 3g}}}(p)$, defined in Eq. (9.2). To that end, and given the similarity between the fourteen charges displayed in the right panel of Fig. 12, we opt to represent them collectively by means of the blue band shown in Fig. 13. The band is delimited by the uppermost and lowermost cases, namely $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(c_1,p)$ and $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(c_{11},p)$, respectively [see Eq. (6.15) for the numerical values of the $c_i$].

For momenta $p\lessapprox 1.5~\text {GeV}$ there is a clear hierarchy, which is expressed by the inequality $\alpha _{\mathrm{{\scriptscriptstyle 3\,g}}}(p)< \alpha _{\mathrm{{\scriptscriptstyle 4\,g}}}(x,p) < \alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)$, independently of the collinear configuration chosen for $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$. In fact, the same hierarchy was obtained in [8, 25] for charges defined by the three- and four-gluon vertices in their totally symmetric configurations, and the soft-ghost kinematics for the ghost-gluon vertex.

Fig. 13

Comparison of the effective charges $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$, $\alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)$, and $\alpha _{\mathrm{{\scriptscriptstyle 3g}}}(p)$, defined in Eqs. (9.1) and (9.2), respectively. The blue band delimits the upper and lower cases of $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x,p)$, evaluated with the configurations $c_1$ and $c_{11}$ of Eq. (6.15). In the inset, we show a zoom of the behavior of three effective charges in the deep infrared region

Focusing on the deep infrared, we note that none of the charges turns negative, and that all go to zero for $p=0$, albeit at different rates. In fact, given that F(0), $\Delta (0)$, $B_{sg}(0)$ are all positive and finite, whereas $L _{{sg}}(p) \sim \ln (p^2/\mu ^2)$ for small p (see Fig. 4), one easily derives that

$$\begin{aligned}{} & {} \alpha _{cg}(p) \sim c_{cg} p^2 , \qquad \alpha _{4g}(x,p) \sim c_{4g} p^4 , \nonumber \\{} & {} \alpha _{3g}(p) \sim c_{3g} p^6 \ln ^2(p^2/\mu ^2) , \end{aligned}$$

(9.3)

at small p, for some positive constants $c_{cg}$, $c_{4\,g}$ and $c_{3g}$. These asymptotics match the observed behavior, according to which $\alpha _{cg}(p)$ goes to zero at the slowest rate, while $\alpha _{3g}(p)$ at the fastest. Moreover, $\alpha _{3g}(p)$ touches zero at a nonzero momentum,⁷ due to the zero crossing of the $L _{{sg}}(p)$ shown in the lower left panel of Fig. 4; however, $\alpha _{3g}(p)$ does not reverse sign, because its dependence on $L _{{sg}}(p)$ is quadratic.

In the ultraviolet, the different charges slowly merge into each order. Nevertheless, even at $p = 5$ GeV, the $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}$, $\alpha _{\mathrm{{\scriptscriptstyle 3g}}}$ and $\alpha _{\mathrm{{\scriptscriptstyle cg}}}$ are visibly different. Moreover, for $p > rapprox 3.5$ GeV, the charge hierarchy is modified with respect to the infrared: $\alpha _{\mathrm{{\scriptscriptstyle 4\,g}}}(x,p)< \alpha _{\mathrm{{\scriptscriptstyle cg}}}(p) < \alpha _{\mathrm{{\scriptscriptstyle 3\,g}}}(p)$. To verify that this ordering and the overall sizes of the charges in the ultraviolet are correct, rather than a numerical or truncation artifact, we compute the relation between these charges at one loop.

Perturbatively, one charge can be expanded in powers of any other [116]; in particular, taking $x = x_0$

$$\begin{aligned} \alpha {\mathrm{{\scriptscriptstyle 3g}}}(p)= & {} \alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x_0,p) + a_1\alpha _{\mathrm{{\scriptscriptstyle 4g}}}^2(x_0,p) + \cdots , \nonumber \\ \alpha _{\mathrm{{\scriptscriptstyle cg}}}(p)= & {} \alpha _{\mathrm{{\scriptscriptstyle 4g}}}(x_0,p) + b_1\alpha _{\mathrm{{\scriptscriptstyle 4g}}}^2(x_0,p) + \cdots , \end{aligned}$$

(9.4)

where the ellipses denote higher powers of $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}$. Then, our task reduces to determining the one-loop coefficients $a_1$ and $b_1$. Using the results of [140] for $B_{sg}(p^{2})$, $F(p^{2})$, ${{\mathcal {Z}}}(p^{2})$, and $L _{{sg}}(p^{2})$, together with the one-loop result for $G_1(x_0,p)$ given in Eq. (B10), we find that

$$\begin{aligned} a_{1}&= \frac{1}{96\pi }\left[ 161 + 28\ln (2)\right] \approx 0.60, \nonumber \\ b_{1}&= \frac{1}{96\pi }\left[ 47 + 28\ln (2)\right] \approx 0.22. \end{aligned}$$

(9.5)

Since $a_1> b_1 > 0$, Eq. (9.4) implies that the hierarchy found in Fig. 13 at large p agrees with perturbation theory. In fact, it is straightforward to confirm that the agreement is not just qualitative, but quantitative. In particular, setting $p = 4.3$ GeV and $\alpha _{\mathrm{{\scriptscriptstyle 4g}}}= 0.23$ [see Eq. (B14)] into Eq. (9.4), we get $\alpha _{\mathrm{{\scriptscriptstyle cg}}}= 0.24$, and $\alpha _{\mathrm{{\scriptscriptstyle 3\,g}}}= 0.26$; these values match those obtained from the full nonperturbative calculation (i.e., the corresponding curves in Fig. 13), namely $\alpha _{\mathrm{{\scriptscriptstyle cg}}}= 0.26$ and $\alpha _{\mathrm{{\scriptscriptstyle 3g}}}= 0.27$, within $8\%$ and $3\%$, respectively.

10 Conclusions

We have presented a comprehensive nonperturbative study of the transversely-projected four-gluon vertex by means of the SDE obtained within the 4PI effective action formalism. For the purposes of this work we have restricted our attention to the case of the collinear kinematics, which simplify considerably the complexity associated with this vertex. This kinematic choice, in conjunction with the elimination of color terms of the type $f^{abx} d^{cdx}$ by virtue of the charge conjugation symmetry, reduces the number of possible form factors down to fifteen. A special subset of three form factors, including the one associated with the tree-level (classical) tensorial structure, is subsequently singled out and studied in detail. Our treatment of the SDE uses as external inputs results obtained from lattice QCD and previous continuous studies.

The most outstanding nonperturbative feature that emerges from our analysis is the “planar degeneracy” of the form factors considered. Specifically, at a high level of accuracy, all kinematic configurations that lie on a given plane share the same form factors in the infrared. This special property, first observed at the level of the three-gluon vertex  [58, 89,90,91], appears to be shared by the four-gluon vertex, at least in the context of the collinear configurations that we have studied. It would be clearly important to probe the extent of validity of the planar degeneracy for more complicated configurations of momenta, such as general soft-gluon, where one momentum vanishes and the other three are completely arbitrary; calculations in this direction are already in progress.

It would be of course particularly interesting to confront our findings with lattice QCD, as has been the case with all other fundamental vertices of the theory. Unfortunately, the preliminary data available [92,93,94] are not sufficiently conclusive for confirming any of the main features encountered in the present study. It would be interesting to refine the lattice simulations, in order for a meaningful comparison with the results of functional methods to become feasible. In this context, the assumption of planar degeneracy might prove particularly useful, because it would increase significantly the available statistics.

In principle, the methods of the present study may be applicable to other 1PI four-point functions of QCD, such as the gluon-gluon-ghost-ghost and four-ghost functions, previously considered in in [79], as well as the quark-quark-gluon-gluon, quark-quark-ghost-ghost, and four-quark vertices. A common characteristic of all these functions is the absence of classical (tree-level) contribution, and the ensuing ultraviolet finiteness. These Green’s functions are usually components of the kernels appearing in the SDEs; it would be therefore valuable to determine their overall numerical impact. In this context, the choice of collinear configurations is again expected to simplify the analysis. Of course, in such a case, the infrared safety of the entire calculation needs be evaluated, keeping in mind that the infrared stabilization caused by the gluon and quark propagators is counteracted by the infrared divergences induced by the ghost propagators. In addition, since the aforementioned Green’s functions do not display full Bose-symmetry with respect to all their legs, planar degeneracy is not expected to be valid at any useful level of approximation.

Let us finally point out that in our analysis we have not considered dynamical quarks. The inclusion of quarks may proceed straightforwardly, by making two basic modifications to the treatment presented here. First, in the diagrammatic representation of the SDE in Fig. 3, one has to include additional diagrams containing quark-loops [141, 142]. Second, the inputs employed, such as gluon and ghost propagators, as well as ghost-gluon and three-gluon vertices, must be replaced by their “unquenched” counterparts, see [47, 119, 143, 99, 144, 145], and [119], respectively. We hope to be able to present a study of the four-gluon vertex with $2+1$ quark flavors in the near future.

Appendices

Bose symmetric basis for collinear configurations

In this appendix we briefly describe the $S_4$ permutation group formalism employed for the construction of the tensor basis of Eq. (4.4) for $\overline{{\textrm{I}}\!\Gamma }^{abcd}_{\mu \nu \rho \sigma }(x,p)$. A detailed account of this method in the context of four-point functions is given in [107].

The primary objective of this construction is to obtain tensors $t_{i,\mu \nu \rho \sigma }^{abcd} (x,p)$ that are invariant under a permutation of any two external legs of the vertex. To accomplish this, one first identifies multiplets of the $S_4$ permutation group, which transform nontrivially under permutations (see Eq. (47) of [107]). Then, one can construct singlets (invariants) by taking appropriately defined products of these multiplets.

We begin by rearranging the momenta $p_i$ into the Mandelstam momenta, which for collinear configurations read

$$\begin{aligned} q:= & {} p_1 + p_3 = ( x_1 + x_3 )p, \nonumber \\ t:= & {} p_2 + p_3 = ( x_2 +x_3 )p ,\nonumber \\ k:= & {} p_1 + p_2 = ( x_1 + x_2 )p . \end{aligned}$$

(A1)

From these momenta, we form six scalars which are chosen to be

$$\begin{aligned} q^2 =&( x_1 + x_3 )^2 p^2, \quad w_{1} := q\cdot k = ( x_1 + x_3 )( x_1 + x_2 )p^2,\nonumber \\ k^2 =&( x_1 + x_2 )^2 p^2, \quad w_{2} := t\cdot k = ( x_2 + x_3 )( x_1 + x_2 )p^2, \nonumber \\ t^2 =&( x_2 + x_3 )^2 p^2, \quad w_{3} := q\cdot t = ( x_1 + x_3 )( x_2 + x_3 )p^2. \end{aligned}$$

(A2)

The above scalars can then be combined to form an $S_4$ singlet,

$$\begin{aligned} \bar{s}^{2} = \frac{1}{2}(t^{2} + q^{2} + k^{2}) = \frac{p^{2}}{2}\left[ x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}\right] , \end{aligned}$$

(A3)

together with a doublet, $\overline{\mathcal {D}}$, and a triplet, $\overline{\mathcal {T}}$, given by

$$\begin{aligned}&\overline{\mathcal {D}} = \frac{1}{2 \bar{s}^{2}} \begin{bmatrix} \sqrt{3}(q^{2}-t^{2})\\ t^{2}+q^{2}-2k^{2} \end{bmatrix},\nonumber \\&\overline{\mathcal {T}} = \frac{1}{8 \bar{s}^{2}} \begin{bmatrix} 2(w_{1} + w_{2} + w_{3})\\ \sqrt{2}(w_{1} + w_{2} -2w_{3})\\ \sqrt{6}(w_{2} - w_{1}) \end{bmatrix}. \end{aligned}$$

(A4)

Note that the denominator $\bar{s}^2$ in Eq. (A4) is introduced such that $\overline{\mathcal {D}}$ and $\overline{\mathcal {T}}$ are dimensionless.

Next, the three Lorenz tensors in Eq. (4.3) can be organized into a singlet, $\mathcal {S}_{L}$, and a doublet, $\mathcal {D}_{L}$, given respectively by

$$\begin{aligned} \mathcal {S}_{L}&= P_{\mu \sigma }P_{\nu \rho } + P_{\mu \rho }P_{\nu \sigma } + P_{\mu \nu }P_{\rho \sigma }, \nonumber \\ \mathcal {D}_{L}&= \begin{bmatrix} \sqrt{3}(P_{\mu \rho } P_{\nu \sigma }-P_{\mu \sigma }P_{\nu \rho }) \\ P_{\mu \sigma }P_{\nu \rho } + P_{\mu \rho }P_{\nu \sigma } -2 P_{\mu \nu } P_{\rho \sigma } \end{bmatrix}. \end{aligned}$$

(A5)

Similarly, the five color tensors of Eq. (3.21) may be collected into a singlet,

$$\begin{aligned} \mathcal {S}_{C} = \delta ^{ab} \delta ^{cd}+\delta ^{ac} \delta ^{bd}+\delta ^{ad} \delta ^{bc} , \end{aligned}$$

(A6)

and two doublets,

$$\begin{aligned} \mathcal {D}_{C}^{(1)}&= \frac{1}{2}\begin{bmatrix} \sqrt{3} (\delta ^{ac} \delta ^{bd}-\delta ^{ad} \delta ^{bc})\\ (-2 \delta ^{ab} \delta ^{cd}+\delta ^{ac} \delta ^{bd}+\delta ^{ad} \delta ^{bc}) \end{bmatrix},\nonumber \\ \mathcal {D}_{C}^{(2)}&= \frac{1}{2}\begin{bmatrix} \frac{1}{ \sqrt{3}}(f^{cae} f^{bde}-2 f^{abe} f^{cde}+f^{ade} f^{bce})\\ (f^{ade} f^{bce}-f^{cae} f^{bde}) \end{bmatrix}. \end{aligned}$$

(A7)

At this point, we define special products of $S_4$ multiplets that will be used to construct invariants. To this end, let ${{\mathcal {S}}}$ denote a generic singlet, and

$$\begin{aligned} \mathcal {D} = \begin{bmatrix} a\\ s \end{bmatrix}, \quad \mathcal {T} = \begin{bmatrix} u\\ v\\ w \end{bmatrix}, \end{aligned}$$

(A8)

denote generic doublets and triplets, respectively. Then we define the dot (“$\cdot$”) product as

$$\begin{aligned} \mathcal {D}\cdot \mathcal {D}^\prime =a a^\prime + s s^\prime , \qquad \mathcal {T}\cdot \mathcal {T}^\prime = uu' + vv' + ww' , \end{aligned}$$

(A9)

together with “star” (“$\star$”) and “wedge” (“$\wedge$”) products given by

$$\begin{aligned} \mathcal {D}*\mathcal {D}'&= \begin{bmatrix} a s' + s a'\\ a a' - s s' \end{bmatrix}, \nonumber \\ \mathcal {T}*\mathcal {T}'&= \begin{bmatrix} v w' + w v' + \sqrt{2}(u w' + wu')\\ w w' - v v' + \sqrt{2}( u v' + v u') \end{bmatrix}, \end{aligned}$$

(A10)

and

$$\begin{aligned} \mathcal {T}\wedge \mathcal {D} = \begin{bmatrix} va-ws\\ ua - \frac{1}{\sqrt{2}}(va + ws)\\ -us - \frac{1}{\sqrt{2}}(vs-wa) \end{bmatrix},{} & {} \mathcal {D}\wedge \mathcal {D}' = as' - sa'. \end{aligned}$$

(A11)

Using the above products, it can be shown that combinations of the types

$$\begin{aligned}&{{\mathcal {S}}} {{\mathcal {S}}}^\prime , \quad \mathcal {D}\cdot \mathcal {D}, \quad \mathcal {T}\cdot \mathcal {T}, \quad \mathcal {D}\cdot (\mathcal {D}^\prime *\mathcal {D}^{\prime \prime }),\quad (\mathcal {T}*\mathcal {T}^\prime )\cdot \mathcal {D},\nonumber \\&(\mathcal {T}*\mathcal {T}^\prime )\cdot (\mathcal {D}*\mathcal {D}^\prime ), \quad \left[ \mathcal {T}\cdot (\mathcal {T}^\prime \wedge \mathcal {D})\right] (\mathcal {D}^\prime \wedge \mathcal {D}^{\prime \prime }), \end{aligned}$$

(A12)

are $S_4$ singlets [107]. Hence, to construct a Bose symmetric tensor basis for collinear configurations, we form all possible combinations of the above types using the multiplets in Eqs. (A3) through (A7), and select from these 15 linearly independent singlets.

From the procedure outlined above, we obtain the following basis

$$\begin{aligned}&t_{1} = - \mathcal {D}_{L}\cdot \mathcal {D}_{C}^{(2)}, \quad t_{6} = \mathcal {S}_{C} (\overline{\mathcal {D}} \cdot \mathcal {D}_{L}),\nonumber \\&t_{11}= (\overline{\mathcal {T}}*\overline{\mathcal {T}})\cdot (\mathcal {D}_{L}*\mathcal {D}_{C}^{(1)})\quad t_{2} = - \mathcal {D}_{L}\cdot \mathcal {D}_{C}^{(1)},\nonumber \\&t_{7} = \mathcal {S}_{L} [(\overline{\mathcal {T}}*\overline{\mathcal {T}})\cdot \mathcal {D}_{C}^{(1)}],\quad t_{12}= (\overline{\mathcal {T}}*\overline{\mathcal {T}})\cdot (\mathcal {D}_{L}*\mathcal {D}_{C}^{(2)}),\nonumber \\&t_{3} = - \mathcal {S}_{L} \mathcal {S}_{C},\quad t_{8} = \mathcal {S}_{L} [(\overline{\mathcal {T}}*\overline{\mathcal {T}})\cdot \mathcal {D}_{C}^{(2)}],\nonumber \\&t_{13}= \mathcal {S}_{C} [(\overline{\mathcal {T}}*\overline{\mathcal {T}})\cdot \mathcal {D}_{L}], t_{4} = - \mathcal {S}_{L} (\overline{\mathcal {D}} \cdot \mathcal {D}_{C}^{(1)})\nonumber \\&t_{9} = \overline{\mathcal {D}}\cdot (\mathcal {D}_{L}*\mathcal {D}_{C}^{(1)}),\quad t_{14}= [\overline{\mathcal {T}}\cdot (\overline{\mathcal {T}}\wedge \overline{\mathcal {D}})](\mathcal {D}_{L}\wedge \mathcal {D}_{C}^{(1)}),\nonumber \\&t_{5} = \mathcal {S}_{L} (\overline{\mathcal {D}} \cdot \mathcal {D}_{C}^{(2)}), \quad t_{10}= \overline{\mathcal {D}}\cdot (\mathcal {D}_{L}*\mathcal {D}_{C}^{(2)}), \nonumber \\&t_{15}= [\overline{\mathcal {T}}\cdot (\overline{\mathcal {T}}\wedge \overline{\mathcal {D}})](\mathcal {D}_{L}\wedge \mathcal {D}_{C}^{(2)}). \end{aligned}$$

(A13)

Note that the dependence on the $x_i$ appears only through the scalar multiplets, $\bar{s}$, $\overline{{\mathcal {D}}}$ and $\overline{{\mathcal {T}}}$, of Eqs. (A3) and (A4). Hence, the tensors $t_{1,2,3}$ are independent of $x_i$, whereas all others depend on it.

Changing renormalization schemes

The data for the three-gluon and ghost-gluon form factors, $L _{{sg}}(s^2)$ and $B_1(q,r,p)$, respectively, used as external inputs in our SDE, were originally renormalized in a scheme different than that of Eqs. (5.10) and (5.11) that we employ in our analysis. Specifically, $L _{{sg}}(s^2)$ and $B_1(q,r,p)$ were computed in [58, 120] in the “asymmetric MOM scheme”, defined by

$$\begin{aligned} \Delta ^\mathrm{{\scriptscriptstyle asym}}(\mu ^2) = \mu ^{-2} , \qquad F^\mathrm{{\scriptscriptstyle asym}}(\mu ^2) = 1 , \qquad L _{{sg}}^\mathrm{{\scriptscriptstyle asym}}(\mu ^2) = 1 , \nonumber \\ \end{aligned}$$

(B1)

where we introduce the superscript “$\textrm{asym}$” to denote quantities renormalized in this scheme.

Then, from the multiplicative renormalizability expressed by Eq. (5.7) it follows that

$$\begin{aligned} {{\widetilde{Z}}}_{A} =&\, \Delta _{\mathrm{{\scriptscriptstyle B}}}(\mu ^2)/\Delta (\mu ^2), \quad Z_{A}^\mathrm{{\scriptscriptstyle asym}}=\, \Delta _{\mathrm{{\scriptscriptstyle B}}}(\mu ^2)/\Delta ^{\mathrm{{\scriptscriptstyle asym}}}(\mu ^2), \nonumber \\ {{\widetilde{Z}}}_{c} =&\, F_{\mathrm{{\scriptscriptstyle B}}}(\mu ^2)/F(\mu ^2), \quad Z_{c}^\mathrm{{\scriptscriptstyle asym}}=\, F_{\mathrm{{\scriptscriptstyle B}}}(\mu ^2)/F^{\mathrm{{\scriptscriptstyle asym}}}(\mu ^2), \end{aligned}$$

(B2)

where the index “$\textrm{B}$” denotes unrenormalized quantities.⁸ Hence, since the bare $\Delta _{\mathrm{{\scriptscriptstyle B}}}(\mu ^2)$ and $F_{\mathrm{{\scriptscriptstyle B}}}(\mu ^2)$ are scheme-independent, and the renormalization prescriptions of Eqs. (B1) and (5.10) coincide for the propagators, the renormalization constants $Z_A$ and $Z_c$ have the same values in both schemes⁹, i.e.,

$$\begin{aligned} {{\widetilde{Z}}}_{A} = Z_{A}^\mathrm{{\scriptscriptstyle asym}}= \mu ^2 \Delta _{\mathrm{{\scriptscriptstyle B}}}(\mu ^2) , \quad {{\widetilde{Z}}}_c = Z_c^\mathrm{{\scriptscriptstyle asym}}= F_{\mathrm{{\scriptscriptstyle B}}}(\mu ^2) . \end{aligned}$$

(B3)

Therefore, it follows that $\Delta ^\mathrm{{\scriptscriptstyle asym}}(q^2) = \Delta (q^2)$ and $F^\mathrm{{\scriptscriptstyle asym}}(q^2) = F(q^2)$.

The formal equality between ${{\widetilde{Z}}}_{A}$ and $Z_{A}^\mathrm{{\scriptscriptstyle asym}}$ expressed in Eq. (B3) is violated at the level of finite-order perturbation theory, because the value of the coupling therein varies from one scheme to the other. For example, at one loop

$$\begin{aligned} {{\widetilde{Z}}}_A = 1 + \frac{\alpha _s C_{\textrm{A}}}{144\pi }\left\{ 78\left[ \frac{1}{\epsilon } - \gamma _{\mathrm{{\scriptscriptstyle E}}} + \ln (4\pi ) - \ln \left( \frac{\mu ^2}{\nu ^2}\right) \right] {+} 97\right\} , \end{aligned}$$

(B4)

where $C_{\textrm{A}}$ is the Casimir eigenvalue of the adjoint representation [$C_{\textrm{A}} = 3$ for SU(3)], $\gamma _{\mathrm{{\scriptscriptstyle E}}}$ is the Euler–Mascheroni constant, and $\nu$ is the ’t Hooft mass, while $Z_A^\mathrm{{\scriptscriptstyle asym}}$ satisfies an identical expression with $\alpha _s\rightarrow \alpha _s^\mathrm{{\scriptscriptstyle asym}}$. Given that $\alpha _s$ and $\alpha _s^\mathrm{{\scriptscriptstyle asym}}$ have different values, Eq. (B3) appears to be violated.

However, since in the perturbative framework one coupling can always be expanded in a power series of the other [116], i.e.,

$$\begin{aligned} \alpha _{s} = \alpha _{s}^\mathrm{{\scriptscriptstyle asym}}+ {{\mathcal {O}}}((\alpha _{s}^\mathrm{{\scriptscriptstyle asym}})^2), \end{aligned}$$

(B5)

${{\widetilde{Z}}}_A$ and $Z_A^\mathrm{{\scriptscriptstyle asym}}$ can actually be made equal, in agreement with Eq. (B3); the apparent deviation from that relation is ${{\mathcal {O}}}((\alpha _{s}^\mathrm{{\scriptscriptstyle asym}})^2)$, and cannot be disentangled from the truncation of the series. Evidently, this still leaves an ambiguity as to whether $\alpha _s$ or $\alpha _s^\mathrm{{\scriptscriptstyle asym}}$ should be used in numerical evaluations of the perturbative expressions. Ambiguities of this nature are intrinsic to perturbative calculations, and have been discussed extensively in the literature (see e.g., [135, 146, 147] and references therein). In what follows, we take the asymmetric scheme value, $\alpha _s^\mathrm{{\scriptscriptstyle asym}}$, as reference for numerical evaluations, and assume that the errors resulting from this scheme ambiguity are small.

On the other hand, the vertex form factors and the value of the coupling are different in the two schemes considered. Specifically, Eq. (5.7) implies

$$\begin{aligned}&L _{{sg}}(r^2) = \frac{{{\widetilde{Z}}}_{3}}{Z_{3}^\mathrm{{\scriptscriptstyle asym}}} L _{{sg}}^\mathrm{{\scriptscriptstyle asym}}(r^{2}), \ B_{1}(q,r,t) = \frac{{{\widetilde{Z}}}_{1}}{Z_{1}^\mathrm{{\scriptscriptstyle asym}}} B_{1}^\mathrm{{\scriptscriptstyle asym}}(q,r,t), \nonumber \\&\alpha _{s}= \left( \frac{Z_{g}^\mathrm{{\scriptscriptstyle asym}}}{{{\widetilde{Z}}}_{g}}\right) ^{\!\!\!2}\!\alpha _{s}^\mathrm{{\scriptscriptstyle asym}}. \end{aligned}$$

(B6)

Then, it is easily shown from the STIs of Eq. (5.8) that ${{\widetilde{Z}}}_{3} = ({{\widetilde{Z}}}_{4}{{\widetilde{Z}}}_{A})^{1/2}$, ${{\widetilde{Z}}}_{1} = {{\widetilde{Z}}}_{3}{{\widetilde{Z}}}_{c}{{\widetilde{Z}}}_{A}^{-1}$, and ${{\widetilde{Z}}}_{g} = {{\widetilde{Z}}}_{1}{{\widetilde{Z}}}_{c}^{-1}{{\widetilde{Z}}}_{A}^{-1/2}$, and identical relations with “asym” superscripts instead of tildes in all Zs. Hence, using Eq. (B3), the ratios in Eq. (B6) can be expressed as

$$\begin{aligned} \frac{{{\widetilde{Z}}}_{3}}{Z_{3}^\mathrm{{\scriptscriptstyle asym}}} = \frac{{{\widetilde{Z}}}_{1}}{Z_{1}^\mathrm{{\scriptscriptstyle asym}}} = \frac{{{\widetilde{Z}}}_{g}}{Z_{g}^\mathrm{{\scriptscriptstyle asym}}} = \left( \frac{{{\widetilde{Z}}}_{4}}{Z_{4}^\mathrm{{\scriptscriptstyle asym}}}\right) ^{\!\!1/2}. \end{aligned}$$

(B7)

Thus, in order to convert between the asymmetric MOM and the prescription of Eqs. (5.10) and (5.11), we simply need to obtain the finite, and regulator independent, ratio $Z_{4}^\mathrm{{\scriptscriptstyle asym}}/{{\widetilde{Z}}}_{4}$.

In what follows, we assume that the renormalization point $\mu = 4.3$ GeV is sufficiently large such that ${{\widetilde{Z}}}_{4}/Z_4^\mathrm{{\scriptscriptstyle asym}}$ can be approximated by a one-loop calculation.

We begin by computing the one-loop ${{\widetilde{Z}}}_{4}$ by imposing the renormalization scheme of Eq. (5.11). To that end, we substitute in Eq. (6.7) the tree-level forms of all inputs, i.e., $\Delta (q^2)\rightarrow 1/q^2$, $L _{{sg}}(r^2) \rightarrow 1$ and $G_1^{*} \rightarrow 1$. Using dimensional regularization with $d = 4 - 2\epsilon$ space-time dimensions, this procedure yields

$$\begin{aligned}{} & {} G_1^{(1)}(0,p,p,-2p) \nonumber \\{} & {} \quad = {{\widetilde{Z}}}_4 - \frac{\alpha _s}{96\pi }\left\{ 48\left[ \frac{1}{\epsilon } - \gamma _{\mathrm{{\scriptscriptstyle E}}} + \ln (4\pi ) - \ln \left( \frac{p^2}{\nu ^2}\right) \right] \right. \nonumber \\{} & {} \qquad + 28 \ln (2) - 11 \Bigg \rbrace . \end{aligned}$$

(B8)

Then, the renormalization condition of Eq. (5.11) determines ${{\widetilde{Z}}}_{4}$ as

$$\begin{aligned} {{\widetilde{Z}}}_{4}&= 1 + \frac{\alpha _{s}}{96 \pi } \left\{ 48\left[ \frac{1}{\epsilon } - \gamma _{\mathrm{{\scriptscriptstyle E}}} + \ln ( 4 \pi ) - \ln \left( \frac{\mu ^2}{\nu ^2}\right) \right] \right. \nonumber \\&\quad + 28 \ln (2) - 11 \Bigg \rbrace , \end{aligned}$$

(B9)

and finally

$$\begin{aligned} G_{1}^{(1)}(0,p,p,-2p)&= 1+\frac{\alpha _{s}}{2 \pi } \ln \left( \frac{p^{2}}{\mu ^{2}}\right) . \end{aligned}$$

(B10)

Next, $Z_{4}^\mathrm{{\scriptscriptstyle asym}}$ can be determined by invoking the STIs of Eq. (5.8), which together imply $Z_4^\mathrm{{\scriptscriptstyle asym}}= (Z_3^\mathrm{{\scriptscriptstyle asym}})^2 /Z_A^\mathrm{{\scriptscriptstyle asym}}$. Using Eq. (B4) and textbook results [140] for $Z_3^\mathrm{{\scriptscriptstyle asym}}$ entails

$$\begin{aligned} Z_{4}^\mathrm{{\scriptscriptstyle asym}}= 1 + \frac{ \alpha _{s}^\mathrm{{\scriptscriptstyle asym}}}{24 \pi }\left\{ 12 \left[ \frac{1}{\epsilon } - \gamma _{\mathrm{{\scriptscriptstyle E}}} + \ln (4 \pi ) - \ln \left( \frac{\mu ^2}{\nu ^2}\right) \right] - 43\right\} . \end{aligned}$$

(B11)

At this point, Eqs. (B9) and (B11) involve couplings, $\alpha _{s}^\mathrm{{\scriptscriptstyle asym}}$ and $\alpha _s$, in two different renormalization schemes. Then, using Eq. (B5), yields

$$\begin{aligned} \left( \frac{{{\widetilde{Z}}}_{4}}{Z_{4}^\mathrm{{\scriptscriptstyle asym}}}\right) ^{\!\!1/2} = 1 + \frac{7\alpha _s^\mathrm{{\scriptscriptstyle asym}}}{192\pi }\left[ 23 + 4\ln (2) \right] . \end{aligned}$$

(B12)

Note that this ratio differs from unity at order $\alpha _s^\mathrm{{\scriptscriptstyle asym}}$ already, in contrast to the apparent scheme dependence of Eq. (B4), which is ${{\mathcal {O}}}((\alpha _s^\mathrm{{\scriptscriptstyle asym}})^2)$. As such, it represents a genuine difference between ${{\widetilde{Z}}}_4$ and $Z_{4}^\mathrm{{\scriptscriptstyle asym}}$, rather than an artifact of the perturbative expansion.

Finally, using the value of $\alpha _{s}^\mathrm{{\scriptscriptstyle asym}}(\mu ^2) = 0.27$, for $\mu = 4.3$ GeV, determined in [118], we obtain

$$\begin{aligned} \left( \frac{{{\widetilde{Z}}}_{4}}{Z_{4}^\mathrm{{\scriptscriptstyle asym}}}\right) ^{\!\!1/2}\approx 1.08. \end{aligned}$$

(B13)

Combining Eqs. (B12) and (B7) into Eq. (B6) we obtain the final conversion factors and value of $\alpha _s$,

$$\begin{aligned}{} & {} L _{{sg}}(r^2) = 1.08 \, L _{{sg}}^\mathrm{{\scriptscriptstyle asym}}(r^{2}), \ B_{1}(q,r,t) = 1.08 \, B_{1}^\mathrm{{\scriptscriptstyle asym}}(q,r,t), \nonumber \\{} & {} \alpha _{s}(\mu ^2) = 0.23 , \end{aligned}$$

(B14)

valid for $\mu = 4.3$ GeV.