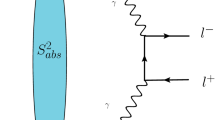
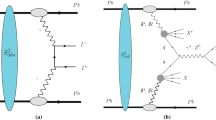
The advent of the high energy colliders has allowed us to study the hadron structure at high energies and to achieve a deeper knowledge of the hadronic structure. Several studies have demonstrated that a 3 dimensional description of the quark and gluon content of hadrons [1, 2] can be revealed in exclusive processes (for recent reviews see, e.g. Refs. [3,4,5,6,7,8,9,10]). In these processes, the scattering amplitude can be factorized in terms of generalized parton distributions (GPDs) [11,12,13,14] and hard scattering kernels, which can be estimated at different orders of the perturbative expansion. Some examples of exclusive processes are the exclusive vector meson production (EVMP), the deeply virtual Compton scattering (DVCS) and the timelike Compton scattering (TCS). In the TCS process, one has the exclusive photoproduction of a lepton pair with large invariant mass [15,16,17,18,19]. Such process can occur in photon-induced interactions, as those present in ultraperipheral collisions [20,21,22,23,24,25,26,27,28], which are collisions where the two incident charged hadrons (or nuclei) interact at impact parameters larger than the sum of their radii, with the hadrons acting as a source of almost real photons. In this case, the exclusive dilepton production occurs through the subprocess \(\gamma h \rightarrow \gamma ^*h \rightarrow l^+ l^- h\), with the real photon in the initial state being emitted by one of the incident charge hadrons (see, e.g. Refs. [29,30,31,32,33]). The representation of the TCS process in pp/pAu collisions at RHIC is presented in Fig. 1.

In contrast to the EVMP and DVCS processes, which have been largely discussed in the literature and a reasonable amount of data is available, the number of phenomenological analysis of the TCS process is still small and its measurement was performed only recently by the CLAS Collaboration [34]. In addition, the calculations of the TCS process has been performed considering distinct theoretical approaches and/or at leading order of the strong running coupling constant \(\alpha _s\), in which the Compton amplitude is dominated by the quark handbag diagrams described in terms of the quark GPDs. Our goal in this letter is to derive, for the first time, the next-to-leading order predictions for the TCS process in pp and pAu collisions at RHIC energies, taking into account of the contributions associated to quark and gluon GPDs. We will provide results for the differential distributions considering distinct values for the rapidity of the dilepton system in the final state. As we will demonstrate below, these results indicate that a future experimental analysis of TCS process at RHIC is, in principle, feasible and can be useful to improve our understanding of the hadronic structure.

Fig. 1
figure 1

Timelike Compton scattering in photon-induced interactions at pp and pAu collisions

Full size image

Initially, let’s present a brief review of the formalism needed to describe the exclusive dilepton photoproduction in ultraperipheral collisions. As in previous studies, we will assume the validity of the Equivalent Photon Approximation (EPA) [20,21,22,23,24,25,26,27,28]. It allow us to factorize the differential cross section for a \(h_1 h_2\) collision in terms of the photon fluxes associated to the incident particles and the photon-hadron cross sections as follows

$$\begin{aligned}{} & {} \left. \frac{d\sigma _{h_1 \, h_2 \rightarrow h_1 \, l^+l^- \, h_2}}{dydQ^{2}dtd(\cos \theta )d\phi }\right| _{\sqrt{s_{NN}}} \nonumber \\{} & {} \quad = n_{h_1}(\omega _1)\cdot \left. \frac{d\sigma _{\gamma \, h_2 \rightarrow l^+l^- \, h_2}}{dQ^{2}dtd(\cos \theta )d\phi }\right| _{\sqrt{s_{\gamma h_2}}} \nonumber \\{} & {} \qquad + n_{h_2}(\omega _2)\cdot \left. \frac{d\sigma _{\gamma \, h_1 \rightarrow l^+l^- \, h_1}}{dQ^{2}dtd(\cos \theta )d\phi }\right| _{\sqrt{s_{\gamma h_1}}} \,\,, \end{aligned}$$
(1)

where \(n_{h_i}\) is the photon flux associated to the hadron \(h_i\) and \(Q^2\) is the timelike virtuality of the final state photon, which is equal to the squared invariant mass (\(M^2\)) of the dilepton system that has a rapidity y in the center-of-mass frame. Moreover, the polar and azimuthal angles, \(\theta \) and \(\phi \), of the lepton in the final state are defined as in Ref. [29] and the photon-hadron center-of-mass energies are given by \(\sqrt{s_{\gamma h_i}} = \sqrt{4 \omega _i E}\), where \(E = \sqrt{s_{NN}}/2\) and \(\omega _i\) is the photon energy which are related to the rapidity of the dilepton system by the kinematical relations \(\omega _1 = M/2 \exp (+ y)\) and \(\omega _2 = M/2 \exp (- y)\). As in Ref. [33], we will assume that the equivalent photon spectrum generated by the hadrons can be described by the relativistic point-like charge model [20,21,22,23,24,25,26,27,28]. As the nuclear flux is enhanced by a factor \(Z^2\) (Z is the nuclear charge), one has that in pAu collisions the differential cross section will be dominated by photon-proton interactions.

One has that Bethe-Heitler (BH) process generates the same final state than the timelike Compton scattering, which implies that both processes contribute at the amplitude level. As a consequence, the differential cross section for the exclusive dilepton production in ultraperipheral collisions will be expressed as a sum of three contributions: \(d\sigma ^{total} = d\sigma ^{TCS} + d\sigma ^{BH} + d\sigma ^{INT}\), where INT denotes the term associated to the TCS - BH interference. The differential cross section for the BH contribution in photon–proton interactions is well known and has been derived in detail e.g. in Ref. [15] (For a recent discussion see Ref. [35]). It is important to emphasize that several theoretical studies have demonstrated that the BH process can be used to probe the linear polarization of coherent photons in ultraperipheral heavy ion collisions [36,37,38], with the predictions in a reasonable agreement with the recent data for the the angular distributions of the dileptons obtained by the STAR collaboration [39, 40].

The TCS and INT contributions are given by [15, 30]

$$\begin{aligned} \frac{d\sigma ^{TCS}_{\gamma \, p \rightarrow l^+l^- \, p}}{dQ^{2}dtd(\cos \theta )d\phi }= & {} \frac{\alpha ^3_{em}}{8\pi s_{\gamma p}^2}\frac{1}{Q^{2}}\frac{1+\cos ^2\theta }{2}\nonumber \\{} & {} \times \left\{ (1-\eta ^2)(|{\mathcal {H}}_1|^2 + |\widetilde{{\mathcal {H}}}_1|^2) \right. \nonumber \\{} & {} \left. -2\eta ^2Re({\mathcal {H}}_1^*\widetilde{{\mathcal {E}}}_1)-\eta ^2 \frac{t}{4M_p^2}|\widetilde{{\mathcal {E}}}_1|^2\right\} \,, \nonumber \\ \end{aligned}$$
(2)

and

$$\begin{aligned}{} & {} \frac{d\sigma ^{INT}_{\gamma \, p \rightarrow l^+l^- \, p}}{dQ^{2}dtd (\cos \theta )d\phi } = -\frac{\alpha ^3_{em}}{4\pi s^2_{\gamma p}}\frac{\sqrt{t_0 - t}}{-tQ}\frac{\sqrt{1 - \eta }}{\eta } \nonumber \\ {}{} & {} \times \left( \cos \phi \frac{1+\cos ^2\theta }{\sin \theta }\right) \nonumber \\{} & {} \times Re\left[ F_1(t){\mathcal {H}}_1 -\eta (F_1(t) +F_2(t))\widetilde{{\mathcal {H}}}_1 -\frac{t}{4M_p^2}F_2(t){\mathcal {E}}_1\right] \,, \nonumber \\ \end{aligned}$$
(3)

where \(\eta = Q^2/(2s_{\gamma p}^2 - Q^2)\), \(M_p\) is the proton mass, \(t_0 = - 4M_p^2 \eta ^2/(1-\eta ^2)\) and we have neglected the lepton mass and assumed that \(s_{\gamma p},\,Q^2 \gg t, M_p^2\). Moreover, \(F_1(t)\) and \(F_2(t)\) are the usual Dirac and Pauli form factors, with \(F_2(0)\) normalized to the anomalous magnetic moment of the proton. In addition, in NLO calculations, the Form factors \({\mathcal {H}}_1({\mathcal {E}}_1)\) and \(\widetilde{{\mathcal {H}}}_1(\widetilde{{\mathcal {E}}}_1)\) are timelike Form factors that can be obtained from the spacelike Form factors \(^{S}{\mathcal {H}}_1({\mathcal {E}}_1)\) and \(^{S}\widetilde{{\mathcal {H}}}_1(\widetilde{{\mathcal {E}}}_1)\) as follow [16].

$$\begin{aligned}{} & {} {\mathcal {H}}_1 = {\,}^{S}{\widetilde{\mathcal {H}}}^{*} -i\pi {\mathcal {Q}}^{2}\frac{\partial }{\partial {\mathcal {Q}}^{2}} {\,}^{S}{\widetilde{\mathcal {H}}} ^{*}, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} {\widetilde{\mathcal {H}}}_1 = -^{S}{\widetilde{\mathcal {H}}}^{*} +i\pi {\mathcal {Q}}^{2}\frac{\partial }{\partial {\mathcal {Q}}^{2}}{\,}^{S}{\widetilde{\mathcal {H}}}^{*}. \end{aligned}$$
(5)

Moreover, the spacelike Form factors can be expressed in terms of the hard-scattering kernels \(T_{{\mathcal {H}}_1,\widetilde{{\mathcal {H}}}_1,{\mathcal {E}}_1,\widetilde{{\mathcal {E}}}_1}^{q,g}\) and the GPDs H, \({\tilde{H}}\), E and \({\tilde{E}}\), defined in Ref. [1] (For details see Refs. [15, 29]). It is important to emphasize that at leading order, one has that \(T_{{\mathcal {H}}_1,\widetilde{{\mathcal {H}}}_1,{\mathcal {E}}_1,\widetilde{{\mathcal {E}}}_1}^{g} = 0\) and the expressions for the quark sector can be found in Refs. [15, 29, 41]. The expressions for the spacelike Form factors are presented in Refs. [18, 19].

One has that the prediction of the TCS and INT contributions are dependent on the model assumed for the description of the Generalized Parton Distributions. As in our previous study [33], we will consider the Goloskokov–Kroll (GK) model, which is based on fits of meson electroproduction data and is discussed in detail in Refs. [42,43,44]. In this model, the GPDs are expressed by

$$\begin{aligned} F_i(x, \xi , t) = \int _1^1d\beta \int _{-1+|\beta |}^{1-|\beta |}d\alpha \, \delta (\beta + \xi \alpha -x)f_i(\beta , \alpha , t). \nonumber \\ \end{aligned}$$
(6)

where \(F = H\), \({\tilde{H}}\), E, \({\tilde{E}}\) and i denotes the double distribution \(f_i\), which are given by following expressions

$$\begin{aligned}{} & {} f_i(\beta , \alpha , t) \nonumber \\{} & {} = g_i(\beta , t)h_i(\beta ) \frac{\Gamma (2n_i+2)}{2^{2n_i+1} \Gamma ^2(n_i+1)}\frac{[(1-|\beta |)^2-\alpha ^2]^{n_i}}{(1-|\beta |)^{2n_i+1}}. \nonumber \\ \end{aligned}$$
(7)

One has that \(n_i\) is set to 1 for valence quarks and 2 for sea quarks and gluons. Moreover, \(h_{sea}^q (\beta ,0) =q_{sea}(|\beta |)\)sign\((\beta )\), \(h_{val}^q(\beta ,0) = q_{val}(|\beta |)\Theta (\beta )\) and \(h_g (\beta ,0) =|\beta | g(|\beta |)\), where \(q_{sea}\), \(q_{val}\) and g are the usual unpolarized PDFs. Finally, the t-dependence of the double distributions are described by \(g_i(\beta , t)\), which is assumed to have a Regge behavior with linear trajectories, being given by

$$\begin{aligned} g_i(\beta , t) = N e^{b_0 t}|\beta |^{-\alpha (t)}(1-\beta )^n. \end{aligned}$$
(8)

The parameters considered in our analysis are detailed in Refs. [42,43,44]. It is important to emphasize that the GK model provides a satisfactory description of the recent TCS data measured by the CLAS Collaboration [34].

Fig. 2
figure 2

Rapidity distributions for the exclusive lepton pair production in ultraperipheral pp (left panel) and pAu (right panel) collisions at \(\sqrt{s_{NN}} = 200\) GeV for fixed values of \(Q^2\), \(\phi \) and t

Full size image

In what follows we will present our predictions for the differential cross sections associated to the Bethe–Heitler (BH), timelike Compton scattering (TCS) and TCS-BH interference (INT) considering ultraperipheral pp and pAu collisions at \(\sqrt{s_{NN}} = 200\) GeV. Our calculations will be performed using the software PARTONS [45], considering the NLO kernels derived in Refs. [18, 19] and the GPDs provided by the GK model. We will present our predictions for the \(\phi \) and t distributions assuming two distinct values for the rapidity of the dilepton system (\(y = 0\) and \(y = 2\)), and a fixed value for the invariant mass of the dilepton system (\(Q^2 = 5.0\) GeV\(^2\)). Moreover, the predictions for the rapidity distributions for fixed values of t and \(\phi \) and integrated over these variables will also be presented.

In Fig. 2 we present the rapidity distributions for the exclusive lepton pair production in ultraperipheral pp (left panel) and pAu (right panel) collisions at \(\sqrt{s_{NN}} = 200\) GeV for fixed values of \(Q^2\), \(\phi \) and t. The Au beam is assumed to be moving from negative to positive rapidities. The predictions for pAu collisions are asymmetric in rapidity and have a magnitude that is two orders of magnitude larger than those derived for pp collisions. Such result is expected due to \(Z^2\) factor in the nuclear photon flux, which enhances the cross section and implies that \(\gamma p\) interactions dominate in pAu collisions. Moreover, our results indicate that the differential cross section is dominated by the BH contribution and that the interference reduces the magnitude of the cross section in comparison to the BH prediction. The dominance of the BH process is also expected from previous studies [15, 29, 30]. In principle, as the magnitude and the dependence of BH process on the kinematical variables is well known, such a contribution can in principle be subtracted in order to access the TCS and INT contributions. As already emphasized in Refs. [29, 30, 33], its contribution can also be suppressed by (a) choosing a specific set of cuts on the kinematical variables such that the BH and TCS contributions become similar, and/or (b) considering specific observables that are sensitive to the INT contribution, as e.g. the angular distribution of the produced leptons. In what follows we will assume that this subtraction and/or suppression could be performed in future experimental analysis and will present, for completeness, the predictions for the BH, INT and TCS contributions.

Fig. 3
figure 3

Azimuthal distributions for the exclusive lepton pair production in ultraperipheral pp (left panel) and pAu (right panel) collisions at \(\sqrt{s_{NN}} = 200\) GeV for fixed values of \(Q^2\), y and t

Full size image

In Fig. 3 we present our predictions for the azimuthal dependence of the differential cross section \(d\sigma /dydtdQ^2d\phi \) for fixed values of y, t and \(Q^2\), derived integrating Eq. (1) over \(\theta \) in the range \([\pi /4,3\pi /4]\) as in previous studies [29, 30] and considering ultraperipheral pp (left panel) and pAu (right panel) collisions at \(\sqrt{s_{NN}} = 200\) GeV. The results for pp (pAu) collisions are presented for \(y = 0\) (\(y = 2\)), where one has the larger magnitude of the cross section (see Fig. 2). As expected, the BH contribution dominates, with the TCS-BH interference being appreciable for \(\phi \approx \pi \). The results indicate that the contribution of the interference contribution is non -negligible and that the analysis of the angular distribution can be useful to probe the INT and TCS contributions if the BH process is subtracted.

Fig. 4
figure 4

Distributions on the t-momentum transfer for the exclusive lepton pair production in ultraperipheral pp (left panel) and pAu (right panel) collisions at \(\sqrt{s_{NN}} = 200\) GeV for fixed values of \(Q^2\), \(\phi \) and y

Full size image

The predictions for the t-distributions of the BH, TCS and INT contributions are presented in Fig. 4, assuming fixed values for \(Q^2\) and \(\phi \) and \(y = 0\) (\(y = 2\)) for ultraperipheral pp (pAu) collisions. The BH contribution strongly increases for \(|t| \rightarrow 0\), since it is determined by the Dirac and Pauli form factors. The INT contribution diminishes the magnitude of the cross section, decreasing for smaller values of |t|. One has that subtracting the BH contribution and by selecting the small-t events, the INT contribution will be dominant and will allow us to probe the TCS amplitude and consequently the modeling of the quark and gluon GPDs.

Fig. 5
figure 5

Rapidity distributions for the exclusive lepton pair photoproduction in ultraperipheral pp (left panel) and pAu (right panel) collisions derived integrating Eq. (1) over t, \(\theta \) and \(\phi \)

Full size image

Finally, in Fig. 5 we present our predictions for the rapidity distributions of the BH and TCS contributions considering the exclusive dilepton production in ultraperipheral pp (left panel) and pAu (right panel) collisions, derived integrating Eq. (1) over |t|, \(\theta \) and \(\phi \) in the ranges [0.0, 0.5] GeV\(^2\), \([\pi /4,3\pi /4]\) and \([0,2\pi ]\), respectively. As expected from the previous results, the BH contribution dominates, with the larger value occurring for \(y = 0\) (\(y \approx 2\)) in pp (pAu) collisions. The TCS contribution is approximately two orders of magnitude smaller than the BH one for the kinematical range and cuts considered.

As a summary, the exclusive dilepton photoproduction in ultraperipheral pp and pAu collisions at RHIC energy was investigated, motivated by the recent measurement of the timelike Compton scattering by the CLAS Collaboration and by the possibility of use this process to probe the quark and gluon GPDs of the proton. One has estimated the Bethe–Heitler, TCS and interference contributions were estimated and predictions for the kinematical range covered by the RHIC detectors were presented assuming the GK model for the quark and gluon GPDs and the NLO kernels. Our results indicated that the exclusive dilepton photoproduction in ultraperipheral collisions at RHIC is dominated by the BH contribution. However, if this contribution is subtracted, our results indicate that the TCS and INT contributions are not negligible and can be probed in future experimental analysis.