The experimental study of photon – induced interactions in pp/pA/AA collisions became a reality in the last years, motivated by the possibility of improve our understanding of the Standard Model as well as by the opportunity of use these processes as an alternative tool to search for New Physics (for a recent review see e.g. Refs. [1, 2]). Recent results for the exclusive diphoton production in ultraperipheral heavy ion collisions (UPHICs) [3,4,5,6,7,8,9,10,11] provided the first observation of the light – by – light (LbL) scattering [12, 13], which was one of the most important predictions in the beginning of Quantum Electrodynamics (QED). Another important result was the observation of the exclusive dilepton production by photon – photon interactions in heavy ion collisions at the RHIC [14] and LHC [15,16,17], which has demonstrated the feasibility of study this final state and allowed us to improve the description of the nuclear photon flux and the modeling of the absorption effects, that suppress the strong interactions in these collisions [18, 19]. Moreover, both results strongly motivated the studies related to beyond Standard Model (BSM) physics performed in Refs. [20,21,22,23,24], which focused to estimate the impact of the axionlike particle production in the diphoton final state and in the possibility of determine the \(\tau \) lepton electromagnetic moments in the \(\gamma \gamma \rightarrow \tau ^+ \tau ^-\) interactions present in PbPb collisions at the LHC. In particular, the results obtained in Refs. [23, 24] have demonstrated the potentiality of the exclusive dilepton production to constrain BSM physics.

The studies performed in [18, 19, 23, 24] were restricted to the rapidity range covered by the central detectors as e.g. ALICE, ATLAS and CMS. Such selection is justified, since the rapidity distribution is larger for midrapidities. However, for the LHC energies, the exclusive dilepton production for forward rapidities can become of the same order, especially if dileptons with small values of invariant masses and low transverse momenta are measured, as possible in the LHCb detector. One of the goals of this letter is to present, for the first time, predictions for the exclusive \(e^- e^+\), \(\mu ^- \mu ^+\) and \(\tau ^- \tau ^+\) production at forward rapidities considering realistic selection cuts that can implemented by the LHCb Collaboration to select the associated events. As we will show below, a future experimental analysis is feasible. Our second goal is to estimate, for the first time, the background associated to dilepton production in double diffractive processes in PbPb, which also are characterized by two intact nuclei and two rapidity gaps in the final state, i.e., empty regions in pseudo-rapidity that separate the intact very forward nuclei from the \(l^+ l^-\) state. We will demonstrate that such background can be strongly suppressed by the exclusivity cuts, which implies that future data will be a direct probe of the dilepton production by photon – photon interactions. As a by product, we also will show that the diffractive events can be separated using a different set of cuts (For a similar analysis for the diphoton production see Ref. [25]).

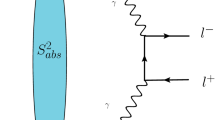
In what follows we will present our predictions for the exclusive dilepton production by photon – photon interactions in ultraperipheral heavy ion collisions, represented in Fig. 1a, which are characterized by an impact parameter b greater than the sum of the radius of the incident nuclei. In such collisions, the strong interactions between the incident nucleus are suppressed and the electromagnetic interaction between them become dominant [3,4,5,6,7,8,9,10,11, 26]. The cross section for the \(PbPb \rightarrow Pb \, l^+ l^- \,Pb \) can be estimated using the equivalent photon approximation [27], which allow us to factorize the elementary \(\gamma \gamma \rightarrow l^+ l^-\) process and describe the intense electromagnetic fields that accompany the relativistic heavy ions in terms of a spectrum of equivalent photons proportional to the square of the nuclear charge Z. As a consequence, the nuclear cross section is proportional to \(Z^4\), implying a very large number of events at RHIC and LHC. Moreover, it is assumed that the photons are coherently radiated by the whole nucleus. Such condition imposes that the minimum photon wavelength must be greater than the nuclear radius R. In other words, the photon virtuality must satisfy \(Q^2 = -q^2 \le 1/R^2\), with the photon four – momentum being \(q^{\mu } = (\omega , \vec {q_{\perp }},q_z = \omega /v)\), where \(\vec {q_{\perp }}\) is the transverse momentum of the photon in a given frame, where the projectile moves with velocity v. Therefore, we have that \(Q^2 = \omega ^2/\gamma _L^2 + q_{\perp }^2\). The coherence condition limits the maximum energy of the photon to \(\omega < \omega _{\text{ max }} \approx \gamma _L/R\) and the perpendicular component of its momentum to \({q_{\perp }} \le 1/R\). Therefore, the coherence condition sets an upper limit on the transverse momentum of the photon emitted by the hadron, which should satisfy \(q_{\perp } \le 1/R\), being \(\approx 28 \) MeV for Pb beams. One has that the photon virtuality can be neglected and the photons can be considered as being real. Moreover, the dilepton pair will be produced with a very small transverse momentum. In the impact parameter representation, the total cross section can be expressed as follows

$$\begin{aligned}&\sigma \left( Pb Pb \rightarrow Pb \otimes l^+ l^- \otimes Pb;s \right) = \int \text{ d}^{2} {\mathbf{r}_{1}} \text{ d}^{2} {\mathbf {r}_{2}} \text{ d }W \text{ d }Y \frac{W}{2} \,\nonumber \\&\quad \hat{\sigma }\left( \gamma \gamma \rightarrow l^+ l^-; W \right) N\left( \omega _{1},{\mathbf {r}_{1}} \right) N\left( \omega _{2},{\mathbf {r}_{2}} \right) S^2_{abs}({\mathbf {b}}) \,, \end{aligned}$$
(1)

where \(\sqrt{s}\) is center - of - mass energy of the PbPb collision, \(\otimes \) characterizes a rapidity gap in the final state, \(W = \sqrt{4 \omega _1 \omega _2}\) is the invariant mass of the \(l^+ l^-\) system and Y its rapidity. The photon energies \(\omega _1\) and \(\omega _2\) are related to W and to the rapidity Y of the outgoing dilepton system by \( \omega _1 = \frac{W}{2} e^Y\) and \(\omega _2 = \frac{W}{2} e^{-Y}\). The cross section \(\hat{\sigma }\) is the elementary cross section to produce a pair of leptons, where l = e, \(\mu \), \(\tau \). Moreover, \(N(\omega _i, {\mathbf {r}}_i)\) is the equivalent photon spectrum with energy \(\omega _i\) at a transverse distance \({\mathbf {r}}_i\) from the center of nucleus, defined in the plane transverse to the trajectory, which is determined by the charge form factor of the nucleus. Finally, the factor \(S^2_{abs}({\mathbf {b}})\) depends on the impact parameter \({\mathbf {b}}\) of the PbPb collision and is denoted by absorptive factor, which excludes the overlap between the colliding nuclei and allows to take into account only ultraperipheral collisions. As in Refs. [19, 25], the nuclear photon flux will be estimated assuming a point – like form factor and that the absorptive factor \(S^2_{abs}({\mathbf {b}})\) will be described by the model proposed by Baur and Ferreira - Filho [28] to exclude the strong interactions between the incident nuclei. One has that the predictions for small invariant masses, which is the kinematical range of interest in this letter, are not dependent on these choices, as demonstrated in Ref. [19]. It is important to emphasize that Eq. (1) is expressed in the impact parameter space and, consequently, does not allow us to estimate the transverse momentum \({\mathbf {q}_{T}}\) spectrum of the photons in the initial state, since \({\mathbf {r}_{i}}\) and \({\mathbf {q}_{T,i}}\) are conjugate variables. In order to include in our calculations the transverse momentum of the incoming photons, we will follow the approach proposed in Ref. [29], where a transverse momentum kick is provided to each photon with a distribution derived using the equivalent photon approximation [27] and that is determined by the nuclear form factor. Finally, our analysis will be performed using the Forward Physics Monte Carlo (FPMC) [30], which allow us to estimate the associated cross sections and distributions taking into account of the detector acceptances.

Fig. 1
figure 1

Dilepton production in a exclusive and b diffractive interactions considering PbPb collisions at the LHC

Full size image

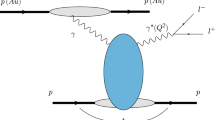
One possible background for the exclusive dilepton production in UPHICs is the Drell - Yan (DY) production in double diffractive processes, represented in Fig. 1b. As shown in Ref. [31] for pp collisions, such process can dominate in some regions of the phase space. However, its contribution for heavy ion collisions is still an open question. In the diffractive DY process, the dilepton is produced through the \(q \bar{q} \rightarrow l^+ l^-\) subprocess, with the partons being constituents of the Pomerons emitted by the incident nuclei, which remain intact after the emission. As the Pomeron is a color – singlet object, two rapidity gaps are expected in the final state, as in the case of the exclusive dilepton production. The main difference between these processes is the presence of the Pomeron remnants X and \(X^{\prime }\) in the double diffractive case, which are expected to generate additional tracks in the final state, in contrast with the exclusive case, where only the dilepton state is present. Moreover, from the analysis of the diphoton production performed in Ref. [25], we can expect that the transverse momentum distribution of the dileptons in these two channels will be different, with the DY process generating dileptons with larger transverse momentum. Such aspects will be considered in what follows in order to suppress the contribution of the diffractive process in comparison to the exclusive one. As in Ref. [25], we will estimate the cross section for the diffractive DY production using the Resolved Pomeron model [32], which implies that the cross section can be expressed by

$$\begin{aligned}&\sigma (Pb Pb \rightarrow Pb \otimes X+l^+ l^-+X^{\prime } \otimes Pb) = S^2_{eik} \nonumber \\&\quad \times \int dx_{1}\int dx_{2} \, \, \left[ q^D_{1}(x_{1},\mu ^2) \cdot \bar{q}^D_{2}(x_{2},\mu ^2) \right. \nonumber \\&\quad + \left. \bar{q}^D_{1}(x_{1},\mu ^2) \cdot {q}^D_{2}(x_{2},\mu ^2) \right] \nonumber \\&\quad \cdot \hat{\sigma }(q \bar{q} \rightarrow l^+l^-) , \end{aligned}$$
(2)

where \( S^2_{eik}\) is the soft survival factor, which takes into account of the soft interactions which lead to an extra production of particles that destroy the rapidity gaps in the final state [33], and \(q^D_i (x_i,\mu ^2)\) and \(\bar{q}^D_i (x_i,\mu ^2)\) are the diffractive quark and antiquark densities of the nucleus i with a momentum fraction \(x_i\). Such quantities will be modeled using the approach proposed in [34] (See also Ref. [35]), which have described the diffractive distributions for a nucleus taking into account the nuclear effects associated to the nuclear coherence and the leading twist nuclear shadowing (For details see Ref. [25]). In this approach the nuclear diffractive quark distribution can be expressed as follows

$$\begin{aligned} {q^D_\mathrm{A}(x,\mu ^2)}= & {} R_g \, \mathrm{A}^2 \, { \int _x^1 \frac{dx_{\mathbb {P}}}{x_{\mathbb {P}}} \left[ \int dt \, f_{\mathbb {P}/\mathrm{p}}(x_{{\mathbb {P}}}, t) \right. }\nonumber \\&{\left. \cdot F_\mathrm{A}^2(t)\right] q_{\mathbb {P}}\left( \frac{x}{x_{\mathbb {P}}}, \mu ^2\right) } \,\,, \end{aligned}$$
(3)

where \(R_g\) is the suppression factor associated to the nuclear shadowing, \(F_\mathrm{A}(t)\) is the nuclear form factor and \(q_{\mathbb {P}}\) is the quark distribution in the Pomeron, which is given by the parameterization obtained by the H1 Collaboration [36]. As in Ref. [34] we will assume \(R_g = 0.15\) and \(F_\mathrm{A}(t) \propto e^{R_\mathrm{A}^2 t/6}\), with \(R_\mathrm{A}\) being the nuclear radius. In our analysis we will estimate the associated cross section and distributions using the FPMC generator, where the hard matrix elements are treated by interfacing FPMC with HERWIG v6.5. The treatment of the soft interactions, which lead to an extra production of particles that destroy the rapidity gaps in the final state, is still a challenge. In our analysis, such soft survival corrections are modelled by the factor \(S^2_{eik}\) and are calculated using the approach developed in Ref. [37], which generalizes the model described in Ref. [38] for coherent double exchange processes in nuclear collisions. In this approach, the double diffractive cross section is expressed in the impact parameter space, which implies that the double pomeron exchange process becomes dependent on the magnitude of the geometrical overlap of the two nuclei during the collision. As a consequence, it is possible to take into account the centrality of the incident particles and estimate \(S^2_{eik}\) by requiring that the colliding nuclei remain intact, which is equivalent to suppress the interactions at small impact parameters (\(b < 2 R_\mathrm{A}\)). Such approach implies that \(S^2_{eik} = 3.4 \times 10^{-5}\) for PbPb collisions at \(\sqrt{s} = 5.5\) TeV, which can be considered an upper bound, since alternative approaches [39, 40] have derived smaller values.

Fig. 2
figure 2

Results for the invariant mass \(m_{\mu \mu }\), rapidity \(y(\mu \mu )\) and acoplanarity distributions of the \(\mu ^{+}\mu ^{-}\) pair at generation level for \(\sqrt{s}=5.5\) TeV in PbPb collisions at the LHC

Full size image

In what follows we will present our results for the exclusive and diffractive dilepton production in PbPb collisions at \(\sqrt{s} = 5.5\) TeV. In our analysis we will use the FPMC event generator [30] to estimate the processes represented in the Fig. 1a, b. For the final state selection we use HepMC2 [43] with a plugin called HepPDT [44] which has been designed to be used by any Monte Carlo particle generator or decay package. HepPDT  has the function to store particle information such as charge and nominal mass in a table which is accessed by a particle ID number. The particle ID number is defined according to the Particle Data Group’s Monte Carlo numbering scheme [41]. The final analysis and distributions are done withROOT [45]. We will focus on dileptons with invariant mass in the range \(1.5\, \text{ GeV } \le m_{ll} \le 20\) GeV, removing the dileptons with invariant mass in the ranges \(2.796\, \text{ GeV } \le m_{ll} \le 3.196\, \text{ GeV }\), \(3.586\, \text{ GeV } \le m_{ll} \le 3.786\, \text{ GeV }\), and \(9.0\, \text{ GeV } \le m_{ll} \le 10.6\, \text{ GeV }\), associated to the \(J/\Psi \), \(\Psi (2S)\) and \(\Upsilon \) decays, respectively.

Table 1 Predictions for the dielectron and dimuon production at forward rapidities in PbPb collisions at \(\sqrt{s} = 5.5\) TeV in exclusive and diffractive interactions considering kinematical cuts that select the exclusive contribution
Full size table

Initially, let’s consider the dimuon production and present in Fig. 2 our results for the invariant mass (\(m_{\mu \mu }\)), rapidity (\(y_{\mu \mu }\)) and acoplanarity (\(1 -(\Delta \phi /\pi )\)) distributions considering the exclusive and diffractive channels, which were obtained at the generation level, without the inclusion of any selection in the events. We have that the diffractive contribution is strongly suppressed by the soft survival effects, with the associated invariant mass and rapidity distributions being a factor \(\approx 10^5\) smaller than the photon – induced one in the \(m_{\mu \mu }\) and \(y_{\mu \mu }\) ranges considered. On the other hand, the results for the acoplanarity distribution indicate that in the exclusive case the muons are dominantly produced in a configuration back - to - back. Such result is expected due to the very small transverse momentum carried by the photons in the initial state. In contrast, for the diffractive case, the transverse momentum of the quarks inside the Pomeron that interact to generate the dimuon can be large, which implies a non - negligible contribution associated to muon pairs with a large acoplanarity. Similar results are obtained for the \(e^+ e^-\) and \(\tau ^+ \tau ^-\) production.

In order to obtain realistic estimates of the dilepton production in PbPb collisions, which can be compared with the future experimental data, we will include in our analysis the experimental cuts that are expected to be feasible in the next run of the LHC by the LHCb detector. Due to the distinct characteristics of the \(\tau \) decay, we will study this final state using a different strategy to be discussed below. For the \(e^+ e^-\) and \(\mu ^+ \mu ^-\) production, the selection criteria implemented in our analysis of double diffractive and exclusive diphoton processes at forward rapidities are the following:

  • The initial selection is made on the transverse momentum of the leptons and invariant mass: \(m_{ll}<\) 20 GeV and \(p_{T}(l,l)>\) 0.4 GeV. The notation \(p_{T}(l,l)\) represents that the transverse momentum cut is applied in both leptons separately;

  • We will impose a cut on the acoplanarity (\(1 -(\Delta \phi /\pi )<\) 0.03) and transverse momentum of the dilepton system (\(p_{T}(l l)<\) 2 GeV);

  • We will select only events where leptons are produced in the rapidity range \(2.0< \eta (l,l) < 4.5\) and no other particle with \(p_T > 0.5\) GeV in the range \(5.5< |\eta | < 8.0\) is produced (this corresponds to the HERSCHEL acceptance installed in the LHCb experiment [46]).

Fig. 3
figure 3

Correlation between the rapidity of the \(\tau ^+ \tau ^-\) system and the purely leptonic pair (left panel) and the semileptonic system (right panel) generated in the decays for the 1-prong category

Full size image

The associated predictions are presented in the Table 1. One has that the predictions for the dielectron and dimuon production are very similar, which is expected in the invariant mass range considered, and the cut on the transverse momentum of the pair suppress the diffractive contribution. In addition, the HERSCHEL selection also suppresses this contribution and does not impact the exclusive one. Such results are expected, since in the exclusive case there are no additional tracks beyond those associated with the dilepton, in contrast to the diffractive production, where the remnants of the Pomeron are expected to generate new tracks. One important comment is that the cut on rapidity for the kinematical range covered by the LHCb detector reduces the cross section by approximately one order of magnitude. However, the final values are still very large, implying that the experimental analysis is feasible.

The results presented in Fig. 2 indicated that the acoplanarity distribution for exclusive and diffractive processes are distinct. Therefore we can invert the acoplanarity cut used in our previous analysis in order to select the diffractive events instead of the exclusive one. The results for the dimuon production derived using this new set of cuts are presented in the Table 2. Similar results are obtained for the dielectron production. One has that the exclusive contribution is strongly suppressed and the measurement of dileptons for these selection criteria is a direct probe of the diffractive channel. Such result opens the possibility to constrain the magnitude of the soft survival factor \( S^2_{eik}\) in the dilepton production, which is one of the main sources of theoretical uncertainty in the treatment of diffractive processes at nuclear collisions.

Table 2 Predictions for the dimuon production at forward rapidities in PbPb collisions at \(\sqrt{s} = 5.5\) TeV in exclusive and diffractive interactions considering kinematical cuts that select the diffractive contribution
Full size table

In what follows we will discuss the exclusive and diffractive \(\tau ^+ \tau ^-\) production in UPHICs. The exclusive case was recently investigated in Refs. [23, 24], strongly motivated by the possibility of use this final state to constrain the anomalous magnetic momentum of the \(\tau \) lepton and search for CP violation effects. These studies focused on the kinematical range covered by the ATLAS and CMS detectors. We will complement these analyzes, by analyzing the possibility of measure this final state in the LHCb detector, which collected data with low pile-up and it is able to reconstruct low momentum tracks. We will restrict our study to the Standard Model subprocesses and postpone for a future publication the investigation of the impact of new physics. Differently from the lighter charged leptons, the very short lifetime of the \(\tau \) lepton [\(\mathcal{{O}}(10^{-13}\) s)] implies that it decays into lighter leptons and hadrons before to interact with the detector. As a consequence, the separation of the \(\gamma \gamma \rightarrow \tau ^+ \tau ^-\) events depends on a precise identification of the decay products. The \(\tau \) decays can be classified as one prong decays (\(\approx 80 \%\)), where one charged particle is present in the final state, and three prong decays (\(\approx 20 \%\)), which are characterized by the production of three charged particles. In our analysis, only the 1-prong decays (semi and purely leptonic) production will be considered. Moreover, in order to suppress the contribution of the diffractive DY process for the purely leptonic channel, we will select events where the leptons in the final state have different flavours. Therefore, the following events will be included in our study:

Table 3 Predictions for the ditau production at forward rapidities in PbPb collisions at \(\sqrt{s} = 5.5\) TeV in exclusive and diffractive interactions considering the different decay channels
Full size table
$$\begin{aligned}&\tau \tau \rightarrow (e^{\pm }\nu _{e}\nu _{\tau })\,(\mu ^{\mp }\nu _{\mu }\nu _{\tau }) ,\,\, (e^{\pm }\nu _{e}\nu _{\tau })\, (\pi ^{\mp }\pi ^{0}\nu _{\tau }),\,\,\nonumber \\&\quad (\mu ^{\pm }\nu _{\mu }\nu _{\tau })\, (\pi ^{\mp }\pi ^{0}\nu _{\tau }) \,. \end{aligned}$$
(4)

The HERWIG 6.5 program [42], which incorporates the TAUOLA MC code [47], is used to model \(\tau \) decay for our studies. We select events with \(p_{T}(l,chg) > 1.0\) GeV and \(2.0< \eta ^{l,chg} < 4.5\) with 0 extra tracks and \(p_{T}(l + chg) < 2.0 \) GeV. As considered for lighter leptons, we discard events where particles with \(p_T > 0.5\) GeV are in the range \( 5.5< |\eta | < 8.0\), corresponding to the HERSCHEL acceptance in the LHCb experiment [46]. Some comments are in order before presenting our predictions. First, we also have performed the analysis considering the rapidity range covered for central detectors and obtained a very good agreement with the results presented in Ref. [24]. Second, we have verified that the acoplanarity distribution for the \(\tau ^+ \tau ^-\) pair decaying into a \((e^{\pm }\nu _{e}\nu _{\tau })\,(\mu ^{\mp }\nu _{\mu }\nu _{\tau })\) final state is similar to that presented in Fig. 2 for \(\mu ^+ \mu ^-\) production. Therefore, for this final state, it is also possible to consider an additional cut on the acoplanarity to separate the diffractive events. However, as the resulting value of the diffractive cross section is very small, it is not advantageous to use this final state to investigate the diffractive processes.

In Fig. 3 we present our results for the correlation between the hard process and reconstruction of the \(\tau ^{+}\tau ^{-}\) pair considering the 1-prong category at generation level. The reconstruction of rapidity of the pair is done before the exclusivity cuts and establish a benchmark of the effective combinations resulting in the \(\tau ^{+}\tau ^{-}\) pair products. Our results indicate that the rapidity of the system before decay and the final state charged particle in exclusive and diffractive processes are correlated, with this correlation being larger in the exclusive case. In Table 3 we present our predictions for the \(\gamma \gamma \rightarrow \tau ^{+}\tau ^{-}\) reaction in PbPb collisions at \(\sqrt{s} = 5.5\) TeV considering the different decay channels. As already observed for lighter leptons, the exclusive channel dominates the \(\tau ^{+}\tau ^{-}\) production. Moreover, the semileptonic contribution for the exclusive production is a factor \(\approx 2.5\) larger than the purely leptonic one. Our results indicate that the total cross section for the exclusive \(\tau ^{+}\tau ^{-}\) production in the kinematical covered by the LHCb detector will be \(\approx \) 60 nb, which implies that the number of events expected for the next run of the LHC is \(\approx \) 600 per year. Although smaller than the prediction for central detectors, this result indicates that a future experimental analysis is feasible.

Let’s summarize our main results and conclusions. In this letter, we have investigated, for the first time, the dilepton production at forward rapidities in diffractive and exclusive processes considering ultraperipheral PbPb collisions at the LHC. We have derived predictions for the \(e^+ e^-\), \(\mu ^+ \mu ^-\) and \(\tau ^+ \tau ^-\) cross sections taking into account of realistic cuts that can be implemented by the LHCb experiment in a future data analysis. Our results indicate that the background associated to the diffractive production can be strongly suppressed and the exclusive processes can be cleanly observed. We also demonstrated that selecting events with large acoplanarity, the diffractive events can be studied, allowing to constrain the modeling of the soft survival factor. For the \(\tau ^+ \tau ^-\) production, the semi and purely leptonic decay channels were considered and the final results indicate that the study of the exclusive production can be performed. Finally, the predictions presented in this indicate that a future experimental analysis of the dilepton production at the LHCb is feasible and can be useful to search for BSM physics.