1 Introduction

The well-known charged black hole solutions of the gravitational field equations in general relativity (GR) so-called Reissner–Nordström black hole (RNBH), have been first obtained by Reissner (1916) [1] and independently by Nordström (1918) [2] governing GR coupled with linear Maxwell electrodynamics. However, the solution has a physical singularity at the BH center (\(r = 0\)). There are different solutions for the charged BHs that avoid the physical singularity, also called regular BH solutions, that have been obtained in GR coupling to non-linear electrodynamics (NED) [3,4,5,6,7,8,9], being based on various Lagrangians governing the NED, and the properties of the spacetime. The obtained BH solutions have been studied by many authors [10,11,12,13].

One of the extensions of GR is the low energy limit of string theory, which introduces the dilaton scalar field as well as an extra supplement term to the GR action known as the Einstein–Hilbert action. It has the form of the axion, gauge fields, and another non-trivial coupling of dilaton to fields. In particular, combinations in the causal structures and thermodynamic properties of BH solutions with dilaton have been investigated in Refs. [14,15,16,17,18,19,20,21,22]. The detailed analysis of the BH solutions in the extended gravity theories are given in Refs. [23,24,25,26,27,28].

The heterotic string theory with the scalar dilaton field coupled to the electromagnetic field tensor has been considered in [15]. We investigated the properties of the spacetime around charged BHs in the Einstein–Maxwell-scalar (EMS) theory through detailed studies of the dynamics of test electrically neutral, charged, and magnetized particles, and the quasiperiodic oscillations in our previous works [29,30,31,32,33,34].

Here we plan to study the charged particle dynamics around charged black holes in EMS theory. The paper is organized as follows: the solution of the charged black hole in EMS theory has been reviewed in Sect. 2. Section 3 is devoted to studying the dynamics of charged test particles around the black hole in EMS theory. Synchrotron radiation of charged particles around EMS black hole is studied in Sect. 4. The electric Penrose process around a charged black hole in EMS gravity has been explored in Sect. 5. The collision process of electrically charged particles near the event horizon of the charged black holes in EMS theory has been explored in 6. We summarize our results in Sect. 7.

Throughout this paper, we use the (–, +, +, +) signature for the spacetime metric and system of units where \(G=1=c\).

2 Static black holes in Einstein–Maxwell-scalar theory

In this section, we will briefly review charged black hole solutions in EMS theory. The action is given as [14, 35]

$$\begin{aligned} S=\int d^4x\sqrt{-g}\Big [R-2\nabla _\alpha \phi \nabla ^\alpha \phi -K(\phi ) F_{\alpha \beta }F^{\alpha \beta } \Big ]\, \end{aligned}$$

where \(\nabla _\alpha \) is the covariant derivative, g is the determinant of \(g_{\mu \nu }\), R is the Ricci scalar of the spacetime curvature, \(\phi \) is a massless scalar field, \(F_{\alpha \beta }\) is the electromagnetic field tensor, \(K(\phi )\) is the coupling function between the dilaton and the electromagnetic fields.

The general form of the black hole solution has been obtained in Ref. [35] as,

$$\begin{aligned} ds^2=-U(r)dt^2+\frac{dr^2}{U(r)}+f(r)\left( d\theta ^2+\sin ^2\theta d\varphi ^2\right) \, \end{aligned}$$
(1)

where U(r) and f(r) are radial functions which have the special forms for the function \(K(\phi )\)

$$\begin{aligned} K(\phi )=\frac{2e^{2\phi }}{\beta e^{4\phi }+\beta -2\gamma }\, \end{aligned}$$
(2)

and obtained the solution in the form

$$\begin{aligned} f(r)= & {} r^2\left( 1+\frac{\gamma Q^2}{Mr}\right) , \nonumber \\ U(r)= & {} 1-\frac{2M}{r} +\frac{\beta Q^2}{f(r)}. \end{aligned}$$
(3)

and the total mass M and electric charge Q. \(\beta =0\) is the Schwarzschild limit, and \(\gamma =0\) and \(\beta =1\) is RN one.

It is worth noting that it has been assumed that the vector and the dilaton fields depend on the radial coordinate only as [35]

$$\begin{aligned}{} & {} A_t(r)=\frac{Q}{r}\left[ \gamma -\frac{\beta }{2}\left( 1+\frac{r^2}{f(r)}\right) \right] ,\end{aligned}$$
(4)
$$\begin{aligned}{} & {} \phi (r)=-\frac{1}{2}\ln \left( \frac{f(r)}{r^2}\right) . \end{aligned}$$
(5)

The event horizon structure of the spacetime (1) can be found solving the condition \(U(r)=0\) with respect to r and we have,

$$\begin{aligned} \frac{r_h}{M}= 1-\frac{\gamma Q^2}{2 M^2}+\sqrt{1+\frac{Q^2 (\gamma -\beta )}{M^2}+\frac{\gamma ^2 Q^4}{4 M^4}} \end{aligned}$$
(6)
Fig. 1
figure 1

The radial dependence of the metric function (3) for the different values of the parameters \(\beta \) (top panel) and \(\gamma \) (bottom panel)

Full size image

In Fig. 1 we demonstrate the radial profiles of the radial function of metric (1) for different values of the EMS parameters (\(\beta \) and \(\gamma \)) and the black hole charge. In fact, the zeros of the metric function imply the horizons of the black hole. It is observed from the figure that Cauchy and event horizons come close to each other for large values of \(\beta \). Also, the event horizon increases for the negative values of \(\gamma \), but slightly. While, when \(\gamma >0\) it decreases.

We now examine the characteristics of the extremes in the black hole charge and the minimum in the event horizon radius by setting the following conditions as

$$\begin{aligned} U(r)=U'(r)=0. \end{aligned}$$
(7)

With the aforementioned conditions, we get the radius and charge expressions shown below:

$$\begin{aligned}{} & {} \frac{(r_h)_{min}}{M}=2-\frac{\beta }{\gamma }+ \frac{\sqrt{\beta ^2-2 \beta \gamma }}{\gamma } \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \frac{Q_{extr}^2}{M^2} =\frac{2 \left( \beta -\sqrt{\beta } \sqrt{\beta -2 \gamma }-\gamma \right) }{\gamma ^2}. \end{aligned}$$
(9)
Fig. 2
figure 2

Critic values of the BH charge (dashed lines) and minimal radius of the event horizon (solid lines) as a function of the parameter \(\gamma \) for the different values of \(\beta \)

Full size image

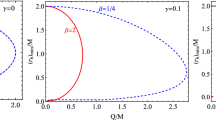
In Fig. 2 we present the dependence of minimum values of the outer horizon and extreme values of the black hole charge from the parameter \(\gamma \) for the different \(\beta \). The solid lines stand for the minimum event horizon, while the dashed ones are for the extreme charge.

It is seen from the figure that the minimum radius of the outer horizon decreases with the increase of \(\gamma \), and also decreases with the increase of \(\beta \) at \(\gamma <0\). Similarly, the extreme in Q also decreases at \(\gamma <0\). When the value of \(\gamma \) reaches a critical value, the event horizon becomes zero, implying that \(\gamma \) must be less than \(\gamma _{cr}\). The critical value of \(\gamma \) increases with the parameter \(\beta \).

Our numerical analysis shows that for all possible values of parameter \(\beta \)

$$\begin{aligned} \lim _{\gamma \rightarrow -\infty } \left\{ (r_h)_\textrm{min}, Q_{\textrm{extr}}\right\} =\{2M,0\}, \end{aligned}$$

and

$$\begin{aligned} \lim _{\gamma \rightarrow \gamma _{\textrm{max}}} \left\{ (r_h)_{\textrm{min}}, Q_{\textrm{extr}}\right\} =\{0, Q_{\textrm{extr}}\}. \end{aligned}$$

The upper value of \(\gamma _{\textrm{max}}\) (\(Q_\textrm{extr}\)) increases (decreases) as \(\beta \) parameter increase. Using the above finding and Eqs. (8) and (9) we can easily get the following relations:

$$\begin{aligned} \gamma _{\textrm{max}}=\frac{\beta }{2}, \qquad Q_\textrm{extr}=\frac{2}{\sqrt{\beta }} \end{aligned}$$
(10)

Below, we will show critical values of \(\gamma \) and corresponding \(Q_{extr}\) to the selected values of \(\beta \) in Table 1.

Table 1 The extremes of the black hole charge and critical value of \(\gamma \) for different values of \(\beta \) at which the event horizon is zero
Full size table

3 Test charged particles around electrically charged EMS black holes

In this section, we will use EMS theory to explore the behaviour of test electrically charged particles surrounding electrically charged black holes. The energy and angular moment of the particles corresponding to the innermost stable circular orbits (ISCOs), synchrotron radiation of the particles, and energy efficiency of the spacetime are all considered here.

3.1 Equations of motion for charged particles

In this subsection, we figure out the effective potential for the radial motion of charged particles in the presence of Coulomb interaction between the particle and the black hole (because both are electrically charged) and investigate the ISCO radius of the charged particle as well as the energy and angular momentum of the particles at their ISCO.

Now, we derive the equations of the motion of test-charged particles in the spacetime of the charged black hole using the following Lagrangian:

$$\begin{aligned} {{{\mathcal {L}}}}_{\mathrm{ch.p}}=\frac{1}{2}g_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }+q A_{\mu }{\dot{x}}^{\mu }. \end{aligned}$$
(11)

where \(q=e/m\) is the charge-to-mass ratio, the so-called specific charge of the particle.

The constants of motion can be determined using timelike and spacelike Killing vectors, and we have

$$\begin{aligned} g_{tt}{\dot{t}}+q A_t=-{{{\mathcal {E}}}}, \qquad g_{\phi \phi }{\dot{\phi }} = {{{\mathcal {L}}}}, \end{aligned}$$
(12)

where \({{{\mathcal {E}}}}\) and \({{{\mathcal {L}}}}\) are the specific energy and angular momentum of the test-charged particle, respectively.

Fig. 3
figure 3

Radial profiles of the effective potential for different values of EMS parameters \(\beta \) and \(\gamma \) and BH charge

Full size image

Finally, equations of motion of a charged particle at a constant plane (\(\theta =const\)) take the form

$$\begin{aligned} {\dot{t}}= & {} \frac{1}{U(r)} \left( {{{\mathcal {E}}}}-q A_t \right) , \end{aligned}$$
(13)
$$\begin{aligned} {\dot{r}}^2= & {} \left( {{{\mathcal {E}}}}-q A_t\right) ^2-U(r)\Big (1+\frac{{{{\mathcal {L}}}}^2}{f(r)\sin ^2\theta }\Big ), \end{aligned}$$
(14)
$$\begin{aligned} {\dot{\phi }}= & {} \frac{{{{\mathcal {L}}}}}{f(r)\sin ^2\theta }. \end{aligned}$$
(15)

The circular motion of test particles can be described using the following equations

$$\begin{aligned} {{{\mathcal {E}}}}=V_{\textrm{eff}} \qquad {\dot{r}}=0 \end{aligned}$$
(16)

In fact, the effective potential is the solution of Eq. (14) with respect to the energy \({{{\mathcal {E}}}}\)

$$\begin{aligned} V^{\pm }_{\textrm{eff}}(r)=q A_t \pm \sqrt{U(r)\left( 1+\frac{\mathcal{L}^2}{f(r)\sin ^2\theta }\right) }. \end{aligned}$$
(17)

One can easily see from the effective potential that it consists of two parts: Column and gravitational interaction and there are two different solutions where the effective potential has the symmetry in the replacement \(qQ \rightarrow -qQ\): \(V^+_{\textrm{eff}} \rightarrow -V^-_{\textrm{eff}}\) and \(V^-_{\textrm{eff}} \rightarrow -V^+_{\textrm{eff}}\).

Analysing the dynamics of charged particles we use \(V^+_{\textrm{eff}}\) as the effective potential corresponding to positive energy [36, 37].

Figure 3 shows radial dependence of the effective potential of test-charged and neutral particles for multiple values of the EMS BH charge and the parameters \(\beta \) and \(\gamma \) together with the comparison of the RN and Schwarzschild BH cases. It is seen from the top left panel of the figure that the maximum effective potential increases due to the Coulomb interaction. Similarly, as \(\beta \) increases the maximum also increases. In the bottom left panel, we can see the dependence of the parameter \(\gamma \) to the maximum of the effective potential. It is shown that an increase in the gamma parameter reduces the maximum effective potential. It is similar to the panel with charge dependence.

Fig. 4
figure 4

Dependence of \(r_{\textrm{ISCO}}\) on Q for different values of EMS parameters \(\beta \) and \(\gamma \) and the particle charge

Full size image

3.2 ISCO of charged particles around charged black holes in EMS theory

Next, we will investigate the ISCO of the charged particle around charged BH. In fact, for the stable circular orbits of particles, the following conditions must be satisfied,

$$\begin{aligned} V_{\textrm{eff}}={{{\mathcal {E}}}},\qquad \partial _rV_{\textrm{eff}}=0, \qquad \partial _{rr}V_{\textrm{eff}} \ge 0. \end{aligned}$$
(18)

where \('\) stands for the radial derivative. We solve the equation \(V'_{\textrm{eff}}=0\) and get the specific angular momentum that corresponds to circular orbits of the charged particle as

$$\begin{aligned}{} & {} {{{\mathcal {L}}}}^2_{\pm }=\frac{1}{\left[ U(r) f'(r)-f(r) U'(r)\right] ^2}\nonumber \\{} & {} \quad \times \Bigg \{ f(r)^2 U(r) f'(r) U'(r) \pm 2 q f(r)^2 U(r) A_t'(r) \nonumber \\{} & {} \quad \times \sqrt{\left( q f(r) A_t'(r)\right) ^2-f'(r)\left[ f(r) U'(r)-U(r) f'(r)\right] }\nonumber \\{} & {} \quad +f(r)^3 \left[ 2 q^2 U(r) A_t'(r)^2-U'(r)^2\right] \Bigg \}. \end{aligned}$$
(19)

In solutions of Eq. (19) the ± signs represent the symmetry with the replacements \(qQ \rightarrow -qQ\) and \(-qQ \rightarrow qQ\). In the Schwarzschild limit \(Q=0\) the angular momentum takes the form

$$\begin{aligned} {{{\mathcal {L}}}}^2_{+}={{{\mathcal {L}}}}^2_{-}=\frac{f(r)^2 U'(r)}{U(r) f'(r)-f(r) U'(r)}. \end{aligned}$$
(20)

The values of the specific angular momentum will be real when the term under the square root is positive

$$\begin{aligned} \left( q f(r) A_t'(r)\right) ^2-f'(r)\left[ f(r) U'(r)-U(r) f'(r)\right] \ge 0\,.\nonumber \\ \end{aligned}$$
(21)

The condition (21) is satisfied, when

$$\begin{aligned} f(r) U'(r)-U(r) f'(r)<0, \end{aligned}$$
(22)

and

$$\begin{aligned} f(r) U'(r)-U(r) f'(r)>0 \end{aligned}$$
(23)

with

$$\begin{aligned} \left( q f(r) A_t'(r)\right) ^2 \ge f'(r)\left[ f(r) U'(r)-U(r) f'(r)\right] . \end{aligned}$$
(24)

The ISCO radius can be found when the following conditions are satisfied:

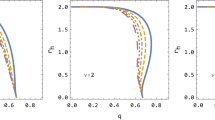
$$\begin{aligned} \partial _rV_{\textrm{eff}}(r)=\partial _{rr}V_{\textrm{eff}}(r)=0. \end{aligned}$$
(25)

In Fig. 4 we plotted the radius of ISCO as a function of Q, for different values of parameter \(\gamma \) (top right panel), q (top left), and \(\beta \) (bottom panel). It is observed from the figure that the positive (negative) values of both the parameters \(\gamma \) and q cause increases (decreases) of the ISCO radius, while the increase of the parameter \(\beta \) cause to decrease in it.

Fig. 5
figure 5

The relationships between the energy \({{{\mathcal {E}}}}\) and angular momentum \({\mathcal {L}}\) of the charged particles at circular orbits around the EMS black hole. The left panel is for the positively charged particles and the right one is for the negatively charged particles

Full size image

Moreover, in Fig. 5 we present the relation between the angular momentum and energy of the charged particles corresponding to the circular orbits around charged EMS black holes for positive (left panel) and negative (right panel) charges of the particles. Interestingly, one can see from the figure that, at two different circular orbits with corresponding angular momentum the particles can be the same energy and in fact, at the ISCO, the two different angular momentums are equal to each other. The angular momentum and energy of the particles at ISCO decreases due to the presence of Coulomb interaction, also the increase of \(\beta \) parameter causes decreasing them. It is also observed that in the \(q>0\) case, at stable circular orbits outer than ISCO the angular momentum becomes different at the same energy, due to Coulomb interaction, and then coincides with each other again which implies the existence of outermost stable circular orbits.

Fig. 6
figure 6

The angular momentum of test charged particles at ISCO \({\mathcal {L}}_{\textrm{ISCO}}\) as a function of the black hole charge Q, for different values of the EMS parameters and the particle charge

Full size image

Figure 6 represents the dependence of specific angular momentum of charged particles at ISCO from the electric charge of charged EMS black holes for different values of the EMS parameter and particle charge. The left panel is for neutral particles, and one can see from the panel that the angular momentum increases due to the presence of positive \(\gamma \), while it decreases for negative values of \(\gamma \). In the middle panel, we have considered the effects of Coulomb interaction on the angular momentum at ISCO, and it shows that the momentum slightly decreases for both positive and negative charges, however, the increase of \(\beta \) decease it sufficiently.

Fig. 7
figure 7

The same figure with Fig. 6, but for the particle energy at ISCO

Full size image

In Fig. 7 we have demonstrated the effects of the EMS parameters and the Coulomb interaction on the energy of charged particles at ISCO. Similar effects of \(\gamma \) and \(\beta \) parameters on \({{{\mathcal {E}}}}_{\textrm{ISCO}}\) have obtained as it has been in the angular momentum at ISCO shown in Fig. 6. However, the effect of negatively charged particles on the energy is not similar, causing it to increase it.

Fig. 8
figure 8

Dependence of \({\mathcal {L}}_{\textrm{ISCO}}\) (the top row) and \({{{\mathcal {E}}}}_{\textrm{ISCO}}\) (the bottom row) on \(r_{\textrm{ISCO}}\)

Full size image

The dependence of the angular momentum and energy of test-charged particles at ISCO from the corresponding ISCO is shown in Fig. 8 for different values of the EMS parameters and the particle charge. In the left panel, the dependence for neutral particles has shown. It is shown in Fig. 4 that the increase of the black hole charge causes decreasing the ISCO radius, and it also causes decreasing the corresponding ISCO radius and the decreasing rate is fast for negative values of \(\gamma \). Also, the rate is faster for positively charged particles than the negative ones. However, the effect of \(\beta \) is small.

4 Synchrotron radiation of charged particles around EMS Black Hole

In this section, we investigate the synchrotron radiation coming out of the charged particles which are accelerated due to electromagnetic forces (Coulomb and Lorentz forces) in the surrounding of charged black holes in EMS theory. The charged particles orbiting the charged EMS black hole emit the synchrotron radiation by the particles accelerated up to relativistic velocities. In order to investigate the synchrotron radiation of the charged particle with orbital motion in the spacetime of the EMS black hole, we use the expression [38]:

$$\begin{aligned} I=\frac{2q^2}{3}\omega _{\alpha }\omega ^{\alpha }, \end{aligned}$$
(26)

where \(\omega _{\alpha }\) is the acceleration of the charged particles orbiting the black hole measured by a proper observer:

$$\begin{aligned} \omega ^{\alpha }=\frac{q}{m}F^{\alpha }_{\beta }u^{\beta },~~~~\omega _{\alpha }u^{\alpha }=0. \end{aligned}$$
(27)

The second part of Eq. (27) implies the velocity of the particle is perpendicular to its acceleration. The charged particle moving along the stable circular orbit with velocity components: \(u^{\alpha } = u^t(1, 0, 0,\varOmega )\), and the acceleration \(\omega ^{\alpha } = (0,\omega ^{r},\omega ^{\theta }, 0)\). The non-zero components of the particle acceleration vector are [39]:

$$\begin{aligned} \omega _r=\frac{q \varOmega F_{rt}}{m\sqrt{-g_{tt}-\varOmega ^2g_{\phi \phi }}}, \quad \omega _{\theta }=0. \end{aligned}$$
(28)

The intensity of the radiation can be easily calculated using Eq. (27) in the following form:

$$\begin{aligned} I=-\frac{2q^4}{3m^2}\frac{g^{rr}F^2_{rt}}{g_{tt}+\varOmega ^2g_{\phi \phi }}. \end{aligned}$$
(29)

Here we are concentrating on the analysis of the effects of EMS parameters on the synchrotron radiation intensity with the comparison of the Reissner–Nordström (RN) black hole.

Fig. 9
figure 9

Comparison of the intensity of synchrotron radiation by charged particles orbiting charged black holes in EMS theory and RN black holes. Here, we analyze the intensity ratios \(I_{EMS}\)/\(I_{RN}\) as a function of radial coordinates for different values of EMS parameters

Full size image

Figure 9 shows the ratios of intensities of synchrotron radiation by charged particles (with \(q=0.1\)) accelerated in the spacetime of a charged black hole in EMS gravity and in an RN black hole with the same charges. The figure demonstrates that the radiation intensity increases with increasing values of the \(\beta \) parameter. In addition, the intensity decreases with positive values of \(\gamma \) and increases with negative values.

5 Penrose process

The Penrose process is one of the most realistic energy-release processes from rotating black holes. According to the process, a particle decays into two parts at the ergoregion around a rotating Kerr black hole. One part falls down the black hole with negative energy, while the other part goes out with positive energy higher than the initial energy of the decayed particle. Following the work of R. Penrose [40], several types of Penrose processes have been developed around various rotating black holes, including magnetic and electric Penrose processes [41,42,43]. In this section, we study the electric Penrose process by charged particles around charged black holes in EMS theory.

5.1 Angular velocity measured at infinity

Assume that the decay of the test particle takes place in the equatorial plane with the four-velocity \(u^{\alpha }=u^t(1,v,0,\varOmega )\), where \(v=dr/dt\) is the radial velocity of the particle and \(\varOmega =d\phi /dt\) is the angular velocity.

One may have the following equation for the angular velocity of the decayed particles using the normalization condition \(u^{\alpha }u_{\alpha }=-k\), where \(k=0\) for massless particle and \(k=1\) for massive particle:

$$\begin{aligned} (u^t)^2\left[ \frac{v^2}{U(r)}-U(r)+\varOmega ^2 f(r)\right] =-k. \end{aligned}$$
(30)

Now, we derive the equation for the angular velocity of the decayed particles measured by a static distant observer located at infinity \(\varOmega =d\phi /dt\) as follows

$$\begin{aligned} \varOmega =\pm \frac{1}{u^t \sqrt{f(r)}}\sqrt{(u^t)^2\left[ U(r)-\frac{v^2}{U(r)}\right] -k}. \end{aligned}$$
(31)

The possible values of \(\varOmega \) are limited by,

$$\begin{aligned} \varOmega _{-}\le \varOmega \le \varOmega _+,\qquad \varOmega _{\pm }=\pm \sqrt{\frac{U(r)}{f(r)}}\, \end{aligned}$$
(32)

corresponding to the Keplerian orbits.

5.2 Conservation laws in the particle decay

We consider a scenario in which a charged particle (1) approaches a charged black hole in EMS theory from infinity and decays into two charged parts (2 and 3) in the vicinity of the event horizon in the equatorial plane. We assume that the decay process satisfies the conservation laws of energy, momentum, and charge

$$\begin{aligned}{} & {} E_1 = E_2 + E_3,\quad L_1 = L_2 + L_3,\quad q_1 = q_2 + q_3, \end{aligned}$$
(33)
$$\begin{aligned}{} & {} m_1\dot{r_1} = m_2\dot{r_2} + m_3\dot{r_3},\quad m_1 \ge m_2 + m_3, \end{aligned}$$
(34)

where the over dots stand for derivatives by the proper time (\(\tau \)). Using the Eqs. (33) and (34), we can find the following equation

$$\begin{aligned} m_1{u_1^\phi } = m_2{u_2^\phi } + m_3{u_3^\phi }\, \end{aligned}$$
(35)

where \(u^\phi =\varOmega {u^t}=\varOmega {e}/f(r)\), \(e_i=(E_i+q_i A_{t})/m_i\), with \(i = 1,2,3 \) indicating the particle’s number, the equation (35) will take the following form

$$\begin{aligned} \varOmega _1m_1e_1=\varOmega _2m_2e_2+\varOmega _3m_3e_3. \end{aligned}$$
(36)

where \(\varOmega _i=d\phi _i/dt\) is an angular velocity of \(i^{th}\) particle given by (31), with restricted values (32). By solving the Eq. (36) we can find the energy of one of the particles, e.g. \(E_3\) [44]

$$\begin{aligned} E_3=\frac{\varOmega _1-\varOmega _2}{\varOmega _3-\varOmega _2}(E_1 + q_1A_t)-q_3A_t, \end{aligned}$$
(37)

5.3 Maximum energy of ionized particle

In order to maximize the energy of the ionized accelerated particle escaping the BH, we let particle 1 be neutral \(q_1 = 0\) and come from infinity with the initial energy equal to its rest mass energy \(E_1 = m_1\) (\({\mathcal {E}} = 1\)). For this case, the angular velocity (31) of the particles takes the simple form,

$$\begin{aligned}{} & {} \varOmega _1^2=\frac{U(r)(1-U(r))}{f(r)}, \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \varOmega _2=\varOmega _{-}, \end{aligned}$$
(39)
$$\begin{aligned}{} & {} \varOmega _3=\varOmega _{+}. \end{aligned}$$
(40)

We assume that particle 3 escapes with higher energy than the initial decayed particle. To find the maximum energy of particle 3, we maximize the expression \((\varOmega _1-\varOmega _2)/(\varOmega _3-\varOmega _2)\). This is achieved by setting the angular momentum of fragments \(\varOmega _i\) to their maximum values. We can then easily find the maximum energy of particle 3

$$\begin{aligned} \frac{\varOmega _1-\varOmega _2}{\varOmega _3-\varOmega _2}=\frac{1}{2}+\frac{\sqrt{1-U(r_{ion})}}{2} \end{aligned}$$
(41)

where \(r_{ion}\) is the ionization radius. We see from the metric functions that the ratio (41) decreases with increasing \(r_{ion}\). Finally, let us write the expression for the energy of the ionized particle in the following form [45]

$$\begin{aligned} E_3=\Bigg [\frac{1}{2}+\frac{\sqrt{1-U(r_{ion})}}{2}\Bigg ] (E_1 + q_1 A_t) - q_3 A_t. \end{aligned}$$
(42)

If \(q_1=0\) and \(q_2 = -q_3\) then we can rewrite

$$\begin{aligned} E_3=\Bigg [\frac{1}{2}+\frac{\sqrt{1-U(r_{ion})}}{2}\Bigg ] E_1 - q_3 A_t \end{aligned}$$
(43)

By dividing the above equation by \(E_1\) we can write the Eq. (43) as

$$\begin{aligned} \frac{E_3}{E_1}=\Bigg [\frac{1}{2}+\frac{\sqrt{1-U(r_{ion})}}{2}\Bigg ] - \frac{q_3 A_t}{E_1} \end{aligned}$$
(44)
Fig. 10
figure 10

Ratio of energies of ionized and neutral particles plotted against the black hole charge Q for different values of spacetime parameters. The black solid line corresponds to RN BH case at \(\beta =1\) and \(\gamma =0\) in the bottom panels of the figure

Full size image

The time component of the electromagnetic four potential depends on Q, therefore the energy of the ionized particle is maximal when \(q_3\) and Q have the same sign, which is also the expected result – the charged particle is accelerated due to the Coulomb repulsion force acting between the black hole and particle. It is useful to define the ratio between the energies of ionized and neutral particles, which would represent the efficiency of the acceleration process. Writing the black hole mass and the speed of light explicitly and substituting \(q_3 = Z e\) and \(m_1 \approx A{m_n}\), where Z and A are the atomic and mass numbers, e is an elementary charge and \(m_n\) is the nucleon mass, we find

$$\begin{aligned} \frac{E_3}{E_1}=\Bigg [\frac{1}{2}+\frac{\sqrt{1-U(r_{ion})}}{2}\Bigg ]-\frac{Z e A_t}{A{m_n}c^2}. \end{aligned}$$
(45)

By writing the mass of the black hole and the speed of light explicitly for the time component of the electromagnetic four potential and metric functions we can find the final equation for \(E_3/E_1\). This equation is complex and difficult to solve. Therefore, we provide graphical analyses of its dependency on the EMS parameters in Fig. 10. In Fig. 10 we plotted the dependence of the efficiency of the acceleration mechanism (ratio of the ionized and neutral particle with \(Z/A=1\)) on the charge of the black hole. The efficiency of the acceleration mechanism increases with the charge of the black hole and decreases slightly as the distance between the black hole and the ionization point increases (as shown in the top panel of Fig. 10). Moreover, the efficiency corresponding to a certain value of the black hole’s charge increases as the \(\beta \) parameter increases and decreases as the \(\gamma \) parameter increases (as shown in the bottom panel of Fig. 10). The ionized particle is accelerated only when the right-hand side of the equation (45) is greater than unity. If the ionization point appears near the event horizon, then the condition \(E_3 > E_1\) is satisfied for arbitrary positive values of the black hole charge, \(Q > 0\).

6 Collisions of electrically charged particles near the event horizon of the EMS black holes

The acceleration of particles colliding near rotating Kerr black holes has been first studied in [46], where the center of mass energy of colliding particles may diverge in the case of the extreme rotating Kerr black hole. Up to now, several authors have investigated the impact of external magnetic fields on the acceleration processes of charged particles in the vicinity of black holes in various gravity models and scenarios (see, for example, Refs. [47,48,49,50]). It has been demonstrated that the efficiency of the energy extraction mechanism is more effective in head-on collisions.

The expression for the center of mass energy for two particles can be found as a sum of two-momenta [51, 52]

$$\begin{aligned} \{E_{cm},0,0,0\}=m_1u_1^{\mu }+m_2u_2^{\mu }\, \end{aligned}$$
(46)

where \(u_1^{\alpha }\) and \(u_2^{\beta }\) are the four-velocity of the two colliding particles with the masses \(m_1\) and \(m_2\), respectively. One can easily calculate the square of center of mass energy defined in (46) and get

$$\begin{aligned} E^2_{cm}=m_1^2+m_2^2-2m_1m_2g_{\mu \nu } u^{\mu }u^{\nu }\, \end{aligned}$$
(47)

or

$$\begin{aligned} \frac{E^2_{cm}}{m_1m_2}=\frac{m_1}{m_2}+\frac{m_2}{m_1}-2g_{\mu \nu } u^{\mu }_1u^{\nu }_2. \end{aligned}$$
(48)

In case when the masses of the colliding particles are \(m_1=X m\) and \(m_2=Y m\).

$$\begin{aligned} \frac{E^2_{cm}}{m^2c^4}=X^2+Y^2-2g_{\mu \nu } u^{\mu }_1u^{\nu }_2. \end{aligned}$$
(49)

Following that, we will analyse the collision of particles of the same masses \(m_1=m_2=m\) and initial energies \(E_1=E_2=m\). Using the standard equation for the center of mass energy of two colliding particles with the same mass, we will investigate the acceleration of charged particles near a magnetically charged RN black hole. As a result, the expression for the center of mass energy becomes.

$$\begin{aligned} {{{\mathcal {E}}}}_{\textrm{cm}}^2=\frac{E^2_{\textrm{cm}}}{4m^2 c^4}=1-g_{\alpha \beta }u_1^{\alpha }u_2^{\beta }\, \end{aligned}$$
(50)

As a result, using the components of the four-velocity, the final expression for the center of mass energy in the equatorial plane (where \(\theta =\pi /2\)) has the following form:

$$\begin{aligned} {{{\mathcal {E}}}}^2_{\textrm{cm}}{} & {} =1+\frac{1}{U(r)}\left( {{{\mathcal {E}}}}_1-q_1 A_t \right) \left( {{{\mathcal {E}}}}_2-q_2 A_t \right) \nonumber \\{} & {} \quad {+}\frac{{\mathcal {L}}_1{{{\mathcal {L}}}}_2}{f(r)} {+}\frac{1}{U(r)}\sqrt{\left( {{{\mathcal {E}}}}_1{-}q_1 A_t\right) ^2{-}U(r)\Bigg (1+\frac{{{{\mathcal {L}}}}_1^2}{f(r)}\Bigg )}\nonumber \\{} & {} \quad \times \sqrt{\left( {{{\mathcal {E}}}}_2-q_2 A_t\right) ^2-U(r)\Bigg (1+\frac{\mathcal{L}_2^2}{f(r)}\Bigg )} \end{aligned}$$
(51)

We now intend to study numerous situations of magnetized particle collisions in the equatorial plane for a variety of circumstances in the proper observer’s frame.

Prior to examining the center-of-mass energy plots, there is an intriguing behaviour of angular momentum, which can be characterized as a “critical value”, that is necessary for approaching a black hole.

Fig. 11
figure 11

Radial dependence of the square of radial velocity for different values of angular momentum of the particle

Full size image

The critical value of angular momentum can be determined by two conditions: (a) \({\dot{r}}=0\) and (b) \(d{\dot{r}}/dr=0\). This is illustrated in Fig. 11. An increase in the angular momentum causes the square of the radial velocity to be negative implying the particles can no longer approach the central object from that value. Therefore, we investigated the allowed values of the angular momentum and determined the critical values.

Fig. 12
figure 12

Dependence of the critical angular momentum on \(\beta \) (top panels) and \(\gamma \) (bottom panels) for different values of the black hole and particle parameters

Full size image

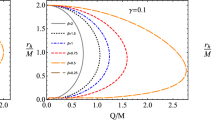
Figure 12 presents the dependence of the critical angular momentum on the EMS parameters for various values of the black hole’s parameters and particle charge. The top three panels show the critical angular momentum as a function of the magnetic parameter (\(\beta \)) for different values of the \(\gamma \) parameter. The left panel shows that increasing \(\gamma \) decreases the permissible value of angular momentum, and there is a linear relationship with the \(\beta \) parameter. The middle panel illustrates that the linearity is disrupted for larger values of black hole charge. The right panel depicts the effect of varying the particle charge. The bottom panels show the angular momentum as a function of \(\gamma \). In most cases, the angular momentum is linearly dependent on \(\gamma \), with an increase in \(\gamma \) causing a decrease in angular momentum, opposite to the behaviour with the \(\beta \) parameter. The middle and right panels replicate the behaviour of the top panel by varying the black hole and particle charge, respectively. The bottom-left figure shows the plot by varying the magnetic parameter \(\beta \) of the black hole.

Fig. 13
figure 13

Radial dependence of CME at \(\beta =\frac{1}{4}\) (top row), \(\beta =1\) (middle row) and \(\beta =\frac{3}{2}\) (bottom row) for different values of \(\gamma \)

Full size image

We have plotted radial profiles of center of mass energy of colliding charged particles with different signs, at three different values of parameters \(\beta \) and \(\gamma \) in Fig. 13, near the corresponding critical values of the black hole charge, \(Q_{cr}\). The figures are plotted for three different cases of fixed values of the particle charges: (i) positive-positive (left column), (ii) positive–negative (middle column) and (iii) negative-negative (right column). The graph of the center of mass energy shows an increasing behaviour by increasing values of parameter \(\gamma \) at \(\beta =\frac{1}{4}\). It can also be observed that, for the collisions of positively charged particles case, the energy shows maximum growth as compared to the other two cases. Similar results in the center of mass energy are also obtained in the cases of \(\beta =1\) and \(\beta =\frac{3}{2}\).

Fig. 14
figure 14

The center of mass energy near the event horizon of the EMS black hole with as a function of the black hole charge Q at different values of EMS parameters \(\beta \) (left) and \(\gamma \) (right). The black dotted line represents graphs for RN BH case at \(\beta =1\) and \(\gamma =0\) in both plots

Full size image

Furthermore, the dependence of the center of mass energy from the EMS black hole charge is shown in Fig. 14. The graphs are plotted for two different cases of black hole parameters \(\beta \) (right) and \(\gamma \) (left). The plot shows that the center of mass energy increases by increasing the EMS parameter \(\beta \). While the energy grows with the increase of the parameter \(\gamma \).

7 Conclusion

This paper is devoted to studying the electrically charged particles’ motion around electrically charged black holes in EMS theory. First, we have studied how the EMS theory parameter changes the event horizon of the black hole and found that an increase of the parameter \(\beta \) decreases the extreme value of the black hole charge as well as the positive values of \(\gamma \). We have also calculated the maximum value of \(\gamma \) and the corresponding extreme black hole charge.

The effective potential for the circular motion of the charged particles at the constant plane around the black hole is also derived. It is obtained that the increase of both \(\beta \) and \(\gamma \) leads to an increase in the effective potential.

The relationship between the energy and angular momentum of the charged particles corresponding to circular stable orbits has also been studied, where test charged particles in the two orbits with different angular momentum, but with the same energy. It is shown that the two angular momentum equals each other at ISCO and an increment in \(\beta \) causes decreasing the angular momentum at ISCO and slightly decreases the energy in the orbit when \(q<0\). In the \(q>0\) case, in two different orbits, the particle has the same angular momentum and energy.

We also have investigated the influence of ISCOs of charged particles around the charged EMS black hole and the obtained results show that the ISCO radius increases with increasing of \(\gamma \), while the \(\beta \) parameter causes the decrease of the radius. The dependence of the energy and angular momentum of the particles at ISCO from the black hole charge is shown graphically. Both parameters of the particle increase in the presence of positive \(\gamma \) and they decrease in the presence of negative \(\gamma \) and \(\beta \).

Moreover, synchrotron radiation of relativistic accelerated charged particles orbiting the EMS black hole has been investigated thoroughly. To show the effect of the EMS field we have compared the intensity of the radiation around the RN black hole and obtained that the parameter \(\beta \) increases the intensity, while the increase of \(\gamma \) decreases.

Finally, we have investigated particle acceleration processes such as electric Penrose processes and BSW effects in collisions of charged particles. We have studied the center of mass energy of two colliding charged particles around a charged black hole. We have observed that an increase in the \(\gamma \) parameter affects an increase in the center of mass energy of the colliding particles. We have examined various scenarios for different values of the \(\beta \) parameter. Lastly, we tested the center of mass energy near the horizon for the critical value of the black hole charge. We discovered that, when the collision occurs near the horizon, the center of mass energy increases dramatically.