1 Introduction

One of the most intriguing results of modern cosmology is the acceleration of the Universe [1,2,3,4], and there are two main theories to explain it. The first is the introduction of a rather exotic form of the component called Dark Energy (DE) [5] keeping Einstein’s theory of General Relativity (GR) as the gravitational theory. The second option is to modify Einstein’s GR theory and introduce a new gravitational theory with more degrees of freedom to explain the Universe’s acceleration [6, 7]. Moreover, in this paper, we will only concern ourselves with DE as a cause of the Universe’s acceleration.

Dark Energy (DE) is a hypothetical form of energy with a repulsive, negative kind of pressure and behaves just the opposite of the force of gravity. Over the years, theorists have come up with several forms of DE candidates while explaining the acceleration, the simplest among them being the cosmological constant \(\Lambda \) [5]. But the DE theory, too, isn’t devoid of complications. With the ever-growing number of DE candidates being developed by cosmologists, the models often suffer from two significant drawbacks − the cosmic coincidence and the fine-tuning problem [8, 9], among many. The primary aim of being a researcher is to improve upon such issues and develop better results.

While there are several cosmological tools that would help us with the effective development of our theories, gravitational lensing (GL) happens to be one of them. Einstein’s theory of GR predicts that space-time gets curved in the presence of massive objects. As a result, light, while passing close to such objects, get bent, thereby enlarging or distorting the background objects. Thus, GL can help us understand the matter content to the geometry and acceleration of the Universe. GL studies were mainly theoretical in the early years, but with the development of observational cosmology, that changed. At present, there are three-technique to study the GL phenomenon [10]. The first is to study the time differences between the images and the subsequent lens map followed by light with the help of Fermat’s principle; the second is to study the bending or deflection angle while they pass close to massive objects and lastly is the study of gravitational lensing statistics.

Statistical studies about GL help us understand the mass distribution of the Universe and also in determining the probability about the occurrence of some specific GL event under some particularly given conditions. The goal of our present work is to study the qualitative behaviour of a few DE models in a non-flat Universe in terms of its lensing probability. We probed our DE models against their various DE parameters and recorded how the optical depth behaves/changes over various source redshift values. It is also worth pointing out that if we have excluded specific cosmological parameters in our study, it would mean that that the change in such parameters value doesn’t affect the overall lensing probability. Lastly, our manuscript here is being organized in the following form: Sect. 2 discusses the various cosmological equations necessary for our study, Sect. 3 deals with the GL probability, in Sect. 4, we presented the few DE models we are going to use in our study, Sect. 5 deals with the comparison of the DE models with \(\Lambda CDM\) and also their corresponding flat Universe’s model, and finally, we conclude with Sect. 6 discussing the results obtained.

2 Cosmology of FRW Universe

Considering the space-time to be isotropic and homogeneous in nature, we have the FRW line element

$$\begin{aligned} ds^2=-c^2{dt}^2+a^2(t)[d\chi ^2+r^2(\chi )\{d\theta ^2+\sin ^2\theta d\phi ^2\}]\qquad \end{aligned}$$
(1)

where \(r(\chi )=\sin {\chi }\), \(r(\chi )=\chi \) or \(r(\chi )=\sinh {\chi }\) depending upon whether the Universe is closed (\(k=1\)), flat (\(k=0\)) or open (\(k=-1\)) respectively. Next, we assume the Universe to be filled with Dark Energy (DE) and Dark Matter (DM) combinations. The Friedmann equations thus, take the form (\(8\pi G=1=c\), and wherever applicable after that.)

$$\begin{aligned}{} & {} \frac{\dot{a}^2}{a^2} + \frac{k}{a^2} = \frac{1}{3}(\rho _m +\rho _x) \end{aligned}$$
(2)
$$\begin{aligned}{} & {} 2\frac{\ddot{a}}{a} + \frac{\dot{a}^2}{a^2} + \frac{k}{a^2} = -(p_m +p_x) \end{aligned}$$
(3)

where \(\rho _i\) and \(p_i (i=m,x)\) respectively denotes the density and pressure of DM and DE. Considering DM and DE are conserved separately, we may write their conservation equations as

$$\begin{aligned} {\dot{\rho }}_m + 3\frac{\dot{a}}{a} (\rho _m+p_m)=0 \end{aligned}$$
(4)

and

$$\begin{aligned} {\dot{\rho }}_x + 3\frac{\dot{a}}{a} (\rho _x+p_x)=0 \end{aligned}$$
(5)

The DM equation of state (EoS) is \(p_m = w_m \rho _m\), where \(w_m\) is the constant EoS parameter. Thus, from the equation (4) we get

$$\begin{aligned} \rho _m = \rho _{m0}a^{-3(1+w_m)} \end{aligned}$$
(6)

where \(\rho _{m0}\) denotes the present-day DM density.

The Hubble parameter is defined by \(H=\frac{\dot{a}}{a}\). Also, we have the redshift definition \(z = \frac{a_0}{a} - 1\) where \(a_0 = a(t_0) = 1\) is the scale factor value at present epoch. Now, we can define the normalized Hubble parameter by

$$\begin{aligned} h(z) = \frac{H^2}{H^2_0} \end{aligned}$$
(7)

Thus, rewriting Eq. (2) in the form of Eq. (7), we get

$$\begin{aligned} h(z) = \frac{1}{3 H^2_0}[(\rho _m + \rho _x) - 3k(1+z)^2] \end{aligned}$$
(8)

In the end, we define the parameters

$$\begin{aligned} \Omega _{m}=\frac{\rho _{m0}}{3H_0^2},\quad \Omega _{x}=\frac{\rho _{x0}}{3H_0^2},\quad \Omega _k = \frac{k}{H^2_0} \end{aligned}$$
(9)

where \(\Omega _m + \Omega _x - \Omega _k = 1\) and all the parameter values are defined at the present time.

3 Gravitational lens probability for multiple images

In the study of Gravitational Lensing Statistics, the natural cosmological distance that we quite often use is the co-moving distance [11]. To demonstrate this, we set \(ds^2 = 0\) (as light rays follow the path of null geodesics). Thus, we get the expression

$$\begin{aligned} \chi = \int \frac{dt}{a(t)} = \int da. \frac{1}{a}.\frac{dt}{da} \end{aligned}$$
(10)

Using the expression \(z = \frac{1}{a(t)}-1\), Eq. (10) can be further reduced to [12]

$$\begin{aligned} \chi = {\left\{ \begin{array}{ll} \int _0^z \frac{dz}{\sqrt{h(z)}} &{} (k=0) \\ |\Omega _k|^{1/2} \int _0^z \frac{dz}{\sqrt{h(z)}} &{} (k=\pm 1) \end{array}\right. } \end{aligned}$$
(11)

where h(z) can be found from Eq. (8) and its value depends upon the various DE model used.

Other kinds of distance measurements fundamental in the study of gravitational lensing are the luminosity distance \(d_L = a(t).r(\chi )\) and the angular diameter distance \(d_A = \frac{r(\chi )}{1+z}\) [13]. All the distance measurements are related to redshift z through Eq. (11) in the form

$$\begin{aligned} d_L=(1+z)^2 d_A = {\left\{ \begin{array}{ll} \frac{(1+z)\chi }{H_0} &{} (k=0) \\ \frac{(1+z)\sin {\chi }}{H_0 \sqrt{|\Omega _k|}} &{} (k=1) \\ \frac{(1+z)\sinh {\chi }}{H_0 \sqrt{|\Omega _k|}} &{} (k=-1) \end{array}\right. } \end{aligned}$$
(12)

Now, the differential optical depth per unit redshift is given by

$$\begin{aligned} \frac{d\tau }{dz_l}=n(1+z_l)^3 \hat{\sigma }\frac{cdt}{dz_l} \end{aligned}$$
(13)

where n is the co-moving number density of lensing galaxies [14,15,16], \(\hat{\sigma }\) is the dimensional cross-section of lensing, and \(cdt/dz_l\) is the proper distance interval. The cross-section \(\hat{\sigma }\) and the proper distance interval are given by

$$\begin{aligned} \hat{\sigma }=16\pi ^3 \sigma ^4\left( \frac{d_A^l d_A^{ls}}{d_A^s}\right) ^2 \end{aligned}$$
(14)

and

$$\begin{aligned} \frac{cdt}{dz_l}=\frac{H_0^{-1}}{(1+z_l)\sqrt{h(z_l)}} \end{aligned}$$
(15)

where \(d_A^l\), \(d_A^{ls}\) and \(d_A^s\) are the angular diameter distances between the observer-lens, lens-source and observer-source, respectively and \(\sigma \) is the velocity dispersion function. Next, considering the contributions of a group of galaxies with varying luminosities and redshifts, the Schechter function may be used to characterise the current luminosity function of galaxies [17, 18]

$$\begin{aligned} \frac{dn}{dL} = \frac{n^*_i}{L^*_i}{\left( \frac{L}{L_i^*}\right) }^{\alpha _i} e^{(-L/L_i^*)} \end{aligned}$$
(16)

where \(i=(S,S_0,E)\) depending upon the galaxy morphology, \(L_i^*\) and \(n_i^*\) are the characteristic luminosity and number density, respectively. Further, using the power-law relation \(L/L_i^*=(\sigma /\sigma _i^*)^{g_i}\) between luminosity and velocity dispersion function, Eq. (16) reduces to

$$\begin{aligned} \frac{dn}{d\sigma }=\frac{n^*_i}{\sigma ^*_i}{\left( \frac{\sigma }{\sigma _i^*}\right) }^{g_i\alpha _i+g_i-1} e^{(-\sigma /\sigma _i^*)^{g_i}} g_i \end{aligned}$$
(17)

Thus, integrating \(d\tau \) from 0 to \(z_s\), we obtain

$$\begin{aligned} \tau (z_s)= \left( \sum _{i=S,S_0,E} F_i \right) \int _{0}^{\chi _s} \left[ \frac{r(\chi _s - \chi _l)}{r(\chi _s)}\right] ^2 r^2(\chi _l) d\chi _l \nonumber \\ \end{aligned}$$
(18)

where \(F_i\) denotes the ability of the ith class of galaxy morphology in generating multiple images and depends solely upon the intrinsic and statistical characteristics of the galaxies. Using Eq. (17), we may calculate \(F_i\) in the form

$$\begin{aligned} F_i= & {} 16 \pi ^3 \sigma ^4 H_0^{-3} \int _0^\infty \frac{n^*_i}{\sigma ^*_i}{\left( \frac{\sigma }{\sigma _i^*}\right) }^{g_i \alpha _i+g_i-1} e^{(-\sigma /\sigma _i^*)^{g_i}} g_i d\sigma \nonumber \\= & {} 16 \pi ^3 \sigma ^4 H_0^{-3} n_i^* \Gamma (\alpha _i+1) \end{aligned}$$
(19)

With the uncertainties widely discussed in the literature [19,20,21,22,23], we will be treating \(F \equiv \sum _{i=S,S_0,E} F_i\) as normalised factor hereafter. Thus, from Eqs. (18) and (19) we derive the simple analytical equation for the gravitational lensing probability of a point source at \(z_s\) for an FRW Universe with DM and DE components given by

$$\begin{aligned} P(lens){} & {} =\frac{\tau (z_s)}{F} \nonumber \\{} & {} = {\left\{ \begin{array}{ll} \frac{\chi _s^3}{30} &{} (k=0) \\ \frac{1}{|\Omega _k|^{3/2}} \left[ \frac{1}{8}(1+3\cot ^2{\chi _s})\chi _s \right. \\ \left. - \frac{3}{8}\cot {\chi _s} \right] &{} (k=1) \\ \frac{1}{|\Omega _k|^{3/2}} \left[ \frac{1}{8}(-1+3\coth ^2{\chi _s})\chi _s \right. \\ \left. - \frac{3}{8}\coth {\chi _s} \right] &{} (k=-1) \end{array}\right. }\nonumber \\ \end{aligned}$$
(20)

4 Lensing for dark energy models

In this section, we study the lensing effects of some dark energy models like Tachyonic Field, Generalised Cosmic Chaplygin Gas, New Variable Modified Chaplygin Gas, Modified Chaplygin–Jacobi Gas and Modified Chaplygin–Abel Gas.

Fig. 1
figure 1

Optical depth vs. source redshift graph for Tachyonic Field in a closed Universe where \(w_m=0.01\), \(m=2\), \(A_t=0.25\) and \(\Omega _k=0.01\)

Full size image
Fig. 2
figure 2

Optical depth vs. source redshift graph for Tachyonic Field in an open Universe where \(w_m=0.01\), \(m=2\), \(A_t=0.25\) and \(\Omega _k=-\,0.01\)

Full size image

  • Tachyonic Field (TF):

    Following the work of A. Sen [24, 25], pressure \(p_x\) and energy density \(\rho _x\) of the “Tachyonic Field” or “TF” are given by

    $$\begin{aligned}{} & {} p_x = - V(\phi )\sqrt{1 - \dot{\phi ^2}} \nonumber \\{} & {} \rho _x = \frac{V(\phi )}{\sqrt{1 - \dot{\phi ^2}}} \end{aligned}$$
    (21)

    where \(\phi \) denotes the TF and \(V(\phi )\) the associated potential. In Eq. (5), we may use the above relation to get

    $$\begin{aligned} \frac{\dot{V}}{V \dot{\phi ^2}} + \frac{\ddot{\phi }}{\dot{\phi }}(1 - \dot{\phi ^2})^{-1} + 3\frac{\dot{a}}{a} = 0 \end{aligned}$$
    (22)

    Assuming (from Ref. [26])

    $$\begin{aligned} V = \frac{1}{(1 - \dot{\phi ^2})^m}, \ (m>0) \end{aligned}$$
    (23)

    we obtain the solution of Eq. (22) in the form

    $$\begin{aligned} \phi= & {} \frac{2 a^{3/2}}{\sqrt{3A}} 2^{F}1 \nonumber \\{} & {} \times \left[ \frac{1+2m}{4}, \frac{3+2m}{4}, \frac{5+2m}{4}, -A^{-\frac{2}{2m+1}}. a^{\frac{6}{2m+1}}\right] \nonumber \\ \end{aligned}$$
    (24)

    where A is the integrating constant. Now, V can be expressed as

    $$\begin{aligned} V = \left[ 1+\left( \frac{A}{a^3}\right) ^{\frac{2}{2m+1}}\right] ^m \end{aligned}$$
    (25)

    Thus, using Eqs. (23) and (25), we get the pressure and energy density expression from Eq. (21) in the form

    $$\begin{aligned}{} & {} p_x = -[1+(A(1+z)^3)^{\frac{2}{2m+1})}]^{\frac{2m-1}{2}}, \nonumber \\{} & {} \rho _x = [1+(A(1+z)^3)^{\frac{2}{2m+1})}]^{\frac{2m+1}{2}} \end{aligned}$$
    (26)

    Equation (26) can be further rewritten as

    $$\begin{aligned}{} & {} p_x = p_{x0}[A_t+(1-A_t)(1+z)^{\frac{6}{2m+1})}]^{\frac{2m-1}{2}}, \nonumber \\{} & {} \rho _x = \rho _{x0}[A_t+(1-A_t)(1+z)^{\frac{6}{2m+1})}]^{\frac{2m+1}{2}} \end{aligned}$$
    (27)

    where \(p_{x0}=-(1+A^{\frac{2}{2m+1}})^{\frac{2m-1}{2}}\) and \(\rho _{x0}=(1+A^{\frac{2}{2m+1}})^{\frac{2m+1}{2}}\) are the pressure and energy density of TF, respectively, at the present time with \(A_t = (1+A^{\frac{2}{2m+1}})^{-1}\).

    Substituting \(\rho _m\) and \(\rho _x\) from Eqs. (6) and (27) respectively in Eq. (8), we get the normalised Hubble parameter in the form

    $$\begin{aligned}{} & {} h(z) = \Omega _m(1+z)^{3(1+w_m)} \nonumber \\{} & {} \quad +\Omega _x[A_t+(1-A_t)(1+z)^{\frac{6}{2m+1})}]^{\frac{2m+1}{2}} - \Omega _k(1+z)^2\nonumber \\ \end{aligned}$$
    (28)

    where \(\Omega _m\), \(\Omega _x\), \(\Omega _k\) are given by (9) and m, \(w_m\) are constants.

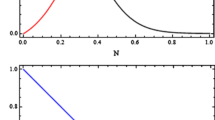
    In order to calculate the optical depth for this model, we substitute Eq. (28) in (11) and later on Eq. (11) in (20). Then we go on plotting the required graphs as shown below. Figures 1 and 2 shows the optical depth vs. source redshift graph for varied \(\Omega _m\) and \(\Omega _x\) while keeping the rest parameters constant. We observe that the lensing probability decreases with an increase in the parameter value of \(\Omega _m\). Moreover, the opposite happens for the \(\Omega _x\) parameter. It is also worth noting that the change in lensing probability isn’t that significant for varied \(\Omega _m\) and \(\Omega _x\) parameters, as evident from the first figure of Figs. 1 and 2. Further, an increase in the source redshift value also increases the optical depth of this model. Again, upon plotting the optical depth vs \(A_t\) graph (Figs. 3, 4), we notice that the optical depth behaviour increases with the increase in \(A_t\) values and the source redshift value.

Fig. 3
figure 3

Optical depth vs. \(A_t\) graph for Tachyonic Field in a closed Universe where \(w_m=0.01\), \(m=2\), \(\Omega _m=0.23\), \(\Omega _x=0.78\) and \(\Omega _k=0.01\)

Full size image
Fig. 4
figure 4

Optical depth vs. \(A_t\) graph for Tachyonic Field in an open Universe where \(w_m=0.01\), \(m=2\), \(\Omega _m=0.23\), \(\Omega _x=0.76\) and \(\Omega _k=-\,0.01\)

Full size image

  • Generalised Cosmic Chaplygin Gas (GCCG):

    “Generalised Cosmic Chaplygin Gas” or “GCCG” was proposed as a dark energy candidate by Gonzalez-Diaz [27]. The EoS of this model is of the form

    $$\begin{aligned} p_x = \rho _x^{-\alpha } [C + (\rho _x^{1+\alpha } - C)^{-\omega }] \end{aligned}$$
    (29)

    where \(C=\frac{A}{1+\omega }-1\) with \(-l<\omega <0 \ (l>1)\) and \(\alpha \), A are constants. Here, when \(\omega \rightarrow 0\) or \(\omega =-1\) or \(A \rightarrow 0\), the GCCG reduces to a Generalised Chaplygin Gas or de-Sitter fluid at late time or \(p_x=\omega \rho _x\) respectively. Further, in the future, GCCG propagates between dust and \(\Lambda CDM\) model.

    Using Eq. (29), we get the solution of (5) as

    $$\begin{aligned} \rho _x= & {} \left[ C + \left( 1+\frac{B}{a^{3(1+\alpha )(1+\omega )}}\right) ^{\frac{1}{1+\omega }}\right] ^{\frac{1}{1+\alpha }} \nonumber \\= & {} \left[ C + \left( 1+B(1+z)^{3(1+\alpha )(1+\omega )}\right) ^{\frac{1}{1+\omega }}\right] ^{\frac{1}{1+\alpha }} \end{aligned}$$
    (30)

    where B is a constant. Using Eqs. (6) and (30) in (8), we get the normalised Hubble parameter in this model of the form

    $$\begin{aligned}{} & {} h(z) = \Omega _m(1+z)^{3(1+w_m)} \nonumber \\{} & {} \quad + \frac{1}{H_0^2} \left\{ C + \left( 1+B(1+z)^{3(1+\alpha )(1+\omega )}\right) ^{\frac{1}{1+\omega }}\right\} ^{\frac{1}{1+\alpha }}\nonumber \\{} & {} \quad - \Omega _k (1+z)^2 \end{aligned}$$
    (31)

    where \(\Omega _m\), \(\Omega _k\) are given by (9) and \(\omega \), B, \(w_m\) are constants.

    As done in the previous model, we calculate the co-moving distance and optical depth for this model as well and plot the necessary graph shown in Figs. 5 and 6. Optical depth vs. source redshift graph of this model with varying \(\Omega _m\) shows that the lensing probability decreases along with the increase in the value of \(\Omega _m\) consistent with our findings in Tachyonic Field.

Fig. 5
figure 5

Optical depth vs. source redshift graph for Generalised Cosmic Chaplygin Gas in a closed Universe where \(\alpha =0.5\), \(\omega =-0.5\), \(B=2\), \(C=3\), \(w_m=0.01\) and \(\Omega _k=0.01\)

Full size image
Fig. 6
figure 6

Optical depth vs. source redshift graph for Generalised Cosmic Chaplygin Gas in an open Universe where \(\alpha =0.5\), \(\omega =-\,0.5\), \(B=2\), \(C=3\), \(w_m=0.01\) and \(\Omega _k=-\,0.01\)

Full size image
Fig. 7
figure 7

Optical depth vs. source redshift graph for New Variable Modified Chaplygin Gas in a closed Universe where \(m=4\), \(n=2\), \(\alpha =0.3\), \(A_0=2\), \(B_0=2\), \(C_0=3\), \(H_0=72\), \(w_m=0.01\) and \(\Omega _k=0.01\)

Full size image
Fig. 8
figure 8

Optical depth vs. source redshift graph for New Variable Modified Chaplygin Gas in an open Universe where \(m=4\), \(n=2\), \(\alpha =0.3\), \(A_0=2\), \(B_0=2\), \(C_0=3\), \(H_0=72\), \(w_m=0.01\) and \(\Omega _k=-\,0.01\)

Full size image

  • New Variable Modified Chaplygin Gas (NVMCG):

    For the unification of DM and DE, the pure “Chaplygin Gas” (CG) model was introduced with the EoS \(p_x=-B/\rho _x \ (B>0)\) [28, 29]. This model was later generalised to \(p_x=-B/\rho _x^\alpha \ (0 \le \alpha \le 1)\) known as the generalised Chaplygin Gas [30, 31]. It was further modified to the form \(p_x = A\rho _x - B/\rho _x^\alpha \ (0 \le \alpha \le 1)\), where \(A>0\), \(B>0\) are constants. This form of CG is named modified Chaplygin Gas [32, 33]. For its in-homogeneity behaviour, assuming B as a function of a(t), the CG in this form is called variable Chaplygin Gas [34, 35]. Also, treating CG as a Born-Infeld scalar field [36], B(a) gets related to the scalar potential. Now, treating the constant B as a variable (\(B=B(a)\)), in the case of generalised Chaplygin Gas, we get variable generalised Chaplygin Gas [37], and the modified Chaplygin Gas gets reduced to variable modified Chaplygin Gas [38]. Further, considering constants A, B too as a function of a(t) in variable modified Chaplygin Gas, we get another new form called the new variable modified Chaplygin Gas or NVMCG [39]. The EoS of NVMCG is given by

    $$\begin{aligned} p_x = A(a)\rho _x - \frac{B(a)}{\rho _x^\alpha } \ (0 \le \alpha \le 1) \end{aligned}$$
    (32)

    Now, assuming \(A(a)=A_0 a^{-n}\) and \(B(a)=B_0 a^{-m}\) where \(A_0\), \(B_0\), n, m are positive constants; we get the solution of Eq. (5) using Eq. (32) as

    $$\begin{aligned} \rho _x(z)= & {} (1+z)^3 e^{\frac{3A_0(1+z)^n}{n}}\nonumber \\{} & {} \times \bigg [C_0+\frac{B_0}{A_0}\left( \frac{3A_0(1+\alpha )}{n}\right) ^{\frac{3(1+\alpha )+n-m}{n}} \nonumber \\{} & {} \times \Gamma \left( \frac{m{-}3(1{+}\alpha )}{n},\frac{3A_0(1{+}\alpha )}{n}(1{+}z)^n \right) \bigg ] ^{\frac{1}{1+\alpha }} \nonumber \\ \end{aligned}$$
    (33)

    where \(C_0\) is the integrating constant and \(\Gamma (a,x)\) the upper incomplete gamma function. Thus, substituting (6) and (33) in (8), we get the normalised Hubble parameter of this model in the form

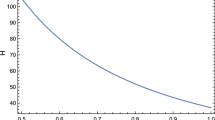
    $$\begin{aligned} h(z)=\Omega _m(1+z)^{3(1+w_m)}+\frac{\rho _x(z)}{3H_0^2}-\Omega _k(1+z)^2 \end{aligned}$$
    (34)

    where \(\rho _x(z)\) can be calculated from (33), \(\Omega _m\), \(\Omega _k\) are given by (9) and m, n, \(B_0\), \(C_0\), \(w_m\) are constants. Calculating optical depth as previously done, we plot our necessary graphs for this model. Firstly, Figs. 7 and 8 shows the optical depth vs source redshift graph with varying \(\Omega _m\) in an open and closed Universe, respectively. It has been found that the optical depth decreases when we increase our \(\Omega _m\) value, which has already been found in our previous two models. However, it should be noted that the graph gets parallel to the \(z_s\) axis for \(z_s>1\), implying that the optical depth behaviour doesn’t get affected for increasing \(z_s\) values. Secondly, we plotted our optical depth vs \(A_0\) graph in Figs. 9 and 10. The lensing probability for \(z_s=2,3\) coincides with each other while for \(z_s=1\), initially, for smaller values of \(A_0\) it gives different lensing probability but ultimately coincide with each other after \(A_0\) crosses certain values in the graph implying for higher \(A_0\) values, change in source redshift (\(z_s\)) does not affect its optical depth behaviour. Further, we also plotted optically depth vs \(H_0\) and optical depth vs \(\alpha \) graphs in Figs. 11, 12, 13 and 14 respectively. We see in the first figure of Figs. 11 and 12 that the lensing probability linearly increases with an increase in \(H_0\) values. Also, the graphs for \(z_s=2,3\) coincide with each other, the reason for which can be verified from the second figure of Figs. 11 and 12 where we see that the graphs get parallel to \(z_s\) axis after crossing \(z_s>1\) value, implying no change in optical depth behaviour for increasing \(z_s\) values. Next, from the first figure of Figs. 13 and 14 the increasing value of \(\alpha \) increases our lensing probability with the graphs for \(z_s=2,3\) coinciding with each other, thereby implying that redshift has no effect in its lensing probability (second figure of Figs. 13, 14).

Fig. 9
figure 9

Optical depth vs. \(A_0\) graph for New Variable Modified Chaplygin Gas in a closed Universe where \(m=4\), \(n=2\), \(\alpha =0.3\), \(B_0=2\), \(C_0=3\), \(w_m=0.01\), \(H_0=72\), \(\Omega _m=0.23\) and \(\Omega _k=0.01\)

Full size image
Fig. 10
figure 10

Optical depth vs. \(A_0\) graph for New Variable Modified Chaplygin Gas in an open Universe where \(m=4\), \(n=2\), \(\alpha =0.3\), \(B_0=2\), \(C_0=3\), \(w_m=0.01\), \(H_0=72\), \(\Omega _m=0.23\) and \(\Omega _k=-\,0.01\)

Full size image
Fig. 11
figure 11

Optical depth vs. \(H_0\) and optical depth vs. source redshift with varied \(H_0\) graphs for New Variable Modified Chaplygin Gas in a closed Universe where \(m=4\), \(n=2\), \(\alpha =0.3\), \(A_0=2\), \(B_0=2\), \(C_0=3\), \(w_m=0.01\), \(\Omega _m=0.23\) and \(\Omega _k=0.01\)

Full size image
Fig. 12
figure 12

Optical depth vs. \(H_0\) and optical depth vs. source redshift with varied \(H_0\) graphs for New Variable Modified Chaplygin Gas in an open Universe where \(m=4\), \(n=2\), \(\alpha =0.3\), \(A_0=2\), \(B_0=2\), \(C_0=3\), \(w_m=0.01\), \(\Omega _m=0.23\) and \(\Omega _k=-\,0.01\)

Full size image
Fig. 13
figure 13

Optical depth vs. \(\alpha \) and optical depth vs. source redshift with varied \(\alpha \) graphs for New Variable Modified Chaplygin Gas in a closed Universe where \(m=4\), \(n=2\), \(A_0=2\), \(B_0=2\), \(C_0=3\), \(H_0=72\), \(w_m=0.01\), \(\Omega _m=0.23\) and \(\Omega _k=0.01\)

Full size image
Fig. 14
figure 14

Optical depth vs. \(\alpha \) and optical depth vs. source redshift with varied \(\alpha \) graphs for New Variable Modified Chaplygin Gas in an open Universe where \(m=4\), \(n=2\), \(A_0=2\), \(B_0=2\), \(C_0=3\), \(H_0=72\), \(w_m=0.01\), \(\Omega _m=0.23\) and \(\Omega _k=-\,0.01\)

Full size image

  • Modified Chaplygin–Jacobi Gas (MCJG):

    Hyperbolic functions are special cases of elliptic functions. “Jacobi elliptic functions” being a collection of fundamental elliptic functions, Villanueva [40] substituted the Jacobi elliptic function in place of the cosine hyperbolic function obtained by the generalised Chaplygin Gas in the Hubble parameter to derive the EoS known as the generalised Chaplygin–Jacobi Gas. Thus, by substituting the “Jacobi elliptic cosine function” \(cn(\Phi )\) for the hyperbolic function, the generating function of Modified Chaplygin Gas

    $$\begin{aligned} H(\phi )=H_c \ Sech^{-\frac{1}{1+\alpha }}(\Phi ) \end{aligned}$$
    (35)

    may be rewritten as

    $$\begin{aligned} H(\phi )=H_c \ cn^{-\frac{1}{1+\alpha }}(\Phi ) \end{aligned}$$
    (36)

    where \(cn(\Phi )\equiv cn(\Phi ,\mu )\) with \(\mu \in [0,1]\) being the elliptic modulus.

    Following the work done by [41], we may write the EoS of “Modified Chaplygin–Jacobi Gas” as

    $$\begin{aligned} p_x{} & {} =[(2\mu -1)(1+A)-1]\rho _x -\frac{\mu B}{\rho _x^\alpha }\nonumber \\{} & {} \quad +\frac{(1-\mu )(1+A)^2}{B}\rho _x^{2+\alpha } \end{aligned}$$
    (37)

    Substituting the value of \(p_x\) from (37) in Eq. (5), we get

    $$\begin{aligned} \rho _x^{1+\alpha }=\frac{B}{1+A}\bigg [\frac{a^{3(1+\alpha )(1+A)}+\mu D}{a^{3(1+\alpha )(1+A)}}-(1-\mu )D\bigg ]\nonumber \\ \end{aligned}$$
    (38)

    where \(D(>0)\) is constant. For larger values of a(t), we have \(\rho _x \simeq (\frac{B}{1+A})^\frac{1}{1+\alpha }\) and \(p_x \simeq -(\frac{B}{1+A})^\frac{1}{1+\alpha }=-\rho _x\) which is equivalent to the “\(\Lambda CDM\) model” where the cosmological constant \(\Lambda =(\frac{B}{1+A})^{\frac{1}{1+\alpha }}\). Also, in the phase of the Universe where \(y=a^{3(1+\alpha )(1+A)}-(1-\mu )D \simeq 0\), we get \(\rho _x\simeq (\frac{B}{1+A} \frac{D}{y})^{\frac{1}{1+\alpha }}\). This relates to a Universe phase in which the polytropic EoS \(p_x=\frac{(1-\mu )(1+A)}{B}\rho _x^{\alpha +2}\) is followed. Thus, the mentioned expression of \(\rho _x\) may be rewritten as

    $$\begin{aligned}{} & {} \rho _x^{1+\alpha }\nonumber \\{} & {} \quad =\frac{B}{1+A}\left[ \frac{(1-A_s)(1+z)^{3(1+\alpha )(1+A)}+A_s}{\mu A_s-(1-\mu )(1-A_s)(1+z)^{3(1+\alpha )(1+A)}}\right] \nonumber \\ \end{aligned}$$
    (39)

    where \(A_s=\frac{1}{1+\mu D}\) with \(1-\mu< A_s < 1\). Thus, the energy density value measured at the present time is \(\rho _{x0}^{1+\alpha }=\frac{B}{(1+A)[\mu A_s-(1-\mu )(1-A_s)]}\). Substituting \(\rho _{m0}\) from Eq. (6) and \(\rho _{x0}\) from the above expression respectively in the Eq. (8), we get the normalised Hubble parameter in the form

    $$\begin{aligned} h(z)= & {} \Omega _m(1+z)^{3(1+w_m)}+\Omega _x[\mu A_s \nonumber \\{} & {} -(1-\mu )(1-A_s)]^{\frac{1}{1+\alpha }} \nonumber \\{} & {} \times \left[ \frac{(1{-}A_s)(1{+}z)^{3(1{+}\alpha )(1{+}A)}{+}A_s}{\mu A_s{-}(1{-}\mu )(1{-}A_s)(1{+}z)^{3(1+\alpha )(1{+}A)}}\right] ^{\frac{1}{1+\alpha }}\nonumber \\{} & {} -\Omega _k(1+z)^2 \end{aligned}$$
    (40)

    where \(\Omega _m\), \(\Omega _x\), \(\Omega _k\) are given by (9) and A, \(\alpha \), \(A_s\), \(\mu \), \(w_m\) are constants.

    Calculating \(\tau (z_s)\), our optical depth vs. source redshift graph with varied \(\Omega _m\) and \(\Omega _x\) is shown in Figs. 15 and 16. Our graph here shows that the lensing probability decreases with an increase in \(\Omega _m\) value (and a decrease in \(\Omega _x\) value). Our findings here are consistent with all the previous models discussed above.

Fig. 15
figure 15

Optical depth vs. source redshift graph for Modified Chaplygin–Jacobi Gas in a close Universe where \(A=0.2\), \(\alpha =0.02\), \(A_s=0.99\), \(\mu =0.89\), \(w_m=0.01\) and \(\Omega _k=0.01\)

Full size image
Fig. 16
figure 16

Optical depth vs. source redshift graph for Modified Chaplygin–Jacobi Gas in an open Universe where \(A=0.2\), \(\alpha =0.02\), \(A_s=0.99\), \(\mu =0.89\), \(w_m=0.01\) and \(\Omega _k=-\,0.01\)

Full size image

  • Modified Chaplygin–Abel Gas (MCAG):

    As already been done in the MCJG model, here too, we replace the hyperbolic function in (35) by the “Abel elliptic functio” \(F(\Phi )\), so that we get the generating function in the form

    $$\begin{aligned} H(\Phi )=H_c F^{-\frac{1}{1+\alpha }}(\Phi ) \end{aligned}$$
    (41)

    where \(F(\Phi )=\sqrt{1+e^2\varphi ^2(\Phi )}\) with \(\varphi (\Phi )\equiv \varphi (\Phi ,c,e)\) which is the “Abel elliptic function” and \(c,e\in \mathrm{I\!R}\). Following the work done by [41], we may write the EoS of “Modified Chaplygin–Abel Gas” in the form

    $$\begin{aligned} p_x= & {} [(e^2+2c^2)(1+A)-1]\rho _x-\frac{c^2B}{\rho _x^\alpha }\nonumber \\{} & {} -\frac{(e^2+c^2)(1+A)^2}{B}\rho _x^{2+\alpha } \end{aligned}$$
    (42)

    Substituting \(p_x\) from (42) in Eq. (5), we get

    $$\begin{aligned}{} & {} \rho _x^{1+\alpha }=\frac{B}{1+A}\left[ \frac{a^{3e^2(1+\alpha )(1+A)}+c^2K}{a^{3e^2(1+\alpha )(1+A)}+(e^2+c^2)K}\right] \nonumber \\ \end{aligned}$$
    (43)

    where \(K(>0)\) is constant. For larger values of a(t), we get \(p_x\simeq -\rho _x\) corresponding to the “\(\Lambda CDM\) model” where the cosmological constant \(\Lambda =\frac{B}{1+A}^{\frac{1}{1+\alpha }}\). For smaller values of a(t), we get \(p_x\simeq -\rho _x\) corresponding to the inflationary phase of the Universe. As a result, MCAG propagates between the phases of inflation and the \(\Lambda CDM\). Thus, the previously described \(\rho _x\) equation may be rewritten as

    $$\begin{aligned}{} & {} \rho _x^{1+\alpha }=\frac{c^2B}{1+A}\nonumber \\{} & {} \times \left[ \frac{(1-B_s)(1+z)^{3e^2(1+\alpha )(1+A)}+B_s}{c^2B_s+(e^2+c^2)(1-B_s)(1+z)^{3e^2(1+\alpha )(1+A)}}\right] \nonumber \\ \end{aligned}$$
    (44)

    where \(B_s=\frac{1}{1+c^2K}\) (\(0<B_s<1\)) with \(\rho _{x0}^{1+\alpha }=\frac{c^2B}{(1+A)[c^2B_s+(e^2+c^2)(1-B_s)]}\) representing the present energy density value. Thus, substituting \(\rho _{m0}\) from Eq. (6) and \(\rho _{x0}\) from the above expression respectively in Eq. (8), we get the normalised Hubble parameter in the form

    $$\begin{aligned}{} & {} h(z)=\Omega _m(1+z)^{3(1+w_m)}\nonumber \\{} & {} \quad +\Omega _x[c^2B_s+(e^2+c^2)(1-B_s)]^{\frac{1}{1+\alpha }} \nonumber \\{} & {} \quad \times \left[ \frac{(1-B_s)(1+z)^{3e^2(1+\alpha )(1+A)}+B_s}{c^2B_s+(e^2+c^2)(1-B_s)(1+z)^{3e^2(1+\alpha )(1+A)}}\right] ^{\frac{1}{1+\alpha }}\nonumber \\{} & {} \quad -\Omega _k(1+z)^2 \end{aligned}$$
    (45)

    where \(\Omega _m\), \(\Omega _x\), \(\Omega _k\) are given by (9) and c, e, \(\alpha \), A, \(B_s\), \(w_m\) are constants.

    As already been done in all the previous models, we calculated our the optical depth and plotted the optical depth vs. source redshift graph for this model as shown in Figs. 17 and 18. The graph shows that the lensing probability decreases with an increase in \(\Omega _m\) value (and decreasing \(\Omega _x\) value) as found in the other models as well.

Fig. 17
figure 17

Optical depth vs. source redshift graph for Modified Chaplygin–Abel Gas in a closed Universe where \(c=0.39\), \(e=0.17\), \(\alpha =0.08\), \(A=0.27\), \(B_s=0.5\), \(w_m=0.01\) and \(\Omega _k=0.01\)

Full size image
Fig. 18
figure 18

Optical depth vs. source redshift graph for Modified Chaplygin–Abel Gas in an open Universe where \(c=0.39\), \(e=0.17\), \(\alpha =0.08\), \(A=0.27\), \(B_s=0.5\), \(w_m=0.01\) and \(\Omega _k=-0.01\)

Full size image
Fig. 19
figure 19

Graphs showing the change in optical depth behaviour of TF and \(\Lambda \)CDM model against source redshift \(z_s\) in an open, flat and closed Universe where the parameter values chosen are as follows TF (open): \(w_m = 0.01, m = 2, A_t = 0.25, \Omega _m = 0.23, \Omega _x = 0.76, \Omega _k = -0.01\); TF (flat): \(w_m = 0.01, m = 2, A_t = 0.25, \Omega _m = 0.23, \Omega _x = 0.77\); TF (closed): \(w_m = 0.01, m = 2, A_t = 0.25, \Omega _m = 0.23, \Omega _x = 0.78, \Omega _k = 0.01\) and \(\Lambda \)CDM (open): \(w_m = 0.01, \Omega _m = 0.23, \Omega _{\Lambda } = 0.76, \Omega _k = -0.01; \Lambda \)CDM (flat): \(w_m = 0.01, \Omega _m = 0.23, \Omega _{\Lambda } = 0.77; \Lambda \)CDM (closed): \(w_m = 0.01, \Omega _m = 0.23, \Omega _{\Lambda } = 0.78, \Omega _k = 0.01\)

Full size image
Fig. 20
figure 20

Graphs showing the change in optical depth behaviour of GCCG and \(\Lambda \)CDM models against source redshift \(z_s\) in an open, flat and closed Universe where the parameter values chosen are as follows GCCG (open): \(\alpha = 0.5, \omega = -0.5,B = 2, C = 3, w_{m} = 0.01, \Omega _m = 0.23, \Omega _k = -0.01\); GCCG (flat): \(\alpha = 0.5, \omega = -0.5,B = 2, C = 3, w_{m} = 0.01, \Omega _m = 0.23\); GCCG (closed): \(\alpha = 0.5, \omega = -0.5,B = 2, C = 3, w_{m} = 0.01, \Omega _m = 0.23, \Omega _k = 0.01\) and \(\Lambda CDM\) (open): \(w_{m} = 0.01, \Omega _m = 0.23, \Omega _\Lambda = 0.76, \Omega _k = -0.01; \Lambda CDM (flat): w_{m} = 0.01, \Omega _m = 0.23, \Omega _\Lambda = 0.77; \Lambda CDM\) (closed): \(w_{m} = 0.01, \Omega _m = 0.23, \Omega _\Lambda = 0.78, \Omega _k = 0.01\)

Full size image
Fig. 21
figure 21

Graphs showing the change in optical depth behaviour of NVMCG and \(\Lambda \)CDM models against source redshift \(z_s\) in an open, flat and closed Universe where the parameter values chosen are as follows NVMCG (open): \(m = 4, n = 2, \alpha = 0.3, A_{0} = 2, B_{0} = 2, C_{0} = 3, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{k} = -0.01\); NVMCG (flat): \(m = 4, n = 2, \alpha = 0.3, A_{0} = 2, B_{0} = 2, C_{0} = 3, w_{m} = 0.01, \Omega _{m} = 0.23\); NVMCG (closed): \(m = 4, n = 2, \alpha = 0.3, A_{0} = 2, B_{0} = 2, C_{0} = 3, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{k} = 0.01\) and \(\Lambda \) CDM (open): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.76, \Omega _{k} = -0.01\); \(\Lambda \) CDM (flat): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.77\); \(\Lambda \) CDM (closed): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.78, \Omega _{k} = 0.01\)

Full size image
Fig. 22
figure 22

Graphs showing the change in optical depth behaviour of MCJG and \(\Lambda \)CDM models against source redshift \(z_s\) in an open, flat and closed Universe where the parameter values chosen are as follows MCJG (open): \(A = 0.2, \alpha = 0.02, A_{s} = 0.99, \mu = 0.89, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{x} = 0.76, \Omega _{k} = -0.01\); MCJG (flat): \(A = 0.2, \alpha = 0.02, A_{s} = 0.99, \mu = 0.89, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{x} = 0.77\); MCJG (closed): \(A = 0.2, \alpha = 0.02, A_{s} = 0.99, \mu = 0.89, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{x} = 0.78, \Omega _{k} = 0.01\) and \(\Lambda \) CDM (open): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.76, \Omega _{k} = -0.01\); \(\Lambda \) CDM (flat): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.77\); \(\Lambda \) CDM (closed): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.78, \Omega _{k} = 0.01\)

Full size image
Fig. 23
figure 23

Graphs showing the change in optical depth behaviour of MCAG and \(\Lambda \)CDM models against source redshift \(z_s\) in an open, flat and closed Universe where the parameter values chosen are as follows MCAG (open): \(c = 0.39, e = 0.17, \alpha = 0.08, A = 0.27, B_{s} = 0.5, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{x} = 0.76, \Omega _{k} = -0.01\); MCAG (flat): \(c = 0.39, e = 0.17, \alpha = 0.08,A = 0.27, B_{s} = 0.5, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{x} = 0.77\); MCAG (closed): \(c = 0.39, e = 0.17, \alpha = 0.08, A = 0.27, B_{s} = 0.5, w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{x} = 0.78, \Omega _{k} = 0.01\) and \(\Lambda \)CDM (open): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.76, \Omega _{k} = -0.01\); \(\Lambda \)CDM (flat): \(w_{m} = 0.01, \Omega _{k} = 0.23, \Omega _\Lambda = 0.77\); \(\Lambda \)CDM (closed): \(w_{m} = 0.01, \Omega _{m} = 0.23, \Omega _{\Lambda } = 0.78, \Omega _{k} = 0.01\)

Full size image

5 Comparison of the DE models with \(\Lambda \)CDM and corresponding flat Universe

The \(\Lambda \)CDM, also known as the concordance model, is the simplest form of dark energy candidate that solves the accelerated expansion of the Universe. The EoS of this model is given by \(p=-\rho \), and thus, the normalised Hubble parameter takes the form

$$\begin{aligned} h(z)=\Omega _m(1+z)^{3(1+w_m)}+\Omega _{\Lambda }-\Omega _k(1+z)^2 \end{aligned}$$
(46)

where \(\Omega _{\Lambda }=\Lambda /3H^2_0\). Here, we proceed by comparing the optical depths of the above-discussed DE models with \(\Lambda \)CDM and also with their corresponding flat models.

  • TF: A comparison of the TF model against \(\Lambda \)CDM is shown in Fig. 19 for the cases of open (\(k=-1\)), flat (\(k=0\)) and closed (\(k=1\)) Universes. In a flat Universe (Fig. 19b), \(\Lambda \)CDM shows a higher possibility of finding multiple images due to a background source than TF. The same holds for the cases of a non-flat open and closed Universe, as seen from Fig. 19a, c respectively.

  • GCCG: The comparison of the GCCG model against \(\Lambda \)CDM is shown in Fig. 20. This model’s lensing probability for open (\(k=-1\)), flat (\(k=0\)) and closed (\(k=1\)) Universe is higher than the corresponding \(\Lambda \)CDM model. Here, Fig. 20a shows the change in optical depth behaviour for the open Universe, Fig. 20b for flat and Fig. 20c for closed Universe.

  • NVMCG: In the NVMCG model, Fig. 21 shows comparison of optical depth behaviour against \(\Lambda \)CDM model. For all the cases of open, flat and closed Universe, NVMCG model shows a higher possibility of finding gravitational lenses when \(z_s <1\) compared to \(\Lambda \)CDM. After \(z_s\) crosses the value 1 lensing probability for NVMCG becomes constant while for \(\Lambda \)CDM it keeps on increasing (Fig. 21a–c).

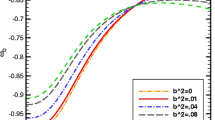
  • MCJG: The graphs for optical depth behaviour are depicted in Fig. 22. The optical depth behaviour of this model is highly consistent with \(\Lambda \)CDM model in an open, flat and closed Universe, unlike the other DE models. Figure 22a shows optical depth behaviour in an open Universe, Fig. 22b in flat and Fig. 22c in closed.

  • MCAG: This model’s optical depth behaviour is similar to that of \(\Lambda \)CDM model. The graph of the optical depth behaviour of this model is shown in Fig. 23. Figure 23a shows the comparison of optical depth in open Universe w.r.t \(\Lambda \)CDM model which is exactly the same as that of \(\Lambda \)CDM model. The same is true for the flat and closed Universe as well (Fig. 23b, c), with graphs of both the models coinciding with each other.

6 Conclusions

In our study, we have considered our Universe to be a non-flat FRW model, which is composed of dark matter and dark energy (DE). Then we studied the optical depth behaviour of some DE models like tachyonic field (TF), generalized cosmic Chaplygin gas (GCCG), new variable modified Chaplygin gas (NVMCG), modified Chaplygin–Jacobi gas (MCJG) and modified Chaplygin–Abel gas (MCAG). Although studies from Refs. [42, 43] showed that cosmological parameters are not the only aspect that affects the strong lensing probability, in our study, however, we have considered them to understand how they affect the strong lensing probability. Later on, we compared our findings in the case of flat Universe of the corresponding DE models and our standard \(\Lambda CDM\) model. It should also be noted that if we avoided specific cosmological parameters in our study, it would mean that the change in such parameter values doesn’t affect our lensing probability. Our findings in the present study can be summarized as follows:

  • With an increasing value of \(\Omega _m\), all the DE models discussed here have decreasing lensing probability.

  • For the parameter \(A_t\) in TF, lensing probability increases with the increase in \(A_t\) and the redshift value. For GCCG, lensing probability decreases with the redshift value.

  • In the NVMCG model, it seems that redshift has little to no effect on its optical depth behaviour (Figs. 7, 8, 9, 10, 11, 12, 13, 14). Initially, when \(0 < z_s \le 1\), the lensing probability increased smoothly, but after \(z_s\) crossed 1, it became constant. Further, while for increasing \(H_0\) and \(\alpha \) in NVMCG the lensing probability increases but the same decreases for increasing \(A_0\) values.

  • For MCJG and MCAG, lensing probability decreases smoothly with the redshift value.

  • Comparison of the DE models with \(\Lambda CDM\) and also their corresponding models in a flat Universe is shown in Figs. 19, 20, 21, 22, 23. Variation in lensing probability can be observed in the case of TF, GCCG and NVMCG when compared with \(\Lambda CDM\) model in an open, flat and closed Universes (Figs. 19, 20, 21). But in the case of MCJG and MCAG, the lensing probability is highly consistent with \(\Lambda CDM\) model (Figs. 22, 23).