Relativistic modeling of stellar objects in a Schwarzschild’s coordinates with embedded class one spacetime

Abstract

In this study, we investigate a new relativistic anisotropic Einstein field equations solution for compact stars under embedding class 1 conditions. In order to do this, we apply the Karmarkar condition and the embedding class one technique. By taking Buchdahl type metric potential $g_{rr}$ into consideration, the precise analytical solution has been investigated. We have studied physical characteristics of various compact star using this analytical solution. Central singularities are absent from the solution. We have explored thermodynamic observables inside the stellar models, such as radial and tangential pressures, matter density, anisotropic factor, energy conditions, TOV, red-shift, and the speed of sound, etc., after establishing this space-time geometry for the stellar models. From the graphical representation of various physical characteristics, it is demonstrated that our model meets all the specification for ultra-high density compact bodies.

1 Introduction

Compact objects are astronomical objects with an extremely high density. For a long time, the study of general relativistic compact objects has been of great interest. Some important parameters, such as mass, radii, internal composition etc., remain difficult to measure because they cannot be inferred directly from the observational data. Many of these physical parameters of compact objects are predicted using theoretical relativistic stellar models. A compact star model provides a detailed understanding of the compact stars that it represents. Modeling compact stars is one of the most challenging tasks in relativistic astrophysics because we know very less about the constituent matter of an ultra-compact star. Schwarzschild had discovered the exact solutions to Einstein’s Field Equations (Efes), since then the theoretical modeling of stellar structure has been a field of active research astrophysical bodies [1]. Oppenheimer and Volkoff were the first to derive computational solutions of Efes for a degenerate neutron gas. It was previously assumed that the nature of a spherically symmetric substance is similar to that of a perfect fluid, in which the radial pressure coincides with the tangential pressure. However, in 1922 the authors [2] proposed that anisotropy should be given importance in studying the nature of matter distribution due to the extreme and unusual conditions that exist in the interior of compact objects. Anisotropy generally describe the direction-dependent properties of materials. In the context of compact stars, however, anisotropy refers to the difference in radial and tangential pressures. When dealing with relativistic fluids, anisotropy must be taken into account. According to Mak and Harko [3], and Sharma et al. [4], anisotropy is sufficient for studying compact stars with dense nuclear matter. Works such that [5,6,7,8,9,10] clarified our understanding of highly dense spherically symmetric fluid spheres with anisotropic pressure. Anisotropy may occur in a compact star due to the presence of a mixture of different types of fluids, rotation, the presence of superfluid, the presence of a magnetic field or an external field, or phase transitions, etc. The primary anisotropic version with tangential stress and consistent density was modeled by Leimatre [11]. Ruderman [6] proposed in 1972 that compact structures are generally anisotropic in nature due to their excessive density $(> 10^{15}~\text {gm}/\text {cc})$. Later, Bowers and Liang [5] conducted extensive research in the field of anisotropic spheres in general relativity and discussed the causes and effects of anisotropy in compact objects. In his work, de Leon [12] obtained two new exact analytical solutions to Einstein’s field equations for a static fluid sphere with anisotropic pressures. Furthermore, Herrera and Santos [8] provided an in-depth review on anisotropic fluids. Herrera along with his colleagues [13,14,15,16] studied and analyzed the stability of the self-gravitating system in the presence of local anisotropy.

An example of a physical system with anisotropic pressure is a scalar field with a nonzero spatial gradient. Anisotropy comes naturally to self-bound systems made up of scalar fields, “boson stars” and the energy–momentum tensor of electromagnetic and fermionic fields [17, 18]. Gravastars and wormholes are likewise regarded as anisotropic objects. The existence of a solid core, several forms of phase transitions [19], pion-condensation [20], slow rotation [21], a strong magnetic field [22], a mixing of two fluids [23, 24], among other factors, have all been shown to cause pressure anisotropy. Additionally, local anisotropy may come from viscosity. Barreto et al. [25, 26] give some numerical calculations on the impact of viscosity-induced anisotropy. The authors in [27] provides an extensive list of the physical processes that cause pressure anisotropy. Herrera [28] recently came to the conclusion that pressure anisotropy will always tend to be produced, even if the system is initially assumed to be isotropic due to physical processes like dissipative fluxes, energy density inhomogeneities, or the appearance of shear in the fluid flow that are anticipated in stellar evolution. Since any equilibrium configuration is the culmination of a dynamic regime, anisotropy acquired during this dynamic process will not vanish in the final equilibrium state. Although the initial configuration had isotropic pressure, but the resulting configuration should always (theoretically) exhibit pressure anisotropy. This is why pressure anisotropy must be taken into account whenever relativistic fluids are involved.

Dev and Gleiser [29, 30] confirmed the significance of physical parameters such as mass, structure, and so on, in presence of anisotropic fluid. Bohmer and Harko [31] made a claim that anisotropic compact stellar-type objects can be much more compact than isotropic ones, with radii that are close to their corresponding Schwarzschild radii. The role of pressure anisotropy has been extensively studied in the context of stability of compact objects. Recently, considering the Tolman VII form for the gravitational potential $g_{rr}$ together with the linear equation of state, Bhar et al. [32] studied the behavior of relativistic objects with locally anisotropic matter distribution. Also, Bhar [33] proposed a new model for an anisotropic strange star which admits the Chaplygin equation of state. In this connection some other useful solutions for a compact star in a different context have been obtained by several authors in [34,35,36,37,38,39]. Certain assumptions like considering barotropic equation of state, [40, 41], pressure anisotropy in (3 + 1)D spacetime [33, 42, 43], quadratic equation of state for stellar interior [44], quadratic envelope [45] and so on are made in order to modeled anisotropic stellar objects. Some other remarkable models for the anisotropic compact stars can be found in [46,47,48]. In this paper, we present a viable and stable anisotropic compact star model in the class-one metric that can describe such ultra-compact stars. The idea about the class one metric is that if we embed our space-time into a higher dimensional flat space-time then this extra dimension will be the class one metric [49]. The beauty of class-one condition is that both the metric functions are dependent on each other. Thomas [50] provided the necessary and sufficient conditions for embedding class one in 1936. These conditions, however, concern extremely heavy algebraic manipulations and have not been widely explored. Although understanding this is still an open problem in astrophysics, the nature and precise structure of ultra-compact neutron stars have become a focus of recent research. The proposal of Randall and Sundrum [51] and discussions by Anchordoqui and Perez Berglia [52] has reignited interest in the concept. Some recent works on anisotropic compact stars of embedding class one can be found in [53, 54].

The paper is organized in the following manner:

In Sect. 2, we calculated Einstein’s field equations and the general solution of the class one Metric. In Sect. 3, we discuss the parameters of our model and a comparison with relevant observational data. In Sect. 4, we discuss the boundary conditions. Where in Sect. 5, we define the physical properties of the Anisotropic solution. Finally, we concluded our work in Sect. 6.

2 Basic field equations and the general solutions of the class 1 metric

In curvature coordinates, consider the static spherically symmetric spacetime metric:

$$\begin{aligned} ds^{2}=-e^{\lambda (r)}dr^{2} -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2})+e^{\nu (r)}dt^{2}. \end{aligned}$$

(1)

The gravitational potential for the interior anisotropic fluid distribution is represented by $e^{\lambda (r)}$ and $e^{\nu (r)}$. The anisotropic fluid distribution’s energy momentum tensor takes the form

$$\begin{aligned} -\kappa T^{i}_{j}= & {} R^{i}_{j}-\dfrac{1}{2}R\delta ^{i}_{j}\nonumber \\= & {} -\kappa \big [(c^{2}\rho +p_t)\nu ^{i}\nu _{j}-p_t\delta ^{i}_{j}+(p_r-p_t)u^iu_j\big ]\nonumber \\ \end{aligned}$$

(2)

where $R^{i}_{j}$ and $\delta ^{i}_{j}$ being respectively the Ricci and the metric tensors, and R being the Ricci scalar (with the assumption of natural units $G = c = 1)$, the contravariant quantity $\nu _i$ is the four-velocity vector and $u_i$ is the unit spacelike vector in the radial direction. Here $p_r$,$p_t$ and $\rho$ denote the radial pressure, tangential pressure and matter density for anisotropic matter with $\kappa =\dfrac{8\pi G}{c^{4}}$. With the metric (1) together with the energy momentum (2) Einstein’s field equations take the form

$$\begin{aligned}{} & {} \dfrac{\nu '}{r}e^{-\lambda }-\dfrac{(1-e^{-\lambda })}{r^{2}}=\kappa p_{r} \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \bigg (\dfrac{\nu ''}{2}-\dfrac{\lambda '\nu '}{4}+\dfrac{\nu ^{'2}}{4}+\dfrac{\nu '-\lambda '}{2r}\bigg )e^{-\lambda }=\kappa p_{t} \end{aligned}$$

(4)

$$\begin{aligned}{} & {} \dfrac{\lambda '}{r}e^{-\lambda }+\dfrac{(1-e^{-\lambda })}{r^{2}}=\kappa c^{2}\rho . \end{aligned}$$

(5)

The differentiation with regard to the radial coordinate r is denoted by the term prime. According to Herrera and Leon [14], $\varDelta = p_t - p_r$ is the anisotropy factor, which measures the fluid’s pressure anisotropy. It should be emphasised that $\varDelta = 0$, i.e. $p_t = p_r = p$, is a special instance of isotropic pressure at the start of the stellar configuration. We obtain the basic form of anisotropic factor using Eqs. (3) and (4):

$$\begin{aligned}{} & {} \varDelta =\kappa \, (p_{t} -\, p_{r} ) \nonumber \\{} & {} \quad = e^{-\lambda } \left[ \frac{\nu ''}{2} -\frac{\lambda ' \nu '}{4} +\frac{{\nu '}^{2} }{4} -\frac{\nu '+\lambda '}{2r} -\frac{1}{r^{2} } \right] \, +\frac{1}{r^{2} }, \end{aligned}$$

(6)

where $\varDelta =\kappa [p_t(r)-p_r(r)]$. As a result, a force owing to anisotropic pressure is represented by $\varDelta /r$, which is repulsive if $p_{t} > p_{r}$ of the stellar model and attractive if $p_{t} < p_{r}$. In comparison to the isotropic fluid sphere, assuming matter dispersion when $p_{t} > p_{r}$ permits the development of more compact objects [55]. This is a three-equation system with five unknowns. As a result, the system of equations is undetermined, and we must limit the number of unknown functions by selecting appropriate conditions.

2.1 Class-one conditions

As is well known, the manifold $V_n$ may always be embedded in the m-dimensional pseudo-Euclidian space $E_m$ with $m = n(n+1)/2$ [49]. The class of the manifold $V_n$ is the least additional dimension Kof the pseudo-Euclidian space with regard to embedding $V_n$ in $E_m$, and it must be less than or equal to the number $(m-n)$ or the same as $n(n-1)/2$.In the instance of relativistic space-time $V_4$, the embedding classK turns out to be 6. Spherically symmetric space-time belongs to class 2, whereas plane symmetric space-time belongs to class 3. The external and interior solutions of the Schwarzschild are classified as class 2 and 1, respectively. Moreover the renowned Friedman–Robertson–Lemaitre space-time [56,57,58] is of class 1, while the famous Kerr metric [59] is of class 5. Higher-dimensional embedding space has no physical value according to general relativity’s postulates. It does, however, give novel characterizations of the gravitational field, which may be linked to basic particle physics’ inherent symmetries [60]. Extrinsic gravity, threads and membranes, and the new brain world are all examples of embeddings (Pavsic and Tapia [61]).

If the Karmarkar condition [62] is satisfied, the metric (1) may now be used to describe the space-time of embedding class one in a more concise form as

$$\begin{aligned} R_{0202} R_{1313} = R_{0101} R_{2323}+ R_{1202} R_{1303}. \end{aligned}$$

(7)

For the postulated interior spacetime Eq. (1), the needed Riemannian symbols are

$$\begin{aligned}{} & {} R_{0101}=-\frac{1}{4} e^{\nu }(-\nu ^{'} \lambda ^{'}+\nu ^{'^{2}}+2\nu ^{''}), \end{aligned}$$

(8)

$$\begin{aligned}{} & {} R_{0202}=-\frac{1}{2}r\nu ^{'} e^{\nu -\lambda }, \end{aligned}$$

(9)

$$\begin{aligned}{} & {} R_{1202}=0= R_{1303},, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} R_{1313}=-\frac{1}{2} r \lambda ^{'} sin^{2}\theta , \end{aligned}$$

(11)

$$\begin{aligned}{} & {} R_{2323}=-r^{2} sin^{2}\theta (1-e^{-\lambda }). \end{aligned}$$

(12)

Substituting Eqs. (8)–(12) in (7) we get differential equation

$$\begin{aligned} e^{\lambda } \lambda ^{'} \nu ^{'}-e^{\lambda }\nu ^{'^{2}}-2e^{\lambda }\nu ^{''}+\nu ^{'^{2}}+2\nu ^{''} =0. \end{aligned}$$

(13)

2.2 A new class of solution for anisotropic compact stars

Now find the anisotropic solution of model, we adopt a specific metric potential $g_{rr}$ [63] which is given by

$$\begin{aligned} \lambda = \ln \{K(1+Cr^2) \}-\ln (K+Cr^2). \end{aligned}$$

(14)

Here discuss about Buchdahl metric.

By using the Eq. (14) in the Eq. (13) we get the metric potential $\nu$ as follows

$$\begin{aligned} \nu = 2\ln \Bigg [A+\frac{B}{\sqrt{C}}\sqrt{(K-1)(K+Cr^2)}\Bigg ]. \end{aligned}$$

(15)

Using the Eqs. (14) and (15), we obtain the density $(\rho )$, radial pressure$( p_r )$, transverse pressure $( p_t )$ and anisotropy $( \varDelta )$ as

$$\begin{aligned}{} & {} \rho = \dfrac{C(K-1)(3+Cr^2)}{8\pi \,K(1+Cr^2)^2} \end{aligned}$$

(16)

$$\begin{aligned}{} & {} p_r = \dfrac{1}{8\pi \,K(1+Cr^2)}\nonumber \\{} & {} \quad \times \left[ \frac{\Big (2\sqrt{C\,(K-1)(K+Cr^2)}\Big )}{\Big ( \frac{A}{B}+\frac{1}{\sqrt{C}}\sqrt{(K-1)(K+Cr^2)}\Big )}-C(K-1)\right] \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \varDelta = \nonumber \\{} & {} \frac{8\pi \,\frac{A}{B}C^2r^2(K-1)+C^{3/2}r^2(K-2)\sqrt{(K-1)(K+Cr^2)}}{K(1+Cr^2)^2\Big [ \frac{A}{B}+\frac{1}{\sqrt{C}}\sqrt{(K-1)(K+Cr^2)}\Big ]} \nonumber \\ \end{aligned}$$

(18)

$$\begin{aligned}{} & {} p_t = p_r + \varDelta . \end{aligned}$$

(19)

We can see from Figs. 1, 2, 3 that the density and pressures are both monotonically decreasing, as would be predicted. We also see that as the radius increases, the anisotropic factor increases monotonically (Fig. 4).

Fig. 1

Behaviour of $\rho$ are shown vs. fractional radius r/R

Fig. 2

Behaviour of $p_r$ are shown vs. fractional radius r/R

Fig. 3

Behaviour of $p_t$ are shown vs. fractional radius r/R

Fig. 4

Behaviour of $\varDelta$ are shown vs. fractional radius r/R

3 The parameters of our model and a comparison with relevant observational data

In this section, we created data plots to compare our model parameters to some of the star candidates. These data points values will be utilized to determine the physical properties of theoretical compact objects and to draw their graphs in the sections above and below.

In Table 1, we selected some realistic values for (C, K, A,  and B) that assisted in estimating the value of $\frac{M}{R}$ for this model and Table 2 displays several physical quantities represented numerically in different units.

Table 1 The estimated, observed and chosen values of the mass M, radius R and parameters for the star candidates

Table 2 The numerical representations of several physical quantities (central density $(\rho _c)$, surface density $(\rho _s)$, central pressure $( p_{c} )$, surface anisotropic factor $(\varDelta _s)$, surface redshift $( Z_s )$ and value of $\Gamma _{critical})$

4 Boundary conditions

It is necessary that the interior solution should connect smoothly with vacuum exterior Schwarzschild solution and is given by

$$\begin{aligned} ds^{2}= & {} -\bigg (1-\dfrac{2M}{r}\bigg )^{-1}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2})\nonumber \\{} & {} +\bigg ( 1-\dfrac{2M}{r}\bigg )dt^{2} \end{aligned}$$

(20)

where M represents the mass of compact stars. Now imposing the continuity of metric function at the boundary $(r=R)$ and vanishing radial pressure at boundary, we get

$$\begin{aligned}{} & {} e^{-\lambda }= 1-\dfrac{2M(R)}{R}\quad \text {and}\quad e^{\nu } = 1-\dfrac{2M(R)}{R} \end{aligned}$$

(21)

$$\begin{aligned}{} & {} p_r(R)= 0. \end{aligned}$$

(22)

For continuity of the first derivative:

$$\begin{aligned} \Bigg (\frac{\partial g^{-}_{tt}}{\partial r}\Bigg )_{r=R} =\Bigg (\frac{\partial g^{+}_{tt}}{\partial r}\Bigg )_{r=R} \end{aligned}$$

(23)

and

$$\begin{aligned} g^{-}_{tt}= e^\nu ,\quad g^{+}_{tt}=\left( 1-\frac{2M}{R}\right) . \end{aligned}$$

(24)

Now from Eqs. (23) and (24) we get,

$$\begin{aligned}{} & {} e^{\nu (R)} ~\nu ^{'}(R)= 0+\frac{2M}{R^2} \\{} & {} \nu ^{'}(R)= \frac{2M}{R^2} \times \frac{1}{e^{\nu (R)}} \\{} & {} \nu ^{'}(R)=\frac{2M}{R^2} \times \frac{1}{(1-\frac{2M}{R})} ~~\Big (Since~~ e^{\nu (R)}=\Big (1-\frac{2M}{R}\Big ) \Big ) \\ \end{aligned}$$

$$\begin{aligned} \nu ^{'}(R)=\frac{2M}{R(R-2M)}. \end{aligned}$$

(25)

Now we have $p_{r}(R)=0$

$$\begin{aligned}{} & {} e^{-\lambda (R)} \Big (\frac{\nu ^{'}(R)}{R}+\frac{1}{R^2}\Big )-\frac{1}{R^2} =0 \\{} & {} \frac{\nu ^{'}(R)}{R}=\frac{1}{R^2 e^{-\lambda (R)}}-\frac{1}{R^2} \\{} & {} \frac{\nu ^{'}(R)}{R}=\frac{1}{R^2 (1-\frac{2M}{R})}-\frac{1}{R^2}\\{} & {} \quad \Big (Since~~ e^{-\lambda (R)}=\Big (1-\frac{2M}{R}\Big ) \Big ) \\{} & {} \frac{\nu ^{'}(R)}{R}=\frac{R}{R^2 (R-2M)}-\frac{1}{R^2} \end{aligned}$$

$$\begin{aligned} \nu ^{'}(R)=\frac{2M}{R (R-2M)}. \end{aligned}$$

(26)

From Eqs. (25) and (26) shows the continuity of the first derivative at $r=R$.

Now using the boundary conditions (21) and (22) we get the values of constant of integration as follows

$$\begin{aligned} \dfrac{A}{B} = \dfrac{(3-K)\sqrt{(K-1)(K+CR^2)}}{(K-1)\sqrt{CR^2}}. \end{aligned}$$

(27)

Now differentiating equations (16)–(19) we get the density, radial and transverse pressure gradient as

$$\begin{aligned}{} & {} \dfrac{d\rho }{dr} = \dfrac{C^2r(1-K)(5+Cr^2)}{4\pi \,K(1+Cr^2)^3} \end{aligned}$$

(28)

$$\begin{aligned}{} & {} \dfrac{dp_r}{dr}= \nonumber \\{} & {} \quad \dfrac{Cr\,\sqrt{C(K{-}1)}(1{-}2K{-}Cr^2)f(r)-2\,Cr\,(1{+}Cr^2)(K{-}1)\sqrt{K+Cr^2}}{4\pi \,K\Big ((1{+}Cr^2)f(r)\Big )^2} \nonumber \\{} & {} + \dfrac{C^2\,r(K-1)}{4\pi \,K(1+Cr^2)^2} \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \dfrac{dp_t}{dr}=\dfrac{\frac{A}{B}(1-K)C^3r^3}{32\pi \,K(K+Cr^2)(1+Cr^2)^2\,f(r)}\nonumber \\{} & {} + \dfrac{Cr\Big [ \frac{A}{B}\sqrt{C}(K-1)(K-2)\sqrt{(K-1)(K+Cr^2)} \Big ]g(r)}{8\pi \,K(K+Cr^2)} \end{aligned}$$

(30)

where

$$\begin{aligned} f(r)= & {} \dfrac{A}{B} + \sqrt{\frac{(K-1)(K+Cr^2)}{C}},\\ g(r)= & {} f(r)\,(3Cr^2 + 2K)(1+Cr^2)^2\sqrt{C}\, -\, Cr^2(1+Cr^2)\\{} & {} \times \Big ( 4\,f(r)\sqrt{C(K+Cr^2)}+(1+Cr^2)\sqrt{(K-1)} \Big ). \end{aligned}$$

5 Physical properties of the anisotropic solution

5.1 Singularity at the center

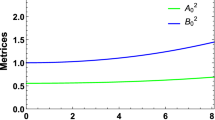
From Eqs. (14) and (15),We observe $e^{\lambda (0)}=1$ and $e^{\nu (0)} = \Bigg [A+\frac{B}{\sqrt{C}}\sqrt{K(K-1)}\Bigg ]^2$. This demonstrates that the metric potentials are positive and singularity-free at the origin. Additionally, they monotonically increase as the star’s radius increases. Because of the energy density at the centre, $r = 0$, it is implied that $\rho (0)=\dfrac{3C(K-1)}{8\pi \,K}$.Since density at the center should be positive,then $K>1$ and $K<0$.

5.2 Causality condition

We will determine the subconscious velocity of sound in this part. The radial and transverse sound velocities must be less than 1, or what is known as causality conditions, for an anisotropic fluid sphere model to be physically viable.The speed of sound propagation $V^2_s$, denoted by the formula $V^2_s=dp/d\rho$, is a crucial factor that has to be examined. It goes without saying that sound cannot travel faster than light. As we fix $c = 1$ here, the behavior of the sound speed is thus always smaller than unity. We look into the sound’s speed in both radial and transverse directions to examine the situation. This should always fulfil $0< V^2_r <1$ and $0< V^2_t <1$ for an anisotropic fluid distribution and a stable equilibrium configuration, as in [13] for a subluminal sound speed. Canuto [69] suggested that with an ultrahigh distribution of matter, the speed of sound should decrease monotonically towards the surface of the star. In our study, an anisotropic fluid distribution has been graphically shown while studying the sound velocity. We have drawn some figures for the strange star candidates 4U 1820, PSR J1903+327, 4U 1608-52, Vela X-1, PSR J1614-2230, Cyg X-2 and PSR B1913+16 in order to see this (Figs. 5, 6).

Fig. 5

The nature of the radial velocity of sound is shown on the versus of the fractional radius (r/R)

Fig. 6

The nature of the tangential velocity of sound is shown on the versus of the fractional radius (r/R)

5.3 Adiabatic index

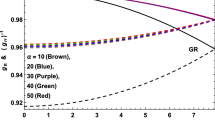
The adiabatic index affects the relativistic anisotropic star’s stability as well. According to Heintzmann and Hillebrandt [70], anisotropic equation of state neutron star models are stable if $\gamma > 4/3$. The isotropic neutron star model, however, has no upper mass limit for the adiabatic index $\gamma > 4/3$ [71], according to Newton’s theory of gravity (Fig. 7).

The adiabatic index $\Gamma$ is described by

$$\begin{aligned} \Gamma _{r}=\Bigg (\frac{\rho +p_{r}}{p_{r}} \Bigg )\Bigg (\frac{dp_{r}}{d\rho }\Bigg ). \end{aligned}$$

(31)

The collapsing scenario is described by for an anisotropic fluid [72],

$$\begin{aligned} \Gamma _r< \frac{4}{3}+max\bigg (-\frac{4}{3}\frac{p_{r}-p_{t}}{r|p_{r}'|}+\frac{\kappa }{3}\frac{r\rho p_{r}}{|p_{r}'|}\bigg ). \end{aligned}$$

(32)

Later Moustakidis [73], discovered the adiabatic index $(\Gamma _{critical})$ critical value

$$\begin{aligned} \Gamma _{critical}=\frac{4}{3}+\frac{19}{21}\frac{M}{R}. \end{aligned}$$

(33)

Fig. 7

Adiabatic index for compact stars vs. fractional radius r/R

5.4 Energy conditions

The energy–momentum tensor has to conform to the following energy conditions in order to have a physically reasonable anisotropic solution:

• 1. According to the null energy condition (NEC), the local mass-energy density cannot be negative, i.e. (NEC): $\rho \ge 0$.

• 2. According to the weak dominant energy condition (WDEC), a star’s internal energy flow cannot be greater than the speed of light, i.e. (WDEC): $\rho -p_r\ge 0$, $\rho -p_t\ge 0$.

• 3. According to the strong dominant energy condition (SDEC), the star’s internal energy flow cannot be greater than one-third the speed of light, i.e. (SDEC): $\rho -3p_r\ge 0$, $\rho -3p_t\ge 0$.

Fig. 8

Nature of NEC is shown versus the fractional radius (r/R)

Fig. 9

Nature of $WEC_r$ is shown versus the fractional radius (r/R)

Fig. 10

Nature of $WEC_t$ is shown versus the fractional radius (r/R)

Fig. 11

Nature of $SEC_r$ is shown versus the fractional radius (r/R)

Fig. 12

Nature of $SEC_t$ is shown versus the fractional radius (r/R)

With regard to the radial coordinate r/R, which has been displayed for several compact stars, we illustrate various energy conditions in this graph from top to bottom. Figures 8, 9, 10, 11, 12 depicts how these energy situations behave. This picture unequivocally shows that the interior portion of the spherical distribution satisfies all of the energy conditions in our model.

5.5 Hydrostatic equilibrium through generalized Tolman–Oppenheimer–Volkoff (TOV) equation

The Tolman–Oppenheimer–Volkoff (TOV) equation in the presence of charge is given by

$$\begin{aligned} -\frac{M_G(c^2\rho +p_r)}{r^2}e^{\frac{\lambda -\nu }{2}}-\frac{dp_r}{dr}+ \dfrac{2(p_t-p_r)}{r} =0 \end{aligned}$$

(34)

where, $M_G$ is the effective gravitational mass given by:

$$\begin{aligned} M_G(r)=\frac{1}{2}r^2 \nu ^{\prime }e^{(\nu - \lambda )/2}. \end{aligned}$$

(35)

From the Eq. (35) the value of $M_G(r)$ we get

$$\begin{aligned} -\frac{\nu '}{2}(c^2\rho +p_r)-\frac{dp_r}{dr}+ \dfrac{2(p_t-p_r)}{r} =0. \end{aligned}$$

(36)

The Eq. (36) can be expressed into three different elements gravitational $(F_g)$, hydrostatic $(F_h)$ and electric $(F_e)$, which are defined as:

$$\begin{aligned} F_g= & {} -\frac{\nu '}{2}(c^2\rho +p_r) \end{aligned}$$

(37)

$$\begin{aligned} F_h= & {} -\frac{dp}{dr} \end{aligned}$$

(38)

$$\begin{aligned} F_a= & {} \dfrac{2\varDelta }{r}. \end{aligned}$$

(39)

Fig. 13

Variation of the three forces-gravitational force $(F_g)$, hydrostatic force $(F_h)$, and anisotropic force $(F_a)$ versus radial fraction r/R for 4U 1820-30

Fig. 14

Variation of the three forces-gravitational force $(F_g)$, hydrostatic force $(F_h)$, and anisotropic force $(F_a)$ versus radial fraction r/R for PSR J1903+327

Fig. 15

Variation of the three forces-gravitational force $(F_g)$, hydrostatic force $(F_h)$, and anisotropic force $(F_a)$ versus radial fraction r/R for 4U 1608-52

Fig. 16

Variation of the three forces-gravitational force $(F_g)$, hydrostatic force $(F_h)$, and anisotropic force $(F_a)$ versus radial fraction r/R for Vela X-1

Fig. 17

Variation of the three forces-gravitational force $(F_g)$, hydrostatic force $(F_h)$, and anisotropic force $(F_a)$ versus radial fraction r/R for PSR J1614-2230

Fig. 18

Variation of the three forces-gravitational force $(F_g)$, hydrostatic force $(F_h)$, and anisotropic force $(F_a)$ versus radial fraction r/R for Cyg X-2

Fig. 19

Variation of the three forces-gravitational force $(F_g)$, hydrostatic force $(F_h)$, and anisotropic force $(F_a)$ versus radial fraction r/R for compact star candidates

Figures 13, 14, 15, 16, 17, 18 and 19 represents the behavior of the generalized TOV equations. We can observe from these figures that the system is counterbalanced by the components the gravitational force $(F_g)$, hydrostatic force$(F_h)$ and anisotropic force $(F_a)$ and the system attains a static equilibrium.

5.6 Redshift

It is required for a stable spherically symmetric anisotropic fluid sphere that the redshift function should gradually decrease inside the star. The gravitational redshift z within the static line element is given by

$$\begin{aligned} z=|e^{\nu (r)}|^{-1/2}-1 =\dfrac{1}{|\sqrt{e^{\nu (r)}}|} -1. \end{aligned}$$

(40)

The surface redshift also establishes the following relationship

$$\begin{aligned} z_s=|e^{\nu (R)}|^{-1/2}-1 = \Bigg (1-\dfrac{2M}{R}\Bigg )^{-1/2}-1. \end{aligned}$$

(41)

Fig. 20

Variation of redshift and fractional radius r/R

Additionally, we were able to determine the surface redshift values for various compact stars, which are displayed in Table 2. In our case, the gravitational redshift z is monotonically decreasing from center to surface.

6 Conclusion and discussion

Einstein’s field equations can be solved by embedding class one spacetime using Karmarkar’s condition, which has been demonstrated to be an effective and straightforward method. Despite its simplicity, the developed model for anisotropic fluid spheres satisfies all necessary conditions to qualify as a valid mathematical and physical solution. In this article, we have calculated relevant values of parameters for compact stars such as 4U 1820-30, PSR J1903+327, 4U 1608-52, Vela X-1, PSR J1614-2230, Cyg X-2, and PSR B1913+16 and obtained some agreeable results. We have also analyzed all physical features in detail and provided figures to support our data. The mass, redshift, and compactness factors are within optimal ranges while the model is stable under the action of hydrostatic, anisotropic, and gravitational forces. The subliminal velocity of sound and the adiabatic index reconfirms the stability of our model. Our analysis in this study demonstrates that masses and radii that are consistent with observations indeed produced when curved geometries are embedded in higher dimensional flat spacetime. The Karmarkar embedding condition was used to find a new solution to the field equations when a specific form of one of the potentials was generated. We have looked at the energy conditions, mass function, compactness, stability, and equilibrium conditions of the stellar model, among other properties, to investigate the physical agreeability of our anisotropic stellar structure. The characteristics of energy density, pressures (radial and tangential), and anisotropic force are shown in Figs. 1, 2, 3, 4 respectively, in Fig. 5 velocity of sounds, in Fig. 7 adiabatic index, in Figs. 8, 9, 10, 11, 12 energy conditions, in Figs. 13, 14, 15, 16, 17, 18 and 19 TOV conditions, and in Fig. 20 redshift etc. We propose that this model is compatible with the compact objects based on the Table 1, and it is free from the central singularity. Therefore, we can state that the physical characteristics of our model are quite realistic and feasible.