1 Introduction

In recent decades, people confirm the fact that black holes are thermodynamics systems [1,2,3] where its area is related with entropy and its surface gravity is connected with temperature [4, 5]. The following important step is to establish the quantum gravity theory. The negative cosmological constant in an Anti-de Sitter (AdS) spacetime with black hole will lead to phase transitions of black holes [6, 7]. And the corresponding conjugate quantity of pressure in an extended phase space for black holes is the volume [8]. The physical implication was related with the holography, where black holes would being a system and dual to conformal field theories [9]. That makes AdS black holes can be identical to the thermodynamics of ordinary systems and their thermodynamics become more complete. Especially there exist several different types of phase transition, the Van de Walls (VdW’s)-like phase transition [10,11,12], reentrant phase transitions [13, 14], the polymer-like phase transition [15], and the triple points [16, 17], along with the novel dual relation of HP phase transition [18]. Meanwhile, the inclusion of the pressure-volume term in the thermodynamical first law makes other model parameters as novel thermodynamical quantities [11] and make it possible to regard AdS black holes as heat engines [19, 20]. All of those developments are in the subdiscipline, black hole chemistry [21].

In the classical thermodynamics, there is a well known process named the Joule–Thomson expansion, i.e., the gas moves from a region of high pressure to a region of low pressure via an equal velocity. Based on this, the JT effect of the charged AdS black hole was firstly investigated in Ref. [22]. Subsequently the JT expansion becomes an active issue and gets more attention, furthermore is extended to the study of other black holes [23,24,25,26,27,28]. Additionally, at the linear level the charged black holes in an AdS spacetime nearby the critical point is of the scaling symmetries, \(S\sim q^2,~P\sim q^{-2},~T\sim q^{-1}\) [29, 30]. It is natural to guess that whether the same scaling symmetry still hole on for the non-linear charged AdS black holes? There are lots of the generalization of the linear charged AdS black hole solution: Einstein–Maxwell–Yang–Mills AdS black hole [31], Einstein–Power–Yang–Mills AdS black hole [32], Einstein–Maxwell–Power–Yang–Mills AdS black hole [33], Einstein–Yang–Mills–Gauss–Bonnet black hole [34], Einstein–Power–Maxwell–Power–Yang–Mills-dilaton [35], and so on. An interesting non-linear generalization of charged black holes involves a Yang–Mills field exponentially coupled to Einstein gravity (i.e., Einstein–Power–Yang–Mills gravity theory) because it possesses the conformal invariance and is easy to construct the analogues of the four-dimensional Reissner–Nordström black hole solutions in higher dimensions. Additionally several thermodynamical features of the EPYM AdS black hole in the extended phase space have been exhibited [33, 36, 37]. Here we pay attention on the JT expansion for the non-linear charged AdS black hole in this theory.

In this paper we study and discuss the Joule–Thomson expansion for black holes in the model of nonlinear electrodynamics (NED) coupled to gravity in AdS spacetime. The interest to NED model [38] considered is due to its simplicity: the metric function is expressed via simple elementary function. This model was explored to study the supermassive black hole M87* [38] and to construct non-singular model of magnetized black hole [39]. In Sect. 2, we briefly review the EPYM AdS black hole solution and its hawking temperature. In Sect. 3, we investigate the Joule–Thomson expansion for the EPYM AdS black hole. A brief summary is given in Sect. 4.

2 EPYM AdS black hole and Hawking temperature

The action for four-dimensional Einstein–Power–Yang–Mills (EPYM) gravity with a cosmological constant \(\Lambda \) was given by [32, 40,41,42]

$$\begin{aligned} I=\frac{1}{2}\int d^4x\sqrt{g} \left( R-2\Lambda -\mathcal {F}^\gamma \right) \end{aligned}$$
(1)

with the Yang–Mills (YM) invariant \(\mathcal {F}\) and the YM field \(F_{\mu \nu }^{(a)}\)

$$\begin{aligned} \mathcal {F}= & {} {\text {Tr}}(F^{(a)}_{{\mu \nu }}F^{{(a)\mu \nu }}),\end{aligned}$$
(2)
$$\begin{aligned} F_{\mu \nu }^{(a)}= & {} \partial _{\mu } A_{\nu }^{(a)}-\partial _{\nu } A_{\mu }^{(a)}+\frac{1}{2 \xi } C_{(b)(c)}^{(a)} A_{\mu }^{(b)} A_{\nu }^{(c)}. \end{aligned}$$
(3)

Here, \({\text {Tr}}(F^{(a)}_{\mu \nu }F^{(a)\mu \nu }) =\sum ^3_{a=1}F^{(a)}_{\mu \nu }F^{(a)\mu \nu }\), R and \(\gamma \) are the scalar curvature and a positive real parameter, respectively; \(C_{(b)(c)}^{(a)}\) represents the structure constants of three-parameter Lie group G; \(\xi \) is the coupling constant; and \(A_{\mu }^{(a)}\) represents the SO(3) gauge group Yang–Mills (YM) potentials defining by the Wu–Yang (WY) ansatz [43,44,45,46]. Variation of the action with respect to the spacetime metric \(g_{\mu \nu }\) yields the field equations

$$\begin{aligned}{} & {} G^{\mu }{ }_{\nu }+\Lambda \delta ^{\mu }{ }_{\nu }=T^{\mu }{ }_{\nu },\end{aligned}$$
(4)
$$\begin{aligned}{} & {} T^{\mu }{ }_{\nu }=-\frac{1}{2}\left( \delta ^{\mu }{ }_{\nu } \mathcal {F}^{\gamma }-4 \gamma {\text {Tr}}\left( F_{\nu \lambda }^{(a)} F^{(a) \mu \lambda }\right) \mathcal {F}^{\gamma -1}\right) . \end{aligned}$$
(5)

Variation with respect to the 1-form YM gauge potentials \(A_{\mu }^{(a)}\) and implement the traceless yields the 2-forms YM equations

$$\begin{aligned} \textbf{d}\left( { }^{\star } \textbf{F}^{(a)} \mathcal {F}^{\gamma -1}\right) +\frac{1}{\xi } C_{(b)(c)}^{(a)} \mathcal {F}^{\gamma -1} \textbf{A}^{(b)} \wedge ^{\star } \textbf{F}^{(c)}=0, \end{aligned}$$
(6)

where \(\textbf{F}^{(a)}=\frac{1}{2}F_{\mu \nu }^{(a)}dx^\mu \wedge dx^\nu ,~\textbf{A}^{(b)}=A_{\mu }^{(b)}\wedge dx^\mu \), and \({ }^{\star }\) stands for the duality. It is obviously that for the case of \(\gamma =1\) the EPYM theory reduces to the standard Einstein–Yang–Mills (EYM) theory [34]. In this work our issue is paid on the role of the non-linear YM charge parameter \(\gamma \).

Here we should point out that the non-Abelian property of the YM gauge field is expressed with its YM potentials

$$\begin{aligned} \textbf{A}^{(b)}=\frac{q}{r^2}C^{(a)}_{(i)(j)}x^idx^j,~r^2=\sum _{j=1}^3x_j^2, \end{aligned}$$
(7)

and q is the YM charge, the indices (a,  i,  j) run the following ranges: \(1\le a,~i,~j\le 3\). The coordinates \(x_i\) take the following forms: \(x_1=r \cos \phi \sin \theta ,~x_2=r \sin \phi \sin \theta ,~x_3=r \cos \theta .\) Since we have utilized the WY ansatz for the YM field, the invariant for this field takes the form [47,48,49]

$$\begin{aligned} {\text {Tr}}(F^{(a)}_{{\mu \nu }}F^{{(a)\mu \nu }})=\frac{q^2}{r^4}. \end{aligned}$$
(8)

This form leads to the disappearance of the structure constants which can be described the non-Abelian property of the YM gauge field. Therefore, under the condition of the WY ansatz we may focus on the role of the non-linear YM charge parameter, instead of the non-Abelian character parameter.

The metric for the four-dimensional EPYM AdS black hole is given as follows [50],

$$\begin{aligned} d s^{2}=-f(r) d t^{2}+f^{-1} d r^{2}+r^{2} d \Omega _{2}^{2}, \end{aligned}$$
(9)

where

$$\begin{aligned} f(r)=1-\frac{2\bar{M}}{r}+\frac{r^{2}}{l^2}+\frac{\left( 2q^{2}\right) ^{\gamma }}{2(4 \gamma -3) r^{4 \gamma -2}}. \end{aligned}$$
(10)

Here \(d\Omega _{2}^{2}\) is the metric on unit 2-sphere with volume \(4\pi \) and q is the YM charge, l is related to the cosmological constant: \(l^2=-\frac{3}{\Lambda }\), \(\gamma \) is the non-linear YM charge parameter and satisfies \(\gamma >0\) [41]. The event horizon of the black hole is obtained from the relation \(f(r_+)=0\). The mass parameter of the black hole can be expressed in terms of the horizon radius as

$$\begin{aligned} \bar{M}=\frac{r_+}{2}\left( 1+\frac{r^2_+}{l^2}+\frac{2^{\gamma -1}q^{2\gamma }}{(4\gamma -3)r_+^{4\gamma -2}}\right) . \end{aligned}$$
(11)

We can also obtain the Hawking temperature of the black hole from Eq. (10) as follows

$$\begin{aligned} T=\frac{1}{4 \pi r_{+}}\left( 1+8 \pi \bar{P} r_{+}^{2}-\frac{\left( 2 q^{2}\right) ^{\gamma }}{2 r_{+}^{(4 \gamma -2)}}\right) . \end{aligned}$$
(12)

From Eqs. (11) and (12) we can calculate the critical value of thermodynamical quantities which are presented in Sec. III A in Ref. [36]. Next we will investigate the effect of the nonlinearity on JT expansion for the AdS black hole in the Einstein-Power Yang-Mills gravity theory.

3 Joule–Thomson expansion

More recently, the authors of [22] have investigated the Joule–Thomson (JT) expansion for AdS charged black holes with the aim to confront the resulting features with those of Van der Waals fluids. The extension to the charged black hole solution in the presence of the quintessence field [51] and rotating-AdS black hole [23] have also been considered. JT expansion [52] is a convenient isoenthalpic tool that a thermal system exhibits with a thermal expansion. It is worth noting that when expanding a thermal system with a temperature T, the pressure always decreases yielding a negative sign to \(\partial P\). In this section, we will investigate the Joule–Thomson expansion of the RN-dS spacetime. In JT expansion for the Van der Waals system as well as AdS black holes, gas/black hole phase is passed at high pressure through a porous plug or small value in the low-pressure section of an adiabatic tube, and the enthalpy remains constant during the expansion. The expansion is characterized by a change in temperature relative to pressure. The JT coefficient, which can describe the expansion process, is read as

$$\begin{aligned} a=\left( \frac{\partial T}{\partial {P}}\right) _{H}, \end{aligned}$$
(13)

where the enthalpy is related with the internal energy

$$\begin{aligned} H=U+ P V. \end{aligned}$$
(14)

We can judge whether the system is in a cooling process or in a heating process by the positive or the negative for the JT coefficient. Namely, if the temperature of the system is increasing with the decreasing of pressure, the JT coefficient is negative and the system is in the heating process, while if the temperature is decreasing with the decreasing of pressure, the JT coefficient is positive and the system is in the cooling process.

In this part, we will investigate the JT expansion of the EPYM AdS black hole. As we know, when the system is in the JT expansion, the enthalpy of system is fixed. In the extended phase space, the mass parameter of AdS black hole is corresponding to the enthalpy and it only just keep a constant when the system is in a JT process. The Joule-Thomson coefficient can be expressed as

$$\begin{aligned} H= & {} \bar{M},\quad a=\left( \frac{\partial T}{\partial \bar{P}}\right) _{H} =\left( \frac{\partial T}{\partial \bar{P}}\right) _{\bar{M},q}\nonumber \\ {}= & {} \left( \frac{\partial T}{\partial r_+}\right) _{\bar{M},q}\bigg /\left( \frac{\partial \bar{P}}{\partial r_+}\right) _{\bar{M},q} \end{aligned}$$
(15)

In order to study the JT expansion of the system more easier, we rewritten the temperature and the pressure as

$$\begin{aligned} T= & {} \frac{1}{2\pi r_+}\left( -1+\frac{3\bar{M}}{r_+}-\frac{\gamma 2^{\gamma } q}{(4\gamma -3)r_+^{4\gamma -2}}\right) ,\end{aligned}$$
(16)
$$\begin{aligned} \bar{P}= & {} \frac{3}{8\pi r_+^2}\left( -1+\frac{2\bar{M}}{r_+}-\frac{2^{\gamma -1}q}{(4\gamma -3)r_+^{4\gamma -2}}\right) . \end{aligned}$$
(17)

From above equations, the JT coefficient becomes

$$\begin{aligned} a= & {} \frac{2r_+}{3}\frac{1-\frac{6\bar{M}}{r_+}+\frac{\gamma (4\gamma -1)2^\gamma q}{(4\gamma -3)r_+^{\gamma -2}}}{1-\frac{3\bar{M}}{r_+}+\frac{\gamma 2^\gamma q}{(4\gamma -3)r_+^{\gamma -2}}}\nonumber \\= & {} \frac{4r_+}{3}\frac{2+8\pi \bar{P}r_+^2-\frac{\left[ 2\gamma (4\gamma -1)-3\right] 2^\gamma q}{2(4\gamma -3)r_+^{4\gamma -2}}}{1+8\pi \bar{P}r_+^2-\frac{2^\gamma q}{2r_+^{4\gamma -2}}}. \end{aligned}$$
(18)

The JT coefficient will be divergent at the point \(r_{+m}\), which is satisfied the following equation

$$\begin{aligned} 1-8\pi \bar{P}r_{+m}^2-\frac{2^\gamma q}{2r_{+m}^{4\gamma -2}}=0. \end{aligned}$$
(19)

It is very interesting that at the point \(r_{+m}\) the hawking temperature in Eq. (12) is just zero, which indicates that the divergent point of the JT coefficient will be reveal the certain information of the extreme EPYM AdS black hole.

In the following, we will focus on the minimum inverse temperature, the minimum inverse mass parameter, the isoenthalpic and inverse curves of this system. When the JT coefficient and the temperature are both zero in Eq. (18), the horizon radius satisfies

$$\begin{aligned} r_i^{4\gamma -2}=\frac{\left[ 2\gamma (4\gamma -1)-3\right] 2^{\gamma } q}{4(4\gamma -3)}, \end{aligned}$$
(20)

then substituting the above expression into Eq. (16), the minimum inverse temperature reads

$$\begin{aligned} T_i^{min}{} & {} =\frac{8\gamma ^2-10\gamma +3}{4\pi (8\gamma ^2-2\gamma -3)}\nonumber \\{} & {} \quad \times \left( \frac{\left[ 8\gamma ^2-2\gamma -3\right] 2^\gamma q}{4(4\gamma -3)}\right) ^{-1/(4\gamma -2)}. \end{aligned}$$
(21)

The ratio between the minimum inverse temperature and the critical one becomes

$$\begin{aligned} \frac{T_i^{min}}{T_c}= & {} \frac{\left( 8\gamma ^2-10\gamma +3\right) (4\gamma -1)}{4\left( 8\gamma ^2-2\gamma -3\right) (2\gamma -1)}\nonumber \\{} & {} \times \left( \frac{8\gamma ^2-2\gamma -3}{4\gamma (4\gamma -3)(4\gamma -1)}\right) ^{-1/(4\gamma -2)}. \end{aligned}$$
(22)
Fig. 1
figure 1

The behavior of the ratio between the minimum inverse temperature and the critical one with the non-linear YM parameter

Full size image
Fig. 2
figure 2

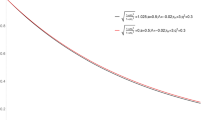
The inverse curves \(T_i-\bar{P}_i\) with different values of \(\gamma \) (see the left) and of q (see the right). In the left the non-linear charge parameter \(\gamma \) is set to 0.85 (the black dashed line), 0.9 (the red thick line), and 1 (the blue thick line). In the right the YM charge is set to 0.85 (the black dashed line), 1 (the red thick line), and 1.2 (the blue thick line)

Full size image

It is obviously that the ratio is independent with the YM charge and its behavior is exhibited in Fig. 1. Note that as \(\gamma \rightarrow \infty \), the above ratio is approach to 1/2. For the non-linear YM field (i.e., \(\gamma \ne 1\)), this ratio is not equal to 1/2, which is just different from that for the linear YM field in this theory as well as the Einstein–Maxwell theory [23, 53]. This difference is induced by the non-linear YM field, or maybe the modification of the thermodynamical volume. Especially, as \(1<\gamma \) this ratio is bigger than 1/2 and it is less than 1/2 for \(1/2<\gamma <1\). In addition when the pressure is zero and the temperature is the minimum inverse temperature, we can obtain the minimum inverse mass by substituting Eq. (20) into Eq. (11) as

$$\begin{aligned} \bar{M}_{min}{} & {} =\frac{8\gamma ^2-2\gamma -1}{2\left( 8\gamma ^2-2\gamma -3\right) }\nonumber \\{} & {} \quad \times \left( \frac{\left( 8\gamma ^2-2\gamma -3\right) 2^\gamma q}{4(4\gamma -3)}\right) ^{1/(4\gamma -2)}. \end{aligned}$$
(23)

Since in the JT process of this system the black hole mass parameter \(\bar{M}\) is unchanging, thus we can check out that whether the system is in a JT process through the minimum inverse mass parameter. That means a JT process of the system can be survive when \(\bar{M} \ge \bar{M}_{min}\). Note that when \(\gamma \rightarrow \infty \) the limitation of the minimum inverse mass approaches \(\frac{1}{2^{3/4}}\) and it is independent with the YM charge. Furthermore as \(3/4<\gamma \), \(\bar{M}_{min}>0\) and it is decreasing with the non-linear YM charge parameter \(\gamma \).

Fig. 3
figure 3

The isoenthalpic and inverse curves with different values of the mass parameter

Full size image

As the JT coefficient is zero, we can obtain the inverse pressure and temperature from Eqs. (12) and (18) as

$$\begin{aligned} \bar{P}_i= & {} \frac{1}{8\pi r_i^2}\left( -2+\frac{\left[ 2\gamma (4\gamma -1)-3\right] 2^\gamma q}{2(4\gamma -3)r_i^{4\gamma -2}}\right) ,\end{aligned}$$
(24)
$$\begin{aligned} T_i= & {} \frac{1}{4\pi r_i}\left( -1+\frac{\gamma 2^\gamma q}{r_i^{4\gamma -2}}\right) , \end{aligned}$$
(25)

where the lower index “i” stands for the inverse meaning. Therefore we can exhibit the inverse curve in the \(\bar{P}-T\) plane with different values of the YM charge q and the non-linear charge parameter \(\gamma \) from above equations in Fig. 2. From Fig. 2 we can see that there exists a inverse curve of the EPYM AdS black hole with the given parameters and it is not a circled one. The inverse temperature is increasing with the increasing of q and \(\gamma \). On the other hand, to better understand the Joule–Thomson expansion from Eqs. (16) and (17) we can depict the isoenthalpic curves, the inverse curves, and the effects of q, \(\gamma \) on them in Fig. 3. The result shows that the inverse curve divide the isoenthalpic one into two parts: one is the cooling phenomena with the positive slope of the \(\bar{P}-T\) curves, the other is the heating process with the negative slope of the \(\bar{P}-T\) curves. And both the inverse temperature and pressure are increasing with the increasing of the non-linear YM charge parameter, while they are decreasing with the YM charge.

4 Discussions and conclusions

In this manuscript we have analyzed the Joule–Thomson expansion of the EPYM AdS black hole in the expanded phase space. Considering the similar process of the gas expansion from a higher pressure section to a lower one by maintaining the fixed enthalpy, we applied it to the EPYM AdS black hole where the mass parameter is identified as enthalpy. Through the analysis of the Joule–Thomson coefficient we calculated the minimum inverse temperature and mass parameter, which could check out where a Joule–Thomson process of the system can be survive. We also presented the inverse curves in the \(\bar{P}-T\) plane and the corresponding isenthalpic curves. Above the inverse curve we obtained the cooling region, while below the inverse curve it corresponds to the heating one. Especially the effect of the Yang Mills charge nonlinearity on the Joule–Thomson expansion was also investigated. The corresponding result can be summarized in the following

  • The ratio between the minimum inverse temperature and the critical temperature is independent with the YM charge and approaches to 1/2 as \(\gamma \rightarrow \infty \). When \(\gamma =1\) it equals to 1/2 and it is bigger than 1/2 for \(1<\gamma \), while less than 1/2 for \(1/2<\gamma <1\).

  • The minimum inverse mass parameter is independent with the YM charge as \(\gamma \rightarrow \infty \), it is positive in the range of \(3/4<\gamma \) and is decreasing with the increasing of the non-linear YM charge parameter.

  • Both the inverse temperature and pressure are increasing with the increasing of the non-linear YM charge parameter, while they are decreasing with the YM charge.