1 Introduction

Over the last decade, a great interest has been aroused in the field of hardon physics, especially heavy baryons. Significant progresses have been achieved in both experiment and theory. For example, the LHCb collaboration observed the doubly charmed baryon \(\Xi _{cc}^{++}\) in the final state \(\Lambda _cK^{-}\pi ^+\pi ^+\) [1] and it has been confirmed in the decays \(\Xi _{cc}^{++}\rightarrow \Xi _{c}^+\pi ^+\)and \(\Xi _{cc}^{++}\rightarrow \Xi _{c}^{'+}\pi ^+\) [2, 3]. On the theory side, multiple approaches have been developed to study the physical properties of heavy baryons, such as decay width. For example, in Refs. [4,5,6] the authors employed light-front quark model (LFQM) to explore the weak decays of doubly heavy baryons. In Ref. [7] the weak decays of doubly heavy baryons were studied within light-cone sum rules. In retrospect, weak decays of the heavy baryons were also studied under the heavy quark limit [8], the relativistic quark model with quark–diquark picture [9], the relativistic three-quark model [10] and the Bethe–Salpeter approach [11].

In Refs. [4,5,6, 12,13,14,15] the LFQM was extended to study the weak decays of the heavy baryons with the quark–diquark picture. However, although the quark–diquark picture is an effective approximation when the diquark is a spectator in the transition, it is not very suitable for studying the decay where the diquark will be broken. Instead, three-quark picture was employed to study the weak decays between two heavy baryons with \(J^P=\frac{1}{2}^+\) in Refs. [16,17,18,19]. In Ref. [12] the transition between \(J^P=\frac{1}{2}^+\) heavy baryon \(({\mathcal {B}}_i(\frac{1}{2}^+))\) and \(J^P=\frac{3}{2}^+\) one \(({\mathcal {B}}_f(\frac{3}{2}^+))\) was studied with the quark–diquark picture. In this work we employ the three-quark picture to study the transition \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) within the LFQM framework. The LFQM is a relativistic quark model which has been applied to study transitions among mesons [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] and has been extended to the case of baryon decay [4,5,6, 12,13,14,15]. We derive general forms of transition amplitude \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\). Then we revisit the transition \(\Sigma _{b}\rightarrow \Sigma _{c}^*\) and study the relative weak decays of the double charmed baryon \(\Xi _{cc}\).

For the weak decay of single heavy baryon, the b quark in the initial state would transit into the c quark in the final state by emitting W bosons. The two light quarks do not take part in the process of the weak decay and the subsystem of the two light quarks can be regarded as a spectator. Under the three-quark picture, the three quarks are regarded as independent individuals. Although the two light quarks are no longer point-like diquark, the subsystem where they reside still has a definite spin, color, isospin and all the quantum numbers of the subsystem keep unchanged so it is treated as the spectator. For the weak decay of doubly charmed baryon \((ccq_2),\) one c quark in the initial state decays to a lighter quark \(q_1\) by emitting W bosons via the weak interaction. The resulting new quark forms a subsystem \((q_1q_2)\) with the light quark \(q_2\) which comes from the initial state. As a result, both cc pair in the initial state and \(q_1q_2\) in the final state which have definite spin cannot be treated as the spectators in the decay. A rearrangement of quarks for the initial and final baryons is necessary to isolate the unchanged subsystem \(cq_2\), which can be viewed as the spectator approximately.

In LFQM, we need to specify the vertex functions of the initial state and the final state according to the total spin and parity of the baryon. Here the quantum numbers of the initial state and the final state are \({1\over 2}^+\) and \({3\over 2}^+\), respectively. We adopt the vertex function of \({1\over 2}^+\) baryon in Ref. [16] and construct the three-body vertex function of \({3\over 2}^+\) in analog to Ref. [16]. Then we derive the transition matrix element, extract the form factors and compute them numerically.

Using these form factors we calculate the associated non-leptonic decays and semileptonic decays. The leptons are not involved in the strong interaction which means the semileptonic decay is less contaminated by the non-perturbative QCD effect, hence the study on semileptonic decay can be very helpful to constrain the model parameters and test model predictions. For the non-leptonic two-body decays \({\Sigma _b}\rightarrow \Sigma _c^*M\), \({\Xi _{cc}}\rightarrow \Sigma _c^*M\) and \({\Xi _{cc}}\rightarrow \Xi _c^{*}M\), by neglecting the interaction between the final states, the transition element is factorized to a product of the meson decay constant and the transition amplitude \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) under the factorization assumption. Future measurement on these channels will be necessary to further test model predictions and elucidate the underlying mechanism of heavy hadron decay.

This paper is organized as follows: in Sect. 2 we present the vertex functions of the heavy flavor baryons, and derive the form factors of the transition \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) in the LFQM. In Sect. 3 we present numerical results for the transition \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) along with all necessary input parameters. We calculate the form factors and the decay widths of related semi-leptonic and non-leptonic decays. Section 4 is devoted to our conclusions and discussions.

2 \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) in the light-front quark model

In this paper we study the transition \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) with the three-quark picture of baryon in LFQM. We focus on the weak decay of single heavy baryon \(\Sigma _{b}\) to \(\Sigma _{c}^*\) and the doubly charmed baryon \(\Xi _{cc}\) to single charmed baryon \(\Sigma _{c}^*\) or \(\Xi _{c}^*\).

2.1 The vertex functions

In Ref. [16], the vertex function of a baryon \({\mathcal {B}}\) with the total spin \(S=1/2\) and total momentum P was discussed.Footnote 1 For a single heavy baryon it could be expressed as

$$\begin{aligned}{} & {} |{\mathcal {B}}(P,S,S_z)\rangle \nonumber \\{} & {} \quad =\int \{d^3\tilde{p}_1\}\{d^3\tilde{p}_2\}\{d^3\tilde{p}_3\} \, 2(2\pi )^3\delta ^3(\tilde{P}-\tilde{p_1}-\tilde{p_2}-\tilde{p_3}) \nonumber \\{} & {} \qquad \times \sum _{\lambda _1,\lambda _2,\lambda _3}\Psi _{S_{q_1q_2}}^{SS_z}(\tilde{p}_1,\tilde{p}_2, \tilde{p}_3,\lambda _1,\lambda _2,\lambda _3) {\mathcal {C}}^{\alpha \beta \gamma }\nonumber \\{} & {} \qquad \times {\mathcal {F}}_{Q,q_1,q_2}\left| \right. Q_{\alpha } (p_1,\lambda _1)q_{1\beta }(p_2,\lambda _2)q_{2\gamma }(p_3,\lambda _3)\rangle , \end{aligned}$$
(1)

where Q denotes heavy quark (b or c), \(q_{1}(q_{2})\) denotes the flavor of the light quark, \(\lambda _i\) and \(p_i\, (i=1,2,3)\) are helicities and light-front momenta of the quarks, \({\mathcal {C}}^{\alpha \beta \gamma }\) and \({\mathcal {F}}_{Q,q_1,q_2}\) are the color and flavor factors. The total spin of \(q_1\) and \(q_2\) is denoted to \(S_{q_1q_2}\) which is 0 for \(\Lambda _b\, ( \Lambda _c)\) and 1 for \(\Sigma _b\, ( \Sigma _c)\), respectively. In light-front approach, the on-mass-shell light-front momentum p is defined as

$$\begin{aligned}{} & {} \tilde{p}=(p^{+},p_{\perp }),\quad p_{\perp } =(p^{1},p^{2}),\quad p^{-} =\frac{m^2+p^2_{\perp }}{p^{+}},\nonumber \\{} & {} \quad \{d^3p\} = \frac{dp^{+}d^2p_{\perp }}{2(2\pi )^3}. \end{aligned}$$
(2)

The momentum-space wave functions \(\Psi ^{SS_z}_0\) and \(\Psi ^{SS_z}_1\)[16, 37] are

$$\begin{aligned} \Psi ^{SS_z}_0(\tilde{p}_i,\lambda _i)= & {} A_0 \bar{u}(p_3,\lambda _3)[(\bar{P}\!\!\!\!/+M_0)\gamma _5]v(p_2,\lambda _2)\nonumber \\{} & {} \quad \times \bar{u}(p_1,\lambda _1) u(\bar{P},S) \phi _{\mathcal {B}}(x_i,k_{i\perp }),\nonumber \\ \Psi ^{SS_z}_1(\tilde{p}_i,\lambda _i)= & {} A_1 \bar{u}(p_3,\lambda _3)[(\bar{P}\!\!\!\!/+M_0) \gamma _{\perp }^\beta ]v(p_2,\lambda _2)\nonumber \\{} & {} \quad \times \bar{u}(p_1,\lambda _1) \gamma _{\perp \beta }\gamma _{5} u(\bar{P},S) \phi _{\mathcal {B}}(x_i,k_{i\perp }).\nonumber \\ \end{aligned}$$
(3)

For a single heavy baryon \({\mathcal {B}}\) with total spin \(S=3/2\) the vertex function is the same as that in Eq. (1) except \(\Psi ^{SS_z}_1\) is replaced by \(\Psi ^{'SS_z}_1\) [38], which is given by

$$\begin{aligned} \Psi ^{'SS_z}_1(\tilde{p}_i,\lambda _i)= & {} A'_1 \bar{u}(p_3,\lambda _3)[(\bar{P}\!\!\!\!/+M_0) \gamma _{\perp }^\alpha ]\nonumber \\{} & {} \times v(p_2,\lambda _2)\bar{u}(p_1,\lambda _1) u_{\alpha }(\bar{P},S)\phi _{\mathcal {B}}(x_i,k_{i\perp }).\nonumber \\ \end{aligned}$$
(4)

Notice that the expressions in Eqs. (3) and (4) contain anti-quark spinor \(v(p_2,\lambda _2)\). This is because the identify \(\bar{u} = v^T C^{-1}\) has been applied to simplify the spin wave function, where \(C^{-1}\) is used to eliminate C in the bispinor matrix of wave function [37, 38] (C denotes charge conjugation operator).

With the normalization of the state \({\mathcal {B}}\)

$$\begin{aligned}{} & {} \langle {\mathcal {B}} (P',S',S'_z)|{\mathcal {B}} (P,S,S_z)\rangle \nonumber \\{} & {} \quad =2(2\pi )^3P^+\delta ^3(\tilde{P}'-\tilde{P})\delta _{S'S}\delta _{S'_zS_z}, \end{aligned}$$
(5)

and

$$\begin{aligned}{} & {} \int \left( \prod ^3_{i=1}\frac{dx_id^2k_{i\perp }}{2(2\pi )^3}\right) 2(2\pi )^3 \delta \left( 1-\sum x_i\right) \delta ^2\left( \sum k_{i\perp }\right) \nonumber \\{} & {} \quad \times \phi ^*_{\mathcal {B}}(x_i,k_{i\perp })\phi _{\mathcal {B}}(x_i,k_{i\perp })=1, \end{aligned}$$
(6)

we can compute the factors \(A_0\), \(A_1\) and \(A'_1\):

$$\begin{aligned} A_0= & {} \frac{1}{4\sqrt{P^+M_0^3(m_1+e_1)(m_2+e_2)(m_3+e_3)}},\nonumber \\ A_1= & {} \frac{1}{4\sqrt{3P^+M_0^3(m_1+e_1)(m_2+e_2)(m_3+e_3)}},\nonumber \\ A'_1= & {} \frac{1}{4\sqrt{2P^+M_0^3(m_1+e_1)(m_2+e_2)(m_3+e_3)}}, \end{aligned}$$
(7)

where \(p_i\cdot \bar{P}=e_iM_0\,(i=1,2,3)\) is used, \(\bar{P}=p_1+p_2+p_3\) and \(e_i\) is defined in Eq. (12).

For the weak decay of doubly charmed baryon, the vertex function with total spin \(S=1/2\) and momentum P is

$$\begin{aligned}{} & {} |{\mathcal {B}}(P,S,S_z)\rangle \nonumber \\{} & {} \quad =\int \{d^3\tilde{p}_1\}\{d^3\tilde{p}_2\}\{d^3\tilde{p}_3\} \, 2(2\pi )^3\delta ^3(\tilde{P}-\tilde{p_1}-\tilde{p_2}-\tilde{p_3}) \nonumber \\{} & {} \qquad \times \sum _{\lambda _1,\lambda _2,\lambda _3}\Psi _{S_{QQ}}^{SS_z}(\tilde{p}_1, \tilde{p}_2,\tilde{p}_3,\lambda _1,\lambda _2,\lambda _3) {\mathcal {C}}^{\alpha \beta \gamma }\nonumber \\{} & {} \qquad \times {\mathcal {F}}_{Q,Q,q_2}\left| \right. Q_{\alpha }(p_1,\lambda _1)Q_{\beta } (p_2,\lambda _2)q_{2\gamma }(p_3,\lambda _3)\rangle . \end{aligned}$$
(8)

In order to describe the momenta of the constituent quarks, the intrinsic variables \((x_i, k_{i\perp })\) (\(i=1,2,3\)) are introduced through

$$\begin{aligned}{} & {} p^+_i=x_i P^+, \quad p_{i\perp }=x_i P_{\perp }+k_{i\perp } \quad x_1+x_2+x_3=1,\nonumber \\{} & {} k_{1\perp }+k_{2\perp }+k_{3\perp }=0, \end{aligned}$$
(9)

where \(x_i\) is the momentum fraction with the constraint \(0<x_1, x_2, x_3<1\). The variables \((x_i, k_{i\perp })\) are Lorentz-invariant since they are independent of the total momentum of the hadron. The invariant mass square \(M_0^2\) is defined as a function of the internal variables \(x_i\) and \(k_{i\perp }\):

$$\begin{aligned} M_0^2=\frac{k_{1\perp }^2+m_1^2}{x_1}+ \frac{k_{2\perp }^2+m_2^2}{x_2}+\frac{k_{3\perp }^2+m_3^2}{x_3}. \end{aligned}$$
(10)

The internal momenta are defined as

$$\begin{aligned} k_i= & {} (k_i^-,k_i^+,k_{i\bot })=(e_i-k_{iz},e_i+k_{iz},k_{i\bot })\nonumber \\= & {} \left( \frac{m_i^2+k_{i\bot }^2}{x_iM_0},x_iM_0,k_{i\bot }\right) . \end{aligned}$$
(11)

It is easy to obtain

$$\begin{aligned} e_i= & {} \frac{x_iM_0}{2}+\frac{m_i^2+k_{i\perp }^2}{2x_iM_0},\nonumber \\ k_{iz}= & {} \frac{x_iM_0}{2}-\frac{m_i^2+k_{i\perp }^2}{2x_iM_0}, \end{aligned}$$
(12)

where \(e_i\) is the energy of the i-th constituent, and they obey the condition \(e_1+e_2+e_3=M_0\). The transverse \(k_{i\bot }\) and z direction \(k_{iz}\) components constitute a momentum vector \(\vec k_i=(k_{i\bot }, k_{iz})\).

The spatial wave function \(\phi _{\mathcal {B}}(x_i, k_{i\perp })\) [39, 40] is defined as

$$\begin{aligned}{} & {} \!\!\!\phi _{\mathcal {B}}(x_1,x_2,x_3,k_{1\perp },k_{2\perp },k_{3\perp })\nonumber \\{} & {} \quad =\frac{e_1e_2e_3}{x_1x_2x_3M_0} \varphi (\overrightarrow{k}_1,\beta _1) \varphi \left( \frac{\overrightarrow{k}_2-\overrightarrow{k}_3}{2},\beta _{23}\right) \end{aligned}$$
(13)

with \(\varphi (\overrightarrow{k},\beta )=4(\frac{\pi }{\beta ^2})^{3/4}\textrm{exp}(\frac{-k_z^2-k^2_\perp }{2\beta ^2})\), where \(\beta \) is a non-perturbative parameter that characterizes the shape of wave function. We will discuss the parameter selection in Sect. 3.

This form of spatial wave function is inspired by the ground-state eigenfunction of Hamiltonian of harmonic oscillator [37]. For such three-body system in the center-of-momentum frame (\(\overrightarrow{p}_1\), \(\overrightarrow{p}_2\), \(\overrightarrow{p}_3\)), the ground-state wave function can be factorized as

$$\begin{aligned} \psi \sim \exp \left( -\frac{3}{2} \cdot \frac{\overrightarrow{p}_1^2 }{2\alpha ^2} \right) \times \exp \left( - \frac{(\overrightarrow{p}_2-\overrightarrow{p}_3)^2 }{2\alpha ^2} \right) . \end{aligned}$$
(14)

2.2 The form factors of \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) in LFQM

The form factors for the transition from initial heavy baryon \({\mathcal {B}}_i(\frac{1}{2}^+)\) (i.e. \(|{\mathcal {B}}(P,1/2,S_z)\)) to final heavy baryon \({\mathcal {B}}_f(\frac{3}{2}^+)\) \((|{\mathcal {B}}(P',3/2,S'_z)\rangle )\) are defined as

(15)
Fig. 1
figure 1

The Feynman diagram for single heavy baryon weak decay, where \(\bullet \) denotes \(V-A\) current vertex

Full size image
Fig. 2
figure 2

The Feynman diagram for doubly charmed baryon weak decay, where \(\bullet \) denotes \(V-A\) current vertex

Full size image

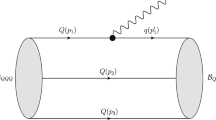
where momentum \(q \equiv P-P'\). \(Q_1\) and \(Q_2\) denote heavy quark operators (see Fig. 1). \(M_{{\mathcal {B}}_i}\) and \(M_{{\mathcal {B}}_f}\) represent the masses of heavy baryon \({\mathcal {B}}_i\) and \({\mathcal {B}}_f\), respectively. For the decay of doubly charmed baryon \(Q_2\) should be replaced by \(q_1\) (see Fig. 2).

Here the momenta of initial and final baryons P and \(P'\) obey the on-shell relations \(E^{(')2}=P^{(')2}+M^{(')2}\). However, in Eqs. (3) and (4) the spinors are function of \(\bar{P}\) and \(\bar{P}'\), which are the sums of the momenta of the involved constituent quarks and do not obey physical on-shell relations. To reconcile the conflict, here we follow the approach in the previous study [12] and assume form factors \((f_1, f_2, f_3, f_4, g_1, g_2, g_3, g_4)\) are the same in both physical and unphysical form. Then Eq. (15) is re-written as the following equation where the spinors are off-shell:

(16)

2.2.1 The transition \(\Sigma _b\rightarrow \Sigma ^*_c\)

The lowest order Feynman diagram responsible for the \(\Sigma _b\rightarrow \Sigma ^*_c\) (\( \Sigma _b\) and \(\Sigma ^*_c\) are \({\mathcal {B}}_i(\frac{1}{2}^+)\) and \({\mathcal {B}}_f(\frac{3}{2}^+)\), respectively) weak decay is shown in Fig. 1. Following the approach given in Refs. [13, 14, 39, 40] the transition matrix element can be calculated with the vertex functions of \(\mid {\mathcal {B}}_i(\frac{1}{2}^+) \rangle \) and \(\mid {\mathcal {B}}_f(\frac{3}{2}^+)\rangle \),

(17)

where for the weak decay of single heavy baryons,

$$\begin{aligned} m_1=m_b, \quad m'_1=m_c, \quad m_2=m_{q_1}, \quad m_3=m_{q_2}. \end{aligned}$$

\(p_1\) denotes the four-momentum of the heavy quark b, \(p'_1\) denotes the four-momentum of the quark c, P \((P')\) stands as the four-momentum of \({\mathcal {B}}_i\) \(({\mathcal {B}}_f).\) Setting \(\tilde{p}_2=\tilde{p}'_2\), \(\tilde{p}_3=\tilde{p}'_3\) we have

$$\begin{aligned}{} & {} x'_{i}=\frac{P^+}{P^{'+}}x_{i}, \quad k'_{1\perp }=k_{1\perp }-(1-x_1)q_{\perp },\nonumber \\{} & {} \quad k'_{2\perp }=k_{2\perp }+x_2q_{\perp }, \quad k'_{3\perp }=k_{3\perp }+x_3q_{\perp }. \end{aligned}$$
(18)

Multiplying the following expressions \(\bar{u}(\bar{P},S_z)\gamma _{\mu }\bar{P}^\xi {u}_{\xi } \)\( (\bar{P}',S'_z)\), \(\bar{u}(\bar{P},S_z)\bar{P}'_{\mu }\bar{P}^\xi {u}_{\xi }(\bar{P}',S'_z)\), \(\bar{u}(\bar{P},S_z) \bar{P}_{\mu }\bar{P}^\xi {u}_{\xi }(\bar{P}', \)\( S'_z)\), \(\bar{u}(\bar{P},S_z) g_{\mu }^{\xi } {u}_{\xi }(\bar{P}',S'_z)\) to the right sides of both Eqs. (16) and (17) and then summing over the polarizations of all states, we can obtain four algebraic equations and each equation contains the form factors \(f_{1}\), \(f_{2}\), \(f_{3}\) and \(f_{4}\). Solving these equations, we can get the explicit expressions of these form factors \(f_{i}(i=1,2,3,4\)) (see Appendix A for detail).

Similarly, multiplying these expressions \( \bar{u}(\bar{P},S_z)\gamma _{\mu } \)\( \bar{P}^\xi \gamma _{5}{u}_{\xi }(\bar{P}',S'_z)\), \(\bar{u}(\bar{P},S_z)\bar{P}'_{\mu }\bar{P}^\xi \gamma _{5}{u}_{\xi }(\bar{P}',S'_z)\), \(\bar{u}(\bar{P},S_z) \bar{P}_{\mu }\)\(\bar{P}^\xi \gamma _{5}{u}_{\xi }(\bar{P}',S'_z)\), and \(\bar{u}(\bar{P},S_z) g_{\mu }^ {\xi }\gamma _{5}{u}_{\xi }(\bar{P}',S'_z)\) to the right sides of both Eqs. (16) and (17) and solving for four algebraic equations, we can obtain analytical expressions of \(g_{i}(i=1,2,3,4).\)

2.2.2 The transition \(\Xi _{cc}\rightarrow \Sigma ^*_c (\Xi ^*_c)\)

For the weak decay of doubly charmed baryon \(\Xi _{cc}\rightarrow \Sigma ^*_c (\Xi ^*_c)\), one c quark in the initial state \(([cc] q_2)\) decays to a light quark \(q_1\) in the final state \((c [q_1 q_2])\) by weak interaction (Fig. 2). This light quark \(q_1\) combines with the light quark \(q_2\) from the initial state to form a physical subsystem \(q_1q_2\) which possesses definite spin i.e. the quark composition in the initial state is \([cc]q_2\), and that in the final state is \(c[q_1 q_2]\) (\(q_1\) and \( q_2\) may be same or not), which means neither the original [cc] nor the final [\(q_1 q_2\)] are spectators. The physical subsystem (diquark) is not spectator in the transition, so the quarks need to be rearranged. Therefore, the [cc] diquark in the initial state needs to be destroyed and then rearranged with another light quark using a Racah transformation. The related transformation is [5]

$$\begin{aligned}{} & {} [c^1c^2]_1[q_2]=\frac{\sqrt{2}}{2}\left( -\frac{\sqrt{3}}{2}[c^2][c^1q_2]_0\right. \nonumber \\{} & {} \quad \left. +\frac{1}{2}[c^2][c^1q_2]_1-\frac{\sqrt{3}}{2}[c^1][c^2q_2]_0+ \frac{1}{2}[c^1][c^2q_2]_1\right) ,\nonumber \\ \end{aligned}$$
(19)

where the subscript after brackets 0 or 1 denotes the total spin of two quarks in the brackets. The superscript for every c quark is added to distinguish each other. After the rearrangement \(\Psi ^{SS_z}_{S_{cc}}(\tilde{p}_i,\lambda _i)\) can be expressed to \(-\frac{\sqrt{6}}{2}\Psi ^{SS_z}_0(\tilde{p}_i,\lambda _i) +\frac{\sqrt{2}}{2}\Psi ^{SS_z}_1(\tilde{p}_i,\lambda _i)\) where the subscript 0 and 1 are the total spin of \(cq_2\) subsystem.

Since the final state baryon \({\mathcal {B}}_f\) (\(\Sigma ^*_c\) or \(\Xi ^*_c\)) has spin of 3/2, the Racah transformation leads to the following rearrangement:

$$\begin{aligned}{}[c][q_1 q_2]_1=[q_1][c q_2]_{1}=[q_2][c q_1]_{1}, \end{aligned}$$
(20)

and the expression \(\Psi ^{'SS_z}_{cq_{1}}(\tilde{p}'_i,\lambda '_i)\) or \(\Psi ^{'SS_z}_{cq_{2}}(\tilde{p}'_i,\lambda '_i)\) is just \(\Psi ^{'SS_z}_1(\tilde{p'}_i,\lambda '_i)\).

After the rearrangement the spectators in the process are isolated so the spectator approximation can be used in the calculation. In terms of the rearrangement the expressions of the form factors for the transition \(\Xi _{cc}\rightarrow {\Sigma ^{*}_c}(\Xi ^{*}_c)\) have an additional factor \(\frac{\sqrt{2}}{2}\) relative to those for \(\Sigma _{b}\rightarrow {\Sigma ^{*}_c}\).

3 Numerical results

Table 1 The masses of the involved quarks and baryons (in units of GeV)
Full size table

3.1 The \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f (\frac{3}{2}^+)\) form factors

In order to compute the relative transition rates of semi-leptonic decays and non-leptonic decays of \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f (\frac{3}{2}^+)\), we need to calculate the aforementioned form factors numerically. First of all, we need to fix the free parameters of the model, including masses of quarks and baryons, and wavefunction \(\beta \) parameters. The masses of quarks given in Ref. [25] and the masses of baryons taken from Refs. [1, 41] are listed in Table 1.

There is no precise measure of the parameters \(\beta _1\), \(\beta _{23}\), \(\beta _1'\) and \(\beta _{23}'\) in the wave functions of the initial and the final baryons. Generally the reciprocal of \(\beta \) is related to the electrical radium of the baryon. Since the strong coupling strength between \(q_1\) and \(q_2\) is half of that between \(q_1\bar{q}_2\). Assuming a Coulomb-like potential, one can expect the radius of \(q_1q_2\) to be \(1/\sqrt{2}\) times that of \(q_1\bar{q}_2\) i.e. \(\beta _{q_1q_2}\approx \sqrt{2}\beta _{q_1\bar{q}_2}\). In Ref. [42] in terms of the binding energy the authors also obtained the same results. Therefore in our work we use the \(\beta \) values in the mesons case \((\beta _{q_1\bar{q}_2})\) [25] to estimate \(\beta _{q_1 q_2}\). As for the value of \(\beta _1\) we refer to the \(\beta \) values of the heavy mesons in Ref. [43].

Since the form factors \(f_{i}(i=1,2,3,4)\) and \(g_{i}(i=1,2,3,4)\) is calculated in the frame \(q^+=0\) i.e. \(q^2=-q^2_{\perp }\le 0\) (the space-like region) one needs to extend them into the time-like region to evaluate the transition rates. In Refs. [39, 40] the form factors were parameterized using the three-parameter form

$$\begin{aligned} F(q^2)=\frac{F(0)}{\left( 1-\frac{q^2}{M_{{\mathcal {B}}_i}^2}\right) \left[ 1-a\left( \frac{q^2}{M_{{\mathcal {B}}_i}^2}\right) +b\left( \frac{q^2}{M_{{\mathcal {B}}_i}^2}\right) ^2\right] }.\nonumber \\ \end{aligned}$$
(21)

However for the decay of doubly charmed baryon this parametric form doesn’t work well, instead a polynomial form was employed [17]. So here we also use the three-parameter polynomial form

$$\begin{aligned} F(q^2)=F(0)+a\frac{q^2}{M_{{\mathcal {B}}_i}^2}+b \left( \frac{q^2}{M_{{\mathcal {B}}_i}^2}\right) ^2, \end{aligned}$$
(22)

where \(F(q^2)\) represents the form factors \(f_i\) and \(g_i\).

Using the form factors calculated numerically in the space-like region we fit the parameters a, b and F(0) in the un-physical region and then extrapolate to the physical region with \(q^2\ge 0\) through Eq. (22).

Fig. 3
figure 3

a The form factors \(f_i\; (i=1,2,3,4)\) and b the form factors \(g_i\; (i=1,2,3,4)\) with \(\beta _{23}= 2.9 \beta _{u\bar{d}}\)

Full size image

3.1.1 The transition \(\Sigma _b\rightarrow \Sigma ^*_c\)

Based on the forementioned discussion, we set \(\beta _1=\sqrt{2}\beta _{b\bar{s}}\) and \(\beta _1'= \sqrt{2}\beta _{c\bar{s}}\). However u and d quarks can be regarded as a \(1^+\) diquark which means the distance between u and d quarks should be smaller than normal case so \(\beta _{23}\) will bigger than \(\sqrt{2}\beta _{u\bar{d}}\). In Ref. [16] we fixed \(\beta _{23}=\beta _{23}'=2.9 \beta _{u\bar{d}}\) and \(\beta _{u\bar{d}}=0.263\) GeV [25], since u and d quarks are in the \(^3S_1\) state. The relevant values of \(\beta \) are presented in Table 2. With these parameters we calculate the form factors and make theoretical predictions on the transition rates. The fitted values of a,  b and F(0) in the form factors \(f_{i}\) and \(g_{i}\) are presented in Table 3. The dependence of the form factors on \(q^2\) is depicted in Fig. 3.

From Fig. 3, one can find that the absolute values of the form factors \(f_1(q^2)\) and \(g_2(q^2)\) are close to 0. The absolute values of \(f_2(q^2)\) and \(f_3(q^2)\) are almost close to each other at the small value of \(q^2\) (\(q^2<6\) Gev). Compared with the results in Ref. [12], the values of the \(f_i\) and \(g_i\) here are similar to those obtained in Scheme II of Ref. [12] where the polarization of the [ud] diquark depends on the momentum of the diquark itself. Considering \(1^+\) diquark is a so called bad diquark [44], which means the distance of ud here is bigger than that for a \(0^+\) diquark case, we estimate \(\beta _{23}=\beta _{23}'< 2.9 \beta _{u\bar{d}}\) so we also set \(\beta _{23}=\beta _{23}'= 2.0 \beta _{u\bar{d}}\) and \(2.5 \beta _{u\bar{d}}\) to do the same calculation and compare the results on the semileptonic and nonleptonic decays later.

Table 2 The values of \(\beta \) parameters (in units of GeV)
Full size table
Table 3 The \(\Sigma _{b}\rightarrow \Sigma _c^*\) form factors given in the three-parameter form with \(\beta _{23}= 2.9 \beta _{u\bar{d}}\)
Full size table
Fig. 4
figure 4

a The form factors \(f_i\; (i=1,2,3,4)\) and b the form factors \(g_i\; (i=1,2,3,4)\) with \(\beta _{1}= 2.9 \beta _{c\bar{c}}\)

Full size image

3.1.2 The transition \(\Xi _{cc}\rightarrow \Sigma ^*_c(\Xi ^*_c)\)

For the doubly baryon \(\Xi _{cc}\), two c quarks consist of a \(1^+\) diquark so we set \(\beta _{1}=\beta _{c[cq_2]}= 2.9 \beta _{c\bar{c}}\) and \(\beta _{23}=\beta _{23}'= \sqrt{2}\beta _{c\bar{q}_2}\). Since the rearrangement for \(\Sigma ^*_c(\Xi ^*_c)\) we choose \(\beta '_{1}=\beta _{d[cq_2]}= \sqrt{2}\beta _{c\bar{d}}\, (\beta '_{1}=\beta _{s[cq_2]}= \sqrt{2}\beta _{c\bar{s}})\). The relevant parameters are collected in Table 2.

The fitted values of a,  b and F(0) in the form factors \(f_{i}\), \(g_{i}\) are presented in Table 4. The dependence of the form factors on \(q^2\) is depicted in Fig. 4. Compared with the curves of the form factors in Fig. 3, those in Fig. 4 change more significantly with \(q^2\), especially when \(q^2>2\) GeV. Similarly we also set \(\beta _{1}=\beta _{c[cq_2]}=2.0 \beta _{c\bar{c}}\) and \(\beta _{1}=\beta _{c[cq_2]}= 2.5 \beta _{c\bar{c}}\) in the calculation.

3.2 Semi-leptonic decay of \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f (\frac{3}{2}^+) +l\bar{\nu }_l\)

3.2.1 Semi-leptonic decay of single heavy baryon: \(\Sigma _b\rightarrow \Sigma _c^* l\bar{\nu }_l\)

Employing these form factors obtained in Sect. 3.1.1, we evaluate the rates of \(\Sigma _{b} \rightarrow \Sigma _{c}^* l\bar{\nu }_l\). At the same time we also depict the differential decay rates of the \(\Sigma _b \rightarrow \Sigma _c^* +l\bar{\nu }_l\) which depend on \(\omega \) (definition can be found in Appendix B) in Fig. 5. We calculate the total decay widths, longitudinal decay widths, transverse decay widths and the ratio of the longitudinal to transverse decay rates R with \(\beta _{23}=\beta _{23}'=2.0 \beta _{u\bar{d}}\), \(2.5 \beta _{u\bar{d}}\), and \(2.9 \beta _{u\bar{d}}\), respectively. The results are listed in Table 5.

As we can see in Table 5, the width increases slowly when the value of \(\beta _{23}\) decreases and the decay width is a little smaller than that in Ref. [12] where quark–diquark picture for baryons within the LFQM was employed. The longitudinal decay rate, transverse decay rate and their ratio R are also a little difference under the two types of models of baryon. In Ref. [10] the authors employed relativistic three-quark model to calculate theses form factor and their predictions on the decay width of \(\Sigma _b \rightarrow \Sigma _c^* +l\bar{\nu }_l\) are almost twice larger than this work. In summary, our results on the decay width of \(\Sigma _b \rightarrow \Sigma _c^* +l\bar{\nu }_l\) are less than the results in Refs. [9,10,11,12], which means a small \(\beta _{23}\) (\(\beta _{23}'\)) is more reasonable if we want to make the prediction close to those in references.

Table 4 The \(\Xi _{cc}\rightarrow \Sigma _c^*\) form factors given in the three-parameter form with \(\beta _{1}= 2.9 \beta _{c\bar{c}}\)
Full size table

We also use the same method to calculate the decay width of \(\Omega _{b}\rightarrow \Omega _{c}^* l\bar{\nu }_l\), \(\Xi _{b}^{'}\rightarrow \Xi _{c}^* l\bar{\nu }_l\) with \(\beta _{23}=\beta _{23}'= 2.0 \beta _{q_1\bar{q}_2}\) and the results are shown in Table 6. From Table 6, we can see that the widths of \(\Sigma _{b} \rightarrow \Sigma _{c}^* l\bar{\nu }_l, \Omega _{b}\rightarrow \Omega _{c}^* l\bar{\nu }_l\) and \(\Xi _{b}^{'}\rightarrow \Xi _{c}^* l\bar{\nu }_l\) are close to each other. Similarly, they are lower than those in the Ref. [9].

Fig. 5
figure 5

Differential decay rates \(d\Gamma /d\omega \) for the decay \(\Sigma _b \rightarrow \Sigma _c^* l\bar{\nu }_l\) with \(\beta _{23}= 2.9 \beta _{u\bar{d}}\)

Full size image
Table 5 The widths and polarization asymmetries of \(\Sigma _b\rightarrow \Sigma _c^* l\bar{\nu }_l\)
Full size table
Table 6 The widths and polarization asymmetries of the semileptonic decay between two single heavy baryons \((\beta _{23}= 2.0 \beta _{u\bar{d}})\)
Full size table

3.2.2 Semi-leptonic decay of doubly charmed baryon: \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} l \bar{\nu }_l\) and \(\Xi _{cc}\rightarrow \Xi _{c}^{*} l \bar{\nu }_l\)

For the weak decay of doubly charmed baryon, we calculate the decay rates of \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} l \bar{\nu }_l\) and \(\Xi _{cc}\rightarrow \Xi _{c}^{*} l \bar{\nu }_l\). The curves of the differential decay widths depending on \(\omega \) for \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} l \bar{\nu }_l\) are depicted in Fig. 6 which is very similar to that for \(\Sigma _b \rightarrow \Sigma _c^* +l\bar{\nu }_l\). The curves for \(\Xi _{cc}\rightarrow \Xi ^*_{c} l \bar{\nu }_l\) are similar to those in Fig. 6 except their peak values are 20 times bigger than those for \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} l \bar{\nu }_l\) so we omit the figure. The numerical results with \(\beta _{1}= 2.0 \beta _{c\bar{c}}\), \(2.5 \beta _{c\bar{c}}\), \(2.9 \beta _{c\bar{c}}\) are presented in Tables 7 and 8, respectively. One can find that the differential decay rate of \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} (\Xi _{c}^{*}) l \bar{\nu }_l\) increases with the decrease of the \(\beta _{1}\) value and the differential decay rate with \(\beta _{1}= 2.0 \beta _{c\bar{c}}\) is close to that in Refs. [5, 45] where the decay was explored with the quark–diquark picture in the LFQM. When \(\beta _{1}= 2.9\beta _{c\bar{c}}\), the result of \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} l \bar{\nu }_l\) is about half of the Refs. [5, 45]. Our results here indicate \(\beta _{1}\) prefers a small number, such as \(2.0\beta _{c\bar{c}}\) if the predictions in references are accurate.

3.3 Non-leptonic decays of \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f (\frac{3}{2}^+)+ M\)

Because of the strong interaction, the non-leptonic decays are more complicated than the semi-leptonic processes. Here we adopt the theoretical framework of factorization assumption, where the hadronic transition matrix element can be factorized into a product of two independent matrix elements of currents.

3.3.1 Non-leptonic decays of single heavy baryon: \(\Sigma _b\rightarrow \Sigma _c^* + M \)

For \(b\rightarrow c\) transition, the hadronic transition matrix element is

$$\begin{aligned}{} & {} \left\langle {\mathcal {B}}_f\left( \frac{3}{2}^+\right) M \right| {\mathcal {H}} \left| {\mathcal {B}}_i\left( \frac{1}{2}^+\right) \right\rangle \nonumber \\{} & {} \quad =\frac{G_FV_{bc}V^*_{q_aq_b}}{\sqrt{2}}\langle M \mid \bar{q_b} \gamma ^{\mu } (1-\gamma _{5}) q_a\nonumber \\{} & {} \qquad \times \mid 0\rangle \left\langle {\mathcal {B}}_f \left( \frac{3}{2}^+\right) \right| \bar{c} \gamma ^{\mu } (1-\gamma _{5}) b \left| {\mathcal {B}}_i\left( \frac{1}{2}^+\right) \right\rangle , \end{aligned}$$
(23)

where the term \(\langle M \mid \bar{q}_b \gamma ^{\mu } (1-\gamma _{5}) q_a \mid 0\rangle \) can be written as the decay constant of meson M (where \(q_a\) and \(q_b\) denote heavy or light quark flavors) and the second one \(\langle {\mathcal {B}}_f (\frac{3}{2}^+)\mid \bar{c} \gamma ^{\mu } (1-\gamma _{5}) b \mid {\mathcal {B}}_i(\frac{1}{2}^+) \rangle \) is determined by the form factors we obtained. The Fermi constant and CKM matrix elements are selected from Ref. [41]

$$\begin{aligned}{} & {} G_F=1.1664\times 10^{-5}~{\textrm{GeV}}^{-2}, \\{} & {} V_{cb}=0.0416, \quad V_{ud}=0.9738,\quad V_{us}=0.2257,\\{} & {} \quad V_{cd}=0.230, \quad V_{cs}=0.957. \end{aligned}$$

In Table 9, we present the results of the main two-body decay channels for \(\Sigma _{b}\) with the different value of \(\beta _{23}(\beta _{23}')\). The decay constants are derived from the Ref. [25]. From the Table 9 one also can notice that the widths increase with the decrease of the value of \(\beta _{23}\,(\beta _{23}')\) and the results with \(\beta _{23}=\beta _{23}'= 2.0 \beta _{u\bar{d}}\) are close to those with the heavy quark limit in Ref. [12].

3.3.2 Non-leptonic decays of doubly charmed baryon: \(\Xi _{cc}\rightarrow \Sigma ^*_c(\Xi ^*_c)+ M\)

The non-leptonic decays results of the doubly charmed baryon are listed in Table 10. As we can see from the table that the non-leptonic decay widths increase significantly with the decrease of the value of \(\beta _{1}\). A smaller value of \(\beta _{1}\) is more consistent with results in previous studies, such as Ref. [5]. Future experiments are needed to constrain the \(\beta \) parameters and test our model predictions.

Fig. 6
figure 6

Differential decay rates \(d\Gamma /d\omega \) for the decay \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} l \bar{\nu }_l\) with \(\beta _{1}= 2.9 \beta _{c\bar{c}}\)

Full size image
Table 7 The widths and polarization asymmetries of the transition \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} l \bar{\nu }_l\)
Full size table
Table 8 The widths and polarization asymmetries of the transition \(\Xi _{cc}\rightarrow \Xi _{c}^{*} l \bar{\nu }_l\)
Full size table
Table 9 The widths (in unit \(10^{10}~{\textrm{s}}^{-1}\)) of the non-leptonic decays \(\Sigma _b\rightarrow \Sigma _c^* + M\)
Full size table
Table 10 The nonleptonic decay widths (in unit \(10^{10}~{\textrm{s}}^{-1}\)) of the doubly charmed baryon to the single charmed baryon
Full size table

4 Conclusions and discussions

In this paper, we study the weak decays between two heavy baryons \({\mathcal {B}}_i(\frac{1}{2}^+)\rightarrow {\mathcal {B}}_f(\frac{3}{2}^+)\) with the three-quark picture of baryon in the LFQM. We derive the general form of transition amplitude, and obtain analytical expression of form factors for specific transition processes: \(\Sigma _{b}\rightarrow \Sigma _{c}^*\) and \(\Xi _{cc}\rightarrow \Sigma ^*_c(\Xi ^*_c)\). For weak decay of \(\Sigma _{b}\rightarrow \Sigma _{c}^*\), the b quark decays to c quark and ud subsystem with definite spin can be regarded as spectator in initial and final states. For the transition \(\Xi _{cc}\rightarrow \Sigma ^*_c(\Xi ^*_c)\), the cc system in initial state and the ud (su or sd) system in final state possess definite spins, but they are not spectators. In that case, quark rearrangement is adopted in our calculation of form factors. We then compute numerical values of these form factors with reasonable assumptions of model parameters. Last, we calculate rate of semi-leptonic and non-leptonic decays of \(\Sigma _{b}\) (\(\Sigma _b\rightarrow \Sigma _c^* l\bar{\nu }_l\), \(\Sigma _b\rightarrow \Sigma _c^* + M\)) and \(\Xi _{cc}\) \((\Xi _{cc}\rightarrow \Sigma _{c}^{*}(\Xi _{c}^{*}) l \bar{\nu }_l,\) \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} (\Xi _{c}^{*}) + M)\) based on numerical results of these form factors.

The weak decays of \(\Sigma _{b}\rightarrow \Sigma _{c}^*\) were studied in Ref. [12] where the quark–diquark picture was employed in the LFQM. Instead of quark–diquark picture, here we use the three-quark picture to revisit the transition of \(\Sigma _{b}\rightarrow \Sigma _{c}^*\). During the transition, the two light quarks serve as the spectators and maintain their all quantum numbers (spin, color). The associated momentum is also unchanged. The b quark in initial state transits to c quark by emitting two leptons mediated by gauge bosons \(W^{\pm }\).

We calculate the form factors for the transition \(\Sigma _{b}\rightarrow \Sigma _{c}^*\). The values of the \(f_i\) and \(g_i\) are similar to those obtained in Scheme II of Ref. [12] where the polarization of the [ud] diquark depends on the momentum of the diquark itself. Considering \(1^+\) diquark is a so-called bad diquark, i.e. the distance between the two quarks is larger than a good diquark case, we estimate \(\beta _{23}=\beta _{23}'< 2.9 \beta _{u\bar{d}}\) so we also set \(\beta _{23}=\beta _{23}'= 2.0 \beta _{u\bar{d}}\) and \(2.5 \beta _{u\bar{d}}\) to perform the same calculation. With computed form factors we evaluate the decay widths of the semi-leptonic \(\Sigma _b\rightarrow \Sigma _c^* l\bar{\nu }_l\) and non-leptonic \(\Sigma _b\rightarrow \Sigma _c^* +M\) with different values of \(\beta _{23}\). Comparing the results in other references, we find \(\beta _{23}\) and \(\beta _{23}'\) prefer a small value if we want our predictions close to those in the references. We also compute the semi-leptonic decay width of \(\Omega _{b}\rightarrow \Omega _{c}^* l\bar{\nu }_l\) and \(\Xi _{b}^{'}\rightarrow \Xi _{c}^* l\bar{\nu }_l\) with \(\beta _{23}=\beta _{23}'=2.0 \beta _{q_1\bar{q}_2}\).

For the weak decay of the doubly charmed baryon \(\Xi _{cc}\), a heavy quark c in the initial state decays to a light quark (s or d) in the final state through the weak interaction. However the cc pair in initial state and ud (us or ds) in the final state possess definite spin which can be regarded as diquarks. In this way, neither the initial physical diquark cc nor the final physical diquark ud (us or ds) are spectators. Therefore, the three-quark picture is more suitable here. We have rearranged the quarks in the initial and final states using the Racah transformation so the effective spectator can be isolated from the baryon. We calculate the form factors in the space-like region and then extend them to the time-like region (the physical region) by using the three-parameter form. Using these form factors we calculate the widths of semi-leptonic decay \(\Xi _{cc}\rightarrow \Sigma ^*_c(\Xi ^*_c) l \bar{\nu }_l\) and non-leptonic decay \(\Xi _{cc}\rightarrow \Sigma ^*_c(\Xi ^*_c)+M\), respectively. For the weak decay of \(\Xi _{cc}\rightarrow \Sigma ^*_c(\Xi ^*_c) l \bar{\nu }_l\), the decay width increases when the \(\beta _{1}\) value decreases. Our results on the semi-leptonic decay \(\Xi _{cc}\rightarrow \Sigma _{c}^{*} (\Xi _{c}^{*} l \bar{\nu }_l) l \bar{\nu }_l\) with \(\beta _{1}=2.0 \beta _{c\bar{c}}\) are close to the Ref. [5]. Future experiments will be necessary to precisely determine the parameters and test model predictions.