1 Introduction

The terminology “dirty” black hole that has been introduced by Matt Visser in [1] refers to black holes surrounded by some kind of classical matter such as electromagnetic or scalar fields. In the latter case, the black holes are also called “hairy”. Therefore, in this regard the Schwarzschild black hole which is characterized only by its mass is not dirty, however, the Reissner–Nordström black hole is a dirty one whose dirt is the electromagnetic static field. In a system of gravity coupled to electromagnetism, adding Dilaton [2,3,4], axion [5,6,7], Dilaton and axion [8] or Abelian Higgs field [9] results in some interesting dirty black holes. The effects of the dirtiness matter fields are on the physical structure of the black holes, for instance, in the Hawking temperature [1], gravitational wave astronomy [10], quasinormal modes [11,12,13,14] and tidal force [15]. In [16], Bronnikov and Zaslavskii have studied generic static spherically symmetric dirty/hairy black holes supported by an energy-momentum tensor expressed by \(T_{\mu }^{\nu }=diag\left( -\rho ,p_{r},p_{t},p_{t}\right) .\) In the latter equation, \(\rho \), \(p_{r},\) and \(p_{t}\), respectively, are the energy density, the radial and transverse pressure of the matter field which is supposed to be in equilibrium with the black hole. In particular, they investigated the equilibrium conditions between the black hole and the classical matter field surrounding the black hole in terms of the radial pressure to density ratio i.e., \(w=\frac{p_{r}}{\rho }\) [16]. Accordingly, the following two cases were reported upon which the equilibrium is possible: (i) \(\lim _{u\rightarrow u_{h}}w\left( u\right) \rightarrow -1\) and (ii) \(\lim _{u\rightarrow u_{h}}w\left( u\right) \rightarrow -1/\left( 1+2k\right) \) and \(\rho \left( u\right) \sim \left( u-u_{h}\right) ^{k}\), in which u is the radial coordinate, \(u_{h}\) is the horizon and \(k>0\). Furthermore, Bronnikov and Zaslavskii have generalized their results for an arbitrary static spacetime in [17] where general static black holes in matter were considered and the case for the nonlinear equation of state has been studied in [18].

Power-law Maxwell nonlinear electrodynamics (PM-NED) model was proposed in [19] and soon after became popular among the other models of NED [20,21,22,23,24,25,26,27,28,29,30,31]. The model is simply given by

$$\begin{aligned} {\mathcal {L}}=\alpha {\mathcal {F}}^{p} \end{aligned}$$
(1)

in which \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\) is the Maxwell invariant, \(p\ne \frac{ 1}{2},0\) is any real number and \(\alpha \) is a dimensionful coupling constant. While the reason for excluding \(p=0\) seems obvious it is not so clear for \(p=\frac{1}{2}.\) To see why let’s consider Maxwell’s nonlinear equation in flat spacetime for a point electric charge sitting at the origin. Maxwell’s field of such configuration is assumed to be

$$\begin{aligned} {\textbf{F}}=E\left( r\right) dt\wedge dr \end{aligned}$$
(2)

where \(E\left( r\right) \) is the radial electric field produced by the electric charge. Maxwell’s equation is given by

$$\begin{aligned} d\left( \frac{\partial {\mathcal {L}}}{\partial {\mathcal {F}}}\tilde{{\textbf{F}}} \right) =0 \end{aligned}$$
(3)

in which

$$\begin{aligned} {\tilde{{\textbf{F}}}}=E\left( r\right) r^{2}\sin \theta d\theta \wedge d\varphi \end{aligned}$$
(4)

is the dual electromagnetic field in the flat spherically symmetric spacetime described by the line element

$$\begin{aligned} ds^{2}=-dt^{2}+dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) . \end{aligned}$$
(5)

Evaluating the Maxwell invariants, one finds \(\mathcal {F}=-2E^{2},\) and consequently Eq. (3) implies

$$\begin{aligned} r^{2}E^{2p-1}=\text {const.,} \end{aligned}$$
(6)

that yields

$$\begin{aligned} E\left( r\right) =\frac{q}{r^{\frac{2}{2p-1}}},\text { (}q\text { is an integration constant).} \end{aligned}$$
(7)

Clearly, (6) is not satisfied for \(p=\frac{1}{2}\) which also causes \( E\left( r\right) \) is undetermined for \(p=\frac{1}{2}.\) Hence one has to exclude \(p=\frac{1}{2}\). We note that the same obstacle pops up when the spacetime is curved but spherically symmetric. Apparently, \(\mathcal {L}=\alpha \sqrt{ {\mathcal {F}}}\) needs special treatment and even a special name separately from the “power low”. In the literature, it is called as square-root nonlinear electrodynamics (SR-NED) model and it was even known before the power-law Maxwell’s model. By properly adjusting the coupling constant \( \alpha \), the electric and magnetic SR models are \(\mathcal {L}_{e}\sim \sqrt{-{\mathcal {F}}}\) and \(\mathcal {L}_{m}\sim \sqrt{{\mathcal {F}}}\) respectively. The magnetic model was proposed long ago by Nielsen and Olesen [32] in string theory and was used by ’t Hooft for introducing the confinement and linear potential for quarks [33]. Adding the electric square root term to the Maxwell linear theory results in an electric confinement field in the black hole spacetime [34,35,36,37,38,39,40]. The SR-NED model is also the strong field limit of the famous Born-Infeld (BI) [41, 42] model when \(\mathrm{E.B}=0.\)

Recently in [43], we have introduced a \(2+1+p\)–dimensional uniform magnetic brane in the context of gravity minimally coupled with the magnetic SR-NED. With \(p=1\) the solution reduces to the Bonnor-Melvin magnetic universe with a cosmological constant studied in [44]. In particular, we have shown that the spacetime is regular and supported by a uniform magnetic field in the sense that Maxwell’s invariant is uniform.

In this research, our aim is to introduce a dirty/hairy black hole solution in the context of Einstein’s gravity coupled to SR-NED and a Dilaton scalar field. In particular, we add the Dilaton field to come over the obstacle that appears in the PM-NED with \(p=1/2.\) We recall that the well-known Einstein–Maxwell–Dilaton theory admits black holes in the asymptotically flat [45, 46] and non-asymptotically flat regimes [47]. There are several research papers based on such a class of black holes that study the various aspects and applications of the theory. Furthermore, Einstein-NED-Dilaton theory with the BI-NED model has also received attention in the literature [48, 49]. Considering the value of such theories, we believe that the Einstein-SR-NED-Dilaton theory which represents the strong field regime of the later theory will find its applications probably in AdS/CFT correspondence. As we shall see the form of the black hole solution is rather simple which more looks like to be a correction in the Schwarzschild black hole. In other words, the effects of the Dilaton and SR-NED are combined in only one additional parameter which we shall call it its dirtiness parameter. Therefore, the final black hole consists of two parameters in comparison with the Schwarzschild black hole which consists of only one parameter.

Let us note that in the string theory, in the low energy limit, the problem is described by the action

$$\begin{aligned} I=\int d^{4}x\left( {\mathcal {R}}-\frac{1}{2}\left( \nabla \psi \right) ^{2}- \frac{1}{4}e^{-2\psi }F_{\mu \nu }F^{\mu \nu }\right) \end{aligned}$$
(8)

in which the Dilaton field is represented by \(\psi \) [50] (also [51]). In other words, the charged black holes in string theory are hairy and the hair/Dilaton is coupled nonminimally to the electromagnetic fields [52]. In the same context i.e., Einstein–Maxwell-Scalar/Phantom theory there have been black hole solutions that are either asymptotically flat or non-asymptotically flat [53,54,55,56,57,58,59,60,61].

The organization of the paper is as follows. In Sect. 2 we introduce the theory by giving the action and the field equations. Also, we solve the field equations exactly and present the results analytically in the same section. In Sect. 3 we study the general properties of the black hole. The physical properties consist of the energy conditions, the null geodesics, the mass of the black hole, the thermal stability analysis, and the first law of thermodynamics of the black hole and the causal structure. In Sect. 4 we study the tidal force of the dirty black hole and we conclude our paper in Sect. 5.

2 The action, the field equations and the solutions

We start with the Einstein-nonlinear electrodynamic-Dilaton action described by

$$\begin{aligned} I=\int d^{4}x\left( {\mathcal {R}}-\frac{1}{2}\partial _{\mu }\psi \partial ^{\mu }\psi +e^{-2b\psi }{\mathcal {L}}\left( {\mathcal {F}}\right) \right) \end{aligned}$$
(9)

in which \(b\ne 0\) is a free Dilaton parameter, \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\) is the electromagnetic invariant with \(\textbf{F}=F_{\mu \nu }dx^{\mu }\wedge dx^{\nu }\) the abelian electromagnetic field satisfying the Bianchi identity

$$\begin{aligned} d{\textbf{F}}=0 \end{aligned}$$
(10)

and \(\psi =\psi \left( r\right) \) is the Dilaton field. The nonlinear electromagnetic Lagrangian model is given by [32, 33]

$$\begin{aligned} {\mathcal {L}}\left( {\mathcal {F}}\right) =\alpha \sqrt{-{\mathcal {F}}} \end{aligned}$$
(11)

where \(\alpha \) is a dimensionful constant parameter. Variation of the action with respect to the metric tensor gives Einstein’s field equations expressed by

$$\begin{aligned} {\mathcal {R}}_{\mu }^{\nu }=2\partial _{\mu }\psi \partial ^{\nu }\psi +\frac{ \alpha e^{-2b\psi }}{\sqrt{-{\mathcal {F}}}}F_{\mu \lambda }F^{\nu \lambda }. \end{aligned}$$
(12)

Furthermore, variation of the action with respect to the Dilaton scalar field yields the Dilaton field equation given by

$$\begin{aligned} \nabla _{\mu }\nabla ^{\mu }\psi \left( r\right) =\frac{\alpha be^{-2b\psi } }{2}\sqrt{-{\mathcal {F}}} \end{aligned}$$
(13)

and finally, variation of the action with respect to the gauge potential yields the NED-Dilaton equation

$$\begin{aligned} d\left( \frac{e^{-2b\psi }}{\sqrt{-{\mathcal {F}}}}\tilde{{\textbf{F}}}\right) =0 \end{aligned}$$
(14)

in which \({\tilde{F}}\) is the dual field two-form of F. Our spacetime is static and spherically symmetric with the line element

$$\begin{aligned} ds^{2}=-f\left( r\right) dt^{2}+\frac{dr^{2}}{f\left( r\right) }+R\left( r\right) ^{2}d\Omega ^{2}, \end{aligned}$$
(15)

where \(d\Omega ^{2}=d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\) is the line element on the 2-sphere. The electromagnetic field is chosen to be a pure electric field produced by a point charge sitting at the origin expressed by

$$\begin{aligned} {\textbf{F}}=E\left( r\right) dt\wedge dr \end{aligned}$$
(16)

with its dual field obtained to be

$$\begin{aligned} \tilde{{\textbf{F}}}=E\left( r\right) R\left( r\right) ^{2}\sin \theta d\theta \wedge d\varphi . \end{aligned}$$
(17)

The electrodynamic invariant is obtained to be

$$\begin{aligned} {\mathcal {F}}=-2E\left( r\right) ^{2} \end{aligned}$$
(18)

upon which the NED-Dilaton equation (14) implies

$$\begin{aligned} R\left( r\right) ^{2}=R_{0}^{2}e^{2b\psi }. \end{aligned}$$
(19)

where \(R_{0}\) is an integration constant related to the electric charge of the electric monopole. We add that Eq. (19) has been found through the NED-Dilaton equation (14) explicitly. In a similar situation with linear or nonlinear electrodynamics in the literature, such a relation is usually considered in the form of an ansatz. For instance, we refer to [62, 63]. Another important observation regarding the NED-Dilaton equation (14) is that it doesn’t identify the form of the electric field E(r) and on the contrary E(r) canceled out. This, however, doesn’t mean that E(r) is an arbitrary function. As we shall see it will be identified from the other field equations, uniquely.

Einstein’s field equations are given by

$$\begin{aligned} {\mathcal {R}}_{t}^{t}= & {} -\frac{\alpha R_{0}^{2}E\left( r\right) }{\sqrt{2} R\left( r\right) ^{2}}, \end{aligned}$$
(20)
$$\begin{aligned} {\mathcal {R}}_{r}^{r}= & {} 2f\left( \psi ^{\prime }\right) ^{2}+{\mathcal {R}}_{t}^{t}, \end{aligned}$$
(21)

and

$$\begin{aligned} {\mathcal {R}}_{\theta }^{\theta }={\mathcal {R}}_{\varphi }^{\varphi }=0, \end{aligned}$$
(22)

where

$$\begin{aligned} {\mathcal {R}}_{t}^{t}= & {} -\frac{1}{2R}\left( Rf^{\prime \prime }+2f^{\prime }R^{\prime }\right) , \end{aligned}$$
(23)
$$\begin{aligned} {\mathcal {R}}_{r}^{r}= & {} -\frac{1}{2R}\left( Rf^{\prime \prime }+4fR^{\prime \prime }+2f^{\prime }R^{\prime }\right) \end{aligned}$$
(24)

and

$$\begin{aligned} {\mathcal {R}}_{\theta }^{\theta }={\mathcal {R}}_{\varphi }^{\varphi }=-\frac{1}{ R^{2}}\left( RR^{\prime }f^{\prime }+fRR^{\prime \prime }-1+\left( R^{\prime }\right) ^{2}f\right) \end{aligned}$$
(25)

are Ricci tensor’s components. Furthermore, the Dilaton field equation (13) explicitly becomes

$$\begin{aligned} \left( R^{2}f\psi ^{\prime }\right) ^{\prime }=\frac{\alpha bR_{0}^{2}\sqrt{2 }E\left( r\right) }{2}. \end{aligned}$$
(26)

Note that wherever needed we used (19) to simplify the equations. Next, we solve (22) for \(f\left( r\right) \) which is given by

$$\begin{aligned} f\left( r\right) =\frac{r-r_{0}}{RR^{\prime }} \end{aligned}$$
(27)

in which \(r_{0}\) is an integration constant. We are, then, left with three equations, namely, (20), (21) and (26), and three unknown functions i.e., \(R\left( r\right) ,\) \(E\left( r\right) \) and \(\psi \left( r\right) .\) Eq. (21) simply becomes

$$\begin{aligned} R^{\prime \prime }+R\psi ^{\prime 2}=0 \end{aligned}$$
(28)

which implies

$$\begin{aligned} \psi ^{\prime }=\pm \sqrt{-\frac{R^{\prime \prime }}{R}}, \end{aligned}$$
(29)

in which without loss of generality we continue with the positive \(\psi ^{\prime }.\) Furthermore, from Eq. (20) one obtains

$$\begin{aligned} E\left( r\right) =-\frac{\sqrt{2}R^{2}}{\alpha R_{0}^{2}}R_{t}^{t} \end{aligned}$$
(30)

which together with (29) simplify Eq. (26) into

$$\begin{aligned}{} & {} \left( 2b\sqrt{-R^{\prime \prime }R}-2R^{\prime }\right) \left( RR^{\prime }R^{\prime \prime \prime }\left( r-r_{0}\right) \right. \nonumber \\{} & {} \quad \left. {-}2R^{\prime \prime }\left( RR^{\prime \prime }\left( r{-}r_{0}\right) {-}\frac{1}{2}R^{\prime }\left( \left( r{-}r_{0}\right) R^{\prime }{+}2R\right) \right) \right) {=}0.\nonumber \\ \end{aligned}$$
(31)

The latter yields the following two possibilities:

$$\begin{aligned} 2b\sqrt{-R^{\prime \prime }R}-2R^{\prime }=0 \end{aligned}$$
(32)

or

$$\begin{aligned}{} & {} RR^{\prime }R^{\prime \prime \prime }\left( r-r_{0}\right) \nonumber \\{} & {} \quad -2R^{\prime \prime }\left( RR^{\prime \prime }\left( r-r_{0}\right) -\frac{1}{2} R^{\prime }\left( \left( r-r_{0}\right) R^{\prime }+2R\right) \right) =0. \nonumber \\ \end{aligned}$$
(33)

Considering the first equation i.e., (32) one finds

$$\begin{aligned} R\left( r\right) =(C_{1}r+C_{2})^{\frac{b^{2}}{b^{2}+1}} \end{aligned}$$
(34)

in which \(C_{1}\) and \(C_{2}\) are two integration constants. To keep the solution physical one has to assume \(C_{1}>0,C_{2}\ge 0\) such that \( -R^{\prime \prime }R\) remains positive. The latter equation further implies

$$\begin{aligned} E\left( r\right) =\frac{\sqrt{2}}{\alpha b^{2}R_{0}^{2}} \end{aligned}$$
(35)

which is uniform and

$$\begin{aligned} \psi =\psi _{0}+\frac{b}{b^{2}+1}\ln \left( C_{1}r+C_{2}\right) \end{aligned}$$
(36)

where \(\psi _{0}\) is an integration constant. Finally, the metric function \( f\left( r\right) \) is obtained from (27) to be

$$\begin{aligned} f\left( r\right) =\frac{\left( b^{2}+1\right) \left( r-r_{0}\right) }{ b^{2}C_{1}}\left( C_{1}r+C_{2}\right) ^{\frac{1-b^{2}}{1+b^{2}}}. \end{aligned}$$
(37)

Here we note that not only the radial electric field is constant/uniform but Maxwell’s invariant of the theory i.e., \(\mathcal {F}\) is also uniform and given by

$$\begin{aligned} {\mathcal {F}}=-2\left( \frac{\sqrt{2}}{\alpha b^{2}R_{0}^{2}}\right) ^{2}. \end{aligned}$$
(38)

The constant \(R_{0}\) can be identified through the solution (36) and its consistency with (19), which implies

$$\begin{aligned} R_{0}=e^{-b\psi _{0}}. \end{aligned}$$
(39)

As we can see, \(R_{0}\) doesn’t appear in the rest of the field equations and the solutions directly and its existence is through \(\psi _{0}.\) Concerning (36) shifting \(\psi \) by \(-\psi _{0}\) doesn’t change the kinematic term in the action (9). Moreover, in the term regarding the coupling of the NED and the Dilaton field i.e.,

$$\begin{aligned} e^{-2b\psi }{\mathcal {L}}\left( {\mathcal {F}}\right) =\frac{2}{b^{2}}\left( C_{1}r+C_{2}\right) ^{\frac{-b^{2}}{b^{2}+1}}, \end{aligned}$$
(40)

the effects of \(-\psi _{0}\) and \(R_{0}^{2}\) have also been canceled out, mutually. These all suggest that we set \(\psi _{0}=0\) which results in \( R_{0}=1.\)

Finally, the other possibility given by Eq. (33) admits an exact solution in the form

$$\begin{aligned} R\left( r\right) =C_{3}\sqrt{\frac{\left( 1+C_{1}^{2}\right) \left( r_{0}^{2}+C_{2}^{2}\right) }{4}+\frac{\left( C_{1}^{2}-1\right) r_{0}C_{2}}{2 }+r^{2}+r\left( C_{2}-r_{0}\right) }\exp \left( -\frac{1}{C_{1}}\arctan \left( \frac{2r+C_{2}-r_{0}}{C_{1}\left( C_{2}+r_{0}\right) }\right) \right) , \end{aligned}$$
(41)

where \(C_{1},\) \(C_{2}\) and \(C_{3}\) are some integration constant. Using (41) one obtains \(R^{\prime \prime }>0\) and consequently from (29) \( \psi ^{\prime }\left( r\right) ^{2}<0\) which implies that the scalar field is actually a phantom field. Hence we exclude this solution at least in this current study.

3 Physical properties of the solution

The exact solutions of the field equations can be summarized as follows. The electric field is radial with uniform magnitude given by Eq. (35) and the spacetime is found to be described by the line element

$$\begin{aligned} ds^{2}= & {} -\frac{\left( b^{2}+1\right) \left( r-r_{0}\right) }{b^{2}C_{1}} \left( C_{1}r+C_{2}\right) ^{\frac{1-b^{2}}{1+b^{2}}}dt^{2}\nonumber \\{} & {} +\frac{dr^{2}}{ \frac{\left( b^{2}+1\right) \left( r-r_{0}\right) }{b^{2}C_{1}}\left( C_{1}r+C_{2}\right) ^{\frac{1-b^{2}}{1+b^{2}}}}\nonumber \\{} & {} \quad +(C_{1}r+C_{2})^{\frac{2b^{2} }{b^{2}+1}}d\Omega ^{2}. \end{aligned}$$
(42)

To see the structure of this spacetime, we apply the following transformation \((C_{1}r+C_{2})^{\frac{b^{2}}{b^{2}+4}}\rightarrow R\) upon which (42) becomes

$$\begin{aligned} ds^{2}= & {} -\frac{\left( b^{2}+1\right) R^{\frac{1-b^{2}}{b^{2}}}}{b^{2}C_{1}} \left[ \frac{1}{C_{1}}\left( R^{\frac{b^{2}+1}{b^{2}}}-C_{2}\right) -r_{0} \right] dt^{2}\nonumber \\{} & {} +\frac{\left( \frac{b^{2}+1}{b^{2}C_{1}}\right) R^{\frac{ b^{2}+1}{b^{2}}}dR^{2}}{\left[ \frac{1}{C_{1}}\left( R^{\frac{b^{2}+1}{b^{2}} }-C_{2}\right) -r_{0}\right] }+R^{2}d\Omega ^{2}. \end{aligned}$$
(43)

This is easily seen that within redefinition of \(r_{0}\rightarrow -\frac{ C_{2}}{C_{1}}+\frac{R_{+}^{\frac{b^{2}+1}{b^{2}}}}{C_{1}}\) and \(t\rightarrow C_{1}t\) one can eliminate \(C_{2}\) such that (43) becomes

$$\begin{aligned} ds^{2}{} & {} =-\eta ^{2}\left( 1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}\right) R^{\frac{2}{b^{2}}}dt^{2}+\frac{\eta ^{2}dR^{2}}{1-\left( \frac{R_{+}}{R} \right) ^{\eta ^{2}}}\nonumber \\{} & {} \quad +R^{2}d\Omega ^{2} \end{aligned}$$
(44)

in which \(R_{+}\) is the new constant in place of \(r_{0},\) and \(\eta ^{2}= \frac{b^{2}+1}{b^{2}}\). The spacetime described by Eq. (44) is a black hole whose event horizon is located at \(R=R_{+}.\) On the other hand with the transformation \((C_{1}r+C_{2})^{\frac{b^{2}}{b^{2}+1}}\rightarrow R\) the scalar field simplifies as

$$\begin{aligned} \psi =\frac{1}{b}\ln R. \end{aligned}$$
(45)

We want to emphasize that \(b=0\) has already been excluded which removes our worries in (45). As a matter of fact, with \(b=0\) the nonlinear Maxwell equation (14) implies \(R=R_{0}\) which doesn’t satisfy Einstein’s equations.

3.1 Energy conditions

One of the physical constraints on any matter field supporting a black hole is the satisfying of the energy conditions. These energy conditions imply whether the matter fields are normal or exotic. Let us write Einstein’s equation in the following form (\(8\pi G=1\))

$$\begin{aligned} G_{\mu }^{\nu }=T_{\mu }^{\nu } \end{aligned}$$
(46)

in which the effective energy-momentum tensor is written as

$$\begin{aligned} T_{\mu }^{\nu }=diag\left[ -\rho ,P_{r},P_{t},P_{t}\right] \end{aligned}$$
(47)

where \(\rho ,\) \(P_{r},\) and \(P_{t}\) are the effective energy density, radial, and transverse pressure densities, respectively. Applying Einstein equation (46) and getting help from Eq. (12) with the line element given by Eq. (44), one obtains

$$\begin{aligned} \rho= & {} \frac{\eta ^{2}-1}{\eta ^{2}R^{2}}\left( 1-\left( \frac{R_{+}}{R} \right) ^{\eta ^{2}}\right) , \end{aligned}$$
(48)
$$\begin{aligned} P_{r}= & {} \frac{\eta ^{2}-1}{\eta ^{2}R^{2}}\left( 1-\left( \frac{R_{+}}{R} \right) ^{\eta ^{2}}\right) , \end{aligned}$$
(49)

and

$$\begin{aligned} P_{t}=\frac{\left( \eta ^{2}-1\right) ^{2}}{\eta ^{2}R^{2}}\left( 1-\frac{1}{ \eta ^{2}-1}\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}\right) . \end{aligned}$$
(50)

Thechnically, having the RHS of the Eqs. (48) and (49) the same is due to the solution of the field equations which is reflected in the line element (44). Recalling \(\eta ^{2}>1,\) outside the black hole where the energy-momentum tensor is described by (47), all components i.e., \(\rho ,\) \(P_{r},\) and \(P_{t}\) are positive definite. Therefore, the null-energy condition (NEC) implying \(\rho +P_{i}\ge 0\), the weak-energy condition (WEC) implying \(\rho \ge 0\) and \(\rho +P_{i}\ge 0,\) and the strong-energy condition (SEC) implying \(\rho +\sum P_{i}\ge 0\) are all satisfied. Furthermore, the effective energy-momentum tensor vanishes at the horizon indicating the regularity of the horizon [16].

In terms of the results obtained in [16], we would like to add that \(w= \frac{\rho }{P_{r}}=1\) which indicates the matter field is normal, however, both \(\rho \) and \(p_{r}\) become zero at the horizon.

3.2 Null geodesic

In this section, we would like to study the photons’ motion in the vicinity of the obtained black hole (44). The Lagrangian of a null-particle moving in the vicinity of the black hole (44) is given by

$$\begin{aligned} L= & {} -\frac{1}{2}\eta ^{2}\left( 1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}\right) R^{\frac{2}{b^{2}}}{\dot{t}}^{2}+\frac{1}{2}\frac{\eta ^{2}R^{2}}{ 1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}}\nonumber \\{} & {} +\frac{1}{2}R^{2}\left( {\dot{\theta }}^{2}+\sin ^{2}\theta {\dot{\varphi }}^{2}\right) \end{aligned}$$
(51)

in which a dot stands for the derivative with respect to an affine parameter. Considering the conserved energy

$$\begin{aligned} {\mathcal {E}}=-\frac{\partial L}{\partial {\dot{t}}}=\eta ^{2}\left( 1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}\right) R^{\frac{2}{b^{2}}}{\dot{t}} \end{aligned}$$
(52)

and the angular momentum

$$\begin{aligned} \ell =\frac{\partial L}{\partial {\dot{\varphi }}}=R^{2}\sin ^{2}\theta {\dot{\varphi }} \end{aligned}$$
(53)

together with the null condition i.e.,

$$\begin{aligned} g^{\mu \nu }{\dot{x}}_{\mu }{\dot{x}}_{\nu }=0 \end{aligned}$$
(54)

one obtains the main geodesic equation given by

$$\begin{aligned} R^{2\left( \eta ^{2}-1\right) }R^{2}+\frac{\ell ^{2}}{\eta ^{2}}\left( 1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}\right) R^{2\left( \eta ^{2}-2\right) }=\frac{{\mathcal {E}}^{2}}{\eta ^{4}}, \end{aligned}$$
(55)

where we have assumed \(\theta =\frac{\pi }{2}.\) Introducing \(r=R^{\eta ^{2}}\) the geodesic equation (55) simplifies significantly as expressed by

$$\begin{aligned} {\dot{r}}^{2}+\eta ^{2}\ell ^{2}\left( 1-\frac{r_{+}}{r}\right) r^{\frac{ 2\left( \eta ^{2}-2\right) }{\eta ^{2}}}={\mathcal {E}}^{2}. \end{aligned}$$
(56)

This is in analogy with the equation of motion of a unit-mass one-dimensional particle with mechanical energy \(\frac{1}{2}E^{2}\) and effective one-dimensional potential

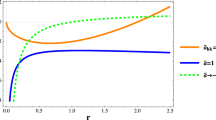
$$\begin{aligned} V_{eff}\left( r\right) =\frac{1}{2}\eta ^{2}\ell ^{2}\left( 1-\frac{r_{+}}{r} \right) r^{\frac{2\left( \eta ^{2}-2\right) }{\eta ^{2}}}. \end{aligned}$$
(57)

In Fig. 1 we plot \(\frac{V_{eff}\left( r\right) }{\frac{1}{2}\eta ^{2}\ell ^{2}}\) in terms of r for \(r_{+}=1\) and various values of \(\eta ^{2}.\) This figure displays that for \(\eta ^{2}\ge 2\) irrespective of the value of \(E^{2}\) and \(\ell ^{2}\) the photon falls into the singularity. On the other hand for \(\eta ^{2}<2\) the effective potential admits a maximum at \(r=r_{c}\) where

$$\begin{aligned} r_{c}=\frac{4-\eta ^{2}}{2\left( 2-\eta ^{2}\right) }r_{+} \end{aligned}$$
(58)

and

$$\begin{aligned} V_{eff}\left( r_{c}\right) =\frac{\eta ^{4}\ell ^{2}}{2\left( 4-\eta ^{2}\right) }\left( \frac{4-\eta ^{2}}{2\left( 2-\eta ^{2}\right) } r_{+}\right) ^{\frac{2\left( \eta ^{2}-2\right) }{\eta ^{2}}}. \end{aligned}$$
(59)

As it is depicted in Fig. 2, with \(\frac{{\mathcal {E}}^{2}}{2\ell ^{2} }<V_{eff}\left( r_{c}\right) \) and \(r_{0}<r_{c\text { }}\) the photon falls into the singularity. Furthermore, with \(\frac{{\mathcal {E}}^{2}}{2\ell ^{2}} <V_{eff}\left( r_{c}\right) \) and \(r_{0}>r_{c\text { }}\)the photon definitely bounces back to infinity. Finally, for \(\frac{{\mathcal {E}}^{2}}{2\ell ^{2}} >V_{eff}\left( r_{c}\right) \) the null particle either falls to the singularity or escapes to infinity depending on its initial condition.

Fig. 1
figure 1

The plots of the effective potential (57) versus r for \(r_{+}=1\) and \(\eta ^{2}=1.1,...,2.6\) with equal steps from bottom to top. The curve corresponding to \(\eta ^{2}=2.0\) is indicated

Full size image
Fig. 2
figure 2

A typical plot of the effective potential (57) versus r when \(\eta ^{2}<2.\) The potential admits an absulot maximum at \( r=r_{c}\) where \(V_{eff}\left( r_{c}\right) =\frac{\eta ^{4}\ell ^{2} }{2\left( 4-\eta ^{2}\right) }\left( \frac{4-\eta ^{2}}{ 2\left( 2-\eta ^{2}\right) }r_{+}\right) ^{\frac{2\left( \eta ^{2}-2\right) }{\eta ^{2}}}.\) The fate of a null particle moving in the vicinity of this potential depends strongly on its initial conditions and the conserved quantities. All cases are stated with arrows in different regions that are highlighted with different colors

Full size image

3.3 The mass of the black hole

The line element (44) represents a singular non-asymptotically flat black hole. Being non-asymptotically flat implies that the standard ADM mass is not defined for such a black hole. Hence we follow the Brown and York (BY) [47, 49, 64] formalism to introduce the so-called “quasilocal (QL) mass”. According to BY formalism, for a non-asymptotically flat line element

$$\begin{aligned} ds^{2}=-F\left( R\right) ^{2}dt^{2}+\frac{dR^{2}}{G\left( R\right) ^{2}} +R^{2}d\Omega ^{2} \end{aligned}$$
(60)

the QL mass is given by

$$\begin{aligned} M_{QL}=\lim _{R_{B}\rightarrow \infty }R_{B}F\left( R_{B}\right) \left[ G_{ref}\left( R_{B}\right) -G\left( R_{B}\right) \right] \end{aligned}$$
(61)

in which \(G_{ref}\left( R_{B}\right) \) is an arbitrary non-negative reference function, which yields the zero of the energy for the background spacetime, and \(R_{B}\) is the radius of the space-like hypersurface. For the line element (44) one finds \(F\left( R\right) ^{2}=\eta ^{2}\left( 1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}\right) R^{\frac{2}{b^{2}}},\) \( G\left( R\right) ^{2}=\frac{1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}}{ \eta ^{2}}\) and \(G_{ref}\left( R_{B}\right) ^{2}=\frac{1}{\eta ^{2}}\) which result in

$$\begin{aligned} M_{QL}=\frac{1}{2}R_{+}^{\eta ^{2}}. \end{aligned}$$
(62)

The line element therefore becomes

$$\begin{aligned} ds^{2}=-\eta ^{2}\left( 1-\frac{2M_{QL}}{R^{\eta ^{2}}}\right) R^{\frac{2}{ b^{2}}}dt^{2}+\frac{\eta ^{2}dR^{2}}{1-\frac{2M_{QL}}{R^{\eta ^{2}}}} +R^{2}d\Omega ^{2}. \nonumber \\ \end{aligned}$$
(63)

The latter line element gives the correct spacetime limit as \(b\rightarrow \infty \) such that \(\eta ^{2}\rightarrow 1\), \(E\left( r\right) \rightarrow 0\) and the solution becomes the standard Schwarzschild black hole and \(M_{QL}\) turns to be identified as the ADM mass of the black hole. Moreover, by scaling the time t and the radial coordinate R the latter line element becomes

$$\begin{aligned} ds^{2}= & {} -\left( 1-\frac{2M}{\rho ^{\eta ^{2}}}\right) \rho ^{2\left( \eta ^{2}-1\right) }d\tau ^{2}+\left( 1-\frac{2M}{\rho ^{\eta ^{2}}}\right) ^{-1}d\rho ^{2}\nonumber \\{} & {} +\varkappa ^{2}\rho ^{2}d\Omega ^{2} \end{aligned}$$
(64)

in which \(\rho =\eta R,\) \(M=M_{QL}\eta ^{\eta ^{2}},\) \(\tau =\eta ^{1-\frac{2 }{b^{2}}}t\) and \(\varkappa ^{2}=\frac{1}{\eta ^{2}}\). Having known that \( \eta ^{2}=\frac{b^{2}+1}{b^{2}}>1\), (64) clearly implies that the Dilaton field causes a sort of conical structure with the deficit angle represented by \(\varkappa ^{2}<1.\)

3.4 Thermal stability and the first law

To investigate the thermal stability of the black hole (63), we calculate the Hawking temperature defined by

$$\begin{aligned} T_{H}=\left( -\frac{g_{tt}^{\prime }}{4\pi \sqrt{-g_{tt}g_{rr}}}\right) _{R=R_{+}}=\frac{\eta ^{2}}{4\pi }R_{+}^{\eta ^{2}-2} \end{aligned}$$
(65)

and upon applying the so-called area law [65], the entropy of the black hole is also given by

$$\begin{aligned} S=\pi R_{+}^{2}. \end{aligned}$$
(66)

Finally, we calculate the specific heat capacity defined by

$$\begin{aligned} C=T_{H}\frac{\partial S}{\partial T_{H}}=\frac{2\pi }{\eta ^{2}-2}R_{+}^{2}. \end{aligned}$$
(67)

The black hole is considered to be thermally stable if both \(T_{H}\) and C are positive. Therefore with \(\eta ^{2}-2>0\) (\(b^{2}<1\)) the black hole is thermally stable. In accordances with (65), with \(\eta ^{2}=2\) the Hawking temperature becomes constant which justifies the infinite heat capacity.

Finally, knowing that in the definition of quasilocal mass i.e., (61) \(\eta ^{2}\) is related to the background, the first law of thermodynamics of the black hole simply becomes

$$\begin{aligned} dM_{QL}=T_{H}dS \end{aligned}$$
(68)

where the variations of \(M_{QL}\) and S are with respect to \(R_{+}\) [49].

3.5 The spacetime structure

The spacetime described by the line element (64) is rather new in the literature and deserves to be more investigated from the spacetime structure aspect. The solution obviously is a black hole with an event horizon located at \(\rho =\rho _{+}=\left( 2\,M\right) ^{\frac{1}{\eta ^{2}}}\)such that it may be written as

$$\begin{aligned} ds^{2}= & {} -\left( \rho ^{\eta ^{2}}-\rho _{+}^{\eta ^{2}}\right) \rho ^{\eta ^{2}-2}d\tau ^{2}\nonumber \\{} & {} +\frac{\rho ^{\eta ^{2}}}{\rho ^{\eta ^{2}}-\rho _{+}^{\eta ^{2}}}d\rho ^{2}+\varkappa ^{2}\rho ^{2}d\Omega ^{2}. \end{aligned}$$
(69)

After transforming \(r=\varkappa \rho \) and redefinition of time one finds

$$\begin{aligned} ds^{2}= & {} -\left( r^{\eta ^{2}}-r_{+}^{\eta ^{2}}\right) r^{\eta ^{2}-2}dt^{2}\nonumber \\{} & {} + \frac{r^{\eta ^{2}}}{\varkappa ^{2}\left( r^{\eta ^{2}}-r_{+}^{\eta ^{2}}\right) }dr^{2}+r^{2}d\Omega ^{2} \end{aligned}$$
(70)

in which \(0<r<\infty \) and \(-\infty<t<\infty \). The Kretschmann scalar of the latter spacetime is given by

$$\begin{aligned} {\mathcal {K}}=\frac{\omega _{0}}{r^{4}}\frac{\omega _{1}}{r^{4+\eta ^{2}}}+ \frac{\omega _{2}}{r^{4+2\eta ^{2}}} \end{aligned}$$
(71)

where \(\omega _{i}\) are some constants. We recall that \(1<\eta ^{2}=\frac{ b^{2}+1}{b^{2}}\) which implies the origin \(r=0\) is a singular point. To find the nature of this curvature singularity we apply the so-called conformal compactification. Hence, we obtain the conformal/tortoise radial coordinate defined by

$$\begin{aligned} r_{*}=\int \sqrt{-\frac{g_{rr}}{g_{tt}}}dr=\frac{1}{\chi }\int \frac{r}{ r^{\eta ^{2}}-r_{+}^{\eta ^{2}}}dr. \end{aligned}$$
(72)

We observe that the conformal/tortoise radial coordinate \(r_{*}\) depends on \(\eta ^{2}\). For technical reasons, we set \(\eta ^{2}=\frac{3}{2}\) as well as 2 and continue our investigation accordingly. In this configurations one finds

$$\begin{aligned} r_{*}=\left\{ \begin{array}{ll} \frac{1}{\chi }\left\{ 2\sqrt{r}+\frac{2}{3}\sqrt{r_{+}}\ln \left| \sqrt{ r}-\sqrt{r_{+}}\right| -\frac{1}{3}\sqrt{r_{+}}\ln \left| r+r_{+}+ \sqrt{r_{+}r}\right| -\frac{2\sqrt{3r_{+}}}{3}\arctan \left( \frac{2 \sqrt{r}+\sqrt{r_{+}}}{\sqrt{3r_{+}}}\right) \right\} , &{} {\small \eta }^{2} {\small =}\frac{3}{2} \\ \frac{1}{2\chi }\ln \left| r^{2}-r_{+}^{2}\right| , &{} {\small \eta } ^{2}{\small =}2 \end{array} \right. \end{aligned}$$
(73)

where \(-\infty<r_{*}<\infty \). Next, we define the retarded and advanced coordinates i.e., \(u=t-r_{*}\) and \(v=t+r_{*}\) (\(-\infty<u<v<\infty \)) such that (70) becomes

$$\begin{aligned} ds^{2}=\left\{ \begin{array}{cc} -r\left( 1-\left( \frac{r_{+}}{r}\right) ^{3/2}\right) dudv+r^{2}d\Omega ^{2}, &{} {\small \eta }^{2}{\small =}\frac{3}{2} \\ -r^{2}\left( 1-\left( \frac{r_{+}}{r}\right) ^{2}\right) dudv+r^{2}d\Omega ^{2}, &{} {\small \eta }^{2}{\small =}2 \end{array} \right. . \end{aligned}$$
(74)

Next, we define the Kruskal–Szekeres coordinate

$$\begin{aligned} U=\left\{ \begin{array}{cc} \frac{4\sqrt{r_{+}}}{3\chi }\exp \left( -\frac{3\chi }{4\sqrt{r_{+}}} u\right) , &{} {\small \eta }^{2}{\small =}\frac{3}{2} \\ \frac{1}{\chi }\exp \left( -\chi u\right) , &{} {\small \eta }^{2}{\small =}2 \end{array} \right. \end{aligned}$$
(75)

and

$$\begin{aligned} V=\left\{ \begin{array}{cc} \frac{4\sqrt{r_{+}}}{3\chi }\exp \left( \frac{3\chi }{4\sqrt{r_{+}}}v\right) , &{} {\small \eta }^{2}{\small =}\frac{3}{2} \\ \frac{1}{\chi }\exp \left( \chi v\right) , &{} {\small \eta }^{2}{\small =}2 \end{array} \right. \end{aligned}$$
(76)

such that (\(r\ge r_{+}\))

$$\begin{aligned} UV=\left\{ \begin{array}{cc} \frac{16r_{+}}{9\chi ^{2}}\frac{1-\sqrt{r_{+}/r}}{\sqrt{1+r_{+}/r+\sqrt{ r_{+}/r}}}\exp \left( 3\sqrt{\frac{r}{r_{+}}}-\sqrt{3}\arctan \left( \frac{2 \sqrt{r/r_{+}}+1}{\sqrt{3}}\right) \right) , &{} {\small \eta }^{2}{\small =} \frac{3}{2} \\ \frac{\left| r^{2}-r_{+}^{2}\right| }{\chi ^{2}}, &{} {\small \eta } ^{2}{\small =}2 \end{array} \right. , \end{aligned}$$
(77)

and \(0<U<V<\infty \). The line element, hence, becomes

$$\begin{aligned} ds^{2}=\left\{ \begin{array}{ll} r\left( 1+r_{+}/r+\sqrt{r_{+}/r}\right) ^{3/2}e^{-3\sqrt{\frac{r}{r_{+}}}}e^{ \sqrt{3}\arctan \left( \frac{2\sqrt{r/r_{+}}+1}{\sqrt{3}}\right) }dUdV+r^{2}d\Omega ^{2}, &{} {\small \eta }^{2}{\small =}\frac{3}{2} \\ dUdV+r^{2}d\Omega ^{2}, &{} {\small \eta }^{2}{\small =}2 \end{array} \right. \end{aligned}$$
(78)

which is regular at \(r=r_{+}\) and singular at \(r=0.\) Introducing

$$\begin{aligned} U=X-T \end{aligned}$$
(79)

and

$$\begin{aligned} V=X+T \end{aligned}$$
(80)

transforms the line element into

$$\begin{aligned} ds^{2}=\left\{ \begin{array}{ll} r\left( 1+r_{+}/r+\sqrt{r_{+}/r}\right) ^{3/2}e^{-3\sqrt{\frac{r}{r_{+}}}}e^{ \sqrt{3}\arctan \left( \frac{2\sqrt{r/r_{+}}+1}{\sqrt{3}}\right) }\left( -dT^{2}+dX^{2}\right) +r^{2}d\Omega ^{2}, &{} {\small \eta }^{2}{\small =} \frac{3}{2} \\ -dT^{2}+dX^{2}+r^{2}d\Omega ^{2}, &{} {\small \eta }^{2}{\small =}2 \end{array} \right. \end{aligned}$$
(81)

such that

$$\begin{aligned} X^{2}-T^{2}=UV \end{aligned}$$
(82)

given in Eq. (77). We see that the singularity at \(r=0\) corresponds to hyperbola

$$\begin{aligned} T^{2}-X^{2}=\left\{ \begin{array}{cc} \left( \frac{4}{3\chi }\right) ^{2}e^{\left( -\frac{\sqrt{3}\pi }{6}\right) }r_{+}, &{} {\small \eta }^{2}{\small =}\frac{3}{2} \\ \frac{r_{+}^{2}}{\chi ^{2}}, &{} {\small \eta }^{2}{\small =}2 \end{array} \right. \end{aligned}$$
(83)

on the TX-plane and is valid for even \(r>0\) which implies

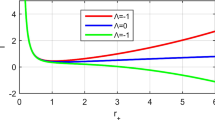
$$\begin{aligned} T^{2}-X^{2}\le \left\{ \begin{array}{cc} \left( \frac{4}{3\chi }\right) ^{2}e^{\left( -\frac{\sqrt{3}\pi }{6}\right) }r_{+}, &{} {\small \eta }^{2}{\small =}\frac{3}{2} \\ \frac{r_{+}^{2}}{\chi ^{2}}, &{} {\small \eta }^{2}{\small =}2 \end{array} \right. . \end{aligned}$$
(84)

In Figs. 3 and 4 we plot the Kruskal–Szekeres diagram and the maximally-extended Carter–Penrose diagram of the black hole spacetime (70) with \(\eta ^{2}=\frac{3}{2}\) and \(\eta ^{2}=2\) that is also applicable for an arbitrary \(\eta ^{2}\). The nature of the singularity at the center of the black hole is spacelike that is the same as the Schwarzschild black hole.

Fig. 3
figure 3

Kruskal–Szekeres diagram of the black hole spacetime (70) with \({\small \eta }^{2}{\small =}\frac{3}{2}\) and \({\small \eta }^{2}{\small =}2\)

Full size image

4 Tidal forces

In this section, we study the so-called tidal force which is an indication of the interaction between a black hole with its surroundings. When an extensive object falls under the gravitational attraction of a black hole, the tidal forces exerted on the object on its geodesic cause either stretching or compressing in different directions. For instance, when such an object falls radially toward the Schwarzschild black hole, it is stretched in the radial direction while compressed in the angular/transverse directions [66,67,68,69]. Unlike the Schwarzschild black hole which is surrounded by a vacuum, in the well-known Reissner-Nordström dirty black hole for the same radially falling extensive object, the tidal forces vanish at some certain radius and its nature changes from stretching to compressing and vice-versa [70]. Similar properties have also been reported in some other black hole spacetimes where the sign-turning point for the tidal force is either outside the event horizon or inside [70,71,72,73].

In [15] the tidal force tensor in the tetrad basis attached to a radially infalling observer has been calculated for a dirty black hole with the line element

$$\begin{aligned} ds^{2}= & {} -f\left( R\right) dt^{2}+\frac{1}{1-\frac{B\left( R\right) }{R}} dR^{2}\nonumber \\{} & {} +R^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) . \end{aligned}$$
(85)

In accordance with the results of [15], the tidal force tensor is given by

$$\begin{aligned} K_{\hat{\mu }}^{\hat{\nu }}=diag\left[ 0,K_{1},K_{2},K_{3}\right] \end{aligned}$$
(86)

in which

$$\begin{aligned} K_{1}= & {} \frac{2B}{R^{3}}-\frac{1}{2}\left( \rho +P_{r}-2P_{t}\right) \end{aligned}$$
(87)
$$\begin{aligned} K_{2}= & {} K_{3}=-\frac{B}{R^{3}}+\frac{1}{2}\rho -\frac{E^{2}}{2f}\left( \rho +P_{r}\right) \end{aligned}$$
(88)

with E the energy per unit mass and \(\rho ,\) \(P_{r}\), and \(P_{t}\) given in (48)–(50). Note that the unit convention in [15] is \( G=1.\) Herein the line element is given by (44) such that

$$\begin{aligned} f\left( R\right) =\eta ^{2}\left( 1-\left( \frac{R_{+}}{R}\right) ^{\eta ^{2}}\right) R^{2\left( \eta ^{2}-1\right) } \end{aligned}$$
(89)
Fig. 4
figure 4

Carter-penrose diagram of the black hole spacetime (70 ) with \({\small \eta }^{2}{\small =}\frac{3}{2}\) and \({\small \eta }^{2}{\small =}2\)

Full size image

and

$$\begin{aligned} B\left( R\right) =\left( 1-\frac{1}{\eta ^{2}}\left( 1-\left( \frac{R_{+}}{R} \right) ^{\eta ^{2}}\right) \right) \frac{R}{2}. \end{aligned}$$
(90)
Fig. 5
figure 5

The radial tidal force in terms of \(\frac{R}{R_{+}}\) and \(\eta \). This figure implies the radial tidal force is always positive and in terms of \(\frac{R}{R_{+}}\) it is a monotonic decreasing function that approaches zero. On the other hand for a given \(\frac{R}{ R_{+}}\), the radial tidal force first decreases in terms of \(\eta \) and then increases

Full size image
Fig. 6
figure 6

The angular tidal force in terms of \(\frac{R}{R_{+}}\) and \(\eta \). The angular tidal force is always negative and in terms of \(\frac{R}{R_{+}}\) for a given \(\eta \), it is a monotonic increasing function that approaches zero. On the other hand for a given \(\frac{R}{ R_{+}}\), the angular tidal force first decreases in terms of \(\eta \) and then increases

Full size image

In Figs. 5 and 6 we plot \(K_{1}\) and \(K_{2}\) in terms of \( \frac{R}{R_{+}}\) (\(\frac{R}{R_{+}}>1\)) and \(\eta \) (\(1<\eta \)) and \(E=1.\) We observe that similar to the tidal force in a Schwarzschild black hole, the radial tidal force is tensile and the transverse is compressive. With increasing the value of \(\eta \) first both forces decrease and then increase and both approach zero at infinity.

5 Conclusion

In the framework of Einstein’s gravity coupled to SR-NED as well as a Dilaton field, we managed to solve the field equations exactly and obtain a black hole solution characterized by two parameters namely, \(R_{+}\) and b. While the latter is a theory constant representing the Dilaton the former is an integration. This non-asymptotically flat black hole is singular at its center where the electric charge is placed. The electric field is radial but uniform in the sense that the electromagnetic invariant is a constant. Since the ADM mass is not defined for non-asymptotically flat black holes, we applied BY formalism to obtain the QL conserved mass expressed as \(M_{QL}\) such that in the Schwarzschild limit (\(\eta ^{2}=1\)), it coincides with the ADM mass of the Schwarzschild black hole. Furthermore, we studied the null geodesic on the equatorial plane and showed that the fate of photons depends on the ratio \(\frac{{\mathcal {E}}^{2}}{\ell ^{2}}\) where E and \(\ell \) are the conserved energy and angular momentum. Moreover, we investigated the thermal stability of the black hole and observed that with \(0<b^{2}<1\) (\( 2<\eta ^{2}\)) the black hole is thermally stable in the sense that both the Hawking temperature and the heat capacity are positive. As it was stated in [16], black holes are not forming in the empty space and rather are surrounded by matter fields that are either falling into the black holes or are in equilibrium with it. The black hole presented in this paper is a typical example of such a black hole called a “dirty” black hole supported by normal/regular matter. The mathematical structure of the spacetime is kind of modified Schwarzschild black hole because with \(\eta ^{2}=1\) it coincides with the Schwarzschild black hole. Therefore, one may call this solution the natural dirty Schwarzschild black hole. Concerning what we have done in this study we may consider the following to be the novelty of our paper: (i) We filled the gap of the PM-NED model which has so far been considered with \(p\ne \frac{1}{2}\). (ii) The black hole in the context of our study has been found to be a new generalization of the Schwarzschild black hole in a practically simple form. We have shown that its casual structure is similar to the Schwarzschild black hole as well. (iii) The dirty-Schwarzschild – this is what we named our solution – the black hole is thermally stable for \(2<\eta ^{2}\). (iv) We calculated the tidal force which clearly is in agreement with the Schwarzschild black hole although its minimum value takes place in \(\eta ^{2}\ne 1,\) recalling that \(\eta ^{2}=1\) is the Schwarzschild limit.