Scrutinizing a hidden SM-like gauge model with corrections to oblique parameters

Abstract

In view of the recent high precision measurement of the Standard Model W boson mass at the CDF II detector, we compute the contributions to the oblique parameters S, T and U coming from the two additional Higgs doublets (one inert and one hidden) as well as the hidden neutral dark gauge bosons and extra heavy fermions in the gauged two-Higgs-doublet model (G2HDM). While the effects from the hidden Higgs doublet and new heavy fermions are found to be minuscule, the hidden gauge sector $SU(2)_H \times U(1)_X$ with gauge coupling strength $\gtrsim 10^{-2}$ and gauge boson mass $\gtrsim 100$ GeV can readily explain the W boson mass anomaly but is nevertheless excluded by the dilepton high-mass resonance searches at the Large Hadron Collider. On the other hand, the new global fits to the oblique parameters due to the new W boson mass measurement can give discernible impacts on the mass splitting and mixing angle for the inert Higgs doublet in G2HDM. We also study the impact on the signal strength of diphoton mode of the 125 GeV Higgs boson $h \rightarrow \gamma \gamma$ and the detectability of the yet to be observed process $h \rightarrow Z \gamma$ at the High Luminosity Large Hadron Collider. Current constraints for the dark matter candidate $W^\prime$ including the dark matter relic density, dark matter direct detections and invisible Higgs decays are also taken into account in this study.

1 Introduction

Based on the data with an integrated luminosity of 8.8 fb$^{-1}$ collected by the CDF II detector between 2002 and 2011, after over 10 years of dedicated analysis, the CDF Collaboration at the Tevatron Collider has recently unveiled a high-precision direct measurement of the standard model (SM) W boson mass. The reported result is [1]

$$\begin{aligned} m_W (\mathrm{CDF\; II}) = 80,433.5 \pm 9.4 \; \mathrm{MeV/}c^2 , \end{aligned}$$

(1)

which is $\sim 7 \sigma$ away from the SM prediction from electroweak (EW) global fits [2]

$$\begin{aligned} m_W (\mathrm{SM - \; Global \, Fits}) = 80,359.1 \pm 5.2 \; \mathrm{MeV/}c^2 . \end{aligned}$$

(2)

The CDF result (1) also represents a $\sim 3 \sigma$ deviation from other direct measurements from the more recent ATLAS [3] and LHCb [4] experiments. This immediately stirs a great deal of excitement in the field and triggers many subsequent studies. This recent measurement has significant implications for the electroweak precision global fit [5,6,7]. Specifically, the fit can accommodate the recent CDF $m_W$ measurement by incorporating a large and nonzero value of the U parameter or a large positive value of T parameter in the case of $U = 0$. These two parameters T and U, together with a third parameter S, are well-known in the community of electroweak precision test as oblique parameters [8]. We will briefly review them later in Sect. 3. We note that the deviation of the CDF W boson mass measurement with the global fit only shifts slightly from $7\sigma$ to 6$\sigma$ if a theoretical calculation tool used by CDF is updated by a more recent version [9]. More important and optimistic view is that the global fit could entail new physics (NP) beyond the SM (BSM).

While combined result of the measurements from LEP, Tevatron and ATLAS are still lacking, pending on evaluation of uncertainty correlations [1, 10], and the new CDF result of $m_W$ is needed to be independently confirmed, BSM enthusiast has already offering various NP interpretations of the new CDF result. See for example, Refs. [11,12,13] for extra U(1) implications, [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] for extended or composite Higgs sectors, [30, 31] for SMEFT, [32, 33] for lepto-quark, [34, 35] for dark matter (DM) models, [36,37,38,39,40] for low energy supersymmetry, and [41,42,43,44] for grand unification, etc. Another interesting point to support the BSM physics as pointed out in [45] is that the hadronic uncertainties in the fine structure constant and hadronic vacuum polarization that affects the SM W boson mass and muon anomalous magnetic dipole moment respectively are anti-correlated with each other.

In this work, we study the impact of the new CDF result to the extra particle mass spectra in the gauged two-Higgs-doublet model (G2HDM) first proposed in [46] and explored further in [47,48,49,50,51,52,53,54,55,56]. G2HDM is a gauged DM model based on the extended electroweak gauge group $G_{\textrm{G2HDM}} = SU(2)_L \times U(1)_Y \times SU(2)_H \times U(1)_X$. The extra gauge group $SU(2)_H \times U(1)_X$ represents the dark gauge sector interacting feebly with the visible SM sector, in the sense that the new gauge couplings $g_H$ and $g_X$ are much smaller than the SM electroweak gauge couplings g and $g^\prime$, as suggested by our recent detailed studies [54, 55]. Additional Higgses and heavy fermions must be included in G2HDM to make it phenomenologically viable and free from gauge and gravitational anomalies. The crucial idea of G2HDM is that the usual two Higgs doublets ($H_1$ and $H_2$) in general two-Higgs-doublet model (2HDM) is lumped together in a 2 dimensional spinor representation $H= (H_1 \, H_2)^{\textrm{T}}$ of a hidden local $SU(2)_H$ gauge group. Hence we christened the model as gauged 2HDM. Nevertheless, a hidden doublet $\Phi _H$ of $SU(2)_H$ is necessarily introduced so as to provide realistic Yukawa couplings and mass spectra for the extra vector bosons and fermions in the model. Effectively we have a tailor-made 3HDM in the scalar sector.

One distinctive feature of the model is that there is no need to impose an ad hoc discrete $Z_2$ symmetry to stabilize the DM. There is a hidden h-parity in the model [52], admitted readily once one writes down all possible gauge invariant and renormalizable interactions, that will guarantee the lightest h-parity odd particle to be the DM candidate, provided that it is not broken spontaneously.¹ Another interesting feature is that the new gauge bosons $W^{\prime \, (p,m)} \equiv (W^\prime _1 \mp i W^\prime _2)/\sqrt{2}$ are electrically neutral and don’t mix with the SM $W^\pm$ bosons. They are also h-parity odd and can be the DM candidate. A scenario of sub-GeV low mass $W^{\prime \, (p,m) }$ as DM was studied in [54, 55]. In this work, we will turn our attention to the scenario of $W^{\prime \, (p,m) }$ as DM candidate with a wider mass range.

The G2HDM model is renormalizable and anomaly-free. Furthermore, the model has a range of intriguing phenomenological implications, including the emergence of new signals from extra gauge bosons at the LHC [50], the enhancement of di-Higgs production [51], and the possibility of charged lepton flavor violation processes [56]. Recent studies also suggest that the G2HDM model has great potential to be probed in both dark matter and dark photon search experiments [54, 55]. In addition, the DM candidate $W^{\prime \, (p,m)}$ has non-abelian and complex nature which can make it to be both asymmetric and self-interacting DM. These features of the $W^{\prime \, (p,m)}$ in G2HDM as DM candidate may be interesting to explore in the future so as to resolve some well-known issues such as the too-big-to-fail and core-cusp problems encountered in the conventional WIMP cold dark matter scenario [57] in astrophysics and cosmology.

In the next Sect. 2, we will briefly review the particle content in the minimal G2HDM [54, 55], their masses and interactions that are relevant to our study. In Sect. 3, we remind ourselves by reviewing the Peskin-Takeuchi oblique parameters [8] that not only entered in the art of global fit analysis which correlates all electroweak observables but also provided important constraints on NP models. In Sect. 4, we compute the new contributions to the oblique parameters from the mixings of the neutral gauge bosons (Sect. 4.1), extended Higgs sector (Sects. 4.2 and 4.3) and extra heavy fermions (Sect. 4.4) in G2HDM. In Sect. 5, we present and discuss our numerical results by including the new contributions to the oblique parameters to compare with the updated global fits [6]. In addition, we will take the opportunity in this section to explore the detectability of the process $h \rightarrow Z \gamma$ in the High Luminosity Large Hadron Collider (HL-LHC). Conclusions are given in Sect. 6. We reserve an appendix for the analytical expressions of the one-loop amplitudes of the two processes $h_i \rightarrow \gamma \gamma$ ($i=1,2$) and $h_i \rightarrow Z_j \gamma$ ($i=1,2;j=1,2,3$) in G2HDM, where $h_1$ and $Z_1$ are identified as the SM 125 GeV Higgs scalar (h) and 91 GeV Z vector boson respectively.

2 Model setup

In this section, we will briefly review the minimal G2HDM. The original model was introduced in Ref. [46], and various refinements [48, 49, 52] and collider implications [47, 50, 51] were pursued subsequently with the same particle content as the original model. As advocated recently in [54, 55], we will drop the triplet field $\Delta _H$ of the extra $SU(2)_H$. This is mainly due to the fact that realistic mass spectra for all particles in G2HDM can be achieved without including the triplet. This important fact has been overlooked in the original work [46] because a couple of terms were missing in the scalar potential. Additionally, removing the triplet field results in a reduction of 6 arbitrary parameters in the scalar potential.

We will refer this as the minimal G2HDM in what follows. The quantum numbers of the matter particles in G2HDM under $SU(3)_C \times SU(2)_L \times SU(2)_H \times U(1)_Y \times U(1)_X$ are ²

Scalars:

$$\begin{aligned} H= & {} \left( H_1 \;\; H_2 \right) ^{\textrm{T}} \sim \left( \textbf{1}, \textbf{2}, \textbf{2}, \frac{1}{2}, { \frac{1}{2} }\right) , \;\\ \Phi _H= & {} \left( \Phi _1 \;\; \Phi _2 \right) ^{\textrm{T}} \sim \left( \textbf{1}, \textbf{1}, \textbf{2}, 0, { \frac{1}{2} } \right) \;; \end{aligned}$$

Spin 1/2 Fermions:

Quarks

$$\begin{aligned} Q_L= & {} \left( u_L \;\; d_L \right) ^{\textrm{T}} \sim \left( \textbf{3}, \textbf{2}, \textbf{1}, \frac{1}{6}, 0 \right) , \;\\ U_R= & {} \left( u_R \;\; u^H_R \right) ^{\textrm{T}} \sim \left( \textbf{3}, \textbf{1}, \textbf{2}, \frac{2}{3}, \frac{1}{2} \right) ,\\ D_R= & {} \left( d^H_R \;\; d_R \right) ^{\textrm{T}} \sim \left( \textbf{3}, \textbf{1}, \textbf{2}, -\frac{1}{3}, - \frac{1}{2} \right) \;;\\ u_L^H\sim & {} \left( \textbf{3}, \textbf{1}, \textbf{1}, \frac{2}{3}, 0 \right) , \; d_L^H \sim \left( \textbf{3}, \textbf{1}, \textbf{1}, -\frac{1}{3}, 0 \right) \;; \end{aligned}$$

Leptons

$$\begin{aligned} L_L= & {} \left( \nu _L \;\; e_L \right) ^{\textrm{T}} \sim \left( \textbf{1}, \textbf{2}, \textbf{1}, -\frac{1}{2}, 0 \right) , \;\\ N_R= & {} \left( \nu _R \;\; \nu ^H_R \right) ^{\textrm{T}} \sim \left( \textbf{1}, \textbf{1}, \textbf{2}, 0, \frac{1}{2} \right) ,\\ E_R= & {} \left( e^H_R \;\; e_R \right) ^{\textrm{T}} \sim \left( \textbf{1}, \textbf{1}, \textbf{2}, -1, - \frac{1}{2} \right) \;;\\ \nu _L^H\sim & {} \left( \textbf{1}, \textbf{1}, \textbf{1}, 0, 0 \right) , \; e_L^H \sim \left( \textbf{1}, \textbf{1}, \textbf{1}, -1, 0 \right) . \end{aligned}$$

The most general renormalizable Higgs potential which is invariant under both $SU(2)_L\times U(1)_Y$ and $SU(2)_H \times U(1)_X$ can be written down as follows

$$\begin{aligned} V =&- \mu ^2_H \left( H^{\alpha i} H_{\alpha i} \right) - \mu ^2_{\Phi } \Phi _H^\dag \Phi _H + \lambda _H \left( H^{\alpha i} H_{\alpha i} \right) ^2 \nonumber \\&+ \lambda _\Phi \left( \Phi _H^\dag \Phi _H \right) ^2 + \frac{1}{2} \lambda '_H \epsilon _{\alpha \beta } \epsilon ^{\gamma \delta } \left( H^{ \alpha i} H_{\gamma i} \right) \left( H^{ \beta j} H_{\delta j} \right) \nonumber \\&+\lambda _{H\Phi } \left( H^\dag H\right) \left( \Phi _H^\dag \Phi _H\right) + \lambda ^\prime _{H\Phi } \left( H^\dag \Phi _H\right) \left( \Phi _H^\dag H\right) , \end{aligned}$$

(3)

where (i, j) and ($\alpha$, $\beta$, $\gamma$, $\delta$) refer to the $SU(2)_L$ and $SU(2)_H$ indices respectively, all of which run from one to two, and $H^{\alpha i} = H^*_{\alpha i}$.

To study spontaneous symmetry breaking (SSB) in the model, we parameterize the Higgs fields according to standard lore

$$\begin{aligned} H_1= & {} \begin{pmatrix} G^+ \\ \frac{ v + h_{\textrm{SM}}}{\sqrt{2}} + i \frac{G^0}{\sqrt{2}} \end{pmatrix}, \; H_2 = \begin{pmatrix} H^+ \\ H_2^0 \end{pmatrix}, \nonumber \\ \Phi _H= & {} \begin{pmatrix} G_H^p \\ \frac{ v_\Phi + \phi _H}{\sqrt{2}} + i \frac{G_H^0}{\sqrt{2}} \end{pmatrix} \; \; \; \end{aligned}$$

(4)

where v and $v_\Phi$ are the only non-vanishing vacuum expectation values (VEVs) in $H_1$ and $\Phi _{H}$ fields respectively. $v = 246$ GeV is the SM VEV.

The relevant interaction Lagrangian for the computation of the one-loop oblique parameters in G2HDM is

$$\begin{aligned} {\mathcal {L}}_{\textrm{int}} = {\mathcal {L}}_{\mathrm{int \, 1}} + {\mathcal {L}}_{\mathrm{int \, 2}} , \end{aligned}$$

(5)

where

$$\begin{aligned} {\mathcal {L}}_{\mathrm{int \, 1}}&\supset&- \frac{1}{2} \left( \partial _\mu h_{\textrm{SM}} \right) \left[ \left( g W_3^\mu - g^\prime B^\mu \right) G^0\right. \nonumber \\{} & {} \left. + i g \left( G^+ W^{- \mu } - G^- W^{+ \mu } \right) \right] \nonumber \\{} & {} + \frac{1}{2} \left( h_{\textrm{SM}} + v \right) \left\{ \left( \partial _\mu G^0 \right) \left( g W_3^\mu - g^\prime B^\mu \right) \right. \nonumber \\{} & {} \left. + i g \left[ \left( \partial _\mu G^+ \right) W^{- \mu } - \left( \partial _\mu G^- \right) W^{+\mu } \right] \right\} \nonumber \\{} & {} + \frac{i}{2} \left( g W_3^\mu - g^\prime B^\mu \right) \left[ \left( \partial _\mu H^{0 \, *}_2 \right) H_2^0 - \left( \partial _\mu H^{0}_2 \right) H_2^{0 \, *} \right] \nonumber \\{} & {} + \frac{i}{2} \left( g W_3^\mu + g^\prime B^\mu \right) \left[ \left( \partial _\mu H^{+} \right) H^- - \left( \partial _\mu H^{-} \right) H^{+} \right] \nonumber \\{} & {} + i \frac{g}{\sqrt{2}} \left\{ W^{-\mu } \left[ \left( \partial _\mu H^{+} \right) H_2^{0 \, *} - \left( \partial _\mu H^{0 \,*}_2 \right) H^{+} \right] \right. \nonumber \\{} & {} \left. - W^{+\mu } \left[ \left( \partial _\mu H^{-} \right) H_2^{0} -\left( \partial _\mu H^{0}_2 \right) H^{-} \right] \right\} \nonumber \\{} & {} + \cdots , \end{aligned}$$

(6)

and

$$\begin{aligned} {\mathcal {L}}_{\mathrm{int \, 2}}&\supset&\frac{1}{8} \left[ g^2 \left( W^\mu _3 W_{3 \mu } + 2 \, W^{+ \mu } W^{-}_{\mu } \right) + g^{\prime \, 2} B^\mu B_\mu \right] \nonumber \\{} & {} \times \left[ \left( h_{\textrm{SM}} + v \right) ^2 + 2 \left( H_2^{0\, *} H_2^0 + H^+ H^- \right) \right] - \frac{1}{4} g g^\prime W^\mu _3 B_\mu \nonumber \\{} & {} \times \left[ \left( h_{\textrm{SM}} + v \right) ^2 + 2 \left( H_2^{0\, *} H_2^0 - H^+ H^- \right) \right] + \cdots . \end{aligned}$$

(7)

Note that the $\cdots$ in (6) and (7) indicate terms of first and second order in $g_H$ and $g_X$ have been ignored under our approximations. Their effects will be taking into account at the tree level via the mass mixings in the neutral gauge bosons in the model as will be explained further in Sect. 4.1.

In G2HDM, the SM $Z_{\textrm{SM}}$ and A fields are defined as usual

$$\begin{aligned} \begin{pmatrix} W_3^ \mu \\ B^\mu \end{pmatrix} = \begin{pmatrix} c_W &{} s_W \\ - s_W &{} c_W \end{pmatrix} \begin{pmatrix} Z_{\textrm{SM}}^\mu \\ A^\mu \end{pmatrix} , \end{aligned}$$

(8)

where

$$\begin{aligned} s_W \equiv \sin \theta _W = \frac{ g^\prime }{\sqrt{g^2 + g'^2 }} , \; c_W \equiv \cos \theta _W = \frac{ g }{\sqrt{g^2 + g'^2 }} , \end{aligned}$$

(9)

and the electric charge e is given by

$$\begin{aligned} e = \frac{ g g'}{\sqrt{g^2 + g'^2 }} \; \;\;\; \textrm{and} \;\;\;\; \alpha = \frac{e^2}{4 \pi } . \end{aligned}$$

(10)

In G2HDM, the SM W boson does not mix with $W^\prime$ and its mass is the same as in SM: $m_W = g v/2$. However in general the SM $Z_{\textrm{SM}}$ will mix further with the gauge field $W^{\prime }_3$ associated with the third generator of $SU(2)_H$ and the $U(1)_X$ gauge field X via the following mass matrix:

$$\begin{aligned} {\mathcal {M}}_Z^2 = \begin{pmatrix} m^2_{Z} &{}\qquad - \frac{1}{2} g_H v m_{Z} &{}\qquad - { \frac{1}{2} } g_X v m_{Z} \\ - \frac{1}{2} g_H v m_{Z} &{}\qquad m^2_{W^\prime } &{}\qquad { \frac{1}{4} } g_H g_X v_{-}^2 \\ - {\frac{1}{2} } g_X v m_{Z} &{} \qquad { \frac{1 }{4} } g_H g_X v_{-}^2 &{}\qquad {\frac{1}{4} } g_X^2 v_{+}^2 + M_X^2 \end{pmatrix} , \end{aligned}$$

(11)

where

$$\begin{aligned} m_{Z}= & {} \frac{1 }{2} v \sqrt{ g^2 + g^{\prime \, 2} }, \end{aligned}$$

(12)

$$\begin{aligned} m_{W^\prime }= & {} \frac{1}{2} g_H \sqrt{ v^2 + v_\Phi ^2 } , \end{aligned}$$

(13)

$v_{\pm }^2 = \left( v^2 \pm v^2_\Phi \right)$ and $M_X$ is the Stueckelberg mass for the $U(1)_X$.

The real and symmetric mass matrix ${\mathcal {M}}_Z^2$ in (11) can be diagonalized by a 3 by 3 orthogonal matrix ${{\mathcal {O}}}^G$, i.e. $({\mathcal {O}}^{G})^{\textrm{T}} {\mathcal {M}}_Z^2 {\mathcal {O}}^G = \textrm{Diag}(m^2_{Z_1}, m^2_{Z_2},m^2_{Z_3})$, where $m_{Z_i}$ is the mass of the physical fields $Z_i$ for $i=1,2,3$. We will identify $Z_1 \equiv Z$ to be the neutral gauge boson resonance with a mass of 91.1876 GeV observed at LEP  [58]. The lighter/heavier of the other two states is the dark photon ($\gamma ^\prime$)/dark Z ($Z^\prime$). These neutral gauge bosons are h-parity even in the model, despite the adjective ‘dark’ are used for the other two states. We note that these neutral gauge bosons can decay into SM particles and thus they can be constrained by experimental data, including the electroweak precision measurement at the Z pole physics from LEP, searches for dark Z and dark photon at colliders, beam-dump experiments, and astrophysical observations. The DM candidate considered in this work is $W^{\prime \, (p,m)}$, which is electrically neutral but carries one unit of dark charge and chosen to be the lightest h-parity odd particle in the parameter space.

In G2HDM there are mixings effects of the two doublets $H_1$ and $H_2$ with the hidden doublet $\Phi _H$. The neutral components $h_{\textrm{SM}}$ and $\phi _H$ in $H_1$ and $\Phi _H$ respectively are both h-parity even. They mix to form two physical Higgs fields $h_1$ and $h_2$

$$\begin{aligned} \left( \begin{matrix} h_{\textrm{SM}} \\ \phi _H \end{matrix} \right) = {{\mathcal {O}}}^S \cdot \left( \begin{matrix} h_1 \\ h_2 \end{matrix} \right) = \left( \begin{matrix} \cos \theta _1 &{} \sin \theta _1 \\ - \sin \theta _1 &{} \cos \theta _1 \end{matrix} \right) \cdot \left( \begin{matrix} h_1 \\ h_2 \end{matrix} \right) . \end{aligned}$$

(14)

The mixing angle $\theta _1$ is given by

$$\begin{aligned} \tan 2 \theta _1 = \frac{\lambda _{H\Phi } v v_\Phi }{ \lambda _\Phi v^2_\Phi - \lambda _H v^2 } . \end{aligned}$$

(15)

The masses of $h_1$ and $h_2$ are given by

$$\begin{aligned} m_{h_1,h_2}^2= & {} \lambda _H v^2 + \lambda _\Phi v_\Phi ^2 \nonumber \\{} & {} \mp \sqrt{\lambda _H^2 v^4 + \lambda _\Phi ^2 v_\Phi ^4 + \left( \lambda ^2_{H\Phi } - 2 \lambda _H \lambda _\Phi \right) v^2 v_\Phi ^2 }. \nonumber \\ \end{aligned}$$

(16)

Depending on its mass, $h_1$ or $h_2 \equiv h$ is identified as the observed Higgs boson at the LHC. Currently the most precise measurement of the Higgs boson mass is $m_{h} = 125.38 \pm 0.14$ GeV [59].

The complex fields $H_2^{0 \, *}$ and $G^p_H$ in $H_2$ and $\Phi _H$ respectively are both h-parity odd. They mix to form a physical dark Higgs $D^*$ and a unphysical Goldstone field ${\tilde{G}}^*$ absorbed by the $W^{\prime \, p}$

$$\begin{aligned} \begin{pmatrix} G^m_H \\ H_2^{0} \end{pmatrix} = {\mathcal {O}}^D \cdot \begin{pmatrix} {\tilde{G}} \\ D \end{pmatrix} = \begin{pmatrix} \cos \theta _2 &{} \sin \theta _2 \\ - \sin \theta _2 &{} \cos \theta _2 \end{pmatrix} \cdot \begin{pmatrix} {\tilde{G}} \\ D \end{pmatrix} . \end{aligned}$$

(17)

The mixing angle $\theta _2$ satisfies

$$\begin{aligned} \tan 2 \theta _2 = \frac{2 v v_\Phi }{v^2_\Phi - v^2} , \end{aligned}$$

(18)

and the mass of D is

$$\begin{aligned} m_D^2 = \frac{1}{2} \lambda ^\prime _{H\Phi } \left( v^2 + v_\Phi ^2 \right) . \end{aligned}$$

(19)

In the Feynman-’t Hooft gauge the Goldstone field ${\tilde{G}}^*$ $({\tilde{G}} )$ has the same mass as the $W^{\prime \, p}$ ($W^{\prime \, m}$) which is given by (13). Finally the charged Higgs $H^\pm$ is also h-parity odd and has a mass

$$\begin{aligned} m^2_{H^\pm } = \frac{1}{2} \left( \lambda ^\prime _{H\Phi } v^2_\Phi - \lambda ^\prime _H v^2 \right) . \end{aligned}$$

(20)

One can do the inversion to express the fundamental parameters in the scalar potential in terms of the particle masses [54, 55]:

$$\begin{aligned} v_\Phi= & {} {\left\{ \begin{array}{ll} \begin{matrix} v \cot \theta _2 , &{}&{} \textrm{for} \; \theta _2 > 0 , \\ - v \tan \theta _2 , &{}&{} \textrm{for} \; \theta _2 \le 0 , \end{matrix} \end{array}\right. } \end{aligned}$$

(21)

$$\begin{aligned} \lambda _H= & {} \frac{1}{2 v^2} \left( m^2_{h_1} \cos ^2 \theta _1 + m^2_{h_2} \sin ^2 \theta _1 \right) , \end{aligned}$$

(22)

$$\begin{aligned} \lambda _\Phi= & {} \frac{1}{2 v_\Phi ^2} \left( m^2_{h_1} \sin ^2 \theta _1 + m^2_{h_2} \cos ^2 \theta _1 \right) , \end{aligned}$$

(23)

$$\begin{aligned} \lambda _{H\Phi }= & {} \frac{1}{2 v v_\Phi } \left( m^2_{h_2} - m^2_{h_1} \right) \sin \left( 2 \theta _1 \right) , \end{aligned}$$

(24)

$$\begin{aligned} \lambda ^\prime _{H\Phi }= & {} \frac{ 2 m_D^2 }{v^2 + v_\Phi ^2} , \end{aligned}$$

(25)

$$\begin{aligned} \lambda ^\prime _{H}= & {} \frac{2}{v^2} \left( \frac{m_D^2 v_\Phi ^2 }{ v^2 + v_\Phi ^2 } - m^2_{H^\pm }\right) . \end{aligned}$$

(26)

From (13), we also have

$$\begin{aligned} g_H = \frac{ 2 m_{W'} }{ \sqrt{v^2 + v^2_{\Phi } }} . \end{aligned}$$

(27)

Thus one can use $m_{h_2}$, $m_{W^\prime }$, $m_D$, $m_{H^\pm }$, $\theta _1$ and $\theta _2$ as input in our numerical scan.

The Feynman rules can be straightforwardly derived by rewriting the two Lagrangians (6) and (7) using the physical fields mentioned above. The h-parity odd particles in G2HDM are $W^{\prime \, (p,m)}$, $D^{(*)}$, ${{\tilde{G}}}^{(*)}$, $H^\pm$, and all new heavy fermions $f^H$. Among them, $W^{\prime \, (p,m)}$, $D^{(*)}$, and $\nu ^H$ are electrically neutral and hence any one of them can be a DM candidate. The connector sector linking the SM particles and the DM $W^{\prime (p,m)}$ consists of the h-parity even or odd particles. Specifically, we have $\gamma$, $Z_i (i=1,2,3)$ and $h_n (n=1,2)$ in the s-channel, and new heavy fermions $f^H$s or even the DM $W^{\prime (p,m)}$ itself in the t-channel and/or u-channel. Phenomenology of a complex scalar $D^{(*)}$ as DM was studied in detail in [52, 53] and for low mass $W^{\prime \, (p,m)}$ as DM, see [54, 55]. For further details of G2HDM, we refer our readers to the earlier works [48, 49]. Phenomenology of a new heavy neutrino $\nu ^H$ as DM in the model, which is necessarily implying both DM and neutrino physics, has yet to be explored.

3 Oblique parameters and W boson mass shift

As is well known, the oblique parameters S, T, and U [8] represent the most important electroweak radiative corrections since they are defined by the transverse pieces of the vacuum polarization tensors of the SM vector gauge bosons. They are process independent whereas the other vertex and box corrections are necessarily attached to the particles in the initial and final states in the elementary processes in high precision experiments.

The vacuum polarization tensor $i \Pi _{IJ}^{\mu \nu }(q)$ involving the SM gauge bosons I and J has the following decomposition

$$\begin{aligned} i \Pi _{IJ}^{\mu \nu }(q) = i \left( \Pi _{IJ} (q^2) g^{\mu \nu } - \Delta _{IJ} (q^2) q^\mu q^\nu \right) . \end{aligned}$$

(28)

The form factor $\Delta _{IJ}(q^2)$ needs no concern to us since at high energy experiments like LEP I and II where electroweak precision measurements were carried out, $q^\mu$ will dot into the helicity spinors of light leptons and will give vanishing results. The vacuum polarization amplitude $\Pi _{IJ} (q^2)$ has the following expansion

$$\begin{aligned} \Pi _{\gamma \gamma } (q^2)= & {} q^2 \Pi ^\prime _{\gamma \gamma }(0) + \cdots , \end{aligned}$$

(29)

$$\begin{aligned} \Pi _{Z\gamma } (q^2)= & {} q^2 \Pi ^\prime _{Z\gamma }(0) + \cdots , \end{aligned}$$

(30)

$$\begin{aligned} \Pi _{ZZ} (q^2)= & {} \Pi _{ZZ}(0) + q^2 \Pi ^\prime _{ZZ}(0) + \cdots , \end{aligned}$$

(31)

$$\begin{aligned} \Pi _{WW} (q^2)= & {} \Pi _{WW}(0) + q^2 \Pi ^\prime _{WW}(0) + \cdots . \end{aligned}$$

(32)

The oblique parameters S, T and U are defined with an overall factor of ${\hat{\alpha }}={\hat{e}}^2/4\pi$ extracted out in front as [8]

$$\begin{aligned} {\hat{\alpha }} S&= 4 {\hat{s}}_W^2 {\hat{c}}_W^2 \left[ \Pi ^\prime _{ZZ}(0) - \frac{{\hat{c}}_W^2 - {\hat{s}}_W^2}{{\hat{s}}_W {\hat{c}}_W} \Pi ^\prime _{Z\gamma }(0) - \Pi ^\prime _{\gamma \gamma }(0) \right] ,\;\;\;\;\; \end{aligned}$$

(33)

$$\begin{aligned} {\hat{\alpha }} T&= \frac{\Pi _{WW}(0)}{m_W^2} - \frac{\Pi _{ZZ}(0)}{m_Z^2} , \end{aligned}$$

(34)

$$\begin{aligned} {\hat{\alpha }} U&= 4 {\hat{s}}_W^2 \big [ \Pi ^\prime _{WW}(0) - {\hat{c}}_W^2 \Pi ^\prime _{ZZ}(0) - 2 {\hat{s}}_W {\hat{c}}_W \Pi ^\prime _{Z\gamma }(0) \nonumber \\&\quad - {\hat{s}}_W^2 \Pi ^\prime _{\gamma \gamma }(0) \big ] . \end{aligned}$$

(35)

The W boson mass shift can be related to the oblique parameters according to [8]

$$\begin{aligned} \frac{ \Delta m_W^2 }{m_Z^2}= & {} {\hat{\alpha }} \frac{{\hat{c}}_W^2 }{{\hat{c}}_W^2 - {\hat{s}}_W^2} \left[ -\frac{S}{2} + {\hat{c}}_W^2 T + \frac{{\hat{c}}_W^2 - {\hat{s}}_W^2}{4 {\hat{s}}_W^2} U \right] . \;\;\; \end{aligned}$$

(36)

Here the hat quantities ${\hat{c}}_W$, ${\hat{s}}_W$ and ${\hat{\alpha }}$ are understood to be evaluated at the Z pole. In order to compare with the difference of the central values of the CDF II result (1) and the global fit number (2), namely, $\Delta m_W \approx$ 75 MeV, we use $\Delta m_W \approx \left( \Delta m_W^2 + m_W^2 \right) ^{1/2} - m_W$ with $m_W$ given by the SM expression $m_W = g v/2$ and $\Delta m_W^2$ by (36).

4 New contributions to the oblique parameters in G2HDM

In this section, we compute the contributions to the oblique parameters from all the new particles introduced in G2HDM. First, we will handle the tree level contributions to the oblique parameters coming from the mass mixing matrix for the three massive neutral gauge bosons given in (11).

Fig. 1

Tree level diagrams (to second orders of $g_H$ and $g_X$) that contribute to the oblique parameters from the mass mixings (11) between the $Z_{\textrm{SM}}$, $W^\prime _3$ and X in G2HDM

Fig. 2

The W mass shift from the tree level mixing of the neutral gauge bosons spanned on the ($m_{W'}$, $g_H$) plane. Here we set $g_X = 0$. The solid green, solid blue and solid red lines represent the W mass shift of 1 MeV, 20 MeV and the one measured at the CDF II, respectively. The light gray shaded region is the excluded region ($\Delta m_Z > 2.1$ MeV) from the measurement of Z boson mass at LEP  [58]. The orange region is the excluded region from the di-lepton high mass resonance search from ATLAS [62]

4.1 Contributions from the tree level mixings of $Z_{\textrm{SM}}$, $W^\prime _3$ and X

The kinetic and mass mixings of an extra U(1) boson with the SM B and $W^3$ gauge fields violate the custodial symmetry in the SM at the tree level and can give rise to the effective shift of the oblique parameters [60] (see also [13]). The neutral gauge boson mass mixings (11) of $Z_{\textrm{SM}}$, $W^\prime _3$ and X in G2HDM also violate the custodial symmetry in the SM and can give rise to a non-vanishing vacuum polarization amplitude $\Pi _{ZZ}(q)$ at the tree level. The other 3 vacuum polarization amplitudes vanish at tree level in the model. For $g_H, g_X \ll g, g^\prime$, from the Feynman diagram in Fig. 1, one obtains

$$\begin{aligned} \Pi _{ZZ} (q^2) \approx \frac{1}{4} v^2 m_Z^2 \left( \frac{g_H^2}{q^2 - m_{W^\prime }^2} + \frac{g_X^2}{q^2 - m_X^2} \right) , \end{aligned}$$

(37)

where $m^2_{W^\prime }$ is given by (13) and $m_X^2$ is the 33 entry of (11), namely

$$\begin{aligned} m_X^2 = \left( {\mathcal {M}}_Z^2 \right) _{33} = \frac{1}{4} g_X^2 \left( v^2 + v_\Phi ^2 \right) + M_X^2 . \end{aligned}$$

(38)

The Z boson propagator is modified as

$$\begin{aligned} i \Delta _Z^{\mu \nu } (q) = - i \left( \frac{ g^{\mu \nu } }{q^2 - m_Z^2 - \Pi _{ZZ}(q^2) } - q^{\mu } q^{\nu } \; \textrm{term} \right) . \end{aligned}$$

(39)

This modified propagator implies a mass correction $\delta m^2_Z$ and a wave function renormalization constant ${\mathcal {Z}}$ for the Z boson, viz.

$$\begin{aligned} \delta m_Z^2\approx & {} \Pi _{ZZ}(m_Z^2) - m_Z^2 \Pi ^\prime _{ZZ} (m_Z^2) , \end{aligned}$$

(40)

$$\begin{aligned} \sqrt{\mathcal {Z}}\approx & {} 1 + \frac{1}{2} \Pi _{ZZ}^\prime (m_Z^2) . \end{aligned}$$

(41)

The mass shift for the physical Z field is then given by $\Delta m_Z^2 \approx \delta m_Z^2 + m_Z^2 ( {\mathcal {Z}} - 1) \approx \Pi _{ZZ}(m_Z^2)$.³ One can then deduce the effective oblique parameters by using the EFT approach with the following effective Lagrangian [61]

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{eff}}= & {} {{\mathcal {L}}}_{\textrm{SM}} + {{\mathcal {L}}}_{\textrm{NP}} , \end{aligned}$$

(42)

where ${{\mathcal {L}}}_{\textrm{SM}}$ is the SM Lagrangian and ${{\mathcal {L}}}_{\textrm{NP}}$ is the Lagrangian from NP effects which is defined as

$$\begin{aligned} {{\mathcal {L}}}_{\textrm{NP}}= & {} -\frac{A}{4} \hat{F}_{\mu \nu } \hat{F}^{\mu \nu } -\frac{B}{2} \hat{W}_{\mu \nu }^{\dagger } \hat{W}^{\mu \nu } -\frac{C}{4} \hat{Z}_{\mu \nu } \hat{Z}^{\mu \nu } \nonumber \\{} & {} + \frac{G}{2} \hat{F}_{\mu \nu } \hat{Z}^{\mu \nu } - w \tilde{m}_W \hat{W}_{\mu }^{\dagger } \hat{W}^{\mu } - \frac{z}{2} \tilde{m}_Z \hat{Z}_{\mu } \hat{Z}^{\mu }. \end{aligned}$$

(43)

Here $\hat{F}_{\mu \nu }$ and $\hat{Z}_{\mu \nu }$ represent the usual Abelian field strengths, whereas $\hat{W}_{\mu \nu } = D_\mu \hat{W}_\nu - D_\nu \hat{W}_\mu$ with the covariant $D_\mu \hat{W}_\nu = \partial _\mu \hat{W}_\nu + i e \hat{A}_\mu \hat{W}_\nu$. The $\tilde{m}_{W (Z)}$ is the W(Z) mass in the SM and the coefficients A, B, C, G, w and z represent either the wave function renormalizations or mass corrections from NP. Since neutral gauge boson mass mixings are tree-level effects, this effective Lagrangian approach seems more appropriate to deduce the oblique parameters. We therefore identify $C = - \Pi ^\prime _{ZZ}(m_Z^2)$ and $z = (\Pi _{ZZ}(m_Z^2) - m_Z^2 \Pi ^\prime _{ZZ}(m_Z^2) )/m_Z^2$.⁴ All the other effective parameters A, B, G and w in Eq. (43) are zeros at tree level in G2HDM. Using Eq. (2) in [61], we then obtain the tree level oblique parameters as

$$\begin{aligned} S_{\textrm{tree}} (\{ W^\prime , X \})&\approx - U_{\textrm{tree}} (\{ W^\prime , X \}) \approx - \frac{{\hat{s}}_W^2 {\hat{c}}_W^2 }{ {\hat{\alpha }} } v^2 m_Z^2 \nonumber \\&\quad \times \left[ \frac{g_H^2}{ (m_Z^2 - m^2_{W^\prime } )^2} + \frac{g_X^2}{ ( m_Z^2 - m^2_X )^2 } \right] , \end{aligned}$$

(44)

$$\begin{aligned} T_{\textrm{tree}} (\{ W^\prime , X \})&\approx - \frac{1}{4 \, {\hat{\alpha }} } v^2 \nonumber \\&\quad \times \left[ g_H^2 \frac{ (2 m_Z^2 - m^2_{W^\prime } ) }{(m_Z^2 - m^2_{W^\prime } )^2 } + g_X^2 \frac{ ( 2 m_Z^2 - m_X^2 ) }{ ( m_Z^2 - m^2_X )^2 } \right] . \end{aligned}$$

(45)

Fig. 3

Vacuum polarization diagrams that contribute to the oblique parameters from the mixing between the SM doublet $H_1$ and the hidden doublet $\Phi _H$ in G2HDM

The corresponding W boson mass shift at the tree level can be computed using (36).

Fig. 4

Upper panels: the oblique parameters divided by $\sin ^2\theta _1$ as a function of $m_{h_2}$ (left) and contours for the W boson mass shift, $\Delta m_W$, projected on the ($m_{h_2}$, $\sin ^2\theta _1$) plane (right) for the case where $h_1$ is identified to be the observed Higgs boson. Lower panels: likewise but $\sin ^2\theta _1 \rightarrow \cos ^2 \theta _1$ and $m_{h_2} \leftrightarrow m_{h_1}$, for the case where $h_2$ is identified to be the observed Higgs boson. The dashed black, blue and green (solid black, blue and green) lines on the upper (lower) right panel represent the mass shift $\Delta m_W =$ − 5, − 20 and − 60 (5, 20 and 60) MeV, respectively. The solid red line indicates the upper bound on the mixing angle $\sin ^2\theta _1 \lesssim 0.2$ (upper right panel) or $\cos ^2\theta _1 \lesssim 0.2$ (lower right panel) from the Higgs signal strength measurement at the LHC. We note this upper bound for $\sin ^2 \theta _1$ (or $\cos ^2\theta _1$) changes if $m_{h_2}$ is close to $m_{h_1}$ [65]

In Fig. 2, we show the contours of W boson mass shift from the contribution of the tree level mixings between the neutral gauge bosons projected on the plane of $m_{W'}$ and $g_H$. Here we have fixed $g_X = 0$ for simplicity. Including contributions from both $W^\prime$ and X do not change our conclusions in a significant way. In $m_{W'} \gtrsim m_Z$ regions and for relative large values of $g_H$, one can reach the W boson mass shift ($\Delta m_W \approx 75$ MeV) measured at the CDF II. However these large values of $g_H$ also yield a large Z boson mass shift which is in conflict with the great precision measurement of the Z mass at LEP [58]

$$\begin{aligned} m_Z(\textrm{LEP}) = 91.1876 \pm 0.0021 \; \textrm{GeV} . \end{aligned}$$

(46)

In the heavy mass region of ${W'}$ boson, the gauge coupling $g_H$ is also constrained to be $g_H \lesssim 10^{-2}$ from the di-lepton high mass resonance searches at ATLAS [62]. In the allowed region, the W boson mass shift is relatively small from these extra massive neutral gauge bosons in G2HDM. In other words, the mass mixing effects from (11) to the W boson mass shift is not significant. We note that for lower mass regions of $W'$ and X bosons ($m_{W', X} < m_Z$), the oblique parameters in Eqs. (44, 45) calculated from the EFT approach may not be justified. However in these low mass regions, the gauge couplings are constrained to be smaller ($g_{H, X} \lesssim 10^{-3}$ ) [54, 55], one expects the contribution to the W boson mass shift from these mixing effects is also negligible.

In the next three subsections, we will turn to one-loop contributions to the oblique parameters from all other new particles in G2HDM. We will treat $Z_1 = Z \approx Z_{\textrm{SM}}$ and work in the Feynman-’t Hooft gauge.

4.2 Contributions from the $SU(2)_H$ doublet $\Phi _H$

Since $\Phi _H$ is a $SU(2)_H$ doublet but a $SU(2)_L$ singlet, its contribution can only arise from the mixing effects between $h_{\textrm{SM}}$ and $\phi _2$ and therefore similar to the singlet extension of the SM. The relevant Feynman diagrams are depicted in Fig. 3.

For the $\Delta T$ parameter, we find

$$\begin{aligned} \Delta T (\Phi _H)= & {} \frac{3 \sin ^2 \theta _1}{16 \pi {\hat{s}}_W^2 } \left\{ \biggl [ \frac{m_{h_2}^2}{m_{h_2}^2 - m_W^2} \log \left( \frac{m_{h_2}^2}{m_{W}^2} \right) \right. - \left( \frac{m_Z^2}{m_W^2} \right) \nonumber \\{} & {} \left. \frac{m_{h_2}^2}{m_{h_2}^2 - m_Z^2} \log \left( \frac{m_{h_2}^2}{m_{Z}^2} \right) \biggr ] - \left[ h_2 \rightarrow h_1 \right] \right\} . \end{aligned}$$

(47)

The above result agrees with [63, 64].

Compact expressions for the $\Delta S (\Phi _H)$ and $\Delta U (\Phi _H)$ parameters can also be obtained using their definitions given in (33) and (35).

$$\begin{aligned}{} & {} \Delta S (\Phi _H) = \frac{\sin ^2 \theta _1}{12 \pi } \nonumber \\{} & {} \left\{ - \frac{ 2 \, m_Z^2 \left( m_{h_1}^2 - m_{h_2}^2 \right) \left( 2 m_{h_1}^2 m_{h_2}^2 + 3 m_Z^2 \left( m_{h_1}^2 + m_{h_2}^2 \right) - 8 m_Z^4 \right) }{ \left( m_{h_1}^2 - m_Z^2 \right) ^2 \left( m_{h_2}^2 - m_Z^2 \right) ^2 } \right. \nonumber \\{} & {} \qquad + \left. \left[ \frac{ m_{h_2}^2 \left( m_{h_2}^4 - 3 m_{h_2}^2 m_Z^2 + 12 m_Z^4 \right) }{ \left( m_{h_2}^2 - m_Z^2 \right) ^3 }\right. \right. \nonumber \\{} & {} \qquad \times \left. \left. \log \left( \frac{m_{h_2}^2 }{ m_Z^2 } \right) - \left( m_{h_2} \rightarrow m_{h_1} \right) \right] \right\} , \end{aligned}$$

(48)

and

$$\begin{aligned}{} & {} \Delta U (\Phi _H)= \frac{\sin ^2 \theta _1}{12 \pi } \nonumber \\{} & {} \Biggl \{ \Biggl [ \frac{ 2 \, m_Z^2 \left( m_{h_1}^2 - m_{h_2}^2 \right) \left( 2 m_{h_1}^2 m_{h_2}^2 + 3 m_Z^2 \left( m_{h_1}^2 + m_{h_2}^2 \right) - 8 m_Z^4 \right) }{ \left( m_{h_1}^2 - m_Z^2 \right) ^2 \left( m_{h_2}^2 - m_Z^2 \right) ^2 } \Biggr . \Biggr . \nonumber \\{} & {} \qquad - \Biggl . \frac{ m_{Z}^4 \left( 9 m_{h_2}^2 + m_Z^2 \right) }{ \left( m_{h_2}^2 - m_Z^2 \right) ^3 } \log \left( \frac{m_{h_2}^2 }{ m_Z^2 } \right) \nonumber \\{} & {} \qquad + \frac{ m_{Z}^4 \left( 9 m_{h_1}^2 + m_Z^2 \right) }{ \left( m_{h_1}^2 - m_Z^2 \right) ^3 } \log \left( \frac{m_{h_1}^2 }{ m_Z^2 } \right) \Biggr ] \nonumber \\{} & {} \qquad - \biggl . \biggl [ \left( m_{Z} \rightarrow m_{W} \right) \biggr ] \biggr \} . \end{aligned}$$

(49)

As one expects, all three $\Delta S(\Phi _H)$, $\Delta T(\Phi _H)$ and $\Delta U(\Phi _H)$ vanish as $m_{h_2} \rightarrow m_{h_1}$ or $\theta _1 \rightarrow 0$. In this limit, from Eq. (16), we must require $\lambda _{H\Phi }=0$, $\lambda _H = \lambda _\Phi$ and $\mu _H^2 = \mu _\Phi ^2$. The scalar potential with $\lambda _{H\Phi }=0$, $\lambda _H = \lambda _\Phi$ and $\mu _H^2 = \mu _\Phi ^2$ for the three doublets $H_1$, $H_2$ and $\Phi _H$ can then be simplified to manifest a custodial symmetry of SO(12), preventing the deviation of the oblique parameters from nil for the degenerated $h_1$ and $h_2$. The other two couplings $\lambda _H^\prime$ and $\lambda _{H\Phi }^\prime$ in the scalar potential break this custodial symmetry but they are not relevant for the masses of $h_1$ and $h_2$.

We note that the above expressions (47), (48), and (49) are written down assuming the lighter $h_1$ is identified as the observed Higgs boson. If instead the heavier $h_2$ is identified to be the observed Higgs boson, analogous expressions can be obtained by setting $\sin ^2\theta _1 \rightarrow \cos ^2\theta _1$ and $m_{h_1} \leftrightarrow m_{h_2}$ in (47), (48), and (49).

Fig. 5

Vacuum polarization diagrams that contribute to the oblique parameters from the inert doublet $H_2$ in G2HDM

We will first study the case where $h_1$ is the observed Higgs boson. In the upper left panel of Fig. 4, we show the oblique parameters divided by $\sin ^2\theta _1$ calculated from (47), (48), and (49) as a function of $m_{h_2}$. One can see that $\Delta S$ is positive value while $\Delta T$ is opposite, and $|\Delta U|$ is much smaller than $|\Delta S|$ and $|\Delta T|$. In the upper right panel of Fig. 4, we show the contours for the W mass shift projected on the ($m_{h_2}$, $\sin ^2\theta _1$) plane. The W boson mass shift is seen to be negative for $m_{h_2} > m_{h_1}$.

Similar plots in the lower left and right panels of Fig. 4 are made for the case where the heavier $h_2$ is the observed Higgs boson. In this case, the oblique parameters flip their signs as compared with the previous case as shown in the lower left panel in Fig. 4. As a result, a positive W boson mass shift is obtained as shown in the lower right panel in Fig. 4. The mass shift can be large in the large $\cos ^2\theta _1$ and small $m_{h_1}$ regions.

Due to the Higgs data at the LHC which require $\sin ^2 \theta _1 (\textrm{or}\, \cos ^2 \theta _1) \lesssim 0.2$ (from the Higgs boson coupling modifier $\kappa _Z = 0.99\pm 0.06$ [66]) for the case where $h_1$ (or $h_2$) is the observed Higgs boson, the W boson mass shift from this contribution is constrained to be relatively small in both cases and thus makes it difficult for the hidden $SU(2)_H$ doublet $\Phi _H$ to explain the CDF W boson mass anomaly.

4.3 Contributions from the inert Higgs doublet $H_2$ in G2HDM

The second Higgs doublet $H_2$ in G2HDM plays a similar role as the inert Higgs doublet in I2HDM [67,68,69,70]. However the neutral component $H_2^0$ of $H_2$ can be treated as a complex scalar field in G2HDM instead of decomposing into $(S+iA)/\sqrt{2}$ in I2HDM, where S and A are the scalar and pseudo-scalar fields. In addition, as already given in (17), $H_2^0 (H_2^{0 \, *})$ mixes with $G^m_H (G^p_H)$ from the hidden doublet $\Phi _H$ to form a physical dark Higgs $D (D^*)$ and a Goldstone boson ${\tilde{G}} ({\tilde{G}}^*)$, with the latter of which absorbed by the complex gauge fields $W^{\prime \,m} (W^{\prime \,p})$ of $SU(2)_H$. The relevant Feynman diagrams for the inert Higgs doublet contributions are depicted in Fig. 5.

For the T parameter, we got

$$\begin{aligned} \Delta T ( H_2)= & {} \frac{1 }{8 \pi ^2 {\hat{\alpha }} v^2 } \biggl [ F(m_{H^{\pm }},m_D)\cos ^2 \theta _2 \nonumber \\{} & {} + F(m_{H^{\pm }},m_{W'})\sin ^2 \theta _2\nonumber \\{} & {} - \, \frac{1}{4} \, F(m_D,m_{W'})\, \sin ^2 2\theta _2 \biggr ] . \end{aligned}$$

(50)

where $m_{W'}$ is the mass the Goldstone boson $\tilde{G}$ which is absorbed by the new gauge boson $W^{\prime \, (p,m)}$ of $SU(2)_H$, and the function $F(m_1,m_2)$ is defined as

$$\begin{aligned} F(m_1,m_2) = {\left\{ \begin{array}{ll} \frac{m_1^2 + m_2^2}{2} - \frac{m_1^2 m_2^2}{m_1^2 - m_2^2} \log \left( \frac{m_1^2}{m_2^2} \right) ,&{}\textrm{for} \; m_1 \ne m_2\, , \\ 0 &{}\textrm{for} \; m_1 = m_2 . \end{array}\right. } \end{aligned}$$

(51)

Again, analytical formulas for the $\Delta S (H_2)$ and $\Delta U (H_2)$ parameters can be obtained using their definitions given in (33) and (35).

$$\begin{aligned} \Delta S (H_2)= & {} \frac{1}{36 \pi } \Bigg \{ - 3 \log \Bigg ( \frac{ m_{H^\pm }^2 }{ m_D^2 } \Bigg ) + 6 \Bigg (\cos ^4\theta _2 - 1 \Bigg ) \nonumber \\{} & {} + 3 \Bigg ( 2 - \log \Bigg ( \frac{ m_{D}^2 }{ m_{W'}^2 } \Bigg ) \Bigg ) \sin ^4\theta _2 \nonumber \\{} & {} + \frac{1}{4} G ( m_D, m_{W'} ) \sin ^2 2 \theta _2 \Bigg \} \end{aligned}$$

(52)

and

$$\begin{aligned} \Delta U (H_2)= & {} \frac{1}{36 \pi } \Bigg \{ - 3 \log \Bigg ( \frac{ m_{H^\pm }^2 }{ m_D^2 } \Bigg ) - 6 \Bigg (\cos ^4\theta _2 + 1 \Bigg ) \nonumber \\{} & {} + G \Bigg ( m_D, m_{H^\pm } \Bigg ) \cos ^2\theta _2 \nonumber \\{} & {} - 3 \Bigg ( 2 - \log \Bigg ( \frac{m_D^2}{m_{W'}^2} \Bigg ) \Bigg ) \sin ^4 \theta _2 \nonumber \\{} & {} - \Bigg ( \, 6 \log \Bigg ( \frac{m_D^2}{m_{W'}^2} \Bigg ) - G ( m_{W'}, m_{H^\pm } ) \Bigg ) \sin ^2\theta _2 \nonumber \\{} & {} - \frac{1}{4} G \Big ( m_D, m_{W'} \Big ) \sin ^2 2 \theta _2 \Bigg \} , \end{aligned}$$

(53)

where

$$\begin{aligned} G \left( m_1, m_2 \right)= & {} \frac{\left( 7 m_1^4 - 2 m_1^2 m_2^2 + 7 m_2^4 \right) }{\left( m_1^2 - m_2^2 \right) ^2} \nonumber \\{} & {} - \frac{ 6 m_2^4 \left( 3 \, m_1^2 - m_2^2 \right) }{\left( m_1^2 - m_2^2 \right) ^3} \log \left( \frac{m_1^2}{m_2^2} \right) . \end{aligned}$$

(54)

Note that in the limit of $m_2 \rightarrow m_1$, $G (m_1,m_1)=12$.

In the pure inert limit of $\theta _2 \rightarrow 0$, $D \rightarrow {H_2^0}$ and we simply have

$$\begin{aligned} \lim _{\theta _2 \rightarrow 0} \Delta S(H_2)= & {} - \frac{1}{12 \pi } \log \left( \frac{m_{H^\pm }^2}{m_{H_2^0}^2} \right) , \end{aligned}$$

(55)

$$\begin{aligned} \lim _{\theta _2 \rightarrow 0} \Delta T ( H_2)= & {} \frac{1 }{8 \pi ^2 {\hat{\alpha }} v^2 } F(m_{H^{\pm }},m_{H_2^0}) , \end{aligned}$$

(56)

$$\begin{aligned} \lim _{\theta _2 \rightarrow 0} \Delta U(H_2)= & {} - \frac{1}{12 \pi } \log \left( \frac{m_{H^\pm }^2}{m_{H_2^0}^2} \right) \nonumber \\{} & {} + \frac{1}{36 \pi } \left( G \left( m_{H_2^0}, m_{H^\pm } \right) - 12 \right) . \end{aligned}$$

(57)

The above expressions of (55) and (56) are consistent with the inert Higgs results [68]. Furthermore, if $m_{H^\pm }=m_{H_2^0}$, $\Delta S(H_2) = \Delta T(H_2) = \Delta U(H_2) = 0$ in this limit.

4.4 Contributions from the new heavy fermions in G2HDM

Since all the new heavy fermions $f^H$ in G2HDM are $SU(2)_L$ singlets, they don’t interact with the charge $W^\pm$ bosons. Under the assumption that $g_H, g_X \ll g, g^\prime$, the heavy fermions interacts with both the SM $\gamma$ and Z are vector-like described by the following Lagrangian

$$\begin{aligned} {\mathcal {L}} ( f^H ) = e Q_{ f^H } \left( {\bar{f}}^H \gamma _\mu f^H \right) \left( A^\mu - \tan \theta _W Z^\mu \right) + \cdots \; , \end{aligned}$$

(58)

where we have dropped terms that are proportional to $g_H$ or $g_X$. Thus we have

$$\begin{aligned} \Pi _{WW}^{ f^H} ( q^2 )= & {} 0 , \end{aligned}$$

(59)

$$\begin{aligned} \Pi _{ \gamma \gamma }^{ f^H} ( q^2 )= & {} N_C e^2 Q^2_{f^H} \Pi _{QQ} ( q^2 ) , \end{aligned}$$

(60)

$$\begin{aligned} \Pi _{ \gamma Z }^{ f^H} ( q^2 )= & {} - N_C e^2 Q^2_{f^H} \tan \theta _W \Pi _{QQ} ( q^2 ) , \end{aligned}$$

(61)

$$\begin{aligned} \Pi _{ ZZ }^{ f^H} ( q^2 )= & {} N_C e^2 Q^2_{f^H} \tan ^2 \theta _W \Pi _{QQ} ( q^2 ) , \end{aligned}$$

(62)

where $\Pi _{QQ}$ is the oblique loop amplitude $\Pi _{\gamma \gamma }$ with both the color and electric charge factors trimming off [71], i.e.

$$\begin{aligned} \Pi _{QQ} ( q^2 )= & {} \frac{1}{2 \pi ^2} q^2 \Big [ \frac{1}{6} E - \int _0^1 dx \, x (1-x) \nonumber \\{} & {} \times \log \frac{m^2_{f^H} - x \left( 1 - x \right) q^2}{ \mu ^2} \Big ] \;\;\;\;\; \end{aligned}$$

(63)

with $E \equiv \frac{2}{\epsilon } - \gamma _E + \log 4 \pi$. Using the above expressions (59)–(63), we can demonstrate easily that all the oblique parameters from the heavy fermions $f^H$s in G2HDM vanish:

$$\begin{aligned} \Delta S (f^H) = \Delta T (f^H) = \Delta U (f^H) = 0 . \end{aligned}$$

(64)

The non-trivial leading contributions from the heavy fermions in G2HDM to the oblique parameters start at order $g_H^2/16 \pi ^2$ and $g_X^2/16\pi ^2$, which we are neglecting in this study.

The rationale behind the vector-like results in Eqs. (59)–(62) and (64) is as follows. From Eq. (11), we can see that setting $g_H$ and $g_X$ to zeros implies there are no mixings in the neutral gauge bosons. As a result, from the quantum numbers of the heavy fermions $f^H$ given in Sect. 2 for the model setup, we know that all $f^H$s are strictly singlets under $SU(2)_L$, i.e. $T_i (f^H) = 0$ where $T_i \, (i=1,2,3)$ are the three generators of $SU(2)_L$. This immediately implies $\Pi _{11}^{f^H} = \Pi ^{f^H}_{33} =\Pi _{3Q}^{f^H} = 0$. In this case, the only SM gauge field that $f^H$s couple to is the hypercharge B field. Since both left-handed and right-handed heavy fermions have the same hypercharge, we left with $\Pi _{YY}^{f^H}=\Pi _{QQ}^{f^H} \ne 0$. Furthermore, it is well-known that all oblique parameters vanish for the electroweak singlets with arbitrary hypercharge.

To summarize, we have computed all possible nontrivial sources of new physics effects to the oblique parameters $\Delta S$, $\Delta T$ and $\Delta U$ in G2HDM under the approximation of $g_H, g_X \ll g, g^\prime$. While the tree level mixings of the neutral gauge bosons and the extra heavy fermions in G2HDM contribute to the oblique parameters are of order $g_{H,X}^2$ and $g_{H,X}^2/16\pi ^2$ respectively and therefore not significant, there are new contributions from the inert doublet $H_2$ and the $H_2$-$\Phi _H$ mixings, as well as from the hidden doublet $\Phi _H$ through the $H_1$-$\Phi _H$ mixings. These new contributions from the extended scalar sector in G2HDM are of order $g^2/16\pi ^2$ and $g^{\prime 2}/16\pi ^2$ which are the same order as the SM one-loop contributions. In the next section, we will focus on the detailed numerical analysis of these new contributions.

Table 1 The parameter space setup for the scan. For the light DM mass scenario, $m_{W^{\prime }}$, $m_{X}$ and $g_{X}$ are scanned in log scale while the rest are in linear scale. All the new heavy fermion masses are set equal to 3 TeV

5 Numerical results

In this section we present the numerical results in the light of new W boson mass measurement at the CDF II. Among the h-parity odd particles, we require $W'$ to be the lightest particle so that it can be a DM candidate in this model. We propose two setups of scan based on the mass of the DM, one is the light DM mass scenario and another is the heavy DM mass scenario. The parameter space setup for these two scenarios is given in Table 1. We sample the parameter space in the model using MCMC scans emcee [72]. For the light DM mass scenario, $m_{W^{\prime }}$, $M_{X}$ and $g_{X}$ are scanned in the log scale, while the rest are in the linear scale in both scenarios except $M_{X}$ and $g_X$ are fixed in the heavy DM mass scenario. We also assume that the lighter $h_1$ is the observed Higgs boson and all heavy fermion masses are degenerated and fixed to be 3 TeV.

We closely follow the analysis for the current constraints in the model from [54, 55]. In particular, we take into account the theoretical constraints on the scalar potential, the collider physics from the LHC including the signal strengths of $h \rightarrow \gamma \gamma$ [73], $h \rightarrow W^+W^-, ZZ$ [66] and $h \rightarrow \tau ^+ \tau ^-$ [74] from the gluon-gluon fusion, the constraints from the electroweak precision measurement at Z pole [58] and from $Z'$ [62] and dark photon $\gamma '$ physics (see [75] for a recent review). To take into account the new W boson mass measurement at the CDF II, the recent global fit values for the oblique parameters due to NP contributions is adapted from [6], which are given as

$$\begin{aligned} \Delta S= & {} 0.005 \pm 0.096 , \nonumber \\ \Delta T= & {} 0.04 \pm 0.12 , \nonumber \\ \Delta U= & {} 0.134 \pm 0.087 , \end{aligned}$$

(65)

and the correlation coefficients are $0.91, -0.65$ and $-0.88$ for ($\Delta S, \Delta T$), ($\Delta S, \Delta U$) and ($\Delta T, \Delta U$), respectively.

We also take into account the constraints from DM searches including the DM relic density $\Omega \textrm{h}^2 = 0.120 \pm 0.001$ measured from Planck collaboration [76], DM direct detections from CRESST III [77], DarkSide-50 [78], XENON1T [79, 80], PandaX-4T [81] and LZ [82], and the Higgs invisible decays constraint from the LHC [83]. We note that, due to the kinematical forbiddance, the Higgs invisible decays constraint is not applied for the heavy DM mass scenario. The branching ratio of invisible Higgs decay is given in [54, 55]. We use micrOMEGAs package [84] to calculate the DM relic density and the DM-proton scattering cross section. We note that the production cross section of the mono-jet signals $pp \rightarrow W'^{p} W'^{m} j$ in the model is small due to the smallness of the gauge coupling $g_H$ [54, 55] and hence evading the current constraint from the LHC [85, 86]. Thus we do not include the mono-jet constraint in our analysis.

Hereafter, we denote the scan without the DM constraints as CDF-2022 and with the DM constraints as CDF-2022+DM. To see the impacts due to the CDF II W boson mass measurement, we employ other scans with the old global fit values for the oblique parameters taken from the Particle Data Group (PDG) [58] which are given as

$$\begin{aligned} \Delta S= & {} -0.01 \pm 0.1 , \nonumber \\ \Delta T= & {} 0.03 \pm 0.12 , \nonumber \\ \Delta U= & {} 0.02 \pm 0.11 , \end{aligned}$$

(66)

and the correlation coefficients are $0.92, -0.8$ and $-0.93$ for ($\Delta S, \Delta T$), ($\Delta S, \Delta U$) and ($\Delta T, \Delta U$), respectively. We then denote the PDG scan without the DM constraints as PDG-2021 and with the DM constraints as PDG-2021+DM.

Fig. 6

The favored regions projected on the planes of $(\Delta m \equiv m_{H^{\pm }} - m_D, \theta _2)$ (left panel) and $(m_{W^{\prime }}, m_{H^{\pm }})$ (right panel) for the heavy DM mass scenario. The dark (light) orange region represents the $1\sigma$ ($2\sigma$) favored by CDF-2022, while the dark (light) gray region indicates the $1\sigma$ ($2\sigma$) favored by PDG-2021

5.1 Heavy DM mass scenario

In Fig. 6, we show first the favored regions from CDF-2022 (orange regions) and PDG-2021 (gray regions) spanned on the parameter space without imposing the DM constraints. On the left panel of Fig. 6, we project the favored regions on the plane of the mass splitting ($\Delta m \equiv m_{H^\pm } - m_D$) and the mixing angle $\theta _2$. The mixing angle $\theta _2$ is allowed to be either a nearly maximal mixing region ($\theta _2 \sim -\pi /2$) or a tiny mixing region ($\theta _2 \lesssim 5\times 10^{-3}$). Since the relation between $\theta _2$ and $g_H$ is given as

$$\begin{aligned} g_H = \frac{2 \,m_{W'}}{v} \times {\left\{ \begin{array}{ll} \begin{matrix} |\sin \theta _2| \, , &{}&{} \textrm{for} \; \theta _2 > 0 , \\ |\cos \theta _2| \, , &{}&{} \textrm{for} \; \theta _2 \le 0 , \end{matrix} \end{array}\right. } \end{aligned}$$

(67)

the upper bound on $\theta _2$ is due to the upper bound on the gauge coupling $g_H$ which is from the constraints of the Z mass shift and the di-lepton high mass resonance search at the LHC as shown in Fig. 2. For the tiny mixing $\theta _2$ region, the impact from the new W mass measurement at CDF II is significant. In particular, within $2\sigma$ favored region, CDF-2022 prefers a large mass splitting between the charged Higgs and dark Higgs, while the PDG-2021 prefers a smaller mass splitting and even allows the degenerated case. On the other hand, for the nearly maximal mixing region, both CDF-2022 and PDG-2021 allow the degenerated mass between the charged Higgs and dark Higgs. However CDF-2022 still allows for a larger mass splitting as compared with the region favored by PDG-2021.

On the right panel of Fig. 6, we project the favored regions on the plane of the charged Higgs and $W'$ masses. The favored regions from CDF-2022 and PDG-2021 are almost the same. For the region of $m_{W'} \gtrsim 1.4$ TeV, the favored region has a thin cigar shape indicating the charged Higgs and $W'$ masses are correlated linearly and hence their mass ratio is close to unity.

Fig. 7

The DM annihilation and coannihilation processes in the model. The top left, top right and bottom left panels represent the DM annihilation processes mediated by the scalar $h_i$, the neutral gauge boson $Z_i$ via the s-channel and the heavy hidden fermions $f^H$ via the t-channel, respectively. The bottom right panel indicates the DM coannihilation processes where $\chi _{i} = \{W', H^{\pm }, {D}\}$ and $i \ne j$

Fig. 8

The $1\sigma$ (dark) and $2\sigma$ (light) favored regions of the data from CDF-2022+DM (blue) and PDG-2021+DM (gray) projected on the plane of the mass splittings $(m_{H^\pm } - m_{W^{\prime }})/{m_{W^{\prime }}}$ and $(m_{D} - m_{W^{\prime }})/{m_{W^{\prime }}}$ for the heavy DM mass scenario

Fig. 9

The $1\sigma$ (dark) and $2\sigma$ (light) favored regions of the data from CDF-2021+DM (blue) and PDG-2022+DM (gray) projected on the planes of $(\Delta m \equiv m_{H^{\pm }} - m_D, \theta _2)$ (left panel) and $(m_{W^{\prime }}, m_{H^{\pm }})$ (right panel) for the heavy DM mass scenario

Similar to the well known WIMP DM scenario, the DM candidate $W'$ is kept in the chemical equilibrium with the SM thermal bath via its $2\leftrightarrow 2$ annihilations before starting to freeze-out due to the expansion of the universe. The DM relic abundance can be determined by solving the Boltzmann equation for the evolution of the DM number density which heavily influenced by the $2 \leftrightarrow 2$ annihilations between the DM and SM particles.

In G2HDM, beside the standard annihilation of the $W^{\prime \, (p,m)}$ pair to pairs of SM particles, the coannihilation—mutual annihilation of multiple h-parity odd species—to pairs of SM particles can be also occurred. The Feynman diagrams for the DM annihilation and coannihilation processes are depicted in Fig. 7. In the coannihilation limit, the $\chi _i \leftrightarrow \chi _j$ with $\chi _i = \{W', H^{\pm }, D\}$ and $i \ne j$, is rapid until after annihilations decouple. The effective annihilation rate in this limit can be given by [87]

$$\begin{aligned} \sigma ^{\textrm{coann}} = \sum _{i,j}^{3} \sigma _{ij} \frac{g_i g_j}{g_{\textrm{eff}}^2} (1+ \Delta _i)^{3/2} (1+ \Delta _j)^{3/2} e^{-x(\Delta _i + \Delta _j)}, \end{aligned}$$

(68)

where $\sigma _{ij}$ is the annihilation cross section, $x = m_{W'}/T$ with T is the temperature, $\Delta _i = (m_i - m_{W'})/{m_{W'}}$, ${g_i}$ counts the number of internal degrees of freedom and

$$\begin{aligned} g_{\textrm{eff}} = \sum _{i =1}^{3} g_i (1+ \Delta _i)^{3/2} e^{-x \Delta _i}. \end{aligned}$$

(69)

From Eq. (68), we see that the coannihilation process can be significant if the masses of $W'$ and the other h-parity odd particles are nearly degenerated.

For large mass splittings between $W'$ and other h-parity odd particles, the pairs of $W^{\prime \, (p,m)}$ mainly annihilate into pairs of SM fermions and $W^{+} W^{-}$, which are mediated by the neutral gauge bosons $Z, Z', \gamma '$ and scalar bosons $h_1, h_2$ via the s-channel as well as the new heavy fermions via the t-channel. The cross sections of such processes are proportional to $g_H^2$, thus they are suppressed due to constraints on this new gauge coupling unless a resonant DM annihilation process occurs through the s-channel. To fulfill the resonant condition, the mediator mass must be nearly twice that of the $W^\prime$ mass.

Fig. 10

The $1\sigma$ (dark blue) and $2\sigma$ (light blue) favored regions of the data from CDF-2022+DM projected on the plane of the DM mass and spin independent DM-proton scattering cross section for the heavy DM mass scenario. The dark and light gray regions are the exclusion from PandaX 4T [81] and LZ [82] experiments. The dashed green, red and purple lines represent future sensitivities from the DM direct detections at XENONnT [88], DarkSide-20k [89] and DARWIN [90], respectively. Green region is the neutrino floor background

Fig. 11

The favored regions projected on the planes of $(\Delta m \equiv m_{H^{\pm }} - m_D, m_{H^{\pm }})$ (left panel) and $(m_{W^{\prime }}, \theta _2)$ (right panel) for the light DM mass scenario. The dark (light) orange region represents the $1\sigma$ ($2\sigma$) favored by CDF-2022, while the dark (light) gray region indicates the $1\sigma$ ($2\sigma$) favored by the PDG-2021

For the heavy DM mass scenario, we found out that the main contribution that yields the DM relic density observed at Planck Collaboration is the coannihilation channels. The annihilation processes are subdominant because the cross sections are suppressed due to the smallness of the new gauge couplings $g_H$ and $g_X$. Figure 8 shows the mass difference between the DM $W'$ and h-parity odd particles $H^{\pm }$ and D when the DM constraints are included. The mass differences $(m_{H^\pm } - m_{W^{\prime }})/{m_{W^{\prime }}}$ and $(m_{D} - m_{W^{\prime }})/{m_{W^{\prime }}}$ are required to be ${{\mathcal {O}}} (10^{-2} - 10^{-1})$ within $2\sigma$ region. The CDF-2022+DM prefers a larger region of the mass differences while the PDG-2021+DM can extend to a lower region.

Figure 9 shows the favored regions on $(\Delta m, \theta _2)$ (left panel) and $(m_{W^{\prime }}, m_{H^{\pm }})$ (right panel) planes when the DM constraints are taken into account. As compared with the results without the DM constraints (shown in Fig. 6), the nearly maximal mixing regions of the angle $\theta _2$ are not favored anymore. The degeneracy of the charged Higgs and dark Higgs (i.e. $\Delta m = 0$) favored by the PDG-2021 is no longer favored when the DM constraint is included. Within $2\sigma$ region, it requires the mass splitting to be in the range of $33 \,\textrm{GeV} \lesssim \Delta m \lesssim 78 \,\textrm{GeV}$ for PDG-2021+DM and $72 \,\textrm{GeV} \lesssim \Delta m \lesssim 100 \,\textrm{GeV}$ for CDF-2022+DM. The mixing angle is also required to be smaller $\theta _2 \lesssim 2 \times 10^{-3}$. The cigar shape of the favored region on the right panel of Fig. 9 is due to the happenstance of DM coannihilation i.e. $(m_{H^\pm } - m_{W^{\prime }})/{m_{W^{\prime }}} \sim {{\mathcal {O}}} (10^{-2} - 10^{-1})$ as suggested already in the right panel of Fig. 6 for $m_{W^\prime } \gtrsim 1.4$ TeV even before imposing DM constraints. The DM mass is predicted to be $m_{W'} > 700$ GeV while the charged Higgs mass is $m_{H^\pm } > 800$ GeV within $2\sigma$ region. The CDF-2022+DM prefers a bit higher in the charged Higgs mass region as compared with the result from PDG-2021+DM.

In Fig. 10, we show the CDF-2022+DM favored region on the $(m_{W^\prime },\sigma _{W^\prime p}^{\textrm{SI}})$ plane for the DM direct detection. Due to the constraint from the di-lepton high mass resonance search at the LHC [62], the gauge coupling is required to be $g_H \lesssim 10^{-2}$ in the favored DM mass region. It results in a small DM-proton spin-independent scattering cross section $\sigma _{W^\prime p}^{\textrm{SI}}$ and thus the favored region lies far below the current limits from PandaX 4T [81] and LZ [82] (gray regions). Most of the CDF-2022+DM favored region overlaps with the neutrino floor background region. However a portion of the favored region predicted by the model can be probed by future DM direct detections at DarkSide-20k [89] and DARWIN [90].

Fig. 12

Same as Fig. 11 for the light DM mass scenario but with the DM constraints included. The dark (light) blue region represents the $1\sigma$ ($2\sigma$) favored by the CDF-2022+DM, while the dark (light) gray region indicates the $1\sigma$ ($2\sigma$) favored by the PDG-2021+DM

5.2 Light DM mass scenario

Again we show first the favored regions from CDF-2022 and PDG-2021 for the light DM mass scenario in Fig. 11 without the DM constraints imposed. Similar to the heavy DM mass scenario, the significant difference between CDF-2022 and PDG-2021 is the favored region projected on the mass splitting between the charged Higgs and dark Higgs which is shown in the left panel of Fig. 11. In particular, within $2\sigma$ region, CDF-2022 prefers a mass splitting $60 \,\textrm{GeV} \lesssim \Delta m \lesssim 100$ GeV, while PDG-2021 favors a smaller region $10 \,\textrm{GeV} \lesssim \Delta m \lesssim 75$ GeV. However, unlike the heavy DM mass scenario, both CDF-2022 and PDG-2021 in this scenario disfavor the degeneracy of the charged Higgs and dark Higgs masses. The favored regions projected on ($m_{W'}-\theta _2$) plane is shown in the right panel of Fig. 11. The results between CDF-2022 and PDG-2021 projected on this plane is slightly different. CDF-2022 prefers a region with the DM mass ($m_{W'} \lesssim 20$ GeV within $2 \sigma$ region) and the mixing angle ($\theta _2 \lesssim 0.15$ rad within $2 \sigma$ region) while PDG-2021 favors a bit lighter DM mass and larger mixing angle region. There is a lower bound on the DM mass ($m_{W'} \gtrsim 0.02$ GeV within $2 \sigma$ region) which is due to the constraints from the dark photon searches [54, 55]. In particular, because the relation between $m_{W'}$ and $m_{Z'}$ shown in (11), the lower bound on $m_{Z'}$ due to NA64 [91], E141 [92] $\nu$-CAL I [93] experiments can be translated to a lower bound on the DM mass. The constraints from the dark photon searches also put a strong upper limit on the gauge couplings $g_H$ and $g_X$ [54, 55]. Since the relation between $g_H$ and $\theta _2$ given in (67), the upper limit on $g_H$ induces the upper limit on $\theta _2$ as shown in the right panel of Fig. 11.

Fig. 13

The $1\sigma$ (dark blue) and $2\sigma$ (light blue) favored regions of the data from CDF-2022+DM projected on the plane of the DM mass and spin independent DM-proton scattering cross section for the light DM mass scenario. The gray regions are the exclusion from CRESST-III [77], DarkSide-50 [78] and XENON1T [80] experiments. The dashed green, red, purple and orange lines represent the future sensitivities from DM direct detection experiments at NEWS-G [94], SuperCDMS [95], CDEX [96] and HeRALD [97], respectively. Green region is the neutrino floor background

Next, we take into account the DM constraints for this light DM mass scenario. Due to the scanned mass ranges of $D, H^{\pm }$ and $W'$, the mass splitting between DM and other $h-$parity odd particles $H^{\pm }$ and D are relatively large and hence forbids the DM coannihilation channels. The annihilations of $W'^{p} W'^{m}$ to the SM fermion pairs via s-channel with the mediation of $Z', \gamma '$ are dominant processes. However the cross sections of such processes are suppressed due to the smallness of the gauge couplings $g_H$ and $g_X$ except near the resonant regions where the mass of mediators are about twice DM mass. Because the mass of the lighter $\gamma '$ can not satisfy the resonant condition i.e. $m_{\gamma '} \not \approx 2 \times m_{W'}$, only the annihilation process with a heavier mediator $Z'$ near the resonance can provide a DM relic density observed at the Planck Collaboration.

We show the results with the DM constraints included in Fig. 12. In this scenario, since the DM physics is not significantly impacted by the charged Higgs and dark Higgs, the favored regions projected on ($\Delta m$, $m_{H^{\pm }}$) plane as shown in the left panel of Fig. 12 are almost unchanged as compared with the one without DM constraints as shown in the left panel of Fig. 11. On the other hand, due to the DM direct detection constraints from CRESST-III [77], DarkSide-50 [78] and XENON1T [80] experiments, the DM mass is required to be $m_{W'} \lesssim 2$ GeV within $2\sigma$ region as shown in the right panel of Fig. 12. In the same panel, we also see that it is required to have a lower bound on $\theta _2 \gtrsim 1.8 \times 10^{-2}$ rad. This is because of the DM relic density observed at the Planck Collaboration. A smaller $\theta _2$ results in a smaller $g_H v/{m_{W'}}$ value as shown in (67), which can cause a smaller DM annihilation cross section and eventually lead to an overabundant DM in the universe.

In Fig. 13, we project the favored regions from the CDF-2022+DM data on the plane of the DM mass and spin independent DM-proton scattering cross section. The current constraints from CRESST-III [77], DarkSide [78] and XENON1T [80] experiments are shown as the gray shaded regions. These constraints put an upper limit on the DM mass in this scenario. We find out that a portion of the favored region at $m_{W'} \sim 1$ GeV and $\sigma _{W'p}^{\textrm{SI}} \sim [10^{-44} - 10^{-39}] \, \textrm{cm}^2$ can be probed by future DM direct detection experiments at NEWS-G [94], SuperCDMS [95], CDEX [96] and HeRALD [97]. Note also a small fraction of the $2 \sigma$ favored region lies below the neutrino floor background (light green).

Fig. 14

The one-loop form factors for the individual particle running inside the loop of $h \rightarrow \gamma \gamma$ (left panel) and $h \rightarrow Z \gamma$ (right panel) processes as a function of $|\sin \theta _1|$. The data points are taken in $\Delta \chi ^2 < 5.99$ region from CDF-2022+DM for the heavy DM mass scenario. The orange, green and red points represent the form factors for the SM fermions, charged Higgs, new heavy fermions respectively. The blue points represent the negative value of form factor for the W boson. Note that $F_{\gamma \gamma }(X) \equiv F_{1} (X)$ defined in Eqs. (93, 94, 95, 96) and $F_{Z \gamma }(X) \equiv F_{11} (X)$ defined in Eqs. (73, 80, 81, 87) in the Appendix. Here $X \equiv (W^\pm , f^{\textrm{SM}}, f^H, H^{\pm })$

Fig. 15

Same as Fig. 14 but for the light DM mass scenario

s

Fig. 16

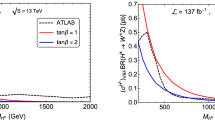
The favored data points from CDF-2022+DM for the heavy DM mass scenario projected on the ($\mu ^{\textrm{ggh}}_{\gamma \gamma }, |\delta _{hZ\gamma }|$) plane. In the left panel the color gradient represents the mixing angle $|\sin {\theta _1}|$ while on the right panel it represents the charged Higgs mass $m_{H^\pm }$. The region between the two vertical red lines is $2\sigma$ region of the expected diphoton signal strength measurement with a $4\%$ uncertainty at the HL-LHC [100]. The horizontal dashed blue line represents the expected measurement precision of $24\%$ for $Z \gamma$ production at the HL-LHC [100]

Fig. 17

Same as Fig. 16 but for the light DM mass scenario

5.3 The processes $h \rightarrow \gamma \gamma$ and $h \rightarrow Z \gamma$ at the LHC

Given the favored parameter space obtained in previous two subsections for the heavy and light DM scenarios, one would like to study their impacts to the diphoton and $Z \gamma$ channels from the 125 GeV Higgs decays and the future searches for these processes at the hadron collider. A precise measurement of the signal strength of these processes at the colliders could reveal the existence of new particles coupled to the Higgs (see e.g. [98, 99]). For the diphoton channel, measurements with the current 13 TeV LHC data yield a signal strength via the gluon-gluon fusion production mechanism: $\mu ^{\textrm{ggh}}_{\gamma \gamma } = 0.96 \pm 0.14$ [73]. For 14 TeV LHC with $3\,\textrm{ab}^{-1}$ luminosity, the signal strength is expected to be measured with a $\pm 0.04$ uncertainty [100]. On the other hand, the $Z \gamma$ channel has not yet been observed with the current data at the LHC [101, 102]. With an expected uncertainty of $24\%$ for the signal strength measurement at the 14 TeV LHC with $3\,\textrm{ab}^{-1}$ luminosity, this $Z\gamma$ channel can be observed with 4.9 $\sigma$ significance at ATLAS experiment [100].

The analytical expressions for the one-loop amplitudes of $h \rightarrow \gamma \gamma$ and $h \rightarrow Z \gamma$ in the G2HDM are given in the Appendix. As compared with the SM predictions, the production rates of these two channels can be modified due to new contributions from the charged Higgs and new charged heavy fermions running inside the loops as well as effects from the mixing angle $\theta _1$ between the SM Higgs boson $h_{\textrm{SM}}$ and the hidden scalar $\phi _H$ in the model. We note again that in this analysis, we assume all new heavy fermions to be degenerated and fixed their masses to be 3 TeV. We select the data points from CDF-2022+DM with $\Delta \chi ^2 = \chi ^2 - \chi ^2_{\textrm{min}} < 5.99$ where $\chi ^2$ is the total $\chi ^2$ calculated from the Higgs data at the LHC, Z-boson mass measurement from LEP II, oblique parameters from Ref. [6], DM relic density from Planck collaboration and the one-side limits from $Z'$ searches, DM direct detection and Higgs invisible decay.

Figure 14 shows the one-loop form factor for the individual particle including $W^{\pm }$, $H^\pm$, charged SM fermions (mainly top quark) and new charged heavy fermions running inside the loop of $h \rightarrow \gamma \gamma$ (left panel) and $h \rightarrow Z \gamma$ (right panel) processes as a function of $|\sin \theta _1|$ in the heavy DM scenario. The current data from ATLAS [66] puts an upper limit on the mixing angle $|\sin \theta _1| \lesssim 0.35$. In both $h \rightarrow \gamma \gamma$ and $h \rightarrow Z \gamma$ processes, the $W^\pm$ form factor gets negative values but its magnitude is dominant. From the right panel of Fig. 9 and the left panel of Fig. 12, we learnt that our scan results prefer a heavy charged Higgs mass in both heavy and light DM mass scenarios. One expects the charged Higgs form factor is rather small. From Fig. 14, we have $F_{\gamma \gamma , Z\gamma } (H^{\pm }) \sim {{\mathcal {O}}} (10^{-7} - 10^{-5})/$ GeV. The charged Higgs form factor is smaller than the SM top quark form factor in the $h \rightarrow \gamma \gamma$ process but it can be larger in the $h \rightarrow Z \gamma$ process. We also see that the new charged heavy fermions are suppressed due to the large VEV $v_\Phi$ in this data. We note that the SM fermion and new heavy fermion form factors for the $h \rightarrow \gamma \gamma$ process are about one order of magnitude larger than those for the $h \rightarrow Z \gamma$ process, while the W boson (as well as the charged Higgs) form factors stay almost the same for these two processes. In the limit of no mixing between the SM Higgs boson $h_{\textrm{SM}}$ and the hidden scalar $\phi _H$, i.e. $\sin \theta _1 = 0$, the new heavy fermion form factor would be vanished.

Figure 15 shows a similar plot as Fig. 14 but for the light DM mass scenario. In this scenario, $m_{h_1} > 2 \,m_{W'}$, the Higgs boson can decay invisibly into a pair of $W^{\prime (p,m)}$. Furthermore, a lighter DM mass also results in a smaller $v_\Phi$ value, this would enhance the contribution of new heavy fermions in the loop. As shown in the left panel of Fig. 15 for the $\gamma \gamma$ case, the contribution from the new heavy fermions can be comparable with the charged Higgs when $|\sin \theta _1| \gtrsim 0.1$.

In Fig. 16, we project the favored data points from CDF-2022+DM for the heavy DM mass scenario on the ($\mu ^{\textrm{ggh}}_{\gamma \gamma }, |\delta _{hZ\gamma }|$) plane, where

$$\begin{aligned} \delta _{hZ\gamma } = 1 - \frac{\Gamma ({h \rightarrow Z \gamma )}}{ \Gamma ({h_{\textrm{SM}} \rightarrow Z_{\textrm{SM}} \gamma }) } \end{aligned}$$

(70)

is the normalized deviation of the $h \rightarrow Z\gamma$ decay width from its SM value. The signal strength of diphoton production from the gluon-gluon fusion is given by

$$\begin{aligned} \mu _{\gamma \gamma }^{\textrm{ggh}} = \frac{\Gamma _{h_{\textrm{SM}}}}{\Gamma _{h}} \frac{\Gamma ({h \rightarrow gg}) \Gamma ({h \rightarrow \gamma \gamma }) }{\Gamma ({h_{\textrm{SM}} \rightarrow gg}) \Gamma ( {h_{\textrm{SM}} \rightarrow \gamma \gamma } )} , \end{aligned}$$

(71)

where the decay width of h into two gluons in the model can be found in [46].

The deviation $|\delta _{hZ\gamma }|$ can be large if the mixing angle $\theta _1$ is large as shown in the left panel of Fig. 16. Similarly, $\mu ^{\textrm{ggh}}_{\gamma \gamma }$ can be also impacted by this mixing effects, a larger mixing angle $\theta _1$ results in a wider region of $\mu ^{\textrm{ggh}}_{\gamma \gamma }$. Moreover, due to the destructive interference between the charged Higgs and W boson contributions, the diphoton signal strength becomes smaller when the charged Higgs has a lighter mass as shown in the right panel of Fig. 16. Future measurements for the diphoton and $Z\gamma$ production from the HL-LHC can probe a large portion of the CDF-2022+DM favored region in this heavy DM scenario. The low mass region of charged Higgs can be probed by the expected diphoton signal strength measurement with a $4\%$ uncertainty at the HL-LHC [100].

Similar plots as Fig. 16 but for the light DM mass scenario are shown in Fig. 17. Similar to the heavy DM mass scenario, both $|\delta _{hZ\gamma }|$ and $\mu ^{\textrm{ggh}}_{\gamma \gamma }$ can be impacted by the mixing effects and the charged Higgs mass. We note that, in this scenario, Higgs boson is kinematically allowed to decay into light neutral gauge bosons $Z'Z'$, $\gamma '\gamma '$, $ZZ'$ and $Z \gamma '$, however the branching ratio of these processes are minuscule due to the smallness of the gauge couplings $g_H$ and $g_X$. As also shown in Fig. 17, precision measurements on the diphoton and $Z\gamma$ productions at the HL-LHC can further constraint the parameter space of the model especially on the mixing angle $\theta _1$ and charged Higgs mass for the light DM mass scenario.

6 Conclusions

Motivated by the new high-precision measurement of the SM W boson mass by the CDF II [1], we scrutinize the minimal G2HDM by computing the contributions from the inert Higgs doublet, hidden Higgs doublet, hidden neutral dark gauge bosons and extra heavy fermions in the model to the oblique parameters S, T, and U. We found out that only inert Higgs doublet can give a significant contribution while contributions from other new particles in the model are minuscule.

The favored regions on the model parameter space are obtained using the updated electroweak global fits of these oblique parameters [2, 6] and the current constraints in the model including the theoretical constraints on the scalar potential, the Higgs data from the LHC, $Z'$, dark photon physics constraints as well as relic density, direct detection and Higgs invisible decays constraints for the dark matter candidate $W'$. We initiated two scenarios based on the dark matter mass, one is heavy DM mass scenario and another is light DM mass scenario. By comparing with the old global fit values for the oblique parameters from PDG, we found out that the CDF W boson mass measurement significantly impacts the mass splitting $\Delta m = (m_H^\pm - m_D)$ in the inert h-parity odd Higgs doublet $H_2$. In particular, the result using the updated global fit values [6] favors a larger mass splitting ($72 \,\textrm{GeV} \lesssim \Delta m \lesssim 100 \,\textrm{GeV}$ for the heavy DM mass scenario and $60 \,\textrm{GeV} \lesssim \Delta m \lesssim 100 \,\textrm{GeV}$ for the light DM mass scenario) as compared with one using the old global fit values ($33 \,\textrm{GeV} \lesssim \Delta m \lesssim 78 \,\textrm{GeV}$ for the heavy DM mass scenario and $10 \,\textrm{GeV} \lesssim \Delta m \lesssim 75 \,\textrm{GeV}$ for the light DM mass scenario) from the PDG. We also found that to satisfy the DM relic density observed at the Planck collaboration, it is required the $W'$ coannihilation processes to be occurred for the heavy DM mass scenario and the nearly resonant annihilation process with the dark photon as a mediator for the light DM mass scenario. The former requires the differences $(m_{H^\pm } - m_{W^{\prime }})/{m_{W^{\prime }}}$ and $(m_{D} - m_{W^{\prime }})/{m_{W^{\prime }}}$ to be in $\sim {{\mathcal {O}}}(10^{-2}, 10^{-1})$, while the latter requires the mediator mass to be around twice the DM mass. For the heavy DM mass scenario, the favored dark matter mass is around 1 TeV and can be probed by future dark matter direct detection experiments at DarkSide-20k and DARWIN as shown in Fig. 10. Whereas, for the light DM mass scenario, the favored DM mass locates at sub-GeV $\sim {{\mathcal {O}}}(0.1-1)$ GeV and also can be probed by future dark matter direct detections at CDEX, NEWS-G, SuperCDMS, and HeRALD as shown in Fig. 13.

Furthermore we studied the diphoton and $Z \gamma$ productions from the Higgs decays and the detectability of these processes at the LH-LHC. We showed that the contribution from the charged Higgs can be larger than the SM fermions (mainly top quark) for the $h \rightarrow Z \gamma$ process but not for the diphoton channel. In the low charged Higgs mass region, the contribution from charged Higgs can be significant and thus reduces the decay widths of $h \rightarrow \gamma \gamma$ and $h \rightarrow Z \gamma$ due to the destructive interference with the W boson contribution. We also showed that the deviations of the diphoton and $Z \gamma$ productions from the SM predictions are highly depending on the mixing angle $\theta _1$ between the SM Higgs boson and the scalar from the hidden doublet. A large portion of the favored region, especially the large mixing angle $\theta _1$ and low charged Higgs mass regions, can be probed by more precise measurement of the $h \rightarrow \gamma \gamma$ signal strength and the detection of $h \rightarrow Z \gamma$ process at the HL-LHC.

Other rare decay modes $h \rightarrow \gamma \gamma ^\prime , \gamma Z^\prime$ (one-loop) and $h \rightarrow \gamma ^\prime \gamma ^\prime , Z^\prime Z^\prime$, and $\gamma ^\prime Z^\prime$ (tree) in G2HDM may be kinematical allowed and thus have important impacts at collider physics. For instance, the dark photon ($\gamma ^\prime$) and dark Z ($Z^\prime$) may be long-lived, traversing some macroscopic distances for small enough $g_X$ and $g_H$ before they decay into SM light fermion pairs. We reserve the exploration of these modes for future studies. For a recent analysis of $h \rightarrow \gamma \gamma ^\prime$ at the LHC, see [103].

Before closing, we reiterate that the results of the present work are obtained under the approximation of the new gauge couplings of $SU(2)_H \times U(1)_X$ are much smaller than the SM gauge couplings, as suggested from the analysis of Z mass shift and dark matter direct detection in our previous works [54, 55]. Consequently we can ignore the loop contributions from the extra gauge bosons $(W^{\prime \, (p,m)}, Z^\prime , \gamma ^\prime$) to the oblique parameters since the effects would be down by the loop factor $1/16\pi ^2$ compared with the tree level mass mixing effects studied in Sect. 4.1. Furthermore, in analogous to the SM case, there should be 8 more vacuum polarization amplitudes $i \Pi ^{\mu \nu }_{W^{\prime \, p} W^{\prime \, m}}$, $i \Pi ^{\mu \nu }_{Z^\prime Z^\prime }$, $i \Pi ^{\mu \nu }_{\gamma ^\prime \gamma ^\prime }$, $i \Pi ^{\mu \nu }_{Z^\prime \gamma ^\prime }$, $i \Pi ^{\mu \nu }_{\gamma \gamma ^\prime }$, $i \Pi ^{\mu \nu }_{\gamma Z^\prime }$, $i \Pi ^{\mu \nu }_{Z \gamma ^\prime }$, and $i \Pi ^{\mu \nu }_{Z Z^\prime }$ that are needed to be worried about. The formalism of the oblique parameters by Peskin and Takeuchi [8] would have to extend properly so as to take into account all new hidden particle contributions to all possible oblique parameters in G2HDM. Such a task is very interesting but beyond the scope of this present work. We hope to return to this challenge in the future.

Appendix

In this Appendix we provide the corrected general analytical expressions for the one-loop amplitudes of the two processes $h_i \rightarrow \gamma \gamma$ and $h_i \rightarrow Z_j \gamma$⁵ in G2HDM. As mentioned in the text, the $h_1$ and $Z_1$ are identified as the observed $125.38 \pm 0.14$ GeV [59] Higgs (h) and $91.1876 \pm 0.0021$ GeV [58] neutral gauge boson (Z) respectively. Under the assumption that $g_H, g_X \ll g, g^\prime$ used in the present analysis, one can set the couplings $g_H$ and $g_X$ to be zero and the mixing matrix element ${{\mathcal {O}}}^G_{ij} = \delta _{ij}$ in the following formulas. However the analytical expressions are valid for general mixing cases.

$\underline{h_i \rightarrow Z_j \gamma }$

The decay rate for $h_i \rightarrow Z_j \gamma$ is

$$\begin{aligned} \Gamma ( h_i \rightarrow Z_j \gamma ) = \frac{1}{32 \pi } m_{h_i}^3 \left( 1 - \frac{m_{Z_j}^2}{m_{h_i}^2} \right) ^3 \biggl \vert F^1_{i j } + F^{1/2}_{i j } + F^0_{i j } \biggr \vert ^2 , \end{aligned}$$

(72)

where $F^s_{ij}$ with $s=0,1/2,1$ denotes the loop form factor for charge particle with spin equals 0, 1/2, 1 respectively running inside the loop.

In G2HDM, the only charged spin 1 particle is the SM $W^\pm$, thus $F^1_{i j } = F_{i j } (W^\pm )$,

$$\begin{aligned}{} & {} F_{ij} (W^\pm )\nonumber \\{} & {} \quad = \frac{1}{16 \pi ^2} \cdot e \cdot g m_W \cdot g c_W \cdot \frac{1}{m_W^2} \cdot {{\mathcal {O}}}^S_{1i} {{\mathcal {O}}}^G_{1j} \nonumber \\{} & {} \qquad \times \left\{ \left[ 5 + \frac{2}{ \tau _{iW}} + \left( 1 + \frac{2}{ \tau _{iW}} \right) {\left( 1 - \frac{4}{ \lambda _{jW}} \right) } \right] \right. \nonumber \\{} & {} \qquad \left. I_1 \left( \tau _{iW}, \lambda _{jW} \right) - 16 {\left( 1 - \frac{1}{ \lambda _{jW}} \right) } I_2 \left( \tau _{iW}, \lambda _{jW} \right) \right\} .\nonumber \\ \end{aligned}$$

(73)

We note that the two factors $(1 - 4/\lambda _{jW})$ and $(1 - 1/\lambda _{jW})$ in (73) were not taken into account properly in [46]! Here and in the following, we denote $\tau _{il} = 4\,m^2_l / m^2_{h_i}$ and $\lambda _{jl} = 4\,m^2_l / m^2_{Z_j}$. The two functions $I_1(\tau ,\lambda )$ and $I_2(\tau ,\lambda )$ are well known and given by [104]

$$\begin{aligned} I_1(\tau ,\lambda )= & {} \frac{\tau \lambda }{2 ( \tau - \lambda )} + \frac{\tau ^2 \lambda ^2}{2 ( \tau - \lambda )^2} \left[ f(\tau ) - f(\lambda ) \right] \nonumber \\{} & {} + \frac{\tau ^2 \lambda }{2 ( \tau - \lambda )^2} \left[ g(\tau ) - g(\lambda ) \right] , \end{aligned}$$

(74)

$$\begin{aligned} I_2(\tau ,\lambda )= & {} - \frac{\tau \lambda }{2 ( \tau - \lambda )} \left[ f(\tau ) - f(\lambda ) \right] , \end{aligned}$$

(75)

with

$$\begin{aligned} f( x )= & {} \left\{ \begin{array}{ll} \left[ \textrm{arcsin} (1 / \sqrt{x} ) \right] ^2 , &{}\quad (x \ge 1) , \\ - \frac{1}{4} \left[ \ln \left( \eta _+ / \eta _- \right) - i \pi \right] ^2 , &{}\quad (x < 1) ; \end{array} \right. \end{aligned}$$

(76)

$$\begin{aligned} g(x)= & {} \left\{ \begin{array}{ll} \sqrt{x - 1} \, \textrm{arcsin} (1 / \sqrt{x} ) , &{}\quad (x \ge 1) , \\ \frac{1}{2} \sqrt{1 - x} \left[ \ln \left( \eta _+ / \eta _- \right) - i \pi \right] , &{}\quad (x < 1) ; \end{array} \right. \end{aligned}$$

(77)

where

$$\begin{aligned} \eta _\pm \equiv 1 \pm \sqrt{1 - x} . \end{aligned}$$

(78)

We note that the arguments of the functions f(x) and g(x) in (76) and (77) are defined to be the inverse of those in [46].

All the charged fermions in G2HDM, including both the SM fermions $f^{\textrm{SM}}$ and the new heavy fermions $f^{H}$ contribute to $F^{1/2}_{ij}$. Thus

$$\begin{aligned} F^{1/2}_{i j } = \sum _{f^{\textrm{SM}}} F_{ij} ( f^{\textrm{SM}} ) + \sum _{f^H} F_{ij} ( f^H ) , \end{aligned}$$

(79)

where

$$\begin{aligned} F_{ij } ( f^{\textrm{SM}} )= & {} \frac{1}{16 \pi ^2} \cdot N^c_{ f^{\textrm{SM}}} \cdot e Q_{ f^{\textrm{SM}}} \cdot \frac{m_{ f^{\textrm{SM}}}}{v}\nonumber \\{} & {} \quad \cdot C^{f^{\textrm{SM}}}_{Vj} \cdot \frac{-2}{m_{f^{\textrm{SM}}}} \cdot {{\mathcal {O}}}^S_{1i} \nonumber \\{} & {} \times \biggl [ I_1 \left( \tau _{if^{\textrm{SM}}}, \lambda _{jf^{\textrm{SM}}} \right) - I_2 \left( \tau _{if^{\textrm{SM}}}, \lambda _{jf^{\textrm{SM}}} \right) \biggr ] , \nonumber \\ \end{aligned}$$

(80)

and

$$\begin{aligned} F_{ij} ( f^{\textrm{H}} )= & {} \frac{1}{16 \pi ^2} \cdot N^c_{ f^{\textrm{H}}} \cdot e Q_{ f^{\textrm{H}}} \cdot \frac{m_{ f^{\textrm{H}}}}{v_\Phi } \cdot \nonumber \\{} & {} \quad C^{f^{\textrm{H}}}_{Vj} \cdot \frac{-2}{m_{f^{\textrm{H}}}} \cdot {{{\mathcal {O}}}^S_{2i} } \nonumber \\{} & {} \times \biggl [ I_1 \left( \tau _{if^{\textrm{H}}}, \lambda _{jf^{\textrm{H}}} \right) - I_2 \left( \tau _{if^{\textrm{H}}}, \lambda _{jf^{\textrm{H}}} \right) \biggr ] , \end{aligned}$$

(81)

with $N^c_{f}$ being the color factor and $Q_f$ the electric charge of f in unit of $e > 0$; $C_{Vj}^f$ is the vector coupling of $Z_j$ with fermion f given by⁶

$$\begin{aligned} C^f_{Vj} = \frac{1}{2} \left( C^f_{Lj} + C^f_{Rj} \right) , \end{aligned}$$

(82)

where

$$\begin{aligned} C^{f^{\textrm{SM}}}_{Lj}= & {} \frac{g}{c_W} \left( T^3_L \left( f^{\textrm{SM}} \right) - Q \left( f^{\textrm{SM}} \right) s^2_W \right) {{\mathcal {O}}}^G_{1j} , \end{aligned}$$

(83)

$$\begin{aligned} C^{f^{\textrm{SM}}}_{Rj}= & {} \frac{g}{c_W} \left( - Q \left( f^{\textrm{SM}} \right) s^2_W \right) {{\mathcal {O}}}^G_{1j} + g_H T^3_H \left( f^{\textrm{SM}} \right) {{\mathcal {O}}}^G_{2j} \nonumber \\{} & {} + g_X Q_X \left( f^{\textrm{SM}} \right) {{\mathcal {O}}}^G_{3j} , \end{aligned}$$

(84)

$$\begin{aligned} C^{f^{H}}_{Lj}= & {} \frac{g}{c_W} \left( - Q \left( f^{H} \right) s^2_W \right) {{\mathcal {O}}}^G_{1j} , \end{aligned}$$

(85)

$$\begin{aligned} C^{f^{H}}_{Rj}= & {} \frac{g}{c_W} \left( - Q \left( f^{H} \right) s^2_W \right) {{\mathcal {O}}}^G_{1j} + g_H T^3_H \left( f^{H} \right) {{\mathcal {O}}}^G_{2j} \nonumber \\{} & {} + g_X Q_X \left( f^{H} \right) {{\mathcal {O}}}^G_{3j} . \end{aligned}$$

(86)

Table 2 Coupling coefficients $C^f_{Lj}$ and $C^f_{Rj}$ for quarks

Table 3 Coupling coefficients $C^f_{Lj}$ and $C^f_{Rj}$ for leptons

$T^3_{L,H}$ is the third component of the generators of $SU(2)_{L,H}$, $Q=T^3_L + Y$ is the electric charge, and $Q_X$ is the $U(1)_X$ charge. The explicit expressions for $C^f_{Lj}$ and $C^f_{Rj}$ for both the SM fermions and new heavy fermions in G2HDM are listed in Table 2 for quarks and Table 3 for leptons. The vector couplings $C^f_{Vj}$ of quarks and leptons are listed in Tables 4 and 5 respectively.

Table 4 Coupling coefficients $C^f_{Vj}$ for quarks

Table 5 Coupling coefficients $C^f_{Vj}$ for leptons

There is only one charged Higgs $H^\pm$ in G2HDM. Thus $F^0_{ij} = F_{ij} ( H^\pm )$ with

$$\begin{aligned} F_{ij} (H^\pm )= & {} \frac{1}{16 \pi ^2} \cdot e Q_{H^+} \cdot g_{h_i H^+H^-} \cdot g_{Z_j H^+ H^-} \cdot \frac{2}{m^2_{H^\pm }} \nonumber \\{} & {} \cdot I_1 \left( \tau _{i H^\pm }, \lambda _{j H^\pm } \right) , \end{aligned}$$

(87)

where $Q_{H^+} = +1$, and $g_{h_i H^+H^-}$ and $g_{Z_j H^+ H^-}$ are the $h_i H^+ H^-$ and $Z_j H^+ H^-$ couplings in the G2HDM respectively. Explicitly they are

$$\begin{aligned} g_{h_i H^+H^-}= & {} \left( 2 \lambda _H - \lambda ^\prime _H \right) v {{\mathcal {O}}}^S_{1i} + \left( \lambda _{H \Phi } + \lambda ^\prime _{H \Phi } \right) v_\Phi \mathcal {O}^S_{2i} ,\;\;\; \;\; \;\nonumber \\ \end{aligned}$$

(88)

$$\begin{aligned} g_{Z_j H^+H^-}= & {} \; \frac{1}{2} ( g \, c_W - g^\prime s_W ) {{\mathcal {O}}}^G_{1j} - \frac{1}{2} g_H {{\mathcal {O}}}^G_{2j} \nonumber \\{} & {} + {\frac{1}{2} } g_X {{\mathcal {O}}}^G_{3j} . \end{aligned}$$

(89)

$\underline{h_i \rightarrow \gamma \gamma }$

The decay rate for $h_i \rightarrow \gamma \gamma$ is

$$\begin{aligned} \Gamma ( h_i \rightarrow \gamma \gamma ) = \frac{1}{64 \pi } m_{h_i}^3 \left( 1 - \frac{m_{Z_j}^2}{m_{h_i}^2} \right) ^3 \biggl \vert F^1_{ i } + F^{1/2}_{ i } + F^0_{ i } \biggr \vert ^2 , \end{aligned}$$

(90)

with similar definitions of $F^s_{i}$ like $F^s_{ij}$ before. The factor of 1/64 instead of 1/32 is due to Bose statistics in the diphoton final state. The previous formulas of $F_{ij}(W^\pm )$, $F_{ij}( f^{\textrm{SM}} )$, $F_{ij}( f^H )$ and $F_{ij}( H^\pm )$ can be easily translated into the diphoton case by taking $m_{Z_j} \rightarrow 0$ limit or equivalently $\lambda _{jl} = 4\,m^2_l/m^2_{Z_j} \rightarrow \infty$ and noting that

$$\begin{aligned} I_1 ( \tau , \infty )= & {} - \frac{\tau }{2} \left( 1 - \tau f (\tau ) \right) , \end{aligned}$$

(91)

$$\begin{aligned} I_2 (\tau , \infty )= & {} \frac{\tau }{2} f ( \tau ) . \end{aligned}$$

(92)

The results are $F^1_{ i } = F_{ i }( W^\pm )$, $F^{1/2}_{ i } = \sum _{f^{\textrm{SM}}} F_{ i }( f^{\textrm{SM}} ) + \sum _{f^H} F_{ i }( f^H )$, and $F^0_{ i } = F_{ i }( H^\pm )$ with

$$\begin{aligned} F_{ i } ( W^\pm )= & {} \frac{1}{16 \pi ^2} \cdot e^2 \cdot g m_W \cdot \frac{-1}{m_W^2} \cdot {{\mathcal {O}}}^S_{1i} \nonumber \\{} & {} \cdot \left[ 2 + 3 \tau _{iW} + 3 \tau _{iW} \left( 2 - \tau _{iW} \right) f ( \tau _{iW} ) \right] \, \!, \end{aligned}$$

(93)

$$\begin{aligned} F_{ i } ( f^{\textrm{SM}} )= & {} \frac{1}{16 \pi ^2} \cdot N^c_{ f^{\textrm{SM}}} \cdot e^2 Q^2_{ f^{\textrm{SM}}} \cdot \frac{m_{ f^{\textrm{SM}}}}{v} \cdot \frac{4}{m_{f^{\textrm{SM}}}} \cdot {{\mathcal {O}}}^S_{1i} \nonumber \\{} & {} \times \left\{ \tau _{if^{\textrm{SM}}} \left[ 1 + \left( 1 - \tau _{if^{\textrm{SM}}} \right) f ( \tau _{if^{\textrm{SM}}} ) \right] \right\} , \end{aligned}$$

(94)

$$\begin{aligned} F_{ i } ( f^H )= & {} \frac{1}{16 \pi ^2} \cdot N^c_{ f^{\textrm{H}}} \cdot e^2 Q^2_{ f^{\textrm{H}}} \cdot \frac{m_{ f^{\textrm{H}}}}{v_\Phi } \cdot \frac{4}{m_{f^{\textrm{H}}}} \cdot { {{\mathcal {O}}}^S_{2i} } \nonumber \\{} & {} \times \left\{ \tau _{if^{\textrm{H}}} \left[ 1 + \left( 1 - \tau _{if^{\textrm{H}}} \right) f ( \tau _{if^{\textrm{H}}} ) \right] \right\} , \end{aligned}$$

(95)

$$\begin{aligned} F_{ i } ( H^\pm )= & {} \frac{1}{16 \pi ^2} \cdot e^2 \cdot g_{h_i H^+ H^-} \cdot \frac{-1 }{ m^2_{H^\pm } } \nonumber \\{} & {} \cdot \left\{ \tau _{iH^\pm } \left[ 1 - \tau _{iH^\pm } f( \tau _{iH^\pm }) \right] \right\} .. \end{aligned}$$

(96)

Note that both the charged Higgs and new heavy fermion contributions were not handled correctly in $h_i \rightarrow \gamma \gamma$ and $h_i \rightarrow Z_j\gamma$ in [46].