Abstract
In this paper, we explore the collider phenomenology of charged Higgs bosons in the context of a generic Beyond Standard Model scenario with extended gauge and scalar sectors. In such scenarios, the charged Higgs boson can decay via the \(W^{'}Z/ WZ^{'}\) channels. We formulate a search strategy for the \(H^{\pm }\) in the channel \(\sigma (g b \rightarrow H^{\pm }t){\mathcal{B}\mathcal{R}}(H^{\pm } \rightarrow W' Z)\) considering the interesting cascade decay chain \(H^{\pm } \rightarrow W^{'} Z \rightarrow W^{\pm } Z Z\). We find that the charged Higgs can be discovered in final states with multiple hard leptons and/or b-quarks which future LHC experiments with sufficiently large luminosity (\({\mathcal {L}} = 1000~\text {fb}^{-1}\) and above) can probe. We then study the phenomenological implications of our findings in the context of a generic toy model with a \(H^{\pm }\) as well as in a more realistic electroweak symmetry breaking scenario.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Standard Model (SM) of particle physics has enjoyed tremendous success over the years and with the discovery of the Higgs boson at the LHC in 2012 [1, 2], its particle spectrum is now firmly established. However, in parallel, a large body of experimental and theoretical work suggest that there has to lie some physics beyond the SM – generically dubbed BSM physics or New Physics (NP) – at the TeV scale, and the LHC experiments are currently working to uncover hints of BSM physics in a wide variety of final states. Construction of models beyond the SM typically involves enlarging the scalar sector, the gauge sector, or the matter content of the SM – in fact, there are many BSM scenarios in which more than one of these three sectors is modified. Correspondingly, in these models there exist particles (fermions, gauge bosons, or heavy and neutral Higgs bosons) at the TeV scale. Experiments in high energy physics look for these new, heavy states by typically taking advantage of the couplings of these heavy particles to the SM sector. This is a reasonable approach as one expects that the discovery potential should be maximal in processes of the form NP\(\rightarrow \) SM, SM. However, given the non-observation of any BSM particle in the LHC experiments thus far, it behooves one to ask if there are other channels that one could probe that might uncover hints that traditional search channels might have missed. In this work, we undertake one such study for heavy charged Higgs bosons that appear in many scalar extensions of the SM.
Extending the scalar sector with new Higgs fields in doublet or other representations of the SM \(SU(2)_L\) has a long history. Examples include (but are certainly not limited to) the Two Higgs-Doublet Models (2HDMs) [3] and their many variants [4, 5], the minimal supersymmetric Standard Model (MSSM) [6, 7], and other triplet extensions [8] of the SM. Many such models typically involve enlarging only the scalar part of the SM Lagrangian leaving the SM gauge group \(SU(2)_L\times U(1)_Y\) as is. Many of these models include a physical singly charged Higgs boson after electroweak symmetry breaking (EWSB). However, it is equally possible to consider scenarios wherein one extends the SM gauge group simultaneously involving additional Higgs fields thus invoking more complicated patterns of symmetry breaking. In models of this kind, one expects, in addition to traditional searches, process of the form NP\(\rightarrow \) SM, NP to be viable as well. If nature indeed chose to follow such a path, it would be interesting to explore the consequences of what an extended gauge model could mean for charged Higgs search prospects at the LHC – this simple framework forms the motivation for the present work. Hunting for BSM particles in these unconventional channels has already been implemented in case of supersymmetric particles. For example, in case of chargino or neutralino searches one typically assumes that these SUSY particles decay via the lightest SUSY partner (LSP) \({\tilde{\chi }}^{0}_{1}\) and the corresponding SM counterpart (like SM Higgs and W) [9, 10]. Similarly, for gluino searches [11] one can consider the following decay chains \({\tilde{g}} \rightarrow j j {\tilde{\chi }}^{0}_{3}\) (Here \({\tilde{\chi }}^{0}_{3}\) denotes a relatively heavier Bino). These \({\tilde{\chi }}^{0}_{3}\) then further decays via LSP and SM-like Higgs. It is interesting to point out, in both cases LSP is considered as a stable particle and in the detector it will be treated as missing energy. Apart from the Susy searches the heavy BSM higgses both neutral and charged Higgses, are also looked into NP \(\rightarrow \) SM NP channels – example being \(H \rightarrow a a\) (where a is the lightest pseudo-scalar) [12, 13] and \(H^{\pm } \rightarrow W^{\pm } a\) [14].
We begin the paper laying out the essential set up for our study in Sect. 2 and briefly discuss the current collider limits. In Sect. 2.2, we present the detailed collider phenomenology of the charged Higgs boson in various viable modes of the form NP\(\rightarrow \) SM, NP. Till this point, we strive to present our discussions in a model-independent fashion, only assuming a spectrum that contains additional gauge and scalar degrees of freedom as compared to the SM. To understand what these results mean in specific models, in Sect. 3, we comment on the viability of our analysis in the context of both a toy model as well as a more realistic EWSB scenario outlined in Ref. [15]. We summarise and present our conclusions in Sect. 4.
2 The \(H^{\pm }\) boson discovery prospect at LHC
2.1 Set-up and current limits
Here, we will undertake the LHC study of charged Higgs bosons in theories which also have an enlarged gauge symmetry. At the outset, we make no assumptions about the exact gauge group or, for that matter, the representations of the additional Higgs fields under the SM and the extra gauge groups. Our discussion in this section will be mostly model-independent with the following minimal set of assumptions:
-
The BSM sector allows for the existence of heavy, charged Higgs bosons \(H^{\pm }\) in addition to the SM Higgs \(h^0\). There could (and in general, will) be other neutral and/or charged Higgs bosons and perhaps new heavy fermions as well, but our analysis in this section does not depend on these specifics.
-
The model also allows for the presence of new, heavy charged and neutral gauge bosons (\(W'\), \(Z'\)) that are fermiophobic. This last assumption is a critical one as we would like to explore charged Higgs decay to these new gauge bosons, and will therefore require relatively light \(W'\) and \(Z'\) that are not already ruled out by direct searches.
-
There is a non-zero coupling between the heavy gauge bosons and the \(H^\pm \) at tree level, i.e., the vertices of the type \(H^\pm W'^{\mp }Z\) and \(H^\pm W^{\mp }Z'\) exist and are non-vanishing.
Our goal here is to explore the discovery prospects of the charged Higgs in the channel \(H^{\pm }\rightarrow W'^{\pm }~Z\). A simpler alternative would of course, be to simply look for the process \(H^{\pm }\rightarrow W^{\pm }Z\) – the \(H^{\pm }W^{\mp }Z\) is an interesting vertex whose phenomenology has been explored elsewhere [16, 17]. It has been shown [18] that for the Lagrangian term \({\mathcal {L}} = \xi H^{\pm }W^{\mp }_{\mu }Z_{\mu } + h.c.\), the coupling can be expressed in the general fashion
where \(\rho = \frac{m^{2}_{W}}{m^{2}_{Z}\cos ^{2}\theta _{W}}\), \(T_i\) and \(Y_i\) are the \(T_3\) and hypercharge quantum numbers of the ith Higgs field and \(v_i\) is its vacuum expectation value (vev). For the 2HDM, the above coupling vanishes at tree level [18] – in fact, for any model with multiple Higgs fields all in the doublet representation under the SM \(SU(2)_L\), it can be shown that the \(H^{\pm }W^{\mp }_{\mu }Z_{\mu }\) vertex is absent at tree level [19]. On the other hand, the Georgi–Machacek model [8, 20] for instance, where one introduces an additional Higgs triplet, contains in its scalar spectrum a \(H^{\pm }\) which does indeed couple to \(W^{\pm }\) and Z boson at tree level but remains fermiophobic. It is evident that, depending on model construction the phenomenology associated with various BSM states will change significantly. With that in mind, in this article we propose an alternative discovery prospect of the charged Higgs boson within the context of a BSM scenario with enlarged scalar and gauge sectors.
Both ATLAS [21, 22] and CMS [23, 24] have looked for the \(H^{\pm }\) primarily via two mechanisms: (i) where the \(H^{\pm }tb\) vertex comes into play in production or decay mode or both, and (ii) where the \(H^{\pm }\) is produced from the fusion of \(W^{\pm }\) and Z. In Fig. 1, we present the bound (obtained from ATLAS and CMS measurements) on the \(H^{\pm }\) production cross-section for these two mechanisms [24, 25] – understandably, the limits are weaker in the latter case. Depending on the final state, the combined measurement by ATLAS has imposed upper limits on \(\sigma \times \)BR for a charged Higgs in various channels in the mass-range 180 GeV to 3 TeV. The CMS collaboration searches and results can be found in [26]. In Table 1, we summarize the various search channels for the charged Higgs in the ATLAS and CMS experiments and the mass range probed in each case along with the range of cross-section limits. We close this section mentioning that in a realistic model, these limits will be relaxed somewhat as the branching ratio for each channel would typically be less than 100% (experimental numbers are quoted assuming 100% BR in the channel of interest). Indeed in models where the “non-standard” decays of the charged Higgs are sizeable [27, 28], the limits can be substantially weakened – we will illustrate this in Sect. 3 in one specific context. In the section on LHC phenomenology that follows, our discussion will thus not assume any restrictions on the charged Higgs mass or its couplings.
2.2 LHC analysis
In this section, we analyze the feasibility for a 5\(\sigma \) discovery of the charged Higgs concentrating on its decay to particles in the extended gauge sector. We restrict our attention to the associated production mode of the \(H^\pm \) \(g b \rightarrow H^{\pm } t\) and perform the data simulation using the MADGRAPH5aMC@NLO event generator [33] (working in the five flavor scheme). The SM backgrounds which are used for this study are generated via the in-built SM model file in the MADGRAPH repository. The parton level simulation from MADGRAPH is passed on to PYTHIA 6 [34] for jet showering and hadronization followed by detector level simulation in DELPHES 3 [35]. The BSM model file used in the next section has been designed using FEYNRULES [36, 37].
The primary process we are interested in is \(p p \rightarrow H^{\pm } {\bar{t}} \rightarrow W^{'\pm } Z {\bar{t}}\). Since we assume that the \(W'\) does not couple to fermions, we are left with the choice of considering the two decaysFootnote 1\(W^{'\pm } \rightarrow W^{\pm } Z\) and \(W^{'\pm } \rightarrow W^{\pm } h\). Accordingly, we look at three different signals depending on the subsequent decays of the various gauge bosons. These are
-
(a)
Signal 1: \(p p \rightarrow H^{\pm } {\bar{t}} \rightarrow W^{'\pm } Z {\bar{t}} \,(W^{'\pm } \rightarrow W^{\pm } Z) \rightarrow W^{\pm } W^{\mp } Z Z b \rightarrow 4j + 4\ell + b \),
-
(b)
Signal 2:
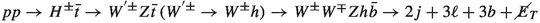 , and
, and -
(c)
Signal 3: \(p p \rightarrow H^{\pm } {\bar{t}} \rightarrow W^{'\pm } Z {\bar{t}}\, (W^{'\pm } \rightarrow W^{\pm } Z) \rightarrow W^{\pm } W^{\mp } Z Z {\bar{b}} \rightarrow 4j + 2\ell + 3b.\)
In choosing the various final states, our consideration has been to both find a channel that would aid a complete reconstruction of the \(H^\pm \) while also minimizing the SM background to the extent possible. This has led us to consider final states that, in addition to hadronic components, also have leptons and missing energy (usually the presence of the latter will lead to one or more electroweak vertex in the corresponding SM Feynman diagrams leading to lower cross-sections). Considering the multijet final states, the major experimental search challenges will arise from SM processes like \(t{\bar{t}}\) + jets and VV + jets with subdominant contributions from VVV + jets etc. In addition, we have also considered \(t{\bar{t}}h\) + jets, Vh + jets, \(t{\bar{t}}V\) and VVh + jetsFootnote 2 as part of the entire SM background. These SM backgrounds are listed in Table 2 along with their corresponding cross-sections. While the \(t{\bar{t}}\) is required to decay leptonically, in the case of VV + jets, we consider different possibilities such that the final state topology of the background processes are closer to the different signals listed above. We employ the following set of basic identification cuts at the time of simulation that would eliminate events with low \(p_T\) jets and leptons:
We have chosen a wider window for the pseudorapidity for jets as compared to the leptons to ensure that we do not lose many signal events. Further, we demand that all pairs of particles are optimally separated:
Within this basic framework, we now move on to the task of optimizing the discovery process of the charged Higgs by designing kinematic cuts for the three different final states given above. No heavy \(W',Z'\) has been discovered at the LHC thus far and so, beyond the assumption of the existence of a heavy gauge boson with a specific mass, we do not use any particular attributes of it to construct our cuts. Specifically, we do not impose an invariant mass cut around the \(W'\) mass to filter out the SM background.Footnote 3 We stress here that what follows is a purely background analysis – the signal is represented by a fiducial cross-section and included here to ensure that the cuts do not affect it too much.
2.2.1 Signal I
We begin our discussion of the process \(p p \rightarrow H^{\pm } {\bar{t}} \rightarrow W^{'\pm } Z {\bar{t}} \,(W^{'\pm } \rightarrow W^{\pm } Z) \rightarrow W^{\pm } W^{\mp } Z Z b \rightarrow 4j + 4\ell + b \) choosing as a benchmark point \(m_{H^{\pm }} = 500\) GeV and \(m_{W^{'}} = 350\) GeV (hereafter dubbed BP1). In Table 3, we present the cut flowchart that minimizes the SM background effectively for this particular choice. While stronger \(p_T\) cuts beyond the identification step would prove to be reasonably useful, we find that for this signal a cut on the hadronic transverse energy proves more efficacious. It can be seen in particular that the \(t{\bar{t}}\) + jets background goes down by more than 50% once we demand \(H_T \ge 400~ \text {GeV}\). We then move to a set of self-evident identification cuts: \(N_j \ge 4 \), \(N_l \ge 4\) as we are dealing with a multi-jet, multi-lepton final state. While this certainly helps us get rid of a major chunk of background, it can be seen that it does so at the cost of signal reduction – this is to be expected given the current lepton identification percentages at the LHC. To deal with the \(t{\bar{t}}\) events that remain after this step (as there are still events with semi-leptonic decays of the top quark that can survive these identification cuts), we demand an upper bound on  for the surviving events. Finally, we reconstruct the harder of the two Z bosons from the more energetic lepton pair (this is from the \(H^{\pm } \rightarrow W^{'\pm } Z\) part of the process). While strictly speaking this step is superfluous given ultimately we want to reconstruct the \(H^\pm \) itself, it is included here for its effect in bringing down the vector boson dominated part of the background.
for the surviving events. Finally, we reconstruct the harder of the two Z bosons from the more energetic lepton pair (this is from the \(H^{\pm } \rightarrow W^{'\pm } Z\) part of the process). While strictly speaking this step is superfluous given ultimately we want to reconstruct the \(H^\pm \) itself, it is included here for its effect in bringing down the vector boson dominated part of the background.
The reason for choosing the particular numbers in Table 3 for the \(H_T\) and  cuts can be inferred from Fig. 2. It can be seen that for the specific benchmark point chosen, the signal events (red curve in the plots) are peaked for larger \(H_T\) (> 400 GeV) and smaller
cuts can be inferred from Fig. 2. It can be seen that for the specific benchmark point chosen, the signal events (red curve in the plots) are peaked for larger \(H_T\) (> 400 GeV) and smaller  (< 50 GeV), regions where the SM background events are (mostly) minimal. While a stronger \(H_T\) cut would undoubtedly help in reducing \(t{\bar{t}}\) even more, we have stuck with a more moderate cut so as to not affect the signal too much. In Fig. 3, we display the invariant mass distribution \(m_{2j+4\ell }\) for the signal and background before and after implementing the kinematic cuts outlined in Table 3 (here the two leading jets in the final state are chosen to reconstruct the \(H^\pm \)). Based on the distribution, we conclude that a slightly asymmetric cut of \(400~\text {GeV}\le m_{2j+4\ell }\le 800~\text {GeV}\) would be quite effective in teasing out the signal in this particular channel.
(< 50 GeV), regions where the SM background events are (mostly) minimal. While a stronger \(H_T\) cut would undoubtedly help in reducing \(t{\bar{t}}\) even more, we have stuck with a more moderate cut so as to not affect the signal too much. In Fig. 3, we display the invariant mass distribution \(m_{2j+4\ell }\) for the signal and background before and after implementing the kinematic cuts outlined in Table 3 (here the two leading jets in the final state are chosen to reconstruct the \(H^\pm \)). Based on the distribution, we conclude that a slightly asymmetric cut of \(400~\text {GeV}\le m_{2j+4\ell }\le 800~\text {GeV}\) would be quite effective in teasing out the signal in this particular channel.
The \({H}_T\) and  distribution for both the signal and the SM backgrounds with \(m_{H^{\pm }} = 500\) GeV and \(m_{W^{'}} = 350\) GeV for Signal 1. Here, the sum of all SM backgrounds has been displayed (blue curve). For information regarding the actual number of events employed in the analysis, please see the first row of the corresponding cut flow chart
distribution for both the signal and the SM backgrounds with \(m_{H^{\pm }} = 500\) GeV and \(m_{W^{'}} = 350\) GeV for Signal 1. Here, the sum of all SM backgrounds has been displayed (blue curve). For information regarding the actual number of events employed in the analysis, please see the first row of the corresponding cut flow chart
The charged Higgs invariant mass distribution before and after implementing the cuts listed in Table 3 for Signal 1. Here, the sum of all SM backgrounds has been displayed (blue curve). For information regarding the actual number of events employed in the analysis, please see the first row of the corresponding cut flow chart
While the benchmark point chosen above certainly seems conducive to discovery in the \(4j + 4\ell + b \) channel, it is instructive to ask how the discovery prospects look like for a case where there is a larger mass splitting between the \(H^\pm \) and the \(W'^\pm \). In Table 4, we present the cut flowchart for the benchmark point \(m_{H^{\pm }} = 700\) GeV and \(m_{W^{'}} = 350\) GeV (hereafter called BP2). Comparing with Table 3, we see a couple of important differences: since we are dealing with a more massive charged Higgs, we have chosen a stronger \(H_T\) cut in this case. Accordingly, there is a larger reduction in the \(t{\bar{t}}\) (and other) backgrounds. In addition, while it was not necessary in the previous benchmark point analysis, in this case we have put in a \(p_T\) cut on the leading lepton to aid suppression of the SM background more effectively. While it can be seen that one can achieve a good \(S/\sqrt{B}\) in this case as well, we need also to consider that in a realistic model scenario the production cross-section for a heavier \(H^\pm \) will be significantly lower.
2.2.2 Signal 2
Since the \(W'\) is assumed to have non-zero couplings to the scalar sector, we now consider the decay chain  – we once again begin with BP1. The cut flowchart for this particular benchmark point for this signal is displayed in Table 5. We begin with a \(H_T\) cut as before, and further demand at least 2 b-jets and 3 leptons. Further, we choose an invariant mass window of the two hardest leptons around the Z mass. Since in this case both the signal and the \(t{\bar{t}}\) background will have a sizeable missing energy, we have not put in a
– we once again begin with BP1. The cut flowchart for this particular benchmark point for this signal is displayed in Table 5. We begin with a \(H_T\) cut as before, and further demand at least 2 b-jets and 3 leptons. Further, we choose an invariant mass window of the two hardest leptons around the Z mass. Since in this case both the signal and the \(t{\bar{t}}\) background will have a sizeable missing energy, we have not put in a  cut. The \(H_T\) and \(M_{\ell \ell }\) distributions for this case are shown in Fig. 4 – it can be seen that the hadronic transverse momentum has the same qualitative features as that of Signal 1 thus explaining the same choice of cuts. The invariant mass distribution \(m_{2b2j2\ell }\) before and after implementation of the cuts is shown in Fig. 5. It can be seen that the choice of cuts has rendered most background negligible except for \(VVV+\text {jets}\) – however this background has a rather small cross-section and should not provide a great impediment to discovery.
cut. The \(H_T\) and \(M_{\ell \ell }\) distributions for this case are shown in Fig. 4 – it can be seen that the hadronic transverse momentum has the same qualitative features as that of Signal 1 thus explaining the same choice of cuts. The invariant mass distribution \(m_{2b2j2\ell }\) before and after implementation of the cuts is shown in Fig. 5. It can be seen that the choice of cuts has rendered most background negligible except for \(VVV+\text {jets}\) – however this background has a rather small cross-section and should not provide a great impediment to discovery.
 channel corresponding to \(m_{H^{\pm }}=500\) GeV and \(m_{W^{'}}=350\) GeV for Signal 2
channel corresponding to \(m_{H^{\pm }}=500\) GeV and \(m_{W^{'}}=350\) GeV for Signal 2The \({H}_T\) and \(M_{\ell \ell }\) distribution for both signal and SM backgrounds with \(m_{H^{\pm }} = 500\) GeV and \(m_{W^{'}} = 350\) GeV for Signal 2. Here, the sum of all SM backgrounds has been displayed (blue curve). For information regarding the actual number of events employed in the analysis, please see the first row of the corresponding cut flow chart
s
The charged Higgs invariant mass distribution before and after implementing the cut mentioned in Table 5. Here, the sum of all SM backgrounds has been displayed (blue curve). For information regarding the actual number of events employed in the analysis, please see the first row of the corresponding cut flow chart
In Table 6, we consider BP2 with a wider mass splitting as before. Comparing with Table 4, we have put in a \(p_T\) cut on the leading jet in lieu of the missing energy cut. In addition, we have resorted to a tight(er) \(m_{\ell \ell }\) cut to minimize backgrounds with vector bosons.
 channel with the signal corresponding to \(m_{H^{\pm }} = 700\) GeV and \(m_{W^{'}} = 350\) GeV
channel with the signal corresponding to \(m_{H^{\pm }} = 700\) GeV and \(m_{W^{'}} = 350\) GeV2.2.3 Signal 3
We now move to the third process \(p p \rightarrow H^{\pm } {\bar{t}} \rightarrow W^{'\pm } Z {\bar{t}} (W^{'\pm } \rightarrow W^{\pm } Z) \rightarrow W^{\pm } W^{\mp } Z Z {\bar{b}} \rightarrow 4j + 2\ell + 3b\). Note that this is quite similar to Signal 1 and the difference here arises only from the way the SM gauge bosons decay. Here we require the Z that comes from the \(H^\pm \) to decay to \(b{\bar{b}}\) while the other Z (from the \(W'\) decay) is required to decay leptonically. While it is certainly advantageous to exploit the b-jet tagging at the LHC in addition to higher branching ratios, the \(t{\bar{t}}\) + jets background would need to be suppressed carefully. However, as we demonstrate in Table 7 for BP1, this can indeed be achieved. We find, as before, that the background events that remain after the \(H_T\) and basic identification cuts can be efficiently reduced with a  cut. In Table 8, we display the efficacy of cuts for the other benchmark point \(m_{H^{\pm }} = 700\) GeV and \(m_{W^{'}} = 350\) GeV – it is seen that the final number of background events is smaller in this case owing to the harder \(H_T\) cuts involved. Thus, the discovery of heavy or light charged Higgses in these channels is a delicate balance between getting enough signal events (which is difficult for heavier \(H^\pm \)) and suppressing the background more effectively (which is easier for heavier \(H^\pm \)). We will revisit this issue in the next section.
cut. In Table 8, we display the efficacy of cuts for the other benchmark point \(m_{H^{\pm }} = 700\) GeV and \(m_{W^{'}} = 350\) GeV – it is seen that the final number of background events is smaller in this case owing to the harder \(H_T\) cuts involved. Thus, the discovery of heavy or light charged Higgses in these channels is a delicate balance between getting enough signal events (which is difficult for heavier \(H^\pm \)) and suppressing the background more effectively (which is easier for heavier \(H^\pm \)). We will revisit this issue in the next section.
We reiterate that the preceding analysis was purely an exercise to suppress SM backgrounds for relevant processes – the signal cross section used was fiduciary. We would like to draw the reader’s attention to an important point raised in Ref. [38] and in related studies [39, 40] that concerns the difference between the four flavour scheme (4FS) and the five flavour scheme (5FS) used at the level of MADGRAPH event generation. The crucial difference between the schemes, as concerns the production of a charged Higgs boson, is that in 4FS the final state b-quark arises due to a hard scattering process and in 5FS the b-quark is part of the parton flux. While inclusive observables like the total cross-section do match between the two schemes, shapes of differential distributions can be potentially different particularly those that involve the soft b-jet. In our analysis, we have made use of cuts on jet and b-jet multiplicities – observables that are sensitive to the differences in the 4FS and 5FS. The agreement between these is better if one uses a shower scale of \(F=4\) (as opposed to the default MADGRAPH value \(F=1\) that we worked with). This could potentially cause a few percent corrections in the results (given that the general conclusion of Ref. [38] is that the 4FS is more robust) – however, given that all our backgrounds are almost completely suppressed, it is reasonable to assume that such differences, at least in the present study, should not affect our overall results as far as model implications are concerned.
Before closing the section, we would like to calculate the actual signal cross section necessary for discovery or exclusion in a specific model for each of the three signals for both benchmark points using [41]
where \(S = \sigma _{S}{\mathcal {L}}\) and \(B = \sigma _{B}{\mathcal {L}}\) are the total number of signal and background events that survive the cuts. In Table 9, we present the corresponding numbers for both the benchmark points and for all three signal scenarios discussed above.
It can be seen that Signal \(( 4j + 2\ell + 3b)\) requires slightly lower values of signal cross-section for both exclusion (the \({\mathcal {Z}}_{E} \ge 1.96\) column) and a \(5\sigma \) discovery compared to the other two. However, the feasibility of one or the other depends on strength of couplings and patterns of decays and can only be answered within a model-specific context. We turn to this issue in the next section.
3 Model implications
3.1 A toy model
We begin our discussion with a toy model to get a sense of the feasibility of the cross-section numbers estimated in Sect. 2. While a typical BSM scenario could have multiple particles and involved patterns of symmetry breaking, herein we concentrate on the minimal set necessary to illustrate our results along the lines of [16]. Thus we consider a toy model that includes a charged Higgs and a heavy \(W'\) in addition to the SM particle spectrum. We begin with the relevant terms in the Lagrangian for the \(W'\).
where S denotes a generic neutral scalar and \(m_{W^{'}}\) is the mass of the additional gauge boson. The interaction terms between the SM and the new gauge bosons come about after rewriting the gauge kinetic energy in terms of the mass eigenstates in the usual manner. For our current purposes, we restrict to the case where the masses of the possible additional neutral scalars (other than the SM-like Higgs boson) are larger than \(m_{W^{'}}\). In addition, since we are dealing with a fermiophobic \(W',\)Footnote 4 we do not consider decays to SM quarks and leptons. Thus the only relevant decay channels are the WZ and the Wh modes – we write down the corresponding decay widths below:
where \(m_{12} = m^{2}_{W} + m^{2}_{Z}\), \(m_{\pm } = m_{W} \pm m_{Z}\), and the EWSB scale \(v=246\) GeV. The couplings \(\xi _{W'WZ}\) are \(\xi _{W'Wh}\) are taken as free parameters (these typically depend on the new gauge couplings in an extended gauge model), and we fix them to reasonable \({\mathcal {O}}(1)\) numbers in what follows. In Fig. 6, we display the branching ratio of the \(W'\) in the mass range 200–600 GeV for two different choices of the couplings. One can notice that even for low values of \(\xi _{W'WZ}\), the WZ channel dominates over the Wh for \(m_{W'}>350\) GeV.
In Fig. 7, we illustrate the variation in branching ratio values for both these decay modes for \(m_{W'}= 350\) GeV. For \(\xi _{W'WZ} \ge 0.4,\) \({\text {BR}}( W' \rightarrow WZ)\) is greater than 90% for entire range of \(\xi _{W'Wh}\). On the other hand, the \({\text {BR}}(W' \rightarrow Wh)\) has an appreciable value (say, \( > rsim \) 30%) in the region \(\xi _{W'WZ} < 0.2.\) In our subsequent analysis, we will fix \({\text {BR}}(W' \rightarrow W Z)\) to 0.95 (for Signals 1 and 3) and \({\text {BR}}(W' \rightarrow W h)\) to 0.7 (for Signal 2) as these numbers represent the best case scenarios under the present considerations.
s
Turning now to the charged Higgs boson, in Eq. (3.4), we write down the most general phenomenological Lagrangian that describes the interaction of the \(H^\pm \) with the SM sector.
where the projection operators are defined in the usual way: \(P_{L/R} = \frac{(1 \mp \gamma _{5})}{2}\), and \(\xi ^{H^{\pm }}_{VS}\), \(\xi ^{H^{\pm }}_{f/f^{'}}\), \(\xi ^{H^{\pm }}_{V^{'}V}\) are model dependent coupling parameters. In the first term, \(V_\mu ^{\pm }\) can denote either the \(W_\mu ^{\pm }\) or its heavy counterpart (the couplings in the two cases would, of course, be different as is evident from the notation). The second term denotes interactions of the \(H^\pm \) with pairs of gauge bosons WZ, \(W'Z\), and \(WZ'\) each with a coupling generically denoted by \(\xi ^{H^{\pm }}_{VV^{'}}\). While one can design models in which these couplings are independent, we assume the following pattern (with the assumption that the charged Higgs belongs in a multiplet that contributes to electroweak symmetry breaking): \(\xi ^{H^{\pm }}_{WZ^{'}}\) = \(\cos ^{2}\theta _{W}\xi ^{H^{\pm }}_{W^{'}Z}\), \(\xi ^{H^{\pm }}_{WZ}\) = \(\left( \frac{m_{W} }{ m_{W^{'}}}\right) \xi ^{H^{\pm }}_{W^{'}Z}\), and similarly in the scalar sector \(\xi ^{H^{\pm }}_{W^{'}h}\) = \(\left( \frac{m_{W}}{m_{W^{'}}}\right) \xi ^{H^{\pm }}_{Wh}\). For example, in a general left-right symmetric model where the symmetry breaking is engineered by a \(Y = \frac{1}{2}\) scalar bidoublet and two \(Y = 1\) complex triplet scalar representations \(\Delta _{L/R}\), one can achieve a similar pattern of couplings. In general, the charged Higgs boson can couple to up- and down-type quarks and to leptons differently. However to reduce the number of free parameters and make our analysis simpler, we assume \(\xi ^{H^{\pm }}_{f} = \xi ^{H^{\pm }}_{f^{'}} = \xi ^{H^{\pm }}_{ff^{'}}\) (for example, like in the Type-I 2HDM [3, 42]). Thus, we are left with three independent coupling parameters \((\xi ^{H^{\pm }}_{W^{'}Z},\) \(\xi ^{H^{\pm }}_{ff^{'}}\) and \(\xi ^{H^{\pm }}_{Wh})\) that we will treat as free parameters in what follows and fix them to reasonable \({\mathcal {O}}(1)\) numbers. In Eqs. (3.5–3.7), we present the decay widths for the charged Higgs in the various available channels.
where \(\lambda \) is the usual Kallen function \(\lambda (x, y, z) = x^{2} + y^{2} + z^{2} - 2xy -2yz -2xz\).
In Fig. 8, we show the \(H^{\pm }\) boson decay branching ratios in different channels for various choices of \(\xi ^{H^{\pm }}_{W'Z}\) and \(\xi ^{\pm }_{ff^{'}}\) fixing \(\xi ^{\pm }_{Wh}\) at 0.1. One can observe that for moderate values of \(\xi ^{H^{\pm }}_{W^{'}Z}\), \({\text {BR}}(H^{\pm }\rightarrow W^{'} Z)\) is non-negligible and can reach \( > rsim \) 20% for \(m_{H^{\pm }} \ge 500\) GeV. For slightly larger values of \(\xi ^{H^{\pm }}_{W'Z}\), this number can be as high as 50% as is demonstrated in the first of the three plots in Fig. 8. Interestingly, the \(H^{\pm } \rightarrow W Z'\) decay channel also has an appreciable contribution for \(m_{H^{\pm }} > rsim 650\) GeV. Moreover, if the \(Z'\) decays to Zh, the cut flow chart presented for Signal 2 can be applicable.
In Fig. 9, we display the branching ratio for a democratic choice of couplings: \(\xi ^{H^{\pm }}_{ff^{'}} = \xi ^{H^{\pm }}_{W^{'}Z} = \xi ^{H^{\pm }}_{Wh} = 0.5.\) Interestingly in this case, for \(m_{H^{\pm }} \ge 550\) GeV, the \(H^{\pm } \rightarrow W' h\) becomes the dominant decay mode. If we choose to decay the \(W'\) to WZ, then the final state topology in this case is identical to that of Signal 2. If we trade the \(M_{\ell {\bar{\ell }}}\) cut with something like 110 GeV \(\le M_{b{\bar{b}}} < 140\) GeV cut in Table 5, a majority of the SM backgrounds can be rejected. However, the \(t{\bar{t}}h\) + jets background would be a challenge in this particular scenario and thus our cut flowchart for Signal 2 might have to be supplanted with additional cuts. If on the other hand we consider \(W'\rightarrow W h\), the final state would be \(WWhh + {\bar{b}}\). Though in the present study, we do not explore the collider phenomenology for these interesting channels and stick to the scenario where \(\xi ^{H^{\pm }}_{Wh} = 0.1,\) we mention them here to give an idea of the kind of rich phenomenology that the charged Higgs can enjoy in many extended gauge models.
To illustrate the differences between the two benchmark points, in Fig. 10, we present the variation of \({\text {BR}}(H^{\pm } \rightarrow W Z)\) in the parameter plane \(\xi ^{H^{\pm }}_{W^{'}Z}\) vs \(\xi ^{H^{\pm }}_{ff^{'}}\) plane for the two different choices of \(m_{H^\pm }\) used in this study. A heavier \(H^\pm \) decays to \(W'h\) more readily and at the cost of the \(W'Z\), and hence we find that this branching ratio cannot reach the numbers that the 500 GeV case can.
Any estimate finally has to involve both the production cross-section (\(pp\rightarrow H^\pm {\bar{t}}\) in our case) and the various branching ratios. In Fig. 11 we present the production cross-section for the charged Higgs boson in the mass range 200–700 GeV at the 14 TeV LHC via the associated production mode for various choices of \(\xi ^{H^{\pm }}_{ff^{'}}\). The black dashed line represents the cross-section values [40, 43, 44] for \(\xi ^{H^{\pm }}_{ff^{'}}=1\).
Having specified the cross-section and the branching ratios, we are now in a position to present the reach plot for the \(H^\pm \) in the various channels within the context of this toy model. For this purpose, we require
where \(\epsilon _{s}\) denotes efficiency of the cut based analysis, a number that is independent of the model dependent parameters. We fix \(\epsilon _{s}\) to a rather modest value of 0.25 in the reach plots presented in Fig. 12 – it should be noted that more parameter space will open up for slightly more liberal choices of efficiency. It can be seen that both Signal 1 and Signal 2 can prove to be quite effective in aiding the discovery of a charged Higgs, while Signal 3 requires higher luminosities. In the plot, the yellow and cyan regions correspond to \(5\sigma \) and \(3\sigma \) discovery regions while the gray region can potentially be excluded. While regions of \(5\sigma \) discovery are admittedly small (particularly for Signal 3), it is clear from these plots that even in this toy model scenario, the extended gauge sector does offer new possibilities for a charged Higgs boson discovery that could be probed at the LHC.
3.2 A not so toy model
In a recent work [15], a BSM scenario with an enlarged gauge symmetry \(SU(2)_{0}\times SU(2)_{1}\times U(1)_{2}\) was proposed which also has an extended scalar sector that includes a charged Higgs. In this section, we understand the reach of the discussed signals in the context of this model. We present here the essential elements of the model for the present purposes – for a complete description of the model, the reader is invited to consult Ref. [15].
Given the extended nature of the gauge group, the model contains new heavy gauge bosons in addition to heavy charged and neutral Higgs bosons. Electroweak symmetry breaking in this set-up is engineered by two Higgs doublets \(\Phi _{1,2}\) and a non linear sigma model field \(\Sigma \). The vevs of \(\Sigma \) and \(\Phi _2\) are denoted by F and that of \(\Phi _1\) is denoted by f – these are parametrized as
The explicit form of these scalar fields are defined in the following mannerFootnote 5
The coupling constants of the \(SU(2)_{0}\), \(SU(2)_{1}\), and \(U(1)_{2}\) gauge groups are denoted by \(g_{0}\), \(g_{1}\) and \(g_{2}\)Footnote 6 respectively and parametrized as
The parametrisation which we have described in Eq. 3.9 is certainly one of many possibilities. A more general parametrization would be to simply label the vevs of the three fields \(f_{1}, f_{2}, \text {and}\ F\). For this choice, the W and \(W^{'}\) mass will take the following forms:
To obtain the correct W boson mass one should equate the combination \(\frac{f^{2}_{1}f^{2}_{2} + F^{2}\left( f^{2}_{1} + f^{2}_{2}\right) }{F^{2} + f^{2}_{2}}\) with \(v^{2}\) and thus only two these vevs can be free parameters. However, even with this constraint, the pattern of EWSB is not “neat” for this model unlike 2HDM to render a clean parametrization of the remaining two vevs. However, one of the prime motivations of this model, as explained in Ref. [15] was to facilitate a comparison with the 2HDM. This prompts one to consider the case \(f_1=f_2\) which would in turn mean that the W boson mass is now
This immediately helps us employ a 2HDM-like parametrization \(F = \sqrt{2}v\cos \beta , ~f = v\sin \beta \). Note that this is still different from the 2HDM parametrization \(v_1 = v\cos \beta , ~v_2 = v\sin \beta \) – the result of this is that the hWW coupling in this model does not factor neatly as in the 2HDM as \(g_{SM}\sin (\beta -\alpha )\) (where \(\alpha \) is the mixing angle in the neutral Higgs sector). So, in what follows, we will be displaying our results in terms of \(\sin \beta \) rather than \(\sin (\beta -\alpha )\).
The general gauge invariant potential takes the following form:
After symmetry breaking the scalar spectrum of the model contains two CP-even Higgs bosons (H, h), a pseudoscalar A, and a pair of charged Higgs bosons \(H^{\pm }\). One can notice that the \(H^{\pm }\) mass comes solely from the \(\lambda _{4}\) term in Eq. 3.14 – the \(\lambda _{5}\) and \(\lambda _{6}\) terms do not contain any terms quadratic in the pions and describe interactions. The mass matrix for the charged scalars thus takes the following form:
The corresponding eigenstates of the Goldstone modes \(G^{\pm }_{1}\), \(G^{\pm }_{2}\) which get eaten by the \(W^{\pm }_{\mu }\) and \(W^{'\pm }_{\mu }\) can be expressed as
On other hand the physical charged Higgs corresponds to the combination
and its mass can be computed to be \(M^{2}_{H^{\pm }} = \frac{\lambda _{4}}{2}(2f^{2} + F^{2})\). The fermionic sector of the model is constructed in such a fashion as to mimic the traditional Type-I 2HDM Higgs-fermion couplings at leading order. In other words, we ensure that the SM fermions get their masses primarily from the \(\Phi _{1}\) doublet. In Table 10 we present various charged Higgs boson couplings that will be relevant for our current discussion in terms of a parameter \(x=m_W/m_{W'}\). We identify the lighter CP-even Higgs as the \(h-125\) GeV SM-like Higgs and fix the other neutral Higgs masses to be heavier than the charged Higgs. As a consequence, the decays \(H^{\pm } \rightarrow VH/VA\) (where \(V = W~ \text {or}~ W^{'}\)) are kinematically disallowed. The mixing angle between the two CP even Higgs is denoted by \(\alpha \) and it follows the same definition as in the 2HDM literature. One can notice the coupling \(\xi ^{H^{\pm }}_{ff^{'}}\) is proportional to ratio of the two vevs similar to the typical Type-I 2HDM. The compelling feature of this model is a non-zero of \(\xi ^{H^{\pm }}_{W^{\mp }Z}\) coupling at tree level which is absent in models where symmetry breaking is engineered purely by singlet or doublet representations of the scalar fields – see Eq. (2.1) [19]. Thus one could potentially study the \(H^{\pm }\) decay via the WZ mode. However the charged Higgs coupling to WZ mode is suppressed by an additional \(x^{2}\) factor, which makes this mode phenomenologically difficult to probe. Interestingly, the coupling between the \(H^{\pm }\) and \(W^{'}Z\) is proportional to \(\sin \beta \) only and thus not necessarily suppressed making this model a good candidate for our present study.
Before moving ahead, let us make a couple of comments regarding the \(W^{'}\) boson. Any BSM scenario where the electroweak symmetry is enlarged by an additional SU(2) group would contain an additional pair of charged gauge bosons after symmetry breaking. In general these \(W^{'}\)s couple to SM fermions and can be observed in different direct search experiments. The current limit on these heavy gauge bosons are set to be in the TeV range from direct searches in the fermionic decay channels. However, in the current model the gauge-fermion interactions are constructed in such a way that the coupling of the \(W^{'}\) to SM fermions is zero at tree level – for details, the reader is referred to [15]. As a result the experimental limits on the \(W^{'}\) from direct searches do not apply and thus one can consider relatively low values of \(m_{W^{'}}\). Due to its fermiophobic nature, the \(W^{'}\) decays primarily via the Wh and WZ modes. The h and the Z can decay via \(b{\bar{b}}\) and the dilepton channels respectively, which leads to multi-lepton or multi-b quark final states for the charged Higgs which is the subject of the analysis in Sect. 2.
We now turn to the charged Higgs boson phenomenology in this model. We begin in Fig. 13 presenting the production cross-section for the charged Higgs boson in the \(p p \rightarrow H^{\pm } t\) channel for the benchmark scenarios \(m_{H^{\pm }} = 500\) GeV and 700 GeV as a function of \(\sin \beta \) (related to the ratio of the vevs – see Eq. 3.9) in the context of the 14 TeV LHC. As this production mode is controlled by \(\xi ^{H^{\pm }}_{tb}\) coupling \((\propto \cot \beta ),\) the cross section falls significantly for higher values of \(\sin \beta \). The cross section is of course independent of the model parameter \(\alpha \) (the mixing between the CP-even neutral Higgs states).
In Fig. 14, we present the \(H^{\pm }\) branching ratios in the various kinematically allowed channels. As expected for low value of \(\sin \beta \), the branching ratio for \(t{\bar{b}}\) channel dominates over \(W^{'}Z\) mode in the mass range up to TeV. However, if we resort to large \(\sin \beta \) value, the above situation is altered significantly due to the suppression of the \(\xi ^{H^{\pm }}_{tb}\) coupling. In our present work, we require the charged Higgs to be produced in association with a top quark and decay via the \(W^{'}Z\) mode. To determine the region of parameter space which favours discovery one needs to take into account the effect of both the production cross section as well as decay branching ratios. Here, we set the Higgs mixing angle \(\sin \alpha =-\frac{1}{\sqrt{2}}\). For this particular choice of \(\sin \alpha \), one can satisfy the recent Higgs discovery data for \(\sin \beta > 0.4.\) For details corresponding to the relevant constraints, interested readers may look into Ref. [15].
It is important to note that in this analysis, it is implicity assumed that the narrow width approximation (NWA) holds so the total cross-section can be neatly factored into production times branching ratio. However, in a model-specific scenario, it needs to be ascertained that the width of the particle in question is not too high to make sure this assumption invalid. For \(m_{H^\pm }=500\) GeV and \(m_{W'}= 350\) GeV, we have checked that \(\Gamma /M\) for either particle is \(\le 10\%\) so that NWA in this regime is valid for this model.
With these numbers in place, we show in Fig. 15, the reach plot in this extended gauge model for Signal 1 and Signal 2 as an illustration of the methods employed in this study. It can be seen that a wide range of \(\sin \beta \) allows for discovery of the charged Higgs in this channel for an integrated luminosity of \({\mathcal {L}}=1000\) fb\(^{-1}\) or higher. We have also imposed the cut efficiency \(\epsilon _{s}\) at 0.25. We choose \(\sin \alpha \) to be \(-\frac{1}{\sqrt{2}}\) which is allowed by various theoretical as well as experimental bounds that are calculated for this model. In case of Signal 1, one can achieve 5\(\sigma \) significance for 1000 \(\text {fb}^{-1}\) luminosity. On the other hand for Signal 2, it is only achievable for the 3000 \(\text {fb}^{-1}\) luminosity. For Signal 3 however, the total signal events which survive after imposing the cuts turns out to not be sufficient for discovery.
4 Conclusion
While the LHC has not produced any new particle beyond the SM-like Higgs, particle physics is entering a stage where more sophisticated analysis methods need to be employed to tease out any hints of new physics. At the same time, care should be taken to exhaust all possible forms of search for possible hints of heavy gauge, scalar, or fermionic degrees of freedom already accessible at the LHC or in the near future by exploring channels and techniques not considered before. In this spirit, in this paper we have presented a case of discovering a charged Higgs boson – traditionally looked for in tb and \(\tau \nu \) modes (or in WA/Wh modes in 2HDM-like scenarios) – via novel decay chains in models with an extended gauge sector.
The extended gauge group immediately presents other, potentially new discovery modes for the charged Higgs. In this paper, we explored the decay mode \(H^\pm \rightarrow W'^{\pm }Z\) and considered three different final states depending on the \(W'\) decay. We have done this study under the assumption that the \(W'\) is fermiophobic (and therefore can evade the direct constraints and be light) – we demonstrated, both in a toy model and in a more realistic scenario, that these new signals have promising discovery potential for the charged Higgs. We further showed that two of the three signals that we have discussed could potentially aid discovery at 500 fb\(^{-1}\) in a toy model, while the third might typically require higher luminosities. In a particular realistic extended gauge model with heavy charged Higgs bosons present in the spectrum, these signals can potentially be realized for \({\mathcal {L}}=1000\) fb\(^{-1}\) or higher. These indicate that a further study of such scenarios in other model-specific contexts is certainly warranted. We close this study with the remark that models with both extended gauge and scalar sectors remain a rich source of exciting phenomenology in new directions that could be probed at the LHC in the near future.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data which we have used in the present study can be classified into two categories: Experimental Data and the data set which are generated using Madgraph. The experimental data is the intellectual property of the ATLAS and CMS collaborations which we can not deposit. The second category of the data is simulated through the Madgraph event generators which is not useful to the community. Thus will not be deposited.]
Notes
Given that we are also dealing with an extended scalar sector, it is equally possible to consider \(W'\rightarrow W H\), with the H being a heavy neutral Higgs. Since \(H\rightarrow b{\bar{b}}\) is in general also admissible, the final state here can be considered within this context as well, assuming, of course, that \(m_{H^{\pm }}>m_{H}\).
In all these backgrounds, “\(+\)jets” includes events with \(+0\), \(+1\), and \(+2\) jets.
While this can certainly be done, as we demonstrate in the next section, we are able to achieve a \(5\,\sigma \) significance without this cut.
It is certainly possible to relax this criterion and consider a \(W'\) with sufficiently weak couplings to the SM fermions to evade the direct search limits and remain light.
Hereafter we will identify \(f_{1} = f\) and \(f_{2} = F\).
In our calculation, we will treat \(\sin \phi \) as a small parameter and diagonalise the gauge boson mass matrix perturbatively in \(\sin \phi \) (which we will relabel as x for notational simplicity).
References
G. Aad et al. (ATLAS), Phys. Lett. B 716, 1 (2012). https://doi.org/10.1016/j.physletb.2012.08.020. arXiv:1207.7214 [hep-ex]
S. Chatrchyan et al. (CMS), Phys. Lett. B 716, 30 (2012). https://doi.org/10.1016/j.physletb.2012.08.021. arXiv:1207.7235 [hep-ex]
G.C. Branco, P.M. Ferreira, L. Lavoura, M.N. Rebelo, M. Sher, J.P. Silva, Phys. Rep. 516, 1 (2012). https://doi.org/10.1016/j.physrep.2012.02.002. arXiv:1106.0034 [hep-ph]
S. De Curtis, S. Moretti, K. Yagyu, E. Yildirim, Eur. Phys. J. C 77, 513 (2017). https://doi.org/10.1140/epjc/s10052-017-5082-4. arXiv:1610.02687 [hep-ph]
H.E. Logan, D. MacLennan, Phys. Rev. D 81, 075016 (2010). https://doi.org/10.1103/PhysRevD.81.075016. arXiv:1002.4916 [hep-ph]
M. Drees, Int. J. Mod. Phys. A 4, 3635 (1989). https://doi.org/10.1142/S0217751X89001448
H.E. Haber, G.L. Kane, Phys. Rep. 117, 75 (1985). https://doi.org/10.1016/0370-1573(85)90051-1
H.E. Logan, V. Rentala, Phys. Rev. D 92, 075011 (2015). https://doi.org/10.1103/PhysRevD.92.075011. arXiv:1502.01275 [hep-ph]
A. Tumasyan et al. (CMS), JHEP 10, 045 (2021). https://doi.org/10.1007/JHEP10(2021)045. arXiv:2107.12553 [hep-ex]
G. Arcadi, A. Djouadi, H.-J. He, J.-L. Kneur, R.-Q. Xiao (2022). arXiv:2206.11881 [hep-ph]
E. Arganda, A. Delgado, R.A. Morales, M. Quirós, Eur. Phys. J. C 82, 971 (2022). https://doi.org/10.1140/epjc/s10052-022-10951-4. arXiv:2107.06034 [hep-ph]
G. Aad et al. (ATLAS), Phys. Rev. D 105, 012006 (2022). https://doi.org/10.1103/PhysRevD.105.012006. arXiv:2110.00313 [hep-ex]
G. Aad et al. (ATLAS), Phys. Rev. D 102, 112006 (2020). https://doi.org/10.1103/PhysRevD.102.112006. arXiv:2005.12236 [hep-ex]
Search for \(H^{\pm } \rightarrow W^{\pm }A \rightarrow W^{\pm }\mu \mu \) in \(pp \rightarrow t{\overline{t}}\) events using an \(e\mu \mu \) signature with the ATLAS detector at \(\sqrt{s}=13\) TeV. Technical Report (CERN, Geneva, 2021) all figures including auxiliary figures are available at https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2021-047
B. Coleppa, A. Sarkar, Eur. Phys. J. C 82, 534 (2022). https://doi.org/10.1140/epjc/s10052-022-10487-7. arXiv:2011.10926 [hep-ph]
J.-Y. Cen, J.-H. Chen, X.-G. He, G. Li, J.-Y. Su, W. Wang, JHEP 01, 148 (2019). https://doi.org/10.1007/JHEP01(2019)148. arXiv:1811.00910 [hep-ph]
A. Adhikary, N. Chakrabarty, I. Chakraborty, J. Lahiri, Eur. Phys. J. C 81, 554 (2021). https://doi.org/10.1140/epjc/s10052-021-09335-x. arXiv:2010.14547 [hep-ph]
J.F. Gunion, H.E. Haber, G.L. Kane, S. Dawson, Front. Phys. 80, 1–404 (2000)
A.A. Johansen, N.G. Uraltsev, V.A. Khoze, JETP Lett. 35, 153 (1982)
C. Degrande, K. Hartling, H.E. Logan, A.D. Peterson, M. Zaro, Phys. Rev. D 93, 035004 (2016). https://doi.org/10.1103/PhysRevD.93.035004. arXiv:1512.01243 [hep-ph]
G. Aad et al. (ATLAS), JHEP 03, 127 (2016). https://doi.org/10.1007/JHEP03(2016)127. arXiv:1512.03704 [hep-ex]
G. Aad et al. (ATLAS), Phys. Rev. Lett. 114, 231801 (2015). https://doi.org/10.1103/PhysRevLett.114.231801. arXiv:1503.04233 [hep-ex]
A.M. Sirunyan et al. (CMS), JHEP 07, 126 (2020). https://doi.org/10.1007/JHEP07(2020)126. arXiv:2001.07763 [hep-ex]
A.M. Sirunyan et al. (CMS) Eur. Phys. J. C 81, 723 (2021)
G. Aad et al. (ATLAS) JHEP 06, 145 (2021)
Search for charged Higgs bosons with the \({{\rm H}}^{\scriptscriptstyle \pm }\rightarrow \tau ^{\scriptscriptstyle \pm }{{\nu }_{\tau }}\) decay channel in the fully hadronic final state at \(\sqrt{s} = 13~{{\rm TeV}}\). Technical Report (CERN, Geneva, 2016). https://cds.cern.ch/record/2223865. https://cds.cern.ch/record/2780092
B. Coleppa, F. Kling, S. Su, JHEP 12, 148 (2014). https://doi.org/10.1007/JHEP12(2014)148. arXiv:1408.4119 [hep-ph]
B. Coleppa, A. Sarkar, S.K. Rai, Phys. Rev. D 101, 055030 (2020). https://doi.org/10.1103/PhysRevD.101.055030. arXiv:1909.11992 [hep-ph]
M. Aaboud et al. (ATLAS), JHEP 09, 139 (2018). https://doi.org/10.1007/JHEP09(2018)139. arXiv:1807.07915 [hep-ex]
M. Aaboud et al. (ATLAS), Phys. Lett. B 759, 555 (2016). https://doi.org/10.1016/j.physletb.2016.06.017. arXiv:1603.09203 [hep-ex]
V. Khachatryan et al. (CMS), JHEP 11, 018 (2015). https://doi.org/10.1007/JHEP11(2015)018. arXiv:1508.07774 [hep-ex]
M. Aaboud et al. (ATLAS), Phys. Lett. B 787, 68 (2018). https://doi.org/10.1016/j.physletb.2018.10.021. arXiv:1806.01532 [hep-ex]
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H.S. Shao, T. Stelzer, P. Torrielli, M. Zaro, JHEP 07, 079 (2014). https://doi.org/10.1007/JHEP07(2014)079. arXiv:1405.0301 [hep-ph]
T. Sjostrand, S. Mrenna, P.Z. Skands, JHEP 05, 026 (2006). https://doi.org/10.1088/1126-6708/2006/05/026. arXiv:hep-ph/0603175
J. de Favereau, C. Delaere, P. Demin, A. Giammanco, V. Lemaître, A. Mertens, M. Selvaggi (DELPHES 3), JHEP 02, 057 (2014). https://doi.org/10.1007/JHEP02(2014)057. arXiv:1307.6346 [hep-ex]
N.D. Christensen, P. de Aquino, C. Degrande, C. Duhr, B. Fuks, M. Herquet, F. Maltoni, S. Schumann, Eur. Phys. J. C 71, 1541 (2011). https://doi.org/10.1140/epjc/s10052-011-1541-5. arXiv:0906.2474 [hep-ph]
A. Alloul, N.D. Christensen, C. Degrande, C. Duhr, B. Fuks, Comput. Phys. Commun. 185, 2250 (2014). https://doi.org/10.1016/j.cpc.2014.04.012. arXiv:1310.1921 [hep-ph]
C. Degrande, M. Ubiali, M. Wiesemann, M. Zaro, JHEP 10, 145 (2015). https://doi.org/10.1007/JHEP10(2015)145. arXiv:1507.02549 [hep-ph]
M. Guchait, A.H. Vijay, Phys. Rev. D 98, 115028 (2018). https://doi.org/10.1103/PhysRevD.98.115028. arXiv:1806.01317 [hep-ph]
M. Flechl, R. Klees, M. Kramer, M. Spira, M. Ubiali, Phys. Rev. D 91, 075015 (2015). https://doi.org/10.1103/PhysRevD.91.075015. arXiv:1409.5615 [hep-ph]
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Eur. Phys. J. C 71, 1554 (2011). https://doi.org/10.1140/epjc/s10052-011-1554-0. arXiv:1007.1727 [physics.data-an]. [Erratum: Eur. Phys. J. C 73, 2501 (2013)]
P. Posch, Phys. Lett. B 696, 447 (2011). https://doi.org/10.1016/j.physletb.2011.01.003. arXiv:1001.1759 [hep-ph]
T. Plehn, Phys. Rev. D 67, 014018 (2003). https://doi.org/10.1103/PhysRevD.67.014018. arXiv:hep-ph/0206121
R.S. Chivukula, E.H. Simmons, B. Coleppa, H.E. Logan, A. Martin, Phys. Rev. D 83, 055013 (2011). https://doi.org/10.1103/PhysRevD.83.055013. arXiv:1101.6023 [hep-ph]
Acknowledgements
BC acknowledges support from the Department of Science and Technology, India, under Grant CRG/2020/004171. GBK is supported by the Prime Minister’s Research Fellowship (Grant No. PMRF-192002-1802) from the Department of Science and Technology, India. AS would like to thank Dr. Satendra Kumar for his help in writing the FeynRules files.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Coleppa, B., Krishna, G.B. & Sarkar, A. Charged Higgs prospects in extended gauge models. Eur. Phys. J. C 83, 363 (2023). https://doi.org/10.1140/epjc/s10052-023-11488-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-023-11488-w




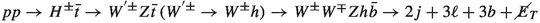 , and
, and












