1 Introduction

Black holes, as one of the most important theoretical predictions of the general relativity (GR), have been demonstrated by gravitational waves from binary black holes merger [1,2,3,4,5,6], by x-ray binary systems (see Refs. [7, 8] and references therein), and by the images for supermassive black holes in the centers of our Galaxy and M87 [9,10,11,12,13,14,15,16,17,18,19,20]. However, central singularities break GR down and event horizons trigger the information paradox. Although GR has passed all of the tests in the Solar System and beyond with flying colors, its great success has not stopped alternatives. The strong gravitational field will provide a unique access for probing alternatives and their information of the curved spacetimes [21, 22]. Given that they have extremely strong gravitational fields in the universe, black holes make a perfect laboratory for testing GR and modified gravity scenarios [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66].

Among these alternative theories, the most eminent and simple case is the scalar-tensor theory just as Horndeski’s theory [67]. In Horndeski’s theory, the action contains a scalar field and the metric tensor field, which gives the metric and scalar fields equations with no derivatives beyond second order. In comparison with GR, Horndeski’s theory has the same symmetry including local Lorentz invariance and diffeomorphism [68, 69]. The spacetime of Horndeski’s theory is invested with the hairy black hole [70,71,72,73,74,75]. The simplest case for the hairy black hole in Horndeski’s theory has the radially dependent scalar field [72, 76,77,78,79,80] and has been paid much attention in its existence and instability [81], in the no-hair theorem [82], in the thermodynamical property [70], in strong gravitational lensing [83, 84], in quasi normal modes at higher-order WKB approach [85], and so on. Neutral timelike particles’ bound orbits around the hairy black hole in Horndeski’s theory [80] are still missing, which will be performed in this paper.

Bound orbits, especially precessing and periodic motions, are paving the way for testing the fundamental theories of gravity. As the precessing motions, the advance of the perihelion of Mercury is one of classical experimental tests of GR [21]. The perihelion precessions for our Solar System’s other planets [86,87,88,89,90,91,92], for exoplanets [93,94,95,96], for binary pulsars [97,98,99,100,101,102] and for stars around Sgr A* [103] have also been studied intensively in GR and modified gravity scenarios. As the periodic motions, one massive particle’s motion nearby one black hole shows the zoom-whirl structure [104,105,106,107]. This structure is described as the ratio of the average angular frequency to the radial frequency per radial cycle [108]. If the ratio is irrational, the particle’s motion is a quasi-periodic one. If the ratio is rational, the particle’s motion is a periodic one. An irrational or a rational number “b” [108] can be generally used to describe this behavior. Although this zoom-whirl structure for the periodic motions has not been apparently observed, the periodic motions might offer computational advantages for adiabatic extreme mass-ratio inspirals [109] and the unique information about some properties of the spacetime in the strong gravitational field that is unavailable from the precessing motions. The periodic motions have widely been investigated in Kerr [108], Reissner–Nordström [110] and others black holes [111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128]. Particularly, the discovery of some stars around Sgr A* in the present and the near future has made it possible to use their precessing and periodic motions for probing the curved spacetime of one black hole [103, 129,130,131,132,133,134].

This paper is structured as follows. In Sect. 2, we briefly review the metric in the hairy black hole and give its geodesics. In Sect. 3, we mainly investigate the bound orbits for a timelike particle around the hole, including the marginally bound orbits and the innermost stable circular orbits, and precessing and periodic motions. Especially, based on the observations of GRAVITY, we estimate the bounds on the coupling parameter of the hole in this section. In Sect. 4, conclusions and discussion are presented.

2 Metric and geodesics

One scalar field \(\varphi \) has been included in Horndeski’s theory [72] in addition to the metric tensor. Four arbitrary functions \(Q_i(\mathrm {\Phi )}(i=2,3,4,5)\) are considered in the action of the theory [72], where \(2\mathrm {\Phi }=- \partial ^{\mu } \varphi \partial _{\mu }\varphi \). Following the previous work [72, 84], we consider the particular quartic type of Horndeski’s theory, namely \(Q_5(\mathrm {\Phi )}=0\). Then, the corresponding action can be written as

$$\begin{aligned} \mathscr {S}= & {} \int \textrm{d}^4 x \sqrt{-g} \bigg \{ Q_2(\mathrm {\Phi })+Q_3(\mathrm {\Phi }) \square \varphi +Q_4(\mathrm {\Phi })R \nonumber \\{} & {} +Q_{4}(\mathrm {\Phi })_{,\mathrm {\Phi }} \Big [(\square \varphi )^2-(\nabla ^{\mu }\nabla ^{\nu } \varphi )(\nabla _{\mu }\nabla _{\nu }\varphi ) \Big ] \bigg \}, \end{aligned}$$
(1)

in which \(g=\textrm{det}(g_{\mu \nu })\) denotes the determinant of metric tensor \(g_{\mu \nu }\), and R is the Ricci scalar. \(\square \) and \(\nabla \) represent the D’Alembert and Nabla operators respectively. And the upper and lower indexes of \(\nabla \) are contra and covariant derivatives. The four-current vector has

$$\begin{aligned} J^{\mu }=\frac{1}{\sqrt{-g}}\frac{\delta \mathscr {S}}{\delta (\varphi _{,\mu })}, \end{aligned}$$
(2)

which is related to the Noether charge [135]. Variation of the action (1) with respect to \(g^{\mu \nu }\) has [72, 80]

$$\begin{aligned} Q_4(\mathrm {\Phi })\left( R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R\right) =T_{\mu \nu }, \end{aligned}$$
(3)

where \(T_{\mu \nu }\) is the stress-energy-momentum tensor of matter.

When we set \(\varphi \equiv \varphi (r)\) as Refs. [72, 80], a static and spherically symmetric solution for the hairy black hole can be read as follows [80]

$$\begin{aligned} \textrm{d}s^2 = -F(r)\textrm{d}t^2+\frac{1}{F(r)}\textrm{d}r^2 +r^2(\textrm{d}\theta ^2+ \sin ^{2}\theta \textrm{d}\phi ^2), \end{aligned}$$
(4)

with

$$\begin{aligned} F(r) = 1-\frac{2M}{r}+\frac{q}{r}\textrm{ln}\frac{r}{2M}, \end{aligned}$$
(5)

where M is the mass of the black hole, q is the coupling parameter in Horndeski’s theory with the dimension of length (see Refs. [72, 80], for details). When \(q=0\), this hole reduces to the classical Schwarzschild one.

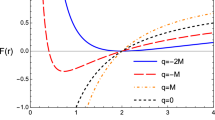
The event horizon(s) can be obtained from \(F(r)=0\) [136]. It indicates that the hairy black hole may have inner and outer event horizons when \(-2<q/M<0\). And one can easily find the hairy black hole always has the same event horizon (\(r=2M\)) as the one in the Schwarzschild black hole when q takes any value. According to Eq. (5), we plot F(r) as a function of r/M with different values of q, see Fig. 1. The figure shows that there are two event horizons when \(-2<q/M<0\), namely inner one and outer one. While the outer one is at \(r=2M\), the inner horizon is away from the central singularity with the decrease of q/M. Only one event horizon can exist when q/M is \(-2\) or 0. The numerical expression of the inner horizon yields

$$\begin{aligned} r=q \ \textrm{ProductLog} \Big (\frac{2M}{q}e^{\frac{2M}{q}} \Big ), \end{aligned}$$
(6)

where ProductLog(z) is Lambert W function. For one arbitrary z, the Lambert W function is defined as the principal solution of \(We^W=z\).

Fig. 1
figure 1

F(r) as a function of r/M with different values of q

Full size image
Fig. 2
figure 2

The Ricci scalar (R), the square of Ricci tensor (\(R^{2}\)) and the Kretschmann scalar (\(K^{2}\)) as a function of the radius r/M for the metric of the hariy black hole

Full size image

Based on the metric (4), we derive the Ricci scalar, the square of Ricci tensor and the Kretschmann scalar

$$\begin{aligned} R= & {} g^{\mu \nu }R_{\mu \nu }=-\frac{qM^{2}}{r^3}, \end{aligned}$$
(7)
$$\begin{aligned} R^{2}= & {} R_{\mu \nu }R^{\mu \nu }=\frac{5q^2M^{4}}{2r^6}, \end{aligned}$$
(8)
$$\begin{aligned} K^{2}= & {} R_{\mu \nu \sigma \rho }R^{\mu \nu \sigma \rho }\nonumber \\= & {} \frac{48M^{6}}{r^{6}}+\frac{40qM^{5}}{r^{6}}+\frac{13q^{2}M^{4}}{r^{6}} -\frac{48qM^{5}}{r^{6}}\ln \bigg (\frac{r}{2M}\bigg )\nonumber \\{} & {} -\frac{20q^{2}M^{4}}{r^{6}}\ln \bigg (\frac{r}{2M}\bigg ) +\frac{12q^{2}M^{4}}{r^{6}}\bigg [\ln \bigg (\frac{r}{2M}\bigg )\bigg ]^{2}, \end{aligned}$$
(9)

where non-zero components in \(R_{\mu \nu }\) are

$$\begin{aligned} R_{tt}= & {} -\frac{qM^{2}}{2r^{4}}\bigg [q\ln \bigg (\frac{r}{2M}\bigg )+r-2M\bigg ], \end{aligned}$$
(10)
$$\begin{aligned} R_{rr}= & {} \frac{qM^{2}}{2r^{2}}\bigg \{\bigg [q\ln \bigg (\frac{r}{2M}\bigg )+r-2M\bigg ]\bigg \}^{-1}, \end{aligned}$$
(11)
$$\begin{aligned} R_{\theta \theta }= & {} -\frac{q}{r}, \end{aligned}$$
(12)
$$\begin{aligned} R_{\phi \phi }= & {} -\frac{q}{r}\sin ^{2}\theta , \end{aligned}$$
(13)

which means the metric of the hariy black hole is not Ricci-flat. From Eqs. (7)–(9), one can see some different properties of the spacetime from the classical one. From Eqs. (7)–(9), it suggests that the coupling constant q affects R, \(R^{2}\) and \(K^{2}\). With \(-2<q/M<0\), \(R\in (0,2M^3/r^3)\), \(R^{2}\in (0, 10M^6/r^6)\) and \(K^{2}\in (0, 48\,M^6/r^6)\). The values of R, \(R^{2}\) and \(K^{2}\) as a function of r/M for the metric of the hairy black hole are shown in Fig. 2, it indicates that three scalars all go to zero when r lies outside the event horizons.

With the spherically symmetric metric Eq. (4), we consider one timelike particle moving on the equatorial plane (\(\theta =\pi /2\)), the corresponding Lagrangian is derived as follows

$$\begin{aligned} 2 \mathscr {L} = -F(r)\dot{t}^2+\frac{1}{F(r)}\dot{r}^2 +r^2\dot{\phi }^2, \end{aligned}$$
(14)

in which “\(\cdot \)” denotes the derivative of an affine parameter, it yields

$$\begin{aligned} P_t= & {} \frac{\partial \mathscr {L}}{\partial \dot{t}}=-F(r)\dot{t} =-E, \end{aligned}$$
(15)
$$\begin{aligned} P_{\phi }= & {} \frac{\partial \mathscr {L}}{\partial \dot{\phi }}=r^2\dot{\phi }=L, \end{aligned}$$
(16)
$$\begin{aligned} P_r= & {} \frac{\partial \mathscr {L}}{\partial \dot{r}}=\frac{1}{F(r)}\dot{r}, \end{aligned}$$
(17)

where E and L indicate the conserved energy and orbital angular momentum per unit mass of the particle respectively. The Hamiltonian for the particle is:

$$\begin{aligned} \mathscr {H} = P_t\dot{t}+P_\phi \dot{\phi }+P_r\dot{r}-\mathscr {L}, \end{aligned}$$
(18)

and we have

$$\begin{aligned} 2\mathscr {H} = -E\dot{t}+\frac{1}{F(r)}\dot{r}^2+L\dot{\phi }=-1. \end{aligned}$$
(19)

Substituting Eqs. (15)–(16) into Eq. (19), they derive the equation of motion for the radial coordinate r

$$\begin{aligned} \dot{r}^2=E^2-F(r) \Big (1+\frac{L^2}{r^2} \Big ). \end{aligned}$$
(20)

It gives us the following effective potential [137]

$$\begin{aligned} V_\textrm{eff} \ {}\equiv & {} \ E^2-\dot{r}^2 \nonumber \\= & {} \ F(r) \Big (1+\frac{L^2}{r^2} \Big ) \nonumber \\= & {} \Big [1-\frac{2M}{r}+\frac{q}{r}\textrm{ln}\frac{r}{2M} \Big ] \Big (1+\frac{L^2}{r^2} \Big ). \end{aligned}$$
(21)

For convenience, some dimensionless parameters can be defined and rewritten as

$$\begin{aligned} x=\frac{r}{2M},\ \ \ l=\frac{L}{2M},\ \ \ \tilde{q}=\frac{q}{2M}, \end{aligned}$$
(22)

Equation (21) can be re-expressed as

$$\begin{aligned} V_\textrm{eff}=\Big [1-\frac{1}{x}+\frac{\tilde{q}}{x}\textrm{ln}x \Big ] \Big (1+\frac{l^2}{x^2} \Big ), \end{aligned}$$
(23)

From Eq. (23), one could find the effective potential \(V_\textrm{eff}\) depends on x, l and \(\tilde{q}\), which presents the bounded orbits around the hairy black hole just as shown in Sect. 3.

3 Bound orbits of neutral timelike particles

3.1 The marginally bound orbits and the innermost stable circular orbits

For a neutral timelike particle around the hairy black hole, the bound orbits can be found between the marginally bound orbits (MBOs) and the innermost stable circular orbits (ISCOs). MBOs are unstable circular orbits around the black hole, which satisfy [136]

$$\begin{aligned} V_\textrm{eff} = 1,\ \ \ \partial _{x}V_\textrm{eff}=0. \end{aligned}$$
(24)

Its algebraic expression is as follows

$$\begin{aligned}{} & {} xl^2 - x^2 - l^2 + \tilde{q} x^2 \ln x + \tilde{q} l^2 \ln x =0, \end{aligned}$$
(25)
$$\begin{aligned}{} & {} x^2 + 3l^2 - \tilde{q} x^2 \ln x - 3\tilde{q} l^2 \ln x \nonumber \\{} & {} \quad + \tilde{q} x^2 + \tilde{q} l^2 - 2xl^2=0. \end{aligned}$$
(26)

ISCOs are the minimum allowed radius for the particle, they are given by the following conditions [136]

$$\begin{aligned} V_\textrm{eff} = E^2,\ \ \ \partial _{x}V_\textrm{eff}=0,\ \ \ \partial _{x}\partial _{x}V_\textrm{eff}=0. \end{aligned}$$
(27)

It gives

$$\begin{aligned}{} & {} x^3 + xl^2 - x^2 - l^2 + \tilde{q} x^2\ln x \nonumber \\{} & {} \quad + \tilde{q}l^2 \ln x - E^2x^3=0, \end{aligned}$$
(28)
$$\begin{aligned}{} & {} x^2 + 3l^2 + \tilde{q} x^2 + \tilde{q} l^2 - 2xl^2 \nonumber \\{} & {} \quad - \tilde{q} x^2 \ln x - 3\tilde{q} l^2 \ln x=0, \end{aligned}$$
(29)
$$\begin{aligned}{} & {} 2x^2 + 12l^2 + 3\tilde{q} x^2 + 7\tilde{q} l^2 - 6xl^2\nonumber \\{} & {} \quad - 2\tilde{q} x^2\ln x - 12\tilde{q} l^2 \ln x=0. \end{aligned}$$
(30)
Fig. 3
figure 3

\(x_\textrm{MBO}\), \(l_\textrm{MBO}\), \(x_\textrm{ISCO}\), \(l_\textrm{ISCO}\) and \(E_\textrm{ISCO}\) of a neutral timelike particle around the hairy black hole with respect to the dimensionless coupling values \(\tilde{q}\)

Full size image

Figure 3a displays the angular momentum \(l_\textrm{MBO}\) and the radial distance \(x_\textrm{MBO}\) of the neutral timelike particle around the hairy black hole with respect to the dimensionless value \(\tilde{q}\) for MBOs. As shown in Fig. 3a, in comparison to \(x_\textrm{MBO}\), \(l_\textrm{MBO}\) decreases sharply with the increase of \(\tilde{q}\). \(x_\textrm{MBO}\) decreases and then increases slightly with \(\tilde{q}\). Apparently, there exists an extreme point when \(-0.64<\tilde{q}<0\). With \(\tilde{q} \approx -0.64\) and \(\tilde{q}=0\), \(x_\textrm{MBO}\) is equal to 2, which is the same result of the Schwarzschild case. Figure 3b–d show the energy \(E_\textrm{ISCO}\), the angular momentum \(l_\textrm{ISCO}\) and the radial distance \(x_\textrm{ISCO}\) as a function of \(\tilde{q}\). \(E_\textrm{ISCO}\) increases sharply with the increasing of \(\tilde{q}\), while \(l_\textrm{ISCO}\) decreases with \(\tilde{q}\). Meanwhile, \(x_\textrm{ISCO}\) decreases and then increases slowly due to the effect of the hairy black hole. It still contains an extreme point with \(\tilde{q}\in (-0.57, 0)\) (see Fig. 3b). By taking \(\tilde{q} \approx -0.57 \) or \(\tilde{q}=0\), \(x_\textrm{ISCO}=3\). It has the same value as the results of the Schwarzschild one.

When the neutral timelike particle locates between MOBs and ISCOs around the black hole, one can analyse the particles’s bound orbits by the aid of its effective potential and radial motion. The left column in Fig. 4 demonstrates \(V_\textrm{eff}\) varies with x for different values of l (represented by various colors) and \(\tilde{q}\). The red curves denote MBOs, which have two extreme points. ISCOs is represented as the purple curves with only one extreme point. It suggests that \(V_\textrm{eff}\) decreases with the angular momentum l. At the same time, the maximum point and the minimum point are getting closer with decrease of l until they become one at ISCOs.

Fig. 4
figure 4

The effective potential \(V_\textrm{eff}\) and radial motion \(\dot{x}^2\) vary with x for a neutral timelike particle around the hairy black hole. Left column: \(V_\textrm{eff}\) varies with different values \(\tilde{q}\) and l. Right column: \(\dot{x}^2\) varies with different values \(\tilde{q}\) and E

Full size image
Fig. 5
figure 5

The (l, E) allowed region of the bound orbits around the hairy black hole with fixed values \(\tilde{q}\). The upper and lower curves in each shadow region represent respectively the upper and lower bounds. Note that the regions with the blue and red ones in the third row are almost the same one because the values of \(\tilde{q}=0\) and \(\tilde{q}=-8.2\times 10^{-5}\) are very close

Full size image

The right column in Fig. 4 shows the variation of \(\dot{x}^2\) with different values \(\tilde{q}\) for \(l=(l_\textrm{MBO}+l_\textrm{ISCO})/2\) and different values of E (displayed by various colors). Bound orbits can not exist when \(\dot{x}^2\) has a root or no root unless the curves have more than one roots and the intersection parts of the colors curves with \(\dot{x}^{2}=0\) are above the black dot dash lines in right column in Fig. 4. For example, orange curves in Fig. 4f–j have two roots, and intersection parts of the orange curves with \(\dot{x}^{2}=0\) belong to bound orbits. Blue and green curves have three roots, the parts between the last two roots also give bound orbits.

According to the above characters, one can plot the (l, E) allowed region for bound orbits shown as Fig. 5. It suggests that the (l, E) allowed regions for bound orbits are extremely sensitive to the coupling parameter \(\tilde{q}\). In the first row of Fig. 5, while the regions of \(\tilde{q}=-0.90\) and \(\tilde{q}=-0.88\) overlap slightly with that of \(\tilde{q}=-1.00\), there are not any overlapping region between the regions of \(\tilde{q}=-1.00\) and \(\tilde{q}=-0.80\). A similar situation also exists in the second and third rows in the figure. Especially, the overlapping regions get smaller or even disappear with the increasing of \(\tilde{q}\). Note that the regions with the blue and red ones in the third row in Fig. 5 are almost the same one because the values of \(\tilde{q}=0\) and \(\tilde{q}=-8.2\times 10^{-5}\) are very close. We also see that, with the increasing of \(\tilde{q}\), the range of l in the (l, E) allowed region gets smaller while the minimum value of E increases. This implies that the bound orbits around the hairy black hole have lower energy and higher angular momentum than the Schwarzschild one.

3.2 Precession and the preliminary bound on the hairy black hole

In the previous research [84], by considering the hairy black hole, the authors detailedly investigate the strong deflection gravitational lensing and the corresponding time delay in the strong deflection gravitational lensing. In their work, the parameter \(q_{s}\) (shown as q in Ref. [84] and also \(\tilde{q}\) in the present work; here we use \(q_{s}\) to avoid confusion with another symbol in the context) was constrained by the shadow size from EHT observations of M87*, which is \(q_{s}\in (-0.281979, 0)\). In this subsection, with deriving the particles’ relativistic periastron precessions, we will strengthen constraints on the coupling parameter \(\tilde{q}\) (\(q_{s}\)) by using the result of the S2 star’s precession with GRAVITY.

When l and E are fixed, the bound orbit of the neutral timelike particle around the black hole can be described by an irrational or a rational number b, which represents \(\Delta \phi \) over one radial cycle as

$$\begin{aligned} \Delta \phi =2\pi (b+1), \end{aligned}$$
(31)

in which b denotes periodic or quasi-periodic orbit [108]. The relationship between the angle \(\Delta \omega \) and b is

$$\begin{aligned} \Delta \omega \equiv \Delta \phi - 2\pi =2\pi b, \end{aligned}$$
(32)

where b is corresponding to three integers (\(z,w,\nu \)) as follows [108]

$$\begin{aligned} b= w + \frac{\nu }{z}, \end{aligned}$$
(33)

the equatorial angle can be written as

$$\begin{aligned} \Delta \phi =2 \int _{x_\textrm{p}}^{x_\textrm{a}} \frac{\textrm{d}\phi }{ \textrm{d}x} \textrm{d}x = 2 \int _{0}^{\pi } \frac{\textrm{d}\phi }{ \textrm{d}\Psi }\textrm{d}\Psi , \end{aligned}$$
(34)

where \(x_\textrm{p}\) and \(x_\textrm{a}\) represent the periastron and apastron of periodic orbit respectively, we obtain

$$\begin{aligned} x= \frac{(a/2M)(1-e^2)}{1+e\textrm{cos }\Psi }, \end{aligned}$$
(35)

with e and a being the eccentricity and the semi-major axis of the orbit. And they satisfy

$$\begin{aligned} x_\textrm{p}=(a/2M)(1-e), \ \ \ x_\textrm{a}=(a/2M)(1+e). \end{aligned}$$
(36)

Based on Eqs. (16), (20) and (35), we derive

$$\begin{aligned} \frac{\textrm{d}\phi }{\textrm{d}\Psi } = \frac{(a/2M)e(1-e^2)l\textrm{sin}\Psi }{x^2(1+e\textrm{cos}\Psi )^2 \sqrt{E^2-F(x)(1+\frac{l^2}{x^2})}}. \end{aligned}$$
(37)

From \(\dot{x}|_{x=x_\textrm{p}}=0\) and \(\dot{x}|_{x=x_\textrm{a}}=0\), \(l^2\) and \(E^2\) are found as

$$\begin{aligned} l^2= & {} \frac{x_\textrm{a }^2 x_\textrm{p }^2\left[ F(x_\textrm{p})-F(x_\textrm{a})\right] }{x_\textrm{p }^2 F(x_\textrm{a})-x_\textrm{a }^2 F(x_\textrm{p})}, \end{aligned}$$
(38)
$$\begin{aligned} E^2= & {} \frac{F(x_\textrm{a}) F(x_\textrm{p})(x_\textrm{p }^2-x_\textrm{a }^2)}{x_\textrm{p }^2 F(x_\textrm{a})-x_\textrm{a }^2 F(x_\textrm{p})}. \end{aligned}$$
(39)

In a weak gravitational field, we expand Eq. (5) as the term M/r by using post-Newtonian approximation and we also consider \(\tilde{q}\) is a small quantity. Substituting l and E into Eqs. (37), (37) becomes

$$\begin{aligned} \frac{\textrm{d}\phi }{\textrm{d}\Psi }= & {} 1 + \frac{M(3 + e\textrm{cos}\Psi )}{a(1-e^2)} +\tilde{q} \Bigg [\frac{(1-e)\ln (1-e)}{2e^2(1+\textrm{cos}\Psi )} \nonumber \\{} & {} +\frac{(1+e) \ln (1+e)}{2e^2(1-\textrm{cos}\Psi )} -\frac{(1+e\textrm{cos}\Psi )\ln ({1+e\textrm{cos}\Psi })}{e^2\textrm{sin}^2 \Psi } \Bigg ] \nonumber \\{} & {} +\mathscr {O}(M^2,\tilde{q}M,\tilde{q}^2). \end{aligned}$$
(40)

Recently, GRAVITY [103] has reported the Schwarzschild precession of the S2 star around Sgr A* by means of spectroscopic and astrometric measurements. The ratio of the measured Schwarzschild precession to the one predicted by general relativity [103] is

$$\begin{aligned} f_\textrm{SP} \equiv \frac{\Delta \omega _\textrm{S2}}{\Delta \omega _\textrm{GR}}=1.10\pm 0.19, \end{aligned}$$
(41)

where

$$\begin{aligned} \Delta \omega _\textrm{GR}=\frac{6\pi M}{a(1-e^2)}. \end{aligned}$$
(42)

If we suppose that the galactic centre supermassive black hole, Sgr A*, is the hairy black hole in Horndeski’s theory, the precession of S2 star around Sgr A* can be derived as

$$\begin{aligned} f_\textrm{SP} \equiv \frac{\Delta \omega _\textrm{hairy}}{\Delta \omega _\textrm{GR}}\simeq 1+\frac{a\tilde{q}(1-e^{2})}{3Me^{2}}(1-\sqrt{1-e^2}), \end{aligned}$$
(43)

in which

$$\begin{aligned} \Delta \omega _\textrm{hairy}= & {} \Delta \phi -2 \pi \nonumber \\\simeq & {} \frac{6\pi M}{a(1 - e^2)}+\frac{2\pi \tilde{q}}{e^2}(1-\sqrt{1-e^2}) \nonumber \\{} & {} +\mathscr {O}(M^2,\tilde{q}M,\tilde{q}^2), \end{aligned}$$
(44)

with the help of Eqs. (34) and (40).

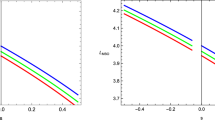
By using the best-fit orbit parameters of the S2 star in Ref. [103], we deduce that

$$\begin{aligned} \tilde{q} = (0.82 \pm 1.57) \times 10^{-4}, \end{aligned}$$
(45)

or

$$\begin{aligned} q = (1.03 \pm 1.97) \times 10^{6}~~\textrm{m}. \end{aligned}$$
(46)

Based on Eq. (45), we have \(\tilde{q} \in [-0.75 \times 10^{-4}, 2.39 \times 10 ^{-4}]\), which is very close to zero. This result still overlaps with the theoretical range \(-1<\tilde{q}<0\). In Ref. [84], the coupling constant \(q_{s}\) in the Horndeski’s theory has been constrained by the shadow size from EHT observations of M87*, which gives \(q_{s}\in (-0.281979, 0)\). And we have the relationship with \(\tilde{q}=q_{s}=q/2M\) because we all set \(2M=1\), see Table 1. We also obtain \(1 - E = (2.000 \pm 0.001) \times 10^{-5}\) and \(l = 36.52\pm 0.04 \). Shape and position of one black hole shadow may be affected by the accretion disk around the hole. It has definitely influence on the bound result constrained by the shadow size as Ref. [84]. We can see that our bound for \(\tilde{q}\) is improved to be higher than the one of previous work [84] by at least four orders of magnitude.

Table 1 Precessing around the hairy black hole in the view of the data for the orbit of the S2 star around Sgr A*
Full size table

In our estimation and uncertainty for \(\tilde{q}\) in Eq. (45), the variances of all the variables in Eq. (43) have been taken into account and we do not consider their covariance. This is because that the correlation coefficients of these variables are not available directly in spite of the posterior distribution of the orbit fit given in Ref. [103]. Our result (see Table 1) is based on the statistics of the best-fit orbit parameters of S2 [103]. And we replace the Schwarzschild black hole with the hairy black hole with Horndeski’s gravity. It is worth emphasizing that the orbital parameters of S2 (e.g., a and e) should be correlated to \(\tilde{q}\) somehow. The precession of S2 star Eq. (44) due to the hairy black hole with Horndeski gravity might be partially reabsorbed in our fitting \(\tilde{q}\). As a result, our estimation may overestimate the constraint on \(\tilde{q}\) due to the correlations between the parameters. For this issue, Ref. [138] gives a more detailed discussion. It was noted that, in the present work, we only give a preliminary bound on \(\tilde{q}\) instead of a genuine constraint on the hairy black hole with Horndeski’s gravity based on a full statistical analysis with the whole observational data set, which will be fully considered in our next step.

Fig. 6
figure 6

Color-indexed b-maps on two dimensionless parameters \(\epsilon \) and \(\eta \) for \(\tilde{q}=0\), \(-\)0.25, \(-\)0.57, \(-\)0.64, \(-\)0.75, and –1

Full size image

3.3 Periodic orbits in the strong gravitational field

A rational or irrational number “b” may be used for describing periodic or quasi-periodic orbits in a strong gravitational field according to Ref. [108]. When “b” is a rational number, it can be specified by three integers (\(z,w,\nu \)) in Eq. (33). z and w shows the zoom-whirl structure for the particle’s motion around the black hole, \(\nu \) denotes the vertex number. Based on Eqs. (31), (34) and (37), we found that the rational number “b” is connected with E, l and the metric F(x) of the hairy black hole. It means that various values of \(\tilde{q}\) make the behaviors of periodic orbits different.

From Fig. 5, it suggests that the allowed regions (l, E) of the bound orbits are extremely sensitive to \(\tilde{q}\). In order to compare the variations of b with E and l in the same figures, we define two dimensionless parameters \(\epsilon \) and \(\eta \) as follows

$$\begin{aligned} \epsilon= & {} \frac{l-l_{\textrm{ISCO}}}{l_{\textrm{MBO}}-l_{\textrm{ISCO}}}, \end{aligned}$$
(47)
$$\begin{aligned} \eta= & {} \frac{E-E_{\textrm{min}}}{E_{\textrm{max}}-E_{\textrm{min}}}, \end{aligned}$$
(48)

where \(E_{\textrm{min}}\) and \(E_{\textrm{max}}\) derive from \(V_{\textrm{eff}}=E^2\) and \(\dot{x}=0\). Equations (47) and (48) indicate \(\epsilon \in [0,1]\) and \(\eta \in [0,1]\).

Figure 6 displays color-indexed b-maps on two dimensionless parameters \(\epsilon \) and \(\eta \) for \(\tilde{q}=0\), \(-\)0.25, \(-\)0.57, \(-\)0.64, \(-\)0.75, and –1. For each graph in Fig. 6, when \(\epsilon \) is fixed, b increases with the increasing of \(\eta \). On the other hand, b decreases with the increasing of \(\epsilon \) with fixed values of \(\eta \). In each graph in Fig. 6, when \(\epsilon \) is close to zero for all values of \(\tilde{q}\), b can increase to more than 2.5 indicated by the orange colors. The b-maps with \(\tilde{q}\) look like similar, while the blue areas become smaller with the change of \(\tilde{q}\) from top to bottom. It indicates that a larger value of \(\tilde{q}\) will lead to the larger value of b.

Fig. 7
figure 7

As the parameter \(\tilde{q}\) takes different values, b varies with E for fixed l (left column) and varies with l for fixed E (right column)

Full size image

Figure 7 shows b varies with E or l under a range of \(\tilde{q} \in [-0.2,0]\). In this figure, the left column shows b varies with respect to the energy E for the fixed l and \(\tilde{q}\). When the value of \(\tilde{q}\) gets smaller, namely from the red curve to the purple one, the corresponding values of b increase significantly. At the same time, the allowed region of E becomes wider with the increase of l from the top to the bottom. For the given \(\tilde{q}\) and E, b as a function of l is as shown in the right column. It indicates b decreases with the increase of l when E is fixed. It suggests that the value of b is larger and the range of l is becoming smaller when the value of \(\tilde{q}\) gets larger.

When the (l, E) allowed region has a overlapping region with two close values \(\tilde{q}\), we can plot the quasi-periodic and periodic orbits around the black hole by taking the same values of l and E into account, see Fig. 8. Similarly, the quasi-periodic or periodic orbits cannot be depicted on condition that there is no overlapping (l, E) region (see Figs. 5 and 6). For instance, we consider \(E = 0.909185\) and \(l= 3.6\) in the first row of Fig. 8. The particle’s motion around hairy black hole has perfect periodic orbits with \(\tilde{q} = 0.88\), the zoom-whirl behavior is (1,1,0) (\(b=1\)), which means the amount of closed leaf is only one in this figure and the amount of nearly circular whirls close to periastron per leaf is also one. However, by sharing the same values of l and E, the particle’s motion shows the quasi-periodic orbits with \(\tilde{q} = 0.90\), whose rational number is \(b = 1+2/3\approx 1.67\), which is quite different from \(\tilde{q} = 0.88\) case. Also, the quasi-periodic orbit with \(\tilde{q}=-0.8\) has another zoom-whirl behavior with \(b=0.517365\). And when \(\tilde{q}=-1.00\) with the same values of l and E, there is no bound orbit for \(\tilde{q}=-1.00\) (denoted as N.A.). For another example, in the last row in Fig. 8, there exists the periodic orbit with \(b=2\) for the Schwarzschild case (\(\tilde{q}=0\)), which is denoted by “Schw”. However, when we take \(\tilde{q}=-8.2 \times 10^{-5}\), the related bound orbit presents a quasi-periodic orbit with \(b=2.207313\), which is very close to the zoom-whirl behavior with \(b=2+1/5\) (5,2,1). Even in some cases, for the fixed energy and angular momentum, small variations in \(\tilde{q}\) can put the bound orbits out of existence. It indicates that periodic and quasi-periodic orbits or even no bound orbits for the hairy black holes are extremely sensitive to small variations of the coupling parameter \(\tilde{q}\). These maybe provide us a chance to identify some information of the hairy black hole in the strong gravitational field.

Fig. 8
figure 8

The quasi-periodic and periodic orbits of a neutral timelike particle around the hairy black hole with the same l and E at each row for different values of \(\tilde{q}\). “N.A” means that there is no bound orbit in specified E and l. “Schw” denotes the Schwarzschild case

Full size image

4 Conclusions and discussion

In this present work, we investigate the dynamics of neutral timelike particles around a hairy black hole in Horndeski’s theory, hoping to provide more clues for probing such a spacetime. Some properties of the metric are displayed in Figs. 1 and 2. We obtain the MBOs and ISCOs for neutral particles around the hole (see Fig. 3). It shows that \(l_{\textrm{MBO}}\) and \(l_{\textrm{ISCO}}\) decrease with the increase of \(\tilde{q}\), while \(E_{\textrm{ISCO}}\) increases with the increase of \(\tilde{q}\). Here \(\tilde{q}\) is a dimensionless coupling parameter and has \(-1\le \tilde{q}\le 0\) because we set \(2M=1\). For \(x_{\textrm{MBO}}\) and \(x_{\textrm{ISCO}}\), it is found that there exists an extreme point between \(-0.64<\tilde{q}<0\). By analysis of the effective potential and radial motion (see Fig. 4) for the neutral particle, the (l, E) allowed regions of the bound orbits around the hole are taken into account (see Fig. 5). It suggests that the allowed regions (l, E) are extremely sensitive to the coupling parameter \(\tilde{q}\).

The precessing and periodic motions for the neutral particle are also considered. With deriving its relativistic periastron precession [Eq. (43)], a preliminary bound on the hairy black hole is obtained by using the result of the S2 star’s precession with GRAVITY, which is \(\tilde{q}=(0.82\pm 1.57)\times 10^{-4}\) [or \(q=(1.03\pm 1.97)\times 10^{6}\) m]. It is tighter than the previous result [84] constrained by the shadow size from EHT observations of M87* by about 3–4 orders of magnitude. We analyse the corresponding periodic motions around the hole (see Figs. 6, 7, 8). It clearly shows that small variations in the coupling parameter can make the neutral particles’ motions back and forth from the periodic orbits to the quasi-periodic orbits or no bound orbit. It suggests that small variations of \(\tilde{q}\) can cause the dynamical characters for the timelike particle’s bound orbits to change dramatically.

Our present work might provide hints for distinguishing the hairy black hole in Horndeski’s theory from the classical hole by using the test particles’ dynamics in the strong gravitational field. The hairy black hole spacetime we considered here is without spin, while celestial bodies are usually spinning in the Universe. Although the non-spin approximation might be suitable for very slowly spinning cases or for the bound orbits adequately far from the hole, one still needs to consider the spin for those much close to its center, bringing more novel and complicated properties. We will leave the detailed research on these issues in our next move. Other effects, such as tidal forces in a black hole on the particle in radial free fall [139, 140] and gravitational radiation reaction to the particle motion [141, 142], will be very interesting topics for testing this spacetime. In future work, we also plan to study in detail such effects on the hairy black hole.