Probing a self-complete and Generalized-Uncertainty-Principle black hole with precessing and periodic motion

Abstract

We investigate the precessing and periodic orbits of timelike particles around a self-complete and Generalized-Uncertainty-Principle (GUP) black hole. After its marginally bound orbit and innermost stable circular orbit are found, we obtain the allowable conditions for the bound orbits. The relativistic periastron advance is worked out, and thereby the minimal resolution length of the GUP is estimated based on the precessing orbit of the S2 star around the Galactic Center. For the periodic motion, we find that when the minimal length approaches its critical value, it would be extremely sensitive for the periodic orbits to disturbance due to any variation of the minimal length so that they would easily become unbound.

Appendices

Appendix A: Determination of marginally bound orbit

Recalling the conditions for the marginally bound orbit (25), which can be rewritten with the dimensionless quantities $x=m_{\bullet }^{-1}\, r$ and $l=m_{\bullet }^{-1}\,L$ as

$$\begin{aligned} V_{\mathrm{eff}}(x) = & 1, \end{aligned}$$

(55)

$$\begin{aligned} V_{\mathrm{eff},x}(x) = & 0, \end{aligned}$$

(56)

we can solve $l^{2}$ from Eq. (55) as

$$ l^{2}=x^{2}\bigg[\frac{1}{A(x)}-1\bigg] , $$

(57)

and substitute it into Eq. (56), which leads to

$$ \frac{P(x)}{x A(x)}=0, $$

(58)

with

$$ P(x)=x A_{,x}(x)+2A^{2}(x)-2A(x). $$

(59)

Since we only consider a timelike particle outside the event horizon $x_{\mathrm{H}}$ of the self-complete and GUP black hole, which means $A(x)>0$ for any given $x>x_{\mathrm{H}}$, we find that Eq. (58) is equivalent to $P(x)=0$. When the self-complete and GUP black hole has only one event horizon for $\eta =\eta _{\mathrm{H,c}}$, it can be shown that $P(x_{\mathrm{H,c}})=0$ due to Eqs. (14) and (15). Since $x_{\mathrm{H,c}}$ is the smallest event horizon of the self-complete and GUP black hole, we can exclude any roots of $P(x)$ which are less than $x_{\mathrm{H,c}}$, in order to avoid making the marginally bound orbit inside the event horizon.

Figure 5 shows $P(x)$ with various $\eta$. We can see that although $P(x)$ might have three roots, there is only one in the allowable range of $x>x_{\mathrm{H,c}}$, meaning that it is the radius of the marginally bound orbit, i.e., $x_{\mathrm{mb}}$. Then, $l_{\mathrm{mb}}$ can be determined by Eq. (57). Therefore, we can find that, for a given $\eta \in \mathcal{D}_{\mathrm{H}}$, the marginally bound orbit of the self-complete and GUP black hole demands that

$$\begin{aligned} l_{\mathrm{mb}} \in & [3.94929,4], \end{aligned}$$

(60)

$$\begin{aligned} x_{\mathrm{mb}} \in & [3.61992,4]. \end{aligned}$$

(61)

When $\eta =0$, the marginally bound orbit returns to the one of the Schwarzschild black hole, i.e., $x_{\mathrm{mb}}=4$ and $l_{\mathrm{mb}}=4$. When $\eta =\eta _{\mathrm{H,c}}$, $l_{\mathrm{mb}}$ and $x_{\mathrm{mb}}$ decrease to their smallest values in the ranges of (60) and (61).

Fig. 5

Curves of $P(x)$ with various $\eta$ and the shadowed region marks the range $x \le x_{\mathrm{H,c}}$ which must be excluded for finding the marginally bound orbit

Appendix B: Determination of innermost stable circular orbit

With the dimensionless quantities $x$ and $l$, we can rewrite the conditions for the innermost stable circular orbit (27) as

$$\begin{aligned} V_{\mathrm{eff}}(x) = & E^{2}, \end{aligned}$$

(62)

$$\begin{aligned} V_{\mathrm{eff},x} = & 0 , \end{aligned}$$

(63)

$$\begin{aligned} V_{\mathrm{eff},xx} = &0 . \end{aligned}$$

(64)

From Eq. (62), $l^{2}$ can be solved as

$$ l^{2}=x^{2}\bigg[\frac{E^{2}}{A(x)}-1\bigg]. $$

(65)

Substituting it into Eq. (63), we can have

$$ V_{\mathrm{eff},x}=\frac{[xA_{,x}(x)-2A(x)] E^{2}+2A^{2}(x)}{xA(x)}=0. $$

(66)

Since $A(x)$ is positive for any timelike particle outside the event horizon, we can find the energy of the innermost stable circular orbit satisfying

$$ E^{2}=\frac{2A^{2}(x)}{2A(x)-x A_{,x}(x)}, $$

(67)

which, with Eq. (65), leads to

$$ l^{2}=\frac{x^{3}A_{,x}(x)}{2A(x)-x A_{,x}(x)} . $$

(68)

Making use of Eqs. (67) and (68), we can express Eq. (64) as

$$ V_{\mathrm{eff},xx}(x)=\frac{Q(x)}{x N(x)}=0, $$

(69)

where

$$\begin{aligned} Q(x) = & 2 x A(x)A_{,xx}(x)-4x [A_{,x}(x)]^{2} \\ & +6A(x)A_{,x}(x), \end{aligned}$$

(70)

$$\begin{aligned} N(x) = & 2 A(x)-x A_{,x}(x). \end{aligned}$$

(71)

It can be straightforwardly checked that $V_{\mathrm{eff},xx}(x_{\mathrm{H,c}})=0$ due to Eqs. (14) and (15). For a given $\eta \in \mathcal{D}_{\mathrm{H}}$ and any $x>x_{\mathrm{H}}$, the root of $Q(x)=0$ gives the radius $x_{\mathrm{isco}}$ of the innermost stable circular orbit for the self-complete and GUP black hole, while the root of $N(x)=0$ leads to the radius $x_{\mathrm{m}}$ of its photon sphere (Claudel et al. 2001; Bozza 2002). It can be checked that $x_{\mathrm{H}}< x_{\mathrm{m}}< x_{\mathrm{isco}}$. It means that Eq. (69) is equivalent to $Q(x)=0$ for any $x>x_{\mathrm{H}}$, because $Q(x)$ and $N(x)$ cannot vanish simultaneously.

Figure 6 shows $Q(x)$ with various $\eta$. For $\eta =\eta _{\mathrm{H,c}}$, $Q(x)$ has two roots and one of them is $x=x_{\mathrm{H,c}}$ which should be excluded. For $0\le \eta <\eta _{\mathrm{H,c}}$, $Q(x)$ has only one root. Therefore, together with Eqs. (67) and (68), we can find that, for a given $\eta \in \mathcal{D}_{\mathrm{H}}$, the innermost stable circular orbit of the self-complete and GUP black hole requires that

$$\begin{aligned} E_{\mathrm{isco}} \in & [0.94199,2\sqrt{2}/3], \end{aligned}$$

(72)

$$\begin{aligned} l_{\mathrm{isco}} \in & [3.45046,2\sqrt{3}], \end{aligned}$$

(73)

$$\begin{aligned} x_{\mathrm{isco}} \in & [5.77957,6]. \end{aligned}$$

(74)

When $\eta =0$, the innermost stable circular orbit returns to the one of the Schwarzschild black hole with $E_{\mathrm{isco}}=2\sqrt{2}/3$, $l_{\mathrm{isco}}=2\sqrt{3}$ and $x_{\mathrm{isco}}=6$. When $\eta =\eta _{\mathrm{H,c}}$, $E_{\mathrm{isco}}$, $l_{\mathrm{isco}}$ and $x_{\mathrm{isco}}$ decrease to their smallest values in the ranges of (72), (73) and (74).

Fig. 6

Curves of $Q(x)$ with various $\eta$ and the shadowed region marks the range $x \le x_{\mathrm{H,c}}$ which must be excluded for the innermost stable circular orbit

Appendix C: More discussion about the bound orbits

For the self-complete and GUP black hole, Fig. 7 shows the (dimensionless) radius of its event horizon $x_{\mathrm{H}}$, the (dimensionless) angular momentum $l_{\mathrm{mb}}$ and the (dimensionless) radius $x_{\mathrm{mb}}$ of its marginally bound orbit, as well as the energy $E_{\mathrm{isco}}$, the (dimensionless) angular momentum $l_{\mathrm{isco}}$ and the (dimensionless) radius $x_{\mathrm{isco}}$ of its innermost stable circular orbit against $\eta \in \mathcal{D}_{\mathrm{H}}$. All of these quantities decrease from their values for the Schwarzschild black hole ($\eta =0$) to those with $\eta =\eta _{\mathrm{H,c}}$, while it can be checked that $x_{\mathrm{mb}}< x_{\mathrm{isco}}$ and $l_{\mathrm{mb}}>l_{\mathrm{isco}}$.

Fig. 7

From top to bottom, it shows the radius of its event horizon $x_{\mathrm{H}}$, the angular momentum $l_{\mathrm{mb}}$ and the radius $x_{\mathrm{mb}}$ of the marginally bound orbit, as well as the energy $E_{\mathrm{isco}}$, the angular momentum $l_{\mathrm{isco}}$ and the radius $x_{\mathrm{isco}}$ of the innermost stable circular orbit for the self-complete and GUP black hole with various $\eta \in \mathcal{D}_{\mathrm{H}}$

The left column of Fig. 8 shows the effect potential $V_{\mathrm{eff}}$ and each panel (a)–(d) has a specific value of $\eta$. Every curve of $V_{\mathrm{eff}}$ has its own angular momentum $l$ denoted by a specific color. Each purple curve of $V_{\mathrm{eff}}$ corresponds to the marginally bound orbit, which has the biggest $l=l_{\mathrm{mb}}$ of the bound motion for a given $\eta$ and has two distinct extreme points. Each red curve demonstrates $V_{\mathrm{eff}}$ with the smallest $l=l_{\mathrm{isco}}$ of the bound motion which gives the innermost stable circular orbit and its the maximum and minimum points merger into one. Those $V_{\mathrm{eff}}$ with $l\in (l_{\mathrm{isco}},l_{\mathrm{mb}})$ are between them. A less $l$ can make $V_{\mathrm{eff}}$ smaller and cause its extreme points to be closer, while a bigger $\eta$ can arise $V_{\mathrm{eff}}$ for a given $l$. The right column of Fig. 8 shows $\dot{r}^{2}$ with a fixed $l=(l_{\mathrm{isco}}+l_{\mathrm{mb}})/2$ and a specific $\eta$ in each panel (e)–(h). Every curve of $\dot{r}^{2}$ has its own energy $E$ denoted by a specific color. It is clear that $E$ must take some certain values to make $\dot{r}^{2}$ have at least two roots, ensuring the existence of the bound motion. A bigger or smaller $E$ will leave $\dot{r}^{2}$ with only one root, causing the test particle to fall into or escape from the self-complete and GUP black hole.

Fig. 8

Left column: $V_{\mathrm{eff}}$ with different $\eta$ and $l$. Right column: $\dot{r}^{2}$ with a fixed $l=(l_{\mathrm{isco}}+l_{\mathrm{mb}})/2$ for various $\eta$ and $E$

Based on the radial equation of motion (21), we can see that the energy $E$, the angular momentum $l$ and the minimal length $\eta$ determine the properties of the motion together. For the bound motion of a test timelike particle, the condition that $\dot{r}^{2}$ has at least two roots, see the right column of Fig. 8, can impose a constraint on $E$, $l$ and $\eta$. After one of these three quantities is fixed, the other two will span an allowable domain for the bound motion, outside which the particle will be either scattered or captured by the self-complete and GUP black hole. If $\eta$ is chosen firstly, $l_{\mathrm{isco}}$ and $l_{\mathrm{mb}}$ set the minimum and maximum points for the allowable range of $l$, and $E_{\mathrm{isco}}$ and $E_{\mathrm{mb}}$ give those for the range of $E$, where all of $l_{\mathrm{isco}}$, $l_{\mathrm{mb}}$, $E_{\mathrm{isco}}$ and $E_{\mathrm{mb}}$ depend on $\eta$, see Fig. 7. For any $l\in (l_{\mathrm{isco}},l_{\mathrm{mb}})$, the range of $E$ for the bound motion can be found by the condition that the curve of $\dot{r}^{2}$ has exactly two roots. The left column of Fig. 9 shows the allowable domain spanned by $l$ and $E$ for the bound motion with some given $\eta$ in the panels (a)–(d). We can see that as $\eta$ increases, the allowable domain of $l$ and $E$ for the bound motion shrinks. It also means that the stronger GUP effects can more easily destabilize the bound motion of a particle, which will be distinctly shown in Sect. 4. Likewise, if $l$ is fixed firstly, the bound-motion domain of $\eta$ and $E$ can be found as well and shown in the right column of Fig. 9 with some given $l$ in the panels (e)–(h). We can see that as $l$ grows, the bound-motion domain of $\eta$ and $E$ becomes bigger. The lower boundary of $E$ barely changes with $\eta$, while its upper boundary increases as $\eta \rightarrow \eta _{\mathrm{H,c}}$. It also means that a larger $l$ can make the particle settle down to a bound orbit more easily.

Fig. 9

The allowable domains for bound motion (shaded area) spanned by $l$ and $E$ for various $\eta$ (left column) and those spanned by $\eta$ and $E$ for $l$ (right column)

For later convenience, we define $\mathcal{B}_{E}(\eta , l)$ to denote the allowable range of $E$ for the bound motion with given $\eta$ and $l$. Therefore, after $\eta$ and $l$ are specified, a timelike test particle can move in a bound orbit as long as its $E$ belongs to $\mathcal{B}_{E}(\eta , l)$. For example, as Fig. 9(g) shown, we can find $\mathcal{B}_{E}(0.55, 3.7)=[0.95351, 0.96636]$. Similarly, we define $\mathcal{B}_{l}(\eta , E)$ to denote the allowable range of $l$ for the bound motion with given $\eta$ and $E$. For instance, it can be read out from Fig. 9(c) that $\mathcal{B}_{l}(0.5, 0.96)=[3.64813, 3.91116]$.

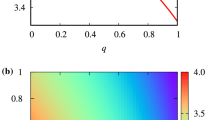
In order to have a whole picture about the dependence of $q$ on $E$, $l$ and $\eta$, we define two dimensionless quantities

$$\begin{aligned} \varepsilon = & \frac{l-l_{\mathrm{isco}}}{l_{\mathrm{mb}}-l_{\mathrm{isco}}}\in [0, 1], \end{aligned}$$

(75)

$$\begin{aligned} \delta = & \frac{E-E_{\mathrm{min}}}{E_{\mathrm{max}}-E_{\mathrm{min}}}\in [0, 1], \end{aligned}$$

(76)

where $\varepsilon =\delta =0$ and 1 correspond to the innermost stable circular orbit and the marginally bound orbit respectively for a given $\eta$, and $E_{\mathrm{min}}$ and $E_{\mathrm{max}}$ are respectively the minimally and maximally allowable energy for the given $l$ and $\eta$. Figure 10 shows color-indexed $q$-maps on the domain of $(\varepsilon , \delta )$ for the bound orbits with $\eta =\{0, 0.2, 0.4, \eta _{\mathrm{H},\mathrm{c}}\}$. As $\varepsilon$ (or $l$) grows, $q$ becomes smaller. Meanwhile, as $\delta$ (or $E$) increases, $q$ becomes bigger. In order to more clearly display these trends in the $q$-maps, we extract some particular slices of the $q$-maps and show $q$ with respect to $E$ for some specific $l$ and $q$ with respect to $l$ for some specific $E$, respectively, in the left and right panels of Fig. 11. Thus, a test particle with its allowably lowest angular momentum ($\varepsilon \sim 0$) and highest energy ($\delta \sim 1$) for the bound motion will have the biggest $q$. Another distinct feature is that the red area with high $q\ge 3$ augments as the increment of $\eta$, meaning that the stronger GUP effects can make a test particle precess more significantly.

Fig. 10

Color-indexed $q$ with respect to $\varepsilon$ and $\delta$ for $\eta =\{0, 0.2, 0.4, \eta _{\mathrm{H},\mathrm{c}}\}$

Fig. 11

Left panel: $q$ against $E$ for some specific $l$. Right panel: $q$ against $l$ with some specific $E$

After having these grand pictures about the bound motion of a timelike particle around the self-complete and GUP black hole, we will pay close attention to its precessing and periodic orbits in the following sections.

Appendix D: More examples of periodic orbits

Figure 12 also shows some examples of the bound orbits. It is similar to Fig. 3 except the facts that the angular momentum is reduced to $l=3.78$ and the periodic orbits are shown in the column of $\eta =0.4$. We can see again that as the GUP effects get stronger, the $q$-values of the bound orbits decrease. However, a more important feature is that no bound orbit exists for some specific $E$ and $l$ in the last four rows under $\eta =0$ and 0.2, which are denoted by “N.A.” in Fig. 12. Based on the previous discussion in Appendix C, we can find the allowable bound-motion range $\mathcal{B}_{E}(\eta ,l)$ of $E$ for these given $\eta$ and $l$ as

$$\begin{aligned} \mathcal{B}_{E}(0,3.78) \approx & \mathcal{B}_{E}(0.2,3.78) \\ = & [0.956194,0.973769]. \end{aligned}$$

(77)

Since none of the energy in the panel marked by “N.A.” in Fig. 12 belongs to these allowable ranges, it makes the bound orbits impossible. Such a trend is more distinctly demonstrated in Fig. 13, in which the angular momentum is further lessen to $l=3.75$ and the periodic orbits are shown in the column of $\eta =\eta _{\mathrm{H,c}}$. These settings make the bound orbits in a large number of panels disappear, marked by “N.A.”, because their energy $E$ are beyond the allowable ranges $\mathcal{B}_{E}(\eta ,l)$ for the specific $\eta$ and $l$ that are

$$\begin{aligned} \mathcal{B}_{E}(0,3.75) = & [0.95522561,\ 0.97041779], \end{aligned}$$

(78)

$$\begin{aligned} \mathcal{B}_{E}(0.2,3.75) = & [0.95522561,\ 0.97041780], \end{aligned}$$

(79)

$$\begin{aligned} \mathcal{B}_{E}(0.4,3.75) = & [0.95522561,\ 0.97051578], \end{aligned}$$

(80)

$$\begin{aligned} \mathcal{B}_{E}(0.5,3.75) = & [0.95522562,\ 0.97118916]. \end{aligned}$$

(81)

Some of these ranges can be verified in Fig. 9.

Fig. 12

Some examples of bound orbits around the self-complete and GUP black hole with $l=3.78$ and the periodic orbits shown in the column of $\eta =0.4$. The notation of “N. A.” means that no bound orbit exists in the panel with particular $E$, $l$ and $\eta$. Other settings are similar to Fig. 3

Fig. 13

Some examples of bound orbits around the self-complete and GUP black hole with $l=3.75$ and the periodic orbits shown in the column of $\eta =\eta _{\mathrm{H,c}}$. The notation of “N. A.” means that no bound orbit exists in the panel with particular $E$, $l$ and $\eta$. Other settings are similar to Fig. 3

Figure 14 also shows some examples of the bound orbits. It is similar to Fig. 4 except the facts that the energy is reduced to $E=0.97$ and the periodic orbits are shown in the column of $\eta =0.4$. We can see again that no bound orbit exists in the last four rows for $\eta =0$ and 0.2, denoted by “N.A.” in Fig. 14, because their angular momentum does not belong to the allowable bound-motion range $\mathcal{B}_{l}(\eta ,E)$ which are

$$\begin{aligned} \mathcal{B}_{l}(0, 0.97) \approx & \mathcal{B}_{l}(0.2, 0.97) \\ = & [3.746220, 4.392108]. \end{aligned}$$

(82)

After the energy is further reduced to $E=0.96$ and the periodic orbits are shown in the column of $\eta =\eta _{\mathrm{H,c}}$, there exist only a few bound orbits and a majority of orbits become unbound as shown in Fig. 15, because their angular momentum $l$ are beyond the allowable ranges $\mathcal{B}_{l}(\eta ,E)$ that are

$$\begin{aligned} \mathcal{B}_{l}(0, 0.96) \approx & \mathcal{B}_{l}(0.2, 0.96) \\ = & [3.652556,\ 3.911155], \end{aligned}$$

(83)

$$\begin{aligned} \mathcal{B}_{l}(0.4, 0.96) = & [3.652036,\ 3.911155], \end{aligned}$$

(84)

$$\begin{aligned} \mathcal{B}_{l}(0.5, 0.96) = & [3.648127,\ 3.911155]. \end{aligned}$$

(85)

Some of them can be verified in Fig. 9 as well.

Fig. 14

Some examples of bound orbits around the self-complete and GUP black hole with $E=0.97$ and the periodic orbits shown in the column of $\eta =0.4$. The notation of “N. A.” means that no bound orbit exists in the panel with particular $E$, $l$ and $\eta$. Other settings are similar to Fig. 4

Fig. 15

Some examples of bound orbits around the self-complete and GUP black hole with $E=0.96$ and the periodic orbits shown in the column of $\eta =\eta _{\mathrm{H,c}}$. The notation of “N. A.” means that no bound orbit exists in the panel with particular $E$, $l$ and $\eta$. Other settings are similar to Fig. 4