Central exclusive diffractive production of two pions from continuum and resonance decay in the Regge-eikonal model

Abstract

Calculations of the central exclusive diffractive production (CEDP) of two pions via continuum and resonance mechanisms are presented in the Regge-eikonal approach. Data from STAR, ISR, CDF and CMS are analysed and compared with theoretical descriptions. The preliminary extraction of $f_0(500)$, $f_0(980)$ and $f_2(1270)$ couplings to pomerons and the $\rho$ meson contribution from the photoproduction mechanism to the CEDP cross-section are considered. We show possible nuances and problems of calculations and prospects of investigations at current and future hadron colliders.

1 Introduction

In previous papers [1, 2], the general properties and calculations of the central exclusive diffractive production (CEDP) were considered. It was shown, in particular in [2], that diffractive patterns (differential cross-sections) of CEDP play a significant role in model verification.

In [3], we considered the low-mass CEDP (LM CEDP) with production of the two-pion continuum. Here, we expand this analysis and add contributions from CEDP of $f_0(500)$, $f_0(980)$ and $f_2(1270)$ and exclusive vector meson photoproduction (EVMP) of a $\rho _0$ meson to this process, also taking into account the interference between continuum and resonance mechanisms.

CEDP of two pions is a basic “standard candle” for LM CEDP. Why do we need exact calculations and predictions for this process?

• Di-pion LM CEDP is a tool for the investigation of hadronic resonances (such as $f_2$ or $f_0$), since one of the basic hadronic decay modes for these resonances is the two-pion one. We can extract different couplings of these resonances to reggeons (pomeron, odderon) to understand their nature (structure and interaction mechanisms).

• We can use LM CEDP to fix the procedure to calculate “rescattering” (unitarity) corrections. In the case of di-pion LM CEDP, there are several kinds of corrections in the proton–proton, pion–proton and pion–pion channels.

• The pion is the most fundamental particle in the strong interactions, and LM CEDP gives us a powerful tool to go deep inside its properties, especially to investigate the form factor and scattering amplitudes for the off-shell pion.

• LM CEDP has rather large cross-sections. This is very important for an exclusive process, since in the special low-luminosity runs (of the LHC) we need more time to get enough statistics.

• As was proposed in [3, 4], it is possible to extract some reggeon-hadron cross-sections. In the case of single and double dissociation, this was the pomeron–proton cross-section. Here, in the LM CEDP of the di-pion, we can analyse the properties of the pomeron–pomeron to pion–pion exclusive cross-section.

• Diffractive patterns of this process are very sensitive to different approaches (subamplitudes, form factors, unitarization, reggeization procedure), especially differential cross-sections in t and $\phi _{pp}$ (azimuthal angle between final protons), and also $M_{\pi \pi }$ dependence. That is why this process is used to verify different models of diffraction.

• All the above items are additional advantages provided by the LM CEDP of two pions, which has the usual properties of CEDP, namely a clear signature with two final protons and two large rapidity gaps (LRG) [5, 6], and the possibility to use the “missing mass method” [7].

Processes of the LM CEDP have been calculated in other works [8,9,10,11,12,13,14,15,16,17,18] which are devoted to the most popular models for the LM CEDP of di-mesons, where the authors considered phenomenological, non-perturbative, perturbative and mixed approaches in the reggeon–reggeon collision subprocess. The nuances of various approaches were analysed in the introduction of [3].

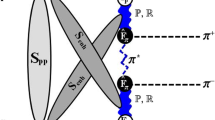
In this article we consider the case depicted in Fig. 1 and show how it can describe the data from the ISR [19, 20], STAR [21,22,23,24,25,26], CDF [27, 28] and CMS [29,30,31] collaborations.

In the first part of the present work, we introduce the framework for calculations of double-pion LM CEDP (kinematics, amplitudes, differential cross-sections) in the Regge-eikonal approach, which was considered in detail in [3]. Here, we take the reggeized full (RF) case from the four approaches of [3], which is the best in the data description.

We also discuss some nuances of the calculations which we should take into account in further more accurate analysis (elastic amplitudes for virtual particles, off-shell pion form factor, pion–pion elastic amplitude at low energies, nonlinearity of the pion trajectory, tensorial couplings and spin effects).

In the second part, we analyze the experimental data on the process at different energies, extract some couplings of resonances the pomeron, find the best approach and make some predictions for LHC experiments.

To avoid complicated expressions in the main text, all the basic formulae are placed in appendixes.

Fig. 1

Primary amplitudes (absorptive corrections are not shown) of the process of double-pion LM CEDP $p+p\rightarrow p+\pi ^++\pi ^-+p$ in the Regge-eikonal approach for a continuum (a, b), LM CEDP of $f_0$ and $f_2$ resonances (c) and EVMP of a $\rho _0$ meson (d, e) with subsequent decay to $\pi ^+\pi ^-$. a, b The central part of the diagram is the primary continuum CEDP amplitude, where $T_{\pi ^{\pm }p}$ are full elastic pion–proton amplitudes, and the reggeized off-shell pion propagator is depicted as a dashed zigzag line. This is the most applicable case from the four approaches considered in [3]. c The central part of the diagram contains pomeron–pomeron-resonance fusion with subsequent decay to pions. The propagator is taken in the Breit–Wigner approximation. d, e The central part of the diagram contains full EVMP amplitude with $\rho _0$ production and decay. Off-shell pion form factor on a, b and other suppression form factors (in the pomeron–pomeron-f or the pion–pion-($f_0$,$f_2$,$\rho _0$ vertices) ) on c–e are presented as black circles

2 General framework for calculations of LM CEDP

LM CEDP is the first exclusive two-to-four process which is driven basically by the pomeron–pomeron fusion subprocess. It serves as a clear process for investigations of resonances such as $f_0(500)$, $f_0(980)$, $f_2(1270)$ and others with masses less than 3 GeV. At the moment, for low central di-pion masses it is a huge problem to use a perturbative approach, which is why we apply the Regge-eikonal method for all the calculations. For proton–proton and proton–pion elastic amplitudes, we use the model of [32, 33], which describes all the available experimental data on elastic scattering. For EVMP we use a similar model [34].

2.1 Components of the framework

The LM CEDP process can be calculated in the following scheme (see Fig. 1):

• 1. We calculate the primary amplitudes of the processes, which are depicted as central parts of diagrams in Fig. 1. Here we consider the case where the bare off-shell pion propagator in the amplitude for continuum di-pion production is replaced by the reggeized one

  $$\begin{aligned} {{\mathcal {P}}}_{\pi }({\hat{s}},{\hat{t}})= & {} \left( \textrm{ctg}\frac{\pi \alpha _{\pi }({\hat{t}})}{2}-\textrm{i} \right) \nonumber \\{} & {} \cdot \frac{\pi \alpha _{\pi }^{\prime }}{2 {\mathrm {\Gamma }}(1+\alpha _{\pi }({\hat{t}}))} \left( \frac{{\hat{s}}}{s_0} \right) ^{\alpha _{\pi }({\hat{t}})}, \end{aligned}$$

  (1)

  where ${\hat{s}}$ is the di-pion mass squared and ${\hat{t}}$ is the square of the momentum transfer between a pomeron and a pion in the pomeron–pomeron fusion process (see Appendix A for details). Reggeization of the virtual pion propagator is not obvious, since the effect of this is expected to be small, and moreover, it is not even clear that we are in the relevant kinematic region ($|{\hat{t}}|\ll {\hat{s}}=M_{\pi \pi }^2$) to include such corrections for central production. It was also verified in the calculations presented in this paper. For example, the authors of [8,9,10] used the replacement

  $$\begin{aligned} \frac{1}{{\hat{t}}-m_{\pi }^2}\rightarrow \frac{\textrm{e}^{\alpha _{\pi }({\hat{t}})|\varDelta Y|}}{{\hat{t}}-m_{\pi }^2}, \end{aligned}$$

  (2)

  which gives the correct “reggeized” behaviour in the relevant kinematic region, and the usual “bare” pion propagator behaviour for the small difference between rapidities of pions. The authors of [11,12,13] used a phenomenological expression for virtual pion propagators (see (1) for notations, and also (3.25), (3.26) of [13])

  $$\begin{aligned}{} & {} \frac{1}{{\hat{t}}-m_{\pi }^2} F(\varDelta Y) + \left( 1-F(\varDelta Y)\right) {{\mathcal {P}}}_{\pi } \left( {\hat{s}},{\hat{t}}\right) ,\nonumber \\{} & {} F(\varDelta Y)=\textrm{e}^{-c_y \varDelta Y},\, \varDelta Y=y_{\pi ^+}-y_{\pi ^-}, \end{aligned}$$

  (3)

  to take into account possible non-Regge behaviour for ${\hat{t}}\sim {\hat{s}}/2$, i.e. for small rapidity separation $\varDelta Y$ between final pions. The Regge model really does not work in this area or it needs to be modified (as was done, for example, in works [11,12,13,14,15,16,17,18] with empirical formulae or additional assumptions). In the present calculations we use linear pion trajectory $\alpha _{\pi }({\hat{t}})=0.7({\hat{t}}-m_{\pi }^2)$. The nonlinear case was also verified, and the difference in the final result is not significant. We use also full eikonalized expressions for proton–proton, pion–proton and photon–proton amplitudes, which can be found in Appendix B.

• 2. After the calculation of the primary LM CEDP amplitudes, we have to take into account all possible corrections in proton–proton and proton–pion elastic channels due to the unitarization procedure (so-called soft survival probability or rescattering corrections), which are depicted as $V_{pp}$, $V'_{pp}$ and $S_{\pi p}$ blobs in Fig. 1. For proton–proton and proton–pion elastic amplitudes we use the model of [32, 33] (see Appendix B). The possible final pion–pion interaction is not shown in Fig. 1, since we neglect it in the present calculations.

In this article we do not consider so-called enhanced corrections [8,9,10], since they give non-leading contributions in our model due to smallness of the triple pomeron vertex. Also, we have no possible absorptive corrections in the pion–pion final elastic channel, since the central mass is low, and there is a lack of data on this process to define parameters of the model. Nevertheless, one can consider these corrections, as was done by some authors recently [35], since they can play a significant role for masses less than 1 GeV.

The exact kinematics of the two-to-four process is outlined in Appendix A.

Here we use the model presented in Appendix B as an example. One can use other models that are proved to effectively describe all the available data on proton–proton and proton–pion elastic processes and exclusive $\rho _0$ photoproduction, but it is currently difficult to find more than a couple of models which have more or less predictable power (see [36] for a detailed discussion). This is why we use the given model, as it is proved to be good in data fitting, especially in our kinematic region of interest.

2.2 Continuum di-pion production

The final expression of the amplitude for the continuum di-pion production with proton–proton and pion–proton “rescattering” corrections (see Fig. 1a, b) can be written as

$$\begin{aligned}{} & {} M^U\left( \{ p \}\right) \nonumber \\{} & {} \quad =\int \int \frac{d^2\textbf{q}}{(2\pi )^2}\frac{d^2\textbf{q}^{\prime }}{(2\pi )^2} \frac{d^2\textbf{q}_1}{(2\pi )^2}\frac{d^2\textbf{q}_2}{(2\pi )^2} V_{pp}(s,q^2) V_{pp}(s^{\prime },q^{\prime 2})\nonumber \\{} & {} \qquad \times \left[ S_{\pi ^-p}({\tilde{s}}_{14},q_1^2) M_0\left( \{ {\tilde{p}}\} \right) S_{\pi ^+p}({\tilde{s}}_{23},q_2^2)+ (3\leftrightarrow 4) \right] \nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned}{} & {} M_0\left( \{ p \}\right) \nonumber \\{} & {} \quad =T^{el}_{\pi ^+p}(s_{13},t_1) {{\mathcal {P}}}_{\pi }({\hat{s}},{\hat{t}}) \left[ {\hat{F}}_{\pi }\left( {\hat{t}}\right) \right] ^2 T^{el}_{\pi ^-p}(s_{24},t_2), \end{aligned}$$

(5)

where functions are defined in (28)–(32) of Appendix B, and sets of vectors are

$$\begin{aligned}{} & {} \{ p \}\equiv \{ p_a,p_b,p_1,p_2,p_3,p_4\} \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \{ {\tilde{p}}\}\equiv \{ p_a-q,p_b+q; p_1+q^{\prime }+q_1,\nonumber \\{} & {} \;\;\;\;\;\;\;\;\;\;\;\; p_2-q^{\prime }+q_2,p_3-q_2,p_4-q_1 \} , \end{aligned}$$

(7)

and

$$\begin{aligned} {\tilde{s}}_{14}= & {} \left( p_1+p_4+q^{\prime } \right) ^2,\; {\tilde{s}}_{23}=\left( p_2+p_3-q^{\prime } \right) ^2, \end{aligned}$$

(8)

$$\begin{aligned} s_{ij}= & {} \left( p_i+p_j \right) ^2,\; t_{1,2}=\left( p_{a,b}-p_{1,2} \right) ^2, \end{aligned}$$

(9)

$$\begin{aligned} {\hat{s}}= & {} \left( p_3+p_4 \right) ^2,\; {\hat{t}}=\left( p_a-p_1-p_3 \right) ^2 \end{aligned}$$

(10)

The off-shell pion form factor is equal to unity on mass shell ${\hat{t}}=m_{\pi }^2$ and taken as exponential

$$\begin{aligned} {\hat{F}}_{\pi }=\textrm{e}^{({\hat{t}}-m_{\pi }^2)/\varLambda _{\pi }^2}, \end{aligned}$$

(11)

where $\varLambda _{\pi }\sim 1.2$ GeV is taken from the fits to the LM CEDP of two pions at low energies (see the next section). In this paper we use only the exponential form, but it is possible to use other parametrizations (see [8,9,10,11,12,13,14,15,16,17,18]). The exponential one shows more appropriate results in the data fitting.

Other functions are defined in Appendix B. Then we can use the expression (19) to calculate the differential cross-section of the process.

2.3 CEDP and EVMP of low mass resonances.

For $f_0(500)$, $f_0(980)$, $f_2(1270)$ and $\rho _0$ resonances, the general unitarized amplitude (see Fig. 1c, d) is similar to the expression (4), where amplitude $M_0\left( \{ p \}\right)$ is replaced by the corresponding central primary amplitude for the resonance production and further decays to $\pi ^+\pi ^-$.

For f mesons, amplitudes are constructed from proton-pomeron form factors, pomeron–pomeron couplings to mesons,¹ off-shell propagators, off-shell form factors and decay vertices.

For the EVMP amplitude of the $\rho _0$ meson, we take the full unitarized photon–proton amplitude contracted with the photon flux, and also with the off-shell meson propagator, off-shell form factors and its decay vertex to pions. Additionally, we have to sum this amplitude with the symmetric one with $t_1\leftrightarrow t_2$.

All the primary amplitudes are presented in Appendix C.

2.4 Nuances of calculations

In the next section, one can see that there are some difficulties and puzzles in the data fitting, which have likewise been presented in other works [11,12,13,14,15,16,17,18]. In this subsection, let us discuss some nuances of calculations which could change the situation.

We have to pay special attention to amplitudes, where one or more external particles are off their mass shell. An example of such an amplitude is the pion–proton one $T_{\pi ^+ p}$ ($T_{\pi ^- p}$), which is part of the CEDP amplitude (see (4)). For this amplitude, here we use the Regge-eikonal model with the eikonal function in the classical Regge form, and the “off-shell” condition for one of the pions is taken into account by the additional phenomenological form factor ${\hat{F}}_{\pi }({\hat{t}})$. However, there are at least two other possibilities.

The first of these was considered in [38]. For an amplitude with one off-shell particle, the formula

$$\begin{aligned} T^*(s,b)=\frac{\delta ^*(s,b)}{\delta (s,b)}T(s,b)=\frac{\delta ^*(s,b)}{\delta (s,b)} \frac{\textrm{e}^{2\textrm{i}\delta (s,b)}-1}{2\textrm{i}} \end{aligned}$$

(12)

was used. In our case,

$$\begin{aligned}{} & {} \delta (s,b) = \delta _{\pi p}(s,b; m_{\pi }^2,m_{\pi }^2,m_p^2,m_p^2),\nonumber \\{} & {} \delta ^*(s,b) = \delta _{\pi p}^*(s,b; {\hat{t}},m_{\pi }^2,m_p^2,m_p^2)\nonumber \\{} & {} \left. \delta _{\pi p}=\delta ^*_{\pi p}\right| _{{\hat{t}}\rightarrow m_{\pi }^2}. \end{aligned}$$

(13)

$\delta _{\pi p}$ is the eikonal function (see (24)). This is similar to the introduction of the additional form factor, but in a more consistent way, which takes into account the unitarity condition (Fig. 2).

Fig. 2

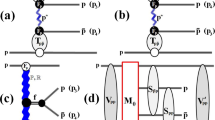
Full unitarized amplitude of the process of double-pion LM CEDP $p+p\rightarrow p+\pi ^++\pi ^-+p$. Proton–proton rescatterings in the initial and final states are depicted as $V_{pp}$ and $V'_{pp}$ blobs, respectively, and pion–proton rescattering corrections are also shown as $S_{\pi p}$ blobs. The sum of primary amplitudes $M_0$ from Fig. 1 is shown as a red rectangle

Fig. 3

Pion–proton on-shell and off-shell elastic differential cross-section (in the model of conserved meson currents presented in Appendix C) for different pion virtualities ${\hat{t}}_{\pi }$: $m_{\pi }^2$(on-shell),$-0.01$ GeV$^2$,$-0.15$ GeV$^2$,$-0.4$ GeV$^2$ in the covariant approach with conserved currents

The second one arises from the covariant reggeization method, which was considered in Appendix C of [3]. For the case of conserved hadronic currents, we have definite structure in the Legendre function, which is transformed in a natural way to the case of the off-shell amplitude. But in this case, the off-shell amplitude has a specific behaviour at low t values (see Fig. 3 and [2] for details). As was shown in [2], unitarity corrections can mask this behaviour.

Since final pion–proton interactions can give rather large suppression (about 10–20% and even more, as in Fig. 4), in our calculations we use the full amplitude as depicted in Fig. 2.

Fig. 4

Predictions of the model for the continuum (see Fig. 1a, b) at 7 TeV. Curves from top to bottom correspond to the Born term, the amplitude with proton–proton rescattering corrections only, and that with all the corrections (proton–proton and pion–proton). $\varLambda _{\pi }=1.2$ GeV

3 Data from hadron colliders versus results of calculations

Our basic task is to extract the fundamental information on the interaction of hadrons from different cross-sections (“diffractive patterns”):

• from the t-distributions we can obtain the size and shape of the interaction region;

• the distribution on the azimuthal angle between final protons gives quantum numbers of the produced system (see [2, 37] and references therein);

• from $M_c$ (here $M_c=M_{\pi \pi }$) dependence and its influence on t dependence we can draw some conclusions about the interaction at different space-time scales and interrelation between them. Also, we can extract couplings of reggeons to different resonances.

Process $p+p\rightarrow p+\pi +\pi +p$ is the first “standard candle”, which we can use to estimate other CEDP processes. In this section, we consider the experimental data on the process attempt to extract the information on couplings of different resonances to the pomeron.

Fig. 5

The data on the process $p+p\rightarrow p+\pi ^++\pi ^-+p$ at $\sqrt{s}=200$ GeV (STAR collaboration [21, 22]): a $|\eta _{\pi }|<1$, $|\eta _{\pi \pi }|<2$, $p_{T\pi }>0.15$ GeV, $0.005<-t_{1,2}<0.03$ GeV$^2$; b plus additional cut $M_c < 1$ GeV. Curves correspond to $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings from (14). Solid upper curves correspond to the sum of all amplitudes, and dashed lower curves represent the continuum contribution. The thickness of the solid curves corresponds to the errors of Monte Carlo calculations. Additional interpolation was used between calculated points for smoothing

Fig. 6

The new data on the process $p+p\rightarrow p+\pi ^++\pi ^-+p$ at $\sqrt{s}=200$ GeV (STAR collaboration [23,24,25]): $|\eta _{\pi }|<0.7$, $p_{T\pi }>0.2$ GeV, $p_x>-0.2$ GeV, 0.2 GeV$<|p_y|<0.4$ GeV, $(p_x+0.3\,\textrm{GeV})^2+p_y^2<0.25$ GeV$^2$, where p denotes the momenta of final protons. Curves correspond to $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings from (14). Solid curves correspond to the sum of all amplitudes, and the dashed lower curve in a represents the continuum contribution. The thickness of the solid curves corresponds to the errors of Monte Carlo calculations. Additional interpolation was used between calculated points for smoothing

3.1 STAR collaboration data versus model cases

In this subsection, the data of the STAR collaboration [21,22,23,24,25,26] and model curves for continuum and the sum of all cases of Fig. 1 are presented. In our approach, we have several free parameters, namely $\varLambda _{\pi }$ (for the continuum) and couplings of resonances to pomeron $g_{{\mathbb {P}}{\mathbb {P}}f}$, which we can extract from the data. All the distributions are depicted here for $\varLambda _{\pi }=1.2$ GeV and couplings from (14).

Fig. 7

The new data on the process $p+p\rightarrow p+\pi ^++\pi ^-+p$ at $\sqrt{s}=200$ GeV (STAR collaboration [23,24,25]): $|y_{\pi \pi }|<0.4$, 0.05 GeV$<|t_{1,2}|<0.16$ GeV$^2$, $\phi _0<45^{o}$. Solid curves represent fits from experimental papers [23,24,25] extrapolated to the full kinematic region. The thick dashed curve corresponds to parameters, fixed from the old data from STAR depicted in Fig. 5 and explained in the text: $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings from (14). The thickness of the solid curves corresponds to the errors of Monte Carlo calculations. Additional interpolation was used between calculated points for smoothing

Fig. 8

The new preliminary data on the process $p+p\rightarrow p+\pi ^++\pi ^-+p$ at $\sqrt{s}=510$ GeV (STAR collaboration [26]): $|\eta _{\pi }|<0.7$, $p_{T\pi }>0.2$ GeV, $p_x>-0.27$ GeV, 0.4 GeV$<|p_y|<0.8$ GeV, $(p_x+0.6\,\textrm{GeV})^2+p_y^2<1.25$ GeV$^2$, where p denotes the momenta of final protons. The theoretical solid curve corresponds to $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings from (14). Fluctuations are due to a complex Monte Carlo integration process, and they can be smoothed by increasing the integration accuracy

We begin our analysis by fitting the data from STAR depicted on the Fig. 5a. Then we make predictions for other available data on this process.

First, we should note a difference between the data and prediction at the same energy. In Fig. 5b, one can see the azimuthal angle distribution. Here we can explain some difference because our pomeron–pomeron–meson couplings are constants, but in reality, they depend on the azimuthal angle. The next case, which is depicted in Fig. 6, is more interesting. We see that predictions underestimate the data in the region of $M_c\sim 0.8\pm 0.1$ GeV as in Fig. 5a. The data are close to predictions in the regions of f mesons. This fact cannot be understood at the moment, since, if we fix parameters using this new STAR data from Fig. 6, we will obtain overestimation of the data at higher energies, which looks strange. We may have to renormalize this part of the STAR data. Also, pomeron–pomeron–meson couplings have some complex dependence on $t_{1,2}$ and $\phi _0$ (see [37] and references therein), and it should be taken into account.

The $\rho$ contribution is small. We also see some differences in Fig. 6b–d.

The data and fits (solid curves) for the extended kinematic region at $\sqrt{s}=200$ GeV are depicted in Fig. 7 with the theoretical curve, which slightly underestimates the data at low masses and overestimates the data at the peak of $f_2(1270)$. Since these data and curves were obtained in [23,24,25] by some extrapolation, they can only be considered qualitatively.

In Fig. 8 we see a similar situation with overestimation at $M_c\sim 0.7\pm 0.2$ GeV and at the peak of $f_0(980)$.

3.2 ISR and CDF data versus the model curves

Fig. 9

Data on the process $p+p\rightarrow p+\pi ^++\pi ^-+p$ (ISR and ABCDHW collaborations [19, 20]): a at $\sqrt{s}=63$ GeV, $|y_{\pi }|<1$, $\xi _p>0.9$; b at $\sqrt{s}=62$ GeV, $|y_{\pi }|<1.5$, $\xi _p>0.9$. Curves correspond to $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings from (14). Solid upper curves correspond to the sum of all amplitudes, and dashed lower curves represent the continuum contribution. Fluctuations in solid curves are due to the complex Monte Carlo integration process, and they can be smoothed by increasing the integration accuracy. The thickness of the solid curves corresponds to the errors of Monte Carlo calculations. Additional interpolation was used between calculated points for smoothing

Fig. 10

Data on the process $p+{\bar{p}}\rightarrow p+\pi ^++\pi ^-+{\bar{p}}$ (CDF collaboration [27, 28]) at $\sqrt{s}=1.96$ TeV: a $|\eta _{\pi }|<1.3$, $|y_{\pi \pi }|<1$, $p_{T,\pi }>0.4$ GeV; b $|\eta _{\pi }|<1.3$, $|y_{\pi \pi }|<1$, $p_{T,\pi }>0.4$ GeV, $p_{T, \pi \pi }>1$ GeV. Curves correspond to $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings from (14). Solid upper curves correspond to the sum of all amplitudes, and dashed lower curves represent the continuum contribution. Fluctuations in solid curves are due to the complex Monte Carlo integration process, and they can be smoothed by increasing the integration accuracy. The thickness of the solid curves corresponds to the errors of Monte Carlo calculations. Additional interpolation was used between calculated points for smoothing

Let us look at the ISR [19, 20] and CDF [27, 28] data with parameter $\varLambda _{\pi }$, which we use to describe the data from the STAR collaboration. Different cases are depicted in Figs. 9 and 10.

We see a strong underestimation of the ISR data (by a factor of 3). For these low energies we have to take into account possible corrections to pion–proton amplitudes (contributions from secondary reggeons are strong), since our approach describes data rather well only for energies greater than $\sim 10$ GeV. In each shoulder ($T_{\pi p}$ amplitude in Fig. 1a, b) the energy can be less than 10 GeV. In the present calculations, just to preliminarily and qualitatively check the effect of secondary reggeons and to improve the situation, we use simple exponential parametrization (Born approximation with secondary reggeons) for pion–proton amplitudes to cover the energy value down to $\sim 3$ GeV. The result depicted in Fig. 9 takes into account this correction. We can observe some improvements (increase by a factor of $\sim 1.3$) in comparison with our previous calculations in [3], but even in this case, the data are underestimated. This should be precisely explained in further research. We may also have significant contributions from single and double dissociations to the data.

As to the CDF data in Fig. 10a, they are close to the predictions at the region of the $f_2(1270)$ meson. Another part of the CDF data in Fig. 10b are close to the prediction, but the curve does not fit the data at the region of the $f_2(1270)$ meson. It also looks strange and has no explanation at the moment, since these are the data from the same experiment. This may be due to interference effects with $\gamma \gamma$ or $\gamma \mathbb {O}$ fusion in the central production process and corrections to the $\pi \pi$ final interaction.

Fig. 11

Data on the process $p+p\rightarrow p+\pi ^++\pi ^-+p$ (CMS collaboration [29, 30]): a at $\sqrt{s}=5$ TeV with cuts $|\eta _{\pi }|<2.4$, $p_{T,\pi }>0.2$ GeV; b at $\sqrt{s}=7$ TeV with cuts $|y_{\pi }|<2$, $p_{T,\pi }>0.2$ GeV; c at $\sqrt{s}=13$ TeV with cuts $|\eta _{\pi }|<2.4$, $p_{T,\pi }>0.2$ GeV. Curves correspond to $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings from (14). Solid upper curves correspond to the sum of all amplitudes, and dashed lower curves represent the continuum contribution. The thickness of the solid curves corresponds to the errors of Monte Carlo calculations. Additional interpolation was used between calculated points for smoothing

3.3 CMS data and predictions

In Fig. 11, one can see the recent data from the CMS collaboration and curves of our model, which correspond to $\varLambda _{\pi }=1.2$ GeV in the off-shell pion form factor (11) and couplings (14) from the fit to the STAR data in Fig. 6. Here our predictions are very close to the data except for the region $M_c\sim 0.8\pm 0.1$ GeV, as in all datasets.

4 Summary and conclusions

In this paper, we have considered the LM CEDP process of di-pions and its description in the framework of the Regge-eikonal approach. Here we summarize all the facts and conclusions:

• The result is crucially dependent on the choice of $\varLambda _{\pi }$ in the off-shell pion form factor, i.e. on ${\hat{t}}$ (virtuality of the pion) dependence. In the present approach, the best description of the old STAR data [21, 22] is given by the case with $\varLambda _{\pi }=1.2$ GeV and couplings:

  $$\begin{aligned} g_{{\mathbb {P}}{\mathbb {P}}f_0(500)}= & {} 0.88,\nonumber \\ g_{{\mathbb {P}}{\mathbb {P}}f_0(980)}= & {} 0.43,\nonumber \\ g_{{\mathbb {P}}{\mathbb {P}}f_2(1270)}= & {} 1.72. \end{aligned}$$

  (14)

  The couplings of the pomeron to $f_{0,2}$ can be compared with the value 0.64, which is obtained in [39].

• The model shows that contributions from the the $\rho$ meson are not so significant at available energies, but we have a dip in the theoretical curves at the region of $\rho$ production (at CMS energies, for example, it is obvious). This should also be explained in further investigations.

• Rescattering corrections (“soft survival probability”) in pp and $\pi p$ contribute significantly to the values and form of distributions.

• If we try to fit the data from STAR [23,24,25,26], we find that the curves with parameters fixed from [21, 22] underestimate the data in the region of the $\rho$ meson as in Fig. 5a. The data are close to predictions only in the regions of f mesons. These effects have no explanation at the moment and may be due to some complex dependence of pomeron–pomeron–meson couplings on $t_{1,2}$ and $\phi _0$, wrong normalization of the data or missed contributions from some other processes such as low mass diffractive dissociation.

• We have strong underestimation of the ISR data (by a factor of 3) [19, 20] and contradictory description of two parts of the CDF data [27, 28] with the same parameters (see Figs. 9, 10).

• However, the CMS data at all energies are described rather well (see Fig. 11). A discrepancy is observed only in the region $M_c\sim 0.8\pm 0.2$ GeV as for other energies.

The main open problems regarding model parameters are related to interference terms (we have to know all cut-off form factor parameters, couplings of pions and reggeons to resonances and their dependence on $t_{1,2}$ and $\phi _0$). To fix the model parameters correctly, we need the comparison with precise (exclusive) experimental data (STAR, ATLAS+ALFA, CMS+TOTEM) simultaneously in several differential observables, e.g. the differential distributions $\mathrm{{d}}\sigma /\mathrm{{d}}t_1$, $\mathrm{{d}}\sigma /\mathrm{{d}}\phi _0$, the angular distributions in the $\pi ^+\pi ^-$ rest system and others. It should be done in further works.

We also have to take into account effects such as the interference with $\gamma \gamma \rightarrow \pi \pi$ and $\gamma \mathbb {O}\rightarrow \pi \pi$ processes, effects related to the irrelevance and possible modifications of the Regge approach (for the virtual pion exchange) in this kinematic region, as was discussed in the introduction, corrections to pion–pion scattering at low $M_{\pi \pi }$, corrections to $T_{\pi p}(s,t)$ for $\sqrt{s}<3$ GeV, and differences of resonance peaks from the Breit–Wigner functions. In further works we will take into account possible modifications of the model for the best description of the data.

This model will be implemented in the Monte Carlo event generator ExDiff [40]. It is possible to calculate LM CEDP for other di-hadron final states ($p{\bar{p}}$ for “odderon” hunting, $K^+K^-$, $\eta \eta ^{\prime }$ and so on), which are also very informative for our understanding of diffractive mechanisms in strong interactions.

Appendices

Appendix A: Kinematics of LM CEDP

The $2\rightarrow 4$ process $p(p_a)+p(p_b)\rightarrow p(p_1)+\pi (p_3)+\pi (p_4)+p(p_2)$ can be described as follows (the notation for any momentum is $k=(k_0,k_z;\textbf{k})$, $\textbf{k}=(k_x,k_y)$):

$$\begin{aligned} p_a= & {} \left( \frac{\sqrt{s}}{2}, \beta \frac{\sqrt{s}}{2}; \textbf{0} \right) ,\; p_b=\left( \frac{\sqrt{s}}{2}, -\beta \frac{\sqrt{s}}{2}; \textbf{0} \right) ,\nonumber \\ p_{1,2}= & {} \left( E_{1,2},p_{1,2z}; \textbf{p}_{1,2\perp } \right) , E_{1,2}=\sqrt{p_{1,2z}^2+\textbf{p}_{1,2\perp }^2+m_p^2},\;\nonumber \\ p_{3,4}= & {} \left( m_{3,4\perp }\textrm{ch}\;y_{3,4}, m_{3,4\perp }\textrm{sh}\;y_{3,4}; \textbf{p}_{3,4\perp } \right) \nonumber \\= & {} \left( \sqrt{m_{\pi }^2+\textbf{p}_{3,4\perp }^2\textrm{ch}^2\eta _{3,4}}, |\textbf{p}_{3,4\perp }|\;\textrm{sh}\;\eta _{3,4}; \textbf{p}_{3,4\perp } \right) , \nonumber \\ m_{i\perp }^2= & {} m_i^2+\textbf{p}_{i\perp }^2,\; m_{1,2}=m_p,\; m_{3,4}=m_{\pi }, \nonumber \\ \textbf{p}_{4\perp }= & {} -\textbf{p}_{3\perp }-\textbf{p}_{1\perp }-\textbf{p}_{2\perp },\; \nonumber \\ \beta= & {} \sqrt{1-\frac{4m_p^2}{s}},\; s=(p_a+p_b)^2,\; s^{\prime }=(p_1+p_2)^2. \end{aligned}$$

(15)

Here, $y_i$ ($\eta _i$) are rapidities (pseudorapidities) of the final pions.

The phase space of the process in terms of the above variables is as follows

$$\begin{aligned} \mathrm{{d}}\mathrm {\Phi }_{2\rightarrow 4}= & {} \left( 2\pi \right) ^4\delta ^4\left( p_a+p_b-\sum _{i=1}^4p_i\right) \prod _{i=1}^4 \frac{d^3p_i}{(2\pi )^32E_i} \nonumber \\= & {} \frac{1}{2^4(2\pi )^8} \prod _{i=1}^3 p_{i\perp }\mathrm{{d}}p_{i\perp }\mathrm{{d}}\phi _i\cdot \mathrm{{d}}y_3\mathrm{{d}}y_4 \cdot {{\mathcal {J}}}; \nonumber \\ {{\mathcal {J}}}= & {} \frac{\mathrm{{d}}p_{1z}}{E_1} \frac{\mathrm{{d}}p_{2z}}{E_2} \delta \left( \sqrt{s}-\sum _{i=1}^4 E_i\right) \delta \left( \sum _{i=1}^4 p_{iz}\right) \nonumber \\= & {} \frac{1}{\left| {\tilde{E}}_2{\tilde{p}}_{1z}-{\tilde{E}}_1{\tilde{p}}_{2z}\right| }, \end{aligned}$$

(16)

where $p_{i\perp }=\left| \textbf{p}_{i}\right|$, ${\tilde{p}}_{1,2z}$ are appropriate roots of the system

$$\begin{aligned}{} & {} {\left\{ \begin{array}{ll} &{}A=\sqrt{s}-E_3-E_4=\sqrt{m_{1\perp }^2+p_{1z}^2}+ \sqrt{m_{2\perp }^2+p_{2z}^2},\\ &{}B=-p_{3z}-p_{4z}=p_{1z}+p_{2z}, \end{array}\right. }\nonumber \\ \end{aligned}$$

(17)

$$\begin{aligned}{} & {} {\tilde{p}}_{1z}= \frac{B}{2}+\frac{1}{2(A^2-B^2)}\left[ B\left( m_{1\perp }^2-m_{2\perp }^2\right) + A\cdot \lambda _0^{1/2} \right] ,\nonumber \\{} & {} \lambda _0=\lambda \left( A^2-B^2,m_{1\perp }^2,m_{2\perp }^2\right) . \end{aligned}$$

(18)

Here $\lambda (x,y,z)=x^2+y^2+z^2-2xy-2xz-2yz$, and then ${{\mathcal {J}}}^{-1}=\lambda _0^{1/2}/2$.

For the differential cross-section we have

$$\begin{aligned} \frac{\mathrm{{d}}\sigma _{2\rightarrow 4}}{\prod _{i=1}^{3} \mathrm{{d}}p_{i\perp }\mathrm{{d}}\phi _i\cdot \mathrm{{d}}y_3\mathrm{{d}}y_4 }= & {} \frac{1}{2\beta s}\cdot \frac{\prod _{i=1}^3 p_{i\perp }}{2^4(2\pi )^8\cdot \frac{1}{2}\lambda _0^{1/2}} \left| T\right| ^2 \nonumber \\= & {} \frac{\prod _{i=1}^3 p_{i\perp }}{2^{12}\pi ^8\beta s \lambda _0^{1/2}}\left| T \right| ^2. \end{aligned}$$

(19)

Pseudorapidity is a more convenient experimental variable, and we can use the transform

$$\begin{aligned} \frac{\mathrm{{d}}y_i}{\mathrm{{d}}\eta _i}=\frac{p_{i\perp }\textrm{ch}\eta _i}{\sqrt{m_i^2+p_{i\perp }^2\textrm{ch}^2\eta _i}} \end{aligned}$$

(20)

to obtain the differential cross-section in pseudorapidities.

Fig. 12

Total amplitude of the process of double-pion LM CEDP $p+p\rightarrow p+\pi ^++\pi ^-+p$ with detailed kinematics. Proton–proton rescatterings in the initial and final states are depicted as black filled circles, and pion–proton subamplitudes are shown as shaded circles. All momenta are shown. The basic part of the amplitude, $M_0$ (see Eq. (5)), without corrections is circled by a dotted line. Crossed lines are on the mass shell. Here, $\varDelta _{1\perp }=\varDelta _1-q-q^{\prime }$, $\varDelta _{2\perp }=\varDelta _2+q+q^{\prime }$, ${\hat{t}}=k^2=(\varDelta _{1\perp }-q_1-p_3+q_2)^2$, ${\hat{u}}=(\varDelta _{1\perp }-q_1-p_4)^2$, ${\hat{s}}=(p_3+p_4-q_1-q_2)^2$

In some cases it is convenient to use other variables for the integration of the cross-section and calculation of distributions on central mass. For these cases we have

$$\begin{aligned} \mathrm{{d}}\mathrm {\Phi }_{2\rightarrow 4}= & {} \frac{1}{2^4(2\pi )^8} \prod _{i=1}^2 \mathrm{{d}}t_i \mathrm{{d}}\phi _i\cdot M_c \mathrm{{d}}M_c \mathrm{{d}}\eta _c \mathrm{{d}}c^* \mathrm{{d}}\phi ^*\cdot {{\mathcal {J}}}^{\prime }; \nonumber \\ {{\mathcal {J}}}^{\prime }= & {} \frac{\beta _M}{4\beta _1\beta _2 s} \frac{\mathrm{{d}}y_c}{\mathrm{{d}}\eta _c},\, \,\,\,\, \beta _i \simeq \sqrt{1+\frac{4(m_p^2-(1-\xi _i)t_i)}{\beta ^2s^2(1-\xi _i)^2}}; \nonumber \\ \beta _M= & {} \sqrt{1-\frac{4m_{\pi }^2}{M_c^2}},\, \, \frac{\mathrm{{d}}y_c}{\mathrm{{d}}\eta _c}=\frac{p_{c\perp }\textrm{ch}\eta _c}{\sqrt{M_c^2 +p_{c\perp }^2\textrm{ch}^2\eta _c}}; \end{aligned}$$

(21)

$$\begin{aligned} \frac{\mathrm{{d}}\sigma \mathrm{{d}}\sigma _{2\rightarrow 4}}{\prod _{i=1}^{2} \mathrm{{d}}t_{i}\mathrm{{d}}\phi _i \mathrm{{d}}M_c \mathrm{{d}}\eta _c \mathrm{{d}}c^* \mathrm{{d}}\phi ^*}= & {} \frac{1}{2\beta s}\cdot \frac{M_c \beta _M \frac{\mathrm{{d}}y_c}{\mathrm{{d}}\eta _c}}{2^4(2\pi )^8\cdot 4\beta _1\beta _2 s} \left| T\right| ^2 \nonumber \\= & {} \frac{M_c \beta _M \frac{\mathrm{{d}}y_c}{\mathrm{{d}}\eta _c}}{2^{15}\pi ^8\beta \beta _1\beta _2 s^2 }\left| T \right| ^2, \end{aligned}$$

(22)

where $c^*=\cos \theta ^*$, $\theta ^*$ and $\phi ^*$ are the polar and azimuthal angles of the pion momenta in the $\pi ^+\pi ^-$ rest frame, $M_c$ is the di-pion mass, $\eta _c$ is the di-pion pseudorapidity, $t_1=(p_a-p_1)^2$, $t_2=(p_b-p_2)^2$ and

$$\begin{aligned} \xi _{1,2}\simeq \sqrt{\frac{M_c^2-t_1-t_2+2\sqrt{t_1t_2}\cos (\phi _1-\phi _2)}{s}} {\textbf {e}}^{\pm y_c}. \end{aligned}$$

For exact calculations of elastic subprocesses (see Fig. 12) of the type $a(p_1)+b(p_2)\rightarrow c(p_1-q_{el})+d(p_2+q_{el})$:

$$\begin{aligned} q_{el}= & {} \left( q_0,q_z; \textbf{q}\right) ,\nonumber \\ q_z= & {} -\frac{b}{2a}\left( 1-\sqrt{1-\frac{4ac}{b^2}}\right) ,\nonumber \\ q_0= & {} \frac{A_0q_z+\textbf{p}_{1\perp }\textbf{q}+\textbf{p}_{2\perp }\textbf{q}}{A_z},\nonumber \\ a= & {} A_z^2-A_0^2,\; b=-2 \left( A_z\cdot {{\mathcal {D}}}+A_0 \left( \textbf{p}_{1\perp }\textbf{q}+\textbf{p}_{2\perp }\textbf{q}\right) \right) ,\nonumber \\ c= & {} 2 A_z B_z-\left( \textbf{p}_{1\perp }\textbf{q}+\textbf{p}_{2\perp }\textbf{q}\right) ^2 +\textbf{q}^2A_z^2,\nonumber \\ A_0= & {} p_{1z}+p_{2z},\; A_z=p_{10}+p_{20}, \nonumber \\ B_0= & {} p_{1z}\cdot \textbf{p}_{2\perp }\textbf{q}-p_{2z}\cdot \textbf{p}_{1\perp }\textbf{q},\nonumber \\ B_z= & {} p_{10}\cdot \textbf{p}_{2\perp }\textbf{q}-p_{20}\cdot \textbf{p}_{1\perp }\textbf{q},\nonumber \\ {{\mathcal {D}}}= & {} p_{1z}p_{20}-p_{2z}p_{10}, \end{aligned}$$

(23)

and $q_{el}^2\simeq -\textbf{q}^2$.

Appendix B: Regge-eikonal model for elastic proton–proton and pion–proton scattering

Here is a short review of formulae for the Regge-eikonal approach [32, 33], which we use to estimate rescattering corrections in the proton–proton and pion–proton channels.

Amplitudes of elastic proton–proton and pion–proton scattering are expressed in terms of eikonal functions

$$\begin{aligned}{} & {} T_{pp,\pi p}^{el}(s,b)=\frac{\textrm{e}^{-2\varOmega _{pp,\pi p}^{el}(s,b)}-1}{2\textrm{i}},\nonumber \\{} & {} \varOmega _{pp, \pi p}^{el}(s,b) = -\textrm{i}\,\delta _{pp,\pi p}^{el}(s,b),\nonumber \\{} & {} \delta ^{el}_{pp,\pi p}(s,b)=\frac{1}{16\pi s}\int _0^\infty d(-t) J_0(b\sqrt{-t}) \delta ^{el}_{pp,\pi p}(s,t). \end{aligned}$$

(24)

$$\begin{aligned}{} & {} \delta ^{el}_{pp}(s,t)\nonumber \\{} & {} \simeq g_{pp\mathbb {P}}(t)^2\left( \textrm{i}+\tan \frac{\pi (\alpha _{\mathbb {P}}(t)-1)}{2}) \right) \pi \alpha ^{\prime }_{\mathbb {P}}(t) \left( \frac{s}{2s_0}\right) ^{\alpha _{\mathbb {P}}(t)},\nonumber \\{} & {} \alpha _{\mathbb {P}}(t)=1+\frac{\alpha _{\mathbb {P}}(0)-1}{1-\frac{t}{\tau _a}},\, g_{pp\mathbb {P}}(t)=\frac{g_{pp\mathbb {P}}(0)}{\left( 1-a_g t\right) ^2}. \end{aligned}$$

(25)

$$\begin{aligned}{} & {} {}\delta ^{el}_{\pi p}(s,t)\nonumber \\{} & {} \simeq \left( \text {i}+\tan \frac{\pi (\alpha _{\mathbb {P}} (t)-1)}{2}) \right) \beta _{\mathbb {P}}(t) \left( \frac{s}{s_0}\right) ^{\alpha _{\mathbb {P}} (t)}\nonumber \\{} & {} +\left( \textrm{i}+\tan \frac{\pi (\alpha _{f}(t)-1)}{2}) \right) \beta _{f}(t) \left( \frac{s}{s_0}\right) ^{\alpha _{f}(t)}, \end{aligned}$$

(26)

$$\begin{aligned}{} & {} \alpha _{\mathbb {P}}(t)=1+p_1\left[ 1-p_2 t\left( \arctan \left( p_3-p_2t\right) -\frac{\pi }{2} \right) \right] ,\nonumber \\{} & {} \alpha _f(t)=\left( \frac{8}{3\pi }\gamma (\sqrt{-t+c_f}) \right) ^{1/2},\nonumber \\{} & {} \gamma (\mu )=\frac{4\pi }{11-\frac{2}{3}n_f}\left( \frac{1}{\ln \frac{\mu ^2}{\varLambda ^2}}+\frac{1}{1-\frac{\mu ^2}{\varLambda ^2}} \right) ,\nonumber \\{} & {} \beta _{\mathbb {P}}(t)=B_{\mathbb {P}}\textrm{e}^{b_{\mathbb {P}}t} (1+d_1t+d_2t^2+d_3 t^3+d_4 t^4),\nonumber \\{} & {} \beta _f(t)=B_f \textrm{e}^{b_f t}. \end{aligned}$$

(27)

Table 1 Parameters for proton–proton elastic scattering amplitude

Table 2 Parameters for pion–proton elastic scattering amplitude

Parameters can be found in Tables 1 and 2.

$$\begin{aligned} V_{pp}(s,q^2)= & {} \int d^2\textbf{b} \,\textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \sqrt{1+2\textrm{i}T_{pp}^{el}(s,b)}\nonumber \\= & {} \int d^2\textbf{b}\, \textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \textrm{e}^{-\varOmega _{pp}^{el}(s,b)}\nonumber \\= & {} (2\pi )^2\delta ^2\left( \textbf{q}\right) + 2\pi {\bar{T}}_{pp}(s,q^2), \end{aligned}$$

(28)

$$\begin{aligned} {\bar{T}}_{pp}(s,q^2)= & {} \int _0^\infty b\,\mathrm{{d}}b\, J_0\left( b\sqrt{-q^2}\right) \left[ \textrm{e}^{-\varOmega _{pp}^{el}(s,b)}-1 \right] \end{aligned}$$

(29)

$$\begin{aligned} S_{\pi p}(s,q^2)= & {} \int d^2\textbf{b} \,\textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \left( 1+2\textrm{i}T_{\pi p}^{el}(s,b) \right) \nonumber \\= & {} \int d^2\textbf{b}\, \textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \textrm{e}^{-2\varOmega _{\pi p}^{el}(s,b)}\nonumber \\= & {} (2\pi )^2\delta ^2\left( \textbf{q}\right) + 2\pi {\bar{T}}_{\pi p}(s,q^2), \end{aligned}$$

(30)

$$\begin{aligned} {\bar{T}}_{\pi p}(s,q^2)= & {} \int _0^\infty b\,\mathrm{{d}}b\, J_0\left( b\sqrt{-q^2}\right) \left[ \textrm{e}^{-2\varOmega _{\pi p}^{el}(s,b)}-1 \right] \end{aligned}$$

(31)

Here we take $S_{\pi p}(s,t)=S_{\pi ^+ p}(s,t)=S_{\pi ^- p}(s,t)$ and

$$\begin{aligned} T^{el}_{\pi ^+p}(s,t)=T^{el}_{\pi ^-p}(s,t)=-4\text {i} \pi s {\bar{T}}_{\pi p}(s,t) \end{aligned}$$

(32)

Approach (26) describes the data on pion–proton scattering better even at low energies, which is why we use it instead of the one presented in [32].

Functions ${\bar{T}}_{pp}$ and ${\bar{T}}_{\pi p}$ are convenient for numerical calculations, since its oscillations are not so strong.

Appendix C: Primary amplitudes for CEDP and ERVM resonance production

Here is a short review of the formulae, which can be obtained from Refs. [14,15,16,17, 34, 39].

Let us introduce the general diffractive factor

$$\begin{aligned} F_{\mathbb {P}}(t,\xi ) = g_{pp\mathbb {P}}(t)^2\left( \textrm{i}+\tan \frac{\pi (\alpha _{\mathbb {P}}(t)-1)}{2}) \right) \frac{\pi \alpha ^{\prime }_{\mathbb {P}}(t)}{\xi ^{\alpha _{\mathbb {P}}}(t)}. \end{aligned}$$

(33)

1.1 $f_0$ production

For $f_0$ production we have the following expression

$$\begin{aligned}{} & {} \!\!\!\!\!M_0^{pp\rightarrow p \{f_0\rightarrow \pi ^+\pi ^- \} p} \nonumber \\{} & {} \quad = -F_{\mathbb {P}}(t_1,\xi _1) F_{\mathbb {P}}(t_2,\xi _2) \, g_{\mathbb {P}\mathbb {P}f_0}(t_1,t_2,M_c^2) \nonumber \\{} & {} \qquad \times \frac{g_{f_0\pi \pi } \left( {{\mathcal {F}}}(M_c^2,m_{f_0}^2)\right) ^2F_M(t_1)F_M(t_2)}{(M_c^2-m_{f_0}^2) +B_{f_0}(M_c^2,m_{f_0}^2)}, \end{aligned}$$

(34)

where ($M_c > 2m_{\pi }$)

$$\begin{aligned}{} & {} \!\!B_{f_0}(M_c^2,m_{f_0}^2) \nonumber \\{} & {} \quad = \textrm{i}\; \varGamma _{f_0} \left( {{\mathcal {F}}}(M_c^2)\right) ^2\left[ \frac{1-4m_{\pi }^2/M_c^2}{1-4m_{\pi }^2/m_{f_0}^2}\right] ^{1/2} \end{aligned}$$

(35)

$$\begin{aligned}{} & {} {{\mathcal {F}}}(M_c^2,m_f^2) = F^{\mathbb {P}\mathbb {P}f} (M_c^2,m_f^2)=F^{f\pi \pi }(M_c^2,m_f^2)\nonumber \\{} & {} \quad =\exp \left( \frac{-(M_c^2-m_{f}^2)^2}{\varLambda _{f}^4}\right) ,\, \varLambda _{f}\sim 1\,\textrm{GeV}, \end{aligned}$$

(36)

$$\begin{aligned}{} & {} F_M(t) = 1/(1-t/m_0^2),\, m_0^2 = 0.5\,\textrm{GeV}^2 \end{aligned}$$

(37)

${{\mathcal {F}}}(M_c^2,m_f^2)$ and $F_M(t)$ are off-shell phenomenological form factors introduced in [14,15,16,17] to better describe the data. Here we fix the mass and width of $f_0(500)$ and $f_0(980)$ mesons as in [15]

$$\begin{aligned} m_{f_0(500)}= & {} 0.6\,\textrm{GeV},\, \varGamma _{f_0(500)} = 0.5\, \textrm{GeV}, \end{aligned}$$

(38)

$$\begin{aligned} m_{f_0(980)}= & {} 0.98\,\textrm{GeV},\, \varGamma _{f_0(980)} = 0.07\,\textrm{GeV}, \end{aligned}$$

(39)

and also their couplings to pions

$$\begin{aligned} g_{f_0(500)\pi \pi } = 3.37,\, g_{f_0(500)\pi \pi } = 1.55, \end{aligned}$$

(40)

also assuming $\varGamma (f_0\rightarrow \pi \pi )/\varGamma _{f_0}=100\%$.

In this work, coupling of pomerons to mesons $g_{\mathbb {P}\mathbb {P}f_0}$ is the constant and can be extracted from the experimental data as a free parameter. In [39] this coupling is proposed to be 0.64 GeV for all mesons related to the “glueball state”. Here, due to simplifications, these couplings are of the same order but may differ by factor $2\div 3$ (see the main text).

1.2 $f_2$ production

For $f_2(1270)$ production we have to modify the expression (34) due to the tensor nature of this meson. Finally, we have

$$\begin{aligned}{} & {} M_0^{pp\rightarrow p \{f_2\rightarrow \pi ^+\pi ^- \} p} \nonumber \\{} & {} \quad = F_{\mathbb {P}}(t_1,\xi _1) F_{\mathbb {P}}(t_2,\xi _2) \,g_{\mathbb {P}\mathbb {P}f_2} \nonumber \\{} & {} \qquad \times \frac{(g_{f_2\pi \pi }/2) \left( {{\mathcal {F}}}(M_c^2,m_{f_2}^2)\right) ^2F_M(t_1)F_M(t_2)}{(M_c^2-m_{f_2}^2) +B_{f_2}(M_c^2,m_{f_2}^2)} {{\mathcal {P}}}_2, \end{aligned}$$

(41)

where

$$\begin{aligned} {{\mathcal {P}}}_2 = (\varDelta _1\varDelta _{34})^2-\frac{(M_c^2-4m_{\pi }^2)\lambda (M_c^2,t_1,t_2)}{12 M_c^2} \end{aligned}$$

(42)

is the additional function which can be obtained by contraction of the pomeron–pomeron–meson vertex with the pion–pion–meson one, $\varDelta _1=p_a-p_1$, $\varDelta _{34}=p_3-p_4$.

$$\begin{aligned}{} & {} B_{f_2}(M_c^2,m_{f_2}^2) \nonumber \\{} & {} \quad =\textrm{i}\; \varGamma _{f_2} \left( {{\mathcal {F}}}(M_c^2,m_{f_2}^2)\right) ^2\left[ \frac{1-4m_{\pi }^2/M_c^2}{1-4m_{\pi }^2/m_{f_0}^2}\right] ^{5/2} \frac{M_c^4}{m_{f_2}^4} \end{aligned}$$

(43)

Fixed parameters for $f_2(1270)$ are

$$\begin{aligned} m_{f_2(1270)}= & {} 1.275\,\textrm{GeV},\, \varGamma _{f_2(1270)} = 0.1851\, \textrm{GeV},\nonumber \\ g_{f_2(1270)\pi \pi }= & {} 9.26\,\textrm{GeV}^{-1},\, \varLambda _{f_2}=1\,\textrm{GeV}. \end{aligned}$$

(44)

After the data analysis, the “scalar” coupling of the $f_2(1270)$ to the pomeron is found to be of the order of 2. Since the pomeron does not behave as a simple scalar, the structure of the coupling is, of course, more complicated. In the “exact” model as in [14], the pomeron can be a coherent sum of different spins and can have several couplings to f mesons. But in real life we have to obtain the vertex for any spin J and then make a continuation to the complex plane in J, such as in classical Regge theory. This is the conceptual question which was partially discussed in [3], but we postpone it to our further theoretical works. In the present work we use the simplified model for the $f_2$ production. This is why the extracted value of the “constant” coupling could differ from the real set of tensor couplings.

1.3 $\rho _0$ production

For $\rho _0$ the situation is somewhat complicated, since we have to take into account vector dominance and also $\rho -\omega$ mixing. After all contractions, the primary amplitude looks like

$$\begin{aligned}{} & {} M_0^{pp\rightarrow p \{\rho _0\rightarrow \pi ^+\pi ^- \} p} = \textrm{i}\;T^{el}_{\rho _0 p}(s_2,t_2)\frac{C_T^{\rho _0}(t_1){{\mathcal {P}}}_{\rho }}{|t_1|} \nonumber \\{} & {} \quad \times \frac{(g_{\rho _0\pi \pi }/2) {{\mathcal {F}}}_{\rho }(M_c^2){{\mathcal {F}}}_{\rho }(t_1)}{(M_c^2-m_{\rho _0}^2)+B_{\rho _0} (M_c^2,m_{\rho _0}^2)}+(1\leftrightarrow 2), \end{aligned}$$

(45)

$$\begin{aligned}{} & {} s_2=(p_3+p_4+p_2)^2=(p_a-p_1+p_b)^2,\\{} & {} s_1=(p_3+p_4+p_1)^2=(p_b-p_2+p_a)^2. \end{aligned}$$

Amplitude $T^{el}_{\rho _0 p}(s,t)$ can be obtained by the use of the formulae similar to (24)–(26) with

$$\begin{aligned} \delta ^{el}_{\rho _0 p}(s,t)\simeq & {} g_{pp\mathbb {P}}(t)g_{\rho \rho \mathbb {P}}(t)\left( \textrm{i}+\tan \frac{\pi (\alpha _{\mathbb {P}}(t)-1)}{2}) \right) \nonumber \\{} & {} \times \pi \alpha ^{\prime }_{\mathbb {P}}(t) \left( \frac{s}{2s_0}\right) ^{\alpha _{\mathbb {P}}(t)},\nonumber \\ g_{\rho \rho \mathbb {P}}(t)= & {} g_{\rho \rho \mathbb {P}}(0) = 7.07\,\textrm{GeV}\,\,\,\text{(see } \text{[34]) }; \end{aligned}$$

(46)

$$\begin{aligned} C_T^{\rho _0}(t)= & {} \sqrt{\frac{3\varGamma _{\rho \rightarrow e^+e^-}}{\alpha _e m_{\rho }}} \frac{m_{\rho }^2}{m_{\rho }^2-t}, \end{aligned}$$

(47)

$$\begin{aligned} {{\mathcal {F}}}_{\rho }(p^2)= & {} (1+p^2(p^2-m_{\rho }^2)/\varLambda _{\rho }^4)^{-n_{\rho }}, \end{aligned}$$

(48)

$$\begin{aligned} F_1(t)= & {} \frac{1-\kappa \, t/(4 m_p^2)}{1-t/(4m_p^2)}(1-t/m_D^2)^{-2}, \end{aligned}$$

(49)

$$\begin{aligned} \kappa= & {} \mu _p/\mu _N=2.7928,\, m_D^2=0.71\,\textrm{GeV}^2, \end{aligned}$$

(50)

$$\begin{aligned}{} & {} \!\!\!\!\!\varGamma _{\rho \rightarrow e^+e^-}= 7.04\cdot 10^{-6}\,\textrm{GeV}, \end{aligned}$$

(51)

$$\begin{aligned}{} & {} \!\!\!\!{{\mathcal {P}}}_{\rho } \simeq 2\sqrt{4\pi \alpha _e}F_1(t) \left( \mathbf {\varDelta }_{34}^*\textbf{p}_a^* \right) , \end{aligned}$$

(52)

${{\mathcal {P}}}_{\rho }$ is the factor that is equal to the “scalar proton–proton–photon vertex” contracted with the vector of the $\rho \pi \pi$ vertex, and the scalar product of transverse vectors $\left( \mathbf {\varDelta }_{34}^*\textbf{p}_a^* \right)$ in the $\rho$ meson rest frame with

$$\begin{aligned} \varDelta _1^*=\{(M_c^2+t_1-t_2)/(2M_c),0,0,\lambda ^{1/2}/(2M_c)\} \end{aligned}$$

can be expressed in terms of four vectors in the central mass frame of colliding protons:

$$\begin{aligned}{} & {} \left( \mathbf {\varDelta }_{34}^*\textbf{p}_a^* \right) = -\varDelta _{34}p_a -\varDelta _{34,z}^*p_{a,z}^*,\nonumber \\{} & {} \varDelta _{34,z}^* = -\varDelta _1\varDelta _{34}\frac{2M_c}{\lambda ^{1/2}},\nonumber \\{} & {} p_{a,z}^* = \left( \frac{p_ap_c(M_c^2+t_1-t_2)}{2M_c^2}-\frac{t_1}{2} \right) \frac{2M_c}{\lambda ^{1/2}},\nonumber \\{} & {} \lambda \equiv \lambda (M_c^2,t_1,t_2),\, p_c=p_3+p_4. \end{aligned}$$

(53)

Other functions and parameters are

$$\begin{aligned}{} & {} B_{\rho _0}(M_c^2,m_{\rho _0}^2) \nonumber \\{} & {} \quad = \textrm{i}\; \varGamma _{\rho _0} \left( {{\mathcal {F}}}_{\rho }(M_c^2)\right) ^2\left[ \frac{1-4m_{\pi }^2/M_c^2}{1-4m_{\pi }^2/m_{\rho _0}^2}\right] ^{3/2} \frac{M_c^2}{m_{\rho _0}^2} \end{aligned}$$

(54)

$$\begin{aligned}{} & {} m_{\rho _0} = 0.7737\,\textrm{GeV},\, \varGamma _{\rho _0} = 0.1462\,\textrm{GeV},\nonumber \\{} & {} g_{\rho _0\pi \pi } = 11.51\,\textrm{GeV},\, \varLambda _{\rho }=1\,\textrm{GeV}, \, n_{\rho }=0.5. \end{aligned}$$

(55)

Here we take for all off-shell propagators of resonances the simple Breit–Wigner form, but we can use more complicated expressions, which can be found, for example, in [14,15,16,17].

$$\begin{aligned}{} & {} M^U\left( \{ p \}\right) \\{} & {} \quad =\int \int \frac{d^2\textbf{q}}{(2\pi )^2}\frac{d^2\textbf{q}^{\prime }}{(2\pi )^2} \frac{d^2\textbf{q}_1}{(2\pi )^2}\frac{d^2\textbf{q}_2}{(2\pi )^2} V_{pp}(s,q^2) V_{pp}(s^{\prime },q^{\prime 2})\\{} & {} \qquad \times \; \left[ \left[ S_{{\bar{h}}p}({\tilde{s}}_{14},q_1^2) M_0^{C}\left( \{{\tilde{p}}\} \right) S_{hp}({\tilde{s}}_{23},q_2^2)+ (3\leftrightarrow 4) \right] +M_0^R\left( \{{\tilde{p}}\} \right) \right] \\{} & {} \quad \approx \int \int \frac{d^2\textbf{q}}{(2\pi )^2} \frac{d^2\textbf{q}_1}{(2\pi )^2}\frac{d^2\textbf{q}_2}{(2\pi )^2} S_{pp}(s,q^2) \\{} & {} \qquad \times \left[ \left[ S_{{\bar{h}}p}({\tilde{s}}_{14},q_1^2) M_0^{C}\left( \{{\tilde{p}}\} \right) S_{hp}({\tilde{s}}_{23},q_2^2)+ (3\leftrightarrow 4) \right] {+}M_0^R\left( \{{\tilde{p}}\} \right) \right] _{q^{\prime }\rightarrow 0} \\{} & {} M_0^{C}\left( \{ p \}\right) = T^{el}_{hp}(s_{13},t_1) {{\mathcal {P}}}_{h}({\hat{s}},{\hat{t}}) \left[ {\hat{F}}_{h}\left( {\hat{t}}\right) \right] ^2 T^{el}_{{\bar{h}}p}(s_{24},t_2), \end{aligned}$$

where functions are defined in (28)–(32) of Appendix B, and sets of vectors are

$$\begin{aligned}{} & {} \{ p \}\equiv \{ p_a,p_b,p_1,p_2,p_3,p_4\}\\{} & {} \{ {\tilde{p}}\}\equiv \{ p_a-q,p_b+q; p_1+q^{\prime }+q_1,\\{} & {} \;\;\;\;\;\;\;\;\;\;\;\; p_2-q^{\prime }+q_2,p_3-q_2,p_4-q_1\}, \end{aligned}$$

and

$$\begin{aligned} {\tilde{s}}_{14}= & {} \left( p_1+p_4+q^{\prime } \right) ^2,\; {\tilde{s}}_{23}=\left( p_2+p_3-q^{\prime } \right) ^2, \end{aligned}$$

(56)

$$\begin{aligned} s_{ij}= & {} \left( p_i+p_j \right) ^2,\; t_{1,2}=\left( p_{a,b}-p_{1,2} \right) ^2, \end{aligned}$$

(57)

$$\begin{aligned} {\hat{s}}= & {} \left( p_3+p_4 \right) ^2,\; {\hat{t}}=\left( p_a-p_1-p_3 \right) ^2 \end{aligned}$$

(58)

$$\begin{aligned} S_{h_1h_2}(s,q^2)= & {} \int d^2\textbf{b} \,\textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \left( 1+2\textrm{i}T_{h_1h_2}^{el}(s,b) \right) \\= & {} \int d^2\textbf{b}\, \textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \textrm{e}^{-2\varOmega _{h_1h_2}^{el}(s,b)}{=} (2\pi )^2\delta ^2\left( \textbf{q}\right) {+} 2\pi {\bar{T}}_{h_1h_2}(s,q^2), \\ {\bar{T}}_{h_1h_2}(s,q^2)= & {} \int _0^\infty b\,\mathrm{{d}}b\, J_0\left( b\sqrt{-q^2}\right) \left[ \textrm{e}^{-2\varOmega _{h_1h_2}^{el}(s,b)}-1 \right] \\ T_{h_1h_2}^{el}(s,b)= & {} \frac{\textrm{e}^{-2\varOmega _{h_1h_2}^{el}(s,b)}-1}{2\textrm{i}},\\ \varOmega _{h_1h_2}^{el}(s,b)= & {} -\textrm{i}\,\delta _{h_1h_2}^{el}(s,b),\\ \delta ^{el}_{h_1h_2}(s,b)= & {} \frac{1}{16\pi s}\int _0^\infty d(-t) J_0(b\sqrt{-t}) \delta ^{el}_{h_1h_2}(s,t)\\ {\hat{F}}_{h}= & {} \textrm{e}^{({\hat{t}}-m_{h}^2)/\varLambda _{h}^2},\\ M_0^{C,\pi }\left( \{ p \}\right)= & {} T^{el}_{\pi ^+p}(s_{13},t_1) {{\mathcal {P}}}_{\pi }({\hat{s}},{\hat{t}}) \left[ {\hat{F}}_{\pi }\left( {\hat{t}}\right) \right] ^2 T^{el}_{\pi ^-p}(s_{24},t_2), \\ {{\mathcal {P}}}_{\pi }({\hat{s}},{\hat{t}})= & {} \left( \textrm{ctg}\frac{\pi \alpha _{\pi }({\hat{t}})}{2}-\textrm{i} \right) \cdot \frac{\pi \alpha _{\pi }^{\prime }}{2\!\!\mathrm {\Gamma } (1+\alpha _{\pi }({\hat{t}}))} \left( \frac{{\hat{s}}}{s_0} \right) ^{\alpha _{\pi }({\hat{t}})},\\ \alpha _{\pi }({\hat{t}})= & {} 0.7({\hat{t}}-m_{\pi }^2)\\ M_0^{C,p}\left( \{ p \}\right)= & {} T^{el}_{pp}(s_{13},t_1) {{\mathcal {P}}}_{p}({\hat{s}},{\hat{t}}) \left[ {\hat{F}}_{p}\left( {\hat{t}}\right) \right] ^2 T^{el}_{{\bar{p}}p}(s_{24},t_2),\\ {{\mathcal {P}}}_{p} ({\hat{t}})= & {} {} \left( \textrm{ctg}\frac{\pi \alpha _p({\hat{t}})}{2}- \text {i} \right) \cdot \frac{\pi \alpha _p ^{\prime }}{2\mathrm {\Gamma } (1+ \alpha _p({\hat{t}}))} \left( \frac{{\hat{s}}}{s_0} \right) ^{\alpha _p({\hat{t}})},\\ \alpha _p({\hat{t}})\simeq & {} ({\hat{t}}-m_p^2)\, \mathrm{(for~ the ~``scalar\hbox {''}\, proton)}\\ V_{h_1h_2}(s,q^2)= & {} \int d^2\textbf{b} \,\textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \sqrt{ 1+2\textrm{i}T_{h_1h_2}^{el}(s,b)}\\= & {} \int d^2\textbf{b}\, \textrm{e}^{\textrm{i}\textbf{q}\textbf{b}} \textrm{e}^{-\varOmega _{h_1h_2}^{el}(s,b)}= (2\pi )^2\delta ^2\left( \textbf{q}\right) + 2\pi {\tilde{T}}_{h_1h_2}\\ {\tilde{T}}_{h_1h_2}= & {} \int _0^\infty b\,\mathrm{{d}}b\, J_0\left( b\sqrt{-q^2}\right) \left[ \textrm{e}^{-\varOmega _{h_1h_2}^{el}(s,b)}-1 \right] \end{aligned}$$