1 Introduction

Strong electromagnetic fields polarize the quantum vacuum and produce charged particle-antiparticle pairs. The corresponding electromagnetic theory is described by the effective Lagrangian consisting of the usual Maxwell Lagrangian and the loop corrections due to the strong fields. Heisenberg and Euler found the one-loop effective Lagrangian in a uniform electromagnetic field by solving the Dirac equation [1]. Schwinger implemented quantum field theory to derive the effective Lagrangian in the form of the proper-time integral, in which the fermion or scalar boson coupled to the electromagnetic field is integrated out [2]. The simple poles in the proper-time integral endow the effective Lagrangian with an imaginary part, which is interpreted as the loss of the vacuum persistence due to pair production. In fact, a pure electric field or an electric field parallel to a magnetic field in a proper Lorentz frame can produce electron-positron pairs from the Dirac sea via quantum tunneling through the tilted mass gap. Even when pair production does not occur, strong electromagnetic fields polarize the vacuum so that photons propagating through the vacuum experience the prominent phenomena of vacuum polarization such as vacuum birefringence, photon splitting, and photon-photon scattering (for review, see [3, 4]).

The pair production, called the Schwinger effect, is an epitome of non-perturbative quantum field effects. Electron-positron pairs can be efficiently produced when the electric field is comparable to the critical field \(E_{c}=m^{2}c^{3}/e\hbar =1.3\times 10^{16}\,\mathrm {V/cm}\) as the pair production per unit four Compton volume is given by a Boltzmann factor of which exponent is given as the negative of the ratio of the critical field to the electric field. An magnetic field comparable to the critical field \(B_{c}=m^{2}c^{3}/e\hbar =4.4\times 10^{13}\,\textrm{G}\) makes the lowest Landau level energy equal to the electron rest mass energy. The extreme field strengths \(E_{c}\) and \(B_{c}\) are called the Schwinger limit. The physics under such strong electromagnetic fields, described by the effective Lagrangian, should drastically differ from that under weak fields.

In experiments, the Schwinger pair production is still impossible to realize because no terrestrial mean provides an electric field comparable to the Schwinger limit. In spite of the recent progress in high-intensity lasers based on chirped pulsed amplification (CPA) technique, the current highest laser intensity is \(1.1\times 10^{23}\,\mathrm {W/cm^{2}}\), achieved by CoReLS [5], of which field strength is still lower than \(E_{c}\) by three orders. Several laser facilities are being constructed for higher intensities, but the target field strengths are still lower by order one or two [6].

In contrast, the effects of vacuum polarization such as photon-photon scattering have been experimentally investigated. The Delbrück scattering, in which a photon is scattered by a Coulomb field, was observed with MeV photons [7, 8]. Photon splitting, in which a photon is split into two by a Coulomb field, was also observed by exploiting the strong nuclear Coulomb field [9]. The photon-photon scattering without a Coulomb field is more difficult to realize but was recently evidenced from heavy ion collision experiments: the ATLAS experiment [10, 11], the CMS experiment [12], and the STAR experiment [13, 14].

Photon-photon scattering can also occur under a magnetic field. The Delbrück scattering by a magnetic field leads to vacuum birefringence: the vacuum under a strong magnetic field can act as a birefringent medium to low-energy photons. Compared to the Schwinger pair production and the photon-photon scattering by the nuclear Coulomb field, vacuum birefringence has the advantage of accumulating the effect over a macroscopic length scale. To realize vacuum birefringence, the PVLAS project used the magnetic field of a strong permanent magnet as the background field and optical laser photons as the probe photons [15]. Also, it was proposed to use the field from an ultra-intense laser as the background field and the strong X-rays from an X-ray free electron laser as the probe photons [16, 17]. These proposals rely on the state-of-arts scientific technologies such as ultra-intense lasers [6], X-ray free electron lasers [18], and ultra-high-precision X-ray polarimetry [19]. Albeit challenging, the goal of the PVLAS project and the laser-based proposals is limited to the vacuum birefringence in subcritical fields.

On the other hand, neutron stars can have magnetic fields comparable to the critical field, and particularly magnetars (highly magnetized neutron stars) have magnetic fields stronger than the critical field by a factor of up to 50 [20,21,22,23]. Thus, the study of QED vacuum polarization effect in such supercritical magnetic fields can provide a diagnostics for the strong magnetic fields of those stars [24]. Recently, a polarimetry of the X-rays from a magnetar has been reported [25], and similar projects has been proposed [26, 27]. The macroscopic length scale of field variation, comparable to the radius of neutron stars, would facilitate the formulation because the Heisenberg–Euler–Schwinger (HES) one-loop effective Lagrangian for uniform electromagnetic fields [1, 2] can be used locally for such a large-scale variation.

To analyze the vacuum birefringence in supercritical magnetic fields, a closed analytic expression of one-loop effective action is necessary instead of the proper-time integral expression obtained by Heisenberg–Euler and Schwinger. Dittrich employed the dimensional regularization method to perform the proper-time integral in terms of the Hurwitz zeta-function and logarithmic functions in either a pure magnetic field or an electric field perpendicular to the magnetic field [28, 29]. In Ref. [30], the in-out formalism leading to the proper-time integral also directly gives another closed analytic expression for the one-loop effective Lagrangian in the same field configuration, which is identical to the Dittrich’s formula. Furthermore, the imaginary part of the one-loop Lagrangian in the closed form yields the same result obtained by summing the residues of all simple poles of the proper-time integral [30].

In this paper, we further develop the method in [31] to find a closed analytic expression for the one-loop effective Lagrangian in a supercritical magnetic field combined with a subcritical electric field. Provided that the fields vary little over the Compton length and time, one may use the HES one-loop effective Lagrangian in the gauge-and Lorentz-invariant form as a good approximation and can express the Lagrangian as a power series of a small quantity representing the electric field component along the magnetic field.Footnote 1 Using the closed expression, we study the propagation modes of weak low-energy probe photons in a vacuum under such electromagnetic fields. For this purpose, we find the permittivity and permeability tensors, work out the vacuum birefringence for parallel electric and magnetic fields, and apply the results to the Goldreich–Julian model.

To provide a more accurate formulation of the X-ray polarimetry for neutron stars, especially magnetars, we include electric field in our formulation. According to the Goldreich and Julian’s rotating dipole model, the dipole’s rotation induces a weak electric field so that an electromagnetic wrench is produced (\(G=-{\textbf{E}}\cdot {\textbf{B}}\ne 0\)) [39]. The electromagnetic wrench can significantly change vacuum birefringence. Previous studies on vacuum birefringence have focused on the wrenchless case (\(G=0\)) [4, 40,41,42,43], due to the lack of a sufficiently concise closed expression of the one-loop effective Lagrangian with the electromagnetic wrench. Although the results without wrench may give a lowest-order description, an accurate quantitative analysis requires a formulation incorporating wrench. In this paper, we provide such a concise closed expression of the one-loop Lagrangian, the optical response functions of field-modified vacua, and the photon propagation modes for parallel electric and magnetic fields to reveal that electromagnetic wrench can significantly alter the vacuum birefringence around astrophysical bodies. Our work will have an immediate application to the space missions that include X-ray polarimetry for neutron stars, especially magnetars, such as the Imaging X-ray Polarimetry Explorer (IXPE) [25], the enhanced X-ray Timing and Polarimetry (eXTP) [26], and the Compton Telescope project [27].

Table 1 Symbols referring to electric and magnetic fields and their values in special conditions
Full size table

This paper is organized as follows. In Sect. 2, an explicit expression of the one-loop effective Lagrangian is derived for the vacuum under an arbitrarily strong magnetic field superposed with a weaker electric field. The expression is given as a Taylor series in a parameter that quantifying the electric field component along the magnetic field with respect to the magnetic field. Then, in Sect. 3, the series is used to obtain the permittivity and permeability tensors for a weak low-frequency probe field. These tensors are used in Sect. 4 to find the modes of the probe field (the refractive indices and associated polarization vectors) for the configuration in which the electric field is parallel to the magnetic field. As a concrete application of the formulation, we analyze the vacuum birefringence in a hypothetical neutron star’s magnetosphere described by the Goldreich–Julian model. Finally, a conclusion is given with a discussion on further development. We use the Lorentz–Heaviside (LH) units with \(\hbar =c=1\), in which the fine structure constant is \(\alpha =e^{2}/(4\pi )\) (e is the elementary charge).

2 One-loop QED effective Lagrangian in a uniform electromagnetic field: \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\)

2.1 Invariant parameters and classification of uniform electromagnetic fields

When dealing with the QED effective Lagrangian in a uniform electromagnetic field, the following Lorentz- and gauge-invariant parameters are convenient for analysis [44]:

$$\begin{aligned} a=\sqrt{\sqrt{F^{2}+G^{2}}+F},\quad b=\sqrt{\sqrt{F^{2}+G^{2}}-F}, \end{aligned}$$
(1)

where \(F=F^{\mu \nu }F_{\mu \nu }/4\) and \(G=F^{\mu \nu }F_{\mu \nu }^{*}/4\), i.e., the Maxwell scalar and pseudoscalar; \(F^{\mu \nu }\) and \(F^{*\mu \nu }=\varepsilon ^{\mu \nu \alpha \beta } F_{\alpha \beta }/2\) (\(\varepsilon ^{0123}=1\)) are the field-strength tensor and its dual, respectively [45]. Then F and G are given as

$$\begin{aligned} F= & {} \frac{1}{4}F^{\mu \nu }F_{\mu \nu }=\frac{1}{2}\left( {\textbf{B}}^{2}-{\textbf{E}}^{2}\right) =\frac{1}{2}\left( a^{2}-b^{2}\right) ,\nonumber \\ G= & {} \frac{1}{4}F^{\mu \nu }F_{\mu \nu }^{*} =-{\textbf{E}}\cdot {\textbf{B}}=\sigma ab, \end{aligned}$$
(2)

where \(\sigma \) denotes the sign of G. As will be shown later, the formulation in terms of a and b, instead of F and G or \({\textbf{E}}\) and \({\textbf{B}}\), has the advantage to facilitate the expansion of the effective Lagrangian as a series. These symbols and their values in the special conditions considered in this paper are summarized in Table 1.

The parameters a and b can be used to classify the cases of uniform electromagnetic fields, as shown in Fig. 1. The sign of the Maxwell scalar F determines which field is stronger between the electric and magnetic fields, dividing the ab-plane into two regions: the upper left where the electric field is stronger and the lower right where the magnetic field is. The condition \(G=0\) shrinks each region to its attached coordinate axis. The cases with \(G=0\) are called wrenchless, while the fields with \(G\ne 0\) are said to have an electromagnetic wrench [3]. In the wrenchless case, an appropriate Lorentz transformation can eliminate the weaker field between the magnetic field and the electric field [45]. Thus, the a-axis (b-axis) in Fig. 1 represents the condition of essentially being under a magnetic (electric) field; of course, it includes the case of a pure magnetic (electric) field. In studying the vacuum birefringence of astrophysical relevance, the magnetic field is much stronger than the electric field, and thus the region of \(a\gg b\) in Fig. 1 is of our interests.

2.2 Integral expression of \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) and closed expression of \(\bar{\mathcal {L}}^{(1)}(\bar{a},0)\)

The physics of the vacuum in intense electromagnetic fields has been studied with the effective Lagrangian, which is obtained by integrating out the matter field degrees of freedom in the complete Lagrangian [46]. In the effective Lagrangian, the term other than the free-field part, the Maxwell theory (\({\mathcal {L}}^{(0)}(a,b)=(b^{2}-a^{2})/2\)), is responsible for the phenomena such as pair production, vacuum birefringence, photon splitting, etc. As the term is dominantly contributed from the one-loop [47,48,49] at least for the magnetic field strengths of astrophysical relevance, we consider the effective Lagrangian up to the one-loop:

$$\begin{aligned} {\mathcal {L}}_{\textrm{eff}}(a,b)={\mathcal {L}}^{(0)}(a,b)+{\mathcal {L}}^{(1)}(a,b) =\frac{b^{2}-a^{2}}{2}+{\mathcal {L}}^{(1)}(a,b). \end{aligned}$$
(3)

The one-loop contribution \({\mathcal {L}}^{(1)}(a,b)\) for the spinor QED is given as a proper-time integral [1, 2, 50]:

$$\begin{aligned}{} & {} {\mathcal {L}}^{(1)}(a,b)\nonumber \\{} & {} \quad =-\frac{1}{8\pi ^{2}}\int _{0}^{\infty }ds\frac{e^{-m^{2}s}}{s^{3}} \left\{ (eas)\coth (eas)(ebs)\cot (ebs)\right. \nonumber \\{} & {} \qquad \left. -\left[ 1+\frac{(eas)^{2}-(ebs)^{2}}{3}\right] \right\} , \end{aligned}$$
(4)
Fig. 1
figure 1

Classification of uniform electromagnetic fields in the ab-plane. The diagonal line \(b=a\) corresponds to the condition of equally strong electric and magnetic fields, i.e., \(\vert {\textbf{B}}\vert =\vert {\textbf{E}}\vert \) (\(F=\left( {\textbf{B}}^{2}-{\textbf{E}}^{2}\right) /2=0\)). The horizontal and vertical axes correspond to the wrenchless condition, i.e., \(G=-{\textbf{E}}\cdot {\textbf{B}}=0\)

Full size image

where m is the electron mass, and \(1+(es)^{2}\left( a^{2}-b^{2}\right) /3\) is subtracted to remove the zero-point energy and renormalize the charge and fields for yielding a finite physical quantity [2]. This expression can be rewritten in a form convenient for the case of \(a\gg b\), i.e., \(\tilde{b}=b/a\ll 1\):

$$\begin{aligned}{} & {} {\mathcal {L}}^{(1)}(a,b)=\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\nonumber \\{} & {} \quad =\frac{m^{4}}{8\pi ^{2}}\frac{1}{4\bar{a}^{2}}\int _{0}^{\infty }\textrm{d}z\frac{e^{-2\bar{a}z}}{z^{3}} \left[ 1+\frac{z^{2}(1-\tilde{b}^{2})}{3}\right. \nonumber \\{} & {} \qquad \left. -\tilde{b}z^{2}\coth (z)\cot (z\tilde{b})\right] , \end{aligned}$$
(5)

where the dimensionless quantities are

$$\begin{aligned} z=eas,\quad \bar{a}=\frac{m^{2}}{2ea}, \quad \bar{b}=\frac{m^{2}}{2eb},\quad \tilde{b}=\frac{b}{a}=\frac{\bar{a}}{\bar{b}}. \end{aligned}$$
(6)

For a pure magnetic field, \(\bar{a}=B_{c}/(2B_0)\) and \(\bar{b}=\infty \), where \(B_{c}=m^{2}/e=4.4\times 10^{13}\,\textrm{G}=1.2\times 10^{13}\,\mathrm {LH~units}\)Footnote 2 is the critical magnetic field strength (see Table 1).

This integral can be numerically evaluated as described in Appendix  A, but an explicit closed expression is favored for theoretical analysis. For the case of \(b=0\), an explicit expression was obtained either by the dimensional regularization of (4) [28] or by the Schwinger–DeWitt in-out formalism combined with \(\Gamma \)-function regularization [30]:

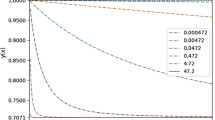
$$\begin{aligned}{} & {} \bar{\mathcal {L}}^{(1)}(\bar{a},0)\equiv \frac{m^{4}}{8\pi ^{2}\bar{a}^{2}}H(\bar{a})\nonumber \\{} & {} \quad =\frac{m^{4}}{8\pi ^{2}\bar{a}^{2}}\left[ \zeta '(-1,\bar{a})-\frac{1}{12} +\frac{\bar{a}^{2}}{4}-\left( \frac{1}{12}-\frac{\bar{a}}{2}+\frac{\bar{a}^{2}}{2}\right) \ln \bar{a}\right] ,\nonumber \\ \end{aligned}$$
(7)

where \(\zeta (s,\bar{a})\) is the Hurwitz zeta function, and \(\zeta '(-1,\bar{a})=d\zeta (s,\bar{a})/ds\vert _{s=-1}\) [51] (see Appendix B for more details). This expression perfectly matches the numerical evaluation of (5) with \(\tilde{b}=0\), as shown in Fig. 2.

Fig. 2
figure 2

Comparison of the integral and closed expressions of \(\bar{{\mathcal {L}}}^{(1)}(\bar{a},0)\). The integral expression is (5) with \(\tilde{b}=0\), and the closed one is (7). The plotted values are in units of \(m^{4}/8\pi ^{2}\). The parameter \(\bar{a}\) ranges from 0.001 to 100, corresponding to \(B/B_{c}\) from 500 to 0.005 for the purely magnetic case. The inset shows the values in linear scale for the range of \(\bar{a}\) from 0.002 to 0.01. The plots of the two expressions perfectly overlap each other

Full size image

2.3 Imaginary part of \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\)

The effective Lagrangian \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) in (5), despite an integral of real functions along a real axis, acquires an imaginary part due to the simple poles at \(z=n\pi /\tilde{b}\) (\(n=1,2,\ldots \)) arising from \(\cot (z\tilde{b})\). The imaginary part represents the loss of vacuum persistence due to the Schwinger pair production and can be obtained analytically by using the Sokhotski–Plemelj theorem [2, 52]:

$$\begin{aligned}{} & {} \bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})= \bar{\mathcal {L}}^{(1)}_\textrm{Re} + i \bar{\mathcal {L}}^{(1)}_\textrm{Im} \nonumber \\{} & {} \quad = \mathrm {P.V.} + i \frac{m^{4}}{8\pi ^{2}}\frac{1}{4\bar{a}^{2}} \sum _{n=1}^{\infty } \frac{\tilde{b}}{n} e^{-2\bar{b}n\pi } \coth \frac{n\pi }{\tilde{b}}, \end{aligned}$$
(8)

where \(\mathrm {P.V.}\) refers to the principal value of the integral, which is real. The factor \(e^{-2\bar{b}n\pi }\) implies that the imaginary part \(\bar{\mathcal {L}}^{(1)}_\textrm{Im}\) is small unless \(2\bar{b}\pi \lesssim 1\), which reduces to \(E_0 \gtrsim \pi E_c\) for the parallel field configuration in Table 1; the Schwinger pair production is appreciable only when the electric field is comparable to or larger than \(E_c\). In such a case, the refractive indices for probe photons becomes complex, as is shown by Heyl and Hernquist for a pure electric field [42]. More generally, the generation and subsequent dynamics of pair plasmas becomes significant to eventually induce the vacuum’s back-reaction to the applied fields [3, 53]. The formulation including such effects is beyond the scope of the present paper and will be studied in a future work.

In developing a formulation without \(\bar{\mathcal {L}}^{(1)}_\textrm{Im}\), we need to identify the parameter region where it can be neglected to a good approximation. Noting that the polarization and the magnetization are obtained by differentiating \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) by \({\textbf{E}}\) and \({\textbf{B}}\), respectively (see Sect. 3), we may use the ratios, the imaginary polarization to the real polarization and the imaginary magnetization to the real magnetization, as the parameters representing the significance of \(\bar{\mathcal {L}}^{(1)}_\textrm{Im}\) compared to \(\bar{\mathcal {L}}^{(1)}_\textrm{Re}\). The ratios are given in the parallel field configuration as

$$\begin{aligned} \frac{P_\textrm{Im}}{P_\textrm{Re}} = \frac{\partial _{\tilde{b}} I_{\textrm{Im}} (\bar{a},\tilde{b}) }{\partial _{\tilde{b}} I_{\textrm{Re}}(\bar{a},\tilde{b}) }, \quad \frac{M_\textrm{Im}}{M_\textrm{Re}} = \frac{(-2 + \bar{a} \partial _{\bar{a}} + \tilde{b} \partial _{\tilde{b}} ) I_{\textrm{Im}} (\bar{a},\tilde{b})}{(-2 + \bar{a} \partial _{\bar{a}} + \tilde{b} \partial _{\tilde{b}} ) I_{\textrm{Re}} (\bar{a},\tilde{b})},\qquad \end{aligned}$$
(9)

where \(I_{\textrm{Re}}(\bar{a},\tilde{b})\) and \(I_{\textrm{Im}}(\bar{a},\tilde{b})\) are the real and imaginary parts of the integral in (5), respectively (except the factor \(m^4 / (32 \pi ^2 \bar{a}^2 )\)). Not understanding the exact physical meaning of \(P_\textrm{Im}\) and \(M_\textrm{Im}\) for now, we treat them as mathematical variations induced by \(\bar{\mathcal {L}}^{(1)}_\textrm{Im}\).

Fig. 3
figure 3

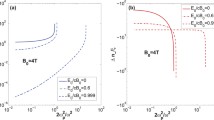
The influence of the imaginary part of part of \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\): (a) \(P_\textrm{Im} / P_\textrm{Re}\) and (b) \(M_\textrm{Im} / M_\textrm{Re}\). The parallel field configuration in Table 1 was assumed, and \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) was calculated numerically with the first 10 poles, as described in Appendix A. The filled squares mark the points of \(\bar{b}=0.5\) (\(E_0=E_c\)), and the empty ones do the points of \(\bar{b}=1\) (\(E_0=0.5E_c\)). In (a), the horizontal cut at \(P_\textrm{Im}/P_\textrm{Re}=10^{-2}\) crosses the others at \(\bar{a}=0.034,~0.068,~0.14,~0.30\), corresponding to \((B/B_c,E/E_c)=(15,0.37),~(7.4,0.37),~(3.6,0.36),~(1.7,0.33)\)

Full size image

Figure 3 shows the ratios \(P_\textrm{Im} / P_\textrm{Re}\) and \(M_\textrm{Im} / M_\textrm{Re}\) for \(\tilde{b}=0.2,~0.1,~0.05,~0.025\). In Fig. 3a, the array of filled squares marks the points of \(E_0=E_c\) for different \(B_0\), indicating that \(E_0\) dominantly determines \(P_\textrm{Im} / P_\textrm{Re}\). The array of empty squares marks the points of \(E_0=0.5E_c\), and the dependence is similar. When the electric field is sufficiently strong, e.g., \(\bar{a}=0.04\) and \(\tilde{b}=0.2\) corresponding to \(E_0=2.5E_c\), \(P_\textrm{Im} / P_\textrm{Re}\) reaches 1 and become even larger at higher \(E_0\) values. As the criterion for neglecting \(\bar{\mathcal {L}}^{(1)}_\textrm{Im}\), we choose \(P_\textrm{Im} / P_\textrm{Re} \lesssim 10^{-2}\), which implies \(E_0 \lesssim 0.33E_c\) (consider the points at which the horizontal line at \(P_\textrm{Im} / P_\textrm{Re} = 10^{-2}\) crosses the other curves). Unlike the polarization ratio, the magnetization ratio \(M_\textrm{Im} / M_\textrm{Re}\) has a strong dependence on the magnetic field, as is indicated by the arrays of filled and empty squares in Fig. 3b. It also never overcome 0.2 in the investigated parameter regime, indicating that \(\bar{\mathcal {L}}^{(1)}_\textrm{Im}\) is the minor in determining the magnetization. The condition \(M_\textrm{Im} / M_\textrm{Re}=10^{-2}\) gives a threshold value higher than \(0.33E_c\). One may consider to plot the ratio of the Langrangian itself \(\bar{\mathcal {L}}^{(1)}_\textrm{Im} / \bar{\mathcal {L}}^{(1)}_\textrm{Re}\). Although not shown here, the curve shows a behavior lying between the behavior of \(P_\textrm{Im} / P_\textrm{Re}\) and that of \(M_\textrm{Im} / M_\textrm{Re}\).

We adopt the validity condition \(E_0 \lesssim E_c/3\) obtained from \(P_\textrm{Im} / P_\textrm{Re}\) as it is the most restrictive. The condition can be rewritten as \(\bar{b} \gtrsim 3/2\) or \(\bar{a} \gtrsim \bar{a}_\textrm{thres} \equiv 3\tilde{b}/2 \) for general field configurations, resulting in the exponential factor \(e^{-2\bar{b}\pi } \lesssim 8\times 10^{-5}\). Below we neglect \(\bar{\mathcal {L}}^{(1)}_\textrm{Im}\) in our formulation, and \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) refers only to its real part.

2.4 Expansion of \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) in \(\tilde{b}\)

In the magnetosphere of neutron stars, the magnetic field is much stronger than the electric field, and thus \(a\gg b\), or equivalently \(\bar{a}\ll \bar{b}\), from (1) and (2). For example, the Goldreich–Julian model [39] gives \(\tilde{b}\) (\(=b/a=\bar{a}/\bar{b}\)) as a function decreasing with the distance from the star center: \(\tilde{b}(r=R)\le 0.2\) and \(\tilde{b}(r=10R)\le 0.02\), where R is the star’s radius. For such a condition, the expansion of \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) in \(\tilde{b}\) is useful for analysis.

In the integral expression of \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\), (5), \(\cot (\tilde{b}z)\) has poles at \(z=n\pi /\tilde{b}\) (\(n=1,2,\dots \)), which may make the integral diverge. However, the principal value of the integral is finite because the symmetric behavior of the cotangent function around the poles. Furthermore, if \(\exp (-2\bar{a}z)\) suppresses the integrand sufficiently much before the first pole, i.e., \(1/(2\bar{a})\ll \pi /\tilde{b}\), or equivalently \(\bar{b}\gg 1/(2\pi )\), an asymptotic expression valid for \(\bar{b}\gg 1/(2\pi )\) can be obtained. The condition \(\bar{b}\gg 1/(2\pi )\) is reasonably satisfied by the validity condition \(\bar{b} \gtrsim 3/2\) given in Sect. 2.3.

To proceed, we substitute the series form of \((\tilde{b}z)\cdot \cot (\tilde{b}z)\) in (5) (4.19.6 of [51]):

$$\begin{aligned} (\tilde{b}z)\cdot \cot (\tilde{b}z)=\sum _{n=0}^{\infty }\frac{B_{2n}(-1)^{n}(2\tilde{b}z)^{2n}}{(2n)!}, \end{aligned}$$
(10)

where \(B_{2n}\) are the Bernoulli numbers. The series is convergent only for \(\vert \tilde{b}z \vert <\pi \) due to the nearest poles at \(\tilde{b}z=\pm \pi \). Upon substitution, the contribution outside the region of convergence asymptotically vanishes as \(\bar{b}\rightarrow \infty \). Then, the integral in (5) is written as

$$\begin{aligned}{} & {} \int _{0}^{\infty }\textrm{d}z\frac{e^{-2\bar{a}z}}{z^{3}}\left\{ 1+\frac{z^{2}(1-\tilde{b}^{2})}{3}\right. \nonumber \\{} & {} \quad \left. -z\coth (z)\sum _{n=0}^{\infty }\frac{(-1)^{n}B_{2n}(2\tilde{b}z)^{2n}}{(2n)!}\right\} . \end{aligned}$$
(11)

To evaluate the integral, we use the integral representation of \(H(\bar{a})\) in (7), which is derived by comparing (7) with (B3):

$$\begin{aligned} H(\bar{a})=\frac{1}{4}\int _{0}^{\infty }\textrm{d}z\frac{e^{-2\bar{a}z}}{z^{3}}\left\{ 1+\frac{z^{2}}{3}-z\coth (z)\right\} . \end{aligned}$$
(12)

Differentiating (12) 2n times by \(\bar{a}\) yields a useful formula:

$$\begin{aligned}{} & {} \left( \frac{\textrm{d}}{\textrm{d}\bar{a}}\right) ^{2n}H(\bar{a})\equiv H^{(2n)}(\bar{a})\nonumber \\{} & {} \quad =\frac{2^{2n}}{4}\int _{0}^{\infty }\textrm{d}z\frac{e^{-2\bar{a}z}}{z^{3}}\left\{ 1+\frac{z^{2}}{3}-z\coth (z)\right\} z^{2n}, \end{aligned}$$
(13)

of which closed form is given as (see App. C for the derivation).

$$\begin{aligned} H^{(2n)}(\bar{a})= & {} \psi ^{(2n-2)}(\bar{a})+\frac{1}{12}\frac{\Gamma (2n)}{\bar{a}^{2n}} +\frac{1}{2}\frac{\Gamma (2n-1)}{\bar{a}^{2n-1}}\nonumber \\{} & {} +\frac{\Gamma (2n-2)}{\bar{a}^{2n-2}}\theta (n-2)-\delta _{n1}\ln \bar{a},\quad (n\ge 1),\nonumber \\ \end{aligned}$$
(14)

where \(\psi ^{(m)}(\bar{a})\) is the polygamma function. By using (13) and (14) and the integral representation of the \(\Gamma \) function, one can integrate (11) term-by-term to obtain an asymptotic series of \({\bar{{\mathcal {L}}}}^{(1)}(\bar{a},\tilde{b})\):

$$\begin{aligned} {\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b}) =&\frac{m^{4}}{8\pi ^{2}}\left[ \frac{H(\bar{a})}{\bar{a}^{2}}+\left( \frac{1}{144\bar{a}^{4}} -\frac{H^{(2)}(\bar{a})}{12\bar{a}^{2}}\right) \tilde{b}^{2}\right] \nonumber \\&+\frac{m^{4}}{8\pi ^{2}}\sum _{n=2}^{\infty }(-1)^{n}B_{2n}\left[ \frac{H^{(2n)}(\bar{a})}{(2n)!\bar{a}^{2}}\right. \nonumber \\&\left. -\frac{1}{2n(2n-1)(2n-2)\bar{a}^{2n}}-\frac{1}{24n\bar{a}^{2n+2}}\right] \tilde{b}^{2n}, \end{aligned}$$
(15)

in which all the terms are given in terms of special functions. Thus, (15) provides a systematic explicit expression of \(\bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})\) in powers of \(\tilde{b}\) for an arbitrary value of \(\bar{a}\). For example, the first three leading orders are given as

$$\begin{aligned} \bar{\mathcal {L}}^{(1)}(\bar{a},\tilde{b})&= \frac{m^{4}}{8\pi ^{2}}\frac{1}{\bar{a}^{2}}\left[ \zeta '(-1,\bar{a})-\frac{1}{12} +\frac{\bar{a}^{2}}{4}\right. \nonumber \\&\quad -\left. \left( \frac{1}{12}-\frac{\bar{a}}{2}+\frac{\bar{a}^{2}}{2}\right) \ln \bar{a}\right] \nonumber \\&\quad +\frac{m^{4}}{8\pi ^{2}}\left( -\frac{1}{24\bar{a}^{3}} +\frac{\ln \bar{a}-\psi ^{(0)}(\bar{a})}{12\bar{a}^{2}}\right) {\tilde{b}^{2}}\nonumber \\&\quad +\frac{m^{4}}{8\pi ^{2}}\left( -\frac{1}{720\bar{a}^{5}}-\frac{\psi ^{(2)}(\bar{a})}{720\bar{a}^{2}}\right) \tilde{b}^{4}+O(\tilde{b}^{6}). \end{aligned}$$
(16)

A concise expression of the one-loop effective Lagrangian for general field configuration such as (15) and (16) is crucial for the analysis of the vacuum birefringence, especially for the case with an electromagnetic wrench. The lack of such a systematic expression has limited the vacuum birefringence analysis to the wrenchless case. Previously, Heyl and Hernquist obtained the lowest-order correction due to electromagnetic wrench in the strong magnetic field limit [54].

When both electric and magnetic fields are highly subcritical, i.e., \(\bar{a}\gg 1\) and \(\bar{b}\gg 1\) hold, the lowest order can be obtained from the expansion up to \(O(\tilde{b}^{4})\), and the second lowest from the expansion up to \(O(\tilde{b}^{6})\):

$$\begin{aligned} {\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})&= \frac{m^{4}}{8\pi ^{2}}\frac{1}{\bar{a}^{4}}\left[ \frac{1}{720}+\frac{\tilde{b}^{2}}{144} +\frac{\tilde{b}^{4}}{720}\right] \nonumber \\&\qquad +\frac{m^{4}}{8\pi ^{2}}\frac{1}{\bar{a}^{6}}\left[ -\frac{1}{5040} -\frac{\tilde{b}^{2}}{1440}+\frac{\tilde{b}^{4}}{1440}+\frac{\tilde{b}^{6}}{5040}\right] \nonumber \\&\quad = \frac{m^{4}}{8\pi ^{2}}\left[ \frac{1}{720\bar{a}^{4}}+\frac{1}{144\bar{a}^{2}\bar{b}^{2}} +\frac{1}{720\bar{b}^{4}}\right] \nonumber \\&\qquad +\frac{m^{4}}{8\pi ^{2}}\left[ -\frac{1}{5040\bar{a}^{6}}-\frac{1}{1440\bar{a}^{4}\bar{b}^{2}}\right. \nonumber \\&\qquad \left. +\frac{1}{1440\bar{a}^{2}\bar{b}^{4}}+\frac{1}{5040\bar{b}^{6}}\right] \end{aligned}$$
(17)

The term with the first bracket is written in terms of \({\textbf{E}}\) and \({\textbf{B}}\) as

$$\begin{aligned} \frac{e^{4}}{360\pi ^{2}m^{4}}\left[ ({\textbf{B}}^{2}-{\textbf{E}}^{2})^{2}+7({\textbf{E}} \cdot {\textbf{B}})^{2}\right] , \end{aligned}$$
(18)

which was obtained by Heisenberg and Euler [1], and Schwinger [2].

It is worthy to mention that the one-loop effective Lagrangian \({\mathcal {L}}^{(1)}(a,b)\) (4) can be expressed as a convergent series of which terms are some special functions of a and b [55,56,57]. The expansion may be exact but is not very convenient for the condition of an arbitrarily strong magnetic field combined with a weak electric field because the expansion needs an infinite sum. The convergence of the sum is slow, and thus its evaluation needs acceleration techniques [56]. In this regard, the expansion (16) is more convenient for theoretical analysis and practical applications.

2.5 Behavior of \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\) and the validity of its expansion form

The exact dependence of \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\) with \(\tilde{b}\) can be investigated by numerically evaluating the integral expression (5), as described in Appendix  A. As \({\bar{\mathcal {L}}}^{(1)}(\bar{a},0)\) is completely known, the ratio \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})/{\bar{\mathcal {L}}}^{(1)}(\bar{a},0)\) represents the dependence on \(\tilde{b}\) alone. In Fig. 4, the offset difference of \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\) from \({\bar{\mathcal {L}}}^{(1)}(\bar{a},0)\) (the difference as \(\bar{a} \rightarrow \infty \)) increases with \(\tilde{b}\). Furthermore, additional significant differences appear as \(\bar{a}\) decreases below certain onset values. For example, when \(\tilde{b}=0.2\), the ratio is close 1.2 until \(\bar{a}\) decreases to 1, but, as \(\bar{a}\) decreases below 1, it significantly increases and then decreases. When \(\tilde{b}\) is smaller, the behavior is similar except that the offset difference is smaller, and the onset value of \(\bar{a}\) for the additional difference decreases. This additional difference is attributed to the pair production because it becomes significant as the validity condition \(\bar{a} \gtrsim \bar{a}_\textrm{thres} \equiv 3\tilde{b}/2 \) begins to be violated.

Fig. 4
figure 4

\({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})/{\bar{\mathcal {L}}}^{(1)}(\bar{a},0)\) for \(\tilde{b}=0.2,\,0.1,\,0.05,\,0.025\). \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\) was obtained by the direct integration of (5) with the first 10 poles

Full size image

By using the numerical evaluation of \(\mathcal {\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\), we can find the parameter range in which the expansion (15) is accurate. The ratio \({\bar{\mathcal {L}}}_{\textrm{exp}}^{(1)}(\bar{a},\tilde{b},n)/{\bar{\mathcal {L}}}_{\textrm{int}}^{(1)}(\bar{a},\tilde{b})\) is plotted for \(n=0,\,1,\,2,\,3\) and \(\tilde{b}=0.2,\,0.05\), where \({\bar{\mathcal {L}}}_{\textrm{exp}}^{(1)}(\bar{a},\tilde{b},n)\) is the expansion (15) up to \(O(\tilde{b}^{2n})\), and \({\bar{\mathcal {L}}}_{\textrm{int}}^{(1)}(\bar{a},\tilde{b})\) is the numerical evaluation of (5). In Fig. 5a, \({\bar{\mathcal {L}}}_{\textrm{exp}}^{(1)}(\bar{a},\tilde{b}=0.2,n\ge 1)\) is accurate within 1% for \(\bar{a}\ge 0.3\). The 1%-accuracy threshold of \(\bar{a}\), denoted by \(\bar{a}_{1\%}\), decreases slightly as n increases, but a higher-n expansion blows up faster below \(\bar{a}_{1\%}\): a typical behavior of Taylor expansions. When \(\tilde{b}\) is not taken into account, the error becomes larger than 17%, as can be seen in the \(n=0\) plot in Fig. 5a. Therefore, the correction due to \(\tilde{b}\ne 0\) should be taken into account for accuracy. At a lower value of \(\tilde{b}=0.05\) (Fig. 5b), the overall behavior is similar to the case of \(\tilde{b}=0.2\), but \(\bar{a}_{1\%}\) is lowered to 0.025, and the minimum error of the \(n=0\) expansion decreases to 2%.

Actually \(\bar{a}_{1\%}\) is closely connected to the validity condition \(\bar{a} \gtrsim \bar{a}_\textrm{thres} \equiv 3\tilde{b}/2 \). Note that \(\bar{a}_\textrm{thres}=\bar{a}_{1\%}\) for \(\tilde{b}=0.2\) and \(\bar{a}_\textrm{thres}=3\bar{a}_{1\%}\) for \(\tilde{b}=0.05\): \(\bar{a}_\textrm{thres}\) is more restrictive than \(\bar{a}_{1\%}\). Figure 5 suggests the \(n=2\) expansion as the optimal expansion, albeit the \(n=1\) expansion is reasonable within the valid parameter space.

Fig. 5
figure 5

\({\bar{\mathcal {L}}}_{\textrm{exp}}^{(1)}(\bar{a},\tilde{b},n)/{\bar{\mathcal {L}}}_{\textrm{int}}^{(1)}(\bar{a},\tilde{b})\) for \(n=0,\,1,\,2,\,3\) when (a) \(\tilde{b}=0.2\) and (b) \(\tilde{b}=0.05\). \({\bar{\mathcal {L}}}_{\textrm{exp}}^{(1)}(\bar{a},\tilde{b},n)\) is the expansion (15) up to \(O(\tilde{b}^{2n})\), and \({\bar{\mathcal {L}}}_{\textrm{int}}^{(1)}(\bar{a},\tilde{b})\) is the numerical evaluation of (5) including the first 10 poles

Full size image

3 Response of the vacuum in strong electromagnetic fields

In contrast to the classical vacuum, the quantum vacuum in electromagnetic fields behaves as a medium, of which response is quantified by the polarization (\({\textbf{P}}\)) and the magnetization (\({\textbf{M}}\)), or equivalently by the electric induction (\({\textbf{D}}\)) and magnetic field strength (\({\textbf{H}}\)). These quantities can be obtained by considering the variation of the effective Lagrangian with respect to that of the electromagnetic field [1, 58]:

$$\begin{aligned} {\textbf{D}}= & {} {\textbf{E}}+{\textbf{P}}=\frac{\partial {\mathcal {L}}_{\textrm{eff}}}{\partial {\textbf{E}}}={\textbf{E}}+\frac{\partial {\mathcal {L}}^{(1)}}{\partial {\textbf{E}}},\nonumber \\ {\textbf{H}}= & {} {\textbf{B}}-{\textbf{M}}=-\frac{\partial {\mathcal {L}}_{\textrm{eff}}}{\partial {\textbf{B}}} ={\textbf{B}}-\frac{\partial {\mathcal {L}}^{(1)}}{\partial {\textbf{B}}}. \end{aligned}$$
(19)

In this section, we derive expressions of \({\textbf{P}}\) and \({\textbf{M}}\) for an arbitrary \({\mathcal {L}}^{(1)}(a,b)\) and use the result to obtain the permittivity and permeability tensors for weak low-frequency (\(\omega \ll m\)) probe fields. These tensors are necessary to analyze the vacuum birefringence in the next section. These results can be obtained also in an explicitly Lorentz covariant manner by using photon polarization tensors [3, 43, 44, 59,60,61].

3.1 Polarization and magnetization of the vacuum in uniform electric and magnetic fields

The effective Lagrangian is a function of a and b (1) and (2), and thus we consider the variation of a general differentiable function f(a, b):

$$\begin{aligned} \delta f=\delta a\cdot \partial _{a}f+\delta b\cdot \partial _{b}f. \end{aligned}$$
(20)

As a and b are functions of F and G, the variations \(\delta a\) and \(\delta b\) can be written in terms of the variations \(\delta F\) and \(\delta G\):

$$\begin{aligned} \delta a=\frac{\partial a}{\partial F}\delta F+\frac{\partial a}{\partial G}\delta G, \quad \delta b=\frac{\partial b}{\partial F}\delta F+\frac{\partial b}{\partial G}\delta G. \end{aligned}$$
(21)

In turn, the variations of \(\delta F\) and \(\delta G\) can also be written in terms of \(\delta {\textbf{E}}\) and \(\delta {\textbf{B}}\):

$$\begin{aligned} \delta F=\frac{\partial F}{\partial {\textbf{E}}}\cdot \delta {\textbf{E}} +\frac{\partial F}{\partial {\textbf{B}}}\cdot \delta {\textbf{B}}, \quad \delta G=\frac{\partial G}{\partial {\textbf{E}}}\cdot \delta {\textbf{E}} +\frac{\partial G}{\partial {\textbf{B}}}\cdot \delta {\textbf{B}}. \nonumber \\ \end{aligned}$$
(22)

Thus, using the chain rules, the coefficients in these variations can be calculated by using (1) and (2) to express \(\delta f\) in terms of \(\delta {\textbf{E}}\) and \(\delta {\textbf{B}}\):

$$\begin{aligned} \delta f=\delta {\textbf{E}}\cdot \left( -{\textbf{E}}\hat{S}-{\textbf{B}}\hat{A}\right) f +\delta {\textbf{B}}\cdot \left( {\textbf{B}}\hat{S}-{\textbf{E}}\hat{A}\right) f, \end{aligned}$$
(23)

where

$$\begin{aligned}&\hat{S}=\frac{\left( a\cdot \partial _{a}-b\cdot \partial _{b}\right) }{a^{2}+b^{2}} =\partial _{F},\quad \hat{A}=\frac{\sigma \left( b\cdot \partial _{a}+a\cdot \partial _{b}\right) }{a^{2}+b^{2}}=\partial _{G},\nonumber \\&\hat{S}\hat{A}=\hat{A}\hat{S}=\partial _{F}\partial _{G}. \end{aligned}$$
(24)

The operators \(\hat{S}\) and \(\hat{A}\) are symmetric and anti-symmetric under the parity inversion, respectively. Note that \((a^{2}+b^{2})\hat{S}\) measures the difference of homogeneity of polynomials such that \((a^{2}+b^{2})\hat{S}(a^{m}b^{n})=(m-n)(a^{m}b^{n})\), while \((a^{2}+b^{2})\hat{A}\) measures the mixed homogeneity of polynomials such that \((a^{2}+b^{2})\hat{A}(a^{m}b^{n})=(mb^{2}+na^{2})(a^{m-1}b^{n-1})\). In addition, \((a^{2}+b^{2})\hat{S}\) preserves the polynomial order (m, n), while \((a^{2}+b^{2})\hat{A}\) changes it to \((m-1,n+1)\) and \((m+1,n-1)\) while maintaining the sum of the orders of a and b. Replacing f with \({\mathcal {L}}^{(1)}\) and using (19), one can obtain \({\textbf{P}}\) and \({\textbf{M}}\) from \({\mathcal {L}}^{(1)}(a,b)\):

$$\begin{aligned}&{\textbf{P}}=\frac{\partial {\mathcal {L}}^{(1)}}{\partial {\textbf{E}}} =-{\textbf{E}}\hat{S}{\mathcal {L}}^{(1)}-{\textbf{B}}\hat{A}{\mathcal {L}}^{(1)},\nonumber \\&{\textbf{M}}=\frac{\partial {\mathcal {L}}^{(1)}}{\partial {\textbf{B}}} ={\textbf{B}}\hat{S}{\mathcal {L}}^{(1)}-{\textbf{E}}\hat{A}{\mathcal {L}}^{(1)}. \end{aligned}$$
(25)

Despite the appearance, this relation is not linear in \({\textbf{E}}\) and \({\textbf{B}}\), as \(\hat{S}{\mathcal {L}}^{(1)}\) and \(\hat{A}{\mathcal {L}}^{(1)}\) are nonlinear functions of \({\textbf{E}}\) and \({\textbf{B}}\).

3.2 Permittivity and permeability tensors for weak low-frequency probe fields

The material-like vacuum with the nonlinear response relation (25) affects the propagation of photons. When the photon energy is much smaller than the electron’s rest mass energy (\(\omega \ll m=0.5\,\textrm{MeV}\)), the photon can be treated as a weak perturbation field (probe field) added to the strong background field [62, 63]. Then, \({\textbf{E}}\), \({\textbf{B}}\), \({\textbf{D}}\), \({\textbf{H}}\), \({\textbf{P}}\), and \({\textbf{M}}\) can be decomposed as

$$\begin{aligned} {\textbf{A}}={\textbf{A}}_{0}+\delta {\textbf{A}}, \end{aligned}$$
(26)

where \({\textbf{A}}_{0}\) (\(\delta {\textbf{A}}\)) refers to the quantities of the background (probe) field. Furthermore, as \({\textbf{A}}_{0}\) is uniform, while \(\delta {\textbf{A}}\) is varying, the relation (19) should be satisfied separately between the uniform and varying quantities:

$$\begin{aligned} {\textbf{D}}_{0}&={\textbf{E}}_{0}+{\textbf{P}}_{0},\quad {\textbf{H}}_{0}={\textbf{B}}_{0}-{\textbf{M}}_{0}, \end{aligned}$$
(27)
$$\begin{aligned} \delta {\textbf{D}}&=\delta {\textbf{E}}+\delta {\textbf{P}},\quad \delta {\textbf{H}}=\delta {\textbf{B}}-\delta {\textbf{M}}. \end{aligned}$$
(28)

Then, \(\delta {\textbf{D}}\) and \(\delta {\textbf{H}}\) can be obtained by varying the relation (25) around \(({\textbf{E}}_{0},{\textbf{B}}_{0})\), for which the formula (23) is convenient. A straightforward but lengthy calculation yields the linear relations among the varying quantities relevant to the probe field:

$$\begin{aligned} \delta {\textbf{D}}=\varvec{\epsilon }_{E}\cdot \delta {\textbf{E}}+\varvec{\epsilon }_{B} \cdot \delta {\textbf{B}},\quad \delta {\textbf{H}}=\bar{\varvec{\mu }}_{B}\cdot \delta {\textbf{B}} +\bar{\varvec{\mu }}_{E}\cdot \delta {\textbf{E}}, \end{aligned}$$
(29)

where \(\varvec{\epsilon }_{E}\), \(\varvec{\epsilon }_{B}\), \(\bar{\varvec{\mu }}_{B}\), and \(\bar{\varvec{\mu }}_{E}\) are 3-by-3 tensors. Their components are as follows:

$$\begin{aligned}&\epsilon _{E,ij} =\delta _{ij}(1-{\mathcal {L}}_{S}^{(1)})\nonumber \\&\quad +\left[ E_{0i}E_{0j}{\mathcal {L}}_{SS}^{(1)} +\left( E_{0i}B_{0j}+B_{0i}E_{0j}\right) {\mathcal {L}}_{SA}^{(1)}+B_{0i}B_{0j}{\mathcal {L}}_{AA}^{(1)}\right] , \nonumber \\&\epsilon _{B,ij} =-\delta _{ij}{\mathcal {L}}_{A}^{(1)}\nonumber \\&\quad +\left[ -E_{0i}B_{0j}{\mathcal {L}}_{SS}^{(1)} +\left( E_{0i}E_{0j}-B_{0i}B_{0j}\right) {\mathcal {L}}_{SA}^{(1)}+B_{0i}E_{0j}{\mathcal {L}}_{AA}^{(1)}\right] , \nonumber \\&\bar{\mu }_{B,ij} =\delta _{ij}(1-{\mathcal {L}}_{S}^{(1)})\nonumber \\&\quad +\left[ -B_{0i}B_{0j}{\mathcal {L}}_{SS}^{(1)} +\left( B_{0i}E_{0j}+E_{0i}B_{0j}\right) {\mathcal {L}}_{SA}^{(1)}-E_{0i}E_{0j}{\mathcal {L}}_{AA}^{(1)}\right] , \nonumber \\&\bar{\mu }_{E,ij} =\delta _{ij}{\mathcal {L}}_{A}^{(1)}\nonumber \\&\quad +\left[ B_{0i}E_{0j}{\mathcal {L}}_{SS}^{(1)} +\left( B_{0i}B_{0j}-E_{0i}E_{0j}\right) {\mathcal {L}}_{SA}^{(1)}-E_{0i}B_{0j}{\mathcal {L}}_{AA}^{(1)}\right] , \end{aligned}$$
(30)

where

$$\begin{aligned} {\mathcal {L}}_{S}^{(1)}= & {} \hat{S}{\mathcal {L}}^{(1)} \vert _0,\quad {\mathcal {L}}_{A}^{(1)} =\hat{A}{\mathcal {L}}^{(1)} \vert _0,\quad \nonumber \\ {\mathcal {L}}_{SS}^{(1)}= & {} \hat{S}\hat{S}{\mathcal {L}}^{(1)} \vert _0, \quad {\mathcal {L}}_{SA}^{(1)} =\hat{S}\hat{A}{\mathcal {L}}^{(1)} \vert _0,\quad {\mathcal {L}}_{AA}^{(1)} =\hat{A}\hat{A}{\mathcal {L}}^{(1)} \vert _0.\nonumber \\ \end{aligned}$$
(31)

Here, the subscript 0 means that \(\hat{S}\) and \(\hat{A}\) are evaluated at \(({\textbf{E}}_{0},{\textbf{B}}_{0})\). Note that these formulae are valid for any effective Lagrangian. From now on, we shall focus on the HES Lagrangian (4).

The tensors \(\varvec{\epsilon }_{B}\) and \(\bar{\varvec{\mu }}_{E}\) represent the magneto-electric response to the probe field, in which a magnetic (electric) field induces polarization (magnetization) [64], unlike usual dielectric and magnetic materials (see [65, 66] for the recent studies of the magneto-electric response in condensed matter). Such response disappears as the background electric field vanishes: when \({\textbf{E}}_{0}=0\), \({\mathcal {L}}_{A}^{(1)}\) and \({\mathcal {L}}_{SA}^{(1)}\) in (30) vanishes for the Lagrangian (4) to yield \(\varvec{\epsilon }_{B}=\bar{\varvec{\mu }}_{E}=0\).

The quantities in (31) have the complete information for the analysis of vacuum birefringence because they immediately lead to the permittivity and permeability for an arbitrary background field configuration through (30). By using the expansion (16), we can obtain the formulae of (31) contributed from each order of \(\tilde{b}\). For example, the contributions from the lowest three orders are shown in Tables 2, 3, and 4. In Table 2, the dependence on \(\bar{b}\) appears due to the \(b\cdot \partial _{a}\) term in \(\hat{A}\) although \({\bar{\mathcal {L}}}^{(1)}(\bar{a},0)\) does not depend on \(\bar{b}\). As the combined field of the background field and the probe field is not wrenchless in general, the expression of \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b}\ne 0)\) is necessary for wrenchless background fields.

For the case of \(b=0\) with an arbitrary value of a, i.e., the wrenchless case, the exact expressions of (31) can be obtained first by combining the results in Tables 2 and 3 and then by taking the limit of \(\bar{b}=\infty \). Higher order contributions are absent in this case. The results are shown in Table 5. The same results were obtained by Karbstein and Shaisultanov [43], who expanded the one-loop effective action up to the second order of the probe field and specified the calculation to the wrenchless case.

Table 2 Contribution to \({\mathcal {L}}_{S}^{(1)}\), \({\mathcal {L}}_{A}^{(1)}\), \({\mathcal {L}}_{SS}^{(1)}\), \({\mathcal {L}}_{SA}^{(1)}\), and \({\mathcal {L}}_{AA}^{(1)}\) from the \(O(\tilde{b}^{0})\) term in the expansion of \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\) (16). Each contribution is obtained by multiplying the quantities in the second and third columns
Full size table
Table 3 Contribution to \({\mathcal {L}}_{S}^{(1)}\), \({\mathcal {L}}_{A}^{(1)}\), \({\mathcal {L}}_{SS}^{(1)}\), \({\mathcal {L}}_{SA}^{(1)}\), and \({\mathcal {L}}_{AA}^{(1)}\) from the \(O(\tilde{b}^{2})\) term in the expansion of \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\) (16). Each contribution is obtained by multiplying the quantities in the second and third columns
Full size table
Table 4 Contribution to \({\mathcal {L}}_{S}^{(1)}\), \({\mathcal {L}}_{A}^{(1)}\), \({\mathcal {L}}_{SS}^{(1)}\), \({\mathcal {L}}_{SA}^{(1)}\), and \({\mathcal {L}}_{AA}^{(1)}\) from the \(O(\tilde{b}^{4})\) term in the expansion of \({\bar{\mathcal {L}}}^{(1)}(\bar{a},\tilde{b})\) (16). Each contribution is obtained by multiplying the quantities in the second and third columns
Full size table
Table 5 \({\mathcal {L}}_{S}^{(1)}\), \({\mathcal {L}}_{SS}^{(1)}\), and \({\mathcal {L}}_{AA}^{(1)}\) for \(\tilde{b}=0\). \({\mathcal {L}}_{A}^{(1)}={\mathcal {L}}_{SA}^{(1)}=0\). Each quantity is obtained by multiplying the quantities in the second and third columns
Full size table

In the special limit of weak fields, the quantities in (31) can be obtained by combining the results in Tables 2, 3, and 4, and finding the asymptotic form for the limit of \(\bar{a},\bar{b}\rightarrow \infty \). Alternatively, the weak-field limit of the effective Lagrangian (17) can be used to evaluate (31):

$$\begin{aligned} {\mathcal {L}}_{S}^{(1)}=\frac{e^{2}}{360\pi ^{2}}\left( \frac{1}{\bar{a}^{2}}-\frac{1}{\bar{b}^{2}}\right) , \quad {\mathcal {L}}_{A}^{(1)}=\frac{7e^{2}\sigma }{720{\bar{a}}\bar{b}\pi ^{2}}, \nonumber \\ {\mathcal {L}}_{SS}^{(1)}=\frac{e^{4}}{45m^{4}\pi ^{2}},\quad {\mathcal {L}}_{SA}^{(1)}=0, \quad {\mathcal {L}}_{AA}^{(1)}=\frac{7e^{4}}{180m^{4}\pi ^{2}}, \end{aligned}$$
(32)

which are obtained with the quantities of the first bracket in (17) only. When \(\bar{b}=\infty \), these expressions yields the permittivity and permeability tensors obtained by Adler for the case of a weak magnetic field [63]:

$$\begin{aligned} \epsilon _{E,ij}=\delta _{ij}\left( 1-\frac{2\kappa }{4\pi }B_{0}^{2}\right) +B_{0i}B_{0j}\frac{7\kappa }{4\pi }, \quad \epsilon _{B.ij}=0, \nonumber \\ \bar{\mu }_{B,ij}=\delta _{ij}\left( 1-\frac{2\kappa }{4\pi }B_{0}^{2}\right) -B_{0i}B_{0j}\frac{4\kappa }{4\pi },\quad \bar{\mu }_{E,ij}=0 \end{aligned}$$
(33)

where \(\kappa =e^{4}/\left( 45\pi m^{4}\right) \). If the quantities in the second bracket of (17) is used, higher-order contributions are obtained.

4 Vacuum birefringence for \({\textbf{B}}_{0}\parallel {\textbf{E}}_{0}\) and \(\vert {\textbf{B}}_{0}\vert \gg \vert {\textbf{E}}_{0}\vert \)

In this section, we work out the refractive indices and the polarization vectors for the case of an arbitrarily strong magnetic field superposed with a weak electric field in the direction of the magnetic field, as shown in Fig. 6. In such a configuration, \(a=B_{0}\), \(b=E_{0}\), \(\bar{a}=B_\textrm{c}/(2B_{0})\), \(\bar{b}=E_\textrm{c}/(2E_{0})\), and \(\tilde{b}=E_0/B_0\) (see Table 1). This configuration, looking too restrictive at a first glance, is actually general enough to include the non-parallel cases, too. By choosing an appropriate Lorentz transformation, one can transform non-perpendicular configurations into parallel ones and the perpendicular configuration into that of a pure magnetic one as far as the electric field is weaker than the magnetic field [3, 45]. However, the Lorentz transformation of the permittivity and permeability of anisotropic media is a highly non-trivial issue [67], and thus eventually we need a formulation for an arbitrary field configuration [68]. In this paper, we focus on the parallel configuration to reveal the effect of the electromagnetic wrench in the simplest setting.

Fig. 6
figure 6

Configuration of the background fields (\({\textbf{E}}_{0}\), \({\textbf{B}}_{0}\)) and the probe field. The probe field has its propagation vector \({\textbf{k}}\) on the xz-plane and its two polarization vectors \(\delta {\textbf{E}}_{\pm }\) associated with the refractive indices \(n_{\pm }\). Unless \(E_{0}=0\) (thus \(\epsilon _{2}=0\)), \(\delta {\textbf{E}}_{+}\) is not along the y-axis, and \(\delta {\textbf{E}}_{-}\) is not on the xz-plane

Full size image

The refractive indices and the associated polarization vectors are found by solving the Maxwell equations for the probe field. When the probe field is a plane wave with the propagation vector \({\textbf{k}}\) and the angular frequency \(\omega \) (\({\textbf{k}}=\omega {\textbf{n}}=\omega n\hat{k}\)), the Maxwell equations for the probe field reduce to

$$\begin{aligned} \omega \delta {\textbf{B}}={\textbf{k}}\times \delta {\textbf{E}}, \quad \omega \delta {\textbf{D}}=-{\textbf{k}}\times \delta {\textbf{H}}. \end{aligned}$$
(34)

By substituting (29) into these equations, we obtain a matrix–vector equation for the polarization vector:

$$\begin{aligned} \varvec{\epsilon }_{E}\cdot \delta {\textbf{E}}+\varvec{\epsilon }_{B} \cdot {\textbf{n}}\times \delta {\textbf{E}}+{\textbf{n}}\times \left( \bar{\varvec{\mu }}_{B} \cdot {\textbf{n}}\times \delta {\textbf{E}}+\bar{\varvec{\mu }}_{E}\cdot \delta {\textbf{E}}\right) =\varvec{\Lambda }\cdot \delta {\textbf{E}}=0,\qquad \end{aligned}$$
(35)

where \(\varvec{\Lambda }\) is a \(3\times 3\) matrix incorporating \(\varvec{\epsilon }_{E}\), \(\varvec{\epsilon }_{B}\), \(\bar{\varvec{\mu }}_{B}\), \(\bar{\varvec{\mu }}_{E}\), and \({\textbf{n}}\). For this equation to have non-trivial solutions, \(\textrm{det}\varvec{\Lambda }=0\) should hold, from which refractive indices (\(n_{\pm }\)) are obtained. Substituting each of the refractive indices into the matrix–vector equation, one can obtain the associated polarization vectors (\(\delta {\textbf{E}}_{\pm }\)).

Table 6 Components of the permittivity and permeability tensors for the configuration in Fig. 6. These tensors have the shape of (36)
Full size table

In the configuration in Fig. 6, the parallel field condition \({\textbf{B}}_{0}=B_{0}\hat{z}\) and \({\textbf{E}}_{0}=E_{0}\hat{z}\) (\(E_{0}\ge 0\) and \(B_{0}>0\)) forces the permittivity and permeability tensors \(\varvec{\epsilon }_{E}\), \(\varvec{\epsilon }_{B}\), \(\bar{\varvec{\mu }}_{B}\), and \(\bar{\varvec{\mu }}_{E}\) in (29) to have the following structure:

$$\begin{aligned} {\varvec{r}}= \begin{pmatrix} r &{}\quad 0 &{}\quad 0\\ 0 &{}\quad r &{}\quad 0\\ 0 &{}\quad 0 &{}\quad r+\tilde{r} \end{pmatrix}, \end{aligned}$$
(36)

where r and \(\tilde{r}\) are given in Table 6 for each tensor. Furthermore, without loss of generality, the propagation vector can be assumed to be in the xz-plane: \({\textbf{k}}=\omega n(\sin \theta ,0,\cos \theta )\). Then the matrix \(\varvec{\Lambda }\) becomes

$$\begin{aligned} \varvec{\Lambda }= \begin{pmatrix} 1-n^{2}\cos ^{2}\theta &{}\quad 0 &{}\quad n^{2}\sin \theta \cos \theta \\ 0 &{} \quad 1-n^{2}(1+\mu \sin ^{2}\theta ) &{}\quad \epsilon _{2}n\sin \theta \\ n^{2}\sin \theta \cos \theta &{} \quad \epsilon _{2}n\sin \theta &{}\quad 1+\epsilon _{1}-n^{2}\sin ^{2}\theta \end{pmatrix}, \end{aligned}$$
(37)

where

$$\begin{aligned} \mu =\frac{\tilde{\bar{\mu }}_{B}}{\epsilon _{E}},\quad \epsilon _{1}=\frac{\tilde{\epsilon }_{E}}{\epsilon _{E}}, \quad \epsilon _{2}=\frac{\tilde{\epsilon }_{B}}{\epsilon _{E}}. \end{aligned}$$
(38)

By solving \(\textrm{det}(\varvec{\Lambda })=0\), which is a quadratic equation in \(n^{2}\), two values of \(n^{2}\) are obtained, i.e., birefringence:

$$\begin{aligned} n_{\pm }^{2}=\frac{1+\epsilon _{1}\cos ^{2}\theta +\sin ^{2}\theta \cdot f_{\pm }(\epsilon _{1}+\mu +\epsilon _{1}\mu ,\epsilon _{2}^{2})}{(1+\epsilon _{1}\cos ^{2}\theta )(1+\mu \sin ^{2}\theta ) +\epsilon _{2}^{2}\cos ^{2}\theta \sin ^{2}\theta }, \end{aligned}$$
(39)

where

$$\begin{aligned} f_{\pm }(\eta ,\lambda )\equiv \frac{(\eta +\lambda )\pm \sqrt{(\eta +\lambda )^{2}+4\lambda }}{2}. \end{aligned}$$
(40)

When \(\lambda \ne 0\) (non-zero wrench), \(f_{+}(\eta ,\lambda )\) and \(f_{-}(\eta ,\lambda )\) undergo an avoided crossing, as shown in Fig. 7. In contrast, when \(\lambda =0\) (wrenchless), \(f_{+}(\eta ,\lambda )\) and \(f_{-}(\eta ,\lambda )\) are swapped to each other in the crossing. Consequently, \(n_{+}^{2}\) and \(n_{-}^{2}\) exhibit the same behaviors for \(\epsilon _{2}\ne 0\) and \(\epsilon _{2}=0\) as \(\epsilon _{1}+\mu +\epsilon _{1}\mu \) crosses the origin (\(\eta =\epsilon _{1}+\mu +\epsilon _{1}\mu \), \(\lambda =\epsilon _{2}^{2}\)). The avoided crossing is the consequence of the electromagnetic wrench because \(\epsilon _{2}\) vanishes as \(E_{0}\) does (In Table 6, \({\mathcal {L}}_{SA}^{(1)}=0\) when \(E_{0}=0\)) for the configuration in Fig. 6. By the same token, the swapping is a signature of the wrenchless case.

Fig. 7
figure 7

Behavior of \(f_{\pm }(\eta ,\lambda )\) (40) near \(\eta =0\), where \(\eta =\epsilon _{1}+\mu +\epsilon _{1}\mu \) and \(\lambda =\epsilon _{2}^{2}\)

Full size image

With the two indices (39), the matrix equation \(\varvec{\Lambda }\cdot \delta {\textbf{E}}=0\) can be solved straightforwardly, but the general results are too lengthy to be presented. Instead, noting that \(\epsilon _{2}\) vanishes in the wrenchless case, we present only the expansions of the refractive indices and the polarization vectors up to \(O(\epsilon _{2}^{2})\). The swapping behavior for \(\epsilon _{2}=0\) makes the expansion depend on the sign of \(\epsilon _{1}+\mu +\epsilon _{1}\mu \). From now on, it is assumed that \(\epsilon _{1}+\mu +\epsilon _{1}\mu <0\) (the region of \(\eta <0\) in Fig. 7) below as it holds in the most wrenchless cases. Then the two refractive indices are expanded from (39) as

$$\begin{aligned} n_{+}^{2} \simeq&\,\frac{1}{1+\mu \sin ^{2}\theta }-\frac{(1+\mu )\sin ^{2}\theta }{(\epsilon _{1} +\mu +\epsilon _{1}\mu )(1+\mu \sin ^{2}\theta )^{2}}\epsilon _{2}^{2}, \nonumber \\ n_{-}^{2} \simeq&\,\frac{1+\epsilon _{1}}{1+\epsilon _{1}\cos ^{2}\theta }\nonumber \\&+\frac{(1+\epsilon _{1})\sin ^{2}\theta }{(\epsilon _{1}+\mu +\epsilon _{1}\mu )(1+\epsilon _{1}\cos ^{2}\theta )^{2}}\epsilon _{2}^{2}. \end{aligned}$$
(41)

Then, the polarization vectors corresponding to \(n_{\pm }^{2}\) are obtained by solving \(\varvec{\Lambda }_{\pm }\cdot \delta {\textbf{E}}_{\pm }=0\), where \(\varvec{\Lambda }_{\pm }\) is \(\varvec{\Lambda }\) (37) with \(n^{2}=n_{\pm }^{2}\). The components of \(\varvec{\Lambda }_{\pm }\) are denoted by \(\Lambda _{\pm ,ij}\). However, a blind application of the Gauss elimination fails to find the correct solution that becomes the wrenchless solution as \(\epsilon _{2}\) vanishes. By considering the limiting behavior of \(\Lambda _{\pm ,ij}\) for \(\epsilon _{2}\rightarrow 0\) and requiring the solution’s limiting behavior be consistent with that of \(\Lambda _{\pm ,ij}\), one can make \(\varvec{\Lambda }_{\pm }\), \(\delta {\textbf{E}}_{\pm }\), and \(\varvec{\Lambda }_{\pm } \cdot \delta {\textbf{E}}_{\pm }=0\) safely reduce those of the wrenchless case as \(\epsilon _{2}\rightarrow 0\).

For example, as \(\epsilon _{2}\rightarrow 0\), \(\Lambda _{+,22}\rightarrow \epsilon _{2}^{2}\), and \(\Lambda _{+,23}\rightarrow \epsilon _{2}\), while other non-zero components do not vanish. Then, the solution of the type \(\left( O(\epsilon _{2}),1,O(\epsilon _{2})\right) ^{T}\) yields the correct solution in terms of \(\Lambda _{+,ij}\):

$$\begin{aligned} \delta {\textbf{E}}_{+}= & {} \begin{pmatrix} \frac{\Lambda _{+,13}\Lambda _{+,23}}{\Lambda _{+,11}\Lambda _{+,33}-\Lambda _{+,13}^{2}}\\ 1\\ -\frac{\Lambda _{+,11}\Lambda _{+,23}}{\Lambda _{+,11}\Lambda _{+,33}-\Lambda _{+,13}^{2}} \end{pmatrix} \simeq \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix}\nonumber \\{} & {} \quad + \begin{pmatrix} \frac{1}{\epsilon _{1}+\mu +\epsilon _{1}\mu }\frac{\cos \theta }{\sqrt{1+\mu \sin ^{2}\theta }}\\ 0\\ -\frac{1}{\epsilon _{1}+\mu +\epsilon _{1}\mu }\frac{(1+\mu )\sin \theta }{\sqrt{1+\mu \sin ^{2}\theta }} \end{pmatrix} \epsilon _{2}, \end{aligned}$$
(42)

where the denominator \(\Lambda _{+,11}\Lambda _{+,33}-\Lambda _{+,13}^{2}\) does not vanish as \(\epsilon _{2}\rightarrow 0\). In solving \(\varvec{\Lambda }_{+}\cdot \delta {\textbf{E}}_{+}=0\), one obtains two sets of solutions, but they are the same for \(\epsilon _{2}\ne 0\) because of the constraint on the matrix elements, i.e., \(\det (\varvec{\Lambda }_{+})=0\). Between the two sets, we choose the set of which denominators do not vanish for \(\epsilon _{2}=0\) because the set correctly reduces to the wrenchless solution in the limit of \(\epsilon _{2}\rightarrow 0\). Note that \(\delta {\textbf{E}}_{+}\) can be normalized arbitrarily for convenience because solving the homogeneous equation \(\varvec{\Lambda }_{+}\cdot \delta {\textbf{E}}_{+}=0\) determines \(\delta {\textbf{E}}_{+}\) up to an overall factor.

Similarly, as \(\epsilon _{2}\rightarrow 0\), \(\Lambda _{-,23}\rightarrow \epsilon _{2}\), \(\Lambda _{-,33}-\Lambda _{-,13}^{2}/ \Lambda _{-,11}\rightarrow \epsilon _{2}^{2}\), while other non-zero components do not vanish. Then the solution of the type \(\left( x,O(\epsilon _{2}),1\right) ^{T}\), where x is non-vanishing, yields the following solution:

$$\begin{aligned} \delta {\textbf{E}}_{-}= & {} \begin{pmatrix} -\frac{\Lambda _{-,13}}{\Lambda _{-,11}}\\ -\frac{\Lambda _{-,23}}{\Lambda _{-,22}}\\ 1 \end{pmatrix} \simeq \begin{pmatrix} -(1+\epsilon _{1})\cot \theta \\ 0\\ 1 \end{pmatrix}\nonumber \\{} & {} +\begin{pmatrix} 0\\ \frac{\sqrt{1+\epsilon _{1}}}{\epsilon _{1}+\mu +\epsilon _{1}\mu }\frac{\sqrt{1+\epsilon _{1}\cos ^{2}\theta }}{\sin \theta }\\ 0 \end{pmatrix}\epsilon _{2}+ \begin{pmatrix} -\frac{(1+\epsilon _{1})\cot \theta }{\epsilon _{1}+\mu +\epsilon _{1}\mu }\\ 0\\ 0 \end{pmatrix}\epsilon _{2}^{2},\nonumber \\ \end{aligned}$$
(43)

where \(\Lambda _{-,11}\) and \(\Lambda _{-,22}\) do not vanish as \(\epsilon _{2}\rightarrow 0\).

In the wrenchless case, \(E_{0}=0\) and, thus, \(\epsilon _{2}=0\) hold. The corresponding refractive indices and polarization vectors are the zeroth-order terms in (41) and (43), which are consistent with those obtained by Melrose [3]. Unlike in the background-field-free vacuum, \({\textbf{k}}\), \(\delta {\textbf{E}}_{+}\), and \(\delta {\textbf{E}}_{-}\) do not form an orthogonal triad in general, albeit \({\textbf{k}}\perp \delta {\textbf{E}}_{+}\) and \(\delta {\textbf{E}}_{+}\perp \delta {\textbf{E}}_{-}\). The polarization vector \(\delta {\textbf{E}}_{+}\) is along the y-axis, while \(\delta {\textbf{E}}_{-}\) lies in the xz-plane but not necessarily \({\textbf{k}}\perp \delta {\textbf{E}}_{-}\) [69]. An orthogonal triad is formed only when \(\theta =\pi /2\): \(\delta {\textbf{E}}_{-}\) is aligned along the z-axis.

When \(\theta =0\), i.e., \({\textbf{k}}\) is along the z-axis, \(n_{\pm }^{2}=1\) and \(\delta {\textbf{E}}_{\pm ,z}=0\) regardless of the wrench: the background field does not affect the propagation of the probe field because of the equal and opposite contributions from the virtual electrons and positrons.

Fig. 8
figure 8

Effect of the electromagnetic wrench on vacuum birefringence: (a) \(n_{+}-n_{-}\) and (b) the angle (degree) of \(\delta {\textbf{E}}_{+}\) with respect to the y-axis for \(\tilde{b}=0,\,0.025,\,0.05,\,0.1,\,0.2\). The propagation vector \({\textbf{k}}\) of the probe field is chosen to be along the x-axis (\(\theta =\pi /2\)) to maximize the difference in a given field configuration. The vertical lines mark \(\bar{a}_\textrm{thres}\) for \(\tilde{b}=0.1,\, 0.2\): below \(\bar{a}_\textrm{thres}\), the corresponding plots become to lose its validity. The plots of the other \(\tilde{b}\) values are valid in the whole range

Full size image

The electromagnetic wrench (\(\tilde{b}\ne 0\)) can significantly affect the vacuum birefringence, as shown in Fig. 8. In Fig. 8a, the difference of the two refractive indices, \(n_{+}-n_{-}\), decreases noticeably in the supercritical region (\(\bar{a} \le 0.5\)) as \(\tilde{b}\) increases: at \(\bar{a}=0.3\) (\(\bar{a}_\textrm{thres}\) for \(\tilde{b}=0.2\)), the decrease is 5.0% when \(\tilde{b}=0.1\) but increases to 17% when \(\tilde{b}=0.2\). The absolute decrease for \((\bar{a},\tilde{b})=(0.15,0.1)\) is \(1.6 \times 10^{-5}\), which is quite close to the same as that for (0.3, 0.2), \(1.7 \times 10^{-5}\); the electric field is \(E_c/3\) at both cases.

In addition, the polarization vectors rotates due to the wrench. When \({\textbf{k}}\) is along the x-axis (\(\theta =\pi /2\)), \(\delta {\textbf{E}}_{+}\) and \(\delta {\textbf{E}}_{-}\) on the yz-plane, being perpendicular to each other in the wrenchless case. However, \(\delta {\textbf{E}}_{+}\) rotates further from the y-axis toward the z-axis in the wrenched case, and the amount of rotation increases with either \(\bar{a}\) or \(\tilde{b}\), as shown in Fig. 8b. In contrast to \(n_{+}-n_{-}\), the rotation angle is already as high as \(1^\circ \) even with the small value of \(\tilde{b}=0.025\). The rotation angle is \(5.5^\circ \) for \((\bar{a},\tilde{b})=(0.15,0.1)\) but increases to \(12.5^\circ \) for (0.3, 0.2), albeit the electric field remains the same. These results show that the rotation angle of the polarization vector is a more sensitive indicator of the wrench.

Both the reduction of the differences of the refractive indices and the rotation of polarization vectors are new features of vacuum birefringence introduced by the non-zero electromagnetic wrench. These results suggest that the electromagnetic wrench should be taken into account in analyzing the vacuum birefringence when the electric field is a fraction of a supercritical magnetic field. Such a situation is anticipated in the magnetosphere of neutron stars, especially magnetars.

5 Vacuum birefringence in pulsar magnetosphere

For a more concrete connection of the results in the previous sections to astrophysical phenomena, we consider the aligned rotator model suggested by Goldreich and Julian [39, 70]. The model provides the electric and magnetic fields around a neutron star by considering it as a magnetic dipole rotating along its dipole axis. Albeit the model cannot describe the pulsar radiation, it has been used as the basic model of pulsar magnetospheres because it predicts some phenomena observed in real pulsars and provides simple analytic expressions. In our context, it plays the role of a theoretical model for studying strong-field QED, classical and quantum. This model contains the essential element of the vacuum birefringence considered in our study, i.e., the wrench effect due to an electric field along the background magnetic field.

Fig. 9
figure 9

Vacuum birefringence in pulsar magnetosphere. a The directions of the magnetic (red arrow) and electric (green arrow) fields, b the configuration of the background fields and the photon propagation vector near the north pole (\(\theta <25^{\circ }\)), c the distribution of \(\tilde{b}=b/a\) for a pulsar with \(\Omega =2\pi /(1~\textrm{ms})\) and \(R=10~\textrm{km}\), and d the difference of the refractive indices multiplied by a factor of \(10^6\), i.e., \((n_+ - n_-)\times 10^6 \), for the photon propagating along the z-axis (\(\bar{a}=0.2\) and \(\tilde{b}=0,~0.1,~0.2\) corresponding to \(B_0 =2.5B_c\) and \(E_0=0,~0.25E_c,~0.5E_c\), respectively). When \(\bar{a}=\tilde{b}=0.2\), the ratio \(P_\textrm{Im}/P_\textrm{Re}\) is 0.07

Full size image

Using the model, we find that the region near the pole of a pulsar realizes the parallel field configuration considered in Sect. 4. According to the model, the electric and magnetic fields around a pulsar and their inner product are given as follows [70]:

$$\begin{aligned}&{\textbf{B}}_0(r,\theta _n) =\frac{{\mathcal {B}}}{(r/R)^{3}}\left( \cos \theta _n\hat{r} +\frac{1}{2} \sin \theta _n\hat{\theta }_n\right) , \nonumber \\&{\textbf{E}}_0(r,\theta _n)=\frac{{\mathcal {B}}}{(r/R)^{4}}\frac{R\Omega }{c} \left[ \left( \frac{3}{2}\sin ^{2}\theta _n-1\right) \hat{r}-\frac{1}{2}\sin 2\theta _n\hat{\theta }_n\right] , \nonumber \\&{\textbf{E}}_0\cdot {\textbf{B}}_0=-\frac{{\mathcal {B}}^{2}}{(r/R)^{7}}\frac{R\Omega }{c}\cos ^{3}\theta _n, \end{aligned}$$
(44)

where \({\mathcal {B}}\), \(\Omega \), and R are the magnetic field strength at the north pole, the angular frequency of rotation, and the pulsar’s radius, respectively. The position is specified by \((r,\theta _n,\varphi )\) in the spherical coordinate system of the pulsar; \(\varphi \) is absent in these expressions due to the azimuthal symmetry. As illustrated in Fig. 9a, the electric and magnetic fields are anti-parallel near the poles. The degree of parallelization, defined as \(\left( {\textbf{E}}_0\cdot {\textbf{B}}_0\right) ^{2}/\left( {\textbf{E}}_0^{2}{\textbf{B}}_0^{2}\right) \), is over 0.99 when \(\theta _n<11.2^{\circ }\) and over 0.95 when \(\theta _n<22.9^{\circ }\), regardless of the other parameters. Moving from the pole to the equator, the magnetic field becomes tangential, while the electric field reverses its sign in the radial direction at \(\theta _n<54.7^{\circ }\). Therefore, we can use the results in Sect. 4 to analyze the vacuum birefrigence in the region with \(\theta _n\lesssim 10^{\circ }\). Figure 9b shows the configuration of the background fields and the photon propagation vector \({\textbf{k}}\) at a position \({\textbf{r}}\) with a polar angle of \(\theta _n\): the magnetic field \({\textbf{B}}_0\) is inclined by an angle \(\alpha \simeq \theta _n/2\) with respect to \({\textbf{r}}\). The electric field \({\textbf{E}}_0\) is almost anti-parallel to the magnetic field. For the photon propagating along the z-axis, the angle between \({\textbf{k}}\) and \({\textbf{B}}_0\) is \(\theta \simeq 3\theta _n/2\). Furthermore, the parameter \(\tilde{b}=b/a\), an indicator for the wrench effect, is significant in this region for millisecond pulsars with a radius comparable to 10 km, as shown in Fig. 9c.

The wrench effect on the vacuum birefringence near the pole is seen in Fig. 9d, which shows the difference in the refractive indices for the photons propagating in the \(+z\) direction. As the wrench parameter \(\tilde{b}\) increases to 0.2, the difference decreases by about \(2\times 10^{-6}\) at a polar angle of \(10^\circ \). The difference increases with the polar angle mainly because the angle between \({\textbf{k}}\) and \({\textbf{B}}_0\), i.e., \(\theta \) in Fig. 9b, increases with the polar angle. Though small, the difference can lead to a substantial change because the birefringence effect accumulates over a distance comparable to the pulsar radius, which is much larger than the photon wavelength.

6 Conclusion

We have derived a concise expression of the one-loop effective Lagrangian for the vacuum under an arbitrarily strong magnetic field superposed with a weak electric field (15); \(G=-{\textbf{E}}\cdot {\textbf{B}}\) can be non-zero to allow the electromagnetic wrench. The expression is valid as far as the pair production is not significant because, in the case of significant pair production, a plasma of produced electron-positron pairs affects the vacuum polarization. As a criterion for neglecting pair production, we suggested the condition \(E_0 \lesssim E_c/3\), based on the exact numerical evaluation of the one-loop effective Lagragian. The lack of such a concise expression for general field configuration has restricted the vacuum birefringence analysis to the wrenchless case in the literature.

By using the derived one-loop effective Lagrangian, we have calculated the linear optical response of such vacuum to weak low-frequency fields. The permittivity and permeability tensors are given as (30) for an arbitrary one-loop effective Lagrangian. When the expansion form (16) of the HES effective Lagrangian is used, these tensors have values specified in Tables 2, 3, and 4. The known results for the wrenchless and the weak-field cases in the literature are obtained by taking the limit of \(b\rightarrow 0\) for arbitrary a (the wrenchless case) and \(a,b\rightarrow 0\) (the weak-field case) in our general expression, respectively.

With the permittivity and permeability tensors, we have worked out the modes of the probe field for the case where the background electric and magnetic fields are parallel to each other. The refractive indices (41) clearly exhibit birefringence, with the associated polarization vectors (42) and (43). In the case with an electromagnetic wrench, we have found that the electromagnetic wrench can reduce the difference of the refractive indices and rotate the polarization tensor significantly; these effects have not been reported so far to our knowledge.

Our result is crucial for the X-ray polarimetry of highly magnetized neutron stars and magnetars because the magnetospheres of such astrophysical objects have both a magnetic field comparable to or higher than the Schwinger limit and a weak induced electric fields. The electric field along the magnetic field can noticeably change the polarimetric results, as shown in Fig. 8. For instance, when \(B=1.7{\textrm{c}}\) and \(E=0.33E_{\textrm{c}}\), the difference of the refractive indices changes by 17%, and the polarization vectors rotate by \(12.5^{\circ }\) due to the non-negligible electric field along the magnetic field. At smaller values of E, the change is reduced but can accumulate to a significant level because the probe’s propagation length is comparable to the size of the stars. Thus, our formulae incorporating the electromagnetic wrench enable us to more accurately analyze the vacuum birefringence at such astrophysical conditions and, therefore, have a direct impact on the space missions such as Imaging X-ray Polarimetry Explorer (IXPE), the enhanced X-ray Timing and Polarimetry (eXTP), and the Compton Telescope project.

Our results have indicated the significance of the electromagnetic wrench in the vacuum birefringence around neutron stars. However, for a more accurate analysis, we need to extend the formulation in several aspects. First, the formulation should be generalized to include the imaginary part of the Lagrangian for the case pair production is significant. Second, the mode analysis in Sect. 4 should be extended to arbitrary angles among the photon propagation vector, the electric field, and the magnetic field. Recently, we made such an analysis for an arbitrary nonlinear Lagrangian and derived the formulae of refractive indices and polarization vectors [68]. We leave the application of the analysis with the current Lagrangian for a future work. Third, the spatial variation of electric and magnetic fields should be addressed. The formulation discussed so far assumes homogeneous fields but effectively gives the local values of the vacuum response because the length scale of field variation is about the size of neutron stars. Under such a spatial variation, the photon propagation vector and the photon polarization vectors can change their directions during the propagation. Then, the wave equation or its approximated version needs to be solved. Fourth, the contribution from the plasma surrounding neutron stars should be included in addition to the contribution from nonlinear vacuum discussed so far. Once the plasma distribution is estimated, its contribution to photon propagation can be included by using the standard formulae in plasma physics. Finally, the gravity may need to be incorporated because neutron stars have non-negligibly strong gravitational fields. Each of these points are highly non-trivial and requires substantial amount of theoretical and numerical investigations.