Constraints on primordial curvature spectrum from primordial black holes and scalar-induced gravitational waves

Abstract

The observational data of primordial black holes and scalar-induced gravitational waves can constrain the primordial curvature perturbation at small scales. We parameterize the primordial curvature perturbation by a broken power law form and find that it is consistent with many inflation models that can produce primordial black holes, such as nonminimal derivative coupling inflation, scalar–tensor inflation, Gauss–Bonnet inflation, and K/G inflation. The constraints from primordial black holes on the primordial curvature power spectrum with the broken power law form are obtained, where the fraction of primordial black holes in dark matter is calculated by the peak theory. Both the real-space top-hat and the Gaussian window functions are considered. The constraints on the amplitude of primordial curvature perturbation with Gaussian window function are around three times larger than those with real-space top-hat window function. The constraints on the primordial curvature perturbation from the NANOGrav 12.5 years data sets are displayed, where the NANOGrav signals are assumed as the scalar-induced gravitational waves, and only the first five frequency bins are used.

1 Introduction

Primordial black holes (PBHs) are formed from the overdense regions of the Universe by gravitational collapse during radiation domination [1, 2]. They can explain the source of the gravitational waves (GWs) events detected by the Laser Interferometer Gravitational Wave Observatory (LIGO) Scientific Collaboration and the Virgo Collaboration [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. They are also dark matter (DM) candidates [18,19,20,21,22,23,24,25,26,27] due to the non detection of particle dark matter. For the PBHs with masses around $10^{-17}-10^{-15} M_{\odot }$ and $10^{-14}-10^{-12} M_{\odot }$, they can make up almost all dark matter because of no observational constraints on the abundances of PBHs at these two mass windows. The seed of the overdense regions that collapse to form PBHs can come from the primordial curvature perturbations generated during inflation [28,29,30,31]. To produce enough PBHs DM, the amplitude of the power spectrum of the primordial curvature perturbations should be around $A_\zeta \sim {\mathscr {O}}(0.01)$. From the observation of cosmic microwave background (CMB) anisotropy measurements, the constraints on the primordial curvature perturbations are $A_\zeta =2.1\times 10^{-9}$ [32] at large scales, $k\lesssim {\mathscr {O}}(1)\,\text {Mpc}^{-1}$. Therefore, to produce enough PBHs DM, the primordial curvature power spectrum should be enhanced by about seven orders of magnitude at small scales, compared with the constraints at larger scales [33].

The amplitude of the primordial curvature perturbations can be sharply enhanced if there is an ultra-slow-roll phase in the inflation model [34,35,36]. For the single field inflation models, the ultra-slow-roll phase can be realized by the canonical inflation models with an inflection point [33, 37,38,39,40,41,42,43,44], and the ultra-slow-roll phase can also be realized by many noncanonical inflation models [45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. The speed of the enhancement of the primordial curvature perturbations of the single field inflation can not be arbitrarily fast; the steepest enhancement obeys the power law form, ${\mathscr {P}}_\zeta \sim k^4$ [65, 66]. Guided by this property, the typical peaks in the power spectrum of the primordial curvature perturbations generated by single field inflation can be approximated by a broken power law, ${\mathscr {P}}_{ peak}(k)=A(\alpha +\beta )/[\beta (k/k_p)^{-\alpha }+\alpha (k/k_p)^\beta ]$ [67]. Considering the large scales constraints, the power spectrum of the primordial curvature perturbations can be approximated by ${\mathscr {P}}_{ \zeta }(k)=A(\alpha +\beta )/[\beta (k/k_p)^{-\alpha }+\alpha (k/k_p)^\beta ]+A_*(k/k_*)^{n_{s*}-1}$. In this paper, we show that the broken power law form of the primordial curvature perturbation is consistent with many inflation models such as the inflation model with nonminimal derivative coupling [46], scalar–tensor inflation model [59], Gauss–Bonnet inflation model [60], and inflation model with non-canonical kinetic term (K/G inflation) [57].

The observational data of PBHs can provide constraints on the primordial curvature perturbations at small scales. There are many works on this topic. The constraints on the primordial curvature perturbations from the PBHs observational data with Press–Schechter theory and Gaussian window function are discussed in ref. [68]. The constraints considering all the steps from gravitational collapse to PBHs formation in real space are obtained in ref. [69]. And the constraints with peak theory are given in ref. [70] where the power spectrum of the primordial curvature perturbation is chosen as the log-normal form. As the broken power law form of the primordial curvature perturbation are consistent with many inflation models, in this paper, we use the broken power law form and give the constraints on primordial curvature perturbation from the observational data of PBHs with peak theory. Both Gaussian and real-space top-hat window functions are considered.

Accompanying the formation of PBHs, the large scalar perturbations can induce secondary gravitational waves after the horizon reentry during the radiation-dominated epoch [71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105]. The scalar-induced gravitational waves (SIGWs), containing much information about the early Universe, have wide frequency distribution and can be detected by pulsar timing arrays (PTA) [106,107,108,109,110] and the future space-based GW detectors such as Laser Interferometer Space Antenna (LISA) [111, 112], Taiji [113], and TianQin [114]. The stochastic process with a common amplitude and a common spectral slope across pulsars detected by the North American Nanohertz Observatory for Gravitational Wave (NANOGrav) Collaboration [115] and other pulsar timing arrays [116, 117] can be explained by SIGWs [58, 67, 118,119,120]. In this paper, we give the constraints on the primordial curvature perturbation from the NANOGrav 12.5 years data sets by regarding the NANOGrav signals as GWs induced from the primordial curvature perturbation with the broken power law form.

This paper is organized as follows. In Sect. 2, we calculate the abundance of PBHs from the power spectrum of primordial curvature perturbation by peak theory. In Sect. 3, we give the energy density of SIGWs. We discuss the constraints from the PBHs and SIGWs on the power spectrum of primordial curvature perturbation in Sect. 4. We conclude the paper in Sect. 5.

2 The primordial black holes

The fraction of the Universe in PBHs at the formation is denoted by

$$\begin{aligned} \beta =\frac{\rho _{\text {PBH}}}{\rho _b}, \end{aligned}$$

(1)

where $\rho _\text {PBH}$ is the energy density of PBHs and $\rho _b$ is the background energy density of the Universe. From the peak theory, the energy density of PBHs is [70, 121,122,123,124,125]

$$\begin{aligned} \rho _{\text {PBH}}=\int _{\nu _c}^{\infty }M_{\text {PBH}}(\nu ){\mathscr {N}}_{pk}(\nu )d\nu , \end{aligned}$$

(2)

where $\nu =\delta /\sigma$ and $\nu _c=\delta _c/\sigma _0$, $\delta _c$ is the threshold of the smoothed density contrast for the formation of PBHs and $\sigma _0$ is the variance of the smoothed density contrast. $M_\text {PBH}$ is the mass of PBHs and ${\mathscr {N}}_{pk}$ is the number density of PBHs [121],

$$\begin{aligned} {\mathscr {N}}_{pk}(\nu )=\frac{1}{a^3}\frac{1}{(2\pi )^2}\left( \frac{\sigma _1}{\sqrt{3}\sigma _0}\right) ^3 \nu ^3\exp \left( -\frac{\nu ^2}{2}\right) . \end{aligned}$$

(3)

The moment of the smoothed density power spectrum $\sigma _n$ is defined by

$$\begin{aligned} \sigma ^2_n=\int _{0}^{\infty }\frac{dk}{k}k^{2n} T^2(k,R_H)W^2(k,R_H){\mathscr {P}}_\delta (k), \end{aligned}$$

(4)

where $\sigma _0$ and $\sigma _1$ are obtained by choosing $n=0$ and $n=1$, respectively. The power spectrum of the density contrast ${\mathscr {P}}_\delta$ is related to the power spectrum of primordial curvature perturbations ${\mathscr {P}}_\zeta$ by

$$\begin{aligned} {\mathscr {P}}_\delta (k)=\frac{4(1+w)^2}{(5+3w)^2}\left( \frac{k}{aH}\right) ^4 {\mathscr {P}}_{\zeta }(k), \end{aligned}$$

(5)

where the state equation $w=1/3$ during the radiation domination. The most considered window functions $W(k,R_H)$ in Eq. (4) are the real-space top-hat window function [126],

$$\begin{aligned} W(k,R_H)=3\left[ \frac{\sin \left( kR_H\right) -\left( kR_H\right) \cos \left( kR_H\right) }{\left( kR_H\right) ^3}\right] , \end{aligned}$$

(6)

and the Gaussian window function

$$\begin{aligned} W(k,R_H)=\exp \left( \frac{-k ^2 R_H^2}{2}\right) , \end{aligned}$$

(7)

with the smoothed scale $R_H\sim 1/aH$. In this paper, both these two window functions are considered. The transfer function in Eq. (4) is

$$\begin{aligned} T(k,R_H)=3\left[ \frac{\sin \left( \frac{kR_H}{\sqrt{3}}\right) -\left( \frac{kR_H}{\sqrt{3}}\right) \cos \left( \frac{kR_H}{\sqrt{3}}\right) }{\left( {kR_H}/{\sqrt{3}}\right) ^3}\right] . \end{aligned}$$

(8)

The mass of primordial black holes in Eq. (2) obeys the critical scaling law [127,128,129],

$$\begin{aligned} M_{\text {PBH}}=\kappa M_H(\delta -\delta _c)^{\gamma }, \end{aligned}$$

(9)

where $\gamma =0.36$ in the radiation domination [127, 128] and $M_H$ is the mass in the horizon,

$$\begin{aligned} M_H\approx 13\left( \frac{g_*}{106.75}\right) ^{-1/6}\left( \frac{k}{10^6 \text {Mpc}^{-1}}\right) ^{-2}M_\odot , \end{aligned}$$

(10)

$g_*$ is the number of relativistic degrees of freedom at the formation of PBHs. The parameter $\kappa$ in the critical scaling law and PBHs formation threshold $\delta _c$ are dependent on the window function, and the relations of them between the two window functions are [125]

$$\begin{aligned} \delta _{c(G)}\approx \frac{\delta _{c(TH)}}{2.17},\quad \kappa _G\approx \frac{2.74^2\times 2.17^\gamma }{4} \kappa _{TH}, \end{aligned}$$

(11)

where $\gamma$ is the index in the critical scaling law (9). For the real-space top-hat window function, we choose $\delta _{c(TH)}=0.51$ and $\kappa _{TH}=3.3$ [130, 131]; from Eq. (11), the corresponding values for the Gaussian window function are $\delta _{c(G)}\approx 0.24$ and $\kappa _{G}=8.2$.

Combining the mass fraction of the Universe which collapses to form PBHs, Eq. (1), with the background equation of the energy density of the Universe, we obtain the density parameter of PBHs at present [132],

$$\begin{aligned} \varOmega _\text {PBH}=\int _{M_\text {min}}^{M_\text {max}} d \ln M_H \left( \frac{M_{eq}}{M_H}\right) ^{1/2}\beta (M_H), \end{aligned}$$

(12)

where we use the relations $\rho _\text {PBH}\propto a^{-3}$ and $\rho _b\propto a^{-n}$, with $n=4$ during radiation domination and $n=3$ during matter domination; and $M_{eq}=2.8\times 10^{17}M_{\odot }$ is the horizon mass at the matter-radiation equality. The limits of the integral are taken as $M_\text {min}=0$ and $M_\text {max}=\infty$ because of $\beta (M_H)\rightarrow 0$ at the condition $M_H\rightarrow 0$ or $M_H\rightarrow \infty$. The fraction of primordial black holes in the dark matter at present is defined as

$$\begin{aligned} f_{\text {PBH}}=\frac{\varOmega _{\text {PBH}}}{\varOmega _\text {DM}}=\int f(M_\text {PBH}) d\ln M_\text {PBH}, \end{aligned}$$

(13)

where $\varOmega _\text {DM}$ is the density parameter for dark matter, and the PBHs mass function is

$$\begin{aligned} f(M_\text {PBH})=\frac{1}{\varOmega _{\text {DM}}}\frac{d \varOmega _{\text {PBH}}}{d \ln M_{\text {PBH}}}. \end{aligned}$$

(14)

Substituting Eq. (12) into definition (14) and combining the above equations, we can obtain the PBHs mass function [132],

$$\begin{aligned} f(M_\text {PBH}){} & {} =\frac{1}{\varOmega _{\text {DM}}} \int _{M_\text {min}}^{M_\text {max}}\frac{d M_H}{M_H} \frac{M_\text {PBH}}{\gamma M_H} \sqrt{\frac{M_{eq}}{M_H}}\nonumber \\{} & {} \quad \times \frac{1}{3\pi } \left( \frac{\sigma _1}{\sqrt{3}\sigma _0 aH}\right) ^3\frac{1}{\sigma _0^4} \left( \mu ^{1/\gamma }+\delta _c\right) ^3 \nonumber \\{} & {} \quad \times \mu ^{1/\gamma } \exp \left[ -\frac{\left( \mu ^{1/\gamma }+\delta _c\right) ^2}{2\sigma _0^2}\right] , \end{aligned}$$

(15)

where $\mu =M_{\text {PBH}}/(\kappa M_H)$ and the relation $d\delta /d\ln M_{\text {PBH}}=\mu ^{1/\gamma }/\gamma$ derived from Eq. (9) is used.

3 The scalar-induced gravitational waves

Accompanying the formation of PBHs, the large scalar perturbation can induce secondary gravitational waves during the radiation domination. The metric with perturbation in the cosmological background and Newtonian gauge is

$$\begin{aligned} d s^2{} & {} =-a^2(\eta )(1+2\varPhi )d\eta ^2 \nonumber \\{} & {} \quad +a^2(\eta )\left[ (1-2\varPhi )\delta _{ij}+\frac{1}{2}h_{ij}\right] d x^i d x^j, \end{aligned}$$

(16)

where the anisotropic stress is neglected, $\eta$ is the conformal time, $\varPhi$ is the Bardeen potential, and $h_{ij}$ are the tensor perturbations. The tensor perturbations in the Fourier space can be obtained by the transform

$$\begin{aligned} h_{ij}(\varvec{x},\eta )=\int \frac{ d^3k e^{i\varvec{k}\cdot \varvec{x}}}{(2\pi )^{3/2}} [h_{\varvec{k}}(\eta )e_{ij}(\varvec{k})+{\tilde{h}}_{\varvec{k}}(\eta ){\tilde{e}}_{ij}(\varvec{k})], \end{aligned}$$

(17)

where $e_{ij}(\varvec{k})$ and ${\tilde{e}}_{ij}(\varvec{k})$ are the plus and cross polarization tensors,

$$\begin{aligned} e_{ij}(\varvec{k})= & {} \frac{1}{\sqrt{2}}\left[ e_i(\varvec{k})e_j(\varvec{k})-{\tilde{e}}_i(\varvec{k}){\tilde{e}}_j(\varvec{k})\right] , \end{aligned}$$

(18)

$$\begin{aligned} {\tilde{e}}_{ij}(\varvec{k})= & {} \frac{1}{\sqrt{2}}\left[ e_i(\varvec{k}){\tilde{e}}_j(\varvec{k})+{\tilde{e}}_i(\varvec{k})e_j(\varvec{k})\right] , \end{aligned}$$

(19)

with the basis vectors satisfying $\varvec{e}\cdot \tilde{\varvec{e}}=\varvec{e} \cdot \varvec{k}= \tilde{\varvec{e}}\cdot \varvec{k}$.

The tensor perturbations in the Fourier space with either polarization induced by the second order of the linear scalar perturbations satisfy [73, 74]

$$\begin{aligned} h''_{\varvec{k}}+2{\mathscr {H}}h'_{\varvec{k}}+k^2h_{\varvec{k}}=4S_{\varvec{k}}, \end{aligned}$$

(20)

where a prime denotes the derivative with respect to the conformal time $\eta$, $h'_{\varvec{k}}=dh_{\varvec{k}}/d\eta$, and ${\mathscr {H}}=a'/a$ is the conformal Hubble parameter. The second order source from the linear scalar perturbations $S_{\varvec{k}}$ is

$$\begin{aligned} S_{\varvec{k}}{} & {} =\int \frac{d^3{\tilde{k}}}{(2\pi )^{3/2}}e_{ij}(\varvec{k}){\tilde{k}}^i{\tilde{k}}^j \left[ 2\varPhi _{\tilde{\varvec{k}}}\varPhi _{\varvec{k}-\tilde{\varvec{k}}} \right. \nonumber \\{} & {} \quad \left. +\frac{1}{{\mathscr {H}}^2} \left( \varPhi '_{\tilde{\varvec{k}}}+{\mathscr {H}}\varPhi _{\tilde{\varvec{k}}}\right) \left( \varPhi '_{\varvec{k}-\tilde{\varvec{k}}}+{\mathscr {H}}\varPhi _{\varvec{k}-\tilde{\varvec{k}}}\right) \right] , \end{aligned}$$

(21)

where $\varPhi _{\varvec{k}}$ is the Bardeen potential in the Fourier space and can be related to the primordial curvature perturbations $\zeta _{\varvec{k}}$ generated in the inflation by the transfer function

$$\begin{aligned} \varPhi _{\varvec{k}}=\frac{3+3w}{5+3w}T(k,\eta ) \zeta _{\varvec{k}}, \end{aligned}$$

(22)

where $T(k,\eta )$ is the transfer function (8).

To solve the tensor perturbations Eq. (20), the Green function method is used, and the solution is

$$\begin{aligned} h_k(\eta )=\frac{4}{a(\eta )}\int _{\eta _k}^{\eta }d {\tilde{\eta }}g_k(\eta ,{\tilde{\eta }})a({\tilde{\eta }})S_k({\tilde{\eta }}), \end{aligned}$$

(23)

where the corresponding Green function is

$$\begin{aligned} g_k(\eta ,\eta ')=\frac{\sin \left[ k(\eta -\eta ')\right] }{k}. \end{aligned}$$

(24)

Substituting the solution of $h_k$ (23) into the definition of the power spectrum of tensor perturbations,

$$\begin{aligned} \langle h_{\varvec{k}}(\eta )h_{\tilde{\varvec{k}}}(\eta )\rangle =\frac{2\pi ^2}{k^3}\delta ^{(3)}(\varvec{k}+\tilde{\varvec{k}}){\mathscr {P}}_h(k,\eta ), \end{aligned}$$

(25)

we can obtain [73, 74, 88, 89, 133]

$$\begin{aligned} {\mathscr {P}}_h(k,\eta ){} & {} = 4\int _{0}^{\infty }dv\int _{|1-v|}^{1+v}du \left[ \frac{4v^2-(1-u^2+v^2)^2}{4uv}\right] ^2\nonumber \\ {}{} & {} \quad \times I_{RD}^2(u,v,x){\mathscr {P}}_{\zeta }(kv){\mathscr {P}}_{\zeta }(ku), \end{aligned}$$

(26)

where $u=|\varvec{k}-\tilde{\varvec{k}}|/k$, $v={\tilde{k}}/k$, $x=k\eta$, and the integral kernel $I_{\text {RD}}$ is

$$\begin{aligned} I_{\text {RD}}(u, v, x){} & {} =\int _1^x dy\, y \sin (x-y)\{3T(uy)T(vy) \nonumber \\{} & {} \quad +y[T(vy)u T'(uy)+v T'(vy) T(uy)] \nonumber \\{} & {} \quad +y^2 u v T'(uy) T'(vy)\}. \end{aligned}$$

(27)

The energy density of Gravitational waves is defined as

$$\begin{aligned} \varOmega _{\textrm{GW}}(k,\eta )=\frac{1}{24}\left( \frac{k}{aH}\right) ^2\overline{{\mathscr {P}}_h(k,\eta )}. \end{aligned}$$

(28)

Substituting Eq. (26) into the definition (28), we get [89, 133]

$$\begin{aligned} \varOmega _{\textrm{GW}}(k,\eta )&=\frac{1}{6}\left( \frac{k}{aH}\right) ^2\int _{0}^{\infty }dv\int _{|1-v|}^{1+v}du\nonumber \\&\quad \times \left[ \frac{4v^2-(1-u^2+v^2)^2}{4uv}\right] ^2\nonumber \\&\quad \times \overline{I_{\text {RD}}^{2}(u, v, x)} {\mathscr {P}}_{\zeta }(kv){\mathscr {P}}_{\zeta }(ku), \end{aligned}$$

(29)

where $\overline{I_{\text {RD}}^{2}}$ is the oscillation time average of the integral kernel. The evolution of the energy density of the gravitational waves is the same as that of radiation; with the help of this property, the energy density of the gravitational waves at present can be obtained easily,

$$\begin{aligned} \varOmega _{\textrm{GW}}(k,\eta _0)=\frac{c_g\varOmega _{r,0} \varOmega _{\textrm{GW}}(k,\eta )}{\varOmega _{r}(\eta )}, \end{aligned}$$

(30)

where $\varOmega _{r,0}$ is the energy density of the radiation at present and $\varOmega _{r}(\eta )=1$ at the generation of SIGWs, and [67, 118]

$$\begin{aligned} c_g=0.387\left( \frac{g_{*,s}^4g_*^{-3}}{106.75}\right) ^{-1/3}. \end{aligned}$$

(31)

4 The constraints on the primordial power spectrum

At large scales, the constraints on the primordial curvature perturbations from the observation of CMB anisotropy measurements are strong, $A_\zeta =2.1\times 10^{-9}$ [32]. At the same time, there are few constraints on the primordial curvature perturbations at small scales. Because PBHs and scalar-induced GWs are produced from the primordial curvature perturbations with large amplitude at small scales, the successful or failed detection of PBHs and SIGWs can provide constraints on the primordial curvature perturbations at small scales. To produce enough PBHs DM and SIGWs, the power spectrum of the primordial perturbations should be around ${\mathscr {P}}_\zeta \sim {\mathscr {O}}(0.01)$, which is about seven orders of magnitudes larger than that at large scales. For the single field inflation models, the profile of the enhancement of the power spectrum can be governed by the power law form, and the steepest enhancement is about the order of $\sim k^4$ [65, 66]. To fit the enhanced primordial power spectrum, we consider the broken power law parameterization [67]

$$\begin{aligned} {\mathscr {P}}_\zeta (k)=\frac{A(\alpha +\beta )}{\beta (k/k_p)^{-\alpha }+\alpha (k/k_p)^\beta }+A_*(k/k_*)^{n_{s_*}-1}. \end{aligned}$$

(32)

The first term is the broken power law form to fit the enhanced peak at small scales, $0.5 \lesssim \alpha \lesssim 4$ controls the speed of enhancement, and $0.5 \lesssim \beta \lesssim 4$ determines the speed of decline in the power spectrum. A pair of smaller parameters, $\alpha$ and $\beta$, gives a broader peak in the spectrum. The lower limit of the parameters ensures the curvature power spectrum between the end of inflation and the peak obeys a power law [67]. The second term in Eq. (32) is the near scale-invariant power law form to fit the Planck 2018 constraints [134] at large scales, and the parameters are chosen as $k_*=0.05\text {Mpc}^{-1}$, $n_{s_*}=0.965$, and $A_*=2.1\times 10^{-9}$.

In Fig 1, we compare the parameterization (32) with some real inflation models. The black dashed lines denote the power spectra from real inflation models, and the red solid lines represent the results from parameterization (32). The power spectra in the left upper panel, right upper panel, left lower panel, and right lower panel are from the inflation model with nonminimal derivative coupling [46], scalar–tensor inflation model [59], Gauss–Bonnet inflation model [60], and inflation model with a non-canonical kinetic term (K/G inflation model) [57], respectively. Figure 1 shows that the power spectra from parameterization (32) are consistent well with those from real inflation models both at large and peak scales. The features of PBHs and SIGWs are mainly determined by the high peak region of the power spectrum of the primordial curvature perturbations. Therefore, we can safely use parameterization (32) to research the topic of PBHs and SIGWs.

Fig. 1

The difference between the power spectra from real inflation models (denoted by black dashed lines) and parameterization (32) (marked by solid red lines). The left upper panel, right upper panel, left lower panel, and right lower panel are the power spectra from inflation model with nonminimal derivative coupling [46], scalar–tensor inflation model [59], Gauss–Bonnet inflation model [60], and inflation model with non-canonical kinetic term (K/G inflation) [57], respectively

4.1 Constraints from PBHs

Combining the parameterization (32) and PBHs mass function (15), we can transfer the constraints on PBHs DM to those on the primordial curvature power spectrum. The left panel of Fig. 2 shows the main observational data of PBHs DM at present, and the right panel of Fig. 2 displays the corresponding constraints on the primordial curvature power spectrum from the left panel PBHs DM observational data. In the right panel of Fig. 2, the red and black bands are the results with the choice of top-hat and Gaussian window functions, respectively. The lower and upper limits of each band are from the parameterization (32) with $\alpha =\beta =0.5$ and $\alpha =\beta =4$, respectively. For the choice of the top-hat window function, the constraints on the primordial curvature power spectrum from PBHs DM are more robust than those from BBN and PTA; and for the choice of the Gaussian window function, the constraints are weaker than those from PTA. The uncertainty of the constraints caused by the choice of the window function is more significant than that by the profile of the peak in the primordial curvature power spectrum. The magenta line denotes the constraints from PBHs DM with Press–Schechter theory and Gaussian window function given in ref. [68], and the constraints are weaker than that with peak theory. The reason is that the PBHs abundance calculated by the peak theory is larger than that by the Press–Schechter by about one order magnitude for the same primordial power spectrum [122].

Fig. 2

The left panel shows the observational constraints on the PBHs abundance: the cyan region from accretion constraints by CMB [135, 136], the red region from LIGO-Virgo Collaboration measurements [137,138,139,140,141,142], the gray region from the EROS/MACHO [143], the green region from microlensing events with Subaru HSC [144], the blue region from the Kepler satellite [145], the orange region from white dwarf explosion (WD) [146], the yellow region from galactic center 511 keV gamma-ray line (INTEGRAL) [147,148,149], and the brown region from extragalactic gamma-rays by PBH evaporation (EG$\gamma$) [150]. The right panel shows the constraints on the primordial curvature spectrum. The light green shaded region is excluded by the CMB observations [134]. The cyan, orange and blue regions show the constraints from the EPTA observations [151], the effect on the ratio between neutron and proton during the big bang nucleosynthesis (BBN) [152] and $\mu$-distortion of CMB [153], respectively. The red and black bands are from the left panel PBHs observational data. The black curve in the right panel is the parameterization (32) with the best parameter values (33) and (34) obtained from the Bayesian analysis of PTA data, and the black curve in the left panel is the corresponding mass function calculated by the peak theory with the Gaussian window function

Fig. 3

The convex curves denote the energy density of SIGWs with peak frequencies around $10^{-9}$ Hz, $10^{-3}$ Hz, and $10^{2}$ Hz, respectively. The dashed and solid lines are related to the black and red bands in the right panel of Figure 2, respectively. The concave curves represent the GWs detectors limits: the black dashed curve denotes the EPTA limit [106,107,108,109, 154], the green dot-dashed curve denotes the PPTA limit [155], the gray dotted curve denotes the SKA limit [110], the red dotted curve in the middle denotes the TianQin limit [114], the magenta dot-dashed curve shows the Taiji limit [113], the brown dashed curve shows the LISA limit [112], and the gray dashed curve in the right denotes the aLIGO limit [156, 157]

Accompanying the PBHs formation, the large scalar perturbations can induce the secondary gravitational waves. Substituting the parameterization (32) into Eq. (30), we can obtain the energy density of the corresponding SIGWs. According to the lower limits of each band displayed in the right panel of Fig. 2, we choose the parameter values listed in Table 1 to generate SIGWs with peak frequencies around $10^{-9}$ Hz, $10^{-3}$ Hz, and $10^2$ Hz, and the results are shown in Fig. 3. The labels “Gauss” and “TopHat” in Table 1 denote the choices according to the lower limits of the black and red bands in the right panel of Fig. 2, respectively. The parameter $f_p$ is the peak frequency of the SIGW. The solid and dashed lines in Fig. 3 are the energy density of the SIGWs with the parameter value choices labeled as “TopHat” and “Gauss” in Table 1, respectively. The green, red, and black lines denote the SIGWs with peak frequencies around $10^{-9}$ Hz, $10^{-3}$ Hz, and $10^2$ Hz, respectively. The SIGWs with $10^{-9}$ Hz can explain the stochastic common-spectrum process detected by the NANOGrav and other PTA groups recently. In the future, more and more SIGWs with peak frequency around $10^{-9}$ Hz may be detected by PTA groups. The SIGWs with $10^{-3}$ Hz can be detected by the future space-based GWs detectors such as LISA, Taiji, and TianQin. Under the present PBHs DM observational data constraints, the corresponding SIGWs can be detected by both the present PTA and future space-based GW detectors. More information about inflation at small scales will be obtained with more observational data about SIGWs being detected. The SIGWs with peak frequencies around $10^2$ Hz cannot be detected by the aLIGO detector; therefore, the aLIGO detector can tell us little information about the inflation at small scales through SIGWs at present.

Table 1 The parameter values of the parameterization (32) with $\alpha =\beta =0.5$

4.1.1 Constraints from all dark matter

Due to the failure of direct detection of particle dark matter, it is warranted to consider the possibility of PBHs as a DM candidate. There are no constraints on PBHs DM abundance at the two mass windows $10^{-17}$–$10^{-15} M_{\odot }$ and $10^{-14}$–$10^{-12}M_{\odot }$, as displayed in the left panel of Fig. 2; therefore, PBHs with masses locating at these two windows can make up all the dark matter. Combining the parameterization (32) and PBHs mass function (15), we can obtain the constraints on the primordial power spectrum if the PBHs DM make up all the dark matter, and the results are shown in Fig. 4, where the peak scale $k_p$ in parameterization (32) is chosen as $k_p=10^{13} ~\text {Mpc}^{-1}$. The solid lines denote the results with the Gaussian window function, and the dashed lines represent those with the real-space top-hat window function. The required amplitude A of the primordial power spectrum is increasing along with the parameter $\alpha$ and $\beta$. The reason is that the fraction of PBHs in the dark matter is the integration of mass function among the whole range as shown in Eq. (13), so a narrower peak in the primordial power spectrum requires a larger amplitude A to give the same fraction. A narrower peak is from a pair of larger $\alpha$ and $\beta$, so the amplitude A increases along with the parameter $\alpha$ and $\beta$. For the top-hat window function, the smallest value of the required amplitude is $A\approx 3.24\times 10^{-3}$; and for the Gaussian window function, it is $A\approx 8.92\times 10^{-3}$, which is about three times larger than that with the top-hat window function. For the top-hat window function, the largest value of the required amplitude is $A\approx 5.32\times 10^{-3}$; and for the Gaussian window function, it is $A\approx 1.51\times 10^{-2}$, which is also about three times larger than that with the top-hat window function. The largest value of A is around 1.7 times larger than the smallest value for each window function.

Fig. 4

The required of amplitude A to explain all the dark matter. The solid and dashed lines are the results with the Gaussian and top-hat window functions, respectively

For the case where PBHs explain all the dark matter, the corresponding SIGWs are displayed in Fig. 5. The black lines denote the energy density of SIGWs where the Gaussian window function is chosen to calculate the corresponding PBH mass function, and the red lines denote those with the top-hat window function being chosen. The dashed lines are the energy density of the GWs induced from the primordial power spectra with the broadest peak, $\alpha =\beta =0.5$; and the solid lines are from the primordial power spectra with the narrowest peak, $\alpha =\beta =4$. If the PBHs formed from the primordial curvature perturbations can explain all the dark matter, the corresponding SIGWs will be detected by the future space-based GW detectors, and the profile of SIGWs can determine the profile of the peak in the primordial curvature power spectrum. If the future space-based GW detectors do not detect the SIGWs, it indicates that the PBHs can only account for a part of dark matter.

Fig. 5

The convex curves denote the energy density of SIGWs, where the corresponding PBHs can explain all dark matter. The black and red curves represent the situations where the Gaussian window function and real-space top hat window function are chosen to calculate the corresponding PBH mass function, respectively. The dashed and solid lines are from the parameterization (32) with the broadest peak and the narrowest peak, respectively

Fig. 6

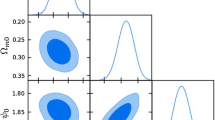
The posteriors on the parameters in parameterization (32) from the first five frequency bins of NANOGrav 12.5 years data set, and the shaded areas denote $1\,\sigma$ and $2\,\sigma$ confidence regions

4.2 Constraints from SIGWs

The scalar-induced gravitational waves generated during the radiation domination are the components of the stochastic background of gravitational waves. The North American Nanohertz Observatory for Gravitational Wave (NANOGrav) Collaboration has published an analysis of the 12.5 years pulsar timing array (PTA) data, where strong evidence of a stochastic process with a common amplitude and a common spectral slope across pulsars was found [115]. The same signal is also detected by other pulsar timing array groups [116, 117]. Although this process lacks quadrupolar spatial correlations, it is worth interpreting as a stochastic GW signal, which the SIGWs can explain with frequencies around $10^{-9}$ Hz [58, 67, 118,119,120].

This paper constrains the power spectrum of the primordial curvature perturbation from the NANOGrav 12.5 years data, assuming that the NANOGrav 12.5 years signals are from SIGWs. We follow the analysis in ref. [158] and focus on the results of the NANOGrav free-spectrum analysis, where the signal in each frequency bin is fitted separately. Only the posteriors on the first five frequency bins are used due to the most constraining measurements coming at the lowest frequencies [115, 158]. The public data products are from https://data.nanograv.org. The log-likelihood function is obtained by evaluating the energy density of the SIGWs at the five values $f_i$ and summing the log probability density functions of the five independent kernel density estimates at these values [158]. The posteriors on the parameters of parameterization (32) are shown in Fig. 6, where the sampling is performed with the DYNESTY [159] implementation of the nested sampling algorithm [160]; and the marginalized posterior distributions lead to the following mean values and one-sigma confidence intervals,

$$\begin{aligned} \log _{10}A= & {} -1.95_{-0.15}^{+0.37},\quad \log _{10}k=6.04_{-0.66}^{+0.29}, \end{aligned}$$

(33)

$$\begin{aligned} \alpha= & {} 1.96_{-1.08}^{+1.32},\quad \beta =1.04_{-0.38}^{+0.89}. \end{aligned}$$

(34)

By choosing these best parameter values (33) and (34), the power spectrum with the broken-power-law-parameterization (32) is displayed in the right panel of Fig. 2 and denoted by the black line. The corresponding mass function of PBHs calculated with peak theory and the Gaussian window function are shown in the left panel of Fig. 2 and represented by the black line, which are under the PBHs observational constraints. For the peak theory with the top-hat window function, the mass function at the peak is about $f_\text {PBH}(M_\text {PBH}^\text {peak})\sim 10^{4}$, exceeding the PBHs observational constraints, which can also be understood from the right panel of Fig. 2, so we don’t display them in the left panel of Fig. 2.

In Fig. 7, we take together the posteriors distribution from NANOGrav 12.5 years data and other constraints on the primordial power spectrum. The blue regions are the $1\,\sigma$ and $2\,\sigma$ posteriors on the amplitude and scale, respectively. The orange and cyan regions are excluded by the BBN [152] and EPTA [151]. The black and red bands are the upper limits constrained from the PBHs observational data, as displayed in the right panel of Fig. 2.

Fig. 7

The constraints on the primordial curvature power spectrum. The orange and cyan regions are excluded by BBN [152] and EPTA [151]. The blue area is the allowed region to explain the NANOGrav 12.5 years data sets; the two contours denote the $1\sigma$ and $2\sigma$ confidence regions, respectively. The black and red bands are the upper limits constrained from the PBHs observational data, as displayed in the right panel of Fig. 2

5 Conclusion

The primordial black holes and scalar-induced gravitational waves can be produced from the large scalar perturbations in the early Universe. They can tell us information about the small-scale primordial curvature perturbation generated in the inflation. To form enough PBHs DM and induce detectable GWs, the amplitude of the primordial curvature power spectrum should be around ${\mathscr {P}}_\zeta \sim {\mathscr {O}}(0.01)$, which is about seven orders of magnitude larger than the constraints from CMB observational data at large scales. Generally, the enhanced region of the primordial power spectrum can be parameterized as the power law form. For the whole primordial power spectrum, we use the broken power law form to parameterize their profile, where the parameterization form is ${\mathscr {P}}_\zeta (k)=A(\alpha +\beta )/[\beta (k/k_p)^{-\alpha }+\alpha (k/k_p)^\beta ]+A_*(k/k_*)^{n_{s*}-1}$ with $k_*=0.05\text {Mpc}^{-1}$, $n_{s*}=0.965$, and $A_*=2.1\times 10^{-9}$. The primordial curvature power spectrum with the broken power form can be produced from many inflation models, such as nonminimal derivative coupling inflation, scalar–tensor inflation, Gauss–Bonnet inflation, and K/G inflation.

The fraction of PBHs in the dark matter is calculated by the peak theory, where both Gaussian and top-hat window functions are considered. With the help of the fraction equation, we obtain the constraints on the primordial curvature power spectrum from the present primary PBHs DM observational data. The results are displayed in the right panel of Fig. 2. For the choice of the top-hat window function, the constraints on the primordial curvature power spectrum from PBHs DM are more robust than those from BBN and EPTA. For the Gaussian window function, the constraints from PBHs DM are weaker than those from EPTA. The uncertainty of the constraints caused by the choice of the window function is more significant than that by the profile of the peak in the primordial curvature power spectrum; we should take care of the choice of the window function. Under the constraints of PBHs DM, the corresponding SIGWs with frequencies around $10^{-9}$ Hz, $10^{-3}$ Hz, and $10^2$ Hz are shown in Fig. 3. The SIGWs with frequencies around $10^{-9}$ Hz and $10^{-3}$ Hz can be detected by PTA and the future space-based detectors, respectively. The SIGWs with frequencies around $10^2$ Hz cannot be detected presently, and we will get little information about the early Universe from them. The required amplitudes of the primordial curvature power spectrum to explain all the dark matter are displayed in Fig. 4, and they depend on the shape of the spectrum peak and window function. For the top hat window function, to explain all the dark matter, the amplitude of the primordial power spectrum with the narrowest peak requires $A\approx 5.32\times 10^{-3}$ and $A\approx 3.24\times 10^{-2}$ with the broadest peak; for the Gaussian window function, it requires $A\approx 1.51 \times 10^{-2}$ with the narrowest peak and $A\approx 8.92\times 10^{-3}$ with the broadest peak. The largest required amplitude is about 1.7 times larger than the smallest for each window function. The corresponding SIGWs can be detected by future space-based detectors, and the SIGWs can be used to verify whether PBHs can explain all the dark matter.

The constraints on the primordial curvature power spectrum from NANOGrav 12.5 years data sets are displayed in Fig. 6 by assuming the NANOGrav signals are from SIGWs. The mean values and one-sigma confidence intervals of the broken power law parameterization of primordial curvature power spectrum obtained from the first five frequency bins of NANOGrav 12.5 years data sets are $\log _{10}A=-1.95_{-0.15}^{+0.37}$, $\log _{10}k=6.04_{-0.66}^{+0.29}$, $\alpha =1.96_{-1.08}^{+1.32}$, and $\beta =1.04_{-0.38}^{+0.89}$. The allowed region of the curvature power spectrum from the NANOGrav 12.5 years data sets, the upper limits from the PBH observational data, and the excluded regions from BBN and EPTA are taken together in Fig. 7.

In conclusion, we give the constraints on the primordial curvature perturbations from the present primary PBHs observational data, where the fraction of PBHs in dark matter is calculated by the peak theory and the primordial curvature spectrum is parameterized by the broken power law form. The region of the primordial curvature spectrum to explain the NANOGrav 12.5 years data sets is also obtained by assuming the NANOGrav signals are from SIGWs.