1 Introduction

The strong interaction is one of the fundamental forces of nature, which guides the dynamics of quarks and gluons. The theory that describes the dynamics of the strong interaction, quarks and gluons, is quantum chromodynamics (QCD). It also explains the whole nuclear physics, from the hadronic mass spectrum to the synthesis of the heavy elements in the cosmos. The quark model [1, 2] classifies hadrons into conventional mesons (\(q\bar{q}\)) and baryons (qqq or \(\overline{qqq}\)). Furthermore, it advocates the existence of exotic hadrons like tetraquarks (\(qq\overline{qq}\)) and pentaquarks (\(qqq\overline{qq}\)). These newly discovered particles are clearly exotic states. Exotic states provide an unrivaled environment to peruse the confinement mechanism and the strong interaction [3]. The posibility of existence of exotic multiquark hadrons was proposed at the beginning of the quark model, although the lack of convincing experimantal evidence for such multiquark states made their investigation of unusual interest. To date, more and more tetraquark and pentaquark states have been discovered and confirmed by various experiments. The first tetraquark (TQ) candidate was the particle X(3872), discovered in 2003 by the Belle collaboration [4], and a number of other candidates followed, referred to as “X,” “Y,” and “Z” [5]. The \(Z_c^{+}\)(3900) discovered by BESIII in 2013 clearly cannot be explained by a conventional heavy quarkonium state [6]. In 2020, LHCb reported a narrow X(6900) structure in the di-\(J/\Psi \) channel [7]. The structure could be interpreted as a tetraquark with four charm quarks, \(T_{cc\bar{c}\bar{c}}\). Amplification near the di-\(J/\Psi \) mass threshold was also observed in the LHCb data, which may be due to final-state rescattering, the interference of two resonances, or reflections associated with genuine resonances [8]. Experimental data on mesons with hidden-charm and exotic properties were published in Table 1, [9,10,11,12,13]. The XYZ-naming scheme, where X are neutral exotic charmonium-like states observed in hadronic decays, Y are neutral exotic charmonium-like states with\(J^{PC} = 1^{--}\) observed in \(e^- e^+\) collisions, and Z are charged (isospin triplet \(I=1\)) charmonium-like states [14]. The experimentally determined quantum numbers \(J^{PC}\), the masses M, the observational channels, and the names of the experiments in which they were first observed are given in Table 1 [11,12,13]. In this work, we consider only diquarks and antidiquarks in the ground state.

Table 1 Experimental data on hidden-charm exotic mesons
Full size table

The manuscript is structured as follows. In Sect. 2, we introduce the spinless Betht-Salpeter equation to achieve the two-body equation. The QCD-motivated Coulomb-plus-linear potential, also known as Cornell potential, it has received a great deal of attention in particle physics, more precisely in the context of meson spectroscopy in Sect. 3. We calculated the mass od diquarks in Sect. 4. In Sect. 5, we invoke using the spinless Bethe–Salpeter equation for calculating of the energy eigenvalue and mass spectrum, the tetraquark masses then becomes the sum of diquar-anidiquark masses and the energy of perturbed system. Finally, in summary we give a preliminary study about the mass spectra of heavy tetraquarks in Sect. 6.

2 The spinless relativistic Bethe–Salpeter

The relativistic wave-Salpeter equation [15,16,17,18] is established by considering the kinetic energies of the constituents and the interaction potential. The spinless Salpeter (SS) for the case of two particles with unequal masses \(m_1\) and \(m_2\) interacting via a spherically symmetric potential V(r) in the centre-of-mass system of the two particles is given by

$$\begin{aligned} \left[ \sum _{\begin{array}{c} i=1,2 \end{array} }\sqrt{-\Delta _{N}+m_i^2}+V(r) - M \right] \chi (\textbf{r})=0 , \end{aligned}$$
(1)

where the kinetic terms involving the operation \(\sqrt{-\Delta _{N}+m_i^2}\) are non-local operators and \(\chi (\textbf{r})=Y_{l,m}(\theta ,\phi )R_{n,l}(\textbf{r})\) denotes the Salpeter wave function. For heavy quarks, the kinetic energy operators in Eq. (1) can be approximated (cf. e.g. Jaczko and Durand in Refs. [19,20,21,22]), as

$$\begin{aligned} \sum _{\begin{array}{c} i=1,2 \end{array}}\sqrt{-\Delta +m_i^2}=m_1+m_2-\frac{\Delta _N}{2\mu }-\frac{\Delta _N^2}{8\eta ^3}+\cdots , \end{aligned}$$
(2)

where \(\mu =\tfrac{m_1m_2}{m_1+m_2}\) denotes the reduced mass and \(\eta =\mu (\tfrac{m_1m_2}{m_1m_2 - 3\mu ^2})^{1/3}\) is a useful mass parameter. This equation of type SS retains its relativistic kinematics and is suitable for describing the spin-averaged spectrum of two bound particles of masses \(m_1\) and \(m_2\) and the total binding mass \(M_{nl}\). The Hamiltonian containing the relativistic corrections up to order \(\tfrac{v^2}{c^2}\) is called the generalized Breit–Fermi Hamiltonian (see, Lucha et al. from Refs. [23,24,25]). Therefore, the spinless Salpeter equation (in units \(\hbar =c=1\)) [15,16,17,18] can be written as

$$\begin{aligned} \left[ - \frac{\Delta _N}{2\mu }-\frac{\Delta _N^2}{8\eta ^3}+V(r)\right] R_{n,l}(\textbf{r}) = E_{n,l}R_{n,l}(\textbf{r}) , \end{aligned}$$
(3)

where \(E_{n,l}=M_{n,l} - m_1- m_2\) refers to the Salpeter binding energy with \(M_{n,l}\) is the semi-relativistic-bound-state masses of the tetraquark and \(\Delta _N = \nabla _N^2\)Footnote 1. To obtain a Schrödinger-like equation, the perturbed term in Eq. (3) is treated using the reduced Schrödinger equation [27]

$$\begin{aligned} p^4 = 4\mu ^2[ E_{n,l} - V(r)]^2 , \end{aligned}$$
(4)

with \(p^4 = \Delta _N^2\), and consequently, one would reduce Eq. (3) to the Schrödinger form [15,16,17,18]

$$\begin{aligned}{} & {} \left[ -\frac{\Delta _N}{2\mu }\!-\!\frac{\mu ^2}{2\eta ^3}[E_{n,l}^2 + V^2(r) \!- \!2E_{n,l}V(r)] \!+\! V(r)\right] R_{n,l}(\textbf{r})\nonumber \\{} & {} \quad = E_{n,l}R_{n,l}(\textbf{r}) \end{aligned}$$
(5)

Furthermore, the N-dimensional space operator in spherical polar coordinates is

$$\begin{aligned} \Delta _N = \frac{\partial ^2}{\partial r^2} + \frac{N-1}{r}\frac{\partial }{\partial r} - \frac{L_{N-1}^2}{r^2}, \end{aligned}$$
(6)

with \(L_{N-1}^2 =l(l + N - 2) \). After applying the following transformation

$$\begin{aligned} R_{n,l}(r) = \frac{u_{n,l}(r)}{r^{(N-1)/2}} , \end{aligned}$$
(7)

l is the angular momentum number, for \(N=3\) we obtain [15,16,17,18]

$$\begin{aligned} \Delta = \frac{\partial ^2}{\partial r^2} - \frac{l(l+1)}{r^2} , \end{aligned}$$
(8)

and

$$\begin{aligned} \Delta ^2{} & {} = \frac{\partial ^4}{\partial r^4} - \frac{2l(l+1)}{r^2}\frac{\partial ^2}{\partial r^2}\nonumber \\{} & {} \quad + \frac{4l(l+1)}{r^3}\frac{\partial }{\partial r}+ \frac{l(l+1)[l^2+l-6]}{r^4}. \end{aligned}$$
(9)

Using Eqs. (8) and (9), and after a lengthy but straightforward manipulation, we can write Eq. (5) in a simpler, clearer and less ambiguous form than for 3D space

$$\begin{aligned} \left[ -\frac{1}{2\mu }\frac{d^2}{dr^2} + \frac{l(l+1)\hbar ^2}{2\mu r^2} + W_{n,l}(r) - \frac{W_{n,l}(r)^2}{2\widetilde{m}}\right] u_{n,l}(r) = 0 , \end{aligned}$$
(10)

with

$$\begin{aligned} W_{n,l}(r) = V(r) - E_{n,l}, \end{aligned}$$
(11)

and the effective mass

$$\begin{aligned} \widetilde{m} = \frac{\eta ^3}{\mu ^2} = \frac{(m_1 m_2 \mu )}{(m_1 m_2 - 3\mu ^2)}. \end{aligned}$$
(12)

It is worth noting that Eq. (10) is in complete agreement with the expansion formula of Durand in Refs. [19,20,21,22]. The perturbation term, \(W_{n,l}(r)^2\); that is, \((\frac{v^2}{c^2})\) term in Eq. (10) is significant only when it is small (i.e., \(W_{n,l}(r)/\widetilde{m}\ll 1\)). This condition is confirmed by the confining potentials used to describe heavy−quark systems, except near the colour−Coulomb singularity at the origin, and for \(r\rightarrow \infty \) (i.e. the wave function vanishes at 0 and \(\infty \)). However, on average it is always satisfied, as stated by Durand [19,20,21,22].

3 Cornell potential

The static potential we consider is the Cornell potential, which is one of the earliest QCD-motivated Coulomb-plus-linear potentials

$$\begin{aligned} V(r) = \frac{a}{r}+br, \end{aligned}$$
(13)

where

$$\begin{aligned} a=\kappa _s\alpha _s=-\frac{4}{3}\alpha _s \end{aligned}$$

for \((qq-q\bar{q})\) system and

$$\begin{aligned} a=\kappa _s\alpha _s=-\frac{2}{3}\alpha _s \end{aligned}$$

for (qq and \(\bar{q}\bar{q}\)) system. Where \(\alpha _s\) is the QCD coupling constant. b is constant and r is the hyperradius \((0< r < 1 fm)\) [28]. Then, in order to respect the Pauli principle (the two quarks of the same flavor are identical fermions), the diquark total spin S must be 1. To calculate diquark mass, we took the color factor as \(-\frac{2}{3}\) and for calculating the tetraquark mass, we took the color factor as \(-\frac{4}{3}\). In other words, substituting the color factor \(\kappa _s=-\frac{4}{3}\) (for quark–antiquark system in color singlet state) with \(\kappa _s=-\frac{2}{3}\) (quark–quark system in the anti triplet color state) is equivalent of introducing a factor of \(\frac{1}{2}\) in the Coulomb part of the Cornell potential for the conventional quark–antiquark system. It has received considerable attention in particle physics, more specifically in the context of meson spectroscopy, where it is used to describe systems of bound quark and antiquark states [29]. The potential includes the Coulomb interaction of quarks over short distances, known from perturbation-theoretic quantum chromodynamics (QCD), and quark confinement over long distances, known from lattice QCD, via the linear term in simple form. The Coulombic term alone is not sufficient, as it would allow free quarks to ionize out of the system. All results presented in this paper are based on the Cornell potential, i.e.. In the first step, by substituting the Cornell potential Eq. (13) into Eq. (10). We obtain

$$\begin{aligned}{} & {} \left[ - \frac{1}{2\mu } + \left( \frac{l(l+1)}{2\mu } - \frac{b^2}{2\widetilde{m}}\right) \frac{1}{r^2} - \frac{a^2}{2\widetilde{m}}r^2 \right. \nonumber \\{} & {} \quad \left. + \left( a + \frac{E_{n,l}a}{\widetilde{m}}\right) r + \left( \frac{E_{n,l}b}{\widetilde{m}} - b\right) \frac{1}{r}\right] u_{n,l}(r) = 0. \end{aligned}$$
(14)

where a and b in Eq. (14) are the Cornell potential coefficients. Now we introduce an ansatz of the form Refs. [30]

$$\begin{aligned} u_{n,l}(r) = h_n(r)\exp {(s_l(r))}, \end{aligned}$$
(15)
$$\begin{aligned} h_n(r) = {\left\{ \begin{array}{ll} 1, &{}if \ n=0 , \\ \prod _{i=1}^{n} (r- \alpha _i^n), &{} if \ n \ge 1 . \end{array}\right. } \end{aligned}$$
(16)

The exponential term is

$$\begin{aligned} s(r) = \alpha r^2 + \beta r + \gamma \ln (r), \end{aligned}$$
(17)

we have

$$\begin{aligned} \begin{aligned} 4\alpha ^{2}&= - \frac{\mu a^2}{{\widetilde{m}}\hbar ^{2}},\\ \gamma ^2 - \gamma&= L(L+1) - \frac{\mu b^2}{{\widetilde{m}}\hbar ^2},\\ 4 \alpha \beta&= \frac{2 \mu a}{\hbar ^2} + \frac{2\mu Ea}{\widetilde{m}\hbar ^2},\\ 2 \beta \gamma&= \frac{2 \mu }{\hbar ^2}\left( \frac{Eb}{\widetilde{m}}-b\right) ,\\ \beta ^2 + 4\alpha \gamma + 2\alpha&= \frac{2\mu }{\hbar ^2}\left( \frac{ab}{\widetilde{m}} - E - \frac{E^2}{2\widetilde{m}}\right) . \end{aligned} \end{aligned}$$
(18)

The parameters of the given potential can be obtained by Eq. (18)\((\hbar = c =1)\)

$$\begin{aligned} \begin{aligned} \alpha&= \frac{a}{2} \sqrt{\frac{\mu }{\widetilde{m}}},\\ \beta&= \frac{\widetilde{m}}{2\sqrt{\frac{\mu }{\widetilde{m}}}+ \frac{\widetilde{m}}{2 \mu b}},\\ \gamma&= \frac{1}{2}. \end{aligned} \end{aligned}$$
(19)

where the \(\alpha , \beta \) and \(\gamma \) coefficients are obtained according to \(\mu \) and \(\widetilde{m}\) parameters and \(\gamma =\frac{1}{2}\) for \(l=0\). We will get Eq. (21) by having of the Cornell potential coefficients, \(\mu \) and \(\widetilde{m}\). Eventually, we calculate the energy-eigenvalue equation of the system

$$\begin{aligned} E_{n,l} = - \widetilde{m} + \sqrt{\widetilde{m}^2 - f}, \end{aligned}$$
(20)

where f is

$$\begin{aligned} f = - 2ab + 2a\sqrt{\tfrac{\widetilde{m}}{\mu }} + \frac{\widetilde{m}}{\mu }\left( \frac{\widetilde{m}}{2\sqrt{\tfrac{\widetilde{m}}{\mu }} + \tfrac{\widetilde{m}}{2\mu b}}\right) ^2. \end{aligned}$$
(21)

4 Mass of diquark–antidiquark

The contribution of spin-dependent potentials, a spin-spin \(V_{SS}(r)\), spin-orbit \(V_{LS}(r)\), and tensor \(V_{T}(r)\), that makes significant contributions particularly for excited states, is necessary to better understand the splitting between orbital and radial excitations of different combinations of quantum numbers of tetraquarks. All three spin-dependent terms are driven by the Breit–Fermi Hamiltonian for one-gluon exchange [23,24,25, 31] and yields

$$\begin{aligned} V_{SS}(r)= & {} C_{SS}(r)S_1\cdot S_2, \end{aligned}$$
(22)
$$\begin{aligned} V_{LS}(r)= & {} C_{LS}(r)L\cdot S, \end{aligned}$$
(23)
$$\begin{aligned} V_{T}(r)= & {} C_{T}(r)S_{12}, \end{aligned}$$
(24)

The matrix element \(S_1\cdot S_2\) acts on the wave function, and generates a constant factor, but the \(V_{SS}(r)\) remains a function of only r, and the expectation values of \(\left<S_1\cdot S_2\right>\) are available through a quantum-mechanical formula [32].

$$\begin{aligned} \left<S_1\cdot S_2\right>=\left<\frac{1}{2}(S^2-S_1^2-S_2^2)\right> \end{aligned}$$
(25)

where, \(S_1\) and \(S_2\) denote the spins of constituent quarks for quarkonium and diquarks for tetraquarks, respectively. \(C_{SS}(r)\) may be defined as follows

$$\begin{aligned} C_{SS}(r)=\frac{2}{3m^2}\nabla ^2V_V(r)=-\frac{8\kappa _s\alpha _s\pi }{3m^2}\delta ^3(r), \end{aligned}$$
(26)

A fair agreement may be achieved by adding spin-spin interactions in a zero-order potentials using the Schrödinger equation in heavy quarkonium spectroscopy by including the spin-spin interaction using the artefact providing a new parameter \(\sigma \) instead of the Dirac delta. So now \(V_{SS}(r)\) can be redefined as

$$\begin{aligned} V_{SS}(r)=-\frac{8\kappa _s\alpha _s\pi }{3m^2}\left( \frac{\sigma }{\sqrt{\pi }}\right) ^3\exp ^{-\sigma ^2(r)^2}S_1\cdot S_2, \end{aligned}$$
(27)

The expectation value of operator \(\left<L\cdot S\right>\) is mainly dependent on the total angular momentum J which is calculated using the formula \(J=L+S\),

$$\begin{aligned} \left<L\cdot S\right>=\left<\frac{1}{2}(J^2-L^2-S^2)\right> \end{aligned}$$
(28)

where, L denotes the total orbital angular momentum of quarks and diquarks, respectively, in the case of quarkonium and tetraquark. The following equation may be used to compute \(C_{LS}(r)\),

$$\begin{aligned} C_{LS}(r)=-\frac{3\kappa _s\alpha _s\pi }{2m^2}\frac{1}{(r)^2}-\frac{c}{2m^2}\frac{1}{(r)} \end{aligned}$$
(29)

The second component in the spin-orbit interaction is called Thomas Precession, and it is proportional to the scalar term. It is thought that confining interaction originates from the Lorentz scalar structure. In higher excited states, the contribution of the spin-tensor becomes quite important, which requires a little algebra and may be calculated by

$$\begin{aligned} V_{T}(r)=C_{T}(r) \left( \frac{(S_1\cdot (r))(S_2\cdot (r))}{(r)^2}-\frac{1}{3}(S_1\cdot S_2)\right) \end{aligned}$$
(30)

where

$$\begin{aligned} C_{T}(r)=-\frac{12\kappa _s\alpha _s\pi }{4m^2}\frac{1}{(r)^3} \end{aligned}$$
(31)

The results of \((S_1\cdot S_2)\) may be obtained by solving the diagonal matrix elements for the spin \(\frac{1}{2}\) and spin 1 particles, as detailed in the following references [33]. To solve the tensor interaction, the simpler formulation may be used.

$$\begin{aligned} S_{12}=12\left( \frac{(S_1\cdot (r))(S_2\cdot (r))}{(r)^2}-\frac{1}{3}(S_1\cdot S_2)\right) \end{aligned}$$
(32)

and which can be redefined as

$$\begin{aligned} S_{12}=4[3(S_1.\hat{(r)})(S_2.\hat{(r)})-(S_1\cdot S_2)] \end{aligned}$$
(33)

Pauli matrices and spherical harmonics with their corresponding eigenvalues may be used to achieve the results of the \(S_{12}\) term. The following conclusions are valid for bottomonium and diquarks [37]

$$\begin{aligned} \begin{aligned} \left<S_{12}\right>_{\frac{1}{2}\otimes \frac{1}{2}\rightarrow S=1,l\ne 0}&=\left\{ \begin{array}{lr} -\frac{2l}{2l+3} \ {} &{}for \ J=l+1,\\ \\ -\frac{2(l+1)}{(2l-1)} \ {} &{} for\ J=l-1,\\ \\ 2 \ {} &{}for\ J=l, \end{array} \right. \end{aligned} \end{aligned}$$
(34)

when \(l=0\) and \(S=0\) the \(\left<S_{12}\right>\) always vanishes, but it yields a non-zero value for exited states in mesons

$$\begin{aligned} \begin{aligned} \left<S_{12}\right>&=\left\{ \begin{array}{lr} -\frac{2}{5} \ for \ {} &{}J=2,\\ \\ +2 \ for\ {} &{}J=l,\\ \\ -4 \ for\ &{}J=0, \end{array} \right. \end{aligned} \end{aligned}$$
(35)

these value are valid only for bottomonium and diquarks that are specifically spin-half particles, but in the case of tetraquarks when spin-1 diquarks are involved, it needs a laborious algebra, which is not discussed in depth here, rather one can refer Refs. [37] for detailed discussion. When the two-body problem is solved to obtain the masses of the tetraquarks, the interaction between the two (anti) quarks inside the (anti) diquark is identical; because (anti) diquarks are only considered in the S-wave state, only the spin-spin interaction is relevant; the spin-orbit and tensor are both identically zero. We have obtained the mass-spectra of diquarks.

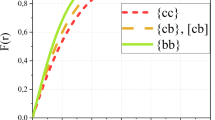
$$\begin{aligned} M_{diquark}= M_{q_1.} + M_{q_2.} + E_{n,l}+\left\langle V_{SS}(r)\right\rangle . \end{aligned}$$
(36)

In the present work there are four fitting parameters \(\alpha _s, b,c, \sigma \). The existence parameters [28, 36] are \(0.5,0.14\ GeV^2,0.19 \ GeV^2,\) and \(0.4\ GeV\) respectively. To obtain the mass-spectra of diquarks and to obtain the mass-spectra of diquarks and tetraquarks. The (qq) diquark, which is made of quarks of various flavours, may have spins S = 0,1 (scalar [qq], axial vector \(\{qq\}\) diquarks), while the \(\{qq\}\) diquark, which is composed of quarks of the same flavour, can only have spin \(S=1\). Because of the stronger attraction owing to the spin-spin interaction, the scalar S diquark is frequently referred to as a “good” diquark, while the heavier axial vector A diquark is referred to as a “bad” diquark [34].

Table 2 The masses of conventional diquarks are calculated in units of MeV. S and A denote scalar and axial vector diquarks which are antisymmetric \([\cdots ]\) and symmetric \(\{\cdots \}\) in flavour, respectively. \(\delta \) is the percentage difference between our results and [38]
Full size table
Table 3 Masses M of the neutral heavy diquark (QQ)-antidiquark \((\bar{Q}\bar{Q})\) states are calculated by us. T is the threshold for decays into two heavy-\((Q\bar{Q})\) mesons and the percentage difference is \(\Delta =(M-T)100\) and \(\delta _1\) and \(\delta _2\) are the percentage difference between our results and Refs. [41, 42] respectively. D.C., is the diquark content and \(E_b\) is the binding energy. All values are given in MeV
Full size table
Table 4 Comparison of theoretical predictions for the masses of the ground states of the heavy tetraquarks. \(E_b\) is the binding energy. \(\delta _1\) and \( \delta _2 \) are the percentage difference between our results and Refs. [40, 54]. \(\delta _3\) is the percentage difference between our results and Refs. [28, 40]. T is the lowest threshold for decays into two mesons and \(\Delta =(M-T)100\) is the percentage difference between our results and T [40](in MeV)
Full size table

5 Heavy tetraquark masses

This work encourages us to further investigate the heavy tetraquarks. We use the spinless Bethe–Salpeter equation to calculate the energy-eigenvalue (Eq. (20)) and mass spectrum (Eq. (36)). For this purpose, we calculate the masses of the heavy tetraquarks, which are considered as bound states of diquark and antidiquark. For the potential of the diquark–antidiquark interaction, we obtain the Cornell potential. The tetraquark masses are then the sum of the diquark–antidiquark masses and the energy of the perturbed system [35].

$$\begin{aligned} M_{tetraquark}= M_{diqu.} + M_{anti-diqu.} + E_{n,l}+\left< V_{SS}(r)\right>. \end{aligned}$$
(37)

In order to properly calculate the spin-dependent corrections we need to remember that the diquarks have spin 1. Then, for the coupling of a spin 1 diquark and spin 1 antidiquark, we will have the total tetraquark spin \(S_T=0,1,2\). The spin contribution is added to the Eq. (35) as a perturbation term. The calculated masses M of the ground states [39] of the neutral \(QQ\bar{Q}\bar{Q}\) tetraquarks composed of the heavy diquark \(QQ,=b,c\), and heavy antidiquark \(\bar{Q}\bar{Q}\) are given in Table 3 estimate the masses of tetraquark states, so we need some diquarks masses, These conventional diquarks are listed in Table 2.

As we know in QQ heavy diquark with two identical flavors, the spin can be 0 or 1, considering that \(L+S \) must be odd, in the ground state of \( L=0 \), the diquark spin must be equal to 1. That is, we have the axial vector diquark. For this reason, in Table 2, for heavy diquarks \( \lbrace Q,Q\rbrace \), we only have the A state.

The double and four heavy tetraquarks are considered as the bound system of the heavy(light) diquark and the light(heavy) antidiquark. It is important to study the possible stability of tetraquarks since they are explicitly exotic states with a heavy flavour number of 1, 2 or larger. Thus, their observation would be a direct proof for the existence of the multiquark states. Estimates of the production rates of such tetraquarks indicate that they could be produced and detected in present and future facilities. We calculated the masses M of the ground states (1 S) tetraquarks with open charm and bottom composed of the heavy diquark, containing two heavy quarks and the light antidiquark.

Tables 3 and 4 lists the calculated masses M of tetraquarks consisting of a diquark and an antidiquark. It is important to note that the comparison of the masses of heavy tetraquarks in Tables 3 and 4, gives the values of the lowest thresholds T for decays into two corresponding heavy-light mesons calculated using the measured masses of these mesons [36]. We also show the values of \(\Delta = M_{tetra}-M_{threshold}\), where \(M_{tetra}\) is the tetraquark mass and \(M_{threshold}\) is the mass of its lowest meson-meson threshold. A negative \(\Delta \) means that the tetraquark lies below the threshold of the fall-apart decay into two mesons and thus should be a narrow state. Besides that a state with small positive \(\Delta \) value could also be observed as a resonance since its decay rate will be suppressed by the phase space. All other states with large positive \(\Delta \) values are expected to be broad and difficult to observe in the experiments. The results are presented in Tables 3 and 4, we considered \(\Delta \) in these tables as the percentage difference. For cc and bb because the two quark flavors in diquark are the same, so only axial vector diquark exists, then the ground tetraquark is composed of two axial vector diquark (AA). Also, in tetraquarks \(cc\bar{u}\bar{d}\) and \(bb\bar{u}\bar{d}\) due to the fact that the heavy diquark spin is 1 (A state), we do not have the SS state, so we have the \(A\bar{S}\) state.

6 Summary

In summary, we present a preliminary study of the mass spectra of heavy tetraquarks. Despite the drawback of insufficient experimental data, these studies have become a topic of interest in recent years, with calculations yielding satisfactory results as more and more data are collected. In this work, we have calculated the masses of the ground states of tetraquarks with two and four heavy quarks assuming the diquark–antidiquark structure. Such an approximation allowed us to reduce the very complicated four-body relativistic problem to the solution of much simpler two-body relativistic problems. We then turn to calculating the energy-eigenvalues for tetraquarks via the Bethe–Salpeter equation, using the Cornell potential. We then determine the masses of these particles. These values are in remarkable agreement with previous measurements, both experimental and theoretical. We sincerely hope that our calculations will motivate others to become more involved in this subject and expect that further experimental information may reveal more features of exotic particles.