Muon and electron $(g-2)$ anomalies with non-holomorphic interactions in MSSM

Abstract

The recent Fermilab muon $g-2$ result and the same for electron due to fine-structure constant measurement through ${}^{133}\textrm{Cs}$ matter-wave interferometry are probed in relation to MSSM with non-holomorphic (NH) trilinear soft SUSY breaking terms, referred to as NHSSM. Supersymmetric contributions to charged lepton $(g-2)_l$ can be enhanced via the new trilinear terms involving a wrong Higgs coupling with left and right-handed scalars. Bino-slepton loop is used to enhance the SUSY contribution to $g-2$ where wino mass stays at 1.5 TeV and the left and right slepton mass parameters for the first two generations are considered to be the same. Unlike many MSSM-based analyses completed before, the model does not require a light electroweakino, or light sleptons, or unequal left and right slepton masses, or a very large higgsino mass parameter. In absence of popular UV complete models, we treat the NH terms at par with MSSM soft terms, in a model independent framework of Minimal Effective Supersymmetry. The first part of the analysis involves the study of $(g-2)_\mu$ constraint along with the limits from Higgs mass, B-physics, collider data, direct detection of dark matter (DM), while focusing on a higgsino DM which is underabundant in nature. We then impose the constraint from electron $g-2$ where a large Yukawa threshold correction (an outcome of NHSSM) and opposite signs of trilinear NH coefficients associated with $\mu$ and e fields are used to satisfy the dual limits of $\Delta {a_\mu }$ and $\Delta {a_e}$ (where the latter comes with negative sign). Varying Yukawa threshold corrections further provide the necessary flavor-dependent enhancement of $\Delta {a_e}/m_e^2$ compared to that of $\Delta {a_\mu }/m_\mu ^2$. A larger Yukawa threshold correction through $A^\prime _e$ for $y_e$ also takes away the direct proportionality of $a_e$ with respect to $\tan \beta$. With a finite intercept, $a_e$ becomes only an increasing function of $\tan \beta$. We identified the available parameter space in the two cases while also satisfying the ATLAS data from slepton pair production searches in the plane of slepton mass parameter and the mass of the lightest neutralino.

1 Introduction

The discovery of the Higgs boson [1, 2] at the Large Hadron Collider (LHC) almost a decade ago gave the Standard Model (SM) of particle physics [3] a strong foundation. However, SM has its limitations both in the theoretical as well as in the observational sides. The gauge hierarchy problem, matter-antimatter asymmetry, no candidate for dark matter [4, 5] are to name a few in this regard. This demands the existence of a Beyond the Standard Model (BSM) physics. Low energy Supersymmetry (SUSY) [6,7,8,9,10,11,12,13,14,15] is especially attractive in this context since it can address the gauge hierarchy problem associated with the Standard Model (SM) and also it is able to provide with particle dark matter candidates. Additionally, we must not forget that the Higgs boson is found to have a mass of 125 GeV, which is well below the predicted upper limit for an SM-like Higgs particle of the Minimal Supersymmetric Standard Model (MSSM) [9,10,11,12,13,14,15]. Thus, over the past decades, SUSY, with its strong theoretical appeal and its ability to influence a variety of observables of phenomenological interest, continues to remain as the most attractive candidate for a BSM physics.

Undoubtedly, a BSM physics demands nothing less than direct observations of new particles at the LHC. This will then lead us to the possible new symmetries and interactions present in nature. However, even after a decade of running of the LHC, we are yet to see a cherished new particle. We may as well need to accept the fact that BSM particles could perhaps be staying quite far from our experimental reach. Keeping hope for a collider discovery, we must at the same time continue to look for possible indirect signatures of SUSY. This may come from flavor physics, electroweak physics precision tests and dark matter. Concerning the above, we remember that the anomalous magnetic moment of muon, $a_\mu = \frac{1}{2} (g-2)_\mu$, stands out prominently over the past two decades showing some degree of disagreement (over 2 to 3$\sigma$) of the experimental result as obtained in Brookhaven [16] with that of SM evaluations performed at different times. The hadronic vacuum polarization part of the SM result has a large uncertainty, particularly the lowest order part of the same that requires analysis in the non-perturbative regime. The non-perturbative aspect may require input from effective field theory like chiral perturbation theory, hadronic models, dispersion relations together with experimental data like $e^+e^- \rightarrow \textrm{hadrons}$, and Lattice Quantum Chromodynamics (LQCD). A comprehensive analysis explaining the break-up of different contributions to the SM result of $a_\mu$ may be seen in Ref. [17].¹ While the recent Fermilab $a_\mu$ data [19, 20] is consistent with the same from Brookhaven, the difference $\Delta a_\mu$ has grown larger. The combined data from Fermilab and Brookhaven show a $4.2 \sigma$ level of discrepancy [20] as given below.

$$\begin{aligned} \Delta a_\mu =a_\mu ^\textrm{exp}- a_\mu ^\textrm{SM}=(251 \pm 59)\times 10^{-11}. \end{aligned}$$

(1)

Interestingly, $\Delta a_\mu$ can be ascribed to $a_\mu ^\textrm{SUSY}$, the SUSY contributions to $a_\mu$ which in turn will help us to constrain the SUSY model parameter space.

With further results to come from the Fermilab in the near future and the data from upcoming experiment JPARC [21], muon $g-2$ can shed light on various BSM physics models. In this context, we must point out the recent Lattice result [22] for the hadronic vacuum polarization. This has effectively shifted $a^\textrm{SM}_\mu$ to move toward $a^\textrm{exp}_\mu$ rather closely causing tension between the dispersive and LQCD modes of evaluations of the hadronic uncertainty amount within $a^\textrm{SM}_\mu$. We would also like to point out that an agreement between $a_\mu ^\textrm{exp}$ and $a_\mu ^\textrm{SM}$ may invite issues with global electroweak fits to electroweak precision observables. This is because the existing deviation of the above two $a_\mu$ values is related to precision electroweak predictions via the common dependence on hadronic vacuum polarization effects [23,24,25]. In any case, such important issues will be transparent in future, but at this point we will use Eq. (1) for $a_\mu ^\textrm{SUSY}$.

On the top of $(g-2)_\mu$, we would also include the existing deviation for $(g-2)_e$, the anomalous magnetic moment for electron. A smaller but not insignificant discrepancy exists for the electron $g-2$ anomaly arising out of the measurement of the fine-structure constant that used ${}^{133}\textrm{Cs}$ matter-wave interferometry. An approximately $2.5\sigma$ level of discrepancy is given below [26],

$$\begin{aligned} \Delta a_e=a_e^\textrm{exp}- a_e^\textrm{SM}=(-8.8 \pm 3.6)\times 10^{-13}. \end{aligned}$$

(2)

Unlike the above cases of muon and electron anomalies of Eqs. (1) and (2) where they come with opposite signs, a newer measurement of fine-structure constant based on ${}^{87}\textrm{Rb}$ [27] shows a 1.6$\sigma$ deviation in the positive side.

$$\begin{aligned} \Delta {a_e}^{Rb}=a_e^\textrm{exp}- a_e^\textrm{SM}=(4.8 \pm 3.0)\times 10^{-13}. \end{aligned}$$

(3)

In many new physics models with flavor universality, one finds $\frac{m_\mu ^2}{m_e^2}\frac{\Delta a_{e}}{\Delta a_{\mu }} \simeq 1$. This is also true in SUSY.² In contrast to the above, the measurement values referred to in Eqs. (1) and (2) lead to an appreciably larger negative value for the above quantity, namely:

$$\begin{aligned} R_{e,\mu }=\frac{m_\mu ^2}{m_e^2}\frac{\Delta a_{e}}{\Delta a_{\mu }} \simeq -15. \end{aligned}$$

(4)

Thus, using the two constraints simultaneously leads to a rather difficult situation. We note that the right hand side of Eq. (4) is only the central value. Appropriate error estimates of the two magnetic moments may be used for obtaining the combined uncertainty values. On the other hand, use of Eqs. (1) and (3) lead to $R_{e,\mu } \simeq 8$. Clearly, the later case of having simultaneous positive values for the two deviations with also a smaller $R_{e,\mu }$ is easier to accommodate in SUSY analyses. In the absence of a resolution of the $\Delta a_e$ puzzle, we choose to consider the rather difficult ${}^{133}\textrm{Cs}$-based value of Eq. (2).

This will analyze ${(g-2)}_{\mu ,e}$ in the framework of Non-standard soft SUSY breaking terms [28, 29] contrast it with other SUSY-based analyses that also used the ${}^{133}\textrm{Cs}$-based result of Eq. (2). We will also show the result of using the ${}^{87}\textrm{Rb}$ data briefly just for the sake of completeness.

Besides ${(g-2)}_{\mu ,e}$ we will also include dark matter constraints in our analysis. The plan of our work is given below. In Sect. 2 we will describe the Non-holomorphic MSSM (NHSSM) model and its signature on the SUSY spectra. We will also discuss the constraints arising from avoiding charge and color breaking (CCB) minima. Apart from the above, we will also mention the difference of status between the non-holomorphic soft parameters with the ones of regular MSSM soft terms in the context of ultraviolet (UV) completion. In Sect. 3 we will discuss the SUSY contributions to the magnetic moment of charged leptons. The above will also emphasize the role of Yukawa threshold corrections in MSSM that may be important for satisfying Eq. (2). We will then discuss the effect of non-holomorphic trilinear interactions on leptonic magnetic moments ${(g-2)}_l$ and how the trilinear NH terms may provide the necessary threshold effects appropriate for Eq. (2). We will particularly outline the parameter zone that would be consistent with a higgsino dark matter as a multi-component dark matter element with relic density obeying only the upper limit from the PLANCK data. Then we will discuss the combined case of obeying ${(g-2)}_\mu$ and ${(g-2)}_e$ in MSSM and see how NHSSM effects can generate appropriate threshold corrections to $y_e$ and also to some lesser extent to $y_\mu$. We will discuss the essential points of past MSSM-based analyses in contrast to the features of NHSSM. We will see that there is no need to assume a flavor unfriendly choice for slepton masses in NHSSM, neither we do we need to consider any superheavy higgsino state to generate Yukawa threshold corrections. In Sect. 4 we will present the results in two separate parts namely ${(g-2)}_\mu$ with DM and inclusion of ${(g-2)}_e$ for the combined analysis. We will also use LHC constraints from slepton pair-production. Finally, we will conclude in Sect. 6.

2 MSSM with non-holomorphic soft terms

2.1 MSSM: superpotential and soft terms

The MSSM Superpotential is given by [9],

$$\begin{aligned} \mathcal {W}= & {} \mu H_D. H_U -Y_{ij}^e H_D.L_i {{\bar{E}}}_j -Y_{ij}^d H_D.Q_i {{\bar{D}}}_j \nonumber \\ {}{} & {} -Y_{ij}^u Q_i.H_U {{\bar{U}}}_j. \end{aligned}$$

(5)

Here, for two doublet chiral superfields A and B, one has $A.B=\epsilon _{\alpha \beta }A^\alpha B^\beta$, where $\epsilon _{\alpha \beta }$ is an antisymmetric (Levi-Civita) tensor in 2-dimension. $Y_{ij}^e$, $Y_{ij}^u$ and $Y_{ij}^d$ are lepton, up and down type of Yukawa matrices respectively. $H_D$ and $H_U$ with hypercharges -1 and 1 respectively refer to down and up type of doublets of Higgs chiral superfields that contain both the Higgs scalars and and their fermionic partners higgsinos. $L_i,Q_i$ and $E_i,U_i$ are left handed doublet and right handed singlet chiral superfields of applicable fermions and their scalar superpartners.

The MSSM soft terms including the non-holomorphic scalar mass terms and the holomorphic trilinear coupling terms are as given below [9].

$$\begin{aligned} -{\mathcal {L}}_{soft}= & {} [{{\tilde{q}}}_{iL}.h_u{(Y^u A_u)}_{ij} {{\tilde{u}}}^*_{jR}+ h_d.{{\tilde{q}}}_{iL}{(Y^d A_d)}_{ij} {\tilde{d}}^*_{jR}\nonumber \\{} & {} +h_d.{{\tilde{l}}}_{iL}{(Y^e A_e)}_{ij} {{\tilde{e}}}^*_{jR}+ h.c.] \nonumber \\{} & {} +\left( B\mu h_d.h_u + h.c. \right) + m_d^2 {|h_d|}^2 +m_u^2 {|h_u|}^2\nonumber \\{} & {} + {{\tilde{q}}}_{iL}^*{({M}_{{\tilde{q}}}^2)}_{ij} {{\tilde{q}}}_{jL}+ {{\tilde{u}}}_{iR}^* {({M}_{{\tilde{u}}}^2)}_{ij} {{\tilde{u}}}_{jR} + {{\tilde{d}}}_{iR}^* {({M}_{{\tilde{d}}}^2)}_{ij} {{\tilde{d}}}_{jR}\nonumber \\{} & {} +{\tilde{l}}_{iL}^* {({M}_{{\tilde{l}}}^2)}_{ij} {{\tilde{l}}}_{jL}+ +{\tilde{e}}_{iR}^* {({M}_{{\tilde{e}}}^2)}_{ij} {{\tilde{e}}}_{jR} \nonumber \\{} & {} + \textrm{gaugino}~\textrm{mass}~\mathrm{terms.} \end{aligned}$$

(6)

Here, $h_d$ and $h_u$ are doublets of Higgs scalar fields. The other terms contain mass terms and trilinear terms involving the scalar parts of the associated matter superfields. Finally, there are Majorana mass terms involving the gauginos. With $v_u,v_d$ as the vacuum expectation values (vevs) of the neutral components of Higgs scalar fields $h_u$ and $h_d$, one has $\tan \beta =v_u/v_d$ and $M_Z^2=\frac{1}{4}(g_Y^2+g_2^2)(v_u^2+v_d^2)$, leading to $\sqrt{(v_u^2+v_d^2)}\simeq 246$ GeV. The Yukawa couplings and masses are related via the vevs as $y_e=\frac{m_e}{(v_d/\sqrt{2})}$, $y_u=\frac{m_u}{(v_u/\sqrt{2})}$ etc. The above $y_e$ relates to $Y_{ij}^e$ the leptonic Yukawa matrix as $Y_{11}^e=y_e,Y_{22}^e=y_\mu , Y_{33}^e=y_\tau$.³ Similar notation holds good for the quark Yukawa matrices.

2.2 Non-holomorphic soft terms

Reference [28] enumerated the MSSM soft terms shown as $-{\mathcal {L}}_{soft}$ in Eq. (6). It also listed a few additional SUSY breaking interactions in a general sense that would be regarded as hard SUSY breaking terms in presence of a gauge singlet scalar field [30]. On the other hand, in absence of any such singlets as in MSSM, such terms grouped within $-{\mathcal {L}'}_{soft}$ shown as below, are no longer of hard SUSY breaking type [29,30,31] and these are labelled as non-holomorphic soft SUSY breaking terms or the so-called “C-terms” in SUSY texts [10]. In MSSM these are regarded as soft SUSY breaking terms.

$$\begin{aligned} -{\mathcal {L}'}_{soft}= & {} h_d^c.{{\tilde{q}}}_{iL}{(Y^u A_u^\prime )}_{ij} {{\tilde{u}}}^*_{jR}+ {{\tilde{q}}}_{iL}.h_u^c{(Y^d A_d^\prime )}_{ij} {{\tilde{d}}}^*_{jR}\nonumber \\{} & {} + {{\tilde{l}}}_{iL}.h_u^c {({Y^e A}_e^\prime )}_{ij} {{\tilde{e}}}^*_{jR}+ \mu ' {{\tilde{h}}}_u.{\tilde{h}}_d+ h.c. \end{aligned}$$

(7)

Here, instead of the Higgs scalar doublets one has their conjugates $h_d^c$ and $h_u^c$. With appropriate hypercharges, $h_d^c$ couples with the up-type of squarks and $h_u^c$ goes with the down type of squarks and sleptons. This is why the above is often referred as a scenario with wrong Higgs coupling.

Reference [29] analyzed such terms (along with the MSSM soft terms) in a model independent way. Instead of a model based analysis, in an agnostic point of view the authors named the framework as “Minimal Effective Supersymmetry” where the new soft parameters considered were to be treated at par with the ones of Eq. (6) and these were left to be determined from low energy data only.

In the quest of a model, Ref. [31] considered a hidden sector based F-type supesymmetry breaking scenario including two chiral superfields. The author obtained terms of $-{\mathcal {L}'}_{soft}$ terms to be of the order $\frac{{|F|}^2}{M^3}\sim \frac{M_W^2}{M}$ indicating suppression by the scale of mediation M of SUSY breaking. Arising from the same analysis, there is no such supression for the MSSM soft terms of Eq. (6). Clearly, according to the model of Ref. [31] these are highly suppressed terms if the scale of mediation is close to the grand unification theory (GUT) scale or the Planck scale. However, Ref. [31] also pointed out that the above does not make the terms of $-{\mathcal {L}'}_{soft}$ irrelevant for issues starting from a possible incorrectness in using a simplistic form of spontaneous SUSY breaking to involvement of multiple high scales etc.

It is known that building models for nonstandard soft SUSY breaking terms or the “C-terms” is difficult [10]. We cite a few available analyses here. References [32,33,34] may be seen for analyses with generalized supersoft SUSY breaking that have relations to non-holomorphic soft terms. Generating non-holomorphic terms based on gauge mediated SUSY breaking may be seen in Ref. [35]. Here, the authors discussed the possibility of finding gauge invariant supersymmetric direct Yukawa couplings between the Higgs and the messenger fields. One-loop corrections involving messenger fields in the loop may lead to the wrong-Higgs gaugino operators [35] that may become important in the low energy theory below the scale of SUSY breaking.⁴ Reference [37] relates to non-holomorphic terms arising out of D-brane instantons stretched between SUSY breaking and visible sectors.

It is clear that the NH terms of $-{\mathcal {L}'}_{soft}$ are not friendly to supergravity [31, 38] types of scenarios or they may be difficult to be found from a popular UV complete theory. Similar to Ref. [10, 31] we are also of the opinion that the NH terms are hardly irrelevant in spite of their difficulty in model building and we may consider the approach of “Minimal Effective Supersymmetry” of Ref. [29]. Based on the inputs given at a high or a low scale we classify below the past phenomenological analyses with non-standard soft terms that considered no explicit model or in other words were consistent with the “Effective” approach of Ref. [29]. Analyses of Refs. [39,40,41,42,43,44,45,46,47,48] used renormalization group evolutions within a Constrained MSSM (CMSSM [9]) like setup. Here the NH parameters were considered to be of unknown origin and were at par with other CMSSM mass and trilinear parameters. Similarly, there are works with phenomenological MSSM (pMSSM) [49] like inputs [50,51,52,53] where the NH parameters given at a low scale were treated at par with the MSSM soft SUSY breaking parameters. Thus as with previous analyses, we consider the new parameters to be of unknown origin given at a low scale. The tree-level Higgs potential is unaffected, but this is not so for the charge and color breaking terms of the scalar potential [51]. The presence of the higgsino mass soft terms with coupling $\mu ^\prime$ may cause isolation of a fine-tuning from the Higgsino mass $\mu$ since at tree level higgsino mass would have components from the superpotential (Eq. 5) as well as from the soft term of (Eq. 7) [46, 47, 50]. The mass matrices for the scalars get modified in the off-diagonal component involving L-R mixing. For example, a slepton mass matrix may be written as,

$$\begin{aligned} M_{\tilde{e}}^2=&\left( \begin{matrix} M_{\tilde{l_L}}^2+M_Z^2(T_{3L}^{\tilde{e}}-Q_e\sin ^2\theta _{W})\cos 2\beta +m_e^2 &{} -m_e({A}_e-(\mu +{A}_e')\tan \beta ) \\ -m_e({A}_e-(\mu +{A}_e')\tan \beta ) &{} M_{\tilde{l_R}}^2+M_Z^2 Q_e\sin ^2\theta _{W}\cos 2\beta +m_e^2 \end{matrix} \right) . \end{aligned}$$

(8)

We note that going from MSSM to NHSSM, $\mu \tan \beta$ gets replaced by $(\mu + {A}_l^\prime )\tan \beta$ in the off-diagonal entries. In the electroweakino sector the higgsino mass entries are altered from $\mu$ to $\mu +\mu '$ leading to the following neutralino and chargino mass matrices in NHSSM.

$$\begin{aligned}{} & {} M_{\widetilde{\chi ^0}}=\left( \begin{matrix} M_1 &{} 0 &{} -M_Z\cos \beta \sin \theta _W &{} M_Z\sin \beta \sin \theta _W \\ 0 &{} M_2 &{} M_Z\cos \beta \cos \theta _W &{} -M_Z\sin \beta \cos \theta _W \\ -M_Z\cos \beta \sin \theta _W &{} M_Z\cos \beta \cos \theta _W &{} 0 &{} -(\mu +\mu ')\\ M_Z\sin \beta \sin \theta _W &{} -M_Z\sin \beta \cos \theta _W &{} -(\mu +\mu ') &{} 0 \end{matrix} \right) . \end{aligned}$$

(9)

$$\begin{aligned}{} & {} M_{\widetilde{\chi ^{\pm }}}=\left( \begin{matrix} M_2 &{} \sqrt{2} M_W\sin \beta \\ \sqrt{2} M_W\cos \beta &{} -(\mu +\mu ')\\ \end{matrix}\right) . \end{aligned}$$

(10)

The present analysis will consider vanishing $\mu ^\prime$.

2.3 Charge and color breaking

Avoiding a Charge and Color Breaking (CCB) minima in NHSSM [51] while considering both the holomorphic and non-holomorphic trilinear couplings requires a 4-vev scenario, like the vevs for $H_u$, $H_d$, ${{\tilde{f}}}_L$ and ${{\tilde{f}}}_R$. Here ${\tilde{f}}$ stands for the concerned sfermion. With $A_f$ and $A_f^\prime$ both present there is no possibility of considering a 3-vev scenario unlike in MSSM. A rather straigtforward computation as shown in Ref. [51] results into the following inequalities for avoiding a CCB minima. It is seen that unlike MSSM, there is no D-flat direction so that terms with $g_1^2+g_2^2$ come into the picture arising out of the D-term potential.

$$\begin{aligned} \left[ |A_t|+|\mu | + |A_t'| \right] ^2< & {} 3 \left( m_1^2 + m_2^2 + m_{\tilde{t}_L}^2 + m_{\tilde{t}_R}^2 -2B_{\mu }\right) , \nonumber \\ \left[ |A_b|+|\mu | + |A_b'| \right] ^2< & {} 3 \left\{ 1+\frac{g_1^2+g_2^2}{24y_b^2}\right\} \nonumber \\{} & {} \times \left( m_1^2 + m_2^2 + m_{\tilde{b}_L}^2 + m_{\tilde{b}_R}^2 -2B_{\mu }\right) , \nonumber \\ \left[ |A_\tau |+|\mu | + |A_\tau '| \right] ^2< & {} 3 \left\{ 1+\frac{g_1^2+g_2^2}{24y_\tau ^2}\right\} \nonumber \\{} & {} \times \left( m_1^2 + m_2^2 + m_{\tilde{\tau }_L}^2 + m_{\tilde{\tau }_R}^2 -2B_{\mu }\right) , \nonumber \\ \end{aligned}$$

(11)

where $m_{1,2}^2=m_{{H_d},{H_u}}^2+\mu ^2$. One finds that even with a very large $A_e^\prime$ as in our analysis, the above constraint is easily satisfied because of the $g_1^2+g_2^2$ term that becomes very large due to a small $y_e$ in the denominator. This is entirely different from the MSSM case that has a D-flat direction coming out in a 3-vev based scenario.⁵

Apart from a global vacuum stability where a lot of MSSM parameter space can be excluded for a large value of $A_f$ corresponding to the first two generations of leptons ($f\equiv e,\mu$), we must point out that for a long-lived universe, the CCB conditions corresponding to the light fermion cases are readily evaded. The above is quite commonly used in SO(10) based analyses (e.g Ref. [57]) to label a parameter point valid even when the absolute stability is affected. This is true as long as the CCB inequalities are satisfied for the large Yukawa coupling cases i.e. the inequalities involving the third generation trilinear couplings like $A_t$. The rate of tunneling from the Standard Model like false vacuum to a CCB true vacuum is proportional to $e^{-a/y^2}$ [56] (follows from Eq. 9 and 11 of Ref. [58]), where a is a constant and y is the associated Yukawa coupling for the colored/charged fields. If the dangerous third generation of sfermion constraints are already avoided, the rate of tunneling corresponding to a small Yukawa case may be very small. As mentioned in Ref. [58] these are the cases where D-term contributions to the potential cannot be neglected. NHSSM with large values of $A_e^\prime$ also falls into this class and it is thus additionally consistent with a long-lived universe consideration. Thus for NHSSM, the inqualities involving $A_e$, $A_e^\prime$ and $A_\mu$, $A_\mu ^\prime$ are either satisfied for absolute stability or they can be ignored as in MSSM for a long-lived universe leading to cosmological stability [57, 58].

3 Leptonic $(g-2)$ and Yukawa threshold corrections in MSSM

In MSSM, as shown in Fig. 1, at the one-loop level the leading contributions to $a_{\mu }^{\textrm{SUSY}}$ come from ${\tilde{\chi }}^0-{\tilde{\mu }}$ and ${{\tilde{\chi }}}^\pm -{\tilde{\nu }}_\mu$ loops [59,60,61,62,63,64,65,66,67,68,69,70,71]. The required chirality flip may be found from a SUSY Yukawa coupling of a higgsino to a lepton, an appropriate slepton (${\tilde{\mu }}$) or sneutrino ${{\tilde{\nu }}}_\mu$. Otherwise, the chirality flip may be associated at a slepton $\tilde{\mu }$ line corresponding to the transition ${{\tilde{\mu }}}_L-{\tilde{\mu }}_R$ [72]. Using Ref. [73] the one-loop contributions are given as follows.

$$\begin{aligned} a_\mu ^{{{\tilde{\chi }}}^0}= & {} \frac{m_\mu }{16\pi ^2} \sum _{i,m}\left\{ -\frac{m_\mu }{ 12 m^2_{{\tilde{\mu }}_m}} (|n^L_{im}|^2+ |n^R_{im}|^2)F^N_1(x_{im}) \right. \nonumber \\{} & {} \left. +\frac{m_{{\tilde{\chi }}^0_i}}{3 m^2_{{\tilde{\mu }}_m}} \textrm{Re}[n^L_{im}n^R_{im}] F^N_2(x_{im})\right\} \end{aligned}$$

(12)

$$\begin{aligned} a_{\mu }^{{{\tilde{\chi }}}^\pm }= & {} \frac{m_\mu }{16\pi ^2}\sum _k \left\{ \frac{m_\mu }{ 12 m^2_{{\tilde{\nu }}_\mu }} (|c^L_k|^2+ |c^R_k|^2)F^C_1(x_k) \right. \nonumber \\{} & {} \left. +\frac{2m_{{\tilde{\chi }}^\pm _k}}{3m^2_{{\tilde{\nu }}_\mu }} \textrm{Re}[ c^L_kc^R_k] F^C_2(x_k)\right\} \end{aligned}$$

(13)

where i and m refer to the four neutralino and two chargino states whereas k indicates the two smuon states. The referred couplings are given by,

$$\begin{aligned} n^R_{im}= & {} \sqrt{2} g_1 N_{i1} X_{m2} + y_\mu N_{i3} X_{m1}, \end{aligned}$$

(14)

$$\begin{aligned} n^L_{im}= & {} {1\over \sqrt{2}} \left( g_2 N_{i2} + g_1 N_{i1} \right) X_{m1}^* - y_\mu N_{i3} X^*_{m2}, \end{aligned}$$

(15)

$$\begin{aligned} c^R_k= & {} y_\mu U_{k2}, \end{aligned}$$

(16)

$$\begin{aligned} c^L_k= & {} -g_2V_{k1}. \end{aligned}$$

(17)

The loop functions for the neutralino and chargino loops namely $F^{N,C}_{1,2}$ may be seen in Ref. [73]. A simplified result follows when the loops that contribute most are the ones with chargino-sneutrino and bino-smuon fields [74].

$$\begin{aligned} a_{\mu }^{{{\tilde{\chi }}}^\pm }\simeq & {} \frac{\alpha _2 \, m^2_\mu \, \mu \,M_{2} \tan \beta }{4\pi \sin ^2\theta _W \, m_{\tilde{\nu }_\mu }^{2}}\nonumber \\{} & {} \times \left( \frac{f_{\chi ^{\pm }}(M_{2}^2/m_{\tilde{\nu }_{\mu }}^2) -f_{\chi ^{\pm }}(\mu ^2/m_{\tilde{\nu }_{\mu }}^2)}{M_2^2-\mu ^2} \right) \!{,} \end{aligned}$$

(18)

$$\begin{aligned} a_\mu ^{{{\tilde{\chi }}}^0}\simeq & {} \frac{\alpha _1 \, m^2_\mu \, \,M_{1}(\mu \tan \beta - {A}_\mu )}{4\pi \cos ^2\theta _W \, (m_{\tilde{\mu }_R}^2 - m_{\tilde{\mu }_L}^2)}\nonumber \\{} & {} \times \left( \frac{f_{\chi ^0}(M^2_1/m_{\tilde{\mu }_R}^2)}{m_{\tilde{\mu }_R}^2} - \frac{f_{\chi ^0}(M^2_1/m_{\tilde{\mu }_L}^2)}{m_{\tilde{\mu }_L}^2}\right) \!{,} \end{aligned}$$

(19)

where the loop functions f are as given in Ref. [74].

Fig. 1

One-loop contributions to $a_{\mu }^{\textrm{SUSY}}$

3.1 Yukawa threshold corrections

In MSSM, the Yukawa couplings are modified because of soft interactions. We would now like to discuss Yukawa threshold corrections for fermions that affects ${(g-2)}_l$ as a higher order effect. At one-loop level, the lepton Yukawa coupling in MSSM can be given as,

$$\begin{aligned} y_{l} = \frac{m_l}{(v/ \sqrt{2})}\sqrt{1+\tan ^2\beta } \frac{1}{1+\Delta _l} \left( 1+ O(\cot \beta )\right) . \end{aligned}$$

(20)

Here $\Delta _l$ in MSSM is given by [75],

$$\begin{aligned} \Delta _l= & {} -\frac{g_2^2\ M_2}{16\pi ^2}\tan \beta \Big [ \mu I(m_1,m_2,m_{{{\tilde{\nu }}_l}}) + \mu \frac{1}{2} I(m_1,m_2,m_{\tilde{l}_L})\Big ] \nonumber \\{} & {} -\frac{g_1^2\ M_1}{16\pi ^2}\tan \beta \Big [\mu I(\mu ,M_1,m_{\tilde{l}_R}) \nonumber \\{} & {} - \mu \frac{1}{2}I(\mu ,M_1,m_{\tilde{l}_L})- \mu I(M_1,m_{\tilde{l}_L},m_{\tilde{l}_R}) \Big ]. \end{aligned}$$

(21)

Here, $m_{1,2}$ are the chargino masses and the loop function I is as given in Ref. [75]. As we will discuss for NHSSM, the last term $\mu I(M_1,m_{\tilde{l}_L},m_{\tilde{l}_R})$ will be altered via $\mu \rightarrow (\mu +A_l^\prime )$. Including these corrections, the one-loop contributions get modified as,

$$\begin{aligned} a_l^{\textrm{SUSY,1L}} \longrightarrow a_l^{\textrm{SUSY,1L}} \frac{1}{1+\Delta _l}. \end{aligned}$$

(22)

$\Delta _l$, which is proportional to $\tan \beta$, contains the all order re-summation of the $\tan \beta$ enhanced contributions [76, 77]. We further note that with the assumption that all the SUSY masses are equal and much larger than the W-boson mass $M_W$, $\Delta _\mu =-0.0018\tan \beta ~\mathrm{sign (\mu )}$ [75, 76]. $\Delta _\mu$ may be much larger for unequal SUSY particle mass parameters [75]. A larger $\Delta _l$ that is itself proportional to $\tan \beta$, can even influence $a_l$’s $\tan \beta$-dependence via $y_l$. In the limit of radiative mass generations of fermions, $a_l$ can become almost independent of $\tan \beta$ [78]. Such effects of the radiative generation of mass of fermions in analyzing $g-2$ were considered in Refs. [75, 78,79,80,81,82,83]. The authors pointed out the role of non-holomorphic trilinear interactions on lepton Yukawa couplings $y_l$ and $(g-2)_l$. A similar control of $(g-2)_e$ via enhancement of Yukawa threshold corrections in MSSM was used in Ref. [84] where the authors considered very large values of $\mu$ (up to 500 TeV). We will discuss some details of the work in Sect. 3.2.

Following Sect. 2, an off-diagonal element of a slepton matrix would look like $m_l(A_l-(\mu +A_l^\prime )\tan \beta )$, indicating a generic alteration of $\mu$ of MSSM going to $\mu +A_l^\prime$ in NHSSM wherever there is an L-R mixing. The same will be true in the last term (L-R) of the last line of Eq.  (21). Since for an electron the aforesaid off-diagonal term is multiplied by $m_e$ which is too small, one must have a very large value of $(\mu +A_e^\prime )$ so as to get a finite L-R mixing effect in relation to the diagonal terms. With an electroweak fine-tuning-friendly low $\mu$, we see that $A_l^\prime$ has to be very large so that $\mu$ may be ignored in $\mu +A_l^\prime$. Thus, with an appropriately large ${A}^\prime _l$, $\Delta _l$ in NHSSM may be approximately proportional to ${A}^\prime _l$, and the effect on $y_l$ can be much larger than what may be possible in MSSM due to a potentially large enhancement factor $1/(1+\Delta _e)$. We will demonstrate how the radiatively corrected Yukawa coupling $y_e$ may become very important while discussing the case of $a_e$ in Sect. 4. Additionally, the sign correlation of $a_l$ with respect to $A_l^\prime$ can be ascertained from the relevant bino-slepton loop result of Eq. (19) when one changes $\mu$ to $\mu +A_l^\prime$. Since $\Delta _e$ is proportional to $\tan \beta$ we will see that the threshold corrections to $y_e$ will cause $a_e$ to be a slowly increasing function of $\tan \beta$ with some intercept, but unlike MSSM it would no longer be proportional to $\tan \beta$ (Eq. 22).

There have been an appreciable number of SUSY-based analyses on ${(g-2)}_\mu$ after the announcement of Fermilab result [85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114]. Some of the above works also involve dark matter constraints. DM relic density could be satisfied via higgsino or wino type of LSPs provided one considers underabundant scenarios with the possibility of multiple candidates for DM. In this case, ${\widetilde{\chi }}^{\pm }-{\tilde{\nu }}_\mu$ loop may contribute dominantly to $a_\mu$. One can similarly consider bino-wino mixed LSP in this regard. One can also consider bino type of LSP which obtains correct relic density by self-annihilation via s-channel H/A boson, with $a_\mu$ constraint being satisfied via the contribution from the bino-smuon loop with relatively light smuons. Alternatively, bino-stau coannihilation may be used for DM relic density generation and $a_\mu$ constraint may be similarly addressed. As we will see in our work with nonstandard trilinear soft terms, we consider higgsino to be the LSP (in an underabundant choice for DM). Regarding $a_\mu$, we use the contribution from the bino-smuon loop that is enhanced by larger L-R mixing due to the above soft terms. We will further see that the large threshold corrections (due to the nonstandard soft terms) to leptonic Yukawas, particularly $y_e$, can be useful to accommodate the $a_e$ constraint simultaneously.

3.2 Accommodating $a_e$ constraint in addition to $a_\mu$ limits

Equation (4) summarizes the requirement for a new physics to accommodate both the constraints. The ratio is required to be not only large but also negative. We would like to address the essential parts of a few past MSSM analyses in this regard. References [74, 84, 109] analyzed the $a_\mu$ and $a_e$ constraints in the context of MSSM. Reference [109] used 1-3 flavor violation in the bino-slepton loop to get the desired outcome for $a_e$ while satisfying the $\tau \rightarrow e \gamma$ bound. There was no flavor violation to use for $a_\mu$. The essential focus of Ref. [74] was to satisfy $(g-2)_\mu$ and $(g-2)_e$ either via the lighter chargino-sneutrino loop or via the neutralino-slepton loop diagrams with appropriate signs of the U(1) and SU(2) gaugino masses $M_1$ and $M_2$. The analysis of Ref. [74] that could only have a light electroweakino spectra, used different mass parameters for the sleptons of the first two generations (apart from the sneutrinos). The work considered differing right and left slepton mass parameters, a highly unfriendly choice for flavor. Clearly, such large mass splittings in the sleptons of the first two generations are prone to create large flavor-violating off-diagonal entries in the slepton mass matrices when lepton matrices become diagonalized. It can easily give rise to lepton flavor violation, which is severely limited via the $\mu \rightarrow e \gamma$ constraint. Alignment of slepton and lepton matrices were to be invoked in order to meet the above constraint. Apart from the above, a generally light SUSY spectrum in satisfying the $(g-2)_l$ magnetic moment data while having strong LHC constraints on sparticle masses forces one to have only a compressed scenario involving light sleptons and wino-like chargino along with a bino-like LSP. Reference [110] also used differing mass parameters between the two generations of sleptons, whereas an overabundant bino DM was avoided by considering a superWIMP dark matter scenario.⁶ As mentioned earlier, Ref. [84] explored the above magnetic moment constraints also in the MSSM context using a very large $\mu$ (up to $\sim 500$ TeV) to generate large threshold corrections to the relevant Yukawa couplings in the analysis. A large degree of sensitivity of the above corrections to the slepton masses is used to accommodate the $(g-2)$ constraints. Selectron masses were considered to be heavy (multi TeV) whereas smuon masses are less than a TeV in order to satisfy both the $g-2$ constraints. The analysis required a very large $\tan \beta$($=70$) and light wino ( 500 GeV) and massive higgsinos. The work that is associated with a large value for the electroweak fine-tuning complied with the vacuum stability condition to find the valid parameter space. On the theoretical side, both the analyses [74, 84] discussed the flavor dependence of the slepton masses by considering a Higgs mediation scenario [115, 116] so as to have an alignment of the slepton and lepton matrices. Reference [117] addressed the magnetic moment constraint pair by considering CP-violating phases and the constraint from electron dipole moment (EDM).

In contrast to the above analyses that had to manage the flavor issues carefully and are strongly constrained by $\mu \rightarrow e \gamma$ or may have to live with light SUSY spectra or very large $\tan \beta$, we focus on including nonstandard soft terms. We must emphasize here that as mentioned before, the MSSM soft terms and the nonstandard soft SUSY breaking terms do not have the same status. While the regular soft terms are highly supported by popular UV complete models, the NH terms are in general difficult for modelling. As mentioned earlier, in a model independent standpoint, we analyze the effect of the nonstandard terms considering an approach of “Minimal Effective Supersymmetry” of Ref. [29]. An analysis with NH terms would not demand any large $\mu$, or light spectra and we will use a flavor friendly scenario of having identical slepton masses for the first two generations with equal coefficients for the left and right mass parameters. However, we will use two different non-holomorphic trilinear parameters for the first two generations of leptons, both given as inputs at the low scale. In general, had these been given at a much higher scale like the grand unification scale we might run into flavor issues. Nevertheless, a detailed analysis of the exact degree of flavor violation, is beyond the scope of this work.

4 Results

4.1 Muon magnetic moment in NHSSM

Our NHSSM analysis on lepton $g-2$ in its first part involves studying the effects of the nonstandard soft terms on the enhancement of the SUSY contributions to muon g$-2$. We will explore at the beginning the constraints from $(g-2)_\mu$ data and analyze the parameter space that would be consistent with dark matter (DM) and other constraints. We will demonstrate the mechanism that enhances $(g-2)_\mu$ in NHSSM. For DM, we will consider the case where the lightest supersymmetric particle (LSP) is expected to obey only the upper limit of the relic density bound from PLANCK data [118]. We will identify the parameter space that would satisfy all the direct detection limits from XENON1T namely both the spin-independent [119] and spin-dependent [120] type of data. Once the above analysis delineates the parameter space, we will explore the effect of imposing the constraint from the electron’s magnetic moment $(g-2)_e$ due to fine-structure constant measurement. We will see how the Yukawa threshold corrections due to NHSSM effects can affect leptonic $g-2$, particularly $(g-2)_e$. Because of the above, we will see that it is indeed possible to find NHSSM parameter regions such that the scaled magnetic moment ratio of interest $R_{e,\mu }$ as discussed before may be consistent with Eq. (4). We use SARAH-4.14.4 [121, 122] and SPheno 4.0.4 [123, 124] to implement the model and for computing SUSY spectra and observables.

In order to generate a sufficient amount of SUSY contributions to leptonic $g-2$ in NHSSM we take the help of chirality flip via the Left-Right scalar mixing due to the non-holomorphic trilinear SUSY breaking interaction parametrized by ${A}^\prime _l$. We use $T_l^\prime$ as an input defined via $T^\prime _l =y_l {A}^\prime _l$ (with $y_l=\frac{m_l}{(v_d/\sqrt{2})}$). This follows the input convention used in the codes SARAH-SPheno (for example see Ref. [46]) for all the trilinear soft parameters. We should point out that with this parametrization a value of a few GeV for $T^\prime _l$ may mean a large value for ${A}^\prime _l$. The largeness is most prominent for electron, whereas for top quark, the associated values of $T_t$ and $A_t$ are not so different from each other. We must also remember that because of the appearance of the fermionic mass $m_e$ in the off-diagonal entry of Eq. (8), any non-negligible L-R mixing of selectrons would need a significantly large ${A}^\prime _e$ because of the smallness of the electronic mass. In one-loop vertex correction radiative diagrams (Fig. 1), this is achieved via the NH trilinear interactions of scalars in the bino-slepton loops.⁷ Thus, both the above trilinear parameters and the mass of bino $M_1$ will have significant roles in our analysis apart from the masses of sleptons for which we consider equal left and right mass parameters $m_L,m_R$ for the first two generations. We must emphasize that the above NH terms may potentially enhance $a_l$ significantly in comparison with the MSSM contributions involving chargino or neutralino loops.

In order to probe NHSSM effects clearly we keep the SU(2) gaugino mass to be sufficiently heavy, much above $\mu$ or $M_1$. A large part of parameter space where $(g-2)_e$ can be accommodated in our work involves (i) direct effect of larger $A_e^\prime$ on the bino-seletron loop of Fig. 1 (i.e. through Eq. (19) with $\mu \rightarrow \mu +A_e^\prime$) and (ii) via the effect of the enhancement factor $\frac{1}{1+\Delta _e}$ directly on $a_e$ (Eq. 22). Of course, $\frac{1}{1+\Delta _e}$ influences the Yukawa coupling for electron ($y_e$) directly via $A_e^\prime$ through the same L-R mixing. The effect of the said NH trilinear mixing may easily supersede the contribution from the higgsino mixing superpotential term characterized by $\mu$. On the other hand, the corrections may become smaller for larger slepton mass values. Keeping our choice of scalar mass spectra in tact, we will rather limit the associated NH trilinear SUSY breaking parameters such as $A^\prime _e$ so as to limit $y_e$. We will label the above as the “Limited Threshold Corrections of Yukawa Coupling (LTCYC)” zone. To specify explicitly, by LTCYC zone of $y_e$ we mean that the radiatively corrected value of $y_e$ can at most be twice the corresponding MSSM value, or in other words $\frac{1}{1+\Delta _e} < 2$. However, with the chosen SUSY mass parameters we will see that the required agreement with data for ${(g-2)}_e$ range is possible even with a factor quite smaller than two. As we will point out in Sect. 4.3.2 the chosen SUSY parameter space that satisfies ${(g-2)}_\mu$ requires only moderately large $A_\mu ^\prime$ in contrast to $A_e^\prime$ for the case of ${(g-2)}_e$. Thus, LTCYC for $y_\mu$ is automatically satisfied for all the parts of our analysis meant for ${(g-2)}_\mu$. We will explore explicitly how far LTCYC for $y_e$ as a condition becomes important when we incorporate $(g-2)_e$ as a constraint in Sect. 4.3.

Toward the end, we will impose the constraints from ATLAS search for slepton-pair production [125] in the LSP-slepton mass plane and explore a few benchmark points that would satisfy all the constraints. While the neutralino-slepton loop dominated by bino type of neutralino would enhance $(g-2)_l$, we will primarily consider higgsino as the LSP which would be suitable for satisfying the DM relic density data from PLANCK (only the upper limit, in a multi-component DM scenario) as well as the spin independent (SI) direct-detection (DD) scattering cross section data of LSP-nucleon scattering. The bino-higgsino mixed region would obviously be disfavored or discarded via the SI DD constraints. Below, we focus on the minimal requirement for enhancing SUSY contributions to leptonic $g-2$ and the variables that are closely connected to $g-2$ and dark matter. With the above in mind, we keep the squark masses decoupled to large values and we do the same for the tau-sleptons too. All the left and right handed scalars including that of the first two generations of sleptons will assume equal SUSY breaking mass parameter input values ($m_L=m_R$). We keep the trilinear coefficient for top-squark namely $T_t$ at a high negative value that would be consistent with Higgs mass data. The Table 1 refers to the input parameter values/ranges.⁸

Table 1 SUSY scale input ranges of Soft masses and Trilinear SUSY breaking parameters. Quantities labelled by T are scaled trilinear parameters, e.g. $T_t =y_t {A}_t$ or $T^\prime _\mu =y_\mu {A}^\prime _\mu$. Masses and trilinear couplings are in GeV. All the trilinear parameters not mentioned here are understood to assume zero values

With the above parameter space been defined, some of our constraints are that from the Higgs data, $Br(b \rightarrow s \gamma )$, relic density upper limit from PLANCK. This is apart from the $(g-2)_\mu$ and $(g-2)_e$ constraints mentioned earlier and the SI and SD direct detection constraints from XENON1T that depend on the mass of the LSP. With $M_{\textrm{SUSY}}$ being large, we consider a 3 GeV theoretical uncertainty in SUSY Higgs mass leading to the following as the acceptable range [126] for the SM-like Higgs in MSSM.

$$\begin{aligned} 122<m_h<128~\textrm{GeV}. \end{aligned}$$

(23)

The flavor limits at 2$\sigma$ are $3.02 \times 10^{-4}< Br(b \rightarrow s \gamma )< 3.62 \times 10^{-4}$ [127] and $2.23 \times 10^{-9}<Br(B_s \rightarrow \mu ^+ \mu ^-)< 3.63 \times 10^{-9}$ [128]. Considering the PLANCK result for dark matter namely $\Omega _{{{\tilde{\chi }}}^0} h^2=0.120 \pm 0.001$ [118], the $2\sigma$ level limits are ${[\Omega _{{{\tilde{\chi }}}^0} h^2]}_{\textrm{min}}=0.118$ and ${[\Omega _{{{\tilde{\chi }}}^0} h^2]}_{\textrm{max}}=0.122$. The DM relic density is expected to satisfy only the upper bound. In our generally underabundant scenario, for the purpose of direct detection cross-section, we define a scale factor $\xi$ [129] as given below.

$$\begin{aligned} \xi =\Omega _{{{\tilde{\chi }}}^0} h^2 /{[\Omega _{{{\tilde{\chi }}}^0} h^2]}_{\textrm{min}} ~\textrm{if}~ \Omega _{{{\tilde{\chi }}}^0} h^2 \le {[\Omega _{{{\tilde{\chi }}}^0} h^2]}_{\textrm{min}}, \textrm{else}~ \xi =1. \end{aligned}$$

(24)

We plot Fig. 2 that describes our result of the SUSY contributions to $a_{\mu }$ (referred hereafter as $a_{\mu }$ itself) in relation to the relevant SUSY breaking parameter $M_1$, the mass of bino. Figure 2a shows the variation of $a_{\mu }$ with the mass of bino ($M_1$) for $\tan \beta =$ 10 to 50 in steps of 10. Here, the fixed parameters used are $T^\prime _\mu =200$ GeV, $m_L(=m_R)=600$ GeV, $\mu =600$ GeV, and $M_2=1.5$ TeV. As we will see later (Fig. 17), the NHSSM contributions to $a_\mu$ are much larger than the corresponding MSSM ones (i.e. with vanishing $T^\prime _\mu$) for the chosen regions of values of mass and coupling parameters of Table 1. The black horizontal lines are the 1$\sigma$ limits of $a_\mu$. For each $\tan \beta$, $a_{\mu }$ increases with $M_1$, and then it decreases. The peaks occur at around a given value of $M_1$ and the corresponding locations are almost independent of $\tan \beta$. Figure 2b shows the variation of $a_{\mu }$ with $M_1$ for specific values of slepton mass parameters $m_L ~(=m_R)$ corresponding to the first two generations. The fixed parameters chosen are $T^\prime _\mu =200$ GeV, $\mu =1$ TeV and $\tan \beta =10$ with $M_2$ taking an identically large value as before. The curves show similar peaks and their locations depend on the slepton mass parameter $m_L$.

Fig. 2

a Variation of SUSY contributions to $a_{\mu }$ (referred as $a_{\mu }$ itself) with respect to the mass of bino ($M_1$) for a few values of $\tan \beta$. Fixed parameters are as mentioned in the plots. The black horizontal lines are the 1$\sigma$ limits of $a_\mu$. For each $\tan \beta$, $a_{\mu }$ has an ascending and a descending part over the range of variation of $M_1$. The location of the peaks depend on $m_L(=m_R)$, and these are essentially unchanged with respect to $M_1$. b Same as a except for a given value of $\tan \beta$ and varying $m_L$. There are similar peaks in $a_{\mu }$, but they shift with varying $m_L$

We continue to study the behavior of $a_\mu$ concerning the relevant SUSY breaking parameters in Fig. 3. Undoubtedly, $a_\mu$ is enhanced most prominently via the trilinear parameter $A_\mu ^\prime$ via its strong effect through chirality flipping L-R scalar interaction in the bino-smuon loop. For $\tan \beta =10$, $m_L=\mu =600$ GeV and $M_2=1.5$ TeV, Fig. 3a shows the variation of $a_\mu$ with respect to $M_1$ for a few different values of $T_\mu ^\prime$, 100–500 GeV in steps of 100 GeV. A substantial amount of enhancement of $a_\mu$ occurs due to a change in $T_\mu ^\prime$. In this analysis, we satisfy all the charge-breaking related constraints for NHSSM (Eq. 11) [51] and stay within the LTCYC zone for the threshold corrections to $y_l$ due to the variation over $T_l^\prime$. Figure 3b refers to the variation of $a_{\mu }$ over $T_\mu ^\prime$ for different values of $M_1$. $|a_{\mu }|$ generally decreases with $M_1$ for values above 400 GeV. The exceptions are the cases of $M_1=200$ and 400 GeV, which are flipped because they belong to the ascending and the descending parts of the corresponding curve for $m_L=600$ GeV of Fig. 2b. Furthermore, the sign of $a_\mu$ is approximately given by the sign of $T^\prime _\mu$. In the NHSSM scenario of interest where non-vanishing ${A}^\prime _\mu$ enhances the bino-smuon loop contribution causing the same loop to dominate over all the other diagrams, at the lowest order, $\mu \tan \beta$ gets replaced by $(\mu +{A}^\prime _\mu )\tan \beta$ in Eq. (19). With vanishing ${A}_\mu$, and ${A}^\prime _\mu ~(=T^\prime _\mu /y_\mu )$ large enough to offset $\mu$, the sign of $a_\mu$ is determined by the sign of $A^\prime _\mu$. Numerically this is seen to be valid as long as  GeV or so. Consistency with the 1$\sigma$ band demands that $(g-2)_\mu$ data can be satisfied with only positive $T^\prime _\mu$. Figure 3c displays the variation of $a_{\mu }$ with $M_1$ for $\mu$ satisfying $150<\mu <1000$ GeV. The blue and red regions refer to $\tan \beta =10$ and 40 respectively. The limited level of thickening of lines even for a large $\tan \beta$ demonstrates that there is only a mild degree of dependence of $a_{\mu }$ on $\mu$ over the range mentioned above. This is consistent with the fact that a higgsino-smuon or a charged higgsino-sneutrino loop for $a_\mu$ are hardly important in our analysis with a dominant effect due to a NH trilinear term.

Fig. 3

a Variation of $a_{\mu }$ with the mass of bino ($M_1$) for a few values of $T_\mu ^\prime$ where $T_\mu ^\prime$ relates to ${A}^\prime _\mu$ of Eq. (7) via $T^\prime _\mu =y_\mu {A}^\prime _\mu$. b Variation of $a_{\mu }$ over $T_\mu ^\prime$ for different values of $M_1$. $|a_{\mu }|$ generally decreases with $M_1$ for values above 400 GeV. The exceptions are the cases of $M_1=200$ and 400 GeV, which are flipped because they belong to the ascending and the descending zones of the corresponding curve for $m_L=600$ GeV of b. c Variation of $a_{\mu }$ with $M_1$ for the scanned range of $\mu$ satisfying $150<\mu <1000$ GeV. The blue and red regions refer to $\tan \beta =10$ and 40 respectively. The limited level of thickening of lines even for a large $\tan \beta$ demonstrates only a mild degree of dependence of $a_{\mu }$ on $\mu$ over the range. The black horizontal lines are the 1$\sigma$ limits of $a_\mu$

We now use the $(g-2)_\mu$ constraint in the most important $M_1-T^\prime _\mu$ plane in Fig. 4a. The fixed parameter under the study are $\tan \beta =10$, $\mu =300$ GeV, $m_L=600$ GeV and $M_2=1.5$ TeV. We divide the region into 1$\sigma$ (blue), 2$\sigma$ (green), and 3$\sigma$ (gray) zones with respect to the $(g-2)_\mu$ constraint. The 1$\sigma$ region extends from $T^\prime _\mu =175$ to 450 GeV while $M_1$ spans the entire space chosen in our analysis. The region bents toward the left and this is indeed consistent with what follows from Fig. 3a. Figure 4b shows similarly constrained region with the same color convention as above. A generic decrease of $a_\mu$ with increase in $m_L$ is apparent since large $T^\prime _\mu$ is necessary to stay in a given fixed colored zone for large $m_L$ values.

Fig. 4

a Display of 1$\sigma$ (blue), 2$\sigma$ (green), and 3$\sigma$ (gray) regions with respect to the $(g-2)_\mu$ constraint in the $(T^{\prime }_\mu -M_1)$ plane for fixed parameters mentioned in the figure. b Similar display in the $(T^{\prime }_\mu -m_L)$ plane

Figure 5 shows a few $a_\mu$ contours in the plane of $M_1-m_L$ for $\tan \beta =10$ and 40 for $T^\prime _\mu =400$ and 700 GeV. The cyan-colored points represent unconstrained parameter values that only satisfy the basic constraints like Higgs data, $Br(b \rightarrow s \gamma )$, lightest neutralino to be the LSP, and restriction from charge-breaking minima. The blue and green shaded regions are $1\sigma$ and $2\sigma$ bands for the ${(g-2)}_\mu$ constraint. Three lines are drawn for $a_\mu =5\times 10^{-9}$, $a_\mu =10\times 10^{-9}$, and $a_\mu =15\times 10^{-9}$. Clearly, $a_\mu$ is large for small $m_L$ or small smuon mass regions. We must note that the reach of the smallness of $m_L$ to obtain an enhanced $a_\mu$ effectively may lead to picking up small $M_1$ regions. This is particularly true for higher $\mu$ cases. The requirement of ${{\tilde{\chi }}}^0_1$ to be the LSP, which in our case is either a bino or a higgsino dominated state, to a reasonable degree of approximation demands $m_L$ to be higher than $M_1$ or $\mu$ whichever is the lowest among the last two. There are other reasons why the bottom white regions of each of the figures are excluded. These may be due to the requirements of avoidance of tachyonic sleptons or charge-breaking minima. On the other hand, small $m_L$ regions find stringent constraints from the LHC data which we will discuss later. Comparing the figures, we can further see that, as expected, larger $T^\prime _\mu$ values enhance $a_\mu$. For a given $a_\mu$, and a fixed $M_1$, a larger $T^\prime _\mu$ creates a possibility to accommodate a larger $m_L$. A large $\tan \beta$ like 40 enhances $a_\mu$.

Fig. 5

a Plot in $M_1-m_L$ plane for $\tan \beta =10$, $\mu =400$ GeV and $T^\prime _\mu =400$ GeV with all other fixed parameters same as mentioned in Table 1. The cyan-colored points represent unconstrained parameter values that only satisfy the basic constraints like Higgs data, $Br(b \rightarrow s \gamma )$, lightest neutralino to be the LSP, and restriction from charge breaking minima. The blue and green shaded regions are $1\sigma$ and $2\sigma$ bands for the ${(g-2)}_\mu$ constraint. Three lines are drawn for $a_\mu =5\times 10^{-9}$, $a_\mu =10\times 10^{-9}$, and $a_\mu =15\times 10^{-9}$. Clearly, $a_\mu$ is large for small $m_L$ or small smuon mass regions. The white region at the bottom refers to a discarded parameter zone. This refers to not satisfying the requirements like LSP has to be the lightest neutralino ${\tilde{\chi }}^0_1$, avoidance of tachyonic sleptons or any presence of charge-breaking minima. b Same as above except $T^\prime _\mu =700$ GeV. A larger $T^\prime _\mu$ enhances $a_\mu$, leading the possibility to accommodate a larger $m_L$ value for a given $a_\mu$ at a given $M_1$ in comparison with a. There is however no $a_\mu =15\times 10^{-9}$ line because of unavailability of valid parameter space. c, d are similar figures as above for $\tan \beta =40$. The lower discarded (white) regions extend with respect to $\tan \beta =10$

4.2 Constraints from dark matter

We now include the constraints from dark matter in this NHSSM $(g-2)_\mu$ analysis. Of course, with our choice of an underabundant scenario of a higgsino dark matter, no NHSSM trilinear parameter would directly affect the DM analysis. We will study DM for its effects on the combined parameter space. In our analysis, wino mass $M_2$ is chosen to be quite heavy (1.5 TeV), whereas the higgsino mass has a range of $150<\mu <1000$ GeV, and for bino, we have $100<M_1<1000$ GeV. Our parameter space further consists of heavy tau-sleptons (2 TeV) along with decoupled squarks, whereas we choose the range of the first two generations of sleptons to vary within 200 GeV to 1 TeV. With $m_A=2.5$ TeV as an input the neutral CP-even or CP-odd Higgs masses are way above to encounter the so-called funnel region that is characterized by bino-dominated LSPs undergoing self-annihilation via s-channel processes involving A or H-bosons. Coming to the higgsinos, the chosen mass range is such that the upper limit of 1 TeV is what is necessary for higgsino LSP to become a single component DM but the upper limit of $M_1$ is also chosen to be the same. A chance equality of $M_1$ and $\mu$ would produce a large bino-higgsino mixing, but this would not be friendly with the SI direct detection. On the other hand, regions with $M_1<\mu$ would produce overabundance. Hence, in most of the available parameter space, the LSP is of higgsino type, except in a few occasions when there is a possibility of $\widetilde{\chi }_1^0$-slepton coannihilations. With higgsino LSPs to have mass below a TeV the associated relic density is supposed to satisfy only the upper limit of DM relic density constraint from PLANCK data. One of the important channels for DM production would be the coannihilation channel between the higgsno LSP with the lighter chargino state (${{\tilde{\chi }}}^0_1-{{\tilde{\chi }}}^\pm _1$) which is also higgsino dominated in nature. Figure 6a shows the Spin-independent scattering cross-section of the LSP with a proton ($\sigma ^\textrm{SI}_{\chi p}$) as a function of the LSP mass for $\tan \beta = 10$ for the parameter space mentioned in Table 1. We used micrOMEGAs 5.2.13 for dark matter-related computations [130,131,132]. Considering the large number of points with underabundance of DM we multiply $\sigma ^\textrm{SI}_{\chi p}$ with a scale factor $\xi$ which was defined in Eq. (24). Only those points satisfying the DM relic density upper bound, Higgs mass data, B-physics related limits and $(g-2)_\mu$ at 2$\sigma$ level are plotted and these are shown in green. The blue line is the constraint from the spin-independent (SI) direct detection (DD) experiment of XENON1T indicating discarded regions above the line (at 90%CL). Using interpolation we will further use the XEONON1T line to judge whether a parameter point with a given mass of the LSP would survive the SI DD experiment limit. Figure 6b shows the results for $\tan \beta =40$.

Fig. 6

a Spin-independent (SI) scattering cross-section of the LSP with a proton $\sigma ^\textrm{SI}_{\chi p}$ as a function of the LSP mass for $\tan \beta = 10$. Considering the large number of points with underabundance of DM we multiply $\sigma ^\textrm{SI}_{\chi p}$ with a scale factor $\xi$ (Eq. 24). The points satisfying the DM relic density upper bound and $(g-2)_\mu$ limits at 2$\sigma$ level are shown in green. The blue line is the constraint from $\sigma ^\textrm{SI}_{\chi p}$, the spin-independent (SI) direct detection (DD) experiment of XENON1T indicating discarded regions above the line (at 90% CL). b Similar figure for $\tan \beta = 40$

Figure 7a shows the projection of the analysis of Fig. 6 on the $M_1-\mu$ plane. Points shown in green satisfy the DM relic density upper bound, the XENON1T spin-independent direct detection cross-section limit at 90% CL as well as $(g-2)_\mu$ values within 2$\sigma$ level. The parameter zone with bino-higgsino mixed type of LSPs ($M_1 \simeq \mu$) are typically discarded via the XENON1T SI-DD limits. Generally, LSPs are visibly higgsino-dominated in nature and satisfy all the constraints within the mass range of 150 (the chosen lower limit of $\mu$) to 780 GeV. Apart from higgsinos, additionally, there are a very few parameter points corresponding to bino-like LSPs undergoing occasional coannihilations with sleptons for $m_{\widetilde{\chi }_1^0}$ between 250 and 350 GeV. Figure 7b, shows a similar plot for $\tan \beta =40$. Here $m_{\widetilde{\chi }_1^0}$ ranges from 150 to 760 GeV. Both for $\tan \beta =10$ and 40, the upper limit of the mass of $\widetilde{\chi }_1^0$ is restricted via the XENON1T SI-DD data.

Fig. 7

a Scatter plot in $M_1-\mu$ plane for the analysis of Fig. 6. Points shown in green satisfy the $(g-2)_\mu$ and the DM relic density limits both at $2\sigma$ level while also having $\sigma ^\textrm{SI}_{\chi p}$ value below the XENON1T limit at 90% CL. The LSP is generally of higgsino type. There are a few isolated points in the small $M_1$($<\mu$) zone with $m_{\widetilde{\chi }_1^0}$ between 250 to 350 GeV that correspond to bino-dominated LSPs satisfying the DM relic density limits via slepton coannihilations. An appropriately large choice of $m_{A/H}$ avoids pair-annihilations of essentially binos via the s-channels Higgs process. b Similar figure for $\tan \beta =40$

We now include the Spin-dependent direct detection of DM study in our analysis. Figure 8a shows the Spin-dependent (SD) scattering cross-section of the LSP with a neutron ($\sigma ^\textrm{SD}_{\chi n}$) as a function of the LSP mass for $\tan \beta = 10$. As before, we multiply $\sigma ^\textrm{SD}_{\chi n}$ with a scale factor $\xi$ (Eq. 24). Only those points satisfying the DM relic density upper bound as well as $(g-2)_\mu$ at 2$\sigma$ level are plotted and these are shown in green. The blue line is the constraint from the SD direct-detection experiment of XENON1T indicating discarded regions above the line at 90% CL. We further checked that the constraint from $\sigma ^\textrm{SD}_{\chi p}$ is weaker than $\sigma ^\textrm{SD}_{\chi n}$. Figure 8b is a similar plot for $\tan \beta = 40$. Compared to the SI DD cross-sections of Fig. 6, here we do not find any new discarded region. This is true for both choices of $\tan \beta$. Hence, all our conclusion for the SI DD cross-section analysis remain valid and analyzing $\sigma ^\textrm{SI}_{\chi p}$ itself is sufficient for a conclusion regarding the direct detection of DM.

Fig. 8

a Spin-dependent (SD) scattering cross-section of the LSP with a neutron $\sigma ^\textrm{SD}_{\chi n}$ multiplied by the previously mentioned scale factor $\xi$, as a function of the LSP mass, for $\tan \beta = 10$. The points satisfying the DM relic density upper bound and $(g-2)_\mu$ limits at 2$\sigma$ level are shown in green. The blue line refers to the constraint from the SD direct-detection experiment of XENON1T at 90% CL. The constraint from $\sigma ^\textrm{SD}_{\chi p}$ is weaker than $\sigma ^\textrm{SD}_{\chi n}$. b Similar figure for $\tan \beta = 40$

Fig. 9

a Scatter plot of $a_\mu$ for varying $M_1$ and other parameters as mentioned in the text for $\tan \beta = 10$. The parameter points shown in green satisfy the dark matter constraints including the direct detection limits from XENON1T. In order to probe the extent to which NHSSM can enhance $a_{\mu }^{\textrm{SUSY}}$, the maroon points refer to the result of a similar scanning in an MSSM parameter space (using $T^\prime _l=0$). None of the dark matter constraints are applied here. Throughout the analyses, we confirm that the points that satisfy $\sigma ^\textrm{SI}_{\chi p}$ also respect both n and p SD DD cross-sections namely, $\sigma ^\textrm{SD}_{\chi n}$ and $\sigma ^\textrm{SD}_{\chi p}$ respectively. The $1\sigma$ allowed band for $a_{\mu }$ is shown as black horizontal lines. b Similar figure for $\tan \beta =40$

Below, we probe how large $a_\mu$ can go depending on the variation of basic MSSM parameters like $M_1$ and $m_L$ and NHSSM parameter $T^\prime _\mu$. Thus, Fig. 9a shows a scatter plot of $a_\mu$ vs. $M_1$ for $\tan \beta = 10$. The parameter points shown in green satisfy the dark matter constraints including the direct detection limits from XENON1T. For comparison purposes, we draw maroon points located near the bottom of the $a_\mu$ axis. These points refer to the result of a similar scanning in an MSSM parameter space (by using $T^\prime _\mu =0$). None of the dark matter constraints are however applied here in the MSSM case. The smallness of the MSSM $a_\mu$ values shows that the bino-smuon loop contribution with effects from $T^\prime _\mu$ supersedes all the MSSM loop contributions. This indeed helps us in explaining the sign-correlation of $a_\mu$ with $T^\prime _\mu$ as mentioned earlier. The regions with large $a_\mu$ typically arise in small $M_1$ zones and this is likely to be case due to the associated smallness of slepton masses (see Fig. 5). The figure shows that the SI direct detection cross-section is below the XENON1T limit throughout the domain of variation chosen for $M_1$. The results shown in Fig. 9b confirm larger MSSM contributions to $a_\mu$ for an increase of $\tan \beta$ to 40, although the enhancement is much smaller than the NHSSM effects toward $a_\mu$, hence not so visible.

Figures 10 and  11 are the scatter plots for the dependence of $a_\mu$ on $T^\prime _\mu$ and $m_L$ when other parameters are varied. Figure 10a displays a scatter plot of $a_\mu$ for varying $T^\prime _\mu$ for $\tan \beta = 10$. The points shown in green satisfy the dark matter relic density upper bound and their SI direct detection (DD) cross-section $\sigma ^\textrm{SI}_{\chi p}$ values fall below the XENON1T limit. The large $a_\mu$ region of Fig. 10 refers to small $m_L$ values. This in turn correspond to small $M_1$ zones with enhanced $a_\mu$. The blanck (white) strip near the $T^\prime _\mu$ axis i.e., near the region with very small $a_\mu$ denotes the absence of valid parameter points, and this is related to the blanck region for smaller $m_L$ values (near the $m_L$ axis) of Fig. 11a. In combination, the resulting off-diagonal slepton mass values for large $T^\prime _\mu$ and small $m_L$ are likely to generate excluded regions because of the appearance of tachyonic slepton states or vacuum instability. With $T^\prime _\mu =y_\mu {A}_\mu$, the effect becomes more prominent for a larger $\tan \beta$ as may be seen in Figs. 10b and 11b. We further note that the large $a_\mu$ regions corresponding to small $m_L$ values in each of the parts of Fig. 11 refer to small $M_1$ and large $T^\prime _\mu$ zones. The LSP that satisfies the DM constraints is of higgsino type and associated with underabundance.

Fig. 10

a Scatter plot of $a_\mu$ vs. $T^\prime _\mu$ for $\tan \beta = 10$ for varying parameters as mentioned in the text. All the green points satisfy the same constraints as mentioned in Fig. 9. b Similar figure for $\tan \beta =40$

Fig. 11

a Same as Fig. 10a for $\tan \beta = 10$ except for varying $m_L$ instead of $T^\prime _\mu$. b Similar plot for $\tan \beta =40$

Fig. 12

a Display of the effect of $T^\prime _e$ on the electron Yukawa coupling $y_e$ for the shown values of the SUSY parameters. For each $\tan \beta$, the solid lines refer to $M_1=300$ GeV whereas the dotted lines are drawn for $M_1=700$ GeV. A large negative value for $T^\prime _e$ gives rise to a larger $|y_e|$ compared to the same for a similar positive value for $T^\prime _e$. $y_e$ is also seen to flip its sign as $T^\prime _e$ becomes positive. A larger $M_1$ also enhances $|y_e|$. No LTCYC condition for $y_e$ is applied here in order to display the extent of the Yukawa threshold correction of $y_e$. b Display of the electron magnetic moment $a_e$ for two different values of $\tan \beta$ as well as $M_1$. The other SUSY parameters are shown within the figure. The two solid lines refer to $\tan \beta =10,40$ for $M_1=300$ GeV, and the two dotted lines stand for $\tan \beta =10,40$ where $M_1=700$ GeV. Unless $T^\prime _e$ is tiny, negative values of $a_e$ that is required via the experimental limits follow from negative values of $T^\prime _e$. c A similar plot like a for electron. d A similar plot like b for muon

4.3 Inclusion of electron magnetic moment limits; Yukawa coupling enhancement in NHSSM

We will now probe the effect of including the ${}^{133}\textrm{Cs}$-based fine-structure constant measurement derived electron $g-2$ data in our analysis on top of the muon $g-2$ constraint. We will only consider the necessary amount for $T^\prime _e$ that would generate the required value for $a_e$. We will also highlight the threshold corrections to the electron Yukawa coupling $y_e$ due to $T^\prime _e$ and constrain the NHSSM parameter space accordingly. This will involve both cases namely a free enhancement of $y_e$ as well as limiting $y_e$ by requiring to stay within the LTCYC zone as mentioned earlier. Figure 12a shows the effect of $T^\prime _e$ on the electron Yukawa coupling $y_e$ for $\mu =400$ GeV and $m_L(=m_R)=500$ GeV. The blue lines are for $\tan \beta =10$, and the red lines are for $\tan \beta =40$. For each $\tan \beta$, the solid lines refer to $M_1=300$ GeV whereas the dotted lines are drawn for $M_1=700$ GeV. No LTCYC condition for $y_e$ is applied here in order to display the extent of the Yukawa threshold correction of $y_e$. A large negative value for $T^\prime _e$ gives rise to a larger $|y_e|$ compared to the same for an identical positive value of $T^\prime _e$. $y_e$ is also seen to flip its sign as $T^\prime _e$ becomes positive. A larger $M_1$ also enhances $|y_e|$. We point out that no LTCYC condition is applied here in order to show the extent how $y_e$ is affected due to an increased $T^\prime _e$. Depending on the value of $m_L$ and $M_1$, the above may in turn cause appearance of tachyonic selectron states. We now try to understand how $a_e$ behaves as $T^\prime _e$ is varied. Figure 12b displays $a_e$ for two different values of $\tan \beta$, and two different values of $M_1$ identical with those of Fig. 12a. The other SUSY parameters are $\mu =400$ GeV and $m_L(=m_R)=500$ GeV as used before. Unless $T^\prime _e$ is tiny, negative value of $a_e$ that is required due to the experimental data is correlated with negative value of $T^\prime _e$. We note that the solid lines of $a_e$ for $\tan \beta =10$ and 40 for $M_1=300$ GeV are very close to each other. The same is true for the two dotted lines corresponding to $M_1=700$ GeV. The reason for the approximate independence of $a_e$ on $\tan \beta$ would be clear in Sect. 4.3. The display of $y_\mu$ for a variation of $T^\prime _\mu$ as shown in Fig. 12c indicates a larger available zone of variation of $T^\prime _\mu$ compared to that of $T^\prime _e$ of Fig. 12a. This arises because of the difference of mass values of electron and muon. No LTCYC for $y_\mu$ is an issue here since the threshold correction of $y_\mu$ is moderate corresponding to the given span of variation of $T^\prime _\mu$ and the chosen SUSY mass parameters. A large negative value for $T^\prime _\mu$ gives rise to a larger $|y_\mu |$ compared to the same for a similar positive value for $T^\prime _\mu$. Unlike the case of $y_e$ of Fig. 12a, here $y_\mu$ does not change sign when $T^\prime _\mu$ becomes positive, albeit within its given range of interest for our study. A larger $M_1$ also enhances $|y_\mu |$. Figure 12d shows the variation of $a_\mu$ over $T^\prime _\mu$. We note that with a given value $T^\prime _{(e,\mu )}$, varying $M_1$ will alter $y_{(e,\mu )}$ which in turn would affect $a_{e,\mu }$.

4.3.1 Absence of $\tan \beta$ scaling in $a_l$ within NHSSM because of large ${A}^\prime _l$

In Sect. 4.3, we discussed the effects on the $\tan \beta$ related behavior of magnetic moments of leptons in scenarios that may induce large threshold corrections to the associated Yukawa couplings. In the above context, an NHSSM study of $a_l$ becomes quite relevant. With no LTCYC conditions applied Fig. 13 shows the scaling-related behaviors of $a_e$,$a_\mu$ with respect to a variation over $\tan \beta$ for the MSSM and the NHSSM cases. Here, $a_e$,$a_\mu$ are appropriately multiplied by powers of 10 so that all of them may be plotted in a single graph. The solid blue line refers to $a_e \times 10^{13}$ for $T^\prime _e=-5$ GeV, whereas the dashed blue line corresponds to $a_e \times 10^{14}$ for the MSSM case (i.e. $T^\prime _e=0$). Clearly, $a_e$ satisfies proportional relationship with $\tan \beta$ in MSSM, but this is no longer true in NHSSM, where $a_e$ is only a slowly increasing function of $\tan \beta$ with a large intercept.⁹ Showing identical behavior, the solid and dashed red lines are similar results for $a_\mu$.

Fig. 13

Display of scaling related behavior of $a_e$,$a_\mu$ with respect to $\tan \beta$ for the MSSM and the NHSSM cases. No LTCYC conditions are used here. Here, $a_e$,$a_\mu$ are appropriately multiplied by appropriate powers of 10. The solid blue line refers to $a_e \times 10^{13}$ for $T^\prime _e=-5$ GeV, whereas the dashed blue line corresponds to $a_e \times 10^{14}$ for the MSSM case (i.e.$T^\prime _e=0$). Clearly, $a_e$ satisfies proportional relationship with $\tan \beta$ in MSSM, but $a_e$ is merely a slowly increasing function of $\tan \beta$ with large intercept. Showing identical behavior, the solid and dashed red lines are similar results for $a_\mu$

4.3.2 Limiting the degree of threshold corrections of Yukawa couplings for leptons: LTCYC criterion vs the $a_e$ constraint

The non-holomorphic soft terms may be able to cause large Yukawa corrections for fermions, particularly the leptons so that the radiatively corrected values may be a few times the MSSM specified value namely $y_{l,(ref)} \equiv y_l=\frac{m_e}{(v_d/\sqrt{2})}$. This was already discussed for phenomenological analyses in Refs. [75, 78,79,80,81,82,83] where lepton masses were generated radiatively, obviously requiring a large radiative corrections. We should also point out that the present Higgs decay to $e^+ e^-$ from the LHC can only give an upper bound for $y_e$ which is about a few hundred times of its SM value [133,134,135].¹⁰ In our analysis, a negative $a_e$ may be accommodated by a relatively large radiative corrections to $y_e$. Of course a choice of a very large slepton mass would be able to suppress the radiative corrections, but here we want to explore the minimal zone of values of $|T^\prime _e|$ that with the chosen SUSY mass spectra of our analysis would be consistent with limits from $a_e$. Since $a_e$ is driven by $y_e$, in general, both for muon and electron, as mentioned before we choose to discard any parameter point that leads to ${y_l/y_{l(ref)}}>2$ with $l \equiv e,\mu$ and denote it as Limited Threshold Corrections of Yukawa Coupling (LTCYC) criterion. Figure 14a shows a scatter plot in the $(y_e/y_{e(ref)}- T^\prime _e)$ plane satisfying the LTCYC criterion in addition to all other constraints like DM relic density upper bound and direct detection limits, Higgs mass data, B-physics related limits and $(g-2)_{e,\mu }$ at 2$\sigma$ level for $\tan \beta =10$. The result is a bound of 14 GeV for $|T^\prime _e|$ and there are significant amount of parameter space with much smaller values like a range of 1.5–1.8 for ${y_e/y_{e(ref)}}$. Figure 14b shows a similar result for $\tan \beta =40$ showing the same cut-off at 13 GeV. We observe that for both the values of $\tan \beta$ there are appreciable amount of parameter space where the ratio ${y_e/y_{e(ref)}}$ stays between 1.5 and 1.8 (much below the maximum of 2). This corresponds to $-4 \mathrm{~GeV}<T^\prime _e<-2 \mathrm{~GeV}$. Figure 14c and d display the required values of the above Yukawa coupling ratio for correct $a_e$. LTCYC issue is important for $a_e$ only. For muon, the experimental limits of the magnetic moment is hardly stringent. Unlike the case of electron, the chosen region of variation of $T^\prime _\mu$ does not produce any appreciably large amount of radiative corrections to $y_\mu$. Hence, LTCYC for $y_\mu$ is not an issue for $a_\mu$, so that the condition gets automatically satisfied for the full parameter space under consideration. Indeed it may be seen that a positive $T^\prime _\mu$ as required for positive $a_\mu$ leads to values below unity for $y_\mu /y_{\mu (ref)}$.

Fig. 14

Limiting the level of leptonic Yukawa radiative corrections in NHSSM at the weak scale: $y_l$ refers to output Yukawa coupling value that is obtained after radiative corrections whereas $y_{l(ref)}$ is the tree level MSSM input value out of leptonic mass $m_l$. We choose to discard any parameter point that leads to $y_l/y_{l(ref)}>2$ and denote it as Limited Threshold Corrections of Yukawa Coupling (LTCYC) criterion. a Scatter plot in $(y_e/y_{e(ref)}- T^\prime _e)$ plane satisfying the LTCYC criterion in addition to all other constraints like DM relic density upper bound and direct detection limits, Higgs mass data, B-physics related limits and $(g-2)_{e,\mu }$ at 2$\sigma$ level for $\tan \beta =10$. A larger $|T^\prime _e|$ above 14 is seen not to satisfy the said limit. b Same as a for $\tan \beta =40$. c $(a_e-y_e/y_{e(ref)})$ plot showing a possibility of finding the desired $a_e$ for radiative corrections above 45%. d Same as c for $\tan \beta =40$

The fact that NHSSM parameter $T^\prime _e$ is able to generate a significant amount of correction to $y_e$, while on the other hand there is an approximate sign correlation between $a_{e,\mu }$ with $T^\prime _{e,\mu }$ gives one a reasonable expectation for the scaled magnetic moment ratio $R_{e,\mu }=\frac{(a_e/m_e^2)}{(a_\mu /m_\mu ^2)}$ to be within the desired zone, namely $R_{e,\mu } \simeq -15$ (see Eq. 4). Figure 15 is a scatter plot of the above ratio with parameters in the x-axis, namely $T^\prime _e$ and $M_1$ that are important for the radiative corrections to Yukawa coupling $y_e$. All other parameters including also $T^\prime _\mu$ are varied according to the mentioned respective ranges of Table 1 considering $\tan \beta =10$ while also applying the LTCYC conditions for the two leptons as mentioned earlier. All the points (shown in green) satisfy the DM relic density constraint for its upper limit, the XENON1T data for SI direct detection, $a_e$ and $a_\mu$ limits showing the desired $R_{e,\mu }$ values well within its uncertainty limits. Figure 15b for $\tan \beta =10$ shows scatter points in the $M_1-R_{e,\mu }$ plane. The points with large $R_{e,\mu }$ correspond to smaller $M_1$ values. The DM satisfied (green) region satisfy  GeV.

Fig. 15

a Scatter plot of magnetic moment ratio $a_e/a_\mu$ scaled with ${m_\mu }^2/{m_e}^2$ against $T_e^\prime$ for $\tan \beta =10$. All the points (shown in green) satisfy the DM relic density constraint for its upper limit, the XENON1T data for SI direct detection, $a_e$ and $a_\mu$ limits. LTCYC conditions are applied in addition. b Similar scatter plot for a variation of $M_1$

We will now investigate how the conclusion of Sect. 4.2 gets modified when we further restrict the NHSSM parameter space toward satisfying the $(g-2)_e$ constraint. First, since we demand $y_e$ to be within the LTCYC zone, $|T_e^\prime |$ should be small and this comes to around 14 GeV or less. Considering the fact that SUSY contributions to $a_e$ needs to be negative, the limits on $T^\prime _e$ becomes . Figure 16a shows the combined results (green points) of imposing all the constraints like Higgs mass data, B-physics limits, DM constraints for relic density and SI direct detection in addition to $a_\mu$ and $a_e$ limits drawn in the plane of $M_1-T_e^\prime$. Here and henceforth in all the subsequent figures of this work LTCYC limits for $y_e$ and $y_\mu$ are understood to have been applied by default. The valid region for $M_1$ that satisfy all the constraints comes out to be $230<M_1<800$ GeV for $\tan \beta =10$. Figure 16b, a similar plot for $\tan \beta =40$ has a valid $M_1$ zone satisfying $230<M_1<660$ GeV.

Fig. 16

a Scatter plots in the $M_1 - T^{\prime }_{e}$ plane for $\tan \beta = 10$. The points shown in green arise from imposing all the constraints like Higgs mass data, B-physics limits, DM constraints for relic density and SI direct detection in addition to $a_\mu$ and $a_e$ limits. Here and henceforth in all the subsequent figures of this work LTCYC limits for $y_e$ and $y_\mu$ are understood to have been applied by default. b Similar plot for $\tan \beta =40$

Figure 17 shows similar scatter plots in the $M_1-T^\prime _\mu$ plane. The larger range of variation of $T^\prime _\mu$ compared to $T^\prime _e$ arises from the way $T^\prime _{e,\mu }$ are defined, namely these are scaled with the respective Yukawa couplings. The conclusion for valid upper limit of $M_1$ remains the same as before for both values of $\tan \beta$.

Fig. 17

a Scatter plots in the $M_1 - T^{\prime }_{\mu }$ plane for $\tan \beta = 10$. The color scheme is same as that of Fig. 16. b Similar plot for $\tan \beta =40$

Fig. 18

a Scatter plot in $M_1-\mu$ plane for $\tan \beta = 10$. All the points shown in green satisfy $(g-2)_{e,\mu }$, dark matter relic density upper bound and XENON1T provided $\sigma ^\textrm{SI}_{\chi p}$ bounds. b Similar plot for $\tan \beta =40$

Fig. 19

a Scatter plots in $T^{\prime }_e - T^{\prime }_{\mu }$ plane for $\tan \beta =10$. The color scheme is same as that of Fig.16. b Similar plot for $\tan \beta =40$

We are to explore now the effect of imposing ${(g-2)}_e$ constraint on the $M_1-\mu$ plane of Fig. 18. We will compare the above with the corresponding result of Fig. 7 drawn for ${(g-2)}_\mu$. The availability of NHSSM parameter space gets reduced significantly because the threshold corrections to $y_e$ should not become too large. We remember that the above corrections at least involve masses of bino, sleptons, as well as the trilinear NH coupling $T^\prime _e$. Hence, a given set of $M_1$ and $m_L$ that is available in the muon $(g-2)$ analysis, may not be consistent when combined with non-vanishing $T^\prime _e$ to satisfy ${(g-2)}_e$. Thus, when one imposes the ${(g-2)}_e$ constraint, that in turn is sensitive on the corrections to $y_e$, the reduction of parameter space is rather unavoidable. The green points of Fig. 18a satisfy $(g-2)_{e,\mu }$ constraints at 2$\sigma$ level in addition to obeying the dark matter relic density bound. The associated $\sigma ^\textrm{SI}_{\chi p}$ values also fall below the XENON1T limit. Figure 18b shows a similar result for $\tan \beta =40$ where a largeness of $\textrm{tan}\beta$ further takes away a significant amount of parameter space so as to have $y_e$ within LTCYC zone.

Figure 19a is a scatter plot in the plane of trilinear NH parameters for electron and muon for $\tan \beta =10$. The points shown in green satisfy the DM relic density constraint, the XENON1T $\sigma ^\textrm{SI}_{\chi p}$ data along with $(g-2)_\mu$ and $(g-2)_e$ limits at $2\sigma$ level. The points also have $y_e$ in the LTCYC zone. Clearly, $T^\prime _e$ should be appreciably large so as to satisfy $(g-2)_e$ data. We find the valid region to have $-14~\textrm{GeV}<T^\prime _e<0$.

4.4 LHC constraints from slepton pair production and constraint from compressed higgsino LSP scenario

4.4.1 Both $(g-2)_\mu$ and $(g-2)_e$

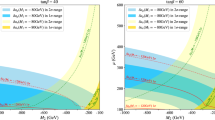
With no difference in SUSY sparticle content between NHSSM and MSSM, we directly apply the SUSY constraints from LHC data on our analysis. We intend to identify the exclusion region of NHSSM parameter space from the ATLAS data for slepton pair production that considered selectron and smuon in the analysis [125]. The later gives an exclusion region in the $(m_{\tilde{\chi }^0_1}-m_L)$ plane. We note here that by directly applying the ATLAS bound on our parameter space we are taking a conservative approach as the exclusion can potentially get somewhat weaker for the higgsino LSP scenario. The reason is as follows. The ATLAS limit is derived for a simplified model assuming $BR({\tilde{l}} \rightarrow l \widetilde{\chi }_1^0) = 100 \%$, This criterion is not strictly satisfied in the higgsino LSP region, where the proximity of $m_{\widetilde{\chi }_1^0}$ and $m_{{\widetilde{\chi }_1}^{\pm }}$ allows for a significant branching ratio of the sleptons to final states involving $\nu _l$ and ${\widetilde{\chi }_1}^{\pm }$. This may lead to a reduction in the number of signal leptons and thus to the weakening of the exclusion limit.

We will further analyze the constraint from a compressed scenario with higgsino as LSP that is associated with closely spaced values for the masses $m_{\widetilde{\chi }_1^0}$, $m_{{\widetilde{\chi }_1}^{\pm }}$ and $m_{\widetilde{\chi }_2^0}$. This is based on the ATLAS result given in Fig. 14a of Ref. [136].

Focusing on higgsino type of LSPs, we show Fig. 20 drawn in the plane of $m_{\widetilde{\chi }_2^0}-\Delta _{21}$ where $\Delta _{21}=m_{\widetilde{\chi }_2^0}-m_{\widetilde{\chi }_1^0}$. The above-mentioned 1$\sigma$ contour of the ATLAS result is shown in black. The red colored points appearing to the left of the contour form the discarded zone, whereas the cyan colored points survive the constraint. Clearly, a compressed scenario with $\Delta _{21}$ having values up to 10–15 GeV are eliminated for  GeV. Larger values of $\Delta _{21}$ in the same zone of $m_{\widetilde{\chi }_2^0}$ are alright. The corresponding lower limit of $m_{\widetilde{\chi }_1^0}$ is approximately 185 GeV. Thus, we may conclude that not all values of LSP masses below 185 GeV are valid. Hence, with a conservative standpoint we henceforth consider the lowest value for a higgsino type of LSP to be 185 GeV.¹¹

Figure 21a shows a scatter plot in $m_L - m_{\tilde{\chi }^0_1}$ plane for $\tan \beta =10$. All the points satisfy the perturbativity of $y_e$. Considering the constraint for compressed higgsino states as mentioned above, $m_{\tilde{\chi }^0_1}$ is allowed to have values above 185 GeV. The points shown in green satisfy the DM relic density constraint, the XENON1T $\sigma ^\textrm{SI}_{\chi p}$ data along with $(g-2)_\mu$ and $(g-2)_e$ limits at $2\sigma$ level. The points also have $y_e$ in the LTCYC zone. On the top of the figure we draw the black line that indicates the current exclusion bounds in the $m_L - m_{\tilde{\chi }^0_1}$ plane at the LHC. The green points that stay outside the contour are the residual parameter points that would also satisfy the LHC limit. On the higher LSP mass side, irrespective of slepton masses, for $\tan \beta =10$ a value of $m_{{{\tilde{\chi }}}^0_1}$ between 400 to 500 GeV would satisfy all the constraints considered in this analysis. For slepton masses above 700 GeV, valid LSP mass would lie below 350 GeV. Figure 21b shows a similar result for $\tan \beta =40$. Here, the LHC contour engulfs a lot of region of the parameter space with a larger mass of the LSP as shown in green. The region with slepton masses above 700 GeV allows valid LSP mass up to 275 GeV. Apart from the above, the LSP mass values for valid parameter points outside and near the black contour in its lower side are correlated with $m_L$ in an approximately linear fashion. One finds that with $\tan \beta =10$, $m_{{{\tilde{\chi }}}^0_1}$ can be as large as 400 GeV when $m_L=550$ GeV whereas the later numbers are 400 GeV and 500 GeV respectively for $\tan \beta =40$.

Fig. 20

Allowed (cyan) and disallowed (red) regions in the plane of $m_{\widetilde{\chi }_2^0}-\Delta _{21}$ with respect to the 1$\sigma$-level contour (black line) as given by the ATLAS data namely Fig.14a of Ref. [136]. The corresponding lower limit of $m_{\widetilde{\chi }_1^0}$ satisfying the above constraint is about 185 GeV in this higgsino dominated $\widetilde{\chi }_1^0$-$\widetilde{\chi }_2^0$-${\widetilde{\chi }_1}^{\pm }$ scenario

Fig. 21

a Scatter plot in $m_{\tilde{\chi }^0_1}-m_L$ plane for $\tan \beta =10$. The points shown in green satisfy the DM relic density constraint, the XENON1T $\sigma ^\textrm{SI}_{\chi p}$ data along with $(g-2)_\mu$ and $(g-2)_e$ limits at $2\sigma$ level. The points also have $y_e$ in the LTCYC zone. The black line indicates the current exclusion bounds in the slepton-neutralino plane as obtained from slepton pair production data from ATLAS, LHC [125]. All the points pass the compressed higgsino constraint as mentioned in the text. b Similar plot for $\tan \beta =40$

4.4.2 Only $(g-2)_\mu$

Since the LHC data is seen to affect the combined analysis of ${(g-2)}_\mu$ and ${(g-2)}_e$ with dark matter rather strongly, we feel that it is important to go back and examine the situation of considering only the ${(g-2)}_\mu$ constraint with dark matter (as in Sect. 4.2) in relation to the ATLAS constraints described above. The results are seen in Fig. 22a and b. Figure 22a shows the ATLAS data [125] satisfied appropriate mass values of sparticles in the $m_L - m_{\tilde{\chi }^0_1}$ plane. As before, we also impose the constraint from the compresed higgsino scenario. For $\tan \beta =10$, satisfying all the constraints, valid $m_{\tilde{\chi }^0_1}$ ranges from 400 GeV to 750 GeV for any value of $m_L$. On the other hand when $m_L>700$ GeV, $m_{\tilde{\chi }^0_1}$ assumes values up to the same upper limit namely 750 GeV. For $\tan \beta =40$, as seen in Fig. 22a the above numbers for $m_{\tilde{\chi }^0_1}$ are in between 400 and 775 GeV, whereas for $m_L>700$ GeV, valid $m_{\tilde{\chi }^0_1}$ zone extends to 775 GeV. Apart from the above, the LSP mass values for valid (green) parameter points outside and near the black contour in its lower side are correlated with $m_L$ in an approximately linear fashion. One finds for both the values of $\tan \beta$, $m_{{\tilde{\chi }}^0_1}$ can be as large as 400 GeV when $m_L=550$ GeV.

Fig. 22

a Scatter plot in $m_{\tilde{\chi }^0_1}-m_L$ plane for $\tan \beta =10$. The points shown in green satisfy the DM relic density constraint, the XENON1T $\sigma ^\textrm{SI}_{\chi p}$ data along with $(g-2)_\mu$ and $(g-2)_e$ limits at $2\sigma$ level. The points also have $y_e$ in the LTCYC zone. The black line indicates the current exclusion bounds in the slepton-neutralino plane as obtained from slepton pair production data from ATLAS, LHC [125]. All the points pass the compressed higgsino constraint as mentioned in the text. b Similar plot for $\tan \beta =40$

We now show two representative points of our analysis in Table 2 for two values of $\textrm{tan}\beta$. Referring to Fig. 21a that corresponds to satisfying both $(g-2)_\mu$ and $(g-2)_e$ constraints, the two points are chosen based on the ATLAS provided contours [125] for slepton pair production shown in black. We choose $tan\beta =10$ and 40 for specifying two benchmark points BP1 and BP2 both of which correspond to moderate values of $m_{\widetilde{\chi }_1^0}$ and slepton mass parameter $m_L$. The points are far away from having any effect due to the constraints from compressed spectra. We remind that all the left and right slepton mass parameters are taken to be equal. The LSP is almost a higgsino in nature. The relic density is satisfied via like ${\tilde{\chi }}_1^0- {\tilde{\chi }}_2^0$ or ${\tilde{\chi }}_1^0-{\tilde{\chi }}_1^{\pm }$ coannihilation mechanisms. Apart from other constraints like ${(g-2)}_{e,\mu }$ and dark matter, the constraints from B-physics are easily satisfied because of large squark masses of the third generation. With a larger stop-mixing via $A_t$, the Higgs mass is satisfied within the limits of Eq. (23). Notably, $a_e$ value of BP2 for $\tan \beta =40$ is similar to that of BP1 corresponding to $\tan \beta =10$. This is because, as discussed earlier, in NHSSM, the SUSY contributions to $a_e$ has a milder $\tan \beta$ dependence unlike a proportional relationship as seen in MSSM. With LSP as a higgsino it is a candidate of a subdominant component of DM. Hence we use a scale factor $\xi$ (Eq. 24) that further reduces the SI and SD direct detection cross sections. Certainly, the valid parameter space would be larger for both small and large $\tan \beta$ if we had chosen only $(g-2)_\mu$ among the two magnetic moment constraints.

Table 2 Representative Points in NHSSM corresponding to SUSY scale input of soft parameters that satisfy all the constraints considered in the analysis along with $a_\mu$ and $a_e$ (using data from ${}^{133}\textrm{Cs}$-based measurement). All the dimensionful parameters are in GeV. Here, $T_e^\prime =y_e A_e^\prime$ and $T_t=y_t A_t$

5 Results for $a_e$ constraint from the ${}^{87}\textrm{Rb}$-based experiment

Finally, we briefly discuss the effects of using the $a_e$ constraint from Eq. (3), i.e. from the ${}^{87}\textrm{Rb}$-based experiment as mentioned earlier. There is a 1.6$\sigma$ deviation from the SM result and the spread is more toward the positive side, unlike the case of Eq. (2) corresponding to the experiment using ${}^{133}\textrm{Cs}$ matter-wave interferometry. Focusing on only $\tan \beta =10$, the scatter-plot of Fig. 23a in the $T^{\prime }_e - T^{\prime }_{\mu }$ plane shows the requirement of both positive and negative signs of $T^{\prime }_e$ in relation to the results shown in Fig. 12. The points shown in green satisfy the DM relic density constraint, the XENON1T $\sigma ^\textrm{SI}_{\chi p}$ data along with $(g-2)_\mu$ and $(g-2)_e$ limits at $2\sigma$ level. The points also have $y_e$ in the LTCYC zone. A milder deviation corresponding to Eq. (3) makes the result to have similarity with the case of using only the $a_\mu$ constraint. Similarly, we plot Fig. 23b indicating parameter points in the $m_{\tilde{\chi }^0_1}-m_L$ plane. Further details regarding constraint from the ATLAS data are same as those of Fig. 21. Expectedly, the result is closer to that of Fig. 22a for the only $(g-2)_i$ case.

Fig. 23

a Analysis with ${}^{87}\textrm{Rb}$ data for $a_e$ for scatter-plots in the $T^{\prime }_e - T^{\prime }_{\mu }$ plane $\tan \beta =10$. The color scheme and constraints imposed are same as that of Fig. 19. b Analysis with ${}^{87}\textrm{Rb}$ data for $a_e$ for scatter-plots in the $m_{\tilde{\chi }^0_1}-m_L$ plane for $\tan \beta =10$. Further details are same as those of Fig. 21

6 Conclusion

The Standard Model of particle physics has achieved a remarkable degree of success ever since the discovery of the Higgs Boson. Apart from the above discovery itself, the measurements of Higgs couplings, various results from the ATLAS and the CMS experiments of the LHC, several results from low energy precision measurements involving flavor physics also point towards a strong validity of SM. However, theoretical issues such as the gauge hierarchy problem, and observational evidences like the dark matter, baryon asymmetry, non-zero neutrino mass etc. demands the SM to be extended beyond its current boundary. Hence, a search for a BSM physics is highly relevant in the present era. In this connection, we note that the recent Fermilab experiment on muon $g-2$ measurement has confirmed the deviation from the SM value obtained in the previous measurement at BNL. Assuming that the SM result that depends on low energy $e^+ e^-$ data will not get drastically altered in the near future, or in other words, it would take a while for the lattice-based computations of the hadronic error to reach a definite conclusion, it is important to pursue the implications of the Fermilab announcement from the BSM physics perspective.

The combined discrepancy of the Fermilab and the BNL data is at an impressive level of 4.2$\sigma$. The anomaly amount itself is of the order of electroweak corrections in SM. Thus, it is very crucial to probe a BSM physics scenario that may produce a large contribution to the above observable at the same energy scale. SUSY, undoubtedly one of the most important candidates for new physics, is well-known to be capable of producing a large correction to ${(g-2)}_\mu$. There are regions of parameter space in MSSM with appropriate wino, bino, higgsino and left and right handed smuon masses that can explain the Fermilab result, typically for a large $\tan \beta$. There are also dedicated beyond the MSSM models that can enhance the $(g-2)_\mu$ contribution by virtue of the model properties, including new symmetries. In this analysis, staying within the MSSM sparticle spectra, we augment MSSM with non-holomorphic trilinear soft breaking interactions. We also pointed out that unlike MSSM soft terms, the non-holomorphic terms which for MSSM are soft SUSY breaking in nature do not have the privilege of being supported by popular UV complete models. The appropriate NH term generates an enhancement of the SUSY contributions to $(g-2)_\mu$ via a coupling effect which helps to easily accommodate the data. The model neither demands any flavor unfriendly choice of different right and left slepton masses nor does it demand a large $\tan \beta$ or a light chargino. One uses a large bino-smuon loop contribution with stronger mixing of the L-R smuons to produce the desired effect. Using the Fermilab data to constrain the model, we further impose constraints due to dark matter related observables. It is found that a higgsino-dominated dark matter having an underabundant contribution to the DM relic density can be consistent with direct detection cross-section as well as ${(g-2)}_\mu$. For ${(g-2)}_\mu$, a scenario with dominant bino-smuon loop contribution can satisfy the data via a large L-R mixing caused by the wrong Higgs couplings of the non-holomorphic terms.

We further impose the relevant direct search bounds from the LHC, e.g. the constraints from the slepton pair production searches from ATLAS as well as the constraint coming from the compressed higgsino searches. The conclusion of the combined ${(g-2)}_\mu$ analysis with dark matter and collider limits is the following (Fig. 22). For $\tan \beta =10$ and 40, satisfying all the constraints, valid $m_{\tilde{\chi }^0_1}$ ranges from 400 GeV to 750 GeV for any value of $m_L$. On the other hand when $m_L>700$ GeV, $m_{\tilde{\chi }^0_1}$ stays in between the lower limit of $\sim 185$ GeV to the same upper limit namely 750 GeV. Apart from the above, the LSP mass values for the valid parameter points outside and near the ATLAS provided contour in its lower side are correlated with $m_L$ in an approximately linear fashion. One finds for both the values of $\tan \beta$, $m_{{{\tilde{\chi }}}^0_1}$ at its minimum can be around 400 GeV when $m_L \simeq 600$ GeV.

We then extend the muon $g-2$ analysis in NHSSM to include the electron $g-2$ data as derived from the fine-structure constant measurement based on ${}^{133}\textrm{Cs}$ matter-wave interferometry. The resulting ${(g-2)}_e$ shows an approximately $2.5\sigma$ level of discrepancy, but interestingly, it comes with a negative sign. It becomes very challenging to accommodate the muon and electron g-2 anomalies simultaneously in MSSM. This measurement is in contrast to the ${}^{87}\textrm{Rb}$-based measurement which shows a smaller positive deviation. Here, we use the more unfriendly ${}^{133}\textrm{Cs}$-based data in our work to compare our results with previous MSSM-based analyses and for probing the potential of the non-standard soft terms in relation to any related phenomenology. The present work approaches to accommodate $a_e$ via appropriately enhancing the Yukawa threshold corrections for $y_e$ by using minimum possible $T^\prime _e$ values for the chosen mass spectra. The analysis satisfies constraints from vacuum stability and charge and color breaking minima. The negative sign for the SUSY contributions to $a_e$ could be generated by negative $T^\prime _e$. An interesting feature of $a_e$ in NHSSM is that one cannot enhance it appreciably by increasing $\tan \beta$. $a_e$ at best can be a slowly increasing function of $\tan \beta$, but unlike MSSM, it is no longer proportional to $\tan \beta$, an effect that arises out of a large threshold correction to $y_e$.

The conclusion of the combined ${(g-2)}_\mu$ and ${(g-2)}_e$ analysis with dark matter and collider limits is the following (see Fig. 21). For $\tan \beta =10$, satisfying all the constraints, valid $m_{\tilde{\chi }^0_1}$ ranges from 400 to 500 GeV for any value of $m_L$. On the other hand when $m_L>700$ GeV, $m_{\tilde{\chi }^0_1}$ stays in between the lower limit of $\sim$185 GeV to the same upper limit namely 500 GeV. For $\tan \beta =40$, the ATLAS contour engulfs a lot of parameter space with larger mass of the LSP leaving a small window of $m_{\widetilde{\chi }_1^0}$ between 400 to 425 GeV for any $m_L$. For $m_L>700$ GeV, the valid $m_{\tilde{\chi }^0_1}$ zone is from 185 GeV to 275 GeV. Apart from the above, the LSP mass values for valid parameter points outside and near the ATLAS provided contour in its lower side are correlated with $m_L$ in an approximately linear fashion. One finds that for $\tan \beta =10$, $m_{{{\tilde{\chi }}}^0_1}$ can be as large as 410 GeV for $m_L$ below 550 GeV. For $\tan \beta =40$, $m_{{{\tilde{\chi }}}^0_1}$ can be as large as 425 GeV when $m_L$ is below 440 GeV. Finally, we presented two representative points that satisfy all the constraints considered in this analysis. We also discussed briefly the results of considering the limits of $a_e$ as coming from the ${}^{87}\textrm{Rb}$-based experiment indicating a smaller deviation from the SM result.