1 Introduction

The accelerated expansion of the late Universe is commonly attributed to the existence of an extra cosmic constituent known collectively as “Dark Energy”. In the context of the concordance \(\Lambda \)CDM scenario, dark energy is just the standard cosmological constant and this scenario is very successful in interpreting observations such as Cosmic Microwave Background (CMB) [1], Supernovae Ia (SNIa) [2], Large Scale Structure (LSS) [3], etc.

However, recently various observational issues have gain attention, for example the Hubble constant tension, that is the discrepancy between the value of the Hubble constant from the CMB and the corresponding one from Cepheids up to  5\(\sigma \) (see [4] for a thorough and recent review). Another example is the difference of the root-mean-square amplitude of matter over-density perturbation \(\sigma _{8}\), between the value extracted from the CMB (imposing \(\Lambda \)CDM) and the corresponding value extracted by fitting on the Large Scale power spectrum [5]. Furthermore, the value of the cosmological constant in the late Universe seems to be inconsistent with the corresponding value at the early Universe [6].

On the other hand, the current gravitational theory, namely General Relativity (GR), cannot be re-normalized and thus it is difficult to be consistent with a quantum description [7]. Hence, a large portion of the literature follows the direction of modified gravity, which seems promising to solve the latter problem [8], and in addition it is very efficient in describing the two phases of accelerated expansion of the universe [9, 10]. Finally, note that modified gravity can be efficient in alleviating the two aforementioned tensions of \(\Lambda \)CDM cosmology, namely the \(H_{0}\) and the \(\sigma _{8}\) ones [11].

Along these lines and due to the fact that the Einstein-Hilbert Lagrangian is just one of many possible Lagrangians that could lead to the same field equations, the community has developed many frameworks of modified gravity. A class of gravitational modification arises from the extension of the Einstein-Hilbert Lagrangian with extra terms, however maintaining its geometrical structure, i.e. its Riemannian formulation, resulting for instance in f(R) gravity [12], in Gauss-Bonnet and f(G) gravity [13, 14], in Weyl gravity [15], etc. A more radical approach to follow is to modify the building blocks of General Relativity, that is the underlying geometrical structure. An instance of this kind of modification arises from the torsional formulation of gravity, namely the modified teleparallel theories, such as the f(T) gravity [16, 17], the \(f(T,T_{G})\) gravity [18], the scalar-torsion theories [19, 20] etc. In contrast to the standard GR and the corresponding f(R) extensions, which are based on curvature, in modified teleparallel formulation gravity is manifested via the torsion tensor, with curvature being zero.

There is yet another possibility, which is formulated using the non-metricity Q of the connection. In this setup, only the non-metricity is non-zero while curvature and torsion both vanish. Hence, non-metricity can be used in order to describe gravity through geometry, leading to the so-called Symmetric Teleparallel Equivalent to General Relativity (STEGR) [21]. It is interesting to note that although Teleparallel Equivalent of General Relativity (TEGR) as well as STEGR, are completely equivalent to General Relativity at the level of equations, when we modify them the resulting theories f(R), f(T) and f(Q) are different theories. These types of modifications have in general more degrees of freedom than the two of standard GR, unless specific constraints are imposed in the functional forms. Thus, during the last years f(Q) gravity, its application to cosmology and generalizations has attracted the interest of the literature [22,23,24,25,26,27,28,29, 29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48].

A very strong constraint on modified gravity models in the early Universe comes from the era of Big Bang Nucleosynthesis (BBN) [49,50,51,52,53,54]. In the present work we are interested in imposing BBN constraints on f(Q) gravity, within an analytical approach, following [55,56,57,58,59]. Specifically, we use observational data on primordial abundances of \( {}^{4}{He}\) to constrain all known f(Q) models along some that are proposed for the first time inspired by the successful f(T) models. The plan of the manuscript is the following. In Sect. 2 we provide a formal description of Symmetric Teleparallel gravity and its f(Q) extension, while in Sect. 3 we present the cosmological solutions of the theory alongside the specific f(Q) models that are going to be studied. In Sect. 4 we briefly review the formalism of BBN constraints, and then in Sect. 5 we apply it in the framework of f(Q) gravity. Finally, in Sect. 6 we derive our conclusions and we point out further directions.

2 Symmetric teleparallel gravity

General Relativity is built upon Lorentzian Geometry which is specified by choosing a connection that is symmetric and metric compatible. The latter is the Levi-Civita connection and due to its properties it only produces non-zero curvature, whilst torsion and non-metricity are zero [60]. Nevertheless, a different kind of connection can be utilized when using geometrodynamics as the mathematical framework for gravity. As a matter of fact the most general connection is called metric-affine it is described by the formula

$$\begin{aligned} \Gamma ^{\alpha }{}_{\mu \nu }&=\mathring{\Gamma }^{\alpha }{}_{\mu \nu }+K^{\alpha }{}_{\mu \nu }+L^{\alpha }{}_{\mu \nu }, \end{aligned}$$
(1)

where \(\mathring{\Gamma }^{\alpha }{}_{\mu \nu }\) represents the Christoffel symbols of the Levi-Civita connection, \(K^{\alpha }{}_{\mu \nu }\) is the contorsion tensor and \(L^{\alpha }{}_{\mu \nu }\) is the disformation tensor related to the non-metricity [61]

$$\begin{aligned} Q_{\alpha \mu \nu }&:=\nabla _{\alpha }g_{\mu \nu }. \end{aligned}$$
(2)

The disformation tensor can then be expanded as [21]

$$\begin{aligned} L^{\alpha }{}_{\mu \nu }&:=\frac{1}{2}g^{\alpha \beta }\left( -Q_{\mu \beta \nu }-Q_{\nu \beta \mu }+Q_{ \beta \mu \nu }\right) , \end{aligned}$$
(3)

and encapsulates all the information coming from the non-metricity tensor of the general affine connection. In summary, these three types of geometric deformation \(\mathring{\Gamma }^{\alpha }{}_{\mu \nu }\), \(K^{\alpha }{}_{\mu \nu }\) and \(L^{\alpha }{}_{\mu \nu }\) form a kind of “trinity of gravity”, which encompasses all components of the general connection \(\Gamma ^{\alpha }{}_{\mu \nu }\) [62]. This practically implies that it is possible to express the geometry of a gravitational theory in either curvature, non-metricity or torsion. A connection which admits only non-metricity, whilst curvature and torsion are zero, is called Symmetric Teleparallel Gravity (STG) connection, while connections which have only zero curvature are called teleparallel connections [63, 64].

Similarly to TEGR, which is based on a connection which has only torsion [65], the STG connection has only non-metricity and hence STEGR is equivalent to GR at the level of field equations, since its action differs by a boundary term from the Einstein-Hilbert. In particular, defining the non-metricity scalar as [21]

$$\begin{aligned} Q:= & {} -\frac{1}{4}Q_{\alpha \mu \nu }Q^{\alpha \mu \nu }+\frac{1}{2}Q_{\alpha \mu \nu }Q^{ \mu \alpha \nu }\nonumber \\ {}{} & {} +\frac{1}{4}Q_{\alpha }Q^{\alpha }-\frac{1}{2}{\bar{Q}}_{\alpha }Q^{ \alpha }, \end{aligned}$$
(4)

with

$$\begin{aligned} Q_{\mu }&:=Q_{\mu }{}^{\alpha }{}_{\alpha },\quad \quad {\bar{Q}}_{\mu }:=Q{}_{\alpha }{}^{ \alpha }{}_{\mu }, \end{aligned}$$
(5)

one has the relation

$$\begin{aligned} \mathring{R}&=Q+B, \end{aligned}$$
(6)

where \(\mathring{R}\) is the Ricci scalar of the Levi-Civita connection, and the boundary term is

$$\begin{aligned} B:=\mathring{\nabla }_{\alpha }\left( {\bar{Q}}^{\alpha }-Q^{\alpha }\right) \!. \end{aligned}$$
(7)

Therefore, General Relativity, which uses \(\mathring{R}\) as the Lagrangian density, and STEGR, which uses Q, lead to exactly the same equations.

One can extend STEGR by extending the Lagrangian to an arbitrary function, resulting to f(Q) gravity, with action [21, 66]

$$\begin{aligned} S_{G}&={\displaystyle \int d^{4}x\,\sqrt{-g}\left[ -\frac{1}{16\pi G}f(Q)+\mathcal {L}_{m} \right] ,} \end{aligned}$$
(8)

where G is the gravitational constant and \(\mathcal {L}_{m}\) the matter Lagrangian. The corresponding field equations are

$$\begin{aligned}{} & {} \sqrt{-g} \left( \frac{1}{2}fg_{\mu \nu }- \frac{\partial f}{\partial g^{\mu \nu }}\right) -2\nabla _{\alpha }\left( \sqrt{-g}P^{\alpha }{}_{\mu \nu }\right) \nonumber \\{} & {} \quad =8\pi G\sqrt{-g} \,T_{\mu \nu }, \end{aligned}$$
(9)

with

$$\begin{aligned} \frac{\partial f}{\partial g^{\mu \nu }}&=-\frac{f_{\text {Q}}}{\sqrt{-g}}\left( \frac{\partial \left( \sqrt{-g}Q\right) }{ \partial g^{\mu \nu }}-\frac{1}{2}\sqrt{-g}Qg_{\mu \nu }\right) \nonumber \\&=-f_{\text {Q}}\biggl [c_{1}\left( 2Q_{\alpha \beta \mu }Q^{\alpha \beta }{}_{\nu }-Q_{ \mu \alpha \beta }Q^{\nu }{}_{\alpha \beta }\right) \nonumber \\&\quad +c_{2}Q_{\alpha \beta \mu }Q^{\beta \alpha }{}_{\nu }+c_{3}\left( 2Q_{\alpha }Q^{\alpha } {}_{\mu \nu }\!-\!Q_{\mu }Q_{\nu }\right) \nonumber \\&\quad +c_{4}{\widetilde{Q}}_{\mu }{\widetilde{Q}}_{\nu }+c_{5}{\widetilde{Q}}_{\mu }Q^{\alpha }{ }_{\mu \nu }\biggl ], \end{aligned}$$
(10)

and where the conjugate to f(Q) is defined as [21]

$$\begin{aligned} P^{\alpha }{}_{\mu \nu }&:=\frac{1}{2\sqrt{-g}}\frac{\partial (\sqrt{-g}f(Q))}{\partial Q{}_{\alpha }{}^{\mu \nu }}\,\nonumber \\&=-f_{\text {Q}}\biggl \{c_{1}Q^{\alpha }{}_{\mu \nu }+c_{2}Q_{(\mu }{}^{\alpha }{}_{\nu )}+c_{3}g_{\mu \nu }Q^{\alpha }\nonumber \\&\quad \,+c_{4}\delta {}^{\alpha }{}_{(\mu }{\widetilde{Q}}_{\nu )}+\frac{c_{5}}{2}\bigl [{\widetilde{Q}}^{\alpha }g_{\mu \nu }+\delta {}^{\alpha }{}_{(\mu }Q_{\nu )}\bigr ]\biggl \}, \end{aligned}$$
(11)

while as usual the matter energy momentum tensor is defined as

$$\begin{aligned} T_{\mu \nu }&:=-\frac{2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}\mathcal {L}_{m})}{\delta g^{\mu \nu }}. \end{aligned}$$
(12)

The field equations (9) are quite general with respect to both their normalizations described by G and also the defined constants \(c_i\) of Q. For instance, by choosing Q as in Eq. (4) then we retrieve the standard modified class of f(Q) gravity [21]. In the rest of this work we deal with this standard modified class of f(Q) theories.

3 Cosmological application of f(Q) gravity

In this section we proceed to the cosmological application of f(Q) gravity. We impose a spatially flat Friedmann–Robertson–Walker (FLRW) metric of the form

$$\begin{aligned} ds^{2}&=-dt^{2}+a^{2}(t)\delta _{ij}dx^{i}dx^{j}, \end{aligned}$$
(13)

with a(t) the scale factor. In this case Eq. (9) gives rise to the two Friedmann equations [22]

$$\begin{aligned} 6f_{\text {Q}}H^{2}-\frac{1}{2}f&=8\pi G(\rho _{m}+\rho _{r}), \end{aligned}$$
(14)
$$\begin{aligned} \big (12H^{2}f_{\text {QQ}}+f_{\text {Q}}\big ){\dot{H}}&=-4\pi G(\rho _{m}+p_{m}+\rho _{r}+p_{r}), \end{aligned}$$
(15)

where \(H={\dot{a}}/a\) is the the Hubble function and with \(\rho _{m}\), \(\rho _{r}\) and \(p_{m}\), \(p_{r}\) the energy densities and pressures of the matter and radiation perfect fluids respectively.

The non-metricity scalar Q, in an FRW background becomes \(Q=6H^{2}\). Note that this is only valid in the Coincident Gauge or when the linear affine connection has been chosen to respect the symmetries of spacetime. In the case of Coincident Gauge, a global coordinate system is chosen such that it trivializes the coefficients of the linear affine connection (1) globally. The choice of such a coordinate system reflects the fixing of a gauge freedom enjoyed by the Symmetric Teleparallel Gravity. Thus fixing this type of gauge is not the general case for the Flat FLRW background but rather a special case which may reduce to GR as argued in [67,68,69].

Finally, the equations constitute a close system by considering the matter and radiation conservation equations, namely

$$\begin{aligned} {\dot{\rho }}_{m}+3H(\rho _{m}+p_{m})&=0, \end{aligned}$$
(16)
$$\begin{aligned} {\dot{\rho }}_{r}+3H(\rho _{r}+p_{r})&=0. \end{aligned}$$
(17)

We can re-write Eqs. (14)–(15) as

$$\begin{aligned} H^{2}&=\frac{8\pi G}{3}\left( \rho _{m}+\rho _{r}+\rho _{DE}\right) , \end{aligned}$$
(18)
$$\begin{aligned} {\dot{H}}&=-4\pi G\left( \rho _{m}+p_{m}+\rho _{r}+p_{r}+\rho _{DE}+p_{DE}\right) , \end{aligned}$$
(19)

where we have defined the energy density and pressure of the effective dark energy sector as

$$\begin{aligned} \rho _{DE}= & {} \frac{1}{16\pi G}\left[ 6H^{2}\left( 1-2f_{\text {Q}}\right) +f\right] , \end{aligned}$$
(20)
$$\begin{aligned} \nonumber \\ p_{DE}= & {} \frac{1}{16\pi G}\left[ 4\left( f_{\text {Q}}-1\right) {\dot{H}}-f\right. \nonumber \\{} & {} \left. +6H^{2}\left( 8f_{\text {QQ}}{\dot{H}}+2f_{\text {Q}} -1\right) \right] . \end{aligned}$$
(21)

Finally, it proves convenient to introduce the density parameters for the various sectors us

$$\begin{aligned} \Omega _i=\frac{8\pi G\rho _i}{3H^2}, \end{aligned}$$
(22)

where “i” stands for matter, radiation and dark energy.

Let us now focus on particular f(Q) forms that are of interest for the late Universe description. As the exact modification in the action that could solve or at least alleviate the problems of the concordance model in not known, the community proposed various terms, serving different purposes. For example, some of us proposed a model that is able to describe the accelerated expansion of the universe slightly better than the concordance one, while is free of cosmological constant value problem, [43]. Other models are proposed with the aim to solve the \(H_0\) tension, which is achieved if they posses equation of state parameter that crosses the phantom divide [70].

In general, any model that exhibits identical Hubble rate with the concordance one (see [28]) can pass the BBN constraints trivially, hence we do not examine models of this kind. Note also that we consider versions of our models in their “bare” form, i.e. without explicitly containing the cosmological constant, in order to avoid re-introducing the cosmological constant problem and also to keep the smallest possible set of free parameters. One could in principle combine any selection of the following models, however the final model could have a large number of free parameters, thus it could be penalized by the various fitting quality metrics (i.e. information criteria).

  1. 1.

    Polynomial model The polynomial model was introduced in [22], as a generalization of the square-root model. The latter imposes modifications on the evolution of the perturbations while maintaining the standard GR background evolution. The polynomial model allows for modifications in both background and perturbation levels, thus is principle could alleviate both \(\sigma 8\) and \(H_0\) tensions. The polynomial model is given as

    $$\begin{aligned} f(Q)&=Q-6\lambda M^{2}\left( \frac{Q}{6M^{2}}\right) ^{\alpha }, \end{aligned}$$
    (23)

    where \(\lambda \) and \(\alpha \) are dimensionless parameters. The parameter M corresponds to a mass scale that should be of the order \(\sqrt{\Lambda }\), with \(\Lambda \) the standard cosmological constant. The case of \(\alpha =0\) gives STEGR plus a cosmological constant equal to \(6\lambda M^{2}\), while the case \(\alpha =1\) corresponds to STEGR with \(G\rightarrow G/(1-\lambda )\). More generally, \(\alpha >1\) is mostly relevant to early Universe, while \(\alpha <1\) is able to describe dark energy and thus it is relevant to late Universe. Moreover, in the latter case the existence of an asymptotic GR limit at early times is apparent. Finally, note that the case \(\alpha =-1\) has been confronted with late universe observations in [34]. In this model for the effective dark-energy density (20) we obtain

    $$\begin{aligned} \rho _{\text {DE}}=\frac{1}{16\pi G}\left[ 6^{-\alpha }\Omega _{\text {F0}}H_{0}^{-2\alpha }Q ^{\alpha +1 }\right] , \end{aligned}$$
    (24)

    where \(\Omega _{F0} = 1 - \Omega _{m0} - \Omega _{r0}\), and with the subscript denoting the value of a quantity at present time. Calculating the first Friedmann (14) at present time we find that the free parameter \(\lambda \) can be eliminated in terms of \(\alpha \) and M as

    $$\begin{aligned} \lambda =\frac{1}{12\alpha +6}\left( \Omega _{\text {F0}}H_{0}{}^{-2\alpha }M^{ 2\alpha -2}\right) . \end{aligned}$$
    (25)
  2. 2.

    Power-Exponential model This model has proposed in [43] and has been proven able to provide slightly better fits to observational data than the concordance model [43]. It is characterized by

    $$\begin{aligned} f(Q)&=Qe^{\lambda \frac{Q_{0}}{Q}}. \end{aligned}$$
    (26)

    As it is apparent, in case \(\lambda =0\) GR without a cosmological constant is recovered. In the past, where the term \(Q_{0}/Q\) decreases, since the Hubble function increases, the model at hand effectively reduces to the power-law model, thus alleviating the cosmological constant problem. In a sense, this model behaves as infinite number of different power-law models that coexist, and at each moment of the cosmic history one of them becomes dominant. Another advantage of the model is that it has the same number of free parameters with the concordance one, while additionally containing rich phenomenology. In this case (20) gives

    $$\begin{aligned} \rho _{\text {DE}}=\frac{1}{16\pi G}\left[ Q -e^{\frac{\lambda Q_{0}}{Q }}\left( Q -2\lambda Q_{0}\right) \right] . \end{aligned}$$
    (27)

    The parameter \(\lambda \) is expressed from the first Friedmann Eq. (14) at present as

    $$\begin{aligned} \lambda =\frac{1}{2}+W\left( \frac{\Omega _{\text {F0}}-1}{2\sqrt{e}}\right) , \end{aligned}$$
    (28)

    where W is the Lambert function.

  3. 3.

    Log-square-root model Let us now propose a new f(Q) model. In particular, following the approach of [71], we introduce a logarithmic-square-root f(Q) model as:

    $$\begin{aligned} f(Q)&=Q+nQ_{0}\sqrt{\frac{Q}{\lambda Q_{0}}}\ln \left( \lambda \frac{Q_{0}}{Q}\right) , \end{aligned}$$
    (29)

    with n and \(\lambda >0\) the model parameters. This model possess an effective equation of state parameter that remains strictly non- phantom. As shown at [71], it can be combined with an exponential one and provide crossing of the phantom divide. The corresponding effective energy density (20) gives

    $$\begin{aligned} \rho _{\text {DE}}&=\frac{1}{16\pi G}\Omega _{\text {F0}}\sqrt{Q_{0}Q }, \end{aligned}$$
    (30)

    and the first Friedmann equation at present leads to

    $$\begin{aligned} n&=\frac{\Omega _{\text {F0}}}{2}\sqrt{\lambda }. \end{aligned}$$
    (31)
  4. 4.

    Hyperbolic tangent-power model We consider the hyperbolic tangent power model, in similar lines with [72], namely we choose

    $$\begin{aligned} f(Q)&=Q+\lambda Q_{0}\left( \frac{Q}{Q_{0}}\right) {}^{n}\tanh \left( \frac{Q_{0}}{Q}\right) \, . \end{aligned}$$
    (32)

    This model permits a phantom divide crossing for the equation of state parameter. Moreover, as \(\lim _{Q \rightarrow +\infty } \tanh \left( \frac{Q_{0}}{Q}\right) \) goes to zero, it behaves as bare GR in early times, thus resolves the cosmological constant problem. In late times, where \(Q_0 \sim Q\) it reduces to the polynomial model, with \(M = H_0^2\) and \(\lambda \rightarrow -\lambda \). For the particular case of \(n = 0\), one obtains a \(\Lambda \) CDM-like behavior in redshifts close to 0. In a sense, the hyperbolic tangent power model, in parallel with the power-exponential model are generalizations of the polynomial model. For the hyperbolic tangent power model case, the effective Dark Energy density reads as

    $$\begin{aligned} \rho _{\text {DE}}= & {} \frac{1}{16\pi G}Q_{0}^{1-n}Q ^{n-1}\nonumber \\{} & {} \cdot \left[ (1\!-\!2n)Q \tanh \left( \!\frac{Q_{0}}{ Q } \!\right) \!+\!2Q_ { 0}\text {sech}^{2}\left( \!\frac{Q_{0}}{Q }\!\right) \right] , \nonumber \\ \end{aligned}$$
    (33)

    while

    $$\begin{aligned} n&=\frac{1}{2}\left[ -\coth (1)\Omega _{\text {F0}}+1+4\text {csch}(2)\right] . \end{aligned}$$
    (34)
  5. 5.

    DGP-like f(Q) model-I In the recent work [73] two new f(Q) models were introduced, by requiring the extra terms in the modified Friedman equation to be of the form \(\sim H\). It was argued that a term proportional to Q is responsible for the \(H^2\) term, thus adding a term proportional to \(\sqrt{Q}\) leads to a term \(\sim H\) in the Friedman equation. These two models resemble the Dvali–Gabadadze–Porrati cosmology [74] at the background level, and this is where they acquire their names from. We mention here that this resemblance is only at the background level, since the perturbations in the usual DGP model and f(Q) gravity are fundamentally different, and hence the present scenario does not share the known problem of usual DGP model in fitting the perturbation-related data (such as LSS and CMB temperature/polarization) [75, 76]. The first model of this kind reads as

    $$\begin{aligned} f(Q)=\alpha \sqrt{Q}\log Q+2\beta Q, \end{aligned}$$
    (35)

    where \(\alpha , \ \beta \) are free parameters. We mention that in the original parametrization the free parameter \(\alpha \) is not dimensionless, and we use the form (35) in order to maintain compatibility with the results of [73] (although it would be more convenient to impose a re-scaling \(\alpha \rightarrow \sqrt{Q_{0}} \alpha \) to ensure that \(\alpha \) is dimensionless). Nevertheless, we stress that inside the logarithm one should explicitly include a constant value of dimension \(H_0^{-2}\), and for consistency in the present work we do apply this modification. In this case (20) gives

    $$\begin{aligned} \rho _{\text {DE}}= & {} \frac{1}{16\pi G}\big [\sqrt{6}H_{0}\sqrt{Q }\left( 2\beta +\Omega _{\text {F0}}-1\right) \nonumber \\{} & {} -2\beta Q +Q \big ], \end{aligned}$$
    (36)

    Note the existence of \(\sqrt{Q} \sim H\) terms on the effective Dark Energy Density, Eq. 36. There is an obvious resemblance with the Running Vacuum (RV) class of cosmologies, [77] and specifically the “type-G” models. RV cosmologies although they do not possess a Lagrangian formulation, they fit the data exceptionally well, while they are also able to alleviate the Hubble constant and \(\sigma 8\) tensions, [78]. Thus, this resemblance imply the possibility for the DGP-like models considered here to share the aforementioned nice properties of RV models, while in the meantime possessing a Lagrangian description. Moreover, the first Friedmann equation gives

    $$\begin{aligned} \alpha =-\sqrt{\frac{3}{2}}H_{0}\left( 2\beta +\Omega _{\text {F0}}-1\right) . \end{aligned}$$
    (37)

    Finally, note that near the current time, the term \(\sim H\) ceases to be negligible in comparison to \(H^2\), thus giving rise to new phenomenology. However, in the past this term is negligible and the model is very close to the concordance one.

  6. 6.

    DGP-like f(Q) model-II The second model introduced in [73] reads as

    $$\begin{aligned} f(Q) = \frac{Q\sqrt{u(Q)}\left[ \!\sqrt{u(Q)}\!-\!\sqrt{\gamma }\text {arctanh} \left( \!\frac{ \sqrt{u(Q)}}{\sqrt{\gamma }}\right) \!\right] }{8\pi G\sqrt{Qu(Q)}},\nonumber \\ \end{aligned}$$
    (38)

    where \(u(Q) = \gamma + \beta ^2 Q\), and \(\beta \),\(\gamma \) are free parameters, different than zero. Note that the arctanh(x) function is defined at \(x \in (-1,1)\), so the Lagrangian description for the model is valid for \(0< \sqrt{u(Q)}/\sqrt{\gamma } < 1\). The particular choice of u is motivated from the previous case and includes also a mixing between \(H^2\) and H terms [73]. In this case we acquire

    $$\begin{aligned} \rho _{\text {DE}}&=\frac{1}{16\pi G}\left[ Q -\sqrt{Q }\sqrt{\gamma +\beta ^{2}Q }\right] , \end{aligned}$$
    (39)

    while

    $$\begin{aligned} \gamma&=-6H_{0}{}^{2}\left( \beta -\Omega _{\text {F0}}+1\right) \left( \beta +\Omega _{\text { F0}}-1\right) . \end{aligned}$$
    (40)

    Similarly to the previous case, in order to maintain dimensional consistency within the square root, we include an \(H_0^{-2}\) normalization (i.e. we apply the re-scaling \(\gamma \rightarrow Q_{0} \gamma \)).

4 Big bang nucleosynthesis constraints

In this section we review the Big Bang Nucleosynthesis (BBN) formalism following [49,50,51,52]. The BBN takes place during the radiation era and thus the energy density of relativistic particles needs to be taken into account, namely

$$\begin{aligned} {\displaystyle \rho _{r}}&=\frac{\pi ^{2}}{30}g_{*}T^{4}, \end{aligned}$$
(41)

where

$$\begin{aligned} g_{*}\sim 10\, \end{aligned}$$
(42)

is the effective number of degrees of freedom and T is the temperature (for more details of the BBN framework used in this work see the appendix of [53]). The calculation of the neutron abundance is realized by taking into account the protons-neutron conversion rate

$$\begin{aligned} \lambda _{pn}(T){} & {} =\lambda _{(n+\nu _{e}\rightarrow p+e^{-})}+\lambda _{(n+e^{+}\rightarrow p+{\bar{\nu }}_{e})}\nonumber \\{} & {} \quad +\lambda _{(n\rightarrow p+e^{-}+{\bar{\nu }}_{e})},\ \end{aligned}$$
(43)

and its inverse \(\lambda _{np}(T)\), thus the total rate is

$$\begin{aligned} \lambda _{tot}(T)=4A\,T^{3}(4!T^{2}+2\times 3!\mathcal{Q}T+2!\mathcal{Q}^{2}), \end{aligned}$$
(44)

where \(\mathcal{Q}=m_{n}-m_{p}=1.29\times 10^{-3}\) GeV is the neutro-proton mass difference and \(A=1.02\times 10^{-11}\) GeV\(^{-4}\).

Regarding the primordial mass fraction of \(^{4}He\), it can be estimated [50] as

$$\begin{aligned} Y_{p}:=\lambda \,\frac{2x(t_{f})}{1+x(t_{f})}, \end{aligned}$$
(45)

with \(\lambda =e^{-(t_{n}-t_{f})/\tau }\), \(t_{f}\) the freeze-out time of the weak interactions, \(t_{n}\) the corresponding freeze-out time of nucleosynthesis, \(\tau \) the neutron mean lifetime and \(x(t_{f})=e^{-\mathcal{Q}/T(t_{f})}\) the neutron-to-proton equilibrium ratio. The role of the function \(\lambda (t_{f})\) is to account for the fraction of neutrons that decay into protons during the time interval \(t\in [t_{f},t_{n}]\).

In case of modified gravity models, in general the Friedmann equations will contain extra terms than the standard GR ones. The BBN is realized in the radiation epoch and according to observations these extra contributions have to be small compared to the radiation sector in the Standard Model of particles physics in the framework of General Relativity, whilst we can safely neglect the matter sector as we are deep in the radiation era. Thus, the first Friedmann equation can be approximated as

$$\begin{aligned} H^{2}&\approx \frac{8\pi G}{3}\rho _{r}=:H_{GR}^{2}, \end{aligned}$$
(46)

where the scale factor evolves as \(a\sim t^{1/2}\), with t the cosmic time. Consequently, temperature and time are related by \({\displaystyle \frac{1}{t}\simeq \left( \frac{32\pi ^{3}g_{*}}{90}\right) ^{1/2}\frac{T^{2}}{M_{P}}}\) (or \(T(t)\simeq (t/\text {sec})^{-1/2}\) MeV), which can further lead to

$$\begin{aligned} H&\approx \left( \frac{4\pi ^{3}g_{*}}{45}\right) ^{1/2}\frac{T^{2}}{M_{P}}, \end{aligned}$$
(47)

where

$$\begin{aligned} M_{P}=(8\pi G)^{-1}=1.22\times 10^{19}\text { GeV}, \end{aligned}$$
(48)

is the Planck mass.

Assuming that the expansion time is much smaller than the interaction time, then the interaction rate \(\lambda _{tot}(T)\) given in (44) satisfies \(\frac{1}{H}\ll \lambda _{tot}(T)\), which means that all processes can be approximated as being in thermal equilibrium [50, 79]. In contrast, if the particles do not have the necessary time intervals to interact then \(\frac{1}{H}\gg \lambda _{tot}(T)\) and thus they decouple. The temperature at which the particles decouple is called freeze-out temperature and is denoted as \(T_{f}\), and it is defined through \(H=\lambda _{tot}(T)|_{T=T_f}\). Using \(H\approx \left( \frac{4\pi ^{3}g_{*}}{45}\right) ^{1/2}\frac{T^{2}}{M_{P}}\), while \(\lambda _{tot}(T)\approx qT^{5}\), with

$$\begin{aligned} q=4A4!\simeq 9.8\times 10^{-10}\text { GeV}{}^{-4}, \end{aligned}$$
(49)

the freeze-out temperature is provided as

$$\begin{aligned} T_{f}&=\left( \frac{4\pi ^{3}g_{*}}{45M_{P}^{2}q^{2}}\right) ^{1/6}\sim 0.0006\,\text {GeV}. \end{aligned}$$
(50)

In the realm of modified gravity, the Hubble function H will, in general, deviate from \(H_{GR}\). This in turn means that the corresponding freeze-out temperatures will also deviate by an amount of \(\delta T_{f}\). This deviation induces a difference \(\delta Y_{p}\) of the fractional mass \(Y_{p}\)

$$\begin{aligned} \delta Y_{p}&=Y_{p}\left[ \left( 1-\frac{Y_{p}}{2\lambda }\right) \ln \left( \frac{2\lambda }{Y_{p}}-1\right) -\frac{2t_{f}}{\tau }\right] \frac{\delta T_{f}}{T_{f}}, \end{aligned}$$
(51)

where \(\delta T(t_{n})=0\) was imposed due to the fact that \(T_{n}\) is fixed by the binding energy of deuterium [55,56,57,58,59]. Thus, the observational imprints of the mass fraction \(Y_{p}\) of baryons that convert to \(^{4}He\) during the BBN epoch, are [80,81,82,83,84,85,86]

$$\begin{aligned} Y_{p}&=0.2476,\qquad |\delta Y_{p}|<10^{-4}. \end{aligned}$$
(52)

By replacing these into (51), the upper bound of \(\frac{\delta T_{f}}{T_{f}}\) is obtained as

$$\begin{aligned} \left| \frac{\delta T_{f}}{T_{f}}\right|&<4.7\times 10^{-4}, \end{aligned}$$
(53)

which quantifies the allowed deviation from the cosmology of GR.

As we mentioned above, the effective dark energy \(\rho _{DE}\) of modified gravity is present during the BBN times too, and compared to \(\rho _{r}\), \(\rho _{DE}\) should be smaller and thus it can be considered as a first-order deviation. Hence, the Hubble function is

$$\begin{aligned} H&=H_{GR}\sqrt{1+\frac{\rho _{DE}}{\rho _{r}}}=H_{GR}+\delta H, \end{aligned}$$
(54)

where

$$\begin{aligned} \delta H&=\left( \sqrt{1+\frac{\rho _{DE}}{\rho _{r}}}-1\right) H_{GR}. \end{aligned}$$
(55)

The deviation \(\delta H\) from standard \(H_{GR}\) will induce the deviation \(\delta T_{f}\) from \(T_{f}\), and according to the relation \(H_{GR}=\lambda _{tot}\approx qT^{5}\) it turns out that

$$\begin{aligned} \left( \sqrt{1+\frac{\rho _{DE}}{\rho _{r}}}-1\right) H_{GR}=5qT_{f}^{4}\delta T_{f}. \end{aligned}$$
(56)

Since \(\rho _{DE}\ll \rho _{r}\) we finally obtain

$$\begin{aligned} \frac{\delta T_{f}}{T_{f}}\simeq \frac{\rho _{DE}}{\rho _{r}}\frac{H_{GR}}{10qT_{f}^{5}}. \end{aligned}$$
(57)

We have now all the information needed to proceed to the investigation of the BBN bounds on the parameters of the f(Q) models introduced above.

5 BBN constraints on f(Q) gravity

In this section, the models introduced in Sect. 3 will be tested against the constraint (53). This will be realized by calculating (57) for each of the models. In general, we are interested in the regions of the parameter space where the constraint (57) is satisfied. Obviously, all models are expected to satisfy the constraint trivially for the case \(\Omega _{\text {F0}}=0\), i.e. in the case where there is no effective dark energy. In the following, in all figures the drawn parts correspond to satisfaction of the aforementioned BBN constraint. For the standard free parameters we impose the ranges \(h\in [0.6,0.9]\) and \(\Omega _{\text {F0}}\in [0,1]\). For the case of free model parameters we use the mathematically allowed ranges.

5.1 1. Polynomial model

Substituting Eq. (25) along with Eq. (24) in Eq. (57) we obtain

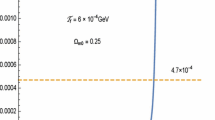
$$\begin{aligned} \frac{\delta T_{f}}{T_{f}}&\simeq \frac{1}{q}2^{4\alpha +3}3^{\frac{1}{2}-\alpha }5^{-\alpha -\frac{3}{2}}\pi ^{3\alpha +2}H_{0}\Omega _{\text {F0}}\text {}\nonumber \\&\quad \cdot g_{*}^{\alpha +\frac{1}{2}}T_{f}^{4\alpha -3}\left( H_{0}M_{p} \right) {}^{-2\alpha -1}. \end{aligned}$$
(58)

Imposing the constraint (53) on the parameter space of the polynomial model using (58), we obtain Fig. 1. Note that we imposed the relation \(H_{0}=2.12 \cdot 10^{-42}h\) GeV and we have also replaced the numerical values (49), (42), (50) and (48).

From Fig. 1 we deduce that the model parameter \(\alpha \) should be in the range \(\alpha \lesssim 0.88\) in order for the model to satisfy the BBN constraints. However, if we additionally desire the model to be able to describe dark energy in the late-time Universe, then we obtain the combined constraint \(\alpha <0\).

5.2 2. Power-exponential model

Substituting Eq. (28) alongside with (27) into (57) we acquire

$$\begin{aligned} \frac{\delta T_{f}}{T_{f}}\simeq \frac{8\sqrt{\frac{3}{5}}\pi ^{2}\sqrt{g_{*}}T_{0}^{4}\left\{ e^{\lambda \left( \frac{T_{0}}{T_{f}}\right) ^{4}}\left[ 2\lambda -\left( \frac{T_{f}}{T_{0}}\right) ^{4}\right] +\left( \frac{T_{f}}{T_{0}}\right) ^{4}\right\} }{5qT_{f}^{7}M_{p}}. \nonumber \\ \end{aligned}$$
(59)

Inserting this expression into (53) we find that for the range of values \(0.5\le h\le 0.9\) and \(0\le \Omega _{\text {F0}}\le 1\), the constraint (53) is satisfied trivially for all parameter values. This result is intuitively expected, since as we mentioned above the past asymptotic behavior of the model recovers pure GR at early times, and thus during the BBN epoch [43]. This is a great advantage of this particular model.

Fig. 1
figure 1

The parameter space of the polynomial model (23) that is consistent with the BBN constraints. If we also desire the model to be able to describe dark energy in the late-time Universe we obtain the combined constraint \(\alpha <0\)

Full size image

5.3 3. Log-square-root

In this case, inserting (31) and (30) in (57) we find

$$\begin{aligned} \frac{\delta T_{f}}{T_{f}}\simeq 8\pi ^{2}\sqrt{\frac{3g}{5}}\frac{\Omega _{\text {F0}}T_{0}^{2}}{5qT_{f}^{5}M_{p}}. \end{aligned}$$
(60)

Therefore, substituting (60) in (53) we observe that for the range of values \(0.5\le h\le 0.9\) and \(0\le \Omega _{\text {F0}}\le 1\), the constraint (53) is always satisfied. This is an advantage of the model, and supports its viability. Definitely, one should confront the model with late-time observational data, too.

5.4 4. Hyperbolic tangent-power model

In the case of the hyperbolic tangent-power model (32), substituting (34) and (33) into (57) we obtain

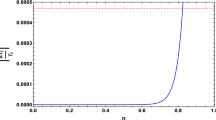
$$\begin{aligned} \frac{\delta T_{f}}{T_{f}}\simeq & {} \sqrt{\frac{3}{5}}\frac{8\pi ^{2}\sqrt{g_{*}}}{5qM_{p}T_{f}^{7}} \left( \frac{T_{f}}{T_{0}}\right) ^{4n-4}\nonumber \\{} & {} \cdot \left\{ \! (1\!-\!2n)T_{f}^{4}\tanh \!\left[ \!\left( \frac{T_{0}}{T_{f}}\right) ^{4}\right] \!+\!2T_{ 0} ^{ 4 } \text {sech}^{2}\!\left[ \!\left( \frac{T_{0}}{T_{f}}\right) ^{4}\right] \!\right\} . \nonumber \\ \end{aligned}$$
(61)

In Fig. 2 we depict the constraint (53) by using (61). The procedure is the same as in case of Fig. 1 above. As we observe, the BBN constraints are satisfied for \(n\lesssim 1.88\).

Fig. 2
figure 2

The parameter space of the hyperbolic tangent-power model (32) that is consistent with the BBN constraints. If we also desire the model to be able to describe dark energy in the late-time Universe we obtain the combined constraint \(n\lesssim 1.88\)

Full size image

5.5 5. DGP-like model-I

For the DGP-like model-I (35), if we insert (37) and (36) into (57), we acquire

$$\begin{aligned} \frac{\delta T_{f}}{T_{f}} \simeq \frac{8\sqrt{\frac{3}{5}}\pi ^{2}\sqrt{g_{*}}T_{0}{}^{2}\left[ 2\beta \!+\!\Omega _{ \text {F0}}\!-\!2\beta \left( \frac{T_{f}}{T_{0}}\right) ^{2} \!+\!\left( \frac{T_{f}}{T_{0}} \right) ^{2}\!-\!1\right] }{5qM_{p}T_{f}{}^{5}} . \nonumber \\ \end{aligned}$$
(62)

Furthermore, numerical exploration of this equation for the standard parameter ranges \(0.5\le h\le 0.9\) and \(0\le \Omega _{\text {F0}}\le 1\), shows that the constraint (53) is satisfied only in the tuned interval \(0.499984< \beta < 0.500016\).

5.6 6. DGP-like model-II

Finally, let us come to the DGP-like model-II of (38). The constraint (57), after inserting (40) and (39), reduces to

$$\begin{aligned} \frac{\delta T_{f}}{T_{f}}\simeq & {} \sqrt{\frac{3}{5}}\frac{8\pi ^{2}\sqrt{g_{*}}T_{0}{}^{2}}{5qM_{p}T_{f}^{5}} \nonumber \\{} & {} \cdot \left\{ \!\!\left( \frac{T_{f}}{T_{0}}\right) ^{2}\!\!-\!\sqrt{\!\left( \Omega _{ \text { F0 }} \! -\!2\right) \!\Omega _{\text {F0}}\!+\!\beta ^{2}\!\left[ \!\left( \frac{T_{f}}{T_{0}} \right) ^ {4 } \!-\!1\!\right] \!+\!1}\right\} . \nonumber \\ \end{aligned}$$
(63)

Examining this expression for the range of values \(0.5\le h\le 0.9\) and \(0\le \Omega _{\text {F0}}\le 1\), we deduce that the constraint (53) is satisfied in the tuned window \(0.999969< |\beta | < 1.00003\).

Fig. 3
figure 3

Plot of \(\text {log}_{10}f(Q)/Q_0\) over \(\text {log}_{10}Q/Q_0\) for models 1 to 5. Red dashed-dotted line corresponds to GR limit

Full size image

Lastly, at Fig. 3 we plot models 1 to 5, employing the BBN constraints extracted previously on their free parameters and \(\Omega _{m0} \sim 0.3\). A rather useful finding is that in order to maintain the standard thermal history, a model should converge to \(f(Q) \sim Q^{\alpha }\), with \(\alpha \in (1.00, 1.088)\) at \(Q/Q_0 \sim 10^4\).

The latter is similar to the result of [87], where it was found that for the case of f(Q,T) model of the form (using our formalism) \(f(Q,T)= Q(Q^{a} - 1) + bT\), i.e. \(f(Q,T) \sim \mathcal {O}\left( Q^{a+1}\right) \), \(0.99 \lesssim a+1 \lesssim 1.01\), regardless of the presence of the torsion term.

6 Conclusions

We use the Big Bang Nucleosynthesis formalism and observations in order to extract constraints on f(Q) gravity. The latter is a modified gravitational theory arising from the consideration of non-metricity as the basic geometric quantity. We investigated various classes of f(Q) models, and we additionally introduced a number of new ones, inspired by other modified gravities, that are capable of describing the late-time Universe evolution. We applied the semi-analytic approach of [56,57,58] for the physics of the BBN epoch, and we calculated the deviations that f(Q) terms bring on the freeze-out temperature \(T_f\) in comparison to that of the standard \(\Lambda \)CDM evolution. We then imposed the observational bound on \( \left| \frac{\delta {T}_f}{{T}_f}\right| \) to extract constraints on the involved parameters of the considered models. We report the constraints imposed by BBN, narrowing the prior range of the free parameters, thus paving the road for their exhaustive observational analysis.

Concerning the polynomial model, we showed that the exponent parameter \(\alpha \) should be in the interval \(\alpha <0\) if we desire the model to simultaneously pass the BBN constraints and be able to describe the late-time Universe acceleration. On the other hand, the power-exponential model is found to pass the BBN constraints trivially, which was expected since this model recovers general relativity at early times. This is a significant advantage, since this particular model is known to be compatible with late-time observational datasets slightly more efficiently than \(\Lambda \)CDM scenario [43], and thus it can be considered as a good candidate for the description of Nature.

In the case of the new proposed Log-square-root models we showed that BBN constraints are also trivially satisfied. However, in the new hyperbolic tangent-power model we showed that the combined BBN and late-time constraints require the model parameter to lie in the range \(n \lesssim 1.88\). Finally, we examined the two DGP-like f(Q) models that have recently appeared in the literature. In both cases we found that the BBN constraints are satisfied for a very narrow window for the model parameter \(\beta \). We also arrived at a more general result, namely that all allowed instances of the considered models should fall close to GR limit at \(Q/Q_0 \sim 10^4\). The latter could used to optimize a given heuristic approach towards solving \(\sigma _8\) and \(H_0\) tensions, as before undertaking time-consuming calculations and/or fittings for a particular f(Q) model, one could easily check if the model pass our criterion.

In summary, we showed that f(Q) gravity can safely pass the BBN constraints, and in some cases this is obtained trivially. This is an important advantage, since many gravitational modifications, although able to describe the late-time evolution of the Universe, fall to pass the BBN confrontation since they produce too-much modification at early times. Hence, f(Q) gravity proves to be a class of modified gravity that deserves further investigation. One could try to proceed beyond the semi-analytical approach of this work, using numerical codes like Parthenope [88] and AlterBBN [89], in the same lines with [90]. Such a detailed investigation lies beyond the scope of the present work and it is left for a future project.