1 Introduction

The \(\Lambda \)CDM cosmological model also known as standard cosmological model has been successfully explained the dynamic and evolution of the universe from its beginning (big bang) to the present accelerated phase assuming that Einstein’s general relativity (GR) defines gravity. But standard cosmological model has no proofs about dark energy (DE) and dark matter (DM). It is also unable to explain matter-antimatter asymmetry [1]. Researchers are of the opinion on the basis of observational data coming from Supernova Ia [2, 3], cosmic microwave background [4, 5] and large scale structure formation [6,7,8] that presented accelerated expansion of the universe is due the presence of DE. The DE sector commands over the cold dark matter and navigate the universe towards accelerated expansion due to its enough negative pressure [2, 9, 10].

The evolution of the universe starting with big bang expanded rapidly from its initial singularity and its density exceeded from critical density in \(t<10^{-43}\) seconds (s) called Planck epoch. After that separation between fundamental forces such as gravitational and electro-nuclear forces took place in \(t<10^{-36}\) s followed by a very rapid expansion called inflationary phase completed in \(t<10^{-32}\) s. Hereafter the electroweak force decomposed into the weak nuclear and electromagnetic forces when \(t=10^{-12}\) s and at the same time there was a decrease in the energy density of the universe such that matter can exist in the form of quarks [11].

For physicists, there are many puzzles related to the early universe among which one is the formation of light elements after the explosion. Bethe in 1939 first time presented the idea of big bang nucleosynthesis (BBN) which is also known as primordial nucleosynthesis [12]. It is a prime prediction of big bang cosmology which took place after baryogenesis. Most cosmologists believe that it took place about 10–20 s after the big bang and concluded in just 20 min approximately [13]. It was time when formation of stable neutrons and protons came into exist as universe became cool enough. This cooling allowed protons and neutrons to fuse to become isotopes of Hydrogen \(^1H\) and Helium \(^4He\). This phenomenon elaborates the relative abundance of Helium in the universe.

The primordial \(^4He\) came into exist when temperature of the cosmos was \(T\sim 100\) MeV, while energy and number density were under the effects of relativistic leptons (electrons, protons, neutrinos) and light emitting particles photons (where protons and neutron do not contribute in the total energy density) [14]. These particles remain in thermal equilibrium retaining their collisions, while the following relationships to protons and neutrons with lepton

$$\begin{aligned} \nu _e+n&\leftrightarrow&p+e^-, \end{aligned}$$
(1)
$$\begin{aligned} e^+ +n&\leftrightarrow&p+{\bar{\nu }}_e,\end{aligned}$$
(2)
$$\begin{aligned} n&\leftrightarrow&p+e^- +{\bar{\nu }}_e, \end{aligned}$$
(3)

hold the particles in thermal equilibrium (where e represents number of electrons, p describes number of protons, n is number of neutrons and \(\nu _e\) gives number of neutrinos in the system). Moreover, in accelerated universe, the conversion rate of protons into neutrons is used to estimate the neutron abundance.

Moreover, there are some other evolutionary era of the universe which are of much importance such as radiation dominated era, matter dominated era and the formation of large scalae structures. In the beginning, after big bang explosion the universe was so hot that energy density of electromagnetic radiation was greater than the density of matter and was driving the expansion called radiation dominated era. It take 47,000 years when energy density of matter overtaken the density of radiation and hence matter became driver of universe’s evolution called matter dominated era. Furthermore, the source for the formation of larger structure was smaller structure which come into exist first and built up into the larger structure. Scientists are of the opinion that at \(t=700\) Myr stars (population III stars) come into exist and then dwarf galaxies and quasars yet to be detected observationally [11].

To analyze the historical background and recent picture of universe, the modified theories of gravity have much prominent role as compared to Einstein’s GR. The above motivation can be fulfilled by numerous gravitational modifications. Cosmological models which deal with higher-order corrections to the Einstein–Hilbert Lagrangian have additional motivation of improving the renormalizability of GR [15, 16]. These higher-order cosmological models come into exist when an additional term in Einstein–Hilbert action is added such as f(R) gravity [17] with R as Ricci curvature, Weyl gravity [18, 19], Lovelock cosmology [20], Galileon theory of gravity [21, 22], Einstein cubic gravity [23, 24] etc. For current analysis on DE issue including modified theories of gravity, a lot of work have been done in the literature [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53].

Many physicists worked on constraining BBN under the realm of various cosmological models to analyze the formation of light in early universe. Capozziello et al. [13] used BBN observational bounds on the primordial abundance of photons to constrain f(T) cosmology (where T is torsion scalar) and studied three different models in order to examine BBN constraints on their free parameters. Barrow et al. [54] used BBN observational data to impose the BBN constrains on the exponent \(\Delta \) of Barrow entropy. Bhattacharjee [55] constrained model \(f(Q,T)=Q^{n+1}+mT\) under f(Q, T) gravity (where Q is non-metricity) to investigate the viability in cosmology and found that this cosmological model can explain the observed abundances of Helium and Deuterium while Lithium problem persists. Ghoshal and Lambiase [14] used Tsallis cosmology to examine the bound on Tsallis parameter to be \(\beta <2\) by using the constraints coming from the formation of light element from the BBN observational data which permit a very small deviation from GR. Asimakis et al. [56] used BBN data to impose observational constraints on higher-order modified theories of gravity particularly Gauss–Bonnet f(G) gravity, f(P) cubic gravity and running vacuum gravity. They have given a detailed discussion of BBN epoch and investigated the deviation of freeze-out time with a comparison to \(\Lambda \)CDM regime. They found BBN constraints by using the observational data on involved free parameters of various models.

The aim and motivation of this work is to address the implications of Einstein-Aether and modified Hořava–Lifshitz theories of gravity on BBN which is a source to form the light element in the early universe as the cosmological models are assumed viable if and only if they satisfy some suitable conditions imposed by BBN. Since BBN occurred in first 10–20 s after big bang and completed in approximately twenty minutes when the universe was hot and dense (indeed BBN, together with cosmic microwave background radiation, provides the strong evidence about the high temperatures characterizing the primordial universe). It reports that nuclear reactions happened in a sequence that yield the synthesis of photons [57,58,59] and therefore drive the observed universe. Thus from BBN physics, one can deduce stringent constraints on a given theory of gravity related models. Hence, in this paper, we shall confront Einstein-Aether and modified Hořava–Lifshitz theories of gravity models with BBN depending upon recent observational data. We shall consider different models related to Einstein-Aether gravity and modified Hořava–Lifshitz theories of gravity that mimic \(\Lambda \)CDM model.

The arrangement of this paper is as follows: In upcoming section, we review the Einstein-Aether and modified Hořava–Lifshitz theories of gravity. In Sect. 3, we calculate the BBN constraints. In Sect. 4, we review the chi-square test and discussed observational values of the Hubble parameter H. In Sect. 5, we analyze BBN in Einstein-Aether gravity. In Sect. 6, we analyze BBN constraints in modified Hořava–Lifshitz gravity. In the last section, we conclude our findings.

2 Modified theories of gravity

In this section, we present two different theories of gravity. The first one is Einstein-Aether gravity in which Lorentz invariance is breakup by unit time like vector field (Aether) [60]. The other one is modified Hořava–Lifshitz gravity also known as \(f({\tilde{R}})\) gravity. We consider homogeneous, flat and isotropic FRW universe for which line element is

$$\begin{aligned} ds^{2}=-N^{2} dt^{2}+a^{2}\bigg (dr^2+r^2(d\theta ^2+\sin ^2 \theta d\phi ^2)\bigg ), \end{aligned}$$
(4)

where N is lapse variable depends on time t (for Einstein-Aether gravity \(N=1\)) and \(a=a(t)\) is scale factor of the universe [61, 62]. The energy momentum tensor for this model is

$$\begin{aligned} T_{ab}^{m}=\rho U_a U_b+p(g_{ab}+U_a U_b), \end{aligned}$$
(5)

where \(U_a\) is the four velocity, \(\rho \) is the energy density and p describes pressure of the universe respectively. For both theories, continuity equation is given by \({\dot{\rho }}+3H(p+\rho )=0\), where H is the Hubble parameter. In upcoming subsections, we analyze both theories of gravity separately.

2.1 Einstein-Aether gravity

As it is believed by the physicists that Aether is a physical medium that exists everywhere in this universe homogeneously. It is the medium which is reason to travel the light from one place to the other even in vacuum. Physicists are of the opinion that Aether provides a specific static frame of reference in which every traveling object has absolute relative velocity and is well suitable for Newtonian dynamics. But Einstein in his theory of relativity rejected it by performing various experiments on optics. When the concept of cosmic microwave background come into exists, many scientists considered it as modern form of Aether. Gasperini [63] boosted up the Einstein-Aether theory which is said to be covariant moderation of general relativity [60]. The action of Einstein-Aether theory is given as [64, 65]

$$\begin{aligned} {\mathcal {S}}=\int {\sqrt{-g}\Bigg (\frac{R}{4\pi G}+{\mathcal {L}}_{EA}+{\mathcal {L}}_m\Bigg )d^4 x}, \end{aligned}$$
(6)

where g represents the determinant of metric tensor \(g^{\mu \nu }\) and G is the gravitational constant. Moreover, \({\mathcal {L}}_{m}\) is the Lagrangian density of matter while \({\mathcal {L}}_{EA}\) is the Lagrangian density for the vector field which can be given by

$$\begin{aligned} {\mathcal {L}}_{EA}= & {} \frac{1}{16\pi G}\Bigg (M^2 F(K)+\uplambda (A^a A_a+1)\Bigg ), \end{aligned}$$
(7)

where M is a coupling constant, \(\uplambda \) referred as Lagrangian multiplier and \(A^a\) is a vector (tensor of rank one) to have time-like direction which satisfies the relation \(A^a A_a=-1\). Furthermore, F(K) is an arbitrary function involved due to theory with argument K which is given by

$$\begin{aligned} K= & {} \frac{K_{cd}^{ab} \nabla _{a} A^c \nabla _{b} A^{d} C}{M^2}, \end{aligned}$$
(8)
$$\begin{aligned} K_{cd}^{ab}= & {} c_1 g^{ab}g_{cd}+c_2 g_{c}^{a}g_{d}^{b}+c_3 g_{d}^{a}g_{c}^{b},\quad a,b=0,1,2,3, \nonumber \\ \end{aligned}$$
(9)

where \(c_1,~c_2,~c_3\) are constants without dimensions. Einstein field equations for this theory can be obtained from Eq. (6) as

$$\begin{aligned} G_{ab}= & {} T_{ab}^{EA}+8\pi G T_{ab}^{m}, \end{aligned}$$
(10)
$$\begin{aligned} \nabla _a \bigg (F' J_b^a\bigg )= & {} 2\uplambda A_b, \end{aligned}$$
(11)

where prime denotes the derivative w.r.t the argument K, \(T_{ab}^{m}\) is the energy momentum tensor for matter field and is given in Eq. (5), \(J_b^a=-2K_{bc}^{ad}\nabla _d A^c\) and \(T_{ab}^{EA}\) represents energy momentum-tensor for vector field which is given by

$$\begin{aligned} T_{ab}^{EA}= & {} \uplambda A_a A_b+\frac{g_{ab} M^2 F}{2}-Y_{(a~b)} F' \nonumber \\&+\frac{1}{2}\nabla _d \bigg [\bigg (J(_a~^{d}A_b)-J^d (_a A_b)-J_{(ab)} A^d\bigg )F'\bigg ],\nonumber \\ \end{aligned}$$
(12)

where indices (ab) represents symmetry, \(A_a\) is time-like unitary vector and is defined as \(A_a=(1,0,0,0)\) and \(Y_{(ab)}\) is given as

$$\begin{aligned} Y_{(ab)}=-c_1[(\nabla _d A_a)(\nabla ^d A_b)-(\nabla _a A_d)(\nabla _b A_d)]. \end{aligned}$$
(13)

The Friedmann equations for Einstein-Aether theory of gravity become

$$\begin{aligned}&\gamma \Bigg (\frac{1}{2}F K^{-1}-F'\Bigg )H^2+\Bigg (\frac{K}{a^2}+H^2\Bigg ) =\frac{8\pi G}{3}\rho , \end{aligned}$$
(14)
$$\begin{aligned}&\gamma \Bigg ({\dot{H}} F' +H \frac{dF'}{dt}\Bigg ){+}\Bigg (\frac{2K}{a^2}-2{\dot{H}}\Bigg ) = 8\pi G(\rho +p), \end{aligned}$$
(15)

where overhead dot means derivative w.r.t cosmic time ‘t’, the constant parameter \(\gamma =c_1+3c_2+c_3\) and the argument \(K=\frac{3\gamma H^2}{M^{2}}\). If \(\rho _{EA}\) is the effective energy density and \(p_{EA}\) is the effective pressure in Einstein-Aether gravity then Eqs. (14) and (15) becomes as

$$\begin{aligned} \Bigg (\frac{K}{a^2}+H^2\Bigg )= & {} \frac{8\pi G}{3}\rho +\frac{1}{3}\rho _{EA}, \end{aligned}$$
(16)
$$\begin{aligned} \Bigg (\frac{2K}{a^2}-2{\dot{H}}\Bigg )= & {} 8\pi G(\rho +p)+(\rho _{EA}+p_{EA}), \end{aligned}$$
(17)

where

$$\begin{aligned} \rho _{EA}= & {} 3\gamma H^2\Bigg (F'-\frac{1}{2}F K^{-1}\Bigg ), \end{aligned}$$
(18)
$$\begin{aligned} p_{EA}= & {} -\gamma \Bigg ({\dot{H}} F' +H \frac{dF'}{dt}\Bigg )-3\gamma H^2 \Bigg (F'-\frac{F}{2K}\Bigg ). \end{aligned}$$
(19)

2.2 Modified Hořava–Lifshitz gravity

In this subsection, we will discuss the modified Hořava–Lifshitz gravity. The generalized action term for this gravity is [61, 66]

$$\begin{aligned} S_{F({\tilde{R}})}=\int {d^{4}x \sqrt{-g}F({\tilde{R}})}+S_{m}, \end{aligned}$$
(20)

where \(\sqrt{-g}=\sqrt{g^{(3)}} N\) and \(S_m\) is the matter part of action. Also,

$$\begin{aligned} {\tilde{R}}= & {} K_{ab} K^{ab}-\uplambda K^{2} +2 \mu \nabla _{\sigma }(n^{\sigma } \nabla _{\nu } n^{\nu }-n^{\nu } \nabla _{\nu } n^{\sigma })\nonumber \\&-{\mathcal {L}}_{R}^{(3)}(g_{ab}^{(3)}), \end{aligned}$$
(21)

where \(\mu \), \(\uplambda \) are real numbers, \({\mathcal {L}}_{R}^{(3)}\) is a function depending on three dimensional metric \(g_{ab}^{(3)}\) and the covariant derivatives \(\nabla _{a}^{(3)}\) are defined by the metric given in Eq. (4). In this scenario the argument \({\tilde{R}}\) takes the form

$$\begin{aligned} {\tilde{R}}=\frac{(3-9\uplambda ) H^{2}}{N^{2}}+\frac{6\mu }{a^{3}N} \frac{d}{dt}\Bigg (\frac{H a^{3}}{N}\Bigg ). \end{aligned}$$
(22)

The argument \({\tilde{R}}\) reduces to R and hence usual f(R)-gravity is obtained if we choose parameters \(\uplambda =\mu =1\) with flat FRW metric. If we select \(\mu =0\), \({\tilde{R}}\) reduces to \(R_{HL}\) (Ricci scalar for Hořava–Lifshitz gravity) [66] and thus action (20) becomes similar to the action term of Hořava–Lifshitz-like f(R)-gravity [67]. Hence, this assumption (\(\mu =0\)) corresponds to some degenerate limit of general f(R) Hořava–Lifshitz gravity. We call this limit degenerate as it is very difficult to obtain (might be impossible).

Considering FRW cosmology for action (20) for which the spatial curvature \(R_{ab}^{(3)}=R^{(3)}\) vanishes and thus, \({\mathcal {L}}_{R}^{(3)}\) does not contribute any thing (same FRW cosmology obtained for any choice of \({\mathcal {L}}_{R}^{(3)}\)). It is obvious that this situation varies when black hole or solutions with non-trivial dependence are considered. Suppose that universe is composed with perfect fluid, by varying (20) w.r.t \(g_{ab}^{(3)}\) and setting \(N=1\), the Friedmann equations for modified Hořava–Lifshitz gravity are given by

$$\begin{aligned} \rho= & {} F({\tilde{R}})-6\bigg [(1-3\uplambda +3\mu )H^{2}+\mu {\dot{H}}\bigg ]F'({\tilde{R}}) \nonumber \\&+ \,6 \mu H \frac{d F'({\tilde{R}})}{dt}-c a^{-3}, \end{aligned}$$
(23)
$$\begin{aligned} p= & {} -F({\tilde{R}})+2\bigg [(1-3\uplambda +3\mu )({\dot{H}}+3H^{2})\bigg ]F'({\tilde{R}})\nonumber \\&+2(1-3\uplambda ) H \frac{d F'({\tilde{R}})}{dt}-2\mu \frac{d^2 F'({\tilde{R}})}{dt^{2}}, \end{aligned}$$
(24)

where prime denotes the derivative of respective function with respect to argument. Here c is the constant of integration and the term \(ca^{-3}\) represents the dark matter part when \(c>0\) [68]. As during BBN, dark matter part vanishes (i.e. \(c=0\)) [66], therefor Friedmann equations (23) and (24) become

$$\begin{aligned} \rho _{DE}= & {} F({\tilde{R}})-6\bigg [(1-3\uplambda +3\mu )H^{2}+\mu {\dot{H}}\bigg ]F'({\tilde{R}})\nonumber \\&+6 \mu H \frac{d F'({\tilde{R}})}{dt}, \end{aligned}$$
(25)
$$\begin{aligned} p_{DE}= & {} p. \end{aligned}$$
(26)

The value of argument \({\tilde{R}}\) from Eq. (22) reduces to

$$\begin{aligned} {\tilde{R}}=3(1-3\uplambda +6\mu ) H^2 +6\mu {\dot{H}}. \end{aligned}$$
(27)

3 BBN constraints: basic scenario

In this section, we will develop the relation for deviation of freeze-out time \(T_f\) and BBN constraints. Since BBN noticed in radiation era [58, 69, 70], thus during BBN for standard model radiation in context of GR, the first Friedmann equation can be approximated as

$$\begin{aligned} H^2\approx \frac{\rho _r}{3 M_p^2}=H_{GR}^2, \end{aligned}$$
(28)

where \(M_p=\frac{1}{\sqrt{8\pi G}}\) is reduced Planck mass, \(\rho _r\) is energy density of a relativistic particles filling the universe and is given as

$$\begin{aligned} \rho _r=\frac{\pi ^2 g_* T^4}{30}. \end{aligned}$$
(29)

Here T represents the temperature and \(g_*=g(T)\) is the effective number of the degree of freedom usually approximated as \(g_* \sim 10\). Substituting the values of \(\rho _r\) and \(M_p\) in Eq. (28), we get

$$\begin{aligned} H(T)=\Bigg (\frac{4 \pi ^3 g_*}{45}\Bigg )^{\frac{1}{2}} \frac{T^2}{M_{p\ell }}, \end{aligned}$$
(30)

where \(M_{p\ell }=\sqrt{8\pi } M_P\) is referred to as Plank mass. Due to radiation conservation, the scale factor of universe evolves as \(a(t)\sim \sqrt{t}\), where t is the cosmic time. The Hubble parameter H in terms of cosmic time t becomes as\(H=\frac{1}{2t}\) which leads to relation between temperature T and cosmic time t as \(\frac{1}{t}=\bigg (\frac{16 \pi ^3 g_*}{45}\bigg )^\frac{1}{2} \frac{T^2}{M_{p\ell }}\) (or \(T(t)\simeq (t/\text {s})^{-1/2}\) MeV). Since number of neutron arises during BBN due to conversion of some protons-neutron rate [70, 71] which is given as

$$\begin{aligned} \Lambda _{pn}(T)= & {} \Lambda _{(n+\nu _e \rightarrow p+e^-)}+\Lambda _{(n+e^+ \rightarrow p+{\bar{\nu }}_e)}\nonumber \\&+\Lambda _{(n\rightarrow p+e^- +{\bar{\nu }}_e)}, \end{aligned}$$
(31)

and its inverse \(\Lambda _{np}(T)\). Thus the total rate can be given as \(\Lambda _{tot}(T)=\Lambda _{pn}(T)+\Lambda _{np}(T)\). Considering all these particles at same temperature which is low enough causes to use Boltzmann distribution instead of the Fermi-Dirac distribution. Assuming electron mass negligible as compared to electron and neutrino energies, some simple mathematics can be used to calculate neutron abundance via conversion rate of proton into neutron which gives the relation for total rate as [13, 54, 72, 73]

$$\begin{aligned} \Lambda _{tot}(T)=8(12T^2+6Q T+Q^2)A T^3, \end{aligned}$$
(32)

where Q is the mass difference between neutron and proton given as \(Q=m_n -m_p =1.29\times 10^{-3}\) GeV and \(A=1.02\times 10^{-11}\) GeV\(^{-4}\). The relation \(Y_p=\uplambda \frac{2x(T_f)}{1+x(T_f)}\), where \(\uplambda =e^{(T_f-T_n)/\tau }\) with \(T_f\) means freeze-out of weak interaction while \(T_n\) represents the farsee-out of nucleosynthesis, \(x(T_f)=e^{-\frac{Q}{\tau (T_f)}}\) gives the neutron to proton equilibrium ratio and \(\tau =8803\pm 1.1\) s is the neutron average life time [74]. Moreover, the function \(\uplambda (T_f)\) represents the portion of neutrons that decay into proton in the interval [\(T_f,T_n\)]. Now we compare the universe expansion rate \(H^{-1}\) and the function \(\Lambda _{tot}(T)\) given in (32) to calculate the freeze-out time \(T_f\). We can consider system in thermal equilibrium if interaction time is much larger then expansion time (i.e. \(H^{-1}\ll \Lambda _{tot}(T)\)) [57, 69]. On the other hand, the particles decouple if expansion time is much larger then interaction time (i.e. \(H^{-1}\gg \Lambda _{tot}(T)\)). The temperature during which decoupling takes place is freeze-out temperature \(T_f\) that corresponds to \(H(T_f)=\Lambda (T_f)\simeq c_q T_f^5\), where \(c_q\equiv 96A\simeq 9.8\times 10^{-10}~\hbox {GeV}^{-4}\) [13, 54, 72, 73]. Using Eqs. (30) and (32), above requirement leads to the relation

$$\begin{aligned} T_f=\Bigg (\frac{4 \pi ^3 g_*}{45 c_q^2 M_{p\ell }^2}\Bigg )^{1/6}. \end{aligned}$$
(33)

The Hubble parameter H will deviate from \(H_{GR}\) in context of modified cosmology, due to which freeze-out time also presents a deviation \(\Delta T_f\) from (28). Due to this deviation in fractional mass, \(Y_p\) is given as

$$\begin{aligned} \Delta Y_p=Y_p \Bigg [\Bigg (1-\frac{Y_p}{2\uplambda }\Bigg )\ln \Bigg (\frac{2\uplambda }{Y_p}-1\Bigg )-\frac{2T_f}{\tau }\Bigg ]\frac{\Delta T_f}{T_f}, \end{aligned}$$
(34)

where we take \(\Delta T(T_n)=0\) as \(T_n\) is fixed by deuterium binding energy [72, 73, 75]. During BBN era, the observational estimation of mass fraction is [76,77,78,79,80,81]

$$\begin{aligned} Y_p=0.2476,\quad |\Delta Y_p|<10^{-4}. \end{aligned}$$
(35)

One can obtain an extra term in Friedmann equations by using any modified theories of gravity which needs to be small compared to the radiation sector of standard cosmology during BBN era so that observational facts may not be spoiled. Thus, from the general modified Friedmann equation, \(3M_p^2 H^2=\rho _m+\rho _r+\rho _{DE}\), we can obtain

$$\begin{aligned} H=H_{GR}\Bigg (1+\frac{\rho _{DE}}{\rho _r}\Bigg )^{1/2}=\Delta H+H_{GR}, \end{aligned}$$
(36)

where \(H_{GR}=M_p \sqrt{\frac{\rho _r}{2}}\) is the rate at which universe expands in standard cosmology. Thus, we obtain

$$\begin{aligned} \Delta H=H_{GR}\Bigg (\sqrt{1+\frac{\rho _{DE}}{\rho _r}}-1\Bigg ). \end{aligned}$$
(37)

This deviation from standard cosmology will lead to a deviation in the freeze-out temperature \(\Delta T_f\). Since \(H_{GR}=\Lambda _{tot}\approx c_q T_f^5\). This relation along with (33) leads to the relation

$$\begin{aligned} H_{GR}\Bigg (\sqrt{1+\frac{\rho _{DE}}{\rho _r}}-1\Bigg )=5c_q T_f^4 \Delta T_f. \end{aligned}$$
(38)

In the regime \(\rho _{DE}\ll \rho _r\), one can find finally

$$\begin{aligned} \frac{\Delta T_f}{T_f}\simeq \frac{\rho _{DE}}{\rho _r}\frac{H_{GR}}{10 c_q T_f^5}. \end{aligned}$$
(39)

The above theoretically evaluated relation should be compared with the following observational bound

$$\begin{aligned} \Bigg |\frac{\Delta T_f}{T_f}\Bigg |<4.7\times 10^{-4}, \end{aligned}$$
(40)

which is found by using observation estimation of the baryon mass fraction converted into \(^4He\) [76,77,78,79,80,81] which is given in Eq. (35).

4 Chi-square test

A statistical test Chi-square developed by Pearson in 1900 [82] is used for a comparison between the observed values and expected values. Pearson also applied it to test the goodness of fit for frequency curves. This test exhibits, whether the difference between two data sets is due to chance or due to relationship of variables under consideration. The condition to perform Chi-square test is that data set must have points more than five. The outcome of Chi-square test is a single number which analyze the difference between the observed values and expected values of the data sets. There is no difference between two data sets (data sets are identical) if the value of Chi-square is zero. A larger value of \(\chi ^2\) exhibits bigger difference between the two data sets as compared to a smaller value of \(\chi ^2\). To evaluate the limit and best fitting values for different models, we use the \(\chi ^2\) static as

$$\begin{aligned} \chi ^2(p)=\sum \Bigg (\frac{O_i -E_i}{\sigma _i}\Bigg )^2, \end{aligned}$$
(41)

where i counts the data points, \(O_i\) represents the observed value, \(E_i\) is the corresponding expected value, \(\sigma _i\) is the error associated with ith observed value in the data and p denotes the set of model parameters. To observe the compatibility of models with the recent observational data, we will calculate the Hubble parameter H for each model in upcoming sections and compare the corresponding values of H with recent data. Bhardwaj et al. [83] presented the observed values of H for 46 different points against redshift parameter z along with their observational error evaluated by using various age approach by different cosmologists presented in the Table 1 as

Table 1 The behavior of Hubble parameter H against redshift parameter z [83]
Full size table

5 BBN of various models in Einstein-Aether gravity

In this section, we apply the formalism obtained in the Sect. 3 to find the BBN constraints under the realm of Einstein-Aether gravity. We use DE relation (18) which holds in the contexts of Einstein-Aether gravity to find the BBN constraints as well as the Hubble parameter H. We will focus on three different models to examine the BBN constraints and Hubble parameter.

5.1 Model 1

The first model which we use to inspect BBN constraints in context of Einstein-Aether gravity is

$$\begin{aligned} F(K)=f_0 K^n,\quad K>0, \end{aligned}$$
(42)

where \(f_0\) is a positive constant as cosmic acceleration is observed only for \(f_0>0\) [100] and n is the only free parameter. Moreover, \(f_0\) can be expressed in terms of \(H_0\) (i.e. present value of Hubble parameter) as \(n\ne 1\). The present value of DE density can be given as

$$\begin{aligned} \Omega _{DE0}=\frac{\rho _{DE0}}{3M_p^2 H_0^2}, \end{aligned}$$
(43)

where \(\Omega _{DE0}\) is the current matter density parameter and is approximately equivalent to 0.7 while

$$\begin{aligned} H_{0}= & {} 73.02\pm 1.79~\text {km/(sMpc)},\\\sim & {} 2.1\times 10^{-42}~\text {GeV}. \end{aligned}$$

is the Hubble parameter at present [13]. The best fit on other free parameters can be obtained by taking the CC + \(H_0\) + SNeIa + BAO observational data [101]. During BBN era, assuming \(\rho _{DE}=\rho _{DE0}\) and inserting its value along with F(K) in Eq. (18), we get

$$\begin{aligned} f_0=\frac{2 M_p^2 \Omega _{DE0} \left( \frac{\gamma H_0^2 }{M^2}\right) ^{1-n}}{3^{n-1}(2 n-1) \gamma }. \end{aligned}$$
(44)

Inserting Eq. (42) along with (44) into (18) and then simplifying (39), we have

$$\begin{aligned} \frac{\Delta T_f}{T_f}=\frac{\Omega _{DE0} H_0^{2-2n} \xi ^{2n-1} T_f^{4n-7}}{10 c_q}, \end{aligned}$$
(45)

where \(T_f\) is given in (33) and

$$\begin{aligned} \xi =\frac{1}{M_{p\ell }}\Bigg (\frac{4 \pi ^3 g_*}{45}\Bigg )^{\frac{1}{2}}. \end{aligned}$$
(46)
Fig. 1
figure 1

Variation of \(\left| \frac{\Delta T_f}{T_f}\right| \) given in Eq. (45) against free parameter n

Full size image

We depict \(\left| \frac{\Delta T_f}{T_f}\right| \) in Fig. 1 against the free parameter n appearing in (45) with an upper bound coming in (40). It can be observed from the figure that the mathematical relation (45) satisfies the bound (40) for \(n\le 0.8247\). The fixed parameters to plot (45) are chosen as \(H_0=0.69\), \(\gamma =1\), \(\Omega _{DE0}=0.7\) and \(M=5\). It is of great interest that under the requirement, Einstein-Aether gravity describes DE at late universe, conditions (44) must be satisfied. If n is restricted near zero then constraint given in Eq. (39) becomes constant which describes \(\Lambda \)CDM regime. To observe the compatibility of model with observations, we insert the value of \(\rho =\rho _0 a^{-3(1+\omega )}\) where \(\rho _0=3 M_p^2 H_0^2 \Omega _{DE0}\) from continuity equation and \(\rho _{EA}\) from Eq. (18) in Eq. (16), we have

$$\begin{aligned} 2H^2+(\gamma F K^{-1}-2\gamma F')H^2=\frac{16 \pi G}{3}\rho _0 a^{-3(1+\omega )}-\frac{2K}{a^2},\nonumber \\ \end{aligned}$$
(47)

where \(8\pi G=1\). Substituting the values of \(F,~F'\), K in the above equation and using the transformation from cosmic time t to the redshift parameter z given as \(\frac{dH}{dt}=-(1+z)H \frac{dH}{dz}\), simplification leads to the relation

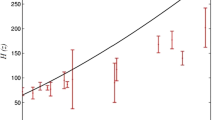
$$\begin{aligned} H'(z)=\frac{3 H_0^2 \Omega _{DE0}(\omega +1) (z+1)^{3 \omega +2} M^2-6 \gamma (z+1) H^2}{f_0 3^{n-1} n (1-2 n) \gamma ^n M^{4-2 n} H(z)^{2 n-1}+6 \gamma (z+1)^2 H(z) +2 H(z) M^{2}}. \end{aligned}$$
(48)

The above equation is a complicated first order ordinary differential equation from which it is difficult to obtain the exact solution. To overcome this complexity, we solve the above equation numerically by using the software mathematica and extract the 43 different values of H against z given in serial number 1 to 43 in Table 1 and plots are in Fig. 2. The error bars representing observations given in [83] are also added to the figure for comparison. Our estimated values for various cosmological parameters for minimum \(\chi ^2\) are computed \(H_0=0.69,~M=5,~\gamma =1,~\omega =-1/3,~\Omega _{DE0}=0.7\) which are identical to the values used to plot Fig. 1 with five different values of n mentioned in the panel of Fig. 2. The values of \(\chi ^2\) obtained for different values of n are as follows

Fig. 2
figure 2

The evolution of the Hubble parameter H against redshift z for different values of \(n = 1.08\) (purple), 1.085 (magenta), 1.09 (green), 1.095 (orange), 1.1 (black). The dashed red line relates to the \(\Lambda \)CDM model. The error bars represent the observational values. We consider that \(H_0=0.69,~M=5,~\gamma =1,~\omega =-1/3,~\Omega _{DE0}=0.7\) and \(f_0\) is given in Eq. (44)

Full size image
$$\begin{aligned} \chi ^2= & {} ~{\left\{ \begin{array}{ll} 224.9193&{}\text {for}\ n=1.080,\\ 152.3425&{}\text {for}\ n=1.085,\\ 176.7795&{}\text {for}\ n=1.090,\\ 224.0224&{}\text {for}\ n=1.095,\\ 271.6758&{}\text {for}\ n=1.100. \end{array}\right. } \end{aligned}$$

The Chi-square analysis (to test the goodness of fit for the curves) depicts that the obtained results are closed to the observations when \(n=1.085\) and differ utmost from the observational data when \(n=1.1\). Moreover, the values of model parameters which are estimated to analyze the BBN compatibility are best fit according to \(\chi ^2\) test.

5.2 Model 2

The second model which we inspect for BBN constraints under the realm of Einstein-Aether gravity is given as

$$\begin{aligned} F(K)=\alpha K^n +\beta , \end{aligned}$$
(49)

where \(\alpha \) and \(\beta \ne 0\) are real constants. This model is more generalized as the model given in (42) and reduces to the model (42) if we choose \(\beta =0\). We can find mathematical relation for the constant \(\alpha \) for BBN era as

$$\begin{aligned} \alpha =\frac{M^{2(n-1)} \left[ \beta M^2+6H_0^2 M_p^2 \Omega _{DE0}\right] }{M^2 (2 n-1)}. \end{aligned}$$
(50)

Substituting Eq. (49) along with (50) into (18) and then simplifying for the constraints given in (39), we have

$$\begin{aligned} \left| \frac{\Delta T_f}{T_f}\right| =\frac{\xi ^{2n} T_f^{4n} (\beta M^2+6H_0^2 M_p^2 \Omega _{DE0})-\beta M^2 H_0^{2n}}{60 c_q M_p^2 H_0^{2n} \xi T_f^7}.\nonumber \\ \end{aligned}$$
(51)
Fig. 3
figure 3

Variation of \(\left| \frac{\Delta T_f}{T_f}\right| \) given in Eq. (51) against free parameter n

Full size image

We plot \(\left| \frac{\Delta T_f}{T_f}\right| \) versus n in Fig. 3 appearing in Eq. (51) with an upper bound coming in (40). We have chosen the fixed constants as \(H_0=0.69\), \(\beta =0.6\) and \(M=5\). It can be observed from the figure that the mathematical relation (51) satisfies the bound (40) for \(n\le 0.7498\). Moreover, if we restrict the free parameter n near zero, then the bound coming in (39) becomes constant which justify the \(\Lambda \)CDM regime. For comparison with recent observational data, we substitute \(\rho \) with from continuity equation and \(\rho _{EA}\) from Eq. (18) in Eq. (16), we have

$$\begin{aligned}&2H^2+\beta \gamma K^{-1} H^2+\alpha \gamma K^{n-1}(1-2n)H^2\nonumber \\&\quad =\frac{2}{3}\rho _0 a^{-3(1+\omega )}-\frac{2K}{a^2}. \end{aligned}$$
(52)

Substituting the corresponding values in the above equation and using the transformation from t to z, simplification leads to the equation

$$\begin{aligned} H'(z)=\frac{3 H_0^2 \Omega _{DE0}(\omega +1) (z+1)^{3 \omega +2} M^2-6 \gamma (z+1) H^2}{3^{n-1} n \alpha (1-2 n) \gamma ^n M^{4-2 n} H(z)^{2 n-1}+6 \gamma (z+1)^2 H(z) +2 H(z) M^{2}}. \end{aligned}$$
(53)

We solved the above equation numerically using the software mathematica due to its complexity and extracted 43 different values of Hubble parameter H for various values of z given in serial number 1 to 43 in Table 1 and plotted in Fig. 4. The error bars added to the figure for comparison representing observations given in [83]. The estimated values for different parameters for minimum \(\chi ^2\) have been computed as \(n=1.096,~M=5,~\beta =0.6,~\gamma =1,~\omega =-1/3,~\Omega _{DE0}=0.7\) and \(\alpha \) is given in Eq. (50) which are similar to the values chosen to plot Fig. 3. The values of \(\chi ^2\) obtained for different values of \(H_0\) are as follow

Fig. 4
figure 4

Hubble parameter versus redshift error bar plot comparing with \(\Lambda \)CDM

Full size image
$$\begin{aligned} \chi ^2= & {} {\left\{ \begin{array}{ll} 473.4646&{}\text {for}\ H_0=64, \\ 277.9502&{}\text {for}\ H_0=68,\\ 157.3789&{}\text {for}\ H_0=72,\\ 110.8029&{}\text {for}\ H_0=76,\\ 139.4633&{}\text {for}\ H_0=80. \end{array}\right. } \end{aligned}$$

With five different values of \(H_0\) mentioned in the panel, the goodness of fit (\(\chi ^2\)) for the curves shows that it is least for the curve having \(H_0=76\) which is closest value to observations and most difference occur with the observations when \(H_0=64\). The \(\chi ^2\) test exhibits that model parameters estimated to analyze BBN consistency are best fit compared to the observational data and the \(\Lambda \)CDM regime.

5.3 Model 3

The third model which we assume to investigate BBN constraints under the realm of Einstein-Aether gravity is much more generalized as compared to both of the previous models and is given as

$$\begin{aligned} F(K)=K+\alpha K^2+\beta K^n,\quad K>0, \end{aligned}$$
(54)

where \(\alpha \) and \(\beta \) are real constants. As in BBN era, DM does not exist. Thus the mathematical relation for constant \(\beta \) in BBN era can be obtained as

$$\begin{aligned} \beta =-\frac{M^{2n} \left( 9 \alpha \gamma ^2 H_0^2 +M^2 (\gamma -2 M_p^2 \Omega _{DE0})\right) }{(2 n-1)3^{n-1} H_0^{2(n-1)} \gamma ^n M^4}. \end{aligned}$$
(55)

Inserting Eqs. (54) and (55) into (18), the simplification of Eq. (39) yields

$$\begin{aligned} \frac{\Delta T_f}{T_f}=\frac{\gamma H_0^{2(n-1)} (M^2+9 \alpha \xi ^2 T_f^4 \gamma )-\xi ^{2n-1} T_f^{4n-4} (9 \alpha H_0^2 \gamma ^2+M^2 (\gamma -2 M_p^2 \Omega _{DE0}))}{20 M^2 c_q M_p^2 T_f^3 H_0^{2(n-1)}}. \end{aligned}$$
(56)
Fig. 5
figure 5

Variation of \(\left| \frac{\Delta T_f}{T_f}\right| \) given in (56) against free parameter n for the model \(F(K)=K+\alpha K^2+\beta K^n\) in Einstein-Aether cosmology

Full size image

Figure 5 describes the graph of above equation against the free parameter n having an upper bound \(4.7 \times 10^{-4}\). It is easy to observe from the Fig. 5 that the absolute value of above mathematical relation remains less than the upper bound (\(4.7 \times 10^{-4}\)) when \(n\le 0.8071\). The other fixed parameters are chosen as \(H_0=0.69\), \(\gamma =0.002\), \(\alpha =10^{-9}\) and \(M=5\). Moreover, the bound existing in Eq. (39) becomes constant if we restrict the free parameter n near zero which favors the \(\Lambda \)CDM regime. For comparison with recent observational data, we substitute \(\rho =\rho _0 a^{-3(1+\omega )}\) with \(\rho _0=3 M_p^2 H_0^2 \Omega _{DE0}\) from continuity equation and \(\rho _{EA}\) from Eq. (18) in (16), we have

$$\begin{aligned}&2H^2+\frac{3 \alpha \gamma ^2 H^4}{M^2}-\gamma H^2-\frac{6\alpha \gamma ^2 H^4}{M^2}+\frac{3^{n-1} \beta \gamma ^n H^{2n} (1-2n)}{M^{2n-2}}\nonumber \\&\quad =\frac{2}{3}\rho _0 a^{-3(1+\omega )}-\frac{6\gamma H^2}{M^2 a^2}. \end{aligned}$$
(57)

Using the transformation from t to z and differentiating w.r.t. redshift z, simplification leads to the relation

$$\begin{aligned} H'(z)=\frac{3 H_0^2 M^2 (\omega +1) \Omega _{DE0} (z+1)^{3 \omega +2}-6 \gamma (z+1) H^2}{6 \gamma (z+1)^2 H-6 \alpha \gamma ^2 H^3 +(2-\gamma ) H M^{2}+\beta 3^{n-1} n (1-2 n) \gamma ^n H^{2 n-1} M^{4-2n}}. \end{aligned}$$
(58)

We proceed the above equation numerically by using mathematica software as it is a complex first order differential equation and extracted 43 different values of Hubble parameter H for various values of z given in serial number 1 to 43 in Table 1 and plot is in Fig. 6. The error bars representing the recent observational data given in [83] are also added to the figure for comparison. The estimated values for different parameters for minimum \(\chi ^2\) are computed as \(H_0=0.69,~\alpha =10^{-9},~M=1.2,~\gamma =0.002,~\omega =-1/3,~\Omega _{DE0}=0.7\) with five different values of \(n = 1.0358\) (purple), 1.0362 (magenta), 1.0366 (green), 1.037 (orange), 1.0374 (black). The values of \(\chi ^ 2\) obtained for different values of n are as follows

Fig. 6
figure 6

The evolution of the Hubble parameter H against redshift z for different values of n along with the \(\Lambda \)CDM model and the error bars representing the observational values

Full size image
$$\begin{aligned} \chi ^2= & {} ~{\left\{ \begin{array}{ll} 48.9366&{}\text {for}\ n~=~1.0358,\\ 122.6629&{}\text {for}\ n~=~1.0362,\\ 147.6971&{}\text {for}\ n~=~1.0366,\\ 207.2323&{}\text {for}\ n~=~1.0370,\\ 260.3635&{}\text {for}\ n~=~1.0374. \end{array}\right. } \end{aligned}$$

The Chi-square analysis depicts that the values of Hubble parameter are closed to the observations when \(n=1.0358\) and differ utmost from the observational data when \(n=1.0374\). It can be seen from the \(\chi ^2\) analysis that the model parameters estimate best to analyze BBN compatibility with the observational data and the \(\Lambda \)CDM regime.

6 BBN in modified Hořava–Lifshitz gravity

In this section, we use the formalism to impose the BBN constraints obtained in Sect. 3 under the realm of modified Hořava–Lifshitz gravity. We use DE relation (25) which holds in context of modified Hořava–Lifshitz gravity. We will concentrate on distinct models to examine the BBN constraints.

6.1 Model 1

The first model with which we inspect BBN constraints in context of modified Hořava–Lifshitz gravity is given as

$$\begin{aligned} F({\tilde{R}})=\alpha {\tilde{R}}^n, \end{aligned}$$
(59)

where \(\alpha \) is a real constant and \({\tilde{R}}\) is given in (27). Since DM does not exist during BBN era, we can get expression for the constant \(\alpha \) as

$$\begin{aligned} \alpha =-\frac{H_0^2 M_p^2 \Omega _{DE0} (3 \uplambda -2 \mu -1) \left( H_0^2 (-3 \uplambda +2 \mu +1)\right) ^{-n}}{3^{n-1} [1-3 \uplambda +2 \mu +2 n (3 \uplambda +\mu -2 \mu n-1)]}. \end{aligned}$$
(60)

Inserting Eqs. (59) and (60) into (25), the simplification of Eq. (39) yields

$$\begin{aligned} \frac{\Delta T_f}{T_f}=\frac{\Omega _{DE0} T_f^{4n-7} \xi ^{2n-1} }{10 c_q H_0^{2n-2}}. \end{aligned}$$
(61)
Fig. 7
figure 7

Variation of \(\left| \frac{\Delta T_f}{T_f}\right| \) given in Eq. (61) against free parameter n

Full size image

Figure 7 describes the graph of \(\left| \frac{\Delta T_f}{T_f}\right| \) against the free parameter n having an upper bound \(4.7\times 10^{-4}\). It is easy to observe from the figure that the mathematical relation (61) satisfies the bound (40) for \(n\le 0.8246\). The other fixed parameters are chosen as \(H_0=69,~H'(0)=1,~\uplambda =0.31,~\omega =-1/3,~\Omega _{DE0}=0.7\) and \(\mu =0.009\). Moreover, the bound existing in Eq. (39) becomes constant if we restrict the free parameter n near zero which favors the \(\Lambda \)CDM regime. For comparison with recent observational data, we substitute \(\rho =\rho _0 a^{-3(1+\omega )}\) with \(\rho _0=3 M_p^2 H_0^2 \Omega _{DE0}\) from continuity equation and \({\tilde{R}}\) from Eq. (27) in Eq. (25), we have

$$\begin{aligned}&2H^2+\frac{3 \alpha \gamma ^2 H^4}{M^2}-\gamma H^2-\frac{6\alpha \gamma ^2 H^4}{M^2}\nonumber \\&\qquad +\frac{3^{n-1} \beta \gamma ^n H^{2n} (1-2n)}{M^{2n-2}}\nonumber \\&\quad =\frac{2}{3}\rho _0 a^{-3(1+\omega )}-\frac{6\gamma H^2}{M^2 a^2}. \end{aligned}$$
(62)

Substituting the transformation from t to z and differentiating w.r.t. redshift z, simplification leads to the relation

$$\begin{aligned}&\alpha (1-6 n) [3 H^2 (-3 \uplambda +6 \mu +1)-6 \mu (z+1) H(z) H']\nonumber \\&\quad -3 H_0^2 \Omega (z+1)^{3 (\omega +1)}+6 \alpha \mu (n-1) nH(-3 (z+1) H^2 \nonumber \\&\quad \times (-3 \uplambda +6 \mu +1) H') \bigg (6 \mu (z+1)^3 H H''-6 (z+1) H^2 \nonumber \\&\quad \times (-3 \uplambda +6 \mu +1) H' +12 \mu (z+1)^2 H H'\nonumber \\&\quad -6 \mu (z+1) H^2 H'+(z+1)^2 H H'^2\bigg )=0. \end{aligned}$$
(63)

The above equation is a complicated second order differential equation from which it is difficult to obtain the exact solution. To overcome this complexity, we solve this equation numerically by using the software mathematica and extracted 43 different values of H against z given in serial number 1 to 43 in Table 1 and plot them in Fig. 8 for different choices of the parameter \(\mu \). The error bars representing observations given in [83] are also added to the figure for comparison. The estimated values for different parameters for minimum \(\chi ^2\) are computed as \(H_0=69,~H'(0)=1,~\uplambda =0.31,~\omega =-1/3,~\Omega _{DE0}=0.7\) which are same as the values chosen to plot Fig. 7 with five different values of \(\mu \) mentioned in the panel. The values of \(\chi ^2\) obtained for different values of \(\mu \) are

Fig. 8
figure 8

Graph Hubble parameter H against redshift z for different values of \(\mu = 0.003\) (purple), 0.006 (magenta), 0.009 (green), 0.012 (orange), 0.015 (black). The dashed red line relates to the \(\Lambda \)CDM regime. The error bars represent the observational values. In plotting the figures, we have chosen \(H_0=69,~H'(0)=1,~\uplambda =0.31,~\omega =-1/3,~\Omega _{DE0}=0.7\) and \(\alpha \) is given in Eq. (60)

Full size image
$$\begin{aligned} \chi ^2= & {} ~{\left\{ \begin{array}{ll} 80.0307&{}\text {for}\ \mu ~=~0.003,\\ 41.7924&{}\text {for}\ \mu ~=~0.006,\\ 59.4275&{}\text {for}\ \mu ~=~0.009,\\ 141.9066&{}\text {for}\ \mu ~=~0.012,\\ 295.6098&{}\text {for}\ \mu ~=~0.015. \end{array}\right. } \end{aligned}$$

To test the goodness of fit for the curves (the Chi-square test), we find that the value of Hubble parameter are closed to the observations [83] when \(\mu =0.006\ \text {and}\ 0.009\) while differ utmost from the observations when \(\mu =0.015\). It can be seen from the \(\chi ^2\) analysis that the values of model parameters (\(H_0=69,~H'(0)=1,~\uplambda =0.31,~\omega =-1/3,~\Omega _{DE0}=0.7\)) estimate best to analyze BBN compatibility with the observational data and the \(\Lambda \)CDM regime.

6.2 Model 2

The second model which we use to investigate BBN constraints under the realm of modified Hořava–Lifshitz gravity is

$$\begin{aligned} F({\tilde{R}})=\alpha {\tilde{R}} + \beta {\tilde{R}}^n, \end{aligned}$$
(64)

where \(\alpha \) and \(\beta \) are real constants. During BBN era when DM does not exist, the value of constant \(\beta \) can be obtained as

$$\begin{aligned} \beta =-\frac{(3 \uplambda -2 \mu -1) \left( 2 \mu -3 \uplambda +1\right) ^{-n} \left( \alpha (3 \uplambda -1)-M_p^2 \Omega _{DE0} \right) }{3^{n-1}[1-3 \uplambda +2 \mu +2 n (3 \uplambda +\mu (3-4 n)-1)]H_0^{2(n-1)}}.\nonumber \\ \end{aligned}$$
(65)

Inserting Eqs. (64) and (65) into (25), the simplification of Eq. (39) yields

$$\begin{aligned} \frac{\Delta T_f}{T_f}= & {} (10 c_q M_p^2 \xi T_f^7)^{-1}[\alpha (3 \uplambda -1) \xi ^2 T_f^4 \nonumber \\&-H_0^2 (H_0^2 (-3 \uplambda +2 \mu +1))^{-n} (-3 \alpha \uplambda +\alpha \nonumber \\&+M_p^2 \Omega _{DE0} ) (\xi ^2 T_f^4 (-3 \uplambda +2 \mu +1))^n]. \end{aligned}$$
(66)
Fig. 9
figure 9

Variation of \(\left| \frac{\Delta T_f}{T_f}\right| \) given in (66) against free parameter n for the model \(F({\tilde{R}})=\alpha {\tilde{R}} + \beta {\tilde{R}}^n\) in the Modified Hořava–Lifshitz cosmology

Full size image

In Fig. 9, we present the graph of \(\left| \frac{\Delta T_f}{T_f}\right| \) versus free parameter n with an upper bound given in (40). It can be observed from the figure that the mathematical relation (66) satisfies the upper bound for \(n\le 0.824\). The fixed parameters to plot the figure are chosen as \(H_0=0.69,~\uplambda =0.334,~\mu =0.0001\) and \(\alpha =0.001\). Moreover, the bound existing in (39) presents \(\Lambda \)CDM regime if we restrict n near zero. For comparison with recent observational data, we substitute \(\rho \) from continuity equation and \({\tilde{R}}\) from Eq. (27) in (25), we have

$$\begin{aligned}&6n H \mu \beta (n-1){\tilde{R}}^{n-2}[6(1-3\uplambda +6\mu )H {\dot{H}}+6\mu {\ddot{H}}]\nonumber \\&\quad -6[(1-3\uplambda +3\mu )H^2+\mu {\dot{H}}](\alpha +n \beta {\tilde{R}}^{n-1})\nonumber \\&\quad +\,\alpha {\tilde{R}} +\beta {\tilde{R}}^n=\rho _0 a^{-3(1+\omega )}. \end{aligned}$$
(67)

Substituting the transformation from t to z and differentiating w.r.t redshift z, simplification leads to the relation

$$\begin{aligned}&6n\beta H(H (3 \uplambda -3 \mu -1)+\mu (z+1) H') \nonumber \\&\quad \times \left[ 3 H^2 (6 \mu -3 \uplambda +1)-6 \mu (z+1) H H'\right] ^{n-1}-H_0^2 \nonumber \\&\quad \times 3 \Omega _{DE0} (z+1)^{3 (\omega +1)} -6 \alpha H(H (3 \mu -3 \uplambda +1)\nonumber \\&\quad -\mu (z+1) H')+\beta H (3 H (6 \mu 3 \uplambda +1)\nonumber \\&\quad -6 \mu (z+1) H')+3 \alpha H (H (-3 \uplambda +6 \mu +1)\nonumber \\&\quad -2 \mu (z+1) H')+36n \beta \mu H (n-1) (3 H^2 \nonumber \\&\quad \times (-3 \uplambda +6 \mu +1)-6 \mu (z+1) H H')^{n-2} \nonumber \\&\quad \times \bigg [6 \mu (z+1)^3 H H''-H^2 (z+1) (6 \mu -3 \uplambda +1) H'\nonumber \\&\quad +(z+1)^2 H H'^2+2 (z+1)^2 H H'-(z+1) H^2 H'\bigg ]=0.\nonumber \\ \end{aligned}$$
(68)

We solved the above equation numerically using the software mathematica due to its complexity and calculated first 43 values of H against z listed in serial number 1 to 43 in Table 1 and plotted in Fig. 10. The error bars representing observations given in [83] are also added to the figure for comparison. The estimated values for different parameters for minimum \(\chi ^2\) have been computed as \(H'(0)=1\), \(\uplambda =0.334\), \(\mu =0.0001\) and \(\alpha =0.001,~\omega =-1/3,~\Omega _{DE0}=0.7\) and \(\beta \) is given in Eq. (65) for five different values of \(H_0= 60\) (purple), 63 (magenta), 66 (green), 69 (orange), 72 (black). The values of \(\chi ^2\) obtained for different values of \(H_0\) as follows

Fig. 10
figure 10

Hubble parameter versus redshift error bar plot comparing with \(\Lambda \)CDM

Full size image
$$\begin{aligned} \chi ^2= & {} ~{\left\{ \begin{array}{ll} 65.1115&{}\text {for}\ H_0~=~60,\\ 38.7577&{}\text {for}\ H_0~=~63,\\ 105.4443&{}\text {for}\ H_0~=~66,\\ 223.1631&{}\text {for}\ H_0~=~69,\\ 406.6963&{}\text {for}\ H_0~=~72. \end{array}\right. } \end{aligned}$$

The Chi-square analysis (to test the goodness of fit for the curves) gives that the obtained results are closed to the observations [83] when \(H_0=63\) and differ utmost from the observational data when \(H_0=72\). It is easy to deduct from the \(\chi ^2\) analysis that the values of model parameters \(H'(0)=1,~\uplambda =0.334,~\mu =0.0001\) and \(\alpha =0.001,~\omega =-1/3,~\Omega _{DE0}=0.7\) estimate best to analyze BBN compatibility with the observational data and the \(\Lambda \)CDM regime.

7 Concluding remarks

In this paper, BBN phenomenon has been investigated in Einstein-Aether and modified Hořava–Lifshitz theories of gravity in the presence of observational bounds on the primordial abundance of \(^4He\). These theories efficiently describe the late time accelerated expansion of the universe and do not spoil the behavior of early universe, particularly BBN era. Firstly, we have investigated BBN for three different models of Einstein-Aether gravity. We have attained the BBN bound \(\bigg |\frac{\Delta T_f}{T_f}\bigg |<4.7\times 10^{-4}\) as per recent observations for \(F(K)=f_0 K^n\) (with \(n\le 0.824\)), \(F(K)=\alpha K^n +\beta \) (with \(n\le 0.752\)) and \(F(K)=K+\alpha K^2+\beta K^n\) (with \(n\le 0.807\), \(\gamma =0.002\) and \(\alpha =10^{-9}\)) as shown in Figs. 1, 3 and 5 respectively. It is of great interest that all three models described the \(\Lambda \)CDM regime for free parameter \(n\rightarrow 0\). Moreover, Chi-square analysis has been performed for the same three models to estimate the values of model parameters and have been plotted in Figs. 2, 4 and 6 along with error bars of observational data [83]. The estimated values of the parameters for the model \(F(K)=f_0 K^n\) are \(H_0=0.69,~M=5,~\gamma =1\), for the model \(F(K)=\alpha K^n +\beta \) are \(n=1.096,~M=5,~\beta =0.6,~\gamma =1\) and for the model \(F(K)=K+\alpha K^2+\beta K^n\) are \(H_0=0.69,~\alpha =10^{-9},~M=1.2,~\gamma =0.002\). Chi-square test showed that obtained results of Hubble parameter H are very near to the observational data.

Secondly, we have investigated BBN phenomenon for two models of modified Hořava–Lifshitz gravity. We have obtained BBN bound for both models \(F({\tilde{R}})=\alpha {\tilde{R}}^n\) (with \(n\le 0.824\)) and \(F({\tilde{R}})=\alpha {\tilde{R}} + \beta {\tilde{R}}^n\) (with \(n\le 0.824\)) as shown in Figs. 7 and 9, respectively. Moreover, both models described \(\Lambda \)CDM regime if we restrict the free parameter n near zero. Additionally, Chi-square has computed for the same two models for an estimation of parameters values existing in the model which have been plotted in Figs. 8 and 10. The error bars of observational data are also mentioned in these plots. The estimated values of the parameters for the model \(F({\tilde{R}})=\alpha {\tilde{R}}^n\) are \(H_0=69,~H'(0)=1,~\uplambda =0.31\) and for the model \(F({\tilde{R}})=\alpha {\tilde{R}} + \beta {\tilde{R}}^n\) are \(H'(0)=1\), \(\uplambda =0.334,~\mu =0.0001,~\alpha =0.001\).

In Figs. 1, 3, 5, 7 and 9, it can be seen \(\left| \frac{\Delta T_f}{T_f}\right| \) (presented in blue curve) remained less than \(4.7\times 10^{-4}\) (given in red line) up to some values of free parameter n for each model belonging to Einstein-Aether and modified Hořava–Lifshitz theories of gravity. This \(\left| \frac{\Delta T_f}{T_f}\right| <4.7\times 10^{-4}\) confirms the primordial abundance of Helium (\(^4He\)) which is a confirmation to the idea of photon (light-element) production in the early history of universe. In Figs. 2, 4, 6, 8 and 10, the Chi-square test confirms the estimation of parameter values presented in the models of Einstein-Aether and modified Hořava–Lifshitz theories. In future, we can study the effects of Einstein-Aether and modified Hořava–Lifshitz theories of gravity on the primordial gravitational wave backgrounds. Since its observational evidence of number of existing polarizations are a successful tool for testing GR and extended theories of gravity. We expect that our contribution will be a source for cosmologists to explore more about BBN as it is an interesting addition in modified theories of gravity.