1 Introduction

Black holes created in astrophysical processes are expected to be well described by asymptotically flat solutions of Einstein equations. However, there is also great interest in black holes with other kinds of asymptotic infinities. In particular, it is of interest to determine the effects that occur when black holes are placed in an external background field, extending to infinity. Moreover, observational evidence indicates that in the center of each galaxy there are black holes [1] along with magnetic fields whose origin may be external or generated by currents in the accretion disk. In this context, a non-asymptotically flat exact solution of Einstein–Maxwell equations describing a black hole in a background magnetic universe was constructed about 30 years ago by Ernst [2], which is also known as a Schwarzschild–Melvin black hole. In this model the external field is able to distort the spherical symmetry of the geometry. The magnetic field has the effect of elongating the event horizon into a cigarette-shaped object, with the long axis parallel to the magnetic field lines. However, for astrophysical reasons, the magnetic field is supposed to be weak enough that the metric in this regime is well approximated by the Schwarzschild one; that is, the magnetic field does not distort the geometry of the spacetime, but only interacts with other electromagnetic charges in the system. Also, it was shown that the Ernst metric permits solutions of the Dirac monopole types to be obtained for the Maxwell equations, and the nontrivial topological properties of the spacetimes may play an important role in the quantum geometry of the fields [3].

Here, we study the propagation of charged massive scalar fields in Ernst black hole backgrounds. In this context, quasinormal modes (QNMs) and quasinormal frequencies (QNFs) [4,5,6,7,8,9,10,11,12] have recently attracted great interest due to the detection of gravitational waves [13]. Although the detected signal is consistent with Einstein gravity [14], there are possibilities for alternative theories of gravity due to the large uncertainties in mass and angular momenta of the ringing black hole [15]. Different investigations have emerged about QNMs of Ernst black holes; for example, in [16], the authors studied massless scalar field perturbations and found that in the presence of a magnetic field, the QNMs are longer-lived and have larger oscillation frequencies, and in [17, 18], unstable modes in magnetized black holes were found. On the other hand, super-radiant instability and the behavior of the QNMs of a massive scalar field were investigated in [19, 20]. Their numerical results show that increasing the field effective mass and the magnetic field strength B gives rise to a decrease in the imaginary part of the QNMs until reaching a vanishing damping rate. Also, it should be pointed out that other important studies about Ernst spacetime have been reported in other contexts. For example, frequency shifts of light emitted by particles describing stable circular geodesics were analyzed [21], and it was shown how magnetic fields can influence the dynamics of particles [22] and epicyclic motions around a black hole [3]. For other non-asymptotically flat spacetimes, see [23,24,25,26,27,28,29].

One aim of this work is to study the effect of an external magnetic field on the anomalous decay rate of QNMs using the sixth-order Wentzel–Kramers–Brillouin (WKB) method. It has been shown that in the imaginary part of the photon sphere, QNFs have an anomalous behavior for a scalar field mass less than a critical mass, i.e., the decay rate of the QNMs decreases when the harmonic angular number \(\ell \) increases. And for a scalar field mass greater than the critical mass, the behavior is inverted: the longest-lived modes are always those with the lowest angular number recovering the standard behavior. The critical mass corresponds to the value of the scalar field mass where the behavior of the decay rate of the QNMs is inverted and can be obtained from the condition \(\text {Im}(\omega )_{\ell }=\text {Im}(\omega )_{\ell +1}\) in the eikonal limit, that is, when \(\ell \rightarrow \infty \), and this behavior has been studied in different black hole geometries including Schwarzschild, Schwarzschild–(A)dS, Reissner–Nordström, black hole in f(R) gravity, for scalar and Dirac fields [30,31,32,33,34,35], and Bronnikov–Ellis and Morris–Thorne wormhole geometries [36]. Also, the existence of a critical scalar field charge for a Reissner–Nordström dS black hole was shown [35]. Here, we show that there is a critical scalar field mass. Furthermore, there is a critical external magnetic field that exhibits the same behavior with respect to the angular harmonic numbers, as well as a critical scalar field charge, for charged massive scalar fields in Ernst black hole backgrounds.

Then, we study the spectrum of quasibound states (QBS) in this background by using the continued fraction method (CFM). QBS are localized in the black hole potential well and tend to zero at spatial infinity, and they have been studied over the years [37,38,39,40,41,42]. Here, we show that the spectrum splits into \(2 \ell +1\) branches, and the separation between the branches increases with the magnetic field, analogous to the splitting of the energy levels of an atom in an external magnetic field, which is the well-known Zeeman effect.

Finally, we study the connection between the unstable null geodesics and the QNMs. It was shown that it occurs in Schwarzschild black holes [43]. However, such a link is violated in an asymptotically flat black hole in the Einstein–Lovelock theory [44] and Schwarzschild AdS black holes [43], see also [45] for further clarification. We will show that unstable null geodesics in the equatorial plane are connected with the QNMs via the WKB method for the case \(m = \pm \ell \) in the eikonal limit \(\ell \rightarrow \infty \), for the four-dimensional Ernst black hole. In order to see this phenomena for other spacetimes, see [46,47,48], and references therein.

This work is organized as follows. In Sect. 2, we give a brief review of Ernst black holes. Then, in Sect. 3, we study the charged scalar field perturbations, and in Sect. 4 we calculate the QNFs by using the WKB method in order to study the anomalous decay rate for high values of \(\ell \), and the CFM for small values of \(\ell \). We then study the QBS in Sect. 5 and the unstable null geodesic in Sect. 6 to determine whether there is a link between the unstable null geodesics and the QNMs. Finally, we conclude in Sect. 7.

2 Ernst black holes

The Ernst metric is an exact solution of the Einstein–Maxwell action. The Ernst solution can be interpreted as providing a model for the exterior spacetime due to a massive body which is placed in an external magnetic field, and has the feature of not being asymptotically flat. Its line element in a Schwarzschild-like coordinate system is given by [2]

$$\begin{aligned} {\textrm{d}}s^{2}= & {} \Lambda ^2 \left( \left( 1-\frac{2M}{r}\right) {\textrm{d}}t^2-\left( 1-\frac{2M}{r}\right) ^{-1} {\textrm{d}}r^2-r^2{\textrm{d}}\theta ^2\right) \nonumber \\{} & {} -\,\frac{r^2\sin ^2\theta }{\Lambda ^2}{\textrm{d}}\phi ^2, \end{aligned}$$
(1)

where

$$\begin{aligned} \Lambda =1+B^2r^2\sin ^2\theta , \end{aligned}$$
(2)

and B is the strength of the external magnetic field. It should be noted that the external magnetic field \(B_{\textrm{Ernst}}\) in the original Ernst black holes [2] is twice what we have used here, \(B_{\textrm{Ernst}}=2 B\). The vector potential for the magnetic field is given by

$$\begin{aligned} A_{\mu }{\textrm{d}}x^{\mu }=-\frac{Br^2\sin ^2\theta }{\Lambda }{\textrm{d}}\phi . \end{aligned}$$
(3)

As pointed out, in this model, the external field is capable of distorting the spherical symmetry of the geometry. The magnetic field has the effect of elongating the event horizon into a cigarette-shaped object, with the long axis parallel to the magnetic field lines. The magnetic field lines remain perpendicular to all points on the event horizon, analogous to electric lines of force about a conductor. However, it was shown that the external magnetic field can be considered as a test field when the strength of the magnetic field satisfies the condition \(B<<B_M=\frac{c^{4}}{G^{3/2}}M_{\odot }(\frac{M_{\odot }}{M})\sim 10^{19}(\frac{M_{\odot }}{M})G\) [49]. On the other hand, from an astrophysical point of view, the magnetic field near the event horizon of stellar black holes \((10 M_{\odot })\) and supermassive black holes \((10^{9}\odot )\) is very small compared with \(B_M\), and thus it is reasonable to neglect the distortions of curvature due to the external magnetic field around black holes. Note that the Schwarzschild black holes and the Melvin metric can be obtained when \(B=0\) and \(M=0\), respectively.

3 Charged scalar field perturbations

A massive charged scalar field satisfies the Klein–Gordon equation,

$$\begin{aligned} \left( \nabla _{\alpha }+ i qA_{\alpha }\right) \left( \nabla ^{\alpha }+ iqA^{\alpha }\right) \Psi + \mu ^2 \Psi =0 , \end{aligned}$$
(4)

where \(\mu \) is the mass of the scalar field, and q its charge. The problem can be reasonably simplified by making the following assumption: for small B, terms higher than \(B^{2}\) can be safely neglected, which allows us to separate the radial and angular variables. In this manner, by taking into account the spacetime symmetry, we can write \(\Psi \) as

$$\begin{aligned} \Psi (t,r,\theta ,\phi )=\frac{1}{r}R(r)S(\theta ){\textrm{e}}^{-i\omega t}{\textrm{e}}^{i m\phi } \end{aligned}$$
(5)

where m is the azimuthal quantum number and \(\omega \) is the QNF of the mode. Thus, the Klein–Gordon equation reads

$$\begin{aligned}{} & {} \frac{1}{r}\frac{{\textrm{d}}}{{\textrm{d}}r}\left( r^{2}f(r) \frac{{\textrm{d}}}{{\textrm{d}}r}\left( \frac{R(r)}{r}\right) \right) \nonumber \\{} & {} \quad +\left( \frac{\omega ^{2}}{f}-4B^{2}m^{2}+2mqB-\mu ^{2}-\frac{\ell (\ell +1)}{r^{2}}\right) =0, \end{aligned}$$
(6)

where \(\ell \) is the harmonic angular number, and \(f(r)= 1-2M/r\). Now, by using the tortoise coordinate \(r^{*}\) given by \({\textrm{d}}r^{*}=\frac{{\textrm{d}}r}{f(r)}\), the Klein–Gordon equation can be written as a one-dimensional Schrödinger-like equation,

$$\begin{aligned} \frac{{\textrm{d}}^{2}R(r^{*})}{{\textrm{d}}r^{*2}}+(\omega ^{2}-V_{\textrm{eff}}(r))R(r^{*}) =0, \end{aligned}$$
(7)

with an effective potential \(V_{\textrm{eff}}(r)\) given by

$$\begin{aligned} V_{\textrm{eff}}(r)=f(r)\left( \frac{f'(r)}{r}+\frac{\ell (\ell +1)}{r^{2}} +4B^{2}m^{2}-2mqB+\mu ^{2}\right) ,\nonumber \\ \end{aligned}$$
(8)

whose asymptotic behaviors near the event horizon and at spatial infinity are

$$\begin{aligned} V_{\textrm{eff}}(r\rightarrow r_{h})&=0 ,\\ V_{\textrm{eff}}(r\rightarrow \infty )=\mu _{\textrm{eff}}^{2}&=\mu ^{2}-2mqB+4m^2B^{2}. \end{aligned}$$

Clearly, the potential coincides with the Schwarzschild potential of a massive scalar field when its mass is replaced by the effective mass

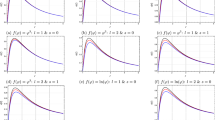
$$\begin{aligned} \mu _{\textrm{eff}}^{2}=4 m^{2} B^{2}-2mqB+\mu ^{2}. \end{aligned}$$
(9)

Note that the value of the squared effective mass can be negative, depending on the values of mass and charge of the scalar field, azimuthal number, and strength of the magnetic field, which is associated with the existence of unstable modes [17, 18]. In Fig. 1, the radial dependence of the effective potential is illustrated, where it is possible to observe a potential barrier. In Sect. 5 we will show that the potential can also have the shape of a potential well for some values of the parameters. Also, as was pointed out, if the value of the squared effective mass is positive, there is some threshold value of the effective mass after which the effective potential loses its barrier-like form and the QNMs disappear; beyond this value, there are arbitrarily long-lived QNMs, so-called quasi-resonance modes [50,51,52].

Fig. 1
figure 1

Effective potential for the multipole number \(\ell =2\) with \(B=0.05\), \(q=1\), \(M=1\) and \(\mu =0.1\)

Full size image

4 Quasinormal modes

In this section we calculate the QNFs of the scalar field using the semi-analytical WKB method and numerically using the CFM. We study the anomalous decay rate of the QNMs and also the splitting of the spectrum due to the external magnetic field.

4.1 QNMs using WKB method

In order to gain analytical insight about the behavior of the QNFs, we use the WKB method [53,54,55,56,57,58], which can be used for effective potentials that have the form of a potential barrier, approaching a constant value at the event horizon and cosmological horizon or spatial infinity [10]. Here, we consider the eikonal limit \(\ell \rightarrow \infty \) to estimate the critical scalar field mass, by considering \(\omega _I^\ell =\omega _I^{\ell +1}\) as a proxy for where the transition or critical behavior occurs [30]. The QNMs that belong to the photon sphere family are determined by the behavior of the effective potential near its maximum value, located at the position \(r^*_{\textrm{max}}\). The Taylor series expansion of the potential around its maximum is given by

$$\begin{aligned} V(r^*)= V(r^*_{\textrm{max}})+ \sum _{i=2}^{\infty } \frac{V^{(i)}}{i!} (r^*-r^*_{\textrm{max}})^{i} , \end{aligned}$$
(10)

where

$$\begin{aligned} V^{(i)}= \frac{{\textrm{d}}^{i}}{{\textrm{d}} r^{*i}}V(r^*) \Big |_{r^*=r^*_{\textrm{max}}} \end{aligned}$$
(11)

corresponds to the i-th derivative of the potential with respect to the tortoise coordinate \(r^*\) evaluated at the position of the maximum \(r^*_{\textrm{max}}\). Using the WKB approach carried to the third order beyond the eikonal approximation, it was found that the QNFs are given by (see, e.g., [59])

$$\begin{aligned} \omega ^2 = V(r^*_{\textrm{max}}) -2 i U , \end{aligned}$$
(12)

where

$$\begin{aligned} U= & {} N\sqrt{-V^{(2)}/2}\nonumber \\{} & {} +\frac{i}{64} \left( -\frac{1}{9}\frac{V^{(3)2}}{V^{(2)2}} (7+60N^2)+\frac{V^{(4)}}{V^{(2)}}(1+4 N^2) \right) \nonumber \\{} & {} +\frac{N}{2^{3/2} 288} \Bigg ( \frac{5}{24} \frac{V^{(3)4}}{(-V^{(2)})^{9/2}} (77+188N^2) \nonumber \\{} & {} +\frac{3}{4} \frac{V^{(3)2} V^{(4)}}{(-V^{(2)})^{7/2}}(51+100N^2) \nonumber \\{} & {} + \frac{1}{8} \frac{V^{(4)2}}{(-V^{(2)})^{5/2}}(67+68 N^2)\nonumber \\{} & {} +\frac{V^{(3)}V^{(5)}}{(-V^{(2)})^{5/2}}(19+28N^2)+\frac{V^{(6)}}{(-V^{(2)})^{3/2}} (5+4N^2) \Bigg ),\nonumber \\ \end{aligned}$$
(13)

and \(N=n+1/2\), with \(n=0,1,2,\ldots ,\) the overtone number.

Defining \(L^2= \ell (\ell +1)\), we find that for large values of L, the maximum of the potential is located approximately at

$$\begin{aligned} r_{\textrm{max}} \approx r_0+ \frac{1}{L^2} r_1 + {\mathcal {O}}(L^{-4}), \end{aligned}$$
(14)

where

$$\begin{aligned} r_0= & {} 3M ,\nonumber \\ r_1= & {} (-1+108m^2 B^2 M^2 -54 m B M^2 q +27 \mu ^2 M^2) \frac{M}{3}, \nonumber \\ \end{aligned}$$
(15)

and

$$\begin{aligned}{} & {} V(r^*_{\textrm{max}}) \approx \frac{1}{27 M^2} L^2 \nonumber \\{} & {} \quad +\frac{2+108 m^2 B^2 M^2 -54 m q B M^2 +27 \mu ^2 M^2}{81 M^2} +{\mathcal {O}}(L^{-2}) . \nonumber \\ \end{aligned}$$
(16)

The second derivative of the potential evaluated at \(r^*_{\textrm{max}}\) is given by

$$\begin{aligned}{} & {} V^{(2)}(r^*_{\textrm{max}}) \approx -\frac{2}{729 M^4} L^2 \nonumber \\{} & {} \quad +\frac{4 (-4+108 m^2 B^2 M^2 -54 m q B M^2 +27 \mu ^2 M^2)}{6561 M^4} +{\mathcal {O}}(L^{-2}),\nonumber \\ \end{aligned}$$
(17)

and the higher derivatives of the potential evaluated at \(r^*_{\textrm{max}}\) yield the following expressions:

$$\begin{aligned} V^{(3)}(r^*_{\textrm{max}})\approx & {} \frac{4}{6561 M^5} L^2 + {\mathcal {O}}(L^0) , \\ V^{(4)}(r^*_{\textrm{max}})\approx & {} \frac{16}{19683 M^6} L^2 + {\mathcal {O}}(L^0) , \\ V^{(5)}(r^*_{\textrm{max}})\approx & {} -\frac{40}{59049 M^7} L^2 + {\mathcal {O}}(L^0) , \\ V^{(6)}(r^*_{\textrm{max}})\approx & {} -\frac{64}{177147 M^8} L^2 + {\mathcal {O}}(L^0) . \end{aligned}$$

Using these results together with Eq. (12), we obtain

$$\begin{aligned} \omega\approx & {} \frac{1}{3 \sqrt{3} M} L - \frac{1+2n}{6 \sqrt{3} M} i +\, \frac{17-15n (n+1)+1944 m^2 B^2 M^2 - 972 m q B M^2}{324 \sqrt{3} M} L^{-1} \nonumber \\{} & {} -\, \frac{(1+2n)(137+235 n (n+1) -116640 m^2 B^2 M^2 + 58320 m q B M^2-29160M^{2}\mu ^{2})}{23328 \sqrt{3} M} i L^{-2} +\,{\mathcal {O}} (L^{-3}). \end{aligned}$$
(18)

The term of order \(L^{-2}\) vanishes at the value of the critical mass \(\mu _c\), which is given by

$$\begin{aligned} \mu _c M = \frac{1}{54} \sqrt{\frac{137}{10} + \frac{47}{2} n (n+1)-11664 m^2 B^2 M^2 + 5832 m q B M^2}.\nonumber \\ \end{aligned}$$
(19)

For \(B=0\), the critical mass of the scalar field in a Schwarzschild background is recovered [30]. Also, it is possible to obtain a critical value of the magnetic field, even for zero scalar field mass \(\mu \), which is given by

$$\begin{aligned} M B_c = \frac{270 m q M + \sqrt{10 m^2 (137+235 n (n+1)+ 7290 M^2 (q^2-4\mu ^2))}}{1080 m^2}.\nonumber \\ \end{aligned}$$
(20)

For \(\mu =0\), \(q=0\), and \(m \ne 0\), this yields \(M B_c = \frac{1}{108 m} \sqrt{\frac{137}{10} + \frac{47}{2} n (n+1)}\). Also, there is a critical charge for the scalar field given by

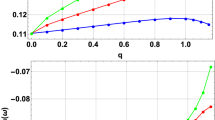
$$\begin{aligned} M q_c = \frac{-137 - 235 n(n+1)+29160 M^2(\mu ^2 + 4 m^2 B^2)}{58320 m M B} . \end{aligned}$$
(21)

In Fig. 2 we show the behavior of \(-\text {Im}(\omega )\) as a function of the scalar field mass \(\mu \). We can observe a critical scalar field mass, where for small values of the scalar field mass, the longest-lived mode is the mode with the highest angular number \(\ell \), while for values of the scalar field mass greater than the critical one, the longest-lived mode is the mode with the smallest angular number. Also, in Fig. 3 we can observe a similar behavior for an external magnetic field and for the charge of the scalar field in Fig. 4.

Fig. 2
figure 2

The behavior of \(-\hbox {{Im}}(\omega )\) as a function of \(\mu \), with \(n=0\), \(M=1\), \(B=0.01\), \(q=0.1\), and \(m=1\), using the sixth-order WKB method. Here, the WKB method via Eq. (19) gives \(\mu _c \sim 0.0794\), the vertical dotted line. Black line for \(\ell =30\), red line for \(\ell =40\), and blue line for \(\ell =50\)

Full size image
Fig. 3
figure 3

The behavior of \(-\hbox {Im}(\omega )\) as a function of B, with \(n=0\), \(M=1\), \(q=0.1\), \(m=1\), and \(\mu =0\), using the sixth-order WKB method. Here, the WKB method via Eq. (20) gives \(B_c \sim 0.0674\), vertical dotted line. Black line for \(\ell =30\), red line for \(\ell =40\), and blue line for \(\ell =50\)

Full size image
Fig. 4
figure 4

The behavior of \(-\text {Im}(\omega )\) as a function of q, with \(n=0\), \(M=1\), \(B=0.01\), \(m=-1\), and \(\mu =0\), using the sixth-order WKB method. Here, the WKB method via Eq. (21) gives \(q_c \sim 0.215\), vertical dotted line. Black line for \(\ell =30\), red line for \(\ell =40\), and blue line for \(\ell =50\)

Full size image

4.2 QNMs using the CFM

In this section, we investigate the behavior of the QNMs of charged massive scalar fields around the Ernst black hole using the CFM, devised by Leaver to compute the QNMs of Schwarzschild and Kerr black holes [60, 61], and improved later by Nollert [62]. It has been used to compute the QNMs in several situations and in particular for charged fields around charged black holes in [63,64,65].

The boundary conditions are given by ingoing waves at the event horizon and outgoing waves at spatial infinity. Thus,

$$\begin{aligned} R(r) \approx \left\{ \begin{array}{ll} (r-r_h)^{- i \omega r_h}&{}\quad \text {as}\ r \rightarrow r_h \\ {\textrm{e}}^{i \Omega r} r^{i r_h (\Omega ^2 + \omega ^2) /2 \Omega } &{}\quad \text {as} \ r \rightarrow \infty \end{array} \right. , \end{aligned}$$
(22)

where \(\Omega = \sqrt{\omega ^2 - \mu ^2 + 2 m q B - 4 m^2 B^2}\). Now, considering the following ansatz for the solution to the radial equation (6) which incorporates the desired boundary conditions

$$\begin{aligned} R(r)= & {} (r-r_h)^{- i\omega r_h} {\textrm{e}}^{i \Omega r} r^{i r_h (\Omega ^2 + \omega ^2)/2 \Omega + i \omega r_h}\nonumber \\{} & {} \times \sum _{n=0}^{\infty } a_n \left( \frac{r-r_h}{r} \right) ^n, \end{aligned}$$
(23)

and substituting it in Eq. (6), a three-term recurrence relation is obtained for the coefficients

$$\begin{aligned} \alpha _0 a_1 + \beta _0 a_0= & {} 0 , \\ \alpha _n a_{n+1} + \beta _n a_n + \gamma _n a_{n-1}= & {} 0, \end{aligned}$$

where

$$\begin{aligned} \alpha _n= & {} -4 \Omega ^2 (1+n)(1+n -2 r_h i \omega ) , \nonumber \\ \beta _n= & {} -2 \Omega \bigg ( -2 \Omega (1+ \ell (\ell +1)+ 2n (n+1)) \nonumber \\{} & {} +\, (1+2n) i r_h (\omega +\Omega ) (\omega +3\Omega ) + 2 r_h^2 (\omega +\Omega )^3 \bigg ) , \nonumber \\ \gamma _n= & {} - (2n \Omega - i r_h (\omega + \Omega )^2)^2 . \end{aligned}$$
(24)

The recursion coefficients must satisfy the following continued fraction relation for the convergence of the series:

$$\begin{aligned} \beta _0 - \frac{\alpha _0 \gamma _1}{\beta _1-}\frac{\alpha _1 \gamma _2}{\beta _2-} \cdots \frac{\alpha _n \gamma _{n+1}}{\beta _{n+1}-} \cdots = 0. \end{aligned}$$
(25)

And the continued fraction must be truncated at some large index N. The QNFs are obtained solving this equation numerically.

In Table 1 we show the QNFs for \(\mu =0.1\), \(r_h=1\), and \(q=0.1\). The results show the splitting of the spectrum of the QNFs due to the Zeeman effect which increases with the magnetic field, and in Fig. 5 we plot the different branches. Note that for \(m=-1\) (red line), the real oscillation frequency increases, and the damping rate decreases when the magnetic field increases, whereas for \(m=1\) (green line), the real oscillation frequency decreases very slightly and then begins to grow, and the damping rate increases and then decreases when the magnetic field increases. On the other hand, for \(m=0\), we recover the QNFs of Schwarzschild [66], because the effective mass reduces to the mass of the scalar field.

Table 1 Fundamental QNFs for \(\mu =0.1\), \(r_h=1\), \(q=0.1\), and different values of the angular number and B
Full size table
Fig. 5
figure 5

Real and imaginary parts of fundamental QNFs as a function of B for \(\mu =0.1\), \(r_h=1\), and \(q=0.1\) using the CFM. Black line for \(\ell =m=0\), red line for \(\ell =1\) and \(m=-1\), blue line for \(\ell =1\) and \(m=0\), and green line for \(\ell =1\) and \(m=1\)

Full size image

5 Quasibound states

In this section we investigate the behavior of the QBS of massive scalar fields around the Ernst black hole using the CFM. The computations of QBS and QNMs are very similar; however, the boundary conditions are different. For the QBS, we must consider ingoing waves at the event horizon and evanescent waves at spatial infinity. In Fig. 6, we show the effective potential for \(r_h = 2\), \(\mu = 0.4\), \(B = 0.1\), \(q = 0.1\), and different values of \(\ell \) and m. Note that for some values of the parameters, the effective potential allows potential wells, and therefore QBS eventually can appear.

Fig. 6
figure 6

Effective potential as a function of r for \(r_h = 2\), \(\mu = 0.4\), \(B = 0.1\), \(q = 0.1\), and different values of \(\ell \) and m

Full size image

Now, the boundary conditions are given by

$$\begin{aligned} R(r) \approx \left\{ \begin{array}{ll} (r-r_h)^{- i \omega r_h} &{}\quad \text {as}\ r \rightarrow r_h \\ {\textrm{e}}^{- \Omega r} r^{- r_h (\Omega ^2 - \omega ^2) /2 \Omega } &{}\quad \text {as} \ r \rightarrow \infty \end{array} \right. , \end{aligned}$$
(26)

where \(\Omega = \sqrt{ \mu ^2 -\omega ^2 - 2 m q B + 4 m^2 B^2}\). So, considering the following ansatz for the radial function R(r) which incorporates the desired boundary conditions,

$$\begin{aligned} R(r) = (r-r_h)^{- i\omega r_h} {\textrm{e}}^{- \Omega r} r^{-r_h (\Omega ^2 - \omega ^2)/2 \Omega + i \omega r_h} \sum _{n=0}^{\infty } a_n \left( \frac{r-r_h}{r} \right) ^n,\nonumber \\ \end{aligned}$$
(27)

and substituting it in Eq. (6), we obtain a three-term recurrence relation for the coefficients

$$\begin{aligned} \alpha _0 a_1 + \beta _0 a_0= & {} 0 , \\ \alpha _n a_{n+1} + \beta _n a_n + \gamma _n a_{n-1}= & {} 0, \end{aligned}$$

where

$$\begin{aligned} \alpha _n= & {} 4 \Omega ^2 (1+n)(1+n -2 r_h i \omega ) , \nonumber \\ \beta _n= & {} 2 \Omega \bigg ( -2 \Omega (1+ \ell (\ell +1)+ 2n (n+1)) \nonumber \\{} & {} \quad + (1+2n) r_h (\omega + i \Omega ) (\omega +3 i \Omega ) + 2 r_h^2 (i \omega -\Omega )^3 \bigg ) , \nonumber \\ \gamma _n= & {} (2n \Omega + r_h (\Omega -i \omega )^2)^2 . \end{aligned}$$
(28)

The recursion coefficients must satisfy the following continued fraction relation for the convergence of the series

$$\begin{aligned} \beta _0 - \frac{\alpha _0 \gamma _1}{\beta _1-}\frac{\alpha _1 \gamma _2}{\beta _2-} \cdots \frac{\alpha _n \gamma _{n+1}}{\beta _{n+1}-} \cdots = 0, \end{aligned}$$
(29)

and the continued fraction must be truncated at some large index N. The frequencies are obtained solving this equation numerically.

In Table 2 we show the fundamental frequencies of the QBS for \(\mu =0.4\), \(r_h=2\), and \(q=0.1\), and different values of \(\ell \), m, and B. The results show the splitting of the spectrum of the QBS due to the Zeeman effect, which increases with the magnetic field. In Fig. 7 we plot the different branches. Also, we observe that the effective mass of the scalar field is slightly larger than the real part of the frequency, and the real part is much larger than the imaginary part, which are typical characteristics of QBS. The imaginary part is negative, and therefore the modes are stable. Also, note that for \(m = -1\) (red line), the real oscillation frequency increases and the damping rate increases as the magnetic field increases, whereas for \(m=1\) (green line), the real oscillation frequency decreases very slightly and then begins to grow, and the damping rate increases and then decreases when the magnetic field increases. Thus, the real oscillation frequency behavior is similar between the QNMs and QBS, whereas for the damping rate, the behavior is the opposite when the magnetic field is increasing. On the other hand, for \(m=0\), we recover the QBS of Schwarzschild [39], because the effective mass reduces to the mass of the scalar field.

Table 2 Fundamental frequency of the QBS for \(\mu =0.4\), \(r_h=2\), \(q=0.1\), and different values of the angular number and B
Full size table

6 Unstable null geodesics

In this section we investigate whether it is possible to establish a connection between null geodesics and QNFs in the eikonal approximation by computing the Lyapunov exponent. Firstly, in order to study the unstable null geodesics in the equatorial plane (\(\theta =\pi /2\)), we use the standard Lagrangian formalism [67], so that the corresponding Lagrangian associated with the line element (1) reads

$$\begin{aligned} {\mathcal {L}}=\frac{1}{2}\left( \Lambda ^{2}\left( f(r)\dot{t}^{2}-\frac{\dot{r}^{2}}{f(r)}\right) -\frac{r^{2}}{\Lambda ^{2}}{\dot{\phi }}^{2}\right) . \end{aligned}$$
(30)

Therefore, from this Lagrangian the generalized momenta are

$$\begin{aligned} p_t&=\Lambda (r)^{2}f(r) \dot{t}=E, \end{aligned}$$
(31)
$$\begin{aligned} p_\phi&=\frac{r^{2}}{\Lambda (r)^{2}}{\dot{\phi }}=L, \end{aligned}$$
(32)
$$\begin{aligned} p_r&=\frac{\Lambda (r)^{2}}{f(r)}\dot{r}. \end{aligned}$$
(33)

Note that the Lagrangian is independent of both t and \(\phi \), so \(p_t\) and \(p_\phi \) are two integrals of motion. Also, the Hamiltonian is given by

$$\begin{aligned} 2{\mathcal {H}}= & {} 2(p_{t}\dot{t}-(p_{r}\dot{r}+p_{\phi }{\dot{\phi }})-{\mathcal {L}}\nonumber \\= & {} \frac{E^{2}}{\Lambda ^{2} f(r)}-\frac{L^{2}\Lambda ^{2}}{r^{2}}-\frac{\Lambda ^{2}\dot{r}^{2}}{f(r)}=0. \end{aligned}$$
(34)

Thus, from the above equation we have

$$\begin{aligned} V_r(r)=\frac{E^{2}}{\Lambda ^{4}}-\frac{f(r)L^{2}}{r^{2}}, \end{aligned}$$
(35)

where we have used \(V_{r}=\dot{r}^{2}\). Now, in order to obtain the circular geodesics, two conditions must be satisfied, namely \(V_{r}(r_c) =V'_{r}(r_c) =0\), which yields

$$\begin{aligned} \frac{E^{2}}{L^{2}}&=\frac{f(r_c)\Lambda (r_c)^{4}}{r_c^{2}}, \end{aligned}$$
(36)
$$\begin{aligned} L^{2}&=\frac{4 r_c^{3}E^{2}\Lambda '(r_c)}{\Lambda ^{5}(r_c)(2 f(r_c)-r_c f'(r_c))}. \end{aligned}$$
(37)
Fig. 7
figure 7

Real and imaginary parts of fundamental frequencies of the QBS as a function of B for \(\mu =0.4\), \(r_h=2\), and \(q=0.1\) using the CFM. Black line for \(\ell =m=0\), red line for \(\ell =1\) and \(m=-1\), blue line for \(\ell =1\) and \(m=0\), and green line for \(\ell =1\) and \(m=1\)

Full size image

As was pointed out in [68, 69], the condition for the existence of two possible radii in the region outside the event horizon \(r=2M\) is that \(MB< 0.09468\). The inner radius is unstable and the outer one is stable. In order to obtain the unstable radius that satisfies

$$\begin{aligned} 3 r_{c}^3B^{2}-5Mr_{c}^{2}B^{2}-r_{c}+3 M=0, \end{aligned}$$
(38)

we consider for convenience the dimensionless units \(x_c=\frac{r_c}{M}\) and \(\beta =BM\). Also, we expand the radius of circular geodesics in terms of small magnetic field B in the following form:

$$\begin{aligned} r_{c}= r_{0}+r_{1}\beta +r_{2} \beta ^{2}. \end{aligned}$$
(39)

Now, by replacing Eq. (39) into (38), we obtain

$$\begin{aligned} x_{c}=3+36 B^2 M^{2}. \end{aligned}$$
(40)

Note a small correction to the Schwarzschild radius of circular geodesics due to the magnetic field. The unstable circular geodesics possess a larger radius than that of the Schwarzschild \(x_c=3\).

On the other hand, it is known that the relation between QNMs and unstable circular null geodesics in the eikonal limit can be established for some spacetimes. For that we will use the WKB method because it gives the correct approximation of QNMs in the eikonal limit. Here, the central wave equation is given by (7), and the effective potential in the eikonal limit \(\ell \rightarrow \infty \) takes the form

$$\begin{aligned} V(r)\approx f(r)\left( \frac{\ell ^{2}}{2 r^{2}}+4 m^{2}B^{2}\right) , \end{aligned}$$
(41)

where the magnetic terms will be always small in comparison with the centrifuge terms. Then the obtained effect is a small correction to the Schwarzschild metric. The maximum value of the potential is found at \(r_{0}=3M+\frac{36 B^{2} m^{2} M^{3}}{\ell ^{2}}\). The QNMs lead to the following form:

$$\begin{aligned} \frac{Q_{0}(r_0)}{\sqrt{2 Q_{0}''(r_0)}}=i\left( n+\frac{1}{2}\right) , \end{aligned}$$
(42)

where \(Q_{0}=\omega ^{2}-V(r)\), \(Q_0''\equiv \frac{d^{2}Q_{0}}{dr_{*}^{2}}\). Following Ref. [43], where the authors showed that angular velocity \(\Omega _c\) at the unstable null geodesic and the Lyapunov exponent \(\lambda \), determining the instability timescale of the orbit, agree with analytic WKB approximations for QNMs,

$$\begin{aligned} \omega _{QNM}=\ell \Omega _{c}-i\left( n+\frac{1}{2}\right) |\lambda |, \end{aligned}$$
(43)

where \(\Omega _{c}=\Lambda ^{2}(r_{c})\sqrt{\frac{f(r_{c})}{r_{c}^{2}}}\), \(\lambda =\frac{\Lambda (r_{c})}{\sqrt{2}}\sqrt{\frac{f(r_{c})r_{c}^{2}V^{\prime \prime }_{r}(r_{c})}{L^{2}}}\), and

$$\begin{aligned} V^{\prime \prime }_{r}(r_{c})= & {} \frac{L^{2}}{r_{c}^{2}}\left( -6\frac{f(r_{c})}{r_{c}^{2}}\right. \nonumber \\{} & {} \left. +\,4\frac{f^{\prime }(r_{c})}{r_{c}}-f^{\prime \prime }(r_{c})-4f(r_{c})\frac{\Lambda {\prime \prime }(r_{c})}{\Lambda (r_{c})}\right) . \end{aligned}$$
(44)

Thus, by using Eq. (43), we obtain

$$\begin{aligned} \omega _{QNM}= & {} \ell (1+B^{2}r_{c}^{2})^{2}\sqrt{\frac{r_c-2M}{r_{c}^{3}}}\nonumber \\{} & {} -\,i\left( n+\frac{1}{2}\right) \frac{1+B^{2}r_c^{2}}{r_c^{2}}\nonumber \\{} & {} \times \left( (r_c-2M)(3(r_c-4 M)-4r_c^{2}B^{2}(r_c-2 M))\right) ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$
(45)

Clearly, the QNMs in the eikonal limit are modified by the presence of the magnetic field B. Note that the above equation for \(m=\pm \ell \), \(r_c= 3M+ 36 B^{2} M^{3}\), can be written as

$$\begin{aligned} \omega _{QNM}= & {} \ell \left( \frac{1}{3\sqrt{3}M}+\frac{6 M B^{2}}{\sqrt{3}}\right) \nonumber \\{} & {} -\,i\left( n+\frac{1}{2}\right) \left( \frac{1}{3\sqrt{3}M}-\frac{5}{\sqrt{3}}M B^{2}\right) , \end{aligned}$$
(46)

which matches with Eq. (18) for the same parameters. In this way, at the equatorial plane, and with \(m=\pm \ell \), there is a connection between the null geodesics and QNMs in the eikonal limit. The reason for this is that the position of the maximum of the potential given by (14) converges to the radius of circular geodesics when \(m = \pm \ell \) in the eikonal limit. It is possible to think about the coincidence from another point of view; it is well known that in classical mechanics, a particle orbiting on the equatorial plane and immersed in a uniform magnetic field perpendicular to that plane will have an orbital angular momentum \(L=L_{z}\). Now, if we want to recover the classical situation from quantum mechanics, we should first recall that the orbital angular momentum vector is quantized, its magnitude is given by \(L^2=\ell (\ell +1)\hbar ^2\), and the projection along the z-axis is \(L_{z}=m\hbar \); therefore, in the particular case when \(m= \ell \) or \(m=-\ell \), and taking the limit \(\ell \rightarrow \infty \), it is possible to recover the classical setting. It is worth noting that for \(B=0\), the Schwarzschild QNMs in the optic geometric limit are recovered [43].

7 Final remarks

In this work, we studied the propagation of charged massive scalar fields in the background of four-dimensional Ernst black holes. Then, by using the WKB method, we showed that there is a critical scalar field mass, i.e., for a scalar field mass less than a critical mass, the decay rate of the QNMs decreases when the harmonic angular number \(\ell \) increases, and for a scalar field mass greater than the critical mass, the behavior is inverted, i.e., the longest-lived modes are always the ones with lowest angular number recovering the standard behavior. Additionally, we showed that there is a critical external magnetic field that exhibits the same behavior with respect to the angular harmonic numbers, as well as a critical scalar field charge. On the other hand, concerning the QNFs, for small values of \(\ell \), we showed that for negative values of m, the real oscillation frequency increases and the damping rate decreases as the magnetic field increases, whereas for positive values of m, the real oscillation frequency decreases very slightly and then begins to grow, and the damping rate increases and then decreases when the magnetic field increases.

On the other hand, we have shown that the spacetime allows stable quasibound states, which the spectrum splits into \(2 \ell +1\) branches, and the separation between the branches increases with the magnetic field, which is the analogous to the splitting of the energy levels of an atom in an external magnetic field, the well-known Zeeman effect. For the QBS, and negative values of m, the real oscillation frequency increases and the damping rate increases as the magnetic field increases, whereas for positive values of m, the real oscillation frequency decreases very slightly and then begins to grow, and the damping rate increases and then decreases when the magnetic field increases. Thus, the real oscillation frequency behavior is similar between the QNMs and QBS, whereas for the damping rate, the behavior is opposite when the magnetic field is increasing. Finally, we have shown that the unstable null geodesic in the equatorial plane is connected with the QNMs for \(m = \pm \ell \) when \(\ell \rightarrow \infty \).