1 Introduction

The nature of dark matter (DM) constitutes one of the most long-standing and puzzling questions in cosmology. There is abundant evidence that nonluminous matter makes up a large fraction of all matter in our universe. Results from cosmological measurements have now determined with exquisite precision the abundance of DM [1]. But the identity of DM remains a mystery. Recently, Barranco et al. proposed that the scalar dynamical resonances could form long-lived configurations around black holes [2,3,4]. This ultralight scalar resonance might be regarded as a candidate for DM. Such long-lived distribution was then generalized to the Dirac field by Zhou et al. [5]. Since then, these massive dynamical resonances around black holes have garnered much attention [6,7,8,9,10,11,12,13,14,15]. The study of resonances of various fields around black holes has stimulated our interest in the evolution of resonances in theories of extra dimensions and braneworld.

The history of extra dimensions and braneworld dates back to the last century. In the 1920s, Kaluza and Klein (KK) proposed a five-dimensional spacetime theory to unify electromagnetic and gravitational interactions [16, 17]. Subsequently, extra-dimensional theories remained silent for more than 70 years, until the 1990s when, to solve the huge hierarchy between the Planck and weak scales, some braneworld models were proposed. Two of them have attracted the attention of many researchers. One is the large extra-dimensional model proposed by Arkani-Hamed et al. [18], and the other is the warped extra-dimensional model proposed by Randall and Sundrum [19]. The size of the extra dimensions is finite in these braneworld models. Subsequently, Antoniadis et al. embedded the braneworld model with large extra dimensions into string theory [20]. A notable development was attained in Ref. [21], which showed that even the extra dimension is infinite, and four-dimensional gravity can also be recovered on the brane. Since then, extra-dimensional theories have attracted considerable attention [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44].

In this paper, we focus on the evolution of the scalar KK resonances on the thick brane, which is generated dynamically by a background scalar field. In a braneworld model, to recover the physics in our four-dimensional spacetime, the zero modes of various fields should be localized on the brane. But in addition to zero modes, there are massive KK modes which might propagate into extra dimensions. KK resonances are a specific class of massive KK modes in braneworld models. Usually, for a volcano-like potential, although massive KK modes cannot be localized on the brane, KK resonances can be quasi-localized [45]. Previous studies have investigated resonances of various fields on thick branes [45,46,47,48,49,50,51,52,53,54,55]. To the best of our knowledge, no studies to date have explored the evolution of KK resonances of various fields in thick brane. The dynamics and the final state of such long-lived modes are still unclear. In the thin brane, scattering of KK gravitons in the Randall–Sundrum II model has been considered [56, 57]. It was proved that the brane possesses a set of discrete quasi-normal modes that appear as scattering resonance, and the graviton KK modes have a very short lifetime on the brane. Can KK modes exist in a thick brane for a long period like the long-lived resonance modes around a black hole? To answer this question, we take the scalar field as a simple example to study the evolution of scalar KK modes numerically. We will show the evolution behaviors of the scalar KK modes and obtain their half-life time on a brane. We will further analyze the feasibility of the KK resonances as a dark matter candidate. Although our research is still crude, it provides a stepping stone to further investigation of KK resonances of various fields on a thick brane.

The layout of the remaining part of this paper is as follows. In Sect. 2, we construct a thick brane solution in five-dimensional spacetime as the background of a test scalar field evolution. In Sect. 3, the scalar field is evolved with the maximally dissipative boundary condition. Both resonances and nonresonances are used as initial data, and their evolution behaviors are compared. Finally, the conclusions and discussion are presented in Sect. 4.

2 Braneworld model in general relativity

Firstly, we consider the thick brane in five-dimensional spacetime. For the simplest case of general relativity with a canonical scalar field, the action is given by [23, 24, 36]

$$\begin{aligned} S=\int {\textrm{d}}^5x\sqrt{-g}\left( \frac{1}{2\kappa ^{2}_{5}}R-\frac{1}{2}g^{MN}\partial _{M} \phi \partial _{N}\phi -V(\phi )\right) , \end{aligned}$$
(1)

where \(\kappa _{5}\) is the five-dimensional gravitational constant. We set \(\kappa _{5}=1\) in this paper for convenience. The five-dimensional metric for our thick brane model is given by

$$\begin{aligned} {\textrm{d}}s^2={\textrm{e}}^{2A(y)}\gamma _{\mu \nu }{\textrm{d}}x^\mu {\textrm{d}}x^\nu +{\textrm{d}}y^2, \end{aligned}$$
(2)

where \({\textrm{e}}^{2A(y)}\) is the warp factor and \(\gamma _{\mu \nu }\) is the induced metric on the brane with four-dimensional Poincareé invariance:

$$\begin{aligned} \gamma _{\mu \nu }{\textrm{d}}x^{\mu }{\textrm{d}}x^{\nu }=\left\{ \begin{array}{l} \eta _{\mu \nu }{\textrm{d}}x^\mu {\textrm{d}}x^\nu , \\ -{\textrm{d}}t^{2}+{\textrm{e}}^{2kt}({\textrm{d}}x^{2}_{1}+{\textrm{d}}x^{2}_{2}+{\textrm{d}}x^{2}_{3}), \\ {\textrm{e}}^{2kx_{3}}(-{\textrm{d}}t^{2}+{\textrm{d}}x^{2}_{1}+{\textrm{d}}x^{2}_{2})+{\textrm{d}}x^{2}_{3}. \end{array} \right. \end{aligned}$$
(3)

The above three cases correspond to the flat brane, de Sitter brane, and anti-de Sitter brane, respectively. Here, \(\eta _{\mu \nu }=\text {diag}(-1,1,1,1)\) is the four-dimensional Minkowski metric, capital Latin letters \(M,N,\ldots = 0,1,2,3,4\) denote the five-dimensional indices, and Greek letters \(\mu ,\nu ,\ldots = 0,1,2,3\) denote the four-dimensional indices. In this paper, we only consider the flat brane, i.e.,

$$\begin{aligned} {\textrm{d}}s^2={\textrm{e}}^{2A(y)}\eta _{\mu \nu }{\textrm{d}}x^\mu {\textrm{d}}x^\nu +{\textrm{d}}y^2. \end{aligned}$$
(4)

The dynamical field equations are

$$\begin{aligned}{} & {} R_{MN}-\frac{1}{2}Rg_{MN}=T_{MN}, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} g^{MN}\nabla _{M}\nabla _{N}\phi =\frac{\partial V(\phi )}{\partial \phi }. \end{aligned}$$
(6)

By substituting the metric (4) into Eqs. (5) and (6), we can obtain the explicit equations of motion

$$\begin{aligned} 6A'^2 +3A''= & {} -V-\frac{1}{2}\phi '^2, \end{aligned}$$
(7)
$$\begin{aligned} 6A'^2= & {} \frac{1}{2}\phi '^2-V, \end{aligned}$$
(8)
$$\begin{aligned} \phi {''}+4A'\phi '= & {} \frac{\partial V}{\partial \phi }, \end{aligned}$$
(9)

where prime denotes the derivative with respect to the extra-dimensional coordinate y. Note that only two of the above equations are independent, but we must solve three functions: \(A(y),~\phi (y)\), and \(V(\phi )\). So we need to provide one of the three functions to solve these equations. Here, we provide the following warp factor:

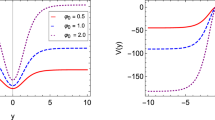
$$\begin{aligned} A(y)=\ln \Big [\tanh \big (k(y+b)\big )-\tanh \big (k(y-b)\big )\Big ], \end{aligned}$$
(10)

where the parameter b has length dimension one and the parameter k has mass dimension one. This warp factor has been thoroughly investigated in previous literature [51, 52, 54]. It can be seen that the parameter b determines the thickness of the thick brane. In the next section, we will see that larger parameter b may result in more resonant KK modes. From Eqs. (7), (8), (9), and (10) we get the solution

$$\begin{aligned} \phi (y)= & {} -i \sqrt{6} \text {sech}(b k)\Big [\cosh (2 b k) \text {F}\big (i k y;\tanh ^2(b k)+1\big )\nonumber \\{} & {} -\,2 \sinh ^2(b k) {\Pi } \big (\text {sech}^2(b k);i k y;\tanh ^2(b k)+1\big )\Big ],\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned} V(y)= & {} \frac{3}{2} k^2 \Big [-4 \big (\tanh (k (y-b))+\tanh (k (b+y))\big )^2\nonumber \\{} & {} +\,\text {sech}^2(k (y-b))+\text {sech}^2(k (b+y))\Big ], \end{aligned}$$
(12)

where \(\text {F}(y,q)\) is the elliptic integral of the first kind and \(\varPi (y,q,p)\) is the elliptic integral of the third kind. This solution was investigated in Ref. [54] in f(T) gravity theory. The energy density for the above brane solution is

$$\begin{aligned} \rho =24k^{2}-6k^{2}\big (\tanh (k (y-b))+\tanh (k (b+y))\big )^2. \end{aligned}$$
(13)

Plots of the above warp factor, scalar field, and energy density are shown in Fig. 1. Based on this braneworld background, we consider a test scalar field and study its evolution. We investigate its dynamic behavior numerically, and clarify whether their KK modes can exist on the brane for a long period.

Fig. 1
figure 1

The shapes of the warp factor (10), scalar field (11), and energy density (13)

Full size image

3 Scalar field resonances and its evolution in braneworld

In this section we will consider the evolution of a scalar field in the thick brane given above. Here we consider a free massless test scalar field \(\psi (x^{M})\). Notice that the scalar field \(\psi (x^{M})\) here is not the background scalar field \(\phi (y)\) that generates the thick brane. The equation of motion for the test field is the Klein–Gordon equation

$$\begin{aligned} \square ^{(5)} \psi =\frac{1}{\sqrt{-g}}\partial _{M}(\sqrt{-g}g^{MN}\partial _{N}\psi )=0. \end{aligned}$$
(14)

With the coordinate transformation \({\textrm{d}}z={\textrm{e}}^{-A}{\textrm{d}}y\), the metric (4) becomes a conformal flat one:

$$\begin{aligned} {\textrm{d}}s^2={\textrm{e}}^{2A(z)}(\eta _{\mu \nu }{\textrm{d}}x^\mu {\textrm{d}}x^\nu +{\textrm{d}}z^2), \end{aligned}$$
(15)

which is very useful in the derivation of the evolution equation and the Schrödinger-like equation of the test scalar field. In black hole physics, there is a similar coordinate, known as the tortoise coordinate. Then Eq. (14) can be written as

$$\begin{aligned} \left[ \partial ^{2}_{z}+3(\partial _{z}A)\partial _{z}+ \eta ^{\mu \nu }\partial _{\mu }\partial _{\nu }\right] \psi =0. \end{aligned}$$
(16)

We then introduce the following decomposition:

$$\begin{aligned} \psi (x^{M})={\textrm{e}}^{-\frac{3}{2}A(z)}\varPhi (t,z)\varXi (x^{i}). \end{aligned}$$
(17)

Substituting the above decomposition (17) into Eq. (16), we get the following equation:

$$\begin{aligned} -\partial _{t}^{2}\varPhi +\partial _{z}^{2}\varPhi -U(z)\varPhi -a^{2}\varPhi =0, \end{aligned}$$
(18)

where a is a constant from the separation of variables. The effective potential U(z) has the following form:

$$\begin{aligned} U(z)=\frac{3}{2}\partial _{z}^{2}A+\frac{9}{4}(\partial _{z}A)^{2}, \end{aligned}$$
(19)

or in the y coordinate equivalently

$$\begin{aligned} U(z(y))=\frac{3}{2}\partial _{y}^{2}A(y){\textrm{e}}^{2A(y)}+ \frac{15}{4}\left( \partial _{y}A(y){\textrm{e}}^{A(y)}\right) ^{2}. \end{aligned}$$
(20)

The function \(\varPhi (t,z)\) can be further decomposed into oscillating modes as

$$\begin{aligned} \varPhi (t,z)={\textrm{e}}^{i\omega t}u(z). \end{aligned}$$
(21)

Substituting the above decomposition in Eq. (18) yields

$$\begin{aligned} -\partial _{z}^{2}u(z)+U(z)u(z)=m^{2}u(z), \end{aligned}$$
(22)

where \(m^2=\omega ^2-a^2\) is the mass of the KK modes. We shall see below that the effective potential U(z) is a volcano-like potential with a double-well. When \(z\rightarrow \pm \infty \), \(U(\pm \infty )\rightarrow 0_{+}\). Thus, all KK modes with \(m^{2}>0\) are free states. Only the modes with \(m^{2}\le 0\) could be bound states. One can show that there is no mode with \(m^{2}<0\). The Schrödinger-like equation (22) can be factorized as the supersymmetric quantum mechanics form

$$\begin{aligned} \left( \partial _{z}+\frac{3}{2}\partial _{z}A(z)\right) \left( -\partial _{z}+ \frac{3}{2}\partial _{z}A(z)\right) u(z)=m^{2}u(z). \end{aligned}$$
(23)

Using this supersymmetric quantum mechanics form with the conditions that A(z) is a real function and the extra dimension z is noncompact, it can be shown that there is no tachyon mode with \(m^{2}<0\) [58, 59]. On the other hand, the solution of the zero mode with \(m^{2}=0\) is

$$\begin{aligned} u_{0}(z)\propto {\textrm{e}}^{\frac{3}{2}A(z)}. \end{aligned}$$
(24)

Obviously, for the warp factor (10), the zero mode \(u_{0}(z)\) is bound on the brane and it has no node along the extra dimension. According to the node theorem, the zero mode must be the ground state, which ensures that \(m^2\ge 0\). Solving Eq. (22), we get a series resonant modes, which can be treated as the initial data for the scalar field. The evolution is dominated by Eq. (18).

3.1 Scalar field resonances

In this part, we give a brief review on how to solve the KK scalar resonances. Substituting the warp factor (10) into Eq. (20), the effective potential in the coordinate y is [54]

$$\begin{aligned} U(z(y))= & {} -\frac{3}{8}k^2 \text {sech}^2\big (k (b-y)\big ) \text {sech}^2\big (k (b+y)\big )\nonumber \\{} & {} \times \Big (\tanh \big (k (b-y)\big ) +\tanh \big (k (b+y)\big )\Big )^{2} \nonumber \\{} & {} \times \Big (-5\cosh (4 k y)+2 \cosh \big (2 k (b-y)\big )\nonumber \\{} & {} +\,2 \cosh \big (2 k (b+y)\big )+9\Big ) . \end{aligned}$$
(25)

Plots of the above effective potential are shown in Fig. 2a. For convenience, we define the dimensionless parameters \(\bar{b}=kb\) and \(\bar{m}=m/k\). We can see that the width of the effective potential increases with \(\bar{b}\). The resonant modes can be studied by the relative probability method which was proposed in Ref. [45]. The relative probability is defined as

$$\begin{aligned} P(m^{2})=\frac{\int ^{z_{b}}_{-z_{b}}|u(z)|^{2}{\textrm{d}}z}{\int ^{z_{\textrm{max}}}_{-z_{\textrm{max}}}|u(z)|^{2}{\textrm{d}}z}, \end{aligned}$$
(26)

where u(z) is solved from Eq. (22), \(z_b\) is approximately the width of the brane, and \(z_{\textrm{max}}\) is a much larger width than \(z_b\), and usually set to \(10z_b\). If the relative probability has a peak with full width at half maximum around \(m=m_{n}\), then there is a resonance with mass \(m_{n}\). In this way, the modes whose amplitudes in the quasi-well are much larger than those outside the quasi-well can be found. These modes will remain on the brane for a longer time. Note that the wave functions can be even or odd because the potential is symmetric. Hence, the following boundary conditions can be used to solve Eq. (22) numerically:

$$\begin{aligned} u_{\textrm{even}}(0)= & {} 1,\quad \partial _{z}u_{\textrm{even}}(0)=0; \end{aligned}$$
(27a)
$$\begin{aligned} u_{\textrm{odd}}(0)= & {} 0,\quad \partial _{z}u_{\textrm{odd}}(0)=1, \end{aligned}$$
(27b)

where \(u_{\textrm{even}}\) denotes the even modes of u(z) and \(u_{\textrm{odd}}\) denotes odd modes of u(z). Substituting the effective potential (25) into the Schrödinger-like equation (22), we can obtain the solution of u(z) numerically for a given mass m. Then the relative probability \(P(m^2)\) can be obtained. The relative probability \(P(m^2)\) of scalar resonances for \(\bar{b}=5,10,15\) are shown in Fig. 2a–c, respectively. The specific parameters of these resonances are listed in Table 1. It can be seen that the number of scalar resonances and their peak values increase with \(\bar{b}\). Usually, the larger peak value means smaller full width at half maximum, and longer lifetime. We will see that in the next subsection.

Fig. 2
figure 2

The shapes of the effective potential (25) for different parameters \(\bar{b}\). The influence of the parameter \(\bar{b}\) on the relative probability P for the odd-parity (red lines) and even-parity (blue dashed lines) massive KK modes. These figures are from Ref. [54]

Full size image

3.2 Evolution of the scalar field resonances

Treating the scalar resonances as the initial data, we can evolve the scalar field under the evolution equation (18). Through the numerical evolution of the scalar field, we can obtain its lifetime on the brane. In this paper, we only consider the case of \(a^2=0\), which means that scalar KK particles travel along the extra dimension at the speed of light at infinity. We also impose the maximally dissipative boundary condition, \(\partial _{n}\varPhi =\partial _{t}\varPhi \) [60], where n is the outward unit normal vector to the boundary. Equation (18) is solved numerically using fourth-order finite differences in space, and evolving in time using a method of lines with a third-order Runge–Kutta integrator.

In order to more intuitively display the evolution of the scalar field, we define the conserved energy of the scalar field [61]

$$\begin{aligned} E=\int _{-\infty }^{\infty }\rho _{E}{\textrm{d}}z, \end{aligned}$$
(28)

where

$$\begin{aligned} \rho _{E}=\frac{1}{2}\left( (\partial _{t}\varPhi )^2+ \left( -\frac{3}{2}\partial _{z}A(z)\varPhi +\partial _{z}\varPhi \right) ^2 \right) . \end{aligned}$$
(29)

Firstly, we consider the evolution of resonances whose parameters are given in Table 1. We integrate the energy density \(\rho _{E}\) over \([-z_{\textrm{max}},z_{\textrm{max}}]\), and the resulting energy will decay due to energy losses through both left and right boundaries. We plot the evolution of the integrated scalar field energy E(t) in Fig. 3. Note that it is plotted on a logarithmic scale. From Fig. 2b–d we can see that there are usually several resonances. Among these resonances, the first one will evolve the longest time. In addition, the evolution time increases with the parameter \(\bar{b}\). This is because the larger \(\bar{b}\), the more energy of the scalar field is concentrated in the potential well. In addition, we plot half-life time of the first resonance with different values of the parameter \(\bar{b}\), which can be seen from Fig. 3d. Note that here we have defined the dimensionless time \(\bar{t}=kt\). It can be clearly seen that the half-life time of the resonances increases with the parameter \(\bar{b}\).

Table 1 Resonant mass spectrum \(\bar{m}_{n}^{2}\), \(\bar{m}_{n}\), and relative probability P for different values of the parameter \(\bar{b}\)
Full size table
Fig. 3
figure 3

a–c The energy of the scalar field vs. time for the evolution of the resonant modes for different values of the parameter \(\bar{b}\). Here, o1 represents the first odd-parity resonance, e1 represents the first even-parity resonance, and so on. d The relation between the half-life of the first scalar resonance and the parameter \(\bar{b}\)

Full size image

The energy decay can be fitted as an exponential function:

$$\begin{aligned} E(t)=E_{0}\text {exp}(-s\bar{t}), \end{aligned}$$
(30)

where s is the fitting parameter and \(E_{0}\) denotes the initial energy of the KK mode. Some results of the fit are listed in Table 2. It can be seen that both the scaled mass \(\bar{m}_1\) and the fitting parameter s of the first resonance decrease with \(\bar{b}\).

Table 2 The first resonant mass spectrum \(\bar{m}_{1}^{2}\), \(\bar{m}_{1}\), fitting parameter s, and half-life \(t_{1/2}\) for different values of the parameter \(\bar{b}\)
Full size table

To better show the evolution of the scalar field over time, we analyze the result of the numerical evolution by extracting a time series for the resonance amplitude at a fixed point \(z_{\text {ext}}\). The results are shown in Fig. 4. It can be seen that the resonance amplitude decreases with evolutionary time, and the amplitude attenuation of the second resonance is significantly faster than that of the first resonance. This also shows that the first resonance will evolve the longest. By comparing the amplitude attenuation at different positions of the same resonance, it can be seen that the attenuation rate and the overall shape are basically the same. In other words, at least for the first two resonances, there is no beating effect found in Ref. [62] for a black hole system.

Fig. 4
figure 4

Upper panel: Time evolution of the first odd resonance (left) and the first even resonance (right) at \(\bar{z}_{\text {ext}}=3\) for \(\bar{b}=15\). Lower panel: Time evolution of the first odd resonance (left) and the first even resonance (right) at \(\bar{z}_{\text {ext}}=30\) for \(\bar{b}=15\). Here \(\bar{z}_{\text {ext}}=kz_{\text {ext}}\)

Full size image
Fig. 5
figure 5

Left panel: The energy of the scalar field vs. time for the evolution of nonresonance for \(\bar{b}=15\). Right panel: Time evolution of the nonresonance with \(\bar{z}_{\text {ext}}=30\) for \(\bar{b}=15\)

Full size image

As a comparison, we also consider the evolution of the nonresonances. These results are shown in Fig. 5. We find that the energy and amplitude of nonresonance decay very fast at the early stage, but later they decay like those of resonances. In order to gain a better understanding of the above results, we perform a spectral analysis. We calculate the discrete Fourier transform in time of the scalar field at a fixed point \(z=z_{j}\). The explicit expression of the discrete Fourier transform is

$$\begin{aligned} F[\varPhi (t)](f):=\left| A\sum _{p}\varPhi (t_{p},z_{j})\text {exp}(-2\pi ift_{p} )\right| , \end{aligned}$$
(31)

where A is normalization constant and \(t_{p}\) are the discrete time values. Plots of the Fourier transform for the first resonance and the nonresonance with \(\bar{m}^2=0.36\) for \(\bar{b}=15\) are shown in Fig. 6. We find that for the Fourier transform of the resonance, there is only one peak corresponding to the resonance frequency. However, for the Fourier transform of the nonresonance, there are several peaks. Thus, nonresonances can evolve into combinations of resonances, and from this point of view, resonances seem to play a similar role in the braneworld as the quasi-normal modes in black holes physics, which deserves further investigation.

Fig. 6
figure 6

Left panel: Discrete Fourier transform in time vs. frequency for the evolution of the nonresonance with \(\bar{m}^2=0.36\) for \(\bar{b}=15\). Right panel: Discrete Fourier transform in time vs. frequency for the evolution of the first resonance with \(\bar{m}_1^2=0.04687\) for \(\bar{b}=15\). The blue dotted lines correspond to the frequencies of the first three odd parity resonances

Full size image

Finally, we consider the half-life time of the scalar resonances. If the exponential decay (30) is sustained throughout all evolution, then it is easy to determine that \(\bar{t}_{1/2}=\frac{\ln (2)}{s}\). For \(k=10^{-10}\text {eV}\) and \(s=10^{-10}\), the half-life time \(t_{1/2}\) of the first scalar resonance will reach \(10^{4}\) seconds. Admittedly, it is still short compared with the age of our universe. But note that the lifetime of resonances increases with the parameter \(\bar{b}\). Thus, for a very large \(\bar{b}\), the lifetime of resonance might reach the cosmological time scale. Here, we can simply estimate the feasibility of resonance as a candidate for dark matter. For the braneworld model in this part, the effective four-dimensional Planck scale \(M_{\text {Pl}}\) and the fundamental five-dimensional scale \(M_{5}\) have the relation

$$\begin{aligned} M_{\text {Pl}}^{2}=\frac{8\bar{b}\coth (2\bar{b})-4}{k}M_{5}^{3}. \end{aligned}$$
(32)

According to the current experiment of the Large Hadron Collider, the collision energy is 13 TeV, but no signal of extra dimensions is seen [63], so the fundamental five-dimensional scale \(M_{5}\) should be greater than 13 TeV. Thus, combining Eq. (32) and the condition \(M_{5} > rsim 13\) TeV, the constraint on the parameter k is given by

$$\begin{aligned} k > rsim (12\bar{b}\coth (2\bar{b})-6)\times 10^{-17}~\text {eV}. \end{aligned}$$
(33)

From Table 2, we can see that the fitting parameter s rapidly decreases with \(\bar{b}\). In fact, when \(\bar{b}\) doubles, the fitting parameter s decreases by an order of magnitude. If we choose \(\bar{b}=10^{8}\), then \(k\ge 10^{-8}\) eV and s might be \(10^{-25}\), and the half-life time \(t_{1/2}\) of the first scalar resonance will reach \(10^{17}\) s, which is the same order of magnitude as the age of our universe (\(4.35\times 10^{17}\) s). On the other hand, the large \(\bar{b}\) means that the first resonance is very light, but they are still hard to spot in the collider. This is because the cross section of any process involving the interaction of the zero mode with the light continuum modes is imperceptibly low. From this perspective, these long-lived resonances with very light mass could be considered as a candidate for dark matter.

4 Conclusion and discussion

In this paper, we numerically investigated the evolution of a free massless scalar field in the thick brane. We find that the resonances decay very slowly compared to the nonresonances and can exist on the brane for a very long period. If the lifetime of these resonances can be as long as the cosmological time scale, they might be a candidate for dark matter. This provides a new idea for dark matter research.

Firstly, we constructed a five-dimensional thick brane generated by a scalar field. Then, we considered the evolution of a test scalar field in this thick brane background. Through the coordinate transformation and the variable separation, we obtained the evolution equation (18) and the Schrödinger-like equation (22) for the extra-dimensional profile of the scalar field. The latter gives us the initial data of the massive KK modes, and the former evolves those initial data. Next we solved the Schrödinger-like equation (22) numerically to obtain the initial data of massive KK modes, in particular the initial data of the resonances. The results were shown in Fig. 2 and Table 1. We found that the relative probability of the first scalar resonance increases with \(\bar{b}\), while the mass \(m_{1}\) of the first scalar resonance decreases with \(\bar{b}\). Using these KK modes as initial data, we investigated their evolution. Considering their energy decay and extracting a time series for the resonance amplitude, the evolution of the scalar field was analyzed. The results were shown in Figs. 3 and 4, and Table 2. The energy decay can be described by a decay parameter s which can be obtained by an exponential fit of \(E/E_{0}\) as the function of \(\bar{t}\). On the other hand, we also considered the evolution of the nonresonances. The energies and amplitudes of nonresonances decay rapidly at the early stage, but later they decay like those of the resonances. The behavior of the nonresonance evolution could be treated as a combination of resonances. Finally, we considered the half-life time of the resonance. For a very large \(\bar{b}\), the lifetime of ultralight resonances can reach the cosmological time scale. These indicate that the scalar resonant mode could be a candidate for dark matter.

There is much to be improved in this paper. Firstly, the mass and interaction of the test scalar field is not taken into account, which might result in more interesting results. Secondly, other test fields such as Dirac spinor fields and gauge fields and their evolution are also worth investigating. These possibilities deserve further study.