Shadowing effects in the diffractive scattering of virtual photons on nuclei and its interference with the process of bremsstrahlung

Abstract

In cosmic ray physics and high-energy neutrino astronomy, muons are ubiquitous. Due to their slow energy loss and consequently large range at high energies, the correct simulation of their transport through matter is especially important for underground experiments. The dominant energy loss processes are ionization and at higher energies pair production, bremsstrahlung and inelastic interaction with nuclei. A muon energy loss process, which has hitherto been neglected in such simulations, is the diffractive scattering of virtual photons on nuclei. As the elastic channel of this process has the same final state as the bremsstrahlung process $(\mu + A \rightarrow \mu + A + \gamma )$, an interference term arises, whose sign depends on the charge of the lepton. It is found that the contribution of this process was overestimated in earlier works and is significantly affected by shadowing.

1 Introduction

High energy muons travel large distances through matter because they lose their energy slowly. This is advantageous for high-energy neutrino astronomy as neutrinos interacting outside the detector can travel into the instrumented volume, thus enlarging the effective volume of the detector. The large range of muons requires that simulations of their transport be sufficiently accurate, in particular the description of their interaction cross sections.

The main energy loss processes of muons are ionisation, electron–positron pair production, bremsstrahlung and photonuclear interaction. Denoting the cross section differential in the relative energy lost per interaction as $d\sigma /dy$, the average energy loss per distance is given by

$$\begin{aligned} \left\langle -\frac{dE}{dx}\right\rangle = \frac{N_A}{A} \rho \int y \sum _{\text {processes}} \frac{d\sigma }{dy} dy, \end{aligned}$$

(1)

where $N_A$ is the Avogadro number, A the mass number, and $\rho$ the mass density of the material. The ionisation leads to small energy losses, which result in a roughly constant contribution to $\langle -dE/dx\rangle$; the other processes lead to an average energy loss that rises approximately linear with energy, such that

$$\begin{aligned} \left\langle -\frac{dE}{dx} \right\rangle \approx a + b E. \end{aligned}$$

(2)

Pair production energy losses are predominantly very small $(y \ll 1),$ while bremsstrahlung and photonuclear interaction also lead to large stochastic losses, in which the muon looses a large fraction of its energy. The dependence of the average energy loss for these dominant processes in water is shown in Fig. 1. While the first calculations of these processes date back to the 1930s [1,2,3], over the decades numerous corrections have been calculated, including the effect of nuclear formfactors [4, 5], atomic electrons as target [6, 7], Coulomb corrections [8, 9], and radiative corrections [10, 11], as well as numerous calculations of photonuclear interaction and nuclear shadowing (e.g. [12,13,14,15]).

Fig. 1

Average energy loss of muons per distance in water

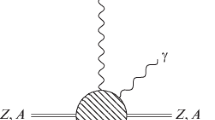
Another process influencing the behaviour of muons is the diffractive scattering of virtual photons to a final-state real photon

$$\begin{aligned} \gamma ^* + A \rightarrow \gamma + A^{(\prime )}. \end{aligned}$$

(3)

This process is known as deeply virtual Compton scattering for photons of high virtuality $Q^2$ and has been studied for the proton, together with other diffractive processes $\gamma ^* + p \rightarrow X + p$, at colliders. For nuclei, deeply virtual Compton scattering has been studied for electron-ion colliders (e.g. [16]).

The diffractive scattering of photons is in principle a subprocess of photonuclear interaction; however, in coherent scattering of virtual photons, where the nucleus stays intact,

$$\begin{aligned} \gamma ^* + A \rightarrow \gamma + A, \end{aligned}$$

(4)

the initial and final state coincide with the bremsstrahlung process when considered on the lepton level

$$\begin{aligned} \mu ^\pm + A \rightarrow \mu ^\pm + \gamma + A. \end{aligned}$$

(5)

This fact gives rise to interference between the bremsstrahlung amplitude ${\mathscr {M}}_{\text {brems}}$ and the diffractive scattering amplitude ${\mathscr {M}}_{\text {diff}}$

$$\begin{aligned} |{\mathscr {M}}_{\text {tot}}|^2 = |{\mathscr {M}}_{\text {brems}}|^2 + |{\mathscr {M}}_{\text {diff}}|^2 + 2 {\text {Re}}\, ({\mathscr {M}}_{\text {diff}} {\mathscr {M}}_{\text {brems}}^*). \end{aligned}$$

(6)

Because the bremsstrahlung amplitude is proportional to the square of the muon charge, while the diffractive amplitude depends linearly on it, the interference term is proportional to the sign of the muon charge. In addition, the bremsstrahlung amplitude is purely real in leading order, such that only the real part of the diffractive scattering amplitude contributes.

In the context of muon transport calculations, the interest lies chiefly in the region of low $Q^2$, as opposed to the deeply virtual region of large $Q^2$ mainly studied in preceding work. The first discussion of diffractive virtual Compton scattering in the context of muon transport was given by [17], which remained largely unnoticed, however.

The article is structured as follows: in Sect. 2, the calculation of [17] is briefly explained; this is done to make the article self-contained, since [17] is difficult to obtain. In Sect. 3, a calculation using the color dipole model is presented, where also the effect of shadowing is taken into account. The article closes in Sect. 4 with a comparison of the results of the different approaches with one another and other corrections to muon energy loss cross sections.

2 Mass-operator calculation of Kelner and Fedotov

The Green’s function for the electromagnetic field in nuclear matter can be obtained by the introduction of a mass operator. The vector potential $A_i$ in a gauge with vanishing scalar potential can be expressed by a current density $j_k$ as

$$\begin{aligned} A_i(x) = -\int D_{ik} (x, x') j_k (x') d^4 x', \end{aligned}$$

(7)

where $D_{ik}(x, x')$ is the quantum retarded Green’s function. The difference between the Feynman propagator and retarded Green’s function can be disregarded according to the authors of [17], since the problem is limited to the evaluation of tree-level diagrams in this formulation. In this case the equation to be solved is given in coordinate-space by

$$\begin{aligned}{} & {} \left( (\omega ^2 + \varDelta + 2 \omega \varPi (\omega ) \rho ({\textbf{r}})) \delta _{ik} - \frac{\partial ^2}{\partial x_i\ \partial x_k}\right) A_k ({\textbf{r}}, \omega )\nonumber \\{} & {} \quad = -j_i ({\textbf{r}}, \omega ), \end{aligned}$$

(8)

where $\omega$ is the energy of the photon, $\varDelta$ is the Laplace operator, $\varPi (\omega )$ the mass operator, and $\rho ({\textbf{r}})$ the number density of nucleons normalized as $\int \rho \ d^3 r = V$ with V the effective nuclear volume. This derivation is analogous to the treatment of diffractive hadron-nucleus reactions in [18], however in the limit of a transparent nucleus (more appropriate to photon-nucleus reactions) instead of a “black” nucleus (appropriate for hadron-nucleus reactions).

A possible dependence on the virtuality of the photon was neglected by [17]. Solving by perturbation theory for a small mass operator $\varPi (\omega )$ the leading approximation for the photon Green’s function is given in momentum space by

$$\begin{aligned} D_{ik} ({\textbf{k}}, {\textbf{l}}, \omega )= & {} (2 \pi )^3 \delta ({\textbf{k}} - {\textbf{l}}) D_{ik}^{(0)} ({\textbf{k}}, \omega ) \nonumber \\{} & {} + D_{il}^{(0)} ({\textbf{k}}, \omega ) 2 \omega \varPi (\omega ) \delta _{lm} V F_n ({\textbf{k}} - {\textbf{l}}) D_{mk}^{(0)} ({\textbf{l}}, \omega ).\nonumber \\ \end{aligned}$$

(9)

Here, $D_{ik}^{(0)}$ is the vacuum photon Green’s function and $F_n({\textbf{q}})$ is the nuclear form factor. This corresponds to a two-photon-nucleus vertex

$$\begin{aligned} M_{ik} (k, l) = 2 \omega \delta _{ik} \varPi (\omega ) V F_n(k - l), \end{aligned}$$

(10)

where k, l are the 4-momenta of the outgoing and incoming photons; this can be expressed in a gauge-invariant way by replacing the Kronecker symbol $\delta _{ik}$ by

$$\begin{aligned} \varDelta _{\mu \nu } = -g_{\mu \nu } + \frac{l_\mu k_\nu }{(k l)} - (k l) \left( \frac{l_\mu }{(k l)} - \frac{U_\mu }{(U k)}\right) \left( \frac{k_\nu }{(k l)} - \frac{U_\nu }{(U l)}\right) ,\nonumber \\ \end{aligned}$$

(11)

where U is the four-velocity of the nucleus and $(Uk) = (Ul) = \omega$, neglecting the energy transfer to the nucleus. The imaginary part of the mass operator is determined by the photoabsorption cross section via the optical theorem

$$\begin{aligned} \sigma _{\gamma A} = \frac{1}{\omega } {\text {Im}}\, {\varepsilon ^*}^\mu (k) M_{\mu \nu } (k, k) {\varepsilon ^\nu } (k) = 2 V {\text {Im}}\, \varPi ; \end{aligned}$$

(12)

the real part follows from dispersion relation.

The interference term of the diffractive amplitude

$$\begin{aligned} {\mathscr {M}}_{\text {diff}} = i e_\mu \frac{[{\bar{u}} (p_2) \gamma _\mu u (p_1)]}{Q^2} M_{\mu \nu } (q, k) \varepsilon ^{* \nu } (k), \end{aligned}$$

(13)

and the bremsstrahlung amplitude

$$\begin{aligned}{} & {} {\mathscr {M}}_{\text {brems}} = i Z e e_\mu ^2 \frac{F_n(\sqrt{-t}) - F_a(\sqrt{-t})}{-t}\nonumber \\{} & {} \quad \times {\bar{u}} (p_2) \left[ \gamma _\alpha \frac{{\hat{p}}_2 + {\hat{k}} + \mu }{2 (p_2 k)} {\hat{U}} - {\hat{U}} \frac{{\hat{p}}_1 - {\hat{k}} + \mu }{2 (p_1 k)} \gamma _\alpha \right] \nonumber \\{} & {} \quad \times u (p_1)\varepsilon ^{* \alpha } (k), \end{aligned}$$

(14)

where $p_{1,2}$ are the incoming and outgoing lepton momenta, q, k the virtual and final state photon momenta, $\varepsilon ^{* \nu } (k)$ the polarization vector of the final state photon, $Q^2 = -q^2$ the virtuality of the virtual photon, and $F_a$ is the atomic formfactor, which turns out to be irrelevant for the interference term, can be evaluated mostly analytically for ultrarelativistic particles ($E_{1,2}^2, \omega ^2 \gg \mu ^2, |t|$, where $\mu$ is the muon mass, t the invariant momentum transfer to the nucleus, and $E_{1,2}, \omega$ the energies of the leptons and final state photons) with the result

$$\begin{aligned} y \frac{d\sigma _{\text {int}}}{dy}= & {} -{\text {sgn}}(e_\mu ) \frac{4 \alpha ^2 Z V}{\pi } {\text {Re}}\, \varPi (\omega ) f(y),\nonumber \\ f(y)= & {} \int _0^\infty \frac{dx}{x} \frac{1 - y + [1 + (1 - y)^2] x^2}{x \sqrt{1 + x^2}} \ln (x + \sqrt{1 + x^2}) \nonumber \\{} & {} \times \left[ F_n^2 (2 \mu x y) - F_n^2 \left( \frac{2 \mu x y}{1 - y}\right) \right] . \end{aligned}$$

(15)

In their numerical calculations, Kelner and Fedotov in [17] used a parametrization of the photoabsorption cross section of the form

$$\begin{aligned} \sigma _{\gamma A} = A (X s^\varepsilon + Y s^{-\eta }) \end{aligned}$$

(16)

with $s = 2 m_p \omega /{{\hbox {GeV}}^2};$ assuming a mass operator of the form $\varPi \propto (-s - i0)^\lambda ,$ they derived the ratio of real and imaginary part of the mass operator as

$$\begin{aligned} \frac{{\text {Re}}\, \varPi }{{\text {Im}}\, \varPi } = \frac{-X s^\varepsilon \cot (\pi \varepsilon ) + Y s^{-\eta } \cot (\pi \eta )}{X s^\varepsilon + Y s^{-\eta }}. \end{aligned}$$

(17)

However, this form of the mass operator leads to an amplitude which is not crossing invariant. The correct form of the mass operator is given by $\varPi \propto (-s - i0)^\lambda - (s + i0)^\lambda$, corresponding to an amplitude ${\mathscr {M}}_{\gamma p \rightarrow \gamma p} \propto (-s - i0)^{1 + \lambda } + (s + i0)^{1 + \lambda }$. This leads to a ratio of the real and imaginary part of the mass operator (and therefore of the amplitude)

$$\begin{aligned} \frac{{\text {Re}}\, \varPi }{{\text {Im}}\, \varPi } = \frac{X s^\varepsilon \tan (\pi \varepsilon /2) - Y s^{-\eta } \tan (\pi \eta /2)}{X s^\varepsilon + Y s^{-\eta }}. \end{aligned}$$

(18)

At large energies, the ratio between (17) and (18) amounts to about a factor of 30 and a difference in the sign of the real part of the amplitude.

3 Calculation of the interference of diffractive Compton scattering and bremsstrahlung in the color dipole approach

3.1 Compton tensor in the color dipole approach

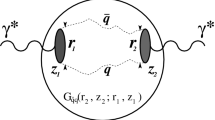
Instead of the mass operator approach used by [17], in this work the color dipole model is used [19,20,21], which expresses the amplitude of diffractive processes on nucleons in the forward direction as

$$\begin{aligned}{} & {} {\mathscr {A}}_{\gamma ^* p \rightarrow X p} \nonumber \\{} & {} \quad = (\beta _{\text {dip}} + i) \int d^2 r \int _0^1 dz\ [\varPsi _X^* \varPsi _{\gamma ^*}] (Q^2, r, z) \sigma _{\text {dip}}(r, W^2),\nonumber \\ \end{aligned}$$

(19)

where $[\varPsi _X^* \varPsi _{\gamma ^*}] (Q^2, r, z)$ is the overlap between the wavefunctions of the initial photon and the final state as a function of photon virtuality $Q^2$, transversal separation of the quark–antiquark pair r and energy fraction of the quark (antiquark) z ($1 - z$), $\beta _{\text {dip}}$ is the ratio between the real and imaginary part of the amplitude, and $\sigma _{\text {dip}}(r, W^2)$ is the dipole cross section describing the interaction of the quark–antiquark pair with the nucleus. For virtual Compton scattering, only transversally polarized virtual photons contribute, with the wave function overlap

$$\begin{aligned}{} & {} {[}\varPsi _\gamma ^* \varPsi _{\gamma ^*}] (Q^2, r, z) = \frac{3 \alpha }{2 \pi ^2}\sum _q \left( \frac{e_q}{e}\right) ^2 \nonumber \\{} & {} \quad \times \{[z^2 + (1 - z)^2] \varepsilon m_q K_1 (\varepsilon r) K_1 (m_q r) \nonumber \\{} & {} \quad + m_q^2 K_0(\varepsilon r) K_0 (m_q r) \}, \end{aligned}$$

(20)

where $\varepsilon = \sqrt{Q^2 z (1 - z) + m_q^2}$, and the sum is over quark flavors q. The dipole cross section cannot be deduced from first principles, so phenomenological parametrizations have to be used. Here, two parametrizations are used, the FKS two-component parametrization [22], unitarized according to the prescription in [13], and the color glass condensate IIMS parametrization [23, 24]. The formulæ for the dipole cross section are given in the Appendix. The FKS model is chosen, despite its age, because it explicitly takes into account the limiting case of real photons and measurements of the photoabsorption cross section are taken into account in fitting, including a phenomenological modification for the photon wave function [cf. (A.5)], whereas more recent models such as the IIMS model are usually more concerned with higher values of $Q^2$.

As in the mass operator calculation by [17], for the calculation of the interference between the bremsstrahlung amplitude and the Compton scattering amplitude the Compton tensor is required. The Compton tensor is not uniquely determined from symmetry considerations: a gauge-invariant rank-two tensor obeying all applicable symmetries for the process $\gamma ^* + N \rightarrow \gamma ^* + N$ is in general described by 21 coefficients [25, 26]; in the spin-independent case this reduces to five coefficients and further to three coefficients in the case of a real photon in the final state, which cannot be unambiguously identified with the amplitudes for transversal-transversal and longitudinal-transversal transition, so to determine the tensorial structure one has to choose a model. The color dipole model [19,20,21], which is commonly used for calculations of forward Compton scattering and diffractive processes (e.g. [16, 27, 28]) and also in this work, does not offer a covariant way to determine this Lorentz tensor structure; the tensor structure would have to be reconstructed from the contraction with the photon polarization vectors for the different helicities. Since the color dipole model corresponds physically to the pomeron exchange, it is much easier to determine the tensor structure using the Feynman rules worked out in [29] to describe hadronic interactions in the Regge regime, treating the pomeron as an effective spin-2 exchange. Calculating the amplitude in the high-energy region, keeping only the leading terms in energy, one obtains the tensorial structure

$$\begin{aligned} M_{\mu \nu }= & {} {\mathscr {A}}_{\gamma ^* A \rightarrow \gamma A} \left\{ \frac{t - l^2 - k^2}{(s - u)^2} (P + P')_\mu (P + P')_\nu \right. \nonumber \\{} & {} - \left. \frac{g_{\mu \nu }}{2} + \frac{k_\mu (P + P')_\nu + (P + P')_\mu l_\nu }{s - u}\right\} \end{aligned}$$

(21)

with $P, P'$ denoting the four-momenta of the nucleus before and after the interaction and s, t, u the usual Mandelstam variables in the photon-nucleus system. In contrast to the preceding calculation, this does not neglect the recoil of the target nucleus. Calculating the interference of this amplitude with the usual bremsstrahlung amplitude is elementary, but tedious. Denoting the scalar products of the final photon momentum and the in- and outgoing lepton momenta as $\eta _1, \eta _2$, respectively, we obtain the expression

$$\begin{aligned}&\overline{2 {\text {Re}} ({\mathscr {M}}_d {\mathscr {M}}_b^*)} \end{aligned}$$

(22)

$$\begin{aligned}&\quad = \frac{(4 \pi \alpha )^2 F_1(t)}{t Q^2} M_{\mu \nu } (P + P')^\rho \left( -g^{\nu \sigma } + \frac{k^\nu k^\sigma }{k^2}\right) \nonumber \\&\qquad \times {\text {Sp}} \Bigg \{ ({\hat{p}}_2 + m) \gamma ^\mu ({\hat{p}}_1 + m)\nonumber \\&\qquad \times \left. \left[ \gamma _\rho \frac{{\hat{p}}_2 + {\hat{k}} + m}{2 \eta _2} \gamma _\sigma - \gamma _\sigma \frac{{\hat{p}}_1 - {\hat{k}} + m}{2 \eta _1} \gamma _\rho \right] \right\} \nonumber \\&\quad = \frac{(4 \pi \alpha )^2}{t Q^2} F_1(t) {\text {Re}}(\mathscr {M}_\text {TT}) \Bigg \{ 2 (\eta _1 + \eta _2) - 4 m_N E (2 - y)\nonumber \\&\qquad + \left( \frac{1}{\eta _1} + \frac{1}{\eta _2}\right) \left( m^2 (t + Q^2) + \left( m^2 - \frac{Q^2}{2}\right) (s - u) \right) \nonumber \\&\qquad - \left( \frac{1}{\eta _1} - \frac{1}{\eta _2}\right) 4 m^2 m_N^2 E (2 - y) \nonumber \\&\qquad + \frac{1}{s - u} \left[ 8 m_N E (2 - y) (s + t - m_N^2 + 7 Q^2) \right. \nonumber \\&\qquad + (\eta _1 + \eta _2) (8 m_N^2 - 10 Q^2 - 4 t) + 16 m_N E ((1 - y) \eta _1 - \eta _2) \nonumber \\&\qquad \times \left( \frac{1}{\eta _1} + \frac{1}{\eta _2}\right) \left( \frac{Q^2}{2} (Q^4 + Q^2 (4 m_N^2 - 7 t) - 4 t m_N^2) \right. \nonumber \\&\qquad \left. + m^2 (t + Q^2) (4 m_N^2 - t) - 56 m_N^2 Q^2 E^2 (1 - y) \right) \nonumber \\&\qquad + \left( \frac{1 - y}{\eta _1} - \frac{1}{\eta _2}\right) 2 m_N^2 Q^2 E (7 Q^2 + t) \nonumber \\&\qquad + \left( \frac{1}{\eta _1} - \frac{1 - y}{\eta _2} \right) 2 m_N E (4 E m_N t y - 2 Q^4 + 5 Q^2 t + t^2) \nonumber \\&\qquad \times \left. \left( \frac{1}{\eta _1} + \frac{(1 - y)^2}{\eta _2}\right) 8 m_N^2 Q^2 E^2 \right] \nonumber \\&\qquad + \frac{1}{(s - u)^2} \left[ 16 m_N E (t + Q^2) (\eta _2 - (1 - y) \eta _1) \right. \nonumber \\&\qquad + (\eta _1 + \eta _2) (-4 Q^4 - 56 Q^2 m_N^2 + 10 Q^2 t - 8 m_N^2 t + 2 t^2) \nonumber \\&\qquad + 4 m_N E (2 - y) (-4 s (t + Q^2) + 32 Q^2 m_N^2 \nonumber \\&\qquad + t (8 m_N^2 - 7 Q^2) - t^2) \nonumber \\&\qquad + 64 m_N^3 E^3 (t + Q^2) (1 - y) \left( \frac{1}{\eta _1} - \frac{1 - y}{\eta _2}\right) \nonumber \\&\qquad - 16 m_N^2 E^2 (t + Q^2) \left( t \left( \frac{1}{\eta _1} + \frac{(1 - y)^2}{\eta _2}\right) \right. \nonumber \\&\qquad \left. + 2 Q^2 (1 - y) \left( \frac{1}{\eta _1} + \frac{1}{\eta _2}\right) \right) \nonumber \\&\qquad - 2 m_N E (t + Q^2) \left( \left( \frac{1}{\eta _1} - \frac{1 - y}{\eta _2}\right) \left( t^2 - 4 m_N^2 t - 2 m^2 t \right. \right. \nonumber \\&\qquad \left. - Q^2 t - 8 m^2 m_N^2 - 12 Q^2 m_N^2 \right) \nonumber \\&\qquad \left. + \left( \frac{1 - y}{\eta _1} - \frac{1}{\eta _2}\right) (-2 Q^4 - 2 m^2 (t - 4 m_N^2)) \right) \nonumber \\&\qquad - \left( \frac{1}{\eta _1} + \frac{1}{\eta _2}\right) \frac{t + Q^2}{2} (2 m^2 (t + Q^2) (t - 4 m_N^2) \nonumber \\&\qquad \left. - Q^2 (t (t - 4 m_N^2) + Q^2 (t - 12 m_N^2))) \right] \Bigg \}. \end{aligned}$$

(23)

This expression differs noticeably from the expression by [17], in particular the nuclear recoil is not neglected and the theoretical basis (pomeron exchange instead of photon mass operator) differs considerably. The phase space integration is elementary (cf. Appendix C).

3.2 Calculation in the color dipole approach with account for nuclear shadowing

The amplitude of nuclear Compton scattering is given in the dilute limit, i.e. without shadowing, by the amplitude on a free nucleon (cf. (19)) multiplied by the nuclear mass number A.

The effect of nuclear shadowing can be taken into account in the color dipole picture using a Glauber–Gribov approach [30,31,32], as was done in [16, 27, 28]. The amplitude for the coherent channel $\gamma ^* A \rightarrow \gamma A$ is then given by

$$\begin{aligned} {\mathscr {A}}_{\gamma ^* A \rightarrow \gamma A}= & {} 2 (\beta _{\text {dip}} + i) \int d^2 b \int d^2 r \int _0^1 dz [\varPsi _\gamma ^* \varPsi _{\gamma ^*}] e^{-i \textbf{b} \cdot \varDelta } \nonumber \\{} & {} \times \left[ 1 - \exp \left( -\frac{1}{2} \sigma _{\text {dip}} A T_A(b) \right) \right] , \end{aligned}$$

(24)

where $T_A$ is the transversal density of the nucleus, defined by the integral over the longitudinal coordinate

$$\begin{aligned} T_A(b) = \int _{-\infty }^\infty d\zeta \rho (b, \zeta ) \end{aligned}$$

(25)

and normalized so that $\int d^2 b\ T_A(b) = 1$, and $\varDelta$ denotes a transverse vector with $\varDelta ^2 = -t$. These expressions are justified for large coherence lengths compared to the dimensions of the nucleus. The used nuclear density is given by a Woods-Saxon distribution

$$\begin{aligned} \rho (\textbf{x}) = \rho _0 \frac{\exp [-(|\textbf{x}| - R_A)/d]}{\exp [-(|\textbf{x}| - R_A)/d] + 1} \end{aligned}$$

(26)

with surface thickness $d = {0.54}{\hbox {fm}}$ and nuclear radius $R_A = ({1.12} A^{1/3} - {0.86} A^{-1/3}) {\hbox {fm}}$.

4 Numerical results and conclusion

The average energy loss divided by the energy is shown in Figs. 2, 3, and 4 for protons, oxygen and standard rock ($Z = 11, A = 22$) as the most important media for large volume neutrino telescopes. For comparison, together with the modulus of the interference correction, the energy loss due to bremsstrahlung and photonuclear interaction is shown, as well as the energy loss according to the calculations of [17] in its original form and with corrected ratio of the real and imaginary part of the Compton amplitude.

Fig. 2

Bremsstrahlung, photonuclear, and interference energy loss of muons on protons

Fig. 3

Bremsstrahlung, photonuclear, and interference energy loss of muons on oxygen

Fig. 4

Bremsstrahlung, photonuclear, and interference energy loss of muons on standard rock

Compared to the bremsstrahlung cross section, the corrections slowly rise with energy and reach the percent level for very high muon energies in the PeV-regime. Since at PeV energies the average energy loss is roughly equally determined by pair production, bremsstrahlung and photonuclear interaction – where the latter slowly rises, while the former two give a constant contribution to the average energy loss –, this correction is of minor importance for energy loss calculations of high-energy muons. Other corrections, such as the uncertainty of the photonuclear energy loss or radiative corrections [33], which are at a percent level or larger already at lower energies, play a larger role.

Appendices

Appendix A: FKS parametrization of the dipole cross section

The two-component parametrization of [22] with the hard component unitarized according to the prescription in [13] is given by

$$\begin{aligned} \sigma _{\text {dip}} (r, s)&= \sigma _{\text {soft}} (r, s) + \sigma _{\text {unit}}(r, s), \end{aligned}$$

(A.1)

$$\begin{aligned} \sigma _{\text {soft}} (r, s)&= a_0^S \left( 1 - \frac{1}{1 + a_4^S r^4}\right) (r^2 s)^{\lambda _S}, \end{aligned}$$

(A.2)

$$\begin{aligned} \sigma _{\text {unit}} (r, s)&= 2 \pi R_u^2 \left\{ \ln \frac{\sigma _{\text {hard}} (r, s)}{2 \pi R_u^2} + C - {\text {Ei}} \left( - \frac{\sigma _{\text {hard}} (r, s)}{2 \pi R_u^2} \right) \right\} , \end{aligned}$$

(A.3)

$$\begin{aligned} \sigma _{\text {hard}} (r, s)&= (a_2^H r^2 + a_6^H r^6) e^{-r \nu _H} (r^2 s)^{\lambda _H}. \end{aligned}$$

(A.4)

The wave function overlap is modified according to [22] by a factor

$$\begin{aligned} f(r) = \frac{1 + B \exp (-c^2 (r - R)^2)}{1 + B \exp (-c^2 R^2)}, \end{aligned}$$

(A.5)

which influences mainly the soft component. The values of the parameters are $\lambda _s = {0.06}$, $\lambda _H = {0.44}$, $a_0^S = {30.0}~{\hbox {GeV}^{-2}}$, $a_4^S = {0.027}~{\text {GeV}^4}$, $a_2^H = {0.072}$, $a_6^H = {1.89}~{\hbox {GeV}^4}$, $\nu _H = {3.27}~{\hbox {GeV}}$, $B = {7.05}$, $R = {6.84}~{\hbox {GeV}^{-1}}$, and $R_u^2 = {10}~{\hbox {GeV}^{-2}}$.

Appendix B: IIMS parametrization of the dipole cross section

The IIMS parametrization [23, 24] of the dipole cross section in the color glass condensate model is given by

$$\begin{aligned} \sigma _{\text {dip}} (x, r) = {\left\{ \begin{array}{ll} {\mathscr {N}}_0 \left( \frac{\tau }{2}\right) ^{2 \left( \gamma _s + \frac{\ln (2/\tau )}{\kappa \lambda Y}\right) } &{} \tau \le 2\\ 1 - \exp [-A \ln ^2 (B \tau )] &{} \tau > 2, \end{array}\right. } \end{aligned}$$

(B.6)

where $\tau = r Q_s$, $Y = \ln (1/x)$, with ${\mathscr {N}}_0 = {0.7}$, $\gamma _s = {0.7376}$, $\kappa = {9.9}$, $\lambda = {0.2197}$, $x_0 = {1.632\times 10^{-5}}$, $Q_s = (x_0/x)^{\lambda /2} {\hbox {GeV}}$, and $\sigma _0 = {27.28}{\hbox {mb}}$. A, B are determined by ${\mathscr {N}}^p$ and its derivative with regard to $\tau$ being continuous at $\tau = 2$ to be

$$\begin{aligned} A&= -\frac{({\mathscr {N}}_0 \gamma _s)^2}{(1 - {\mathscr {N}}_0)^2 \ln (1 - {\mathscr {N}}_0)}, \end{aligned}$$

(B.7)

$$\begin{aligned} B&= (1 - {\mathscr {N}}_0)^{1/\gamma _s - 1/{\mathscr {N}}_0 \gamma _s}/2. \end{aligned}$$

(B.8)

Appendix C: Phase space integration

The corresponding completely differential cross section is given by

$$\begin{aligned} d\sigma _\text {inter}= & {} \frac{\overline{2 {\text {Re}}\,({\mathscr {M}}_d {\mathscr {M}}_b^*)}}{4 \sqrt{(p_1 P)^2 - p_1^2 P^2}} \nonumber \\{} & {} \quad \times (2 \pi )^4 \delta ^{(4)} (p_1 + P - p_2 - k - P') \nonumber \\{} & {} \quad \times \frac{d^4 p_2}{(2 \pi )^3} \delta (p_2^2 - m^2) \frac{d^4 k}{(2 \pi )^3} \delta (k^2) \frac{d^4 P'}{(2 \pi )^3} \delta ({P'}^2 - m_N^2).\nonumber \\ \end{aligned}$$

(C.9)

The phase space element can be transformed as

$$\begin{aligned} d\varPhi= & {} (2 \pi )^4 \delta ^{(4)} (p_1 + P - p_2 - k - P') \nonumber \\{} & {} \quad \times \frac{d^4 p_1}{(2 \pi )^3} \delta (p_2^2 - m^2) \frac{d^4 k}{(2 \pi )^3} \delta (k^2) \frac{d^4 P'}{(2 \pi )^3} \delta ({P'}^2 - m_N^2) \nonumber \\{} & {} = \frac{1}{(2 \pi )^5} \delta ^{(4)} (l + P - k - P') \nonumber \\{} & {} \quad \times d^4 l\ d^4 k\ d^4 P' \delta (l^2 - 2 p_1 l) \delta (k^2) \delta ({P'}^2 - m_N^2) \nonumber \\{} & {} \quad \times dQ^2 \delta (l^2 + Q^2) dt \delta (t + Q^2 + 2 kl) \nonumber \\{} & {} = \frac{1}{(2 \pi )^5} \frac{E}{32 m_N \sqrt{E^2 - m^2} \sqrt{(Ey)^2 + Q^2}} \nonumber \\{} & {} \quad \times dy\ dQ^2\ dt\ d\phi _l\ d\phi _k. \end{aligned}$$

(C.10)

Here, the z-axis is chosen along ${\textbf{l}}$. The azimuthal angle $\phi _l$ can be trivially integrated over, because it corresponds to a rotation of the entire system. The angle $\phi _k$ appears in the scalar products $\eta _{1,2}$ as

$$\begin{aligned} \eta _1 = k p_1 = E_k E_1 - k_{||} p_{1||} - {\textbf{k}}_\perp \textbf{p}_{1\perp }, \eta _2 = k p_2 = \eta _1 - k l,\nonumber \\ \end{aligned}$$

(C.11)

where

$$\begin{aligned} p_{1||}= & {} \frac{\textbf{p}_1 {\textbf{l}}}{|{\textbf{l}}|} = \frac{E E_l - p_1 l}{\sqrt{E^2 - p_1^2}} = \frac{E^2 y + Q^2/2}{\sqrt{(E y)^2 + Q^2}}, \nonumber \\ k_{||}= & {} \frac{{\textbf{l}} {\textbf{k}}}{|{\textbf{l}}|} = \frac{E_k E_l - l k}{\sqrt{E_l^2 + Q^2}} = \frac{E_k E_l + (t + Q^2)/2}{\sqrt{E_k^2 + Q^2}};\nonumber \\ p_{1\perp }= & {} \sqrt{\textbf{p}_1^2 - p_{1||}^2}, \quad k_\perp = \sqrt{{\textbf{k}}^2 - k_{||}^2}. \end{aligned}$$

(C.12)

with $E_l = E y, E_k = E y + t/(2 m_N)$.

The integration over $\phi _k$ reduces to the five integrals

$$\begin{aligned} J_2= & {} \int \eta _2 d\phi _k, \quad J_1 = \int \eta _1 d\phi _k, \quad J_0 = \int d\phi _k, \nonumber \\ J_{-1}= & {} \int \frac{d\phi _k}{\eta _1}, \quad J_{-2} = \int \frac{d\phi _k}{\eta _2}, \end{aligned}$$

(C.13)

which can be solved by elementary integration using the above decomposition into transversal and longitudinal components. Rearranging terms to obtain numerically stable expressions, we obtain

$$\begin{aligned} J_2&= \frac{2 \pi }{E_l^2 + Q^2} \left[ (E - E_l) E_k Q^2 + (E - E_l) E_l \frac{t + Q^2}{2}\right] , \end{aligned}$$

(C.14)

$$\begin{aligned} J_1&= \frac{2 \pi }{E_l^2 + Q^2} \left[ (E - E_l) E_k Q^2 - E E_l \frac{t + Q^2}{2} - \frac{Q^2 (t + Q^2)}{2} \right] , \end{aligned}$$

(C.15)

$$\begin{aligned} J_0&= 2 \pi , \end{aligned}$$

(C.16)

$$\begin{aligned} J_{-1}&= 4 \pi \sqrt{E_l^2 + Q^2} \{[E t + (E - E_k) Q^2]^2 \nonumber \\&\quad + 4 m^2 [E_k^2 Q^2 - E_l E_k (t + Q^2) - (t + Q^2)^2/4]\}^{-1/2}, \end{aligned}$$

(C.17)

$$\begin{aligned} J_{-2}&= 4 \pi \sqrt{E_l^2 + Q^2} \{[(E - E_l) (t + Q^2) + E_k Q^2]^2 \nonumber \\&\quad + 4 m^2 [E_k^2 Q^2 - E_l E_k (t + Q^2) - (t + Q^2)^2/4]\}^{-1/2}. \end{aligned}$$

(C.18)