1 Introduction

Messier and Herschel were the first to discover the clustering tendency of nebulae and prepared the first catalogs of the discovered objects. In the nineteenth and twentieth century, large samples of galaxies were cataloged. In 1920, Hubble proved that the spiral and elliptical nebulae are galaxies like Milky Way located at a large distance [1]. Study of the velocities of galaxies in their respective clusters led to the conclusion of the presence of larger gravitating mass than the total visible mass by a factor of \(\sim 200{-}400\) [2]. This confirmed the presence of extra invisible matter in the system of galaxy.

The quest towards understanding the formation of galaxy clusters and their evolution is at the center of modern day astronomy. Large scale structure formation has been studied extensively on both theoretical and observational grounds. Multi-wavelength observations of galaxy clusters have illustrated all main components like intracluster light (ICL, present due to the stars in the galaxy), intracluster medium (ICM, due to hot gas within the cluster) and the famous Sunyaev–Zel’dovich effect. Micro-wave, mid-infrared and near-infrared wavelengths trace cool gas, obscured cold objects and stellar contents, respectively. The multi-wavelength observations of Abell in 1689 (Z = 0.18) is shown in the Fig. 1. The presence of dark matter (DM) is inferred via gravitational lensing in Abell 1689 [3]. Other probes for the inference of DM include gravitational waves, [4] and rotational curves of galaxies [5].

Theoretical studies of cluster formation have also evolved into a vibrant and mature scientific discipline. Theoretical models of Galaxy clusters have brought forth most important processes that are responsible for the various observed properties of the clusters along with their subsequent evolution. This theoretical development has given clusters the importance of being used as cosmological probes [6]. The current view about the structure formation is the hierarchical sequence of mergers and accretion of small scale systems by the gravitational field of visible matter and DM. A simple model by Kaiser, known as self similar model, predicts cluster properties that are close to observations [7]. Recently, theoretical models employing modified gravity have been employed to predict various aspects of cluster formation [8]. These modified theories include f(R) theory and multidimensional braneworld-modified gravity. These theories provide alternative explanation to dark energy. In f(R) gravity models, a general function of the Ricci Scalar is introduced in the Einstein–Hilbert action which in turn results into cosmic acceleration [9]. Similar results are expected in the brane world-modified gravity models. Galaxy clustering under modified Newtonian potential, motivated by string theory and cosmological constant have also been studied [10, 11]. Similarly, the effect of various other modified gravity laws on the clustering of galaxies has been studied extensively [12,13,14,15,16,17,18,19,20,21].

There are also various theories for cosmological many-body distribution function from thermodynamic point of view. The connection between thermodynamics and gravity first appeared in the works of Bekenstein [22], Hawking [23] and Unruh [24]. Later Jacobson [25] extended this connection to link thermodynamics and general relativity, where in Einstein equation appeared as an equation of state. In Ref. [25], this equation is derived from the proportionality of horizon area and entropy along with the relation, \(\delta Q=T d S\), connecting energy flux \(\delta Q\) and Unruh temperature. Recently, Padmanabhan has discussed the thermodynamic properties of horizons in detail [26].

Fig. 1
figure 1

The image shows combined X-ray/optical of cluster Abell 1689 at z = 0.18. Galaxies in the optical band, colored yellow, are Hubble space telescope observations. The long arcs are due to the gravitational lensing of background galaxies due to the gravitating matter in the cluster. The X-ray emission of the gas (at T 1011 K) is shown in the purple haze. (Credit:X-ray: NASA/CXC/MIT; Optical: NASA/STScI)

Full size image

Recently, Verlinde proposed entropic origin of gravity [27]. The author of [27] argued that in deriving gravity the central notion is the information associated with matter and its location measured via entropy. The displacement of matter leads to a change in entropy that in turn leads to a reaction force which then, under certain reasonable assumptions, takes the form of gravity. This work attempted to established thermodynamics as a basic principle. In Ref. [27], Gravitational law, Einstein’s equations, Poisson’s equation and the equipartition law of energy have found an entropic origin. Following Verlinde’s approach, there is possibility to consider the entropic force in order to derive the correction to the Newton’s force law between two bodies with GUP correction [28, 29].

The structure of the paper is as follows. In Sect. 2, we calculate the gravitational partition function under the GUP corrected gravitational potential. Once the partition function is known, it is a matter of calculation to derive various thermodynamical equations of state. In Sect. 3, we calculate GUP corrected free energy, entropy, internal energy, pressure and chemical potential. By considering the system in quasi-equilibrium as grand canonical ensemble, we estimate general distribution function for gravitating system in Sect. 4. The effect of GUP correction on power-law of two-point function is discussed in Sect. 5. We make final remarks in Sect. 7.

2 Interaction of galaxies under GUP modified potential

In this section, we study the GUP corrected partition function describing galactic clustering.

2.1 GUP modified gravitational potential

In Verlinde’s entropic gravity framework, the Newton’s force law of gravitation can be derived based on a quantum mechanical and thermodynamical set-up. Upon considering GUP contribution and first law of thermodynamics, we write the modified gravity force law as [28]

$$\begin{aligned} F_{GUP}= -\frac{GM^2}{R^2}\frac{2[1+\eta -2\beta (2+\eta )]}{\eta (1+\eta )\left( -4\beta +1+\eta +4\beta \ln \left[ \frac{2\sqrt{\beta }}{1+\eta }\right] \right) }, \end{aligned}$$
(1)

where M is the mass of each galaxy, R is the radial distance, \(\eta =\sqrt{1-4G/ R^2}\) and \(\beta =G /R^2\). Here, both the velocity of light (c) and Heisenberg constant (\(\hbar \)) are set unit. In the large distance limit, \(R \gg L_p = \sqrt{G}\) (Planck length) and therefore \(\beta = G/ R^2\ll 1\). Thus, expanding expression (1) to the first-order of \(\beta \) [28, 29]

$$\begin{aligned} F_{GUP}= -\frac{GM^2}{R^2}\left[ 1+2 \frac{L_p ^2}{R^2} \right] . \end{aligned}$$
(2)

From the standard definition of gravitational potential \(\Phi =-\int F d R\) and Eq. (2), the GUP modified potential reads

$$\begin{aligned} \Phi _{GUP} =-\frac{GM^2}{R}\left[ 1+ \frac{2 L_p ^2}{3 R^2} \right] =-\frac{GM^2}{R}\left[ 1+ \frac{2 }{3 } \beta \right] . \end{aligned}$$
(3)

With this GUP modified potential, we are able to derive the thermodynamics of the galaxy’s cluster along with the distribution function.

2.2 Gravitational partition function

In this section, we calculate the many-body gravitational partition function, for a system of galaxies, treated as point particles, under the modified Newton’s law. This is because the statistical mechanics of an N-body system is based primarily on the partition function. Here, we assume that the system of galaxies made of large ensemble of cells, each of radius R, volume V and average density \({\bar{N}}\) as galaxies are distributed homogeneously over large regions. We let the total number of galaxies and their total energy vary among the cells.

For an N-body system of galaxies each having mass M and the system temperature T, the general partition function (grand canonical) is written as [30]:

$$\begin{aligned} Z_N\left( T,V\right) =\frac{1}{N!}\left( \frac{2\pi MT}{\Lambda ^2}\right) ^{3N/2}Q_N\left( T,V\right) , \end{aligned}$$
(4)

where, \(Q_N (T,V)\), is the configuration part and is given by

$$\begin{aligned} Q_N\left( T,V\right) =\int \cdots \int \prod _{1\le i <j\le N} (1+f_{ij})d^{3N}R. \end{aligned}$$
(5)

Here, two-point function, \(f_{ij}\), is defined as

$$\begin{aligned} f_{ij}=\exp \left( -\frac{\Phi _{GUP}}{T}\right) -1, \end{aligned}$$
(6)

which vanishes in the absence of interactions and in the presence of interactions it takes non-zero value. From the expression (3), it is evident that for point-mass galaxies the potential and, therefore, Hamiltonian of the system diverges. This gives an ill-defined partition function. In order to avoid this discrepancy, we consider the extended nature of galaxies (i.e. galaxies with halos) and introduce a softening parameter \(\epsilon \) which takes a value ranging \(0.01 \le \epsilon \le 0.05\). The confirmation about each galaxy having a finite size is incorporated in the potential of the form \(1/ \sqrt{R^2+\epsilon ^2}\) to the first order [31]. However, at small scales, the density would decrease as \(R^{-2}\), which possibly represents a spherical isothermal halo.

In this consideration, the expression of potential (3) takes following form:

$$\begin{aligned} \Phi _{GUP} =-\frac{GM^2}{(R^2+\epsilon ^2)^{1/2}}\left[ 1+ \frac{2L_P^2}{3(R^2+\epsilon ^2)} \right] . \end{aligned}$$
(7)

From expression (5), we evaluate the configuration integral for the system of single galaxy i.e. \(N = 1\) as follows:

$$\begin{aligned} Q_1(T,V)=V. \end{aligned}$$
(8)

For the system of two galaxies i.e. \(N=2\), the configuration integral is calculated by

$$\begin{aligned} Q_2(T,V)= & {} 4\pi V \int \left[ 1+\frac{GM^2}{T }\left( \frac{1}{(R^2+\epsilon ^2)^{1/2}}\right. \right. \nonumber \\{} & {} \left. \left. +\frac{2L_P^2}{3(R^2+\epsilon ^2)^{3/2}} \right) \right] R^2d R. \end{aligned}$$
(9)

Here we used the fact that effect of long range mean gravitational field is balanced by the expansion of the universe. Upon performing the integration, the above integral yields

$$\begin{aligned}{} & {} Q_2(T,V)\nonumber \\{} & {} \quad =V^2\left[ 1+\frac{3}{2}\frac{GM^2}{RT}\left( \sqrt{1+\frac{\epsilon ^2}{R^2}}+\frac{\epsilon ^2}{R^2} \log \frac{\epsilon /R}{\left[ 1+ \sqrt{1+\frac{\epsilon ^2}{R^2}}\right] } \right. \right. \nonumber \\{} & {} \qquad -\left. \left. \frac{4\beta }{3}\left( \frac{1}{ \sqrt{1+\frac{\epsilon ^2}{R ^2}}}-\frac{1}{ \epsilon }+ \log \frac{{\epsilon /R }}{\left[ 1+\sqrt{1+\frac{\epsilon ^2}{R ^2}}\right] } \right) \right) \right] . \end{aligned}$$
(10)

Under dimensionless scale invariance, we can write

$$\begin{aligned} \frac{GM^2}{RT}\approx \frac{GM^2}{{\bar{N}}^{1/3} T}\xrightarrow {}\frac{ (GM^2)^3}{{\bar{N}} T^3}. \end{aligned}$$
(11)

Using Eq. (11), Eq. (10) can be written in a compact form as

$$\begin{aligned} Q_2(T,V)=V^2\left[ 1+ x\left( \beta _1+\beta _2 \right) \right] , \end{aligned}$$
(12)

where

$$\begin{aligned} x= & {} \frac{3}{2}\frac{(GM^2)^3V}{ {N} T^3}, \end{aligned}$$
(13)
$$\begin{aligned} \beta _1= & {} \sqrt{1+\frac{\epsilon ^2}{R^2}}+\frac{\epsilon ^2}{R^2} \log \frac{\epsilon /R}{\left[ 1+ \sqrt{1+\frac{\epsilon ^2}{R^2}}\right] } , \end{aligned}$$
(14)
$$\begin{aligned} \beta _2= & {} -\frac{4\beta }{3}\left( \frac{1}{ \sqrt{1+\frac{\epsilon ^2}{R ^2}}}-\frac{1}{ \epsilon }+ \log \frac{{\epsilon /R }}{\left[ 1+\sqrt{1+\frac{\epsilon ^2}{R ^2}}\right] } \right) . \end{aligned}$$
(15)

Following the similar procedure, the configuration integral for the system of N-galaxies can be written as

$$\begin{aligned} Q_N(T,V)=V^N\left[ 1+ x\left( \beta _1+\beta _2 \right) \right] ^{N-1}. \end{aligned}$$
(16)

Using Eqs. (4) and (16), the partition function for our system of N gravitationally interacting galaxies is

$$\begin{aligned} Z_N(T,V)=\frac{1}{N!}\left( \frac{2\pi MT}{\Lambda ^2}\right) ^{3N/2}V^N\left[ 1+ x\left( \beta _1+\beta _2 \right) \right] ^{N-1}. \end{aligned}$$
(17)

This partition function includes the uncorrected parameter, \(\beta _1\), and the GUP corrected parameter, \(\beta _2\).

3 Thermodynamics of gravitating system

Knowing the gravitational partition function, various thermodynamics quantities of the system of galaxies can be calculated. The most important among these are Helmholtz free energy, entropy, internal energy, pressure and chemical potential. The general distribution function can also be calculated from the general partition function to know the effect of GUP correction to the distribution of the system galaxies.

3.1 Helmholtz free energy

The Helmholtz free energy for the GUP corrected potential, utilizing standard definition \(F=-T\ln Z_n(T,V)\) (with Boltzmann constant \(k_B = 1\)), can be written for the system of galaxies as

$$\begin{aligned} F=-T\ln \left[ \frac{1}{N!}\left( \frac{2\pi MT}{\Lambda ^2}\right) ^{3N/2}V^N\left[ 1+ x\left( \beta _1+\beta _2 \right) \right] ^{N-1}\right] . \end{aligned}$$
(18)

Since the value of N is very large, so this can further simplified using Stirling’s approximation to

$$\begin{aligned} F= & {} NT\left( \ln \frac{N}{V}T^{-3/2}\right) -NT\nonumber \\{} & {} -NT\ln \left[ 1+ x\left( \beta _1+\beta _2 \right) \right] -\frac{3}{2}NT\ln \left( \frac{2\pi M}{\Lambda ^2}\right) . \end{aligned}$$
(19)

Here, \(N-1\approx N\) is used in view of large N.

3.2 Entropy

Once the expression for Helmholtz free energy is known, other thermodynamic quantities like entropy can be easily derived from it. The entropy is related to the free energy via the relation \(S=-\left( \frac{\partial F}{\partial T}\right) _{N,V}\). Therefore, the entropy of the system is derived from the Helmholtz free energy (19) as

$$\begin{aligned} S= & {} N\ln \left( \frac{V}{N}T^{3/2}\right) +N\ln [1+ x\left( \beta _1+\beta _2 \right) ]\nonumber \\{} & {} -3N\frac{x\left( \beta _1+\beta _2 \right) }{ 1+ x\left( \beta _1+\beta _2 \right) } +\frac{5}{2}N\nonumber \\{} & {} +\frac{3}{2}N\ln \frac{2\pi M}{\Lambda ^2}. \end{aligned}$$
(20)

One can easily see the GUP correction to the entropy embedded in parameter \(\beta _2\).

3.3 Internal energy

Utilizing the relations for free energy and entropy given in Eqs. (19) and (20), respectively, the GUP corrected internal energy for the system of galaxies can be derived using the relation, \(U=F+TS\), as

$$\begin{aligned} U=\frac{3}{2}NT\left[ 1-2\frac{ x\left( \beta _1+\beta _2 \right) }{ 1+ x\left( \beta _1+\beta _2 \right) }\right] . \end{aligned}$$
(21)

3.4 Pressure

The pressure is related to Helmholtz free energy via the relation \(P=-\left( \frac{\partial F}{\partial V}\right) _{N,T}\), which involves first derivative of free energy with respect to volume V keeping particle number (N) and temperature (T) static. Therefore, the pressure for the system of galaxies with GUP modified potential reads

$$\begin{aligned} P=\frac{NT}{V}\left[ 1-\frac{ x\left( \beta _1+\beta _2 \right) }{ 1+ x\left( \beta _1+\beta _2 \right) }\right] . \end{aligned}$$
(22)

The expression of pressure is quite standard as can been seen in [30]. The GUP modification is exhibited in \(\beta _2\).

3.5 Chemical potential

The chemical potential \((\mu )\) of the system of galaxies can be calculated using the standard relation \(\mu = \left( \frac{\partial F}{\partial N}\right) _{T, V}\) for the given F in Eq. (19) as following:

$$\begin{aligned} \mu= & {} T\left( \ln \frac{N}{V}T^{-3/2}\right) +T\ln \left[ 1-\frac{ x\left( \beta _1+\beta _2 \right) }{ 1+ x\left( \beta _1+\beta _2 \right) }\right] \nonumber \\{} & {} -T\frac{ x\left( \beta _1+\beta _2 \right) }{ 1+ x\left( \beta _1+\beta _2 \right) }-\frac{3}{2}T\ln \left( \frac{2\pi M}{\Lambda ^2}\right) . \end{aligned}$$
(23)

Here, in the second term of RHS, we have used simplification

$$\begin{aligned} - T \ln \ [1+ x (\beta _1+\beta _2)] =T\ln \left[ 1-\frac{ x (\beta _1+\beta _2 )}{ 1+ x (\beta _1+\beta _2 )}\right] . \end{aligned}$$

On the comparison of the equations of state, derived utilizing the GUP corrected potential, to their standard form [30], the effect of the correction on the clustering parameter \(B_{GUP}\) is seen, while the basic structure of the equations is preserved. The GUP modified clustering parameter is given by

$$\begin{aligned} B_{GUP}=\frac{ x\left( \beta _1+\beta _2 \right) }{ 1+ x\left( \beta _1+\beta _2 \right) }. \end{aligned}$$
(24)

In the limit of vanishing GUP, i.e. \(\beta _2 \rightarrow 0\), the GUP modified parameter, \(B_{GUP}\), matches with the original clustering parameter defined as [30]

$$\begin{aligned} b=\frac{ x \beta _1 }{ 1+ x \beta _1 }. \end{aligned}$$
(25)

The clustering parameter is important as it takes care of the clustering tendency of the system of gravitationally bound galaxies. The GUP modified clustering parameter in terms of original parameter is given by

$$\begin{aligned} B_{GUP}=\frac{ b+\left( 1-b\right) x\beta _2 }{ 1+ \left( 1-b\right) x\beta _2 }. \end{aligned}$$
(26)

In the limit \( b\rightarrow 0\), the clustering effect vanishes and the galaxies behave as a system of free particles.

4 GUP corrected distribution function

The probability distribution function F(N), which represents void distribution as well as counts of particle number (galaxies) in cells, wherein both particles (galaxies) as well as energy is exchanged between the system and surroundings, can be calculated utilizing grand canonical ensemble. In this section, we analyse the effect of GUP correction in the gravitational potential on the distribution function. The grand canonical partition function (a weighted sum of all canonical partition functions) is given by

$$\begin{aligned} Z_G(T,V,z)=\sum _{N=0}^{\infty } e^{\frac{N\mu }{T}}Z_N(T,V), \end{aligned}$$
(27)

where z is the activity of the system defined by \(z=\exp (\frac{\mu }{T})\).

Now, the probability of finding N-galaxies in a cell of volume V of grand canonical ensemble can be estimated by the following relation:

$$\begin{aligned} F(N)=\frac{\sum _{i}^{}e^{\frac{N\mu }{T}}e^{\frac{U_i}{T}}}{Z_G(T,V,z)}= \frac{e^{\frac{N\mu }{T}}Z_N(T,V)}{Z_G(T,V,z)}. \end{aligned}$$
(28)

The partition function in grand canonical ensemble for the gravitating system under GUP modified Newton’s potential is calculated by

$$\begin{aligned} \log Z_G={\bar{N}}(1-B_{GUP}), \end{aligned}$$
(29)

here, \({\bar{N}}\) refers to the average number of galaxies as system follows grand canonical ensemble.

Using Eqs. (17), (28) and (29), the GUP modified distribution function for the system of galaxies is given as

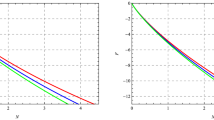
$$\begin{aligned} F(N)= & {} \frac{{\bar{N}}}{N!}(1-B_{GUP})[{\bar{N}}(1-B_{GUP})\nonumber \\{} & {} +NB_{GUP}]^{N-1}e^{-NB_{GUP}-{\bar{N}}(1-B_{GUP})}. \end{aligned}$$
(30)

Remarkably, the basic structure of the distribution function is same to that derived originally by Ahmad et al. [30] and Saslaw and Hamilton [32]. The only difference to the original one is the GUP modified clustering parameter. In order to see the effect of GUP on the distribution function, we plot Fig. 2. From the plot, we confirm that as long as the value of correction parameter increases the maximum (peak) value of F(N) decreases without changing the basic structure of the curve.

Fig. 2
figure 2

Behaviour of the distribution function F(N) as a function of particle number N. Red, blue and green curves represent three different values for the correction parameter \(\beta _2\). Red curve is for \(\beta _2=0\) (i.e. no GUP correction), blue for \(\beta _2=0.5\), and green for \(\beta _2=1\)

Full size image

5 GUP effects on power-law for two-point correlation function

In this section, we study the effect of GUP correction to the power law of the two-point correlation function. Peeble’s assumption about the power-law form of the correlation function [33] has been confirmed via N-body computer simulations [34] as well as analytically in [35]. In order to see the effect of the correction on the correlation function \(\xi _2\), we write the clustering parameter in the form [35]

$$\begin{aligned} B_{GUP}= & {} \frac{{GM^2}{{{\bar{N}}}}}{6T}\int _V \left[ \frac{1}{(R^2+\epsilon ^2)^{1/2}}\right. \nonumber \\{} & {} \left. + \frac{2L_P^2}{3(R^2+\epsilon ^2)^{3/2}}\right] \xi _2 ({{{{\bar{N}}}}, R},T) dV, \end{aligned}$$
(31)
$$\begin{aligned}= & {} \frac{2\pi GM^2 {\bar{N}}}{3T}\int \Bigg [\frac{1}{(R^2+\epsilon ^2)^{1/2}} \nonumber \\{} & {} + \frac{2L_P^2R^2}{3(R^2+\epsilon ^2)^{3/2}}\Bigg ]\xi _2({{{\bar{N}}}},R,T) dR, \end{aligned}$$
(32)

where \({\bar{N}} =N/V\) is the number density.

Fig. 3
figure 3

The plots show the probability distribution function of galaxy clusters in red-shift bins and radius bins. The dotted lines represent the observational data points whereas the solid lines represent the theoretical model considered here

Full size image
Fig. 4
figure 4

The plots show the probability distribution function of galaxy clusters in red-shift bins and radius bins. The dotted lines represent the observational data points whereas the solid lines represent the theoretical model considered here

Full size image

Differentiating (31) with respect to V and using \(\frac{\partial V}{\partial {{\bar{N}}}} =-\frac{V}{{\bar{N}}}\), the expression (31) yields

$$\begin{aligned}{} & {} \frac{{{\bar{N}}}}{V} \frac{\partial }{\partial {{\bar{N}}}} B_{GUP} = \frac{ B_{GUP}}{ V }\nonumber \\{} & {} \quad - \frac{{GM^2}{{{\bar{N}}}}}{6T} \left[ \frac{1}{(R^2+\epsilon ^2)^{1/2}}+\frac{2L_P^2}{3 (R^2+\epsilon ^2)^{3/2}} \right] \xi _2({{{{\bar{N}}}}, R},T).\nonumber \\ \end{aligned}$$
(33)

This above equation upon further simplification gives the following GUP modified two-point function:

$$\begin{aligned} \xi _2 = \frac{{9T} B_{GUP}^2 }{{GM^2}{{{\bar{N}}}} \left[ \frac{2\pi R^3}{(R^2+\epsilon ^2)^{1/2}}+\frac{4\pi R^3L_P^2}{3 (R^2+\epsilon ^2)^{3/2}} \right] }. \end{aligned}$$
(34)

In the limit of point-mass galaxies, the above relation reduces to

$$\begin{aligned} \xi _2= & {} \frac{{9T} B_{GUP}^2 }{{GM^2}{{\bar{\rho }}} \left( 2\pi R^2 +\frac{4\pi \beta R^2}{3 } \right) },\nonumber \\= & {} \frac{{9T} B_{GUP}^2 }{2\pi {GM^2}{{\bar{\rho }}} R^2 }\left( 1 -\frac{2 }{3 } \beta \right) . \end{aligned}$$
(35)

The extra term in the power-law is due to the GUP correction to the Newtonian potential. In the limit of vanishing GUP parameter \(\beta \), one can recover power-law of Newtonian gravity.

6 Data

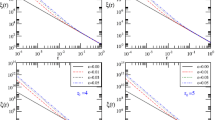
Here we test our model with the data available through Sloan Digital Sky Survey (SDSS-III). The data is available in the data release 12 (DR12). All the necessary data (RA, DEC, z, N etc) is present in the catalog [36] for 132,684 clusters of galaxies in the redshift ranges of \(0.05<z<0.65\). Here we have divide the data in three radius bins (measured in Mpc), \(0.40<R<0.75\), \(0.75<R<1.10\), \(1.10<R<1.45\) and six redshift bins, \(0.05<z<0.15\), \(0.15<z<0.25\), \(0.25<z<0.35\), \(0.35<z<0.45\), \(0.45<z<0.55\) and \(0.55<z<0.65\).

Using the Scipy.optimize.curve_fit API of SciPy python Library we calculated the optimized value of the clustering parameter \(B_{GUP}\). From the plots (Figs. 3 and 4) it can been seen that the fit is accurate in many redshift bins but in the redshift bins \(0.45<z<0.55\) and \(0.55<z<0.65\) within the radius bin \(0.40<R<0.75\). In Fig. 3e, f, the model does not fit properly to the data. The reason could be incomplete sampling of the catalog at low radius and high red-shift range (Tables 1, 2).

Table 1 The table shows different parameters such as number of clusters \(N_{cl}\), number of galaxies \(N_G\), mean number of galaxies per cluster \({\bar{N}}\) and the value of the clustering parameter \(B_{GUP}\) in various radius and red-shift bins
Full size table

Once the optimal value of the clustering parameter is obtained, the value of \(\beta _2\), the GUP correction term, can be easily determined after fixing the values of \(\beta _1\) and x in Eq. (24). Setting the value of \(\beta _1\) and x to unity, the value of \(\beta _2\) in terms of \(B_{GUP}\) can be written as;

$$\begin{aligned} \beta _2=\frac{2B_{GUP}-1}{1-B_{GUP}}. \end{aligned}$$
(36)
Table 2 The table shows various values of \(\beta _2\) for different values of clustering parameter \(B_{GUP}\)
Full size table

The variation of clustering parameter \(B_{GUP}\) with the correction term \(\beta _2\) can be visualized in the Fig. 5.

Fig. 5
figure 5

The variation of correction term \(\beta _2\) with clustering parameter \(B_{GUP}\)

Full size image

7 Conclusion

In Ref. [29], the possibility to apply GUP corrected (entropic) force to the Hubble horizon is discussed. In fact, a non-zero GUP correction to the thermodynamic force is obtained in the context of cosmology. This corrected entropic force gives a corrected Newton’s law of gravity. In this work, we presented a study of clustering of galaxies under the GUP modified Newton’s law. It is observed that the corrected Newtonian potential modify the clustering parameter, which reflects the effect of correction on the clustering. We calculated the grand canonical partition function for the system of gravitationally interacting galaxies. The grand partition function was used to calculate the various GUP corrected thermodynamic quantities like Helmholtz free energy, entropy, pressure, and chemical potential. The GUP corrected general distribution function and the power-law for the two-point correlation function are also calculated. A comparison of the equations of state with their standard form [30] is made and has been found that the equations of state follows the same structure to the original one except of the clustering parameter. We also analyzed the data and compared it with the model to get the optimal value of the clustering parameter \(B_{GUP}\). We could see the model fits the data except in a few redshift ranges e.g., \(0.45<z<0.55\) for the radius range \(0.40<R<1.10\).