Abstract
Poor computing efficiency of precision event generators for LHC physics has become a bottleneck for Monte-Carlo event simulation campaigns. We provide solutions to this problem by focusing on two major components of general-purpose event generators: The PDF evaluator and the matrix-element generator. For a typical production setup in the ATLAS experiment, we show that the two can consume about 80% of the total runtime. Using NLO simulations of \(pp\rightarrow \ell ^+\ell ^-+\text {jets}\) and \(pp\rightarrow t\bar{t}+\text {jets}\) as an example, we demonstrate that the computing footprint of Lhapdf and Sherpa can be reduced by factors of order 10, while maintaining the formal accuracy of the event sample. The improved codes are made publicly available.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Particle colliders have long dominated efforts to experimentally probe fundamental interactions at the energy frontier. They enable access to the highest energy scales in human-made experiments, at high collision rates and in controlled conditions, allowing a systematic investigation of the most basic laws of physics. Event-generator programs have come to play a crucial role in such experiments, starting with the use of early event generators such as JETSET [1] and HERWIG [2] in the discovery of the gluon at the PETRA facility in 1979.
Today, with the Large Hadron Collider (LHC) having operated successfully for over a decade at nearly 1000 times the energy of PETRA, event generators are an ever more important component of the software stack needed to extract fundamental physics parameters from experimental data [3, 4]. Most experimental measurements rely on their precise modelling of complete particle-level events on which a detailed detector simulation can be applied. The experimental demands on these tools continue to grow: the precision targets of the high-luminosity LHC (HL-LHC) [5] will require both high theoretical precision and large statistical accuracy, presenting major challenges for the currently available generator codes. With much of the development during the past decades having focused on improvements in theoretical precision – in terms of the formal accuracy of the elements of the calculation – their computing performance has become a major concern [6,7,8,9].
Event generators are constructed in a modular fashion, which is inspired by the description of the collision events in terms of different QCD dynamics at different energy scales. At the highest scales, computations can be carried out using amplitudes calculated in QCD perturbation theory. These calculations have been largely automated in matrix-element generators, both at leading [10,11,12,13,14], and at next-to-leading [15,16,17,18,19,20] orders in the strong coupling constant, \(\alpha _s\). Matrix-element generators perform the dual tasks of computing scattering matrix elements fully differentially in the particle momenta, as well as integrating these differential functions over the multi-particle phase space using Monte Carlo (MC) methods.
In principle, such calculations can be carried out for an arbitrary number of final-state particles; in practice, the tractable multiplicities are very limited. The presence of quantum interference effects in the matrix elements induces an exponential scaling of computation complexity with the number of final-state particles. This problem is exacerbated further by the rise of automatically calculated next-to-leading order (NLO) matrix elements in the QCD and electroweak (EW) couplings, which not only have a higher intrinsic cost from more complex expressions, but are also more difficult to efficiently sample in phase-space, and introduce potentially negative event weights which reduce the statistical power of the resulting event samples. While theoretical work progresses on these problems, e.g. by the introduction of rejection sampling using neural network event-weight estimates [21], modified parton-shower matching schemes [22, 23] and resampling techniques [24, 25], the net effect remains that precision MC event generation comes at a computational cost far higher than in previous simulation campaigns. Indeed, it already accounts for a significant fraction of the total LHC computing budget [9, 26], and there is a real risk that the physics achievable with data from the high-luminosity runs of the LHC will be limited by the size of MC event samples that can be generated within fixed computing budgets. It is therefore crucial that dedicated attention is paid to issues of computational efficiency.
In this article, we focus on computational strategies to improve the performance of particle-level MC event generator programs, as used to produce large high-precision simulated event samples at the LHC. While the strategies and observations are of a general nature, we focus our attention on concrete implementations in the Sherpa event generator [27] and the Lhapdf library for parton distribution function (PDF) evaluation [28]. Collectively, this effort is aimed at solving the current computational bottlenecks in LHC high-precision event generation. Using generator settings for standard-candle processes from the ATLAS experiment [29] as a baseline, we discuss timing improvements related to PDF-uncertainty evaluation and for event generation more generally. Overall, our new algorithms provide speedups of a factor of up to 15 for the most time-consuming simulations in typical configurations, in time for the LHC Run-3 event-generation campaigns.
This manuscript is structured as follows: Section 2 discusses refinements to the Lhapdf library, including both intrinsic performance improvements and the importance of efficient call strategies. Section 3 details improvements of the Sherpa event generator. Section 4 quantifies the impact of our modifications. In Sect. 5 we discuss possible future directions for further improvements of the two software packages, and Sect. 6 provides an outlook.
2 Lhapdf performance bottlenecks and improvements
While the core machinery of event generators for high-energy collider physics is framed in terms of partonic scattering events, real-world relevance of course requires that the matrix elements be evaluated for colliding beams of hadrons. This is typically implemented through use of the collinear factorisation formula for the differential cross section about a final-state phase-space configuration \(\Phi \),
where \(x_{a,b}\) are the light-cone momentum fractions of the two incoming partons a and b with respect to their parent hadrons \(h_1\) and \(h_2\), and \(\mu _\textrm{R,F} \) are the renormalisation and factorisation scales, respectively. Assuming negligible transverse motion of the partons, this formula yields the hadron-level differential cross section \({\textrm{d}}{\sigma }\) as an integral over the initial-state phase-space, summed over a and b, weighting the differential squared matrix-element \(\textrm{d}\hat{\sigma }\) by the collinear parton densities (PDFs) f for the incoming beams. These PDFs satisfy the evolution equations [30,31,32,33]
with the evolution kernels, \(P_{ab}(z)\), given as a power series in the strong coupling, \(\alpha _s\).
In MC event-generation, the integrals in Eqs. (2.1) and (2.2) are replaced by MC rejection sampling, meaning that a set of PDF values \(f_{a}^{h}(x,\mu _\textrm{F})\) must be evaluated at every sampled phase-space point, for both beams. PDFs are hence among the most intensely called functions within an event generator code, comparable with the partonic matrix-element itself. In particular, Eq. (2.2) is iteratively solved by the backward evolution algorithm of initial-state parton showers [34], requiring two PDF calls per trial emission [35].
This intrinsic computational load is exacerbated by the additional factors that 1) the non-perturbative PDFs are not generally available as closed-form expressions, but as discretised grids of \(f_{}^{}{}(x_i,Q^2_i)\) values obtained from fits to data via QCD scale-evolution, and 2) the PDF fits introduce many new sources of systematic uncertainty, which are typically encoded via \(\mathcal {O}(10\text {--}100)\) alternative sets of PDF functions to be evaluated at the same \((x,Q^2)\) points. In LHC MC-event production, these grids are interpolated to provide PDF values and consistent values of the running coupling, \(\alpha _s\), through continuous \((x,Q^2)\) space by the Lhapdf library.
The starting point for this work is Lhapdf version 6.2.3, the C++ Lhapdf 6 lineage being a redevelopment of the Fortran-based Lhapdf \(\leqslant 5\) series. The Fortran series relied on each PDF fit being supplied as a new subroutine by the fitting group; in principle these used a common memory space across sets, but in practice many separate such memory blocks were allocated, leading to problematically high memory demands in MC-event production. The C++ series has a more restrictive core scope, using dynamic memory allocation and a set of common interpolation routines to evaluate PDF values from grids encoded in a standard data format. Each member of a collinear PDF set is a set of functions \(f_a^h(x, Q^2)\) for each active parton flavour, a, and is independently evaluated within Lhapdf.
The most heavily used interpolation algorithm in Lhapdf is a 2D local-cubic polynomial [36] in \((\log x, \log Q^2)\) space, corresponding to a composition of 1D cubic interpolations in first the x and then the \(Q^2\) direction on the grid. As each 1D interpolation requires the use of four \(f_{a}^{}(x_i,Q_j^2)\) knot values, naively 16 knots are needed as input to construct 4 values at the same x value, used as the arguments for the final 1D interpolation in \(\log Q^2\). The end result is a weighted combination of the PDF values on the 16 knots surrounding the interpolation cell of interest, with the weights as functions of the position of the evaluated point within the cell.
2.1 PDF-grid caching
The first effort to improve Lhapdf ’s evaluation efficiency was motivated by the sum over initial-state flavours in Eq. (2.1), implying that up to 11 calls (for each parton flavour, excluding the top quark) may be made near-consecutively for a fixed \((x,Q^2)\) point within the same PDF.
If such repeated calls use the same \((x,Q^2)\) knot positions for all flavours (which is nearly always the case), much of the weight computation described above can be cached and re-used with a potential order-of-magnitude gain. Such a caching was implemented, with a dictionary of cyclic caches stored specific to each thread and keyed on a hash-code specific to the grid spacing: this ensures that the caching works automatically across different flavours if they use the same grid geometry but does not return incorrect results should that assumption be incorrect. This implementation also has the promising side-effect that, if the set of fit-variation PDFs also use the same grid spacing as the nominal PDF, consecutive accesses of the same \((x,Q^2)\) across possibly hundreds of PDFs would also automatically benefit from the caching.
The practicality of a cache implementation in Lhapdf (with no restructuring of the call patterns from Sherpa) was investigated using the \(e^+ e^-\)+jets setup described below and a 64-entry cyclic cache. This cache is too large to obtain any performance benefits but was useful to explore the caching behaviour. 57% of x and 54% of \(Q^2\) lookups were located within the 64-entry cache. Of these successful cache-hits, the cumulative probability of an x hit rose linearly from 10% in the first check to 50% by the 6th check before slowing down (90% by the 51st check), as illustrated in Fig. 1. For \(Q^2\), the cumulative probability was already at 80% by the third check (90% by the 13th check).
Despite this promise, this caching feature as implemented in Lhapdf 6.3.0 transpired to add little if anything in practical applications with Sherpa generation of these ATLAS-like \(e^+ e^-\)+jets MC events. With a cache depth of 4, the time spent in Lhapdf in the call-stack reduced marginally by a relative 5%, this overall reduction is small due to 29% of the time spent in Lhapdf now being under the newly added _getCacheX and _getCacheQ2 functions. This indicates that, given the Sherpa request pattern, the cost of executing the caching implementation is somewhat comparable to the cost of re-interpolating the quantity.
This experience of caching as a strategy to reduce PDF-interpolation overheads in realistic LHC use-cases highlights the importance of well-matched PDF-call strategies in the event generator. We return to this point later.
2.2 Memory structuring and return to multi-flavour caching
The C++ rewrite of Lhapdf placed emphasis on flexibility and “pluggability” of interpolators to accommodate fitting groups’ requirements, allowing the use of non-uniform grid spacings, functional discontinuities across flavour thresholds, and even different grids for each parton flavour [28], at the cost of a fragmented memory layout. However, much of this flexibility has in practice gone unused.
By disabling the possibility to have fragmented knots for differing flavours, the knots are now stored in a single structure for all flavours. Similarly, the PDF grids are stored in a combined data-structure. This will allow for very efficient caching and even memory accesses due to the contiguous memory layout.
With the observed shortcomings in the caching-strategy implemented in Lhapdf 6.3.0, as described above, in Lhapdf 6.4.0, the caching mechanism focuses on multi-flavour PDFs that are called for explicitly. In this case, large parts of the computations can be shared between the different flavour PDF (for example finding the right knot-indices and computing spacings) due to the fact that the grids have been unified. In principle, the caching of shared computations among the variations is still desirable, given that many variations share grids. However as discussed above, the call strategy of the generator then has to be structured (or, restructured) with this in mind in order to make this caching efficient.
2.3 Finite-difference precomputations
Additionally to the reworked caching strategy, Lhapdf 6.4.0 pre-computes parts of the computations and stores the results. Due to the way the local-cubic polynomial interpolation is set up, the first set of interpolations are always computed along the grid lines. Since these are always the same, in Lhapdf 6.4.0 the coefficients of the interpolation polynomial are pre-computed for the grid-aligned interpolations. This comes with the drawback of the additional memory space that is required to store the coefficients, but it also reduces the interpolation to simply the evaluation of a cubic polynomial (compared to first constructing said polynomial, and then evaluating it). The precomputations reduce the number of “proper” interpolations (in the sense that the interpolation polynomial has to be constructed) from five to one.
Because of these precomputations and the above described memory restructurings, computing the PDF becomes up to a factor of \(\sim \!3\) faster for a single flavour, and with the combination of the multi-flavour caching, computing the PDFs for for all flavours becomes roughly \(\sim \!10\) faster.
3 Sherpa performance bottlenecks and improvements
The computing performance of various LHC event generators was investigated in a recent study performed by the HEP software foundation [7,8,9]. This comparison prompted a closer inspection of the algorithms used and choices made in the Sherpa program. In this section we will briefly review the computationally most demanding parts of the simulation, provide some background information on the physics models, and offer strategies to reduce their computational complexity.
We will focus on the highly relevant processes \(pp\rightarrow \ell ^+\ell ^-+\text {jets}\) and \(pp\rightarrow t\bar{t}+\text {jets}\), described in detail in Sect. 4. They are typically simulated using NLO multi-jet merged calculations with EW virtual corrections and include scale as well as PDF variations. The baseline for our simulations is the Sherpa event generator, version 2.2.11 [37]. In the typical configuration used by the ATLAS experiment, it employs the Comix matrix element calculator [13] to compute leading-order cross sections with up to five final-state jets in \(pp\rightarrow \ell ^+\ell ^-+\text {jets}\) and four jets in \(pp\rightarrow t\bar{t}+\text {jets}\). Next-to-leading order precision in QCD is provided for up to two jets in \(pp\rightarrow \ell ^+\ell ^-+\text {jets}\) and up to one jet in \(pp\rightarrow t\bar{t}+\text {jets}\) with the help of the Open-Loops library [18, 38] for virtual corrections and an implementation of Catani–Seymour dipole subtraction in Amegic [39] and Comix. The matching to a Catani–Seymour based parton shower [40] is performed using the S–Mc@Nlo technique [41, 42], an extension of the Mc@Nlo matching method [43] that implements colour and spin correlations in the first parton-shower emission, in order to reproduce the exact singularity structure of the hard matrix element. In addition, EW corrections and scale-, \(\alpha _s\)- and PDF-variation multiweights are implemented using the techniques outlined in [44,45,46]. A typical setup includes of the order of two hundred multiweights, most of which correspond to PDF variations.
We visualize the imperfect interplay between Sherpa and Lhapdf in Fig. 2. For this test, Sherpa 2.2.11 was compiled against Lhapdf 6.2.3 and Open-Loops 2.1.2 [18, 38]. The performance of generating 1000 partially unweighted MC eventsFootnote 1 was then profiled with the Intel® VTune™ profiler running on a single core of a 2.20GHz Intel®Xeon®E5-2430. The Sherpa run card contains a representative \(pp \rightarrow e^+ e^- + 0,1,2j\)@NLO\(+3,4,5j\)@LO setup at \(\sqrt{s} = 13\) \(\text {TeV} \), including electroweak virtual corrections as well as reweightings to different PDFs and scales; comparable to the setup used in production by the ATLAS collaboration at the time. The total processing time was around 18.5 hours.
The obtained execution profile is visualized in Fig. 2 as a flame-graph [52] where the proportion of the x-axis reflects the proportion of wall-time spent inside a given function, and where the call-stack extends up the y-axis. Calls from Sherpa into the Lhapdf library are highlighted in blue. In total, 79% of the execution time was spent in Lhapdf, with libLHAPDFSherpa.so!PDF::LHAPDF_CPP_Interface::GetXPDF representing the dominant interface call.
In the following, we discuss in detail the major efficiency improvements that have been implemented on the Sherpa side, including the solution to spending so much execution time within Lhapdf. In addition to the major changes, also some minor improvements have been developed, which account for a collective runtime savings of 5-10%. A notable example is the introduction of a cache for the partonic channel selection weights, reducing the necessity to resolve virtual functions in inheritance structures.
3.1 Leading-colour matched emission
A simple strategy to improve the performance of the S–Mc@Nlo matching was recently discussed in [23]. Within the S–Mc@Nlo technique, one requires the parton shower to reconstruct the exact soft radiation pattern obtained in the NLO result. In processes with more than two coloured particles, this leads to non-trivial radiator functions, which are given in terms of eikonals obtained from quasi-classical currents [53]. Due to the involved colour structure of the related colour insertion operators, the radiation pattern can typically not be captured by standard parton shower algorithms. The S–Mc@Nlo technique relies on weighted parton showers [54] to solve this problem. As both the sign and the magnitude of the colour correlators can differ from the Casimir operator used in leading colour parton showers, the weights can become negative and are in general prone to large fluctuations that need to be included in the overall event weight, thus lowering the unweighting efficiency and reducing the statistical power of the event sample.
This problem can be circumvented by assuming that experimentally relevant observables will likely not be capable of resolving the details of soft radiation, and that colour factors in the collinear (and soft-collinear) limit are given in terms of Casimir operators. This idea is also used in the original Mc@Nlo method [43] to enable the matching to parton showers which do not have the correct soft radiation pattern. Within Sherpa, the S–Mc@Nlo matching is simplified to an Mc@Nlo matching, dubbed \(\langle \text {LC}\rangle \)–Mc@Nlo here, using the setting NLO_CSS_PSMODE=1. Without further colour correlators, no additional weight is added, making the unweighting procedure more efficient.
With S–Mc@Nlo , the parton shower needs information about soft-gluon insertions into the Born matrix element, which makes the first step of the parton shower dependent on the matrix-element generator. In fact, within Sherpa the first emission is generated as part of the matrix-element simulation by default. When run in \(\langle \text {LC}\rangle \)–Mc@Nlo mode, the dependence of the parton shower on the matrix-element generator does not exist. Using the flag NLO_CSS_PSMODE=2, the user can then include the generation of the first emission into Sherpa ’s standard Catani–Seymour shower (Css). We will call this configuration \(\langle \text {LC}\rangle \)–Mc@ Nlo–Css in the following. The first emission is then performed after the unweighting step, such that it is not generated any longer for events that might eventually be rejected. This simplification leads to an additional speedup.
The above argument is also employed for spin correlations in collinear gluon splittings, which are normally included in S–Mc@Nlo . Assuming experimentally relevant observables to be insensitive to it, we reduce the corresponding spin-correlation insertion operators to their spin-averaged counterparts present in standard parton shower algorithms in the \(\langle \text {LC}\rangle \)–Mc@Nlo and \(\langle \text {LC}\rangle \)–Mc@ Nlo–Css implementations.
3.2 Pilot-run strategy
In the current implementation of Sherpa ’s physics modules and interfaces to external libraries, physical quantities and coefficients that are needed later in the specified setup, e.g.@ to calculate QCD scale and PDF variations and other alternative event weights such as approximate EW corrections (\(\text {EW}_\text {virt}\)), are calculated when the program flow passes through the specific module or interface. While this is the most efficient strategy for weighted event generation and allows for easy maintainability of the implementation, it is highly inefficient in both partially or fully unweighted event generation and in fact responsible for most of the large fraction of computing time spent in Lhapdf calls in Fig. 2. This is because the unweighting is based solely on the nominal event weight and these additional quantities and coefficients will only be used once an event has been accepted and are thus calculated needlessly for events that are ultimately rejected in the unweighting step.
To improve code performance for (partially) unweighted event generation without compromising on maintainability, we thus introduce a pilot run. This reduces the number of coefficients to be calculated to a minimal set until an event has been accepted. Once such an event is found, we recompute this exact phase space point including all later-on desired coefficients. Thus, the complete set of variations and alternative event weights is computed only for the accepted event, while no unnecessary calculations are performed for the vast number of ultimately rejected events.
The pilot-run strategy is introduced in Sherpa-2.2.12 and is used automatically for (partially) unweighted event generation that includes variations.
3.3 Analytic virtual corrections
Over the past decades fully numerical techniques have been developed to compute nearly arbitrary one-loop amplitudes [15, 16, 18,19,20, 38, 55,56,57,58,59,60,61,62,63,64,65,66,67]. The algorithmic appeal of these approaches makes them prime candidates for usage in LHC event generators. Their generality does, however, come at the cost of reduced computing efficiency in comparison to known analytic results. In addition, the numerical stability of automated calculations can pose a problem in regions of phase space where partons become soft and/or collinear, or in regions affected by thresholds. Within automated approaches, these numerical instabilities can often only be alleviated by switching to higher numerical precision, while for analytic calculations, dedicated simplifications or series expansions of critical terms can be performed. For the small set of standard candle processes at the LHC that require high fidelity event simulation, one may therefore benefit immensely from the usage of the known analytic one-loop amplitudes.
Most of the known analytic results of relevance to LHC physics are implemented in the Monte Carlo for FeMtobarn processes (Mcfm) [68,69,70,71]. A recent project made these results accessible for event generation in standard LHC event generators [72] through a generic interface based on the Binoth Les Houches Accord [73, 74]. A similar interface to analytic matrix elements was provided in the Black Hat library [15].
Since Mcfm does not provide the electroweak one-loop corrections which are relevant for LHC phenomenology in the high transverse momentum region, we use the interface to analytic matrix elements primarily for the pilot runs before unweighting. The full calculation, including electroweak corrections, is then performed with the help of Open-Loops. This switch is achieved by the setting Pilot_Loop_Generator=MCFM.
3.4 Extending the pilot run strategy to reduce jet clustering
For multijet-merged runs using the CKKW-L algorithm [75, 76], the final-state configurations are re-interpreted as having originated from a parton cascade [77]. This is called clustering, and the resulting parton shower history is used to choose an appropriate renormalisation scale for each strong coupling evaluation in the cascade, thus resumming higher-order corrections to soft-gluon radiation [78]. This procedure is called \(\alpha _s\)-reweighting. The clustering typically requires the determination of all possible parton-shower histories, to select one according to their relative probabilities [76, 77]. The computational complexity therefore grows quickly with the number of final-state particles [26]. It can take a significant share of the computing time of a multi-jet merged event, as we will see in Sect. 4.
To alleviate these problems, we have implemented a procedure which uses a surrogate scale choice for the pilot events, while the \(\alpha _s\) reweighting is only done once an event has been accepted, thus avoiding the need to determine clusterings for the majority of trial events. The surrogate scale is defined as
and where j runs over all particles in the final state. In the case of Drell–Yan lepton pair production, the two leptons are combined into a pseudoparticle before computing Eq. (3.1). This functional form of the scale is inspired by various studies in which parton shower predictions and fixed-order results have been compared and found to be in good agreement [79, 80]. It was first proposed in fixed-order studies of W/Z+3 jets [55, 56, 81]. Contrary to the improvements discussed in Sect. 3.2, the usage of a surrogate scale changes the weight of the event. To account for this change, the ratio of the two different cross sections before and after the unweighting must either be used as an additional event weight, or as the basis of an additional second unweighting procedure. In our implementation, we chose the former procedure, expecting a rather peaked weight distribution, such that additional event processing steps (such as a detector simulation) retain a high efficiency even though the events do not carry a constant weight.
4 Observed performance improvements
In this section we investigate the impact of the performance improvements detailed in Sects. 2 and 3. As test cases we use the following setups:
- \(pp \rightarrow e^+e^- + 0,1,2j\text {@NLO}+3,4,5j\text {@LO}\):
-
Drell–Yan production at 13 TeV at the LHC. We bias the partially unweighted event distribution in the maximum of the scalar sum of all partonic jet transverse momenta (\(H_\textrm{T}\)) and the transverse momentum of the lepton pair (\(p_\textrm{T}^V\)), leading to a statistical over-representation of multijet events.
- \(pp \rightarrow t\bar{t} + 0,1j\text {@NLO}+2,3,4j\text {@LO}\):
-
Top-pair production at 13 TeV at the LHC. We bias the partially unweighted event distribution in the maximum of the scalar sum of all non-top partonic jet transverse momenta (\(H_\textrm{T}\)) and the average top-quark (\((p_\textrm{T}^t + p_\textrm{T}^{\bar{t}})/2\)), leading to a statistical over-representation of multijet events.
In each case, the different multiplicities at leading and next-to-leading order are merged using the Me Ps@ Nlo algorithm detailed in [47,48,49]. The setups for both processes reflect the current usage of Sherpa in the ATLAS experiment, and have also been used for a study on the reduction of negative event weights [23]. The corresponding runcards can be found in App. A.
The performance is measured in five variations of the two process setups, with an increasing number of additionally calculated event weights corresponding to QCD variations (scale factors and PDFs) and approximative EW corrections (\(\text {EW}_\text {virt}\)):
- no variations:
-
No variations, only the nominal event weight is calculated.
- \(\text {EW}_\text {virt}\):
-
Additionally, \(\text {EW}_\text {virt}\) corrections are calculated. This requires the evaluation of the EW virtual correction and subleading Born corrections. In particular the evaluation of the virtual part has a significant computational cost. As for the scale and PDF variations, \(\text {EW}_\text {virt}\) corrections are encoded as alternative weights and are not applied to the nominal event weight used for the unweighting.
- \(\text {EW}_\text {virt}\)+scales:
-
Additionally, 7-point scale variations are evaluated, both for the matrix-element and the parton-shower parts of the event generation [46]. This includes the re-evaluation of couplings (when varying the renormalisation scale) and PDFs (when varying the factorisation scale), of which the latter are particularly costly.
- \(\text {EW}_\text {virt}\)+scales+100 PDFs:
-
Additionally, variations are calculated for 100 Monte-Carlo replica of the used PDF set (NNPDF30_nnlo_ as_0118 [82]). This again requires the re-evaluation of the PDFs both in the matrix element and the parton shower. As for the scale variations, the cost scales approximately linearly with the number of variations. Note that this setup variation is closest to what would be typically used in an ATLAS vector-boson or top-pair productions setup, which might however feature a number of PDF variations which is closer to 200.
- \(\text {EW}_\text {virt}\)+scales+1000 PDFs:
-
This setup variation is similar to the previous, with the only difference being that the 1000 instead of the 100 Monte-Carlo replica error set of the NNPDF30_nnlo_as_0118 PDF set is used.
The impact of the performance improvements is investigated in seven steps, with each step adding a new improvement as follows:
- Me Ps@ Nlo baseline:
-
This is our baseline setup, using the pre-improvement versions of Sherpa 2.2.11 and Lhapdf 6.2.3, i.e using the CKKW scale setting procedure throughout as well as the standard S–Mc@Nlo matching technique. All one-loop corrections are provided by Open-Loops.
 Lhapdf 6.4.0:
Lhapdf 6.4.0:-
The version of Lhapdf is increased to Lhapdf 6.4.0, implementing the improvements of Sect. 2.
 \(\langle \text {LC}\rangle \)–Mc@Nlo:
\(\langle \text {LC}\rangle \)–Mc@Nlo:-
The full-colour spin-correlated S–Mc@Nlo algorithm is reduced to its leading-colour spin-averaged cousin, \(\langle \text {LC}\rangle \)–Mc@Nlo, which however is still applied before the unweighting. Note that this is the only step where a physics simplification occurs. For details see Sect. 3.1.
 pilot run:
pilot run:-
The pilot run strategy of Sect. 3.2 is enabled, minimising the number of coefficients and variations needlessly computed for events that are going to be rejected in the unweighting step.
 \(\langle \text {LC}\rangle \)–Mc@ Nlo–Css :
\(\langle \text {LC}\rangle \)–Mc@ Nlo–Css :-
The \(\langle \text {LC}\rangle \)–Mc@Nlo matching is moved into the standard Css parton shower, i.e it is now applied after the unweighting.
 Mcfm:
Mcfm:-
During the pilot run, the automatically generated one-loop QCD matrix elements provided by Open-Loops are replaced by the manually highly optimised analytic expressions encoded in Mcfm. Once the event is accepted, Open-Loops continues to provide all one-loop QCD and EW corrections, see Sect. 3.3.
 pilot scale:
pilot scale:-
Events are unweighted using a simple scale that depends solely on the kinematics of the final state and, thus, does not require a clustering procedure. The correct dependence on the actual factorisation and renormalisation scales determined through the CKKW algorithm is then restored through a residual event weight. For details see Sect. 3.4.
For the benchmarking, a dedicated computer is used with no additional computing load present during the performance tests. The machine uses an Intel®Xeon®E5-2430 with a 2.20 GHz clock speed. Local storage is provided through a RAID 0 array of a pair of Seagate®\(2.5^{\prime \prime }\) 600GB 10kRPM hard-drive with a 12Gb/s SAS interface. Six 8GB DD3 dual in-line memory modules with 1333 million transfers per second are used for dynamic volatile memory.
Reduction in overall run time for different performance improvements, combined with the breakdown of the overall run time into a high-level calculation composition. The timing is assessed by producing 5000 partially unweighted particle-level events for \(pp \rightarrow e^+e^- + 0,1,2j\)@NLO\({}+3,4,5j\)@LO using Me Ps@ Nlo. The scaling with the number of additional variation weights is benchmarked through a few representative setup configurations
4.1 \(pp \rightarrow e^+e^- + 0,1,2j\text {@NLO}+3,4,5j\text {@LO}\).
We begin our analysis by examining the behaviour of the \(e^+e^- + \text {jets}\) setup. Figure 3 shows the impact of each improvement on the total run time to generate 5000 partially unweighted events on the left side, and the composition of these run times for each of the seven steps, respectively, on the right side. For the total run times, horizontal error bars indicate a 10% uncertainty estimate.
First, we note that using Lhapdf 6.4 reduces the overall run time by about 40-50% when many PDF variations are used, i.e. for the setup variants with 100 and 1000 PDF variations. Unsurprisingly, the proportion of total runtime dedicated to PDF evaluation shrinks accordingly.
The effect of additionally enabling \(\langle \text {LC}\rangle \)–Mc@Nlo scales with the number of PDF and scale variations, which also determines the number of required Mc@Nlo one-step shower variations required. Hence, for \(\text {EW}_\text {virt}\)+scales, it gives a speed-up of about 10%, while for the setup with 1000 PDF variations, more than a factor of three is gained.
The biggest impact (apart from the “no variations” setup variant) is achieved when also enabling the pilot run. It removes the overhead of calculating variations nearly entirely, such that the resulting runtimes are then very comparable across all setup variants. Only when calculating 1000 PDF variations there is still a sizeable increase of about 40% in runtime, compared to the “no variations” variant.
Additionally moving the matched first shower emission into the normal Css shower simulation, \(\langle \text {LC}\rangle \)–Mc@ Nlo–Css , gives a speed-up of 5-10% for all setup variants.
Then, switching to use Mcfm for pre-unweighting loop calculations gives another sizeable reduction in runtime by about 80%. This reduction is only diluted somewhat in the 1000 PDF variation case, given the sizeable amount of time that is still dedicated to calculating variations of the partially unweighted events.
Lastly, we observe another 50-60% reduction of the required CPU time when choosing a scale definition that does not need to reconstruct the parton shower history to determine the factorisation and renormalisation scales of a candidate event in the pilot run.Footnote 2 It has to be noted though that the correction to the proper CKKW factorisation and renormalisation scales induces a residual weight, i.e a broader weight distribution, leading to a reduced statistical power of the resulting sample of the same number of events. We will discuss this further below.
The overall reduction in runtime for the setup variants is summed up in Table 1.
It is interesting to note that after applying all of the performance improvements, there is no longer a single overwhelmingly computationally intense component left in the composition shown in Fig. 3 (see the bottom line in each setup variant block): None of the components in the breakdown use more than 40% of the runtime. With the exception of the 1000 PDF variation setup variant, the phase-space and tree-level ME components alone now require more than 50% of the total runtime, such that they need to be targeted for further performance improvements. Also the virtual matrix elements (“loop ME”) are still sizeable (approximately 5-10% of the runtime), albeit much smaller than the time spent on the remainder of the event generation. However, from the perspective of the Sherpa framework this is now irreducible as the runtime is spent in highly optimised external loop matrix-element libraries, and only when it is absolutely necessary.
4.2 \(pp \rightarrow t\bar{t} + 0,1j\text {@NLO}+2,3,4j\text {@LO}\)
Following the analysis of the \(e^+e^- + \text {jets}\) case, we now present the breakdown of \(t\bar{t} + \text {jets}\) run times and their compositions in Fig. 4. Overall, the results are very similar. The most striking difference in the runtime decomposition is that the clustering part is about twice as large compared to the \(e^+e^- + \text {jets}\) case. This is mainly related to the usage of a clustering-based scale definition in the \(\mathbb {H}\)-events, and also to the different structure of the core process. In the \(t\bar{t}\) case, the initial state is dominated by gluons instead of quarks, and the core process comprises four partons instead of two. Therefore, there are considerably more ways to cluster a given jet configuration back into the core process. Secondly, we find that the loop matrix elements have a smaller relative footprint in the \(t\bar{t}\) case, which is due to them only being calculated to NLO accuracy for up to one additional jet (as opposed to two additional jets in the \(e^+e^-\) case).
The speed-ups by the performance improvements are similar, but the larger proportion of the clustering and the smaller proportion of the loop matrix elements results in the pilot run improvement and the analytic loop matrix element improvement having a smaller impact than in the \(e^+e^-\) case. Using the pilot scale also has a smaller effect than in to the \(e^+e^-\) case: the simulation of \(\mathbb {H}\)-events requires the clustering to determine the parton shower starting scale as a phase space boundary for their shower subtraction terms [47].Footnote 3 The large clustering component can only be removed if the \(\mathbb {H}\)-events are calculated using a dedicated clustering-independent scale definition, as is the case in the \(e^+e^-\) setup. Overall, the final runtime improvements as reported in Table 1 are smaller than the ones for the \(e^+e^-\) process, but still very sizeable.
The most notable deviation in the improvement pattern comes from switching to Mcfm for the unweighting step, which only has a minor impact in the \(t\bar{t}\) case. This is due to the fact that only the \(t\bar{t}\) process is implemented in this library while the \(t\bar{t}j\) process, which is much more costly, has to be taken from Open-Loops throughout.
Reduction in overall run time for different performance improvements, combined with the breakdown of the overall run time into a high-level calculation composition. The timing is assessed by producing 1000 partially unweighted particle-level events for \(pp \rightarrow t\bar{t} + 0,1j\)@NLO\({}+2,3,4j\)@LO using Me Ps@ Nlo. The scaling with the number of additional variation weights is benchmarked through a few representative setup configurations
4.3 Weight distribution for pilot scale
Weight distribution of events using either the default Me Ps@ Nlo algorithm (red dashed) or the pilot scale strategy (blue solid) described in Sect. 4. Please note, phase space biasing has been disabled for this figure
The remaining question is whether the pilot run strategy adversely affects the overall event weight distribution to a significant degree. The gain in computing timing observed in the last steps in Figs. 3 and 4 is indeed reduced by a widened weight distribution stemming from the mismatch between the scale definitions. This would be made apparent by applying a second unweighting step to optimise the sample for further post-processing such as a potentially very expensive detector simulation, because the efficiency of the second unweighting step is reduced by a wider weight distribution.
Figure 5 shows the weight distribution of events after the complete simulation, i.e. including the matching and merging procedure. We perform the analysis in partially unweighted mode, which implies that the event weight can be modified by local K-factors [48,49,50,51], and events are hence not fully unweighted. However, we have removed the phase space biasing employed in our benchmark setups above, which is purely kinematical and does not depend on other details, in order to not also conflate this source of residual event weights with the new weight accounting for the differing scales in the unweighting and the final event sample. Note that the distributions are presented on a logarithmic scale. The average weights in the positive (negative) domain are 1.00 (− 1.06) with a weight spread around 0.32 (0.52) when using the Me Ps@ Nlo algorithm and 1.03 (− 1.12) with a weight spread around 0.40 (0.83) when using the pilot scale strategy for \(pp \rightarrow e^+e^- + 0,1,2j\)@NLO\({}+3,4,5j\)@LO. For \(pp \rightarrow t\bar{t} + 0,1j\)@NLO\({}+2,3,4j\)@LO the average weights in the positive (negative) domain are 1.02 (− 1.23) with a weight spread around 0.65 (0.98) when using the Me Ps@ Nlo algorithm and 1.24 (− 1.85) with a weight spread around 0.84 (1.59) when using the pilot scale strategy. The efficiency of a second unweighting step can now be estimated as follows: Determine the number of events to be generated. This corresponds to the area under the curve, integrating from the top.Footnote 4 Find the weight of the right (left) edge of the area integrated over in the positive (negative) half plane. The unweighting efficiency is the value of this weight (i.e. the maximum weight at the given number of events) divided by the average weight. Note that the average weight itself depends on the number of events. For a large number of events and a sharply peaked weight distribution, as in Fig. 5, this effect can be ignored. We find that the effective reduction in efficiency from using the pilot scale approach is typically less than a factor of two if the target number of events is large. The computing time reduction shown in the last steps in Figs. 3 and 4 will effectively be reduced by this amount, but the usage of a pilot scale is in most cases still beneficial.
Predictions for the Born-level observables \(m_{e^+e^-}\) and \(y_{e^+e^-}\), and for the dilepton transverse momentum in comparison between the Me Ps@ Nlo algorithm (red dashed) or the pilot scale strategy (blue solid) described in Sect. 4
Predictions for the Born-level observable \(m_{t\bar{t}}\), for the leading b-jet transverse momentum and the azimuthal difference between the leading b-jet and the leading light-flavour jet in comparison between the Me Ps@ Nlo algorithm (red dashed) or the pilot scale strategy (blue solid) described in Sect. 4
An alternative option to assess the loss in statistical power of a sample by a widened weight spread is provided by the Kish effective sample size [83],
where N is the number of events and \(w_i\) is the ith event weight. We then define the relative effective sample size as the ratio of the effective sample sizes \(N_\text {eff}\) for the setup variants after and before turning on the pilot scale:
We find \(\alpha ^\text {pilot scale} = 0.82\) (0.66) for our \(e^+e^-\) (\(t\bar{t}\)) production setup, confirming that the loss of statistical power is less than a factor of two and thus that the usage of the pilot scale is beneficial in both setups.
Finally, Fig. 6 presents a cross-check between the Me Ps@ Nlo method and the new pilot run strategy for actual \(e^+e^-\) production physics observables given our \(pp \rightarrow e^+e^- + 0,1,2j\)@NLO\({}+3,4,5j\)@LO setup and again including phase space biasing to populate the histograms effectively. We show distributions which can already be defined at Born level (\(m_{e^+e^-}\) and \(y_{e^+e^-}\)), as well as one observable which probes genuine higher-order effects (\(p_\textrm{T}^{e^+e^-}\)). We observe agreement between the two scales at the statistical level, as well as MC uncertainties of the same magnitude. This indicates that our new pilot run strategy will be appropriate not only at the inclusive level, but also for fully differential event simulation. We have confirmed that the same conclusions are true for the \(pp \rightarrow t\bar{t} + 0,1j\)@NLO\({}+2,3,4j\)@LO setup (Fig. 7).
5 Future performance improvements
We have shown, that for a large number of PDF variations, Lhapdf still consumes a significant portion of the computing time. While current realistic setups are of roughly 100–200 variations, future analyses might require an ever increasing number of variations and thus again an improved Lhapdf and a better PDF call alignment in Sherpa.
The presented Lhapdf performance improvements mostly depend on better caching strategies. Future implementations might choose interpolators based on their ability to precompute and store computations. For example, switching from a 2-step local polynomial interpolator to a “proper” bicubic interpolation would allow to precompute all 16 coefficients of a third-order polynomial and only require a matrix-vector multiplication at run-time.
In the context of Sherpa in particular, with the increasing use of multi-weights in the Monte Carlo event generation, the next step to even further increase the caching of common computations would be to also cache the shared computations of the error sets. This requires all the variations to be evaluated at the same time, without changing the \((x,Q^2)\) point before moving to the next one. This could be a further consideration if the number of variations increases but requires a restructuring of the call pattern in Sherpa.
However, currently for the realistic setups we presented, the majority of computing-time is spent on phase space and matrix element computations which would thus be the natural next step for performance improvements. In particular for the high multiplicity matrix elements the generation of any form of unweighted events suffers from low unweighting efficiencies (which is also the reason why the pilot-run yields such significant improvements).
A comparison between Sherpa and Mcfm suggested that this computing time can be further reduced [72]: Firstly, Sherpa could make use of the analytic tree-level matrix elements available in Mcfm. Secondly, the phase-space integration strategy used by Mcfm could be adopted by Sherpa in order to increase efficiency.
In addition to these more traditional techniques, high multiplicity matrix elements could be evaluated on GPUs, a path which has been charted in [84]. We expect significant improvements in this direction in the following years [4].
Finally, the improvements presented in Sect. 3.2 enable Sherpa to be used for the processing of the HDF5 event files introduced in [26], both at leading and at next-to-leading order precision. The corresponding technology is currently being implemented.
6 Conclusion
This manuscript discussed performance improvements of two major software packages needed for event generation at the High-Luminosity LHC: Sherpa and Lhapdf. We have presented multiple simple strategies to reduce the computing time needed for partially or fully unweighted event generation in these two packages, while maintaining the formal precision of the computations. In combination, we achieve a reduction of a factor 15 (7) in the computing requirements for state-of-the-art \(pp \rightarrow e^+e^- + 0,1,2j\)@NLO\({}+3,4,5j\)@LO (\(pp \rightarrow t\bar{t} + 0,1j\)@NLO\({}+2,3,4j\)@LO) simulations at the LHC. With this, we have achieved a major milestone set by the HSF event generator working group and opened a path towards high-fidelity event simulation in the HL-LHC era. Our modifications are made publicly available for immediate use by the LHC experiments.
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and no experimental data has been listed.]
Notes
Unweighted events that acquire further event weights after the principle unweighting of the hard-scattering matrix element configuration are called “partially unweighted”. In addition to intentional phase space biasing, the main sources for such retroactively incurred event weights are overweighted events, i.e. events whose weight exceeds the maximal weight used in the unweighting, and the local K-factor applied to the additional LO multiplicities in an NLO multijet-merged sample [47,48,49,50,51].
From the runtime composition on the right side of Fig. 3, one can see that this is not entirely due to the minimised time spent in the clustering, but also due to a somewhat reduced time usage in the loop matrix elements. This stems from an improved unweighting efficiency for Born-like configuration including virtual corrections when optimising the event generation using the simplified pilot scale, which is likely due to the increased stability of the pilot scale.
The varying phase-space boundary also means that some event weights evaluate to zero with the pilot scale, while they might be non-zero with the nominal scale. This situation would lead to an unweighting rejection probability of unity, while, formally, the correction weight ratio discussed in Sect. 3.4 would become infinite. Note that this is a generic shortcoming of any reweighting-based strategy, which comes into play whenever a hard phase-space boundary might cut off more phase-space for a variation compared to the nominal calculation. In our implementation of the pilot scale, we circumvent this issue by falling back to calculating the event with the nominal scale if a zero is encountered due the pilot scale, and then use the result of this re-run for the unweighting. We find that these re-runs give a non-zero contribution to the run-time in the \(t \bar{t}\) case, and e.g. increase the relative contribution of PDF evaluations in Fig. 4 for the “no variations”, \(\text {EW}_\text {virt}\), \(\text {EW}_\text {virt}\)+scales, and to some degree also the \(\text {EW}_\text {virt}\)+scales+100 PDFs setup variants, where the time spent in PDF variation after accepting an event is not yet too sizeable, such that relatively speaking the time spent in evaluating PDFs for re-runs is not negligible.
In practice, one will need to account for the reduction in statistical power of the event sample due to negative weights: \((1-2f)^2\) for a negative weight fraction of f.
References
T. Sjöstrand, The Lund Monte Carlo for jet fragmentation. Comput. Phys. Commun. 27, 243 (1982)
B.R. Webber, A QCD model for jet fragmentation including soft gluon interference. Nucl. Phys. B 238, 492 (1984)
A. Buckley et al., General-purpose event generators for LHC physics. Phys. Rep. 504, 145–233 (2011). arXiv:1101.2599 [hep-ph]
J.M. Campbell et al., Event generators for high-energy physics experiments. arXiv:2203.11110 [hep-ph]
I. Zurbano Fernandez et al., High-luminosity large hadron collider (HL-LHC): Technical design report
A. Buckley, Computational challenges for MC event generation. J. Phys. Conf. Ser. 1525(1), 012023 (2020). arXiv:1908.00167 [hep-ph]
S. Amoroso et al., HSF Physics Event Generator WG collaboration, Challenges in Monte Carlo event generator software for high-luminosity LHC. Comput. Softw. Big Sci. 5(1), 12 (2021). arXiv:2004.13687 [hep-ph]
HSF Physics Event Generator WG, HSF Physics Event Generator WG collaboration, HL-LHC Computing Review Stage-2, Common Software Projects: Event Generators. arXiv:2109.14938 [hep-ph]
T. Aarrestad et al., HL-LHC computing review: common tools and community software, in 2022 Snowmass Summer Study. ed. by P. Canal et al. (2020)
F. Krauss, R. Kuhn, G. Soff, AMEGIC++ 1.0: a matrix element generator in C++. JHEP 02, 044 (2002). arXiv:hep-ph/0109036
M.L. Mangano, M. Moretti, F. Piccinini, R. Pittau, A.D. Polosa, ALPGEN, a generator for hard multiparton processes in hadronic collisions. JHEP 07, 001 (2003). arXiv:hep-ph/0206293
A. Cafarella, C.G. Papadopoulos, M. Worek, Helac-Phegas: a generator for all parton level processes. Comput. Phys. Commun. 180, 1941–1955 (2009). arXiv:0710.2427 [hep-ph]
T. Gleisberg, S. Höche, Comix, a new matrix element generator. JHEP 12, 039 (2008). arXiv:0808.3674 [hep-ph]
J. Alwall, M. Herquet, F. Maltoni, O. Mattelaer, T. Stelzer, MadGraph 5: going beyond. JHEP 06, 128 (2011). arXiv:1106.0522 [hep-ph]
C.F. Berger, Z. Bern, L.J. Dixon, F. Febres Cordero, D. Forde, H. Ita, D.A. Kosower, D. Maître, An automated implementation of on-shell methods for one-loop amplitudes. Phys. Rev. D 78, 036003 (2008). arXiv:0803.4180 [hep-ph]
G. Cullen, N. Greiner, G. Heinrich, G. Luisoni, P. Mastrolia, G. Ossola, T. Reiter, F. Tramontano, Automated one-loop calculations with GoSam. Eur. Phys. J. C 72, 1889 (2012). arXiv:1111.2034 [hep-ph]
G. Bevilacqua, M. Czakon, M. Garzelli, A. van Hameren, A. Kardos et al., HELAC-NLO. Comput. Phys. Commun. 184, 986–997 (2013). arXiv:1110.1499 [hep-ph]
F. Cascioli, P. Maierhöfer, S. Pozzorini, Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012). arXiv:1111.5206 [hep-ph]
J. Alwall, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H.S. Shao, T. Stelzer, P. Torrielli, M. Zaro, The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301 [hep-ph]
S. Actis, A. Denner, L. Hofer, J.-N. Lang, A. Scharf, S. Uccirati, RECOLA: REcursive Computation of One-Loop Amplitudes. Comput. Phys. Commun. 214, 140–173 (2017). arXiv:1605.01090 [hep-ph]
K. Danziger, T. Janßen, S. Schumann, F. Siegert, Accelerating Monte Carlo event generation—rejection sampling using neural network event-weight estimates. arXiv:2109.11964 [hep-ph]
R. Frederix, S. Frixione, S. Prestel, P. Torrielli, On the reduction of negative weights in MC@NLO-type matching procedures. JHEP 07, 238 (2020). arXiv:2002.12716 [hep-ph]
K. Danziger, S. Höche, F. Siegert, Reducing negative weights in Monte Carlo event generation with Sherpa. arXiv:2110.15211 [hep-ph]
J.R. Andersen, C. Gütschow, A. Maier, S. Prestel, A positive resampler for Monte Carlo events with negative weights. Eur. Phys. J. C 80(11), 1007 (2020). arXiv:2005.09375 [hep-ph]
B. Nachman, J. Thaler, Neural resampler for Monte Carlo reweighting with preserved uncertainties. Phys. Rev. D 102(7), 076004 (2020). arXiv:2007.11586 [hep-ph]
S. Höche, S. Prestel, H. Schulz, Simulation of vector boson plus many jet final states at the high luminosity LHC. Phys. Rev. D 100(1), 014024 (2019). arXiv:1905.05120 [hep-ph]
E. Bothmann et al., Sherpa Collaboration, Event generation with Sherpa 2.2. SciPost Phys. 7(3), 034 (2019). arXiv:1905.09127 [hep-ph]
A. Buckley, J. Ferrando, S. Lloyd, K. Nordström, B. Page, M. Rüfenacht, M. Schönherr, G. Watt, LHAPDF6: parton density access in the LHC precision era. Eur. Phys. J. C 75, 132 (2015). arXiv:1412.7420 [hep-ph]
G. Aad et al., ATLAS Collaboration, Modelling and computational improvements to the simulation of single vector-boson plus jet processes for the ATLAS experiment. arXiv:2112.09588 [hep-ex]
Y.L. Dokshitzer, Calculation of the structure functions for deep inelastic scattering and \(e^+e^-\) annihilation by perturbation theory in quantum chromodynamics. Sov. Phys. JETP 46, 641–653 (1977)
V.N. Gribov, L.N. Lipatov, Deep inelastic \(e\)-\(p\) scattering in perturbation theory. Sov. J. Nucl. Phys. 15, 438–450 (1972)
L.N. Lipatov, The parton model and perturbation theory. Sov. J. Nucl. Phys. 20, 94–102 (1975)
G. Altarelli, G. Parisi, Asymptotic freedom in parton language. Nucl. Phys. B 126, 298–318 (1977)
T. Sjöstrand, A model for initial state parton showers. Phys. Lett. B 157, 321 (1985)
R.K. Ellis, W.J. Stirling, B.R. Webber, QCD and Collider Physics, vol. 8 (Cambridge University Press, Cambridge, 2011)
W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery, Numerical Recipes in C, 2nd edn. (Cambridge University Press, Cambridge, 1992)
E. Bothmann et al., Sherpa Collaboration, Event generation with Sherpa 2.2. SciPost Phys. 7(3), 034 (2019). arXiv:1905.09127 [hep-ph]
F. Buccioni, J.-N. Lang, J. M. Lindert, P. Maierhöfer, S. Pozzorini, H. Zhang, M.F. Zoller, OpenLoops 2. Eur. Phys. J. C 79(10), 866 (2019). arXiv:1907.13071 [hep-ph]
T. Gleisberg, F. Krauss, Automating dipole subtraction for QCD NLO calculations. Eur. Phys. J. C 53, 501–523 (2008). arXiv:0709.2881 [hep-ph]
S. Schumann, F. Krauss, A parton shower algorithm based on Catani–Seymour dipole factorisation. JHEP 03, 038 (2008). arXiv:0709.1027 [hep-ph]
S. Höche, F. Krauss, M. Schönherr, F. Siegert, A critical appraisal of NLO+PS matching methods. JHEP 09, 049 (2012). arXiv:1111.1220 [hep-ph]
S. Höche, M. Schönherr, Uncertainties in next-to-leading order plus parton shower matched simulations of inclusive jet and dijet production. Phys. Rev. D 86, 094042 (2012). arXiv:1208.2815 [hep-ph]
S. Frixione, B.R. Webber, Matching NLO QCD computations and parton shower simulations. JHEP 06, 029 (2002). arXiv:hep-ph/0204244
S. Kallweit, J.M. Lindert, P. Maierhöfer, S. Pozzorini, M. Schönherr, NLO QCD+EW predictions for V + jets including off-shell vector-boson decays and multijet merging. JHEP 04, 021 (2016). arXiv:1511.08692 [hep-ph]
S. Bräuer, A. Denner, M. Pellen, M. Schönherr, S. Schumann, Fixed-order and merged parton-shower predictions for WW and WWj production at the LHC including NLO QCD and EW corrections. JHEP 10, 159 (2020). arXiv:2005.12128 [hep-ph]
E. Bothmann, M. Schönherr, S. Schumann, Reweighting QCD matrix-element and parton-shower calculations. Eur. Phys. J. C 76(11), 590 (2016). arXiv:1606.08753 [hep-ph]
S. Höche, F. Krauss, M. Schönherr, F. Siegert, QCD matrix elements + parton showers: the NLO case. JHEP 04, 027 (2013). arXiv:1207.5030 [hep-ph]
T. Gehrmann, S. Höche, F. Krauss, M. Schönherr, F. Siegert, NLO QCD matrix elements + parton showers in \(e^+e^-\rightarrow \)hadrons. JHEP 01, 144 (2013). arXiv:1207.5031 [hep-ph]
S. Höche, F. Krauss, S. Pozzorini, M. Schönherr, J. Thompson, S. Pozzorini, K.C. Zapp, Triple vector boson production through Higgs–Strahlung with NLO multijet merging. Phys. Rev. D 89, 093015 (2014). arXiv:1403.7516 [hep-ph]
C. Gütschow, J.M. Lindert, M. Schönherr, Multi-jet merged top-pair production including electroweak corrections. Eur. Phys. J. C 78(4), 317 (2018). arXiv:1803.00950 [hep-ph]
E. Bothmann, D. Napoletano, M. Schönherr, S. Schumann, S.L. Villani, Higher-order EW corrections in \(ZZ\) and \(ZZj\) production at the LHC. arXiv:2111.13453 [hep-ph]
B. Gregg, FlameGraph (2011)
A. Bassetto, M. Ciafaloni, G. Marchesini, Jet structure and infrared sensitive quantities in perturbative QCD. Phys. Rep. 100, 201–272 (1983)
S. Höche, S. Schumann, F. Siegert, Hard photon production and matrix-element parton-shower merging. Phys. Rev. D 81, 034026 (2010). arXiv:0912.3501 [hep-ph]
C.F. Berger, Z. Bern, L.J. Dixon, F. Febres-Cordero, D. Forde, T. Gleisberg, H. Ita, D.A. Kosower, D. Maître, Next-to-leading order QCD predictions for W+3-Jet distributions at hadron colliders. Phys. Rev. D 80, 074036 (2009). arXiv:0907.1984 [hep-ph]
C.F. Berger, Z. Bern, L.J. Dixon, F. Febres-Cordero, D. Forde, T. Gleisberg, H. Ita, D.A. Kosower, D. Maître, Next-to-leading order QCD predictions for \(Z,\gamma ^*\)+3-Jet distributions at the Tevatron. Phys. Rev. D 82, 074002 (2010). arXiv:1004.1659 [hep-ph]
C.F. Berger, Z. Bern, L.J. Dixon, F. Febres-Cordero, D. Forde, T. Gleisberg, H. Ita, D.A. Kosower, D. Maître, Precise predictions for W + 4-Jet production at the large hadron collider. Phys. Rev. Lett. 106, 092001 (2011). arXiv:1009.2338 [hep-ph]
H. Ita, Z. Bern, L.J. Dixon, F. Febres-Cordero, D.A. Kosower, D. Maître, Precise predictions for Z + 4 jets at hadron colliders. Phys. Rev. D 85, 031501 (2012). arXiv:1108.2229 [hep-ph]
Z. Bern, L. Dixon, F. Febres Cordero, S. Höche, H. Ita, D.A. Kosower, D. Maître, K.J. Ozeren, Next-to-leading order \(W + 5\)-Jet production at the LHC. Phys. Rev. D 88, 014025 (2013). arXiv:1304.1253 [hep-ph]
V. Hirschi, R. Frederix, S. Frixione, M.V. Garzelli, F. Maltoni, R. Pittau, Automation of one-loop QCD corrections. JHEP 05, 044 (2011). arXiv:1103.0621 [hep-ph]
F. Buccioni, S. Pozzorini, M. Zoller, On-the-fly reduction of open loops. Eur. Phys. J. C 78(1), 70 (2018). arXiv:1710.11452 [hep-ph]
S. Badger, B. Biedermann, P. Uwer, NGluon: a package to calculate one-loop multi-gluon amplitudes. Comput. Phys. Commun. 182, 1674–1692 (2011). arXiv:1011.2900 [hep-ph]
S. Badger, B. Biedermann, P. Uwer, V. Yundin, Numerical evaluation of virtual corrections to multi-jet production in massless QCD. Comput. Phys. Commun. 184, 1981–1998 (2013). arXiv:1209.0100 [hep-ph]
G. Cullen, H. van Deurzen, N. Greiner, G. Heinrich, G. Luisoni et al., GOSAM-2.0: a tool for automated one-loop calculations within the Standard Model and beyond. Eur. Phys. J. C 74(8), 3001 (2014). arXiv:1404.7096 [hep-ph]
S. Actis, A. Denner, L. Hofer, A. Scharf, S. Uccirati, Recursive generation of one-loop amplitudes in the Standard Model. JHEP 04, 037 (2013). arXiv:1211.6316 [hep-ph]
A. Denner, J.-N. Lang, S. Uccirati, NLO electroweak corrections in extended Higgs Sectors with RECOLA2. JHEP 07, 087 (2017). arXiv:1705.06053 [hep-ph]
A. Denner, J.-N. Lang, S. Uccirati, Recola2: REcursive Computation of One-Loop Amplitudes 2. Comput. Phys. Commun. 224, 346–361 (2018). arXiv:1711.07388 [hep-ph]
J.M. Campbell, R.K. Ellis, Update on vector boson pair production at hadron colliders. Phys. Rev. D 60, 113006 (1999). arXiv:hep-ph/9905386
J.M. Campbell, R.K. Ellis, C. Williams, Vector boson pair production at the LHC. JHEP 07, 018 (2011). arXiv:1105.0020 [hep-ph]
J.M. Campbell, R.K. Ellis, W.T. Giele, A multi-threaded version of MCFM. arXiv:1503.06182 [physics.comp-ph]
J. Campbell, T. Neumann, Precision phenomenology with MCFM. JHEP 12, 034 (2019). arXiv:1909.09117 [hep-ph]
J.M. Campbell, S. Höche, C.T. Preuss, Accelerating LHC phenomenology with analytic one-loop amplitudes: a C++ interface to MCFM. Eur. Phys. J. C 81, 1117 (2021). arXiv:2107.04472 [hep-ph]
T. Binoth et al., A proposal for a standard interface between Monte Carlo tools and one-loop programs. Comput. Phys. Commun. 181, 1612–1622 (2010). arXiv:1001.1307 [hep-ph]
S. Alioli, S. Badger, J. Bellm, B. Biedermann, F. Boudjema et al., Update of the Binoth Les Houches Accord for a standard interface between Monte Carlo tools and one-loop programs. Comput. Phys. Commun. 185, 560–571 (2014). arXiv:1308.3462 [hep-ph]
S. Catani, F. Krauss, R. Kuhn, B.R. Webber, QCD matrix elements + parton showers. JHEP 11, 063 (2001). arXiv:hep-ph/0109231
L. Lönnblad, Correcting the colour-dipole cascade model with fixed order matrix elements. JHEP 05, 046 (2002). arXiv:hep-ph/0112284
J. André, T. Sjöstrand, Matching of matrix elements and parton showers. Phys. Rev. D 57, 5767–5772 (1998). arXiv:hep-ph/9708390
D. Amati, A. Bassetto, M. Ciafaloni, G. Marchesini, G. Veneziano, A treatment of hard processes sensitive to the infrared structure of QCD. Nucl. Phys. B 173, 429 (1980)
J. Bellm et al., Jet cross sections at the LHC and the quest for higher precision. Eur. Phys. J. C 80(2), 93 (2020). arXiv:1903.12563 [hep-ph]
A. Buckley et al., A comparative study of Higgs boson production from vector-boson fusion. JHEP 11, 108 (2021). arXiv:2105.11399 [hep-ph]
C.F. Berger, Z. Bern, L.J. Dixon, F. Febres-Cordero, D. Forde, T. Gleisberg, H. Ita, D.A. Kosower, D. Maître, Precise predictions for W + 3 jet production at hadron colliders. Phys. Rev. Lett. 102, 222001 (2009). arXiv:0902.2760 [hep-ph]
R.D. Ball et al., NNPDF Collaboration, Parton distributions for the LHC Run II. JHEP 04, 040 (2015). arXiv:1410.8849 [hep-ph]
L. Kish, Survey Sampling (Wiley, New York, 1965)
E. Bothmann, W. Giele, S. Höche, J. Isaacson, M. Knobbe, Many-gluon tree amplitudes on modern GPUs: a case study for novel event generators. arXiv:2106.06507 [hep-ph]
A. Basden, M. Weinzierl, T. Weinzierl, B.J.N. Wylie, A novel performance analysis workshop series concept, developed at Durham University under the umbrella of the ExCALIBUR programme (2021)
Acknowledgements
The authors would like to thank the Durham Performance Analysis Workshop series [85] which provided an important forum to gain the necessary insights during key phases of this work. This research was supported by the Fermi National Accelerator Laboratory (Fermilab), a U.S. Department of Energy, Office of Science, HEP User Facility. Fermilab is managed by Fermi Research Alliance, LLC (FRA), acting under Contract No. DE-AC02-07CH11359. The work of S.H. was supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Scientific Discovery through Advanced Computing (SciDAC) program. A.B., and M.S. are supported by the UK Science and Technology Facilities Council (STFC) Consolidated Grant programmes ST/S000887/1 and ST/T001011/1, respectively. A.B., I.C., C.G., and M.S. are further supported by the STFC SWIFT-HEP project (grant ST/V002627/1). C.G. wishes to thank Edd Edmondson for technical support and providing exclusive use of a machine for benchmarking. E.B. and M.K. acknowledge support from BMBF (contract 05H21MGCAB) and funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - project number 456104544. M.K. would like to thank the MCnet collaboration for the opportunity to spend a short-term studentship at the University of Glasgow. This work has received funding from the European Union’s Horizon 2020 research and innovation programme as part of the Marie Skłodowska-Curie Innovative Training Network MCnetITN3 (grant agreement no. 722104). M.S. is supported by the Royal Society through a University Research Fellowship (URF \(\backslash \)R1\(\backslash \)180549) and an Enhancement Award (RGF \(\backslash \) EA\(\backslash \)181033, CEC19\(\backslash \)100349, and RF\(\backslash \) ERE\(\backslash \)210397). Our thanks to the MCnetITN3 network for enabling elements of this project, and to Tushar Jain and the Google Summer of Code programme for initial investigations of Lhapdf performance. I.C. and C.G. acknowledge the use of the UCL Myriad and Kathleen High Performance Computing Facilities, and associated support services, in the completion of this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Bothmann, E., Buckley, A., Christidi, I.A. et al. Accelerating LHC event generation with simplified pilot runs and fast PDFs. Eur. Phys. J. C 82, 1128 (2022). https://doi.org/10.1140/epjc/s10052-022-11087-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-11087-1






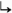
 pilot run:
pilot run:
 pilot scale:
pilot scale:





