The CDF W-mass, muon $g-2$, and dark matter in a $U(1)_{L_\mu -L_\tau }$ model with vector-like leptons

Abstract

We study the CDF W-mass, muon $g-2$, and dark matter observables in a local $U(1)_{L_\mu -L_\tau }$ model in which the new particles include three vector-like leptons ($E_1,~ E_2,~ N$), a new gauge boson $Z'$, a scalar S (breaking $U(1)_{L_\mu -L_\tau }$), a scalar dark matter $X_I$ and its partner $X_R$. We find that the CDF W-mass disfavors $m_{E_1}= m_{E_2}={m_N}$ or $s_L=s_R=0$ where $s_{L(R)}$ is mixing parameter of left (right)-handed fields of vector-like leptons. A large mass splitting between $E_1$ and $E_2$ is favored when the differences between $s_L$ and $s_R$ becomes small. The muon $g-2$ anomaly can be simultaneously explained for appropriate difference between $m_{E_1}$ $(s_L)$ and $m_{E_2}$ $(s_R)$, and some regions are excluded by the diphoton signal data of the 125 GeV Higgs. Combined with the CDF W-mass, muon $g-2$ anomaly and other relevant constraints, the correct dark matter relic density is mainly obtained in two different scenarios: (i) $X_IX_I\rightarrow Z'Z',~ SS$ for $m_{Z'}(m_S)<m_{X_I}$ and (ii) the co-annihilation processes for $min(m_{E_1},m_{E_2},m_N,m_{X_R})$ close to $m_{X_I}$. Finally, we use the direct searches for $2\ell +E_T^{miss}$ event at the LHC to constrain the model, and show the allowed mass ranges of the vector-like leptons and dark matter.

1 Introduction

Recently, the CDF collaboration reported their new measurement of the W-boson mass [1]

$$\begin{aligned} m_W=80.4335 \pm 0.0094~\text {GeV}, \end{aligned}$$

(1)

which approximately has $7\sigma$ deviation from the Standard Model (SM) value, $80.357 \pm 0.006$ GeV [2]. This CDF value is in significant tension with the other experiment measurements including the most precise one reported by the ATLAS collaboration, $m_W=80.370 \pm 0.019$ GeV [3]. Here we take the CDF result seriously and discuss implication of the W-mass shift on new physics models. Besides, the FNAL experiment measurement of the muon anomalous magnetic moment (muon $g-2$) [4], when combined with the result of the BNL experiment [5, 6], has an approximate $4.2\sigma$ discrepancy from the SM prediction [7,8,9],

$$\begin{aligned} \Delta a_\mu =a_\mu ^{exp}-a_\mu ^{SM}=(25.1\pm 5.9)\times 10^{-10}. \end{aligned}$$

(2)

The two anomalies both call for new physics beyond SM. There have been many works explaining the CDF W-mass [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79].

In this paper, we study the CDF W-mass, the muon $g-2$, and the DM observables in a local $U(1)_{L_\mu -L_\tau }$ model in which a singlet vector-like lepton, a doublet vector-like lepton and a complex singlet X field are introduced in addition to the $U(1)_{L_\mu -L_\tau }$ gauge boson $Z'$ [80] and a complex singlet ${{{\mathcal {S}}}}$ breaking $U(1)_{L_\mu -L_\tau }$ symmetry. As the lightest component of X, $X_I$ is a candidate of dark matter (DM) and its heavy partner is $X_R$. The gauge boson self-energy diagrams exchanging the vector-like leptons in the loop can give additional contributions to the oblique parameters (S,  T,  U), and explain the CDF W-mass [24, 53, 55, 76,77,78,79]. The interactions between the vector-like leptons and muon mediated by the $X_I~(X_R)$ can enhance the muon $g-2$ [81,82,83,84,85,86,87,88,89,90,91,92]. These new particles can affect the DM relic density via the DM pair-annihilation and various co-annihilations processes.

Our work is organized as follows. In Sect. 2 we introduce the model. In Sects. 3 and 4 we study the W-boson mass, muon g-2 anomaly, and the DM observables imposing relevant theoretical and experimental constraints. Finally, we give our conclusion in Sect. 5.

2 The model

In addition to the $U(1)_{L_\mu -L_\tau }$ gauge boson $Z'$, we introduce a complex singlet ${{{\mathcal {S}}}}$ breaking $U(1)_{L_\mu -L_\tau }$, a complex singlet X, and the following vector-like lepton fields,

$$\begin{aligned} E^{''}_{L,R}=\left( \begin{array}{c} N_{L,R} \\ e''_{L,R} \end{array}\right) ,E^{'}_{L,R} . \end{aligned}$$

(3)

Their quantum numbers under the gauge group $SU(3)_C\times SU(2)_L\times U(1)_Y\times U(1)_{L_\mu -L_\tau }$ are displayed in Table 1, and the $q_x$ is the $U(1)_{L_\mu -L_\tau }$ charge of the X field.

Table 1 The quantum numbers of the fields charged under $U(1)_{L_\mu -L_\tau }$. The charge of the other field is zero

The new Lagrangian respecting the $SU(3)_C\times SU(2)_L\times U(1)_Y\times U(1)_{L_\mu -L_\tau }$ symmetry is written as

(4)

where $\mu$ and $\tau$ denote the SM muon and tau leptons, and $\nu _{\mu }$ and $\nu _{\tau }$ are the corresponding neutrinos. The $D_\mu$ is the covariant derivative and $g_{Z'}$ is the gauge coupling constant of the $U(1)_{L_\mu -L_\tau }$ group. The kinetic mixing term of gauge bosons of $U(1)_{L_\mu -L_\tau }$ and $U(1)_Y$ is severely constrained from the electroweak precision data [93], and therefore we ignore it simply in this paper. The field strength tensor $Z'_{\mu \nu }=\partial _\mu Z'_\nu -\partial _\nu Z'_\mu$, and V and ${\mathcal {L}}_{\textrm{Y}}$ indicate the scalar potential and Yukawa interactions.

The scalar potential V is written as

$$\begin{aligned} V= & {} -\mu _{h}^2 (H^{\dagger } H) - \mu _{S}^2 ({{{\mathcal {S}}}}^{\dagger } {{{\mathcal {S}}}}) + m_X^2 (X^{\dagger } X) \nonumber \\{} & {} + \left[ \mu X^2 {{{\mathcal {S}}}} + \hbox {h.c.}\right] + \lambda _H (H^{\dagger } H)^2 + \lambda _S ({{{\mathcal {S}}}}^{\dagger } {{{\mathcal {S}}}})^2 \nonumber \\{} & {} +\, \lambda _X (X^{\dagger } X)^2 + \lambda _{SX} ({{{\mathcal {S}}}}^{\dagger } {{{\mathcal {S}}}})(X^{\dagger } X) + \lambda _{HS}(H^{\dagger } H)({{{\mathcal {S}}}}^{\dagger } {{{\mathcal {S}}}}) \nonumber \\{} & {} +\, \lambda _{HX}(H^{\dagger } H)(X^{\dagger } X), \end{aligned}$$

(5)

where the SM Higgs doublet H, the complex singlet fields $\mathcal{S}$ and X are

$$\begin{aligned}{} & {} H=\left( \begin{array}{c} G^+ \\ \frac{1}{\sqrt{2}}\,(h_1+v_h+iG) \end{array}\right) ,\quad {{{\mathcal {S}}}}={1\over \sqrt{2}} \left( h_2+v_S+i\omega \right) ,\nonumber \\{} & {} \quad X={1\over \sqrt{2}} \left( X_R+iX_I\right) . \end{aligned}$$

(6)

Here H and ${{{\mathcal {S}}}}$ respectively acquire vacuum expectation values (VEVs), $v_h=246$ GeV and $v_S$, and the VEV of X field is zero. The parameters $\mu ^{2}_{h}$ and $\mu ^{2}_{S}$ are determined by the minimization conditions for Higgs potential,

$$\begin{aligned}{} & {} \mu _{h}^2 = \lambda _H v_h^2 + {1 \over 2} \lambda _{HS} v_S^2,\nonumber \\{} & {} \mu _{S}^2 = \lambda _S v_S^2 + {1 \over 2} \lambda _{HS} v_h^2. \end{aligned}$$

(7)

The complex scalar X is split into two real scalar fields $X_R$ and $X_I$ by the $\mu$ term after the ${{{\mathcal {S}}}}$ field acquires VEV $v_S$. Their masses are

$$\begin{aligned}&m_{X_R}^2 = m_X^2 + {1 \over 2} \lambda _{HX} v_H^2 + {1 \over 2}\lambda _{SX} v_S^2 + \sqrt{2} \mu v_S\nonumber \\&m_{X_I}^2 = m_X^2 + {1 \over 2} \lambda _{HX} v_H^2 + {1 \over 2}\lambda _{SX} v_S^2 - \sqrt{2} \mu v_S. \end{aligned}$$

(8)

Because the X field has no VEV, there is a remnant discrete $Z_2$ symmetry which makes the lightest component $X_I$ to be stable and as a candidate of DM.

The $\lambda _{HS}$ term leads to a mixing of $h_1$ and $h_2$, and their mass eigenstates h and S are obtained from following relation,

$$\begin{aligned} \left( \begin{array}{c} h_1 \\ h_2 \end{array} \right) = \left( \begin{array}{cc} \cos \alpha &{} \sin \alpha \\ -\sin \alpha &{} \cos \alpha \\ \end{array} \right) \left( \begin{array}{c} h \\ S \end{array} \right) \end{aligned}$$

(9)

with $\alpha$ being the mixing angle. From the $\lambda _{HS}$ term and $\lambda _{HX}$ term, we can obtain the 125 GeV Higgs h coupling to a pair of DM. In order to escape the strong bounds of the DM indirect detection and direct detection experiments, we simply assume the $hX_IX_I$ coupling to be absent, namely choosing $\lambda _{HS}=0$ and $\lambda _{HX}=0$. Thus we obtain

$$\begin{aligned} \alpha =0,\quad \lambda _H=\frac{m_h^2}{2v_h^2},\quad \lambda _S=\frac{m_S^2}{2v_S^2}. \end{aligned}$$

(10)

The gauge boson $Z'$ acquires a mass after ${{{\mathcal {S}}}}$ breaks the $U(1)_{L_\mu -L_\tau }$ symmetry,

$$\begin{aligned} m_{Z'} = 2g_{Z'} \mid q_x\mid v_S. \end{aligned}$$

(11)

The Yukawa interactions with the $U(1)_{L_\mu -L_\tau }$ symmetry are given as

$$\begin{aligned}&-{\mathcal {L}}_{\textrm{Y,mass}}\nonumber \\&\quad = m_1 \overline{E'_L} E'_R + m_2 \overline{E^{''}_L} E^{''}_R + \kappa _{1} \overline{\mu _R} X E'_L+ \kappa _{2} \overline{L_\mu } X E^{''}_R \nonumber \\&\quad \quad + \sqrt{2}y_1 \overline{E^{''}_L} H E'_R + \sqrt{2}y_2 \overline{E^{''}_R} H E'_L \nonumber \\&\quad \quad +\frac{\sqrt{2}m_\mu }{v} \overline{L_\mu }H \mu _R + \hbox {h.c.}, \end{aligned}$$

(12)

where $L_\mu =\left( \nu _{\mu L},\mu _{L}\right)$.

Since the X field has no VEV, there is no mixing between the vector-like leptons and the muon lepton. However, there is a mixing between the vector-like leptons $E''$ and $E'$ after the H acquires the VEV, $v_h= 246$ GeV, and their mass matrix is given as

$$\begin{aligned} M_E = \begin{pmatrix} m_1 &{} y_2 v_h \\ y_1 v_h &{} m_2 \end{pmatrix}. \end{aligned}$$

(13)

We take two unitary matrices to diagonalize the mass matrix,

$$\begin{aligned}&U_L = \begin{pmatrix} c_L &{} -s_L \\ s_L &{} c_L \end{pmatrix}, \quad U_R = \begin{pmatrix} c_R &{} -s_R \\ s_R &{} c_R \end{pmatrix},\nonumber \\&\quad U_L^\dag M_E U_R = {\textrm{diag}}\left( m_{E_1}, m_{E_2}\right) , \end{aligned}$$

(14)

where $c_{L,R}^2 + s_{L,R}^2 = 1$. The $E_1$ and $E_2$ are the mass eigenstates of charged vector-like leptons, and the mass of neutral vector-like lepton N is

$$\begin{aligned} m_{N}=m_2=m_{E_2} c_L c_R+m_{E_1} s_L s_R. \end{aligned}$$

(15)

From the Eq. (12), we can obtain the interactions between the charged vector-like leptons and muon mediated by $X_R$ and $X_I$,

$$\begin{aligned}{} & {} -{\mathcal {L}}_{\textrm{X}} \supset \frac{1}{\sqrt{2}}(X_R+ i X_I)\left[ {\bar{\mu }}_R (\kappa _1 c_L E_{1L} -\kappa _1 s_L E_{2L}) \right. \nonumber \\{} & {} \quad \left. +\, {\bar{\mu }}_L (\kappa _2 s_R E_{1R} + \kappa _2 c_R E_{2R})\right] + h.c., \end{aligned}$$

(16)

and the 125 GeV Higgs interactions to the charged vector-like leptons $E_1$ and $E_2$,

$$\begin{aligned} -{\mathcal {L}}_{\textrm{h}}&\supset&\frac{m_{E_1}(c_L^2 s_R^2 +c_R^2 s_L^2)-2m_{E_2}s_L c_L s_R c_R}{v_h}~ h{\bar{E}}_1E_1,\nonumber \\{} & {} +\,\frac{m_{E_2}(s_L^2 c_R^2 +c_L^2 s_R^2)-2m_{E_1}s_L c_L s_R c_R}{v_h}~ h{\bar{E}}_2E_2.\nonumber \\ \end{aligned}$$

(17)

3 The $S,T,U$ parameters, W-mass, and muon $g-2$

In addition to $m_h= 125$ GeV, $v_h= 246$ GeV, $\lambda _{HS}=0$, $\lambda _{HX}=0$, there are many new parameters in the model. We take $g_{Z'}$, $q_x$, $m_{Z'}$, $\lambda _X$, $\lambda _{SX}$, $m_S$, $m_{X_R}$, $m_{X_I}$, $m_{E_1}$, $m_{E_2}$, $s_L$, $s_R$, $\kappa _1$, and $\kappa _2$ as the input parameters, which can be used to determine other parameters.

In order to maintain the perturbativity, we conservatively take

$$\begin{aligned}{} & {} \mid \lambda _{SX}\mid \le 4\pi ,~~\mid \lambda _X\mid \le 4\pi ,\nonumber \\{} & {} -\,1\le \kappa _1 \le 1,~~-1\le \kappa _2 \le 1 . \end{aligned}$$

(18)

The mixing parameters $s_L$ and $s_R$ are taken as

$$\begin{aligned} -\frac{1}{\sqrt{2}} \le s_L \le \frac{1}{\sqrt{2}}, ~~-\frac{1}{\sqrt{2}} \le s_R \le \frac{1}{\sqrt{2}}. \end{aligned}$$

(19)

We take the random uniform sampling method to scan over the input mass parameters in the following ranges:

$$\begin{aligned}&60~ {\textrm{GeV}} \le m_{X_I} \le 500~ {\textrm{GeV}},~~~ m_{X_I} \le m_{X_R} \le 1 ~\textrm{TeV},\nonumber \\&m_{X_I} \le m_{E_1} \le 1 ~\textrm{TeV},~~~m_{X_I} \le m_{E_2} \le 1 ~\textrm{TeV},\nonumber \\&100 ~{\textrm{GeV}} \le m_{Z'} \le 1 \textrm{TeV},~~~100 ~{\textrm{GeV}} \le m_{S} \le 1 ~\textrm{TeV}. \end{aligned}$$

(20)

The mass of neutral vector-like lepton N is determined by $m_{E_1}$, $m_{E_2}$, $s_L$ and $s_R$, we require $m_N>m_{X_I}$. We choose 0 $<g_{Z'}/m_{Z'}\le$ (550 GeV)$^{-1}$ to satisfy the bound of the neutrino trident process [94]. We take $-2 <q_x\le 2$, and require $\mid g_{Z'}(1-q_x)\mid \le 1$ and $g_{Z'}\le 1$ to respect the perturbativity of the $Z'$ couplings.

The tree-level stability of the potential in Eq. (5) impose the following bounds,

$$\begin{aligned}{} & {} \lambda _H \ge 0 , \quad \lambda _S \ge 0 ,\quad \lambda _X \ge 0 ,\quad \nonumber \\{} & {} \lambda _{HS} \ge - 2\sqrt{\lambda _H \,\lambda _{S}} , \quad \lambda _{HX} \ge - 2\sqrt{\lambda _H \,\lambda _{X}} , \quad \lambda _{SX} \ge - 2\sqrt{\lambda _S \,\lambda _{X}} , \quad \nonumber \\{} & {} \sqrt{\lambda _{HS}+2\sqrt{\lambda _H \,\lambda _S}}~\sqrt{\lambda _{HX}+ 2\sqrt{\lambda _H \,\lambda _{X}}} ~\sqrt{\lambda _{SX}+2\sqrt{\lambda _S\,\lambda _{X}}} \nonumber \\{} & {} \quad +\, 2\,\sqrt{\lambda _H \lambda _S \lambda _{X}} + \lambda _{HS} \sqrt{\lambda _{X}} + \lambda _{HX} \sqrt{\lambda _S} + \lambda _{SX} \sqrt{\lambda _H} \ge 0 . \end{aligned}$$

(21)

The $H\rightarrow \gamma \gamma$ decay can be corrected by the loops of the charged vector-like leptons $E_1$ and $E_2$. We impose the bound of the diphoton signal strength of the 125 GeV Higgs [95],

$$\begin{aligned} \mu _{\gamma \gamma }= 1.10\pm {0.07}. \end{aligned}$$

(22)

3.1 The $S,T,U$ parameters and W-mass

The model contains the interactions of gauge bosons and vector-like leptons,

$$\begin{aligned}{} & {} -{\mathcal {L}}_{\textrm{VG}} = -e \gamma {\bar{E}}_{1,2} \gamma ^\mu E_{1,2} + Z{\bar{E}}_i \gamma ^\mu (L_{ij}P_L+R_{ij}P_R)E_j\nonumber \\{} & {} \quad +\, \frac{g}{2c_W}Z{\bar{N}} \gamma ^\mu (P_L+P_R) N \nonumber \\{} & {} \quad +\,\frac{1}{\sqrt{2}} W^+{\bar{N}}\gamma ^\mu [(c_L P_L+c_R P_R) E_2 \nonumber \\{} & {} \quad +\, (s_L P_L+ s_R P_R) E_1] + h.c., \end{aligned}$$

(23)

where $L_{ij}$ and $R_{ij}$ are

$$\begin{aligned}{} & {} L(R)_{11}=A_1 c_{L(R)}^2 +A_2 s_{L(R)}^2,~~L(R)_{22}=A_1 s_{L(R)}^2 \nonumber \\{} & {} \quad +\, A_2 c_{L(R)}^2,\nonumber \\{} & {} L(R)_{12}=L(R)_{21}=(A_2-A_1) s_{L(R)}c_{L(R)} \end{aligned}$$

(24)

with

$$\begin{aligned} A_1=\frac{g}{c_W}s_W^2,~~A_2=\frac{g}{c_W}\left( -\frac{1}{2}+s_W^2\right) , \end{aligned}$$

(25)

where $s_W\equiv \sin \theta _W$ and $c_W=\sqrt{1-s_W^2}$, and $\theta _W$ is the weak mixing angle.

The gauge boson self-energy diagrams exchanging the vector-like leptons in the loop can give additional contributions to the oblique parameters (S,  T,  U) [96, 97], which are calculated as in Refs. [96,97,98,99]

$$\begin{aligned} \alpha (M_Z^2) \, S= & {} \frac{4 s_W^2 c_W^2}{M_Z^2} \left[ \Pi ^{\text {NP}}_{ZZ} (M_Z^2) - \Pi ^{\text {NP}}_{ZZ} (0) -\Pi ^{\text {NP}}_{\gamma \gamma }(M_Z^2) \right. \nonumber \\{} & {} \left. -\, \frac{c_W^2-s_W^2}{c_W s_W} \, \Pi ^{\text {NP}}_{\gamma Z}(M_Z^2)\right] , \end{aligned}$$

(26)

$$\begin{aligned} \alpha (M_Z^2) \, T= & {} \frac{\Pi ^{\text {NP}}_{WW}(0)}{M_W^2} - \frac{\Pi ^{\text {NP}}_{ZZ}(0)}{M_Z^2} , \end{aligned}$$

(27)

$$\begin{aligned} \alpha (M_Z^2) \, U= & {} 4 s_W^2 \left[ \frac{\Pi ^{\text {NP}}_{WW}(M_W^2)-\Pi ^{\text {NP}}_{WW}(0)}{M_W^2}\right. \nonumber \\{} & {} \left. - c_W^2 \left( \frac{\Pi ^{\text {NP}}_{ZZ}(M_Z^2)-\Pi ^{\text {NP}}_{ZZ}(0)}{M_Z^2}\right) \nonumber \right. \\ {}{} & {} \left. -\, 2 s_W c_W \, \frac{\Pi ^{\text {NP}}_{\gamma Z}(M_Z^2)}{M_Z^2} - s_W^2 \, \frac{\Pi ^{\text {NP}}_{\gamma \gamma }(M_Z^2)}{M_Z^2} \right] , \end{aligned}$$

(28)

where the $\Pi ^{\text {NP}}$ function is given in Appendix A.

Analyzing precision electroweak data and the new CDF W-mass, Ref. [10] gave the values of S,  T and U,

$$\begin{aligned} S=0.06\pm 0.10, ~~T=0.11\pm 0.12,~~U=0.14 \pm 0.09 \end{aligned}$$

(29)

with correlation coefficients

$$\begin{aligned} \rho _{ST} = 0.9, ~~\rho _{SU} = -0.59, ~~\rho _{TU} = -0.85. \end{aligned}$$

(30)

The W-boson mass is given as [97],

$$\begin{aligned} \Delta m_W^2=\frac{\alpha c_W^2}{c_W^2-s_W^2}m_Z^2 \left( -\frac{1}{2}S+c_W^2T+\frac{c_W^2-s_W^2}{4s_W^2}U\right) . \end{aligned}$$

(31)

We perform a fit to the values of S,  T,  U, and require $\chi ^2 < \chi ^2_{\textrm{min}} + 6.18$ with $\chi ^2_{\textrm{min}}$ denoting the minimum of $\chi ^2$. We find the best fit point at which $\chi ^2_{\textrm{min}}=1.77$ and $m_W=80.4381$ GeV. These surviving samples mean to be within the $2\sigma$ range in any two-dimension plane of the model parameters fitting to the S,  T, and U parameters.

Fig. 1

The surviving samples explaining the CDF W-mass within $2\sigma$ range while satisfying the oblique parameters and theory constraints. The varying colors in each panel indicate the values of $\mid m_{E_1}-m_{N}\mid$ and $\mid m_{E_2}-m_{E_1}\mid$, respectively

In Fig. 1, we show the samples explaining the CDF W-boson mass within $2\sigma$ range while satisfying the constraints of the oblique parameters and theoretical constraints. Figure 1 shows that the explanation of the CDF W-mass requires appropriate mass splittings among $E_1,~E_2$ and N, which do not simultaneously equal to zero. For example, when $m_{E_2}=m_N$, the mass splitting between $m_{E_1}$ and $m_{E_2}(m_{N})$ is required to be larger than 100 GeV. The corrections of the model to $m_W$ tend to increase with $\mid m_{E_2}-m_{E_1}\mid$ and $\mid s_L-s_R\mid$. Thus, the measurement of CDF W-mass tends to favor a large (small) $\mid m_{E_2}-m_{E_1}\mid$ for a small (large) $\mid s_L-s_R \mid$, which leads to two clearly distinct populations in $\mid m_{E_2}-m_{E_1}\mid$ of the right panel. From Eq. (15) we obtain

$$\begin{aligned} \mid m_{E_2}-m_{N}\mid =\mid m_{E_2}(1-c_Lc_R)-m_{E_1}s_Ls_R\mid , \end{aligned}$$

(32)

and $\mid m_{E_2}-m_{N}\mid < 50$ GeV favors $s_L$ and $s_R$ to be around 0. However, in such small $s_L$ and $s_R$ region, the CDF W-boson mass and the oblique parameters disfavor a large $\mid m_{E_2}-m_{E_1}\mid$, as shown in the right panel of Fig. 1. As a result, a gulf-like structure appears in the left panel for $\mid m_{E_2}-m_{N}\mid < 50$ GeV and $\mid m_{E_2}-m_{E_1}\mid > 400$ GeV. Assuming $s_L=s_R$ simply we can find that $\mid m_{E_2}-m_{N}\mid$ is proportional to $\mid m_{E_2}-m_{E_1}\mid$ and $s_Ls_R$ from Eq. (32). However, when $\mid m_{E_2}-m_{E_1}\mid$ has a very large value, the CDF W-boson mass and the oblique parameters favor relative small $s_L$ and $s_R$ (see the right panel). Therefore, $\mid m_{E_2}-m_{N}\mid$ has a maximal value for a moderate $\mid m_{E_2}-m_{E_1}\mid$. As a result, a peak-like structure appears in the left panel for which $\mid m_{E_2}-m_{N}\mid$ reaches 250 GeV for $\mid m_{E_2}-m_{E_1}\mid$ around 500 GeV. Also the similar peak-like and gulf-like structures appear in the middle panel since $\mid m_{E_1}-m_{N}\mid$ can be derived from $\mid m_{E_2}-m_{E_1}\mid$ and $\mid m_{E_2}-m_{N}\mid$.

The surviving samples in the Fig. 1 are projected on the plane of U and T, see Fig. 2. The authors of Ref. [10] used $\textsf {GFitter}$ [100] to perform a fit to the new CDF W-mass and precision electroweak data, and gave the values of S, T and U in Eq. (29) [10]. The result of Ref. [10] is independent on model, and the U parameter is pushed to a large value. From Fig. 2, we see that the correction of the model to T is dominant over U and S. Since the values of S, T and U in Eq. (29) are correlated, a large T and a small U can give a well fit to the values of S, T and U in Eq. (29) and explain the CDF W-mass.

Fig. 2

Same as Fig. 1, but projected on the plane of U and T. The varying colors in each panel indicate the values of $\chi ^2$ and S, respectively

Fig. 3

Same as Fig. 1, but projected on the planes of $m_W$ versus $\mid m_{E_2}-m_{N}\mid$ and $\mid m_{E_2}-m_{E_1}\mid$. Here $m_{W_C}$ denotes the central value of the CDF W-mass, 80.4335 GeV. The varying colors in each panel indicate the values of $\mid m_{E_2}-m_{E_1}\mid$ and $\mid m_{E_1}-m_{N}\mid$, respectively

Fig. 4

All the samples explaining the muon $g-2$ anomaly while satisfying the constraints of “pre $(g-2)_\mu$”. The varying colors in each panel indicate the values of $min(m_{E_1},m_{E_2})$ and $s_L$, and the $min(m_i,m_j,\ldots )$ denotes the minimal value of $m_i,m_j,\ldots$

Now we discuss the T parameter. The function $\Pi ^{\text {NP}}_{WW}(0)$ is zero for $m_{E_2}=m_N$ and $m_{E_1}=m_N$, and the $\Pi ^{\text {NP}}_{ZZ}(0)$ is zero for $m_{E_2}=m_{E_1}$. Therefore, from Eq. (27) we see that the corrections of the model to T parameter are absent for $m_{E_2}=m_{E_1}=m_N$, which is disfavored by the CDF measurement of W mass. Because there is no mixing between $E_2$ and $E_1$ for $s_L=s_R=0$, both the $ZE_2E_1$ and $WE_1N$ couplings disappear and $m_{E_2}$ equals to $m_{N}$. Therefore, for $s_L=s_R=0$, both $\Pi ^{\text {NP}}_{WW}(0)$ and $\Pi ^{\text {NP}}_{ZZ}(0)$ are zero, and the corrections to T parameter are also absent. The case of $s_L=s_R=0$ is disfavored by the CDF measurement of W-mass.

The corrections of the model to W-mass are sensitive to the mass differences between the vector-like leptons. In Fig. 3 we show the W-mass as a function of $\mid m_{E_2}-m_{N}\mid$ and $\mid m_{E_2}-m_{E_1}\mid$.

Fig. 5

All the samples explaining the muon $g-2$ anomaly while satisfying the constraints of “pre $(g-2)_\mu$”. The squares and circles are allowed and excluded by the diphoton signal data of 125 GeV Higgs, respectively. The varying colors indicate the values of $\mid m_{E_2}-m_{E_1}\mid$

3.2 The muon $g-2$

The model can give additional corrections to the muon $g-2$ via the one-loop diagrams containing the interactions between muon and $E_1~ (E_2)$ mediated by $X_R$ and $X_I$, and the main corrections are calculated as in Refs. [81, 83, 101]

$$\begin{aligned} \Delta a_\mu= & {} \frac{1}{32\pi ^2}m_\mu \left( \kappa _1 c_L \kappa _2 s_R H(m_{E_1},m_{X_R})\right. \nonumber \\{} & {} \left. -\, \kappa _1 s_L \kappa _2 c_R H(m_{E_2},m_{X_R}) \nonumber \right. \\{} & {} \left. +\, \kappa _1 c_L \kappa _2 s_R H(m_{E_1},m_{X_I})-\kappa _1 s_L \kappa _2 c_R H(m_{E_2},m_{X_I}) \right) ,\nonumber \\ \end{aligned}$$

(33)

where the function

$$\begin{aligned} H(m_{f},m_{\phi })=\frac{m_f}{m_{\phi }^2}\frac{(r^2-4r+2\log {r}+3)}{(r-1)^3} \end{aligned}$$

(34)

with $r=\frac{m_f^2}{m_{\phi }^2}$. Also the one-loop diagram containing the interactions of $Z'\mu ^+\mu ^-$ gives additional correction to the muon $g-2$, which can be safely ignored since the mass of $Z'$ is taken to be ${{{\mathcal {O}}}}{(10^2)}$ GeV. Equation (33) shows that the correction of the model to the muon $g-2$ is absent for $m_{E_1}=m_{E_2}$ and $s_L=s_R$.

We respectively take $s_L=s_R$ and $m_{E_1}=m_{E_2}$, and show the samples explaining the muon $g-2$ anomaly within $2\sigma$ range while satisfying the constraints “pre $(g-2)_\mu$” (denoting theory constraints, the oblique parameters, and the CDF W-mass) in Fig. 4. From Fig. 4, we see that the explanation of the muon $g-2$ anomaly favors $\mid s_L\mid$ to decrease with increasing of $\mid m_{E_1}-m_{E_2}\mid$ for $s_L=s_R$, and $m_{E_1}$ to increase with decreasing of $\mid s_L-s_R\mid$. This characteristic can be well understood from Eq. (33).

Fig. 6

All samples satisfy the constraints of “pre $(g-2)_\mu$”, the diphoton signal data of the 125 GeV Higgs, and muon $g-2$. The squares and circles are allowed and excluded by the DM relic density respectively. The varying colors indicate the values of $m_{X_I}$

After imposing the constraints of the diphoton signal data of the 125 GeV Higgs and “pre $(g-2)_\mu$”, we scan over the parameter space, and project the samples explaining the muon $g-2$ anomaly in Fig. 5. We find that the diphoton signal data of the 125 GeV Higgs exclude some samples explaining the muon $g-2$ anomaly, and favors $s_L$ and $s_R$ to have same sign, especially for large $\mid s_L\mid$ and $\mid s_R\mid$. When $s_L$ and $s_R$ have same sign, the terms of $h{\bar{E}}_1E_1$ ($h{\bar{E}}_2E_2$) coupling in Eq. (17) are canceled to some extent, which suppresses the corrections of $E_1$ and $E_2$ to the $h\rightarrow \gamma \gamma$ decay. The allowed ranges of $s_L$, $c_L$ and $m_{E_{1,2}}$ will be sizably reduced with the enhancement of measurement precision of the diphoton signal. However, it is challenge to completely exclude the parameter space explaining the muon $g-2$ and W-mass via the $h\rightarrow \gamma \gamma$ measurement with the currently expected sensitives at the future LHC.

4 The DM observables

In the model, in addition to $X_IX_I\rightarrow \mu ^+\mu ^-$, and the DM pair-annihilation processes $X_IX_I \rightarrow Z'Z',~SS$ will be open for $m_{Z'}~(m_S)<m_{X_I}$. When the masses of $E_1,~E_2,~N$ and $X_R$ are close to $m_{X_I}$, their various co-annihilation processes will play important roles in the DM relic density. We use $\textsf {FeynRules}$ [102] to generate a model file, and employ $\textsf {micrOMEGAs-5.2.13}$ [103] to calculate the relic density. The Planck collaboration reported the relic density of cold DM in the universe, $\Omega _{c}h^2 = 0.1198 \pm 0.0015$ [104].

After imposing the constraints of “pre $(g-2)_\mu$”, the diphoton signal data of the 125 GeV Higgs, and the muon $g-2$ anomaly, we project the samples achieving the DM relic density within $2\sigma$ range in Fig. 6. Due to the constraints of muon $g-2$ on the interactions between the vector-like leptons and muon mediated by $X_I$, it is not easy to obtain the correct DM relic density only via the $X_IX_I \rightarrow \mu ^+\mu ^-$ annihilation process, and other processes are needed to accelerate the DM annihilation. As shown in Fig. 6, for $min(m_{Z'},m_S) < m_{X_I}$, the $X_I X_I \rightarrow Z'Z'$ or SS will be open and play a main role in achieving the correct relic density. Then the masses of $X_R$, $E_1$, $E_2$ and N are allowed to have sizable deviation from $m_{X_I}$. When $min(m_{Z'},m_S)$ is larger than $m_{X_I}$ and the $X_I X_I \rightarrow Z'Z',~SS$ processes are kinematically forbidden, $min(m_{E_1},~m_{E_2},~m_N,~m_{X_R})$ is required to be close to $m_{X_I}$ so that the correct DM relic density is obtained via their co-annihilation processes.

Fig. 7

For the scenario of $1<m_{X_R}/m_{X_I}<1.15$ and $m_{Z'}~(m_S)>m_{X_R}$, all samples satisfy the constraints of “pre $(g-2)_\mu$”, the diphoton signal data of the 125 GeV Higgs, the muon $g-2$ anomaly, and the DM relic density. The squares and circles are allowed and excluded by the direct searches for $2\ell +E^{miss}_T$ at the LHC. The varying colors in each panel indicate the values of $m_{X_I}$ and $min(m_{E_1},m_{E_2})$, respectively

The $X_I$ has no interactions to the SM quark, and its couplings to the muon lepton and vector-like leptons are constrained by the muon $g-2$ anomaly. Therefore, the model can easily satisfy the bound from the direct detection of DM. At the LHC, the vector-like leptons are mainly produced via electroweak processes,

$$\begin{aligned}{} & {} p~p\rightarrow \gamma / Z^* \rightarrow E_1{\bar{E}}_{1,2},~ E_2{\bar{E}}_{1,2},~N{\bar{N}},\nonumber \\{} & {} p~p\rightarrow W^* \rightarrow E_{1,2} {\bar{N}},~{\bar{E}}_{1,2} N, \end{aligned}$$

(35)

then the decay modes include

$$\begin{aligned} E_{1,2} \rightarrow \mu X_I, ~~N\rightarrow \nu _\mu X_I. \end{aligned}$$

(36)

If kinematically allowed, the following decay modes will be open,

$$\begin{aligned} E_{1,2}\rightarrow \mu X_R,~W N,~~ E_{1,2}\rightarrow Z E_{2,1},~~ N\rightarrow \nu _\mu X_R. \end{aligned}$$

(37)

The $2\mu +E_T^{miss}$ event searches at the LHC can impose strong constraints on the vector-like leptons and DM. The production processes of $2\mu +E_T^{miss}$ in our model are very similar to the electroweak production of charginos and sleptons decaying into final states with $2\ell +E_T^{miss}$ analyzed by ATLAS with 139 fb$^{-1}$ integrated luminosity data [105]. Therefore, we will use this analysis to constrain our model, which is implemented in the $\textsf {MadAnalysis5}$ [106,107,108]. We perform simulations for the samples using MG5_aMC-3.3.2 [109] with PYTHIA8 [110] and Delphes-3.2.0 [111]. We apply $\textsf {MadAnalysis5}$ to identify the best signal region that is statistically the most significant, and check its $1 - \textrm{CL}_s$ value. Assuming 95% confidence level for the exclusion limit, the model with the given parameter space has been excluded if $1 - \textrm{CL}_s > 0.95$, where $\textrm{CL}_s$ is determined by the procedure in [112] and implemented in $\textsf {MadAnalysis5}$.

If the DM relic density is achieved via the co-annihilation processes of vector-like lepton, the mass of vector-like lepton is required to be close to $m_{X_I}$. As a result, the $\mu$ from the vector-like lepton decay is too soft to be distinguished at detector, and the scenario can easily satisfy the constraints of the direct searches at LHC. Here, we employ the ATLAS analysis of $2\ell +E_T^{miss}$ in Ref. [105] to constrain another scenario in which $1<m_{X_R}/m_{X_I}<1.15$ and $m_Z'~(m_S)>m_{X_R}$ is taken, and the co-annihilation processes of $X_R$ can play a main role in achieving the correct relic density. Thus, the masses of the vector-like leptons are allowed to be much larger than $m_{X_I}$.

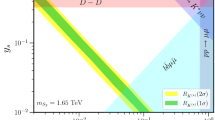
We impose the constraints of “pre $(g-2)_\mu$”, the diphoton signal data of the 125 GeV Higgs, the muon $g-2$ anomaly, the DM relic density, and the direct searches for $2\ell +E^{miss}_T$ at the LHC, and project the surviving samples in Fig. 7. From Fig. 7 we see that the mass of the lightest charged vector-like lepton is allowed to be as low as 120 GeV if $min(m_{E_1},~m_{E_2})-m_{X_I}< 60$ GeV since the muon becomes soft in the region. As $min(m_{E_1},~m_{E_2})-m_{X_I}$ increases, the energy of muon becomes large, and the vector-like lepton needs to be large enough to escape the constraints of direct searches for $2\ell +E^{miss}_T$ at the LHC. For example, $min(m_{E_1},~m_{E_2})$ is favored to be larger than 500 GeV for $min(m_{E_1},~m_{E_2})-m_{X_I}> 300$ GeV. The DM mass is allowed to be as low as 100 GeV if $min(m_{E_1},~m_{E_2})-m_{X_I}< 60$ GeV or $min(m_{E_1},~m_{E_2})-m_{X_I}> 400$ GeV.

The $p~p\rightarrow E_{1,2}{\bar{E}}_{1,2} \rightarrow \mu ^+\mu ^- +E^{miss}_T$ is still the most sensitive channel of detecting the vector-like leptons at future LHC. With the enhancement of the integrated luminosity and center-of-mass energy of the LHC, the current surviving parameter space will be furtherly reduced. However, it is challenge to examine the case of the small mass splitting between $min(m_{E_1},~m_{E_2})$ and $m_{X_I}$ for which the signal contains two soft muon leptons and missing energy. The searches for soft leptons require a dedicated study of the signal and background kinematics beyond a simple cut-and-count analysis. Also the LHC collaborations need design dedicated triggers that have acceptance for leptons with lower transverse momenta. These studies are beyond the scope of this paper.

At the tree-level, the $Z'$ has couplings to the muon lepton, the tau lepton and the new vector-like leptons, and no couplings to the SM quarks. Therefore, for a light $Z'$, the $Z'$ is mainly produced from the decay of Z, and then $Z'$ decays into $\mu ^+\mu ^-,~\tau ^+\tau ^-,~\nu _{\mu }{\bar{\nu }}_{\mu },~\nu _{\tau }{\bar{\nu }}_{\tau }$. Thus, the ATLAS and CMS searches for $4\ell$ can impose strong bound on a light $Z'$. Here we take $m_{Z'}> 100$ GeV to avoid the bound of ATLAS and CMS searches for $4\ell$. Also the $Z'$ can be produced in association with a pair of vector-like leptons, and the final states contain the multi-leptons + $E_T^{miss}$. The LHC sensitivities to such processes are much weaker than those of the $2\ell +E^{miss}_T$ discussed above. The scalar S has no couplings to the SM quark, the SM lepton, the SM-like Higgs boson, and the new vector-like leptons at the tree-level. The S can be produced in association with a $Z'$, and the LHC sensitivities are much weaker than those of $Z'$ production processes. Therefore, $m_S> 100$ GeV is a safe choice in this paper.

5 Conclusion

In this paper we discussed the CDF W-mass, the muon $g-2$, and the DM observables in a local $U(1)_{L_\mu -L_\tau }$ model, and obtained the following observations: (i) The CDF W-mass disfavors $m_{E_1}= m_{E_2}={m_N}$ or $s_L=s_R=0$, and favors a large mass splitting between $E_1$ and $E_2$ when the differences between $s_L$ and $s_R$ becomes small. (ii) The muon $g-2$ anomaly can be simultaneously explained for appropriate difference between $s_L$ $(m_{E_1})$ and $s_R$ $(m_{E_2})$, and some regions are excluded by the diphoton signal data of the 125 GeV Higgs. (iii) Combined with the CDF W-mass, muon $g-2$ anomaly and other relevant constraints, the correct DM relic density is mainly achieved in two different scenarios: (1) $X_IX_I\rightarrow Z'Z',~ SS$ for $m_{Z'}(m_S)<m_{X_I}$ and (2) the co-annihilation processes for $min(m_{E_1},m_{E_2},m_N,m_{X_R})$ close to $m_{X_I}$. (iv) The direct searches for $2\ell +E_T^{miss}$ event at the LHC impose strong bounds on the masses of the vector-like leptons and DM as well as their mass splitting.

Appendix A: The \(\Pi \) function

The $\Pi _{XY}(p^2,m_1^2, m_2^2)$ and $\Pi _{XY}(0,m_1^2, m_2^2)$ are given as [98, 99]

$$\begin{aligned}{} & {} \Pi _{XY}(p^2,m_1^2, m_2^2)\nonumber \\{} & {} \quad = -{N_c\over 16 \pi ^2}\biggl \{ {2\over 3}\biggl (g_{LX}^{f_1f_2}g_{LY}^{f_1f_2}+ g_{RX}^{f_1f_2}g_{RY}^{f_1f_2}\biggr ) \nonumber \\{} & {} \quad \times \, \biggl [m_1^2+m_2^2-{p^2\over 3}- \biggl (A_0(m_1^2)+A_0(m_2^2)\biggr ) \nonumber \\{} & {} \quad +\, {m_1^2-m_2^2\over 2 p^2} \biggl (A_0(m_1^2)-A_0(m_2^2)\biggr )\nonumber \\{} & {} \quad +{2p^4-p^2(m_1^2+m_2^2)-(m_1^2-m_2^2)^2\over 2 p^2} B_0(p^2, m_1^2,m_2^2)\biggr ] \nonumber \\{} & {} \quad +\, 2m_1m_2\biggl (g_{LX}^{f_1f_2}g_{RY}^{f_1f_2}+ g_{RX}^{f_1f_2}g_{LY}^{f_1f_2}\biggr )B_0(p^2,m_1^2,m_2^2)\biggr \},\nonumber \\ \end{aligned}$$

(A1)

$$\begin{aligned}{} & {} \Pi _{XY}(0,m_1^2, m_2^2)= -{N_c\over 16 \pi ^2}\biggl \{ {2\over 3}\biggl (g_{LX}^{f_1f_2}g_{LY}^{f_1f_2}+ g_{RX}^{f_1f_2}g_{RY}^{f_1f_2}\biggr ) \nonumber \\{} & {} \quad \times \, \biggl [m_1^2+m_2^2 - \biggl (A_0(m_1^2)+A_0(m_2^2)\biggr ) \nonumber \\{} & {} \quad -\, {m_1^2+ m_2^2\over 2 } B_0(0,m_1^2, m_2^2) -{(m_1^2-m_2^2)^2\over 2 } B_0^{'}(0, m_1^2,m_2^2)\biggr ] \nonumber \\{} & {} \quad +\, 2m_1m_2\biggl (g_{LX}^{f_1f_2}g_{RY}^{f_1f_2}+ g_{RX}^{f_1f_2}g_{LY}^{f_1f_2}\biggr )B_0(0,m_1^2,m_2^2)\biggr \}. \end{aligned}$$

(A2)

Here the coupling constants $g_{LX}^{f_1f_2}$ and $g_{RX}^{f_1f_2}$ are from

$$\begin{aligned} {{{\overline{f}}}}_1 \biggl (g_{LX}^{f_1f_2} P_L +g_{RX}^{f_1f_2} P_R\biggr )\gamma _\mu f_2 X^\mu , \end{aligned}$$

(A3)

and the $A_0$, $B_0$, and $B_0^{'}$ functions are

$$\begin{aligned} A_0(m^2)= & {} \biggl ({4\pi \mu ^2\over m^2}\biggr )^\epsilon \Gamma (1+\epsilon ) \biggl ({1\over \epsilon }+1\biggr ) m^2 , \nonumber \\ B_0(p^2,m_1^2,m_2^2)= & {} \biggl ({4\pi \mu ^2 \over m_2^2}\biggr )^\epsilon \Gamma (1+\epsilon )\nonumber \\{} & {} \quad \times \, \left[ {1\over \epsilon } -f_1(p^2,m_1^2,m_2^2)\right] ,\nonumber \\ B_0^{'}(p^2,m_1^2,m_2^2)= & {} \frac{\partial }{\partial p^2} B_0(p^2,m_1^2,m_2^2) , \end{aligned}$$

(A4)

and

$$\begin{aligned}{} & {} f_1(p^2, m_1^2,m_2^2)\nonumber \\{} & {} \quad =\int _0^1 dx \log \biggl (x+{m_1^2(1-x)-p^2x(1-x)\over m_2^2} \biggr ). \end{aligned}$$

(A5)