Wormholes, killing horizons and naked singularities: light surfaces in axially symmetric spacetimes

Abstract

We study several classes of exterior and interior axially symmetric spacetimes, such as wormholes, accelerating black holes, and binary black hole systems, from the point of view of light surfaces related to the generators of Killing horizons. We show that light surfaces constitute a useful framework for the study of the more diverse axially symmetric geometries. In particular, we point out the existence of common properties of the light surfaces in different spacetimes. We introduce a deformation of the Kerr–Newman metric and apply the light surfaces framework to analyze several generalizations in a compact form. As particular examples, we analyze static and spinning wormhole solutions, black holes immersed in external (perfect fluid) dark matter, spacetimes with (Taub) NUT charge, acceleration, magnetic charge, and cosmological constant, binary Reissner–Nordström black holes, a solution of a (low-energy effective) heterotic string theory, and the $(1+2)$ dimensional BTZ geometry.

1 Introduction

In this work, we study special light surfaces in axially symmetric spacetimes, which are related to the generators of the Killing horizons and constitute a particular framework to investigate the physical properties of black holes (BH) and other gravitational fields. A Killing horizon is a null hypersurface whose null tangent vector can be normalized to coincide with a Killing vector field. In other words, a Killing horizon is a null surface, whose normal is a Killing vector field. In general, null geodesics whose tangent vectors are normal to a null hypersurface N are called the generators of N. From the Hawking rigidity theorem, it follows that the event horizon of a stationary and asymptotically flat BH geometry is a Killing horizon.¹ Horizons define BHs, fixing their geometrical, thermodynamical and quantum properties. Indeed, a BH macrostate is defined and determined only by the mass M, spin J, and electric charge Q, which corresponds, however, to an enormously large number of microstates, leading eventually to a very high BH entropy. The number of BH microstates increases with the horizon area, which is a function of the outer horizon. The horizon becomes, therefore, a measure of the entropy, where thermodynamic properties seem to be purely intrinsic geometric characteristics.

We examine null hypersurfaces defined by Killing vectors and characterized by a constant photon orbital frequency $\omega$, which defines a unique and alternative framework to analyze solutions with Killing vectors. We perform the analysis in different spacetimes, including internal solutions and wormholes, and find common properties determined by the photon orbits. In the BH case, we use null hypersurfaces with an orbital frequency equal to that of the horizons and perform an analysis of all the geometries with the same frequency. These special light surfaces, define particular structures known as metric Killing bundles (or more simply metric bundles – $\mathcal{M}\mathcal{B}$s).

The starting point of our investigation is the Kerr–Newman (KN) metric, which is the most general asymptotically flat stationary BH solution of the Einstein–Maxwell equations. According to the no hair theorems, the Einstein–Maxwell BH solutions are characterized only by mass, electric charge, and angular momentum.² On the other hand, there is another stationary axisymmetric solution of the Einstein–Maxwell equations with additional parameters such as acceleration, magnetic charge, NUT charge, and cosmological constant. We also study here this general solution with seven parameters.³ A further interesting situation arises from the study of multi-BH configurations with Killing horizons, where, for example, there are several charged spinning sources [8]. Here, we study the case of double extreme Reissner–Nordström (RN) solutions.

To investigate generalizations of the KN spacetime and discuss some aspects of the $\mathcal{M}\mathcal{B}$s for these solutions, we deform the corresponding metric by using the “Pochhammer transformation”, which allows us to find the respective generalized metrics in a simple way. In this work, we also analyze the interior Schwarzschild solution, a (spinning) BH immersed in dark matter represented by a perfect fluid, and the metric of a binary BH system. The main goal of the present work is to prove explicitly the existence of light surfaces in several classes of axially symmetric spacetimes, highlighting the most relevant aspects with potential applications. In the case of the Kerr spacetime, we find all the photon circular orbits with orbital frequency coincident with the inner or outer Kerr BH horizons; these special orbits are known as horizon replicas – see also [18, 19] . In other spacetimes, we explore the structure of the light surfaces in connection with the definition of Killing horizons.

We stress how $\mathcal{M}\mathcal{B}$s establish a new framework of analysis where the entire family of metric solutions is studied as a unique geometric object. $\mathcal{M}\mathcal{B}$s, as collections of light-like surfaces, enlighten some properties of spacetime causal structure as spanning in different geometries. In this scenario, the single spacetime is a part of the plane (extended plane), where $\mathcal{M}\mathcal{B}$s are defined as curves tangent to the Killing horizon curves and the properties of the spacetime solutions are studied as unfolding across the spacetimes of the plane. In this way, we also connect different geometries through metric bundles, constituting an alternative setup for (classical) BH thermodynamics, which can be seen in terms of transitions between different points of the bundle⁴ [38].

By construction, the metric bundle analysis corresponds to the study of the BH Killing horizons. In this work, we explore this aspect focusing on the $\mathcal{M}\mathcal{B}$s significance for the cosmological and acceleration horizons, and the internal solutions matching the exact vacuum solutions of Einstein equations. We extend our previous analysis to include more general spacetimes and to test how the $\mathcal{M}\mathcal{B}$ formalism is a valid tool to analyze very different spacetimes as, for example in the spacetime of multiple BHs. We will address the $\mathcal{M}\mathcal{B}$s framework in connection with the definition of the wormhole throat, which is the analog of the BH horizon.

$\mathcal{M}\mathcal{B}$s and replicas have applications also in the context of alternative theories of gravity to detect possible deviations with the respect to the GR onset – [11]. From an observational viewpoint, it is worth to note that $\mathcal{M}\mathcal{B}$s have been used also to characterize the geometry and causal structure in the regions close to the BH poles and rotational axis – [18, 19]. In particular, replicas connect different spacetime regions allowing to explore, for example, regions close to the BH horizon

Some aspects of the causal structure are determined by the crossings of metric bundles in the extended plane, which has been proved to be essentially regulated by the horizon curves. Bundles are then constructed by photon (circular) orbits which can be measured by observers. Therefore, $\mathcal{M}\mathcal{B}$s have a natural application in BH astrophysics since photon circular orbits can be observed in regions close to the horizons. In particular, the frequencies of stationary observers, which are bounded by the light surfaces considered here, determine many aspect of BH accretion configurations and jets launching.

The plan of this work is as follows: axially symmetric solutions and light surfaces are introduced for the Kerr–Newman geometry in Sect. 2. In Sect. 3, we consider light surfaces in other spacetimes, namely, the interior Schwarzschild solution in Sect. 3.1, the Schwarzschild–Melvin solution in Sect. 3.2, the NUT solution in Sect. 3.3, the C-metric in Sect. 3.4, the metric of an accelerating charged black hole in Sect. 3.5, the Ernst metric in Sect. 3.6, the accelerating and rotating charged black hole in Sect. 3.7, the rotating and accelerating charged BH with cosmological constant in Sect. 3.8, the binary system of two extreme RN BHs in Sect. 3.9, the static and rotating wormhole metric in Sect. 3.10, the rotating charged BH solution of the heterotic string theory in Sect. 3.11, the rotating BH in the presence of perfect-fluid dark matter in Sect. 3.12, and the BTZ solution in Sect. 3.13. Discussion and final remarks follow in Sect. 4. A transformation of the KN metric (“Pochhammer metric”) is studied in Appendix A.

2 Axially symmetric solutions and light surfaces: the Kerr–Newman geometry

The Kerr–Newman (KN) geometry is an electro-vacuum, asymptotically flat, spacetime solution of the Einstein–Maxwell equations, describing the geometry surrounding a rotating charged mass with a mass parameter M, electrical charge parameter Q, and spin parameter a. The line element is (in geometric units with $G=c=1$)

$$\begin{aligned} ds^2= & {} \frac{\sin ^2\theta \left[ d\phi \left( a^2+r^2\right) -a dt\right] ^2}{\varSigma }\nonumber \\{} & {} -\frac{\varDelta \left( a d\phi \sin ^2\theta -dt\right) ^2}{\varSigma }+\frac{ \varSigma dr^2}{\varDelta }+\varSigma d\theta ^2 \end{aligned}$$

(1)

[9]. We adopt the Boyer–Lindquist (BL) coordinate $(t,r,\theta , \phi )$, where

$$\begin{aligned} \varDelta \equiv a^2+Q^2+r^2-2M r\quad \text{ and }\quad \varSigma \equiv a^2 \cos ^2\theta +r^2, \end{aligned}$$

(2)

In the following we shall use also the parameter $\sigma \equiv \sin ^2\theta \in [0,1]$.

The horizons $r_{\pm }\equiv M\pm \sqrt{M^2-Q_t^2}$ in terms of the total charge $Q_t\equiv \sqrt{a^2+Q^2}$, can be written in the plane $Q_t-r$ (extended plane) as $Q_t^{\pm }\equiv \sqrt{-(r-2M) r}$. The metric describes black hole (BH) solutions for $Q_t<M$, extreme BHs for $Q_t=M$ and naked singularities (NSs) for $Q_t>M$. The KN metric reduces to the Kerr solution for $Q=0$, where $Q_t=a$ and the horizons in the extended plane are $a_\pm =Q_t^{\pm }$. For $a=0$ the KN metric is the spherically symmetric Reissner–Nordström (RN) solution, where $Q_t=Q$ and the horizons are $Q_\pm \equiv Q_t^\pm$ in the extended plane $Q-r$. The Schwarzschild metric is for $Q=0$ and $a=0$, where the horizon is $r=2M$.

Let us introduce the Killing vector $\mathcal {L}=\xi ^t +\omega \xi ^{\phi }$, where $\xi ^{t}=\partial _{t}$ and $\xi ^{\phi }=\partial _{\phi }$, and the rotational frequencies $\omega _{\pm }:{g}(\mathcal {L},\mathcal {L})=0$, for null-like circular orbits, where g is the metric tensor. The limiting frequencies (or relativistic velocities) $\omega _H^\pm \equiv \lim _{r\rightarrow r_\pm }\omega _{\pm }$ are the horizons frequencies (relativistic angular velocities), which represent the BH rigid rotation ($\omega _H^\pm$ for the outer and inner horizon, respectively). Therefore, the vector fields $\mathcal {L}_H^{\pm }\equiv \mathcal {L}(r_{\pm })=\xi ^t +\omega _H^{\pm } \xi ^{\phi }$ define the horizons as Killing horizons. The frequencies $\omega _\pm$ are also the limiting frequencies for (time-like) stationary observers. In the static limit, for $a=0$, the horizons of the Schwarzschild and RN BHs are Killing horizons with respect to the Killing field $\xi ^t$ (and the horizons frequencies $\omega _H$ are null).

In this work, we study the so-called metric Killing bundles ($\mathcal{M}\mathcal{B}$s) [10,11,12,13,14,15,16,17,18,19], structures defined as solutions of $\mathcal {L}_{\mathcal {N}}\equiv g(\mathcal {L},\mathcal {L})=0$ with constant $\omega$. For geometries with total charge $Q_t$, metric Killing bundles are the collections of all and only geometries defined as solutions of $g(\mathcal {L},\mathcal {L})=0$, having orbits different from the horizon radii, but corresponding to photon orbits with equal orbital frequency $\omega$, called bundle characteristic frequency. The bundle characteristic frequency coincides always (in magnitude) to an (inner or outer) horizon frequency $\omega _H^{\pm }$ of the bundle. In a fixed spacetime $a=\bar{a}$, there may be more points (orbits r at fixed $\sigma$) of the same bundle with the same photon orbital angular frequency $\omega =\bar{\omega }$ (which is the bundle characteristic frequency). Those orbits are called replicas with frequency $\bar{\omega }$. If $\bar{\omega }$ is the frequency of the inner or outer BH horizon with spin $\bar{a}$, then all the photon orbits $(r,\sigma )$ with frequency $\bar{\omega }$ are known as horizon replicas.

Therefore, (Kerr) metric Killing bundles always contain at least one BH geometry. In this sense, any orbit of a bundle is a BH horizon replica and replicas are also characteristic of the eventual NSs geometries of the bundle. (In the case of the Kerr and KN examples, the characteristic bundle frequency is always a BH horizon frequency and we can defined horizon replicas of a BH in different BH spacetimes or even NS spacetimes. This procedure allows us to relate either different BHs or BHs and NSs through replicas). However, some horizon frequencies are not replicated (horizon confinement). It has been proved that the horizon confinement is a characteristic of some BH inner horizons [17,18,19]).

In spinning solutions, we can consider the co-rotating, $a\omega >0$ and the counter-rotating $a\omega <0$ orbits separately with frequencies that are equal in magnitude to the horizon frequencies. Nevertheless, here we will consider mainly $a\ge 0$ and $\omega \ge 0$.

Below, we consider in details the definitions of extended plane, $\mathcal{M}\mathcal{B}$s characteristics, and horizons replicas. We also investigate metric bundles in the Schwarzschild spacetime and perform a comparison with bundles in the Kerr and RN spacetimes.

The extended plane

Metric Killing bundles can be represented as curves in a plane $\mathcal {P}-r$ called extended plane, where $\mathcal {P}$ is a metric parameter. Each metric bundle is tangent at one point to the horizon curve in the extended plane – see for example Fig. 1 representing the extended plane of the Kerr geometry for $\sigma =1$. The horizon curve in the extended plane is a curve containing all the horizons of the BH solutions. In the extended plane $a-r$ of the Kerr solution, the horizon curve is $a_\pm \equiv \sqrt{r(2M-r)}$; also, for the RN metric the horizon curve in the extended plane $Q-r$ is $Q_\pm \equiv \sqrt{r(2M-r)}$. In the analysis of the counter-rotating replicas with $\omega a<0$, we can consider the extended plane with $a\lessgtr 0$, where the horizon curves are $a_\pm \equiv \pm \sqrt{r(2M-r)}$. In the extended plane, a metric bundle curve can be tangent also to the curve representing the inner horizons; in the examples above, this corresponds to the region $r<M$ and $Q_t<M$. In general, bundle curves can be located in the two regions $r<r_-$ (inner region) and $r>r_+$ (outer region).

In some naked singularity solutions with small values of $a\ge M$, the light surfaces $r_s(\omega )$, i.e. solutions of $g(\mathcal {L},\mathcal {L})=0$ with frequency $\omega$, are characterized in the plane $r-\omega$ by the so-called Killing bottleneck, which consists in a restriction of the light surfaces as functions of the light-like frequencies in the plane $r-\omega$ – see Fig. 1 and [18, 19].

Fig. 1

Left panel: Extended plane $a/M-r/M$ on the equatorial plane $(\sigma =\sin ^2\theta =1)$ of the Kerr geometry. Metric bundles ($\mathcal{M}\mathcal{B}$s) with characteristic frequency $\omega =1/a_0=$constant are shown for different $\omega$, where $a_0$ is the bundle origin spin (bundles value at $r=0$). The black region represents the BH region with the outer and inner horizons $a_\pm$, as functions of r/M (M is the mass). A horizontal line on the extended plane at $\sigma =1$ represents a fixed spacetime $a/M=$constant. In particular, $a=0$ corresponds to the Schwarzschild BH spacetime and $a=M$ to the extreme Kerr BH. The frequencies of the inner and outer horizons curve are clearly distinguished. The frequency $\omega ^{\pm }_H=1/2$ corresponds to the extreme Kerr BH. On the equatorial plane, the point $r=2M$ is the outer ergosurface (the Schwarzschild BH horizon for $a=0$). Right panel: Light surfaces $r_s^{\pm }(\omega ;a)$ on the equatorial plane, solutions of condition $\mathcal {L}_{\mathcal {N}}=0$, as functions of the frequency $\omega$, for different spacetimes. Here, $\omega =1/a_0$ corresponds to $r=0$. The extreme BH spacetime and the bottleneck region are also pointed out

$\mathcal{M}\mathcal{B}$ s characteristics in the extended plane

The concept of metric bundles and some of their main features are illustrated in Fig. 1, using the extended plane $a/M-r/M$ of the Kerr geometry on the equatorial plane $(\sigma =\sin ^2\theta =1)$. Below we list some of the main features, focusing on the definition of replicas. Then, we discuss the $\mathcal{M}\mathcal{B}$s of the Schwarzschild geometry.

Figure 1 shows metric bundles at $\sigma =1$ for different characteristic frequencies $\omega =1/a_0=$constant, where $a_0$ is the bundle origin spin (or bundle origin). For $\sigma \in ]0,1[$ the bundle origin spin is $\mathcal {A}_0\equiv 1/\omega \sqrt{\sigma }$, corresponding to the solution $a:\mathcal {L}_{\mathcal {N}}=0$ for $r=0$. The black region represents the BH region bounded by the outer $(r\in [M,2M])$ and inner $(r\in ]0,M])$ horizons curves $a_\pm \in [0,M]$.

The frequencies of the inner $(\omega _H^-\in ]+\infty ,1/2])$ and outer $(\omega _H^+\in [1/2,0])$ horizons curves are clearly distinguished. The frequency $\omega ^{\pm }_H=1/2$ corresponds to the extreme Kerr BH. On the equatorial plane, the point $r=2M$ corresponds to the outer ergosurface for $a>0$ and to the Schwarzschild BH horizon for $a=0$. On the extended plane at $\sigma =1$, a horizontal line represents a fixed spacetime $a/M=$constant.

Replicas in the extended plane

We can clarify the concept of replicas using the extended plane, for example, of the Kerr geometry as illustrated in Fig. 1. Replicas are light-like (circular) orbits whose orbital frequency $\omega$ coincides with the BH horizon frequency, which is also the bundle characteristic frequency. In general, we consider BH horizon replicas in the same spacetime. Therefore, the frequency $\omega$, defined on an orbit with radius r, is “replicated” on an orbit $r_1\ne r$ if $\omega (r)=\omega (r_1)$. Clearly, the curve defined by the classes of points $(r,r_1)$ defines the bundles (which can include eventually the dependence from $\sigma$, thus $\omega (r, \sigma )=\omega (r_1,\sigma _1)$, where $\sigma \equiv \sin ^2\theta$) [10, 12, 13, 17]. It should be noted that in the Kerr spacetime at a point r, in general, there are two different limiting photon frequencies $\omega _\pm$ for the stationary observers, then it follows that at each point of the extended plane (at fixed $\sigma$ with the exception of the horizon curve) there have to be a maximum of two different crossing metric bundles.

The confinement analysis, which is the study of the topology of the curves ${\omega }=$constant in the extended plane, provides information about the local properties of the spacetime replicated in regions more accessible to the observes; for example, in the case of properties defined in the proximity of the BH poles or of the inner horizons. Replicas also connect measurements in different spacetimes characterized by the same value of the property $\mathcal {Q}$ function of $\omega$, by connecting two null vectors, $\mathcal {L}(r_\pm ,a,\sigma )$ and $\mathcal {L}(r_p,a,\sigma _p)$, where $r_\pm$ is the outer or inner Killing horizon (we also consider the special case $\sigma =\sigma _p$).

From the phenomenological view point, an observer can detect the presence of a replica at the point p of the BH spacetime with spin $a_p$, by measuring the BH horizon frequency $\omega _H^+(a_p)$ or $\omega _H^-(a_p)$ (the outer or inner BH horizon frequency) at the point p. It has been proved in [18, 19] that it is possible to measure the Kerr inner horizons replicas in regions very close to the BH rotational axes. Therefore, one of the intriguing applications of $\mathcal{M}\mathcal{B}$s in BH physics is the possibility to explore the regions close to the BH rotational axes (poles). All the horizon replicas for some fixed Kerr BH are shown in Fig. 2. In Fig. 3, the horizon replicas are shown for NS geometries [18, 19].

Fig. 2

Replicas in a fixed Kerr BH geometry with dimensionless spin a/M. $\omega _H^\pm$ are the outer and inner BH horizons frequencies, respectively. The inner and outer horizons spheres are shown as blue and orange spheres, respectively, and the analysis covers the replicas structure in the region $[r_+,+\infty [$. The replicas structures in the region $]0, r_-]$ is also included, where $r_\pm$ are the outer and inner BH horizon. In some panels, the inner and outer horizon spheres can be seen as embedded in replicas. In the plots $\{z=r \cos \theta , y=r \sin \theta \sin \phi , x=r \sin \theta \cos \phi \}$. Co-rotating outer and inner horizon replicas with frequency $\omega =+\omega _H^\pm$ and counter-rotating outer and inner horizon replicas $\omega =-\omega _H^\pm$ are shown. Left panels show the outer horizon co-rotating replicas (pink surfaces with frequencies $\omega =+\omega _H+$) and the inner horizons co-rotating replicas (gray surfaces with frequency $\omega =+\omega _H^-$). Center panels show the outer horizon counter-rotating replicas (purples surfaces with frequency $\omega =-\omega _H^+$) and the inner horizons counter-rotating replicas (green surfaces with frequency $\omega =-\omega _H^-$). The right panels show replicas with frequencies $\omega =\{+\omega _H^\pm ,-\omega _H^{\pm }\}$, i.e., combinations of the left and center panels. The replica of the BH horizons in different NS geometries are shown in Fig. 3

Fig. 3

Replicas of the BH horizons represented in Fig. 2 for different values of a/M corresponding to naked singularities. Here, $\{z=r \cos \theta , y=r \sin \theta \sin \phi , x=r \sin \theta \cos \phi \}$. The central singularity is the point $x=0,y=0,z=0$. $\omega _H^\pm$ are the outer and inner BH horizon frequencies, respectively. Co-rotating outer and inner horizon replicas with frequency $\omega =+\omega _H^\pm (a^*)$ and counter-rotating outer and inner horizon replicas $\omega =-\omega _H^\pm (a^*)$ for the BH spacetime with spins $a^*$ are shown. Pink surfaces correspond to the outer horizon co-rotating replicas (with frequency $\omega =+\omega _H^+(a^*)$). Grey surfaces denote the inner horizon co-rotating replicas (with frequency $\omega =+\omega _H^-(a^*)$). Purple surfaces correspond to the outer horizon counter-rotating replicas (with frequency $\omega =-\omega _H^+(a^*)$). Green surfaces correspond to inner horizon counter-rotating replicas (with frequency $\omega =-\omega _H^-(a^*)$). The second and fourth columns are close-up views of the first and third columns, respectively. They show the innermost replicas (the outermost surfaces are not included for graphic reasons). Some surfaces are embedded in the outermost replicas. The presence of a bottleneck region is clear in the NS spacetime with $a=1.05M$ (third and fourth rows). In this case, the close-up view highlights the emergence of the bottleneck

Metric bundles in the Schwarzschild spacetime

As shown above, $\mathcal{M}\mathcal{B}$s contain information about the symmetries and horizons of the corresponding spacetime. It is, therefore, convenient to consider Schwarzschild $\mathcal{M}\mathcal{B}$s as a limiting case of the Kerr $\mathcal{M}\mathcal{B}$s. In fact, the symmetries of the Schwarzschild spacetime, spherical symmetry and staticity, can be considered as a limiting case of axial symmetry and stationarity, respectively. Moreover, the event horizon is a Killing horizon with respect to the vector $\xi _t$ (not $\mathcal {L}$), which can also be used to define the corresponding $\mathcal{M}\mathcal{B}$s. On the other hand, the Schwarzschild spacetime can also be considered as a limiting case of the RN solution, which is spherically symmetric and static and, in the BH case, possesses two event horizons that are Killing horizons with respect to the field $\xi _t$ – [10, 17]. However, the RN solution contains NS spacetimes, absent in the Schwarzschild solution.

The bundle characteristic frequencies, solutions of $\mathcal {L}_{\mathcal {N}}=0$, are null in the RN and Schwarzschild spacetimes. Thus, in this case, the tangency condition of the metric bundles with respect to the horizons curves should be understood as an asymptotic condition.⁵ (In the RN case however, in the extended plane $Q-r$, the horizons curve is $Q_\pm =\sqrt{r(2M-r)}$. In the Schwarzschild case, the horizon is the axis $r=2M$.) In this context, the horizon replicas are asymptotic solutions for orbits far from the gravitational source – see also [11].

Therefore, it is useful and convenient to study the $\mathcal{M}\mathcal{B}$s of the Schwarzschild geometry as limits in the extended planes of the RN and Kerr spacetimes – Fig. 1. Then, in the RN geometry, the Schwarzschild case occurs for $Q=0$ and $\omega \rightarrow 0$, or in the Kerr geometry for $a=0$ and $\omega \rightarrow 0$ or $\mathcal {A}_0\rightarrow \infty$. Furthermore, it is also possible to study $\mathcal{M}\mathcal{B}$s in the Schwarzschild case as the zeros of the metric bundles in the RN and Kerr extended planes, respectively. (We shall see that $\mathcal{M}\mathcal{B}$s of the Schwarzschild geometry can also be seen as the limiting cases and the zeros of bundles in cosmological or accelerating in Sect. 3). For the sake of simplicity, in the following analyses we use geometric units with $M=1$.

The Schwarzschild $\mathcal{M}\mathcal{B}$ s as zeros in the extended planes

The zeros of the metric bundles on the Kerr and RN spacetimes, i.e., the solutions $a_{\omega }(r)=0$ and $Q_\omega (r)=0$ correspond to the static case described by the Schwarzschild metric, where the photon orbital frequencies, limiting the stationary observers frequencies, are $\omega _\pm =\omega _{Schw}$,

$$\begin{aligned}{} & {} \omega _{Schw}=\pm \frac{\sqrt{r-2}}{r^{3/2} \sqrt{\sigma }}, \end{aligned}$$

(3)

with $\omega _{Schw}=0$ on the BH horizon $r=2M$. The radii of the light surfaces associated to the metric bundles, solutions of $\mathcal {L}_{\mathcal {N}}=0$, are

$$\begin{aligned}{} & {} r_L^+(W)\equiv \frac{2 \cos \left[ \frac{\chi _w}{3}\right] }{\sqrt{3}\sqrt{W}},\quad r_L^-(W)\equiv -\frac{2 \cos \left[ \frac{\chi _w+\pi }{3} \right] }{\sqrt{3}\sqrt{W}},\nonumber \\{} & {} \quad \text{ where }\quad W\equiv \sigma \omega ^2\ge 0,\quad \chi _w \equiv \cos ^{-1}\left( -3 \sqrt{3}\sqrt{W}\right) ,\nonumber \\{} & {} \quad \text{ and } \nonumber \\{} & {} r_L^+(W)=r_L^-(W)=3\quad \text{ for }\quad W=W_{\max }\equiv \sigma \omega ^2=1/27.\nonumber \\ \end{aligned}$$

(4)

The limiting value, $W_{\max }$, occurs for $r=r_{\gamma }=3$, which is the photon (last) circular orbit in the Schwarzschild spacetime and is also an extremum of the frequency $\omega _{Schw}$ for r, where $\omega _{Schw}(W_{\max })={1}/{3 \sqrt{3} \sqrt{\sigma }}$.

The Schwarzschild $\mathcal{M}\mathcal{B}$ s as limits of RN $\mathcal{M}\mathcal{B}$ s

Let us consider the metric bundle $Q_{\omega }$ for the RN spacetimes. Using the Killing field $\mathcal {L}$ and the zero-quantity $\mathcal {L}_{\mathcal {N}}$, we find the limiting (photon orbital) frequencies $\omega _\pm$ and the metric bundles $Q_\omega$ as follows:

$$\begin{aligned}{} & {} \mathcal {L}\equiv \xi _t+\omega \xi _{\phi };\quad \mathcal {L}_{\mathcal {N}}\equiv {\textbf {g}}(\mathcal {L},\mathcal {L})=g_{tt}+g_{\phi \phi }\omega ^2,\nonumber \\{} & {} \omega _{\pm }=\pm \frac{-g_{tt}}{g_{\phi \phi }}={\pm } \frac{\sqrt{Q^2+(r-2) r}}{\sqrt{\sigma }r^2},\nonumber \\{} & {} \quad Q_{\omega }\equiv \sqrt{r} \sqrt{r^3 \sigma \omega ^2-r+2}. \end{aligned}$$

(5)

As the RN solution is static, on the RN horizons $\omega _\pm =0$. Therefore, also in the RN spacetime, horizon replicas are a limiting concept for the asymptotic regions $r\rightarrow \infty$. The frequency $\omega _{\pm }$ in the Schwarzschild geometry is a solution

$$\begin{aligned}{} & {} Q_{\omega }=0,\quad \text{ for }\quad \omega =\omega _{Sch} \quad (or \quad r=0). \end{aligned}$$

(6)

The Schwarzschild $\mathcal{M}\mathcal{B}$ s as limits of the Kerr $\mathcal{M}\mathcal{B}$ s

The metric bundles of the Schwarzschild geometry can also be studied as the limiting case $a=0$ of the metric bundles of the Kerr geometry. The Kerr BH horizon frequencies are

$$\begin{aligned}{} & {} \forall \theta \ne 0,\quad \omega _H^\pm (r)\equiv \omega _{\pm }(a_{\pm })= \frac{\sqrt{(2-r) r}}{2 r},\nonumber \\{} & {} \quad \text{ then }\quad \lim _{a\rightarrow 0}\omega _H^\pm =0. \end{aligned}$$

(7)

Let us consider then the bundle tangent radius $r_g(\omega )$ to the horizons curve in the extended plane as a function of the bundle frequency $\omega$, an alternative way of writing the horizons curve as a function of the horizon frequencies, and the bundle tangent spin $a_g(a_0,\sigma )\in [0,1]$ to the horizon curve in the extended plane, which is the horizon curve as function of the bundle origin spin $a_0$ and the plane $\sigma$. Then, for the Schwarzschild limit, i.e. $\omega \rightarrow 0$, we obtain

$$\begin{aligned} r_g(\omega )= & {} \frac{2}{4 \omega ^2+1}\ ,\lim _{\omega \rightarrow 0}r_g(\omega )=2;\nonumber \\ a_0= & {} \frac{1}{\sqrt{\sigma }\omega },\quad \lim _{\omega \rightarrow 0} a_0=\infty ;\nonumber \\ a_g(a_0)\equiv & {} \frac{4 a_0\sqrt{\sigma }}{a_0^2 \sigma +4},\quad \lim _{a_0\rightarrow \infty }a_g=0. \end{aligned}$$

(8)

Equation (8) are in agreement with Fig. 1 where, in the extended plane for the Kerr spacetimes, the bundle tangent to the Schwarzschild BH horizon (as limit of the Kerr BH with $a=0$) is the bundle tangent to the outer horizons curve for the bundle origin spin $a_0\rightarrow +\infty$ or, equivalently, bundle frequency $\omega \rightarrow 0$.

Note that for spherically symmetric solutions we can use, if convenient, $\sigma =1$, i.e., we fix an arbitrary equatorial plane without loss of generality. On the other hand, the re-parametrization $\sigma \omega ^2\rightarrow \omega ^2$ is an important identification, which is also used in the axially symmetric cases as, for example, for the Kerr $\mathcal{M}\mathcal{B}$s.

In Appendix A, we introduce a metric deformation of the KN geometry the “Pochhammer metric”, with the exact stationary solution as a limit. This analysis points out some geometrical properties of the $\mathcal{M}\mathcal{B}$s of interior solutions (following the metric deformation) and relates some curvature properties and metric singularities with the metric bundles, showing the emergence of the envelope surfaces with a radial cyclicality. These results anticipate and generalize some aspects discussed in Sect. 3, where several axially symmetric solutions including internal solutions are examined.

3 Particular solutions

In this section, we briefly consider the bundle structure in other axially symmetric solutions. We do not dwell on the details of each solution, referring instead to the comprehensive literature such as [20]. Therefore, following mostly the conventions and notation of the literature, we provide below only the non-zero metric components relevant in the definition of bundles, mainly the components $\{g_{tt},g_{t\phi },g_{\phi \phi }\}$ (and their conformal transformations) in Boyer–Lindquist coordinates $(t,r,\theta ,\phi )$. A $\mathcal{M}\mathcal{B}$, defined by the condition $\mathcal {L}_\mathcal {N}=0$, is a metric conformal invariant. In the following, we will consider the best adapted metric conformal transformation.

We explore the interior Schwarzschild solution in Sect. 3.1, the Schwarzschild–Melvin solution in Sect. 3.2, and the NUT solution in Sect. 3.3. Moreover, the C-metric is considered in Sect. 3.4, the accelerating charged black hole solution in Sect. 3.5, the Ernst metric in Sect. 3.6, the accelerating and rotating charged black holes in Sect. 3.7, the rotating and accelerating charged BH with cosmological constant in Sect. 3.8, the extreme RN black hole binary metric in Sect. 3.9, the static and rotating wormhole solution in Sect. 3.10, the rotating charged BH solution of the heterotic string theory in Sect. 3.11, the rotating BH in perfect-fluid dark matter in Sect. 3.12, and the BTZ solution in Sect. 3.13.

3.1 The interior Schwarzschild solution

In Schwarzschild coordinates, we consider the line element in the interior region $r < R$, where R is the radius of the surface of the gravitational source, for which we assume a vanishing pressure. Using Einstein’s field equations, we obtain the Tolman–Oppenheimer–Volkov equation with a barotropic equation of state (EoS). The regularity condition on the pressure and density sets the limit $R > 9/ 4 M$. Therefore, while the external solution is Schwarzschild, the internal solution is a function of the radius R – see for example [20]. The metric components read

$$\begin{aligned}{} & {} g_{tt}\equiv -e^{2 \xi },\quad g_{\phi \phi }\equiv r^2 \sin ^2\theta ,\nonumber \\{} & {} \text{ where }\quad e^{\xi }\equiv \frac{3}{2} \sqrt{1-\frac{2 M}{R}}-\frac{1}{2} \sqrt{1-\frac{2 M r^2}{R^3}}. \end{aligned}$$

(9)

In the following analysis we will set $M=1$. From the condition $\mathcal {L}_\mathcal {N}\equiv g(\mathcal {L},\mathcal {L})=0$, with $\omega =0,$ we obtain the radius $r= \sqrt{(9-4 R) R^2}$ (dimensionless quantities), which is not verified for the regularity condition on the pressure and, therefore, constraints the extended plane.⁶ The bundles characteristic frequencies on the equatorial plane are

$$\begin{aligned} \omega _\pm =\pm \frac{\sqrt{-3 \sqrt{\frac{R-2}{R}} \sqrt{1-\frac{2 r^2}{R^3}}-\frac{9 R^2+r^2}{R^3}+5}}{\sqrt{2} r}\ . \end{aligned}$$

(10)

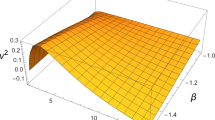
In general, solutions of $\mathcal {L}_{\mathcal {N}}=0$ are for $(R={9}/{4}, r=0, \forall \omega )$, and $(R\ge 2, r\in ] 0,r_a])$, where $r_a\equiv \sqrt{R^3/2}$. Metric bundles are shown in Fig. 4. It is natural to choose the surface radius R as the parameter of the extended plane. So, we show the function $R_a: r=r_a$. It is clear how $R_a$ ($r_a$) constitutes an upper bound for the metric bundles.

Fig. 4

Left panel: Interior Schwarzschild geometry $(M=1)$ of Eq. (9). Metric bundles in the plane $R-r$ where R is the surface radius with vanishing pressure. $\omega$ is the bundle characteristic frequency. The purple curve corresponds to light-like orbital frequency $\omega =0$. The radius $R_a\equiv \root 3 \of {2} r^{2/3}$ is also plotted as a black curve. The interior solution is for $r<R$. The radius $r_{\gamma }$ is the last circular photon circular orbit of the Schwarzschild spacetime. The radii r and R at $\{2, 9/4\}$ are also shown. Right panel: Schwarzschild–Melvin solution $(M=1)$ of Eq. (12). Metric bundles are represented in the plane $B-r$, where B is the “electro-magnetic” parameter. The value $B=1$ is also shown. The horizon corresponds to $r=2$ (the mass parameter is $M=1$)

In this case, the surface of the internal solution acts as envelope surfaces in the $\mathcal{M}\mathcal{B}$s construction. For completeness we have shown also the bundles in the region $r\ge R$ and $R<9/4$. The internal solution is well defined however for $r<R$ and $R>9/4$. Therefore, we show the limits $r=R$ and $R=\{2,9/4\}$. As the metric is spherically symmetric we considered only solutions $\omega \ge 0$.

As it is clear from Fig. 4, $\mathcal{M}\mathcal{B}$s point out the two main constraints to the interior Schwarzschild solution (9). The limiting radius defining the orbits where $\omega =0$ (the metric is static) is represented as a purple curve (existing only for $R<9/4$), the second constraint is the limit $R_a$ emerging from the $\mathcal{M}\mathcal{B}$s structure as $\mathcal{M}\mathcal{B}$s bottom boundary. Figure 4 highlight also the curves topology in the extended plane $R-r$, where it is clear that around $r=3$ (last photon circular orbit of the Schwarzschild spacetime) there is an extremum for the bundles, giving an immediate indication of the existence of replicas. At fixed R (defining the surface of the internal solution), there are replicas in different regions with $R>r$ or $r=R$ and $r\in [R,R_a].)$

Considering the description provided by the analysis of the extended plane, it is interesting to consider the limits

$$\begin{aligned} \lim _{R\rightarrow +\infty }\omega ^2_\pm =\frac{1}{r^2},\quad \lim _{R\rightarrow r}\omega ^2_\pm = \frac{r-2}{r^3}=\omega _{Schw}^2, \end{aligned}$$

(11)

where $\omega _{Schw}$ is in Eq. (3). The limit $R\rightarrow r$, represented in Fig. 4, shows how at $r= R$ (surface of the internal solution) the frequencies $\omega$ coincide with the vacuum Schwarzschild solution.

3.2 The Schwarzschild–Melvin solution

The interior Schwarzschild–Melvin solution has an electromagnetic component B governed by one metric parameter. It can be interpreted as modeling a BH in a uniform background electric or magnetic field. This solution can be derived from the Ernst solution and is not asymptotically flat. The event horizon is at $r_+ = 2M$, where M is the mass parameter. The condition $MB > 1$ is associated to a negative Gaussian curvature – [21]. The metric components are

$$\begin{aligned}{} & {} g_{tt}\equiv -\mathcal {\tilde{D}}^2\left( 1-\frac{2 M}{r}\right) ,\quad g_{\phi \phi }\equiv \frac{r^2 \sin ^2\theta }{\mathcal {\tilde{D}}^2},\nonumber \\{} & {} \text{ where }\quad \mathcal {\tilde{D}}\equiv \frac{1}{4} B^2 r^2 \sin ^2\theta +1. \end{aligned}$$

(12)

The limit $B=0$ is the Schwarzschild solution, while for $M=0$ the metric is the Melvin solution. Here we consider the solution with $M>0$, assuming $M=1$ to simplify the analysis. The bundles characteristic frequencies on $\theta =\pi /2$ are

$$\begin{aligned} \omega _{\pm }=\pm \frac{\sqrt{r-2} \left( B^2 r^2+4\right) ^2}{16 r^{3/2}}. \end{aligned}$$

(13)

For $r=2$, it is $\omega =0$. Metric bundles for this metric are shown in Fig. 4 in the extended plane $B-r$. Solutions are for $r\ge 2$. The figure points out the limit $B=1$, $r=2$ and the emergence of the photon circular orbit $r_\gamma =3$ of the Schwarzschild metric as an extreme of the bundles in the region $B<1$. As discussed in Sect. 2, the “zeros” of the metric bundles in the extended plane, describe the Schwarzschild solution. The curves topology in the extended plane, informs on the presence of replicas (at fixed B). It is clear that the configuration is different for the region $B<1$ (where multiple replicas appear) and the region $B>1$.

3.3 NUT solution

We consider in Sect. 3.3.1, the NUT solutions – [22, 23] – see also [20] as a generalization of the Schwarzschild spacetime, characterized by three metric parameters: the mass parameter M, the l NUT parameter (sometimes called magnetic mass or the gravitomagnetic monopole moment) and $\epsilon$, a discrete 2-space curvature parameter. The Taub solution we consider here corresponds to $\epsilon =+1$ and has as a limit the Schwarzschild solution.⁷ In the limit $l=0$, the metric tensor reduces to the Schwarzschild metric. Usually, it is assumed that $M>0$. For $M<0$, however, we can implement the metric symmetries and reverse the sign of r. The spacetime does not have a well-behaved axis at both $\theta = 0$ and $\theta = \pi$. However, it is possible to introduce a regular axis at $\theta = 0$ by applying the transformation $t\rightarrow (t + 2l\phi )$. We analyze this case in Sect. 3.3.2. For details on the asymptotic flatness of the metric and the local curvature see [20].

Fig. 5

Left panel: NUT1-solution of Eq. (15). Metric bundles are represented in the plane $l-r$, where l is the NUT-parameter, and on the equatorial plane $\theta =\pi /2$. The horizon is also represented for $\omega =0$. Right panel: NUT2-solution of Eq. (16). The characteristic frequencies are defined in Eq. (17). Curves $\omega _\pm =$constant, defining the $\mathcal{M}\mathcal{B}$s are shown in the extended plane $l-r$, for $\theta =\pi /2$

3.3.1 NUT1-metric

The metric components are

$$\begin{aligned}{} & {} g_{tt}\equiv -f_s(r),\quad g_{t\phi }\equiv 2 l f_s(r) \cos \theta ,\nonumber \\{} & {} \quad g_{\phi \phi }\equiv \sin ^2\theta \left( l^2+r^2\right) -4 f_s(r) l^2 \cos ^2\theta ,\nonumber \\{} & {} \quad \text{ where }\quad f_s(r)\equiv \frac{r^2-l^2-2 M r}{l^2+r^2}. \end{aligned}$$

(14)

In the following analysis we assume $M=1$. For $f_s(r)=0$ the metric has singularities which are related to the two Killing horizons associated with the metric symmetries and, in the extended plane $l-r$, there is $f_s(r)=0$ for $l_{\pm }=\pm \sqrt{r(r-2)}$. Note that $l_{\pm }$ exists for $r\in ]0,2]$, and $l_{\pm }=0$ for $r=0$ and $r=2$. In the following, similarly to the Kerr geometry, we consider a restriction of the extended plane $l-r$ for $l>0$. On the equatorial plane, for $\theta =\pi /2$, the bundle characteristic frequencies are

$$\begin{aligned} \omega _{\pm }=\sqrt{\frac{(r-2) r-l^2}{\left( l^2+r^2\right) ^2}}. \end{aligned}$$

(15)

However, as it is clear from Eq. (14), $\mathcal{M}\mathcal{B}$s (and their characteristic frequencies) would differ largely when analyzed closed to the axis $\theta =0$. On the horizon curve $l_\pm$, there is $\omega =0$. The metric bundles are shown in Fig. 5. Notice that the frequencies cancel each other out on the horizon. From Fig. 5, it is possible to note that bundles are defined in the region $r>2$. At $r_\gamma =3$ there is an extreme of the bundle curves in the extended plane where the $\mathcal{M}\mathcal{B}$s zeros correspond to the Schwarzschild case. The curve $l=l_\pm$, where $\omega =0$ (on the plane $\theta =\pi /2$), upper bounds the metric bundles curves. The curvature of the $\mathcal{M}\mathcal{B}$s curves in the extended plane shows the existence of a pair of replicas at fixed l, and the existence of a maximum l for fixed $\omega =$constant.

3.3.2 NUT2-solution

With the transformation $t\rightarrow (t+2l\phi )$, the metric tensor components become

$$\begin{aligned}{} & {} g_{tt}\equiv -f_n(r), \quad g_{\phi \phi }\equiv \sin ^2\theta \left( l^2+r^2\right) \nonumber \\{} & {} \qquad -16 f_n(r) l^2 \sin ^4\frac{\theta }{2},\nonumber \\{} & {} g_{t\phi }\equiv -4 f_n(r) l \sin ^2\frac{\theta }{2},\nonumber \\{} & {} \text{ where }\quad f_n(r)\equiv \frac{r^2-l^2-2 M r}{l^2+r^2},\nonumber \\ \end{aligned}$$

(16)

with a regular axis at $\theta =0$. The bundles characteristic frequencies are (assuming $M=1$ and $\theta =\pi /2$)

$$\begin{aligned} \omega _\pm = \frac{2l[(r-2) r- l^2]\pm (r^2 +l^2)\sqrt{(r-2) r-l^2}}{5 l^4-2 l^2 (r-4) r+r^4}. \end{aligned}$$

(17)

The frequency vanishes at the horizons $l_\pm$. The metric bundles are shown in Fig. 5, where the horizons are evident. The bundles frequencies $\omega _\pm$ are represented in the extended plane $l-r$ where $l>0$. Bundles are defined for $r\ge 2$. The solution $\omega =0$ represents the upper bound of the metric bundles. It is clear that in this case there can be multiple replicas at fixed l. There is also an extreme of the metric bundles for different $l\ge 0$ and different r.

3.4 The C-metric

With the analysis of the C-metric we start the study of $\mathcal{M}\mathcal{B}$s in geometries having BH horizons and acceleration horizons.

The C-metric can be interpreted as a generalization of the Schwarzschild geometry, describing an accelerating BH, whose acceleration is regulated by a metric parameter $\alpha$. The limit $\alpha =0$ is the Schwarzschild spacetime.⁸

The metric components are

$$\begin{aligned}{} & {} g_{tt}\equiv -f_C(r),\quad g_{\phi \phi }\equiv P_C(r) r^2 \sin ^2\theta ,\nonumber \\{} & {} \text{ where }\quad P_C(r)\equiv 1-2 \alpha M\cos \theta , \nonumber \\{} & {} f_C(r)\equiv \left( 1-\frac{2 M}{r}\right) \left( 1-\alpha ^2 r^2\right) . \end{aligned}$$

(18)

The metric has a conformal factor $\varOmega \equiv {1}/{(1-\alpha r \cos \theta )^2}$, which we have not considered in the study of the geometry of the $\mathcal{M}\mathcal{B}$s.

The radius $r_+ = 2M$ is the BH horizon while the acceleration horizon is $r = 1/\alpha$, which are Killing horizons associated with the Killing vector $\partial _t$. Considering $M=1$ and $\theta =\pi /2$, the bundle characteristic frequencies are

$$\begin{aligned} \omega _\pm =\pm \sqrt{\frac{(\alpha ^2 r^2-1)(2-r)}{r^3}}. \end{aligned}$$

(19)

On the (BH and acceleration) horizons, the frequency vanishes, $\omega =0$. The metric bundles are represented in Fig. 6. It is clear that bundles exist for $(2-r)(\alpha ^2 r^2-1)\ge 0$. Therefore, for different values of the acceleration $\alpha$, $\mathcal{M}\mathcal{B}$s exist also in a range $r<2$. In Fig. 6 we showed the extended plane $\alpha -r$, parameterizing the metric tensor for the acceleration $\alpha >0$. In this plane, the BH horizon is the axis $r=2$. It is clear that both the horizons $(r=2, r=1/\alpha )$, where $\omega =0$ bound the metric bundles. The zeros of the metric bundles describes $\mathcal{M}\mathcal{B}$s in the Schwarzschild spacetime. It is interesting to note how the presence of the acceleration $\alpha$ allows the description through $\mathcal{M}\mathcal{B}$s of the region internal to $r<2$, which is inaccessible in the case of null accelerations. The orange curve represents the extreme of the bundle curves in the extended plane. The curves are different according if $r<2$ or $r>2$, distinguishing also the limiting value of the acceleration parameter $\alpha =1/{2}$: for $\alpha >1/{2}$ bundles are for $r\in ]1/\alpha ,2[$, viceversa for $\alpha \in ]0,1/{2}[$ bundles are for $r>2$ bounded by the acceleration horizon. For $r>2$ it is clear the role of the photon marginally circular orbit $r=3$ of the Schwarzschild spacetime. It appears evident that at fixed $\alpha$ there are up to two replicas, close to the acceleration and BH horizons. As the acceleration horizon is a Killing horizon of the metric, $\mathcal{M}\mathcal{B}$s are bounded by the effects of the BH acceleration.

Fig. 6

Metric bundles for the C-metric of Eq. (18)-left panel and of Eq. (20)-center panel on the equatorial plane. There is $M=1$ and $\theta =\pi /2$, $\alpha$ is the acceleration parameter and $\omega =0$ sets the horizons (blue curve). Blue curves are the BH horizons, $r=2$, and the acceleration horizon $r=1/\alpha$. The orange curve represents the extreme points of the curves $\omega =$constant. The right panel shows the Minkowski-limit

The C-metric (II)

We examine here a modified (and conformally deformed) C-metric with

$$\begin{aligned} g_{\phi \phi }\equiv \frac{P_C(r) r^2\sigma }{(2 \alpha M+1)^2} \end{aligned}$$

(20)

– [20]. The metric bundles are represented in Fig. 6, where the characteristic frequencies are ($M=1$ and $\theta =\pi /2$)

$$\begin{aligned} \omega ^2=\frac{(2 \alpha +1)^2 (2-r) \left( \alpha ^2 r^2-1\right) }{r^3}. \end{aligned}$$

(21)

The BH horizon is at $r=2$, while the acceleration horizon is at $r=1/\alpha$. Comparing Eqs. (21) and (19), bundles are defined in the same regions of the extended plane $\alpha -r$. Figure 6 show the similarities among the two cases, where however the curves at $\alpha <1/2$ and $r>2$ bounded by the acceleration horizon, are distinguished by the presence of replicas. Also in this case we can see the role of the marginally circularly photon orbit. In Fig. 6, we have also considered the (Minkowski) limit $M=0$, in the extended plane $\alpha -r$. There is therefore only the acceleration horizon where $\omega =0$ bounding the metric bundles. We could compare therefore the case $M=1$ (C-metrics) and the case $M=0$, focusing on the role played by the BH horizon. At fixed $\alpha$ no replicas are shown. It is also interesting that at large r, the acceleration horizon decreases with r, reducing the range in which $\mathcal{M}\mathcal{B}$s are defined and consequently stationary observes in the C-spacetime .

3.5 Accelerating charged black holes

We take into consideration the following (electrically) charged version of the (conformally deformed) C-metric of Eq. (18) with

$$\begin{aligned}{} & {} g_{\phi \phi }\equiv P_Q(r) r^2 \sin ^2\theta ; \quad g_{tt}\equiv -f_Q(r),\quad \text{ where }\nonumber \\{} & {} P_Q(r)\equiv -2 \alpha M \cos \theta +\alpha ^2 Q^2 \cos ^2\theta +1\nonumber \\{} & {} \text{ and }\quad f_Q(r)\equiv \left( 1-\alpha ^2 r^2\right) \left( -\frac{2 M}{r}+\frac{Q^2}{r^2}+1\right) \end{aligned}$$

(22)

[20]. The metric bundles for this geometry are represented in Fig. 7. It is interesting to note that the introduction of an electromagnetic charge in an accelerated solution leads to an essential change in the $\mathcal{M}\mathcal{B}$s structure.

Fig. 7

Metric bundles in the accelerating charged BH spacetimes of Eq. (22) are shown in the plane $\alpha -r$ (upper line) and $Q-r$ (bottom lime), where Q is the charge parameter, $\alpha$ is the acceleration parameter. Here $M=1$ and $\theta =\pi /2$. Blue curves represent horizons

The metric limits are the RN solution and the C-metric. (In the following we shall consider $M=1$). The horizons coincide with the RN horizons and the acceleration horizon, i.e., $Q= \sqrt{r(2 -r)}$ (defined for $r\le 2$) and $r=1/\alpha$. The characteristic frequencies of the bundles are ($\theta =\pi /2$)

$$\begin{aligned} \omega _\pm =\pm \sqrt{-\frac{\left( Q^2+r^2-2 r\right) \left( \alpha ^2 r^2-1\right) }{r^4}}. \end{aligned}$$

(23)

Fig. 8

Ernst solution of Eq. (24) for $\theta =\pi /2$. Metric bundles are represented in the plane $\alpha -r$ (upper line panels) and $Q-r$ (bottom line panels) for different values of the metric parameters, where the mass parameter is $M=1$, B is a parameter representing the electromagnetic field strength, and $\alpha$ and Q are acceleration and charge parameters. Horizon curves are also shown (blue curves). Orange curves are extreme curves with respect to the radius r

From Fig. 7, we see how the acceleration and BH horizons play a role on the metric bundles structure, differently according to $\alpha >1$or $\alpha <1$. In presence of non-null acceleration, $\mathcal{M}\mathcal{B}$s fill regions of the extended plane, bounded by the BH horizons, which are inaccessible in absence of acceleration. In Fig. 7, we have used two $\mathcal{M}\mathcal{B}$s representation in two extended planes according to the adopted $\mathcal{M}\mathcal{B}$s parametrization. In the upper panels, we consider the plane $\alpha -r$ for different charges $Q<1$ (RN-BH), $Q=1$ (for $\alpha =0$ it corresponds to extreme RN-BH) and $Q>1$ (corresponding to RN-NSs for $\alpha =0$). We can compare this case with the C-metrics of Fig. 6, seeing the electric charge as a deformation of the C-metric. From the Fig. 7 it is clear that the introduction of the charge Q introduces two BHs events horizons $r_-\le r_+$. Metric bundles are bounded at $r<r_+$ by the acceleration horizon, approaching the inner horizon. The acceleration horizon coincides with the outer (inner) BH horizon for $\alpha =1/r_+(1/r_-)$. The topology of the curves in the extended plane is similar to that of the C-metrics. An interesting case is represented by the charge $Q=1$, for the extreme RN-BH, where $r_\pm =1$. It is also clear the existence of the extreme points of the bundle curves, corresponding at $\alpha =0$ to the last photon circular orbit in the RN spacetime. Interestingly, at $Q=1$ in the “inner” region of the extended plane $(r<1,\alpha <1)$ the $\mathcal{M}\mathcal{B}$s show similarities with the $\mathcal{M}\mathcal{B}$s in the Minkowski case of Fig. 6. The Minkowski case is also similar to the NS case represented in Fig. 7, where no replicas appear. In this case, therefore, the region of the extended plane corresponding to NSs is similar to that of the accelerated Minkowski spacetime.

Bundles are also shown in the extended plane $Q-r$ for different acceleration $\alpha$. This case can be compared to the RN $\mathcal{M}\mathcal{B}$s in the extended plane $Q-r$ – see also Eq. (5). There are the limiting cases $\alpha =1$, where the acceleration horizon coincides with the BH horizons $r_\pm =1$ for $Q=1$, and $\alpha =1/2$, where the acceleration horizon coincides with the limiting Schwarzschild BH horizon $r_\pm =2$ for $Q=0$ as represented in the Fig. 7. Differently from the RN case (the zeros of the $\mathcal{M}\mathcal{B}$s in the extended plane $\alpha -r$) metric bundles are confined by the acceleration horizon, but they can exist in the region $Q<Q_\pm$. There are then two ranges of accelerations. For $\alpha =1/2$, where bundles are only in $r<2$ and $Q>Q_{\pm }$ (on the equatorial plane). For $\alpha <1/2$, bundles are defined also for $r>2$. For $\alpha =1$, bundles are inside the BH outer horizon region (region of the extended plane upper bounded by the corresponding outer horizons curve in the limiting RN case) and out the BH inner horizon region, where the curves topology is similar to the Minkowski spacetime case. For $\alpha \in ]1/2,1[$ $\mathcal{M}\mathcal{B}$s are also defined in the region inside the BH inner horizon, as shown in Fig. 7. Replicas exist in the region bounded (from below and from above) by the outer horizons curves and for $r>2$.

3.6 The Ernst metric

The Ernst solution can be interpreted as describing a charged accelerating BH, whose acceleration, regulated in the metric by the parameter $\alpha$, can be induced by an external electric or magnetic field, represented in the metric by the parameter B. The metric has the charged C-metric solution as limiting case for $B=0$; it reduces to the Schwarzschild–Melvin metric when $\alpha = 0$ and $Q = 0$ (Q is the electric charge). Finally, it reduces to the Melvin geometry for $\{\alpha =0,Q=0,M=0\}$, where M is the mass parameter. The metric components are

$$\begin{aligned}{} & {} g_{\phi \phi }\equiv \frac{P_D(r) r^2 \sin ^2\theta }{\mathcal {D}_D^2},\quad g_{tt}\equiv -\mathcal {D}_D^2 f_D(r),\nonumber \\{} & {} \quad \text{ where }\quad f_D(r)\equiv \left( 1-\alpha ^2 r^2\right) \left( \frac{Q^2}{r^2}+1-\frac{2 M}{r}\right) ,\nonumber \\{} & {} \text{ and }\quad P_D(r)\equiv \alpha ^2 Q^2 \cos ^2\theta +1-2 \alpha M \cos \theta ,\nonumber \\{} & {} \quad \mathcal {D}_D\equiv \frac{B^2 P_D(r) r^2 \sin ^2\theta }{4 (1-\alpha r \cos \theta )^2}+\left( 1-\frac{1}{2} B Q \cos \theta \right) ^2. \end{aligned}$$

(24)

The metric has a conformal factor $\varOmega \equiv {1}/{(1-\alpha r \cos \theta )^2}$, neglected in the $\mathcal{M}\mathcal{B}$s study. There are the acceleration horizon and the RN horizons. The metric bundle characteristic frequencies are ($M=1$ and $\theta =\pi /2$)

$$\begin{aligned} \omega _\pm =\pm \sqrt{-\frac{\left( B^2 r^2+4\right) ^4 \left( Q^2+r^2-2 r\right) \left( \alpha ^2 r^2-1\right) }{256 r^4}}. \end{aligned}$$

(25)

The metric bundles are represented in Fig. 8, where the role of the acceleration and BH horizons is emphasized. On the horizons, $\omega _\pm =0$. The metric tensor has three parameters $\{\alpha ,Q,B\}$, and as the horizons are independent of the B parameter, in Fig. 8 the extended planes $\alpha -r$ and $Q-r$ are shown, where B is considered as a deformation parameter with respect to the case of charged and accelerated spacetime shown in Fig. 7. It is clear that the limiting values of r and $\alpha$ discussed in Sect. 3.5 are unaffected by the introduction of the B-parameter. There is a change in the $\mathcal{M}\mathcal{B}$s topology, the existence of the extreme points and the replicas, at different fixed values of Q or $\alpha$, showing an articulated situation characterizing also the region close to the inner horizons. The extension of this region decreases (in the radial distance for the bundle origins axes $r=0$) increasing the acceleration parameter or the electric charge.

3.7 Accelerating and rotating charged black holes

We continue the analysis of the accelerating solutions by considering an accelerating, electrically charged BH with a spin parameter a. The (conformally transformed) metric components are

$$\begin{aligned} g_{tt}\equiv & {} \frac{\left[ {a^2 P_J(r) \sin ^2\theta }-{f_J(r)}\right] }{\tilde{\rho }^2},\nonumber \\ g_{\phi \phi }\equiv & {} \frac{\sin ^2\theta \left[ {P_J(r) \left( a^2+r^2\right) ^2 }-{a^2 f_J(r) \sin ^2\theta } \right] }{\tilde{\rho }^2},\nonumber \\ g_{t\phi }\equiv & {} \frac{a\sin ^2\theta \left[ {f_J(r)}-{P_J(r) \left( a^2+r^2\right) }\right] }{\tilde{\rho }^2},\nonumber \\{} & {} \text{ where }\nonumber \\{} & {} \quad f_J(r)\equiv \left( 1-\alpha ^2 r^2\right) \left( a^2-2 M r+Q^2+r^2\right) , \nonumber \\ P_J(r)\equiv & {} \alpha ^2 \left( a^2+Q^2\right) \cos ^2\theta -2 \alpha M \cos \theta +1,\quad \text{ and } \nonumber \\ \tilde{\rho }\equiv & {} \sqrt{a^2 \cos ^2\theta +r^2}, \quad A\equiv -\frac{Q r \left( d t-a d \phi \sin ^2\theta \right) }{\tilde{\rho }^2},\nonumber \\ \end{aligned}$$

(26)

where A is the vector potential of the electromagnetic field – [20]. The metric has an acceleration horizon and the Kerr–Newman horizons.

On the equatorial plane $\theta =\pi /2$ and considering $M=1$, the bundles characteristic frequencies $\omega$ are

$$\begin{aligned}{} & {} \omega _\mp =\frac{a \left[ \alpha ^2 r^2 \left( a^2+S\right) -Q^2+2 r\right] \mp \sqrt{r^4 \left( 1-\alpha ^2 r^2\right) \left( a^2+S\right) }}{\alpha ^2 a^4 r^2+r^4+a^2 \left[ \alpha ^2 r^2 S-Q^2+r (r+2)\right] },\nonumber \\ \end{aligned}$$

(27)

where $S\equiv Q^2+(r-2) r$. The characteristic frequencies evaluated on the acceleration horizon and the inner and outer BH horizons are

$$\begin{aligned} \omega _{acc}\equiv & {} \frac{a \alpha ^2}{a^2 \alpha ^2+1}, \omega _H^-\equiv \frac{a \left( 2 \sqrt{1-a^2-Q^2}-Q^2+2\right) }{4 a^2+Q^4},\nonumber \\ \omega _H^+\equiv & {} \frac{a}{2 \sqrt{1-a^2-Q^2}-Q^2+2}, \end{aligned}$$

(28)

respectively – Fig. 9.

Fig. 9

Accelerating and spinning charged black holes of Eq. (26). Metric bundles on the equatorial plane are represented in the plane $a-r$ for different charge Q and acceleration $\alpha$ values. Here $M=1$ and a is the dimensionless BH spin parameter. Blue curves are the metric horizons

It is interesting to note how $\omega _{acc}$ does depend on $\{a,\alpha \}$ but not on the electric charge Q, while the inner and outer BH horizons (KN horizon frequencies) depend on the BH spin and charge but not on the acceleration parameter. As the metric depends (for $M=1$) on the three parameters $\{\alpha ,a,Q\}$, we could analyse $\mathcal{M}\mathcal{B}$s in the extended planes $\alpha -r$, $a-r$, and $Q-r$. In Fig. 9, we show the extended planes $\alpha -r$ for fixed $\{Q,a\}$, considered as deformation parameters for the cases in Fig. 7, or $a-r$ for fixed $\{\alpha ,Q\}$, considered as deformation parameters with respect to the Kerr case – see also Fig. 1.

Fig. 10

Accelerating charged spinning BH with cosmological constant of Eq. (29). Metric bundles on the equatorial plane are shown in the plane $a-r$, where a is the spin parameter ($M=1$), for different values of the charge parameter Q, acceleration parameter $\alpha$, and cosmological constant $\varLambda$. The horizon curves $a_\pm$ of Eq. (30) are also represented (blue curves)

Fig. 11

Metric bundles of the double extreme RN BHs, with metric components given in Eq. (33) and $\theta =\pi /2$ in the plane $r-M_1$ (left panel), $r-M_2$ (center panel) and $(r-b)$ (right panel). $(M_1,M_2)$ are the two BH mass parameters, b is the BHs (radial) distance, $\omega$ is the bundle characteristic frequency. The radius $r_+=M_1$ is the BH horizon. The blue line corresponds to $r=M_2$. The arrow indicates the increase of frequency values

Considering $\mathcal{M}\mathcal{B}$s in the extended plane $\alpha -r$ for fixed $\{Q,a\}$, and comparing with Fig. 7, it is clear how the combined presence of electric charge and spin changes the topology of the curves in the plane, particularly in the inner region for $r\in ]r_-,r_+[$ ($r_\pm$ being the Kerr–Newman BH inner and outer horizons), allowing the existence of multiple replicas. The bundles analysis in the plane $a-r$ shows a situation largely different from the Kerr case. Bundles are bounded by the Kerr–Newman BH inner and outer horizons and the acceleration horizon. For $Q<1$ it is evidenced the tangency condition to the horizon curve in the extended plane, absent for $Q>1$ where the extended plane describes accelerated Kerr–Newman NSs. The plots show the articulated structure of the bundles in the plane, stressing the presence of multiple replicas for selected ranges of the spin parameter. A notable difference appears for NSs with $Q\ge 1$ in the extended plane $a-r$, where limiting surfaces (curve a(r)) appear between two sections of the plane for $r<1$ and $r>1$. This is a special characteristic of NSs for this geometry.

3.8 Rotating accelerating charged BH with cosmological constant

In this section, we study the structure of metric bundles in spacetimes with cosmological constant, considering an accelerating and rotating BH with a non zero cosmological constant $\varLambda$. The case of a rotating BH with a cosmological constant has been considered in [15]. The (conformally deformed) metric components are

$$\begin{aligned} g_{tt}\equiv & {} \frac{\left[ a^2 P_{\tilde{\rho }}(r) \sin ^2\theta -{f_{\tilde{\rho }}(r)}\right] }{\tilde{\rho }^2},\nonumber \\ g_{\phi \phi }\equiv & {} \frac{\sin ^2\theta \left[ P_{\tilde{\rho }}(r) \left( a^2+r^2\right) ^2-a^2 f_{\tilde{\rho }}(r) \sin ^2\theta \right] }{\tilde{\rho }^2},\nonumber \\ g_{t\phi }\equiv & {} \frac{ a \sin ^2\theta \left[ f_{\tilde{\rho }}(r) - P_{\tilde{\rho }}(r) \left( a^2+r^2\right) \right] }{\tilde{\rho }^2}, \nonumber \\{} & {} \text{ where }\quad \tilde{\rho }\equiv \sqrt{a^2 \cos ^2\theta +r^2},\nonumber \\ P_{\tilde{\rho }}(r)\equiv & {} \cos ^2\theta \left[ \frac{a^2 \varLambda }{3}\!+\!\alpha ^2 \left( a^2+Q^2\right) \right] -2 \alpha M \cos \theta \!+\!1, \nonumber \\{} & {} \text{ and } \nonumber \\ f_{\tilde{\rho }}(r)\equiv & {} \left( 1-\alpha ^2 r^2\right) \left( a^2-2 M r+Q^2+r^2\right) \nonumber \\{} & {} \qquad -\frac{1}{3} \varLambda r^2 \left( a^2+r^2\right) \nonumber \\ \end{aligned}$$

(29)

– [20]. On this spacetime, there are an inner BH (Cauchy) horizon, an outer (event) BH horizon, and an acceleration horizon, when the corresponding conditions on the metric parameters $(Q,a, \varLambda , \alpha )$ are satisfied. We do not enter here into the details of the interpretation of horizons and the geometry, referring instead to the literature on the matter.⁹ In the following we shall consider $M=1$.

The horizon curves in the extended planes $\varLambda -r$, $Q-r$, $\alpha -r$ and $a-r$ are:

$$\begin{aligned} \varLambda _{\pm }\equiv & {} -\frac{3 \left( \alpha ^2 r^2-1\right) \left( a^2+S\right) }{r^2 \left( a^2+r^2\right) },\nonumber \\ Q_\pm\equiv & {} \frac{\sqrt{-3 \left[ a^2+(r-2) r\right] \left( \alpha ^2 r^2-1\right) -\left[ \varLambda r^2 \left( a^2+r^2\right) \right] }}{\sqrt{3 \alpha ^2 r^2-3}}, \nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned} \alpha _{\pm }\equiv & {} \frac{\sqrt{3 \left( a^2+S\right) -\varLambda r^2 \left( a^2+r^2\right) }}{\sqrt{3} \sqrt{r^2 \left( a^2+S\right) }},\nonumber \\ a_{\pm }\equiv & {} \frac{\sqrt{-3 S \left( \alpha ^2 r^2-1\right) -\varLambda r^4}}{\sqrt{r^2 \left( 3 \alpha ^2+\varLambda \right) -3}},\nonumber \\ \end{aligned}$$

(31)

respectively, where $S\equiv Q^2+(r-2) r$. The bundles characteristic frequencies on the equatorial plane ($\theta =\pi /2$) can be written as:

$$\begin{aligned}{} & {} \omega _\mp = \frac{\tilde{\wp }\mp \tilde{\wp }_1}{\tilde{\wp }_2},\nonumber \\{} & {} \quad \text{ where } \quad \tilde{\wp }\equiv 3 a \left[ \alpha ^2 r^2 \left( a^2+S\right) -Q^2+2 r\right] \nonumber \\{} & {} \quad +a \varLambda r^2 \left( a^2+r^2\right) , \quad \text{ and } \nonumber \\{} & {} \quad \tilde{\wp }_1\equiv \sqrt{9 r^4 \left( 1-\alpha ^2 r^2\right) \left( a^2+S\right) -3 \varLambda r^6 \left( a^2+r^2\right) },\nonumber \\{} & {} \quad \tilde{\wp }_2\equiv a^4 r^2 \left( 3 \alpha ^2+\varLambda \right) +\tilde{\wp }_3+3 r^4,\nonumber \\{} & {} \quad \tilde{\wp }_3\equiv a^2 \left[ 3 \alpha ^2 r^2 S-3 Q^2+\varLambda r^4+3 (r+2) r\right] . \end{aligned}$$

(32)

The corresponding metric bundles are represented in Fig. 10, where we note the emergence of horizons from the bundles. $\mathcal{M}\mathcal{B}$s are bounded by the horizons curves. For some values of the metric parameters $\mathcal{M}\mathcal{B}$s are tangent to the horizons. It is interesting to note the presence of disconnected regions of the extended plane $a-r$ for positive $\varLambda >0$, where $\mathcal{M}\mathcal{B}$s are confined close to the bundles origin axis and the central singularity.

Fig. 12

Metric bundles of the static wormhole metric of Eq. (38) for $\theta =\pi /2$ and $M=1$. The plotted radii $\{r_0, r_{\max },r_\star \}$ are defined in Eqs. (41) and (40). $\lambda$ is a dimensionless parameter defining the throat. $\omega$ is the bundle frequency. Purple curves are the limiting bundles with frequency $\omega ={1}/{3 \sqrt{3}}$

3.9 Binary extreme RN BHs

We investigate the metric featuring a binary extreme RN BHs system, having masses $(M_1, M_2)$ and electro-magnetic charges $Q_1 = \pm M_1, Q_2 = \pm M_2$ ($Q_1 Q_2=M_1 M_2>0$) at a relative distance $r=2b$. The geometry can be included in the Majumdar–Papapetrou family of solutions, providing singularity-free stationary electrovacuum spacetimes with multiple BHs. The binary BH geometry is regulated by the balance between the BH gravitational attraction and the electric repulsion. Then, the binary BH system can be considered in static equilibrium. The line element is

$$\begin{aligned}{} & {} \text {ds}^2=-N^2 d t^2+\frac{dr^2}{N^2}+\frac{r^2 \left( 1-\frac{M_1}{r}\right) ^2d \varOmega ^2}{N^2},\nonumber \\{} & {} \quad \text{ where }\nonumber \\{} & {} N\equiv \left[ {\frac{M_2}{\sqrt{4 b^2+4 b \cos (\theta ) (r-M_1)+(M_1-r)^2}}-\frac{r}{M_1-r}}\right] ^{-1}\nonumber \\ \end{aligned}$$

(33)

and $d\varOmega ^2\equiv d\theta ^2+d \phi ^2 \sin ^2\theta$. The spheroidal coordinates are adapted to a BH with mass $M_1$ and horizon $r = M_1$. Therefore, the second (point-like) BH lies on $r = M_1 + 2b$. N is the lapse function adapted to the BH with mass $M_1$. The second BH, with mass $M_2$, is point-like and located on $\theta =\pi$. The limit of a single BH is obtained for $M_2 = 0$. The singularity (for the first BH with $M=M_1$) is on $1/N = 0$ – see for example [24] – and also [25]. The electromagnetic field is given by the potential $A^\mu _\nu = (\pm N, 0, 0, 0)$. The metric can be interpreted as describing a BH geometry with the deformation induced by another BH.

The bundles characteristic frequencies are

$$\begin{aligned} \omega = \frac{N(r,\theta )\sqrt{N(r,\theta )^2}}{\sqrt{\sigma (M_1-r)^2}}. \end{aligned}$$

(34)

The following notable limits exist for the lapse function N

$$\begin{aligned} \lim _{\beta }N= & {} \left\{ \frac{1}{\frac{M_2}{\sqrt{4 b^2+(M_1-r)^2}}+\tilde{g}_1^{-1}},\frac{1}{\frac{M_2}{\sqrt{(2 b-M_1+r)^2}}+\tilde{g}_1^{-1}},\right. \nonumber \\{} & {} \frac{1}{\frac{M_2}{\sqrt{4 b^2+4 b r \cos \theta +r^2}}+1},\nonumber \\{} & {} \tilde{g}_1,\frac{1}{\frac{M_2}{\sqrt{4 b^2+4 b \cos \theta (r-M_2)+(M_2-r)^2}}-\frac{r}{M_2-r}},\nonumber \\{} & {} \left. \tilde{g}_1,\frac{1}{\frac{M_2}{\sqrt{(M_1-r)^2}}+\tilde{g}_1^{-1}}\right\} \end{aligned}$$

(35)

where

$$\begin{aligned}{} & {} \beta \equiv \left\{ \theta \rightarrow \frac{\pi }{2}, \theta \rightarrow 0, M_1\rightarrow 0, M_2\rightarrow 0, \right. \nonumber \\{} & {} \quad \left. M_1\rightarrow M_2,b\rightarrow +\infty ,b\rightarrow 0\right\} , \tilde{g}_1\equiv 1-\frac{M_1}{r}. \end{aligned}$$

It is clear the emergence of the limit $r=M_1$. The limiting case $N^{-1}=0$ is valid for

$$\begin{aligned}{} & {} r<M_1:\left[ \left( b\in [0,b_+[, \sigma \in [0,1]\right) , \left( b=b_+, \sigma \in ]0,1]\right) ,\right. \\ {}{} & {} \quad \left. \left( b>b_+,\sigma \in [0,1]\right) \right] ,\text{ where }\quad b_+\equiv \frac{M_1-r}{2}, \end{aligned}$$

It is $b_+\ge 0$ for $r\le M_1$. With the parametrization $r\rightarrow (M_1+x)$, we obtain the following four solutions

$$\begin{aligned}{} & {} x_\pm ^q=\frac{\breve{\tau }-q\left( \sqrt{\mathcal {P}_-}\pm \sqrt{\mathcal {P}_+-\mathcal {I}_q}\right) }{2},\nonumber \\{} & {} \quad \text{ where }\quad q\equiv \pm , \quad \breve{\tau }\equiv -\left( 2 b \sqrt{1-\sigma }+M_1\right) ,\nonumber \\{} & {} \quad \mathcal {P}_+\equiv \frac{\tilde{\xi }_2+\hat{\xi }_2+\breve{\xi }_2}{12 \root 3 \of {\mathcal {D}}}. \end{aligned}$$

(36)

and

Fig. 13

Metric bundles analysis in rotating wormhole geometries. Upper left panel: Radii $r_{m}^\pm$ of Eq. (45). The envelope surfaces for the metric bundles $r_\omega ^\pm$ are plotted as functions of the spin a/M and the parameter $\lambda$. Metric bundles ($r_\omega ^0$) of the rotating wormhole of Eq. (42), and ($r_\omega ^\pm$) of Eqs. (43, 44) are shown for $M=1$ in the extended plane $\lambda -r$ and $a-r$ for different values of the metric parameters with $\theta =\pi /2$ and $\sigma \equiv \sin \theta ^2=0.1$ (bottom right panel). The radii $r_\kappa ^\pm$ (blue curves), are shown, where the radius $r_\kappa ^+$ defines the wormhole throat connecting two asymptotically flat regions. The radii $r_m^\pm$ (purple curves) and Kerr BH horizons $r_\pm$ (green curves) as envelope surfaces of the metric bundles are also shown

Fig. 14

Metric bundles in the geometry of a rotating charged BH solution of the heterotic string theory given by Eq. (46) for $\theta =\pi /2$ and $M=1$. The red curves are the BH horizons and metric bundles envelope surfaces. The blue line is the limiting value $Q=\sqrt{2}M$. The planes $Q-r$ and $a-r$ are shown explicitly, where Q and a are the BH charge and spin, respectively

Fig. 15

Metric bundles for BHs in perfect-fluid dark matter of Eq. (49) for $\theta =\pi /2$ and $M=1$. The red curves are the horizons and envelope surfaces of the metric bundles. Different values of $k > rless 0$, describing the intensity of the perfect-fluid dark matter, are considered. k is in the ranges $k/M\in ]-7.18, 2[$. For $k=0$ the line element describes the Kerr geometry

Fig. 16

Metric bundles of the BTZ geometry of Eq. (50). Dashed curves are for light-like orbital frequencies $\omega _-=$constant and plain curves are for $\omega _+=$constant. Upper left panel: The horizons $r_{\pm }$ as functions of the angular momentum J (dashed) and $\ell$ (plain), being related to the cosmological constant by $\varLambda =-1/\ell ^2$, for selected values of the metric parameters. Blue curves are the zero of the characteristics frequencies. (The characteristic frequencies are null $\omega _\pm =0$ for $r= \sqrt{\ell ^2 M}$, with $M>0$ and $\forall J$). In the plane $J-r$, the bundle is null (non-rotating solutions) for $r= \sqrt{{M\ell ^2}/({1-\ell ^2\omega ^2})}$, red curves are the horizons curves in the extended plane

$$\begin{aligned} \mathcal {I}_q\equiv & {} \mathcal {I}_\mp \equiv \frac{\tilde{\xi }_\mp }{12 \sqrt{\mathcal {P}_-}},\quad \mathcal {P}_-\equiv \frac{\tilde{\xi }_3+\hat{\xi }_3+\breve{\xi }_3}{6 \root 3 \of {\mathcal {D}}},\\ \tilde{\xi }_\mp\equiv & {} 2\ 2^{2/3} \sqrt{\mathcal {P}_-} \root 3 \of {\mathcal {D}}\mp 48 b^2 (4 M_1-\tilde{S})\mp \tilde{\xi }_1,\\ \tilde{S}\equiv & {} 2 M_1+4 b \sqrt{1-\sigma }, \\ \tilde{\xi }_1\equiv & {} 3 \tilde{S} \left( \tilde{S}^2-4 M_1^2+4 M_2^2\right) +96 b M_1 (\tilde{S}-M_1) \sqrt{1-\sigma }, \\ \hat{\xi }_2\equiv & {} 16 b^2 \left[ (3 \sigma -7) \root 3 \of {\mathcal {D}}+2 \root 3 \of {2} \left[ (2 \sigma -3) M_1^2+M_2^2\right] \right] , \\ \breve{\xi }_2\equiv & {} 128 \root 3 \of {2} b^3 M_1 \sqrt{1-\sigma }\\{} & {} +16 b M_1 \left[ 2 \root 3 \of {2} \left( M_1^2+2 M_2^2\right) -11 \root 3 \of {\mathcal {D}}\right] \sqrt{1-\sigma }, \\ \tilde{\xi }_2\equiv & {} \left( 9 \tilde{S}^2-28 M_1^2+16 M_2^2\right) \root 3 \of {\mathcal {D}}-64 \root 3 \of {2} b^4-4 \root 3 \of {2} \left( M_1^2-M_2^2\right) ^2 \\ \breve{\xi }_3\equiv & {} -64 \root 3 \of {2} b^3 M_1 \sqrt{1-\sigma }-8 b M_1 \left[ \root 3 \of {\mathcal {D}}+2 \root 3 \of {2} \left( M_1^2+2 M_2^2\right) \right] \sqrt{1-\sigma }, \\ \hat{\xi }_3\equiv & {} 8 b^2 \left[ \root 3 \of {\mathcal {D}} (1-3 \sigma )-2 \root 3 \of {2} \left[ (2 \sigma -3) M_1^2+M_2^2\right] \right] , \\ \tilde{\xi }_3\equiv & {} 2 \left( M_1^2+2 M_2^2\right) \root 3 \of {\mathcal {D}}+2^{2/3} \mathcal {D}^{2/3}+32 \root 3 \of {2} b^4+2 \root 3 \of {2} \left( M_1^2-M_2^2\right) ^2,\\ \mathcal {D}\equiv & {} \mathcal {D}_a+\sqrt{\tilde{\mathcal {D}}_a+\mathcal {D}_a^2}; \\ \tilde{\mathcal {D}}_a\equiv & {} 4 \left[ \tilde{\xi }_4-\left( 4 b^2+8 M_1 \sqrt{1-\sigma } b+M_1^2-M_2^2\right) ^2\right] ^3,\\ \mathcal {D}_a\equiv & {} 2 \left( \tilde{\xi }_5+16 M_1 \left[ 2 M_1^2 (2 \sigma -5)-3 M_2^2\right] \sqrt{1-\sigma } b^3+\right. \\{} & {} \left. \tilde{\xi }_6-12 M_1 \left( M_1^4+M_2^2 M_1^2-2 M_2^4\right) \sqrt{1-\sigma } b+\left( M_1^2-M_2^2\right) ^3\right) ;\\ \tilde{\xi }_4\equiv & {} 24 b M_1 \left[ 4 \sqrt{1-\sigma } b^2-2 M_1 (\sigma -1) b+M_1^2 \sqrt{1-\sigma }\right] , \\ \tilde{\xi }_5\equiv & {} 64 b^6-192 M_1 \sqrt{1-\sigma } b^5-48 \left[ (4 \sigma -5) M_1^2+M_2^2\right] b^4,\\ \tilde{\xi }_6\equiv & {} 12 \left[ (5-4 \sigma ) M_1^4+2 M_2^2 (5 \sigma +3) M_1^2+M_2^4\right] b^2. \end{aligned}$$

Moreover, $N=0$ for $r=r_+=M_1$. More precisely,

$$\begin{aligned}{} & {} N=0\quad \text{ for } r=0: \left( M_1>0, b=\frac{M_1}{2}, \sigma =0\right) , \nonumber \\{} & {} r=M_1: \left( b>0, M_2\ge 0, \sigma \in [0,1]\right) ,\nonumber \\{} & {} r<M_1: \left( b=b_+, M_2>0, \sigma =0\right) . \end{aligned}$$

(37)

$\mathcal{M}\mathcal{B}$s have proved to be a useful tool for the analysis of solutions with multiple gravitational sources (in presence of certain symmetries). Considering then that the $\mathcal{M}\mathcal{B}$s formalism is constructed on special light surfaces and photon circular orbits constraining stationary observers, this can give indications on the analysis of the causal structure (within the symmetries explored here) also in the regions between the two sources as in the case illustrated in Fig. 11.

The corresponding metric bundles are in Fig. 11. The horizon $r=M_1$ delimits also in this geometry the region of $\mathcal{M}\mathcal{B}$s existence.

$\mathcal{M}\mathcal{B}$s are constructed in Fig. 11 in the extended planes $M_1-r$ and $M_2-r$ at fixed $(M_1,b)$ on the equatorial plane and in the plane $b-r$ for fixed $(M_1,M_2)$. In the plane $M_1-r$, the radius $r_+$ bounds from below the metric bundles where, at fixed $M_1$, there are two replicas. On the plane $M_2-r$, it is evidenced the emergence of two regions $r>r_+$ (where there are up to two replicas) and $r<r_+$. On the extended plane $b-r$, the solutions $\omega <0$ and $\omega >0$ are represented. Also in this case, it is clear the existence of (up to two) replicas in the region $r>r_+$. $\mathcal{M}\mathcal{B}$s are distinct for $b\ll 1$ (close BHs) and $b\gg 1$.

3.10 Wormholes

In this section, we analyze different wormhole spacetimes. We investigate the static Damour–Solodukhin wormhole [26] in Sect. 3.10.1 and a rotating generalization that approximates a Kerr BH outside the throat [27] in Sect. 3.10.2.

3.10.1 Static wormhole

We consider the static wormhole [26] (see also [27]) with metric functions:

$$\begin{aligned}{} & {} g_{tt}\equiv -f_{\tilde{W}}(r),\quad g_{\phi \phi }\equiv r^2 \sin ^2\theta ; \nonumber \\{} & {} \quad \text{ and }\quad f_{\tilde{W}}(r)\equiv \lambda ^2-\frac{2 M}{r}+1. \end{aligned}$$

(38)

In the limiting case $\lambda =0$, this metric reduces to the Schwarzschild BH metric. For $\lambda \ne 0$ there is a throat at $r=2M$, joining two isometric, asymptotically flat regions (Lorentzian wormhole). To recover the physical time at infinity (t as time for the asymptotic observers), it is necessary to apply the transformations $t\rightarrow t/\sqrt{1+\lambda ^2}$ and $M\rightarrow M(1+\lambda ^2)$. In this frame, $f_{\tilde{W}}(r)=1-2M/r$ leads to the Schwarzschild BH horizon $r=2M$ as a solution of $f(r)=0$ and the metric bundles reduce to the Schwarzschild $\mathcal{M}\mathcal{B}$s.

In the following, we consider $M=1$ and $\theta =\pi /2$. In the frame (38), the null frequency $(\mathcal {L}_{\mathcal {N}}=0)$ and the bundles equation for the bundles $\lambda (r;\omega )$ in the $\lambda$-parametrization are

$$\begin{aligned} \omega = \pm \frac{\sqrt{r(1+\lambda ^2)-2}}{r^{3/2}},\quad \lambda =\pm \frac{\sqrt{2 +r(r^2 \omega ^2-1)}}{\sqrt{r}}. \end{aligned}$$

(39)

For $\omega =0$, we obtain $r=r_0$ with

$$\begin{aligned} r_0\equiv \frac{2}{\lambda ^2+1}, \end{aligned}$$

(40)

which is shown in Fig. 12 in the extended plane $\lambda -r$ for the entire region of positive and negative values of the $\lambda$-parameter, where $r_0$ and other quantities are even functions of $\lambda$. It is clear that $r_0=2$ is the limiting case of $\lambda =0$ (a Schwarzschild BH). The curve $r_0$ represents the bottom boundary of the metric bundles, symmetric around the value $\lambda =0$, representing an extreme point of the bundles curves seen as a function $r(\lambda )$. We have pointed out the ranges delimited by the values $r=2$ (throat of the wormhole and BH horizon for $\lambda =0$), and the radius $r_\gamma =3$, marginally photon circular orbit.

We introduce also the radii:

$$\begin{aligned}{} & {} r_{\max }\equiv \frac{3}{\lambda ^2+1}:\partial _r\omega =0,\nonumber \\{} & {} \quad r_\star \equiv \left( \sqrt{1+\frac{4}{\lambda ^2}}-1\right) :\omega (r_\star )=\omega (r=2), \end{aligned}$$

(41)

shown in Fig. 12 with the $\mathcal{M}\mathcal{B}$s in the extended plane $\lambda -r$. Note the role of the radii $r=2$ and $r=3$. The radius $r_{\max }$ is the maximum of the bundle curves as functions of r. The radius $r_\star$ is the replica of the frequencies on the wormhole throat (wormhole replicas). It is $\omega (r=2)=0$ only for $\lambda =0$. The limiting bundles with characteristic frequency $\omega =1/3 \sqrt{3}$ are also shown. At fixed $\lambda$ there are generally two replicas. Considering $\lambda \ge 0$, the extended plane shows the presence of four regions, which are significant for the wormhole geometry and their metric bundles, bounded by the curves $r_0$, with limiting bundles at $\omega =1/3\sqrt{3}$, and the axes $\lambda =0$. The frequency $\omega =1/3\sqrt{3}$ corresponds to the limiting value $W_{\max }$ in Eq. (4), occurring at $r=r_{\gamma }=3$, which is the photon (last) circular orbit in the Schwarzschild spacetime and is also an extreme of the frequency $\omega _{Schw}$ for r, where $\omega _{Schw}(W_{\max })={1}/{3 \sqrt{3} \sqrt{\sigma }}$.

3.10.2 Rotating wormhole

Here, we investigate the rotating wormhole obtained in [27] from the Kerr geometry. The metric components are

$$\begin{aligned}{} & {} g_{tt}\equiv -\left( 1-\frac{2 M r}{\varSigma }\right) , g_{\phi \phi }\equiv \sigma \left( \frac{2 a^2 M r \sigma }{\varSigma }+a^2+r^2\right) ,\nonumber \\{} & {} g_{t\phi }\equiv -\frac{2 a M r \sigma }{\varSigma }, \text{ where }\quad \varSigma \equiv a^2 (1-\sigma )+r^2. \end{aligned}$$

(42)

Proceeding as in Sect. 3.10.1, we note that the solutions $f_W(r)\equiv a^2-2 \left( \lambda ^2+1\right) M r+r^2=0$ provide the radii $r_k^\pm \equiv \lambda ^2 M+M \pm \sqrt{\left( \lambda ^2+1\right) ^2 M^2-a^2}$. The (outer) radius $r_\kappa ^+$ is not a horizon, but defines the wormhole throat connecting two asymptotically flat regions. We use the following two transformations, $(-)$ and $(+)$, of the line element $\textrm{d}s^2$ defined by the metric (42):

$$\begin{aligned}{} & {} (-):\quad \textrm{d}s_{(-)}^2\equiv \left. \textrm{d}s^2\right| \nonumber \\{} & {} \quad \left\{ \textrm{d}t\rightarrow \textrm{d}t \sqrt{\lambda ^2+1}, M\rightarrow \frac{M}{\lambda ^2+1}, \textrm{d}\phi \rightarrow \textrm{d}\phi \sqrt{\lambda ^2+1}\right\} , \nonumber \\ \end{aligned}$$

(43)

$$\begin{aligned}{} & {} (+):\quad \textrm{d}s_{(+)}^2\equiv \left. \textrm{d}s^2\right| \left\{ \textrm{d}t\rightarrow \textrm{d}t \sqrt{\lambda ^2+1}, M\rightarrow \frac{M}{\lambda ^2+1}\right\} .\nonumber \\ \end{aligned}$$

(44)

The curves $r(\omega ,\lambda ,a)$ defining the bundles are $r_\omega ^-$ and $r_\omega ^+$, for the first and second transformations respectively, having envelope surfaces with radii $r_m^\pm$, where

$$\begin{aligned} r_m^\pm\equiv & {} \frac{1}{\lambda ^2+1}\pm \sqrt{\frac{1}{\left( \lambda ^2+1\right) ^2}-a^2},\quad \text{ or, } \text{ alternatively }\nonumber \\ \lambda _m\equiv & {} \frac{\sqrt{(2-r) r-a^2}}{\sqrt{a^2+r^2}},\quad a_m\equiv \frac{\sqrt{r} \sqrt{\left( 2-\lambda ^2 r-r\right) }}{\sqrt{\lambda ^2+1}}. \end{aligned}$$

(45)

Here, $\lambda \ge 0$, and $a\in [0,{1}/({\lambda ^2+1})]$. In Fig. 13, the radii $r_m^\pm$ are shown explicitly. It is clear how $r_{m}^\pm$ are the envelope surfaces of the $\mathcal{M}\mathcal{B}$s in Eqs. (43, 44), while the Kerr BH horizons are the envelope surfaces of the metric bundles for Eq. (42).

The metric bundles $r_\omega ^0$ of the metric (42) correspond to the $\mathcal{M}\mathcal{B}$s of the Kerr geometry with envelope surfaces defined by the Kerr BH horizons $r_\pm$ – see also Fig. 1. In Fig. 13, the $\mathcal{M}\mathcal{B}$s $r_\omega ^0$ of the rotating wormhole of Eq. (42), and $r_\omega ^\pm$ of Eqs. (43, 44) are shown (for $M=1$) in the extended planes $\lambda -r$ and $a-r$ for different values of the metric parameters for $\theta =\pi /2$ and for $\sigma \equiv \sin \theta ^2=0.1$. The radii $r_k^\pm$ (blue curves), $r_m^\pm$ (purple curves) and Kerr BH horizons $r_\pm$ (green curves) are also shown. The curves $r_m^\pm$ bound the metric bundles $r_\omega ^\pm$. It is clear the tangency condition which ensures the interpretation of the metric bundles characteristic frequencies as horizons/wormhole throat replicas. This property can be seen also in the extended plane $r-\lambda$. The $\mathcal{M}\mathcal{B}$s topology and curvature in the extended planes contain information about the existence of replicas, which is regulated also by the parameter $\lambda$. The influence of $\lambda$ on the $\mathcal{M}\mathcal{B}$s construction is more evident in the regions close to the rotational axis ($\sigma > rsim 0)$.

3.11 Rotating charged BH solution of the heterotic string theory

We explore a solution of the low-energy effective field theory of a heterotic string theory, describing a four dimensional BH with mass, (electric) charge and angular momentum – [28]. In Boyer–Lindquist coordinates, the metric components are ($M=1$)

$$\begin{aligned} g_{tt}= & {} -\left( 1-\frac{2 r}{\varSigma _K}\right) ,\quad g_{t\phi }=-\frac{2 a r \sigma }{\varSigma _K},\nonumber \\ g_{\phi \phi }= & {} \sigma \left[ \frac{2 a^2 r \sigma }{\varSigma _K}+a^2+r \left( Q^2+r\right) \right] \nonumber \\{} & {} \text{ where }\quad \varSigma _K\equiv a^2 (1-\sigma )+r \left( Q^2+r\right) . \end{aligned}$$

(46)

[29]. The horizons are

$$\begin{aligned}{} & {} r_K^\pm \equiv \frac{1}{2}\left[ 2-Q^2\pm \sqrt{\left( Q^2-2\right) ^2-4 a^2}\right] \end{aligned}$$

(47)

in the ranges

$$\begin{aligned}{} & {} \left( Q\in [0,\sqrt{2}], a\in [0,a_K], r=r_K^\pm \right) ,\nonumber \\{} & {} \left( Q=\sqrt{2}, a=0, r=0\right) , \nonumber \\{} & {} \quad \left( Q>\sqrt{2}, a=0, r=r_K^\pm \right) ,\nonumber \\{} & {} \text{ where }\quad a_K\equiv \frac{\left( 2-Q^2\right) }{2}. \end{aligned}$$

(48)

As we have restricted the analysis to the values $a\ge 0$ and $Q\ge 0$, the spin $a_K$ is well defined only for $Q\in [0,\sqrt{2}]$, where $a_K\in [0,1]$.

In Fig. 14, the $\mathcal{M}\mathcal{B}$s are represented in the planes $Q-r$ and $a-r$, on the equatorial plane for fixed $M=1$. The horizons as $\mathcal{M}\mathcal{B}$s envelope curves are evident.

In Fig. 14, we consider the extended plane $Q-r$ and $a-r$. We can compare these $\mathcal{M}\mathcal{B}$s with those of the KN spacetimes (see Sect. 2). As it is clear from the curvature of the $\mathcal{M}\mathcal{B}$s curves in the extended planes, the replicas analysis (on the equatorial plane) shows the existence of multiple orbits for a fixed spacetime (fixed parameters (Q, a)). Metric bundles are not defined in the region upper bounded by the horizons, but the $\mathcal{M}\mathcal{B}$s zeros inform on the limiting cases of the geometries (at $Q=0$ or for $a=0$).

3.12 Rotating BHs in perfect-fluid dark matter

A rotating BH solution in perfect-fluid dark matter has been discussed in [30, 31].

The metric components are ($M=1$)

$$\begin{aligned} g_{\phi \phi }= & {} \sigma \left[ \frac{a^2 \sigma [2 r-f_D(r)]}{\varSigma _D}+\left( a^2+r^2\right) \right] ,\nonumber \\ g_{t\phi }= & {} -\frac{\sigma [a (2 r-f_D(r))]}{\varSigma _D}, \quad g_{tt}=-\left[ 1-\frac{2 r-f_D(r)}{\varSigma _D}\right] ;\nonumber \\ \varDelta _D\equiv & {} a^2+f_D(r)+r^2-2 r,\quad \varSigma _D\equiv a^2 (1-\sigma )+r^2,\nonumber \\{} & {} f_D(r)\equiv k r \log \left( \frac{r}{| k| }\right) , \end{aligned}$$

(49)

where k is the parameter describing the intensity of the perfect-fluid dark matter and has been chosen in the ranges $k\in ]-7.18M, 2M[$. For $k=0$ the line element reduces to the Kerr metric. The $\mathcal{M}\mathcal{B}$s for these geometries have been plotted in Fig. 15. It can be seen that the tangency condition, shown for $\sigma =1$ and $M=1$, defines the curve of the horizons even for negative dark matter k parameter. Dark matter acts as a deformation of the $\mathcal{M}\mathcal{B}$s of the Kerr geometry extended plane (see Fig. 1). However, the situation for $r>r_+$, where $r_+$ is the outer horizon at $a=0$, describing the zeros of the $\mathcal{M}\mathcal{B}$s in the extended plane $a-r$ differs from the spacetime in absence of dark matter. Furthermore, the condition $k<0$ provides a deformation of the $\mathcal{M}\mathcal{B}$s in the inner horizons region (close to the BH axis and $\mathcal{M}\mathcal{B}$s origin at $r=0$), with a maximum as a function of r. It is evident then that the replica analysis would provide a clear discriminant in the determination of a possible dark matter parameter.

3.13 The BTZ solution

The BTZ metric is a $2 + 1$ stationary and axially symmetric BH solution with a negative cosmological constant and was proposed by Bañados, Teitelboim and Zanelli in [32]. The metric is¹⁰

$$\begin{aligned}{} & {} g_{\phi \phi }=r^2, \quad g_{t\phi }=N_{\phi } r^2,\quad g_{tt}=N_{\phi }^2 r^2-N_{a}^2,\nonumber \\{} & {} \quad \text{ where } \quad N_{\phi }\equiv -\frac{J}{2 r^2},\quad N_{a}^2\equiv \frac{J^2}{4 r^2}+\frac{r^2}{\ell ^2}-M. \end{aligned}$$

(50)

The two constants of integration M and J are the mass and angular momentum, respectively. A BH occurs for $|J|\le M \ell$, the parameter $\ell$ being related to the cosmological constant by $\varLambda =-1/\ell ^2$.

The lapse function N(r) vanishes for two values of r providing the horizons at

$$\begin{aligned} r_\pm \equiv \sqrt{\frac{\ell ^2 M\pm \sqrt{\ell ^4 M^2-J^2 \ell ^2}}{2}}. \end{aligned}$$

(51)

For $J= M\ell$, the horizons coincide $r_+=r_-$. More specifically, for $M>0$, we obtain that $N_a>0$ for

$$\begin{aligned}{} & {} \ell ^2>0:\quad J^2\ge \ell ^2 M^2,\quad (J^2=0, r^2\ge \ell ^2 M); \nonumber \\{} & {} \quad (J^2\in ]0,\ell ^2 M^2[, (r\in ]0,r_-]\cup r\ge r_+)), \end{aligned}$$

(52)

which define the horizons $r_{\pm }$. A particular case is for $M=1/\ell ^2$ and $M=J$.

In the extended planes, the horizons can also be expressed as

$$\begin{aligned}{} & {} M_\pm \equiv \frac{J^2}{4 r^2}+\frac{r^2}{\ell ^2},\quad J_\pm \equiv \frac{2 \sqrt{\ell ^2 M r^2-r^4}}{\ell },\nonumber \\{} & {} \quad \times \ell _\pm \equiv \frac{2 r^2}{\sqrt{4 M r^2-J^2}} \end{aligned}$$

(53)

where the values $M<0$, $J<0$ and $\ell <0$ are allowed. The vacuum empty state is obtained with $M=0$ and $J=0$. The singularity and horizons disappear for $M =-1$ and $J=0$. Then,

$$\begin{aligned} g_{tt}>0 \quad \text{ for }\quad M>0,\quad \ell \ne 0,\quad r\in ]0, \ell \sqrt{M}] \end{aligned}$$

(54)

defines an “ergosurface”. For $M=\{0,-1\}$ or $M>0$ and $J^2\ge \ell ^2 M^2$, there are no horizons and $N_a>0$ for $r> 0$.

The $\mathcal{M}\mathcal{B}$s analysis is independent of the sign of $\ell$, but depends on the sign of $J \omega$. The horizon frequencies are

$$\begin{aligned} \omega (r_-)= & {} -\frac{J}{\sqrt{\ell ^4 M^2-J^2 \ell ^2}-\ell ^2 M}, \nonumber \\ \omega (r_+)= & {} \frac{J}{\sqrt{\ell ^4 M^2-J^2 \ell ^2}+\ell ^2 M}, \end{aligned}$$

(55)

while the light surfaces and the bundles characteristic frequencies $\omega _\pm$ (solutions of $\mathcal {L}_{\mathcal {N}}=0$) are

$$\begin{aligned} r=\frac{\sqrt{M-J \omega }}{\sqrt{\frac{1}{\ell ^2}-\omega ^2}} ,\quad \omega _\pm = \frac{J\pm \sqrt{J^2+\frac{4 r^4}{\ell ^2}-4 M r^2}}{2 r^2}, \end{aligned}$$

(56)

respectively.

The frequencies are null for $r\rightarrow \sqrt{\ell ^2M}$ (where there is also a second photon-like frequency $\omega \rightarrow {J}/{\ell ^2 M}$) – see also Eq. (54). The special case $\omega =M/J$ and $\omega =1/\ell$ is notorius. The bundles can be expressed as

$$\begin{aligned} \ell =\frac{r}{\sqrt{\omega \left( r^2 \omega -J\right) +M}},\quad J= \frac{r^2 \left( \omega ^2-\frac{1}{\ell ^2}\right) +M}{\omega }. \end{aligned}$$

(57)

In the plane $J-r$, the bundle is null (non-rotating solutions) for $r= \sqrt{{M\ell ^2}/({1-\ell ^2\omega ^2})}$, see Fig. 16. The characteristic frequencies are null $\omega _\pm =0$ for $r= \sqrt{\ell ^2 M}$, with $M>0$ and $\forall J$. Also in this case we see the presence of the horizons in the extended plane as a condition defined by the $\mathcal{M}\mathcal{B}$s even in the plane $(\ell -r/M)$.

In Fig. 16-upper left panel, we have shown the horizons $r_\pm$ in the extended planes $J-r$ (where $J\lesseqgtr 0$) and $\ell -r$ (where $\ell \lesseqgtr 0$) for fixed $\ell$ and J, respectively. The horizons largely differ in the two cases. On the plane $J-r$, $\mathcal{M}\mathcal{B}$s can be compared with the the Kerr geometry case. It can be noted that the $\mathcal{M}\mathcal{B}$s are bounded by the horizons curves, but the condition for large r distinguished the BTZ solution with respect to the Kerr spacetime. Conditions for the existence of the replicas at fixed $(J, \ell )$ appear dependent from the parameter $\ell$ and it could be up to two replicas. The situation for $M=0$ is also shown.

The extended plane $\ell -r$ is also considered for $M=\pm 1$ and $M=0$, showing the radii $r= \sqrt{\ell ^2 M}$, (for $M>0$ and $\forall J$) where the characteristic bundle frequencies are null ($\omega _\pm =0$). We could see that asymptotically (for large r) the horizons curve approaches the radii $r= \sqrt{\ell ^2 M}$. The metric bundles are upper bounded by the horizons curves. The extended plane, in the situation where the horizons are not defined, are also represented – see Eq. (52).

4 Discussion and final remarks

Metric bundles have direct observational implications thro ugh the corresponding photon orbiting replicas. In Figs. 2 and 3, we show the horizon replicas in Kerr BH and NS spacetimes. Metric bundles can be generally defined for axially symmetric spacetimes. In the case of spacetimes with Killing horizons, metric bundles are sets of either only BH or BH and NS geometries. Each metric of a bundle has the same photon (orbital) frequency (characteristic bundle frequency), which is also the limiting orbital frequency for stationary observers. This defines the $\mathcal{M}\mathcal{B}$s characteristic frequency as a Killing BH horizon frequency in the extended plane, where $\mathcal{M}\mathcal{B}$s are curves tangent to the horizon curve, representing all the Killing horizons.

From the definition of $\mathcal{M}\mathcal{B}$s, it follows that all the points of a $\mathcal{M}\mathcal{B}$ are replicas of the horizon. Some (horizon) frequencies are not replicated (in the case of solutions with BHs, this is known as horizon confinement [17,18,19]), which are characteristic for some inner horizons.¹¹ In [18, 19], the phenomenological aspects of horizon replicas were discussed, particularly in the regions close to the BH rotation axis. Replicas in a given spacetime prove the existence of photon orbits, whose frequency equals the horizon frequency. The replicas may be detected, for example, in the emission spectra of BH spacetimes. It has been shown that such observations can be performed close to the rotation axis of the Kerr geometry [18, 19]. In [10, 18], metric bundles were used to explore the so-called BH–NS correspondences by using replicas.

In this analysis, grounded on the extended plane and metric bundles, the entire family of metric solutions can be studied as a geometric object. The single spacetime in this framework is, therefore, seen as a single part of the extended plane and its features can be interpreted considering the entire family of metric tensors, focusing on the geometry properties unfolding across the spacetimes of the plane. In this way, different spacetimes are related through metric bundles, possibly reinterpreting the (classical) BH thermodynamics in terms of transitions from one point to another of the extended plane¹² – see also [38, 39]. Metric bundle analysis is also a study of the BH horizons (and, as seen in Sect. 3.8, also of the cosmological horizons¹³ and acceleration horizon in Sects. 3.4, 3.5, 3.6, 3.7, 3.8), therefore, related to BH thermodynamics.

It should also be mentioned how the analysis of the light surfaces is intrinsically related to the study of the spacetime causal structure. Here we have considered an intriguing $\mathcal{M}\mathcal{B}$s application to the case of internal solutions in Sect. 3.1, or to the accelerated solutions as in Sects. 3.4, 3.5, 3.6, 3.7, 3.8) or in presence of a cosmological constant. Furthermore, replicas connect equal properties (frequencies $\omega$) in different spacetime regions, and causal limits imposed in the internal solutions are pointed out in the extended plane by the $\mathcal{M}\mathcal{B}$s analysis. However, bundles characteristic frequencies, determining also the causal properties at the regions of the Kerr poles or close to the BH rotational axis, are sets of photon circular orbital frequencies, limiting the stationary observes in the Kerr spacetimes. Therefore, the causal structure at a point in the extended plane is determined by the crossing of metric bundles (in the Kerr spacetime and RN or KN, for example, there is a maximum of two crossing $\mathcal{M}\mathcal{B}$s). Because of the tangency condition of the $\mathcal{M}\mathcal{B}$s to the horizons curve in the extended plane, the causal structure determined by the $\mathcal{M}\mathcal{B}$s is essentially regulated by the horizons curves in the extended plane. (For example, the spacetime causal structure of the Kerr geometry can be then studied by considering also stationary observers [35]). Metric bundles define, in fact, the causal structure in the extended plane (where a spacetime is a single part of the plane) and also the emergence of the Killing horizons, the BHs and the acceleration horizons as discussed in Sects. 3.4, 3.5, 3.6, 3.7, 3.8.¹⁴

$\mathcal{M}\mathcal{B}$s can be used in the context of modified gravity and more generally alternative theory of gravity to detect the hints of deviances with the respect to current GR frame – [11]. The discrepancies highlighted between the predictions of these models and the general relativistic ones may be detectable. The orbital light-like frequency $\omega (r)$, the bundle characteristic frequency, can be measured by an observer at a point r of the extended plane where the MBs are defined. Replicas establish also a BHs–NSs connection.

As based on photon (circular) orbits, $\mathcal{M}\mathcal{B}$s have natural applications in BH astrophysics in relation to the BH observation of the regions close to the horizons, BH shadows, accretion phenomena and jets launching. In fact, light-surfaces at the base of $\mathcal{M}\mathcal{B}$s definitions, have a wide field of application in many different aspects of BH astrophysics especially for the exploration of the region closed to $(\theta \approx 0, \sigma \approx 0)$. The other significant aspect is the possibility of extracting information from counter-rotating orbits.

In this work, we extended our previous analysis to include more general spacetimes. We proved the existence of $\mathcal{M}\mathcal{B}$s in the following cases: interior solutions, wormhole solutions, BHs immersed in perfect-fluid dark matter, spacetimes with NUT charges, acceleration, magnetic charges, and cosmological constant, BH binary systems, geometries of a (low-energy) heterotic string theory, and the $(1+2)$ dimensional BTZ geometry. The results of our analysis prove that $\mathcal{M}\mathcal{B}$s are a useful frame to explore the properties of very diverse geometries. First, we studied replicas in the Kerr geometry for co-rotating and counter-rotating orbits, showing the relation with the Killing horizons and with the NS case. The introduction of a metric deformation, the “Pochhammer metric” of Appendix A, with the exact stationary solution as a limit, allows us to derive the geometrical properties of the $\mathcal{M}\mathcal{B}$s for interior solutions (which follow from the metric deformation) and for the curvature and metric singularities, showing the emergence of the envelope surfaces with a radial cyclicality. The difference between $\mathcal{M}\mathcal{B}$s in static and stationary spacetimes was discussed.

Fig. 17

Pochhammer symbol $P(r)\equiv b(f r)_y$ as function of r (where $M=1$) for different values of (b, f), signed on the curves, and for y even (left panel) and y odd (right panel). The black line is $P(r)\equiv b(f r)_y=r$ (for $b=f=y=1$)

Fig. 18

Pochhammer symbol $P(r)\equiv b(f r)_y=o$ in the plane $r-o$ for different values of y, signed on the panels, where $\{b,f\}=\pm 1$. For $y=$(odd, even) different regions of the parameters $(b,f)=\pm 1$ are signed as the (o, r) regions, respectively. The zeros $o=0$ are shown. Orange dotted lines are $r=2$ (where $M=1$) and $o=2$, orange region is $o\in [0,2]\times r\in [0,2]$. The black line is $P(r)\equiv b(f r)_y=r$ (for $b=f=y=1$)

Fig. 19

Deformation of the Reissner–Nordström geometry. Upper left panel: Solution $P_{\pm }(r): Q_{\pm }=Q_{\omega }$ of Eq. (A.4), as function $P(r)\equiv b(f r)_y=o$ for different frequencies $\omega$ signed on the panel, the limiting frequency $\omega =1/4$ and $\omega =0$ where $\mathcal {Q}_\pm$ is the RN BH horizon curve in the plane $Q-r$. Shaded region is the horizons region where $P(r)\in [0,2]$. Upper right panel: black region is the BH in the extended plane, where $Q_\pm$ is the horizon curve in the extended plane, $Q_\delta$ in Eq. (A.5) is the curve of minimum points of the metric bundles. The bundles characteristic frequencies are signed on the panel. Special frequencies $\omega \in \{1/\sqrt{27},1/4,\sqrt{2}/{27}\}$ are pointed out, shaded regions are identified as bottlenecks. Bottom left panel: Horizons curve $Q_\pm$, the curve of minimum $Q_\delta$, the frequencies of bundles minimum $\omega _\delta$ are plotted as functions of P(r), gray region is the bottleneck region. Bottom right panel: Horizons curves $Q_\pm (r)$ for different values of parameters (b, f, y) signed on the curves, where the RN metric has been transformed according to the $r\rightarrow P(r)=b(fr)_y$

Fig. 20

Deformation of the Reissner–Nordström reference metric with $\theta =\pi /2$. Curvature scalar R (upper line panels) and Einstein tensor component $G^t_t$ (bottom line panels) for different charge parameter Q signed on panels. Blue, Green, Purple, Orange curves refer to $\{(b,f),y\}=\{(-1,-1),y=6\};\{(+1,+1),y=6\};\{(+1,+1),y=5\};\{(-1,-1),y=5\}$, respectively

Fig. 21

Deformation of the Reissner–Nordström reference metric with $\theta =\pi /2$ ($M=1$). Metric bundles $Q_\omega$, Ricci curvature scalar R and Einstein tensor component $G^t_t$ are shown for different metric deformation parameters $\{(b,f),y\}$ (metric signature $(-,+,+,+)$), where $\{blue,purple,orange,brown\}$ curves refer to frequencies $\{\omega =0.1;\omega =0.5;\omega =1;\omega =7\}$, respectively. Dotted-dashed black line are singularities $b(fr)_y=0$, black circles are the horizons in the plane $Q-r$, $\{dashed-blue,light-gray,dotted-blue,light-pink\}$ curves correspond to $\{(R, Q=0.9),(R, Q=0),(G^t_t, Q=0.9),(G^t_t, Q=0.9)\}$ respectively

Fig. 22

Deformation of the Kerr–Newman reference metric and Kerr reference metric $(Q=0)$ in Boyer–Lindquist coordinates (metric signature $(-,+,+,+)$) on the equatorial plane ($\theta =\pi /2$). Ricci curvature scalar R and Einstein tensor component $G^t_t$ are shown for different BH and NS spin a and charge parameter Q , where $\{blue,green,purple,orange\}$ curves correspond $\{(b,f),y\}=\{(+1,-1),y=6\};\{(+1,+1),y=6\};\{(+1,+1),y=5\};\{(-1,-1),y=5\}$, respectively

Fig. 23

Deformation of the Kerr–Newman reference metric in Boyer–Lindquist coordinates (metric signature $(-,+,+,+)$) on the equatorial plane ($\theta =\pi /2$) where $M=1$. Metric bundles $Q_\omega$, Ricci curvature scalar R and Einstein tensor component $G^t_t$ are shown for spin $a=0.5$ and different deformation parameters $\{(b,f),y\}$, where $\{blue,purple,orange,brown\}$ curves refer to $\mathcal{M}\mathcal{B}$s frequencies $\{\omega =0.1;\omega =0.5;\omega =1;\omega =7\}$ respectively. Dotted-dashed black lines are singularities $b(fr)_y=0$, black circles are the horizons in the plane $Q-r$, $\{dashed-blue,light-gray,dotted-blue,light-pink\}$ curves correspond to $\{(R, Q=0.9),(R, Q=0),(G^t_t, Q=0.9),(G^t_t, Q=0)\}$ respectively

Fig. 24

Deformation of the Kerr–Newman reference metric in Boyer–Lindquist coordinates (metric signature $(-,+,+,+)$) on the equatorial plane ($\theta =\pi /2$) and $M=1$. Metric bundle $a_\omega$, Ricci curvature scalar R and Einstein tensor component $G^t_t$ are shown for charge $Q=0.5$ and different deformation parameters $\{(b,f),y\}$, where $\{blue,purple,orange,brown\}$ curves refer to frequencies $\{\omega =0.1;\omega =0.5;\omega =1;\omega =7\}$ respectively. Dotted-dashed black lines are singularities $b(fr)_y=0$, black circles are the horizons in the plane $a-r$, $\{dashed-blue,light-gray,dotted-blue,light-pink\}$ curves correspond to $\{(R, a=0.9),(R, a=0),(G^t_t, a=0.9),(G^t_t, a=0)\}$ respectively. See also Fig. 25

Fig. 25

Deformation of the Kerr–Newman reference metric in Boyer–Lindquist coordinates (metric signature $(-,+,+,+)$) on the equatorial plane for charge $Q=0.5$ and $M=1$. Metric bundle $a_\omega$ in the extended plane $a-r$, Ricci curvature scalar R and Einstein tensor component $G^t_t$ are plotted for different deformation parameters $\{(b,f),y\}$, where $\{blue,purple,orange,brown\}$ curves refer to frequencies $\{\omega =0.1;\omega =0.5;\omega =1;\omega =7\}$. Dotted-dashed black lines are singularities $b(fr)_y=0$, black circles are the horizons in the plane $a-r$, $\{dashed-blue,light-gray,dotted-blue,light-pink\}$ curves correspond to $\{(R, a=0.9),(R, a=0),(G^t_t, a=0.9),(G^t_t, a=0)\}$ respectively–see also Fig. 24

Fig. 26

Deformation of the Kerr geometry (from KN deformed metric with electric change $Q=0$ ), with Kerr reference metric in Boyer–Lindquist coordinates (metric signature $(-,+,+,+)$) on the equatorial plane, where $M=1$. Metric bundle $a_\omega$ in the extended plane $a-r$, Ricci curvature scalar R and Einstein tensor component $G^t_t$ are plotted for different $\{(b,f),y\}$, where $\{blue,purple,orange,brown\}$ curves refer to the bundles characteristic frequencies $\{\omega =0.1;\omega =0.5;\omega =1;\omega =7\}$ respectively. Dotted-dashed black lines are singularities $b(fr)_y=0$, black circles are the horizons in the plane $a-r$, $\{dashed-blue,light-gray,dotted-blue,light-pink\}$ curves correspond to $\{(R, a=0.9),(R, a=0),(G^t_t, a=0.9),(G^t_t, a=0)\}$ respectively. See also Fig. 27

Fig. 27

Deformation of the Kerr geometry (KN geometry with $Q=0$), with Kerr reference metric in Boyer–Lindquist coordinates (metric signature $(-,+,+,+)$) on the equatorial plane, where $M=1$. Metric bundle $a_\omega$, Ricci curvature scalar R and Einstein tensor component $G^t_t$ are plotted for different deformation parameters $\{(b,f),y\}$, where $\{blue,purple,orange,brown\}$ curves refer to bundles characteristic frequencies $\{\omega =0.1;\omega =0.5;\omega =1;\omega =7\}$ respectively. Dotted-dashed black lines are singularities $b(fr)_y=0$, black circles are the horizons in the plane $a-r$, $\{dashed-blue,light-gray,dotted-blue,light-pink\}$ curves correspond to $\{(R, a=0.9),(R, a=0),(G^t_t, a=0.9),(G^t_t, a=0)\}$ respectively. See also Fig. 26

In the case of interior spacetimes, the surface of the star replaces the envelope surface in solutions with Killing horizons. In the case of NUT solution, the NUT parameter plays the role of the spin in the Kerr solution. The analysis of the accelerated and charged solutions allows us to evaluate how the acceleration and the electric charge parameters differently affect the horizon tangency condition of the $\mathcal{M}\mathcal{B}$s; we have also analyzed the Minkowski limit and the relations between the Killing horizons (defined by the electrical charge) and the acceleration horizon. The Ernst solution, characterized by the metric parameter B, shows a $\mathcal{M}\mathcal{B}$s structure similar to the one of the $\textbf{C}$-solution. The corresponding spacetime has BH horizons and an acceleration horizon. The $\mathcal{M}\mathcal{B}$s are modified by the presence of the parameter B. Furthermore, we considered an accelerating and spinning solution as well as a generalization that includes the cosmological constant. Interestingly, in this case the $\mathcal{M}\mathcal{B}$s are contained in the internal region of the extended plane delimited by the Killing horizons, which are inaccessible in the case of zero acceleration. In spacetimes with cosmological constant, spin, electric charge, and acceleration, the extended plane $a-r$ is bounded by the horizons and contains disconnected regions, where metric bundles can exist. Moreover, the sign of the cosmological constant modifies the accessible regions of the extended plane.

Finally, we analyzed $\mathcal{M}\mathcal{B}$s in the spacetime of two extreme RN BHs, located at a distance b. We noted the role of the horizon at $r=M_1$. Here, we have mainly considered for simplicity $\mathcal{M}\mathcal{B}$s on the equatorial plane. The analysis for different planes and especially close to the central symmetry axis can be done following [18, 19]. A further interesting case is represented by wormhole geometries, where we considered the analysis of [26, 27]. It turns out that for the static and spinning geometries, metric bundles are connected to the wormhole definition from the tangency condition. The cases of a black hole surrounded by dark matter and the spacetime of a heterotic string model were are also analyzed, considering the tangency conditions for the bundles. Analogously, for the BTZ solution in the extended plane $J-r$ (see [15] for the Kerr de-Sitter case) we can note the similarity with the accelerated solutions.

In this work, we have shown that the formalism of metric bundles can be used to analyze very different spacetimes. We focused mainly on the technical aspects of the formalism in each of the analyzed cases. The physical consequences of this analysis constitute a different problem that should be investigated separately for each spacetime, using, however, the geometric similarities that we have established in this work. We expect to continue this investigation in future works.

Appendix A: Light surfaces in deformed spacetimes

In general, the $\mathcal{M}\mathcal{B}$s structure remains unchanged for all metric deformations leaving $\mathcal {L}_{\mathcal {N}}=0$ unchanged. Any metric with $g_{tt}+2\omega g_{t\phi }+g_{\phi \phi }\omega ^2=K \mathcal {L}_{\mathcal {N}}$ for a general non-null K, has the same metric bundles of the geometry with $\mathcal {L}_{\mathcal {N}}$ generating function. (In particular $\mathcal{M}\mathcal{B}$s, defined by the condition $\mathcal {L}_\mathcal {N}=0$, are metric conformal invariants and inherit some of the properties of the Killing vector $\mathcal {L}$.¹⁵)

In this section, we study the horizons deformations of the KN, RN and Kerr geometries in the extended plane. In fact, we consider a particular deformation of the radius r to show how deformations of the bundles reflect on horizons deformation, by performing a comparison with the KN limit. The exact solutions of Einstein equations or other non general relativistic gravitational field equations in Sect. 3 could be studied as deformations of the KN spacetimes. Thus, in this section, we use a deformation of the KN metric, which also includes a deformation of the corresponding limiting cases, i.e., Kerr metric, RN metric, and Schwarzschild metric. Generally, a deformed solution is described by deformed bundles regulated by the deformation parameters of the metric. This allows us to establish relations between metric singularities and curvature singularities in the $\mathcal{M}\mathcal{B}$s formalism. This issue is deepen also in Sect. 3 in the case of different axially symmetric exact solutions, including internal solutions, wormholes, BHs with external fields and dark matter, and BHs in $2+1$ dimensions.

In the following analysis, we use $M=1$ as convenient.

The deformation consists in applying in (1), the transformation

$$\begin{aligned}{} & {} r\rightarrow P(r)\equiv b (f r)_y,\nonumber \\{} & {} \quad \text{ where }\nonumber \\{} & {} \quad (r)_y\equiv r (r+1) \ldots (r+y-1)\nonumber \\{} & {} \quad =\varGamma (r+y)/\varGamma (r),\quad y\in N-\{0\}, \end{aligned}$$

(A.1)

where $(r)_y$ the Pochhammer symbol¹⁶ and $\varGamma (r)$ is the Euler gamma function, where the deformation parameters of the metric (b, f, y) are constant. Below we discuss in details the parameters significance in the cases analyzed and with respect to the reference not-deformed metric. In Figs. 17 and 18, we illustrate the behavior of the Pochhammer symbols for some particular values. In general, a deformed metric corresponds to a non-vacuum solution.¹⁷ To distinguish the deformed metric (1) as compared to the standard not deformed Kerr–Newman solution, we refer to the deformed spacetime tensor as “Pochhammer metric”, where the KN solution is obtained for $P(r)=r$.

On the metric deformation parameters

Our analysis focuses on the cases $(b, f)\in \{\pm 1\}$. Therefore, indicating with $\bullet$ a value in $\{\pm 1\}$, the following conditions hold:

• For $f>0$, $(b, f)=(\bullet ,+)$, solution $r=0$ is mapped, with $P(r)=0$, into $r=0$ and $(y-1)$ negative ($r<0$) zeros;

• For $f<0$,$(b, f)=(\bullet ,-)$, solution $r=0$ is mapped, with $P(r)=0$, into $r=0$ and $(y-1)$ positive ($r>0$) zeros, $r=(y-n)$ where $n\in [1,y]$;

• For $bf=+1$, ($(b, f)=\pm (+,+)$), there is $P(r)=r$ at $y=1$;

• For $bf=-1$, ($(b, f)=\pm (+,-)$), there is $P(r)=-r$ at $y=1$;

Details are given in Figs. 17, 18. We take into account the asymptotic condition, $r\rightarrow +\infty$, leading to $P(r)\rightarrow +\infty$ for $(b,f)=\{(+,+),(+,-)\}$, for y even, and $(b,f)=\{(+,+),(-,-)\}$ for y odd – see Figs. 17 and 18. In particular:

• For $(b,f)= (+,+)$, there is $P(r)>0$ for $r>0$ and any y, satisfying the asymptotic condition, and as $bf=+1$, there is $P(r)=r$ at $y=1$ – Fig. 18. For $f>0$, there is only one zero for $r=0$.

• For $(b,f)= (+,-)$ we have that $P(-r)\ge 0$ for $r\in [n, n + 1]$ for y odd where $n\in [1, y - 2]$ is odd (with y zeros, according to the conditions for $f<0$). If $bf=-1$, then $P(r)=-r$ at $y=1$. Then, $r\in [n,n+1]\cup r\ge y-1$ for $n\in [1,y-3]$ odd, for y even (satisfying the asymptotic condition).

• For $(b,f)= (-,-)$ we obtain $-P(-r)\ge 0$ for y even and $r\in [n, n + 1]$, where $n\in [0, y - 2]$ is even; for y odd (satisfying the asymptotic condition) and $r\in [n, n + 1]\cup r \ge y - 1$ with $n\in [0, y - 3]$ even. As $bf=+1$, we obtain $P(r)=r$ at $y=1$. This case ($y=$odd) has y zeros $r\ge 0$ according to the condition $f<0$ – Fig. 17.

• For $(b,f)= (-,+)$ we obtain no solution $-P(r)<0$ and there is only the zero $P(r)=0$ for $r=0$. The asymptotic condition is not satisfied.

Deformed bundles and deformed horizons

In the study of the horizons deformation in the extended plane, we also consider solutions of $P (r) = o\ge 0$. The case $o=0$ has been analyzed above. We explore the case $o=r_{\pm }\in [0,2]$ for the Kerr–Newman horizons – see Fig. 18. The Kerr and Reissner–Nordström cases, where $\mathcal {Q}_t=a$ and $\mathcal {Q}_t=Q$ respectively, are also considered, showing the situation for the Kerr–Newman metrics, the limiting cases of Schwarzschild, the Kerr and Reissner–Nordström metrics, and the reference exact solutions. (In general, the deformed metric corresponds to a non-vacuum solution while the asymptotic condition $r\rightarrow +\infty$ also ensures the asymptotic flatness of the metric and the match with the reference exact solution.). We search for the solutions of $P(r)=0$ and $P(r)=r_{\pm }$. Solutions $P(r)=0$ are mapped into $r=0$ for $f>0$, or n solutions for $f<0$. Therefore, we consider the deformed bundles as the tangent curves to deformed horizon curves. The horizon curve in the extended plane is $\mathcal {Q}_t=\sqrt{r(2-r)}\equiv \mathcal {Q}_t^H(r)$. In the Kerr–Newman case, the metric bundle structure is studied considering the two horizons representations:

$$\begin{aligned}{} & {} {\textbf { 1.}}:\quad Q=\sqrt{(\mathcal {Q}_t^H)^2-a^2}\quad \text{ and }\quad {\textbf {2.:}}\quad a=\sqrt{(\mathcal {Q}_t^H)^2-Q^2},\nonumber \\{} & {} \quad \text{ where } \quad \mathcal {Q}_t^H\equiv \sqrt{r(2-r)}, \end{aligned}$$

(A.2)

defined in the extended planes $Q-r$ and $a-r$ respectively.

To simplify the discussion, we consider below explicitly the deformation of RN metric, while in Figs. 22, 24, 25 and Figs. 26, 27 deformation of KN and Kerr geometries are discussed.

Some notes on the bundles in the deformed RN geometry

Metric bundles in the spherical symmetric case of the deformed RN solution can be written as:

$$\begin{aligned}{} & {} Q_{\tilde{\omega }}=\pm \sqrt{P(r)[P(r)^3 \tilde{\omega }^2-P(r)+2]},\nonumber \\{} & {} \text{ where }\quad \tilde{\omega }\equiv \omega \sqrt{\sigma },\nonumber \\ \end{aligned}$$

(A.3)

see Eq. (5). In the following analysis, without loss of generality, we consider $\sigma =1$ where $\tilde{\omega }=\omega$.

In the RN metric, $P(r)=r$ – see also Eq. (5).

As it is clear from Figs. 21 and 19, for the deformation of the RN geometry there is, therefore, a number of deformed horizons $P(r)=r_{\pm }(Q)$, in general, superior to 2 and the radii are according to y odd or even.

For the Reissner–Nostström metric we consider the following horizons curve as function of the bundle frequency:

$$\begin{aligned}{} & {} P_{\pm }(r)\equiv 1\pm \sqrt{(P(r)-1)^2-P(r)^4 \omega ^2}:\nonumber \\{} & {} \quad Q_{\pm }(P_\pm )=Q_{\omega }(P),\nonumber \\{} & {} \quad \text{ where }\quad Q_{\pm }\in [0,1]\quad \text{ and }\quad P_\pm \in [0,2],\nonumber \\ \end{aligned}$$

(A.4)

and $P_\pm =P$ only for $\omega =0$ or $P(r)=0$, crossing of the metric bundle with the horizon in the extended plane, illustrating the metric bundles for the spherically symmetric case – Fig. 19.

In the NSs case, the bottleneck region boundary is related to the extremes of the bundles curves with respect to r; this can be clearly seen in the case of spherically symmetry of the RN solution, where we will consider the extreme frequencies $\omega _\delta$ and the charge $Q_\delta$ defined from the metric bundles $Q_\omega$ as follows,

$$\begin{aligned}{} & {} \omega _\delta \equiv \sqrt{\frac{P(r)-1}{2 P(r)^{3}}}:\quad \partial _r Q_\omega =0,\nonumber \\{} & {} \quad \text{ where }\quad Q_\delta \equiv Q_\omega (\omega _\delta )=\sqrt{\frac{P(r)(3-P(r))}{2}}, \end{aligned}$$

(A.5)

where it is evident the role of the photon geodetic circular orbits $r_\gamma =3$ in the limit of the Schwarzschild geometry – see also Eq. (5). The maximum of $Q_\delta$ with respect to P(r) defines a bottleneck region (in the plane $Q-P(r)$), where the maximum frequency $\omega =\sqrt{2/27}$ and $Q_\omega =3/2 \sqrt{2}\approx 1.06066M$ with $P(r)=3/2$.

In Fig. 19, we evidence the aspects (radii P(r), characteristic frequencies, extreme points) determining and characterizing the bottleneck region. We point out also, with reference to the construction of the bottleneck region, the minimum curve $Q_\delta$ of the limiting frequency $\omega =1/\sqrt{27}$ related to the Schwarzschild solution, the frequency $\omega =1/4$ (minimum) and $\omega =\sqrt{2/27}$ construct the bottleneck (for $\sigma =1$.) The spherically symmetric cases are characterized by the asymptotic condition on the bundles curves approaching the horizons curve in the extended plane. The horizons are obviously related to the limit $\omega =0$ (note also the frequency $\omega =1/4$). It is clear that the case $Q=0$ ($\omega =1/\sqrt{27}$) acts as a discriminant case for the frequencies. The curvature of the bundle depends on the frequency and the limiting case $\omega =1/4$ corresponds to the extreme RN metric.

Notes on the bundles in the deformed axially symmetric spacetimes

The metric and geometric deformation of the Ricci scalar (R) and Einstein tensor (we consider here the component $G^t_t$), in the Pochhammer metric with respect to the reference RN solution are plotted for different values of the deformation parameters $\{(b,f),y\}$ in Fig. 20 – see also Fig. 19. Following these deformations, the metric bundle $Q_\omega$, Ricci curvature scalar R and Einstein tensor component $G^t_t$ for different $\{(b,f),y\}$ are shown in Fig. 21.

Considering the analogue analysis performed in Figs. 22, 24, 25 and Figs. 26, 27 for the KN and Kerr geometry, it is clear that an interesting aspect of the Pochhammer metric, as a deformation of an exact metric, with respect to the Kerr and Kerr–Newman reference metrics, is the presence, for some values of the parameters, of a repetition in the bundle structure, often in disconnected regions of the extended plane, as an indication of the presence of more envelope surfaces (horizons or surfaces defined by the analysis of the scalar R and the Einstein tensor) appearing with fixed “cycles” – see also the zero analysis of Fig. 18.

Therefore the bundles structure is compared to the curvature scalar and Einstein tensor, providing for example the analysis of some internal solutions in the $\mathcal{M}\mathcal{B}$s framework and anticipating some aspects considered in Sect. 3, where different particular solutions are addressed with metric bundles.

The metric and geometric deformations induced in the Pochhammer metric with respect to the reference KN solution for different values of the deformation parameters $\{(b,f),y\}$ are plotted in Fig. 22. The study of the bundles deformation is illustrated in Figs. 22 and 23.

The analysis shows the repetitiveness of the $\mathcal{M}\mathcal{B}$s structures for some parameters in the plane $Q-r$, while the asymptotic condition sets the metric at infinity (Figs. 24, 25). The cancellation of the constant R or of the Einstein tensor is an indication of the singularity and matter structure in the internal solution. Figure 26 shows a similar analysis for the deformation of the Kerr metric.