1 Introduction

Cosmology has made tremendous advancements both observationally and theoretically during the past few decades. As a result, the cosmological perspective has moved from being viewed as a theoretical science to a precise and a quantitative field that can be compared to reliable observational facts. Due to the theoretical developments in understanding Einstein’s general theory of relativity (GR) and data measurements, new mysteries have emerged that are challenging for the research community. Although GR has been demonstrated to be incredibly effective as a classical theory of gravitational interactions, the current cosmological picture admits several uncertainties. These cosmological puzzles involve the assumption of undefined cosmic ingredients, characterized as dark energy (DE) and dark matter (DM), which are required for understanding the current observations. It is considered that DM is an essential cosmic component for the development of large-scale structures and various astrophysical paradigms along the cosmic evolution. It is still unclear if DM is governed by a weakly interacting massive particle or is merely a demonstration of a modified form of GR [1]. On the other hand, DE is the name given to another mysterious fluid, which is essentially responsible for the accelerated cosmological expansion, supported by several observations [2, 3].

Among all the theoretical endeavors, geometrically modified gravity theories provide one of the most favorable frameworks for consistently describing the DE era [4,5,6]. In this context, \(f(\textbf{R})\) gravity is the most primary and promising geometrical model of gravitational interaction, which emerges by the addition of a generic function of curvature scalar \(\textbf{R}\) in the standard GR-action instead of \(\textbf{R}\) alone [7]. This type of gravitational model effectively describes the unification of early and late-time cosmological acceleration [8]. Nojiri and Odintsov showed that the framework of \(f(\textbf{R})\) model is compatible with the usual solar system test and is promising for describing series of cosmological events from matter-dominated to DE-dominated universe [9, 10].

Several geometrical theories of gravitation by modifying/extending GR have been suggested and analyzed against the backdrop of cosmology. One promising sector of these geometrical theories is the modified Gauss–Bonnet gravity (GBG), where the Gauss–Bonnet term \(\mathcal {G}\) appears in the standard GR-action in a non-linear fashion [9, 11, 12]. This cosmological theory is considered as a viable candidate for the unified description of gravitational DE and DM [9]. Moreover, some significant cosmological effects such as primordial inflation, late-time universe acceleration and rotational curves of distant galaxies can also be described within the dynamics of GBG-theory [13]. The GBG-theories are also expected to be useful in the field of high-energy physics, i.e., unification of gravity with GUTs or for the description of hierarchy problem [11]. Some modified GBG models of the late-time cosmological evolution are also predicted by low-energy effective string theory action [14]. The modified versions of GBG cosmologies can be used for understanding the evolution of complex self-gravitational systems with the help of structure scalars as well as gravitational waves’ events [15,16,17,18,19,20,21].

The assumption of local isotropy has been extensively used as a fluid approximation to study the mechanism of compact relativistic self-gravitational fluids. This Pascalian nature (equal principal stress) of the fluid distribution is supported by a large number of observational data demonstrating the equality of the radial and tangential pressures under several conditions. On the other hand, substantial theoretical pieces of evidence suggested by different researchers indicate that the occurrence of different types of physical processes for some specific density ranges may result in the emergence of local anisotropy [22,23,24]. Several physical phenomena taking place during the stellar evolution, are responsible for deviations from local isotropy in the low as well as high-density regimes. These physical phenomena, for example, the presence of bosons stars, slow rotations, viscosity, the existence of solid cores, Minkowskian core, and exotic phase transitions during the stellar evolutionary scenarios [25,26,27,28,29]. It is well established that the existence of pressure anisotropies allowed a better understanding of stellar evolution and could exhibit a more realistic description of the astrophysical scenarios. Furthermore, there is a recently obtained result that somehow supersedes all previous arguments, and forces us to consider pressure anisotropy whenever relativistic fluids are involved. According to this result, even though if the relativistic system is considered to be originally isotropic, several physical phenomena of the type expected during the evolutionary phases of the system that will always generate local anisotropy [30]. The fact is that any equilibrium composition is the terminal phase of the dynamical regime and therefore, no reason to suppose that during this process the attained local anisotropy would vanish in the terminal equilibrium phase. Thus, the final composition, despite the fact that it was originally isotropic, should become anisotropic.

Besides considering local anisotropy as a variable playing an an essential role in the evolutionary scenarios of the astrophysical systems, we might also investigate it in the form of another physical quantity including both the pressure anisotropy and density inhomogeneity, dubbed as a complexity factor (\(\textrm{C}_{\textbf{F}}\)). The concept of “complexity” is deeply related to the fundamental structural properties of the system. The appropriate description of the notion of complexity has been quite an attractive problem for researchers in different scientific fields [31,32,33,34]. In this respect, several definitions have been proposed and analyzed for different systems. Most of them are associated with the concepts of information and entropy. However, irrespective of all the attempts, there is still no consensus on a particular description. On the other hand, in the case of relativistic self-gravitational fluids, the notion of complexity is composed of two fundamental structural variables of the fluid (i.e., anisotropy of the pressure and energy density irregularity). From this perspective, Herrera [35] presented an entirely new proposal regarding the phenomenon of complexity in terms of a scalar function (denoted by \(Y_{\textbf{TF}}\)), which constitutes a particular combination of density inhomogeneity and pressure anisotropy. The scalar \(Y_{\textbf{TF}}\) originates from the orthogonal splitting of the curvature tensor. This novel scheme of complexity is based on the fundamental assumption that less complex systems comprises of homogeneous (in the energy density) and isotropic pressure fluid configurations. The perspective applications regarding the complexity of self-gravitational systems within the frameworks of different geometrically modified gravitational models has been discussed in detail [16,17,18,19,20,21]. This investigation is endeavored to analyze the physical features of locally anisotropic, hyperbolically symmetric self-gravitational fluids in terms of geometrical and physical variables that seem to play a significant role in the evolution of such objects. These variables include inhomogeneous density, Weyl tensor, anisotropic pressure, and four-acceleration. The role of these variables in exploring different physical features of static hyperbolically symmetric fluids is analyzed in detail within the realm of the GBG cosmological model.

Recently, a generic approach has been discussed to study the Schwarzschild’s black hole that significantly deviates from the the standard description of a spherically symmetric black hole. This scheme was motivated by two well-known facts [36, 37].

  • Any equilibrium condition of the physical system should be eventually static, which requires a static solution over the entire spacetime manifold.

  • The coordinate singularity appearing in the metric cannot be removed via any coordinate transformation maintaining the static version of Schwarzschild’s line element [38].

Specifically, any transformation that allows the extension of the manifold across the whole spacetime requires the non-staticity of the metric inside the horizon. In [36, 37], it was proposed that inside the horizon the signature of the Schwarzschild’s metric changes from \((-,+,+,+)\) to \((+,-,-,-)\) and an apparent singularity occurs at \(R=2m\). It is well-established that these difficulties may be avoided with the help of suitable coordinate transformations. These transformations provide physically acceptable solutions of the gravitational equations of motion with the altered signature but they are time-independent. In this context, Herrera and Witten [36] proposed a model to keep the time-dependence at the interior of the horizon. This model characterizes the entire spacetime by a four-dimensional manifold both on the exterior and the interior side. Thus, the \(\theta -\phi \) model exhibit hyperbolic symmetry inside the horizon, while spherical symmetry outside the horizon. Hence the presented model allows a change of symmetry from outside to inside the horizon, thereby describing a generic time-independent solution.

Harrison [39] was the first to examine a solution to the GR equations of motion under the background of hyperbolic symmetry. The study of hyperbolic configurations had been a topic of great interest and attracted several researchers in different scenarios [40,41,42,43]. Herrera et al. [37] presented a global description of geodesics with hyperbolically symmetric metric and found some fascinating results about the nature of test particles. More recently, a comprehensive analysis of the global properties of the relativistic, hyperbolically symmetric self-gravitational fluids with different backgrounds have been carried out in [44,45,46]. The same authors discussed the complexity of hyperbolically symmetric fluids by formulating the scalar quantity, known as \(\textrm{C}_{\textbf{F}}\). By imposing different conditions on the anisotropic fluid configuration along with the vanishing complexity condition (\(Y_{\textbf{TF}}=0\)), several analytical hyperbolically symmetric solutions are presented and examined [44]. Many studies in the context of modified theories of gravitation have been proposed recently for understanding the evolution and mechanism of hyperbolically symmetric configurations [46,47,48].

We have extended Herrera’s approach to exploring the physical characteristics inherent to all the self-gravitational fluids admitting hyperbolic symmetry. The article is structured in the following manner: in the next section, we present the basic formalism of GBG-cosmology, variables, and conventions defining the hyperbolically symmetric fluid configurations. Sections 3 and 4 are dedicated to describing the notions of Weyl tensor and Tolmann mass functions and their relationships with physical and geometric variables, respectively. In Sect. 5, we propose the fundamental procedure of the orthogonal splitting of the Riemann curvature tensor to obtain certain scalar quantities describing the formation and evolutions of relativistic fluids. One of these scalars (\(Y_{\textbf{TF}}\)) appears to measure the degree of complexity of the system, dubbed as the \(\textrm{C}_{\textbf{F}}\). The influence of these scalars on the Tolman mass is also discussed in the same section. In Sect. 6, we provide several analytical hyperbolically symmetric solutions satisfying different conditions, describing different evolution of anisotropic fluid configurations. Finally, Sect. 7 is devoted to explain the summary of all the presented results.

2 Fundamental formalism of \(f(\mathcal {G})\) cosmology

In this section, we briefly present the basic structure of GBG in the presence of locally anisotropic distribution of matter. We start by defining the standard gravitational action in the context of GBG as [49]

$$\begin{aligned} \mathcal {A}_{f(\mathcal {G})}\equiv \mathcal {A}_{\textrm{G}}+\mathcal {A}_{m}=\int \left[ \frac{\textbf{R}}{2\kappa ^{2}}+f(\mathcal {G})+L_{m}\right] \sqrt{-\textit{g}}d^{4}x, \end{aligned}$$
(1)

where \(\mathcal {A}_{\textrm{G}}\), \(\mathcal {A}_{m}\) symbolize the action due to gravity and usual matter, respectively. Further, \(\textbf{R}\) stands for the Ricci scalar, \(\textit{g}\) exhibits the determinant of the metric tensor \(\textit{g}_{\mu \eta }\) and \(\kappa ^{2}\) dentes the coupling constant, while \(L_{m}\) describes the Lagrangian associated with the matter field. In addition, \(f(\mathcal {G})\) is an analytic function of the Gauss–Bonnet curvature invariant \(\mathcal {G}\), which is defined in terms of Riemann curvature tensor \(R_{\mu \eta \sigma \upsilon }\), Ricci curvature tensor \(R_{\mu \eta }\) as well as curvature invariant \(\textbf{R}\) as

$$\begin{aligned} \mathcal {G}\equiv \textbf{R}^{2}+R_{\mu \eta \sigma \upsilon }R^{\mu \eta \sigma \upsilon }-4R_{\mu \eta }R^{\mu \eta }. \end{aligned}$$
(2)

This unique form of curvature squared terms, inspired by string/M-theory, has gained special interest in the field of modern cosmology [11, 13, 50, 51]. Another well-known feature of the Gauss–Bonnet combination is its ability to minimize the occurrence of spin-2 ghosts instabilities. Being a topological invariant, the four-dimensional curvature invariant \(\mathcal {G}\) exhibits no dynamical effects upon addition in the gravitational action. However, recently Glavan and Lin [52] presented a new covariant modification of GBG theory by defining the product of \(\mathcal {G}\) and the factor \(\frac{1}{(D-4)}\), and defined the four-dimensional cosmology by the limit as \(D\rightarrow 4\). In this way, the term \(\mathcal {G}\) gives rise to a non-trivial ghost-free generalization of the gravitational action and contributes to the gravitational dynamics.

Now, varying the standard action (15) with respect to \(g_{\mu \eta }\), we obtain the gravitational field equations for GBG theory as

$$\begin{aligned}&G_{\mu \eta }+8 \left[ R_{\mu \sigma \eta \upsilon }+R_{\sigma \eta }\textit{g}_{\mu \upsilon }-R_{\sigma \upsilon }\textit{g}_{\eta \mu }-R_{\mu \eta }\textit{g}_{\sigma \upsilon }\right. \nonumber \\ {}&\qquad \left. +R_{\mu \upsilon }\textit{g}_{\eta \sigma } +\frac{\textbf{R}}{2}(\textit{g}_{\mu \eta }\textit{g}_{\sigma \upsilon }-\textit{g}_{\mu \upsilon }\textit{g}_{\eta \sigma })\right] \nonumber \\&\qquad \times \nabla ^{\upsilon }\nabla ^{\sigma }f_{\mathcal {G}}+(\mathcal {G}f_{\mathcal {G}}-f)\textit{g}_{\mu \eta }=\kappa ^{2}T_{\mu \eta }, \end{aligned}$$
(3)

where \(f_{\mathcal {GG...}}\equiv \frac{\partial ^{n}f(\mathcal {G})}{\partial \mathcal {G}^{n}}\). The trace of the above equation yields

$$\begin{aligned} \textbf{R}+8G_{\mu \eta }\nabla ^{\mu }\nabla ^{\eta } f_{\mathcal {G}}-4(\mathcal {G}f_{\mathcal {G}}-f)=\kappa ^{2}(\rho -3P). \end{aligned}$$
(4)

In this equation, \(G_{\mu \eta }\) is the Einstein tensor, while the operator \(\nabla ^{\mu }\) denotes the covariant-differentiation. We first assume a hyperbolically symmetric, static spacetime in terms of polar coordinates \((r, \theta )\) with the signature \((+,-,-,-)\) as

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2}-r^{2}(d\theta ^{2}+\sinh ^{2}\theta ) d\phi ^{2}, \end{aligned}$$
(5)

where \(\nu (r)\) and \(\lambda (r)\) are functions of the radial coordinate r, only. We label the coordinates as (\(x^{0}\), \(x^{1},\) \(x^{2},\) \(x^{3}\))=(t,  r,  \(\theta ,\) \(\phi \)). Now, we consider that the geometry of the static stellar configuration exhibiting hyperbolical symmetry is filled with locally anisotropic fluid, which may be identified with the following stress-energy tensor as

$$\begin{aligned} T_{\mu \eta }=(\rho +P) U_{\mu }U_{\eta }-P\textit{g}_{\mu \eta }+\Pi _{\mu \eta }, \end{aligned}$$
(6)

where \(\rho \) denotes the energy density of the fluid, \(U^{\mu }\) is the four-velocity vector, \(\Pi _{\mu \eta }\) is the anisotropic stress tensor, and P represents the isotropic stress. Since we are assuming the Eckart frame in which the elements of the fluid are considered to be at rest. This follows that

$$\begin{aligned} \rho&=T_{\mu \eta }U^{\mu }U^{\eta }, \\ P&=-\frac{1}{3}\textit{h}^{\mu \eta }T_{\mu \eta }, \\ \Pi _{\sigma \upsilon }&=\textit{h}^{\sigma }_{\mu }\textit{h}^{\upsilon }_{\eta }(T_{\mu \eta }+P\textit{h}_{\mu \eta }), \quad with \\ \textit{h}_{\mu \eta }&=\textit{g}_{\mu \eta }-U_{\mu }U_{\eta }. \end{aligned}$$

As we consider the fluid to be comoving with respect to our coordinates, therefore

$$\begin{aligned} U^{\mu }=(e^{-\frac{\nu }{2}},0,0,0), \quad U_{\mu }=(e^{\frac{\nu }{2}},0,0,0). \end{aligned}$$
(7)

By using the Bondi approach, the stress-energy tensor (6) in locally Minkowski frame takes the following form

$$\begin{aligned} T_{\mu \eta }=(\rho +P_{\bot }) U_{\mu }U_{\eta }-P_{\bot }\textit{g}_{\mu \eta }+(P_{r}-P_{\bot })K_{\mu }K_{\eta }, \end{aligned}$$
(8)

where \(K_{\mu }=(0,-1,0,0)\) is the component of tetrad field as described in [44]. The anisotropic tensor could be expressed as follows

$$\begin{aligned} \Pi _{\mu \eta }&=\Pi \left( K_{\mu }K_{\eta }+\frac{1}{3}\textit{h}_{\mu \eta }\right) , \quad with \quad \Pi =P_{r}-P_{\bot }, \,\, and \nonumber \\ P_{\bot }&=P-\frac{1}{3}\Pi , \quad P_{r}=P+\frac{2}{3}\Pi . \end{aligned}$$
(9)

In the above equation, \(P_{r}\) and \(P_{\bot }\) are the components of pressure in the radial and transverse directions, respectively.

2.1 Modified field equations

We can easily transform Eq. (3) in the following form

$$\begin{aligned} G_{\mu \eta }\equiv T^{eff }_{\mu \eta }=\kappa ^{2}T_{\mu \eta }+\mathcal {X}^{\textbf{D}}_{\mu \eta }. \end{aligned}$$
(10)

The non-trivial components of the above equation corresponding to the metric (15) and the source (8)

$$\begin{aligned} G_{00}&=\kappa ^{2}T_{00}+\mathcal {X}^{\textbf{D}}_{00} \nonumber \\&=8\pi \rho -\frac{8}{r^{2}}\left[ \mathcal {G}'^{2}f_{\mathcal {G}\mathcal {G}\mathcal {G}}+\mathcal {G}''f_{\mathcal {G}\mathcal {G}}\right] \left( e^{-\lambda }-1\right) e^{-2\lambda } \nonumber \\&\quad +\frac{4}{r^{2}}(e^{-\lambda }-3)\times e^{-2\lambda }\lambda '\mathcal {G}'f_{\mathcal {G}\mathcal {G}}-(\mathcal {G}f_{\mathcal {G}}-f), \end{aligned}$$
(11)
$$\begin{aligned} G_{11}&=\kappa ^{2}T_{11}+\mathcal {X}^{\textbf{D}}_{11}\nonumber \\&=8\pi P_{r}-\frac{4}{r^{2}}(e^{-\lambda }-3)e^{-2\lambda }\nu '\mathcal {G}'f_{\mathcal {G}\mathcal {G}}+(\mathcal {G}f_{\mathcal {G}}-f), \end{aligned}$$
(12)
$$\begin{aligned} G_{22}&=\kappa ^{2}T_{22}+\mathcal {X}^{\textbf{D}}_{22} \nonumber \\&=8\pi P_{\bot }-\frac{4}{r}\left[ \mathcal {G}'^{2}f_{\mathcal {G}\mathcal {G}\mathcal {G}}+\mathcal {G}''f_{\mathcal {G}\mathcal {G}}\right] \nu 'e^{-2\lambda } \nonumber \\&\quad -\frac{2}{r}\nu '^{2}e^{-2\lambda }\mathcal {G}'f_{\mathcal {G}\mathcal {G}}-\frac{2}{r}(2\nu ''-3\nu '\lambda ')e^{-2\lambda }\mathcal {G}'f_{\mathcal {G}\mathcal {G}} \nonumber \\&\quad +(\mathcal {G}f_{\mathcal {G}}-f), \end{aligned}$$
(13)

where primes denote r-derivatives. Here, it is important to emphasize the differences between the above-stated equations and the ones that correspond to the case of the spherically symmetric sources [53].

The additional geometric degrees of freedom mediating from the GBG model can be invoked by considering the power-law form of the function \(f(\mathcal {G})\), given as

$$\begin{aligned} f(\mathcal {G})=\alpha \mathcal {G}^{n}, \end{aligned}$$
(14)

where \(\alpha \), n \(\in \) \(\mathbb {R}\) (\(\mathbb {R}\) being the set of real numbers). For the sake of simplicity, we consider \(n=2\). This cosmic model was initially proposed by Cognola et al. [11]. The assumption of the above-stated geometrically modified gravitational models may be considered as viable corrections to the GBG gravity, suggested by Nojiri and Odintsov [9]. Notably, the power-law GBG cosmological model is physically viable and compatible with the observational data. In addition, this form is also be used for understanding the unification of primordial inflation and late-time DE era [54]. Such types of GBG corrections may be used as possible toy models for studying the formation of complex cosmic structures well as the dark section (the puzzles of DM and DE) of our universe [16, 55, 56]. Just like Einstein’s GR, the modified GBG cosmological model is also conserved (see [57, 58] and references therein), i.e., \(\nabla ^{\mu }T^{eff }_{\mu \eta }=0\) that provides a generalized hydrostatic continuity equation corresponding to the considered hysterically symmetric static source as

$$\begin{aligned} P_{r}'+\left[ \rho +P_{r}+\eta ^{(0)}\right] \frac{\nu '}{2}+\left[ \Pi + \eta ^{(1)}\right] \frac{2}{r}+\eta ^{(2)}=0,\nonumber \\ \end{aligned}$$
(15)

where the values of \(\eta ^{(0)}\), \(\eta ^{(1)}\), and \(\eta ^{(2)}\) are given in the appendix. Next, the generalized mass function corresponding the hyperbolically symmetric static sources can be defined as [44]

$$\begin{aligned} \textit{m}(r)=-\left( \frac{r}{2}\right) R^{3}_{~232}=\frac{r}{2}(1+e^{-\lambda }), \end{aligned}$$
(16)

where \(R^{3}_{~232}\) is the component of Riemann tensor. Now, using Eqs. (11) and (16), we obtain

$$\begin{aligned} \textit{m}(r)'=-4\pi r^{2}\rho +\frac{\alpha }{2} r^{2}\mathcal {G}^{2}+\eta ^{(0)}, \end{aligned}$$
(17)

whose integration provides

$$\begin{aligned} \textit{m}(r)=4\pi \int ^{r}_{0}\left[ -\rho r^{2}+\frac{1}{4 \pi }\left( \frac{\alpha }{2} r^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) \right] dr. \end{aligned}$$
(18)

Equation (16) shows that the mass function m(r) is a positive quantity, then it follows that the quantity \(\rho \) should be negative and consequently the weak energy condition is violated, as already discussed in [59]. In this respect, several comments are discussed in [44] that allows us to right the mass function in the following form

$$\begin{aligned} \textit{m}(r)=4\pi \int ^{r}_{0}\left[ |\rho | r^{2}+\frac{1}{4 \pi }\left( \frac{\alpha }{2} r^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) \right] dr, \end{aligned}$$
(19)

which is obtained after replacing \(\rho \) by \(-|\rho |\), because \(\rho \) is negative. The combination of Eqs. (12) and (16) produces

$$\begin{aligned} \nu '=\frac{8\pi r^{3}P_{r}-2\textit{m}+r^{2}\eta ^{(1)}+\alpha r^{3}\mathcal {G}^{2}}{r(2m-r)}. \end{aligned}$$
(20)

Using the value of \(\nu '\) in Eq. (15), we have

$$\begin{aligned}&P_{r}'+\left( P_{r}-|\rho |+\eta ^{(0)}\right) \frac{8\pi r^{3}P_{r}-2\textit{m}+r^{2}\eta ^{(1)}+\alpha r^{3}\mathcal {G}^{2}}{2r(2m-r)} \nonumber \\&\quad +\left( \Pi + \eta ^{(1)}\right) \frac{2}{r}+\eta ^{(2)}. \end{aligned}$$
(21)

The above equation is called the hydrostatic continuity equation for the considered fluid configuration. Now, we describe the physical significance arising from its different terms. The term \(P_{r}'\) represents the pressure gradient, which is generally negative and opposes the gravity. The second physical quantity exhibits the gravitational force containing the contributions of two different terms:

  1. (i)

    The term \(P_{r}-|\rho |+\eta ^{(0)}\), which is defined as passive gravitational mass density (PGMD) and is expected to be zero in case of stiff equation of state.

  2. (ii)

    The term \(8\pi r^{3}P_{r}-2\textit{m}+r^{2}\eta ^{(1)}+\alpha r^{3}\mathcal {G}^{2}\), which is negative for \(8\pi r^{3}P_{r}<\textit{m}-r^{2}\eta ^{(1)}-\alpha r^{3}\mathcal {G}^{2}\) and is proportional to the active gravitational mass (AGM).

The last two terms characterize the influence of anisotropic pressure and the extra degrees of freedom due to the GBG cosmological model. At this stage, two key points may be provided:

  • It should be notable that if both PGMD and AGM are negative, the impact of gravitational interactions would be opposing to that of negative of the pressure gradient as usual. But the gravitational and hydrostatic force term reverse their roles concerning to the positive value of \(\rho \) due to the equivalence principle.

  • The sign of the self-regenerative impact of pressure (characterized by the term \(8\pi r^{3}P_{r}\) ) is similar to that in the spherically symmetric case, while the second term shows that the contribution of the mass function has the opposite sign respecting to the latter scenario.

3 The Weyl tensor

since it is well established that Riemann–Christoffel curvature tensor can be expressed through other relativistic tensorial quantities such as Weyl curvture tensor \(C_{\mu \eta \sigma }^{\upsilon }\), Ricci curvature tensor \(R_{\mu \sigma }\) and curvature scalar \(\textbf{R}\), as

$$\begin{aligned} R_{\mu \eta \sigma }^{\upsilon }&=C_{\mu \eta \sigma }^{\upsilon }+\frac{1}{2}R_{\mu \sigma }\delta ^{\upsilon }_{\eta }-\frac{1}{2}R_{\mu \eta }\delta ^{\upsilon }_{\sigma } +\frac{1}{2}R^{\upsilon }_{\eta }\textit{g}_{\mu \sigma }-\frac{1}{2}R^{\upsilon }_{\sigma }\textit{g}_{\mu \eta } \nonumber \\&\quad -\frac{1}{6}R(\delta ^{\upsilon }_{\eta } g_{\mu \sigma }-\delta ^{\upsilon }_{\sigma } g_{\mu \eta }) \end{aligned}$$
(22)

Generally, the Weyl curvature tensor can be categorized in terms of magnetic and electrical components. But in this case, the magnetic part turns out to be zero, and we may specify the Weyl tensor via electrical part as

$$\begin{aligned} E_{\mu \eta }=C_{\mu \sigma \eta \upsilon }V^{\sigma }V^{\upsilon }, \end{aligned}$$
(23)

where

$$\begin{aligned} C_{\mu \omega \varsigma \tau }&=(\textit{g}_{\mu \omega \sigma \upsilon }\textit{g}_{\varsigma \tau \alpha \beta }-\tilde{\eta }_{\mu \omega \sigma \upsilon }\tilde{\eta }_{\varsigma \tau \alpha \beta })U^{\sigma }U^{\alpha }E^{\beta \upsilon }, \,\,with \nonumber \\ \textit{g}_{\mu \eta \sigma \upsilon }&=\textit{g}_{\mu \sigma }\textit{g}_{\eta \upsilon }-\textit{g}_{\mu \upsilon }\textit{g}_{\eta \sigma }, \end{aligned}$$
(24)

and \(\tilde{\eta }\) is the Levi-Civita tensor. We may express Eq. (23), in the following form

$$\begin{aligned} E_{\mu \eta }=\mathcal {E}\left( K_{\mu }K_{\eta }-\frac{1}{3}\textit{h}_{\mu \eta }\right) . \end{aligned}$$

Here, \(\mathcal {E}\) is the Weyl curvature scalar, which is given by

$$\begin{aligned} \mathcal {E}=-\frac{(1+e^{-\lambda })}{2r^{2}}-\left[ \nu ''+\frac{\nu '^{2}}{2}-\frac{\nu '}{r}+\frac{\lambda '}{r}-\frac{\lambda '\nu '}{2}\right] \frac{e^{-\lambda }}{2}. \end{aligned}$$
(25)

Next, using the gravitational field equations Eqs. (11)–(13) along with Eqs. (16) and (25), we get the following relationship for the mass function

$$\begin{aligned} \frac{3\textit{m}}{r^{3}}=4\pi |\rho |+4\pi \Pi +\frac{1}{2}\left( \eta ^{(0)}+\eta ^{(1)}-\eta ^{(2)}-\alpha \mathcal {G}^{2}\right) -\mathcal {E}. \end{aligned}$$
(26)

From Eq. (19), we get

$$\begin{aligned} \textit{m}(r)=\frac{4\pi }{3}|\rho |r^{3}-\frac{4\pi }{3}\int ^{r}_{0}|\rho |'\tilde{r}^{3}dr+\int ^{r}_{0}\left( \frac{\alpha }{2} \tilde{r}^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) dr. \end{aligned}$$
(27)

The above-stated equation provides an important representation of the mass of our geometry in terms of its value in homogeneous and inhomogeneous energy-density plus the modification brought about by the GBG model. This relationship can be used to calculate the deviations of the mass function due to density inhomogeneity plus the GBG degrees of freedom. Then, using Eqs. (26) and (27), we get

$$\begin{aligned} \mathcal {E}&=4\pi \Pi +\frac{4\pi }{r^{3}}\int ^{r}_{0}|\rho |'\tilde{r}^{3}dr-\frac{3}{r^{3}}\int ^{r}_{0}\left( \frac{\alpha }{2} \tilde{r}^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) dr \nonumber \\&\quad +\frac{1}{2}\left( \eta ^{(0)}+\eta ^{(1)}-\eta ^{(2)}-\alpha \mathcal {G}^{2}\right) . \end{aligned}$$
(28)

This equation gives a significant representation of the Weyl curvature scalar in terms of two fundamental physical characteristics of the anisotropic fluid configuration such as anisotropic pressure and energy-density inhomogeneity plus the higher degrees of freedom emerging from GBG cosmology. This expression is useful in describing the effects of GBG model on the physical properties of the hyperbolically symmetric anisotropic fluid.

4 Tolman mass

In 1930, Tolman introduced an alternative formalism to characterize the energy-content of the self-gravitational fluids [60]. Thus, the active gravitational mass corresponding to the hyperbolically symmetric fluid using Tolman formalism is defined as

$$\begin{aligned} \textit{m}_{\textit{T}}=\int ^{2\pi }_{0}\int ^{\pi }_{0}\int ^{r}_{0}\left( T^{0}_{0}-T^{1}_{1}-2T^{2}_{2}\right) \sqrt{-\textit{g}}d\tilde{r}d\theta d\phi , \end{aligned}$$
(29)

where \(T^{0}_{0}\), \(T^{1}_{1}\) and \(T^{2}_{2}\) are the non-trivial components of the matter stress-energy tensor. Now, using Eqs. (6) and (29), the above expression takes the following form

$$\begin{aligned} \textit{m}_{\textit{T}}= & {} 2\pi (\cosh \pi -1)\int ^{r}_{0}e^{\frac{(\nu +\lambda )}{2}}\tilde{r}^{2}\nonumber \\{} & {} \times \left( -|\rho |+\eta ^{(0)}+2\alpha \mathcal {G}^{2}+2P_{\bot }+2\eta ^{(2)}+P_{r}+\eta ^{(1)}\right) ,\nonumber \\ \end{aligned}$$
(30)

Next, using the gravitational equations of motion Eqs. (11)–(13) and integrating we have

$$\begin{aligned} \textit{m}_{\textit{T}}=\frac{r^{2}}{4}(\cosh \pi -1)e^{\frac{(\nu -\lambda )}{2}}\nu '. \end{aligned}$$
(31)

The combination of Eqs. (20) and (31) provides

$$\begin{aligned} \textit{m}_{\textit{T}}=\frac{(\cosh \pi -1)}{4}e^{\frac{(\nu +\lambda )}{2}}\left( 8\pi r^{3}P_{r}-2\textit{m}+r^{2}\eta ^{(1)}+\alpha r^{3}\mathcal {G}^{2}\right) . \end{aligned}$$
(32)

Equations (21) and (32) characterize the usual physical meaning of the Tolman mass function in terms of active gravitational mass. It should be notable that \(\textit{m}_{\textit{T}}<0\) for \(8\pi r^{3}P_{r}+r^{2}\eta ^{(1)}+\alpha r^{3}\mathcal {G}^{2}<2\textit{m}\) suggesting that the behavior of gravitational interaction is repulsive, in the background of the considered geometry. As is well-known that the four-acceleration \(a_{\mu }\) can be defined in terms of the four-velocity vector \(U^{\eta }\) as

$$\begin{aligned} a_{\mu }=U_{\alpha ;\eta }U^{\eta }, \end{aligned}$$
(33)

which by using Eqs. (7) and (33), reads as

$$\begin{aligned} a_{\mu }=aK_{\mu }, \quad with \quad a=\frac{\nu '}{2}e^{-\frac{\lambda }{2}}. \end{aligned}$$
(34)

The value of the scalar a, upon substituting the value of \(\nu '\) from Eq. (20), become

$$\begin{aligned} a=\frac{2\textit{m}_{\textit{T}}}{(\cosh \pi -1)}r^{-2}e^{-\frac{\nu }{2}}. \end{aligned}$$
(35)

This shows that if \(8\pi r^{3}P_{r}+r^{2}\eta ^{(1)}+\alpha r^{3}\mathcal {G}^{2}<2\textit{m}\), the quantity \(a_{\mu }\) is directed inward. Since \(a_{\mu }\) describes the radial inertial acceleration, therefore the inward flow of \(a_{\mu }\) manifests the repulsive character of the gravitational interactions. Now, differentiating Eq. (30) with respect to r and combining with Eq. (32), we have

$$\begin{aligned} \textit{m}_{\textit{T}}'-\frac{3}{r}\textit{m}_{\textit{T}}&=-\frac{1}{2}(\cosh \pi -1)e^{\frac{(\nu +\lambda )}{2}}r^{2}\nonumber \\ {}&\quad \left( \mathcal {E}+\eta ^{(1)}+4\pi \Pi -\eta ^{(2)}\right) . \end{aligned}$$
(36)

The integration of the above expression provides

$$\begin{aligned}&\textit{m}_{\textit{T}}=(\textit{m}_{\textit{T}})_{\Sigma ^{e}}\left( \frac{r}{r_{\Sigma ^{e}}}\right) ^{3} \nonumber \\&\quad +\frac{r^{3}}{2}(\cosh \pi -1)\int ^{r_{\Sigma ^{e}}}_{r} \frac{e^{\frac{(\nu +\lambda )}{2}}}{\tilde{r}}\left( \mathcal {E}+\eta ^{(1)}+4\pi \Pi -\eta ^{(2)}\right) dr. \end{aligned}$$
(37)

Then, utilizing Eq. (28), we get

$$\begin{aligned}&\textit{m}_{\textit{T}}=(\textit{m}_{\textit{T}})_{\Sigma ^{e}}\left( \frac{r}{r_{\Sigma ^{e}}}\right) ^{3}+\frac{r^{3}}{2}(\cosh \pi -1)\int ^{r_{\Sigma ^{e}}}_{r} \frac{e^{\frac{(\nu +\lambda )}{2}}}{\tilde{r}} \nonumber \\&\quad \times \left[ 8\pi \Pi ++\frac{4\pi }{r^{3}}\int ^{\tilde{r}}_{0}|\rho |'\tilde{r}^{3}ds-\frac{3}{r^{3}}\int ^{\tilde{r}}_{0}\left( \frac{\alpha }{2} \tilde{r}^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) ds\right. \end{aligned}$$
(38)
$$\begin{aligned} +&\left. \frac{1}{2}\left( \eta ^{(0)}+3\eta ^{(1)}-3\eta ^{(2)}-\alpha \mathcal {G}^{2}\right) \right] d\tilde{r}. \end{aligned}$$
(39)

Under the influence of extra curvature GBG corrections, the above expression is similar to Eq. (54) in the case of spherical symmetry [61].

5 The scheme of orthogonal splitting of curvature tensor

This section deals with the formation of some tensorial quantities obtained through a well-known procedure of orthogonal splitting of the Riemann–Christoffel tensor. This framework was originally presented by Bel [62] and later on extended by many researchers in GR [44, 63, 64] as well as in modified cosmological models [17,18,19]. The scheme of orthogonal decomposition is executed using tensorial terms \(Y_{\mu \eta },~Z_{\mu \eta }\) and \(X_{\mu \eta }\) given by (for details see [62, 63, 65])

$$\begin{aligned}&Y_{\mu \eta }=R_{\mu \sigma \upsilon \eta }U^{\sigma }U^{\eta }, \end{aligned}$$
(40)
$$\begin{aligned}&Z_{\mu \eta }=^{*} R_{\mu \sigma \eta \upsilon }U^{\sigma }U^{\upsilon }=\frac{1}{2}\eta _{\mu \sigma \tau \omega }R^{\tau \omega }_{~~~\eta \upsilon }U^{\sigma }U^{\upsilon }, \end{aligned}$$
(41)
$$\begin{aligned}&X_{\mu \eta }=^{*} R^{*}_{\mu \sigma \eta \upsilon }U^{\sigma }U^{\upsilon }=\frac{1}{2}\eta _{\mu \sigma }^{~~~\tau \omega }R^{*}_{\tau \omega \eta \upsilon }U^{\sigma }U^{\upsilon }, \end{aligned}$$
(42)

where \(*\) represents the dual tensor, i.e., \(R^{*}_{\mu \sigma \eta \upsilon }=\frac{1}{2}\eta _{\tau \omega \sigma \upsilon }R_{\mu \eta }^{~~~\tau \omega }\). Using the orthogonal splitting scheme of \(R_{\mu \sigma \upsilon \eta }\) in terms of matter variables, \(Y_{\mu \eta },~Z_{\mu \eta }\) and \(X_{\mu \eta }\) can be decomposed in terms of their trace and the associated trace-free parts as (see [16, 21, 63, 66])

$$\begin{aligned} X_{\mu \eta }&=\frac{1}{3}\textit{h}_{\mu \eta }X_{\textbf{T}}+\left( K_{\mu }K_{\eta }+\frac{1}{3}\textit{h}_{\mu \eta }\right) X_{\textbf{TF}}, \end{aligned}$$
(43)
$$\begin{aligned} Y_{\mu \eta }&=\frac{1}{3}\textit{h}_{\mu \eta }Y_{\textbf{T}}+\left( K_{\mu }K_{\eta }+\frac{1}{3}\textit{h}_{\mu \eta }\right) Y_{\textbf{TF}}, \end{aligned}$$
(44)

where \(X_{\textbf{T}}\equiv X^{\mu }_{\mu }\) and \(Y_{\textbf{T}}\equiv Y^{\mu }_{\mu }\). Next, using the GBG gravitational equations \(X_{\textbf{T}}\) and \(X_{\textit{TF}}\) become

$$\begin{aligned} X_{\textbf{T}}= & {} -8\pi |\rho |-\alpha G^{2}+\eta ^{(0)}, \end{aligned}$$
(45)
$$\begin{aligned} X_{\textbf{TF}}= & {} 4\pi \Pi +\frac{1}{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) -\mathcal {E}. \end{aligned}$$
(46)

Now, substituting the value of \(\mathcal {E}\) from Eq. (28) in Eq. (46), we have

$$\begin{aligned} X_{\textbf{TF}}&=\frac{1}{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) -\frac{4\pi }{r^{3}}\int ^{r}_{0}|\rho |'\tilde{r}^{3}dr \nonumber \\&\quad +\frac{3}{r^{3}}\int ^{r}_{0}\left( \frac{\alpha }{2} \tilde{r}^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) dr\nonumber \\&\quad -\frac{1}{2}\left( \eta ^{(0)}+\eta ^{(1)}-\eta ^{(2)}-\alpha \mathcal {G}^{2}\right) , \end{aligned}$$
(47)

and

$$\begin{aligned} Y_{\textbf{T}}&=4\pi (-|\rho |+3P)+\frac{1}{2}\left( \eta ^{(0)}-\alpha G^{2}\right) , \end{aligned}$$
(48)
$$\begin{aligned} Y_{\textbf{TF}}&=4\pi \Pi +\frac{1}{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) +\mathcal {E}. \end{aligned}$$
(49)

Next, using the value of \(\mathcal {E}\) from Eq. (28) in Eq. (49), we get

$$\begin{aligned} Y_{\textbf{TF}}&=8\pi \Pi +\frac{1}{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) +\frac{4\pi }{r^{3}}\int ^{r}_{0}|\rho |'\tilde{r}^{3}dr \nonumber \\&\quad -\frac{3}{r^{3}}\int ^{r}_{0}\left( \frac{\alpha }{2} \tilde{r}^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) dr \nonumber \\&\quad +\frac{1}{2}\left( \eta ^{(0)}+\eta ^{(1)}-\eta ^{(2)}-\alpha \mathcal {G}^{2}\right) . \end{aligned}$$
(50)
$$\begin{aligned} X_{\textbf{TF}}+Y_{\textbf{TF}}&=8\pi \Pi +\eta ^{(1)}-\eta ^{(2)}. \end{aligned}$$
(51)

The above result shows that the local anisotropy of pressure in the self-gravitational fluids is controlled by the quantities \(X_{\textbf{TF}}\), \(Y_{\textbf{TF}}\) and the GBG higher degrees of freedom. Now, we describe the physical significance of the terms \(Y_{\textbf{T}}\) and \(Y_{\textbf{TF}}\) by using the expressions Eqs. (38), (48) and (50) as

$$\begin{aligned} \textit{m}_{\textit{T}}&=(\textit{m}_{\textit{T}})_{\Sigma ^{e}}\left( \frac{r}{r_{\Sigma ^{e}}}\right) ^{3}+\frac{r^{3}}{2}(\cosh \pi -1)\int ^{r_{\Sigma ^{e}}}_{r} \frac{e^{\frac{(\nu +\lambda )}{2}}}{\tilde{r}} \nonumber \\&\quad \times \left[ Y_{\textit{TF}}-\frac{1}{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) \right] d\tilde{r}, \end{aligned}$$
(52)

and

$$\begin{aligned} \textit{m}_{\textit{T}}&=\frac{1}{2}(\cosh \pi -1)\int ^{r}_{0}e^{\frac{(\nu +\lambda )}{2}}\tilde{r}^{2} \nonumber \\&\quad \times \left[ Y_{\textit{T}}-\frac{\eta ^{(0)}}{2}+\frac{\alpha }{2}\mathcal {G}^{2} +4\pi \left( 2\alpha \mathcal {G}^{2}+\eta ^{(0)}+\eta ^{(1)}+2\eta ^{(2)}\right) \right] . \end{aligned}$$
(53)

The above equations relate the Tolman mass function with the scalar functions \(Y_{\textbf{T}}\), \(Y_{\textbf{TF}}\) and higher curvature GBG-corrections. The scalar variable \(Y_{\textbf{TF}}\) characterizes the influence of structural variables such as pressure anisotropy, and density inhomogeneity in the presence of higher-order GBG terms upon the mass function. Specifically, the scalar function \(Y_{\textbf{TF}}\) explains how the above-stated terms change the value of the mass function relative to its value in the case of isotropic and homogeneous fluid configuration. This phenomenon provides the basis behind the notion of complexity as described in [16, 20, 35]. This new notion was based on the assumption that a system endowed with isotropic homogeneous configuration exhibits zero complexity. For such type of matter distribution, the scalar \(Y_{\textbf{TF}}\), which we refer to as the complexity factor, vanishes. On the other hand, Eq. (53) shows that in the presence of GBG dark source terms, \(Y_{\textbf{T}}\) serves as Tolman mass density.

6 All static solutions

This section describes a generic framework to manifest a time-independent hyperbolically symmetric model in the form of two generating functions. Following that, we would also discuss several explicit solutions and their generating functions. This methodology is analogous to the one suggested for the case of spherically symmetric fluid [53, 67], in the presence of GBG-corrections.

Therefore, using Eqs. (12) and (13), we get

$$\begin{aligned}&8\pi \Pi +\eta ^{(1)}-\eta ^{(2)}\nonumber \\ {}&\quad =-\frac{1}{2}\left( \nu ''-\frac{\nu '}{r}+\frac{\nu '^{2}}{2}-\frac{\lambda '}{r}-\frac{\nu '\lambda '}{2}+\frac{1}{r^{2}}\right) e^{-\lambda }+\frac{1}{r^{2}}, \end{aligned}$$
(54)

Introducing the new variables

$$\begin{aligned} e^{-\lambda }=\textit{y}; \quad \textit{z}=\frac{\nu '}{2}+\frac{1}{r}, \end{aligned}$$
(55)

Then, Eq. (54) become

$$\begin{aligned}&\textit{y}'+\left( 2\textit{z}+\frac{2\textit{z}'}{\textit{z}}+\frac{4}{\textit{z}r^{2}}-\frac{6}{r}\right) \nonumber \\ {}&\textit{y}=\frac{2}{\textit{z}}\left( \frac{1}{r^{2}}+\eta ^{(2)}-8\pi \Pi -\eta ^{(1)}\right) , \end{aligned}$$
(56)

whose integration gives

$$\begin{aligned} e^{\lambda }=\frac{\textit{z}^{2}e^{\int \left( 2z+\frac{4}{zr^{2}}\right) dr}}{r^{6}\left( 2\int \textit{z}\left( \frac{1+r^{2}\eta ^{(2)}-8\pi \Pi r^{2}-r^{2}\eta ^{(1)} }{r^{8}}\right) e^{\int \left( 2z+\frac{4}{zr^{2}}\right) }dr+A_{3}\right) }. \end{aligned}$$
(57)

Therefore, any time-independent model can be completely defined with the help of two generating functions \(\textit{z}\) and \(\Pi \). Thus the physical variables for this model are given as

$$\begin{aligned} 4\pi |\rho |&=\frac{\textit{m}'}{r^{2}}-\frac{\alpha }{2}\mathcal {G}^{2}+\frac{\eta ^{(0)}}{2}, \end{aligned}$$
(58)
$$\begin{aligned} 4\pi P_{r}&=\frac{\textit{z}\left( 2\textit{m}r-r^{2}\right) +r-\textit{m}}{r^{3}}-\frac{\alpha }{2}\mathcal {G}^{2}-\frac{\eta ^{(1)}}{2}, \end{aligned}$$
(59)
$$\begin{aligned} 8\pi P_{\bot }&=\eta ^{(2)}-\eta ^{(1)}+\left( \frac{\textit{m}}{r}-\frac{\textit{m}'}{r^{2}}\right) \textit{z} \nonumber \\&\quad +\left( \textit{z}^{2}+\textit{z}'-\frac{\textit{z}}{r}+\frac{1}{r^{2}}\right) \left( \frac{2\textit{m}}{r}-1\right) . \end{aligned}$$
(60)

Now, we will discuss some explicit solutions and the respecting generating functions.

6.1 A model with vanishing complexity factor

In this section, we shall discuss a hyperbolically symmetric model satisfying the minimal complexity factor (\(Y_{\textbf{TF}}=0\)) plus the condition \(P_{r}=0\).

It would be curious to observe a stellar model (apart from isotropic and homogeneous solution) under the condition \(Y_{\textbf{TF}}=0\) because the scalar function \(Y_{\textbf{TF}}\) intended to measure the complexity factor of the self-gravitational fluids [35]. To obtain a particular hyperbolically symmetric model, we need to consider an extra constraint on the system as infinitely many solutions can be possible. In this regard, we impose an extra condition \(P_{r}=0\) besides the condition \(Y_{\textbf{TF}}=0\).

Therefore, under the condition \(P_{r}=0\), Eq. (12) become

$$\begin{aligned} \nu '=-\frac{2\textit{g}}{r(2\textit{g}-1)}-\frac{r}{(2\textit{g}-1)}\eta ^{(0)}-\frac{r}{(2\textit{g}-1)}\alpha \mathcal {G}^{2}, \end{aligned}$$
(61)

where \(e^{-\lambda }=2\textit{g}-1\). Further, using the condition \(Y_{\textbf{TF}}=0\) in Eq. (52), we have

$$\begin{aligned} \textit{m}_{\textit{T}}&=(\textit{m}_{\textit{T}})_{\Sigma ^{e}}\left( \frac{r}{r_{\Sigma ^{e}}}\right) ^{3} \nonumber \\&\quad -\frac{r^{3}}{4}(\cosh \pi -1)\int ^{r_{\Sigma ^{e}}}_{r} \frac{e^{\frac{(\nu +\lambda )}{2}}}{\tilde{r}}\left( \eta ^{(1)}-\eta ^{(2)}\right) d\tilde{r}. \end{aligned}$$
(62)

Next, combining Eqs. (31), (61) and (62), we get

$$\begin{aligned} e^{\nu }=\frac{16(2\textit{g}-1)\left[ (\textit{m}_{\textit{T}})_{\Sigma ^{e}}\left( \frac{r}{r_{\Sigma ^{e}}}\right) ^{3}-\frac{r^{3}}{4}(\cosh \pi -1)\int ^{r_{\Sigma ^{e}}}_{r} \frac{e^{\frac{(\nu +\lambda )}{2}}}{\tilde{r}}\left( \eta ^{(1)}-\eta ^{(2)}\right) d\tilde{r}\right] ^{2}}{r^{2}(\cosh \pi -1)^{2}(2\textit{g}-r^{2}\eta ^{(0)}-\alpha r^{2}\mathcal {G}^{2})}, \end{aligned}$$
(63)

and the minimal complexity factor condition yield

$$\begin{aligned} \textit{g}\left( 5\textit{g}-2\right) +\textit{g}'r\left( 1-\textit{g}\right) +2r^{2}\left( 2\textit{g}-1\right) ^{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) =0. \end{aligned}$$
(64)

Thus the associated physical variables turn out to be

$$\begin{aligned} |\rho |&=\frac{3}{4\pi r^{2}}\left[ \frac{\textit{g}(2\textit{g}-1)+\frac{2}{3}r^{2}(2\textit{g}-1)^{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) }{(\textit{g}-1)}\right] \nonumber \\&\quad -\frac{1}{8\pi r^{2}}\left( \eta ^{(0)}-\alpha \mathcal {G}^{2}\right) , \end{aligned}$$
(65)
$$\begin{aligned} P_{\bot }&=\frac{3\textit{g}^{2}}{8\pi r^{2}(2\textit{g}-1)^{2}}\left[ \frac{(2\textit{g}-1)+\frac{2}{3}r^{2}(2-1/\textit{g})^{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) }{(\textit{g}-1)}\right] \nonumber \\&\quad -\frac{1}{8\pi r^{2}}\left( \alpha \mathcal {G}^{2}+\eta ^{(2)}\right) . \end{aligned}$$
(66)

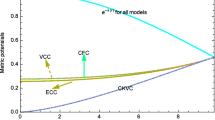
Here, the minimum value of the radial coordinate, fulfilling the condition \(\textit{g}(r_{{\textbf {min}}})>0\), constrains the matter configuration. Furthermore, the continuity of the mass function suggests the appearance of a thin shell over the exterior hypersurface. Eventually, both PGMD and AGM are negative because \(P_{r}=0\).

Thus the corresponding generating functions may be defined as

$$\begin{aligned} \textit{z}&=\frac{2\textit{g}-r^{2}\eta ^{(0)}-r^{2}\alpha \mathcal {G}^{2}-2}{2r(2\textit{g}-1)}, \end{aligned}$$
(67)
$$\begin{aligned} \Pi (r)&=-\frac{3\textit{g}^{2}}{8\pi r^{2}(2\textit{g}-1)^{2}}\nonumber \\ {}&\qquad \left[ \frac{(2\textit{g}-1)+\frac{2}{3}r^{2}(2-1/\textit{g})^{2}\left( \eta ^{(1)}-\eta ^{(2)}\right) }{(\textit{g}-1)}\right] \nonumber \\&\quad +\frac{1}{8\pi r^{2}}\left( \alpha \mathcal {G}^{2}+\eta ^{(2)}+r^{2}\alpha \mathcal {G}^{2}+r^{2}\eta ^{(1)}\right) . \end{aligned}$$
(68)

6.2 The conformally flat solutions

By taking into account the significant role of the Weyl tensor in describing the structure of the matter configuration as stated by the Eqs. (28) and (52), it is important to impose a particular condition of conformal flatness (i.e., \(\mathcal {E}=0\)). Thus under this condition, Eq. (25) yields

$$\begin{aligned} -\left( \frac{1+e^{-\lambda }}{r^{2}}\right) '+\left( \frac{\nu 'e^{-\lambda }}{2r}\right) '+\left( \frac{\nu 'e^{\nu }}{2r}\right) 'e^{-(\lambda +\nu )}=0, \end{aligned}$$
(69)

Considering the intermediate variables

$$\begin{aligned} s=e^{-\lambda }\quad ; \quad \frac{\nu '}{2}=\frac{x'}{x}, \end{aligned}$$
(70)

so that Eq. (69) become

$$\begin{aligned} s'+2\left( \frac{x''-\frac{x'}{x}+\frac{x}{r^{2}}}{x'-\frac{x}{r}}\right) s+\frac{2x}{r^{2}\left( x'-\frac{x}{r}\right) }=0, \end{aligned}$$
(71)

which upon integration gives the following formal solution

$$\begin{aligned} s=\left\{ \int e^{\int u(r)dr}f(r)dr+A_{1}\right\} e^{-\int u(r)dr}, \end{aligned}$$
(72)

where \(A_{1}\) is an integration constant, and

$$\begin{aligned} u(r)=2\frac{d}{dr}\left\{ \ln \left( x'-\frac{x}{r}\right) \right\} , \quad f(r)=-\frac{2x}{r^{2}\left( x'-\frac{x}{r}\right) }. \end{aligned}$$
(73)

Now, transforming Eq. (72) into original variables, we get

$$\begin{aligned} \frac{\nu '}{2}=\frac{1}{r}\left[ \left( \sqrt{\beta r^{2}e^{-\nu }-1}\right) e^{\frac{\lambda }{2}}+1\right] . \end{aligned}$$
(74)

Here, \(\beta \) is an integration constant which can be easily evaluated using the Darmois matching constraints [68] as

$$\begin{aligned} \beta =\frac{\mathbb {M}(9\mathbb {M}-4r_{\Sigma ^{e}})}{r^{4}_{\Sigma ^{e}}}. \end{aligned}$$
(75)

The integration of Eq. (74) provides

$$\begin{aligned} e^{\nu }=\beta r^{2}\sin ^{2}\left( \int \frac{e^{\frac{\lambda }{2}}}{r}dr+\zeta \right) . \end{aligned}$$
(76)

where \(\zeta \) denotes an integration constant, which may be evaluated using Darmois matching constraints [68] as

$$\begin{aligned} \zeta =-\left( \int \frac{e\frac{\lambda }{2}}{r}\right) _{\Sigma ^{e}}+\sin ^{-1}\left( r_{\Sigma ^{e}}\sqrt{\frac{(\frac{2\mathbb {M}}{r_{\Sigma ^{e}}}-1)}{M(9\mathbb {M}-4r_{\Sigma ^{e}})}}\right) . \end{aligned}$$
(77)

Here, it is important to mention a clear difference between Eq. (76) and the respecting expression (Eq. 40 in [69]) in case of spherically symmetric fluid configuration. In order to produce a particular model, we need to impose an extra condition on the hyperbolically symmetric configuration because the condition \(\mathcal {E}=0\) gives only one generating function. In this respect, we impose an extreme the condition, i.e., \(P_{r}=0\). It is notable that this hyperbolically symmetric solution is analogous to the spherically symmetric model presented in [69] plus the higher-order GBG-terms.

Thus under the assumption \(P_{r}=0\), Eq. (12) provides

$$\begin{aligned} \nu '=-\left( \frac{1+e^{\lambda }}{r}\right) -re^{\lambda }\eta ^{(0)}-\alpha re^{\lambda }\mathcal {G}^{2}, \end{aligned}$$
(78)

The combination of Eqs. (78) and (25) along with the condition \(\mathcal {E}=0\), produces

$$\begin{aligned}&8\left( 1+e^{\lambda }\right) +\left( 1+e^{\lambda }\right) \left( \alpha \mathcal {G}^{2}+\eta ^{(0)}\right) e^{\lambda }+3r\lambda ' \nonumber \\&\quad -\alpha e^{\lambda }\left( \mathcal {G}^{2}-r\lambda '\mathcal {G}^{2}-2r\mathcal {G}\mathcal {G}'\right) -r\lambda 'e^{\lambda }+\left( 1+e^{\lambda }\right) ^{2}+\phi , \end{aligned}$$
(79)

where the value of \(\phi \) is given in the appendix. Next, introducing \(e^{-\lambda }+1=2\textit{g}\), we get

$$\begin{aligned} \textit{g}&\left( 9\textit{g}+\alpha \mathcal {G}^{2}+\eta ^{(0)}-4\right) -\textit{g}'r\left( 3\textit{g}+\frac{1}{2}\eta ^{(0)}-2\right) \nonumber \\ {}&\quad +\frac{r^{2}}{4}\left( \alpha \mathcal {G}^{2}+\eta ^{(0)}\right) +\psi , \end{aligned}$$
(80)

where the value of \(\psi \) is given in the appendix.

$$\begin{aligned} A_{2}=\textit{g}-\int \frac{\textit{g}\left( 9\textit{g}+\alpha \mathcal {G}^{2}+\eta ^{(0)}-4\right) +\frac{r^{2}}{4}\left( \alpha \mathcal {G}^{2}+\eta ^{(0)}\right) +\psi }{r\left( 3\textit{g}+\frac{1}{2}\eta ^{(0)}-2\right) }dr. \end{aligned}$$
(81)

where \(A_{2}\) is an integration constant. Now, the combination of Eqs. (74) and (78) produces

$$\begin{aligned} e^{\nu }=\frac{4\alpha r^{2}(2\textit{g}-1)}{\left( 6\textit{g}+r^{2}\eta ^{(0)}+r^{2}\alpha \mathcal {G}^{2}-2\right) ^{2}+4\left( 2\textit{g}-1\right) } \end{aligned}$$
(82)

Finally, by using the above conditions the values of the physical variables become

$$\begin{aligned} |\rho |&=\frac{\textit{g}}{4\pi r^{2}}\left[ \frac{12\textit{g}-6+\frac{3}{2}\eta ^{(0)}+\alpha \mathcal {G}^{2}+\frac{r^{2}}{4\textit{g}} \left( \alpha \mathcal {G}^{2}+\eta ^{(0)}\right) +\frac{\psi }{\textit{g}}}{\left( 3\textit{g}+\frac{1}{2}\eta ^{(0)}-2\right) }\right] \nonumber \\&\quad -\frac{1}{8\pi r^{2}}\left( \eta ^{(0)}-\alpha \mathcal {G}^{2}\right) , \end{aligned}$$
(83)
$$\begin{aligned} P_{\bot }&=\frac{\textit{g}^{2}}{8\pi r^{2}(2\textit{g}-1)}\nonumber \\ {}&\quad \left[ \frac{12\textit{g}-6+\alpha \mathcal {G}^{2}+\frac{3}{2}\eta ^{(0)}+\frac{r^{2}}{4\textit{g}^{2}} \left( \alpha \mathcal {G}^{2}+\eta ^{(0)}\right) +\frac{\psi }{g^{2}}}{\left( 3\textit{g}+\frac{1}{2}\eta ^{(0)}-2\right) }\right] \nonumber \\&\quad -\frac{1}{8\pi r^{2}}\left( \alpha \mathcal {G}^{2}+\eta ^{(2)}\right) . \end{aligned}$$
(84)

The above-stated values of the fluid variables shows that the quantity \(e^{\nu }\) is positive for \(g>\frac{2}{3}\). This solution can also be accomplished by considering an empty vacuole with a hypersurface of \(r=r_{\textbf{min}}\). Also, \(P_{r}=0\) implies that both PGMD and AGM are negative. Although the junction constraints are satisfied over the exterior hypersurface, the mass function becomes discontinuous, thereby appearing a thin shell on the hypersurface \(r=r_{\textbf{min}}\). Finally, the generating functions for this particular hyperbolically symmetric solution can be evaluated as

$$\begin{aligned} \textit{z}=\frac{2\textit{g}-r^{2}\eta ^{(0)}-r^{2}\alpha \mathcal {G}^{2}-2}{2r(2\textit{g}-1)}, \end{aligned}$$
(85)

and

$$\begin{aligned} \Pi (r)&=-\frac{\textit{g}^{2}}{8\pi r^{2}(2\textit{g}-1)}\nonumber \\ {}&\quad \left[ \frac{12\textit{g}-6+\alpha \mathcal {G}^{2}+\frac{3}{2}\eta ^{(0)}+\frac{r^{2}}{4\textit{g}^{2}}\left( \alpha \mathcal {G}^{2}+\eta ^{(0)}\right) +\frac{\psi }{g^{2}}}{\left( 3\textit{g}+\frac{1}{2}\eta ^{(0)}-2\right) }\right] \nonumber \\ {}&\quad +\frac{1}{8\pi r^{2}}\left( \alpha \mathcal {G}^{2}+\eta ^{(2)}+r^{2}\alpha \mathcal {G}^{2}+r^{2}\eta ^{(1)}\right) . \end{aligned}$$
(86)

6.3 The stiff equation of state

Lastly, we discuss some solutions fulfilling the condition known as the stiff equation of state. Lastly, we discuss some solutions fulfilling the condition known as the stiff equation of state. This condition was initially suggested by Zeldovich [70], and is considered to be the most appropriate to explain the ultradense matter. According o his condition, the energy density is assumed o be equal to the pressure. Thus in our case, we have

$$\begin{aligned} |\rho |-\eta ^{(0)}=P_{r}+\eta ^{(1)}. \end{aligned}$$
(87)

Then, Eq. (20) gives

$$\begin{aligned} P_{r}'+\left[ 2\eta ^{(0)}-\eta ^{(1)}\right] \frac{\nu '}{2}+\left[ \Pi +\eta ^{(1)}\right] \frac{2}{r}+\eta ^{(2)}=0. \end{aligned}$$
(88)

In order to get some particular hyperbolic stellar models, further details are needed. In this case, we shall provide some solutions under the following two conditions.

6.3.1 \(P_{\bot }=0\)

In the first case, we consider that the component of pressure in the tangential direction vanishes (i.e., \(P_{\bot }=0\)). Using this condition in Eq. (88), and integrating we get

$$\begin{aligned} P_{r}&=\frac{\mathcal {K}}{r^{2}}-\frac{1}{r^{2}}\int ^{r}_{0} r^{2}\mathcal {X}dr \Rightarrow \nonumber \\ |\rho |&=\frac{\mathcal {K}}{r^{2}}-\frac{1}{r^{2}}\int ^{r}_{0} r^{2}\mathcal {X}dr +(\eta ^{(0)}+\eta ^{(1)}), \end{aligned}$$
(89)

where \(\mathcal {K}\) is an integration constant and \(\mathcal {X}=\left( 2\eta ^{(0)}-\eta ^{(1)}\right) \frac{\nu '}{2}+\frac{2}{r}\eta ^{(1)}+\eta ^{(2)}\).

The combination of the above expression with Eqs. (16)–(18) and (20), produces

$$\begin{aligned} \textit{m}(r)&=4\pi \mathcal {K}r+4\pi \int ^{r}_{0}\mathcal {Z}r^{2}dr, \quad with \nonumber \\ \mathcal {Z}&=-\frac{1}{r^{2}}\int ^{r}_{0} r^{2}\mathcal {X}dr +(\eta ^{(0)}+\eta ^{(1)}), \end{aligned}$$
(90)

and

$$\begin{aligned} e^{-\lambda }&=8\pi \mathcal {K}-1+\frac{4\pi }{r}\int ^{r}_{0}r^{2}\mathcal {Z}dr, \nonumber \\ \nu '&=-\frac{4\pi \left[ r^{3}\int ^{r}_{0}r^{2}\mathcal {X}dr+\int ^{r}_{0}r^{2}\mathcal {Z}dr\right] }{r(2\textit{m}-r)}. \end{aligned}$$
(91)

Here, it is notable that both PGMD and AGM vanish. This hyperbolically symmetric stellar model exhibit non-vanishing pressure surfaces. The corresponding generating functions are defined as

$$\begin{aligned} \textit{z}&=-\frac{4\pi \left[ r^{3}\int ^{r}_{0}r^{2}\mathcal {X}dr+\int ^{r}_{0}r^{2}\mathcal {Z}dr\right] }{2r(2\textit{m}-r)}+\frac{1}{r}; \nonumber \\ \Pi (r)&=\frac{\mathcal {K}}{r^{2}}-\frac{1}{r^{2}}\int ^{r}_{0} r^{2}\mathcal {X}dr\nonumber \\ {}&\quad -\frac{1}{8\pi r^{2}}\left( \alpha \mathcal {G}^{2}+\eta ^{(1)}+\alpha r^{2} \mathcal {G}^{2}+r^{2}\eta ^{(1)}\right) . \end{aligned}$$
(92)

6.3.2 \(Y_{\textit{TF}}=0\)

In this case, we discuss a simplest stiff-fluid stellar solution satisfying the condition \(Y_{\textbf{TF}}=0\), along with the condition (87). Utilizing the above-stated condition in Eq. (50) and then using the final result in Eq. (88), we get

$$\begin{aligned} P_{r}''+\frac{3}{r}P_{r}'-\frac{1}{r}\left( \eta ^{(0)}+\eta ^{(1)}\right) +\frac{\mathcal {A}'}{r}=0, \end{aligned}$$
(93)

where \(\mathcal {A}=-\frac{r^{3}}{8\pi }\left( \eta ^{(0)}+2\eta ^{(1)}-2\eta ^{(2)}-\alpha \mathcal {G}^{2}\right) +\frac{3}{4\pi }\int ^{r}_{0}\left( \frac{\alpha }{2}\tilde{r}^{2}\mathcal {G}^{2}+\eta ^{(0)}\right) dr\). The solution of Eq. (93) reads

$$\begin{aligned} P_{r}=\frac{\textit{b}}{r^{2}}-\textit{a}+\int ^{r}_{0}\left[ \frac{1}{r^{3}}\int ^{r}_{0}\left\{ \frac{\mathcal {A}'}{r}-\frac{1}{r}\left( \eta ^{(0)}+\eta ^{(1)}\right) \right\} dr\right] dr. \end{aligned}$$
(94)

where \(\textit{a}\) and \(\textit{b}\) denote two arbitrary integration constants. Next, utilizing Eqs. (16) and (18), we have

$$\begin{aligned} \textit{m}=4\pi \left( \textit{b}r-\frac{\textit{a}}{3}r^{2}\right) +4\pi \int ^{r}_{0}\left[ \mathcal {W}r^{2}+r^{2}\left( \eta ^{(0)}+\eta ^{(1)}\right) \right] dr, \end{aligned}$$
(95)

where \(\mathcal {W}=\int ^{r}_{0}\left[ \frac{1}{r^{3}}\int ^{r}_{0}\left\{ \frac{\mathcal {A}'}{r}-\frac{1}{r}\left( \eta ^{(0)}+\eta ^{(1)}\right) \right\} dr\right] dr\). The expression (95) can be used to calculate the value of \(\lambda \). Consequently, using these results in Eq. (20), we get the value of \(\nu \).

Now, considering the anisotropic matter configuration to be bounded by the outer hypersurface represented as \(r=r_{\Sigma ^{e}}=constant \), so that we have

$$\begin{aligned} P_{r}=\textit{b}\left( \frac{1}{r^{2}}-\frac{1}{r^{2}_{\Sigma ^{e}}}\right) +\mathcal {W}, \end{aligned}$$
(96)

and

$$\begin{aligned} m&=\frac{4\pi \textit{b}r}{3r^{2}_{\Sigma ^{e}}}\left( 3r^{2}_{\Sigma ^{e}}-r^{2}\right) +\mathcal {Y}, \quad \nonumber \\ {}&\quad with \quad 4\pi \int ^{r}_{0}\left[ \mathcal {W}r^{2}+r^{2}\left( \eta ^{(0)}+\eta ^{(1)}\right) \right] dr. \end{aligned}$$
(97)

Hence the junction constraints are satisfied only on the exterior hypersurface, while not on the interior hypersurface.

Finally, using the above relations we get

$$\begin{aligned} 4\pi r^{3}P_{r}-m=-\frac{8\pi br^{3}}{3r^{2}_{\Sigma ^{e}}}, \end{aligned}$$
(98)

where \(\mathcal {M}=4\pi r^{3}\mathcal {W}-\mathcal {Y}\). Then, for the tangential component of pressure, we obtain

$$\begin{aligned} P_{\bot }=-\frac{\textit{b}}{r^{2}_{\Sigma ^{e}}}-\alpha \mathcal {G}^{2}-\eta ^{(2)}, \end{aligned}$$
(99)

Hence we deduce that PGMD becomes zero for this hyperbolically symmetric model stellar model, however, in the previous model PGMD\(<0\).

7 Discussions and conclusions

We have presented a general framework for understanding the physical characteristics of the static relativistic self-gravitational fluids endowed with hyperbolic symmetry through the principles of one of the most promising geometrical gravitational theories, the modified Gauss–Bonnet gravity (GBG). This study is concerned with the formulations of some scalar quantities commonly known as structure scalars obtained from a well-known procedure of orthogonal decomposition of the curvature tensor. Orthogonal splitting is a way of decomposing the Riemann curvature tensor in terms of some scalar variables, each of which has a distinct physical meaning. The relevance of the structure scalars in understanding the evolution of self-gravitational fluids endowed with spherical, cylindrical, and hyperbolical symmetry has been brought about by many authors in different contexts [44, 63, 64, 71, 72]. In the case of locally anisotropic dissipative fluids, we obtain five scalar functions that reduce to two for non-dissipative dust fluid and remain only one in the case of isotropic static distribution.

The relevance of structure scalars in exploring the complexity of self-gravitational stellar structures cannot be over-emphasized. As described in [35, 73, 74] the scalar variable plays a fundamental role in measuring the complexity of the static and non-static self-gravitational fluids, and for this reason, also defined as the complexity factor (\(\textrm{C}_{\textbf{F}}\)). The motivation to consider these scalar functions in understanding the formation and different evolutionary phases of relativistic self-gravitational stellar structures arises from their unique physical meaning. As it is already established that the structure scalar \(X_{\textbf{T}}\) describe the distribution of energy density, while \(X_{\textbf{TF}}\) define the inhomogeneous character of the energy density of the self-gravitational fluid, in the presence of GBG-corrections. Therefore, in the case of dissipationless fluid configuration, the effect of density inhomogeneities is controlled by a single GBG-corrected scalar \(X_{\textbf{T}}\). For this reason this is considered a primary component in describing the gravitational arrow of time. The GBG-corrected form of two scalar functions \(Y_{\textbf{T}}\) and \(Y_{\textbf{TF}}\) are associated with the Tolman mass function in an obvious way, as described by the Eqs. (52) and (53). On the one hand the scalar \(X_{\textbf{T}}\) serves as the Tolman mass density. On the other hand, the GBG-corrected form of \(Y_{\textbf{TF}}\) describes the effect of two fundamental physical variables (local anisotropy of pressure and the energy density inhomogeneity) on the Tolman mass.

Using the scheme proposed in [44], we have discussed in explicit detail the global physical features of time-independent fluid configurations bestowed with hyperbolic symmetry. In this context, we have presented all possible static hyperbolically symmetric solutions, characterized by vanishing \(\textrm{C}_{\textbf{F}}\) (i.e., \(Y_{\textbf{TF}}=0\)), conformally flat condition, and the stiff equation of state. Some significant findings regarding the dynamics of hyperbolically symmetric configurations are illustrated as

  • Such type of fluid configurations may be locally anisotropic and the energy density is usually negative.

  • The central region of the distribution cannot be completely filled with the fluid. This shows that either there should be a vacuum density inside the horizon, or it should be characterized by some other source.

  • The Tolman mass function appears to be negative for \(8\pi r^{3}P_{r}+r^{2}\eta ^{(1)}+\alpha r^{3}\mathcal {G}^{2}<2\textit{m}\), demonstrating the repulsive nature of the gravitational interactions.

  • The hyperbolically symmetric fluid configurations could be proved more interesting in search of a more complex cosmic model.

It is significant to mention that the first two characteristics are exhibited both by the static as well as non-static regimes. The negative behavior of the energy density is illustrated by the fact that while at a purely classical level energy density is expected to be positive for realistic fluid configurations, however, the scenario is significantly different in the quantum regimes, where energy density could be negative [75,76,77]. This shows that the considered fluid configurations for understanding the type of systems where quantum effects are considered to be significant. On the other hand, the inability of the fluid configuration to fill the central portion gives rise to numerous possible scenarios. It would be significant to carry out a deeper investigation of the physical characteristics of the presented solutions.