1 Introduction

The explorations of Universe as a whole requires the investigation of stellar structures within it. These structures in fact constitute real laboratories, which facilitates the unveiling of the most hidden secrets of the Universe in a fragmented way. Once these hidden secrets are unveiled, they provide us with significant information that will help us to put the pieces of this great puzzle in the corresponding place. In this connection, numerous researchers have explored the existence of collapsed stellar structures through the construction of exact solutions of Einstein’s Field Equations (EFEs). Since the emergence of general theory of relativity (GTR), it has always been a huge challenge to obtain the solutions that could describe physically consistent and well-behaved structures in the Universe. In this direction, Schwarzschild [1] was the first person who developed an analytical solution of EFEs, which describes the exterior of static fluid sphere having spherically symmetric geometry. After that Richard Tolman developed numeral interior solutions of spherically symmetric fluid spheres evolving under isotropic environment [2]. Later on, G. Lamaitre highlighted the fact that all the stellar structures inside the Universe do not necessarily contain anisotropic fluid distributions and elaborated the fact that isotropic condition \((P_r = P_t)\) is not always required by the spherically symmetric geometry [3]. However the work, presented by Bowers and Liang, about the local anisotropies in relativistic fluid spheres provided better understanding of the incidence of anisotropy in matter distributions [4]. Moreover, the theoretical work developed by Ruderman about the physically motivated and realistic stellar models reveal that anisotropy can be emerged in nuclear matter, at least in extremely high density ranges \((\rho > 10^{15}~\hbox {g}/\hbox {cm}^3)\) [5]. The gravitational nature of highly dense objects in extremely high gravitational fields was explored in [6] to obtain new analytical solutions for the stellar interiors.

One can find a detailed discussion on the significance of anisotropic fluids in [7], which highlights the possible causes for the emergence of pressure anisotropy and presents some particular consequences associated with it. Recently, a significant result has been obtained in [8], which somehow supersedes all the previous results based on the assumption of isotropic pressure, and justify the emergence of pressure anisotropy in the relativistic fluids. Moreover, it has been shown that the physical processes of the kind expected in stellar evolution will always tend to produce pressure anisotropy, even if the system is initially assumed to be isotropic. Thus, it should be emphasized here that an equilibrium configuration is the final stage of a dynamic regime and the acquired anisotropy during the dynamic process would never disappear in the final equilibrium state, and therefore the resulting configuration, even if initially had isotropic pressure, should essentially demonstrate pressure anisotropy. In other words, any physical process (expected in a collapse scenario) is not known, which could vanish the anisotropy appearing during the stellar evolution and “isotropize” the relativistic fluid. Thus, the presence of pressure anisotropy in compact stellar objects is not an exception, but an essential feature. In the last few years, a large number of theoretical researches are available that present study on the implications of anisotropic matter distribution on the radius of the stellar system, effective mass, central energy-density, stability of highly compact stellar systems and critical surface redshift [9,10,11,12,13]. It is often observed that presence of anisotropy appears as a repulsive force \((P_t- P_r > 0)\), which counterbalances the gravitational force and contributes in the stability of the system [14, 15].

As EFEs are highly nonlinear equations, so it is not always possible to find their exact solutions. Few years back, a very powerful methodology, termed as gravitational decoupling by means of Minimal Geometric Deformation (MGD) approach in the realm of GTR, has been suggested by Ovalle [16] to obtain the new analytical solutions or to extend the previously known solutions of EFEs. This approach has provided a wide range of opportunities for the extension and construction of the new analytical solutions of EFEs. The gravitational decoupling framework works as follows: In the beginning, an energy-momentum tensor is considered, which consists of the combination of a perfect fluid and some additional source. This additional source can be a scalar, vector or tensor field. Next, a geometric deformation is considered against radial component of a spherically symmetric static line-element, which divides the decoupled field equations into two distinct sets of field equations. These sets of field equations are known as EFEs and quasi-Einstein equation (the later corresponds to the additional source), which are solved independently to get the final solution.

Due to its feasible and versatile features, this approach has been extensively applied in order to study the multiple phenomena, particularly for the construction of anisotropic solutions corresponding to different seed space-times including Tolman IV solutions [17], Tolman VII solution [18], Durgapal solution [19] and FinchSkea solution [20]. Besides, minimally or completely deformed versions of embedding class one solutions [20,21,22] have been established by introducing solution generating scheme for class one condition. Numerous solutions have been established in a variety of contexts by means of the gravitational decoupling approach, for which one can see the Refs. [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55]. It has also been employed to explore a family of black hole solutions together with interior solutions under braneworld gravity [56]. In this regard, Contreras and his collaborators [57] studied hairy rotating black holes with interesting results. Moreover, various stable stellar models have been developed using MGD approach in the frameworks of modified gravitational theories of gravity like f(G) gravity [58], f(R) gravity [59], f(R, T) gravity [60], Lovelock gravity [61], Rastall gravity [62].

A major concern in the implementation of MGD approach is to provide a supplementary condition for the evaluation of the so-called deformation function. In previous literature, mimic constraint for the material variables, regularity condition of the anisotropic function and barotropic equation of state are mostly used as auxiliary conditions. However, we are interested to use complexity factor suggested for self-gravitating systems with static background [63] (for detailed study one can see [64,65,66,67,68,69] including recent works [70,71,72,73,74,75]). In particular, we propose a polynomial complexity factor as an auxiliary condition to evaluate the deformation function, and explore its role on the significance of a relativistic model.

This paper has been arranged as follows: In the next section, we present brief review of major aspects related to the gravitational decoupling. In Sect. 3, we introduce the concept of complexity factor. Section 4 is devoted to the construction of new anisotropic compact stellar models, where Durgapal IV and V are considered as seed solutions and polynomial complexity factor as a supplementary condition. In Sect. 5, we present physical analysis of the constructed models. Last section summarizes the results.

2 Gravitational decoupling

We begin with the brief review of gravitational decoupling by means of MGD. Thus, we start with the gravitationally decoupled field equations, given by

$$\begin{aligned} R_{\alpha \beta }-\frac{1}{2}Rg_{\alpha \beta }=-\kappa ^2 T_{\alpha \beta }^{(tot)}. \end{aligned}$$
(1)

Here, \(T_{\alpha \beta }^{(tot)}\) is linear combination of stress–energy tensors for perfect fluid and some additional source \(\Phi _{\alpha \beta }\), which are combined through intensity parameter \(\beta \), i.e.,

$$\begin{aligned} T_{\alpha \beta }^{(tot)}=T_{\alpha \beta }^{(perfect fluid)}+\beta \Phi _{\alpha \beta }. \end{aligned}$$
(2)

Now, we describe particular expression of stress–energy tensors for perfect fluid, which is given by

$$\begin{aligned} T_{\alpha \beta }^{(perfect fluid)}=({\rho }+P){U_{\alpha }}{U_{\beta }}-Pg_{\alpha \beta }, \end{aligned}$$
(3)

where \({\rho }\) symbolizes the energy density, P denotes the isotropic pressure, and \(U^{\beta }\) represents the four velocity of fluid, satisfying the relation \({U_{\beta }}{U^{\beta }}=1\).

Next, we consider spherically symmetric static stellar configuration whose interior geometry is represented by

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-e^{\omega (r)}dr^{2}-r^2(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(4)

where, \(\nu (r)\) and \(\omega (r)\) are radial dependent functions which ranges from 0 to R. With the above consideration, the field equations (1) takes the following mathematical form

$$\begin{aligned} \kappa ^2\left( \rho +\beta \Phi ^{0}_{0}\right)= & {} e^{-\omega } \left( \frac{\omega '}{r}-\frac{1}{r^2}\right) +\frac{1}{r^2}, \end{aligned}$$
(5)
$$\begin{aligned} \kappa ^2\left( P-\beta \Phi ^{1}_{1}\right)= & {} e^{-\omega } \left( \frac{\nu '}{r}+\frac{1}{r^2}\right) -\frac{1}{r^2}, \end{aligned}$$
(6)
$$\begin{aligned} \kappa ^2\left( P-\beta \Phi ^{2}_{2}\right)= & {} e^{-\omega } \left( \frac{\nu ''}{2}-\frac{\omega '}{2r}+\frac{\nu '}{2r}- \frac{\nu '\omega '}{4}+\frac{\nu '^2}{4}\right) . \nonumber \\ \end{aligned}$$
(7)

The covariant divergence of stress–energy tensor \(T^{(tot)}_{\alpha \beta }\) leads to the following result

$$\begin{aligned}&P'+ \frac{{\eta }'}{2}(\rho +P) -\beta {(\Phi )^{1}_{1}}' +\frac{{\nu }'\beta }{2}(\Phi ^{0}_{0}-\Phi ^{1}_{1})\nonumber \\&\quad +\frac{2\beta }{r}(\Phi ^{2}_{2}-\Phi ^{1}_{1})=0. \end{aligned}$$
(8)

Here, prime has been used to denote the radial derivative. In order to close the above set of field equations (5)–(7), we need to determine seven unknowns, i.e., \(\{\rho , P, \nu , \omega , \Phi _{00}, \Phi _{11}, \Phi _{22} \}\). For the evaluation of these unknown entities, we follow the analytical approach introduced by Ovalle [5]. Before moving towards the implementation MGD approach, it is better to define the physical quantities i.e., \(\rho ^{(tot)}\), \(P_r^{(tot)}\) and \(P_t^{(tot)}\) as

$$\begin{aligned} \rho ^{(tot)}= & {} \rho +\beta \Phi ^{0}_{0}, \end{aligned}$$
(9)
$$\begin{aligned} P_r^{(tot)}= & {} P-\beta \Phi ^{1}_{1}, \end{aligned}$$
(10)
$$\begin{aligned} P_t^{(tot)}= & {} P-\beta \Phi ^{1}_{1}, \end{aligned}$$
(11)

with anisotropic factor given by

$$\begin{aligned} \Delta =P_t^{(tot)}-P_r^{(tot)}=\beta (\Phi ^{1}_{1}-\Phi ^{2}_{2}). \end{aligned}$$
(12)

Next, we consider MGD approach in order to decouple the system (5)–(7). Thus, we consider a linear transformation for radial metric potential and leave the temporal one with no change, i.e.,

$$\begin{aligned} \eta \mapsto e^{-\omega }=\eta +\beta h(r), \end{aligned}$$
(13)

where h(r) is the deformation experienced by the radial metric function, which is responsible for the occurrence of anisotropy in the fluid sphere. We employ the above transformation and divide the system (5)–(7) into two subsystems: one is against \(\beta =0\) and the other is against \(\beta \ne 0\). The first system of equations is given by

$$\begin{aligned} \kappa ^2\rho= & {} \frac{1}{r^2}- \left( \frac{\eta }{r^2}+\frac{{\eta }'}{r}\right) , \end{aligned}$$
(14)
$$\begin{aligned} \kappa ^2P= & {} -\frac{1}{r^{2}}+\frac{\eta }{r}\left( \frac{1}{r}+{\nu }'\right) , \end{aligned}$$
(15)
$$\begin{aligned} \kappa ^2P= & {} \frac{\eta }{4}\left( 2{\nu }''+{{\nu }'}^{2}+ \frac{2{\nu }'}{r}\right) +\frac{{\eta }'}{4}\left( {{\nu }'}+\frac{2}{r}\right) , \end{aligned}$$
(16)

and the second one is given as

$$\begin{aligned} \kappa ^2\Phi ^{0}_{0}= & {} -\frac{h'}{r}-\frac{h}{r^2}, \end{aligned}$$
(17)
$$\begin{aligned} \kappa ^2\Phi ^{1}_{1}= & {} -\frac{h}{r}\left( \frac{1}{r}+{\nu }'\right) , \end{aligned}$$
(18)
$$\begin{aligned} \kappa ^2\Phi ^{2}_{2}= & {} -\frac{h}{4}\left( 2{\nu }''+{{\nu }'}^{2}+ \frac{2{\nu }'}{r}\right) -\frac{h'}{4} \left( {\nu }'+\frac{2}{r}\right) . \end{aligned}$$
(19)

However, the conservation equations for the both scenarios take the form as

$$\begin{aligned}&P'+\frac{\nu '}{2}(\rho +P) = 0, \end{aligned}$$
(20)
$$\begin{aligned}&(\Phi _1^1)'-\frac{\nu '}{2}(\Phi _0^0-\Phi _1^1)-\frac{2}{r}(\Phi _2^2-\Phi _1^1)=0. \end{aligned}$$
(21)

Here, the second equation (21) is related to the quasi-Einstein system of equations, which is similar to the anisotropic Tolman–Oppenheimer–Volkoff (TOV) equation.

Here, we assume Schwarzschild vacuum solution in the exterior region, i.e., \(\rho ^+ =P^+=0\). Thus, the line-element for the exterior geometry can be written as

$$\begin{aligned} ds^{2}= & {} \left( 1-\frac{2M}{r}\right) dt^2-\left( 1-\frac{2M}{r}\right) dr^{2}\nonumber \\&- r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}). \end{aligned}$$
(22)

The continuity of first and second fundamental forms held at the boundary of star \(\Sigma \) provides the following relations

$$\begin{aligned}&\left( 1-\frac{2M}{r}\right) |_{\Sigma _+}=e^{\nu (r)}|_{\Sigma _-}, \end{aligned}$$
(23)
$$\begin{aligned}&\left( 1-\frac{2M}{r}\right) |_{\Sigma _+}= e^{-\eta (r)}|_{\Sigma _-}, \end{aligned}$$
(24)

and

$$\begin{aligned}&\Big (P-\beta (\Phi ^{1}_{1}(r))\Big )|_{\Sigma _-}=0. \end{aligned}$$
(25)

We can conclude this section with the remarks that the first system of equations (14)–(16) will be determined by using well-known Durgapal IV and Durgapal V solution, while the second system of equations (17)–(19), which is comprised of four unknowns, i.e., \(\{\Phi _0^0,~\Phi _1^1,~\Phi _2^2, h(r)\}\), will be closed by using an extra condition. In the present study, this extra condition or information will be based on the complexity factor [63].

3 Complexity of compact stellar systems

In 2018, Herrera presented a definition of complexity for static spherically symmetric self-gravitating systems, which is based on an intuitive idea that simple or less complicated systems correspond to the isotopic pressure and homogeneous energy density. The main ingredient of Herrera’s definition of complexity is complexity factor, which has been chosen among the structure scalars appearing in the orthogonal decomposition of Riemann Tensor. In [63], traced-free scalar \(Y_{TF}\) qualifies as a candidate of complexity factor, which ca be written as

$$\begin{aligned} Y_{TF} = 8\Pi -\frac{4\pi }{r^3}\int _0^r \rho ' \bar{r}^3 d\bar{r}, \end{aligned}$$
(26)

where \(\Pi =P_r-P_t\). Moreover, it can noticed that Tolman active gravitational mass can be defined as

$$\begin{aligned} m_T = \left( \frac{r}{r_\Sigma }\right) ^3 (m_T)_\Sigma +r^3\int _r^{r_\Sigma }\frac{1}{\bar{r}}Y_{TF} e^{(\nu +\omega )/2} d\bar{r}. \end{aligned}$$
(27)

Here, it leads towards the strong argument that complexity factor defined by the traced-free function \(Y_{TF}\) covers all the modifications and alterations produced by the pressure anisotropy and inhomogeneity of energy density on the active gravitational mass. Thus, complexity factor \(Y_{TF}\) provides a relation between local anisotropies of pressure and inhomogeneity of the energy density, as it vanishes for the simplest spherically symmetric self-gravitating systems, i.e., the homogeneous and isotropic systems. However, null complexity condition is not only satisfied in the case of the simplest systems, but also in the scenarios where

$$\begin{aligned} \Pi =\frac{1}{2r^3}\int _0^r \rho ' \bar{r}^3 d\bar{r}. \end{aligned}$$
(28)

This non-local equation of state has been broadly considered as a complementary condition for the closure of the system of EFEs. However, a complexity factor different from zero can also be considered to study the compact stellar systems. In the light of gravitational decoupling by MGD, \(Y_{TF}\) takes the form as

$$\begin{aligned} Y_{TF} =\bar{Y}^1_{TF}+\bar{Y}^2_{TF}. \end{aligned}$$
(29)

Here, \(\bar{Y}^1_{TF}\) represents the complexity factor for the seed gravitational source, and \(\bar{Y}^2_{TF}\) symbolizes complexity factor for additional source with \(\beta =-1\), given by

$$\begin{aligned} \bar{Y}^2_{TF} =8\pi (\Phi _1^1-\Phi _2^2) +\frac{4\pi }{r^3}\int _0^r (\Phi ^0_0)' \bar{r}^3 d\bar{r}, \end{aligned}$$
(30)

which further takes the form as

$$\begin{aligned} \bar{Y}^2_{TF} = \nu ' \frac{h'(r)}{4} + \frac{h(r)}{4}\left[ 2\nu ''+\nu '\left( \nu '-\frac{2}{r}\right) \right] . \end{aligned}$$
(31)

One can observe that the metric potentials \(\{\nu , \eta \}\) can be determined using a known solution, so the expression (28) leads to the differential equation for deformation function h(r), after specifying the complexity factor.

4 Anisotropic solutions with polynomial complexity

4.1 Solution I

Here we consider Durgapal IV Solution in the framework of MGD, which assumes the following form

$$\begin{aligned} e^{\nu (r)}= & {} A^2 \left( C r^2+1\right) ^4, \end{aligned}$$
(32)
$$\begin{aligned} \eta ^{-1}= & {} \frac{B C r^2}{\left( C r^2+1\right) ^2 \left( 5 C r^2+1\right) ^{2/5}}\nonumber \\&+\frac{7-C^2 r^4-10 C r^2}{7 \left( C r^2+1\right) ^2}+\beta h(r). \end{aligned}$$
(33)

In order to evaluate deformation function h(r), we have different choices including mimic constraints and different equation of states. However, we consider a non-zero complexity factor, previously introduced, as an auxiliary condition to find the deformation function h(r) and to close the system. In previous literature, the imposition of null complexity factor condition has been broadly considered, but we are choosing another value for it, i.e.,

$$\begin{aligned} Y_{TF}=\sum _{n=0}^N a_{n} r^n. \end{aligned}$$
(34)

Now, substituting (32) and (33) into the Eq. (34), we obtain the following relation

$$\begin{aligned} \sum _{n=0}^N a_{n} r^n= & {} \frac{1}{7 \psi _1^3 \psi _2^{7/5}}\left[ 2 C r (2 C r (2 \psi _2^{7/5}(C (7 h(r)+1) r^2\right. \nonumber \\&\left. +7 h(r)+5)-7 B(3 C r^2+1))+7 \psi _1^2 \psi _2^{7/5} h'(r)) \right] ,\nonumber \\ \end{aligned}$$
(35)

where \(\psi _1=C r^2+1\) and \(\psi _2=5 C r^2+1\). Moreover, we can see that the above relation represents a differential equation for the deformation function h(r), which is depending on the variation of n. Moreover, we are going to choose \(a_0=0\) and \(a_1=0\), otherwise the expression in (35) leads to the divergence in the stellar interior. After the discard of these possibilities, Eq. (35) reads as

$$\begin{aligned} \sum _{n\ge 2}^N a_{n} r^n= & {} \frac{1}{7 \psi _1^3 \psi _2^{7/5}}\left[ 2 C r (2 C r (2 \psi _2^{7/5}(C (7 h(r)+1) r^2\right. \nonumber \\&\left. +7 h(r)+5)-7 B(3 C r^2+1))\right. \nonumber \\&\left. +7 \psi _1^2 \psi _2^{7/5} h'(r)) \right] . \end{aligned}$$
(36)

As the above equation is depending on the value of n, which can be fixed by choosing a particular value for n. Here, we choose \(n=3\) and integrate the above equation. This yields

$$\begin{aligned} h(r)= & {} \frac{1}{14 \psi _1^2}\left[ \frac{7 a_2 r^2}{8 c}(c^3 r^6+4 c^2 r^4+6 c r^2+4)\right. \nonumber \\&\left. +\frac{7}{9} a_3 c^2 r^9+\frac{7 a_3 r^3}{3 c}+\frac{21 a_3 r^5}{5}+\frac{14 B c r^2}{\psi _2^{2/5}}\right. \nonumber \\&\left. +3 a_3 c r^7-2 c^2 r^4-20 c r^2 +14 C_0 \right] , \end{aligned}$$
(37)

where \(C_0\) is a constant of integration. It can be determined by using the regularity condition of the radial metric potential at the center, which requires \(h(0)=0\). It provides \(C_0=0\). With this development, the particular expressions of thermodynamical variables assume the form as

$$\begin{aligned} \rho ^{(tot)}= & {} \frac{1}{40320 \pi C \psi _1^3 \psi _2^{7/5}} \left[ 720 C^2 (7 B (C r^2 (9 C r^2-10)-3)\right. \nonumber \\&\left. +8 (C r^2 (C r^2+2)+9) \psi _2^{7/5})-\beta (\psi _2^{7/5}(315 a_2 (5 C^4 r^8 \right. \nonumber \\&\left. +21 C^3 r^6+34 C^2 r^4+26 C r^2+12)\right. \nonumber \\&\left. +16 (15 C^4 r^4 (7 a_3 r^5-3)+5 C^3 r^2(89 a_3 r^5+45)\right. \nonumber \\&\left. +27 C^2 (27 a_3 r^5-50)\right. \nonumber \\&\left. +567 a_3 C r^3+210 a_3 r))-5040 B C^2 (9 C^2 r^4\right. \nonumber \\&\left. -10 C r^2-3)) \right] , \end{aligned}$$
(38)
$$\begin{aligned} P_r^{(tot)}= & {} \frac{1}{40320 \pi C \psi _1^3 \psi _2^{2/5}}\left[ \beta (9 C r^2+1) (\psi _2^{2/5} (315 a_2 (C^3 r^6\right. \nonumber \\&\left. +4 C^2 r^4+6 C r^2+4)+8 (5 C^3 r^2 (7 a_3 r^5-18) \right. \nonumber \\&\left. +45 C^2(3 a_3 r^5-20)+189 a_3 C r^3+105 a_3 r))\right. \nonumber \\&\left. +5040 B C^2)+720 C^2 (7 B (9 C r^2+1)\right. \nonumber \\&\left. -16 \psi _2^{2/5} (C r^2 (C r^2+7)-2))\right] , \end{aligned}$$
(39)
$$\begin{aligned} P_t^{(tot)}= & {} \frac{1}{6720 \pi C \psi _1^3 \psi _2^{2/5}}\left[ \psi _2^{2/5}(5 C^4 r^4(\beta (273 a_2 r^4\right. \nonumber \\&\left. +266 a_3 r^5-384)-384)+60 C^3 r^2(\beta (77 a_2 r^4\right. \nonumber \\&\left. +74 a_3 r^5-224) \right. \nonumber \\&\left. -224)+6 C^2 (\beta (945 a_2 r^4+882 a_3 r^5-200)\right. \nonumber \\&\left. +640)+420 \beta C r^2 (7 a_2+6 a_3 r)\right. \nonumber \\&\left. +210 \beta (a_2+a_3 r)) +840 (\beta +1)\right. \nonumber \\&\left. \times B C^2 (9 C r^2+1) \right] . \end{aligned}$$
(40)

Here, the constants B and C have been determined using matching conditions (23) and (24) over the boundary surface \(r = R\), while by means of continuity of the second fundamental form (25), \(a_2\) assumes the following form

$$\begin{aligned} a_2= & {} -\frac{1}{315 \beta R^3 \psi _{2R}^{2/5} (C^3 R^6+4 C^2 R^4+6 C R^2+4)}\nonumber \\&\times \left[ 8 (\psi _{2R}^{2/5} (5 C^3 R^4 (R (-18 \beta +7 \beta a_3 R^5\right. \nonumber \\&\left. -144)+252 M)+45 C^2 R^2 \right. \nonumber \\&\left. \times (R (-20 \beta +3 \beta a_3 R^5-48)+56 M)+63 C (3 \beta a_3 R^6\right. \nonumber \\&\left. +20 M)+105 \beta a_3 R^4)+630 (\beta +1) B C^2 R^3)\right] , \end{aligned}$$
(41)

where \(\psi _{2R}=5 C r^2+1\) is the vale of \(\psi _2\) at the stellar boundary.

Fig. 1
figure 1

Shows the variations of deformation function h(r) (left panel for 1st solution and right panel for 2nd solution) with respect to r

Full size image
Fig. 2
figure 2

Shows the variations of radial metric potential \(e^{\omega }\) (left panel for 1st solution and right panel for 2nd solution) with respect to r

Full size image

4.1.1 Solution II

In the continuing part, we consider Durgapal V Solution in the framework of MGD, which assumes the following form

$$\begin{aligned} e^{\nu (r)}= & {} A^2 \left( C r^2+1\right) ^5, \end{aligned}$$
(42)
$$\begin{aligned} \eta ^{-1}= & {} \frac{1}{\left( C r^2+1\right) ^3}\left[ \frac{B C r^2}{1+6 C r^2}-\frac{1}{112} C r^2 \left( 8 C^2 r^4\right. \right. \nonumber \\&\left. \left. +54 C r^2+309\right) +1\right] +\beta h(r). \end{aligned}$$
(43)

Here, we again consider non-zero complexity factor as an auxiliary condition to find the deformation function h(r). Moreover, we choose the same value for complexity factor that we have considered for the previous solution (34). Thus, by substituting (42) and (43) into the Eq. (34), we obtain the following relation

$$\begin{aligned} \sum _{n=0}^N a_{n} r^n= & {} \frac{1}{112 \psi _1^4 \psi _3^2}\left[ 5 C r (C r (3 \psi _3^2 (112 h(r) \psi _1^2\right. \nonumber \\&\left. +4 C r^2 (2 C r^2+9)+103)-112 B)\right. \nonumber \\&\left. +56 \psi _3^2 \psi _1^3 h'(r))\right] , \end{aligned}$$
(44)

where \(\psi _1=C r^2+1\) and \(\psi _3=6 C r^2+1\). The above relation again provides a differential equation for the deformation function h(r), which is depending on the variation of n. After the choice \(a_0=0\) and \(a_1=0\), Eq. (44) reads as

$$\begin{aligned} \sum _{n\ge 2}^N a_{n} r^n= & {} \frac{1}{112 \psi _1^4 \psi _3^2}\left[ 5 C r (C r (3 \psi _3^2 (112 h(r) \psi _1^2\right. \nonumber \\&\left. +4 C r^2 (2 C r^2+9)+103)-112 B)\right. \nonumber \\&\left. +56 \psi _3^2 \psi _1^3 h'(r))\right] . \end{aligned}$$
(45)

The above equation is depending on the value of N, so we first fix it and then solve the equation. For \(N=3\), the integration of above equation yields

$$\begin{aligned} h(r)= & {} \frac{1}{277200 C \psi _1^3 \psi _3}\left[ \psi _3 (r^2 (11088 a_2 (C r^2 (C r^2 (C r^2 (C r^2+5)\right. \nonumber \\&\left. +10)+10)+5)+C (360 C^3 r^4(28 a_3 r^5-55)+110 C^2 r^2 \right. \nonumber \\&\left. \times (448 a_3 r^5-1215)+1485 C (64 a_3 r^5-515)\right. \nonumber \\&\left. +88704 a_3 r^3)+36960 a_3 r)+277200 C C_0)-46200 B C\right] ,\nonumber \\ \end{aligned}$$
(46)

where \(C_0\) is constant of integration. With all the calculations at hand, we obtain particular expressions of thermodynamical variables in the following form

$$\begin{aligned} \rho ^{(tot)}= & {} \frac{1}{2217600 \pi C r^2 \psi _1^4 \psi _3^2}\left[ 7425 C^2 r^2 (112 B (C r^2 (10 C r^2\right. \nonumber \\&\left. -1)-1)+5(8 C^3 r^6+30 C^2 r^4+C r^2+129) \psi _3^2)\right. \nonumber \\&\left. -\beta (\psi _3^2 \right. \left. \times (360 C^5 r^8 (154 a_2 r^4+168 a_3 r^5-55)\right. \nonumber \\&\left. +2 C^4 r^6(112 r^4 (1287 a_2+1420 a_3 r)-2475)\right. \nonumber \\&\left. +55 C^3 r^4 (16 r^4 (693 a_2+776 \right. \nonumber \\&\left. \times a_3 r)+29565)+495 C^2 r^2(3 (64 r^4 (7 a_2\right. \nonumber \\&\left. +8 a_3 r)-1545)-2800 C_0)+3696 C(105 a_2 r^4\right. \nonumber \\&\left. +124 a_3 r^5+75 C_0)+18480 r^2 (9 a_2+8 a_3 r)) \right. \nonumber \\&\left. +46200 B C (3 C r^2\right. \nonumber \\&\left. +1)(14 C r^2-1))\right] , \end{aligned}$$
(47)
$$\begin{aligned} P_r^{(tot)}= & {} \frac{1}{2217600 \pi C r^2 \psi _1^4 \psi _3} \left[ (\beta (11 C r^2+1) (\psi _3 (72 C^4 r^6 g\right. \nonumber \\&\left. \times (154 a_2 r^4+140 a_3 r^5-275)\right. \nonumber \\&\left. +110 C^3 r^4 (56 r^4 (9 a_2+8 a_3-1215) r)\right. \nonumber \\&\left. +495 C^2 r^2 (32 r^4 (7 a_2+6 a_3 r)-1545)\right. \nonumber \\&\left. +11088 C (10 a_2 r^4+8 a_3 r^5+25 C_0)\right. \nonumber \\&\left. +18480 r^2 (3 a_2+2 a_3 r))\right. \nonumber \\&\left. -46200 B C)) +2475 C^2 r^2(112 B (11 C r^2+1)\right. \nonumber \\&\left. -25 \psi _3 (C r^2 (8 C^2 r^4+42 C r^2+165)-19))\right] , \end{aligned}$$
(48)
$$\begin{aligned} P_t^{(tot)}= & {} \frac{1}{2217600 \pi C \psi _1^4 \psi _3}\left[ 99 C^3 r^2 (\beta (224 r^4 (795 a_2\right. \nonumber \\&\left. +748 a_3 r)+117600 C_0-149475)+30800 B\right. \nonumber \\&\left. -31875)+33 C^2 \right. \nonumber \\&\left. \times (3 \beta (224 r^4 (365 a_2+323 a_3 r)+19600 C_0-7725)\right. \nonumber \\&\left. -1400 (\beta -6) B+35625)\right. \nonumber \\&\left. +432 C^6 r^8 (\beta (5698 a_2 r^4+5600 \times a_3 r^5-6875) \right. \nonumber \\&\left. -6875)+12 C^5 r^6 (\beta (921228 a_2 r^4\right. \nonumber \\&\left. +899080 a_3 r^5-1340625)-1340625)\right. \nonumber \\&\left. +440 C^4 r^4 (\beta (44856 \right. \nonumber \\&\left. \times a_2 r^4+43246 a_3 r^5-145125)-145125)\right. \nonumber \\&\left. +18480 \beta C r^2 (69 a_2+62 a_3 r)+55440 \beta (a_2+a_3 r)\right] .\nonumber \\ \end{aligned}$$
(49)

Here, the constants B and C have been determined using junction conditions (23) and (24) over the stellar surface \(r = R\), while the continuity of the second fundamental form (25) leads to the following expression for \(a_2\)

$$\begin{aligned} a_2= & {} -\frac{1}{\begin{matrix}11088 \beta R^3 \psi _{3R}(C R^2 (C R^2 (C R^2 (C R^2+5)\\ +10)+10)+5)\end{matrix}}\nonumber \\&\times \left[ \beta R(\psi _{3R}(360 C^4 R^6 (28 a_3 R^5-55)+110 C^3 R^4 \right. \nonumber \\&\times \left. (448 a_3 R^5 -1215)+1485 C^2 R^2 (64 a_3 R^5-515)\right. \nonumber \\&\left. +11088 C(8 a_3 R^5+25 C_0)+36960 a_3 R^3)-46200 B C) \right. \nonumber \\&\left. +2475 C(224 M (C R^2+1)^3\psi _{3R}-C R^3 (15\psi _{3R}(8 C^2 R^4\right. \nonumber \\&\left. +26 C R^2+43)-112 B))\right] , \end{aligned}$$
(50)

where \(\psi _{2R}=6 C r^2+1\) is the vale of \(\psi _3\) at the stellar boundary. Moreover, regularity condition of deformed radial metric potential at the center requires \(h(0)=0\), which further provides \(C_0=\frac{B}{6}\).

5 Physical analysis

In the continuing section, we present a detailed physical analysis of our solutions based on the graphical representations by taking into account data of three different real stars, namely Vela X-1, PSR 1937+21 and PSR J164-2230. Let us start by analysing the regularity of deformed metric potential.

5.1 Regularity of deformed metric potential

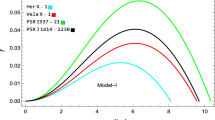
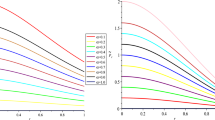
In this study, we have considered gravitational decoupling by means of MGD, which deforms only radial metric function. In order to analyze the behaviour of deformed metric function, we first study the variations of deformation function h(r) inside the stellar system, given in the Fig. 1. It is noted that h(r) is zero at the center, which indicates that radial metric function will be completely regular at the center, i.e., \(e^{\omega }=1|_{r=0}\), and is free of physical and geometrical singularities from the center to the stellar surface. The monotonically increasing profile of \(e^{\omega (r)}\) is given in the Fig. 2. The same scenario has been observed for both anisotropic solutions.

Fig. 3
figure 3

Shows the variations of energy density for the new anisotropic solutions as well as perfect fluid seed solutions (left panel for 1st solution and right panel for 2nd solution) with respect to r

Full size image
Fig. 4
figure 4

Shows the variations of pressure for the new anisotropic solution as well as perfect fluid seed solutions (left panel for 1st solution and right panel for 2nd solution) with respect to r

Full size image

5.2 Thermodynamical observables

The thermodynamical variables of the new anisotropic solutions attain maximum values at the center and then gradually decrease towards the boundary, which is an acceptable trend, when a stable stellar configurations is under consideration. In the Fig. 3, we have graphical profile of energy density, which is positive definite throughout the stellar interior. In the left panel, we have density profile for the new anisotropic Durgapal IV solution, whereas in the right panel we have density profile for the new anisotropic Durgapal V solution. For the seed space-times, the system is found to be less dense as compared to the new anisotropic solutions, however the situation is opposite when one arrives very near the stellar surface. In the Fig. 4, the radial pressure vanishes at the boundary as one expects and there is no energy flux to the exterior space-time. On the other hand, tangential pressure falls rapidly as one moves towards boundary, however this fall is not so rapid as it is in the case of pressure in radial direction. It is important to mention here that we have chosen \(a_3=0\), because it has been observed if we consider even a small non-zero value of \(a_3\), then our solution immediately fails to follow the desired trends. This situation makes us to think that new Durgapal solutions with non-zero coefficient of cubic order term (appearing on the left hand side of Eq. (45)) can not offer a stable stellar configuration. All the plots have been made by fixing \(\beta =0.5\), however it has been checked that all the solutions corresponding to the range of \(\beta \in [0,1]\) present stable stellar configurations. However, for \(\beta \notin [0,1]\) our solutions fail to present a stable configuration.

Fig. 5
figure 5

Shows the variations of anisotropy factor (left panel for 1st solution and right panel for 2nd solution) with respect to r

Full size image
Fig. 6
figure 6

Shows the variations of energy conditions (left panel for 1st solution and right panel for 2nd solution) with respect to r

Full size image

5.3 Anisotropy factor

We have plotted the anisotropy factor in the Fig. 5, where in the left panel we have graphical representation of anisotropic factor for new anisotropic Durgapal IV solution and in the right panel one can see the variations of anisotropic factor for new anisotropic Durgapal V solution. In both cases, we observe that the anisotropy is zero at the center. Moreover, it is positive throughout from the center towards the boundary. This implies that the tangential pressure dominates its radial counterpart, so it gives rise to a repulsive force which counterbalances the inwardly driven gravitational force and stabilizes the stellar system. It increases monotonically from the center towards the surface and is maximum at the stellar surface.

5.4 Energy conditions

An energy-momentum tensor will be physically reasonable, if it obeys the null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC) and the dominant energy condition (DEC). These energy bounds have following mathematical forms

  • NEC: \(\rho ^{(tot)}+P_r^{(tot)}\ge 0\), \(\rho ^{(tot)}+P_t^{(tot)}\ge 0\)

  • WEC: \(\rho ^{(tot)}\ge 0\), \(\rho ^{(tot)}+P_r^{(tot)}\ge 0\), \(\rho ^{(tot)}+P_t^{(tot)}\ge 0\)

  • SEC: \(\rho ^{(tot)}+P_r^{(tot)}\ge 0\), \(\rho +P_t^{(tot)} \ge 0\), \(\rho ^{(tot)}+P_r^{(tot)}+2P_t^{(tot)}\ge 0\)

  • DEC: \(\rho ^{(tot)}-\mid P_r^{(tot)}\mid \ge 0\), \(\rho ^{(tot)} -\mid P_t^{(tot)}\mid \ge 0.\)

Figure 6 presents variations of the mathematical expressions mentioned on the left hand side of the above inequalities, where solid and dashed curves presents evolution of \(\rho ^{(tot)}+P_r^{(tot)}\) and \(\rho ^{(tot)}+P_t^{(tot)}\), respectively, whereas medium-dashed, large-dashed and dotted curves present variations of \(\rho ^{(tot)}+P_r^{(tot)}+2P_t^{(tot)}\), \(\rho ^{(tot)}-\mid P_r^{(tot)}\mid \) and \(\rho ^{(tot)}-\mid P_t^{(tot)}\mid \), respectively. Plots in the both panels depict that all the four inequalities are satisfied at each point within the stellar object, thus it can be said that we have a well-behaved energy–momentum tensor in both cases.

Fig. 7
figure 7

Shows the variations of square speed of sound (left panel for 1st solution and right panel for 2nd solution) with respect to r, for the new anisotropic solutions

Full size image
Fig. 8
figure 8

Shows the variations of adiabatic index (left panel for 1st solution and right panel for 2nd solution) with respect to r, for the new anisotropic solutions

Full size image

5.5 Causality condition

Inside the static configuration the speed of sound must be less than the speed of light, i.e., \(0\le v_r^2\le 1\) and \(0\le v_t^2\le 1\) with \(v_r^2=\frac{dP_r^{(tot)}}{d\rho ^{(tot)}}\) and \(v_t^2=\frac{dP_t^{(tot)}}{d\rho ^{(tot)}}\). From the both panels of Fig. 7, we can observe that our stellar models are satisfying the aforementioned causality conditions. Moreover, the radial and tangential velocities of sound are increasing with the increase of energy density. Moreover, it should be decreasing outwards, and we observe that the speed of sound decreases monotonically from the center of the stellar configuration (more dense region) towards the stellar surface of the star (less dense region). It indicates that our anisotropic solutions are physically well-behaved.

5.6 Adiabatic index

Now we analyze the stability of our new models by using the adiabatic stability or instability criterion. It was first defined by Chandrasekhar [76, 77] for the fluid spheres with isotropic pressure. This stability criterion is developed by using adiabatic index, which is defined as

$$\begin{aligned} \Gamma _r = \left( \frac{\rho ^{(tot)}+P^{(tot)}}{P^{(tot)}}\right) \frac{dP^{(tot)}}{d\rho ^{(tot)}}, \end{aligned}$$
(51)

where \(\Gamma >\frac{4}{3}\) is the limiting case for bounded configurations with isotropic pressure P, and squared speed of sound \(\frac{dP}{d\rho }\). Herrera and co-researchers [78, 79] argued that this stability condition gets altered in the presence of phenomena like anisotropy and dissipation, so aforementioned limiting case is modified and assumes the form as

$$\begin{aligned} \Gamma _r >\frac{4}{3}+\left[ \frac{4(P^{(tot)}_t-P^{(tot)}_r)}{3|(P^{(tot)}_r)'| r}\right] . \end{aligned}$$
(52)

On the right hand side, the second term in Eq. (52) appears due to the relativistic contributions, and absence of this term leads to the Newtonian limit, i.e., \(\Gamma > \frac{4}{3}\) for stable regions. In the Fig. 8, one can see the variations of adiabatic index, which meets the stability criterion in both cases, as at the center it has minimum value which is greater than \(\frac{4}{3}\), and then it increases as one moves towards the stellar boundary.

6 Conclusion

In this manuscript, we have constructed two new families of anisotropic stellar models which describe the implications of polynomial complexity on spherically symmetric astrophysical geometries, in the realm of gravitational decoupling by means of MGD. Thus , we consider MGD approach with two different seed space-times, i.e., Durgapal IV and Durgapal V perfect fluid models, and considered a polynomial complexity factor as an axillary condition for the evaluation of deformation function, which is ultimately required to close the system related to the new additional source. Moreover, we investigated the scenarios where existence of stable stellar configurations is possible. Initially we considered complexity factor equal to a polynomial of order n, but for the sake of convenience we solved the corresponding differential equation for \(n=3\). Thus, the polynomial is reduced to the cubic order, but physical analysis shows that stable solution is possible if we choose \(a_3=0\). For non-zero values of \(a_3\), pressure components fails to follow the accepted trend, and square speed of sound and adiabatic index do not meet the desired criteria near the center.

In order to discuss structural properties of the solution, we considered the radii and mass of three different real stars, named Vela X-1, PSR 1937+21 and PSR J164-2230, and plotted the results for \(\beta =0.5\). We notice that deformed metric potential is regular, and all the thermodynamical variables behave according to the accepted trend. However, the variations of energy density \(\rho ^{(tot)}\) shows that new anisotropic models represent more dense objects as compared to their corresponding seed counterparts, but very near to stellar boundary the situation is opposite. On the other hand, pressure components, i.e., \(P_r^{(tot)}\) and \(P_t^{(tot)}\), of new anisotropic solutions takes smaller values as compared to their seed counterparts, however tangential component takes larger values near the boundary. Anisotropy factor \(\Delta \) is zero at the core, whereas positive throughout in the stellar interior indicating the presence of repulsive force near the stellar surface. It has also been observed that the contributions introduced by the decoupling parameter \(\beta \) on all thermodynamical quantities produce similar results for both stellar models with an inappreciable change in their magnitudes. We have presented the result for \(\beta =0.5\), but checked for different values of \(\beta \). We observed the significance of our models for all values of \(\beta \) lies in the range [0, 1]. However, tangential component of pressure begins to increase near the surface as we choose some value of \(\beta \) greater than one. Energy conditions, square speed of sound, and adiabatic index further confirm the physical existence, physical consistency and stability of the anisotropic stellar models.