Impacts of complexity factor on the transition of fluid configurations from isotropic to anisotropic environment and vice versa

Abstract

This article presents a study on the process of isotropization and properties of stellar models with different complexity factors, which was introduced by Herrera (Phys Rev D 97:044010, 2018). We consider gravitational decoupling via MGD (Minimal Geometric Deformation) approach for spherically symmetric systems with static background and explore the scenarios where the isotropization of an anisotropic solution of Einstein field equations is possible. Moreover, we work on generating the new analogues of Durgapal–Fuloria model under different conditions associated with complexity factor. The physical existence and stability of the new stellar models have been discussed in details with the help of different potent tools.

1 Introduction

The study of exact solution of Einstein field equations (EFEs) plays an important role in the analysis and interpretation of relativistic events. The possibility of existence of collapsed stellar structures is also investigated by developing exact solutions to EFEs. However, it is not always easy to generate analytical solutions which are physically significant [1]. This journey of analytical solutions started when Schwarzschild [2] produced first theoretical solution to the EFEs, which describes a static stellar interior with uniform energy density. After that, Richard Tolman developed a number of analytical solutions that represent spherically symmetric fluid spheres evolving in an isotropic environment [3]. Subsequently, Lemaitre [4] presented his findings and emphasized that it is not necessary that stellar structures in the universe always correspond to isotropic fluid distributions and spherically symmetric geometry always need the isotropic condition ($p_r = p_t$). Though several exact isotropic solutions are presented [5,6,7], nevertheless the majority of these solutions lack the physical validity and cannot meet the fundamental requirements of astrophysical confirmation. However, the study by Bowers and Liang on local anisotropies in a relativistic fluid sphere helped to understand the existence of anisotropy in matter distributions [8], which is frequently observed to act as a repulsive force ($p_ t- p_ r > 0$), balancing the gravitational force and assisting in the stability of the system [9, 10]. Moreover, anisotropic fluids have been the subject of extensive research, with a particular focus on identifying plausible sources of anisotropy. A comprehensive review on the topic can be found in [11]. This review provides a detailed compilation of various physical phenomena that have the potential to induce pressure anisotropy.

There are distinct ways to construct analytical solutions of stellar systems equipped with pressure anisotropy in their interior. For physically viable and competent anisotropic stellar model, one needs to consider some conditions or constraints on the matter variables, space–time geometry or to rely on some specific forms of equation of state. In this regard, one has another interesting mathematical tool, termed as gravitational decoupling by MGD (Minimal Geometric Deformation), which fundamentally has the potential to extend the known isotropic solutions to their anisotropic domains [12, 13]. Originally, Ovalle [14] suggested this technique to obtain an exact solutions of compact stars in the framework of the braneworld. Later on, the mechanism for this methodology has been developed in the framework of general relativity, which has paved the way for a wide range of possibilities for the development of new analytical solutions of EFEs and their extensions. It covers a variety of topics including cosmology, modified gravity theories, anisotropic neutron stars, and black hole solutions [15,16,17,18,19,20,21,22,23,24].

In the framework of gravitational decoupling by MGD, the field equations are modified and assume the following form

$$\begin{aligned} R_{ab}-\frac{1}{2}Rg_{ab}=\kappa \tilde{T}_{ab}, \end{aligned}$$

(1)

where $\tilde{T}_{ab}$ consists of energy momentum tensors (EMT) having at least two sources that interact gravitationally. Thus, EMT $\tilde{T}_{ab}$ can be expressed as

$$\begin{aligned} \tilde{T}_{ab}=T_{ab}^m+\alpha \psi _{ab}, \end{aligned}$$

(2)

where $T_{ab}^m$ corresponds to the seed source, $\psi _{ab}$ is related to some extra source, that introduces anisotropy through a free parameter $\alpha$. Here, solution related to the seed source can easily be fixed by taking into account some known solutions, while the solution for extra source needs some additional constraints. In literature, one can find a large number of articles, where solution for the system of field equations related to the extra source has been explored by virtue of different conditions including mimic constraints on matter variables, regularity condition of the anisotropic function and some plausible equations of states [25,26,27,28,29,30,31,32,33,34,35,36,37,38]. Recently, complexity factor introduced by Herrera [45] has been considered as an auxiliary condition and interesting solutions have been developed in the compact star arena [39,40,41,42,43,44]. Herrera’s definition of complexity for spherically symmetric self-gravitating systems is based on an intuitive idea that the systems with negligible complications correspond to the isotopic pressure and homogeneous energy density. The main ingredient of this definition is complexity factor, which is in fact selected among the four structure scalars emerging in the orthogonal splitting of Riemann Tensor. In [45], a scalar function $\mathcal {Y_{TF}}$ has been considered as strong candidate of a complexity factor. This traced-free function is defined as

$$\begin{aligned} \mathcal {Y_{TF}}=8\pi \bar{\Pi }-\frac{4\pi }{r^3}\int _{0}^{r}\tilde{r}^3\rho 'd\tilde{r}. \end{aligned}$$

(3)

In association with the above quantity, the MGD approach has been frequently used to generate new stellar models. Thus, keeping in view the significance of complexity factor and its use as a supplementary condition for the closure of system of field equations, we consider different conditions against this novel entity and explores some viable situations related to the compact stars. The focus of this work is on demonstrating how GD may be used directly to control particular physical characteristics of a self-gravitating system. To keep things simple, we use the MGD technique, which introduces variations in the metric’s radial component only and prevents a direct transfer of energy between the two EMTs in Eq. (2).

The article is arranged as follows: In Sect. 2, we present a quick review of the MGD. In Sect. 3, we separate the situations for isotropic and anisotropic environments. In Sect. 4, we associate different scenarios with the complexity factor and establish different solutions against those situations. In Sect. 5, we discuss the physical viability and stability of all three solutions using different stability measuring tools like energy conditions, adiabatic Index and causality conditions. Finally in Sect. 6, we conclude our discussion.

2 Field equations for gravitationally decoupled system

In this section, we quickly review the MGD technique in the context of GR. Let us start with the field equations (2), where $T_{ab}^{m}$ is the matter sector and $\psi _{ab}$ is an extra source. The Bianchi identity is satisfied by the system (2), so the divergence of total EMT can be expressed as

$$\begin{aligned} \nabla _a \tilde{T}^{ab}=0. \end{aligned}$$

(4)

As $T^{ab(m)}$ is the solution of EFEs and Einstein tensor is divergence free, so it quickly implies $T^{ab(m)}=0$. Consequently, the following expression will must hold

$$\begin{aligned} \nabla _a \psi ^{ab}=0. \end{aligned}$$

(5)

Here, the extra source can be defined as

$$\begin{aligned} \psi _{b}^{a}=diag(\psi _{0}^{0}, \psi _{1}^{1}, \psi _{2}^{2}, \psi _{3}^{3} ). \end{aligned}$$

(6)

The interior geometry of the spherically symmetric fluid sphere is expressed in Schwarzschild-like coordinates using the following line element

$$\begin{aligned} ds^2=e^{\nu }dt^2-e^{\lambda }dr^2-r^2d\theta ^2-r^2sin^2\theta d\phi ^2, \end{aligned}$$

(7)

where $e^{\nu }$ and $e^{\lambda }$ are the metric potentials, which only depend upon radial coordinate. With the above assumption, the field equations (1) can be written as

$$\begin{aligned} \kappa (\rho ^{m}+\alpha \psi _{0}^{0})= & {} \frac{1}{r^2}+e^{-\lambda }\bigg (\frac{ \lambda '}{r}-\frac{1}{r^2}\bigg ), \end{aligned}$$

(8)

$$\begin{aligned} \kappa (p^{m}_r-\alpha \psi ^{1}_{1})= & {} -\frac{1}{r^2}+e^{-\lambda }\bigg (\frac{1}{r^2}+\frac{v'}{r}\bigg ) , \end{aligned}$$

(9)

$$\begin{aligned} \kappa (p_t^{m}-\alpha \psi ^{2}_{2})= & {} \frac{1}{4}e^{-\lambda }\bigg (2v''-v'\lambda '+v'^2+2\frac{v'-\lambda '}{r}\bigg ).\nonumber \\ \end{aligned}$$

(10)

After renaming the expressions on the left hand side of above equations, we obtain the following terms

$$\begin{aligned} \tilde{\rho }= & {} (\rho ^{m}+\alpha \psi _{0}^{0}), \end{aligned}$$

(11)

$$\begin{aligned} \tilde{p}_r= & {} (p^{m}_r-\alpha \psi ^{1}_{1}), \end{aligned}$$

(12)

$$\begin{aligned} \tilde{p}_t= & {} (p_t^{m}-\alpha \psi ^{2}_{2}). \end{aligned}$$

(13)

The conservation equation of the gravitational system under consideration is given by

$$\begin{aligned}{} & {} p'^{m}_r+v'(\rho ^{m}+p^{m}_r)+\frac{2}{r}(p^{m}_r-p^{m}_t)-(\psi ^1_1)'\nonumber \\{} & {} +\frac{v'}{2}(\psi ^0_0-\psi ^1_1)+\frac{2}{r}(\psi ^2_2-\psi ^1_1)=0 \end{aligned}$$

(14)

Now, we consider MGD approach which introduces deformation in radial metric function in the following form

$$\begin{aligned} e^{-\lambda }\rightarrow & {} e^{-\eta }+\alpha f, \end{aligned}$$

(15)

where f is the function of r. Here it appears as deformation function. Moreover, $\alpha$ is intensity parameter, which controls the effects of $\psi _{ab}$. Having this linear transformation at hand, we are able to divide the entire set of differential equations (8)–(10) into two subsets. Thus, we obtain one set that is related to the seed solution $T_{ab}^{m}$, given by

$$\begin{aligned} \kappa \rho ^{m}= & {} \frac{1}{r^2}+e^{-\eta }\bigg (\frac{ \eta '}{r}-\frac{1}{r^2}\bigg ), \end{aligned}$$

(16)

$$\begin{aligned} \kappa p^{m}_r= & {} -\frac{1}{r^2}+e^{-\eta }\bigg (\frac{1}{r^2}+\frac{v'}{r}\bigg ) , \end{aligned}$$

(17)

$$\begin{aligned} \kappa p_t^{m}= & {} \frac{1}{4}e^{-\eta }\bigg (2v''-v'\eta '+v'^2+2\frac{v'-\eta '}{r}\bigg ). \end{aligned}$$

(18)

and the other set linked with $\psi _{ab}$ is given by

$$\begin{aligned} \kappa \psi _{0}^{0}= & {} -\frac{f}{r^2}-\frac{f'}{r}, \end{aligned}$$

(19)

$$\begin{aligned} \kappa \psi _{1}^{1}= & {} -f\bigg (\frac{v'}{r}+\frac{1}{r^2}\bigg ), \end{aligned}$$

(20)

$$\begin{aligned} \kappa \psi _{2}^{2}= & {} -\frac{f}{4}\bigg (2v''+v'^2+\frac{2v'}{r}\bigg )-\frac{f'}{4}\bigg (v'+\frac{2}{r}\bigg ). \end{aligned}$$

(21)

The component of extra source $\psi _{ab}$ also satisfies the conservation equation (shown in (5)), i.e., $\nabla _a \psi _{a}^{b}=0$. Consequently we have

$$\begin{aligned} \psi _{1}^{'1}-\frac{v'}{2}(\psi ^0_0-\psi ^1_1)-\frac{2}{r}(\psi ^2_2-\psi ^1_1)=0, \end{aligned}$$

(22)

which is linear combination of Eqs. (19–21). In order to describe interior geometry, we consider standard Schwarzschild solution by neglecting any deformation in the exterior region. Thus, we have following line-element for the exterior geometry

$$\begin{aligned} ds^2=\bigg (1-\frac{2M}{r}\bigg )dt^2-\bigg (\frac{r}{r-2M}\bigg )dr^2-r^2 d\Omega , \end{aligned}$$

(23)

where $d\Omega =d\theta ^2+sin^2 \theta d\phi ^2$. With the assumptions for line-elements given in (23), we can define following expressions which need to be satisfied for the smooth matching of the interior and exterior geometries on the boundary $\Sigma$

$$\begin{aligned} e^v\mid _{\Sigma }= & {} \left( 1-\frac{2M}{r}\right) \mid _{\Sigma }, \end{aligned}$$

(24)

$$\begin{aligned} e^{\lambda }\mid _{\Sigma }= & {} \left( 1-\frac{2M}{r}\right) ^{-1}\mid _{\Sigma }, \end{aligned}$$

(25)

$$\begin{aligned} \tilde{p}_r\mid _{\Sigma }= & {} 0, \end{aligned}$$

(26)

where $\Sigma$ indicates that the values evaluated at the boundary, M is the mass and r is the radius of the star. The additional information needed to fully solve the system that is generated by the matching condition (26), is given by

$$\begin{aligned} p_r^{m}(r_b)-\alpha \psi _{1}^1(r_b)=0, \end{aligned}$$

(27)

where $r_b$ shows that the condition is evaluated at boundary. Moreover, the quantities with tilde leads to the total anisotropy of the system as

$$\begin{aligned} \tilde{\Pi }=p_t^{m}-p_r^{m}+\alpha (\psi _{2}^2-\psi _{1}^1)=\Pi _m+\Pi _{\psi }, \end{aligned}$$

(28)

where $\Pi _m$ and $\Pi _{\psi }$ is an anisotropy related to seed and extra sources, respectively.

Now, we close this section with the remarks that the set of equations (16–18) generated by $T_{ab}$ will be determined by using Durgapal–Fuloria solution. On the other hand, the sector related to the additional source Eqs. (19–21), which mainly requires the evaluation of decoupling function f, will be determined by using some extra information. Here, we will adopt different approaches. In the next section, we consider some restrictions against anisotropic factor, while in the Sect. 4 complexity factor will considered under different conditions.

3 Isotropization of compact sources

3.1 Model-I

In this section, we change the anisotropic solution into isotropic one. However, it is worth mentioning here that the study in [46] shows that physical processes occurring during stellar evolution are likely to generate pressure anisotropy, even if the initial assumption is isotropy. The study suggests that equilibrium configurations, which represent the final stage of a dynamic regime, may retain this anisotropy acquired during the evolution process, and there is no inherent reason to expect the acquired anisotropy to disappear in the final equilibrium state, regardless of its initial isotropic conditions. Unless a specific physical process, anticipated in a collapse scenario, acts to counterbalance or ”isotropize” the pressure anisotropy that arises during stellar evolution. Now, we proceed and observe that total anisotropy $\tilde{\Pi }$ given in (28) may be different from the anisotropy generated by the seed sector $T_{ab}^m$. Thus, we can consider an anisotropic system in Eqs. (16–21) with $\Pi _m\ne 0$. With the addition of the extra source $\psi _{ab}$, the system became an isotropic one (8–10), where total anisotropy is vanished, i.e., $\tilde{\Pi } = 0$. Here, $\alpha$ is that coefficient which controls this change. For $\alpha =0$, we have an anisotropic system, while for $\alpha =1$ the system achieves to obey isotropy condition which can be read as

$$\begin{aligned} \tilde{\Pi }=0, \implies \Pi _{\psi }=-\Pi _{m}. \end{aligned}$$

(29)

Replacement of Eqs. (16–21) in the Eq. (29) results into a differential equation, provides

$$\begin{aligned}{} & {} \frac{f'}{4k^2}\left( \Xi '+\frac{2}{r}\right) \nonumber \\ {}{} & {} +\frac{f}{4k^2}\left( 2\Xi ''+\Xi ^{'2}-2\frac{\Xi '}{r}-\frac{4}{r^2}\right) +\Pi _{m}=0, \end{aligned}$$

(30)

where $f'$ represents the derivative of decoupling function w.r.t r. Next, we use the method described above and isotropize the system which is supported by tangential components only [47]. Thus, we have

$$\begin{aligned} e^{\Xi }= & {} B(Ar^2+1)^4, \end{aligned}$$

(31)

$$\begin{aligned} e^{-\eta }= & {} \frac{Ar^2+1}{9Ar^2+1}, \end{aligned}$$

(32)

$$\begin{aligned} \rho= & {} \frac{24A(1+3Ar^2)}{(1+9Ar^2)^2}, \end{aligned}$$

(33)

$$\begin{aligned} p_t= & {} \frac{48A^2 r^2(1+3Ar^2)}{(1+Ar^2)(1+9Ar^2)^2}, \end{aligned}$$

(34)

$$\begin{aligned} p_r= & {} 0, \end{aligned}$$

(35)

where the expressions for A and B are developed by using matching conditions (24–26), where r varies as $0\le r\le R$, and $r=R$ represents the surface of compact stellar system. Following are particular the expressions for above mentioned constants

$$\begin{aligned} A= & {} \frac{M}{R^2(4R-9M)}, \end{aligned}$$

(36)

$$\begin{aligned} B= & {} \frac{R-2M}{R}\biggl (\frac{4R-9M}{4R-8M}\biggl )^4, \end{aligned}$$

(37)

where R can never be less than 9/4. With the help of Eqs. (31–35), we can solve the differential equation (30). It leads to the following result

$$\begin{aligned} f(r)= & {} -\frac{16Ar^2(-2+7Ar^2+A^2r^4)}{7(1+Ar^2)^2(1+9Ar^2)}\nonumber \\{} & {} +\frac{r^2}{\mathcal {Q}(1+Ar^2)^2(1+5Ar^2)^{\frac{2}{5}}}, \end{aligned}$$

(38)

where $\mathcal {Q}$ is the constant of integration. The matching condition (26) at the surface of object requires

$$\begin{aligned} f(R)=0. \end{aligned}$$

(39)

This ultimately results into

$$\begin{aligned} \mathcal {Q}=\frac{7(1+9AR^2)}{16A(1+5AR^2)^{\frac{2}{5}}(-2+7AR^2+A^2R^4)}. \end{aligned}$$

(40)

Eventually, the deformation f(r) takes its final shape as

$$\begin{aligned} f(r)= & {} -\frac{16Ar^2(-2+7Ar^2+A^2r^4)}{7(1+Ar^2)^2(1+9Ar^2)}\nonumber \\{} & {} +\frac{16Ar^2(1+5AR^2)^{\frac{2}{5}}(-2+7AR^2+A^2R^4)}{7(1+Ar^2)^2(1+5Ar^2)^{\frac{2}{5}}(1+9AR^2)}. \end{aligned}$$

(41)

Fig. 1

Represents the deformation function (38) with respect to r. Here, we pick Her X-1 star ($R = 8.10$, $M = 1.25375$), Vela X-1 ($M=1.77$, $R=9.56$), PSR 1937 + 21 ($M=2.4115$, $R=10.3412$) and PSR J 1614-2230 ($M=1.97$, $R=9.69$)

The mass M and the constants A, B remain the same for both cases. With the help of (15) and (41), the new radial component and the solution can be written as

$$\begin{aligned} e^{-\lambda }= & {} \frac{Ar^2+1}{9Ar^2+1}+\frac{16Ar^2}{7(Ar^2+1)^2}\biggl (\frac{-Ar^2(Ar^2+7)+2}{9Ar^2+1}\nonumber \\{} & {} +\frac{(5AR^2+1)^{2/5}(AR^2(AR^2+7)-2)}{(5Ar^2+1)^{2/5}(9AR^2+1)}\biggl ). \end{aligned}$$

(42)

Fig. 2

Figure on the left shows the radial component (42) and the right one shows the behavior of density (43) for $\alpha =1$ (solid lines) and $\alpha =0.5$ (dashed lines)

Fig. 3

The solid lines in figure on the left shows the behavior of radial pressure (44) and the right one shows the tangential pressure (46) for $\alpha =1$, while the dashed lines shows the behavior of $\tilde{p}_r$ and $\tilde{p}_t$ for $\alpha =0.5$

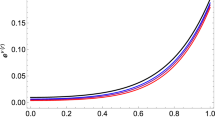
The graphical behavior of $e^{-\lambda }$ for different stars and for different values of $\alpha$ is shown in Fig. 2. The deformation (41) produces an effective density, which is given by

$$\begin{aligned} \tilde{\rho }= & {} \frac{A\alpha }{7\pi }\biggl (\frac{21(1+3Ar^2)}{(1+9Ar^2)^2}-\frac{2P}{(1+Ar^2)^2}\nonumber \\ {}{} & {} \quad \times \biggl (1+\biggl (2Ar^2(1+Ar^2)\nonumber \\{} & {} \quad \times \biggl (-\frac{7+2Ar^2}{1+9Ar^2}+\frac{9(-2+Ar^2(7+Ar^2))}{(1+9Ar^2)^2}\nonumber \\{} & {} \quad -\frac{2(1+5AR^2)^{\frac{2}{5}}(-2+AR^2(7+AR^2))}{(1+5Ar^2)^{\frac{7}{5}}(1+9AR^2)}\biggl )\nonumber \\{} & {} \quad -4Ar^2P+2(1+Ar^2)P\biggl )\div \biggl ((1+Ar^2)P\biggl ). \end{aligned}$$

(43)

The radial pressure is expressed as

$$\begin{aligned} \tilde{p}_r= & {} \frac{2A\alpha }{7\pi (1+Ar^2)^2}\biggl (9-\frac{8}{1+Ar^2}\biggl )P, \end{aligned}$$

(44)

where

$$\begin{aligned} P= & {} \biggl (\frac{2-Ar^2(7+Ar^2)}{1+9Ar^2}\nonumber \\{} & {} +\frac{(1+5AR^2)^{\frac{2}{5}} (-2+AR^2(7+AR^2))}{(1+5Ar^2)^{\frac{2}{5}}(1+9AR^2)}\biggl ). \end{aligned}$$

(45)

However, the tangential pressure $\tilde{p}_t$ is given by

$$\begin{aligned} \tilde{p}_t= & {} \frac{1}{7\pi (1+Ar^2)^3(1+5Ar^2)^{\frac{2}{5}}(1+9Ar^2)^2(1+9AR^2)} \nonumber \\{} & {} \times (2A(21Ar^2(1+5Ar^2)^{\frac{2}{5}}(1+9AR^2)^2+105A^2r^4(1+5Ar^2)^{\frac{2}{5}}\nonumber \\{} & {} \times (1+9AR^2)+147A^3r^6(1+5Ar^2)^{\frac{2}{5}}(1+9AR^2)s\nonumber \\{} & {} +63A^4r^8(1+5Ar^2)^{\frac{2}{5}}(1+9AR^2) -2(1+5AR^2)^{\frac{2}{5}}(1+9Ar^2)^2\alpha \nonumber \\{} & {} -18A(r+9Ar^3)^2(1+5AR^2)^{\frac{2}{5}}\alpha \nonumber \\{} & {} +63A^2r^2(1+9Ar^2)^2R^2(1+5AR^2)^{\frac{2}{5}}\alpha \nonumber \\{} & {} -2(1+5AR^2)^{\frac{2}{5}}(-1+Ar^2(1+6Ar^2)(\nonumber \\{} & {} -4+Ar^2(59+12Ar^2)))(1+9AR^2)\alpha ). \end{aligned}$$

(46)

In this case, anisotropy ($\tilde{\Pi }=\tilde{p}_t-\tilde{p}_r$) of the system takes the following form

$$\begin{aligned} \tilde{\Pi }=\frac{6A^2 r^2(1+3Ar^2)(1-\alpha )}{\pi (1+9Ar^2)^2(1+Ar^2)}, \end{aligned}$$

(47)

which vanishes for $\alpha =1$.

The Eqs. (31–47) are exact solution of the EFEs (8–10) for all values of $\alpha$. Further, it is noticed that the anisotropic model (31)–(35) is obtained by fixing $\alpha =0$, and it is continually transformed into the isotropic case by choosing $\alpha = 1$ (shown in Fig. 4). Therefore, by changing the value of $\alpha$ between [0, 1], we can observe the isotropization process in detail.

Fig. 4

Figure shows the anisotropy factor (47) for $\alpha =0$ (solid lines), $\alpha =0.3$ (dashed lines) and $\alpha =1$

4 Complexity of compact source

The scalar function emerging in the orthogonal splitting of the Riemann tensor is an appropriate quantity to consider it as a complexity factor because it explains how the local anisotropy of pressure and density inhomogeneity change the value of the Tolman mass in comparison to its value for the homogeneous isotropic fluid. This concept of complexity factor was first introduced for static self-gravitating systems in [45], and it was extended to the dynamical case in [48]. The interesting fact about this approach is that it gives zero value to complexity factor for uniform and isotropic systems. The complexity of a given system is measured by complexity factor $\mathcal {Y_{TF}}$, which involves two important quantities: pressure anisotropy and energy density. Mathematically it reads as

$$\begin{aligned} \mathcal {Y_{TF}}= 8\pi \bar{\Pi }-\frac{4\pi }{r^3}\int _{0}^{r}z^3 \rho '(z)dz. \end{aligned}$$

(48)

The vanishing complexity condition ($\mathcal {Y_{TF}}=0$) can be met not only in the simple case of an isotropic and homogeneous system, but in all situations as well, for example if one has

$$\begin{aligned} \bar{\Pi }=\frac{1}{2r^3}\int _{0}^{r}z^3\rho '(z)dz. \end{aligned}$$

(49)

It offers a non-local equation of state that can be used as an additional condition to close the system of EFEs. However, non-vanishing values of $\mathcal {Y}_{TF}$ must be provided because this requirement might not hold in some situations while building particular stellar models.

In this paper, we use the complexity factor as a supplementary condition. For the system represented by (8–10) and (15), the Eq. (48) yields the following expression

$$\begin{aligned}{} & {} \frac{\Xi '}{2}f'+\frac{f}{2}\biggl (\Xi ''-\frac{\Xi '}{r}+\frac{\Xi '^2}{2}\biggl )\nonumber \\{} & {} \quad +\frac{e^{-\eta }}{2}\biggl (\Xi ''-\frac{\Xi '}{r}+\frac{\Xi ^{'2}}{2}-\frac{\Xi '\eta '}{2}\biggl )+\mathcal {Y_{TF}}=0. \end{aligned}$$

(50)

Note that as soon as the ${\{\Xi , \eta \}}$ is defined and the value of $\mathcal {Y_ {TF}}$ is provided, Eq. (50) transforms into a differential equation for the decoupling function f. Here, the complexity factor $\mathcal {Y_{TF}}$ can be defined in its final form as follows

$$\begin{aligned} \mathcal {Y_{TF}}= & {} 8\pi \bar{\Pi }_m-\frac{4\pi }{r^3}\int _{0}^{r}z^3 (\rho ^m)'(z)dz+8\pi \bar{\Pi }_{\psi }\nonumber \\{} & {} -\frac{4\pi }{r^3}\int _{0}^{r}z^3 \rho '_{\psi }(z)dz, \end{aligned}$$

(51)

which can be re-written as

$$\begin{aligned} \mathcal {Y_{TF}}= & {} \tilde{\mathcal {Y}}_{TF}^{m}+\tilde{\mathcal {Y}}_{TF}^{\psi }, \end{aligned}$$

(52)

where $\tilde{\mathcal {Y}}_{TF}^{m}$ is the complexity factor of seed source and $\tilde{\mathcal {Y}}_{TF}^{\psi }$ is the complexity factor associated with extra source $\psi _{ab}$. After having sufficient information about complexity factor, we consider the two different cases of complexity in the next subsections.

4.1 Model-II

First, we deal with a situation in which the sum of complexity factor $\tilde{\mathcal {Y}}_{TF}^{m}$ associated with EMT and $8\pi \Pi _{\psi }$ is equal to zero. The situation can be described mathematically as $\mathcal {Y}_{TF}^m+8\pi \Pi _{\psi }=0$, which leads to a result, i.e., ${\mathcal {Y}}_{TF}=-(4\pi /r^3)\int _{0}^{r}z^3 \rho '_{\psi }(z)dz$. Using Eqs. (19–21), we have

$$\begin{aligned} \frac{4\pi }{r^3}\int _{0}^{r}z^3 \rho '_{\psi }(z)dz=\frac{\alpha }{k^2}\biggl (\frac{f}{r^2}-\frac{f'}{2r}\biggl ). \end{aligned}$$

(53)

Now by using the above condition, we can write

$$\begin{aligned} \mathcal {Y}_{TF}=-\frac{\alpha }{k^2}\biggl (\frac{f}{r^2}-\frac{f'}{2r}\biggl ). \end{aligned}$$

(54)

Finally the condition (50) is transformed into a first order differential equation, given by

$$\begin{aligned}{} & {} \frac{\Xi '}{2}f'+\frac{f}{2}\biggl (\Xi ''-\frac{\Xi '}{r}+\frac{\Xi '^2}{2}\biggl )\nonumber \\{} & {} \quad +\frac{e^{-\eta }}{2}\biggl (\Xi ''-\frac{\Xi '}{r}+\frac{\Xi ^{'2}}{2}-\frac{\Xi '\eta '}{2}\biggl ) -\frac{f}{r^2}+\frac{f'}{2r}=0. \end{aligned}$$

(55)

Fig. 5

Represents the deformation function (62) with respect to r

Fig. 6

Figure on the left shows the new radial component (64) for $\alpha =1$ (solid lines) and for $\alpha =0.5$ (dashed lines). While the right one shows the behavior of effective density (65) for $\alpha =1$ (solid lines) and for $\alpha =0.5$ (dashed lines)

As we can see Eq. (55) doesn’t have $\alpha$ so we can actually require that the complexity be same for all values of $\alpha$. Now we consider Durgapal–Fuloria [49] as a solution to Eqs. (16–18), which is given below

$$\begin{aligned} e^{\Xi }= & {} B(Ar^2+1)^4, \end{aligned}$$

(56)

$$\begin{aligned} e^{-\eta }= & {} 1-\frac{8Ar^2(Ar^2+3)}{7(Ar^2+1)^2}. \end{aligned}$$

(57)

Thus, we have energy density in the following form

$$\begin{aligned} \rho =\frac{8A(A^2r^4+2Ar^2+9)}{7(Ar^2+1)^3}, \end{aligned}$$

(58)

and the isotropic pressure is given as

$$\begin{aligned} p=-\frac{16A(A^2r^4+7Ar^2-2)}{7(Ar^2+1)^3}. \end{aligned}$$

(59)

Here, boundary conditions (24–26) will be used to calculate the constants A and B. Thus, we obtain

$$\begin{aligned} A= & {} \frac{-7+\sqrt{57}}{2R^2}, \end{aligned}$$

(60)

$$\begin{aligned} B= & {} \frac{16 (R - 2 M)}{(\sqrt{57} - 5)^4 R}. \end{aligned}$$

(61)

If we solve Eq. (55) by using the expression for metric function given in (56), then we obtain a particular expression for deformation function given below

$$\begin{aligned} f=\frac{8Ar^2(Ar^2+17)}{49(Ar^2+1)^2}+\frac{r^2}{\mathcal {Q}(Ar^2+1)^2(5Ar^2+1)^{\frac{2}{5}}}, \end{aligned}$$

(62)

where $\mathcal {Q}$ is integration constant. To find $\mathcal {Q}$ we use condition (39), and obtain

$$\begin{aligned} \mathcal {Q}=-\frac{49}{8A(AR^2+17)(5AR^2+1)^{\frac{2}{5}}}. \end{aligned}$$

(63)

With the help of Eq. (15), the new radial metric component therefore solution reads as

$$\begin{aligned} e^{-\lambda }= & {} 1-\frac{8A r^2(Ar^2+3)}{7(Ar^2+1)^2}\nonumber \\{} & {} +\frac{8A\alpha r^2((Ar^2+17)(5Ar^2+1)^{\frac{2}{5}} -(AR^2+17)(5AR^2+1)^{\frac{2}{5}}}{49(5Ar^2+1)^{\frac{2}{5}}(Ar^2+1)^2}.\nonumber \\ \end{aligned}$$

(64)

The boundary conditions can be established by taking new radial component into account. It produces the same results as Eqs. (60, 61). This produces an effective density

$$\begin{aligned} \tilde{\rho }= & {} \frac{A}{49\pi (Ar^2+1)^3}(7(9+Ar^2(Ar^2+2))\nonumber \\{} & {} +\frac{1}{(5Ar^2+1)K}(51(-K+J+A(-5A^2Kr^6\nonumber \\{} & {} +3R^2J+r^2(-243K+170J+10AR^2J)\nonumber \\{} & {} +Ar^4(59P-153J-9AR^2J)))\alpha ). \end{aligned}$$

(65)

The effective pressure is given as

$$\begin{aligned} \tilde{p}_r= & {} \frac{\alpha A}{49\pi (Ar^2+1)^3}\biggl (-14(A^2r^4+7Ar^2-2)\nonumber \\{} & {} +(Ar^2+1)\biggl (1+\frac{8Ar^2}{Ar^2+1}\biggl )\biggl (Ar^2+17\nonumber \\{} & {} -\frac{(AR^2+17)J}{K}\biggl )\biggl ), \end{aligned}$$

(66)

where $K=(5Ar^2+1)^{\frac{2}{5}}$ and $J=(5Ar^2+1)^{\frac{2}{5}}$. However, the anisotropy of the system can be measured through the following expression

Fig. 7

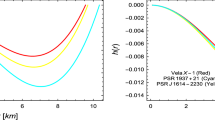
The solid lines in figure on the left and right shows the behavior of radial pressure (66) and the tangential pressure, respectively for $\alpha =1$, while the dashed lines shows the behavior of $\tilde{p}_r$ and $\tilde{p}_t$ for $\alpha =0.5$

$$\begin{aligned} \tilde{\Pi }=\frac{A^2r^2(Ar^2+5)\alpha }{7\pi (Ar^2+1)^3}, \end{aligned}$$

(67)

and the tangential pressure ($\tilde{p}_t$) is expressed as $\tilde{p}_t=\tilde{\Pi }+\tilde{p}_r$.

Fig. 8

Shows the anisotropy (67) of model-II for different values of $\alpha$ with respect to r

4.2 Model-III

In this case, we construct the solution using complexity factor $\mathcal {Y_{TF}}$ again. Here, we consider Eqs. (56), (57), (58) and (59) in the definition (48), and derive a particular expression for complexity factor $\mathcal {Y_{TF}}$. It takes the form as

$$\begin{aligned} \mathcal {Y_{TF}}=\frac{8A^2r^2(Ar^2+5)}{7(Ar^2+1)^3}. \end{aligned}$$

(68)

This expressions for complexity factor is basically established for the seed source. Now, we generalize the expression (68), which is given as

$$\begin{aligned} \mathcal {Y}_{TF}=\frac{c_1r^4+5c_2r^2}{(Ar^2+1)^3}. \end{aligned}$$

(69)

Next, we consider this generalized form to evaluate the deformation function in this subsection. Thus, we replace the above value of $\mathcal {Y}_{TF}$ in Eq. (50), and obtain the following differential equation

$$\begin{aligned}{} & {} \frac{\Xi '}{2}f'+\frac{f}{2}\biggl (\Xi ''-\frac{\Xi '}{r}+\frac{\Xi '^2}{2}\biggl )\nonumber \\{} & {} \quad +\frac{e^{-\eta }}{2}\biggl (\Xi '' -\frac{\Xi '}{r}+\frac{\Xi ^{'2}}{2}-\frac{\Xi '\eta '}{2}\biggl )+\frac{c_1r^4+5c_2r^2}{(Ar^2+1)^3}=0.\nonumber \\ \end{aligned}$$

(70)

To solve (70) we use the Durgapal–Fuloria metric (56–59), the equation yields

$$\begin{aligned} f=\frac{(80 A^2 - 70 c_ 2) r^2 + (8 A^3 - 7 c_ 1) r^4}{56 A (Ar^2 + 1)^2}, \end{aligned}$$

(71)

where $c_1$ and $c_2$ are constants appearing in the generalized form. In this case, the constants A and B (36, 37) are again evaluated using the matching conditions (24–26) with standard Schwarzschild vacuum solution in the outer region. Now using the condition (15), the radial metric function of solution can be expressed as

$$\begin{aligned} e^{-\lambda }=1-\frac{8Ar^2(Ar^2+3)}{7(Ar^2+1)^2}+\alpha f. \end{aligned}$$

(72)

Fig. 9

Represents the Eq. (71) for $\alpha =0.3$ and $c_1=-2\times 10^{-6}$ with respect to r

Fig. 10

In the left figure, the solid and dashed lines shows the new radial component (72) for $\alpha =0.3$, $c_1=-2\times 10^{-6}$ and $\alpha =0.7$, $c_1=-3\times 10^{-7}$ respectively. In the right panel, the solid and dashed lines shows the effective density (73) for $\alpha =0.3$ and $\alpha =0.7$ respectively

Here, the effective density reads as

$$\begin{aligned} \tilde{\rho }= & {} \frac{A (A^2 r^4 + 2 Ar^2 + 9)}{7\pi (Ar^2 + 1)^3} + \frac{(30(-8 A^2 + 7 c_ 2) +5 (8 A^3 - 14 Ac_ 2+ 7 c_ 1 ) r^2 + A (-8 A^3 + 7 c_ 1) r^4)\alpha }{448 A\pi (Ar^2 + 1)^3}, \end{aligned}$$

(73)

while the effective pressure takes the form as

$$\begin{aligned} \tilde{p}_r= & {} \frac{-7 (10 c_ 2 + c_ 1 r^2)\alpha - 63 Ar^2 (10 c_ 2 + c_ 1 r^2)\alpha + 16 A^2 (5\alpha + 16) + 8 A^4 r^4 (9\alpha - 16) + 56 A^3 r^2 (13\alpha - 16)}{448 A\pi (Ar^2 + 1)^3}, \end{aligned}$$

(74)

and the anisotropy is given by

$$\begin{aligned} \tilde{\Pi }=\frac{r^2 (8 A^4 r^2 - 7 Ac_ 1 r^2 + 24 A^3 - 20 Ac_ 2 - c_ 1)\alpha }{64 A\pi (Ar^2 + 1)^3}. \end{aligned}$$

(75)

Fig. 11

In the left figure, the solid and dashed lines shows the radial pressure (74) for $\alpha =0.3$, $c_1=-2\times 10^{-6}$ and $\alpha =0.7$, $c_1=-3\times 10^{-7}$ respectively. In the right panel, the solid and dashed lines shows the tangential pressure for $\alpha =0.3$ and $\alpha =0.7$ respectively

Nevertheless, the corresponding tangential pressure can be determined as $\tilde{p}_t=\tilde{p}_r+\tilde{\Pi }$. Using matching condition at the boundary against radial pressure, we evaluated the constant $c_2$, which takes the following form

$$\begin{aligned} c_2=\frac{8 A^3 R^4 (14 M + R (\alpha - 8)) - 7 c_ 1 R^5\alpha + 16 A^2 R^2 (14 M + R (5\alpha - 12)) + 112 AM}{70 R^3\alpha }. \end{aligned}$$

(76)

5 Physical analysis of the developed solutions

Now we analyze new solutions for physical acceptability as a compact stellar configuration. For this, we have plotted different quantities which will help us in determining the validity of our models. The plots are based on four different configurations of compact stellar objects, namely Her X-1, Vela X-1, PSR 1937+21, PSR J 1614- 2230.

5.1 Model-I

• In Figs. 1, 2, 3 and 4, we have graphical representation of deformation function (f(r)), radial metric function ($e^{-\lambda }$), thermodynamical variables ($\tilde{\rho }$, $\tilde{p}_r$, $\tilde{p}_t$ ) and anisotropy parameter ($\tilde{\Pi }$) for the model-I. In Fig. 1, it is to be noted that deformation function is zero at the center, then it gradually increases and after some distance it begins to decrease, and again it becomes zero at the stellar boundary. It is positive throughout in the stellar configuration. This situations indicates that we have less dense stellar configurations for larger values for $\alpha$. In the left panel of Fig. 2, one can see the regularity of the radial metric function at the center.

• The energy density profiles are plotted in the right panel of Fig. 2, which are positive throughout in the star configuration. All the curves representing energy density have their maxima at the center, then all decease smoothly towards the boundary of the star and indicate towards the robustness of the model.

• The radial and tangential pressure profiles are given in Fig. 3. For $\alpha =1$, isotropic stellar configuration is obtained, while for $\alpha =0.5$ system evolves under anisotropic environment. In both scenarios, pressure profiles remain positive throughout in the stellar interior, maximum at the center and decrease gradually from center towards the boundary. Moreover, tangential pressure dominates its radial counterpart, which can be seen in Fig. 4. Figure 4 combines the trends of both pressure components and articulate them as the pressure anisotropy. It is to note that anisotropy is positive throughout which signifies a positive contribution to the interior forces and and helps the system in having equilibrium.

• In Fig. 13, one can see that the speed of sound in the radial direction satisfies the inequality $0\le v_{r}^{2} \le 1$, where $v_r^2=d\tilde{p}_r/d\rho$, for both values of $\alpha$, while the speed of sound in the tangential direction satisfy the inequality $0\le v_{t}^{2} \le 1$, where $v_r^2=d\tilde{p}_t/d\rho$, for $\alpha =0.7$. However, for $\alpha =0.4$ it assumes negative values near the center. Causality condition for transversal component is basically satisfied for all $\alpha \ge 0.58$, whereas radial component meets the condition for all $\alpha \epsilon [0,1]$.

• The adiabatic index defined by $\Gamma =\frac{\tilde{\rho }+\tilde{p}_r}{\tilde{p}_r}\biggl (\frac{d\tilde{p}_r}{d\tilde{\rho }}\biggl )$, is used to investigate the stability of the developed models. Stellar systems with isotropic fluid distribution resist fluctuations and show behaviour if $\Gamma > \frac{4}{3}$. However, the existence of phenomena like anisotropy leads this stability bound to change, resulting in the modification of the limiting case as $\Gamma > \frac{4}{3}+\frac{4(\tilde{p}_t-\tilde{p}_r)}{3|d\tilde{p}_r/dr|}$ [50]. The extreme left panel of Fig. 16 presents variations of the adiabatic index for model-I, where it is to note that index satisfies the stability condition in all cases. We have also found critical values for the adiabatic index ($\Gamma _{C}$), which is defined by $\Gamma _{C}=\frac{4}{3}+\frac{19}{21}u$ with $u=M/R^2$. The critical values of adiabatic index ($\Gamma _{C}$) are given in Table 1 where it is obvious that $\Gamma >\Gamma _{C}$, It is an accepted trend and ensures the stability of system against radial fluctuations.

• In Fig. 17, energy bounds are displayed which can be written mathematically as

  $$\begin{aligned}&NEC&: \tilde{\rho }+\tilde{p}_r\ge 0, \quad \tilde{\rho }+\tilde{p}_t\ge 0. \end{aligned}$$

  (77)
  $$\begin{aligned}&WEC&: \tilde{\rho }\ge 0, \quad \tilde{\rho }+\tilde{p}_t\ge 0, \quad \tilde{\rho }+\tilde{p}_t\ge 0. \end{aligned}$$

  (78)
  $$\begin{aligned}&SEC&: \tilde{\rho }{+}\tilde{p}_t{\ge } 0, \quad \tilde{\rho }{+}\tilde{p}_t{\ge } 0\quad \tilde{\rho }{+}\tilde{p}_t{+}2\tilde{p}_t{\ge } 0. \end{aligned}$$

  (79)
  $$\begin{aligned}&DEC&: \tilde{\rho }-|\tilde{p}_t|\ge 0, \quad \tilde{\rho }-|\tilde{p}_t|\ge 0. \end{aligned}$$

  (80)

  In Fig. 17, solid curves corresponds to the model-I. The bounds are shown to be satisfied at every point in stars’s interior. Thus, model-I represents the matter source which is realistic and physically accepted as a stellar material (Table 2).

Fig. 12

Shows the anisotropy (75), where the solid and dashed lines shows the anisotropy for $\alpha =0.3$, $c_1=-2\times 10^{-6}$ and $\alpha =0.7$, $c_1=-3\times 10^{-7}$, respectively

Fig. 13

Depicts the variations of sound speed for the Model-I. The left and right panels present the cases for $\alpha =0.4$ and $\alpha =0.7$, respectively

Table 1 Calculated values for various physical quantities of model-I at $r=0$ and $\alpha =0.3$

Table 2 Values of different physical quantities of model-I at $r=0$ and $\alpha =0.3$

Table 3 The values of different parameters for the Model-II by using different values of R and M, along with $\alpha =0.5$

Table 4 Calculated values of different parameters for the second constructed model using $\alpha =0.5$

Table 5 The values of different parameters for the third constructed model by using different values of R and M, along with $\alpha =0.5$

Table 6 Calculated values of different parameters for the third constructed model

Fig. 14

Depicts the variations in sound speed for the model-II. The left and right panels present the cases for $\alpha =0.4$ and $\alpha =0.7$, respectively

Fig. 15

Shows the variations in sound speed for the Model-III. The left and right panels present the cases for $\alpha =0.3$ and $\alpha =0.7$, respectively

Fig. 16

Demonstrates the variations of the adiabatic index (left for the Model-I, central for the Model-II, and right for the Model-III) with respect to r

5.2 Model-II

• Figures 5, 6, 7 and 8 presents graphical analysis of the quantities like deformation function (f(r)), radial metric function ($e^{-\lambda }$), thermodynamical variables ($\tilde{\rho }$, $\tilde{p}_r$, $\tilde{p}_t$ ) and anisotropy parameter ($\tilde{\Pi }$) for the model-II. The mathematical expressions for these quantities are given in Eqs. (62–66). In Fig. 5, it is to be noted that deformation functions is zero at the center and boundary, whereas it has negative range throughout in the stellar interior. This situations indicates that newly established model will represent more dense stellar configurations. The left panel of Fig. 6 exhibits the regularity of the radial metric function at the center. Moreover it is positive throughput in the stellar interior.

• Energy density (65) is graphed in the right panel of Fig. 6, where it is to note that all the curves representing energy density ($\tilde{\rho }$) follow well-accepted trends. Moreover, for higher value of $\alpha$, we obtain more dense stellar configurations. The radial and tangential pressure ($\tilde{p}_r, ~\tilde{p}_t$) are graphed in Fig. 7, where one can see that all the situations happen in a desired way. Pressure in both directions is maximum at the center, then gradually decrease and minimum at the boundary. Radial pressure is zero at the boundary, whereas it is equal to the tangential pressure at the core.

• Pressure anisotropy (67) is plotted on the Fig. 8, which is zero at the center and then monotonically increases. It is maximum at the center for both values of $\alpha$. Its positive range in the stellar interior indicates towards the existence of a repulsive force which will counterbalance the attractive ones and helps to maintain the systems’s equilibrium.

• The speeds of sound plotted in Fig. 14 satisfy the causality condition. In addition to this, $v_t^2-v_t^2 \epsilon [-1,0]$, thus our stellar model possesses stable regions for both cases of intensity parameter, i.e., $\alpha =0.3,~0.7$. On the other hand, the middle panel of Fig. 16 presents variations of adiabatic index for the model-II, where one can see that adiabatic index satisfy the stability bound $\Gamma > \frac{4}{3}+\frac{4(\tilde{p}_t-\tilde{p}_r)}{3|d\tilde{p}_r/dr|}$. Moreover, we have numerical values of adiabatic index and critical adiabatic index in Table 3, which satisfies $\Gamma _C < \Gamma$.

• The expressions on the left hand side of energy bounds (77–78) are graphed in Fig. 17, where dashed curves correspond to the model-II. All the curves are constrained to the first quadrant of the plane, thus our model-II also represents realistic matter configurations. All these features makes it an interesting model (Table 4).

5.3 Model-III

• The expressions in Eqs. (71–75) present main information about the model-III, whereas one can see graphical representation of the solution and thermodynamical variables in Figs. 9, 10, 11, 12, 13, 14, 15, 16, 17. It is to note that all the things in these graphs happen according to the desired trends. The radial metric function (72) is regular at the center, $\tilde{\rho },~\tilde{p}_r,~\tilde{p}_t$ attain their maximum values at the center, and then monotonically decrease towards the stellar boundary. Anisotropy is positive throughout in the interior, moreover it is zero at the center.

• The speed of sound in both principal directions are plotted in Fig. 15. For $\alpha <0.3$, both components satisfy the causality condition for all the selected pairs of radius and mass, however for $\alpha \ge 3$, causality condition is failed to satisfy away from the center for the situation representing Vela X-I. Same scenario can be observed in the case of tangential component of square speed of sound against the radius and mass of PSR 1937+21 for $\alpha \ge 0.44$. Moreover, $v_t^2-v_t^2 \epsilon [-1,0]$, for both selected values of $\alpha =0.3,~0.7$, which means model-III presents stellar configurations having stable regions. Furthermore, the extreme right panel of Fig. 16 presents evolution of adiabatic index for the model-III, which satisfies the stability bound $\Gamma > \frac{4}{3}+\frac{4(\tilde{p}_t-\tilde{p}_r)}{3|d\tilde{p}_r/dr|}$. In addition, the numerical values of adiabatic index and critical adiabatic index are given in Table 5, which satisfies the relation $\Gamma _C < \Gamma$.

• The dashed-dotted curves in the Fig. 17 show that energy bounds (77–80) are all satisfied by the model-III (Table 6).

Fig. 17

Shows the different energy conditions for $\alpha =0.5$. The solid, dashed, and dot-dashed lines are for model-I, model-II, and model-III, respectively

6 Conclusion

In the current manuscript, we have studied the process of isotropization and properties of stellar models with different complexity factors by using a well-known systematic scheme termed as GD by means of MGD. For the study of process of istropization (named model-I in Sect. 3), we considered an anisotropic version of Durgapal–Folouria solution as a seed source and employed isotropy condition $\tilde{p}_r=\tilde{p}_t$ for the evaluation of additional source. The solution obtained in this way is given in Eqs. (42–46), where intensity parameter $\alpha$ varies from 0 to 1. It represents a stellar system which is initially anisotropic for $\alpha =0$, whose anisotropy is gradually decreased when $\alpha$ moves towards 1. For $\alpha =1$, it is disappeared. Next, we developed two interesting anisotropic stellar models, where we have considered definition of complexity introduced by Herrera [45] and imposed additional conditions on complexity factor for the evaluation of system of equations related to the additional source (19–21). We can summarize our results follows:

• The model-I (19–21) describes the process of isotropization, where $\alpha$ works as intensity parameter and controls the whole process. For $\alpha =0$, we have anisotropic stellar configuration, which is less dense as compared to the other anisotropic scenarios which occur between $0<\alpha <1$. For $\alpha =1$, anisotropy is vanished, and a stellar model representing isotropic fluid configuration is obtained. In this case, all the important quantities including $\tilde{\rho }$, $\tilde{p}_r$, $\tilde{p}_t$ behave according to the regular trends (see in the Figs. 1, 2, 3, 4). It has been Adiabatic index ( shown in the extreme left panel of Fig. 16) obeys the stability condition for all scenarios, and energy conditions (representing by solid curves in Fig. 17) maintain their positive profile throughout in the stellar interior for all scenarios. However, square speed of sound is not always under conducive environment. Speed of sound in radial direction always meets the causality condition, whereas transversal component fails to satisfy the causality condition for $\alpha <0.58$ (shown in Fig. 13).

• Model-II presents an anisotropic fluid spheres, which has been developed by using the definition the complexity. Seed source is represented by Durgapal–Folouria perfect fluid solution, while the anisotropic sector has been solved by imposing condition on complexity factor $\mathcal {Y}_{TF}$. We considered complexity of the system mainly depends on the anisotropy of the system. The model obtained in this way is given in (62–66), while graphical description is provided in Figs. 5, 6, 7 and 8. Graphical analysis of the model ensures its physical acceptability. Square speed of sound (Fig. 14), Adiabatic index (middle panel of Fig. 16), and energy conditions (representing by dashed curves in Fig. 17) are completely in agreement with desired trends.

• For the Model-III, we worked out complexity factor $\mathcal {Y}_{TF}$ for the seed source which is Durgpal-Folouria perfect fluid solution (68), and generalized it (69) to obtain a stellar model evolving in anisotropic environment. Radial metric function, thermodynamical variables and anisotropy (71–75) have physically accepted profiles. Adiabatic index (shown in extreme right panel of Fig. 16) meets the stability limit and energy conditions (dot-dashed curves in Fig. 17) re satisfied at each point in the stellar interior, however causality condition is partially satisfied. For $\alpha <0.3$, both components of square speed of sound satisfy the causality condition in all situations and scenarios.