Abstract
In present work, the evolution of scalar field and electromagnetic field under the background of the charged black-bounce spacetimes are investigated, and we obtain an obvious echoes signal which appropriately reports the properties of the charged black-bounce spacetimes and disclose the physical reasons behind such phenomena. Furthermore, by studying the quasinormal ringdown, we analyze the three states of the charged black-bounce spacetimes in detail, our results show that the echoes signal only appears when \((|{Q}|\le m)\) and \((|{l}|> m+ \sqrt{m ^{2}-Q^{2} })\) in this spacetime, while when the parameters demand \((|{Q}|>m)\), the echoes signal will be transformed into a quasinormal ringdown of the two-way traversable wormhole, and the charged black-bounce is a regular black hole with normal horizons by requiring \((|{Q}|\le m)\) and \((|{l}|< m-\sqrt{m ^{2}-Q^{2} })\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, the first measurements of the shadow image captured by Event Horizon Telescope (EHT) [1,2,3,4,5,6] and the gravitational wave (GW) searches by the LIGO Scientific and Virgo collaboration for the merger of compact binaries [7,8,9,10] energized physicists in black hole physics, as the most extremely compact objects characterized by the existence of event horizons, black holes are some of the most important models in GW observations. But in fact, with the development of GW astronomy, one encounters the notion of black hole mimickers, i.e. gravastars, wormholes and so on [11, 12], which can appropriately mimic the results found using black holes in terms of GW observations. Therefore, in order to facilitate the improvement of present templates for black hole mimickers, various properties associated with them are intend to be considered, and one such property is the discussion of quasinormal modes (QNMs) which could be used by observers at GW interferometers aiming to verify a wormhole proposal. Moreover, in view of the hot area of research in wormhole physics [13, 14], it is necessary to find a way distinguishing black holes with wormholes, and one such useful way is to perturb the objects and then observe the time evolution of the perturbation. After that, black holes or wormholes will radiate GWs based on the initial conditions of the perturbations, then they reduce to damped oscillations with complex frequencies, these modes of oscillations are QNMs. In QNMs, we have to mention the notion of echoes, which are generated by the reflected waves of the system. It should be noted that not all wormholes or black holes could generate echoes after perturbations [15], but as a useful way, it can provide some information to examine the properties of black holes and wormholes. In particular, GW echoes from electromagnetic field and scalar field perturbations can help us to study the properties of the compact object itself, and moreover, probably furnish an avenue to the nature of quantum gravity. The notion of GW echoes was proposed in the context of the GW ringdown signals, aiming to study the phenomena in the vicinity of the black holes and their exotic compact alternatives, and it should be noted that echo signals could be used to distinguish the source of gravitational waves, whether it is from a black hole or not [16].
On the other hand, as the characteristic sound of black holes, the QNMs are dominantly governed by the spacetimes in the vicinity of the horizon. It is well known that once a black hole is perturbed [17], there are three stages that are responsible for the perturbations evolution in time. The first one is a relatively short period of initial outburst of radiation, the second one is a usually long period of damping proper oscillations which dominated by the QNM, and the third one is the power-law tail. Here, we focus on the second stage of the evolution of perturbations represented by QNM. One can compute the QNMs by solving the perturbation equations, the potential solution is expressed by the pure ingoing wave at the event horizon and the pure outgoing wave at infinity [18, 19]. Moreover, by studying the black hole QNMs, we can disclose the frequencies of QNMs [20, 21], which are not only related to the basic physical properties of the black hole but also may provide reliable evidence of the existence of the black holes [22]. The QNMs of wormholes have drawn much attention. Roy et al. [23] studied a family of ultra-static Lorentzian wormholes and obtained the scalar QNMs, their results may be used as a template for further studies on the gravitational wave physics of exotic compact objects. In Ref. [24], they studied the phantom wormholes and observe obvious signals of echoes, their results showed that the dark energy equation of state has a clear imprint in echoes in wave perturbations. As stated before, we intend to study the differences between black holes and wormholes in same circumstance, in order to achieve this goal, we must find the theories that admit both the black hole and wormhole solutions, and one such candidate is the regular black hole. Churilova et al. [25] studied the QNM of regular black-hole/wormhole transition and obtained unique wormhole echoes picture near the threshold, their results showed that different parameters corresponding to different spacetime, and only the traversable wormhole spacetime background has a clear echo picture. In addition, more related works can been seen in Refs. [26,27,28,29,30,31,32,33].
Given the demonstrated existence of the black-bounce-Kerr geometries [34] and the black-bounce-Schwarzschild [35], it is reasonably suspect that analogous black bounce variants of the Reissner–Nordström spacetimes will exist. Physically, we can find some answers in Ref. [36], in which the regularizing procedure has been proposed, i.e., the radial coordinate r in the Reissner–Nordström metric is replaced by \(\sqrt{r^{2}+l^{2}}\), here l is the bounce parameter of the charged black-bounce associated with the Plank length. This geometry implies a regularizing procedure: the introduction of bounce parameter or a length scale is applied to the Reissner Nordström geometry black hole, and which is globally free from curvature singularities, passes all weak field observational tests and smoothly interpolates between regular black holes and charged traversable wormholes. Alternatively, we can comprehend the charged black-bounce spacetimes as: an electromagnetic charge is introduced to the black-bounce spacetimes [37, 38], where the black-bounce can be derived from the Schwarzschild black hole in terms of the regularizing procedure. Moreover, a lot of works have studied the ringing of the black hole/wormhole transition, and this transition is characterized by echoes, thus it is necessary to discuss that if there are echoes in the charged black-bounce spacetimes. In this paper, we attempt to provide an investigation to the QNM of the charged black-bounce spacetimes and disclose the physical reasons behind such phenomena. Physically, we analyse the properties of spacetimes in the context of the perturbation of electromagnetic fields and scalar fields, and our results show that echoes signal appears on the condition that the parameters are constrained.
The paper is organized as follows. In Sect. 2, we introduce the charged black-bounce spacetimes, the equations of motion under the influence of scalar field and electromagnetic field perturbation, meanwhile the corresponding effective potential is derived and the figure of the effective potential under the perturbations of scalar field and electromagnetic field are discussed. In Sect. 3, the time domain integration method is introduced. In Sect. 4, the time-domain profiles of the scalar field and electromagnetic field in the context of the black hole and the wormhole by configurating different spacetime parameters are analyzed, including the different ringdown behaviors. In Sect. 5, we use the Prony method to calculate the QNMs frequencies. Finally, the work is summarized in Sect. 6.
2 Scalar field and electromagnetic field perturbation in the charged black-bounce spacetimes
We introduce the charged black-bounce spacetimes, its metric is given by [36]
here m is the mass and Q is the charge of the charged black-bounce respectively. \(r\in (-\infty ,+\infty )\) and \(d{\Omega }^{2}\) represents the line element of a unit 2-sphere. We can see that natural domains for the angular and temporal coordinates are unaffected by the regularisation procedure, then compared with the Reissner–Nordström spacetimes, the natural domain of the r coordinate expands from \(r\in (0,+\infty )\) to \(r\in (-\infty ,+\infty )\). It should be noted that different parameters correspond to different spacetimes, (a) the traversable wormhole:\((|{Q}|\le m)\) and \((|{l}|> m\pm \sqrt{m ^{2}-Q^{2} })\); (b) the two-way traversable wormhole:\((|{Q}|>m)\); (c) the regular black hole:\((|{Q}|\le m)\) and \((|{l}|< m- \sqrt{m ^{2}-Q^{2} })\). Furthermore, the horizons are located at
where \(S_1=S_2=\pm 1\), in particularly, \(S_1=1\) corresponds to our universe, \(S_1=-1\) labels the copy of our universe, \(S_2=1\) indicates outer horizon and \(S_2=-1\) represents inner horizon, respectively.
The general covariant Klein–Gordon equation of scalar field can be expressed as
in order to reduce the above equation, we assume the scalar field separated in the standard form [39]
where \(Y^{{\hat{m}}}_{l_{0}}\) is spherical harmonic function of degree \(l_{0}\) related to the angular coordinates \(\theta \),\(\phi \), and it demands
combination the separated scalar function Eqs. (5) and (4) obtains the following wave equation relating the radial dependence of the scalar function and time
with \(V_{0}= -r ^{2}A^{2}(r ^{2}+l^{2})^{-2}+Ar[2mr(r^{2}+l^{2})^{-\frac{3}{2}}-2rQ^{2}(r ^{2}+l^{2})^{-2}](r ^{2}+l^{2})^{-1}+A^{2}(r ^{2}+l^{2})^{-1}+\frac{Al_0 (l_0+1)}{r ^{2}+l^{2}} \) and the tortoise coordinate \(r_{*}=\int \frac{dr}{A(r)}\).
Furthermore, in view of the formalism of the charged black-bounce spacetimes, here the perturbed metric will be assumed to be axially symmetric, thus we can express the general metric which is time-dependent and axially symmetric as
thus in Eq.(1)
Generally, perturbations of the black hole will lead to non zero values of W, \(q_{2}\), \(q_{3}\), \(\delta v\), \(\delta \mu _{2}\), \(\delta \mu _{3}\) and \(\delta \psi \), in particular, W, \(q_{2}\) and \(q_{3}\) are perturbed, v, \(\mu _{2}\), \(\mu _{3}\) and \(\psi \) are unperturbed, these perturbations are called axial perturbations. In our analysis of axial perturbations, we use Chandrasekhars notations \(x^{0}=t\), \(x^{1}=\phi \), \(x^{2}=r\) and \(x^{3}=\theta \). The nonzero component of electric field strength of unperturbed metric is taken in the form
according to the linearized Maxwell’s equations, since we just consider the magnetic field perturbation, only four relevant equations are listed as
where \(O_{j 0}=\frac{\partial q_{j}}{\partial t}-\frac{\partial W}{\partial x^{j}}\) and \(O_{j {\hat{B}}}=\frac{\partial q_{j}}{\partial x^{{\hat{B}}}}-\frac{\partial q_{{\hat{B}}}}{\partial x^{j}}(j, {\hat{B}}=2,3)\).
Here it should be noted that the first equation in Eq. (11) can be neglected since it just provides the integrability conditions for the next two equations, then we can rewrite this equation in spherical coordinates as
The perturbed components of the Ricci tensor for charged black-bounce spacetimes are computed as follows
in view of the fact that only the axial perturbations are considered in this part, it is characterized by non-zero values W, \(q_{2}\), \(q_{3}\), \(F_{01}\), \(F_{12}\) and \(F_{13}\), and the two equations governing axial perturbations comes from \(R_{12}\) and \(R_{13}\). Besides, it should be noted that before perturbations, \(R_{12}=R_{13}=0\), after perturbations, \(\delta R_{12}=2 \frac{Q}{R^{2}} \delta F_{01}\) and \(\delta R_{13}=0\). Therefore we substitute the changes in the corresponding Ricci tensors and remain the functions v, \(\psi \), \(\mu _{2}\) and \(\mu _{3}\) as same as before the perturbations, one can obtain
eliminating \(F_{12}\) and \(F_{13}\) from Eq. (12) leads to
with \(B=F_{01}sin\theta \). By defining new function \(\eta \)
substituting Eq. (16) into Eq. (14), and taking the time dependence of the perturbed values of W, \(q_{2}\), \(q_{3}\) and O to be \(e^{-i\omega t}\) where \(\omega \) is the frequency of the modes, we have
combining Eqs. (14) and (15) leads to
Next, we deal with the Eqs. (17) and (18) by using the method of separation of variables
with \(C_{n}^{v}(\theta )\) are Gegenbauer polynomials, thus Eqs. (17) and (18) read
with \(u^{2}=2n=(l_{0}-1)(l_{0}+2)\).
In order to facilitate the study, the variable r will be replaced in terms of the tortoise coordinate and we define \(\eta (r)\) and B(r) as
with these definitions, Eq. (20) becomes
here
and \(l=0\) the Eq. (22) approaches the Reissner–Nordström black hole expressions [40]. Furthermore, the Eq. (22) can be considered as two one-dimensional wave equations coupled by the interaction matrix
where
with \(\lambda =2 r^{2}(2 Q^{2}+r^{2}-3 m \sqrt{r^{2}+l^{2}})\).
Noted that the matrix can be diagonalized by a similarity transformation as
where
As stated before, the symbol \(r_{*}\) is the tortoise coordinate which is given by
and the lapse function A(r) decides the event horizon location, i.e., \(r_{*}\) \(\rightarrow \) \(-\infty \) as r \(\rightarrow \) the event horizon of the black hole from infinity, we have \(r_{*}\) \(\in \) (\(-\infty \),\(+\infty \)) for r \(\in \) (\(r_{H}\),\(+\infty \)), therefore Eqs. (7) and (26) are restricted to the regions located outside the event horizon, \(r>r_{H}\). Moreover, the asymptotic regions of the wormhole correspond to \(r_{*}\) \(\rightarrow \) \(\pm \infty \) when the horizons vanish, we express \(\pm r_{*}\) in order to cover the two asymptotic regions connected by the throat, this procedure needs a thin shell joining two copies of the same geometry [41]. Meanwhile, it is also worth pointing that the coordinate \(r_{*}\) is monotonically increasing with r, which appropriately avoids the horizon and more conveniently to discuss the QNMs.
Now, we look for the stationary solutions by using the ansatz \(\Phi _{b} \sim \Psi _{b}e^{-i{\omega }t}\), thus the Schrödinger-like equation transforms into
Before solving Eq. (30), we must state the boundary conditions. Considering Figs. 1, 2, 3 and 4, we have \(r_{*}\) \(\rightarrow \) \(\pm \infty \) and V \(\rightarrow \) 0, thus according to the asymptotic behavior of the effective potential at the boundary, the solution of the wave function at the boundary should have the form of a plane wave, i.e. \(\Psi _b(r_{*}) \sim e^{\pm i{\omega }r_{*}}\), \(r_{*}\) \(\rightarrow \) \(+\infty \) and \(\Psi _b(r_{*}) \sim e^{\pm i{\omega }r_{*}}\), \(r_{*}\) \(\rightarrow \) \(-\infty \). Since we are dealing with the black bounce Reissner Nordström geometry, thus we need to study based on the black hole and the wormhole. For the case of the black hole, the quasinormal boundary conditions imply pure incoming waves at the horizon and pure outgoing waves at spatial infinity, thus for the asymptotically flat solutions, the quasinormal boundary conditions are [42]
For the case of the wormhole, the quasinormal boundary conditions for both infinities are the requirement of purely outgoing waves into both infinities, which implies that no waves are coming from both asymptotically flat regions, i.e. \(\Psi _b \propto e^{\pm i{\omega }r_{*}}, r_{*} \rightarrow \pm \infty \) [43]. Moreover, the solution of a wave function satisfies the above boundary conditions, whose frequencies are a set of discrete complex numbers.
a The effective potentials as a function of tortoise coordinate \(r_{*}\) for perturbations of the scalar field on the regular black hole spacetime with \(m=0.5\), \(l_{0}=1\); b the effective potential(\(V_{1}\)) as a function of tortoise coordinate \(r_{*}\) for perturbations of the electromagnetic field on the regular black hole spacetime with \(m=0.5\), \(l_{0}=1\)
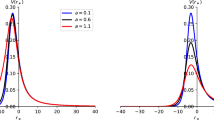
a The effective potentials as a function of tortoise coordinate \(r_{*}\) for perturbations of the scalar field on the traversable wormhole spacetime with \(l=1.01\); b the effective potentials as a function of tortoise coordinate \(r_{*}\) for perturbations of the scalar field on the traversable wormhole spacetime with \(l=1.03\); c the effective potentials as a function of tortoise coordinate \(r_{*}\) for perturbations of the scalar field on the traversable wormhole spacetime with \(l=1.2\); d the effective potentials as a function of tortoise coordinate \(r_{*}\) for perturbations of the scalar field on the traversable wormhole spacetime with \(l=1.7\). In both cases we take \(m=0.5\), \(Q=0.03\) and \(l_{0}=1\)
a The effective potential(\(V_{1}\)) as a function of tortoise coordinate \(r_{*}\) for perturbations of the electromagnetic field on the traversable wormhole spacetime with \(l=1.01\); b the effective potential(\(V_{1}\)) as a function of tortoise coordinate \(r_{*}\) for perturbations of the electromagnetic field on the traversable wormhole spacetime with \(l=1.03\); c the effective potential(\(V_{1}\)) as a function of tortoise coordinate \(r_{*}\) for perturbations of the electromagnetic field on the traversable wormhole spacetime with \(l=1.2\); d the effective potential(\(V_{1}\)) as a function of tortoise coordinate \(r_{*}\) for perturbations of the electromagnetic field on the traversable wormhole spacetime with \(l=1.7\). In both cases we take \(m=0.5\), \(Q=0.03\) and \(l_{0}=1\)
a The effective potentials as a function of tortoise coordinate \(r_{*}\) for perturbations of the scalar field on the two-way traversable wormhole spacetime with \(m=0.5\), \(l_{0}=1\); b the effective potential(\(V_{1}\)) as a function of tortoise coordinate \(r_{*}\) for perturbations of the electromagnetic field on the two-way traversable wormhole spacetime with \(m=0.5\), \(l_{0}=1\)
Figures 1, 2, 3 and 4 report that the effective potentials change with different parameters. In Fig. 1, the value of parameters satisfy the conditions of \(|{Q}|\le m\) and \((|{l}|< m- \sqrt{m ^{2}-Q^{2} })\), so Fig. 1 is the effective potentials of regular black hole, which show that the maximum value of the effective potential reveal no significant changes when we remain the constant charge parameter Q and set the changeable bounce parameter l. In Figs. 2 and 3, the value of parameters satisfy the conditions of \((|{Q}|\le m)\) and \((|{l}|> m+ \sqrt{m ^{2}-Q^{2}})\), so Figs. 2 and 3 are corresponding to the traversable wormhole for perturbations of the scalar field and perturbations of the electromagnetic field respectively. For both cases, which show that the effective potential has obvious double peaks, and with the increasing parameter l, the double peaks will eventually merge to a single peak. While by comparing the maximum value of the effective potential for perturbations of the scalar field and perturbations of the electromagnetic field, we see that the former case is greater than the latter case for the same spacetimes parameters. In Fig. 4, the value of parameters satisfy the conditions of \(|{Q}|> m\), therefore the charged black-bounce spacetimes will transform into the two-way traversable wormhole, we can see that if remaining the constant charge parameter Q, the maximum values of the effective potential decrease with the bounce parameter l.
3 The time domain integration method
The external perturbation field satisfies the equation under the charged black-bounce spacetimes in terms of the tortoise coordinate is given by
since QNMs are complex frequencies related with purely outgoing waves at spatial infinity, from Eq. (32) we have \(\Phi _b(r_{*},t)\) \(\rightarrow \) \(e^{\pm i{\omega }r_{*}}\) \(e^{-i{\omega }t}\) as \(r_{*}\) \(\rightarrow \) \(\pm \infty \), and for an asymptotically flat spacetime, \(V_{b}\) approaches 0. Based on the features of the effective potentials, we will deal with the scalar and vector QNMs in context of the charged black-bounce spacetimes, the existence of QNMs can be directly observed in the time evolution of the scalar field and vector field obtained by integrating the wave equation (Eq. (32)). In view of the obscure expression of the effective potentials, it is difficult to obtain the analytical solutions, here we intend to adopt the time domain integration method which does not depend on the form of the potential barrier, thus we rewritten Eq. (32) in terms of the light-cone variables \(u=t-r_{*}\) and \(v=t+r_{*}\) as
where u and v are integral constants.
Next, we move on towards the numerical integration of the Eq. (33), regarding the characteristic initial value problem, the initial data is specified on the two null surfaces \(u = u_0\) and \(v = v_0\). In view of the fact that the field decay is almost independent of the initial conditions, and the initial condition is the Gaussian wave packet [44,45,46], thus we start with a Gaussian pulse (\(u = u_0\)) and set the field to zero (\(v = v_0\)), i.e.
where the Gaussian pulse with a width is \(\sigma =3\) and the center of the Gaussian pulse is \(v_c=10\). In addition, the appropriate discretization scheme in terms of the Taylors theorem [47, 48] is
where the following designations for the points were used: \(N=(u+\Delta ,v+\Delta )\), \(w=(u+\Delta ,v)\), \(E=(u,v+\Delta )\) and \(S=(u,v)\), thus using the corresponding initial conditions along u and v lines we numerically integrate to derive the time-domain profiles. In addition, in order to facilitate the extraction of the quasinormal frequencies, we will employ the Prony method [49] which helps us to fit the signal by a sum of exponents with some excitation factors.
4 The pictures of echoes for the charged black-bounce spacetimes
In this section, we concentrate on the time evolution under the perturbations of massless scalar field and electromagnetic field in the charged black-bounce spacetimes. Specifically, we depict the time evolution which has the same parameters with the effective potential in order to facilitate the control study, and it should be noted that the necessary condition for the appearance of the echoes is that the potential well must appear.
a The time evolution of traversable wormhole for perturbations of the scalar field with \(l=1.01\); b the time evolution of traversable wormhole for perturbations of the scalar field with \(l=1.03\); c the time evolution of traversable wormhole for perturbations of the scalar field with \(l=1.2\); d the time evolution of traversable wormhole for perturbations of the scalar field with \(l=1.7\). In both cases we take \(m=0.5\), \(Q=0.03\) and \(l_{0}=1\)
a The time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{1}\)) with \(l=1.01\); b the time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{1}\)) with \(l=1.03\); c the time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{1}\)) with \(l=1.2\); d the time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{1}\)) with \(l=1.7\). In both cases we take \(m=0.5\), \(Q=0.03\) and \(l_{0}=1\)
a The time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{2}\)) with \(l=1.01\); b the time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{2}\)) with \(l=1.03\); c the time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{2}\)) with \(l=1.2\); d the time evolution of traversable wormhole for perturbations of the electromagnetic field(\(V_{2}\)) with \(l=1.7\). In both cases we take \(m=0.5\), \(Q=0.03\) and \(l_{0}=2\)
a Time-domain profiles for scalar field in charged black-bounce spacetimes; b time-domain profiles for electromagnetic field(\(V_{1}\)) in charged black-bounce spacetimes; c time-domain profiles for electromagnetic field(\(V_{2}\)) in charged black-bounce spacetimes; In both cases we take \(m=0.5\) and \(l_{0}=3\)
Figure 5 expresses the time evolution of regular black hole (\(|{Q}|\le m\),\(|{l}|< m- \sqrt{m ^{2}-Q^{2} }\)) for perturbations of the scalar field and perturbations of the electromagnetic field, which shows that there are three stages instead of echo signal, moreover, we find that the quasinormal ringdown of regular black hole will decay slighter slower with the decreasing bounce parameter l. Actually, this result can be predicted from Fig. 1, since which reveals no potential well in the effective potential. While for the same parameters, the decay rate of the quasinormal ringdown for perturbations of the scalar field is faster than the decay rate of the quasinormal ringdown for perturbations of the electromagnetic field.
Figures 6 and 7 show that the scalar field perturbation and the electromagnetic perturbation of the charged black-bounce spacetimes for the case of \((|{Q}|\le m)\) and \((|{l}|> m+ \sqrt{m ^{2}-Q^{2} })\), these pictures present the following characteristics:
-
(1)
In terms of the values of the bounce parameter l, the effective potentials (Figs. 2, 3) express two relatively distant peaks. This phenomenon causes modification of the signal at the late times labeled as echoes, which may generate either because of the modification of the black hole metric in the vicinity of its event horizon [50, 51], or by reason of the matter situated at some distance from the compact object [52, 53]. After the black hole/wormhole transition, we find the quasinormal ringdown of the initial black hole followed by a series of echoes in Figs. 6 and 7, and with the parameter l increases, the time interval for the echo signals becomes shorter, which shows that the time interval has a strong dependence on the bounce parameter l, therefore we can see that when the bounce parameter l reaches a certain level (Figs. 6, 7), the echoes signals are not likely to be detected. Actually, these conclusions can be predicted from the effective potential in Figs. 2 and 3, since as the parameter l increases, the width of the potential well becomes smaller and smaller, and finally merges into a single peak potential barrier, thus the echoes signals ultimately vanish.
-
(2)
When the bounce parameter l become larger, the amplitudes of the echoes signal only slightly change, this result is probably due to the corresponding potential function. We can see that as the parameter l increases, the peak value of the potential well only slightly change (such as Figs. 2, 3). It is because the potential well strongly constrain the scalar wave or electromagnetic wave that the echoes are generated. So almost the same height potential wells have the almost the same probability for the scalar wave or electromagnetic wave escaping from the potential well, this is also the reason why the amplitudes of the echoes signal remain almost unchanged.
-
(3)
As the bounce parameter l increases, both peaks of the effective potential become closer and the echo effect decreases rather quickly, and the wormhole still remains a distinctive quasinormal mode. Moreover, from Figs. 6c and 7c, we find that the time evolution of the traversable wormhole have a kind of the initial outburst and obvious quasinormal mode of the wormhole spacetime.
Figure 8 shows the time evolution of the two-way traversable wormhole’s \((|{Q}|>m)\) quasinormal ringing for perturbation of the scalar field and perturbation of the electromagnetic field with different spacetime parameters, and obviously there are no echoes signals, which can be predicted from Fig. 4, since there is no potential well in the figure. Moreover, we can see that the two-way traversable wormhole’s quasinormal ringing will decay slower with the increasing bounce parameter l.
Figures 9 and 10 show that the semi-logarithmic plot of time evolution of electromagnetic perturbations for the charged black-bounce spacetimes with different spacetime parameters, analogy to the cases of the scalar field perturbation and electromagnetic field perturbation(\(V_{1}\)), the echoes signal only appears when \((|{Q}|\le m)\) and \((|{l}|> m+ \sqrt{m ^{2}-Q^{2} })\).
Finally, Figs. 11 and 12 express the time-domain profiles for scalar field and electromagnetic field(\(V_{1}\) and \(V_{2}\)) in charged black-bounce spacetimes, which show that the echoes signal only appears when \((|{Q}|\le m)\) and \((|{l}|> m+ \sqrt{m ^{2}-Q^{2} })\), and this result is independent on the azimuthal quantum number \(l_{0}\).
5 The QNM frequencies of the charged black-bounce spacetimes
In this section, we will study the QNM frequencies of the charged black-bounce spacetimes, as the introduction in Sect. 3, the Prony method is used for extracting the QNM frequencies. As stated before, the frequency of the QNMs is a complex number, i.e. \(\omega =\omega _{Re}+i{\omega }_{Im}\), with \(\omega _{Re}\) is the real oscillation frequency and \(|{\omega }_{Im}|\) is proportional to the decay rate of a given mode. We list the QNM frequencies of the charged black-bounce spacetimes in terms of the different bounce parameter l. It should be noted that the extraction of frequencies from the profiles obtained with the help of time domain integration strongly depends on the temporal range which is determined to be the quasinormal ringing, so in order to have a better comparison with the frequencies under different parameters, we set the almost same temporal range (Table 1). The table presents the following three characteristics:
-
(1)
For the case of the regular black hole, as the bounce parameter l increase, the damping rate is also slighter increasing, which implies the quasinormal ringdown has a faster decay rate, while the bounce parameter l is not sensitive to the decay rate, this result verifies the properties of the Figs. 5 and 9a.
-
(2)
For the case of the traversable wormhole, as the bounce parameter l increase, the imaginary part of the QNM frequencies is decreasing.
-
(3)
For the case of the two-way traversable wormhole, for the smaller bounce parameter l, the bigger \(|{\omega }_{Im}|\) corresponds to the faster decay rate of the QNMs, this result can be predicted from Fig. 8. In addition, for the bigger bounce parameter l, \(\omega _{Re}\) becomes smaller, which implies the real oscillation frequency of the QNMs becomes smaller, but for \(|{\omega }_{Im}|\), it is contrary to the case for the regular black holes.
6 Conclusions
In summary, the charged black-bounce spacetimes (Eq. 1) neatly interpolated between the regular black hole and traversable wormholes, we studied the ringing of the black hole/wormhole transition, which showed that this transition is characterized by echoes, and our results are consistent with the Refs. [25, 54]. For \((|{Q}|\le m)\) and \((|{l}|> m+ \sqrt{m ^{2}-Q^{2} })\), the obvious echoes signal appears after the initial ringdown, while since the increase of the parameter l makes the width of the potential well smaller, the time interval between echoes will gradually decrease, which is consistent with the behavior of the wormholes echo signal given by Ref. [32]. Moreover, when \(|{l}|\gg m+ \sqrt{m ^{2}-Q^{2} }\) (\(|{Q}|\le m\)), the second symmetric peak in the far left region disappears and becomes a single peak potential barrier, thus the echo signal disappears and it turns into a quasinormal ringdown of the traversable wormhole. By studying the effects of spacetime parameter l on the QNM frequency to the two-way traversable wormhole, it shows that QNM frequencies are inversely proportional to the spacetime parameter l. The QNM results of wormholes are likely to be used as a probe for detecting wormholes in the future work.
Moreover, the QNMs of black holes are proper oscillations of black holes under different boundary conditions, which corresponds to purely incoming waves at the event horizon and purely outgoing waves at infinity, and the boundary conditions for a traversable wormhole are the same in terms of the tortoise coordinate, therefore the alternative tools used for finding black holes QNMs can, in some sense, be used for wormholes as well after some necessary corrections [41, 42, 55,56,57]. This work we considered the scalar and electromagnetic perturbations for the charged black-bounce spacetimes, which showed that the echoes signals of the two perturbations have very similar characteristics. Besides, it should be noted that the Refs. [58, 59] are involved in the perturbations of the scalar field or the electromagnetic field on charged black-bounce spacetimes, by using the WKB method, they studied the effects of different spacetimes parameters on the QNMs of the charged black-bounce spacetimes. In our work, by using the time domain integration method, we visually showed the time evolution of scalar field and electromagnetic field in the context of the charged black-bounce spacetimes and studied the ringing of the black hole/wormhole transition, also this transition is characterized by echoes. In particular, regarding the perturbations of electromagnetic field on charged black-bounce spacetimes, we consider the case where the background electromagnetic field is not zero, and we may view that this consideration is more interesting and general [60]. For future work, we can go further to investigate the gravitational field perturbations [61] for the charged black-bounce spacetimes, and this study based on QNMs may be checked in future gravitational wave plans.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: There are no associated data available.]
References
K. Akiyama et al., (Event Horizon Telescope Collaboration), Astrophys. J. 875 L1 (2019)
K. Akiyama et al., (Event Horizon Telescope Collaboration), Astrophys. J. 8, 75 L2 (2019)
K. Akiyama et al., (Event Horizon Telescope Collaboration), Astrophys. J. 875, L3 (2019)
K. Akiyama et al., (Event Horizon Telescope Collaboration), Astrophys. J. 8, 75 L4 (2019)
K. Akiyama et al., (Event Horizon Telescope Collaboration), Astrophys. J. 875, L5 (2019)
K. Akiyama et al., (Event Horizon Telescope Collaboration), Astrophys. J. 875, L6 (2019)
B.P. Abbott et al., LIGO Scientific and Virgo. Phys. Rev. Lett. 116, 061102 (2016)
B.P. Abbott et al., LIGO Scientific and Virgo. Astrophys. J. Lett. 818, L22 (2016)
B.P. Abbott et al., LIGO Scientific and Virgo. Phys. Rev. X 6, 041015 (2016)
B.P. Abbott et al., LIGO Scientific and VIRGO. Phys. Rev. Lett. 118, 221101 (2017)
K. Glampedakis, G. Pappas, Phys. Rev. D 97(4), 041502 (2018)
R.A. Konoplya, A. Zhidenko, JCAP 12, 043 (2016)
P. Kanti, B. Kleihaus, J. Kunz, Phys. Rev. Lett. 107, 271101 (2011)
J.L. Blázquez-Salcedo, C. Knoll, E. Radu, Phys. Rev. Lett. 126, 101102 (2021)
G. D’Amico, N. Kaloper, Phys. Rev. D 102, 044001 (2020)
V. Cardoso, E. Franzin, P. Pani, Phys. Rev. Lett. 116, 171101 (2016)
A. övgün, I. Sakalli, J. Saavedra, Chin. Phys. C 42, 105102 (2018)
D. Du, B. Wang, R. Su, Phys. Rev. D 70, 064024 (2004)
C. Chirenti, Braz. J. Phys. 48, 102 (2018)
S. Iyer, C.M. Will, Phys. Rev. D 35, 3621 (1987)
R.A. Konoplya, Phys. Rev. D 68, 024018 (2003)
M. Saleh, B. Thomas, T.C. Kofane, Astrophys. Space Sci. 350, 721 (2014)
P.D. Roy, S. Aneesh, S. Kar, Eur. Phys. J. C 80, 850 (2020)
H. Liu, P. Liu, Y. Liu, B. Wang, J.P. Wu, Phys. Rev. D 103, 024006 (2021)
M.S. Churilova, Z. Stuchlik, Class. Quantum Gravity 37, 075014 (2020)
V. Cardoso, P. Pani, Nat. Astron. 1, 586 (2017)
P. Bueno, P.A. Cano, F. Goelen, T. Hertog, B. Vercnocke, Phys. Rev. D 97, 024040 (2018)
Y.T. Wang, J. Zhang, S.Y. Zhou, Y.S. Piao, Eur. Phys. J. C 79, 726 (2019)
M.S. Churilova, R.A. Konoplya, A. Zhidenko, Phys. Lett. B 802, 135207 (2020)
C. Vlachos, E. Papantonopoulos, K. Destounis, Phys. Rev. D 103, 044042 (2021)
M.S. Churilova, R.A. Konoplya, Z. Stuchlk, A. Zhidenko, J. Cosmol. Astropart. Phys. 2021, 10 (2021)
Yi. Yang, Dong Liu, Xu. Zhaoyi, Yujia Xing, Wu. Shurui, Zheng-Wen. Long, Phys. Rev. D 104, 104021 (2021)
Dong Liu, Yi. Yang, Wu. Shurui, Yujia Xing, Xu. Zhaoyi, Zheng-Wen. Long, Phys. Rev. D 104, 104042 (2021)
H.C.D.L. Junior, L.C.B. Crispino, P.V.P. Cunha, C.A.R. Herdeiro, Phys. Rev. D 103, 084040 (2021)
F.S.N. Lobo, M.E. Rodrigues, M.V.S. Silva, A. Simpson, M. Visser, Phys. Rev. D 103, 084052 (2021)
E. Franzin, S. Liberati, J. Mazza, A. Simpson, M. Visser, JCAP 07, 036 (2021)
F.S.N. Lobo, A. Simpson, M. Visser, Phys. Rev. D 101, 124035 (2020)
J. Mazza, E. Franzin, S. Liberati, JCAP 04, 082 (2021)
B. Toshmatov, A. Abdujabbarov, Z. Stuchlk, B. Ahmedov, Phys. Rev. D 91, 083008 (2015)
S. Chandrasekhar, The Mathematical Theory of Black Holes (Oxford University Press, Oxford, 1992)
S. Aneesh, S. Bose, S. Kar, Phys. Rev. D 97, 124004 (2018)
K.A. Bronnikov, R.A. Konoplya, A. Zhidenko, Phys. Rev. D 86, 024028 (2012)
R.A. Konoplya, C. Molina, Phys. Rev. D 71, 124009 (2005)
R. Moderski, M. Rogatko, Phys. Rev. D 72, 044027 (2005)
R. Moderski, M. Rogatko, Phys. Rev. D 63, 084014 (2001)
R. Moderski, M. Rogatko, Phys. Rev. D 64, 044024 (2001)
R.A. Konoplya, A.F. Zinhailo, Z. Stuchlk, Phys. Rev. D 99, 124042 (2019)
R.A. Konoplya, C. Posada, Z. Stuchlk, A. Zhidenko, Phys. Rev. D 100, 044027 (2019)
R.A. Konoplya, A. Zhidenko, Rev. Mod. Phys. 83, 793 (2011)
V. Cardoso, E. Franzin, P. Pani, Phys. Rev. Lett. 116, 171101 (2016)
V. Cardoso, S. Hopper, C.F.B. Macedo, C. Palenzuela, P. Pani, Phys. Rev. D 94, 084031 (2016)
R.A. Konoplya, Z. Stuchlk, A. Zhidenko, Phys. Rev. D 99, 024007 (2019)
E. Barausse, V. Cardoso, P. Pani, Phys. Rev. D 89, 104059 (2014)
Kirill A. Bronnikov, Roman A. Konoplya, Phys. Rev. D 101, 064004 (2020)
R.A. Konoplya, A. Zhidenko, Phys. Rev. D 81, 124036 (2010)
R.A. Konoplya, Phys. Lett. B 784, 43 (2018)
M.A. Cuyubamba, R.A. Konoplya, A. Zhidenko, Phys. Rev. D 98, 044040 (2018)
K. Jafarzade, M.K. Zangeneh, F.S.N. Lobo, arXiv:2106.13893 [gr-qc]
Y. Guo, Y.G. Miao, arXiv:2201.02971 [gr-qc]
E. Berti, K.D. Kokkotas, Phys. Rev. D 67, 064020 (2003)
R. Dong, D. Stojkovic, Phys. Rev. D 103, 024058 (2021)
Acknowledgements
The authors are grateful to Dr. Alexander Zhidenko from Brazil for providing us his mathematica code with the implementation of the Prony method. This research was funded by the Guizhou Provincial Science and Technology Project (Guizhou Scientific Foundation-ZK[2022] General 491) and National Natural Science Foundation of China (Grant No.11465006).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Wu, S.R., Wang, B.Q., Liu, D. et al. Echoes of charged black-bounce spacetimes. Eur. Phys. J. C 82, 998 (2022). https://doi.org/10.1140/epjc/s10052-022-10938-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10938-1