1 Introduction

As the first discovery of the gravitational wave (GW) from the binary black hole merged, the study of the gravitational theory enters a new era. Generally, the GW signal from binary massive object merge can be divided into three stages [1,2,3]: the inspiral stage, the merger stage, and the ringdown stage. The post-Newtonian approximation can be used to describe the inspiral stage [4] and the merger stage can only be simulated numerically [5]. As for the ringdown stage, the spacetime is closed to stationary and we can use the quasinormal modes (QNMs) to reflect the ringdown phase if the object formed at the end is a black hole [2, 6].

As more GW signals are detected, more intriguing phenomena are noticed. Particularly, Abedi and collaborators analysed the data of GW150914, GW151226, and LVT151012 and claimed that there are echoes in these signals [7, 8]. However, their analysis is still disputed [9]. In spite of this, many theoretical discussions about echoes arise since echoes contain important information and can help us understand the spacetime structure better. Due to the reflections from the horizonless body surface, a sufficiently compact horizonless object can give rise to some extra echoes of ringdown gravitational waves [10, 11]. Moreover, there are other models of a compact object, such as anisotropic star configurations, which can produce echoes without the need for a reflecting surface [12]. Recently, echoes are also found in the ringdown stage in the wormholes [13,14,15,16,17]. In the beginning, it is believed that whether a final object possesses an event horizon can be determined by the ringdown signal. This perspective is proved to be incorrect since a horizonless compact object, such as a compact horizonless object with negligible reflectivity coefficient on the horizonless body surface, may also produce no echo, and it is shown that the production of the echo in the linear region is associated with the light ring [2, 18], which means the echo signal can also arise in the black holes when the effective potential has at least two peaks. Most recently, it has been shown in Refs. [19, 20] that nonlinear modes in the ringdown stage are excited by the merger of two comparable-mass black holes and thus the non-linear effects are necessary to be considered in gravitational-wave data analysis. Except for the exotic compact object, the echo was also found in quantum black holes [21,22,23]. Moreover, it has been shown in Ref. [24] that the massive gravity also gives a characteristic double-peak potential and it may lead to gravitational waves echoes. Later, in Ref. [25], a classical black hole that satisfies the dominant energy condition is found to have echo signals in an Einstein non-linear electrodynamic theory. This is unusual since the effective potential for most of the classical black hole only has one peak in general. After that, echo signals are also found in the hairy black hole [26].

Most of the previous discussion about the black hole echoes focuses on the case where the effective potential has two peaks. In Ref. [27], Li and Piao first considered the late-time GW ringdown waveform when the potential exhibits more than two peaks, and they observed the characteristic phenomenon of mixing echoes. In their setting, the near-horizon regime of the black hole is modeled as a multiple-barriers filter from the quantum structure, which is implemented by adding some Delta barriers manually at the near-horizon regime and the explicit dynamic remains unknown. It is natural to ask if a similar structure and phenomenon can be found in the dynamical and classical black holes.

In the present paper, we would like to consider the general Einstein non-linear electrodynamic theories. The non-linear electrodynamic theories are first proposed by Born and Infield, which is known as Born–Infeld theory [29, 30], to resolve the issue that the point charge has infinite self-energy. In the gravitational theory, the introduction of the non-linear electromagnetic field may avoid the black hole singularity [31,32,33,34,35]. Moreover, recent study indicate that the non-linear electrodynamic theory allows many horizons [28] and multi-critical points [36]. In 2013, Li and Bambi [37] proposed a hypothesis that the event horizon of a regular black hole in Einstein non-linear electrodynamic theories can be destroyed because these objects have no gravitational singularity and therefore they are not protected by the weak cosmic censorship conjecture [38, 39]. Then, this idea is further verified by Ref. [40]. For the multi-horizon black holes, the destruction of outer horizons also does not violate the weak cosmic censorship. Once the outer horizon is destroyed, the peak inside the horizon will be exposed and the effective potential of the black hole will appear multiple peaks. Moreover, in these cases, multiple peaks can appear away from the event horizon and it is not just a correction to the near event horizon regime. Then, we will calculate the time-domain profile for the scalar perturbation. We find that the three-peak profiles have obvious differences from the two-peak profile. When the number of the peak increases to three, the wave packet will split. The process by which the horizon is destroyed can be reflected through this extraordinary phenomenon and might be found by further GW detection.

This paper is organized as follows: In Sect. 2, we introduce the general Einstein non-linear electrodynamic theories. Then we give the equation of motion of a massless scalar field perturbation and propose the boundary condition. We also introduce the spacetime structure of the multi-horizon black hole and the method of choosing parameters in this section. In Sect. 3, we introduce the numerical method to calculate the time-domain profile. Then, in Sect. 4, we show some representative results. Finally, we draw a conclusion and give a discussion in Sect. 5.

2 Equations of motions in the Einstein-nonlinear electrodynamic theory

The general action of the Einstein gravity minimally coupled with the non-linear electromagnetic field can be written as

$$\begin{aligned} S=\int d^4 x\sqrt{-g}\left( R+{\mathcal {L}}_{\text {EM}} \right) , \end{aligned}$$
(1)

where \({\mathcal {L}}_{\text {EM}}=-\sum _{i=1}^{\infty } a_i {\mathcal {F}}^i\) with \({\mathcal {F}}=F_{ab}F^{ab}\) and \(F_{ab}=\nabla _{a}A_{b}-\nabla _{b}A_{a}\). When \(\alpha _1=1\) and \(\alpha _i=0\) for any \(i>1\), the theory will go back to Einstein–Maxwell theory. The variation of Eq. (1) with respect to \(g_{ab}\) and \(A_{a}\) gives the equation of motion

$$\begin{aligned}{} & {} G_{ab}=-2\frac{\partial {\mathcal {L}}_{\text {EM}}}{\partial {\mathcal {F}}}F_a{}^cF_{bc}+\frac{1}{2}g_{ab}{\mathcal {L}}_{\text {EM}},\nonumber \\{} & {} \nabla _a\left( \frac{\partial {\mathcal {L}}_{\text {EM}}}{\partial {\mathcal {F}}}F^{ab}\right) =0. \end{aligned}$$
(2)

With the spherically symmetric ansatz

$$\begin{aligned} ds^2= & {} -f(r)dt^2+\frac{1}{f(r)}dr^2+r^2\left( d\theta ^2+\sin ^2\theta d\phi ^2\right) ,\nonumber \\ A_a= & {} A_t(r)(dt)_a, \end{aligned}$$
(3)

the general asymptotically flat black hole solution [28]

$$\begin{aligned} f(r)= & {} 1-\frac{2M}{r}+\sum _{i=2}^{\infty }\frac{c_{i}}{r^{i}},\nonumber \\ A_t(r)= & {} \sum _{i=1}^{\infty } b_i r^{-i}\, \end{aligned}$$
(4)

can be found. Here, \(c_i\) and \(b_i\) are constant parameter related to \(\alpha _i\), the charge \(b_1=Q\) and the ADM mass M, and the relationship between the black hole parameters and the coupling constant can refer to Refs. [28, 41, 42].

Next, we consider a massless scalar field perturbation \(\psi \) on this spacetime background. The equation of motion of the scalar field is

$$\begin{aligned} \nabla _a\nabla ^a \psi (t,r,\theta ,\phi )=0. \end{aligned}$$
(5)

Considering the spacetime is spherically symmetric, the scalar field can be separated into

$$\begin{aligned} \psi (t,r,\theta ,\phi )=\sum _{lm}\frac{\Phi (t,r)}{r} Y_{lm}(\theta ,\phi ). \end{aligned}$$
(6)

After replacing \(\psi \) in Eq. (5) by Eq. (6), we can find the equation of motion becomes

$$\begin{aligned} \frac{\partial ^2\Phi }{\partial t^2}-\frac{\partial ^2\Phi }{\partial r_{*}^2}+V(r) \Phi =0, \end{aligned}$$
(7)

where

$$\begin{aligned} V(r)=\frac{l(l+1)f(r)}{r^2}+\frac{f(r)f'(r)}{r} \end{aligned}$$
(8)

l is azimuthal quantum number and \(r_{*}\) is the tortoise coordinate that satisfies

$$\begin{aligned} dr_{*}=\frac{dr}{f(r)}. \end{aligned}$$
(9)

In the physical region, when \(r\rightarrow r_h\) while \(r_{*}\rightarrow -\infty \), V(r) tends to vanish, where we use \(r_h\) to represent the event horizon of the black hole. And when \(r\rightarrow +\infty \) while \(r_{*}\rightarrow +\infty \), V(r) also tends to vanish. Therefore, we can find that the asymptotic solutions of Eq. (7) are

$$\begin{aligned} \Phi \sim e^{-i \omega (t\pm r_{*})},\quad r\rightarrow r_h,+\infty . \end{aligned}$$
(10)

Then, since we require the scalar field is pure outgoing at infinity and pure ingoing at the event horizon, the wave function should satisfy

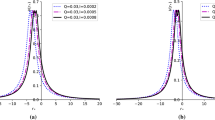
$$\begin{aligned}&\Phi \sim e^{-i \omega (t+r_{*})},\quad r\rightarrow r_h,\nonumber \\&\Phi \sim e^{-i \omega (t-r_{*})},\quad r\rightarrow +\infty . \end{aligned}$$
(11)

In this paper, we would like to consider the \(l=2\) case since \(l=2\) is relevant to the GW observation [26]. The echo will occur when the effective potential V(r) possesses at least two peaks. For the black hole in the Einstein-nonlinear electrodynamic theory, it can exist many horizons [28]. Firstly, we would like to consider a near extremal black hole which has five horizons. The blackening factor of this black is shown by the blue line in the left panel of Fig. 1. Then, we would like to put some charge into this black hole. As Q increases, the outermost horizon will be destroyed one by one without violating the cosmic censorship, which is shown by the orange and green line in Fig. 1. Once a horizon is destroyed, the peak inside the original horizon will be exposed, and then the corresponding effective potential will appear one more peak, which is shown in the right panel of Fig. 1. In short, echo will produce as the destruction of event horizon and the relevant result will be shown in Sect. 4. Moreover, in this figure, we can also find the peak of the effective potential is not always near the horizon.

Fig. 1
figure 1

The left panel shows three black holes in Einstein-nonlinear electrodynamic theory with \(\alpha _1=1, \alpha _2=0.39906, \alpha _3=0.56367, \alpha _4=-1.17846\). \(\alpha _{i>4}\) is obtained by demanding that \(b_{i\ge 17}=0\) according to Ref. [28]. The blue, orange and green line represent black hole with \(Q=2.1946, 2.19506, 2.19556\) respectively. The upper right panel shows the corresponding effective potentials with respect to \(r_h/r\), and the lower right panel shows the corresponding effective potentials with respect to \(r_{*}\)

Full size image
Fig. 2
figure 2

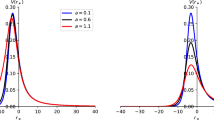
The effective potential as a function of \(r_{*}\) and its corresponding time-domain profile. The parameters of each panel is corresponding to Fig. 1

Full size image

3 Numerical method

In this section, we would like to introduce the finite difference method used to calculate the wave function in this paper and introduce how to extract the quasinormal mode from the wave function.

First, we divide the coordinate into a series of the grids. Each grid point can be represented by \((i \Delta t, j \Delta r_{*})\). Then, the differential equation can be cast into lots of algebraic equations:

$$\begin{aligned}{} & {} \Phi ((i+1)\Delta t,j \Delta r_{*})=-\Phi ((i-1)\Delta t,j\Delta r_{*})\nonumber \\{} & {} \quad +\Phi (i\Delta t,i\Delta r_{*})\left( 2-2\frac{\Delta t^2}{\Delta r_{*}^2}-\Delta t^2 V_{*}(j\Delta r_{*})\right) \nonumber \\{} & {} \quad +\frac{\Delta t^2}{\Delta r_{*}^2}\Big (\Phi \big (i\Delta t,(j+1)\Delta r_{*}\big )+\Phi \big (i\Delta t,(j-1)\Delta r_{*}\big )\Big ),\nonumber \\ \end{aligned}$$
(12)

where \(V_{*}(r_{*})=V(r(r_{*}))\). In this paper, we take \(\Delta t=1/8\), and we choose \(\Delta r_{*}=2 \Delta t=1/4\) considering the Neumann stability condition [43]. we can solve Eq. (7) numerically and we can obtain a time-domain profile after giving the initial condition

$$\begin{aligned} \Phi (0,r_{*})=e^{-\frac{(r_{*}-a)^2}{2}}\,\quad \text {and} \quad \Phi (t<0,r_{*})=0. \end{aligned}$$
(13)

According to Ref. [25], the echo will become more distinct when the initial wave packet is outside the effective potential well. Therefore, we would like to set a, the center of the wave packet, to be zero and outside the potential well for convenience.

Next, we would like to use the Prony method to extract the quasinormal mode at late time. We take the time-domain profile from \(t=t_0\) to \(t=t_0+N h\), where N is an integer and h is the distance between each point. Here, \(t_0,\,N\) and h can be chosen freely. The profile at a certain \(r_{*}\) can be expanded as

$$\begin{aligned} \Phi (t)=\sum _{j=1}^{p} \tilde{C}_j e^{- i \omega _j t}\, \end{aligned}$$
(14)

with \(p=[N/2]\), where [x] denotes the integer part of x.

For any point we choose, this formula establish, i.e.

$$\begin{aligned} x_n=\sum _{j=1}^{p}C_j z_j^n, \end{aligned}$$
(15)

where \(x_n=\Phi (t_0+n h)\), \(z_j=e^{i \omega _j h}\) and \(C_j=\tilde{C_j}e^{- i \omega t_0}\), i.e., we have

$$\begin{aligned} \Phi (t)=\sum _{j=1}^{p} C_j e^{- i \omega _j (t-t_0)}. \end{aligned}$$
(16)

Then we introduce a function

$$\begin{aligned} A(z)=\prod _{i=1}^p(z-z_i)=\sum _{i=0}^p \alpha _i z^i. \end{aligned}$$
(17)

It is easy to find that \(A(z_i)=0\) for any integer i from 1 to p. Then, with an easy calculation, we can find

$$\begin{aligned} \sum _{i=0}^{p}\alpha _i x_{i+j}= & {} \sum _{i=0}^{p}\alpha _i\sum _{k=1}^{p}C_k z_k^{i+j}\nonumber \\= & {} \sum _{k=1}^{p}C_k z_k^j \sum _{i=0}^p \alpha _i z_k^i\nonumber \\= & {} \sum _{k=1}^{p}C_k z_k^j A(z_k)=0. \end{aligned}$$
(18)

According to Eq. (17), we have \(\alpha _p=1\). Therefore, Eq. (18) becomes

$$\begin{aligned} \sum _{i=0}^{p-1}\alpha _i x_{i+j}=-x_{p+j}. \end{aligned}$$
(19)

Taking j from 1 to p, we will obtain p equations and can easily work out \(\alpha _i\). Then, we can get \(z_i\) and then \(\omega _i\) by finding the root of Eq. (17). Finally, the coefficients \(C_i\) can be found using Eq. (15).

4 Numerical results

In this section, we will show some typical results. First, we show the change of the echo signal as Q increases and the horizon is destroyed in Fig. 2. In this series of time-domain profiles, we take the log of the wave function to make the phenomenon more obvious. For the single peak case, the scalar field will decay all the time after an oscillation at the early time. As the destruction of the event horizon, the effective potential becomes two-peak and echoes will arise. In this case, the signal is pretty regular and each wave packet is discrete. Then, when the new event horizon is destroyed and the effective potential becomes three-peak, the echo behavior can distinguish the difference from the two-peak case. It will split and decay more slowly. We also extract the frequency \(\omega _i\) and its corresponding coefficient \(C_i\) at the late time \(t_0=4000\) from the three profiles in Fig. 2, which is shown in Table 1. Note that the absolute value of the coefficients \(C_n\) reflects the contribution of QNMs \(\psi _{n}\equiv C_n \exp [-i \omega _n t]\) to the echoes at \(t=t_0\) and the frequency of these modes only contain a small negative imaginary part. That is to say, in the time range shown in our paper, the contribution from different modes is determined by their coefficient. From Table 1, we can see that the dominate modes are given by \(\psi _3\sim \psi _6\) for the two-peaks case and \(\psi _{12}\sim \psi _{25}\) for the three-peaks case. That is to say, for the one-peak case, there is only one dominant quasinormal mode at late time \(t_0=4000\); for the two-peak cases, the echo will produce by the superposition of long-lived and sub-long-lived modes, which is consistent with Ref. [26]; as for the three-peaks case, there will be more modes that determine the shape of the time-domain profile than in the two-peak case.

Table 1 The quasinormal frequency \(\omega _i\) and its corresponding coefficient \(C_i\) at \(t_0=4000\) of the three profiles in Fig. 2. And the first column of the table is the overtone number n
Full size table

The behavior of the echo from a two-peak effective potential has been studied a lot before [17, 21, 26] while the echo produced by three-peak potential lacks study. In the following content, we would like to choose some typical examples to analyze what phenomena will arise when the number of the peak of the effective potential and the distance between the peaks change.

In Fig. 3, we show the time-domain profile when the number of the peak of the effective potential split from two to three, and the distance between the two peaks on the left increases. We can find that the time-domain profile also split as the potential changes. Except for the main wave packet which already exists in the two-peak case, other wave packets appear near the main wave packet. When the peak separation on the left and right tends to be the same, the distance between two adjacent wave packets is almost the same as in the case where the potential has only two peaks on the right. The difference is that the time-domain profile decays more slowly for the three peaks case.

Finally, in Fig. 4, we show the time-domain profiles and their effective potential. In this set of the effective potential, the space between the three peaks increases gradually. When the space is pretty small, the behavior of the time-domain profile is consistent with the one-peak potential case, where the profile decays all the time and no echo occurs. When the space becomes larger but still is small, the boundary of each wave packet is not obvious. Then, as the space increase, the wave packet becomes more distinct.

Fig. 3
figure 3

The effective potential as a function of \(r_{*}\) and its corresponding time-domain profile. The parameters are \(M=2.24587,\,c_2=5.21202,\,c_6=-3.80336,\,c_{10}=3.23742,\,c_{14}=-1.15436\) for the 1st panel, \(M=2.28227,\,c_2=5.40395,\,c_6=-4.63099,\,c_{10}=4.63569,\,c_{14}=-1.84412\) for the 2rd panel, \(M=2.28229,\,c_2=5.40402,\,c_6=-4.63109,\,c_{10}=4.63528,\,c_{14}=-1.84361\) for the 3th panel, and \(M=2.282306\), \(c_2=5.40408\), \(c_6=-4.63129\), \(c_{10}=4.63522\), \(c_{14}=-1.84339\) for the 4th panel

Full size image
Fig. 4
figure 4

The effective potential as a function of \(r_{*}\) and its corresponding time-domain profile. The parameters are \(M=2.218,\,c_2=5.194,\,c_6=-4.459,\,c_{10}=4.518,\,c_{14}=-1.816\) for the 1nd panel, \(M=2.280,\,c_2=5.408,\,c_6=-4.677,\,c_{10}=4.708,\,c_{14}=-1.879\) for the 2rd panel, \(M=2.282,\,c_2=5.405,\,c_6=-4.642,\,c_{10}=4.652,\,c_{14}=-1.852\) for the 3th panel, and \(M=2.282\), \(c_2=5.404\), \(c_6=-4.631\), \(c_{10}=4.635\), \(c_{14}=-1.843\) for the 4th panel

Full size image
Fig. 5
figure 5

The schematic diagram of echoes from a two-peaks potential case (left panel) and a three-peaks potential case (right panel). (Similar discussions are appeared in Refs. [10, 44,45,46])

Full size image

Analyzing all the above effective potential and time-domain profiles, we can find that the distance between the neighboring main wave packet is associated with the distance between the two peaks on the right side. The distance between the split wave packet and the main wave packet is associated with the distance between the two peaks on the left side. When the length of the left well and the length of the right well is approached, the split signal tends to overlap with the next main wave packet.

To establish a semi-analytic picture that can cumulatively describe the above behaviors, we show the schematic Penrose diagrams of echoes in Fig. 5 for some multi-peaks potential structures. From these diagrams, we can see that the echoes of the ringdown phase are caused by the waves semi-trapped between the different peaks of the potential. For the two-peak case, the positions of the echo signal in the time-domain profile are determined by the reflections from the left peak, and thus the characteristic echo delay time (i.e., the distance between two adjacent wave packets in the time-domain profile) is given by

$$\begin{aligned} \Delta \tau :=\tau _0^{(k)}-\tau _0^{(k-1)}\sim 2 [r_*^{(1)}-r_*^{(2)}]=2\Delta \ell _{12}, \end{aligned}$$
(20)

with

$$\begin{aligned} \ell _{12}\equiv r_*^{(1)}-r_*^{(2)}, \end{aligned}$$
(21)

in which we use \(r_*^{(i)}\) to denote the position of the ith peak to the right, and \(\tau _j^{(k)}\) denotes the position of the wave packet which is reflected k times by the second peak to the right and j times by the third peak to the right, see Fig. 2. That is to say, the time delay between the echoes is roughly \(2l_{12}\). To discuss the three-peak cases, we refer to the wave packet reflected j times by the leftmost peak (third peak to the right) as the jth-order echo signal. Then, from the schematic Penrose diagrams of the three-peaks case, it is straightforward to get

$$\begin{aligned} \tau _j^{(k)}-\tau _0^{0}\sim 2 (j+k)\ell _{12}+2j\ell _{23} \end{aligned}$$
(22)

with

$$\begin{aligned} \ell _{23}\equiv r_*^{(2)}-r_*^{(3)}. \end{aligned}$$
(23)

Then, there are two characteristic quantities as showed in the right panel of Fig. 2,

$$\begin{aligned} \Delta \tau{} & {} :=\tau _j^{(k)}-\tau _j^{(k-1)}\sim 2\ell _{12},\nonumber \\ \Delta \bar{\tau }{} & {} :=\tau _j^{(k+2)}-\tau _{j-1}^{(k)}\sim 2(\ell _{12}-\ell _{23}). \end{aligned}$$
(24)

We showed the corresponding characteristic quantities in the first and third panels of Fig. 3. From the above discussions, it is not hard to see, when \(\ell _{23}\ne n \ell _{12}\) with integer n, there must be some higher-order echo signals that do not coincide with the zero-order signals, which shows the split of the echo signal in time-domain profile. However, when \(\ell _{23} = n \ell _{12}\), the higher-order echo signals will merge with the zero-order signals.

5 Conclusion and discussion

We considered the Einstein gravity coupled with a non-linear electromagnetic field, which admits black hole solutions with multiple horizons. The destruction of the outer horizon can lead to an increase in the peak of the effective potential for the massless scalar field perturbation. For two-peak effective potential, the inner potential peaks can give rise to the echoes and the echo will split for the multi-peak case. This means that the process by which the horizon is destroyed can be reflected by the echo. Then, to study the echo for the multi-peak case, we mainly considered the situation where the effective potential of the black hole has three peaks and consider the process in which the number of peaks changes from two to three and showed how the time-domain profile of the scalar field behaves for multi-peak cases.

In this paper, all the black hole we considered has a singularity. There will be regular black holes for some Einstein-nonlinear electrodynamic theory [47, 48]. And it is not hard to infer that for regular black holes with multi-horizon, the multi-peak effective potential will appear from a similar process. There are still lots of issues that we can consider further except in the discussion presented in this paper. Firstly, we only considered the cases where the effective potential has three peaks in this article. It is also interesting to focus on the more peak cases. Secondly, to get closer to astronomical observations, it is necessary to study echoes of gravitational and electromagnetic waves. Finally, we let the initial wave packet be released outside the peaks. However, it has been shown in Ref. [25] that the echoes will different when the wave packet is released inside the peaks. Moreover, the echo signal will be different if we choose a different initial condition. Therefore, the influence of the initial wave packet is also worthy to be studied in our situation. Besides, our paper only considered the echoes for the spacetime geometry if its outer horizons are destroyed. However, to judge whether the outer horizons can really be destroyed, we need to further consider the dynamic process to study their stability. This is not the focus of this article and will leave for future investigation.